An Analytical Algorithm for Determining Optimal Thin-Walled Hollow Pier Configuration with Sunlight Temperature Differences
Abstract
:1. Introduction
2. Derivation of the Analytical Formula
2.1. Fundamental Assumptions
2.2. Derivation
3. Engineering Profile and Case Study Selection
3.1. Engineering Profile
3.2. Temperature Monitoring Scheme
3.3. Temperature Field Analysis of the Pier Section
3.4. Selection of Calculation Conditions for Sunlight Temperature Differences
4. Basic Theory and Finite Element Methods in Temperature Effect Research
4.1. Basic Theory of Temperature Effect Research
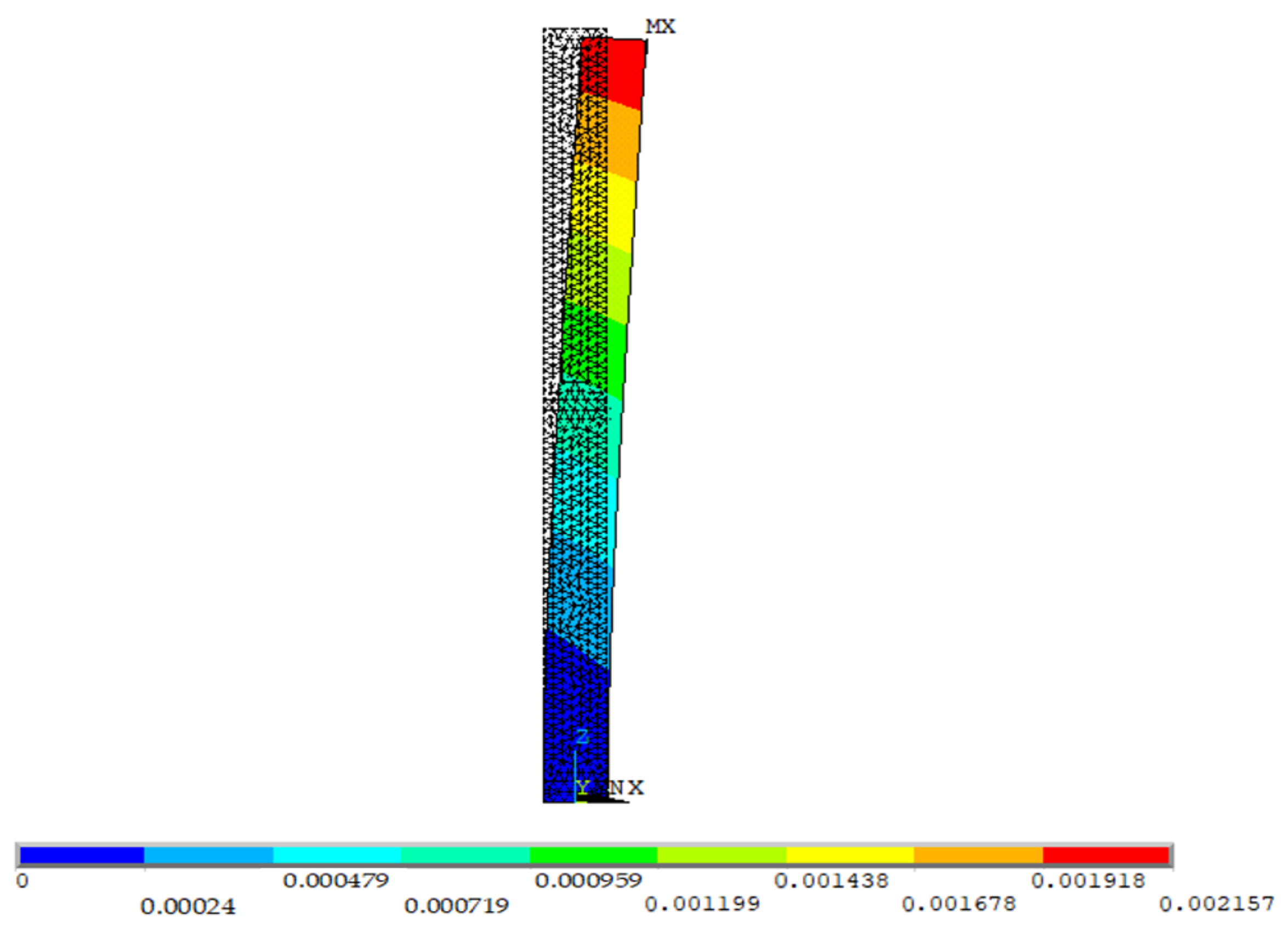
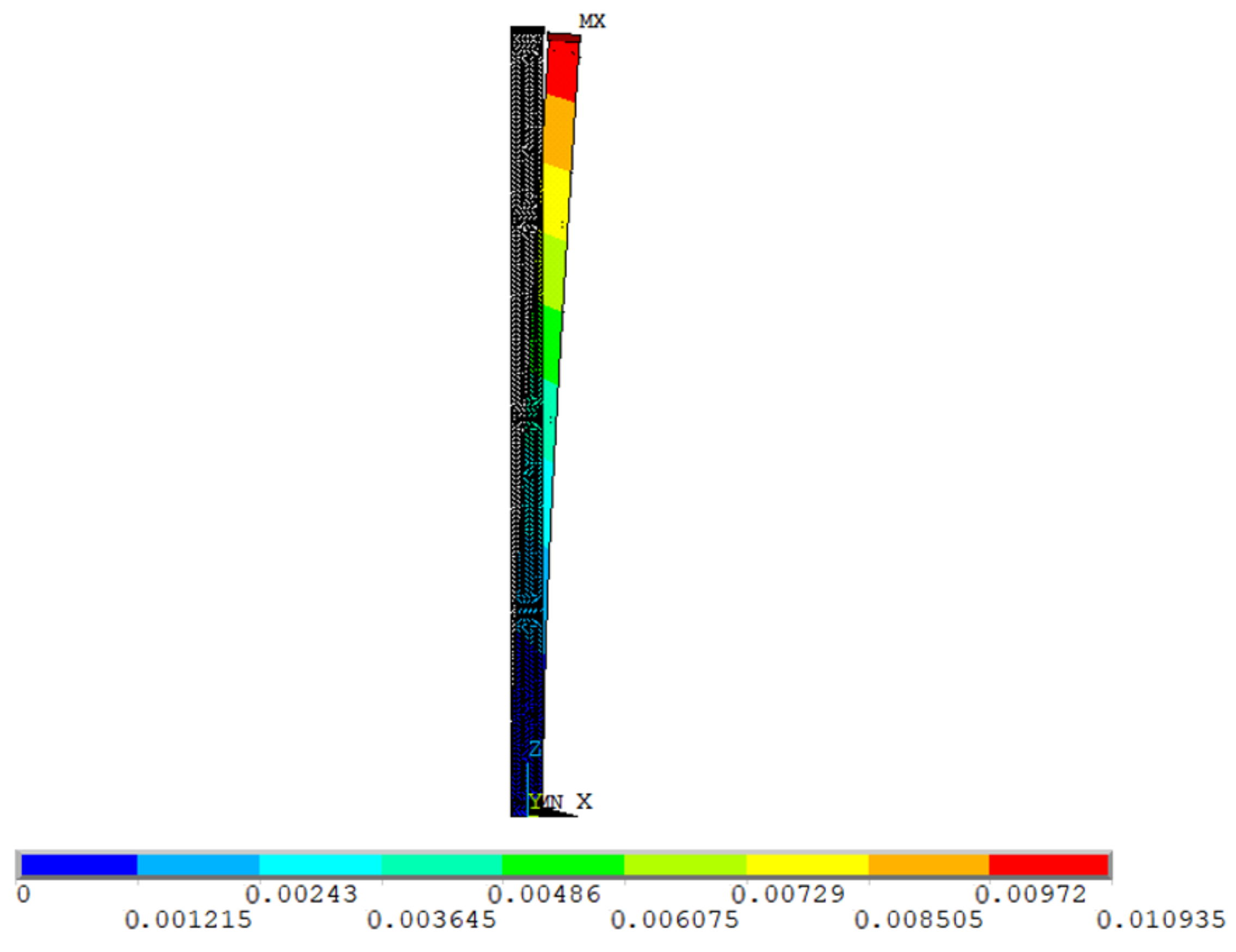
4.2. Finite Element Methods
4.3. A finite Element Model of the No. 5 Pier
5. Comparative Analysis of Algorithm Results
5.1. Finite Element Calculated Values
5.2. Analytic Algorithm Results
5.3. Specification Calculation Results
5.4. Comparative Analysis
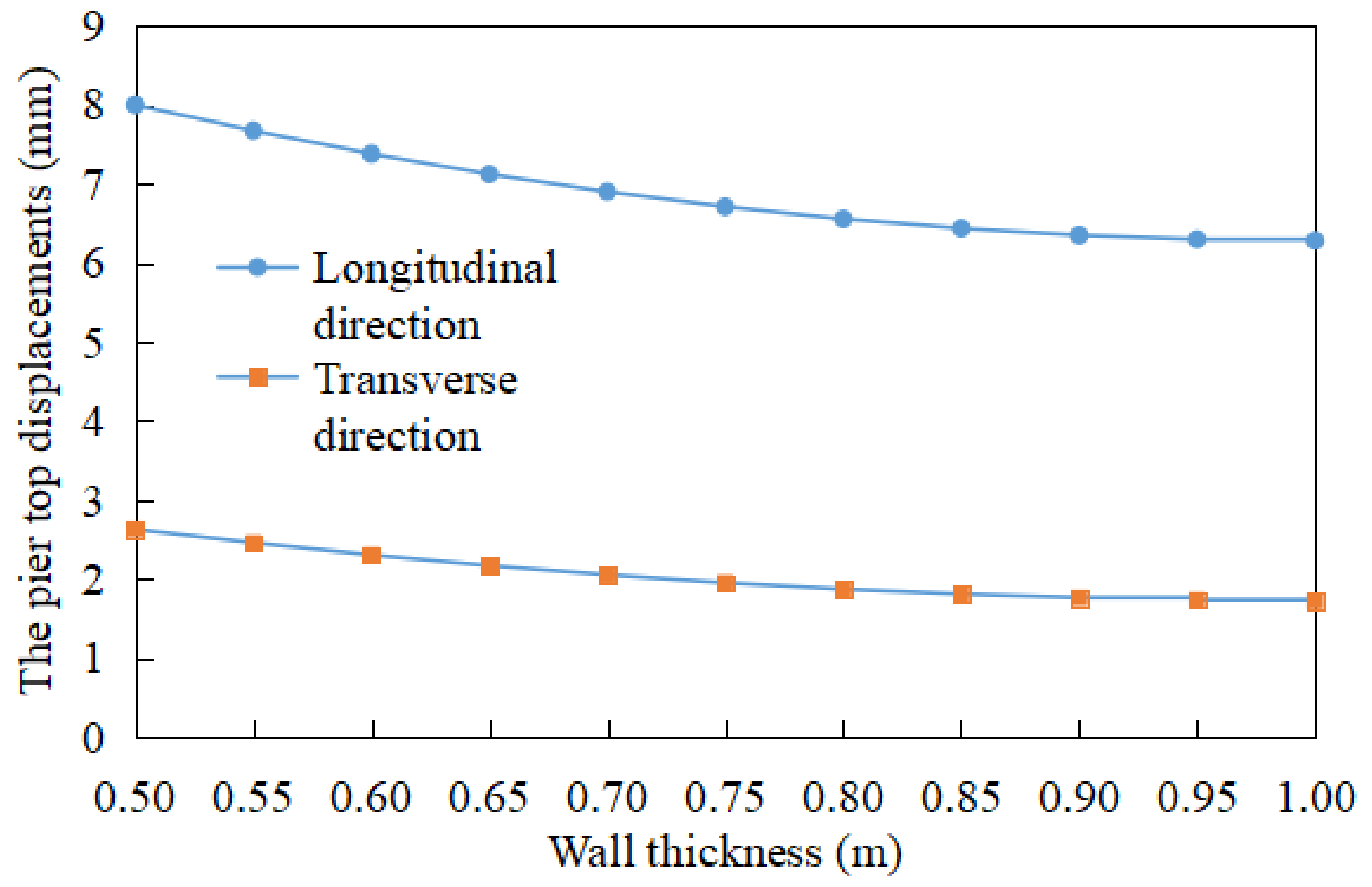
5.5. Parametric Analysis
6. Conclusions
- (1)
- The analytical calculation formula derived in this paper has quite a high accuracy and thus can provide a new means to calculate and control the alignment of thin-walled hollow piers.
- (2)
- The analytical formula is more suitable for the linear calculation of thin-walled hollow piers under the influence of sunlight temperature differences than the formula in the current Chinese railway code. The formula has more specificity to its application, and was also closer to the measured values than the reference formula, with a maximum difference of only 0.507 mm.
- (3)
- The temperature difference due to sunlight has a great influence on the alignment of thin-walled hollow piers, and the greater the temperature difference and height, the more significant the influence on the alignment. When the temperature difference was 10 °C, the displacement of the pier top (75 m high) along the bridge was 1.5 cm. However, increasing pier wall thickness did not significantly limit the pier top displacement.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hu, A.-Q.; Ren, D.-H. Effect of concrete hollow pier wall thickness on the temperature difference distribution of sunlight. J. Shijiazhuang Tiedao Univ. 2021, 34, 21–27. [Google Scholar]
- Yuan, P.; Cai, C.S.; Li, D.; Xu, G.; Li, C. A novel method for determining the spatial responses of a cable-stayed bridge with four cable-planes. Eng. Struct. 2019, 180, 223–233. [Google Scholar] [CrossRef]
- Bi, Z.-G.; Yan, X.-J.; Yu, Y.-J.; Liang, B. Analysis of temperature field and temperature effect of the thin-walled hollow high pier. Henan Sci. 2022, 40, 46–53. [Google Scholar]
- Zhou, L.-Y.; Liu, Z. Investigation of the bucking behavior of thin-walled hollow concrete piers. Struct. Concr. 2020, 22, 1363–1377. [Google Scholar]
- Tayeh, B.; Marijana, H.-N.; Magdy, Y.-R.-R.; Radwa, D.-A.-H. Behavior of Ultra-High-Performance concrete with Hybrid synthetic fiber waste exposed to elevated temperatures. Buildings 2023, 13, 129. [Google Scholar] [CrossRef]
- JTG F80/1-2017; Inspection and Evaluation Quality Standards for Highway Engineering-Section 1 Civil Engineering. China communications press Co., Ltd.: Beijing, China, 2017.
- Zheng, G.; Gu, X.-Y.; Zhang, T.-Q.; Sun, J.-B.; Zheng, W.-H. Random forest method-based prediction and control of bridge pier displacements during construction of two overlapped EPBM tunnels. Eur. J. Environ. Civ. Eng. 2022, 26, 2273–2293. [Google Scholar] [CrossRef]
- Suman, R.; Ikwulono, D.-U.; Andrew, D.-S. Reliability assessment and sensitivity analysis of vehicle impacted reinforced concrete circular bridge piers. Structures 2022, 37, 600–612. [Google Scholar]
- Shim, C.-S.; Dang, S.-N.; Park, S. Three-Dimensional information delivery for design and construction of prefabricated bridge piers. Struct. Eng. Int. 2018, 28, 6–12. [Google Scholar] [CrossRef]
- Editorial Department of China Journal of Highway and Transport. Review on China’s Bridge Engineering Research: 2021. China J. Highw. Transp. 2021, 34, 1–97. [Google Scholar]
- Liu, Y.-J.; Liu, J.; Zhang, N. Review on solar thermal actions of bridge structures. China Civ. Eng. J. 2019, 52, 59–78. [Google Scholar]
- Sun, Z.-G.; Wang, D.-S.; Wang, T.; Wu, S.-W.; Guo, X. Investigation on seismic behavior of bridge piers with thin-walled rectangular hollow section using quasi-static cyclic tests. Eng. Struct. 2019, 200, 109708. [Google Scholar] [CrossRef]
- Chen, H.-H.; Xu, B.; Liu, Q.; Gu, J.-F. Study on failure performance of the thin-walled steel-reinforced concrete pier under low cyclic loading. Buildings 2022, 12, 1412. [Google Scholar] [CrossRef]
- Choi, S.; Won, M.-C. Thermal strain and drying shrinkage of concrete structures in the field. ACI Mater. J. 2010, 107, 498–507. [Google Scholar]
- Rodriguez, L.-E.; Barr, P.-J.; Halling, M.-W. Temperature effects on a box-girder integral-abutment bridge. J. Perform. Constr. Facil. 2014, 28, 583–591. [Google Scholar] [CrossRef]
- Li, Y.; He, S.-H.; Liu, P. Effect of solar temperature field on a sea-crossing cable-stayed bridge tower. Adv. Struct. Eng. 2019, 22, 1867–1877. [Google Scholar] [CrossRef]
- Suzuki, J.; Ohba, Y.; Uchikawa, Y.; Hoshikawa, K.; Kimura, K. Monitoring temperatures on a real box-girder bridge and energy budget analysis for basic information on bridge cooling and surface freezing. J. Bridge Eng. 2014, 12, 45–52. [Google Scholar] [CrossRef]
- Zhao, J.-T.; Cui, C.-Y.; Zhang, P.; Wang, K.-P.; Zhao, M. Parameter sensitivity analysis of the seismic response of a piled wharf structure. Buildings 2023, 13, 349. [Google Scholar] [CrossRef]
- Tang, Z.-Z.; Xue, H.-Y.; Liu, H.; Zhang, W. Prediction of ultralow cycle fatigue damage of thin-walled steel bridge piers. Adv. Steel Constr. 2021, 17, 403–411. [Google Scholar]
- Jelena, P.; Nina, S.; Radenko, P. Damage assessment of road bridge caused by extreme streamflow in Montenegro: Reconstruction and structural upgrading. Buildings 2022, 12, 810. [Google Scholar]
- Hagedorn, R.; Marti-Vargas, J.R.; Dang, C.N.; Hale, W.M.; Floyd, R.W. Temperature gradients in bridge concrete I-girders under a heat wave. J. Bridge Eng. 2019, 24, 04019077. [Google Scholar] [CrossRef]
- Lawson, L.; Ryan, K.L.; Buckle, I.G. Bridge temperature profiles revisited: Thermal analyses based on recent meteorological data from Nevada. J. Bridge Eng. 2020, 25, 11–24. [Google Scholar] [CrossRef]
- Abid, S.R.; Taysi, N.; Ozakça, M. Experimental analysis of temperature gradients in the concrete box–girders. Constr. Build. Mater. 2016, 106, 523–532. [Google Scholar] [CrossRef]
- Abid, S.R.; Taysi, N.; Ozakça, M.; Xue, J.; Briseghella, B. Finite element thermomechanical analysis concrete box-girders. Structures 2021, 33, 2424–2444. [Google Scholar] [CrossRef]
- Deng, Y.; Li, A.; Liu, Y.; Chen, S. Investigation of temperature actions on flat steel box girders of long-span bridges with temperature monitoring data. Adv. Struct. Eng. 2018, 21, 2099–2113. [Google Scholar] [CrossRef]
- Tao, T.; Wang, H.; Zhu, Q.; Zou, Z.; Li, J.; Wang, L. Long-term temperature field of the steel-box girder of a long-span bridge: Measurement and simulation. Eng. Struct. 2021, 236, 111924. [Google Scholar] [CrossRef]
- Sheng, X.-W.; Zheng, Y.-H.; Zheng, W.-Q.; Zhu, Z.-H. Vertical temperature gradient model of concrete box girders based on real-time shadow technology. J. South. China Univ. Technol. 2020, 48, 40–47. [Google Scholar]
- Wang, Z.-W.; Zhang, W.-M.; Zhang, Y.-F.; Liu, Z. Temperature prediction of flat steel box girders of Long-Span bridges utilizing in situ environmental parameters and machine learning. J. Bridge Eng. 2022, 27, 04022004. [Google Scholar] [CrossRef]
- Phuong, H.-H.; Hoang, N.-P. Kriging Metamodel-based seismic fragility analysis of single-bent reinforced concrete highway bridge. Buildings 2021, 11, 238. [Google Scholar]
- Zhang, Y.-B.; Cai, T.-T.; Liu, Y. Effects analysis of the cross-sectional shape on the double-limb thin-walled piers temperature field. J. Railw. Eng. Soc. 2015, 198, 41–45. [Google Scholar]
- Dai, G.-L.; Tang, Y.; Liang, J.-B. Study of temperature load extreme value of a bridge pier base on generalized pares to distribution. Bridge Constr. 2017, 47, 48–53. [Google Scholar]
- Liu, C.-C.; Huang, Y.-J.; Zhang, G.-S.; Liu, W.-H.; Liu, C.; Zhang, Y.-S. Sunshine temperature effect of the thin-wall hollow high pier in high altitude area. J. China Foreign Highw. 2021, 41, 76–79. [Google Scholar]
- Lin, G.-T.; Su, B. Numerical analysis of sunshine temperature effect on a super high pier of mountain bridge. J. Civ. Eng. Manag. 2018, 35, 112–116. [Google Scholar]
- Andrei, K.; Ivar, T. Computationally efficient method for steel colum bucking in fire. Buidings 2023, 13, 407. [Google Scholar]
- Faham, T.; Zhang, L.-D.; Park, S.-W.; Sepasgozar, S. Numerically evaluation of FRP-Strengthened members under dynamic impact loading. Buildings 2021, 11, 14. [Google Scholar]
- TB10052-97; Technical Specification for Flexible Pier Railway Bridge. China railway publishing house Co., Ltd.: Beijing, China, 1997.
- Tang, Y. Active Control of Verticality of Thin-Wall High Pier Based on the Measured Temperature Field; Harbin Institute of Technology: Harbin, China, 2017. [Google Scholar]
- Liu, X.F. Analysis of Thermal Stress Force Concrete Structure; China Communications Press: Beijing, China, 1991. [Google Scholar]
- Tang, F.; Li, D.-J.; An, L.-P. Research of solar radiation influence on pier’s line shape and alignment monitoring of high-pier bridge. J. Railw. Sci. Eng. 2016, 13, 1970–1976. [Google Scholar]
- Yuan, P.; Dong, Y. High-efficient decoupling method for coupling systems with multiple subdomains and time steps. Mech. Syst. Signal. Process. 2022, 163, 15. [Google Scholar] [CrossRef]
- Yuan, P.; Li, D.-J.; Cai, C.-S.; Xu, G.-J. A Novel Decoupling Dynamic Method with Third-order Accuracy and Controllable Dissipation. Comput. Struct. 2021, 249, 44–56. [Google Scholar] [CrossRef]
- Wang, R.F.; Chen, G.R. Temperature Field and Thermal Stress; Science Press: Beijing, China, 2005. [Google Scholar]
- GB50019 2003; Specifications for design of heating ventilation and air conditioning. China nonferrous metal industry’s foreign engineering and construction Co., Ltd.: Beijing, China, 2003.
- Zhang, Z.-M.; Sun, C.; Vahid, J. Structural damage identification of off shore wind turbines:A two-step strategy via FE model updating. Struct. Control. Health Monit. 2021, 29, 1–21. [Google Scholar]
- Song, M.-M.; Silas, C.; Babak, M.; Eric, M.-H. Joint parameter-input estimation for virtual sensing on an offshore platform using output-only measurements. Renew. Energy 2023, 202, 1032–1045. [Google Scholar] [CrossRef]

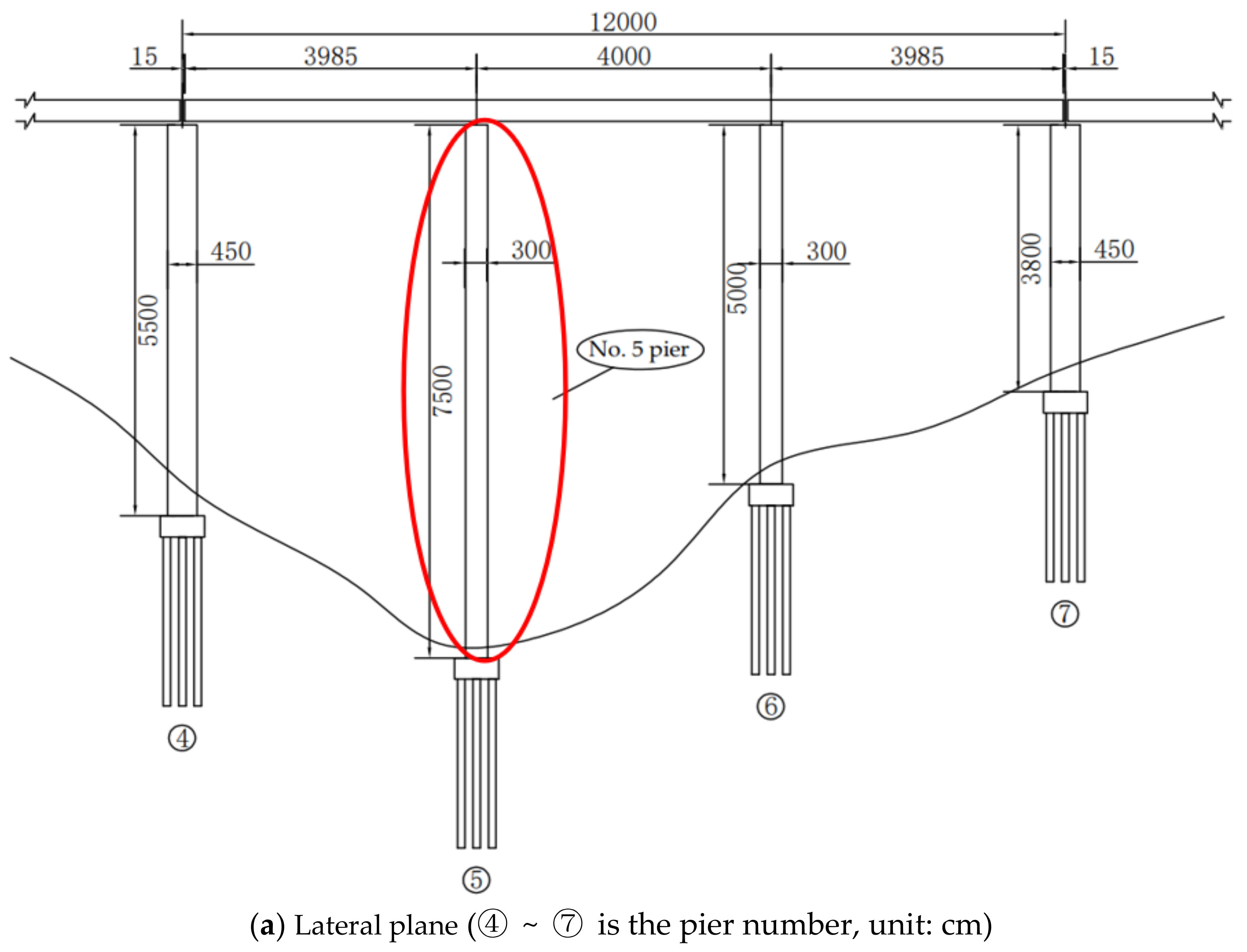
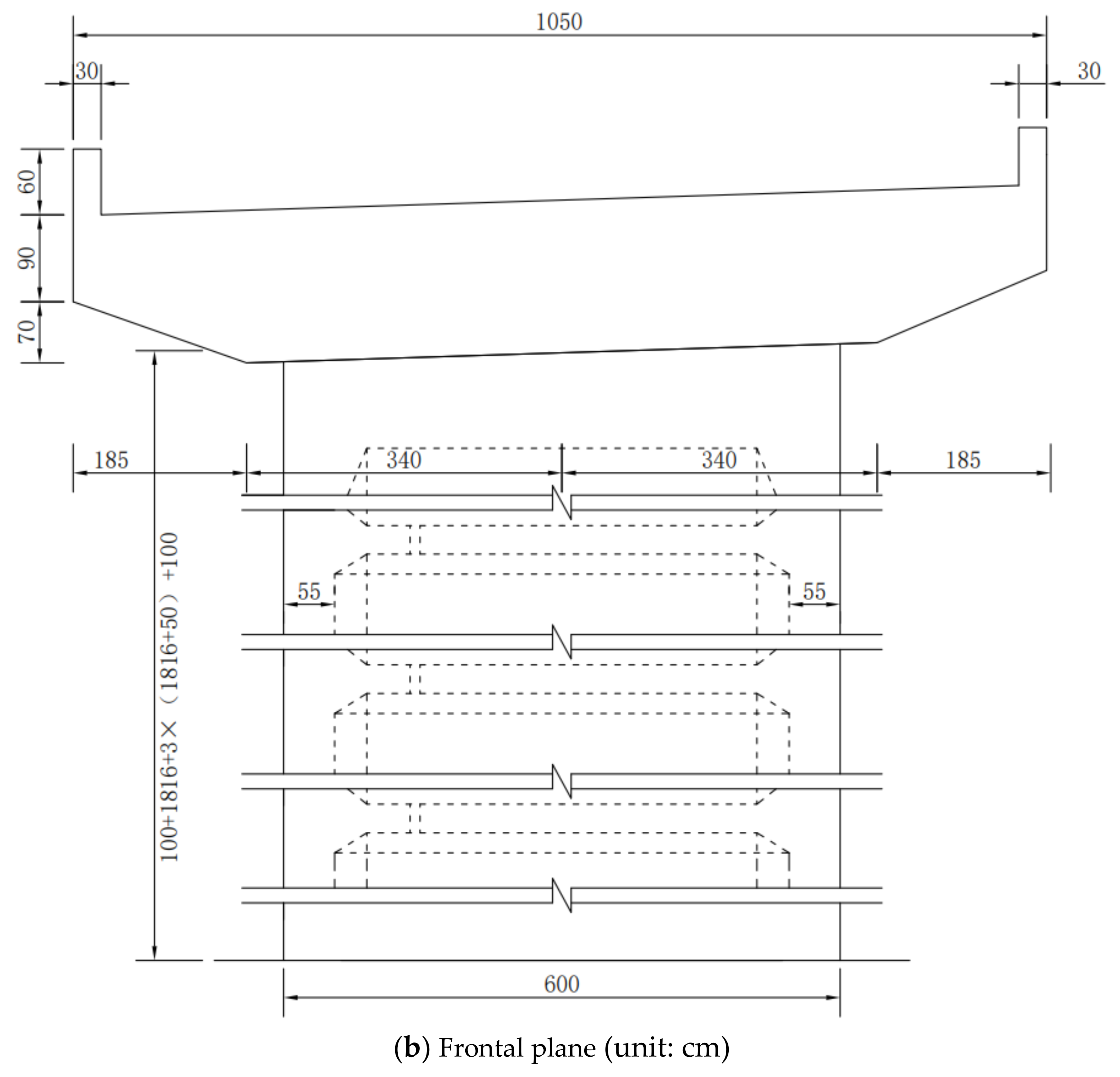
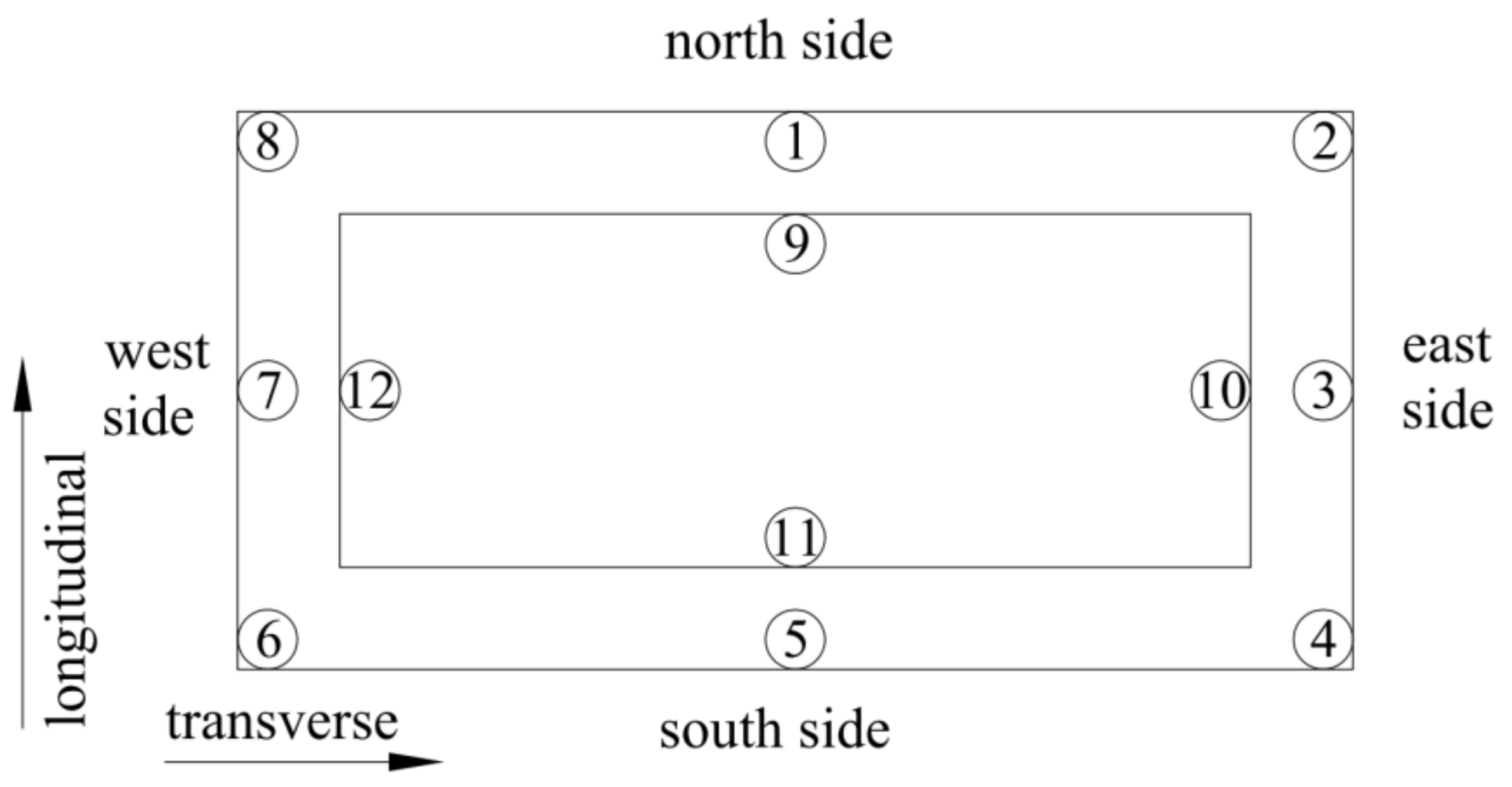



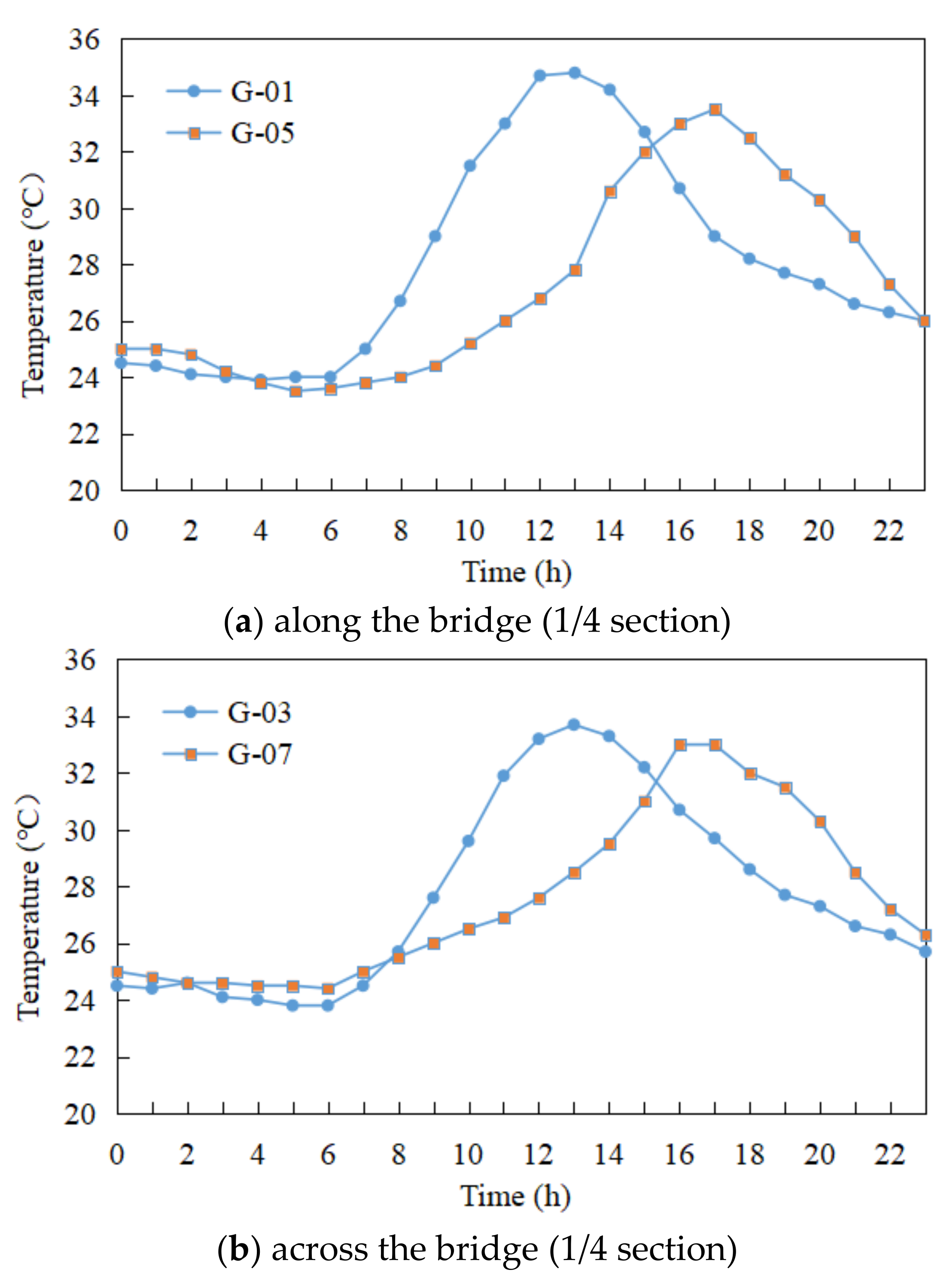
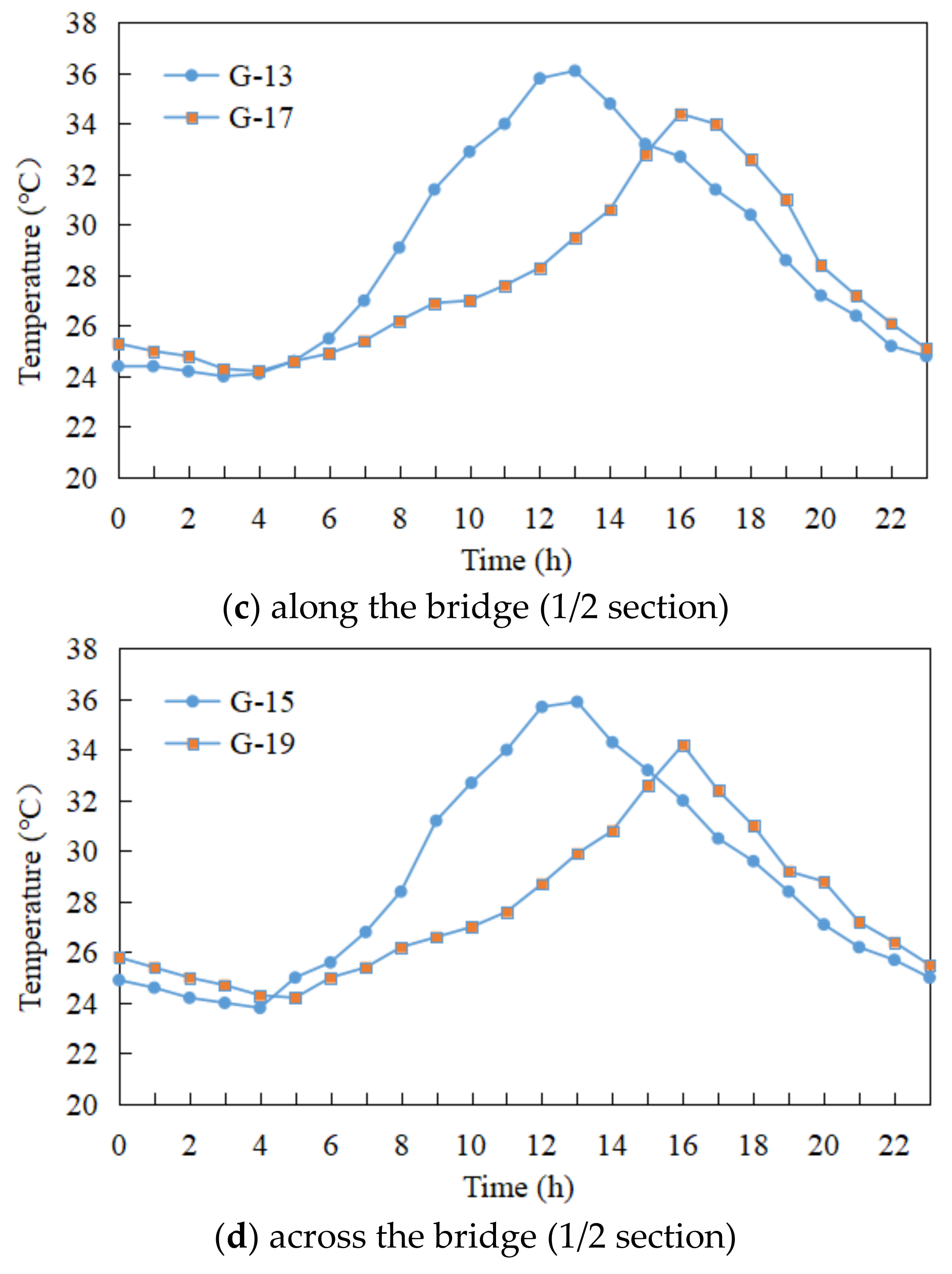
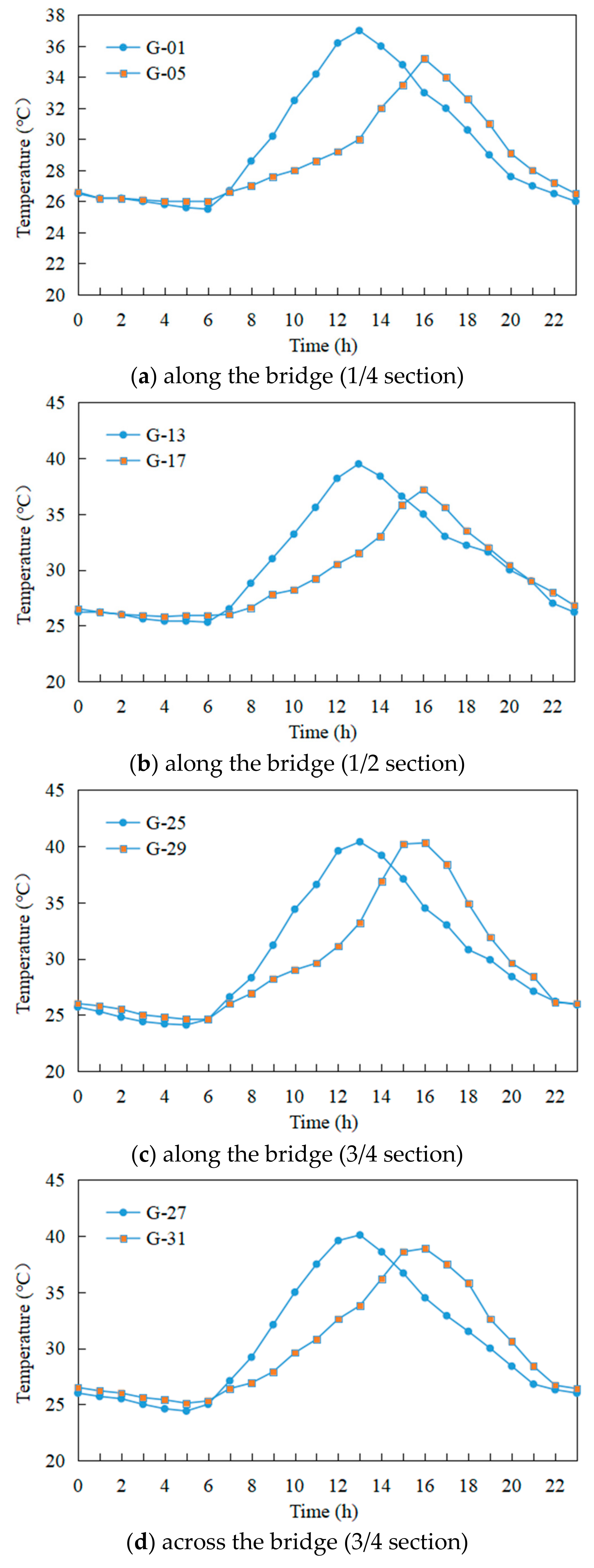





| Condition | Location | Northside | Southside | Temperature Difference |
|---|---|---|---|---|
| Condition 1 | 1/4 section | 29 | 23 | 6 |
| Condition 2 | 1/4 section | 33 | 26 | 7 |
| 1/2 section | 34.5 | 27 | 7.5 | |
| Condition 3 | 1/4 section | 37 | 30 | 7 |
| 1/2 section | 39.5 | 31.5 | 8 | |
| 3/4 section | 40.5 | 32 | 8.5 |
| Condition | Location | Longitudinal Direction |
|---|---|---|
| Condition 1 | total | 2.293 |
| Condition 2 | 0 ~ 1/2 segment | 5.351 |
| 1/2 ~ 3/4 segment | 0.717 | |
| total | 6.068 | |
| Condition 3 | 0 ~ 1/2 segment | 8.027 |
| 1/2 ~ 3/4 segment | 2.293 | |
| 3/4 ~ top segment | 0.807 | |
| total | 11.127 |
| Condition | Location | Longitudinal Direction |
|---|---|---|
| Condition 1 | total | 3.635 |
| Condition 2 | 0 ~ 1/2 segment | 6.946 |
| 1/2 ~ 3/4 segment | 1.136 | |
| total | 8.082 | |
| Condition 3 | 0 ~ 1/2 segment | 9.756 |
| 1/2 ~ 3/4 segment | 3.18 | |
| 1/2 ~ top segment | 1.281 | |
| total | 14.217 |
| Calculated Values | Condition 1 | Condition 2 | Condition 3 |
|---|---|---|---|
| analytical algorithm | 2.293 | 6.068 | 11.127 |
| railway code | 3.635 | 8.082 | 14.217 |
| finite element | 2.157 | 5.801 | 10.935 |
| measured value | 2.8 | 6.48 | 11.36 |
| analysis-measured | 0.507 | 0.412 | 0.233 |
| code-measured | 0.835 | 1.602 | 2.857 |
| digital-measured | 0.643 | 0.679 | 0.425 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
An, L.; Li, D.; Yuan, P.; Chen, P. An Analytical Algorithm for Determining Optimal Thin-Walled Hollow Pier Configuration with Sunlight Temperature Differences. Buildings 2023, 13, 1208. https://doi.org/10.3390/buildings13051208
An L, Li D, Yuan P, Chen P. An Analytical Algorithm for Determining Optimal Thin-Walled Hollow Pier Configuration with Sunlight Temperature Differences. Buildings. 2023; 13(5):1208. https://doi.org/10.3390/buildings13051208
Chicago/Turabian StyleAn, Lipeng, Dejian Li, Peng Yuan, and Peng Chen. 2023. "An Analytical Algorithm for Determining Optimal Thin-Walled Hollow Pier Configuration with Sunlight Temperature Differences" Buildings 13, no. 5: 1208. https://doi.org/10.3390/buildings13051208
APA StyleAn, L., Li, D., Yuan, P., & Chen, P. (2023). An Analytical Algorithm for Determining Optimal Thin-Walled Hollow Pier Configuration with Sunlight Temperature Differences. Buildings, 13(5), 1208. https://doi.org/10.3390/buildings13051208




_Mei.png)




