Classification of Low-Strain Foundation Pile Testing Signal Using Recurrent Neural Network
Abstract
:1. Introduction
2. Related Research
2.1. Theory of Low-Strain Pile Test (LSPT)
2.2. Artificial Intelligence Methods for Pile Test
3. Materials and Methods
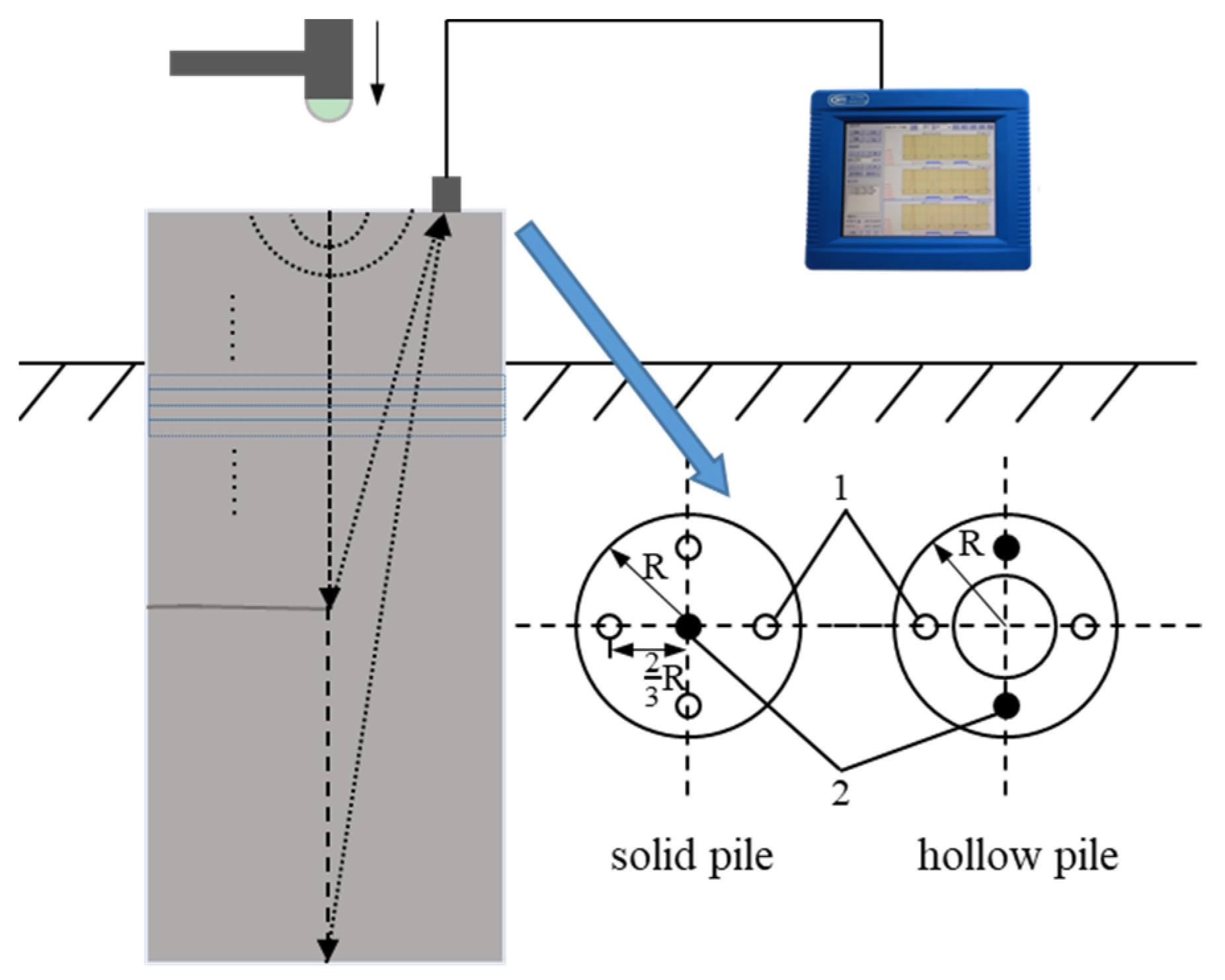
3.1. Concrete Model Pile Used for Testing
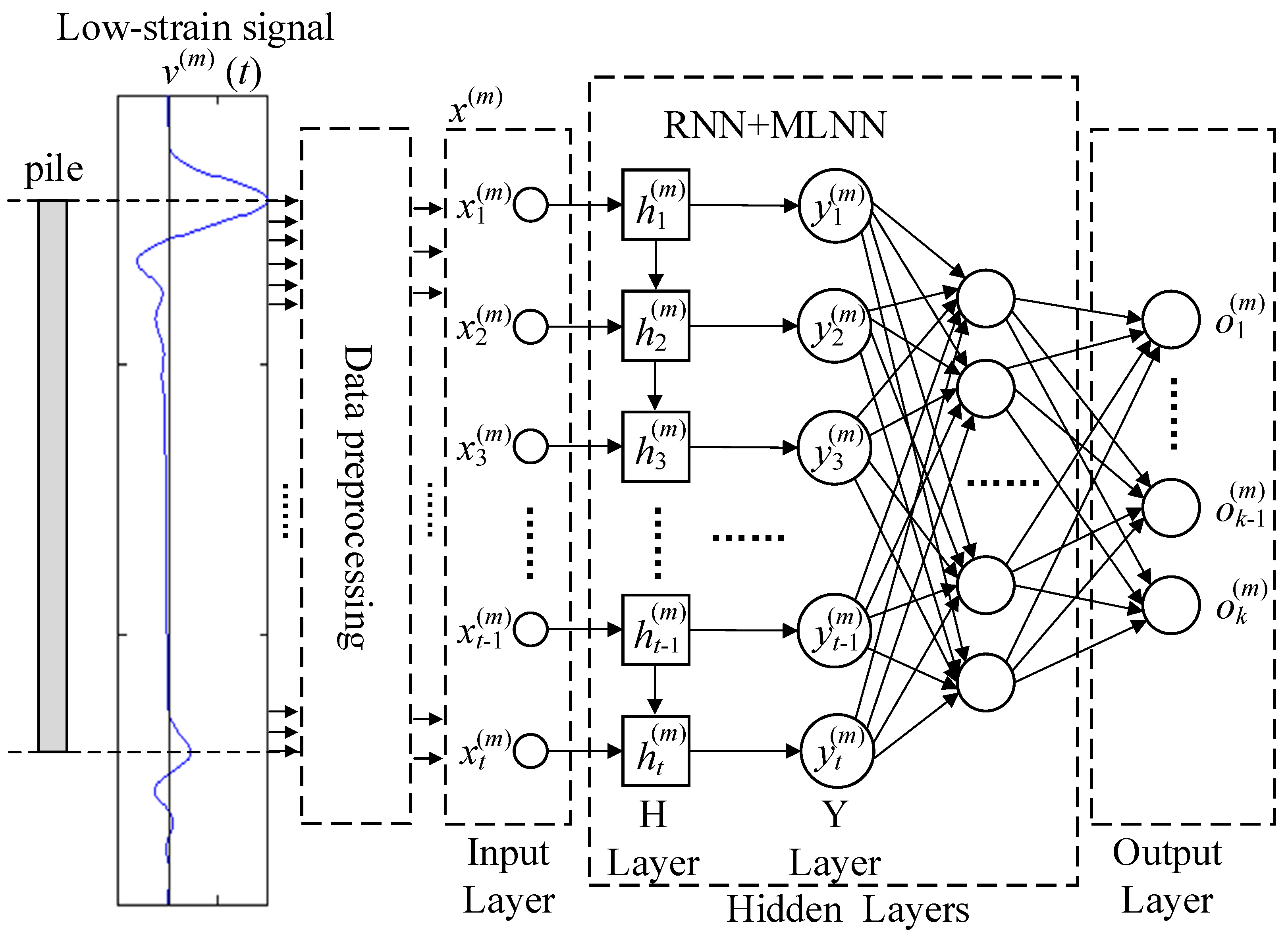
3.2. RNN+MLNN Analysis Model
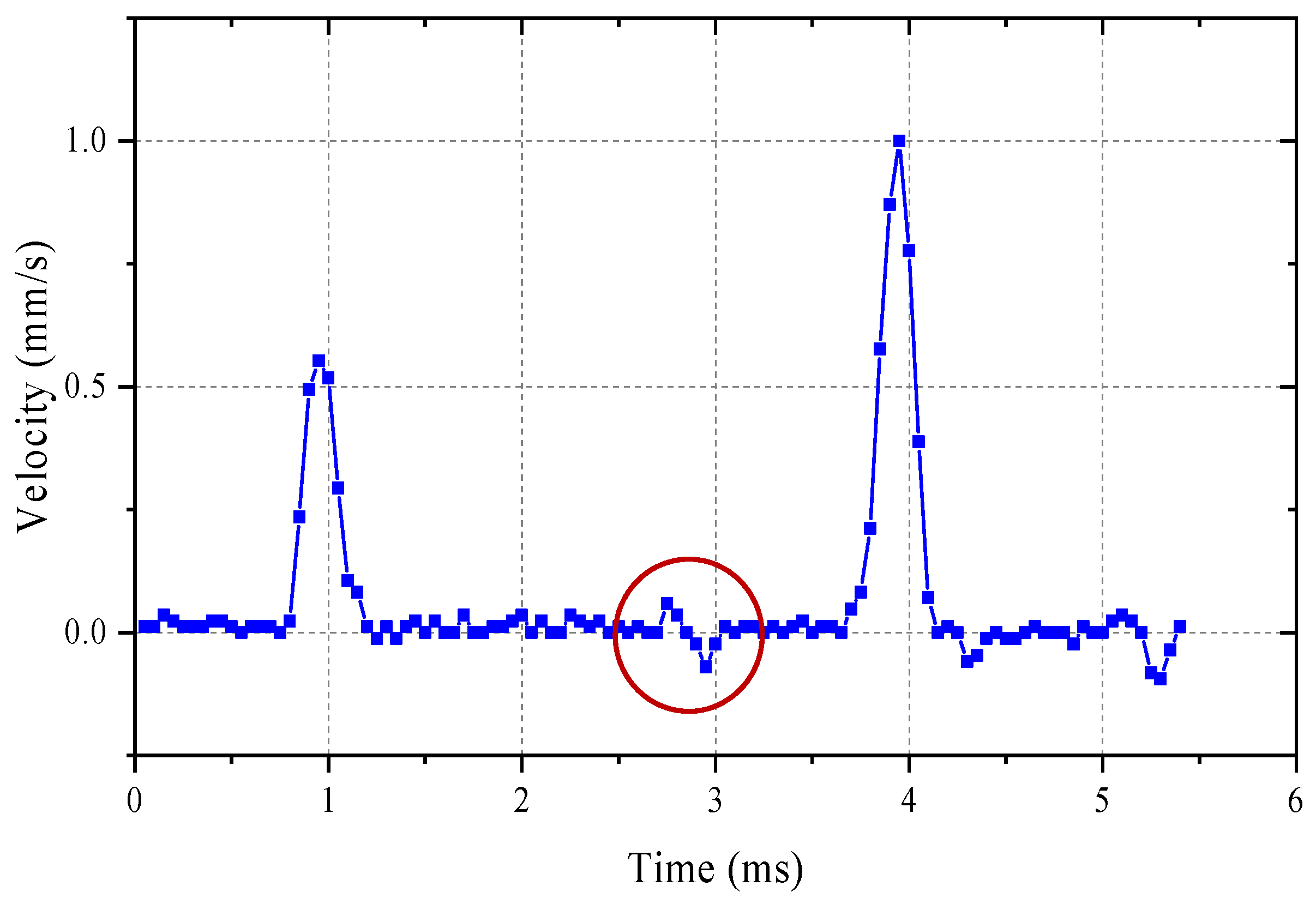
3.3. Data Preprocessing
| Algorithm 1: The initial edge and the peak detection algorithm. | |
| Inputs: | |
| Outputs: | |
| 1 | Calculate the average of the first part of num points ; |
| 2 | Form a new data sequence , ; |
| 3 | Calculate the maximum value of , ; |
| 4 | Set the threshold value as , th is the threshold parameter that can be manually set; |
| 5 | Iterate over all data, starting from 1 until appearing: and The order number i is the starting point of the initial edge: ; |
| 6 | Compute the differential sequence a of |
| 7 | Find the order number j where after , the j is the max value point ; |
| 8 | Return and ; |
4. Experimental Process and Results
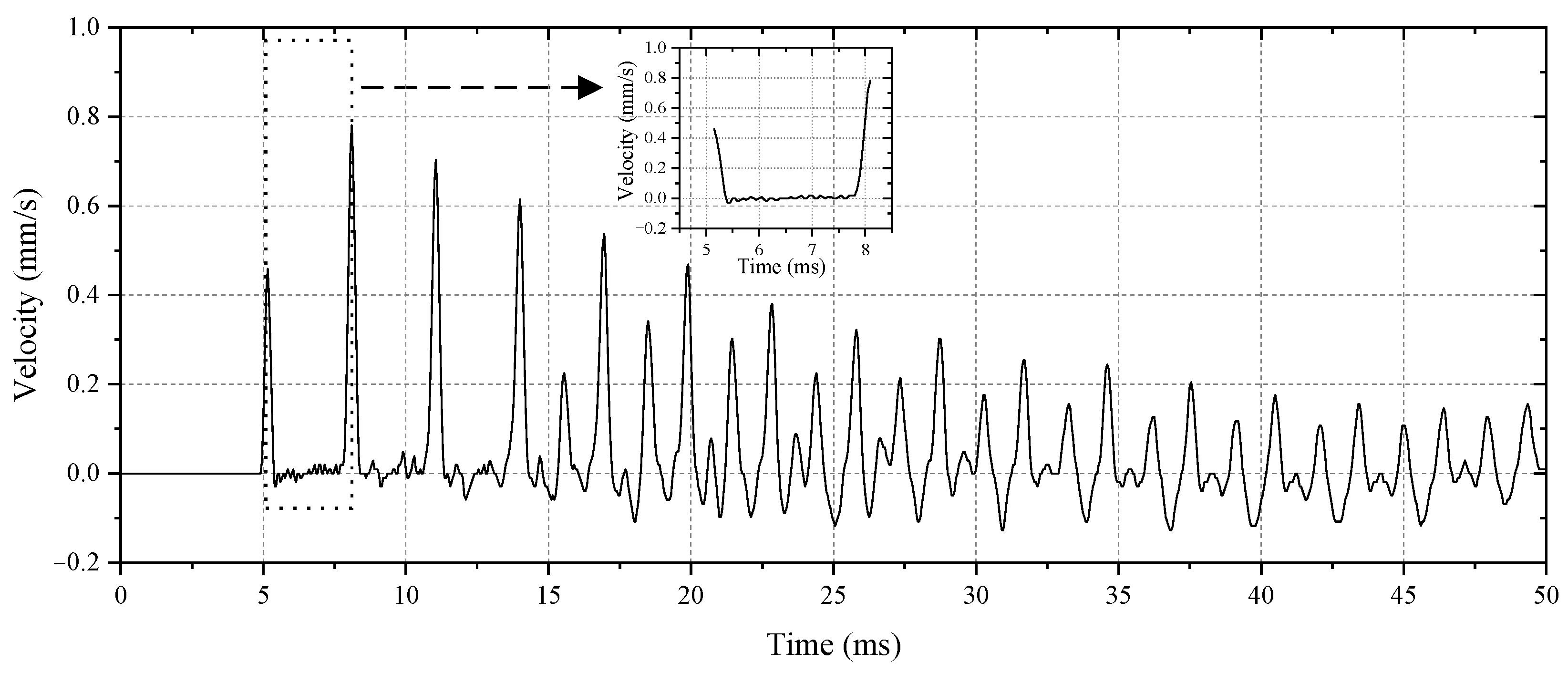
4.1. Data Acquisition
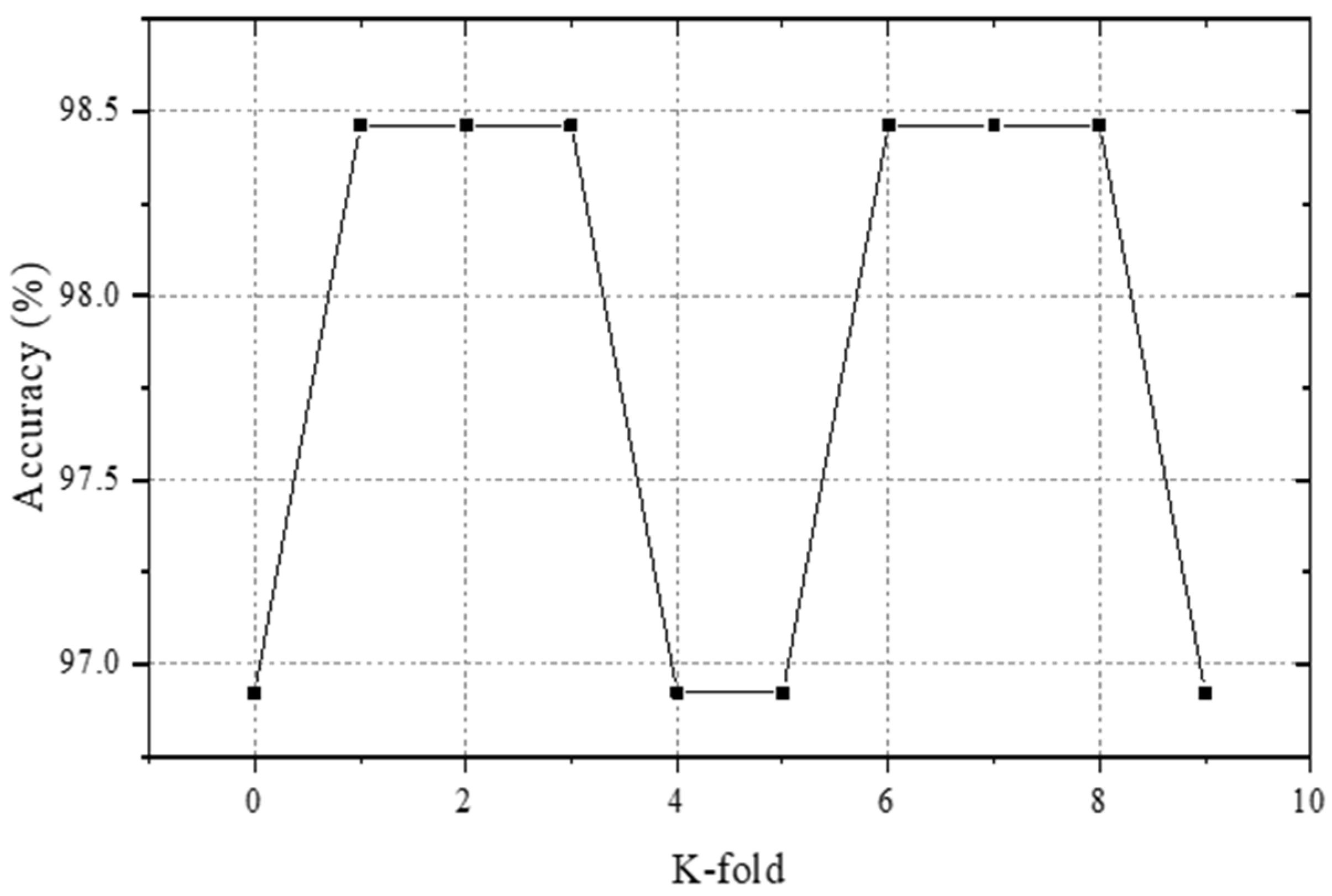
4.2. Data Preparation
- (1)
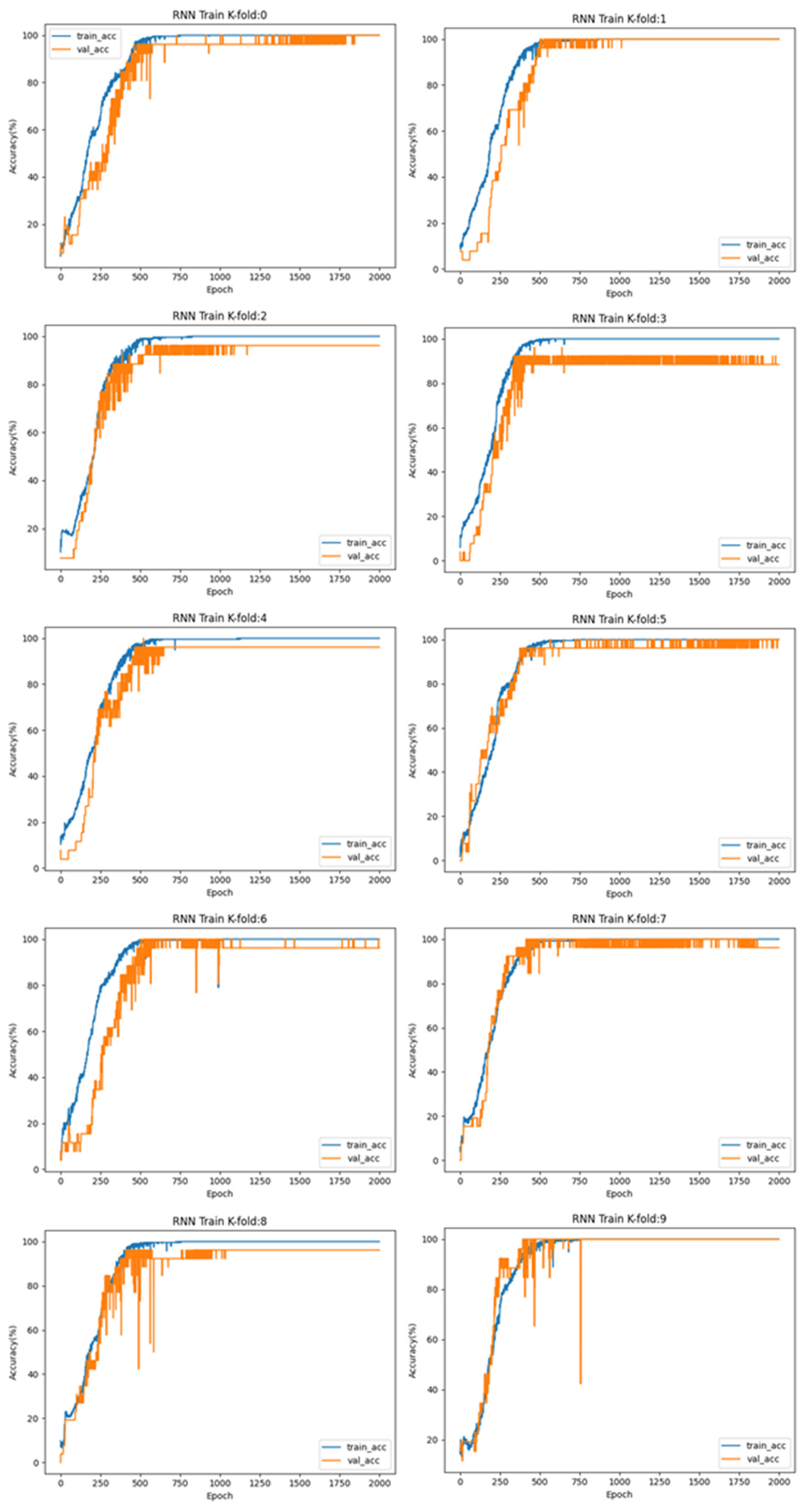
- D0 is used as the verification set, and the rest, D1 to D9, are used as the training sets;
- (2)
- Repeat step (1) until each subset is used as a validation set;
- (3)
- Obtain 10 models with different training parameters and accuracy through steps (1) and (2);
- (4)
- Evaluate the model performance on the test data set T1;
- (5)
- Select the optimal model synthetically.
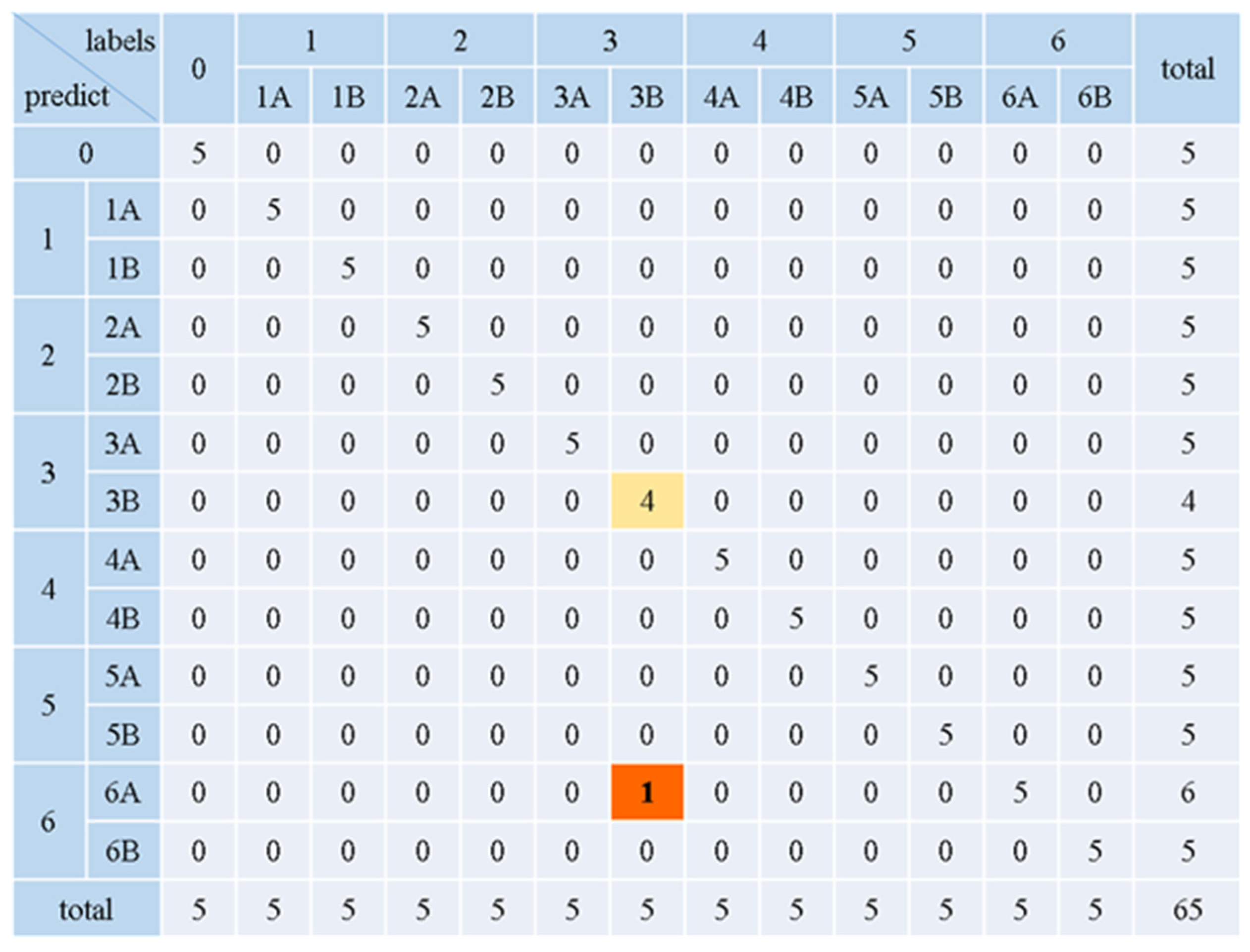
4.3. Test Results
4.4. Discussion
- (1)
- Classification model aspect: Compared with other neural network models, the accuracy of RNN model on test set is improved, but the cost of the computing unit and the training time are increased. Some studies are also trying to unravel the relationship among neurons in the hidden layer of neural networks and form explainable details, but it is still difficult to explain the internal structure of artificial neural networks [66].
- (2)
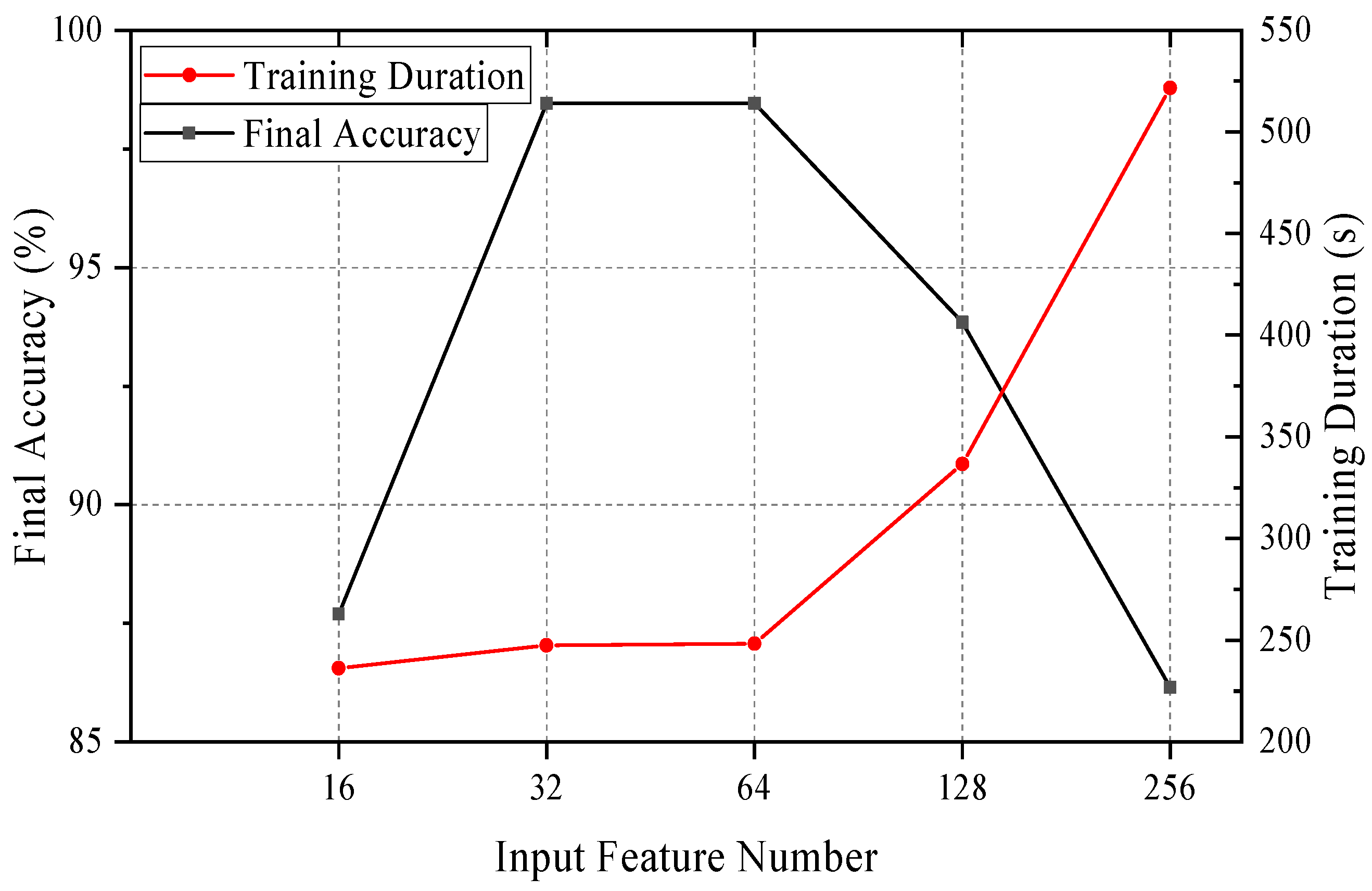
- Input data characteristics: In this stage, the research mainly focuses on the simple combination of time series signals. The input features obtained from the time domain signals will also lose some information details due to the sampling interval. Subsequently, some experts in the foundation pile test are needed to help establish a data feature selection mechanism.
- (3)
- Training data: Since there are thousands of possibilities for the formation of LSPT data in reality, the size of training data will also affect the accuracy of the final model. We need different testing engineers to acquire more data, under different conditions, to form the training data set.
- (4)
- Model application scenarios: The test site of the foundation pile is a scene with pile–soil–human interaction, and each link will affect the final result. This study tries to reduce the relevant influencing factors as much as possible, and it attempts to establish a model with only two key testing factors, namely pile body and particle velocity. If this model is ever going to be put into practice, pile type, pile length, geological data, hammer material, and other factors need to be comprehensively considered, and input characteristics and model structure need to be further expanded on the basis of this research model. Although there is no data to prove that the pile type is related to the pile integrity, the foundation pile is a complex project, which may lead to pile integrity problems in the process of pile construction due to the different construction techniques of different pile types. This issue needs to be further studied on the basis of subsequent massive data collection.
5. Conclusions
- (1)
- Model piles with different shapes are designed and processed to form LSPT signals for training and testing neural network models;
- (2)
- The RNN model is used to fully consider the timing attributes of input features;
- (3)
- The effective interval of input features is verified for the input timing features of different dimensions;
- (4)
- The advantage of using RNN in LSPT signal analysis is illustrated by comparing the RNN model with the traditional BP model and the DL model.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Huang, Z.F.; Bai, X.H.; Yin, C.; Liu, Y.Q. Numerical analysis for the vertical bearing capacity of composite pile foundation system in liquefiable soil under sine wave vibration. PLoS ONE 2021, 16, e0248502. [Google Scholar]
- Wang, G.; Wang, G.; Shen, H.; Xu, G.H. An experimental study on the phase lags in response of pile base pressure to waves at different horizons with silty soil. Coastal Eng. 2012, 31, 21–32. [Google Scholar] [CrossRef]
- You, Y.; Wang, J.; Wu, Q.; Yu, Q.; Wang, X.; Guo, L. Causes of pile foundation failure in permafrost regions: The case study of a dry bridge of the Qinghai-Tibet Railway. Eng. Geol. 2017, 230, 95–103. [Google Scholar] [CrossRef]
- Zheng, J.J.; Liu, Y.; Guo, J.; Xu, Z.J. Probabilistic analysis and reliability assessment for acceptance rate of foundation pile testing. Chin. J. Geotech. Eng. 2009, 31, 1660–1664. [Google Scholar]
- Chen, F.; Jiao, H.; Han, L.; Shen, L.; Yu, G. Real-time monitoring of construction quality for gravel piles based on Internet of Things. Automat. Constr. 2020, 116, 103228. [Google Scholar] [CrossRef]
- Sun, G.; Kong, G.; Liu, H.; Amenuvor, A.C. Velocity response of model ballastless track XCC pile-raft foundation. Can. Geotech. J. 2017, 54, 1340–1345. [Google Scholar] [CrossRef]
- Li, G.S. Discussion on foundation pile test method and loading quantity in static load test. Build. Struct. 2020, 50, 118–129. [Google Scholar]
- Li, L.Z. Discussion about testing the bearing capacity of end bearing large-section in-situ concrete pile by core drilling method. Build. Sci. 2014, 30, 103–107. [Google Scholar]
- Zhang, Y.L.; Tang, D.G. Application of ultrasonic computerized tomography to diagnosis of pile construction integrity. Rock Soil Mech. 2009, 30, 3548–3552. [Google Scholar]
- Wu, B.J.; Wang, K.H.; Tong, W.F.; Xiao, S. Size effect and pile impedance variation in pile integrity test. Chin. J. Rock Mech. Eng. 2019, 38, 3230–3237. [Google Scholar]
- Zhao, S.; Wu, J.T.; Qiu, X.C. Study on defect detection of extended pile shaft under lateral low-strain integrity test. J. Zhejiang Univ. (Eng. Sci.) 2021, 55, 1867–1902. [Google Scholar]
- Fatehnia, M.; Amirinia, G. A review of Genetic Programming and Artificial Neural Network applications in pile foundations. Int. J. Geo-Eng. 2018, 9, 2. [Google Scholar] [CrossRef]
- Eftychios, P.; Marco, S.; Erika, P. A genetically optimized neural classifier applied to numerical pile integrity tests considering concrete piles. Comput. Struct. 2016, 162, 68–79. [Google Scholar]
- Sun, G.; Gu, Y. A pile testing method based on structural dynamic modification. Chin. J. Comput. Mech. 2004, 21, 5. [Google Scholar]
- Zhang, J.; Chen, L. Sonic echo test for pile integrity testing based on wavelet transform. J. Vib. Shock 2014, 33, 179–183. [Google Scholar]
- Wang, L.; Zhang, M.; Zhu, H.; Liu, Y. Review on artificial neural networks and their applications in geoscience. World Nucl. Geosci. 2021, 38, 15–26. [Google Scholar]
- Bai, X.Y.; Zhang, M.Y.; Kou, H.L.; Liu, H. Prediction of time effect of static pile bearing capacity by BP neural network. Geotech. Investig. Survey. 2014, 4, 7–12. [Google Scholar]
- Gao, L.; Xie, K. Application of artificial neural networks to geotechnical engineering. China Civil Eng. J. 2002, 35, 5. [Google Scholar]
- Jebur, A.A.; Atherton, W.; Al Khaddar, R.M.; Loffill, E. Artificial neural network (ANN) approach for modelling of pile settlement of open-ended steel piles subjected to compression load. Eur. J. Environ. Civil Eng. 2021, 25, 429–451. [Google Scholar] [CrossRef]
- Alzo’ubi, A.K.; Ibrahim, F. Predicting Loading–Unloading Pile Static Load Test Curves by Using Artificial Neural Networks. Geotech. Geol. Eng. 2018, 37, 1311–1330. [Google Scholar] [CrossRef]
- Wei, W.; Xie, H.; Mao, X.; Hu, H. Prediction of Bearing Capacity of Composite Foundation of Vibrating Gravel Pile Based on RBF Neural Network. In Proceedings of the 2019 IEEE 14th International Conference on Intelligent Systems and Knowledge Engineering (ISKE), Dalian, China, 14–16 November 2019. [Google Scholar]
- Goudjil, K.; Arabet, L. Assessment of deflection of pile implanted on slope by artificial neural network. Neural Comput. Appl. 2020, 33, 1091–1101. [Google Scholar] [CrossRef]
- He, Z.; Zhang, T.; Lee, R.B. VerIDeep: Verifying Integrity of Deep Neural Networks through Sensitive-Sample Fingerprinting. arXiv 2018. [Google Scholar] [CrossRef]
- Liu, R.; Zhao, Y.; Wei, S.; Yang, Y. Indexing of CNN Features for Large Scale Image Search. Pattern Recognit. 2018, 48, 2983–2992. [Google Scholar] [CrossRef]
- Yan, J.; Jin, L.; Yuan, Z.; Liu, Z. RNN for Receding Horizon Control of Redundant Robot Manipulators. IEEE Trans. Ind. Electron. 2022, 69, 1608–1619. [Google Scholar] [CrossRef]
- Wu, J.; Naggar, M.H.E.; Wang, K.H.; Liu, X. Analytical study of employing low-strain lateral pile integrity test on a de-fective extended pile shaft. J. Eng. Mech. 2020, 146, 04020103. [Google Scholar]
- Cosic, M.; Folic, B.; Folic, R. Numerical simulation of the pile integrity test on defected piles. Acta Geotech. Slovenica 2014, 11, 4–19. [Google Scholar]
- Zheng, C.; Kouretzis, G.P.; Ding, X.; Liu, H.; Poulos, H.G. Three-dimensional effects in low-strain integrity testing of piles: Analytical solution. Can. Geotech. J. 2016, 53, 225–236. [Google Scholar] [CrossRef]
- Chang, D.W.; Cheng, S.H.; Wang, Y.L. One-dimensional wave equation analyses for pile responses subjected to seismic horizontal ground motions. Soils Found. 2014, 54, 313–328. [Google Scholar] [CrossRef]
- Zheng, C.; Ding, X.; Sun, Y. Vertical vibration of a pipe pile in viscoelastic soil considering the three-dimensional wave effect of soil. Int. J. Geomech. 2016, 16, 04015037.1–04015037.10. [Google Scholar] [CrossRef]
- Qu, L.; Ding, X.; Zheng, C.; Liu, H. An analytical solution for wave propagation in a square pile due to transient point load. Comput. Geotech. 2017, 83, 77–82. [Google Scholar] [CrossRef]
- Ziółkowski, W.; Śliwiński, A. Application of a vibrational impedance head to the measurement of the complex elastic modulus by the driving point impedance method. Arch. Acoust. 1991, 16, 591–607. [Google Scholar]
- Ding, X.; Liu, H.; Liu, J.; Chen, Y. Wave propagation in a pipe pile for low-strain integrity testing. J. Eng. Mech. 2011, 137, 598–609. [Google Scholar] [CrossRef]
- Ertel, J.P.; Niederleithinger, E.; Grohmann, M. Advances in pile integrity testing. Near Surf. Geophys. 2016, 14, 503–512. [Google Scholar] [CrossRef]
- Lu, Z.T.; Wang, Z.L.; Liu, D.J. Study on low-strain integrity testing of pipe-pile using the elastodynamic finite integration technique. Int. J. Numer. Anal. Methods Geomech. 2013, 37, 536–550. [Google Scholar] [CrossRef]
- Alkhader, M.; Iyer, S.; Shi, W.; Venkatesh, T.A. Low frequency acoustic characteristics of periodic honeycomb cellular cores: The effect of relative density and strain fields. Compos. Struct. 2015, 133, 77–84. [Google Scholar] [CrossRef]
- Li, H.B.; Li, J.; Farhangi, V. Determination of piers shear capacity using numerical analysis and machine learning for gen-eralization to masonry large scale walls. Structures 2023, 49, 443–466. [Google Scholar] [CrossRef]
- Wang, C.; Zhang, W. A neural network model for diagnosing pile integrity based on reflection wave method. Rock Soil Mech. 2003, 24, 952–956. [Google Scholar]
- Liu, M.; Yue, X.; Yang, Y.; Li, Q. Intelligent identification of pile defect based on sym wavelet and bp neural network. Chin. J. Rock Mechanics Eng. 2007, 26, 5. [Google Scholar] [CrossRef]
- Pham, T.A.; Tran, V.Q.; Vu, H.L.T.; Ly, H.B. Design deep neural network architecture using a genetic algorithm for estimation of pile bearing capacity. PLoS ONE 2020, 15, e0243030. [Google Scholar] [CrossRef]
- Cui, D.M.; Yan, W.Z.; Wang, X.Q.; Lu, L.M. Towards intelligent interpretation of low strain pile integrity testing results using machine learning techniques. Sensors 2017, 17, 2443. [Google Scholar] [CrossRef]
- Jierula, A.; Oh, T.M.; Wang, S.; Lee, J.W. Detection of damage locations and damage steps in pile foundations using acoustic emissions with deep learning technology. Front. Struct. Civil Eng. 2021, 15, 15. [Google Scholar] [CrossRef]
- Zhang, P.Z.; Zhang, Y.C.; Song, X.G.; Yang, H.; Guo, Z.H.; Hu, Y. Modified calculation method of shaft friction for driven pile considering particle size effect. J. Shandong Univ. (Eng. Sci.) 2021, 51, 9. [Google Scholar]
- Yang, R.H. Application of model pile test in low strain inspection of foundation pile. Archit. Technol. 2015, 46, 562–565. [Google Scholar]
- Yang, W.G.; Ma, J.; Li, J.M.; Zhang, F.; Zhang, S.S. Discussion and analysis on the ability of testing pile integrity with low strain variation method. China Inspect. Body Lab. 2021, 29, 101–104. [Google Scholar] [CrossRef]
- Lai, J.; Yang, P.C.; Yang, B.H.; Chang, D.W. Integrity testing of model pile with embedded accelerometers. In Proceedings of the International Conference on Transportation Infrastructure and Materials (ICTIM 2017), Qingdao, China, 9–12 June 2017. [Google Scholar]
- Hu, Y.; Peng, X.; Yang, Z.; Jia, L.; Li, Y.J.; Xue, Q. Temporal representation learning for time series classification. Neural Comput. Appl. 2021, 33, 3169–3182. [Google Scholar] [CrossRef]
- Huesken, M.; Stagge, P. Recurrent neural networks for time series classification. Neurocomputing 2003, 50, 223–235. [Google Scholar] [CrossRef]
- Wei, C.; Kong, Z.; Yang, D.; Jia, Y.W.; Hill, D.J. Short-term residential load forecasting based on LSTM recurrent neural network. IEEE Trans. Smart Grid 2017, 10, 841–851. [Google Scholar]
- Liu, H.; Zhou, J.; Zheng, Y.; Jiang, W.; Zhang, Y. Fault diagnosis of rolling bearings with recurrent neural network-based auto encoders. ISA Trans. 2018, 77, 167–178. [Google Scholar] [CrossRef]
- Liang, H.T.; Liu, S.; Du, J.W.; Hu, Q.; Yu, X. Review of Deep Learning Applied to Time Series Prediction. J. Front. Comput. Sci. Technol. 2023, 1–21. [Google Scholar] [CrossRef]
- Huang, Y.; Han, X.; Zhao, L. Recurrent neural networks for complicated seismic dynamic response prediction of a slope system. Eng. Geol. 2021, 289, 106198. [Google Scholar] [CrossRef]
- Zhang, Q.; Yang, L.T.; Chen, Z.; Li, P. A survey on deep learning for big data. Inf. Fusion 2018, 42, 146–157. [Google Scholar] [CrossRef]
- Young, T.; Hazarika, D.; Poria, S.; Cambria, E. Recent Trends in Deep Learning Based Natural Language Processing. IEEE Computat. Intell. Mag. 2018, 13, 55–75. [Google Scholar] [CrossRef]
- Wang, L.; Zeng, Y.; Chen, T. Back propagation neural network with adaptive differential evolution algorithm for time series forecasting. Expert Syst. Appl. 2015, 42, 855–863. [Google Scholar] [CrossRef]
- Messaoud, S.; Bradai, A.; Moulay, E. Online GMM clustering and mini-batch-gradient descent based optimization for industrial IoT 4.0. IEEE Trans. Ind. Informat. 2020, 16, 1427–1435. [Google Scholar] [CrossRef]
- Shu, Y.; Huang, Y.; Li, B. Design of deep learning accelerated algorithm for online recognition of industrial products defects. Neural Comput. Appl. 2018, 31, 4527–4540. [Google Scholar] [CrossRef]
- Kim, J.Y.; Park, J.H.; Jang, S.Y.; Yang, J.R. Peak detection algorithm for vital sign detection using doppler radar sensors. Sensors 2019, 19, 1575. [Google Scholar] [CrossRef]
- Jiang, H.; Zhang, X.; Li, D.; Zhao, Y.; Zhang, Z. Multi-peak detection algorithm based on wavelength feature recognition in FBG sensor networks. Opt. Eng. 2021, 60, 106104. [Google Scholar] [CrossRef]
- Diaconu, D.C.; Bretcan, P.; Peptenatu, D.; Tanislav, D.; Mailat, E. The importance of the number of points, transect location and interpolation techniques in the analysis of bathymetric measurements. J. Hydrol. 2019, 570, 774–785. [Google Scholar] [CrossRef]
- Wang, H.; Zhang, Y.; Zhang, S.; Li, J.M. Design and implementation of low strain foundation pile dynamic tester. Electron. Des. Eng. 2019, 27, 5. [Google Scholar]
- Jung, K.; Bae, D.H.; Um, M.J.; Kim, S.; Jeon, S.; Park, D. Evaluation of Nitrate Load Estimations Using Neural Networks and Canonical Correlation Analysis with K-Fold Cross-Validation. Sustainability 2020, 12, 400. [Google Scholar] [CrossRef]
- Samek, W.; Binder, A.; Montavon, G.; Lapuschkin, S.; Muller, K.-R. Evaluating the Visualization of What a Deep Neural Network Has Learned. IEEE Trans. Neural Netw. Learn. Syst. 2016, 28, 2660–2673. [Google Scholar] [CrossRef] [PubMed]
- Marcus, G. Deep learning: A critical appraisal. arXiv 2018, arXiv:1801.00631. [Google Scholar]
- Liu, G.G.; Yang, Y.M.; Liu, B.; Zhong, D.Y.; Yang, S.Q. Prediction model of the bird strike risk in the airport sphere by using the artificial neural network. J. Saf. Environ. 2020, 20, 416–422. [Google Scholar]
- Mcgrath, T.; Kapishnikov, A.; Tomaev, N.; Pearce, A.; Hassabis, D.; Kim, B.; Paquet, U.; Kramnik, V. Acquisition of Chess Knowledge in AlphaZero. arXiv 2021, arXiv:2111.09259. [Google Scholar] [CrossRef] [PubMed]





| No. | Paper Author | Number of Features | Model Structure |
|---|---|---|---|
| 1 | Wang et al. [38] | 68 | BP neural network, the input dimension is 68, the number of hidden layers is 1, the number of hidden layer nodes is 50, and the output dimension is 96. The activation function uses logarithmic Sigmoid function |
| 2 | Liu et al. [39] | 4 | BP neural network, the input dimension is 4, the number of hidden layers is 1, the number of hidden layer nodes is 10, and the output dimension is 5. The activation function uses logarithmic Sigmoid function |
| 3 | Tuan et al. [40] | 10 | Multilayer neural network, the input dimension is 10, the number of hidden layers is 4, the number of hidden layer nodes is (74, 17, 24, 12), and the output dimension is 1. The activation function uses relu function |
| 4 | De-Mi et al. [41] | 21 | ELM, the input dimension is 4, the number of hidden layers is 1, the number of hidden layer nodes is 500, and the output dimension is 4. The activation function uses logarithmic Sigmoid function |
| 5 | Alipujiang et al. [42] | 17 | Multilayer neural network, the input dimension is 17, the number of hidden layers is 2, the number of hidden layer nodes is (20, 20), and the output dimension is 2. The activation function uses logarithmic Sigmoid function |
| No. | Pile Shape |
|---|---|
| 0 |  |
| 1 |  |
| 2 |  |
| 3 |  |
| 4 |  |
| 5 |  |
| 6 |  |
| No. | Layer (Type) | Output Shape | Param Number |
|---|---|---|---|
| 1 | gru (GRU) | (None, 16, 32) | 3360 |
| 2 | gru_1 (GRU) | (None, 64) | 18,816 |
| 3 | dense (Dense) | (None, 32) | 2080 |
| 4 | dense_1 (Dense) | (None, 13) | 429 |
| Total Params | 24,685 | ||
| No. | Processing Step | Main Content | Features Number |
|---|---|---|---|
| 1 | Acquire binary signal | Forms the binary data file by the DMI | 1024 |
| 2 | Convert data | Converts binary data to a numeric data array | 1024 |
| 3 | Identify excitation peak | Identify the excitation peak in 1024 data points | 1024 |
| 4 | Intercept the effective length | Intercept the data points of 2 times the pile length from the data of 1024 points | 60 (20 kHz); 149 (50 kHz) |
| 5 | Unify data dimension | Unify the data dimension into 64 by interpolation method | 64 |
| 6 | Normalize data | Adjust data value to [–1, 1] | 64 |
| No. | Type | Network Structure | Trainable Parameters | Duration for 2000 Epochs (s) | Final Accuracy (%) |
|---|---|---|---|---|---|
| 1 | BPN | 13 | 845 | 172.395287 | 95.38 |
| 2 | DL | 32-64-32-13 | 6701 | 211.300839 | 96.92 |
| 3 | RNN+MLNN | 32-64-32-13 | 24,685 | 269.360601 | 98.46 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.; Zhang, S.; Li, J.; Yuan, Y.; Zhang, F. Classification of Low-Strain Foundation Pile Testing Signal Using Recurrent Neural Network. Buildings 2023, 13, 1228. https://doi.org/10.3390/buildings13051228
Wang H, Zhang S, Li J, Yuan Y, Zhang F. Classification of Low-Strain Foundation Pile Testing Signal Using Recurrent Neural Network. Buildings. 2023; 13(5):1228. https://doi.org/10.3390/buildings13051228
Chicago/Turabian StyleWang, Haiyuan, Shen Zhang, Jianmin Li, Yang Yuan, and Feng Zhang. 2023. "Classification of Low-Strain Foundation Pile Testing Signal Using Recurrent Neural Network" Buildings 13, no. 5: 1228. https://doi.org/10.3390/buildings13051228
APA StyleWang, H., Zhang, S., Li, J., Yuan, Y., & Zhang, F. (2023). Classification of Low-Strain Foundation Pile Testing Signal Using Recurrent Neural Network. Buildings, 13(5), 1228. https://doi.org/10.3390/buildings13051228









