A New Kinematical Admissible Translational–Rotational Failure Mechanism Coupling with the Complex Variable Method for Stability Analyses of Saturated Shallow Square Tunnels
Abstract
1. Introduction
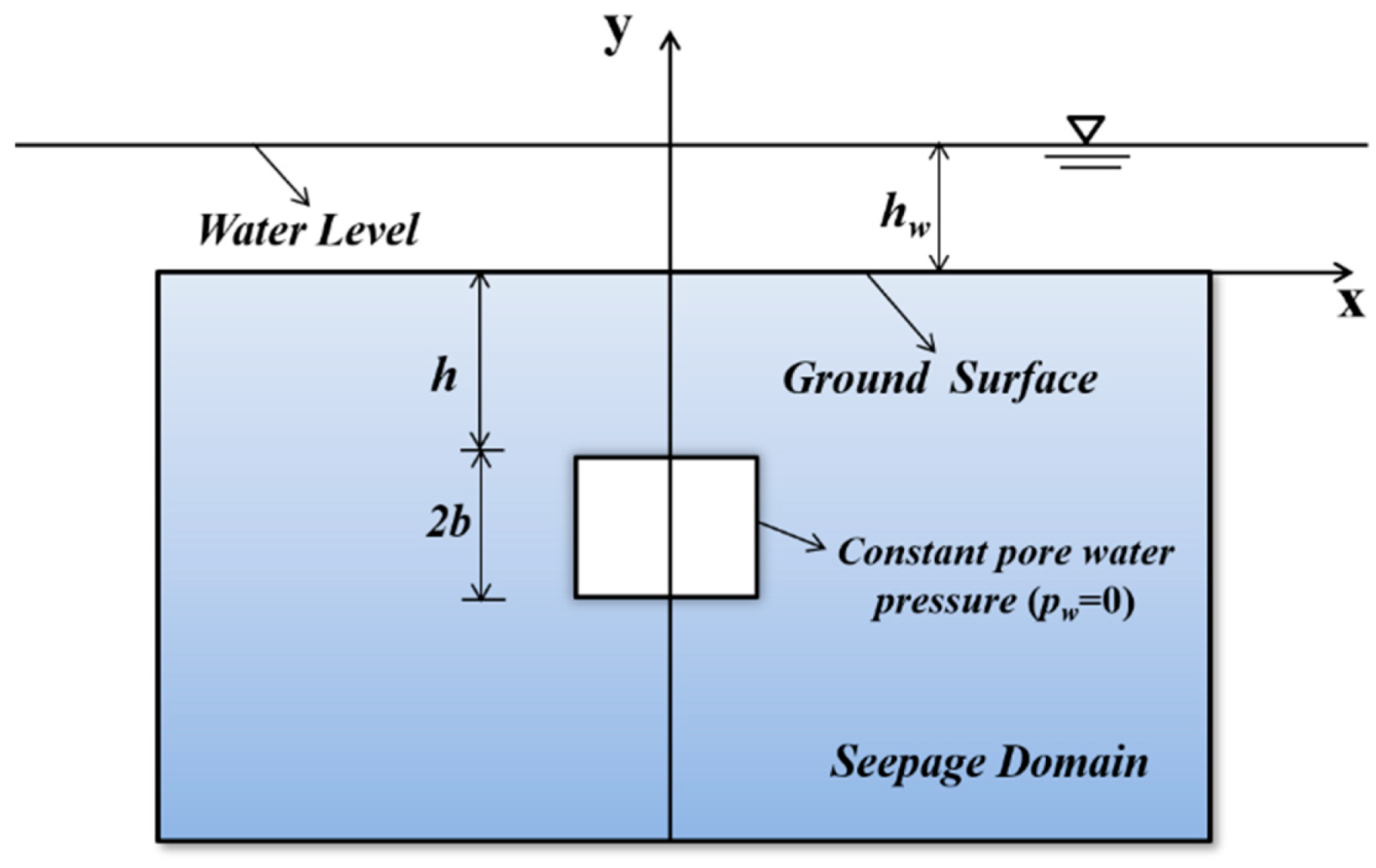
2. Upper Bound Limit Analysis of Shallow Square Tunnels in Water-Bearing Zones
2.1. Upper Bound Limit Analysis Theory
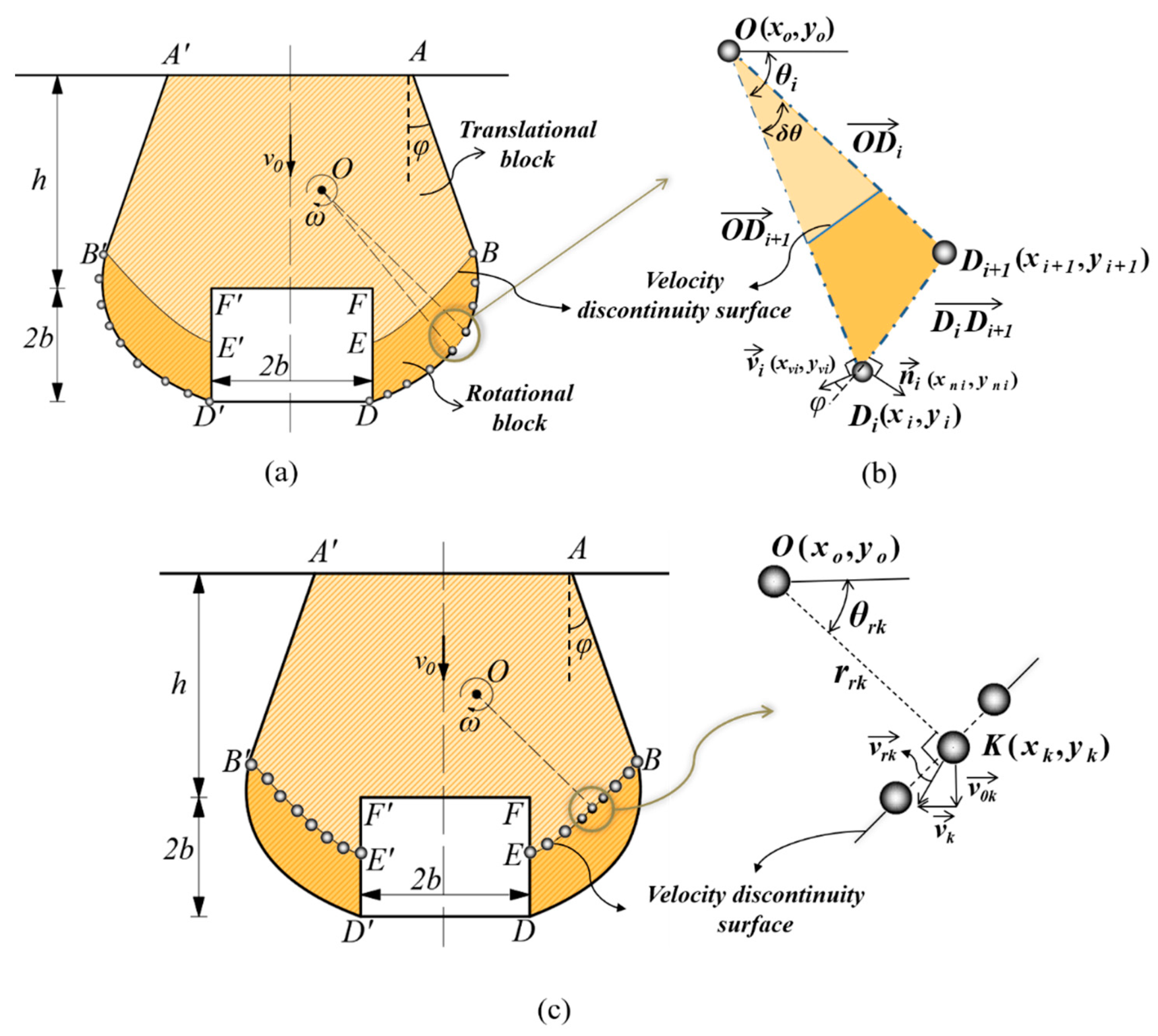
2.2. Translational–Rotational Failure Mechanism of an Underwater Shallow Square Tunnel
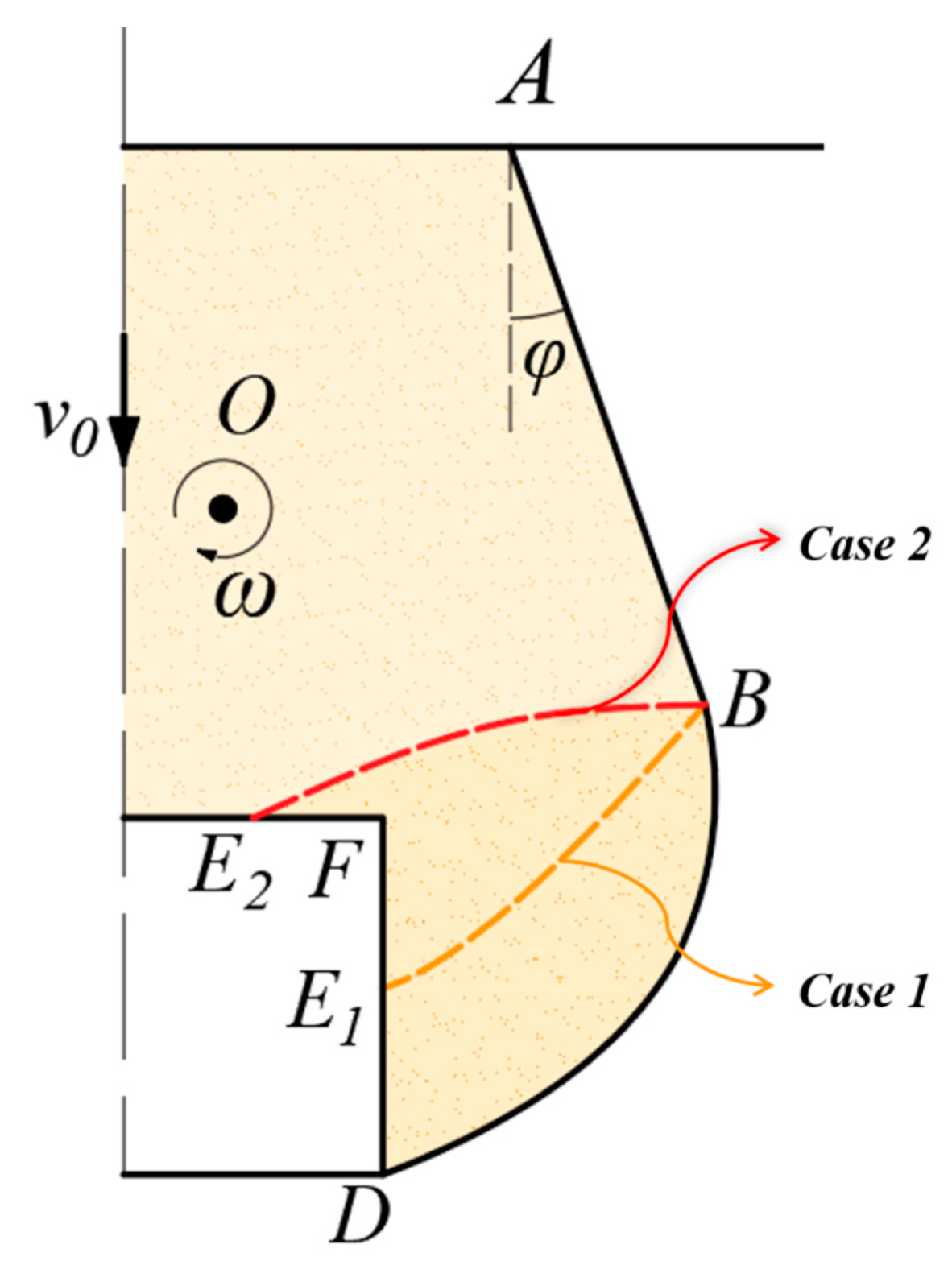
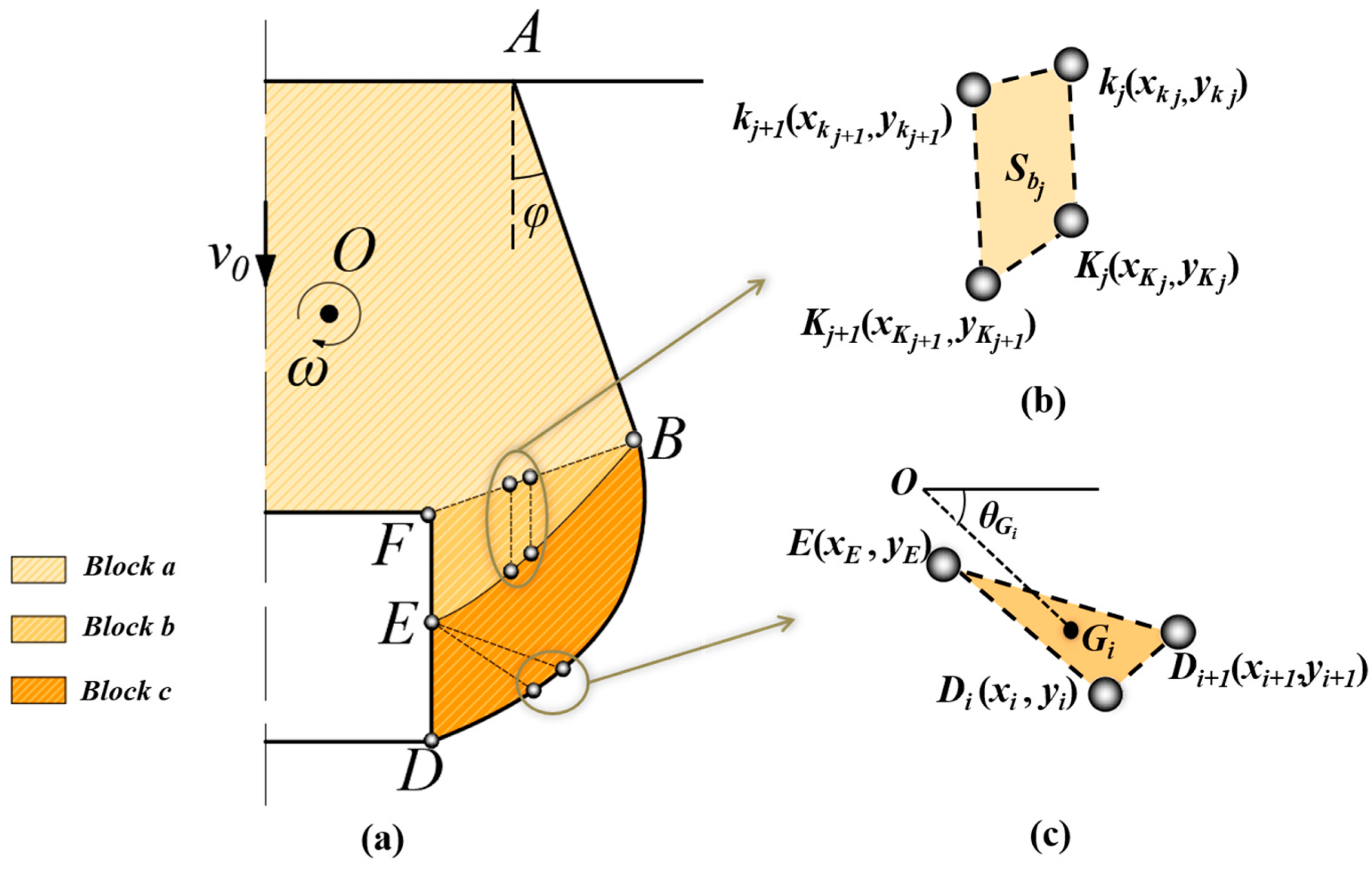
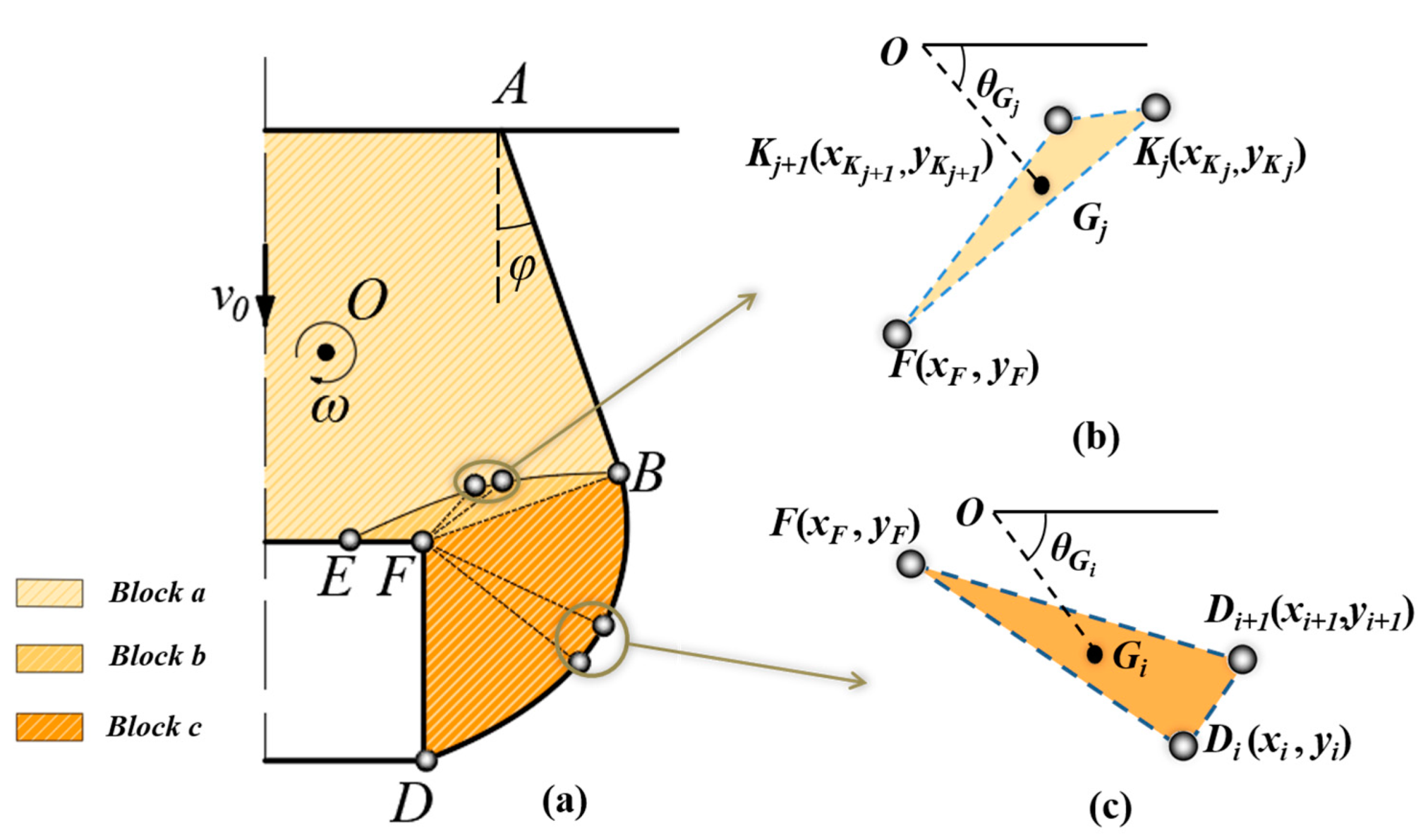
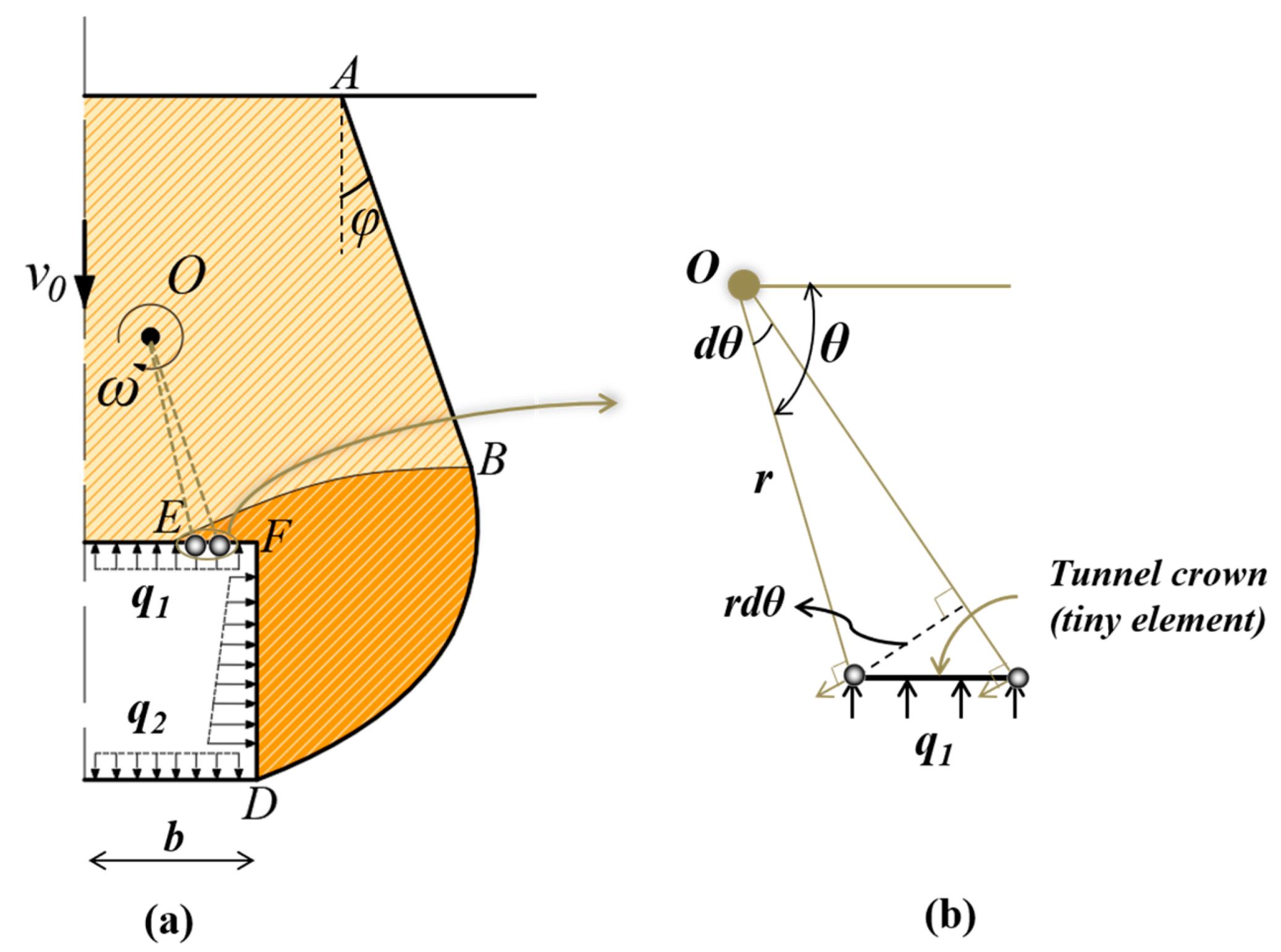
2.2.1. Failure Mechanism Generated by the Discrete Method
2.2.2. Velocity Discontinuity Surfaces and
2.3. Work Rate Calculation
2.3.1. Work Rate of Soils’ Gravity
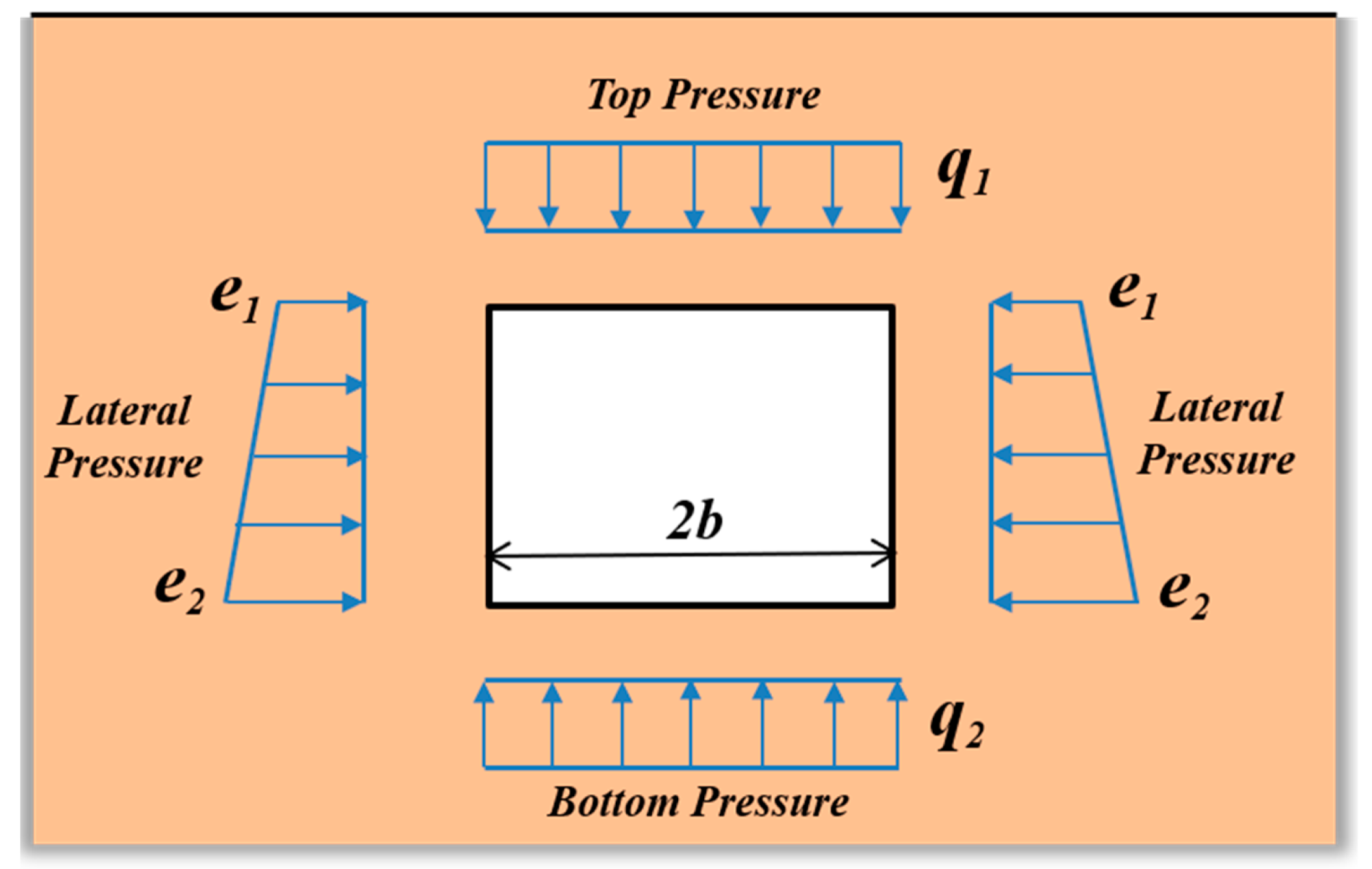
2.3.2. Work Rate of Supporting Pressure
2.3.3. Internal Energy Dissipation Rate
2.4. Analytical Solutions of Pore-Water Pressure Distribution around Tunnels
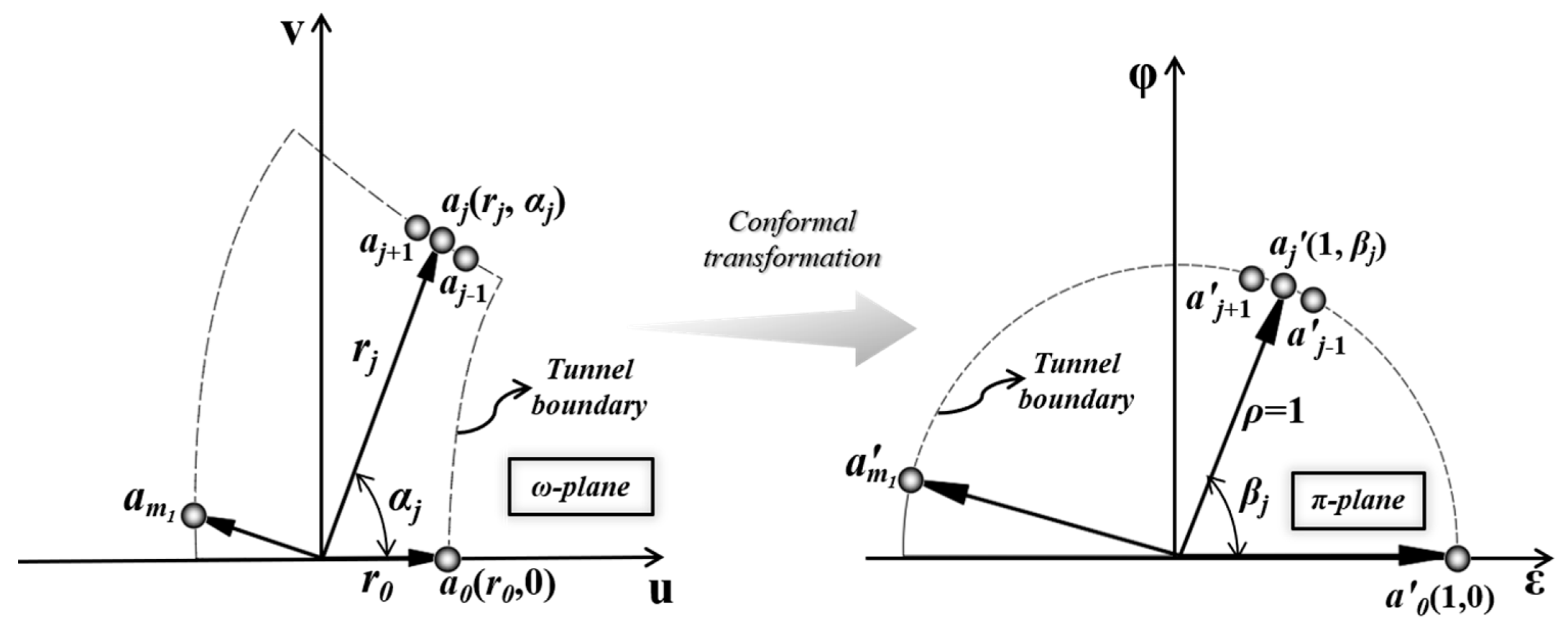
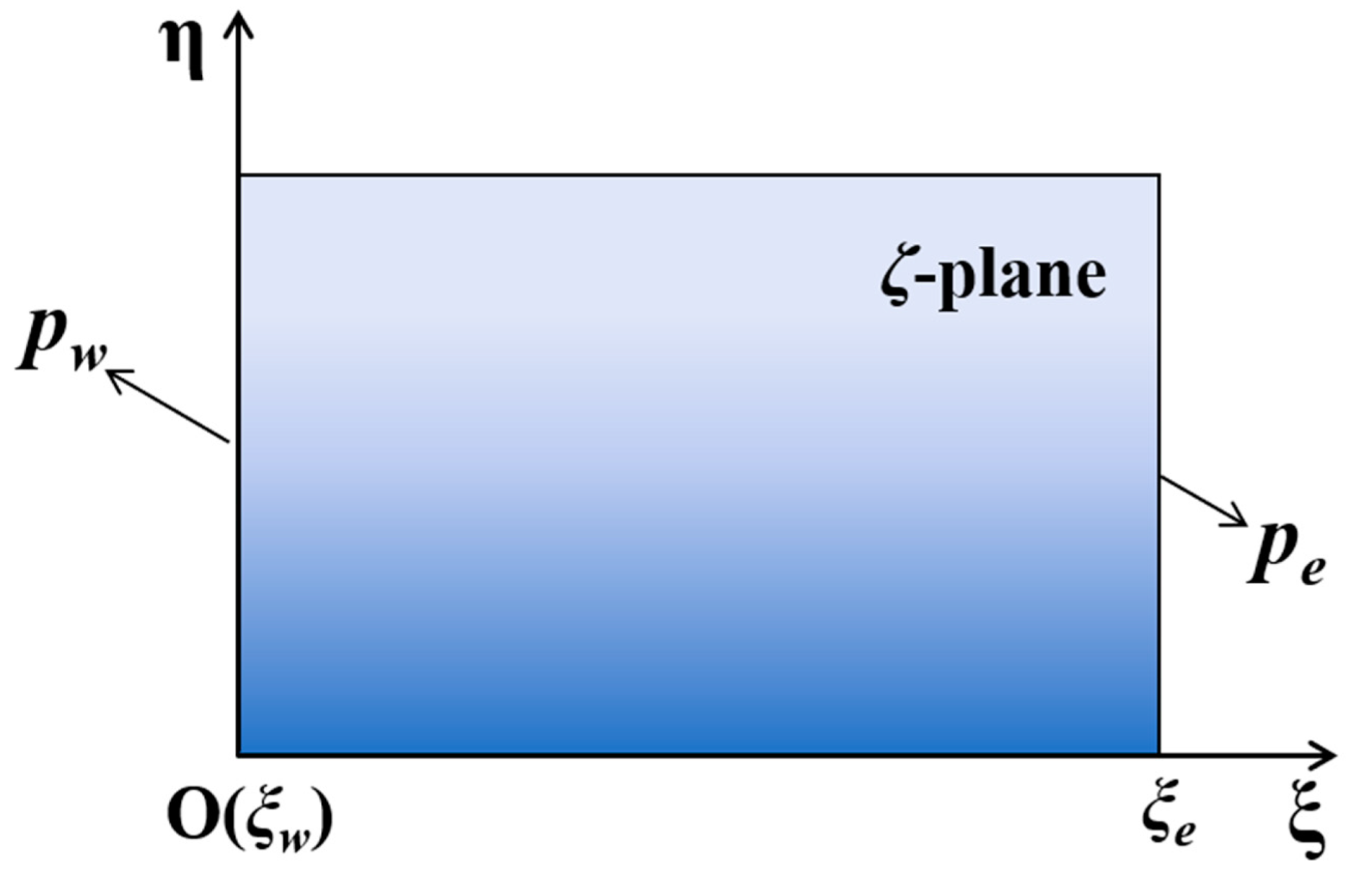
2.4.1. Conformal Mapping
2.4.2. Solutions for Pore-Water Pressure Distribution
2.4.3. Work Rates Performed by the Pore-Water Pressures
3. Verification
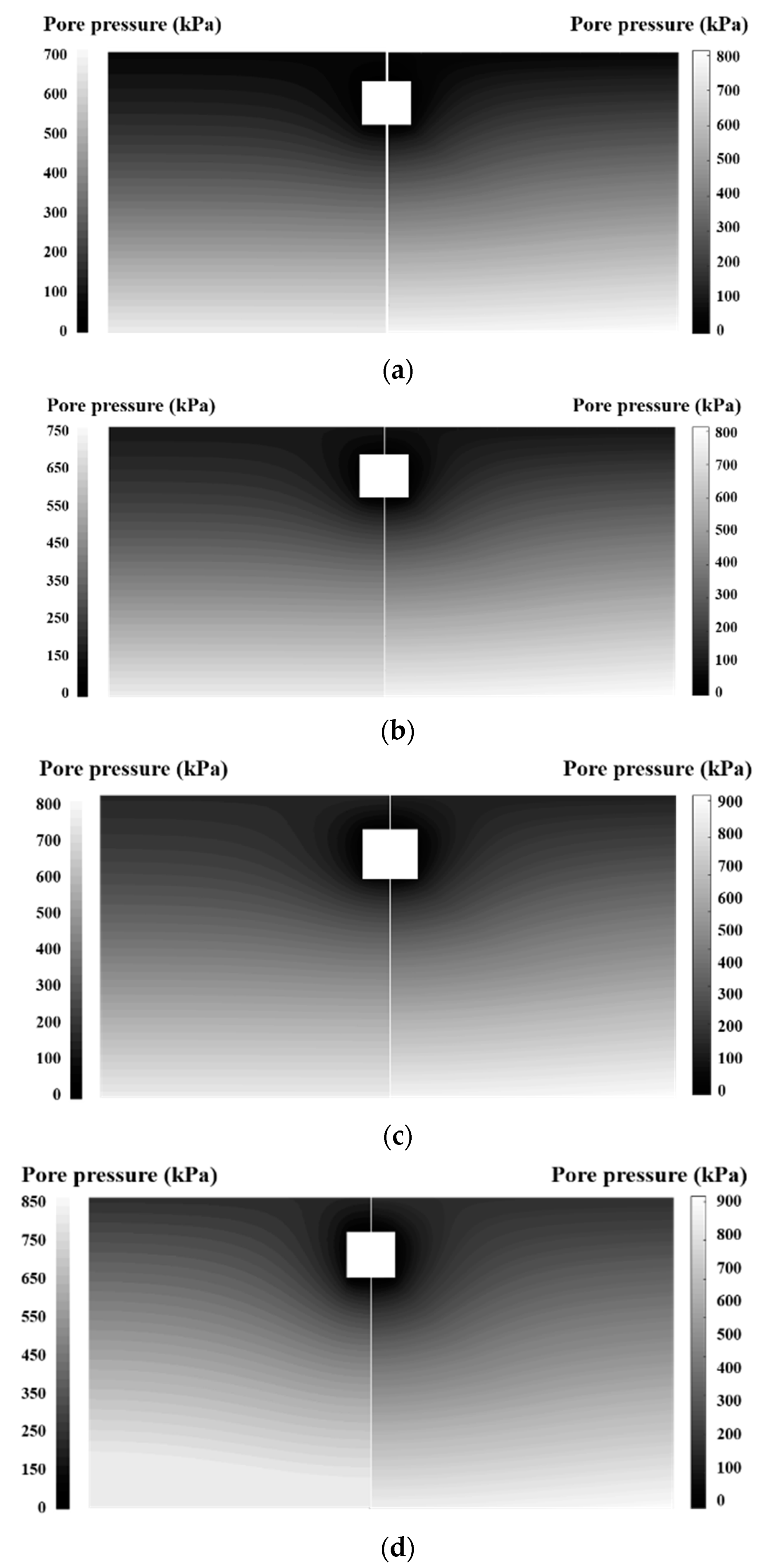
3.1. Verification in Terms of Pore-Pressure Distributions
3.2. Verification in Terms of Existing Solutions
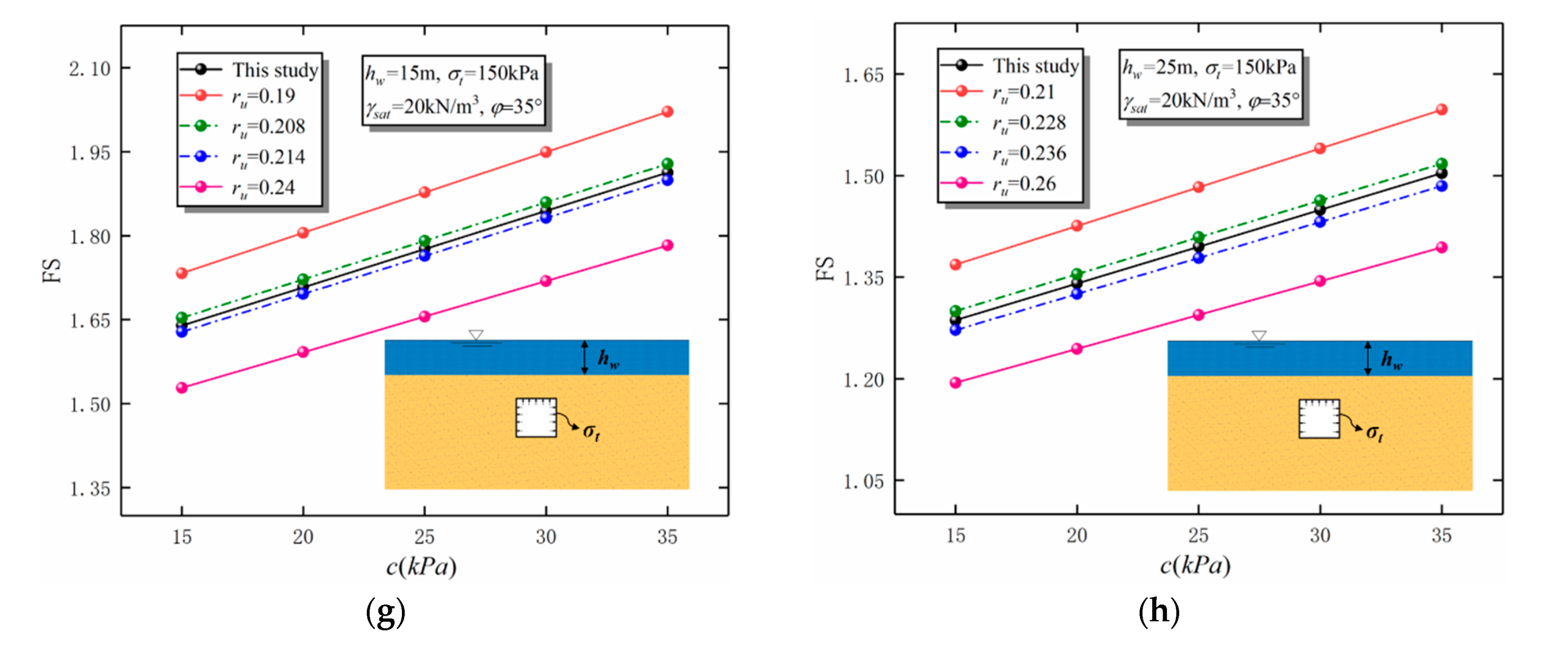
4. Comparisons and Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Broere, W. Urban underground space: Solving the problems of today’s cities. Tunn. Undergr. Space Technol. 2016, 55, 245–248. [Google Scholar] [CrossRef]
- Lv, Y.; Jiang, Y.; Hu, W.; Cao, M.; Mao, Y. A review of the effects of tunnel excavation on the hydrology, ecology, and environment in karst areas: Current status, challenges, and perspectives. J. Hydrol. 2020, 586, 124891. [Google Scholar] [CrossRef]
- Bhattacharya, P.; Dutta, P. Stability of rectangular tunnel in Hoek–Brown rocks under steady-state groundwater flow. Geotech. Lett. 2020, 10, 524–534. [Google Scholar] [CrossRef]
- Dutta, P.; Bhattacharya, P. Stability of rectangular tunnels in weathered rock subjected to seepage forces. Arab. J. Geosci 2022, 15, 61. [Google Scholar] [CrossRef]
- Qin, C.; Chian, S.C. Revisiting crown stability of tunnels deeply buried in non-uniform rock surrounds. Tunn. Undergr. Space Technol. 2018, 73, 154–161. [Google Scholar] [CrossRef]
- Qian, Z.H.; Zou, J.F.; Pan, Q.J. Blowout analysis of shallow elliptical tunnel faces in frictional-cohesive soils. Tunn. Undergr. Space Technol. 2023, 136, 105070. [Google Scholar] [CrossRef]
- Lee, C.J.; Wu, B.R.; Chen, H.T.; Chiang, K.H. Tunnel stability and arching effects during tunneling in soft clayey soil. Tunn. Undergr. Space Technol. 2006, 21, 119–132. [Google Scholar] [CrossRef]
- Wu, B.R.; Lee, C.J. Ground movements and collapse mechanisms induced by tunneling in clayey soil. Int. J. Phys. Model. Geotech. 2003, 3, 15–29. [Google Scholar] [CrossRef]
- Coggan, J.; Gao, F.; Stead, D.; Elmo, D. Numerical modelling of the effects of weak immediate roof lithology on coal mine roadway stability. Int. J. Coal Geol. 2012, 90, 100–109. [Google Scholar] [CrossRef]
- Funatsu, T.; Hoshino, T.; Sawae, H.; Shimizu, N. Numerical analysis to better understand the mechanism of the effects of ground supports and reinforcements on the stability of tunnels using the distinct element method. Tunn. Undergr. Space Technol. 2008, 23, 561–573. [Google Scholar] [CrossRef]
- Verma, A.K.; Singh, T.N. Assessment of tunnel instability—A numerical approach. Arab. J. Geosci. 2010, 3, 181–192. [Google Scholar] [CrossRef]
- Chen, W.F. Limit Analysis and Soil Plasticity; J. Ross Publishing: Amsterdam, Netherlands, 2007. [Google Scholar]
- Davis, E.H.; Gunn, M.J.; Mair, R.J.; Seneviratine, H.N. The stability of shallow tunnels and underground openings in cohesive material. Geotechnique 1980, 30, 397–416. [Google Scholar] [CrossRef]
- Yang, F.; Yang, J.S. Limit analysis method for determination of earth pressure on shallow tunnel. Eng. Mech. 2008, 25, 179–184. (In Chinese) [Google Scholar]
- Fraldi, M.; Guarracino, F. Analytical solutions for collapse mechanisms in tunnels with arbitrary cross sections. Int. J. Solids Struct. 2010, 47, 216–223. [Google Scholar] [CrossRef]
- Assadi, A.; Sloan, S.W. Undrained stability of shallow square tunnel. Int. J. Geotech. Eng. 1991, 117, 1152–1173. [Google Scholar] [CrossRef]
- Sloan, S.W.; Assadi, A. Undrained stability of a square tunnel in a soil whose strength increases linearly with depth. Comput. Geotech. 1991, 12, 321–346. [Google Scholar] [CrossRef]
- Wilson, D.W.; Abbo, A.J.; Sloan, S.W.; Lyamin, A.V. Undrained stability of a square tunnel where the shear strength increases linearly with depth. Comput. Geotech. 2013, 49, 314–325. [Google Scholar] [CrossRef]
- Di, Q.; Li, P.; Zhang, M.; Guo, C.; Wang, F.; Wu, J. Three-dimensional theoretical analysis of seepage field in front of shield tunnel face. Undergr. Space 2022, 7, 528–542. [Google Scholar] [CrossRef]
- Li, P.; Wang, F.; Long, Y.; Zhao, X. Investigation of steady water inflow into a subsea grouted tunnel. Tunn. Undergr. Space Technol. 2018, 80, 92–102. [Google Scholar] [CrossRef]
- Li, W.; Zhang, C.; Tan, Z.; Ma, M. Effect of the seepage flow on the face stability of a shield tunnel. Tunn. Undergr. Space Technol. 2021, 112, 103900. [Google Scholar] [CrossRef]
- Pan, Q.; Dias, D. The effect of pore water pressure on tunnel face stability. Int. J. Numer. Anal. Methods Geomech. 2016, 40, 2123–2136. [Google Scholar] [CrossRef]
- Huang, F.; Yang, X.L. Upper bound limit analysis of collapse shape for circular tunnel subjected to pore pressure based on the Hoek–Brown failure criterion. Tunn. Undergr. Space Technol. 2011, 26, 614–618. [Google Scholar] [CrossRef]
- Qin, C.; Chian, S.C.; Yang, X.; Du, D. 2D and 3D limit analysis of progressive collapse mechanism for deep-buried tunnels under the condition of varying water table. Int. J. Rock Mech. Min. Sci 2015, 80, 255–264. [Google Scholar] [CrossRef]
- Yang, X.L.; Yao, C. Stability of tunnel roof in nonhomogeneous soils. Int. J. Geomech. 2018, 18, 06018002. [Google Scholar] [CrossRef]
- Du, D.; Dias, D.; Yang, X. Analysis of earth pressure for shallow square tunnels in anisotropic and non-homogeneous soils. Comput. Geotech. 2018, 104, 226–236. [Google Scholar] [CrossRef]
- Bishop, A.W.; Morgenstern, N. Stability coefficients for earth slopes. Geotechnique 1960, 10, 129–153. [Google Scholar] [CrossRef]
- Michalowski, R.L. Slope stability analysis: A kinematical approach. Geotechnique 1995, 45, 283–293. [Google Scholar] [CrossRef]
- Viratjandr, C.; Michalowski, R.L. Limit analysis of submerged slopes subjected to water drawdown. Can. Geotech. J. 2006, 43, 802–814. [Google Scholar] [CrossRef]
- Mollon, G.; Dias, D.; Soubra, A.H. Rotational failure mechanisms for the face stability analysis of tunnels driven by a pressurized shield. J. Numer. Anal. Methods Geomech. 2011, 35, 1363–1388. [Google Scholar] [CrossRef]
- Pan, Q.; Dias, D. Three dimensional face stability of a tunnel in weak rock masses subjected to seepage forces. Tunn. Undergr. Space Technol. 2018, 71, 555–566. [Google Scholar] [CrossRef]
- Park, D.; Michalowski, R.L. Three-dimensional stability analysis of slopes in hard soil/soft rock with tensile strength cut-off. Eng. Geol. 2017, 229, 73–84. [Google Scholar] [CrossRef]
- Qian, Z.; Zou, J.; Pan, Q.; Dias, D. Safety factor calculations of a tunnel face reinforced with umbrella pipes. A comparison analysis. Eng. Struct. 2019, 199, 109639. [Google Scholar] [CrossRef]
- Qian, Z.H.; Zou, J.F.; Pan, Q.J.; Chen, G.H.; Liu, S.X. Discretization-based kinematical analysis of three-dimensional seismic active earth pressures under nonlinear failure criterion. Comput. Geotech. 2020, 126, 1037l. [Google Scholar] [CrossRef]
- Qian, Z.H.; Zou, J.F.; Pan, Q.J. 3D discretized rotational failure mechanism for slope stability analysis. Int. J. Geomech. 2021, 21, 04021210. [Google Scholar] [CrossRef]
- Huang, M.S.; Wang, H.; Sheng, D.; Liu, Y. Rotational-translational mechanism for the upper bound stability analysis of slopes with weak interlayer. Comput. Geotech. 2013, 53, 133–141. [Google Scholar] [CrossRef]
- Michalowski, R.L.; Drescher, A. Three-dimensional stability of slopes and excavations. Géotechnique 2009, 59, 839–850. [Google Scholar] [CrossRef]
- Japan Society of Civil Engineers. Japanese Standard for Shield Tunneling; Zhu, W., Translator; China Construction Industry Press: Beijing, China, 2001. (In Chinese) [Google Scholar]
- Zhang, W.; Liu, X.; Liu, Z.; Zhu, Y.; Huang, Y.; Taerwe, L.; De Corte, W. Investigation of the pressure distributions around quasi-rectangular shield tunnels in soft soils with a shallow overburden: A field study. Tunn. Undergr. Space Technol. 2022, 130, 104742. [Google Scholar] [CrossRef]
- Pan, Q.; Dias, D. Safety factor assessment of a tunnel face reinforced by horizontal dowels. Eng. Struct. 2017, 142, 56–66. [Google Scholar] [CrossRef]
- Harr, M.E. Groundwater and Seepage; Courier Corporation: North Chelmsford, MA, USA, 1991. [Google Scholar]
- Huangfu, M.; Wang, M.S.; Tan, Z.S.; Wang, X.Y. Analytical solutions for steady seepage into an underwater circular tunnel. Tunn. Undergr. Space Technol. 2010, 25, 391–396. [Google Scholar] [CrossRef]
- Verruijt, A. A complex variable solution for a deforming circular tunnel in an elastic half-plane. Int. J. Numer. Anal. Methods Geomech. 1997, 21, 77–89. [Google Scholar] [CrossRef]
- Guang-Qin, F.; Deng-Bo, T. Determination of the mapping function for the exterior domain of a non-circular opening by means of the multiplication of three absolutely convergent series. Chin. J. Rock Mech. Eng. 1993, 12, 255–274. (In Chinese) [Google Scholar]
- Zhu, D.; Cai, Y. Method of approaching analytical solution to elastic stress field of an infinite plane containing a single hole. Chin. J. Rock Mech. Eng. 2017, 36, 705–715. (In Chinese) [Google Scholar]
- Box, M.J. A new method of constrained optimization and a comparison with other methods. Comput. J. 1965, 8, 42–52. [Google Scholar] [CrossRef]
- Lu, A.; Wang, Q. New method of determination for the mapping function of tunnel with arbitrary boundary using optimization techniques. Chin. J. Rock Mech. Eng. 1995, 14, 269–274. (In Chinese) [Google Scholar]
- Umeda, T.; Ichikawa, A. A modified complex method for optimization. Ind. Eng. Chem. Process Des. Dev. 1971, 10, 229–236. [Google Scholar] [CrossRef]






| Case | Name | Section Size | Buried Depth | Water Height |
|---|---|---|---|---|
| 1 | Thames Tunnel | 11.4 m × 6.8 m | 4 m | 19 m |
| 2 | Shenzhen Metro Line 8 | 11.8 m × 7.2 m | 4.9 m | / |
| 3 | Underpass of Huguang Road, Xiamen | 17.7 m × 6.2 m | 3 m | / |
| 4 | Hejiangtao tunnel in Hengyang, Hunan | 11.83 m × 7.27 m | 15 m | 8 m |
| 5 | Kunming Metro Line 3 | 11.6 m × 7 m | 6.4 m | / |
| 6 | Guangzhou Metro Line 6 | 6 m × 4.3 m | 4.7 m | / |
| 7 | Urumqi Underground Commercial Street | 20 m × 6 m | 4.9 m | / |
| Case | (kPa) | (degrees) | Du et al. [26] | This Study | Difference (%) | |
|---|---|---|---|---|---|---|
(kPa) | Safety Factor (FS) | |||||
| Dry soil condition | 10 | 15 | / | 186.4 (FS = 1) | 0.946 | 5.4 |
| 18 | / | 158.3 (FS = 1) | 0.980 | 2.0 | ||
| 21 | / | 135.0 (FS = 1) | 1.045 | 4.5 | ||
| 24 | / | 114.3 (FS = 1) | 1.105 | 10.5 | ||
| Saturated soil | 20 | 18 | 0.40 | 158.2 (FS = 1) | 1.161 | 16.1 |
| 0.45 | 156.4 (FS = 1) | 1.156 | 15.6 |
| Case | (degree) | (kPa) | |||
|---|---|---|---|---|---|
| 1 | 20 | 15 | 15~35 | 0.275 | 0.290 |
| 2 | 20 | 25 | 15~35 | 0.295 | 0.312 |
| 3 | 25 | 15 | 15~35 | 0.252 | 0.264 |
| 4 | 25 | 25 | 15~35 | 0.274 | 0.282 |
| 5 | 30 | 15 | 15~35 | 0.231 | 0.238 |
| 6 | 30 | 25 | 15~35 | 0.250 | 0.258 |
| 7 | 35 | 15 | 15~35 | 0.208 | 0.214 |
| 8 | 35 | 25 | 15~35 | 0.228 | 0.236 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peng, Z.-Z.; Qian, Z.-H. A New Kinematical Admissible Translational–Rotational Failure Mechanism Coupling with the Complex Variable Method for Stability Analyses of Saturated Shallow Square Tunnels. Buildings 2023, 13, 1246. https://doi.org/10.3390/buildings13051246
Peng Z-Z, Qian Z-H. A New Kinematical Admissible Translational–Rotational Failure Mechanism Coupling with the Complex Variable Method for Stability Analyses of Saturated Shallow Square Tunnels. Buildings. 2023; 13(5):1246. https://doi.org/10.3390/buildings13051246
Chicago/Turabian StylePeng, Zhong-Zheng, and Ze-Hang Qian. 2023. "A New Kinematical Admissible Translational–Rotational Failure Mechanism Coupling with the Complex Variable Method for Stability Analyses of Saturated Shallow Square Tunnels" Buildings 13, no. 5: 1246. https://doi.org/10.3390/buildings13051246
APA StylePeng, Z.-Z., & Qian, Z.-H. (2023). A New Kinematical Admissible Translational–Rotational Failure Mechanism Coupling with the Complex Variable Method for Stability Analyses of Saturated Shallow Square Tunnels. Buildings, 13(5), 1246. https://doi.org/10.3390/buildings13051246





