Bearing Capacity of Transmission Poles under Combined Wind and Rain Excitations Based on the Deep Learning Method †
Abstract
1. Introduction
2. Ultimate Bearing Capacity of TPs under Combined Wind and Rainfall Effects
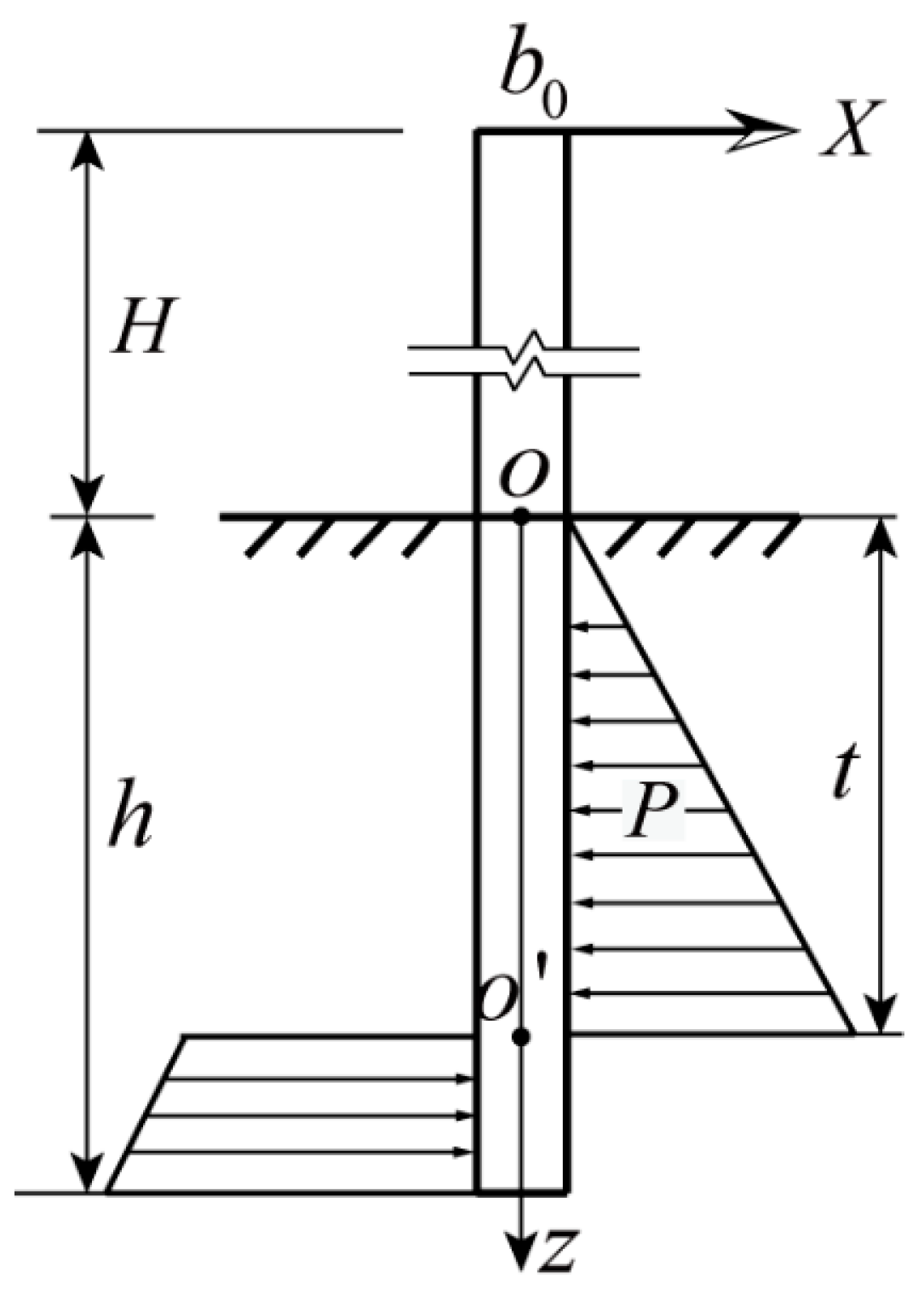
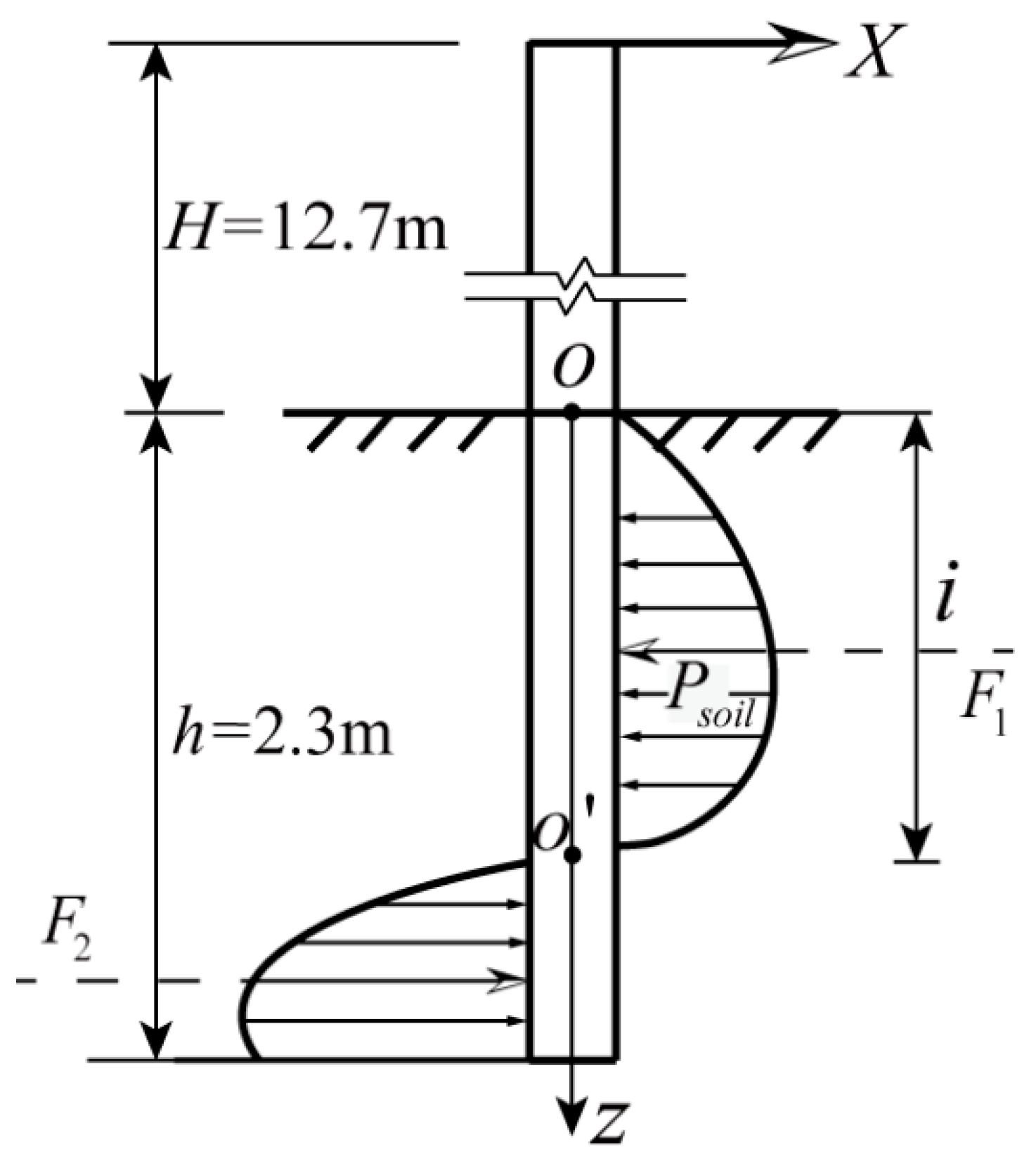
2.1. Ultimate Overturning Moment in the Current Code
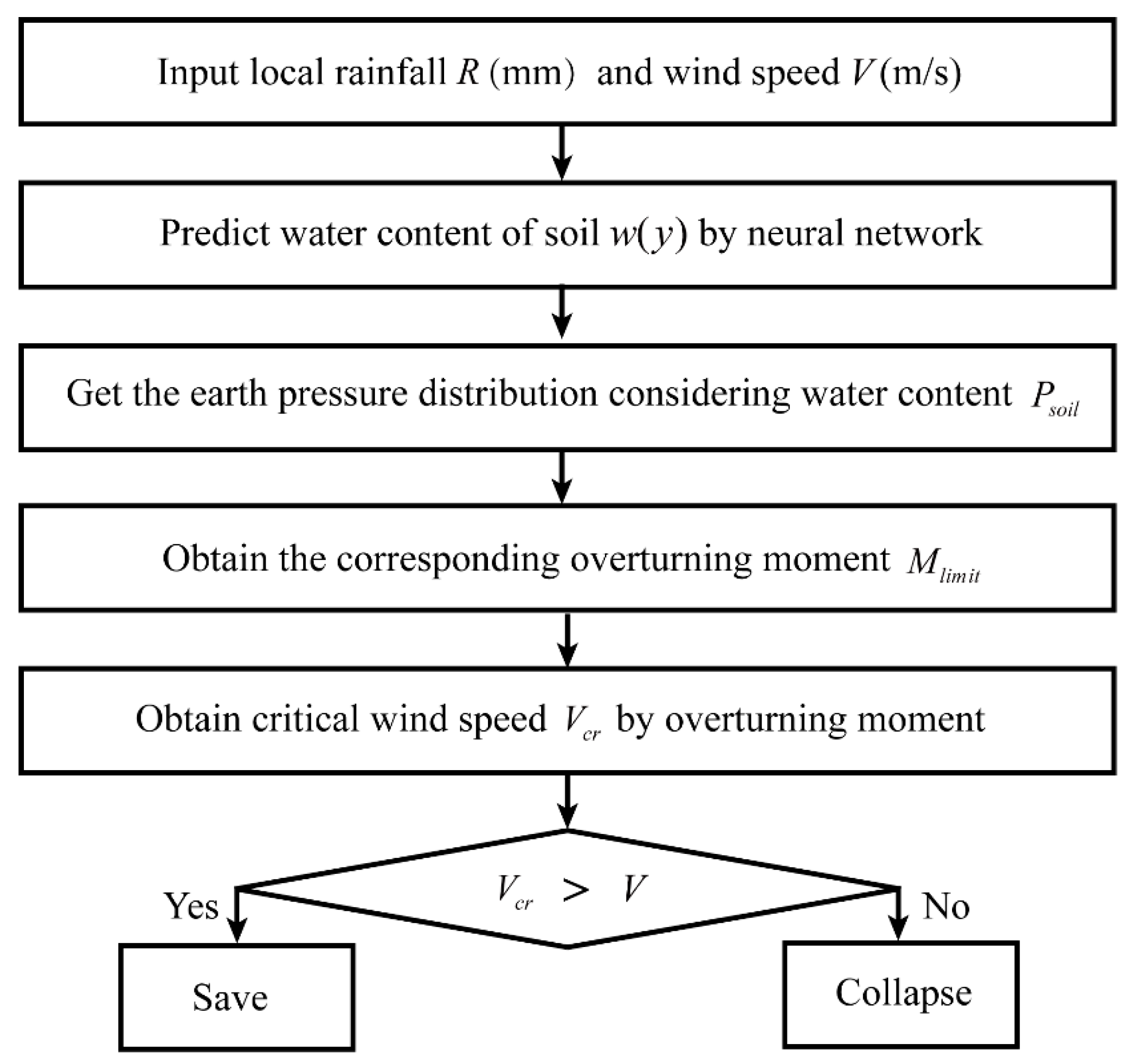
2.2. Evaluation Framework of the Pole-Line System under Rainfall
3. Prediction of the Earth Pressure Distribution after Rainfall Based on the Deep Learning Theory
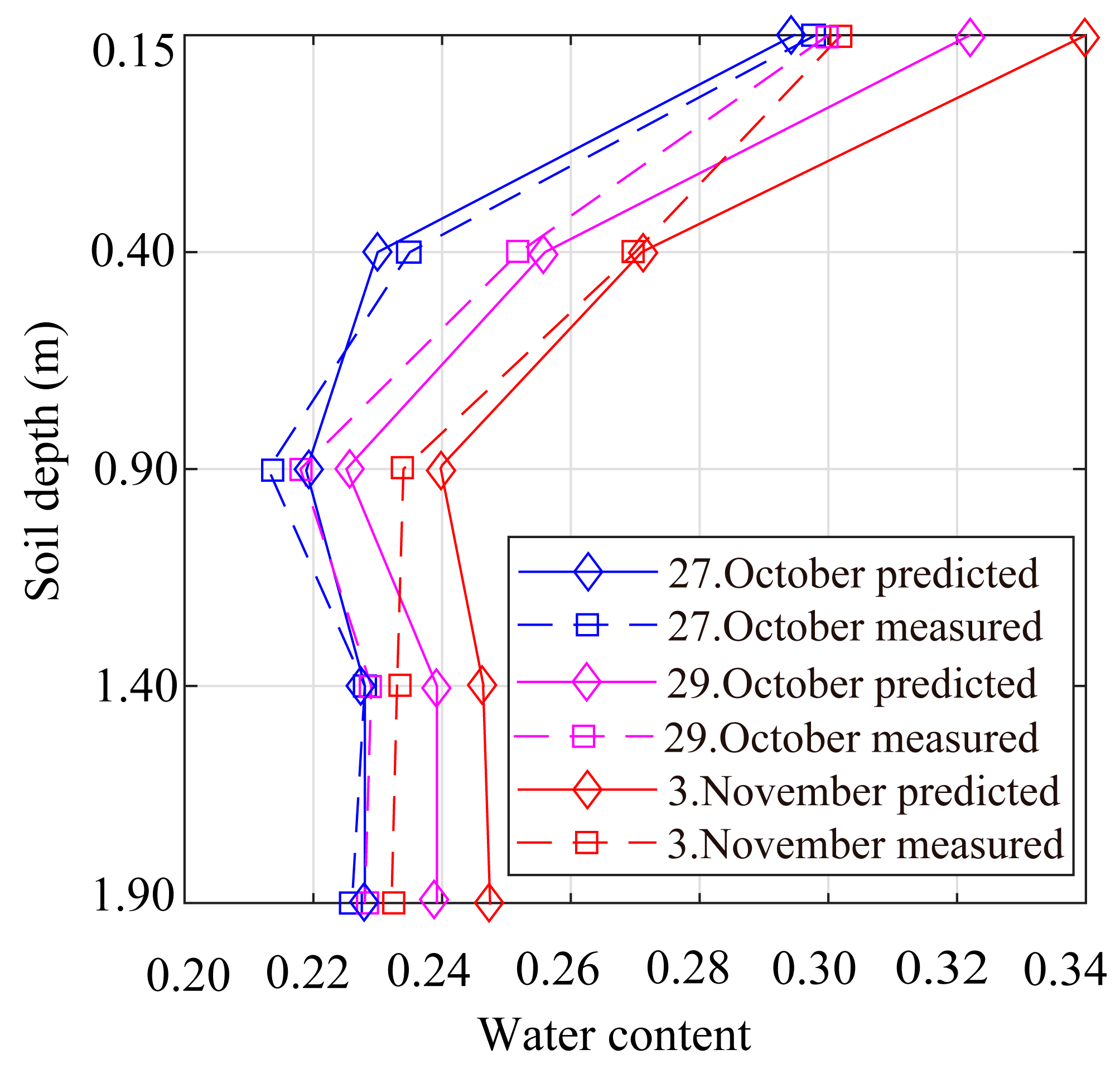
3.1. Neural Network Analysis for Rainfall and Water Content
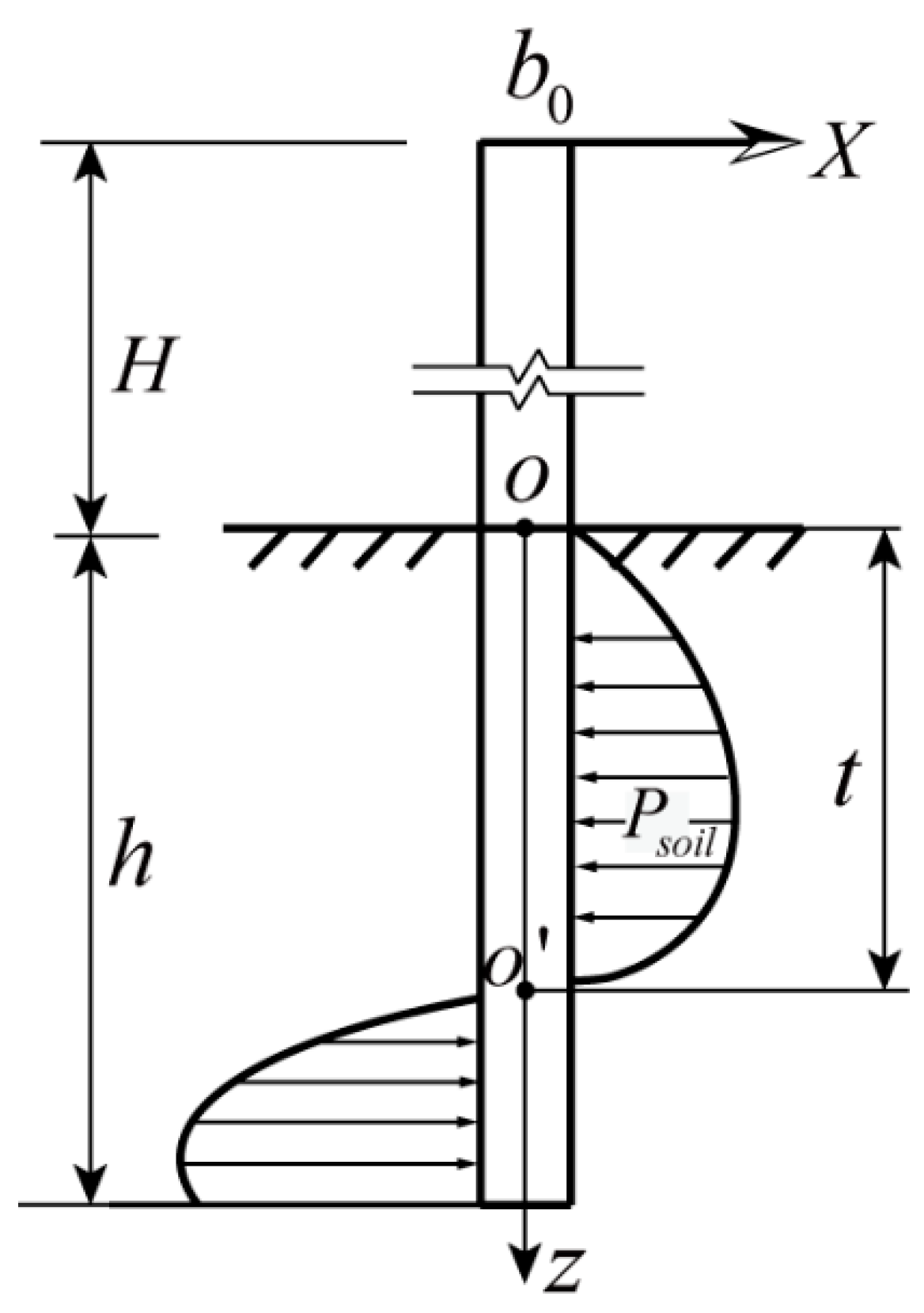
3.2. Mechanical Properties of the Soil after Rainfall
3.3. Ultimate Overturning Moment Considering the Rainfall Effect
4. Performance Estimation of a TP under Combined Wind and Rain Excitations
4.1. Finite Element Model
4.2. Dynamic Structural Analysis
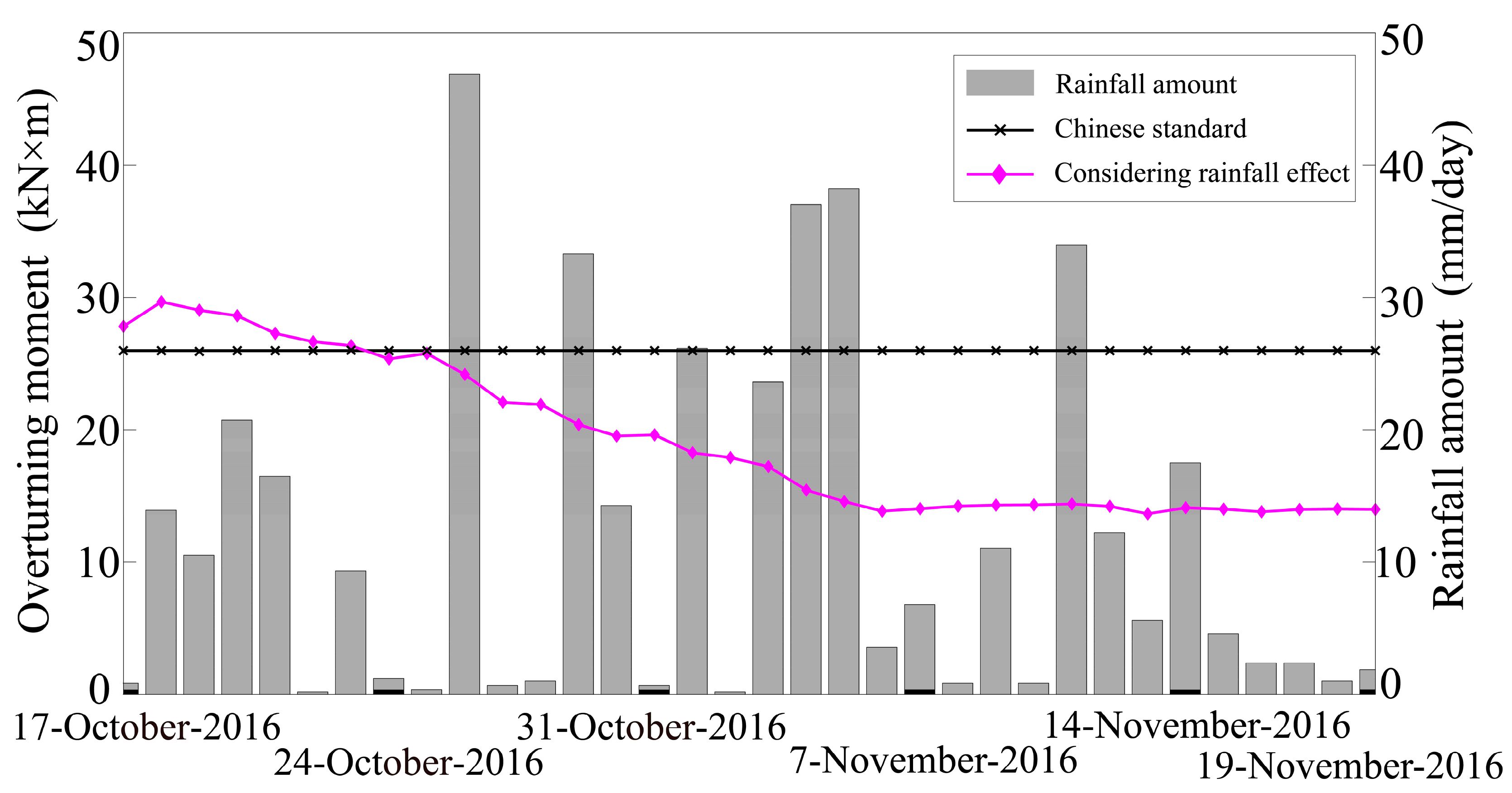
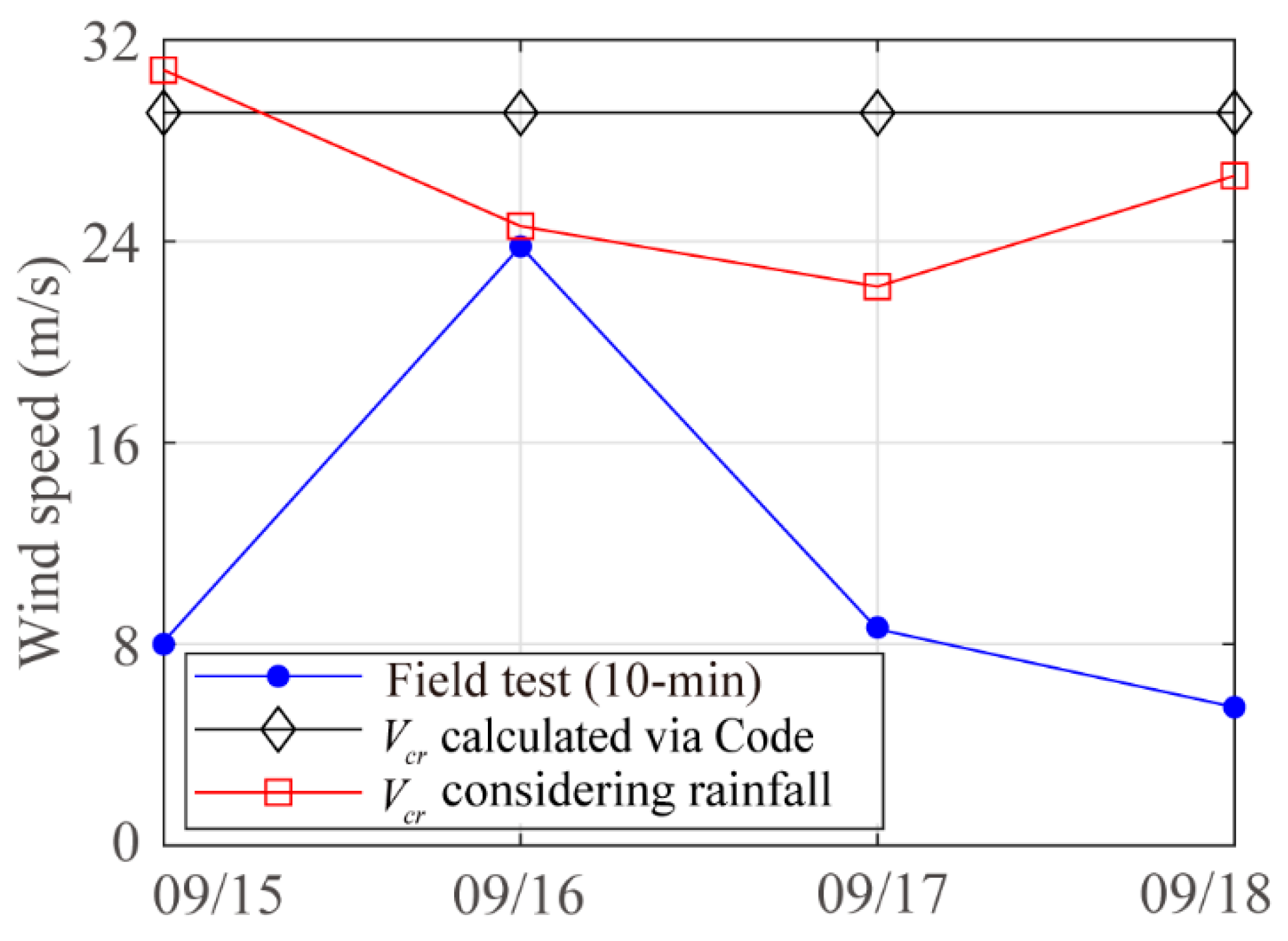
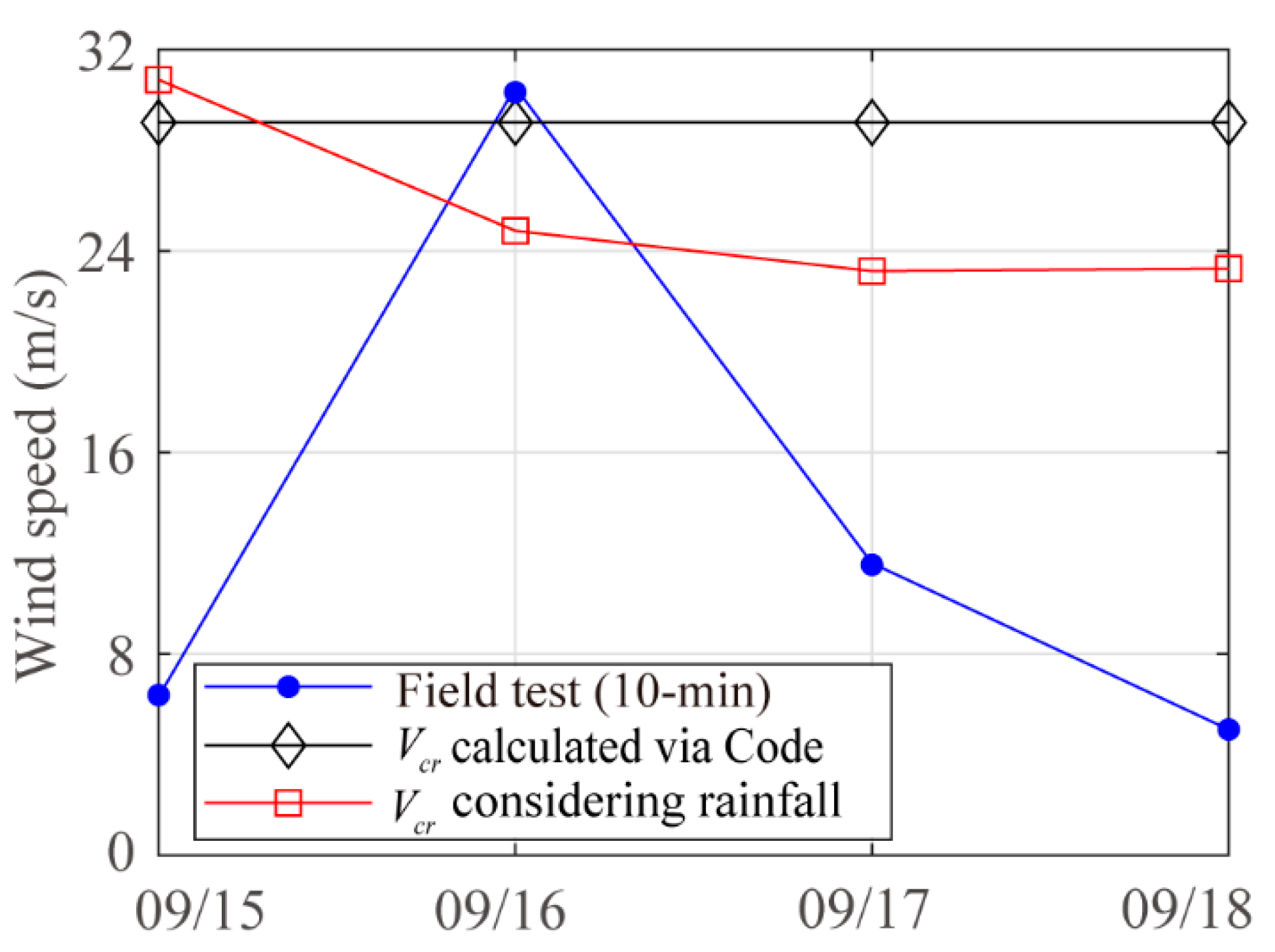
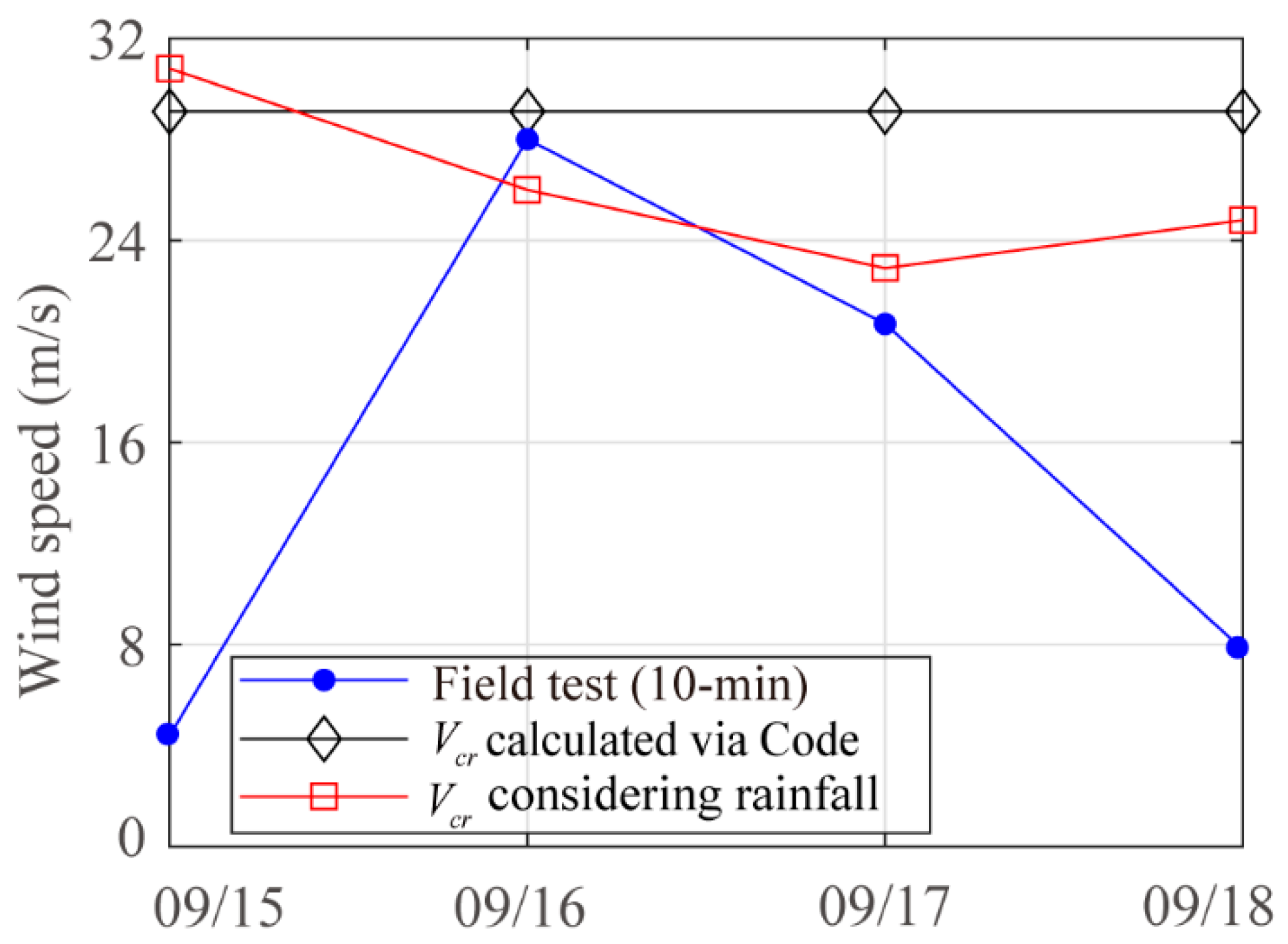
4.3. Collapse Analysis of TPs during the Typhoon Landing
- (1)
- Collapse evaluation for G2990 station.
- (2)
- Collapse evaluation for G1844 station.
- (3)
- Collapse evaluation for G2133 station.
5. Summary and Conclusions
- (1)
- The soil water content is influenced by both the amount and duration of rainfall, which are negatively correlated with the bearing capacity of TPs.
- (2)
- The rainfall effect has a significant impact on the bearing capacity of TPs, and the critical wind speed of TPs will be overestimated if the effect of rainfall is ignored.
- (3)
- For the same typhoon event, different regions give different estimation results, which is mainly caused by the diversity of rainfall events in different locations.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Fu, X.; Li, H.N.; Li, G.; Dong, Z.Q.; Zhao, M. Failure analysis of a transmission line considering the joint probability distribution of wind speed and rain intensity. Eng. Struct. 2021, 233, 11913. [Google Scholar] [CrossRef]
- Choi, M.-G.; Yun, S.; Choi, J.-H.; Ahn, S.-J. A study on the installation of automatic switches considering the characteristics of distribution feeder and importance of customer. Trans. Korean Inst. Electr. Eng. 2019, 68, 1176–1183. [Google Scholar] [CrossRef]
- Fu, X.; Li, H.N.; Wang, J. Failure analysis of a transmission tower subjected to combined wind and rainfall excitations. Struct. Des. Tall Spec. Build. 2019, 28, e1615. [Google Scholar] [CrossRef]
- Zhang, M.; Liu, Y.; Liu, H.; Zhao, G. Dynamic response of an overhead transmission tower-line system to high-speed train-induced wind. Wind Struct. 2022, 34, 335–353. [Google Scholar] [CrossRef]
- Lou, W.; Bai, H.; Huang, M.; Duan, Z.; Bian, R. Wind field generation for performance-based structural design of transmission lines in a mountainous area. Wind Struct. 2020, 31, 165–183. [Google Scholar]
- Yang, S.C.; Liu, T.J.; Hong, H.P. Reliability of tower and tower-Line systems under spatiotemporally varying wind or earthquake loads. J. Struct. Eng. 2017, 143, 04017137. [Google Scholar] [CrossRef]
- He, B.; Zhao, M.X.; Feng, W.T.; Xiu, Y.P.; Wang, Y.; Feng, L.J. A method for analyzing stability of tower-line system under strong winds. Adv. Eng. Softw. 2019, 127, 1–7. [Google Scholar] [CrossRef]
- Sharma, P.; Chen, Z.Q. Probabilistic resilience measurement for rural electric distribution system affected by hurricane events. ASCE-ASME J. Risk Uncertain. Eng. Syst. Part A Civ. Eng. 2020, 6, 04020021. [Google Scholar] [CrossRef]
- Bjarnadottir, S.; Li, Y.; Stewart, M.G. Hurricane risk assessment of power distribution poles considering impacts of a changing climate. J. Infrastruct. Syst. 2013, 19, 12–24. [Google Scholar] [CrossRef]
- Han, S.R.; Rosowsky, D.; Guikema, S. Integrating models and data to estimate the structural reliability of utility poles during hurricanes. Risk Anal. 2014, 34, 1079–1094. [Google Scholar] [CrossRef]
- Dai, K.S.; Chen, S.E.; Luo, M.Y.; Loflin, G., Jr. A framework for holistic designs of power line systems based on lessons learned from super typhoon Haiyan. Sustain. Cities Soc. 2017, 35, 350–364. [Google Scholar] [CrossRef]
- Hou, H.; Zhang, Z.W.; Wei, R.Z.; Huang, Y.; Liang, Y.C.; Li, X.Q. Review of failure risk and outage prediction in power system under wind hazards. Electr. Power Syst. Res. 2022, 210, 108098. [Google Scholar] [CrossRef]
- Nguyen, H.T.; Muhs, J.W.; Parvania, M. Assessing impacts of energy storage on resilience of distribution systems against hurricanes. J. Mod. Power Syst. Clean Energy 2019, 7, 731–740. [Google Scholar] [CrossRef]
- Lee, S.L.; Ham, Y. Probabilistic framework for assessing the vulnerability of power distribution infrastructures under extreme wind conditions. Sustain. Cities Soc. 2021, 65, 102587. [Google Scholar] [CrossRef]
- Yuan, H.; Zhang, W.; Zhu, J.; Bagtzoglou, A.C. Resilience assessment of overhead power distribution systems under strong winds for hardening prioritization. ASCE-ASME J. Risk Uncertain. Eng. Syst. Part A Civ. Eng. 2018, 4, 04018037. [Google Scholar] [CrossRef]
- Vivek, B.; Sharma, S.; Raychowdhury, P.; Ray-Chaudhri, S. A study on failure mechanism of self-supported electric poles through full-scale field testing. Eng. Fail. Anal. 2017, 77, 102–117. [Google Scholar] [CrossRef]
- Fu, X.; Xu, X.; Li, H.N.; Li, G. Bearing capacity of transmission poles under combined wind and rain excitations based on the deep learning method. In Proceedings of the 2022 World Congress on Advances in Structures Engineering and Mechanics, Seoul, Republic of Korea, 16–19 August 2022. [Google Scholar]
- Deng, Y.L.; Ge, S.X.; Lei, F. Effects of pounding and abutment behavior on seismic response of multi-span bridge considering abutment-soil-foundation-structure interactions. Buildings 2023, 13, 260. [Google Scholar] [CrossRef]
- Wang, Z.W.; Hong, B.N.; Liu, X.; Zhou, Q. Water-sensitive properties of shear strength of red clay. J. Sichuan Univ. Eng. Sci. Ed. 2011, 43, 17–22. [Google Scholar]
- Fu, X.H.; Wei, C.F.; Yan, R.T. Research on strength characteristics of unsaturated red clay. Rock Soil Mech. 2013, 34, 204–209. [Google Scholar]
- Cao, W.; Liu, T.; Xu, Z. Calculation of passive earth pressure using the simplified principal stress trajectory method on rigid retaining walls. Comput. Geotech. 2019, 109, 108–116. [Google Scholar] [CrossRef]
- Rankine, W.M. On the stability of loose earth. Proc. R. Soc. Lond. 1857, 147, 9–27. [Google Scholar]
- Fang, Y.S.; Chen, T.J.; Wu, B.F. Passive earth pressures with various wall movements. J. Geotech. Eng.-ASCE 1994, 120, 1307–1323. [Google Scholar] [CrossRef]
- Fang, Y.S.; Ishibashi, I. Static earth pressures with various wall movements. J. Geotech. Eng. 1986, 112, 317–333. [Google Scholar] [CrossRef]
- Yue, G.W.; Feng, F.; Jia, H.N. Numerical simulation of soil arching effect in deep foundation pit with different influencing factors. In Proceedings of the 2011 International Conference on Electrical and Control Engineering, Yichang, China, 16–18 September 2011. [Google Scholar]
- Xie, Y.; Zhang, B.; Liu, B.; Zeng, Z.; Zhang, Y.; Zheng, Y. Shrinkage cracking and strength deterioration of red clay under cyclic drying and wetting. Alex. Eng. J. 2022, 61, 2574–2588. [Google Scholar] [CrossRef]
- DL/T 5219-2014; Technical Regulation for Designing Foundation of Overhead Transmission Line. China Planning Press: Beijing, China, 2014.
- Long, W.X.; Chen, K.S.; Xiao, T.; Peng, X.P. Research of general triaxial test for unsaturated red clay. Rock Soil Mech. 2009, 30, 28–33. [Google Scholar]
- Shen, C.N.; Fang, X.W.; Wang, H.W.; Sun, S.G.; Guo, J.F. Research on effects of suction, water content and dry density on shear strength of remolded unsaturated soils. Rock Soil Mech. 2009, 30, 1347–1351. [Google Scholar]
- Gu, M.X.; Cai, X.C.; Fu, Q.; Li, H.B.; Wang, X.; Mao, B.B. Numerical analysis of passive piles under surcharge load in extensively deep soft soil. Buildings 2022, 12, 1988. [Google Scholar] [CrossRef]
- Thumtuan, P.; Chub Uppakarn, T.; Chalermyanont, T. Real time monitoring of soil moisture content for landslide early warning: Wn experimental study. MATEC Web Conf. 2018, 192, 02032. [Google Scholar] [CrossRef]
- Thumtuan, P. Southern Natural Disaster Research Center 2018. Available online: https://www.nadrec.psu.ac.th/ (accessed on 23 June 2023).
- Wang, J.S.; Xie, Y.Z.; Guo, T.; Du, Z.Y. Predicting the influence of soil-structure interaction on seismic responses of reinforced concrete frame buildings using convolutional neural network. Buildings 2023, 13, 564. [Google Scholar] [CrossRef]
- Ng, C.W.W.; Zhan, L.T.; Bao, C.G.; Fredlund, D.G.; Gong, B.W. Performance of an unsaturated expansive soil slope subjected to artificial rainfall infiltration. Geotechnique 2003, 53, 143–157. [Google Scholar] [CrossRef]
- Zhang, G.; Zhou, G.S.; Yang, F.L. Dynamics of sensible and latent heat fluxes over a temperate desert steppe ecosystem in Inner Mongolia. J. Appl. Ecol. 2010, 21, 597–603. [Google Scholar]
- Huang, Q.X.; Zhang, W.Z. Research on downward crack closing of clay aquiclude in shallow coal seam safety mining. J. Coal Sci. Eng. 2011, 17, 349–354. [Google Scholar] [CrossRef]
- Malizia, J.P.; Shakoor, A. Effect of water content and density on strength and deformation behavior of clay soils. Eng. Geol. 2018, 244, 125–131. [Google Scholar] [CrossRef]
- Ning, Q. Practical Technology for Overhead Distribution Lines; China Water Resources and Hydropower Publishing House: Beijing, China, 2009. [Google Scholar]
- Ryan, P.C.; Stewart, M.G.; Spencer, N.; Li, Y. Probabilistic analysis of climate change impacts on timber power pole networks. Int. J. Electr. Power Energy Syst. 2016, 78, 513–523. [Google Scholar] [CrossRef]
- Rao, N.P.; Gopal, R.B.; Rokade, R.P.; Mohan, S.J. Analytical and experimental studies on 400 and 132 kV steel transmission poles. Eng. Fail. Anal. 2011, 18, 1018–1029. [Google Scholar]
- Raychowdhury, P.; Hutchinson, T.C. Performance evaluation of a nonlinear Winkler-based shallow foundation model using centrifuge test results. Earthq. Eng. Struct. Dyn. 2009, 38, 679–698. [Google Scholar] [CrossRef]
- Ma, X.L.; Zhang, W.; Bagtzoglou, A.; Zhu, J. Local system modeling method for resilience assessment of overhead power distribution system under strong winds. ASCE-ASME J. Risk Uncertain. Eng. Syst. Part A Civ. Eng. 2021, 7, 04020053. [Google Scholar] [CrossRef]
- GB 4623-2014; Circular Concrete Pole. China Planning Press: Beijing, China, 2014.
- Ballaben, J.S.; Sampaio, R.; Rosales, M.B. Uncertainty quantification in the dynamics of a guyed mast subjected to wind load. Eng. Struct. 2017, 132, 456–470. [Google Scholar] [CrossRef]
- Davenport, A.G.; Stagg, J.M. The spectrum of horizontal gustiness near the ground in high winds. Q. J. R. Meteorol. Soc. 1962, 88, 197–198. [Google Scholar] [CrossRef]
- Fu, X.; Zhang, X.H.; Li, H.N.; Li, G.; Liu, H.J. A high-efficiency simulation method of wind field and its application on transmission line. Wind Struct. 2021, 33, 277–288. [Google Scholar] [CrossRef]
- Davenport, A.G.; Sparling, B.F. Dynamic gust response factors for guyed towers. J. Wind Eng. Ind. Aerodyn. 1992, 43, 2237–2248. [Google Scholar] [CrossRef]
- DL/T 5551-2018; Load Code for the Design of Overhead Transmission Line. China Planning Press: Beijing, China, 2018.
- Zhang, S.; Xu, Q.; Zhang, Q. Failure characteristics of gently inclined shallow landslides in Nanjiang, southwest of China. Eng. Geol. 2017, 217, 1–11. [Google Scholar] [CrossRef]
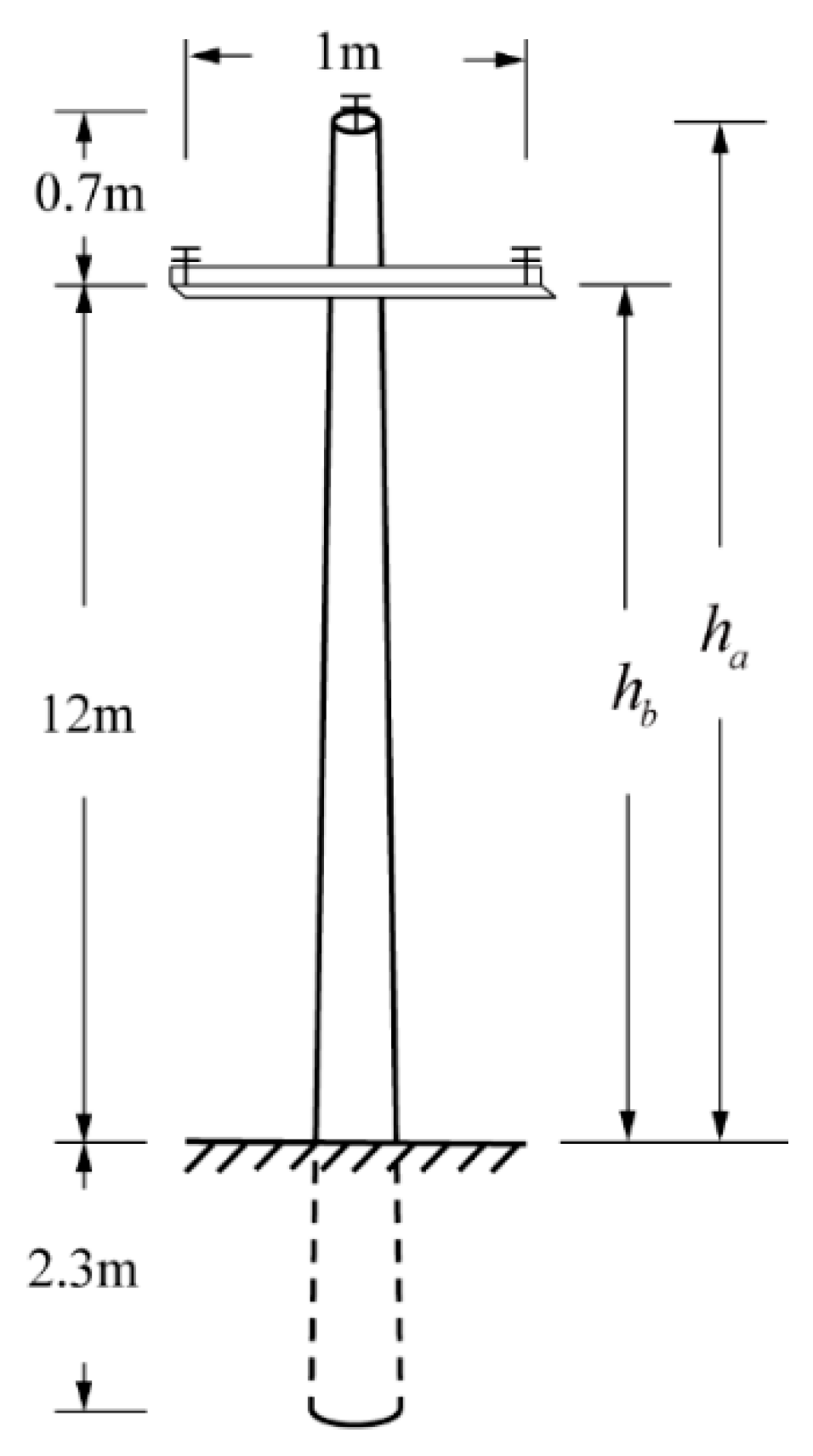
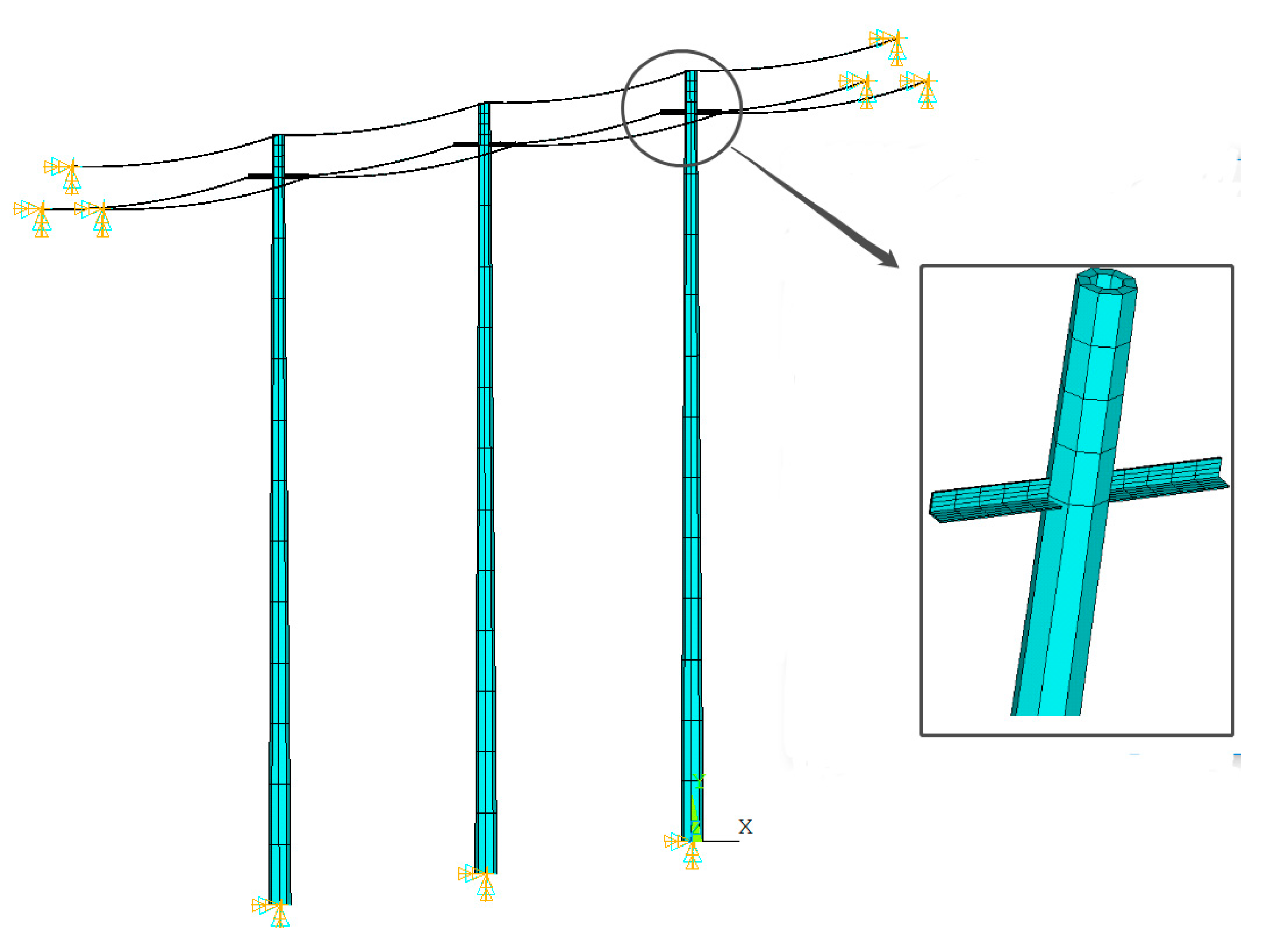



| Material | (kg/m3) | E (GPa) | |
|---|---|---|---|
| Pole | 2500 | 32.5 | 0.2 |
| Cross-arm | 7850 | 200 | 0.31 |
| Line | 2751 | 56 | 0.31 |
| Case No. | First Day (mm) | Second Day (mm) | Third Day (mm) | Fourth Day (mm) |
|---|---|---|---|---|
| Case 1 | 0 | 0 | 0 | 0 |
| Case 2 | 10 | 10 | 10 | 10 |
| Case 3 | 10 | 20 | 30 | 40 |
| Case 4 | 40 | 40 | 40 | 40 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fu, X.; Xu, X.; Liu, H.; Wang, W.; Zhu, D. Bearing Capacity of Transmission Poles under Combined Wind and Rain Excitations Based on the Deep Learning Method. Buildings 2023, 13, 1717. https://doi.org/10.3390/buildings13071717
Fu X, Xu X, Liu H, Wang W, Zhu D. Bearing Capacity of Transmission Poles under Combined Wind and Rain Excitations Based on the Deep Learning Method. Buildings. 2023; 13(7):1717. https://doi.org/10.3390/buildings13071717
Chicago/Turabian StyleFu, Xing, Xu Xu, Huijuan Liu, Wenming Wang, and Dengjie Zhu. 2023. "Bearing Capacity of Transmission Poles under Combined Wind and Rain Excitations Based on the Deep Learning Method" Buildings 13, no. 7: 1717. https://doi.org/10.3390/buildings13071717
APA StyleFu, X., Xu, X., Liu, H., Wang, W., & Zhu, D. (2023). Bearing Capacity of Transmission Poles under Combined Wind and Rain Excitations Based on the Deep Learning Method. Buildings, 13(7), 1717. https://doi.org/10.3390/buildings13071717







