NLFEA of Reinforced Concrete Corbels: Proposed Framework, Sensibility Study, and Precision Level
Abstract
1. Introduction
- Firstly, most previous studies were conducted using material constitutive models other than the Concrete Damaged Plasticity model (CDP), such as the total strain fixed or rotating cracking models. Therefore, it is unclear if modeling choices validated from other material models could be extended to the CDP model.
- In the same way, the influence of considering the elastic modulus degradation (damage evolution) in the ultimate capacity of RC corbels or not is generally not addressed. In fact, the proposed modeling approaches in the literature were frequently validated against specific experimental programs or a specific failure mechanism. Therefore, it is unclear if the presented modeling choices can be directly extended to simulate other RC corbels under the most complex boundary conditions, for which the governing failure mechanism may differ from that observed in the calibration process.
2. Background of the Concrete Damaged Plasticity Model
- (i)
- Stress–strain behavior models (including damage evolution): models that express the behavior of the yield criterion with the evolution of plastic deformation (uniaxial and triaxial behavior).
- (ii)
- Yield criterion: indicates (through the stress tensor) the stress level at which the plastification or yielding of the material will occur (the geometric representation of this is commonly called a failure surface);
- (iii)
- Plastic flow/flow rule: the law that defines the evolution of plastic strains according to the stress level after the yield criterion is achieved.
2.1. Stress–Strain Behavior Models: Hardening/Softening Law
2.2. Yield Criterion
2.3. Plastic Flow Rule
2.4. Summary of Input Parameters Required in CDP
- Ec—concrete elastic modulus and ν—Poisson coefficient;
- σt × εtin and σc × εcin: uniaxial stress—inelastic strain relationship of concrete in tension and compression;
- dt × εtin and dc × εcin: damage—inelastic strain relationship of concrete to tension and compression;
- σbu/σcu: ratio between biaxial and uniaxial compressive yield strengths;
- Kc—shape factor and e—eccentricity;
- ψ—dilation angle and μ—viscosity.
3. Control Tests for Modeling
4. Proposed Modeling Approach
4.1. Overview and Boundary Conditions
4.2. Concrete Modeling
4.3. Reinforcement Material Model
4.4. Mesh
4.5. Solution Procedure and Load Application
5. Validation of the Modeling Approach
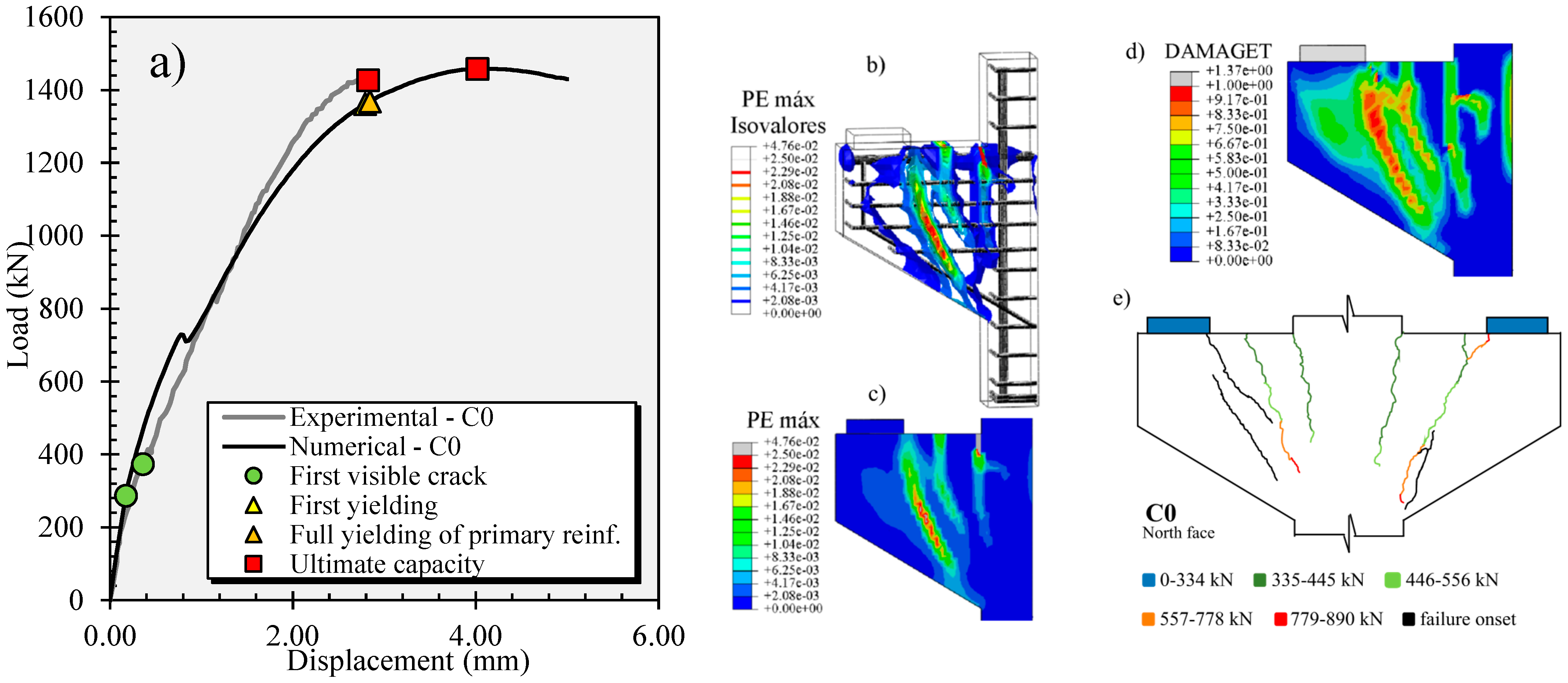
5.1. Load × Displacement Graphs
5.2. Cracking Pattern
5.3. Stresses in the Reinforcing Bars
6. Sensibility Study
6.1. Stress–Strain Behavior in Tensile
6.2. Stress–Strain Behavior in Compression
6.3. Damage Evolution Laws
6.4. Yield Criterion Parameters—σb0/σc0 and Kc
6.5. Plastic Flow Rule Parameters—e and ψ
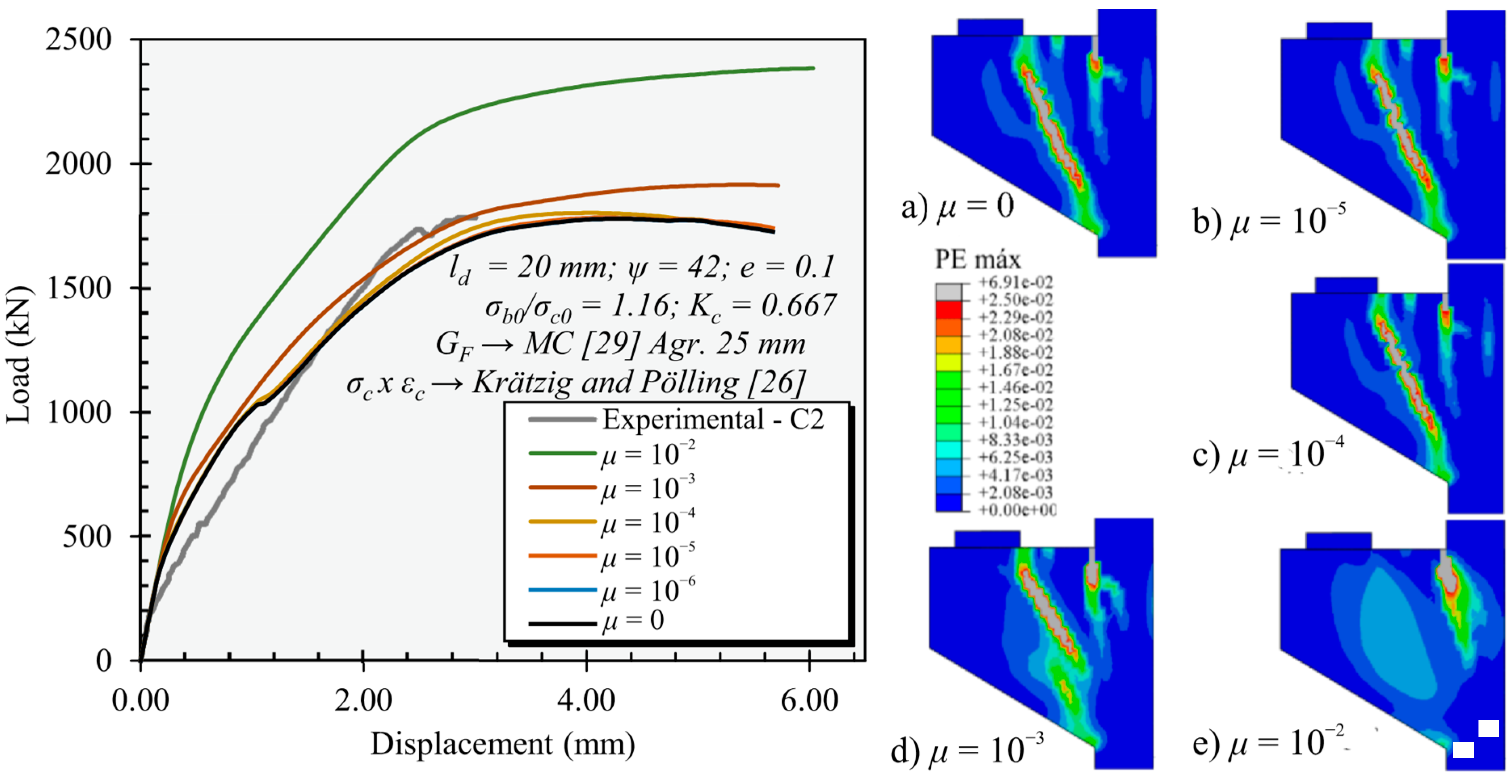
6.6. Viscoplastic Regularization Parameter—μ
7. Level of Accuracy for the Dataset
7.1. Test by Khosravikia et al. [5]
7.2. Tests by Fattuhi
7.3. Summary of the Accuracy Level of the NLFEA
8. Conclusions
- The shape factor Kc, the dilation angle ψ, and the viscosity parameter μ were the most influential parameters in the deformation and ultimate capacity of the numerical models of the RC corbels. After proper calibration, the chosen parameter values were allowed to accurately represent a reasonable number of test results from the literature.
- Values of viscosity parameters higher than 10−4 should be avoided because they significantly change the cracking pattern evolution and the corresponding ultimate capacity of the corbels. In practice, such values may increase the residual tensile and compressive strength of concrete and induce a larger influence zone for the cracks, changing the governing failure mechanisms of the numerical models.
- Different stress–strain behavior models in compression did not significantly change the ultimate capacity of the modeled corbels. This indicates that in practice, the tensile cracks also govern the capacity of the struts.
- The proposed framework for the NLFEA of reinforced concrete corbels was able to satisfactorily predict the global behavior of corbels with different geometries with an a/d varying from 0.4 to 1.4 and a compressive strength of concrete of 28 to 46 MPa.
- The numerical models allowed the accurate prediction of the ultimate loads of RC corbels with varied geometries and material properties. The average ratio between the predicted and tested resistances was 1.015 with a coefficient of variation of 8.57% for the databank, including 36 test results from the literature.
- Different failure mechanisms may govern the ultimate limit states of RC corbels. In this context, the proposed modeling approach allowed the correct prediction of the governing failure mechanism for approximately 88% of the test results. Therefore, an NLFEA can be used not only to assess the ultimate capacity but also to guide eventual strengthening tasks in existing corbels to indicate whether the primary reinforcement or the strut capacity should be improved.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Shu, J. Shear assessment of a reinforced concrete bridge deck slab according to level-of-approximation approach. Struct. Concr. 2018, 19, 1838–1850. [Google Scholar] [CrossRef]
- Lantsoght, E.O.L.; de Boer, A.; van der Veen, C. Distribution of peak shear stress in finite element models of reinforced concrete slabs. Eng. Struct. 2017, 148, 571–583. [Google Scholar] [CrossRef]
- De Sousa, A.M.D.; Lantsoght, E.O.L.; El Debs, M.K. Failure mechanism of one-way slabs under concentrated loads after local reinforcement yielding. Eng. Struct. 2023, 291, 116396. [Google Scholar] [CrossRef]
- Wilson, H.R.; Yousefpour, H.; Brown, M.D.; Bayrak, O. Investigation of Corbels Designed According to Strut-and-Tie and Empirical Methods. ACI Struct. J. 2018, 115, 813–824. [Google Scholar] [CrossRef]
- Khosravikia, F.; Kim, H.S.; Yi, Y.; Wilson, H.; Yousefpour, H.; Hrynyk, T.; Bayrak, O. Experimental and Numerical Assessment of Corbels Designed Based on Strut-and-Tie Provisions. J. Struct. Eng. 2018, 144, 04018138. [Google Scholar] [CrossRef]
- Canha, R.M.F.; Kuchma, D.A.; El Debs, M.K.; de Souza, R.A. Numerical analysis of reinforced high strength concrete corbels. Eng. Struct. 2014, 74, 130–144. [Google Scholar] [CrossRef]
- de Lima Araújo, D.; Azevedo Coelho, S.; Regina Mesquita de Almeida, S.; Khalil El Debs, M. Computational modelling and analytical model for two-step corbel for precast concrete system. Eng. Struct. 2021, 244, 112699. [Google Scholar] [CrossRef]
- Neuberger, Y.M.; Araújo, D.d.L. An improved analytical model for two-step corbels in a precast concrete system. Eng. Struct. 2023, 284, 115947. [Google Scholar] [CrossRef]
- Beshara, F.; Mustafa, T.; Mahmoud, A.; Khalil, M. Constitutive models for nonlinear analysis of SFRC corbels. J. Build. Eng. 2020, 28, 101092. [Google Scholar] [CrossRef]
- Syroka, E.; Bobiński, J.; Tejchman, J. FE analysis of reinforced concrete corbels with enhanced continuum models. Finite Elem. Anal. Des. 2011, 47, 1066–1078. [Google Scholar] [CrossRef]
- Genikomsou, A.S.; Polak, M.A. Finite element analysis of punching shear of concrete slabs using damaged plasticity model in ABAQUS. Eng. Struct. 2015, 98, 38–48. [Google Scholar] [CrossRef]
- De Sousa, A.M.; Lantsoght, E.O.; Genikomsou, A.S.; Krahl, P.A.; El Debs, M.K. Behavior and punching capacity of flat slabs with the rational use of UHPFRC: NLFEA and analytical predictions. Eng. Struct. 2021, 244, 112774. [Google Scholar] [CrossRef]
- Lubliner, J.; Oliver, J.; Oller, S.; Oñate, E. A plastic-damage model for concrete. Int. J. Solids Struct. 1989, 25, 299–326. [Google Scholar] [CrossRef]
- Lee, J.; Fenves, G.L. Plastic-Damage Model for Cyclic Loading of Concrete Structures. J. Eng. Mech. 1998, 124, 892–900. [Google Scholar] [CrossRef]
- Dassault Systems Simulia Corp. Abaqus Analysis User’s Manual 6.14; Dassault Systems Simulia Corp.: Providence, RI, USA, 2014. [Google Scholar]
- Cheng, H.; Paz, C.M.; Pinheiro, B.C.; Estefen, S.F. Experimentally based parameters applied to concrete damage plasticity model for strain hardening cementitious composite in sandwich pipes. Mater. Struct./Mater. Constr. 2020, 53, 78. [Google Scholar] [CrossRef]
- Krahl, P.A.; Carrazedo, R.; El Debs, M.K. Mechanical damage evolution in UHPFRC: Experimental and numerical investigation. Eng. Struct. 2018, 170, 63–77. [Google Scholar] [CrossRef]
- ACI Committee 318. Building Code Requirements for Structural Concrete (ACI 318-14) and Commentary; American Concrete Institute: Indianapolis, IN, USA, 2014; Volume 11, p. 6858. [Google Scholar]
- ASTM C39/C39M-17; Standard Test Method for Compressive Strength of Cylindrical Concrete Specimens. ASTM International: West Conshohocken, PA, USA, 2017.
- ASTM C469/469M-14; Standard Test Method for Static Modulus of Elasticity and Poisson’s Ratio of Concrete in Compression. ASTM International: West Conshohocken, PA, USA, 2014.
- ASTM C496/C496M-04; Standard Test Method for Splitting Tensile Strength of Cylindrical Concrete Specimens. ASTM International: West Conshohocken, PA, USA, 2004.
- ASTM A370-17; Standard Test Methods and Definitions for Mechanical Testing of Steel Products. ASTM International: West Conshohocken, PA, USA, 2017.
- Milligan, G.J.; Polak, M.A.; Zurell, C. Impact of Column Rectangularity on Punching Shear Strength: Code Predictions versus Finite Element Analysis. J. Struct. Eng. 2021, 147, 04020331. [Google Scholar] [CrossRef]
- Fédération Internationale du Béton (fib). fib Model Code for Concrete Structures 2010; Bulletin 65; Ernst & Sohn-Fédération Internationale Du Béton: Lausanne, Switzerland, 2012; Volume 1–2. [Google Scholar]
- EN 1992-1-1:2004 2004; EN 1992-1-1: Eurocode 2: Design of Concrete Structures -Part 1-1: General Rules and Rules for Buildings. CEN: Brussels, Belgium, 2004.
- Krätzig, W.B.; Pölling, R. An elasto-plastic damage model for reinforced concrete with minimum number of material parameters. Comput. Struct. 2004, 82, 1201–1215. [Google Scholar] [CrossRef]
- Oller, S. A continuous Damage Model for Frictional Materials. Ph.D. Thesis, Technical University of Catalonia, Barcelona, Spain, 1988. (In Spanish). [Google Scholar]
- Hordijk, D.A. Tensile and Tensile Fatigue Behaviour of Concrete—Experiments, Modelling and Analyses; Heron: Dronfield, UK, 1992; Volume 37, pp. 3–79. [Google Scholar]
- Comité Euro-International du Béton. CEB-FIP Model Code 1990: Design Code; Comité Euro-International du Béton: Luxembourg, 1993. [Google Scholar] [CrossRef]
- Yu, T.; Teng, J.G.; Wong, Y.L.; Dong, S.L. Finite element modeling of confined concrete-II: Plastic-damage model. Eng. Struct. 2010, 32, 680–691. [Google Scholar] [CrossRef]
- Kupfer, H.B.; Gerstle, K.H. Behavior of Concrete under Biaxial Stresses. J. Eng. Mech. Div. 1973, 99, 853–866. [Google Scholar] [CrossRef]
- Kupfer, H.B.; Hilsdorf, H.K.; Rusch, H. Behavior of Concrete Under Biaxial Stresses. ACI J. Proc. 1969, 66, 656–666. [Google Scholar] [CrossRef]
- Wiliam, K.; Warnke, E. Constitutive Model for the Triaxial Behaviour of Concrete. Seminar on Concrete Structures Subjected to Triaxial Stresses; ISMES: Bergamo, Italy, 1974; pp. 1–30. [Google Scholar]
- Gonzalez-Vidosa, F.; Kotsovos, M.D.; Pavlovic, M.N. Symmetrical Punching of Reinforced Concrete Slabs: An Analytical Investigation Based on Nonlinear Finite Element Modeling. Struct. J. 1988, 85, 241–250. [Google Scholar] [CrossRef]
- Meng, B.; Li, F.; Zhong, W.; Zheng, Y.; Du, Q. Strengthening strategies against the progressive collapse of steel frames with extended end-plate connections. Eng. Struct. 2023, 274, 115154. [Google Scholar] [CrossRef]
- Nana, W.; Bui, T.; Limam, A.; Abouri, S. Experimental and Numerical Modelling of Shear Behaviour of Full-Scale RC Slabs under Concentrated Loads. Structures 2017, 10, 96–116. [Google Scholar] [CrossRef]
- de Sousa, A.M.D.; Lantsoght, E.O.L.; El Debs, M.K. Transition Between Shear and Punching in Reinforced Concrete Slabs: Review and Predictions with ACI Code Expressions. ACI Struct. J. 2023, 120, 115–128. [Google Scholar] [CrossRef]
- de Sousa, A.M.D.; Lantsoght, E.O.L.; El Debs, M.K. Shear and Punching Capacity Predictions for One-Way Slabs under Concentrated Loads Considering the Transition between Failure Mechanisms. Buildings 2023, 13, 434. [Google Scholar] [CrossRef]
- de Sousa, A.M.D.; Lantsoght, E.O.L.; Yang, Y.; El Debs, M.K. Extended CSDT model for shear capacity assessments of bridge deck slabs. Eng. Struct. 2021, 234, 111897. [Google Scholar] [CrossRef]
- De Sousa, A.M.D.; Lantsoght, E.O.L.; El Debs, M.K. One-way shear strength of wide reinforced concrete members without stirrups. Struct. Concr. 2020, 22, 968–992. [Google Scholar] [CrossRef]
- Guo, Z. Principles of Reinforced Concrete Design. Princ. Reinf. Concr. 2014, 587, 89–112. [Google Scholar] [CrossRef]
- Birtel, V.; Mark, P. Parameterised Finite Element Modelling of RC Beam Shear Failure. In Proceedings of the Ababqus User’s Conference, Boston, MA, USA, 23–25 May 2006; pp. 95–108. [Google Scholar]
- Santos, D.P.d.; Fernandes Neto, J.A.D.; Reginato, L.; Carrazedo, R. Optimized design of RC deep beams based on performance metrics applied to strut and tie model and in-plane stress conditions. Lat. Am. J. Solids Struct. 2019, 16, 212. [Google Scholar] [CrossRef]
- Alfarah, B.; López-Almansa, F.; Oller, S. New methodology for calculating damage variables evolution in Plastic Damage Model for RC structures. Eng. Struct. 2017, 132, 70–86. [Google Scholar] [CrossRef]
- Feenstra, P.H.; de Borst, R. Constitutive Model for Reinforced Concrete. J. Eng. Mech. 1995, 121, 587–595. [Google Scholar] [CrossRef]
- Carreira, D.J.; Chu, K.H. Stress-strain relationship for plain concrete in compression. ACI J. 1985, 82, 797–804. [Google Scholar]
- Cantone, R.; Ruiz, M.F.; Muttoni, A. Shear force redistributions and resistance of slabs and wide beams. Struct. Concr. 2021, 22, 2443–2465. [Google Scholar] [CrossRef]
- Setiawan, A.; Vollum, R.L.; Macorini, L.; Izzuddin, B.A. Punching of RC slabs without transverse reinforcement supported on elongated columns. Structures 2020, 27, 2048–2068. [Google Scholar] [CrossRef]
- Earij, A.; Alfano, G.; Cashell, K.; Zhou, X. Nonlinear three–dimensional finite–element modelling of reinforced–concrete beams: Computational challenges and experimental validation. Eng. Fail. Anal. 2017, 82, 92–115. [Google Scholar] [CrossRef]
- Wosatko, A.; Winnicki, A.; Polak, M.A.; Pamin, J. Role of dilatancy angle in plasticity-based models of concrete. Arch. Civ. Mech. Eng. 2019, 19, 1268–1283. [Google Scholar] [CrossRef]
- Michał, S.; Andrzej, W. Calibration of the CDP model parameters in Abaqus. In Proceedings of the 2015 Wourld Congress on Advances in Structural Engineering and Mechanics (ASEM15), Incheon, Republic of Korea, 24–28 September 2015. [Google Scholar]
- Fattuhi, N.I. Strength of SFRC Corbels Subjected to Vertical Load. J. Struct. Eng. 1990, 116, 701–718. [Google Scholar] [CrossRef]
- Fattuhi, N.I. Strength of FRC Corbels in Flexure. J. Struct. Eng. 1994, 120, 360–377. [Google Scholar] [CrossRef]
- Fattuhi, N.I.; Hughes, B.P. Ductility of Reinforced Concrete Corbels Containing Either Steel Fibers or Stirrups. ACI Struct. J. 1989, 86, 644–651. [Google Scholar] [CrossRef]
- Hughes, B.P.; Fattuhi, N.I. Reinforced steel and polypropylene fibre concrete corbel tests. Struct. Eng. 1989, 67, 68–72. [Google Scholar]
- Naegeli, C.H. Estudo de Consolos de Concreto Armado; Universidade Federal do Rio de Janeiro: Rio de Janeiro, Brazil, 1997. [Google Scholar]
- ABNT NBR 6118. NBR 6118; Design of concrete structures—Procedure. Associação Brasileira de Normas Técnicas (ABNT): Rio de Janeiro, Brazil, 2014. (In Portuguese)




























| Proprieties (MPa) | Test Method | C0 | C1 | C2 | C3 | |
|---|---|---|---|---|---|---|
| Concrete | fcm,28 (MPa) | ASTM C39 [19] | 31.72 | 44.82 | ||
| fcm (MPa) | ASTM C39 [19] | 36.54 | 44.82 | 46.88 | 38.61 | |
| Ec (MPa) | ASTM C469 [20] | 33,784 | 43,436 | 44,816 | 34,474 | |
| ftm,sp (MPa) | ASTM C496 [21] | 3.79 | 4.21 | 4.41 | 4.55 | |
| φ 12.7 mm | fym (MPa) | ASTM A370 [22] | 478 | 463 | ||
| fum (MPa) | 683 | 661 | ||||
| φ 25.4 mm | fym (MPa) | 506 | 487 | |||
| fum (MPa) | 701 | 685 | ||||
| φ 28.58 mm | fym (MPa) | 510 | 496 | |||
| fum (MPa) | 741 | 729 | ||||
| Corbel | FEXP (kN) | FFEM (kN) | FFEM/FEXP | Error |
|---|---|---|---|---|
| C0 | 1426.23 | 1458.01 | 1.02 | 2.22% |
| C1 | 1677.65 | 1627.23 | 0.97 | 3.01% |
| C2 | 1784.45 | 1778.17 | 1.00 | 0.35% |
| C3 | 1544.15 | 1346.93 | 0.87 | 12.77% |
| AVG | 0.97 | |||
| COV (%) | 6.79% |
| Reference | Damage Evolution Models | |
|---|---|---|
| Tensile | Compressive | |
| Birtel and Mark [42] | with: ; | with: ; |
| Yu et al. [30] | for | for |
| Alfarah et al. [44] | With: ; | With: ; |
| Property (MPa) | Testing Method | S1 | S2 | S3 | |
|---|---|---|---|---|---|
| Concrete | fcm (MPa) | ASTM C39 [19] | 27.1 | 26.5 | 27.3 |
| Ec (MPa) | ASTM C469 [20] | 27,670 | 27,000 | 27,370 | |
| ftm,sp (MPa) | ASTM C496 [21] | 3.36 | 3.12 | 3.16 | |
| ftm (MPa) | 0.9ftm,sp | 3.02 | 2.81 | 2.84 | |
| φ 9.53 mm | fym | ASTM A370 [22] | 467 | 467 | - |
| φ 25.4 mm | fym (MPa) | 471 | 570 | 471 | |
| Corbel | a (mm) | d (mm) | a/d | c (mm) | h (mm) | bw (mm) | fcm (MPa) | ftm (MPa) | Ec (MPa) | Quant. | ϕ (mm) | d (mm) | fy (MPa) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Fattuhi [52] | |||||||||||||
| 25 | 110 | 123 | 0.89 | 200 | 150 | 150 | 30.50 | 2.718 | 27,513.2 | 2 | 12 | 123 | 452 |
| 26 | 80 | 125 | 0.64 | 200 | 150 | 150 | 30.50 | 2.718 | 27,513.2 | 2 | 10 | 125 | 450 |
| 33 | 75 | 124 | 0.60 | 200 | 150 | 150 | 32.80 | 3.258 | 28,361.7 | 2 | 8 | 124 | 450 |
| 34 | 135 | 122 | 1.11 | 200 | 150 | 150 | 32.80 | 3.258 | 28,361.7 | 2 * | 14.7 * | 122 | 452 |
| 41 | 135 | 123 | 1.10 | 200 | 150 | 150 | 29.44 | 2.889 | 27,110.6 | 2 ** | 13.26 ** | 123 | 452 |
| 42 | 135 | 121 | 1.12 | 200 | 150 | 150 | 29.44 | 2.889 | 27,110.6 | 2 | 18 | 121 | 427 |
| Fattuhi [53] | |||||||||||||
| 65 | 110 | 91.8 | 1.20 | 200 | 147.8 | 150 | 28.29 | 3.024 | 26,670.2 | 2 | 12 | 91.8 | 452 |
| 66 | 135 | 93 | 1.45 | 200 | 149 | 150 | 28.29 | 3.024 | 26,670.2 | 2 * | 14.7 * | 93 | 452 |
| 67 | 110 | 132.4 | 0.83 | 200 | 148.4 | 150 | 30.012 | 3.159 | 27,328.1 | 2 | 12 | 132.4 | 452 |
| 68 | 110 | 112.4 | 0.98 | 200 | 148.4 | 150 | 30.012 | 3.159 | 27,328.1 | 2 | 12 | 112.4 | 452 |
| 69 | 135 | 122.6 | 1.10 | 200 | 148.6 | 150 | 26.24 | 2.799 | 25,864.9 | 2 * | 14.7 * | 122.6 | 452 |
| 70 | 135 | 92.3 | 1.46 | 200 | 148.3 | 150 | 26.24 | 2.799 | 25,864.9 | 2 * | 14.7 * | 92.3 | 452 |
| 71 | 110 | 121.5 | 0.91 | 200 | 147.5 | 150 | 28.29 | 2.79 | 26,670.2 | 2 ** | 13.26 ** | 121.5 | 452 |
| 72 | 110 | 123.2 | 0.89 | 200 | 149.2 | 150 | 28.29 | 2.79 | 26,670.2 | 2 | 12 | 123.2 | 452 |
| 73 | 75.0 | 124 | 0.60 | 200 | 148 | 150 | 28.29 | 2.898 | 26,670.2 | 2 | 8 | 124 | 451 |
| 74 | 75.0 | 94.2 | 0.80 | 200 | 148.2 | 150 | 28.29 | 2.898 | 26,670.2 | 2 | 8 | 94.2 | 451 |
| Fattuhi and Hughes [54] | |||||||||||||
| T1 | 89 | 105 | 0.85 | 200 | 150 | 150 | 41.21 | 3.099 | 29,158.4 | 2 | 10 | 105 | 558 |
| T2 | 89 | 130 | 0.68 | 200 | 150 | 150 | 41.21 | 3.099 | 29,158.4 | 2 2 | 10 10 | 130 76 | 558 |
| T6 | 89 | 137 | 0.65 | 200 | 150 | 150 | 43.05 | 3.213 | 29,707.6 | 2 | 12 | 137 | 491 |
| T7 | 89 | 130 | 0.68 | 200 | 150 | 150 | 39.46 | 2.990 | 28,629.5 | 2 2 | 12 10 | 130 80 | 491 558 |
| T8 | 89 | 130 | 0.68 | 200 | 150 | 150 | 43.05 | 3.213 | 29,707.6 | 2 2 2 | 12 10 10 | 130 93 85 | 491 558 558 |
| T9 | 89 | 130 | 0.68 | 200 | 150 | 150 | 39.46 | 2.990 | 28,629.5 | 2 2 2 | 12 10 10 | 130 69 61 | 491 558 558 |
| Hughes and Fattuhi [55] | |||||||||||||
| C1 | 125 | 120 | 1.04 | 200 | 150 | 150 | 39.57 | 2.996 | 28,659.1 | 2 | 10 | 120 | 558 |
| C21 | 53 | 129 | 0.41 | 200 | 150 | 150 | 38.75 | 2.944 | 28,391.6 | 2 | 8 | 129 | 495 |
| C22 | 89 | 129 | 0.69 | 200 | 150 | 150 | 41.10 | 3.093 | 29,129.2 | 2 | 8 | 129 | 495 |
| C23 | 125 | 129 | 0.97 | 200 | 150 | 150 | 41.10 | 3.093 | 29,129.2 | 2 | 8 | 129 | 495 |
| C24 | 53 | 129 | 0.41 | 200 | 150 | 150 | 38.75 | 2.944 | 28,391.6 | 2 | 10 | 129 | 558 |
| C25 | 65 | 129 | 0.50 | 200 | 150 | 150 | 40.80 | 3.074 | 29,041.6 | 2 | 12 | 129 | 491 |
| C26 | 125 | 129 | 0.97 | 200 | 150 | 150 | 39.57 | 2.996 | 28,659.1 | 2 | 12 | 129 | 491 |
| Reference | Corbel | a/d | fcm (MPa) | FEXP (kN) | FFEM (kN) | FFEM/FEXP | FME | FMF | CP |
|---|---|---|---|---|---|---|---|---|---|
| Wilson et al. [4] | C0 | 0.66 | 36.54 | 1426.2 | 1458.0 | 1.02 | C | T | No |
| C1 | 0.59 | 44.82 | 1677.7 | 1627.2 | 0.97 | T | T | Yes | |
| C2 | 0.59 | 46.88 | 1784.5 | 1778.2 | 1.00 | T | T | Yes | |
| C3 | 0.59 | 38.61 | 1544.2 | 1346.9 | 0.87 | T | T | Yes | |
| Khosravikia et al. [5] | S1 | 0.59 | 27.10 | 1050.0 | 1115.4 | 1.06 | C | C | Yes |
| S2 | 0.59 | 26.50 | 1096.5 | 1073.4 | 0.98 | C | C | Yes | |
| S3 | 0.59 | 27.30 | 772.0 | 860.1 | 1.11 | C | C | Yes | |
| Fattuhi [52] | 25 | 0.89 | 30.50 | 108.5 | 103.1 | 0.95 | T | T | Yes |
| 26 | 0.64 | 30.50 | 112.5 | 114.8 | 1.02 | T | T | Yes | |
| 33 | 0.60 | 32.80 | 91 | 85.3 | 0.94 | T | T | Yes | |
| 34 | 1.11 | 32.80 | 114 | 104.1 | 0.91 | T | T | Yes | |
| 41 | 1.10 | 29.44 | 98 | 92.2 | 0.94 | T | T | Yes | |
| 42 | 1.12 | 29.44 | 111.5 | 99.1 | 0.89 | C | C | Yes | |
| Fattuhi [53] | 65 | 1.20 | 28.29 | 74 | 82.1 | 1.11 | T | T | Yes |
| 66 | 1.45 | 28.29 | 73.5 | 70.7 | 0.96 | T | T | Yes | |
| 67 | 0.83 | 30.01 | 101.3 | 100.9 | 1.00 | T | T | Yes | |
| 68 | 0.98 | 30.01 | 96 | 95.0 | 0.99 | T | T | Yes | |
| 69 | 1.10 | 26.24 | 93.5 | 89.2 | 0.95 | C | T | No | |
| 70 | 1.46 | 26.24 | 67.3 | 65.9 | 0.98 | C | C | Yes | |
| 71 | 0.91 | 28.29 | 116.5 | 110.5 | 0.95 | T | T | Yes | |
| 72 | 0.89 | 28.29 | 101 | 93.3 | 0.92 | T | T | Yes | |
| 73 | 0.60 | 28.29 | 87.5 | 83.5 | 0.95 | T | T | Yes | |
| 74 | 0.80 | 28.29 | 74.3 | 63.5 | 0.86 | T | T | Yes | |
| Fattuhi and Hughes [54] | T1 | 0.85 | 41.21 | 93 | 100.0 | 1.08 | C | C | Yes |
| T2 | 0.68 | 41.21 | 146 | 156.4 | 1.07 | C | T | No | |
| T6 | 0.65 | 43.05 | 136 | 138.0 | 1.01 | T | T | Yes | |
| T7 | 0.68 | 39.46 | 157 | 169.7 | 1.08 | C | C | Yes | |
| T8 | 0.68 | 43.05 | 188 | 212.3 | 1.13 | T | T | Yes | |
| T9 | 0.68 | 39.46 | 153 | 179.9 | 1.18 | C | C | Yes | |
| Hughes and Fattuhi [55] | C1 | 1.04 | 39.57 | 80 | 88.2 | 1.10 | C | C | Yes |
| C21 | 0.41 | 38.75 | 114 | 123.2 | 1.08 | T | T | Yes | |
| C22 | 0.69 | 41.10 | 82 | 81.5 | 0.99 | T | T | Yes | |
| C23 | 0.97 | 41.10 | 47 | 58.0 | 1.23 | T | T | Yes | |
| C24 | 0.41 | 38.75 | 145 | 151.0 | 1.04 | C | T | No | |
| C25 | 0.50 | 40.80 | 151 | 159.3 | 1.06 | T | T | Yes | |
| C26 | 0.97 | 39.57 | 90 | 102.0 | 1.13 | C | C | Yes | |
| Average | 1.015 | 32/36 | |||||||
| Standard deviation | 0.087 | ||||||||
| Coefficient of variation | 8.57% | ||||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Reginato, L.; de Sousa, A.M.D.; Santos, J.V.C.; El Debs, M.K. NLFEA of Reinforced Concrete Corbels: Proposed Framework, Sensibility Study, and Precision Level. Buildings 2023, 13, 1874. https://doi.org/10.3390/buildings13071874
Reginato L, de Sousa AMD, Santos JVC, El Debs MK. NLFEA of Reinforced Concrete Corbels: Proposed Framework, Sensibility Study, and Precision Level. Buildings. 2023; 13(7):1874. https://doi.org/10.3390/buildings13071874
Chicago/Turabian StyleReginato, Luan, Alex M. D. de Sousa, João V. C. Santos, and Mounir K. El Debs. 2023. "NLFEA of Reinforced Concrete Corbels: Proposed Framework, Sensibility Study, and Precision Level" Buildings 13, no. 7: 1874. https://doi.org/10.3390/buildings13071874
APA StyleReginato, L., de Sousa, A. M. D., Santos, J. V. C., & El Debs, M. K. (2023). NLFEA of Reinforced Concrete Corbels: Proposed Framework, Sensibility Study, and Precision Level. Buildings, 13(7), 1874. https://doi.org/10.3390/buildings13071874








