Compressive Strength Prediction of BFRC Based on a Novel Hybrid Machine Learning Model

Abstract

Basalt fiber-reinforced concrete (BFRC) represents a form of high-performance concrete. In structural design, a 28-day resting period is required to achieve compressive strength. This study extended an extreme gradient boosting tree (XGBoost) hybrid model by incorporating genetic algorithm (GA) optimization, named GA-XGBoost, for the projection of compressive strength (CS) on BFRC. GA optimization may reduce many debugging efforts and provide optimal parameter combinations for machine learning (ML) algorithms. The XGBoost is a powerful integrated learning algorithm with efficient, accurate, and scalable features. First, we created and provided a common dataset using test data on BFRC strength from the literature. We segmented and scaled this dataset to enhance the robustness of the ML model. Second, to better predict and evaluate the CS of BFRC, we simultaneously used five other regression models: XGBoost, random forest (RF), gradient-boosted decision tree (GBDT) regressor, AdaBoost, and support vector regression (SVR). The analysis results of test sets indicated that the correlation coefficient and mean absolute error were 0.9483 and 2.0564, respectively, when using the GA-XGBoost model. The GA-XGBoost model demonstrated superior performance, while the AdaBoost model exhibited the poorest performance. In addition, we verified the accuracy and feasibility of the GA-XGBoost model through SHAP analysis. The findings indicated that the water–binder ratio (W/B), fine aggregate (FA), and water–cement ratio (W/C) in BFRC were the variables that had the greatest effect on CS, while silica fume (SF) had the least effect on CS. The results demonstrated that GA-XGBoost exhibits exceptional accuracy in predicting the CS of BFRC, which offers a valuable reference for the engineering domain.

1. Introduction

Concrete is the most widely used material in the building-structure industry, but the demand for its performance is increasing, thus the trend of research and application of advanced and eco-materials is getting more and more attention and development. Many methods have been proposed to improve the performance of concrete materials, and the incorporation of fibers into concrete is a promising solution. Among them, basalt fiber (BF) is an inorganic and environment-friendly green material that is often used as a concrete additive to improve its tensile properties [1,2,3,4]. Basalt-fiber-reinforced concrete (BFRC) has the advantage of superior mechanical properties, durability, crack resistance, and frost resistance and the raw material is readily available, which makes its application promising. It is essential to accurately predict the basic mechanical performance of BFRC to ensure the safety of engineering structures.

Wang D et al. [5] investigated the impacts of BF, polypropylene fibers, and blended fibers on the compressive strength (CS), flexural strength, splitting tensile strength, and stress–strain curves of HPC. The results indicated that fiber admixture could moderately enhance the CS of concrete. Wang X et al. [6] investigated the effects of fiber length and admixture amount on the mechanical properties and crack resistance of BFRC. The results demonstrated that adding the appropriate amount of fiber can increased the CS of BFRC. Chen et al. [7] conducted a comprehensive study on the influence of BF content on basic mechanical properties of concrete. The investigation involved performing compression and cracking tensile experiments. The results demonstrated that BF can enhance the CS of concrete by a moderate amount. Most studies have evaluated the mechanical behavior of BFRC by using experimental methods [8,9,10,11,12,13]. However, BFRC is a mixture of a variety of materials in precise proportions such as basalt fibers, cement, water and aggregate. If the test results are not sufficiently reliable due to mixture design failures, the entire concrete-mixture design procedure has to be restarted. However, experimental studies require a large amount of instrumentation and equipment, which is costly.

In order to surpass the limitations associated with experimental methods, several researchers have turned to machine learning (ML) methods as a means to predict concrete strength [14,15,16]. Hong et al. [17] verified that the RF algorithm can predict the compressive strength of BFRC well. Severcan et al. [18] employed GEP to effectively capture the splitting tensile strength of concrete. Their study demonstrated that GEP exhibited superior performance in predicting the splitting tensile strength compared to other approaches. Nguyen et al. [19] used RF, decision trees (DTs), and XGBoost for the prediction of CS on fly-ash-based polymer concrete and concluded that the XGBoost model outperformed the other two models. In a study by Gupta et al. [20], the optimal proportions of concrete mixes were determined using the Gaussian process, M5P model, random forest (RF), and random tree (RT) techniques and different applied models were evaluated. It was found that Gaussian process regression using RBF kernel produced better results than other models. Asteris et al. [21] used AdaBoost, support vector machine (SVM), RF, DT, and K nearest neighbors to evaluate the behavior of cement-based mortar CS. Kang et al. [22] extended and compared various ML models to forecast flexural strength of steel-fiber-reinforced concrete. Finally, it was found that the CS prediction performance was generally better than the flexural-strength prediction performance regardless of the machine-learning algorithm used. A forest deep neural network (FDNN) algorithm proposed by Altayeb et al. [23] outperformed previous algorithms in predicting the mechanical properties of cementitious composites. Armaghani et al. [24] used models such as artificial neural networks (ANNs), and ANFIS to forecast the CS of cementitious mortar materials with or without biased kaolinite. Ahmed et al. [25] investigated the CS of concrete mixed with fly ash using various techniques such as linear regression, genetic algorithms, and particle-swarm optimization. Nazar et al. [26] used random forest regression, DTs and GEP-model multiple machine-learning approaches for the prediction and valuation of CS in nano-modified concrete and showed that the RFT model performed better in terms of accuracy and precision of the results. Esmaeili and Benemaran [27] used particle-swarm optimization (PSO) and black-widow optimization algorithms (BWOAs) to optimally determine the variables to generate two XGB structures that predicted the modulus of elasticity (MR) of the modified substrate under wet and dry cycling conditions. The results showed that the combination of variables in the M3 model were the most appropriate and that the BWO algorithm was competent in determining the optimal values of the XGB parameters. Benemaran et al. [28] used four different optimization methods (particle-swarm optimization, social-spider optimization, sinusoidal cosine algorithm, and multi-universe optimization) based on the extreme gradient-boosting model to predict the modulus of recovery of flexible pavement foundations. The results showed that all optimization models worked well, but the limit gradient-boosting model based on particle-swarm optimization exhibited the best prediction accuracy. Li et al. [29] developed four hybrid models based on the aquila-optimizer algorithm using an adaptive neuro-fuzzy inference system, support vector regression, random forests, and limiting gradient boosting to accurately predict the unconfined compressive strength of marine clay and recycled tile blends. The results of the study showed that the model of extreme gradient boosting with the aquila-optimizer algorithm had the best performance with a small scatter index and better generalization.

In summary, existing studies have mainly focused on single-scale models without considering the effects of extensive laboratory-work data or factors in the concrete CS. Single algorithms often lead to locally optimal solutions that are difficult to generalize which can ultimately limit their practical application. Many factors influent the CS of concrete, including the mix ratio, water–cement ratio, and shape of the mixture. Therefore, designing a hybrid model integrating multiple algorithms can consider these factors more comprehensively and enhance prediction accuracy and generalizability of concrete CS. Genetic algorithms (GAs) have good global search capability and robustness and can avoid getting trapped in locally optimal solutions. XGBoost is a powerful integrated learning algorithm with efficient, accurate, and scalable features. However, its grid search increases the time significantly as the parameters increase when performing parameter tuning. Therefore, a hybrid model was designed to extend the XGBoost model by using genetic-algorithm parameter optimization (GA-XGBoost) for better and faster prediction of CS on BFRC as well as optimization of concrete mix ratio designs. The main research content was as follows:

• A large dataset on the basic mechanical properties of BFRC was constructed using experimental data on BFRC strength from published literature and made available to the public;
• GA-XGBoost was developed and applied to predict CS on BFRC, and the model was validated by SHAP analysis;
• Six independent regression models—XGBoost, gradient-boosted decision tree (GBDT) regressor, AdaBoost, RF, SVR, and GA-XGBoost—were adopted to predict the concrete CS, and the accuracy of these models’ predictions was compared.

2. Data Preprocessing

Before constructing a model, the dataset must be assembled and preprocessed. Many researchers [14,15,16,17,30,31,32,33,34] have attempted machine-learning predictions, but no studies have been conducted to build shared BFRC model datasets. New datasets needed to be obtained from strength tests of BFRC to develop models for predicting CS.

Since most design criteria for concrete are concerned with strength, this study decided to use and collect test data from several BFRC strengths and form a common dataset. This dataset contained a large amount of data regarding the design parameters of BFRC concrete mixes, as well as several strength parameters. The database included water–cement ratio (W/C), coarse aggregate (CA), silica fume (SF), water–binder ratio (W/B), high-efficiency water reducing agent (S), fine aggregate (FA), and fly ash (F) as concrete-mix design parameters. The ratio of length to diameter of fibers (FL/FD) and fiber content (FC) were used as fiber-property parameters. Finally, the strength parameter recorded in this dataset was compressive strength (CS). The dataset contained 12 parameters, 11 of which are features, and 1 a target.

Table 1. Dataset descriptive statistics.

Feature	Units	Mean	Std	Min	Max	Count
W/C	-	0.450	0.0722	0.280	0.717	346
W/B	-	0.400	0.0753	0.241	0.573	346
C	${\mathrm{k}\mathrm{g}/\mathrm{m}}^3$	395.3	69.25	217	613.3	346
F	${\mathrm{k}\mathrm{g}/\mathrm{m}}^3$	40.92	53.98	0	168	346
SF	${\mathrm{k}\mathrm{g}/\mathrm{m}}^3$	13.14	28.28	0	126	346
CA	${\mathrm{k}\mathrm{g}/\mathrm{m}}^3$	1093	170.6	512	1540	346
FA	${\mathrm{k}\mathrm{g}/\mathrm{m}}^3$	697.9	110.7	507	1194	346
W	${\mathrm{k}\mathrm{g}/\mathrm{m}}^3$	175.2	29.15	112	301	346
S	${\mathrm{k}\mathrm{g}/\mathrm{m}}^3$	3.088	2.292	0	8.360	346
FL/FD	${10}^3$	1.037	0.377	0.345	2	346
FC	%	0.141	0.131	0	0.730	346
CS	MPa	50.15	11.80	15.52	96.25	346

presents descriptive statistics for the dataset utilized in the development of the model.

To enhance the visualization of the graphs, we used Python to create Figure 1 and Figure 2. Figure 1 is a graphical representation of the pairing matrix, and demonstrates how the magnitude of the correlation between the variables changed as different factors changed. Among them, the increase in W/C, W/B, and FA led to a decrease in the concrete CS, while the improvement in C, S, and SF enhanced the CS, and the effect of other factors on CS was not significant. Similar conclusions can be drawn from the correlation coefficient matrix (Figure 2), where W/C, W/B, and FA were negatively correlated with CS with correlation factors of −0.52, −0.52, and −0.2, while C, SF, and S were positively correlated with CS to a comparable extent with correlation factors of 0.32, 0.32, and 0.28. In particular, it was observed from Figure 2 that FC was negatively correlated with CS (−0.15).

According to Oey et al. [35], scaling the training and test sets before segmentation can potentially result in data leakage. In this study, following the separation of the training and test sets, the dataset was scaled using the robust-scaler function from the sklearn library. By utilizing median and quartile scaling, the robustness of machine-learning algorithm was enhanced to minimize the impact of outliers on the model. Then, we could significantly enhance the accuracy of prediction results.

3. Methodology

3.1. Machine-Learning Algorithm

To make it easier to use these machine-learning algorithms, we adopted python as the IDE and used the scikit-learn library from it. The purpose of our study was to validate the GA-XGBoost performance in predicting the CS of BFRC and to compare it with XGBoost, GBDT, AdaBoost, RF, and SVR. To ensure the reliability of the GA-XGBoost model, feature-importance analysis and SHAP analysis were performed, and the findings were analyzed in comparison with previous studies.

3.1.1. Brief Description of RF

RF is described as a consolidated learning model which decreases the variance of an individual decision tree by building the integration of multiple decision trees [36]. This algorithm leverages the definition of bagging, which involves aggregating randomly selected similar datasets from the training set into a forest [37]. In order to randomly select enough features among the nodes, the RF algorithm uses bagging to optimize them. The decision tree partitions the randomly selected sample features into left and right subtrees. This method reduces the instability of the decision tree and improves its generalization ability, but leads to over-fitting in some noisy classification and regression problems. Figure 3 presents the schematic diagram depicting the bagging algorithm.

3.1.2. Brief Description of AdaBoost

The boosting method is a consolidated learning model that constructs a strong learner based on jointing multiple weak learners. In the boosting method, the sample weights of follow-up models are increased based on the learning from the previous model. This iterative process results in the creation of strong learners [38]. AdaBoost is a boosting algorithm that enables training to focus on hard-to-predict samples by dynamically weighting the training samples, ultimately achieving the optimal weak learner [39]. In each iteration, each weak learner dynamically modifies the weights of each sample based on the previously obtained prediction accuracy and trains the new dataset. This algorithm makes the combination of weak learners more likely to produce accurate prediction results. Figure 4 shows the schematic diagram of the boosting algorithm.

3.1.3. Brief Description of GBDT

The definition of the GBDT is a decision-tree-based synthesis algorithm designed to fit the training data by continuously reducing the residuals. Following each round of training for the weak learner, the GBDT adjusts itself by moving in the direction of a decreasing gradient of the loss function [40].

Similar to AdaBoost, the GBDT uses the gradient rather than the weights of error points to locate weak learner deficiencies. The GBDT can use a wider range of objective functions than AdaBoost.

3.1.4. Brief Description of SVR

SVR is an algorithm for solving linear and nonlinear regression problems with a strong generalization capability [41,42]. It predicts export values by combining multiple kernel functions to construct reliable regression models. Another advantage of this algorithm is that the optimal kernel function can be applied to enhance the forecast result accuracy. In addition to regression problems, SVR can be used for pattern recognition and data classification.

3.1.5. Brief Description of XGBoost

XGBoost is an upgraded version of the boosting algorithm based on the GBDT algorithm, and it allows for more accurate and faster fitting by directly using first- and second-order gradients to extend the loss function [43]. This algorithm has been widely used in several fields and offers greater problem-solving capabilities and fewer usage constraints. In contrast to the GBDT, XGBoost exhibits shorter learning times and superior predictive power, particularly when confronted with large-scale datasets. However, the disadvantages of XGBoost are that it requires a lot of memory and computational resources during the training process, and may have overfitting problems for certain datasets. Therefore, careful hyperparameter selection and model optimization are required when using XGBoost.

3.1.6. Features, Advantages, and Disadvantages of the above Five Models

As mentioned above, RF, AdaBoost, GBDT Regressor and XGBoost are all integrated learning algorithms based on decision trees, while SVR is a support vector machine based on a regression algorithm. In general, the DT is the foundation and combinations of DTs creates a RF that has higher accuracy. AdaBoost adjusts the sample weights at each iteration to strengthen those samples that are misclassified. GBDT is designed to fit the training data by continuously reducing the residuals. SVR is a powerful regression algorithm for dealing with nonlinear regression problems. Finally, in order to address the overfitting problem, XGBoost extended and possessed the highest accuracy of the four decision tree methods, while SVR has a high sensitivity to parameters. The main features, advantages, and disadvantages of the above five models are presented in

Table 2. Summary of the above models [44,45,46,47,48].

Model	Main Features	Advantages	Disadvantages
RF	RF is an integrated model consisting of multiple decision trees, which can reduce the variance of individual decision trees.	Improves model accuracy by reducing overfitting; Handles both classification and regression problems; Robust to noise and missing values in the data sets.	The model training time is longer; Larger storage space is required to store multiple decision trees; The presence of outliers in the dataset can influent the accuracy of the model.
AdaBoost	AdaBoost is an integrated model consisting of several weak classifiers for binary and multivariate classification problems.	Manages overfitting to solve dichotomous and multiclassification problems; Handles high-dimensional, unbalanced datasets.	Sensitive to outliers, which may have a significant impact on the model; Longer training time; Tendency to overfit when the data set is too noisy.
GBDT	GBDT Regressor is an integrated decision-tree-based learning algorithm that improves the accuracy and generalization performance through gradient boosting method.	Handles effectively nonlinear relationships and complex feature interactions; Missing values and outliers are handled automatically and with good robustness; Generates feature importance rankings to facilitate subsequent feature engineering.	Sensitive to noise and outliers and prone to overfitting; Relatively slow training speed; Prone to prediction bias for unbalanced datasets.
SVR	SVR is a support vector machine (SVM)-based regression algorithm that can be used to handle nonlinear regression problems.	Handles high-dimensional data sets and non-linear regression problems; There is no requirement for the uniqueness of the solution of the model; Setting the kernel function to be well adapted to different data types.	Time- and memory-consuming when dealing with large data sets; Sensitive to noise and easy to over-fit; Need to solve convex optimization problems with high solution complexity.
XGBoost	XGBoost is a decision-tree-based gradient boosting algorithm that also uses regularization to enhance the accuracy and generalization performance.	Automatic feature selection and excellent performance in handling large scale, high-dimensional data; Handles missing values, outliers, and unbalanced datasets, and is less prone to overfitting; Supports parallel computing and distributed computing with fast processing time.	Requires long training time and large amount of computational resources to handle large-scale datasets; Parameter tuning may lead to over-fitting or under-fitting; Vulnerable to outliers.

.

3.1.7. Combination of Genetic Algorithm and XGBoost

Genetic algorithms (GAs), which originated from computer simulations of biological systems, are stochastic, efficient, and parallel global search and optimization methods. They are able to automatically generate and accumulate knowledge about the search space during the search process and adaptively control the search process to find the optimal solution.

Although XGBoost excels in all aspects, it does have drawbacks, one of which is that many of the parameters are customizable and results can vary from configuration to configuration. When using grid search to adjust parameters, the number of parameters added is correlated with the search time spent. Due to its inherent parallelism and ability to perform distributed computations, GAs quickly traverse all solving methods in the solution space without falling into the trap of rapidly decreasing locally optimal solutions. Consequently, GAs allow faster optimization of many machine-learning parameters and can achieve higher efficiency, outperforming grid searches.

To address the problems of long preparation time and many parameters in XGBoost models, we adopted GAs to improve the efficiency of parameter search process in XGBoost. The individual population of GAs is usually defined as the XGBoost parameters and the fitness function is determined as the average score achieved during XGBoost training. Also, selection, crossover, and variation are used to enhance the operational efficiency of the model. Figure 5 shows a schematic representation of GA-XGBoost.

As a result, GAs should be used to optimize the XGBoost model, so that we find the optimal solution faster, reduce the tuning time, and ease the burden of parameter tuning.

3.2. Model Performance Evaluation

For machine-learning algorithms, we commonly use mean square error (MSE), coefficient of determination (R²), root mean square error (RMSE), and mean absolute error (MAE) to describe the accuracy and stability of a model.

In these regression models, the key to estimation performance is the variance component of the response features, which can have values from negative infinity to 1. Thus, if the algorithm’s model satisfies the data perfectly, its value will be 1 and also explain the data variability. The formulae for the four evaluation indicators are shown below.

$$R^2=1-\frac{\frac{1}{n}{\displaystyle \sum _{i=1}^n{\left(y_i-{\stackrel{\wedge }{y}}_i\right)}^2}}{\frac{1}{n}{\displaystyle \sum _{i=1}^n{\left(y_i-{\stackrel{-}{y}}_i\right)}^2}}$$

(1)

$$MSE=\frac{1}{n}{\displaystyle \sum _{i=1}^n{\left(y_i-{\stackrel{\wedge }{y}}_i\right)}^2}$$

(2)

$$RMSE=\sqrt{\frac{1}{n}{\displaystyle \sum _{i=1}^n{\left(y_i-{\stackrel{\wedge }{y}}_i\right)}^2}}$$

(3)

$$MAE=\frac{{\displaystyle \sum _{i=1}^n\left|y_i-{\stackrel{\wedge }{y}}_i\right|}}{n}$$

(4)

where ${\widehat{y}}_i$ and $y_i$ are the predicted value and true value, $\stackrel{-}{y}$ is the sample mean, and $n$ is the count of data samples.

3.3. Methodology Flowchart

3.3.1. Data Collection

The flowchart of the current work included the four main steps above, as shown in Figure 6.

The database consisted of 346 experimental results collected from 28 published articles about the CS of BFRC. This dataset was randomly divided into a training dataset (accounting for 70%) and a test dataset (the remaining 30%).

3.3.2. Model Training

We used the training dataset to train the ML models mentioned above. These algorithms are described in Section 3.1. The training process was repeated until the above-mentioned models were successfully trained.

3.3.3. Model Verification

After step 2, we used the testing set to validate the above models. That is, we used the GA-XGBoost model proposed in this paper to compare with five other existing models. Additionally, we used the repeated holdout method to ensure the model prediction performance. Model prediction ability was evaluated using four criteria detailed in Section 3.1.

3.3.4. Sensitivity Analysis

Finally, we evaluated the influence of input variables with feature importance and SHAP values to assess the influence of the 11 input parameters.

First, we obtained the original dataset and selected the most relevant features using the feature selection function with reference to Figure 1 and Figure 2. Second, in order to evaluate the performance of the model and ensure the consistency and stability of the model, we randomly divided the dataset into a training set and a test set, and adjusted the random-state parameter of the model to 1. In order to improve the speed and accuracy of the model training, we scaled the training set and the test set by using the median and interquartile spacing. Then, the corresponding datasets were trained and tested, and tuned by traditional grid-search methods to obtain five single machine-learning models. The default settings for the other models’ parameters were used. Finally, we utilize GAs for parameter tuning of the XGBoost models to obtain an integrated model, and the flow is shown in Figure 5.

4. Results and Discussion

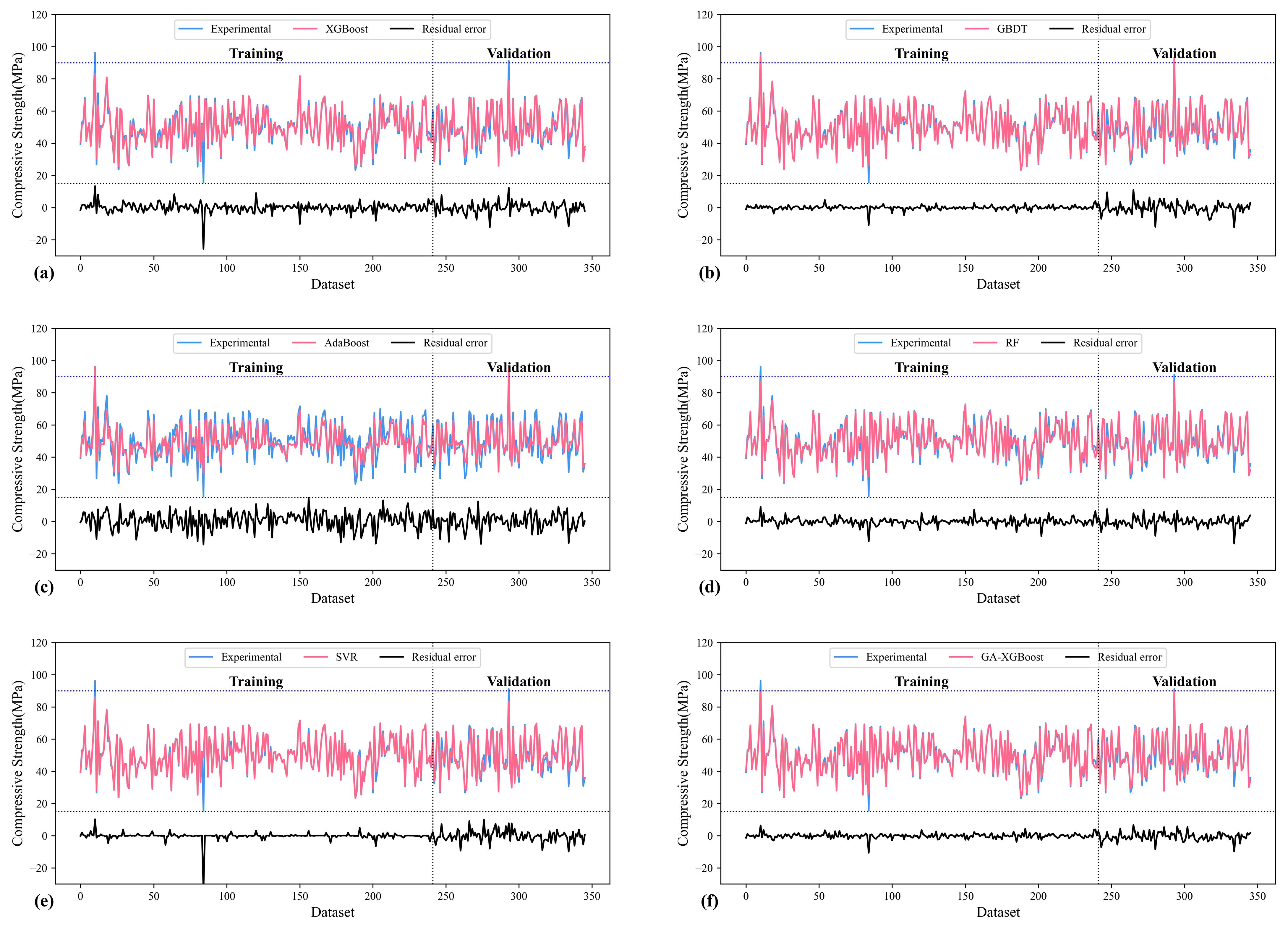
4.1. Evaluation of Six Models

Table 3. Statistical evaluation metrics of models.

Type of Set	Metrics	XGBoost	GBDT	AdaBoost	RF	SVR	GA-XGBoost
Train	R2	0.9307	0.987	0.7822	0.96	0.9527	0.9834
	Rank	5	1	6	3	4	2
	MSE	9.4145	1.7631	29.6077	5.4331	6.4333	2.2596
	Rank	5	1	6	3	4	2
	RMSE	3.0683	1.3278	5.4413	2.3309	2.5364	1.5032
	Rank	5	1	6	3	4	2
	MAE	1.9637	0.8235	4.4515	1.6056	0.758	1.0116
	Rank	5	2	6	4	1	3
Test	R2	0.9133	0.914	0.826	0.9322	0.9123	0.9483
	Rank	4	3	6	2	5	1
	MSE	12.6259	12.5174	25.321	9.8671	12.7635	7.6962
	Rank	4	3	6	2	5	1
	RMSE	3.5533	3.538	5.032	3.1412	3.5726	2.7742
	Rank	4	3	6	2	5	1
	MAE	2.5726	2.473	4.0276	2.2175	2.5728	2.0564
	Rank	4	3	6	2	5	1
Total rank score		36	17	48	21	33	13

shows the results of statistical validation of the model performance on the dataset under four different metrics. Here, the computed results of four performance criteria (R², MSE, RMSE, and MAE) were used to assess the accuracy of the model, a score-based system was designed to assign a score (from 1 to 6) based on the criterion values, and the total score described the ranking of the model. A smaller total score represented a better model performance. Compared to the XGBoost model, the GA-XGBoost model achieved smaller metric errors on the training set (MSE = 2.2596, RMSE = 1.5032, MAE = 1.0116, R² = 0.9834). The results indicated that GAs can be used to maximize performance and enhance the learning ability of the XGBoost model. Also, GA-XGBoost showed the highest score on the test set with a metric error of (MSE = 7.6962, RMSE = 2.7742, MAE = 2.0564, R² = 0.9483). It is reasonable to use GAs to improve parameter tuning of XGBoost to maximize its performance. The performance of other models using grid-search optimization showed that grid-search optimization is also adequate to predict the CS of concrete with considerable model accuracy.

According to the experimental results shown in Figure 7, all models except the AdaBoost model performed well in predicting the CS on BFRC. The predicted values of AdaBoost model showed greater deviations relative to their experimental values due to adaptively increasing the weight of the prediction error. The GA-XGBoost had the best performance and stability, while the RF, GBDT, XGBoost, and SVR performed slightly differently. However, after grid-search optimization, the AdaBoost model still performed poorly because of its lack of sensitivity to noise and outliers. Therefore, we can conclude that GA-XGBoost is the most suitable ML algorithm for predicting the CS on BFRC.

4.2. SHAP Analysis

SHAP analysis is an algorithm used to interpret the prediction results of ML models by providing the magnitude of each feature’s impact on the prediction results. The core of SHAP analysis is based on the Shapley value principle, which assigns each feature’s contribution to all possible subsets of features and calculates the expected value of the feature contribution to obtain the magnitude of each feature’s impact on the prediction results of the model. Shapley values can be used not only to assess the importance of each input variable, but also to calculate the impact of individual input variables on the final result, which is presented in the form of a Shapley plot. Feature-importance analysis is a method used to determine which features or variables have the most influence on the prediction results of a model to help optimize and explain the model’s performance and results.

SHAP analysis can help us interpret the model prediction results and determine which features have the most influence on the prediction results. Also, SHAP can help us validate the reliability of the model to determine if the model uses reasonable features in making predictions on the input data. Finally, SHAP analysis can also help us enhance the model performance by analyzing the impact of each feature on the model’s prediction results and determining which features need more attention and optimization to enhance the prediction performance. For BFRC fit design, it is very important to know the impact of model input variables. In addition, the proposed algorithm should be described in detail to understand how to analyze and calculate the predicted concrete CS. For the global interpretation, we performed SHAP and feature-importance analysis on the best-performing GA-XGBoost model.

To test the effect of features on the prediction of the target variables, Figure 8 indicates the significance of input variables. The results were obtained by averaging the Shapley values throughout the data collection process. We found that W/B dominated the CS of BFRC, which is consistent with the experimental results. The variables FA and W/C were in the second and third place and, in that order, of considerable importance for CS. It is also clear from this figure that CA content was the least important variable, while SF and FL/FD were slightly more important than CA.

Aggregate plots summarize the relative importance of input factors and their relationship with the independent variables and therefore play an important role in SHAP analysis. Figure 9 indicates global interpretation of GA-XGBoost using the SHAP interpretation, showing the distribution of SHAP values for all model features and the main trends of the variables. The figure shows SHAP values of 11 input features, where positive values indicate an aggressive gain to CS and negative values indicate the opposite. Red dots represent those samples with high eigenvalues and blue dots are the opposite.

Figure 9 shows that the W/B variable has a low sample eigenvalue and a high SHAP value. Therefore, the W/B variable with smaller sample eigenvalues has a larger positive gain in improving the CS of BFRC. For the FA and W/C variables, SHAP values with lower sample eigenvalues are positive, which indicates that reducing FA and W/C can improve the CS of BFRC to some extent. Additionally, we can derive from Figure 9 that the SF and FL/FD variables have smaller sample eigenvalues and SHAP values close to 0, which indicates that both of them have little influence on improving the CS of BFRC.

5. Conclusions and Limitations

In order to avoid local optimal solutions and reduce the time for model parameter debugging, an extended XGBoost model (GA-XGBoost) with adoption of GA optimization parameters was designed in this study to facilitate the accuracy and stability of predicting the compressive strength of BFRC. For comparative analysis, we also used XGBoost, GBDT regressor, AdaBoost, RF, and SVR—five other regression models. The following conclusions were reached:

(1)

Compared to other regression models, the GA-XGBoost model shows the best accuracy and stability in predicting CS of BFRC. For the test dataset, the R², MSE, RMSE, and MAE of GA-XGBoost were 0.9483, 7.6962 MPa, 2.7742 MPa, and 2.0564 MPa, and the errors were within the acceptable range.

(2)

By using GAs to tune the parameters in the ML algorithm, a lot of debugging work can be avoided and the best combination of parameters can be obtained. For engineering applications involving ML algorithms, this can greatly assist in developing practical solutions.

(3)

According to SHAP analysis, W/B of BFRC is the most important variable that dominates CS, followed by FA and W/C. The variable FC has some influence on CS, while other variables, such as CA and SF, have less influence on CS. This can provide some reference for the design of BFRC fits.

These results show that the model has high prediction accuracy and stability, and has several application values:

(1)

It can guide the calculation of BFRC compressive strength required for engineering;

(2)

It effectively reduces the difficulty of obtaining BFRC compressive strength, reduces the experimental workload, saves time and cost, and is more economical and environmentally friendly;

(3)

We developed a genetic algorithm for parameter optimization to determine the key parameters of the prediction model, which can provide an effective reference for the optimization of other machine models.

While this study used a large data set containing 11 input variables to build the model, this also increased the complexity of the model. Having more input variables leads to more complex models, which may be detrimental to the generalization ability of the model. At the same time, the presence of these non-independent selected inputs in our input features may have led to redundant information in the data, affecting the performance and generalization ability of the model. We can consider optimizing these non-independent variables by means of feature engineering and quantitative simplification. Therefore, there may be limitations to machine-learning algorithms for practical engineering applications. Future research needs to explore whether input-variable reduction can enhance the accuracy and generalization ability of ML models.