Effect of Geometric Parameters on the Behavior of Eccentric RC Beam–Column Joints

Abstract

Over the last century, the seismic behavior of reinforced concrete (RC) beam–column joints has drawn many researchers’ attention due to their complex stress state. Such joints should possess sufficient capacity and ductility to ensure integrity and safety when subjected to cyclic loading during seismic events. In the literature, while most studies have focused on the behavior of concentric beam–column joints, few studies investigated the response of eccentric beam–column joints, in which the beam’s centerline is offset from the centerline of the column. Recent earthquakes demonstrated severe damage in eccentric beam–column joints due to their brittle torsional behavior, which may threaten the ductility required for the overall structural performance. To investigate the effect of brittle failure on the strength, ductility, and stability of eccentric beam–column joints, nonlinear finite element (FE) models were developed and validated. The FE model was employed to study the effect of some geometric parameters on the global and local behaviors of beam–column joints, including the joint type (exterior and interior), the column aspect ratio, and the joint aspect ratio. The results show that the joint aspect ratio, which is the ratio of beam-to-column depth, has a predominant effect on the failure behavior of the joint. Additionally, the increase in column aspect ratio alters the failure mode from brittle joint shear failure to ductile beam-hinge, although there is an increase in the joint torsional moment. The current study also showed that interior joints exhibited a higher out-of-plane moment as well as more extensive column torsion cracks compared to exterior joints.

1. Introduction

Beam–column joints are the most critical zones in reinforced concrete (RC) moment-resisting frames to withstand seismic loads due to the complex stress state and insufficient ductility compared to other structural components. The inelastic behavior of beam–column joints has been studied since the 1960s [1,2,3]. These studies have served as a basis for the design of beam–column joints, in which details of the requirements and stress limits are given to control the damage and deterioration of strength and stiffness in the connections [4,5,6]. Previous research on RC connections has mainly focused on the concentric configuration between the column and beam [4,7]. On the other hand, limited studies have examined the behavior of eccentric joints where the beam’s centerline is offset, in the plan, from the column centerline. Such eccentric joints are widely constructed, mainly in the perimeters of RC buildings.

The effect of joint eccentricity and other geometrical properties on the behavior of RC beam–column joints subjected to reverse-cyclic lateral loading has been examined [8,9,10,11,12,13]. In the early 1990s, Joh et al. [8], Lawrance et al. [9], and Raffaelle and Wight [13] observed early loss of strength and low ductility of cruciform eccentric beam–column joints due to the noticeable development of torsional cracks. Kusuhara et al. [11] demonstrated the effect of out-of-plane and torsion moments leading to a nonsymmetric yielding in beam reinforcement. Matsumoto et al. [14] emphasized that the reduction in shear strength of eccentric joints could be minimized with an eccentricity ratio, which is the ratio of the beam shift distance to the column width, below 0.25. Raffaele and Wight [13] highlighted the significance of the column aspect ratio on the failure behavior of eccentric beam–column joints. Teng and Zhou [15] tested six interior eccentric beam–column joints with various column aspect ratios and eccentricity ratios. They reported that the increase in eccentricity slightly impacted the joint subassemblies’ global behavior while massively affecting the joint shear distortion. Lee and Ko [16] showed a significant degradation in the joint capacity associated with an increase in the eccentricity ratio from 0.125 to 0.25. Moreover, Burak and Wight [17] indicated that the entire column cross-section works to resist the joint force when its aspect ratio is less than or equal to 1.5. The seismic performance of eccentric knee connections has also been assessed by Mogili et al. [18], with a column aspect ratio of 1.4 and a normalized eccentricity of 0.14. The authors observed lower shear capacity and energy dissipation in the joint opening action compared to concentric joints. Chen and Chen [19] have proposed a geometrical configuration for minimizing the torsional moment and maximizing the effective joint area via expanding the beam width at the beam and column interface, resulting in a remarkable improvement in the global and local behaviors of the joint subassembly.

In addition to the geometrical properties, other factors that influence the failure behavior of eccentric beam–column joints, such as joint reinforcement and level of axial load, were also investigated. Ma et al. [20] and Wong et al. [21] reported that increasing the joint reinforcement helped to improve the plastic deformation capacity and delay the joint deterioration. Goto and Joh [22] and Kusuhara et al. [11] have noted the same results with increased shear reinforcement at the joint region. It was also found that slab reinforcement helps to move the acting line of the resultant force away from the flush face, thus reducing the torsional demand caused by eccentricity [10,14,17,20]. Furthermore, Lee and Yu [23] observed considerable improvements in the seismic behavior of the eccentric beam–column joints using single- and double-headed bars. Moreover, the high level of the column axial load tends to minimize the wide column’s maximum torsional angle and to provide a minor enhancement in the energy dissipation and stiffness before bond failure [24,25].

It is noted from the literature that there is a scarcity of investigations on eccentric joints, especially with various geometrical configurations. This highlights the need for further studies to understand eccentric joint behavior better [26]. Currently, the design provisions of ACI-318 [27] and ACI-352 [26] are found to underestimate eccentric beam–column joint shear capacity [12]. This paper investigated the effect of various geometric design parameters on the failure behavior of eccentric joints. To do so, a finite element model (FEM) was developed and calibrated using the data available in the literature. The calibration models were further extended to study the effects of joint type (exterior or interior), column aspect ratio, and joint aspect ratio (beam-to-column depth ratio) on the global and local behaviors of the eccentric RC beam–column joint subassemblies.

The present study deals with the smeared crack modeling approach, in which local discontinuities (i.e., cracks) are distributed over a specific area within finite elements [28]. One of the most popular smeared crack concrete models is the concrete damage plasticity model (CDP), proposed by Lubliner et al. [29], developed by Lee and Fenves [30], and implemented in ABAQUS [31]. Because of the high computational cost of nonlinear analysis of RC structures, especially for fine mesh sizes between 25 mm and $12.5$ mm [32,33,34], many researchers [35,36,37,38,39,40] successfully obtain the detailed behaviors of different structural elements tested under cyclic loading (i.e., load–displacement backbone curves, cracking patterns, yielding in reinforcement bars) by adopting monotonic loads through the CDP model. On the other side, several researchers [41,42,43,44,45,46] failed to obtain the cyclic characteristics of different structural responses for elements modeled via CDP even at a 30 mm mesh element size [47]. As a result, monotonic loading is typically preferred over cyclic loading when using the CDP model due to the absence of shear retention, which can lead to improper capture of the pinching behavior during load cycles in shear-dominated scenarios [48]. While continuum FEM can be impractical for design or extensive parametric studies compared to physics-based models [49], it offers detailed insights into the internal distribution of stress and strain, as well as the initiation and development of cracking patterns [50]. As such, it is often used in conjunction with laboratory tests and can serve as an alternative means of filling gaps in the data used to develop physics-based models.

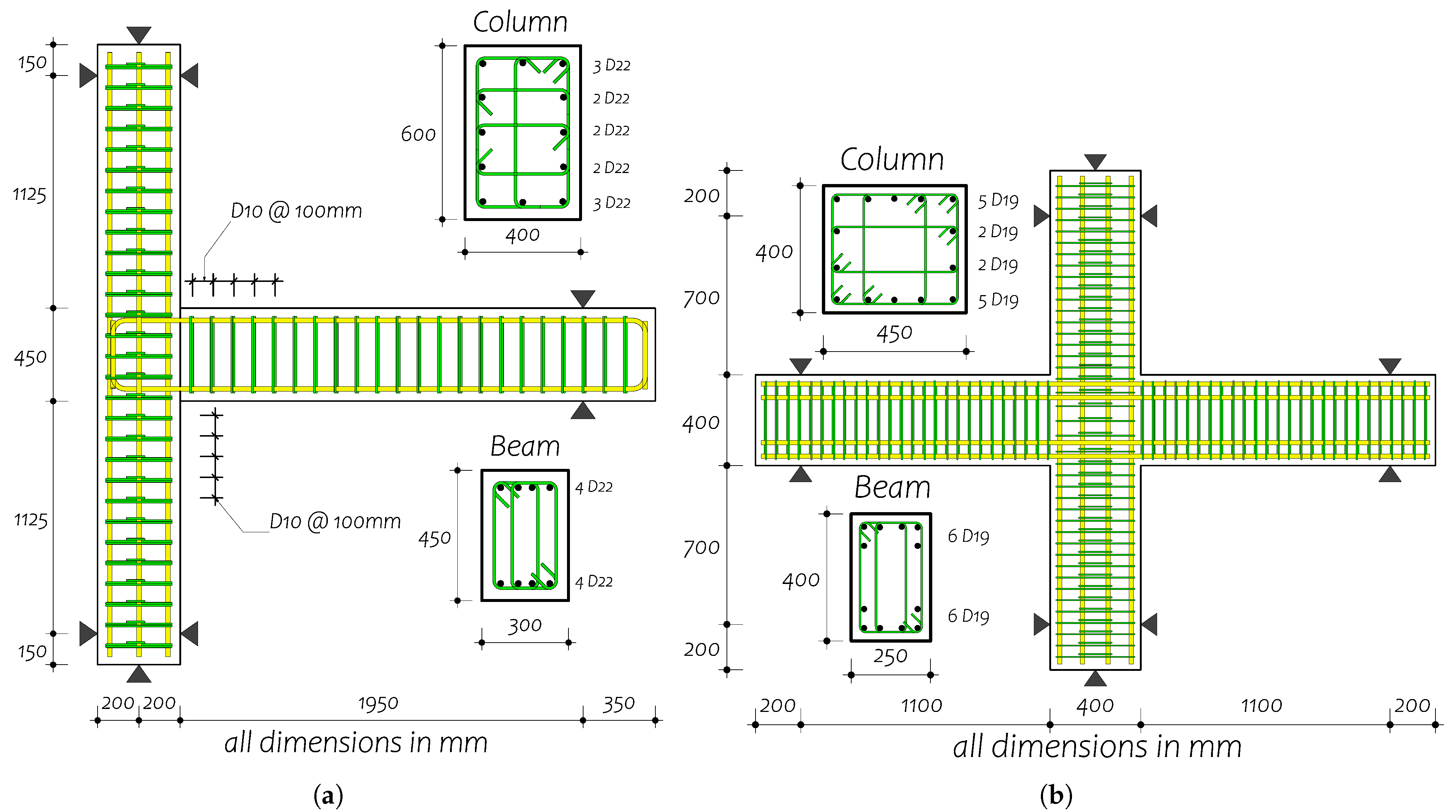
2. Reference Tests for Calibration

The experimental results of two full-scale eccentric beam–column joints (exterior and interior) were utilized to calibrate and validate the FE model. The geometry and reinforcement details for both joint subassemblies are shown in Figure 1a,b. The first joint in Figure 1a, denoted as W150, is an exterior joint examined by Lee and Ko [16] and was designed according to the ACI-318 and ACI-352 guidelines. The specimen was constructed using concrete with a 28-day compressive strength of $29.5$ MPa and a grade ASTM A706 [51] steel reinforcement for the longitudinal bars and stirrups. The second specimen in Figure 1b, denoted as J–10, is an interior joint tested by Matsumoto et al. [14] and was designed according to the Japanese code guidelines AJI [52]. The interior joint was constructed using concrete with a 28-day compressive strength and Young’s modulus of elasticity of 57 MPa and 36 GPa, respectively. In addition, steel grades USD685 [53] and SBPD1275/1420 [54] were used for the longitudinal rebars and stirrups, respectively.

The exterior and interior joints had column aspect ratios of $1.5$ and $1.125$, while the eccentricity ratios were $0.25$ and $0.22$, respectively. Furthermore, the joint aspect ratios were $1.125$ and $1.0$, respectively. The exterior joint exhibited joint deterioration after the beam plastic hinge development, known as beam-joint (BJ) failure mode [4]. In contrast, the interior joint showed early joint distortion even before the beam yield, which refers to the joint (J) failure mechanism [4]. Before applying cyclic load to the beams, axial forces equivalent to $0.1A_g{f}_{cm}$ and $0.2A_g{f}_{cm}$, where $A_g$ is the gross area of the column and $f_{cm}$ is the mean concrete compressive strength, were applied to the columns of the exterior and interior joint subassemblies, respectively. Both researchers reported that the columns’ ends were fully restrained against column rotation around the vertical axis. Moreover, the cyclic load schedules, as shown in Figure 2, were applied to the beam, not the column. As a result, the P-$\Delta$ effect was minimized.

3. Finite Element Model Details

Nonlinear finite element analysis performance and quality depend on all its fundamental components: the material constitutive model, finite element discretization, and solution approach. In this paper, the numerical model was developed using the ABAQUS^® finite element software package [31]. The details of the material constitutive model, model geometry and meshing, boundary conditions, and simulation parameters are discussed below.

3.1. Material Constitutive Models

3.1.1. Concrete

The concrete material was modeled using linear elastic isotropic and CDP models for uncracked and cracked material, respectively. For the elastic properties, the initial modulus of elasticity $E_{ci}$ for concrete was determined following the CEB-FIP model [55] as follows:

$$E_{ci}=E_{c0}{\alpha }_E{\left(\frac{f_{cm}}{10}\right)}^{1/3}$$

(1)

where $E_{c0}$ is $21.5\times {10}^3$ MPa, and ${\alpha }_E$ is assumed here as $0.9$ for limestone aggregates. An average value of $0.2$ for Poisson’s ratio $\nu$ is considered, which is a reasonable assumption for concrete material with a compressive strength ranging between 20 MPa and 120 MPa [56].

CDP was selected due to its unique plasticity mechanics, which describes the concrete pressure sensitivity and the irreversible deformation [57], while the damage can represent material deterioration due to cracking or crushing [58]. For concrete cracking, CDP utilizes the smeared crack model with a fixed orthogonal crack direction [59], where the crack initiation is detected by the simple Rankine criterion [60]. Furthermore, the yield function of CDP was modified based on the classical Drucker–Prager yield function [29,30]. For both nonlinear compression and tension models, the crack band model was utilized to minimize the pathological sensitivity of the numerical results to discretization parameters such as the element size in finite element simulations. The crack band model guarantees that the same amount of energy (i.e., the tensile fracture energy $G_{ft}$ and the compressive crushing energy $G_{fc}$) is dissipated during failures, independent of the element size [61].

For the compression behavior of concrete, the stress–strain curve consists of three stages, as shown in Figure 3a. The first stage is linear elastic up to a stress of $0.4f_{cm}$, in which the stresses and strains are governed by the secant modulus of elasticity $E_c$ at concrete stress of $0.4f_{cm}$ following Equations (2) and (3). The second stage is the strain-hardening part for concrete stress ranging between $0.4f_{cm}$ and $f_{cm}$. The stress in concrete in this stage ${\sigma }_{c\left(2\right)}$ is computed following the expression proposed by the FIB model code (2010) in Equations (4) and (5). In these equations, ${\epsilon }_c$ and ${\epsilon }_{cm}$ represent the compressive strain and the strain at the compressive strength, respectively.

$$E_{c\left(1\right)}=E_c{\epsilon }_c$$

(2)

$$E_c=\left(0.8+0.2\frac{f_{cm}}{88}\right)E_{ci}$$

(3)

$${\sigma }_{c\left(2\right)}=\frac{E_{ci}\frac{{\epsilon }_c}{f_{cm}}-{\left(\frac{{\epsilon }_c}{{\epsilon }_{cm}}\right)}^2}{1+(E_{ci}\frac{{\epsilon }_{cm}}{f_{cm}}-2)\frac{{\epsilon }_c}{{\epsilon }_{cm}}}{f}_{cm}$$

(4)

$${\epsilon }_{cm}=1.6{\left(\frac{f_{cm}}{10}\right)}^{0.25}\times {10}^{-3}$$

(5)

The third stage represents the strain-softening part for concrete passing the peak stress $f_{cm}$ till complete crushing failure. The concrete stress in this stage depends on the compressive crushing energy $G_{fc}$ and the mesh size $l_{ch}$, following the formulas of Krätzig and Pölling [62] in Equations (6) and (7). To determine the crushing energy, Equation (8) was adopted, where the ratio of the crushing energy to the fracture energy can be assumed to be proportional to the square of the ratio of the compressive strength to the tensile strength [63,64]. It was noted through the calibration process that the induced energy from Equation (8) overestimates the post-peak responses of both connections. For this reason, half of the induced crushing energy obtained from Equation (8) was adapted in the FEM. In Equations (6)–(8) ${\epsilon }_c^{pl}$, ${\epsilon }_c^{in}$, and $f_{tm}$ are the compressive damaged plastic strain, the compressive inelastic strain, and the main tensile strength, respectively.

$${\sigma }_{c\left(3\right)}=\frac{1}{\left(\frac{2+{\gamma }_c{f}_{cm}{\epsilon }_{cm}}{2f_{cm}}-{\gamma }_c{\epsilon }_c+\frac{{\epsilon }_c^2{\gamma }_c}{2{\epsilon }_{cm}}\right)}$$

(6)

$${\gamma }_c=\frac{{\pi }^2{f}_{cm}{\epsilon }_{cm}}{2{\left[\frac{G_{fc}}{l_{ch}}-0.5f_{cm}\left({\epsilon }_{cm}\left(1-b\right)+b\frac{f_{cm}}{E_c}\right)\right]}^2},b=\frac{{\epsilon }_c^{pl}}{{\epsilon }_c^{in}}$$

(7)

$$G_{fc}={\left(\frac{f_{cm}}{f_{tm}}\right)}^2{G}_{ft}$$

(8)

On the other side, the formula in Equation (9), proposed by Cornelissen [65] and validated by Hordijk [66], was employed in the present study to model the tension behavior of concrete, as shown in Figure 3b, using the STRA option since it gives the best results compared to the others [67]. In this formula, ${\sigma }_t$ is the tensile stress normal to the crack direction, $f_t$ is the modified tensile strength determined using Equation (10), $w_t$ represents the crack opening displacement at any stress level ${\sigma }_t$, $w_{cr}$ is the crack opening displacement at the complete release of the stress or fracture energy obtained using Equation (11) as a function of the fracture energy $G_{ft}$ and the mean tensile strength $f_{tm}$, and $c_1=3.0$ and $c_2=6.93$ are constants determined from the tensile tests of concrete [66]. The mean tensile strength $f_{tm}$ and the fracture energy $G_{ft}$ can be obtained from Equations (12) and (13), respectively, following the CEB-FIP model code (2010). In Equation (13), $f_{cmo}=10$ MPa and $G_{fo}$ is the base fracture energy depending on the maximum aggregate size $d_{max}$. The value of $G_{fo}$ is selected as $0.028$ N/mm for $d_{max}$ equivalent to $12.5$ mm used in the tested exterior and interior joints. In this study, a reduction factor of $0.7$ is selected for the modified tensile strength $f_t$ to avoid overestimating the tensile softening behavior [68,69]. The descending segment of the tensile stress–strain curve in Figure 3b was obtained in terms of the crack opening from the kinematic relation presented in Equation (14), assuming that there is a single crack per element perpendicular to the tensile stress. In this equation, ${\epsilon }_t$ and ${\epsilon }_{tm}$ represent the tensile strain and the strain at the tensile strength, respectively.

$$\frac{{\sigma }_t}{f_t}=\left[1+{\left(c_1\frac{w_t}{w_{cr}}\right)}^3\right]e^{(-c_2\frac{w_t}{w_{cr}})}-\left[\frac{w_t}{w_{cr}}\left(1+c_1^3\right)\right]e^{-c_2}$$

(9)

$$f_t=0.7\sim 1.3f_{tm}$$

(10)

$$w_{cr}=5.14\frac{G_{ft}}{f_{tm}}$$

(11)

$$f_{tm}=0.317{\left(f_{cm}\right)}^{0.6}$$

(12)

$$G_{ft}=G_{fo}{\left(\frac{f_{cm}}{f_{cmo}}\right)}^{0.7}$$

(13)

$${\epsilon }_t={\epsilon }_{tm}+\frac{w_t}{l_{ch}},{\epsilon }_{tm}=\frac{f_t}{E_{cm}}$$

(14)

Figure 3. Energy-based models for uniaxial behaviors of concrete in (a) compression, and (b) tension.

Figure 3. Energy-based models for uniaxial behaviors of concrete in (a) compression, and (b) tension.

For the damage evaluation, the CDP model utilizes the scalar isotropic damage equation. Two independent uniaxial damage variables, $d_c$ and $d_t$, are used to characterize the responses of the degraded material in compression and tension following Equations (15) and (16), respectively [70]. Moreover, the values used to establish the curves in Figure 3 are summarized in

Table 1. Parameter values for modeling CDP in the exterior and interior connections.

Ref.	${\mathit{f}}_{\mathit{cm}}$ (MPa)	${\mathit{E}}_{\mathit{c}}$ (GPa)	${\mathit{\epsilon }}_{\mathit{cm}}$	$\mathit{\nu }$	${\mathit{f}}_{\mathit{t}}$ (MPa)	${\mathit{G}}_{\mathit{ft}}$ (N/mm)	${\mathit{G}}_{\mathit{fc}}$ (N/mm)	${\mathit{K}}_{\mathit{c}}$	$\mathit{ϵ}$	${\displaystyle \frac{{\mathit{\sigma }}_{\mathit{bo}}}{{\mathit{\sigma }}_{\mathit{co}}}}$	${\mathit{\psi }}^{\mathbf{°}}$
Exterior connection	29.5	23.15	0.0016	0.2	1.7	0.06	4.5	2/3	0.1	1.16	Beam	48
											Column	56
Interior connection	57.0	30.6	0.0017		2.7	0.1	12				Beam	35
											Column	56

.

$$d_c=1-\frac{{\sigma }_c}{f_{cm}}$$

(15)

$$d_t=1-\frac{{\sigma }_t}{f_t}$$

(16)

Furthermore, the multi-axial behavior in the CDP model is characterized by four parameters, i.e., the tensile-to-compressive meridian ratio $K_c$, plastic potential eccentricity $ϵ$, biaxial-to-uniaxial compressive strength ratio $\frac{{\sigma }_{bo}}{{\sigma }_{co}}$, and dilatation angle ${\psi }^{°}$. CDP parameters have been subjected to some degree of uncertainty due to variations in material properties and testing conditions [35]. However, because ${\psi }^{°}$, which is used to define the non-associated potential plastic flow, depends on the confinement pressure and loading history [71], it requires careful calibration to ensure accurate results. To achieve this, $K_c$, $ϵ$, and $\frac{{\sigma }_{bo}}{{\sigma }_{co}}$ are set to the model’s default values, as shown in Table 1. On the other side, a sensitivity analysis has been performed using the values of ${52}^{°}$, ${45}^{°}$, and ${56}^{°}$ for ${\psi }^{°}$. The capacity loads of the exterior and interior joints converged at ${56}^{°}$. However, the numerical curves achieved the convergence at the cracking and yielding stages when ${\psi }^{°}$ of the beam was reduced to ${48}^{°}$ and ${35}^{°}$ for the exterior and interior connections, respectively. This technique provided a good representation of the cracks’ growth and distribution, close to laboratory observations. For the parametric study, dilatation angles of ${48}^{°}$ for the beam and ${56}^{°}$ for the column were used.

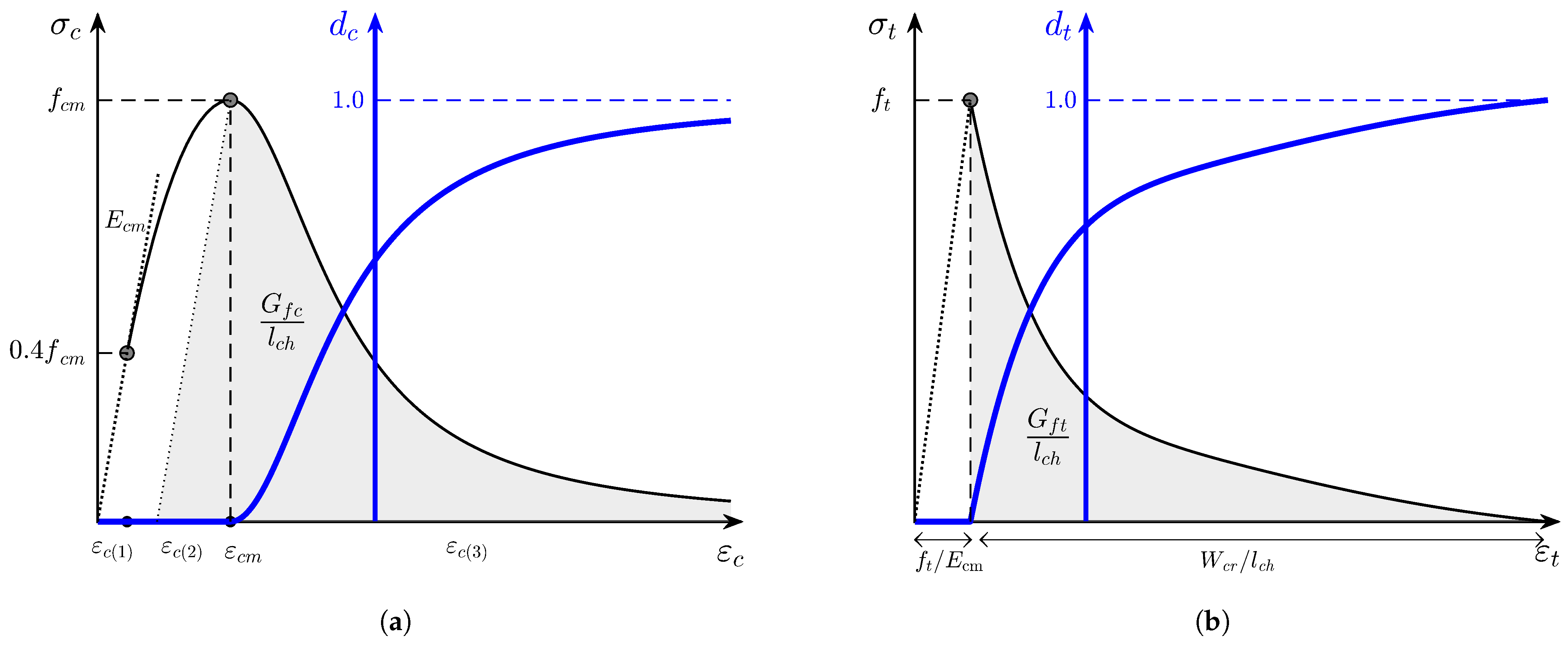
3.1.2. Reinforcing Steel

The steel is modeled using isotropic elasticity and von Mises’ classical metal plasticity yield surface. The associated plastic flow is determined using the uniaxial stress–strain relationship coupled with damage and failure for ductile metals. The stress in the steel rebars is obtained following Mander [72], as in Equation (17).

$$f_s=\left\{\begin{array}{c}{E}_s{\epsilon }_s\\ f_y\\ f_y+{\left(\frac{{\epsilon }_u-{\epsilon }_s}{{\epsilon }_u-{\epsilon }_{sh}}\right)}^p(f_y-f_u)\\ f_u\end{array}\begin{array}{c}\mathrm{for}\hfill \\ \mathrm{for}\hfill \\ \mathrm{for}\hfill \\ \mathrm{for}\hfill \end{array}\right.\begin{array}{c}{\epsilon }_s\le {\epsilon }_y\\ {\epsilon }_y\le {\epsilon }_s\le {\epsilon }_{sh}\\ {\epsilon }_{sh}\le {\epsilon }_s\le {\epsilon }_u\\ {\epsilon }_s\le {\epsilon }_F\end{array}$$

(17)

where $E_s$ is the steel’s modulus of elasticity, $f_y$ is the yield stress of the reinforcing steel, p is a parameter used to define the hardened part of the steel behavior, which is equal to 4, $f_u$ is the ultimate strength of the reinforcing steel, ${\epsilon }_y$ is the yield strain where the yield plateau begins, ${\epsilon }_{sh}$ is the strain where the yield hardening begins, ${\epsilon }_u$ is the steel strain corresponding to $f_u$, and ${\epsilon }_F$ is the steel fracture strain. The properties of the steel rebars used in the exterior and interior eccentric joint specimens W150 and J–10 are listed in

Table 2. Steel material properties for the exterior and interior joints.

Ref.	Steel Type	Bar Size	${\mathit{E}}_{\mathit{s}}$ (MPa)	${\mathit{f}}_{\mathit{y}}$ (MPa)	${\mathit{\epsilon }}_{\mathit{y}}$	${\mathit{f}}_{\mathit{u}}$ (MPa)	el %
Exterior connection	ASTM A706 [51]	No. 7 22 mm long bars for beams and columns	200,000	454.5	0.00227	682.4	10
		No. 3 10 mm stirrups for beams and columns	200,000	471.3	0.00236	715.3	12
Interior connection	USD685 [53]	No. 6 19 mm long bars for columns	202,000	746	0.0055	1011	12
		No. 6 19 mm long bars for beams	185,000	710	0.0056	928	12
	SBPD1275/1420 [54]	6.2 mm stirrups for beams and columns	199,000	1276	0.0077	1453	5

$E_s$ is the elastic modulus of the steel reinforcing bars, $f_y$ is the yield stress, ${\epsilon }_y$ is the yield strain, $f_u$ is the ultimate stress, and $el\%$ is the elongation of the reinforcing bars.

. For the parametric study, the ASTM A706 steel reinforcement is utilized for the longitudinal bars and stirrups.

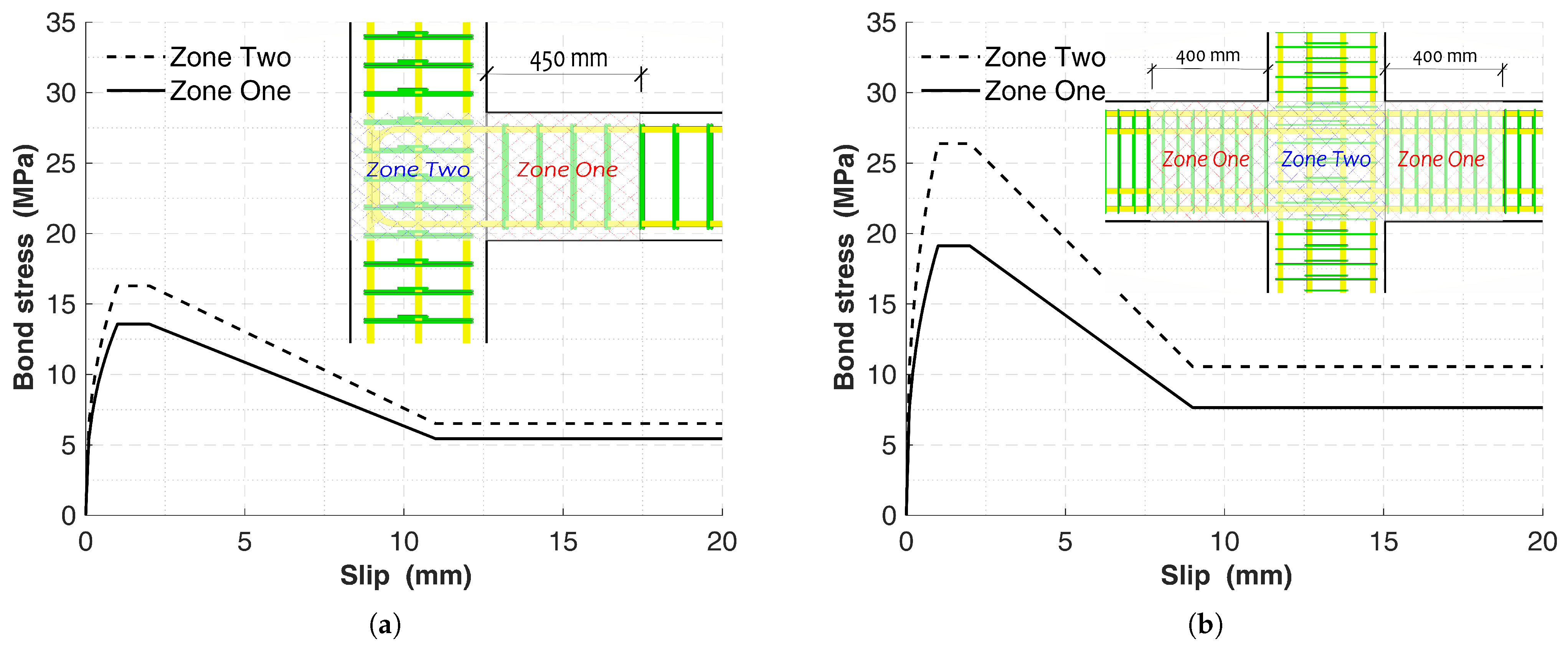
3.1.3. Bond between Concrete and Steel

The bond-slip between the concrete and reinforcing bars plays an essential role in the beam–column joint’s structural behavior, including shear capacity, ductility, and crack propagation [73]. Several techniques exist to simulate the interface contact between the concrete and the reinforcing bars, depending on how the bars are modeled (i.e., continuum solid or structural element). For modeling reinforcing bars as structural elements, the bond-slip behavior can be explicitly modeled via local bond-slip behavior using spring-like contact elements, known as translators, where the interface elements are restrained in the transverse direction and only allowed to move in the rebar direction simulating the slip conditions. The bond-slip relationships for the exterior and interior joints are shown in Figure 4a,b. Zone one and zone two are divided based on the differences in the bond-slip relationships between the concrete and the reinforcing bars within and outside the column of the joint. Zone one extends from the column face to a distance equal to a beam depth from the column face. Zone two is the joint zone within the column. Two different translator types are modeled. The translator for zone one is defined by the bond strength $\tau$, while the translator for zone two is defined via ${\Omega }_{p,tr}\tau$. ${\Omega }_{p,tr}$ accounts for the improvements resulting from the column axial force, while other factors that might impact the bond strength are implicitly modeled through tension-softening behavior. The bond–slip constitutive relationship is assumed following the CEB–FIP model (2010). In the model, the local bond stress $\tau$ is computed as a function of the relative slip s, as in Equation (18):

$$\tau =\left\{\begin{array}{c}{\tau }_{max}{(s⁄s_1)}^{\alpha }\\ {\tau }_{max}\\ {\tau }_{max}({\tau }_{max}-{\tau }_f)\frac{(s-s_2)}{(s_3-s_2)}\\ {\tau }_u\end{array}\begin{array}{c}\mathrm{for}\hfill \\ \mathrm{for}\hfill \\ \mathrm{for}\hfill \\ \mathrm{for}\hfill \end{array}\right.\begin{array}{c}0\le s\le s_1\\ s_1<s\le s_2\\ s_2<s\le s_3\\ s_3<s\end{array}$$

(18)

where ${\tau }_{max}=2.5\sqrt{f_{cm}}$ is the maximum bond strength, and ${\tau }_f=0.4{\tau }_{max}$ is the transferred bond stress by friction, which demolishes at a slip value of 40 × the bar diameter (40D) [74]. The relative slip limits $s_1$ and $s_2$ are selected as 1 mm and 2 mm, respectively. On the other hand, $s_3$ is assumed as the clear distance between the rebar ribs $c_{clear}$, which is equal to 11 mm for the exterior joint and 9 mm for the interior joint. The bond forces for the translator elements for zone one, $F_{Translator\_1}$, are computed using Equation (19) as:

$$F_{Translator\_1}=\tau .l.\pi .D$$

(19)

where l is the spacing between the translator elements is equal to $25.0$ mm, and D is the diameter of the bar. For zone two (joint zone), Equation (19) is modified by the increase factor ${\Omega }_{p,tr}$, which is obtained using Equation (20) [55] as:

$${\Omega }_{p,tr}=1.0-tanh\left(0.2\frac{P_{tr}}{0.1f_{cm}}\right)$$

(20)

where $P_{tr}$ is the transverse compression force. The translator forces in zone two can be, therefore, obtained using Equation (21) as:

$$F_{Translator\_2}={\Omega }_{p,tr}.F_{Translator\_1}$$

(21)

For computational efficiency, a full bond is assumed in the remaining regions of the model since these regions are less susceptible to observing debonding between steel rebars and concrete. The full bond is achieved by utilizing the embedded constraint algorithm between the embedded element (steel parts) and the host element (concrete parts).

3.2. Meshing

Incompatible mesh element C3D8I is used to define the concrete elements over other types of first-order interpolation hexahedral elements (i.e., full C3D8 and reduced C3D8R integration elements) to avoid shear locking and hourglass effects via its extra shape functions [43,75,76,77,78,79,80,81,82]. On the other hand, the steel reinforcement was modeled as discrete structural elements. The stirrups were modeled using the T3D2 truss mesh element type, while the longitudinal bars were modeled using the B31 beam mesh element type to enable rebar compressibility [43]. In addition to the steel material’s Poisson’s ratio of 0.3 utilized with the truss and beam mesh types, a Poisson’s ratio of 0.5 [31] was used in defining the longitudinal bars section.

For the FEM, the element size is selected to satisfy two conditions. First, according to crack band theory, the mesh element size must be in the range of the characteristic length of concrete introduced by Hillerborg et al. [83]. The characteristic length of concrete, also known as the crack band width, represents the part of the crack where the stress transfer is possible, which ranges between $d_a$ to $6d_a$, where $d_a$ is the nominal size of the concrete aggregate [84]. Others developed Equation (22) based on the modulus of elasticity, fracture energy, and main tensile strength to compute the characteristic length of concrete [83]. However, Bažant and Pijaudier-Cabot [85] reported the concrete characteristic length experimentally to be equal $3d_a$. Recently, it has been statistically calculated from many experiments, which have found it to be equal to 26 mm [86]. Second, in order to simulate the stiffening behavior between steel and concrete, the mesh element size must be greater than the magnitude computed from Equation (23) [87]. In the equations, ${\alpha }_{ts}$ and ${\rho }_{s,ef}$ represent the strength level of the interaction stress contribution, ranging between $0.4$ and $1.0$, and the effective reinforcement ratio, respectively. Based on the aggregate size of $12.5$ mm that was used for both experimental reference joints, an element size of 25 mm was selected.

$$h<\frac{E_c{G}_{ft}}{f_{tm}^2}$$

(22)

$$h>\frac{2G_{ft}}{f_{tm}({\epsilon }_y-\frac{{\alpha }_{ts}{f}_{tm}}{{\rho }_{s,ef}{E}_s})}$$

(23)

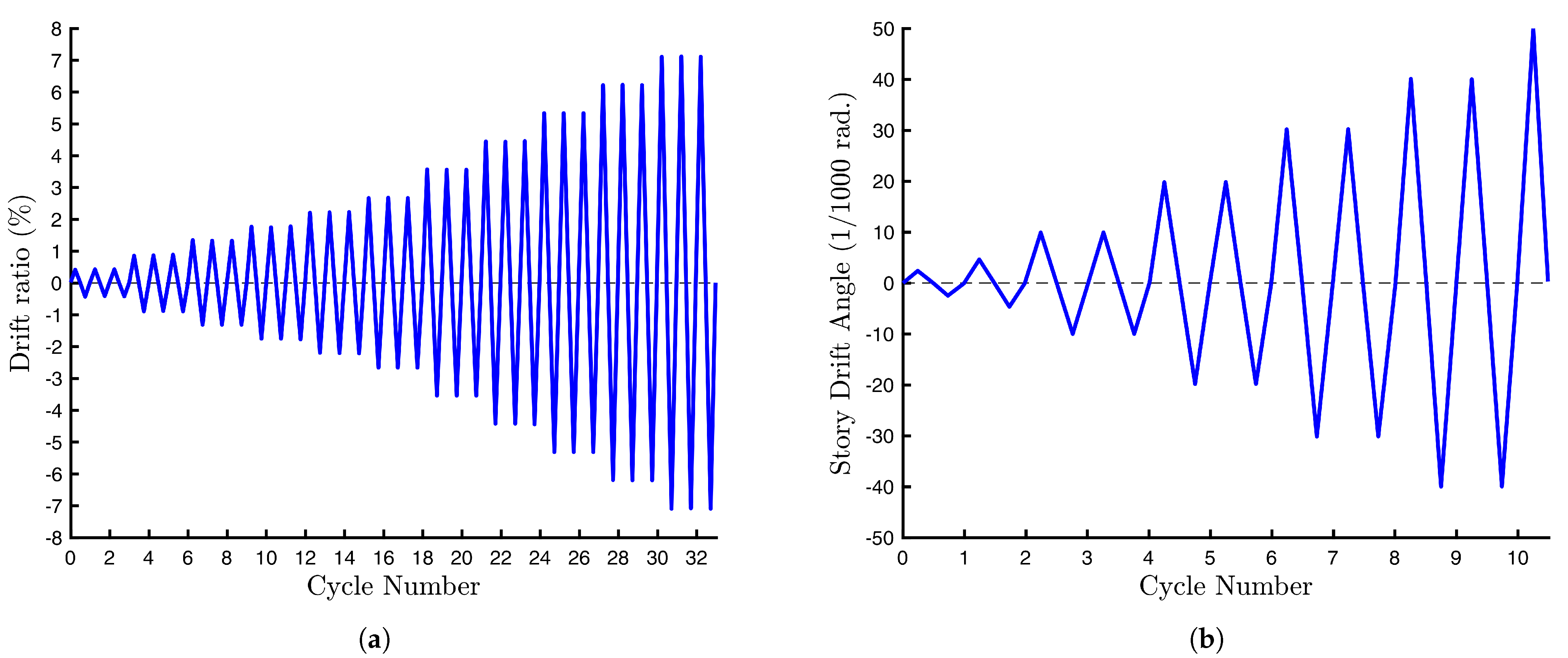
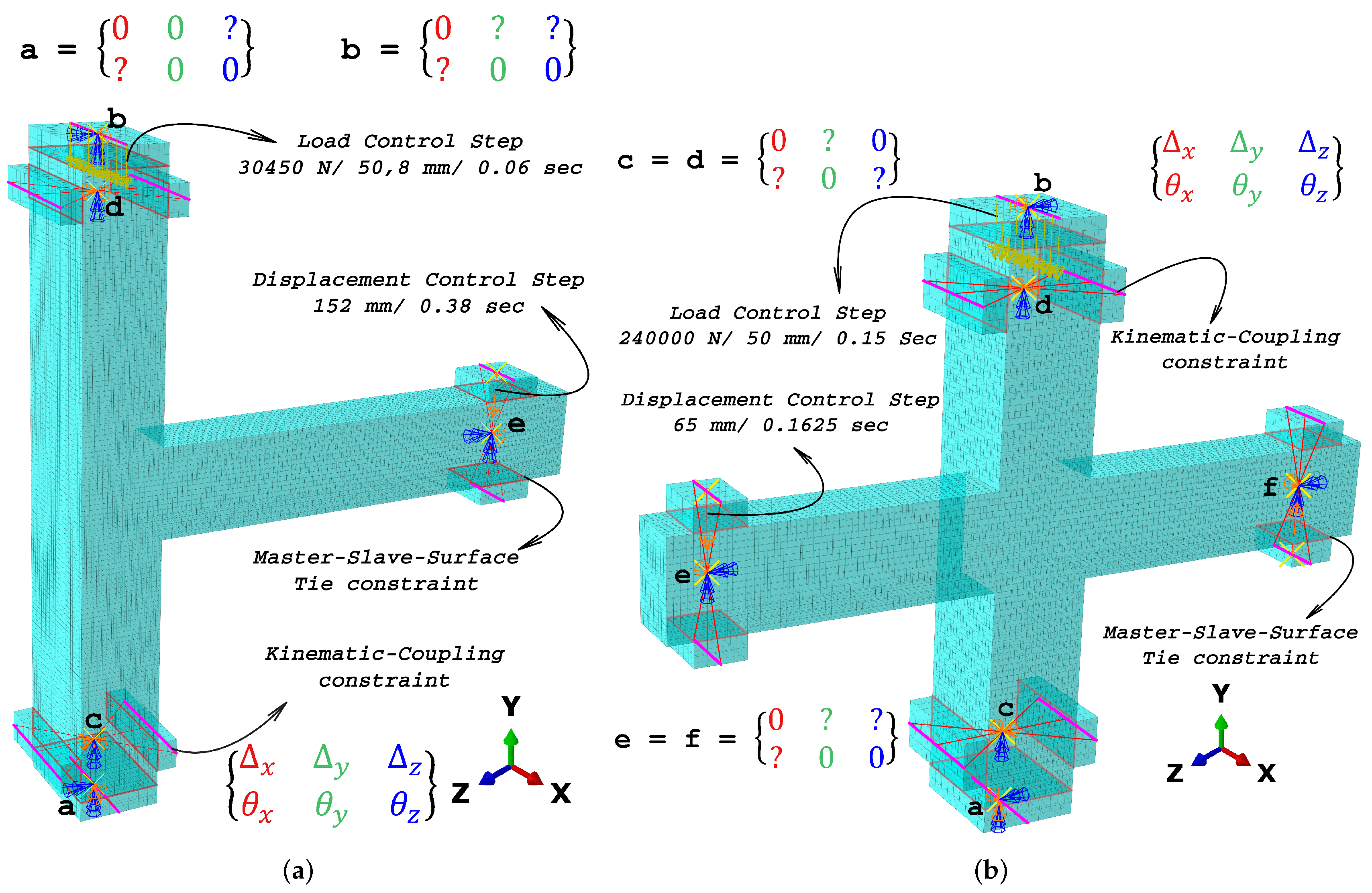
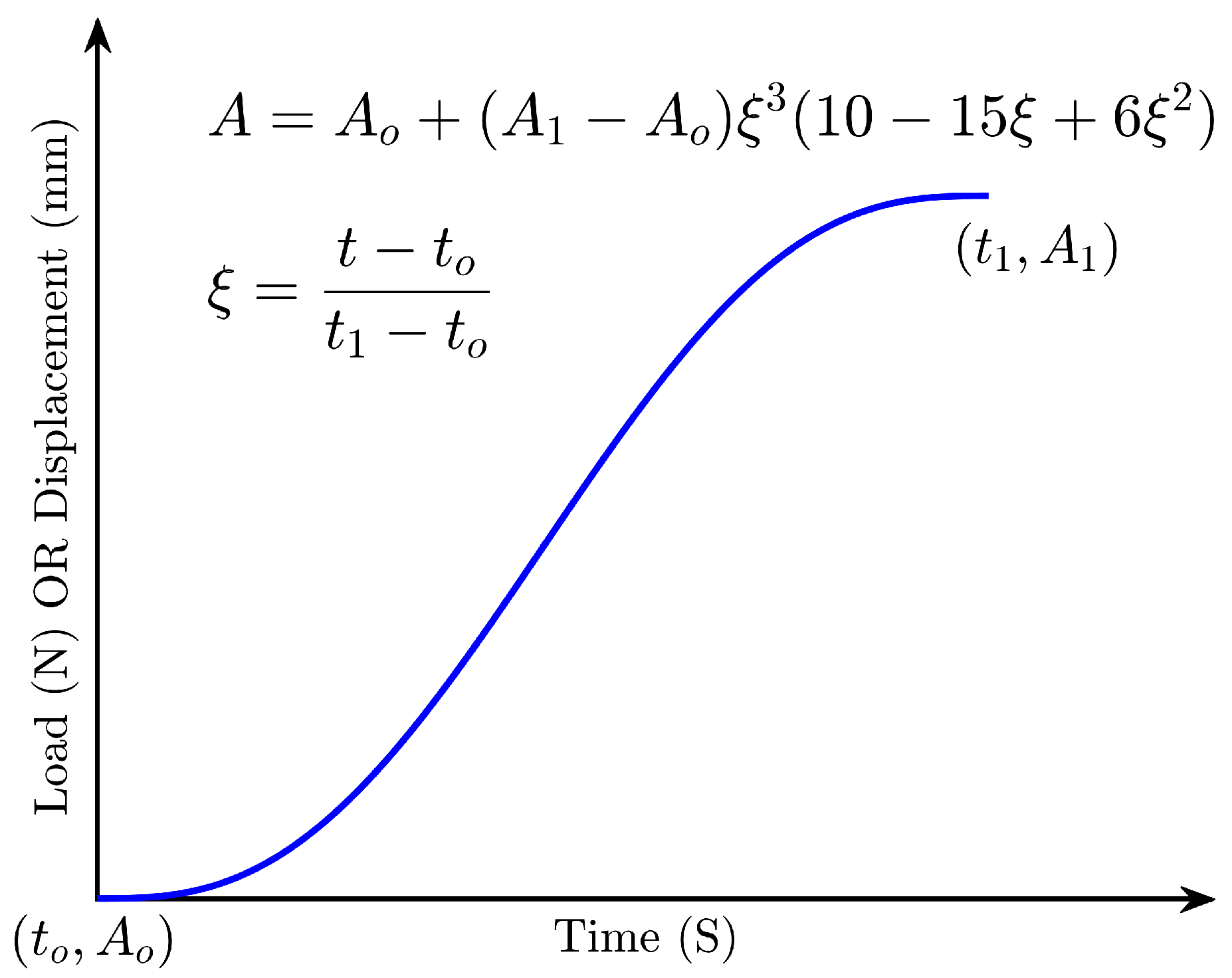
3.3. Boundary Conditions and Simulation Parameters

The ABAQUS\Explicit solver is used to perform the analysis of both joints. The explicit solver was selected over the implicit solver because of its capability to handle problems involving material and geometrical nonlinearities in addition to material damage. The explicit solver uses a time increment close to the stability time $\Delta t=L^e⁄C_d$ of the model based on the smallest element characteristic length $L^e$ and its material dilatational wave speed $C_d=\sqrt{E⁄\rho }$, where E is the modulus of elasticity and $\rho$ is the material density, making the computation time related linearly with the load rate scaling factor and the square root of the mass scaling factor.

The tips of the columns and beams were restrained to mimic pin- and roller-supports, confirming full restraint against the torsion moments about the members’ axes for both exterior and interior joints through implementing kinematic-coupling constraints, as shown in Figure 5a,b. The axial column load was applied at the beginning of the simulation via a load-controlled step and held constant throughout the simulation time. The lateral displacements were further applied monotonically at the beams’ tips. The analysis was carried out using double-precision accuracy through the built-in smooth-step amplitude curve, as shown in Figure 6, to suppress the dynamic oscillation with a velocity of 400 mm/s, similar to those utilized by Thai et al. [88] and Thai and Uy [89], resulting in a small friction of kinematic energy equal to $2\%$ of the internal energy. However, a fixed mass scaling factor was employed to modify the stability time since it reduced significantly through the analysis because of damage and/or plasticity.

4. Parametric Study

The geometric configurations of the beam–column joint have the most significant influence on its behavior after the material strength [4]. Hence, a parametric study was carried out on the geometric parameters of eccentric beam–column joints using the previously calibrated FE configurations. The study matrix consisted of three parameters: the joint type (interior and exterior joints), the joint aspect ratio (the ratio of the beam depth to column depth), and the column aspect ratio, as listed in

Table 3. The matrix of the current beam–column joint study.

Beam Dimensions (mm)	Joint Type	Column Dimensions (mm)	Eccentricity ($\mathit{e}/{\mathit{b}}_{\mathit{c}}$)	Joint Aspect Ratios (${\mathit{d}}_{\mathit{b}}/{\mathit{d}}_{\mathit{c}}$)	Column Aspect Ratios (${\mathit{b}}_{\mathit{c}}/{\mathit{d}}_{\mathit{c}}$)
450 × 300	Interior	600 × 400	0.25	1.125	1.5
		800 × 400	0.3125		2.0
		1000 × 400	0.35		2.5
	Exterior	600 × 400	0.25		1.5
		800 × 400	0.3125		2.0
		1000 × 400	0.35		2.5
600 × 300	Interior	600 × 400	0.25	1.5	1.5
		800 × 400	0.3125		2.0
		1000 × 400	0.35		2.5
	Exterior	600 × 400	0.25		1.5
		800 × 400	0.3125		2.0
		1000 × 400	0.35		2.5
800 × 300	Interior	600 × 400	0.25	2.0	1.5
		800 × 400	0.3125		2.0
		1000 × 400	0.35		2.5
	Exterior	600 × 400	0.25		1.5
		800 × 400	0.312		2.0
		1000 × 400	0.35		2.5

. The cross-section dimensions, reinforcement details, and model properties are all featured in Figure 7. Notably, $b_c$ stands for the column width, while $d_c$ and $d_b$ refer to the depths of the column’s and beam’s cross-sections, respectively, and e is the eccentricity. Symmetrical reinforcement was utilized on both the top and bottom of the beams, whereas the columns were modeled with a reinforcement ratio of $1.8\%$. The ranges for the examined geometrical parameters were selected within the limits of ACI-318 [27].

5. Results and Discussion

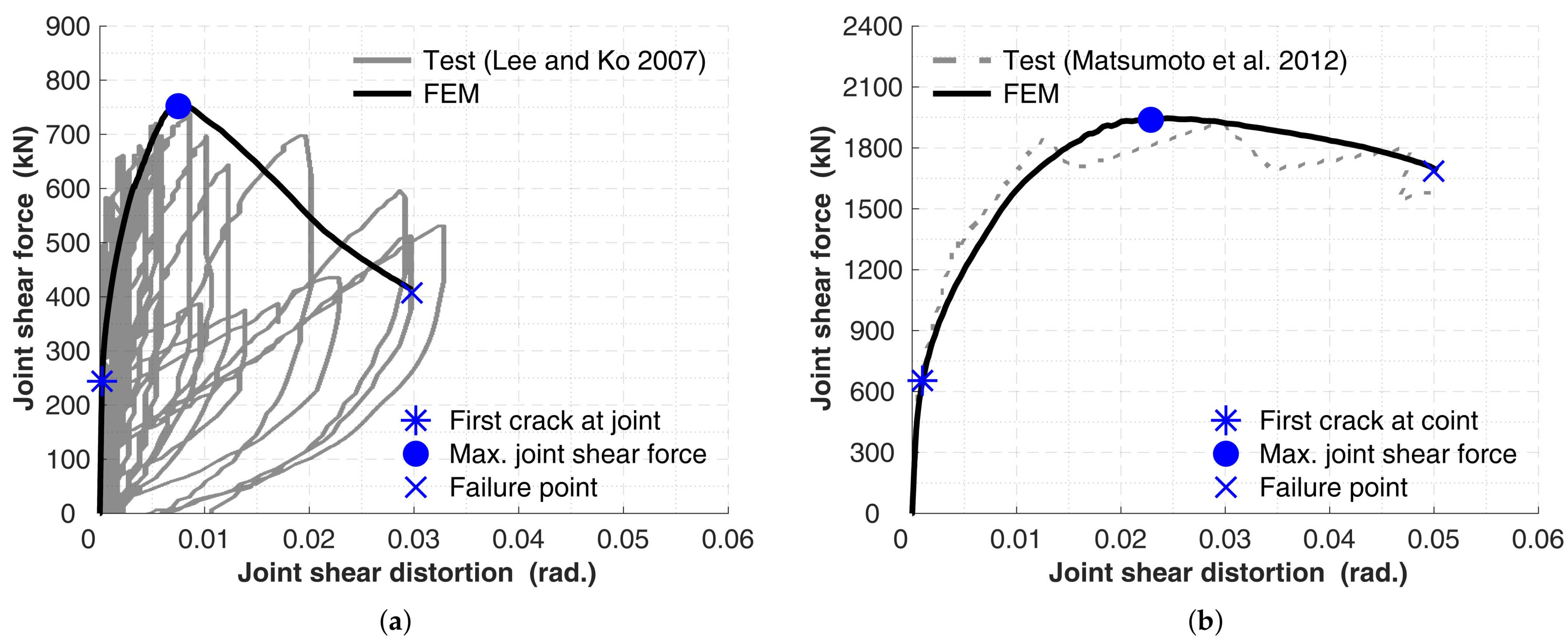
5.1. FE Model Calibration

The accuracy of the nonlinear finite element model using the previously calibrated constitutive model parameters and discretization characteristics is evaluated by comparing the numerical outputs with the experimental results in terms of the global and local behaviors of the joint subassemblies, the cracking pattern, failure mode, and strain profile of the steel reinforcement. In the case of the experiments, the joints were subjected to reversed cyclic loading, and hence, the force–deformation responses in the global and local behaviors are presented by the hysteresis loops. On the other hand, the FE model produced the force–deformation relationship in the form of backbone curves. The validation aims to ensure that the numerical models can predict the experimental behavior of the joints as closely as possible.

5.1.1. Global Behavior

The global behaviors of the exterior and interior joints are shown in Figure 8a,b, respectively. The figures show that the damaged plasticity model with the calibrated parameters can successfully predict the different failure mechanisms for both joints. However, the predicted curve for the exterior joint (W150) was slightly overestimated at the yield point, by about $3\%$, which can be considered negligible. Moreover, although the predicted and experimental readings for the maximum load points were almost identical, the predicted one was observed at a $4.5\%$ drift ratio (DR), while it was located at $4.0\%$ DR for the experimental specimen. This is acceptable since the maximum capacity of the joint is the point of intersection between the beam input shear and the joint shear capacity curves, which is positioned between two load cycles. On the other hand, the predicted interior joint curve is consistent with the experimental one.

5.1.2. Local Behavior

The local behaviors of the joints, involving the forces, moments, and deformations obtained via the integrated variables through the interior cross–section surfaces method, were compared to the laboratory measurements. Figure 9 reveals that the implemented previous method in the FE model can capture the real beam moment–rotations measured at two different locations on the beam of the exterior joint (W150) [16]. On the other side, the predicted joint shear behavior, defined as the joint shear force derived from the preceding technique versus the average of the shear distortions of the mesh elements located in the beam and column intersection, converges to the experimental readings with acceptable accuracy, as shown in Figure 10a,b.

The cracking of the exterior and interior joints was initiated at 254 kN and 640 kN associated with shear distortion angles of $2\times {10}^{-4}$ rad and $8\times {10}^{-4}$ rad. Furthermore, the shear capacities for the exterior and interior joints reached about 750 kN and 1954 kN at shear distortion angles of $0.0075$ rad and $0.024$ rad. At the maximum load, the exterior joint zone was found to resist shear forces six times that of the column, while this value was about four and a half for the interior joint. This agreed with the findings of Paulay [90], that the joint area is subjected to around four to six times the column shear force. Nonetheless, the main reinforcing steel was found to resist about $6\%$ of the joint shear force for the interior joint through the reinforcement dowel action and less than $2\%$ for the exterior joint.

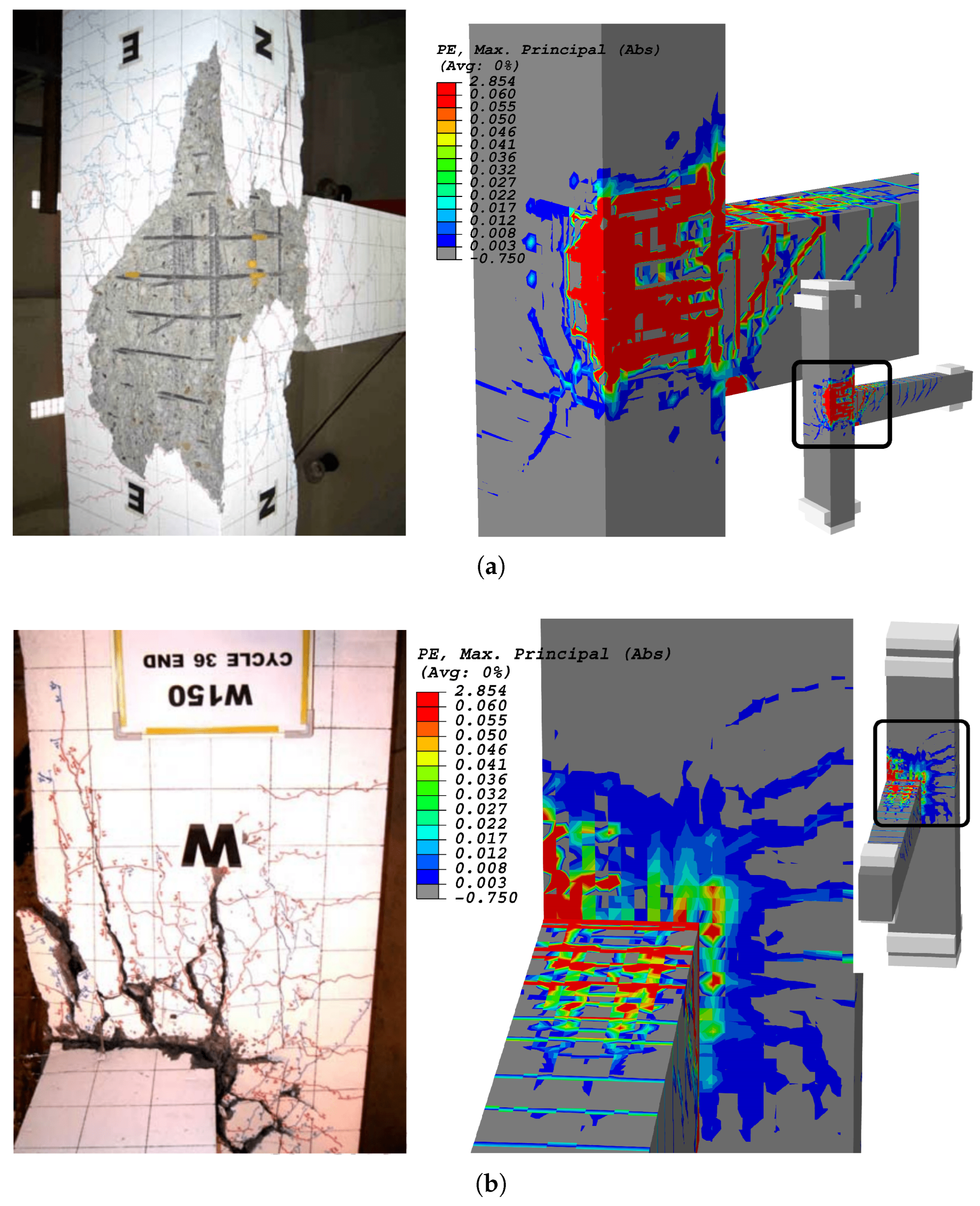
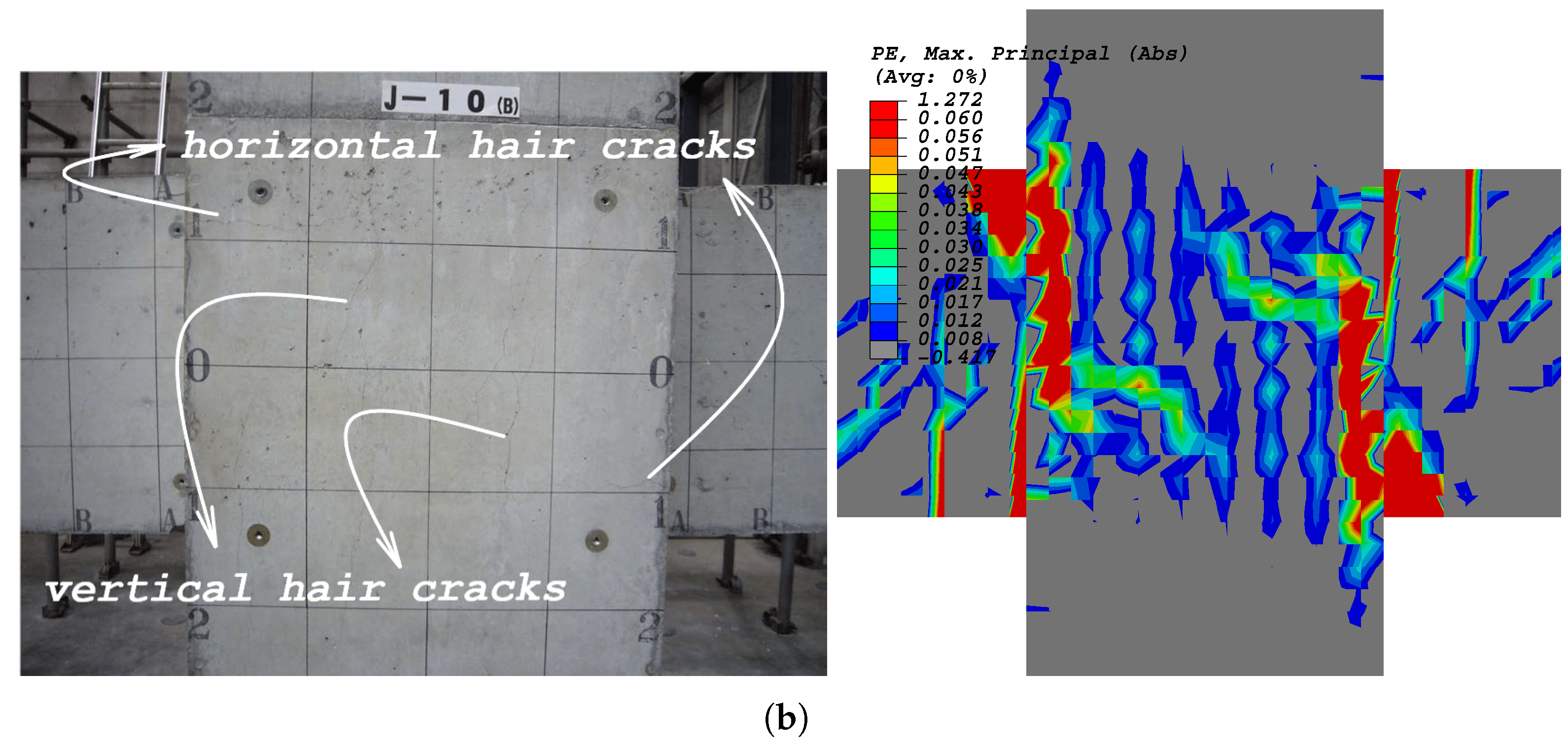
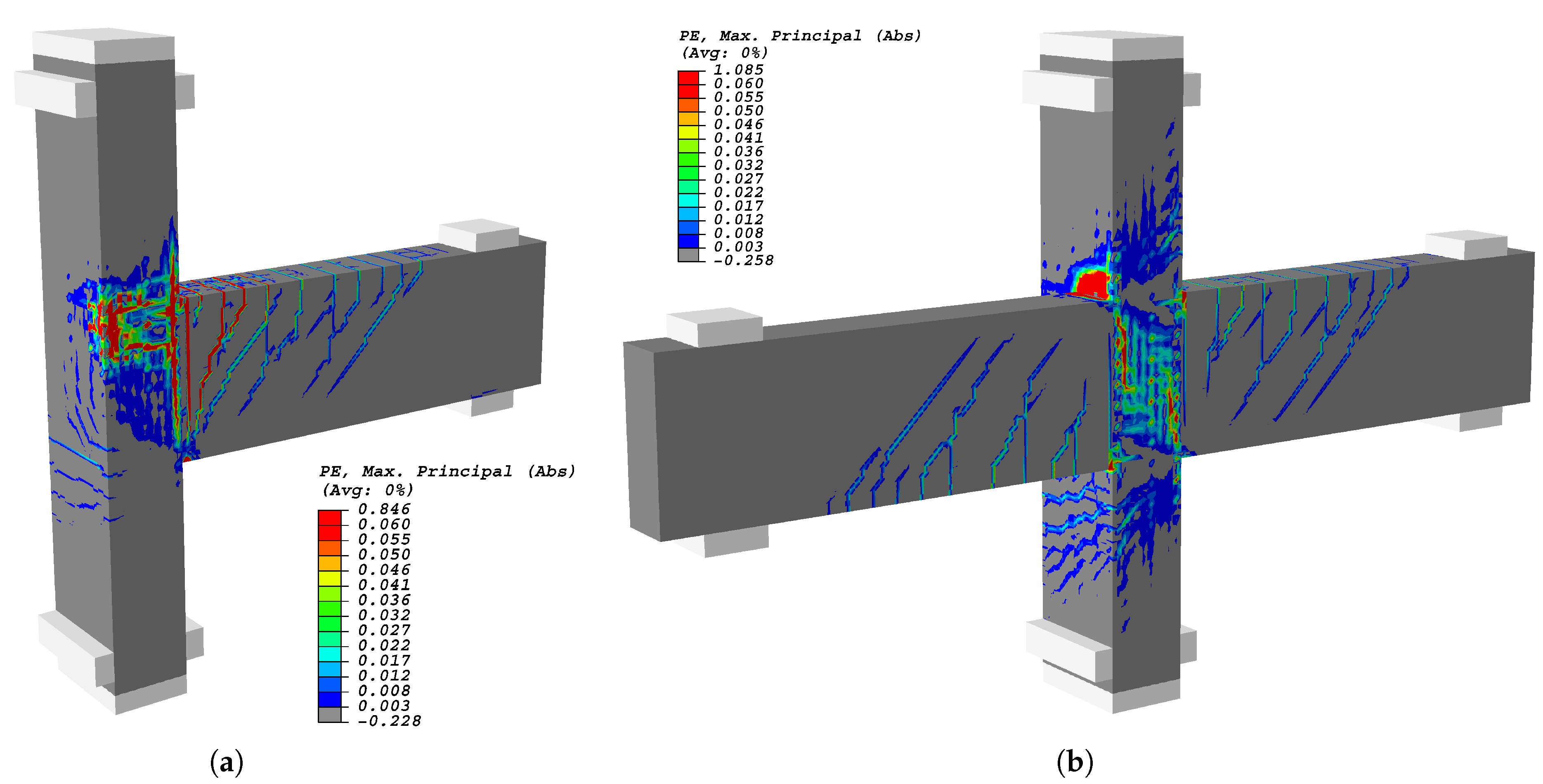
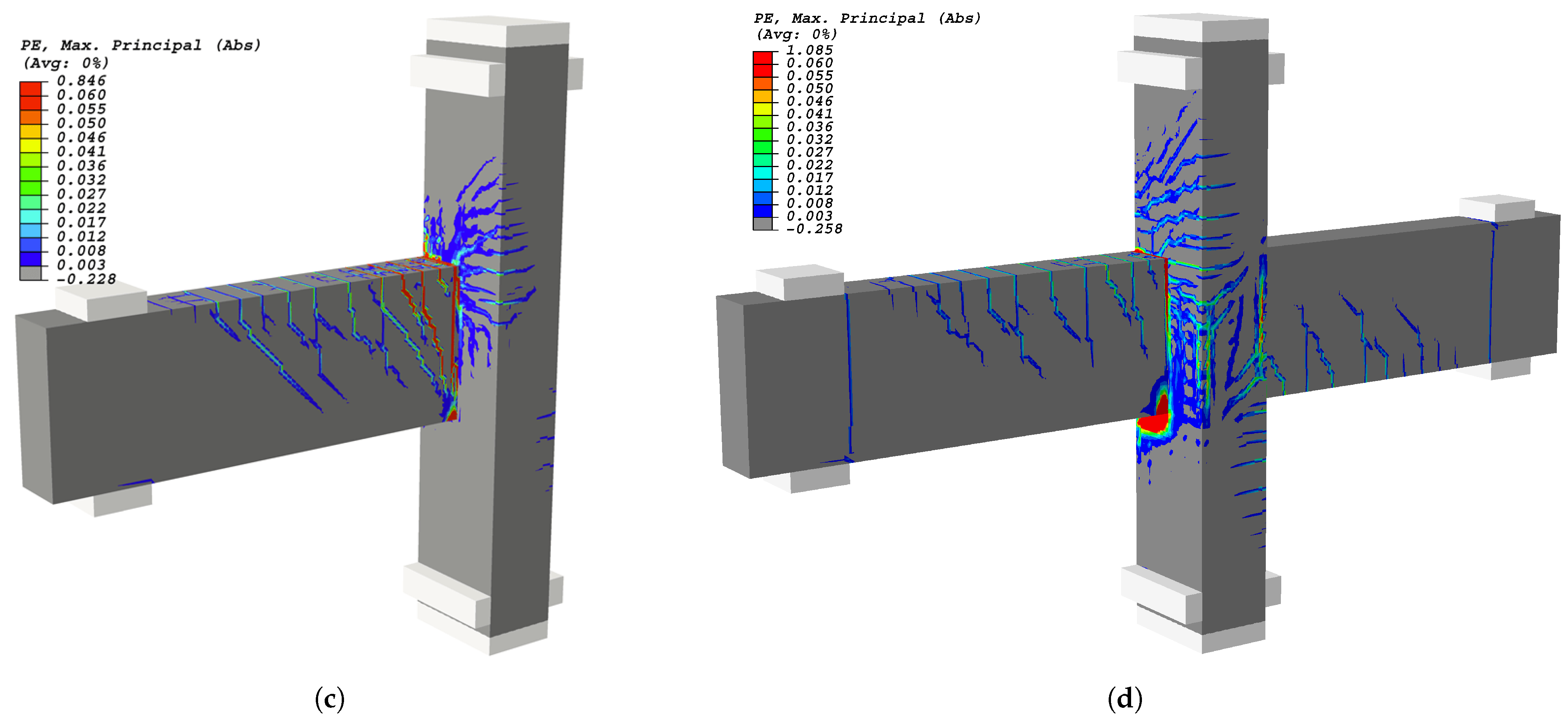
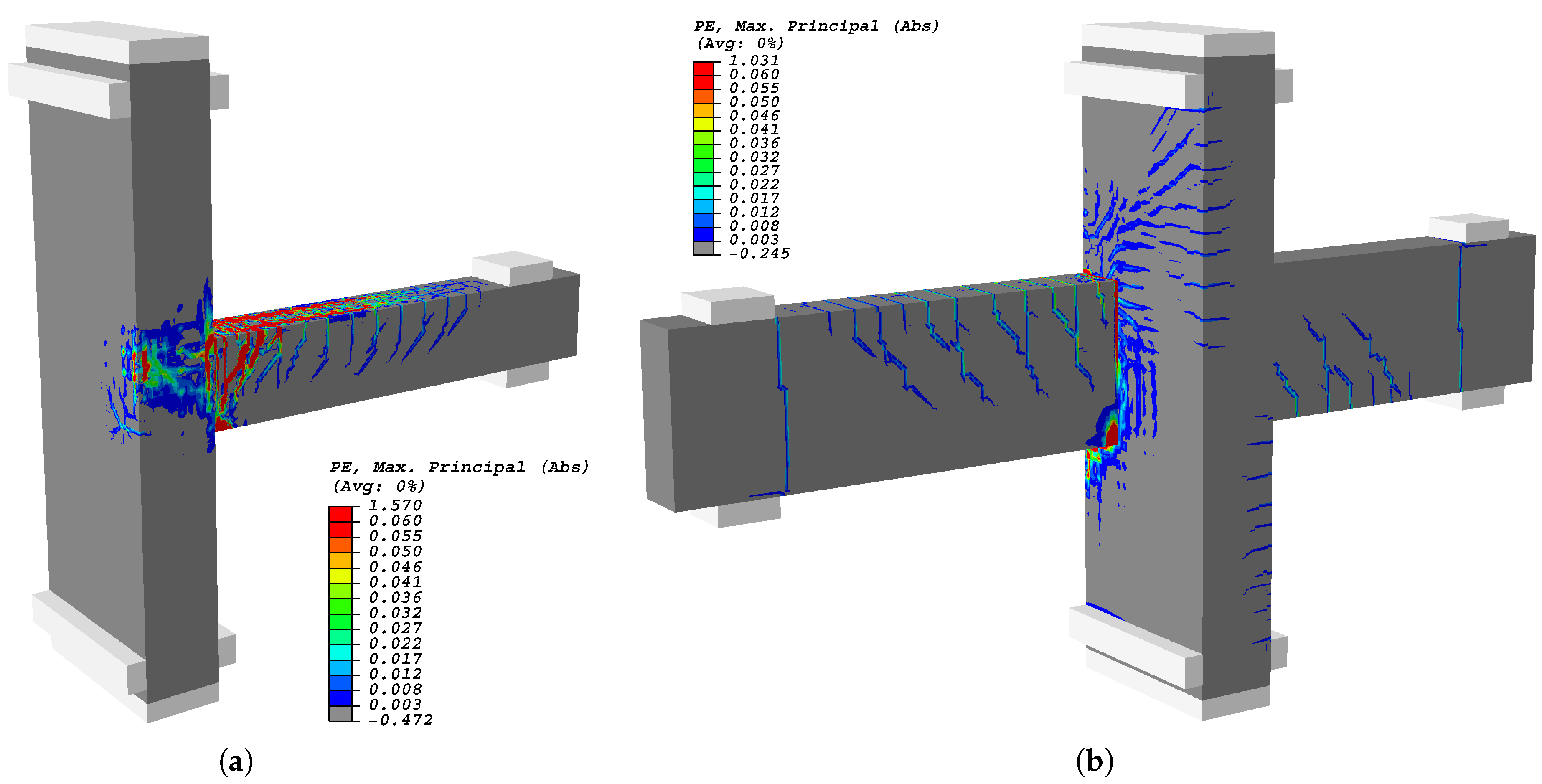
5.1.3. Cracking Pattern

Observing cracking patterns is a cornerstone in assessing the responses of reinforced concrete elements. Since the CDP model does not provide the material cracks, the crack pattern was graphically assessed by examining the contour plots of the maximum principal plastic strain PE. Figure 11 and Figure 12 display the comparisons between the predicted and experimental results of the cracking patterns of the eccentric exterior and interior joint models, respectively, at the end of the test. The flush sides of the joints experienced extensive diagonal shear cracks, which initiated at $0.25\%$ DR and $0.5\%$ DR for the exterior and interior joints, respectively. Later, new cracks grew until the maximum point load, and they expanded rapidly, resulting in concrete spalling at the joint faces, as shown in Figure 11a and Figure 12a. Although the far side of the exterior joint had no cracks, vertical hair cracks developed on the far side of the interior joint, as shown in Figure 12b, which may be attributed to the effect of the intermediate level $\left(0.2A_g{f}_{cm}\right)$ of the column axial load [91]. Moreover, the columns of both joints suffer from flexural and torsional cracks resulting from the joint eccentricity, in addition to a concrete spalling due to the bent bar pushing of the beam for the exterior joint model. Moreover, flexural cracks were initiated at around $1.0\%$ DR for both joints, while the torsional cracks developed at a $2\%$ DR. Furthermore, the cracks of the beam for the interior joint subassembly exhibited uneven depth and width between the beam faces due to the out-of-plane moment, which reached $16\%$ of the in-plane flexure moment. However, this percentage was only $4\%$ for the exterior joint.

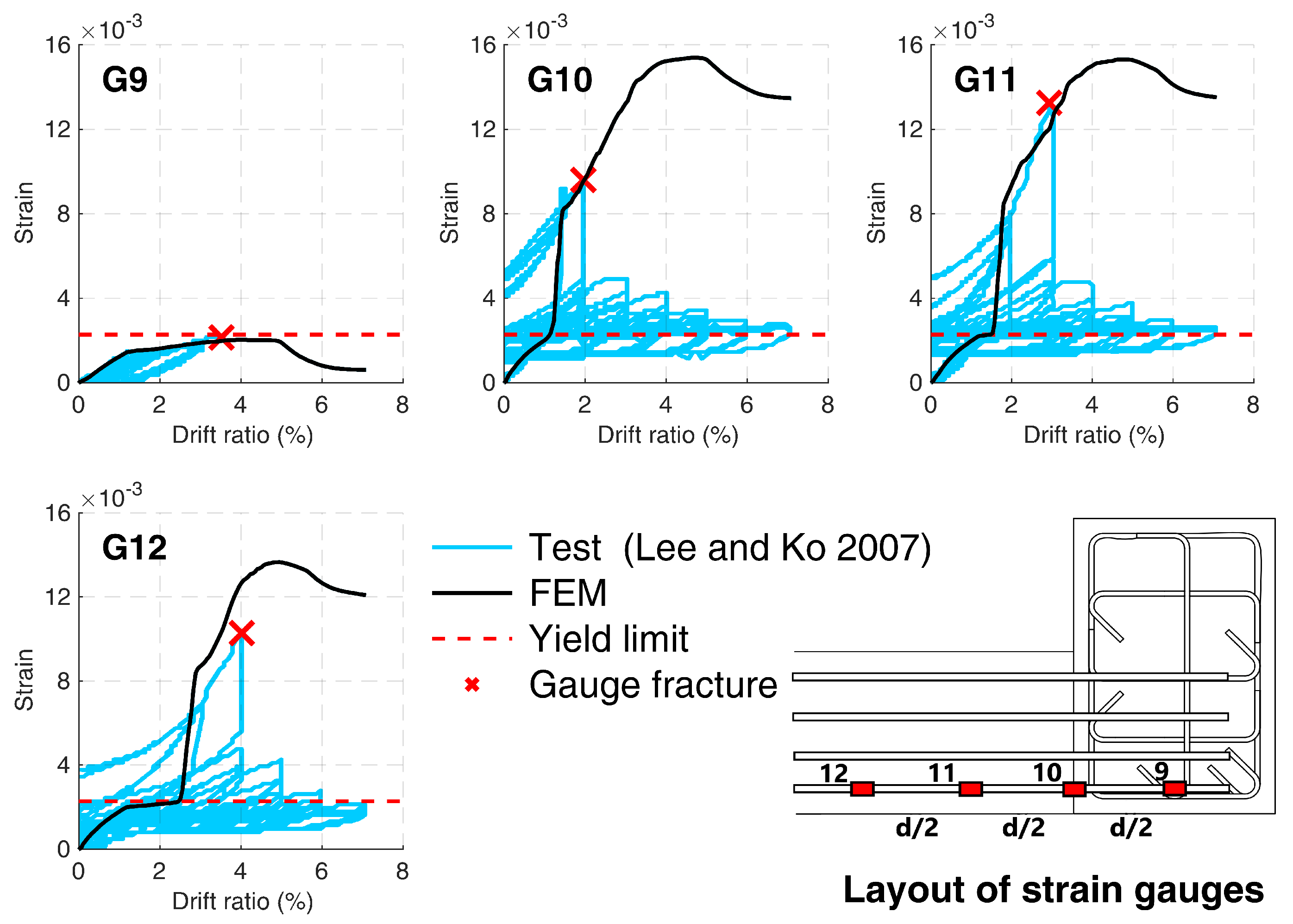
5.1.4. Strains in Steel Rebars

The numerical outputs of logarithmic strain LE11 in Figure 13 show a good agreement with the laboratory measurements reported in [16]. To this end, Figure 14a,b show the plastic strain PE11 of the steel reinforcement for both models. The beam bars yielded for both joints unsymmetrically due to the out-of-plane beam moment. The yielding extended 750 mm and 250 mm away from the column face for the exterior and interior joints, respectively. On the other side, the joint stirrups began to yield after the maximum load since the strain in the inner stirrup legs increased as the joint cracking increased, suggesting its vital role at this stage. These findings align with the research by Hwang et al. [92], which suggests that joint stirrups primarily delay joint collapse by controlling cracking rather than increasing shear strength through confinement.

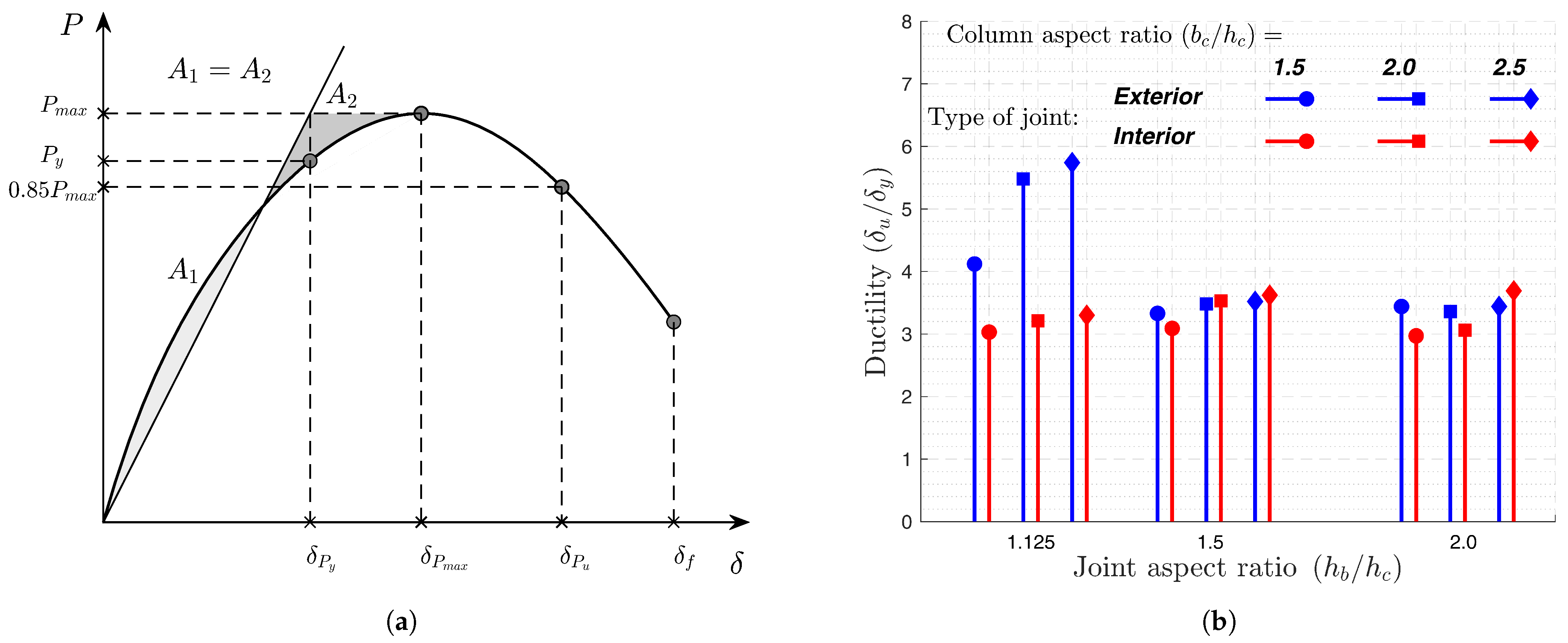
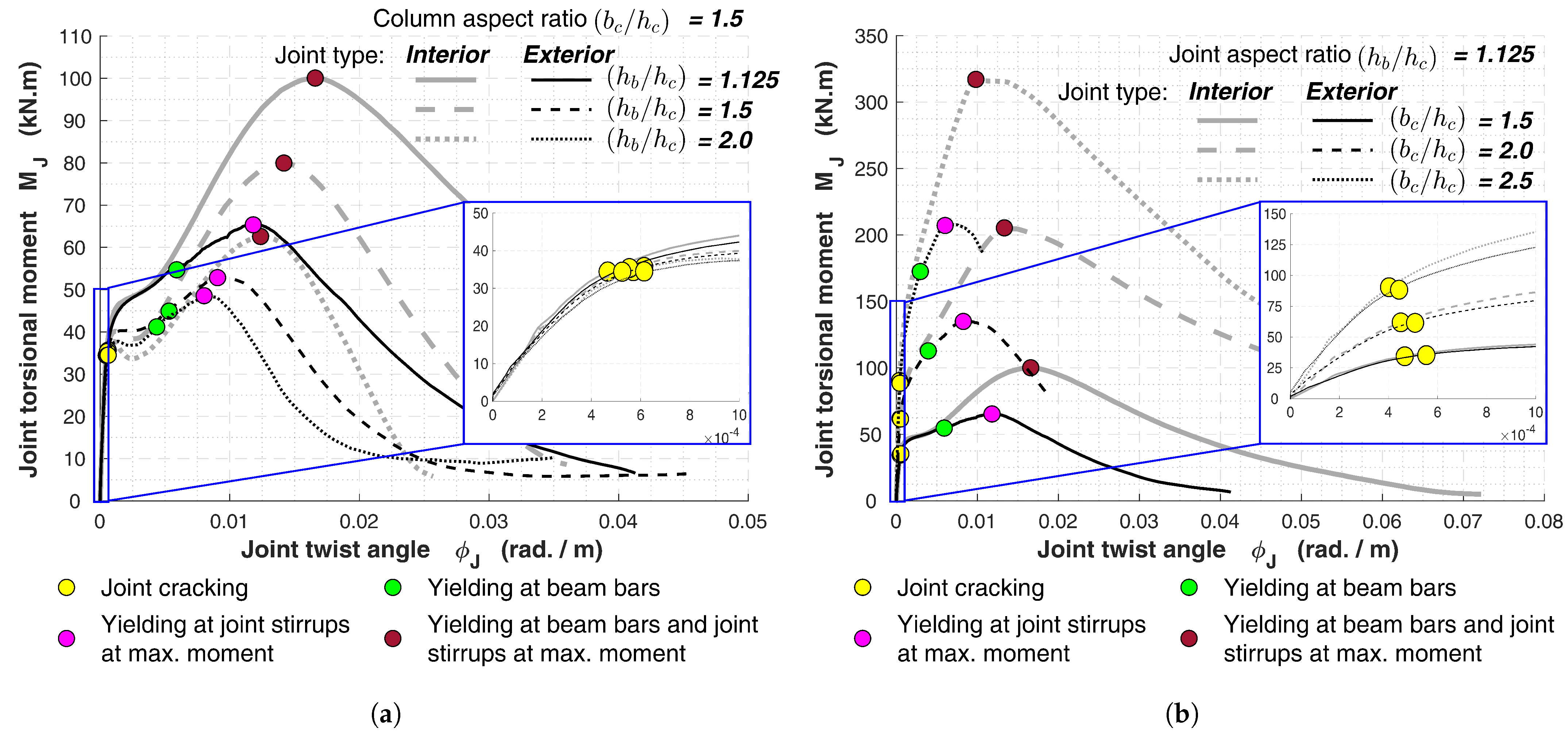
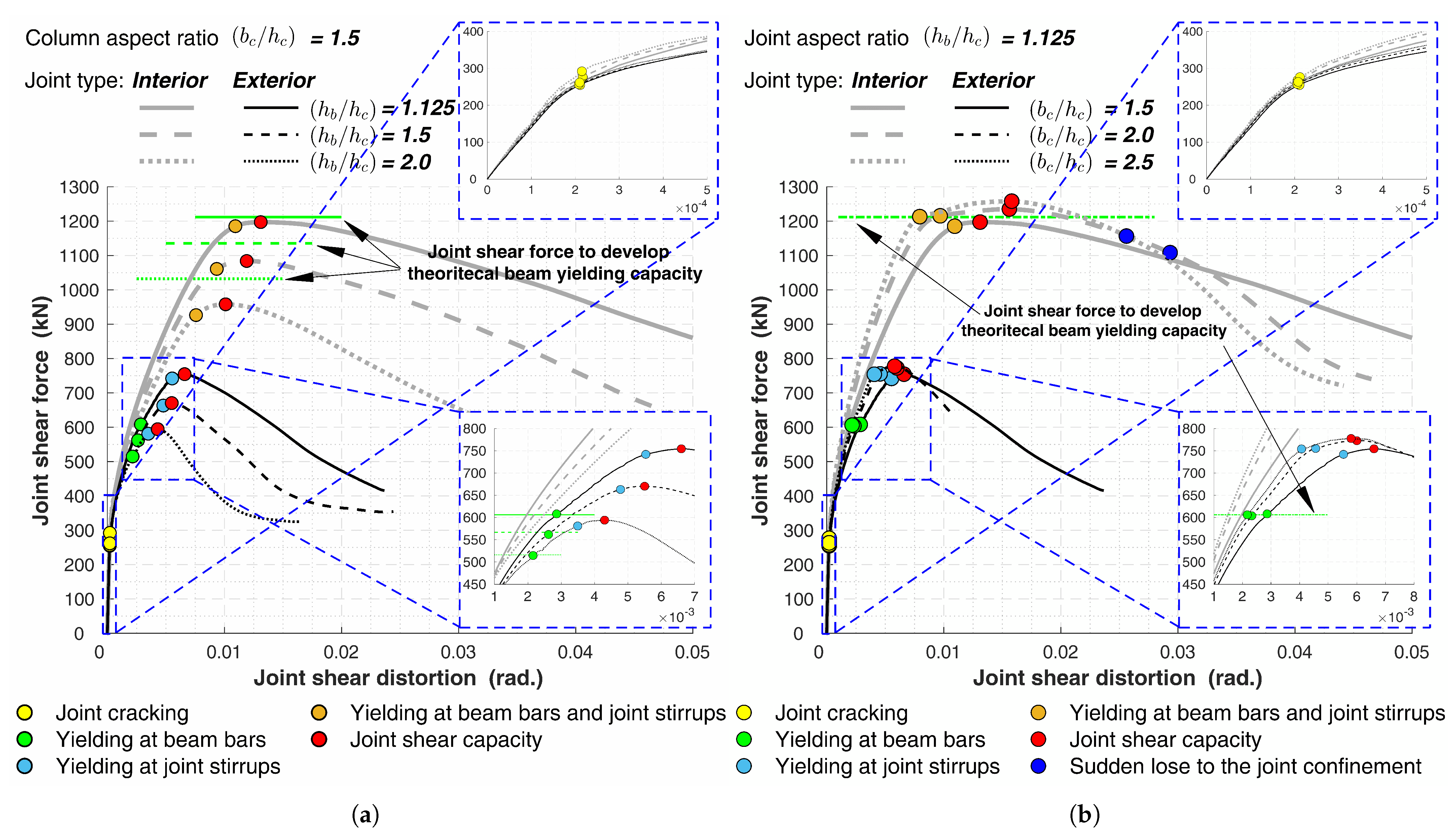
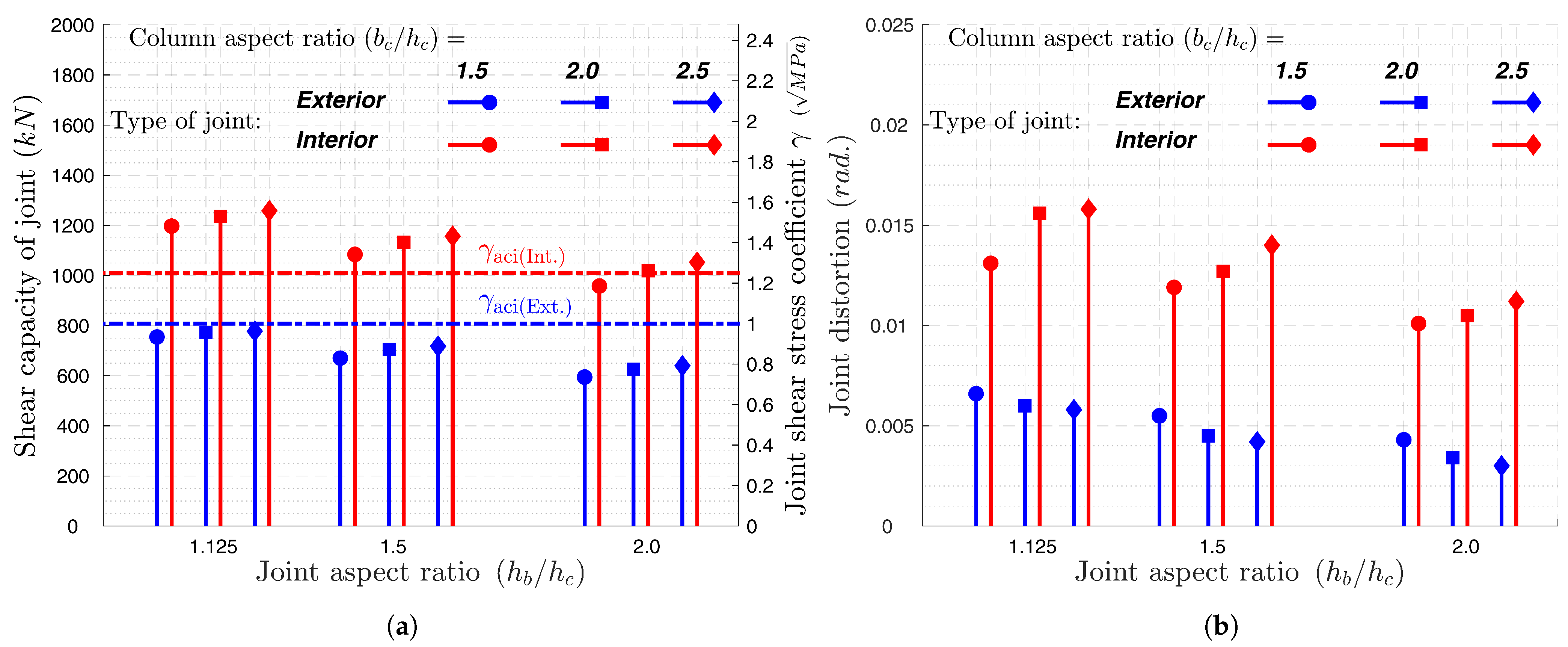
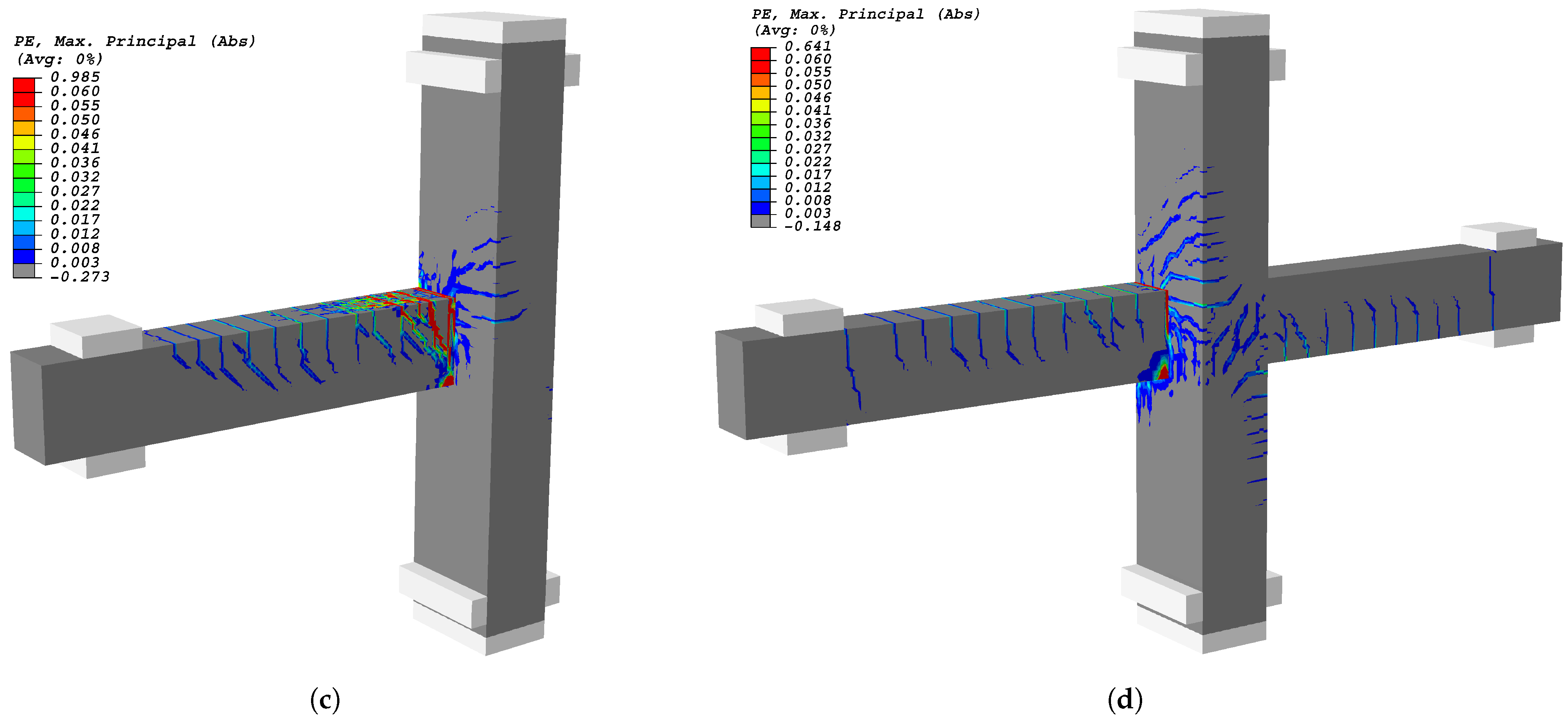
5.2. Parametric Study

The effect of the geometrical parameters on the beam–column joints was assessed by investigating the global behavior, which involves observing the beam load vs. drift ratio, and local behaviors, which involves investigating joint shear force vs. joint shear distortion and joint torsional moment vs. joint twist angle. The cracking pattern of the joints was also investigated to assess the failure behavior.

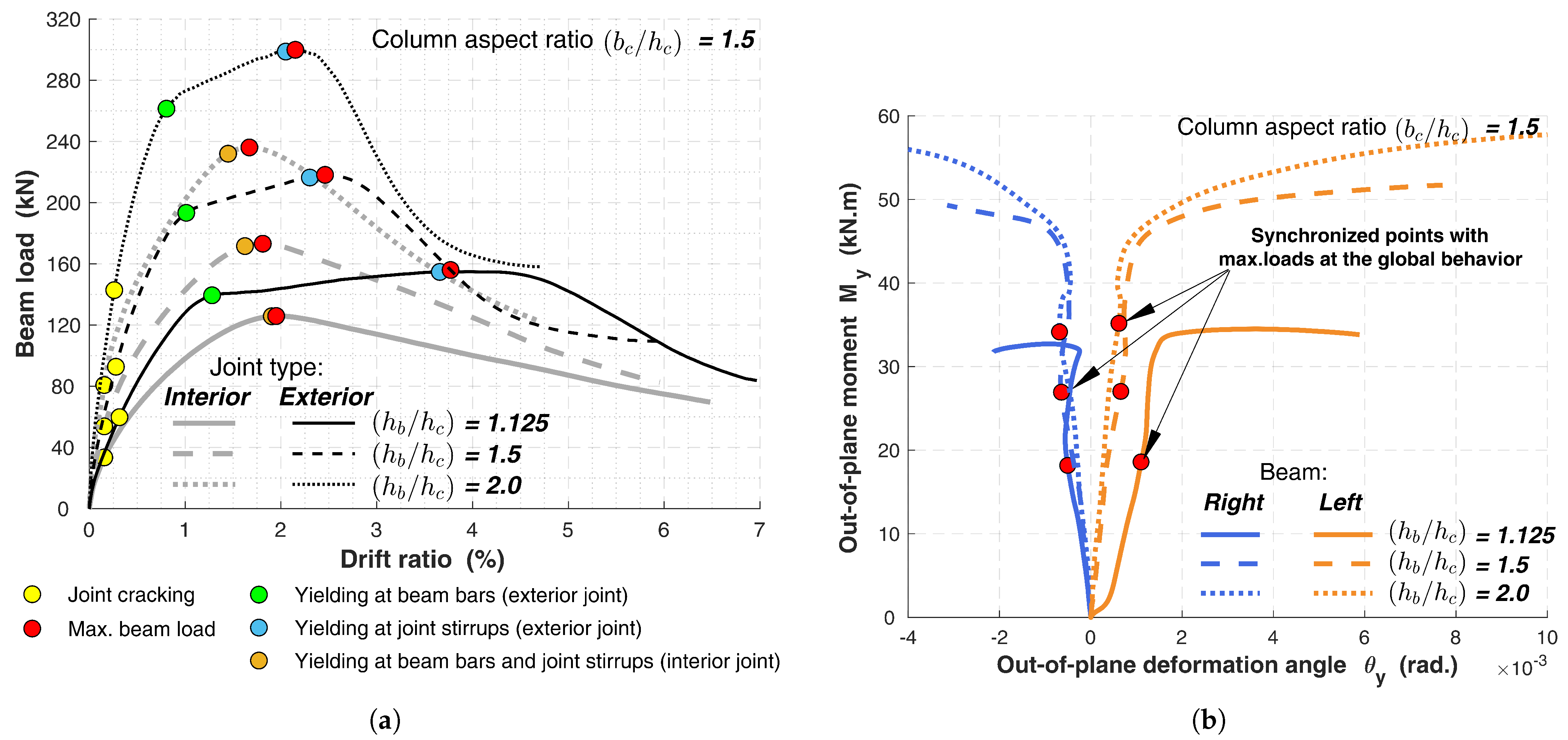
5.2.1. Global Behavior

Figure 15 depicts the performances of both types of joints (exterior and interior) with a constant column aspect ratio of $1.5$ and various joint aspect ratios of $1.125$, $1.5$, and $2.0$. Figure 15a shows that the interior joint collapsed earlier at $6.5\%$ DR compared to the exterior joint, which failed at $7\%$ DR for a $1.125$ joint aspect ratio. However, the collapse becomes faster as the joint aspect ratio increases for both joints. It happens at $6.0\%$ DR and $4.75\%$ DR for the joint aspect ratios of $1.5$ and $2.0$, respectively. The failure point is obtained by observing the kinetic energy profile of the model [93]. Moreover, the post-peak segment of the interior joints became steeper as the joint aspect ratio increased. This can likely be attributed to the out-of-plane moment of the beams [1,11], as shown in Figure 15b, that reaches around $14.5\%$, on average, of the in-plane flexural moment measured at the same section, resulting in a decrease in the joint panel confinement by the beams [94]. Overall, the interior joints have inferior performances, with the maximum loads lower by $25\%$ than the exterior ones. Figure 16 also depicts the effect of changing the column aspect ratio, with values of $1.5$, $2.0$, and $2.5$, while maintaining a constant joint aspect ratio of $1.125$. Figure 16a shows that changing the column aspect ratio can lead to a modest improvement of less than $5\%$ on the max load for the interior joints, while it improves the exterior joints ability to resist the load beyond a $6\%$ DR. Moreover, it was found that the accelerated decrease in the load after $4\%$ DR for the interior joint with column aspect ratios of 2.0 and 2.5 is related to the change in the rotation of the right beam of the joint subassembly, as shown in Figure 16b.

Figure 15a and Figure 16a reveal that the interior joints initiate cracking at half the beam load and drift ratio of the exterior joints. Furthermore, the maximum loads of the exterior joints correlate with the joint stirrups yielding. In contrast, the interior joints experience simultaneous yielding of beam bars and joint stirrups, which is related to their failure type.

On the other side, Figure 17a shows the characteristics of the backbone behavior curve obtained by the equivalent elasto-plastic energy criteria [95] to calculate the ductility ratio $\mu =\frac{{\delta }_{p_y}}{{\delta }_{p_u}}$, where ${\delta }_{p_y}$ is the drift ratio at the yield load $P_y$ and ${\delta }_{p_u}$ is the drift ratio at the load of $0.85P_{max}$. The joint aspect ratio, as shown in Figure 17b, has a predominant impact on the exterior eccentric beam–column joints. The ductility loses more than $20\%$, increasing the joint aspect ratio from $1.125$ to $1.5$ and $2.0$. However, the interior joints preserved an average ductility of about $3.2$ for all joint aspect ratios. On the other hand, the column aspect ratio enhances the ductility depending on the joint type and joint aspect ratio. The exterior joints with a joint aspect ratio of 1.125 have the best performance, with a ductility ratio reaching $5.8$ when the column aspect ratio increases to $2.5$; this effect decreases with the increase in the joint aspect ratio.

5.2.2. Local Behaviors

Figure 18a,b show the torsional behavior of the eccentric joints with the increasing aspect ratios of the joint and column, respectively. The torsional moment at joint cracking does not affect so much by increasing the joint aspect ratio, which is about 35/kNm, on average, as shown in Figure 18a. In contrast, it increases proportionally to the column aspect ratio, as shown in Figure 18b. Furthermore, the maximum torsional moment is directly related to the joint stirrups yielding in the exterior joints and with the simultaneous yielding of the beam bars and joint stirrups for the interior joints.

Figure 19 compares the joint torsional moment capacities and their corresponding rotational angles. The joint rotational angle is computed as the summation of the joint panel’s upper and lower torsional angles over its length. Figure 19 shows that the exterior joints resist $68\%$ and $63\%$ of the torsional moment and rotational angle of the interior joints, respectively. Moreover, the torsional moment capacities for the models with the column aspect ratios of $2.0$ and $2.5$ are about $215\%$ and $335\%$ for $1.5$. The capacities, on the other hand, are reduced by $15\%$, on average, by increasing the joint aspect ratios. Both aspect ratios have the same impact on the rotational angle since they both reduce it by $18\%$, on average, as they increase, as shown in Figure 19b.

Figure 20a,b show the shear behavior of the eccentric joints with points that clarify the significant change in the behavior with their related observations when the joint and column aspect ratios increase, respectively. The joint cracking triggers the first stiffness changing at the shear angle of around $2.2\times {10}^{-4}$ rad, where the corresponding shear forces of the exterior joints are about $93\%$ of those for the interior joints. The concrete began crashing in the joint zone at the maximum joint shear force after developing the theoretical beam yielding capacity for the exterior joints, referred to as BJ failure, followed by the joint stirrups yielding. In contrast, the beam bars and joint stirrups simultaneously yielded for the interior joint without developing the beam yielding capacity, referred to as J failure, especially with the increase in the joint aspect ratio, as shown in Figure 20a. Nevertheless, the increase in the column aspect ratio improves the interior joints to develop the beam yielding capacity, as shown in Figure 20b, and slows down the exterior joint distortion after the maximum shear force. The same observations have been reported by Kim and LaFave [4,96,97], who demonstrated that beam–column joints have distinct changes at key points in their behaviors caused by joint cracking initiation, yielding at beam bars or joint stirrups, and maximum shear force, where the joint begins to lose its resistance. However, a change occurs in the shear behavior for the interior joints with the column aspect ratios of $2.0$ and $2.5$ after the maximum shear force, as shown in Figure 20b, related to the beam out-of-plane deformation, which triggers a sudden decrease in the joint confinement. Moreover, it was found that the capacity points of the shear force and torsional moment behaviors are not synchronized.

Furthermore, Figure 21 compares the joint shear capacities and the corresponding shear distortion angles. The exterior joints sustain a shear force of about $62\%$ of that for the interior joints, which is close to what was reported by Kim and LaFave [4,97] and less than $50\%$ for the corresponding shear distortion angles. As the joint aspect ratio increases, on the other side, the shear capacities decrease by around $10\%$, and the joint distortion angle reduces by $8\%$ and $26\%$ for the aspect ratios of $1.5$ and $2.0$, respectively. Despite only modest enhancements in the shear capacities, of less than $5\%$, due to the increase in the column aspect ratio, the joints are improved, behaving in a ductile manner. Moreover, the shear distortion angles increase by $8\%$, on average, for the interior joints and decrease by $11\%$ for the exterior joints.

The shear stress coefficient $\gamma =V_j⁄\sqrt{f_c}$, on the other hand, is used to consider the joint geometrical shape in calculating the joint shear strength $V_j$ as a function of the number of confined joint faces. According to ACI-318 and ACI-352, it is taken as $1.25$ for the interior joints, while it is reduced to $1.0$ for the exterior joints. Unlike the interior joints, as shown in Figure 21a, the shear stress coefficient overestimates the shear strengths of the exterior joints, especially as the joint aspect ratio increases to a value of more than 1.0, as detected before by Kim and LaFave [97].

5.2.3. Crack Assessment

The plastic strain contours at the maximum load in the global behavior for the joint models have been used in assessing the effect of the geometrical parameters on the behavior of the cracking pattern. Figure 22 depicts the differences in the cracking patterns between the exterior and interior joint models. The damage is concentrated in the beam for the exterior joint, as shown in Figure 22a, since the joint failure occurs after the beam plastic hinge has been developed. On the other hand, the damage is concentrated at the joint zone for the interior joint model that failed before the beam reached its yielding capacity, as shown in Figure 22b. Moreover, both models suffer from torsional cracks, as shown on the far side of the models in Figure 22c,d. Furthermore, unlike the exterior joint, diagonal shear cracks developed on the far side of the interior joint.

Furthermore, by increasing the joint aspect ratio, as shown in Figure 23, the torsional cracks are multiplied and widened. However, the exterior joint model still behaves in a ductile manner where cracks are concentrated at the beam plastic hinge. For the interior joint, on the other hand, it can be seen that the out-of-plane moment became considerable via observing crack depths of the beams in Figure 23b,d, which disappeared in the exterior joint model, as shown in Figure 23a,c. Nevertheless, the increase in the column aspect ratio enhances the cracking behavior, as shown in Figure 24. The shear cracks are eliminated in the joint zone for the exterior joint model, while the beam shear flexural cracks widen, indicating a ductile behavior, as shown in Figure 24a. For the interior joint model, on the other hand, the torsional cracks are reduced, and the joint shear cracks at the far side disappear. In general, the cracking patterns of the models indicate a “strong column–weak beam” response, since the column is still in the elastic stage while the beam or the joint zone have reached their capacity.

6. Conclusions

The paper presented here aimed to study the behaviors of the eccentric beam–column subassembly subjected to lateral loading since they have been poorly investigated so far. For this purpose, a finite element analysis has been conducted using the concrete damage plasticity model with an incompatible mesh element type that provides improved accuracy and resolution. FEM results were validated using experimental readings for exterior and interior joints. Afterwards, the calibrated model parameters were utilized to perform a high-resolution parametric study to assess the impact of the geometrical configurations of the eccentric joints on their behaviors. Based on the observations, the conclusions can be summarized as follows:

• By combining the concrete damage plasticity with the energy-based uniaxial behavior models, employing the incompatible mesh element type, and considering the column axial load effect on the bond behavior, the global and local behaviors of the exterior and interior eccentric beam–column joints could be predicted precisely, as well as their cracking patterns.
• In addition to the anticipated flexure, shear, and normal force actions, the eccentric joint is subjected to a torsional moment, which generates additional shear stress on the joint zone, leading to accelerated joint damage. Moreover, the joints experience an out-of-plane deformation, which can potentially compromise the confinement of the beams within the joint, particularly in the case of interior joints.
• Between the tested parameters, the joint aspect ratio has the dominant impact on the behaviors of the joints by decreasing the joint shear capacity and consequently decreasing the beam–column subassembly capability to develop the beam plastic hinge. Additionally, an increase in the interior joint aspect ratio leads to a higher out-of-plane moment and a loss of joint confinement.
• An increase in the column aspect ratio resulted in slight enhancements in the joint shear capacity. However, it improves the beam–column subassembly’s capability to develop the beam plastic hinge.
• On average, the shear capacities of the exterior joints are three-fifths of the interior joints. However, ACI-318 and ACI-352 assume four-fifths for this percentage. Furthermore, as the joint aspect ratio exceeds 1.0, they overestimate the exterior joint shear strength.