Train-Induced Vibration Prediction and Control of a Metro Depot and Over-Track Buildings
Abstract
:1. Introduction
2. Vibration Measurement in Depot
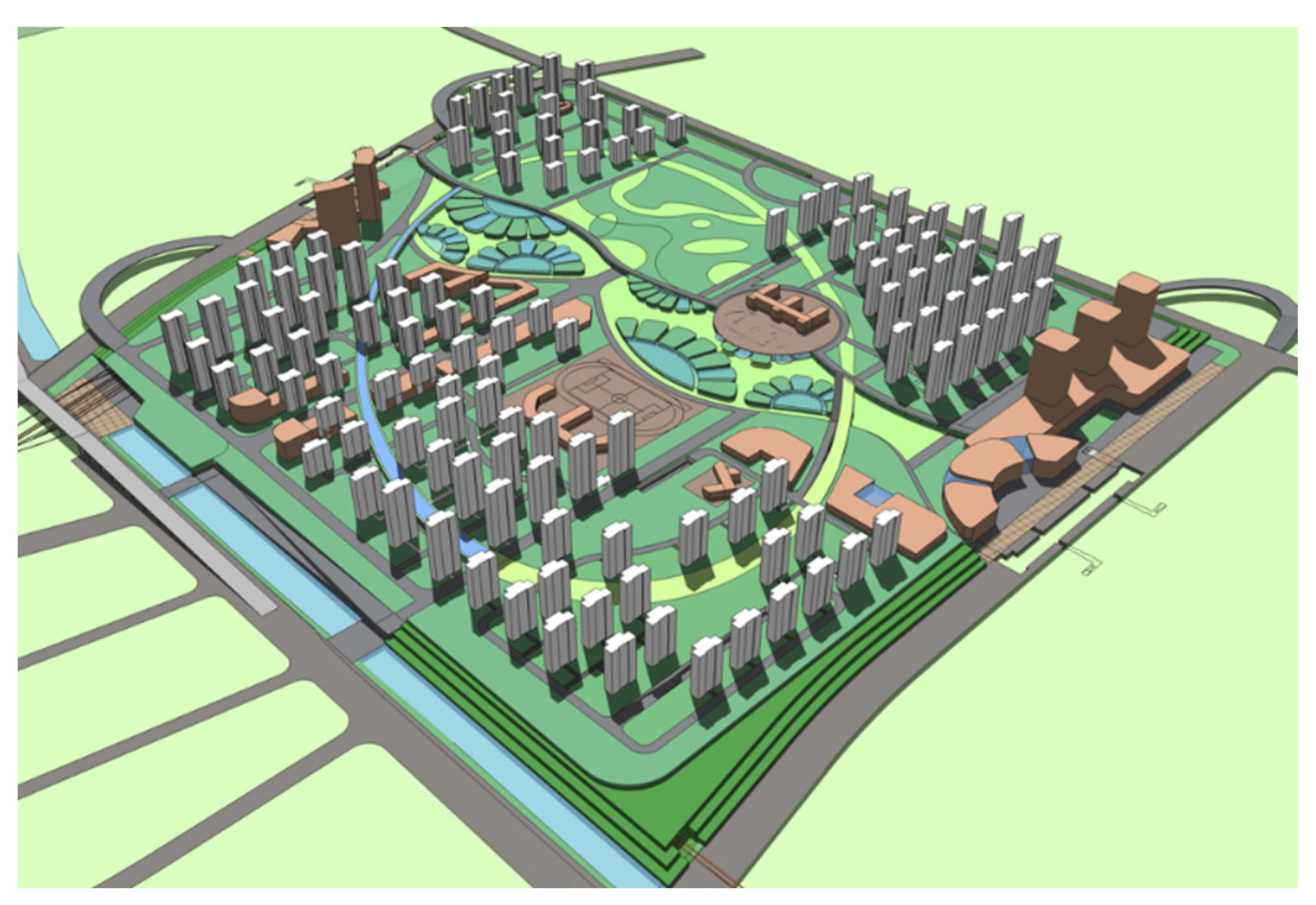
2.1. Project Condition
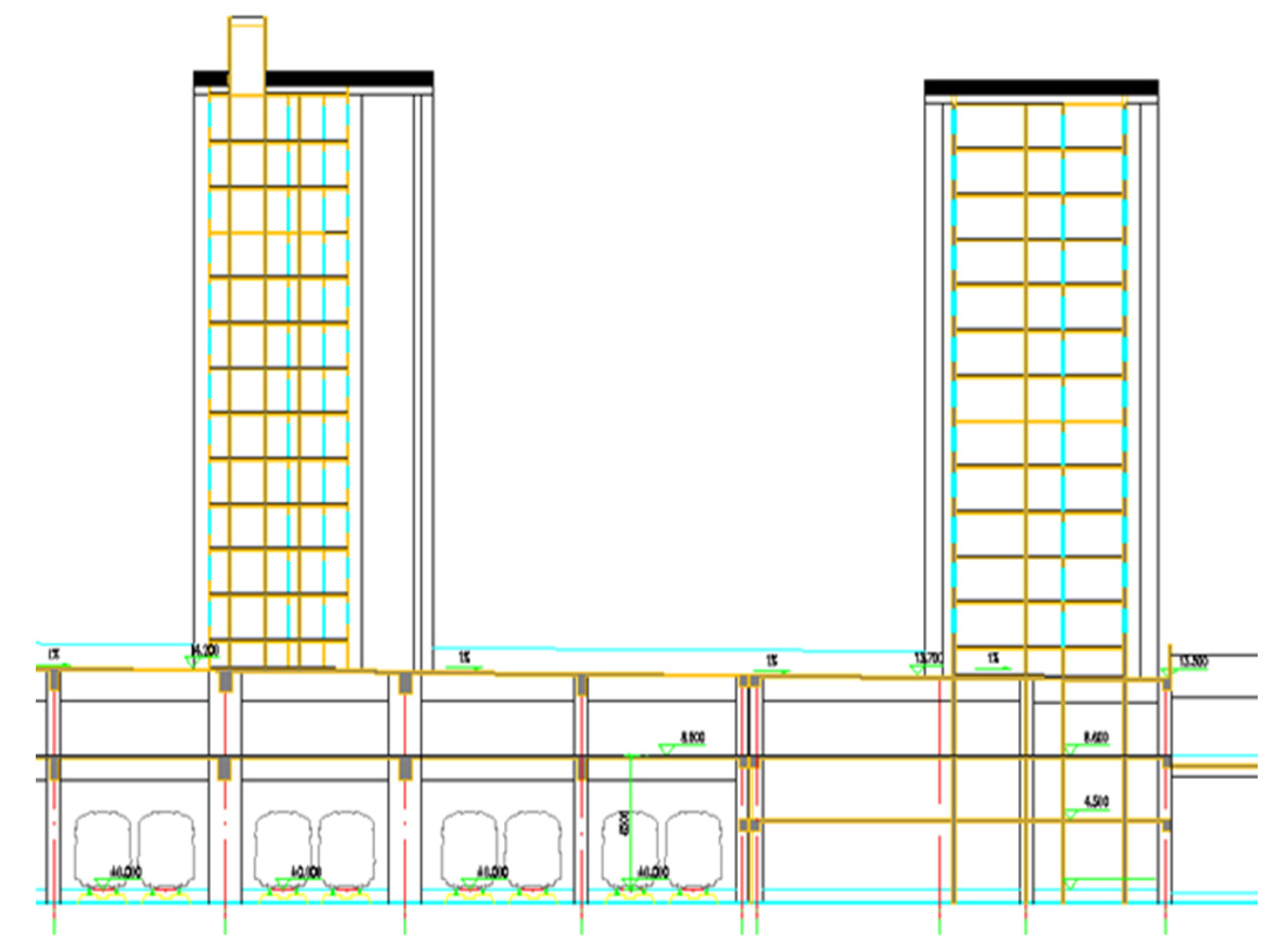
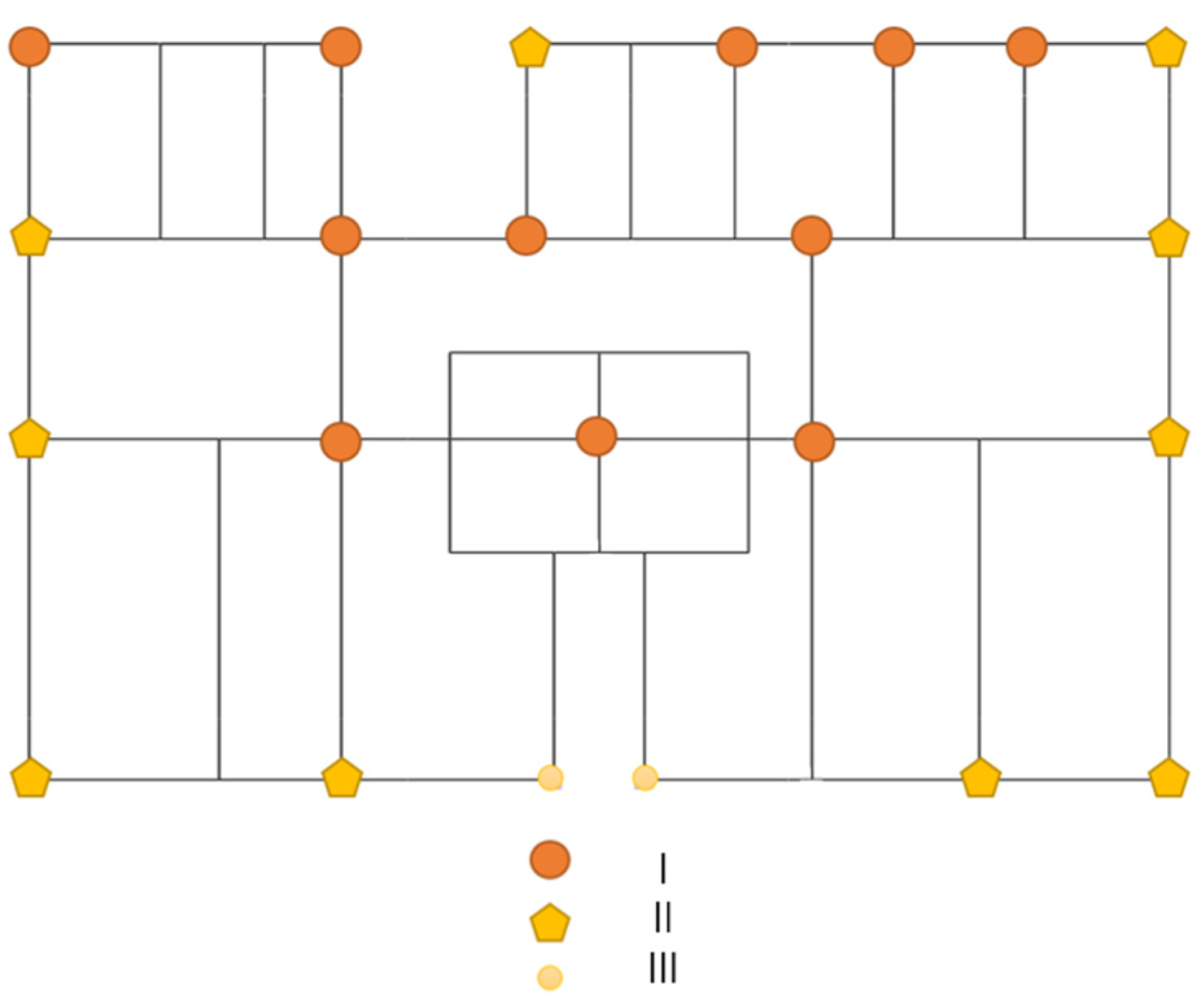
2.2. Measurement Point Arrangement
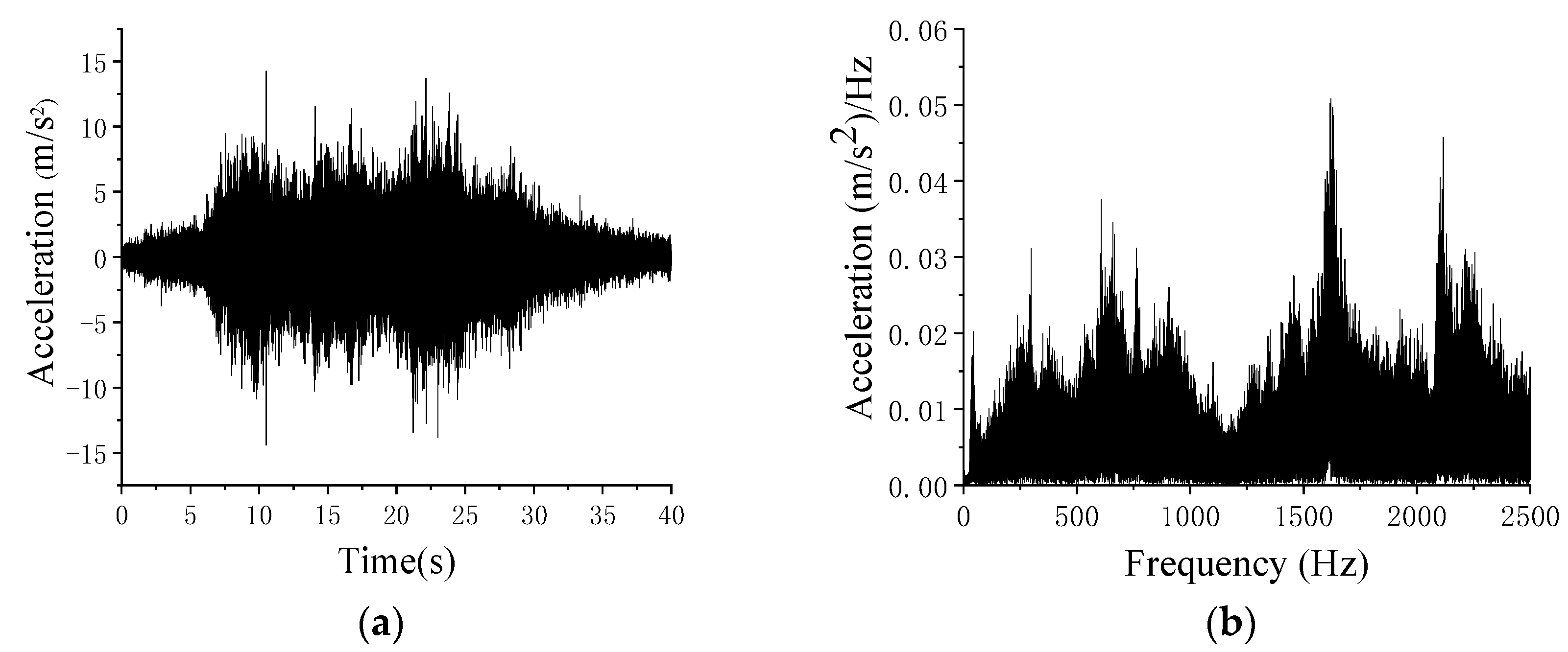
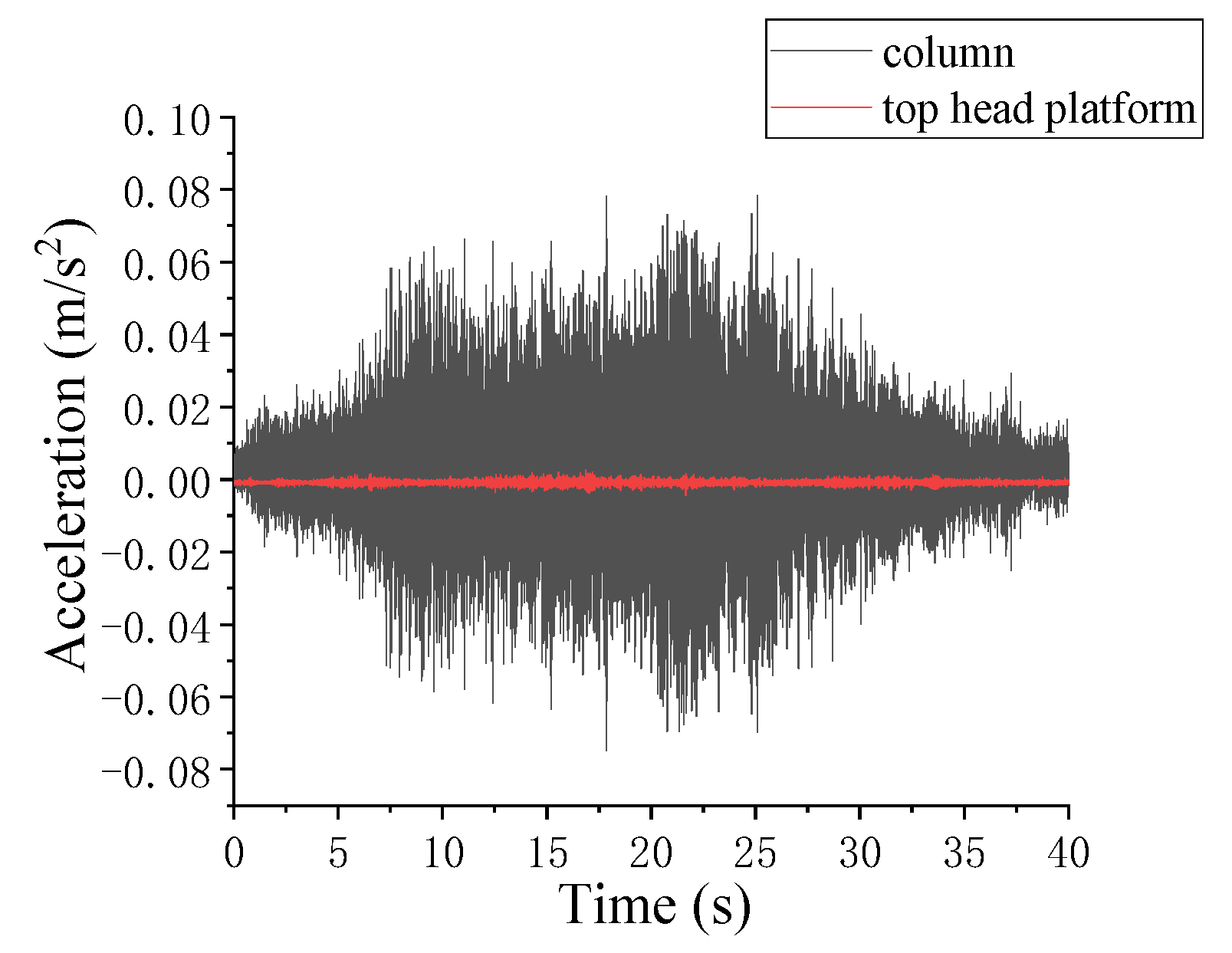
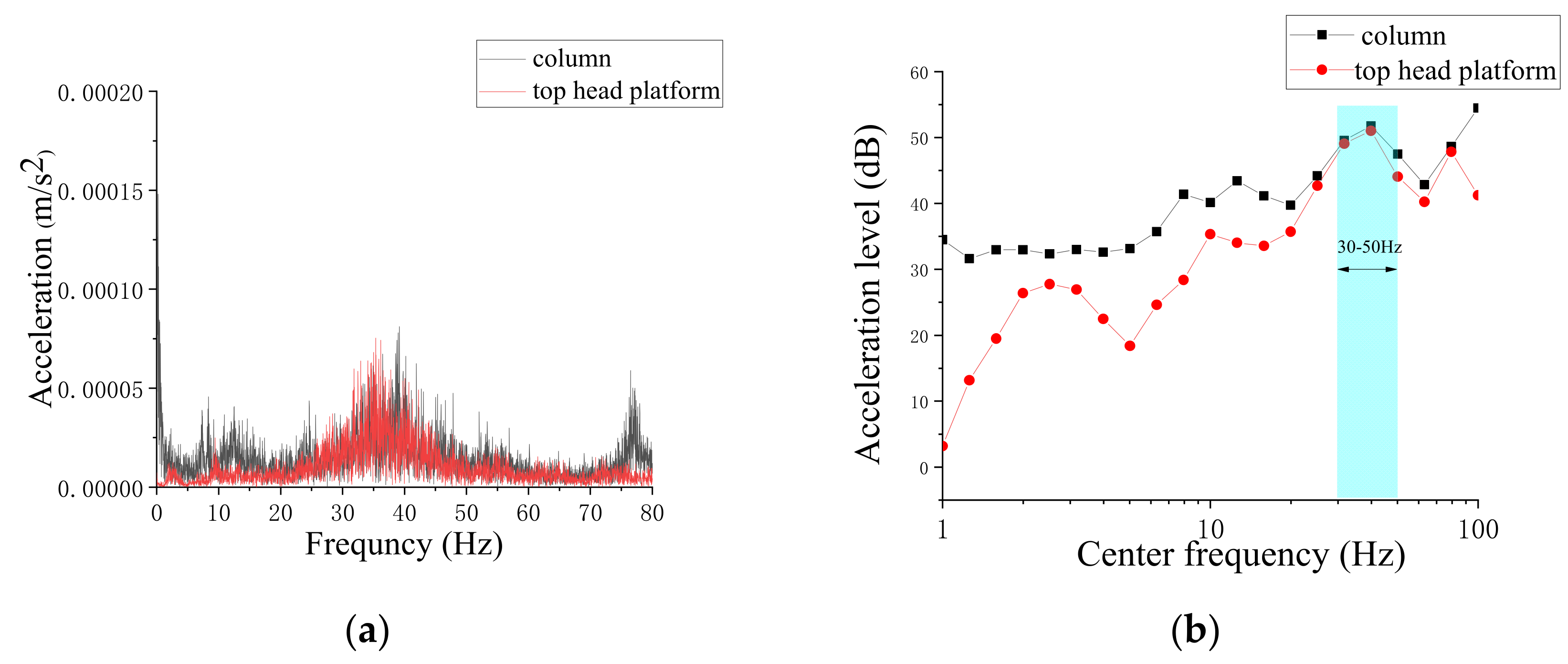
2.3. Measurement Result
3. Numerical Model
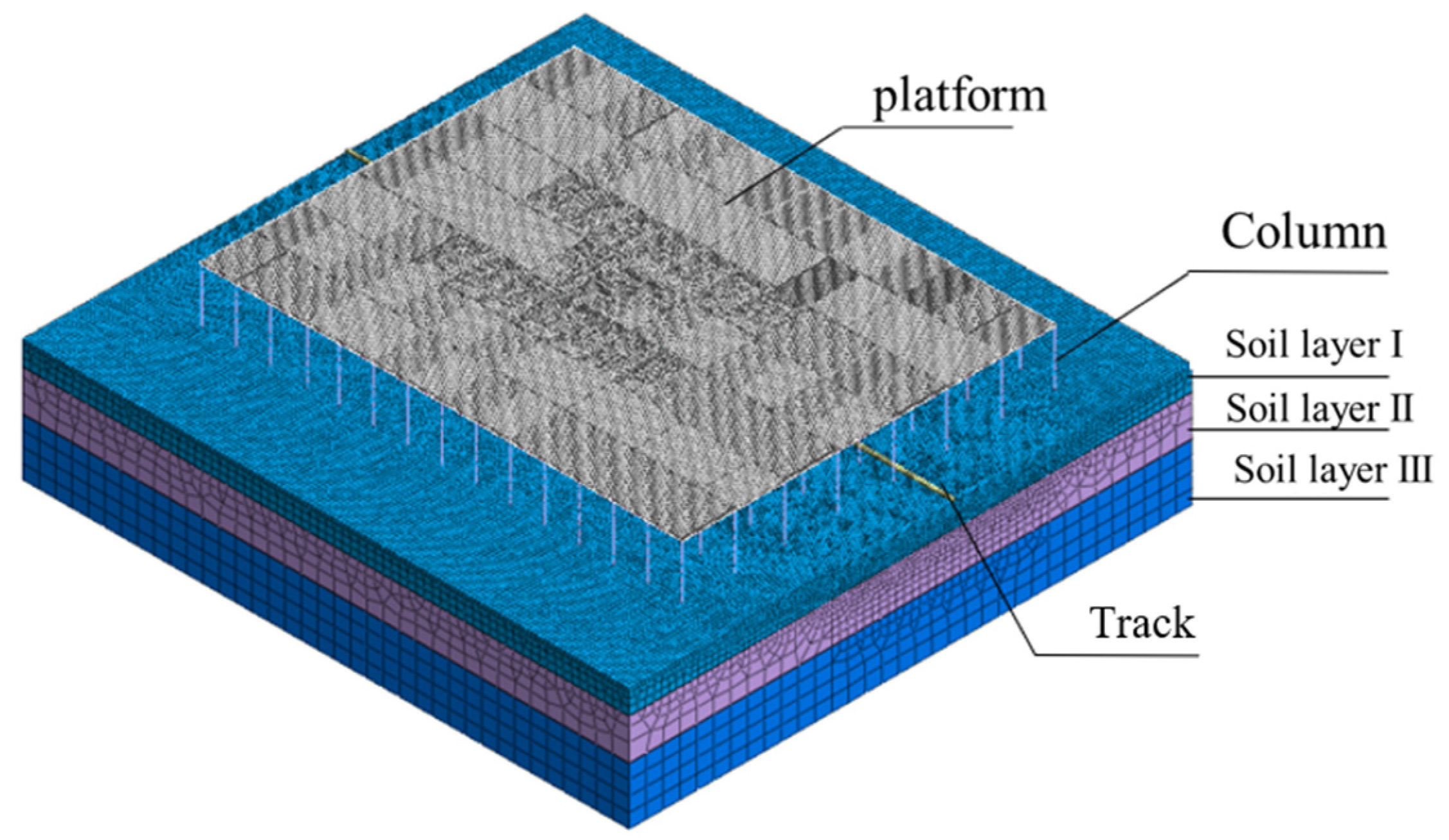
3.1. Track–Soil–Structure 3D FE Model
3.2. Dynamic Train Load
3.2.1. Simulated Acceleration on the Rail
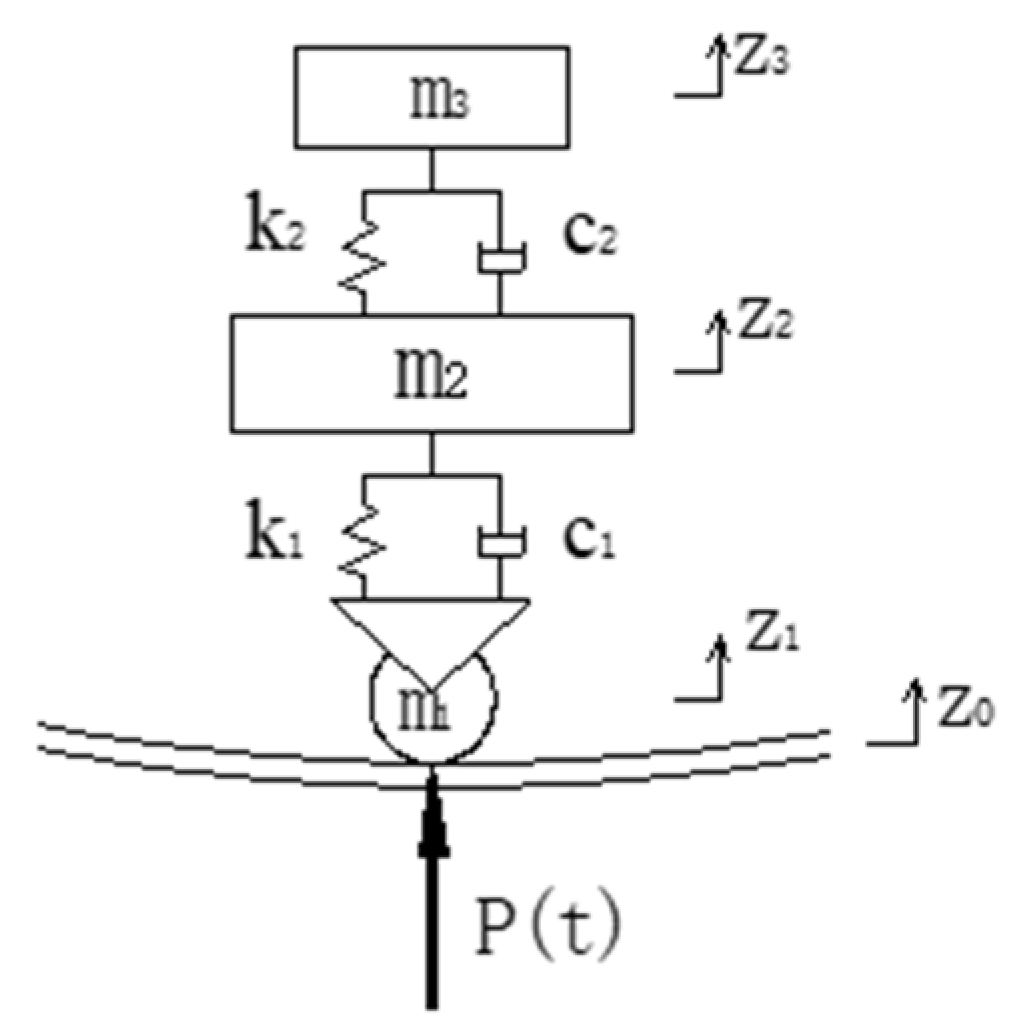
3.2.2. Simplified Model of Metro Trains
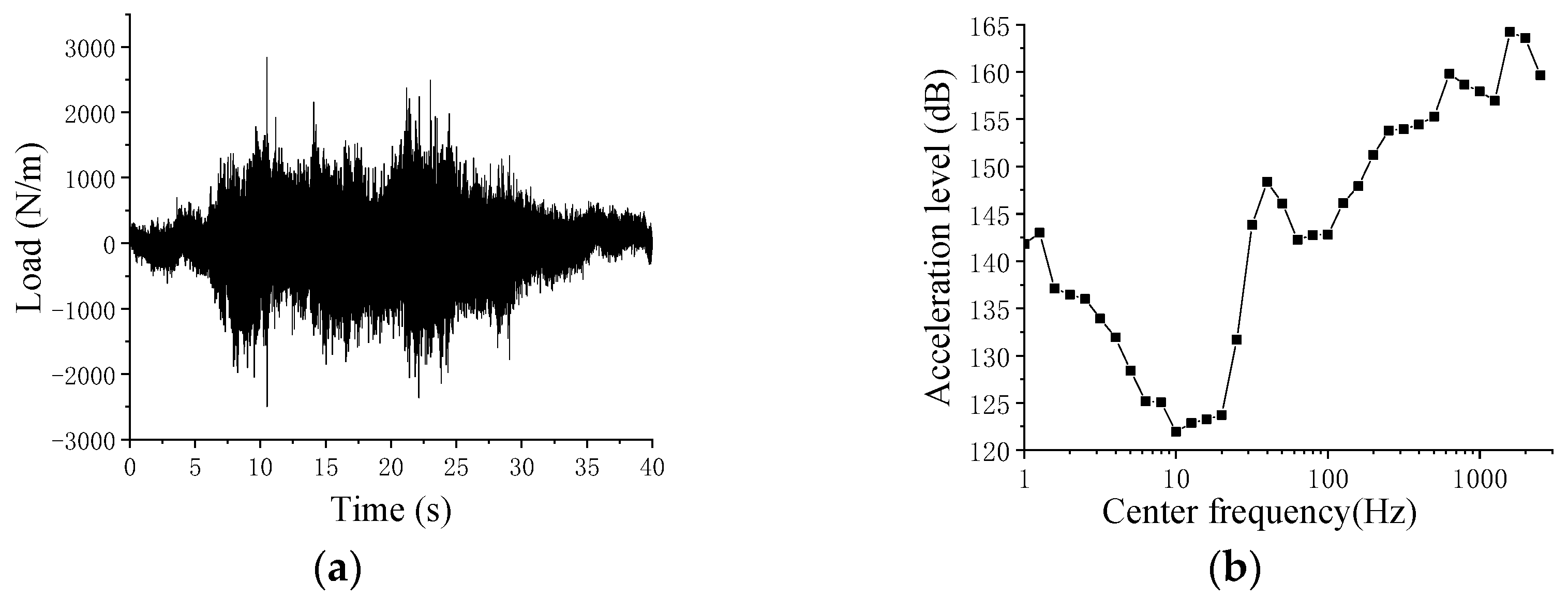
3.2.3. Simulated Train Load
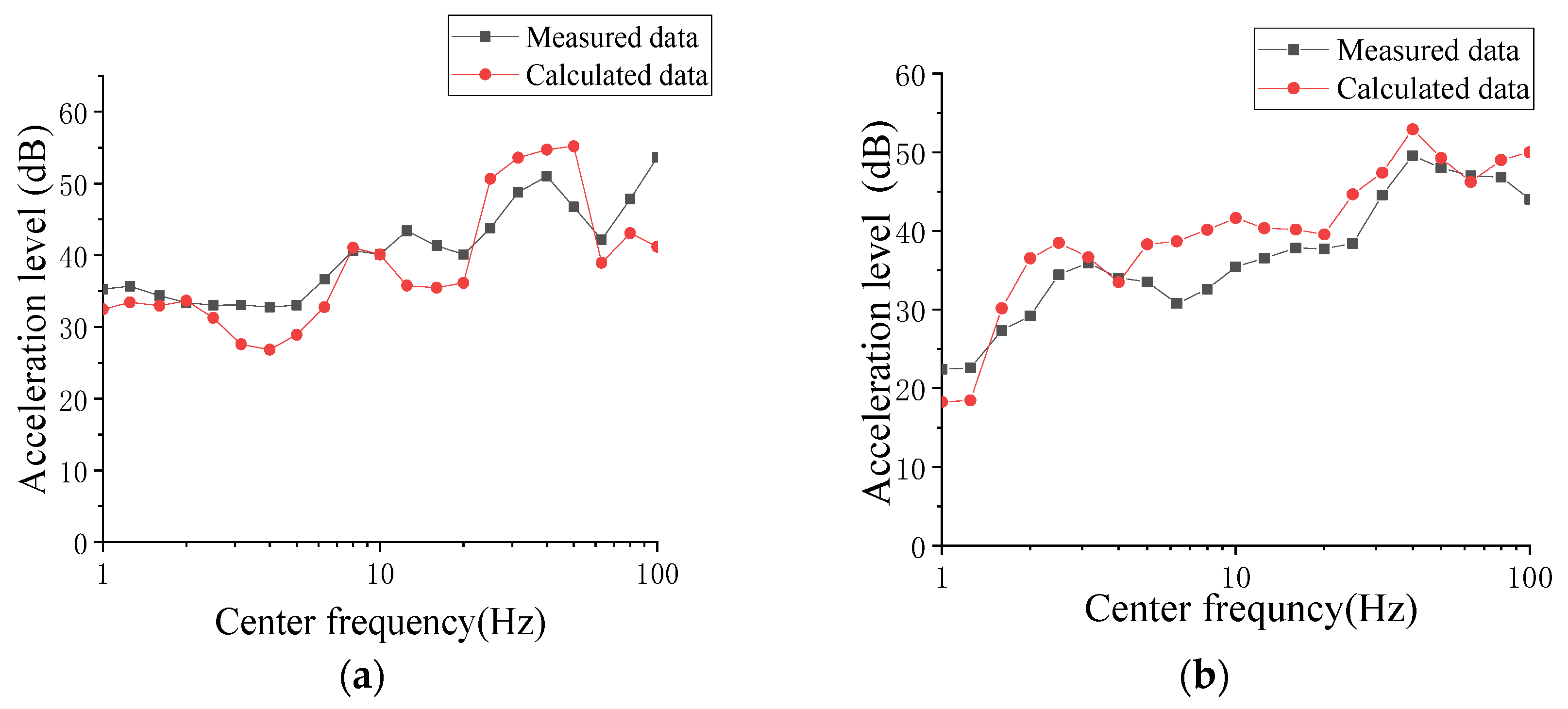
3.3. Model Validation
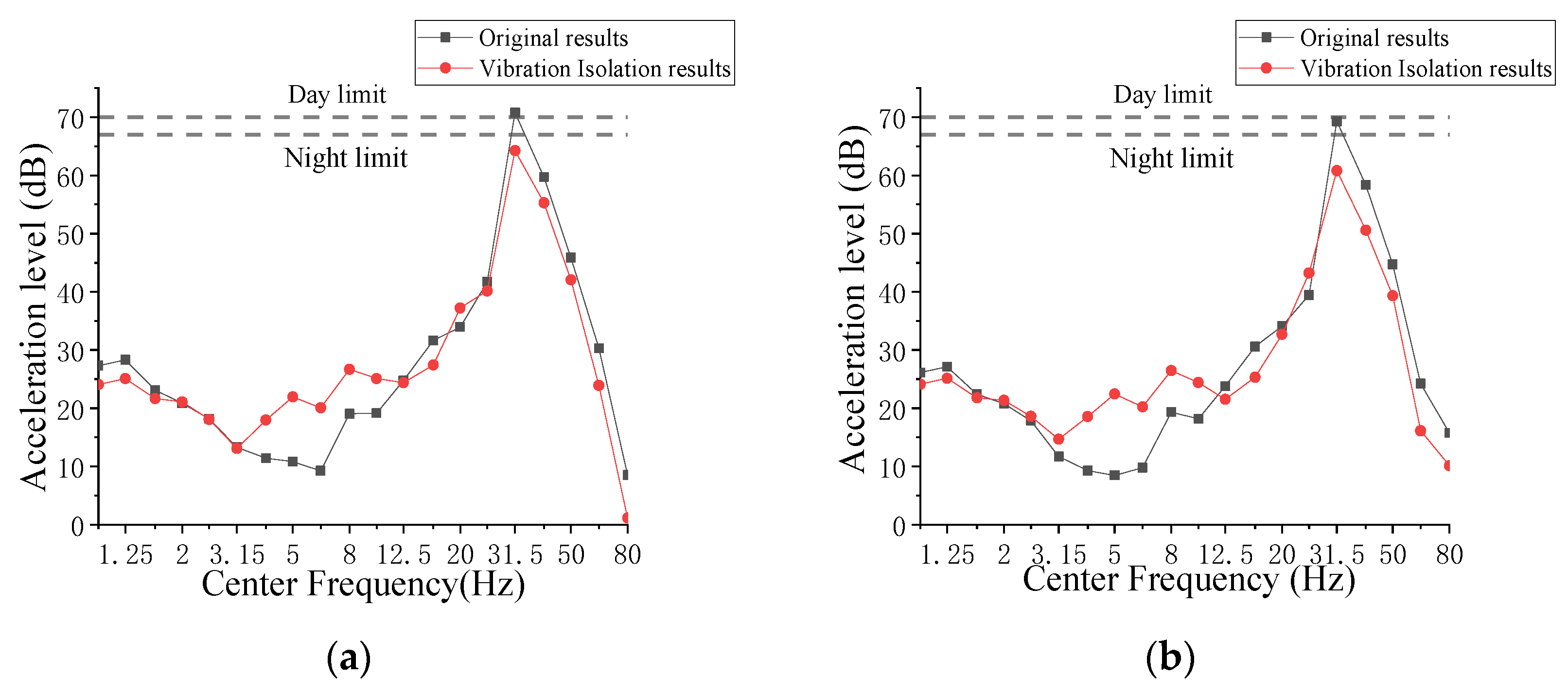
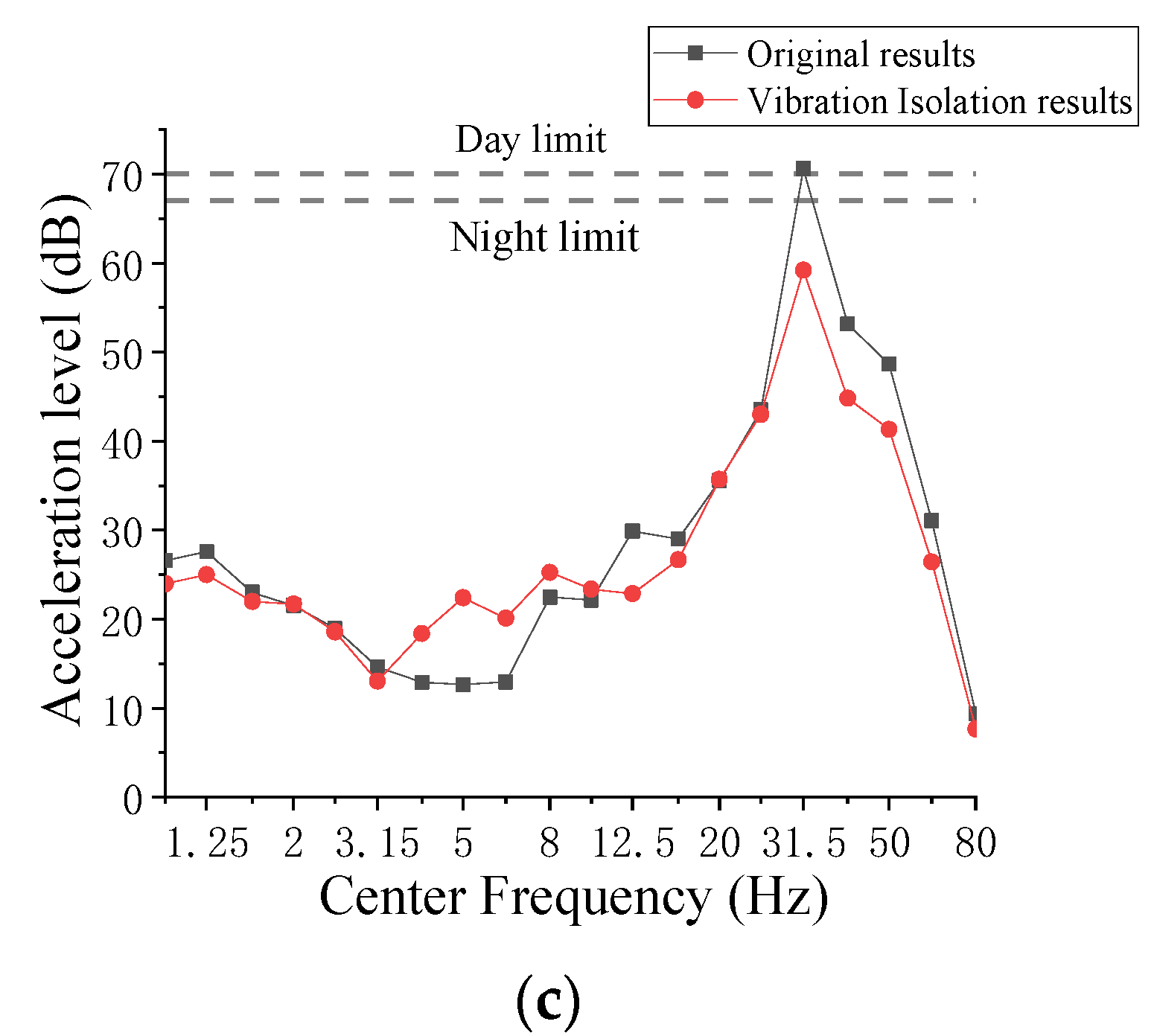
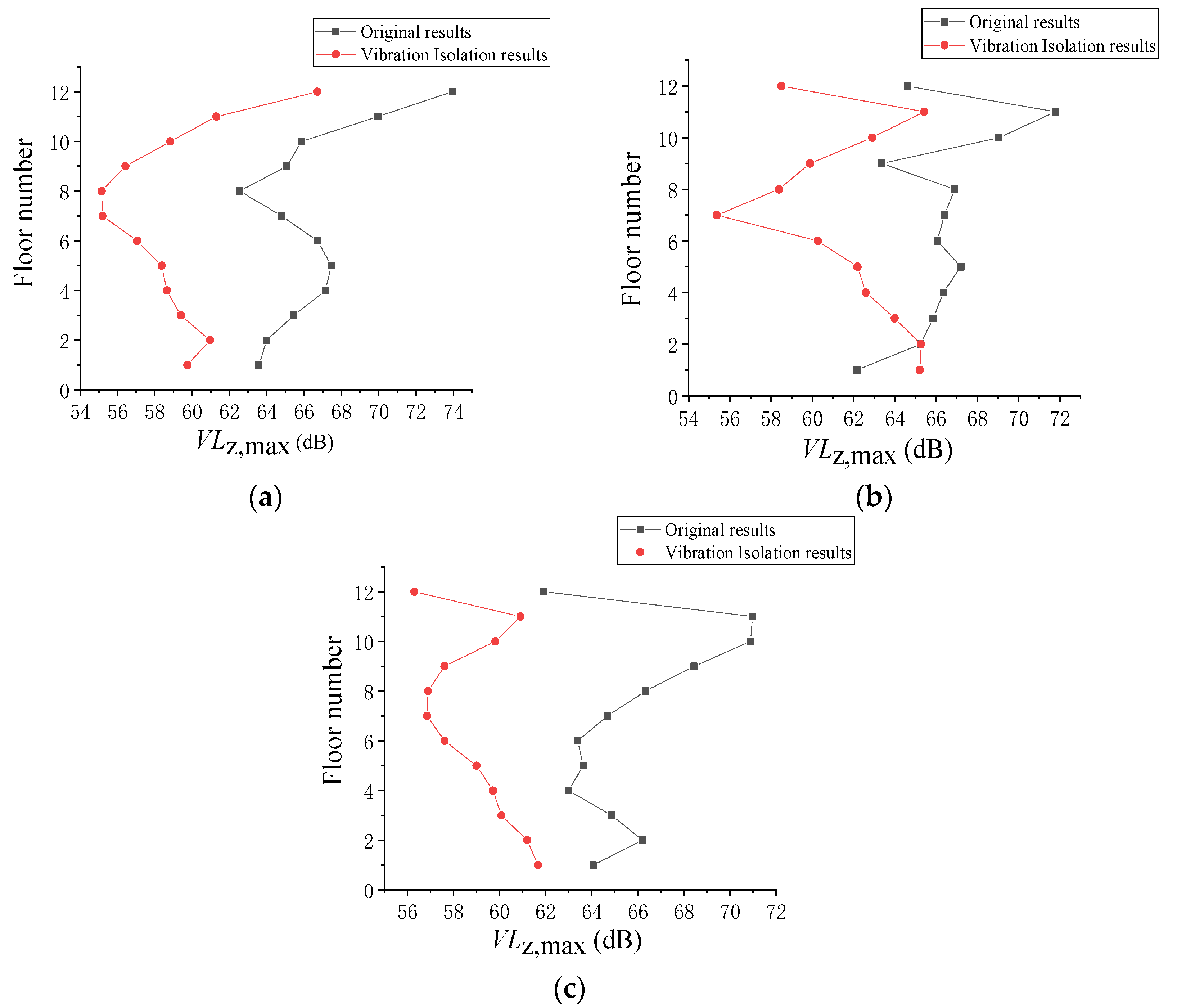
3.4. Prediction Result of Building Vibrations
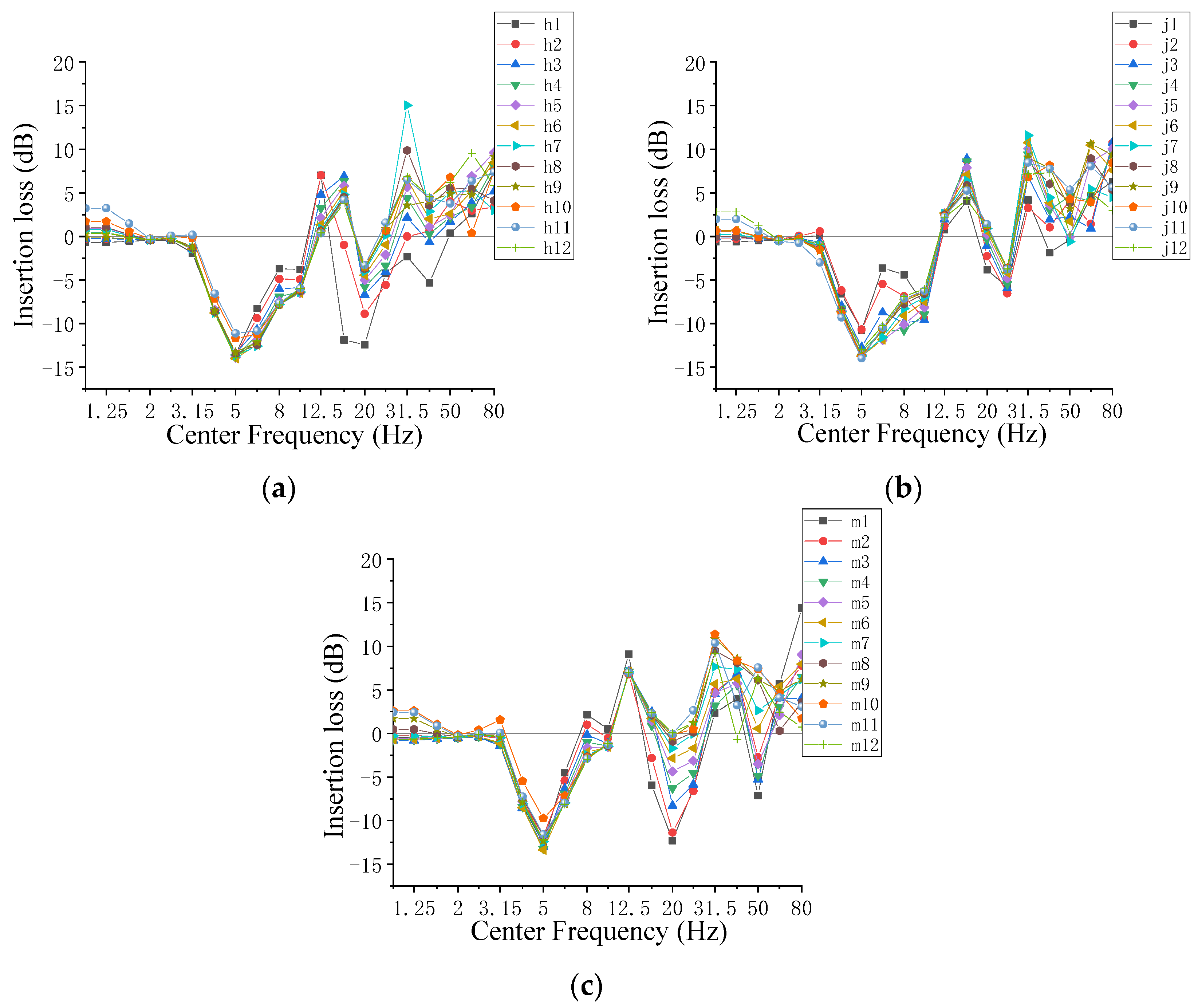
4. Vibration Control Measures
5. Conclusions
- The peak acceleration measured on the rail was approximately 15 m/s2, which was significantly higher than the measurements taken on the column and top head platform, with vibration gradually weakening during transmission.
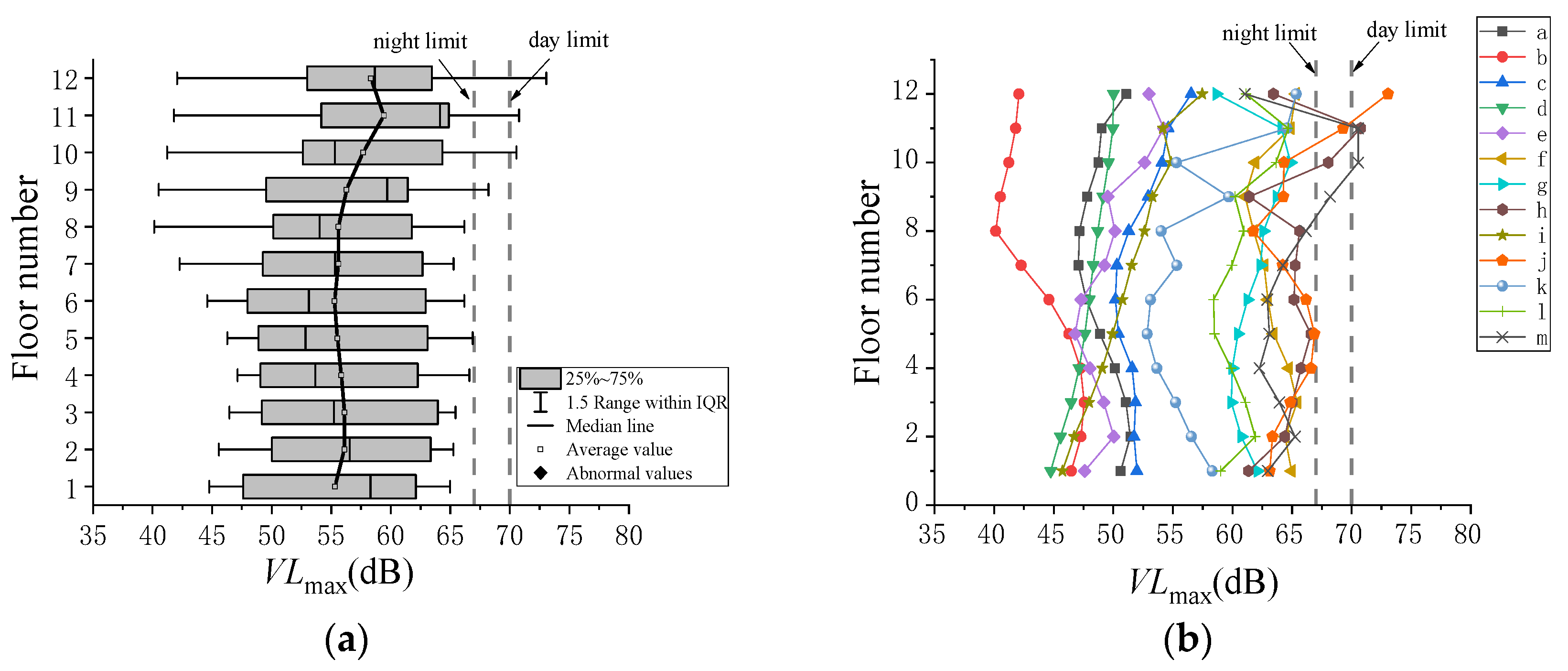
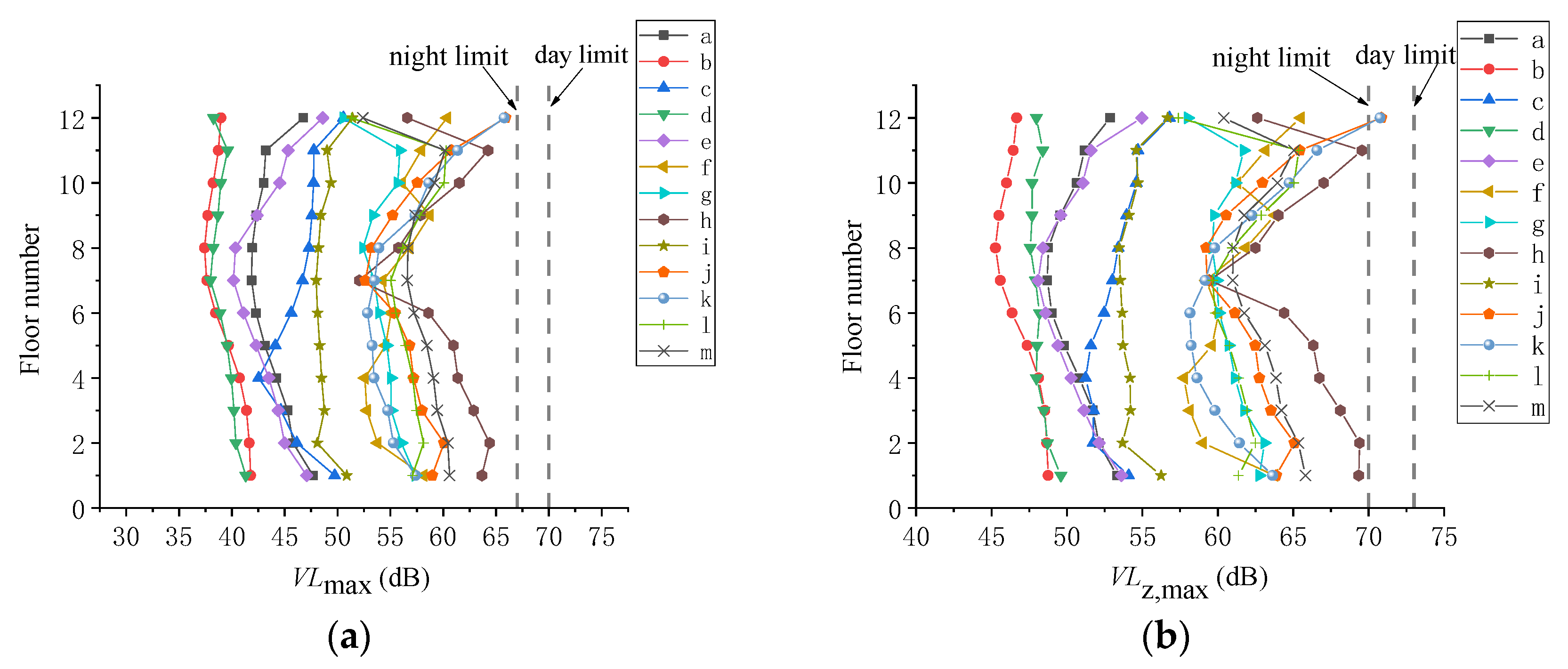
- According to the numerical analysis, without vibration isolation bearings, the overall vibration response of the over-track building decreased and then increased with the increase in the floor number. Rooms h, j, and m significantly exceeded the standard limits. The maximum values of VLmax and VLz,max both appeared in room j on the top floor. The dominant frequency of the building floors was about 31.5 Hz, having a small decrease with the increase in the floor number.
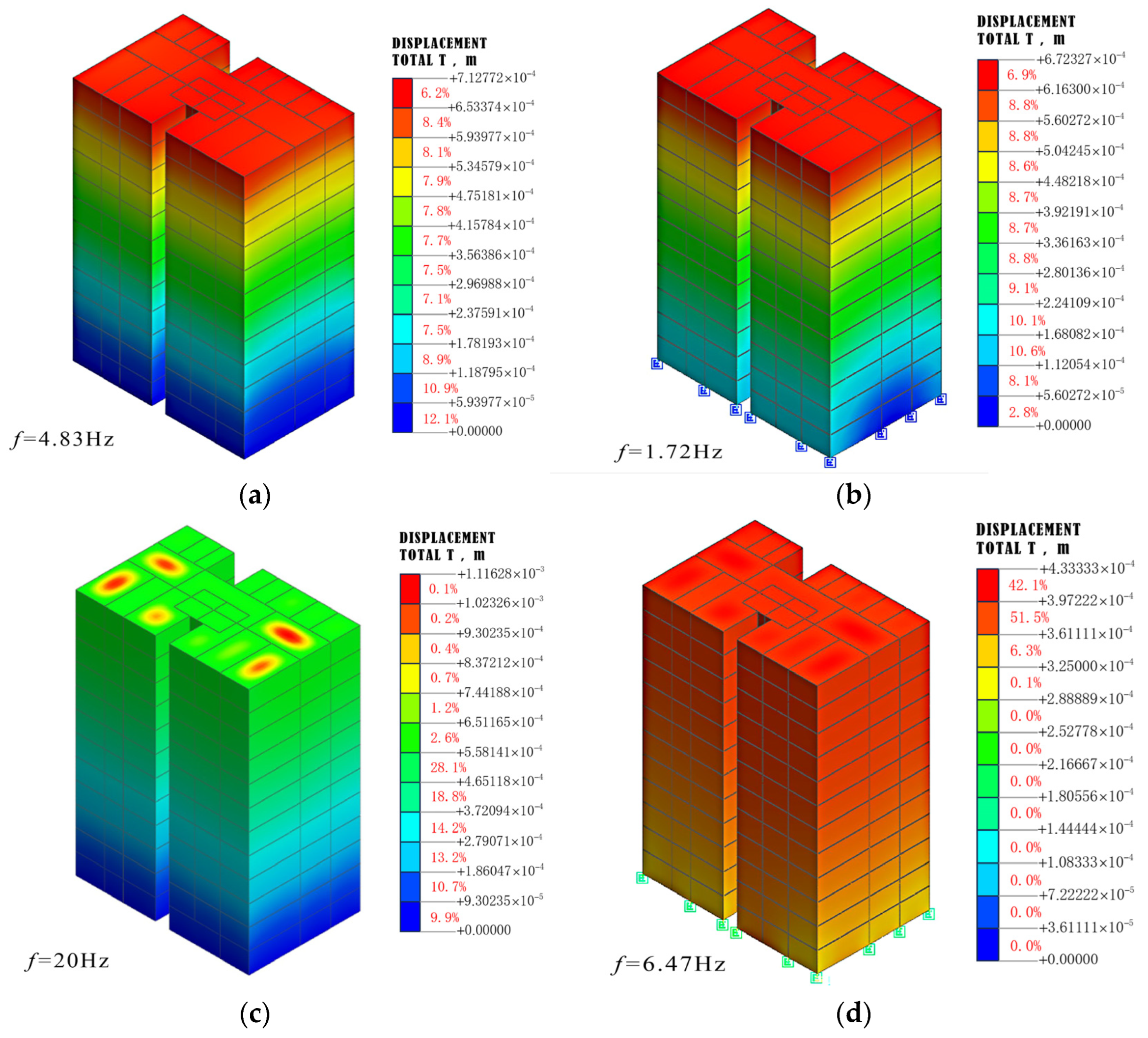
- After adopting vibration isolation bearings, the vertical natural vibration frequency of the superstructure was reduced, resulting in a low frequency of 4–10 Hz; the vibration amplification phenomenon commonly occurred in vibration isolation structures on the building floors.
- Vibration isolation bearings had a significant reduction effect above 30 Hz, with the IL achieving a reduction of 7–15 dB, and the VLz,max values were reduced by 3–12 dB; the reduction effect was more pronounced on floors 7–12 compared to floors 1–6. The vibration response of the building floors has been reduced to meet the standard requirements.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Handy, S. Smart Growth and the Transportation-Land Use Connection: What Does the Research Tell Us? Int. Reg. Sci. Rev. 2005, 28, 146–167. [Google Scholar] [CrossRef]
- Liu, W.; Li, C.; Ma, L.; Du, L. A frequency-domain formulation for predicting ground-borne vibration induced by underground train on curved track. J. Sound Vib. 2023, 549, 117578. [Google Scholar] [CrossRef]
- Hussein, M.; Hunt, H.; Kuo, K.; Costa, P.A.; Barbosa, J. The use of sub-modelling technique to calculate vibration in buildings from underground railways. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2015, 229, 303–314. [Google Scholar] [CrossRef]
- Auersch, L. Building response due to ground vibration—Simple prediction model based on experience with detailed models and measurements. Int. J. Acoust. Vib. 2010, 15, 101. [Google Scholar] [CrossRef]
- Lopes, P.; Ruiz, J.F.; Costa, P.A.; Rodríguez, L.M.; Cardoso, A.S. Vibrations inside buildings due to subway railway traffic. Experimental validation of a comprehensive prediction model. Sci. Total Environ. 2016, 568, 1333–1343. [Google Scholar] [CrossRef] [PubMed]
- Cao, R.; Ma, M.; Sun, X.; Chen, J. Transmission characteristics of train-induced vibration in buildings based on wave propagation analysis. Constr. Build. Mater. 2023, 378, 13115. [Google Scholar] [CrossRef]
- Xu, L.; Ma, M. Analytical solution of ground-borne vibration due to spatially periodic harmonic moving load on a tunnel embedded in layered soil. J. Zhejiang Univ.-Sci. A 2023, 24, 637–652. [Google Scholar] [CrossRef]
- Connolly, D.P.; Marecki, G.P.; Kouroussis, G.; Thalassinakis, L.; Woodward, P.T. The growth of railway ground vibration problems—A review. Sci. Total Environ. 2016, 568, 1276–1282. [Google Scholar] [CrossRef]
- Zou, C.; Wang, Y.; Wang, P.; Gou, J. Measurement of ground and nearby building vibration and noise induced by trains in a metro depot. Sci. Total Environ. 2015, 536, 761–773. [Google Scholar] [CrossRef]
- Zou, C.; Wang, Y.; Moore, J.A.; Sanayei, M. Train-induced field vibration measurements of ground and over-track buildings. Sci. Total Environ. 2017, 575, 1339–1351. [Google Scholar] [CrossRef]
- Cao, Z.; Guo, T.; Zhang, Z.; Li, A. Measurement and analysis of vibrations in a residential building constructed on an elevated metro depot. Measurement 2018, 125, 394–405. [Google Scholar] [CrossRef]
- Liang, R.; Ding, D.; Liu, W.; Sun, F.; Cheng, Y. Experimental study of the source and transmission characteristics of train-induced vibration in the over-track building in a metro depot. J. Vib. Control 2022, 29, 107754632110701. [Google Scholar] [CrossRef]
- Liao, Y.; Zhang, P.; Wu, Q.; Zhang, H. A Case Study on Structural Serviceability Subjected to Railway-Induced Vibrations at TOD Developed Metro Depot. Buildings 2022, 12, 1070. [Google Scholar] [CrossRef]
- Tao, Z.; Hu, Z.; Wu, G.; Huang, C.; Zou, C.; Ying, Z. Train-Induced Vibration Predictions Based on Data-Driven Cascaded State-Space Model. Buildings 2022, 12, 114. [Google Scholar] [CrossRef]
- Clot, A.; Arcos, R.; Romeu, J. Efficient Three-Dimensional Building-Soil Model for the Prediction of Ground-Borne Vibrations in Buildings. J. Struct. Eng. 2017, 143, 04017098. [Google Scholar] [CrossRef]
- Wolf, S. Potential low frequency ground vibration (<6.3 Hz) impacts from underground LRT operations. J. Sound Vib. 2003, 267, 651–661. [Google Scholar]
- Jin, Q.; Thompson, D.J.; Lurcock, D.E.J.; Toward, M.G.R. A 2.5D finite element and boundary element model for the ground vibration from trains in tunnels and validation using measurement data. J. Sound Vib. 2018, 422, 373–389. [Google Scholar] [CrossRef] [Green Version]
- Hung, H.H.; Chen, G.H.; Yang, Y.B. Effect of railway roughness on soil vibrations due to moving trains by 2.5D finite/infinite element approach. Eng. Struct. 2013, 57, 254–266. [Google Scholar] [CrossRef]
- Sanayei, M.; Maurya, P.; Zhao, N.; Moore, J.A. Impedance modeling: An efficient modeling method for prediction of building floor vibrations. Struct. Congr. 2012, 2012, 886–897. [Google Scholar]
- Sanayei, M.; Moore, J.A.; Brett, C.R. Measurement and prediction of train-induced vibrations in a full-scale building. Eng. Struct. 2014, 77, 119–128. [Google Scholar] [CrossRef]
- Zou, C.; Moore, J.A.; Sanayei, M.; Wang, Y. Impedance model for estimating train-induced building vibrations. Eng. Struct. 2018, 172, 739–750. [Google Scholar] [CrossRef]
- Zou, C.; Moore, J.A.; Sanayei, M.; Tao, Z. Efficient impedance model for the estimation of train-induced vibrations in over-track buildings. J. Vib Control 2021, 27, 924–942. [Google Scholar] [CrossRef]
- Tao, Z.; Moore, J.A.; Sanayei, M.; Wang, Y.; Zou, C. Train-induced floor vibration and structure-borne noise predictions in a low-rise over-track building. J. Eng. Struct. 2022, 255, 113914. [Google Scholar] [CrossRef]
- Vogiatzis, K.E.; Kouroussis, G. Prediction and efficient control of vibration mitigation using floating slabs: Practical application at Athens metro lines 2 and 3. Int. J. Rail Transp. 2015, 3, 215–232. [Google Scholar] [CrossRef]
- Ma, M.; Liu, W.; Li, Y.; Liu, W. An experimental study of vibration reduction of a ballasted ladder track. J. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2017, 231, 0954409716642488. [Google Scholar] [CrossRef]
- Sun, X.; Ma, M.; Jiang, B.; Cao, R. Ground vibration from freight railway: Environmental impact and potential mitigation measure at propagation path. Environ. Sci. Pollut. Res. 2022, 29, 44364–44377. [Google Scholar] [CrossRef]
- Li, Z.; Ma, M.; Liu, K.; Jiang, B. Performance of rubber-concrete composite periodic barriers applied in attenuating ground vibrations induced by metro trains. Eng. Struct. 2023, 285, 116027. [Google Scholar] [CrossRef]
- Fiala, P.; Degrande, G.; Augusztinovicz, F. Numerical modelling of ground-borne noise and vibration in buildings due to surface rail traffic. J. Sound Vib. 2007, 301, 718–738. [Google Scholar] [CrossRef]
- Ulgen, D.; Ertugrul, O.L.; Ozkan, M.Y. Measurement of ground borne vibrations for foundation design and vibration isolation of a high-precision instrument. Measurement 2016, 93, 385–396. [Google Scholar] [CrossRef]
- Takei, Y.; Yamada, S.; Izumi, Y.; Fujii, K. Application of seismic and vibration isolation structure system to design of over-track buildings. Q. Rep. RTRI 2007, 48, 50–57. [Google Scholar] [CrossRef] [Green Version]
- Zou, C.; Wang, Y.; Zhang, X.; Tao, Z. Vibration isolation of over-track buildings in a metro depot by using trackside wave barriers. J. Build. Eng. 2020, 30, 101270. [Google Scholar] [CrossRef]
- Yang, J.; Zhu, S.; Zhai, W.; Kouroussis, G.; Wang, Y. Prediction and mitigation of train-induced vibrations of large-scale building constructed on subway tunnel. Sci. Total Environ. 2019, 668, 485–499. [Google Scholar] [PubMed]
- Zhou, Y.; Zhang, Z. Experimental and analytical investigations on compressive behavior of thick rubber bearings for mitigating subway-induced vibration. Eng. Struct. 2022, 270, 114879. [Google Scholar]
- Zhou, Y.; Zhang, Z.; Vassiliou, M.F. Mechanical Properties of Thick Rubber Bearings Used in Over-Track Buildings. In Proceedings of the 17th World Conference on Seismic Isolation (17WCSI), Torino, Italy, 11–15 September 2022; Springer: Cham, Switzerland; pp. 179–189. [Google Scholar]
- Sun, X.J. Prediction of Environment Vibrations Induced by Metro Trains and Mitigation Measures Analysis. Ph.D. Thesis, Beijing Jiaotong University, Beijing, China, 2008. [Google Scholar]
- JGJ/T 170-2009; Standard for Limit and Measuring Method of Building Vibration and Secondary Noise Caused by Urban Rail Transit. Ministry of Housing and Urban-Rural Development of the People’s Republic of China: Beijing, China, 2009.
- GB/T50355-2018; Standard for Limits and Measurement Methods of Vibration in the Room of Residential Building. Ministry of Housing and Urban-Rural Development of the People’s Republic of China: Beijing, China, 2018.
- Muhr, A.H. A comparison of rubber and metal springs for vibration isolation. Plast. Rubber Compos. Process. Appl. 1992, 18, 3–7. [Google Scholar]
- Chen, H.W.; Pan, P.; Liu, J.C.; Sakurai, Y.; Nakamura, M.; Murota, N. Test of thick rubber bearings on its compressive properties. Adv. Mater. 2014, 919, 348–354. [Google Scholar] [CrossRef]









| Title | Depth (m) | Dynamic Elastic Modulus (MPa) | Mass Density (kg/m3) | Poisson’s Ratio | Damping Ratio |
|---|---|---|---|---|---|
| Soil layer I | 6 | 150 | 1920 | 0.4 | 0.05 |
| Soil layer II | 10 | 200 | 2030 | 0.3 | 0.04 |
| Soil layer III | 14 | 600 | 1970 | 0.3 | 0.03 |
| Trackbed/ | / | 42,000 | 2000 | 0.3 | 0.02 |
| Beam/Column/Plate | / | 32,500 | 2500 | 0.35 | 0.02 |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Carriage mass with full passenger capacity m3 (t) | 43.0 | Spring factor of bogie kT (kN/m) | 2080 |
| Carriage mass moment of inertia J (tm2) | 1700 | Damping factor of bogie CT (kN·S/m) | 240 |
| Bogie mass m2 (t) | 3.60 | Spring factor of bogie of wheels (kN/m) | 2450 |
| Bogie mass moment of inertia J (tm2) | 9.62 | Damping factor of bogie of wheels (kN·s/m) | 240 |
| Train length L (m) | 19.52 | Train space L (m) | 12.66 |
| Axle base a (m) | 2.30 | Mass of every two wheels m1 (t) | 1.70 |
| Area | Day | Night |
|---|---|---|
| Special buildings | 65 | 62 |
| Residential and educational buildings | 65 | 62 |
| Residential, commercial, and mixed-use buildings | 70 | 67 |
| Industrial buildings | 75 | 72 |
| Room Type | Limit Value Level | Time Period | Limit Value |
|---|---|---|---|
| Bedroom | Recommended | Day | 73 |
| Night | 70 | ||
| mandatory | Day | 78 | |
| Night | 75 | ||
| Living room | Recommended | Day and night | 73 |
| mandatory | Day and night | 78 |
| Model | Bearing Diameter (mm) | Bearing Height (mm) | Long Term Load (kN) | Vertical Stiffness (kN/mm) | Natural Frequency (Hz) |
|---|---|---|---|---|---|
| I | 800 | 400 | 4538 | 750 | 6.47 |
| II | 700 | 385 | 3327 | 550 | 6.47 |
| III | 500 | 320 | 1936 | 320 | 6.46 |
| Model | 1st Mode Overall Frequency (Hz) | Vertical 1st Mode (Hz) | Floor 1st Mode (Hz) |
|---|---|---|---|
| Original model | 4.83 | 20 | 20 |
| Vibration isolation model | 1.72 | 6.47 | 22.99 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, T.; Jiang, B.; Sun, X. Train-Induced Vibration Prediction and Control of a Metro Depot and Over-Track Buildings. Buildings 2023, 13, 1995. https://doi.org/10.3390/buildings13081995
Wang T, Jiang B, Sun X. Train-Induced Vibration Prediction and Control of a Metro Depot and Over-Track Buildings. Buildings. 2023; 13(8):1995. https://doi.org/10.3390/buildings13081995
Chicago/Turabian StyleWang, Tingting, Bolong Jiang, and Xiaojing Sun. 2023. "Train-Induced Vibration Prediction and Control of a Metro Depot and Over-Track Buildings" Buildings 13, no. 8: 1995. https://doi.org/10.3390/buildings13081995
APA StyleWang, T., Jiang, B., & Sun, X. (2023). Train-Induced Vibration Prediction and Control of a Metro Depot and Over-Track Buildings. Buildings, 13(8), 1995. https://doi.org/10.3390/buildings13081995





