Discussion on Calculation Method of Magnification Factor of Toggle-Brace-Viscous Damper
Abstract
:1. Introduction
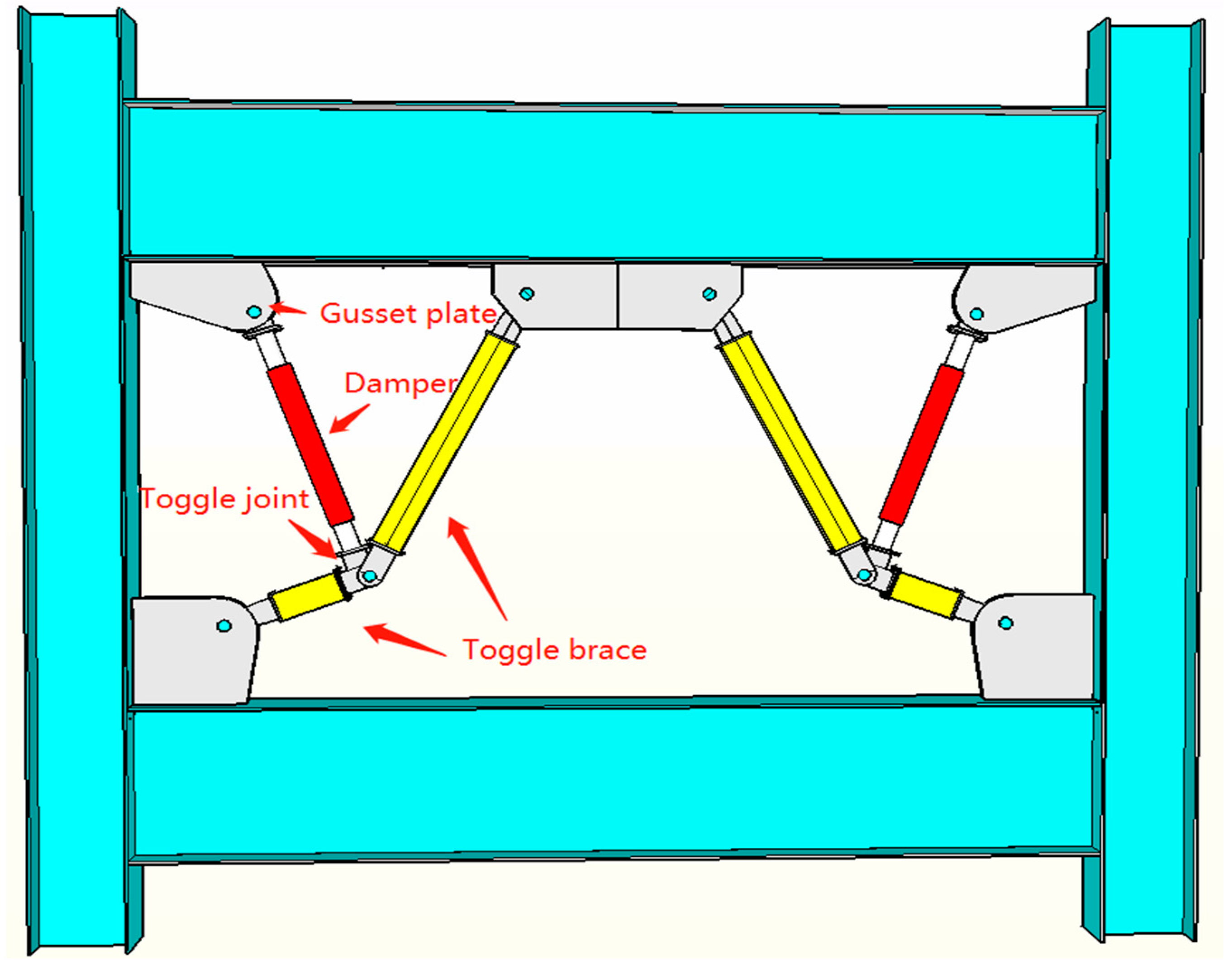
2. Introduction of Improved Algorithm
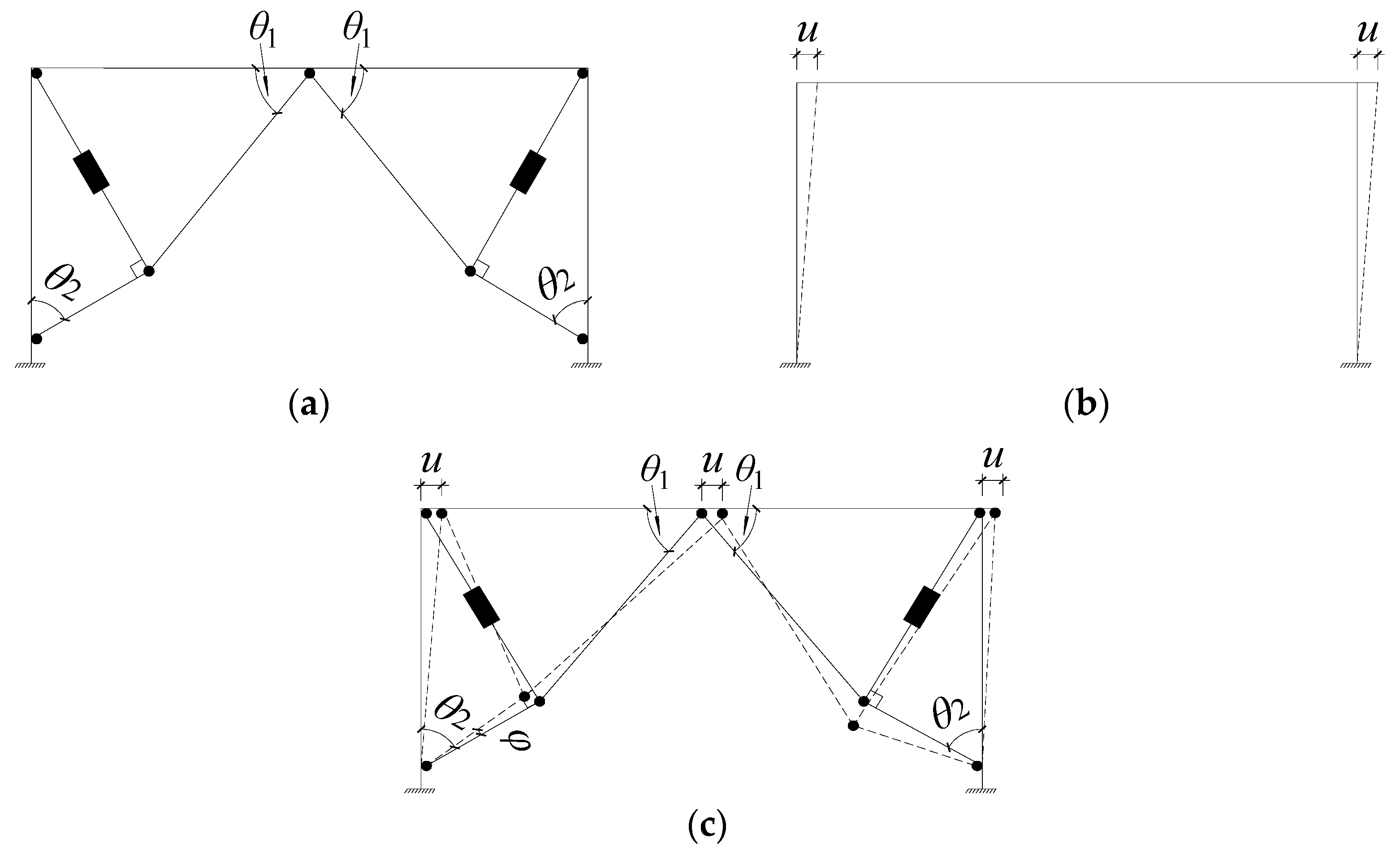
2.1. Existing Algorithm
- (1)
- The frame only performs rigid body motion;
- (2)
- The floor height remains unchanged when the column rotates;
- (3)
- The length of the toggle-joint support is fixed and considered a rigid connecting rod;
- (4)
- Additional dampers can freely contract along the axial direction;
- (5)
- The floor slab has absolute stiffness, and the stiffness ratio of the beams and columns is infinite;
- (6)
- The influence of the connection method between beams and columns on the deformation of dampers can be ignored.
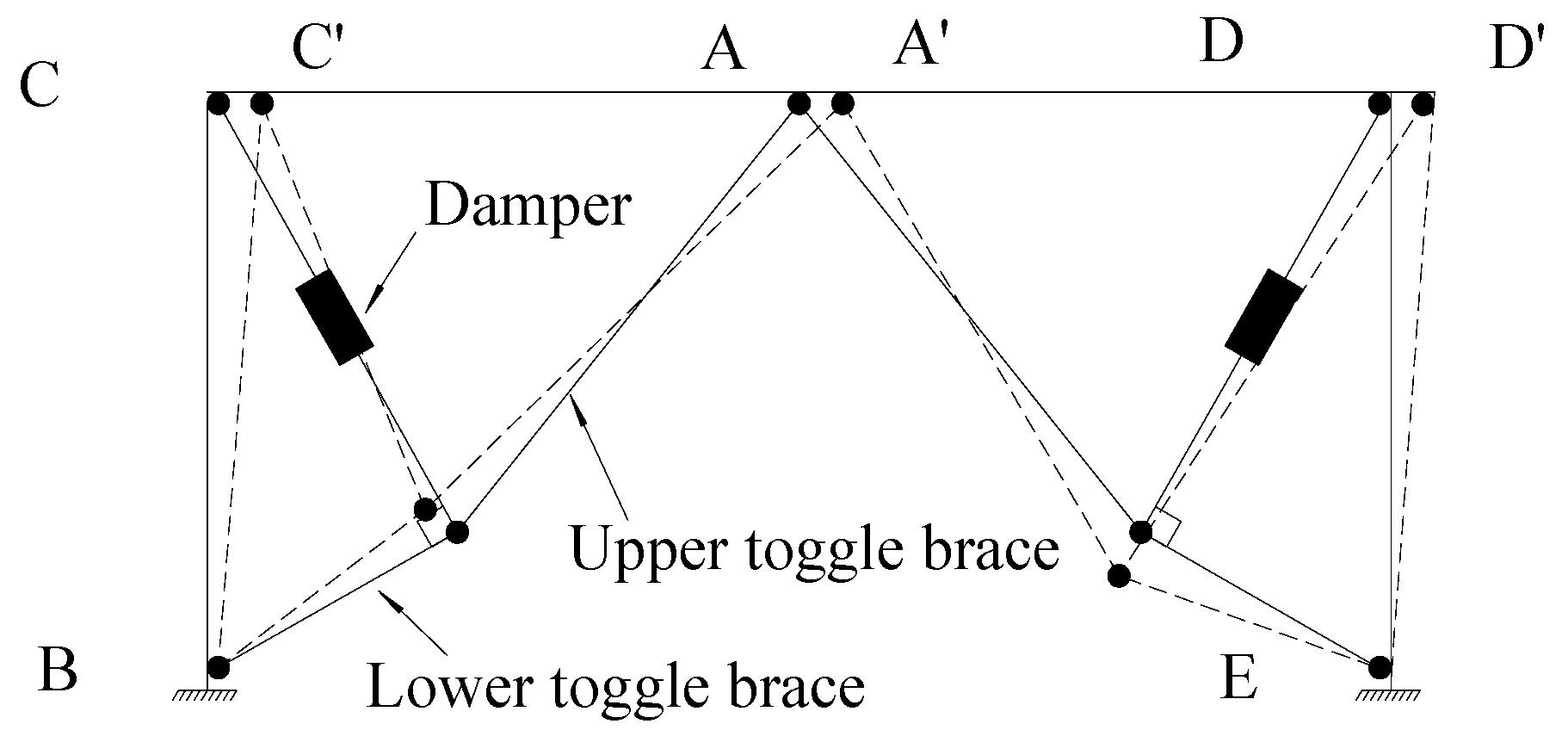
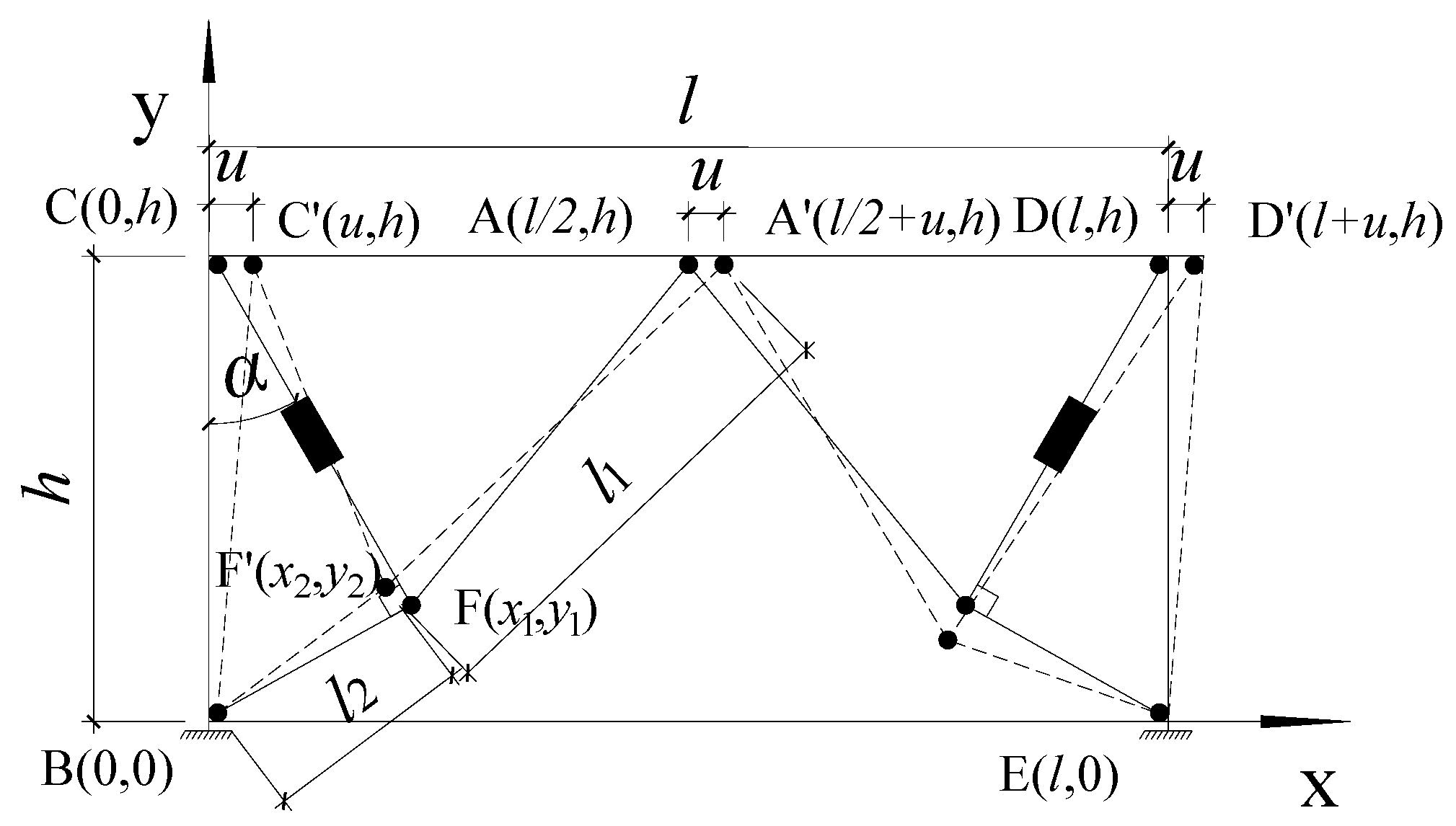
2.2. Improved Algorithm
2.3. Implementation of Improved Algorithms
3. Modeling Program
3.1. Model Overview
3.2. Model Design
3.3. Loading Scheme
4. Discussion of Simulation Results
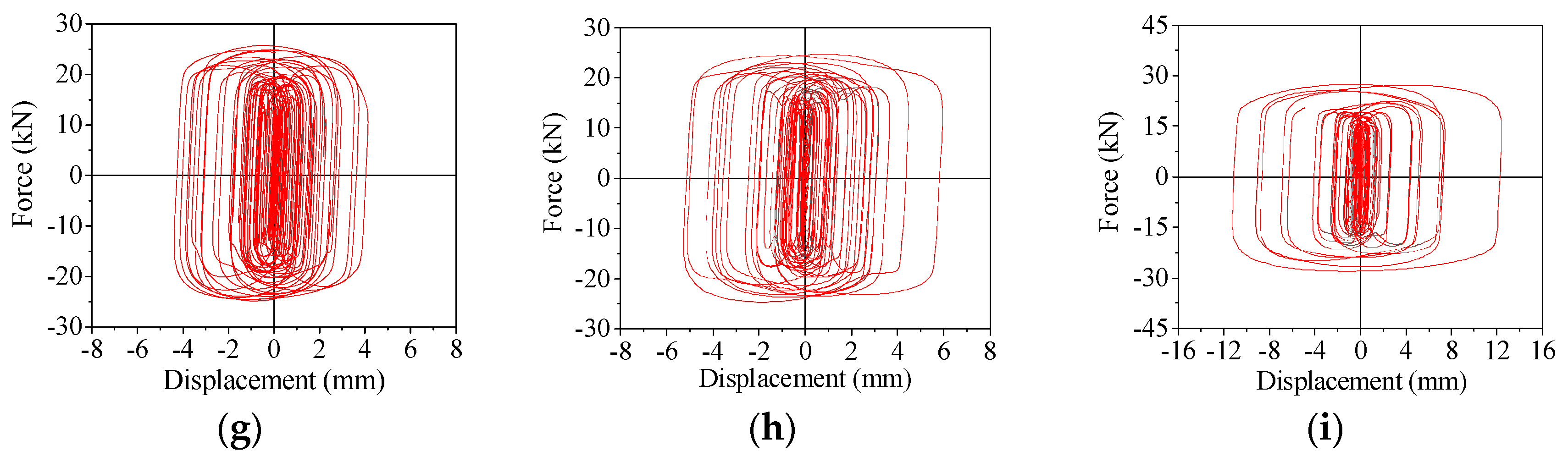
4.1. Hysteresis Curves
4.2. Magnification Factor
5. Optimization of Magnification Factor
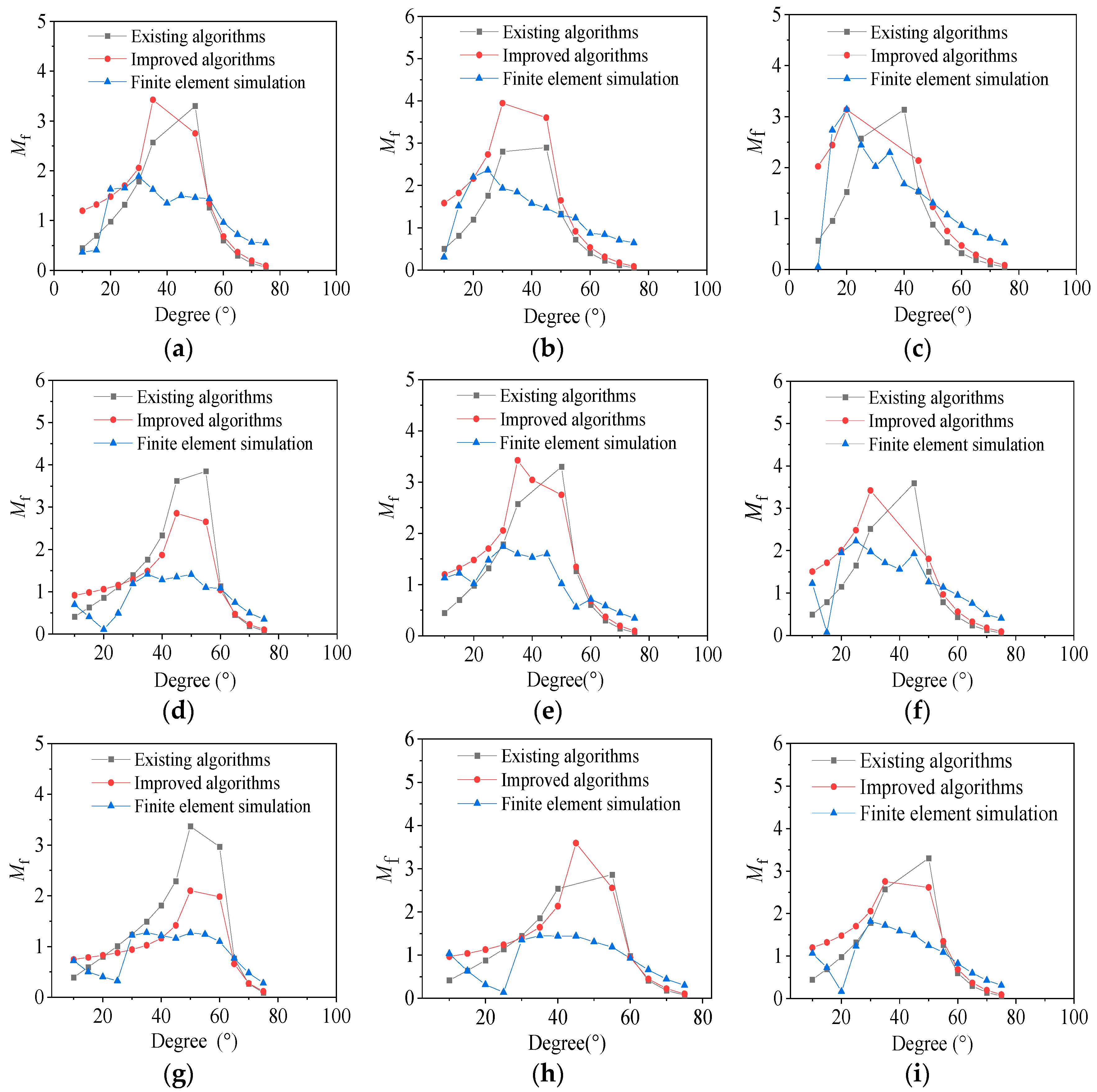
5.1. Relationship between Magnification Factor and Degree
5.2. Hysteresis Curve with Optimal Mf
6. Comparison and Analysis of Algorithms
6.1. Comparison of Algorithms
6.2. Error Analysis
7. Conclusions
- The algorithm for determining the existing Mf is relatively complex and difficult to apply in practical engineering. Considering the insufficient practicality of the existing Mf algorithm, an improved algorithm is formed based on the existing algorithm. Compared with existing algorithms, the improved algorithm optimizes assumptions and calculation methods, and its practicality has been improved.
- The correctness of the improved algorithm was verified using simulation results from nine models. From the numerical simulation results of the TBVD, it can be seen that the TBVD is relatively stable during deformation in the frame structure, and there is no fluctuation in the hysteresis loop. The hysteresis curve is relatively full, and the energy dissipation ability is significant. By comparing with simulation results, the improved algorithm outperforms existing algorithms in calculating Mf and obtaining the optimal angle.
- The Mf is related to the frame size and angle of the damper installation. Under a specific angle condition, the Mf increases with an increase in span and decreases with an increase in story height. When the installation angle range of the viscous damper is 10–20°, its Mf values are all less than 1. When the installation angle range of the viscous damper is 20–65°, the Mf values are greater than 1, and the optimal solution for the Mf is generally within this range. When the installation angle range of the viscous damper is 65–80°, the Mf values are less than 1.
- Based on the above research results, the following suggestions are proposed: designers should use the calculation method for the Mf of TBVDs proposed in this article to estimate the Mf. Designers can determine the angle corresponding to the optimal Mf roughly; TBVDs are recommended to be installed in frames with lower story heights and larger spans, where their performance is superior. The angle between the viscous damper and the frame column should be prioritized at 30 degrees and then further optimize the damping scheme.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Yuan, X.; Chen, G.; Jiao, P.; Li, L.; Han, J.; Zhang, H. A Neural Network-Based Multivariate Seismic Classifier for Simultaneous Post-Earthquake Fragility Estimation and Damage Classification. Eng. Struct. 2022, 255, 113918. [Google Scholar] [CrossRef]
- Nguyen, H.D.; Lafave, J.M.; Lee, Y.J.; Shin, M. Rapid Seismic Damage-State Assessment of Steel Moment Frames Using Machine Learning. Eng. Struct. 2022, 252, 113737. [Google Scholar] [CrossRef]
- Li, H.; Xue, J.; Chen, X.; Tu, G.; Lu, X.; Zhong, R. Experimental Research on Seismic Damage of Cross-Shaped CFST Column to Steel Beam Joints. Eng. Struct. 2022, 256, 113901. [Google Scholar] [CrossRef]
- Reza Khalili, M.; Ghahremani Baghmisheh, A.; Estekanchi, H.E. Seismic Damage and Life Cycle Cost Assessment of Unanchored Brick Masonry Veneers. Eng. Struct. 2022, 260, 114187. [Google Scholar] [CrossRef]
- Li, L.; Wentao, W.; SHI, P. A Visual Data-Informed Fiber Beam-Column Model for the Analysis of Residual Hysteretic Behavior of Post-Earthquake Damaged RC Columns. J. Earthq. Eng. 2023, 1–26. [Google Scholar] [CrossRef]
- Bruschi, E.; Quaglini, V.; Calvi, P.M. A Simplified Design Procedure for Seismic Upgrade of Frame Structures Equipped with Hysteretic Dampers. Eng. Struct. 2022, 251, 113504. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, C.; Xue, Q. Insight into Energy Dissipation Behavior of a SDOF Structure Controlled by the Pounding Tuned Mass Damper System. Earthq. Eng. Struct. Dyn. 2022, 51, 958–973. [Google Scholar] [CrossRef]
- Vinayaravi, R.; Jayaraj, K.; Kumaresan, D.; Asraff, A.K. Study on Energy Dissipation Mechanism of an Impact Damper System. J. Comput. Nonlinear Dyn. 2022, 17, 041003. [Google Scholar] [CrossRef]
- Xu, Y.; Xu, Z.; Guo, Y.; Huang, X.; Dong, Y.; Li, Q. Dynamic Properties and Energy Dissipation Study of Sandwich Viscoelastic Damper Considering Temperature Influence. Buildings 2021, 11, 470. [Google Scholar] [CrossRef]
- Chen, Y.; Yu, W.; Zhang, M.; Li, Y. A Novel Energy Dissipation Damper for Multi-Level Earthquakes. J. Constr. Steel Res. 2022, 192, 107214. [Google Scholar] [CrossRef]
- Nazarimofrad, E.; Shokrgozar, A. Seismic Performance of Steel Braced Frames with Self-Centering Buckling-Restrained Brace Utilizing Superelastic Shape Memory Alloys. Struct. Des. Tall Spec. Build. 2019, 28, e1666. [Google Scholar] [CrossRef]
- Lie, W.; Wu, C.; Luo, W.; Wu, C.; Li, C.; Li, D.; Wu, C. Cyclic Behaviour of a Novel Torsional Steel-Tube Damper. J. Constr. Steel Res. 2022, 188, 107010. [Google Scholar] [CrossRef]
- Zeng, B.; Gao, J.; Qing, Y.; Wang, C.; Sun, X. Seismic Performance of Suspended-floor Structures with Viscous Dampers Considering Acceptable Interstory Drift. Struct. Des. Tall Build 2022, 31, e1912. [Google Scholar] [CrossRef]
- YupengRen; PengzhenLin; ZhigangHe Research on Application of Viscous Dampers in Continuous Steel Truss Gieder with Flexible Arch. J. Eng. Stud. 2018, 10, 546–553. [CrossRef]
- Lin, W.C.; Wang, S.J.; Hwang, J.S. Seismic Retrofit of Existing Critical Structures Using Externally Connected Viscous Dampers. Int. J. Struct. Stab. Dyn. 2022, 22. [Google Scholar] [CrossRef]
- Şigaher, A.N.; Constantinou, M.C. Scissor-Jack-Damper Energy Dissipation System. Earthq. Spectra 2003, 19, 133–158. [Google Scholar] [CrossRef]
- Hwang, J.-S.; Kim, J.; Kim, Y.-M. Rotational Inertia Dampers with Toggle Bracing for Vibration Control of a Building Structure. Eng. Struct. 2007, 29, 1201–1208. [Google Scholar] [CrossRef]
- Gluck, J.; Ribakov, Y. Active Viscous Damping System with Amplifying Braces for Control of MDOF Structures. Earthq. Eng. Struct. Dyn. 2002, 31, 1735–1751. [Google Scholar] [CrossRef]
- Berton, S.; Bolander, J.E. Amplification System for Supplemental Damping Devices in Seismic Applications. J. Struct. Eng. 2005, 131, 979–983. [Google Scholar] [CrossRef]
- Constantinou, M.C.; Tsopelas, P.; Hammel, W.; Sigaher, A.N. Toggle-Brace-Damper Seismic Energy Dissipation Systems. J. Struct. Eng. 2001, 127, 105–112. [Google Scholar] [CrossRef]
- Lee, S.-H.; Min, K.-W.; Chung, L.; Lee, S.-K.; Lee, M.-K.; Hwang, J.-S.; Choi, S.-B.; Lee, H.-G. Bracing Systems for Installation of MR Dampers in a Building Structure. J. Intell. Mater. Syst. Struct. 2007, 18, 1111–1120. [Google Scholar] [CrossRef]
- JGJ 297-2013; Technical Specification for Seismic Energy Dissipation of Buildings. China Architecture and Building Press: Beijing, China, 2012.
- GB 50011-2016; Code for Seismic Design of Buildings. China Architecture and Building Press: Beijing, China, 2016.
- Xue, J.; Luo, Z.; Sui, Y.; Yang, R.; Liu, J.; Ren, R. Seismic Mitigation Effect and Dynamic Test Study of Displacement-Amplified Viscously-Damped Outrigger. J. Build. Struct. 2022, 43, 21–31. [Google Scholar] [CrossRef]
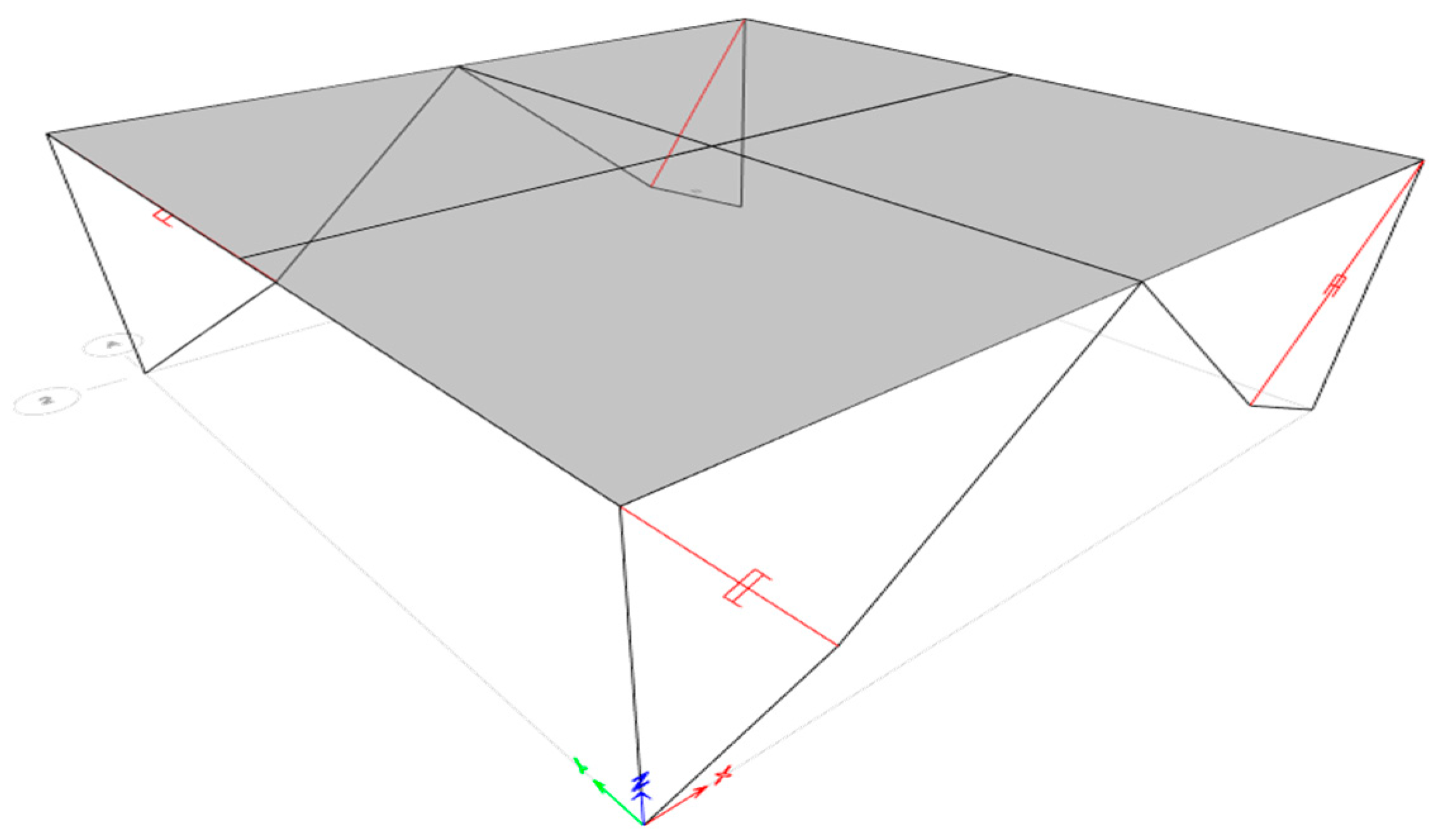
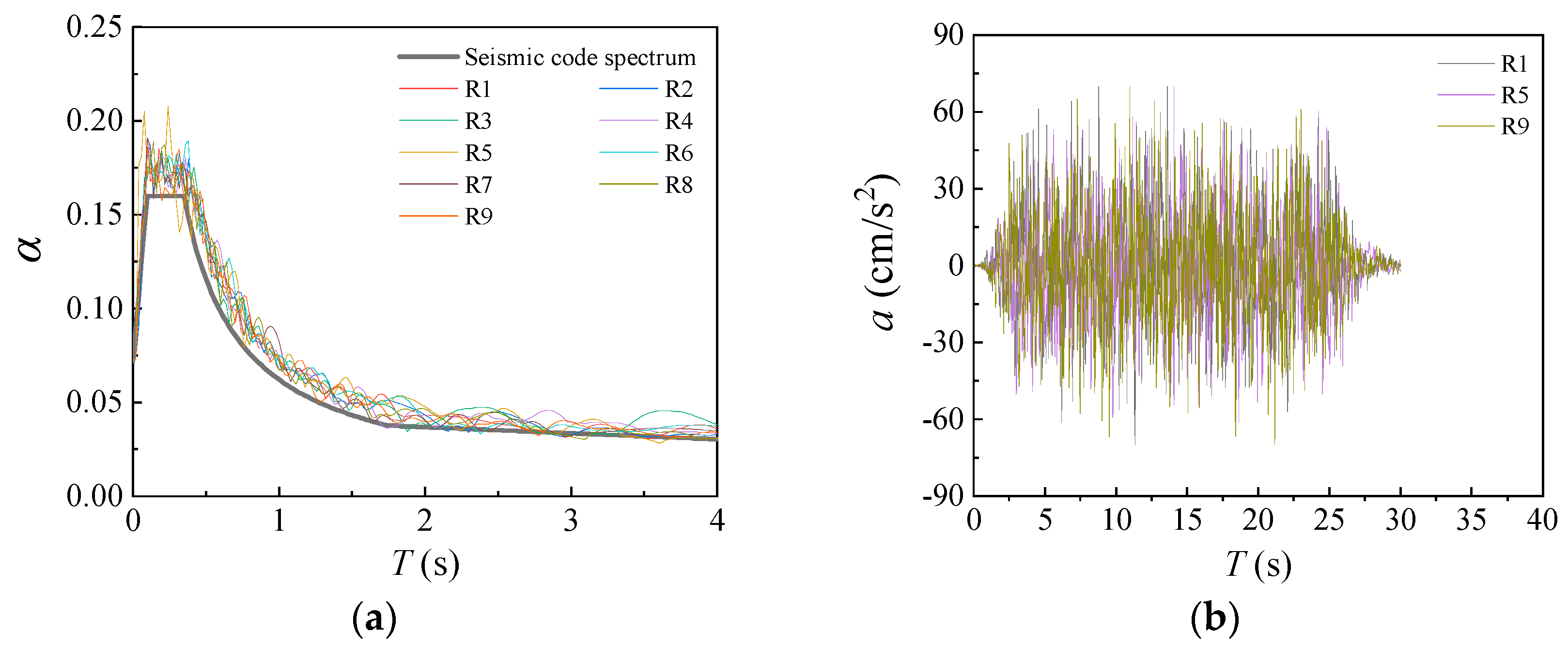

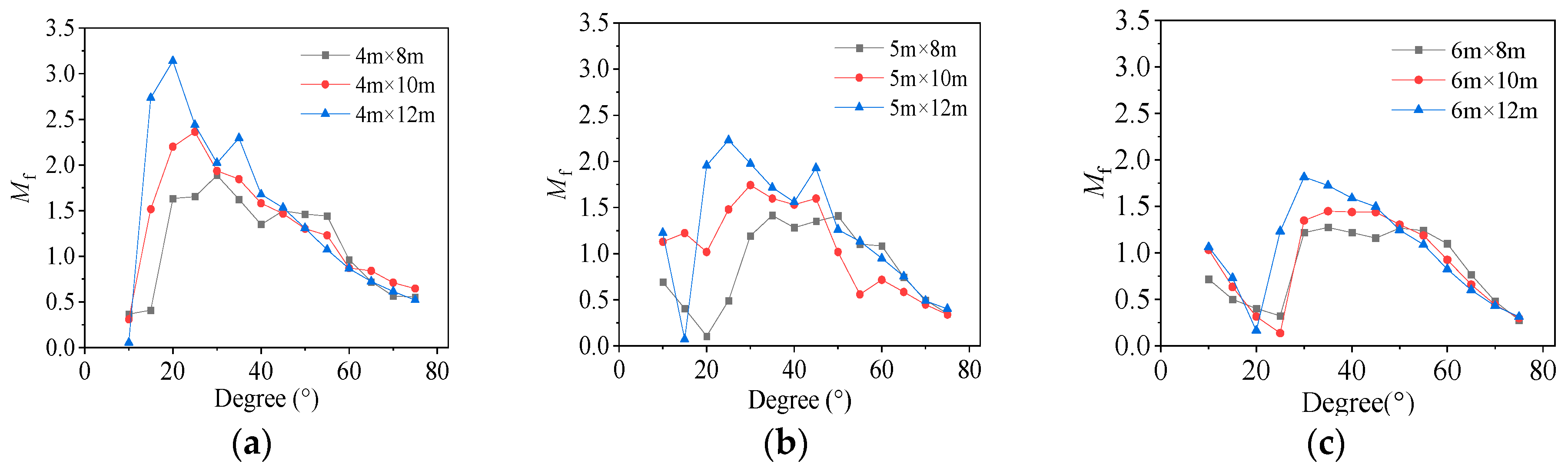
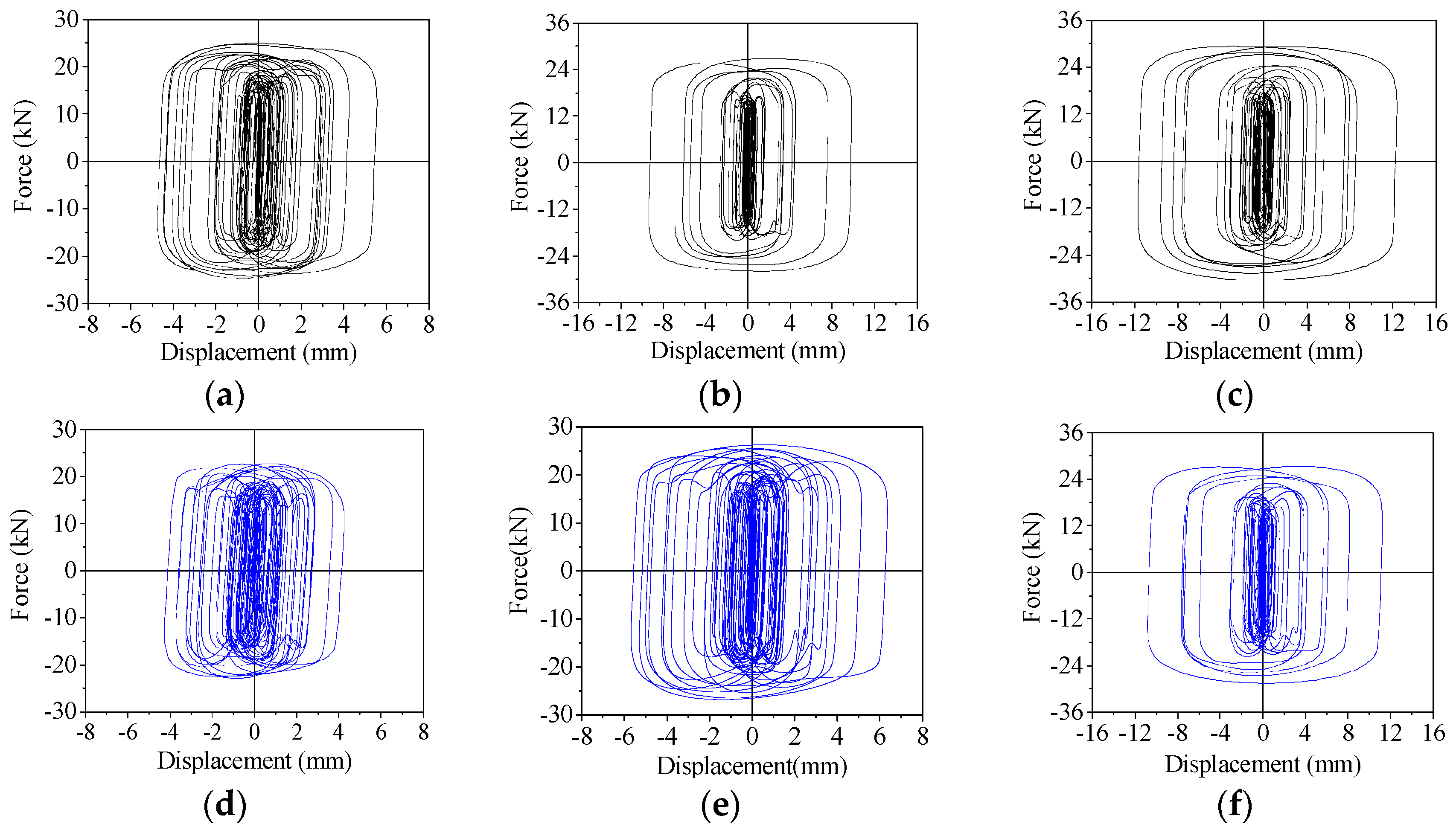

| Model | Height (mm) | Span (mm) |
|---|---|---|
| Model-1 | 4000 | 8000 |
| Model-2 | 4000 | 10,000 |
| Model-3 | 4000 | 12,000 |
| Model-4 | 5000 | 8000 |
| Model-5 | 5000 | 10,000 |
| Model-6 | 5000 | 12,000 |
| Model-7 | 6000 | 8000 |
| Model-8 | 6000 | 10,000 |
| Model-9 | 6000 | 12,000 |
| Part | Section |
|---|---|
| Column | 800 × 800 |
| Primary Beam | 500 × 1400 |
| Secondary beam | 600 × 900 |
| Toggle brace | HW200 × 200 × 20 × 20 |
| Material | Density (kg/m3) | Elastic Modulus (MPa) | Poisson’s Ratio (-) | Strength (MPa) |
|---|---|---|---|---|
| C30 | 2500 | 30,000 | 0.20 | 20.1 (1.43) |
| HRB400 | 7800 | 206,000 | 0.30 | 540 (400) |
| Q345 | 7800 | 206,000 | 0.30 | 470 (345) |
| Model | Mode 1 | Mode 2 | Mode 3 |
|---|---|---|---|
| Model-1 | 0.086 (X) | 0.086 (Y) | 0.057 (Z) |
| Model-2 | 0.127 (X) | 0.127 (Y) | 0.062 (Z) |
| Model-3 | 0.182 (X) | 0.182 (Y) | 0.086 (Z) |
| Model-4 | 0.100 (X) | 0.100 (Y) | 0.078 (Z) |
| Model-5 | 0.136 (X) | 0.136 (Y) | 0.089 (Z) |
| Model-6 | 0.189 (X) | 0.189 (Y) | 0.100 (Z) |
| Model-7 | 0.123 (X) | 0.123 (Y) | 0.101 (Z) |
| Model-8 | 0.142 (X) | 0.142 (Y) | 0.114 (Z) |
| Model-9 | 0.168 (X) | 0.168 (Y) | 0.129 (Z) |
| Height | Span | ||
|---|---|---|---|
| 8 m | 10 m | 12 m | |
| 4 m | 1.887 | 1.9361 | 2.0222 |
| 5 m | 1.2179 | 1.7421 | 1.9753 |
| 6 m | 1.1912 | 1.3484 | 1.8105 |
| Height | Span | ||
|---|---|---|---|
| 8 m | 10 m | 12 m | |
| 4 m | 1.8870 (30°) * | 2.3630 (25°) | 3.1407 (20°) |
| 5 m | 1.4147 (35°) | 1.7421 (30°) | 2.2291 (25°) |
| 6 m | 1.2734 (35°) | 1.4484 (35°) | 1.8105 (30°) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, J.; Ma, P.; Hu, Y.; Yao, J. Discussion on Calculation Method of Magnification Factor of Toggle-Brace-Viscous Damper. Buildings 2023, 13, 2006. https://doi.org/10.3390/buildings13082006
Xu J, Ma P, Hu Y, Yao J. Discussion on Calculation Method of Magnification Factor of Toggle-Brace-Viscous Damper. Buildings. 2023; 13(8):2006. https://doi.org/10.3390/buildings13082006
Chicago/Turabian StyleXu, Jiewei, Pengfei Ma, Yukun Hu, and Jitao Yao. 2023. "Discussion on Calculation Method of Magnification Factor of Toggle-Brace-Viscous Damper" Buildings 13, no. 8: 2006. https://doi.org/10.3390/buildings13082006
APA StyleXu, J., Ma, P., Hu, Y., & Yao, J. (2023). Discussion on Calculation Method of Magnification Factor of Toggle-Brace-Viscous Damper. Buildings, 13(8), 2006. https://doi.org/10.3390/buildings13082006






