Investigation of Uniaxial Compression Stress–Strain Relationship of Early Age Manufactured Sand Concrete and Its Application
Abstract
:1. Introduction
2. Materials and Test Methods
2.1. Materials
2.1.1. Cement
2.1.2. Composition of Concrete
2.2. Test Method
2.2.1. Specimen Preparation
2.2.2. Loading Equipment and Process
2.3. Characteristics of the Stress–Strain Curve
3. Influence of Different Factors on Peak Stresses and Peak Strains
3.1. Effects of Age
3.2. Effects of Water-Binder Ratio
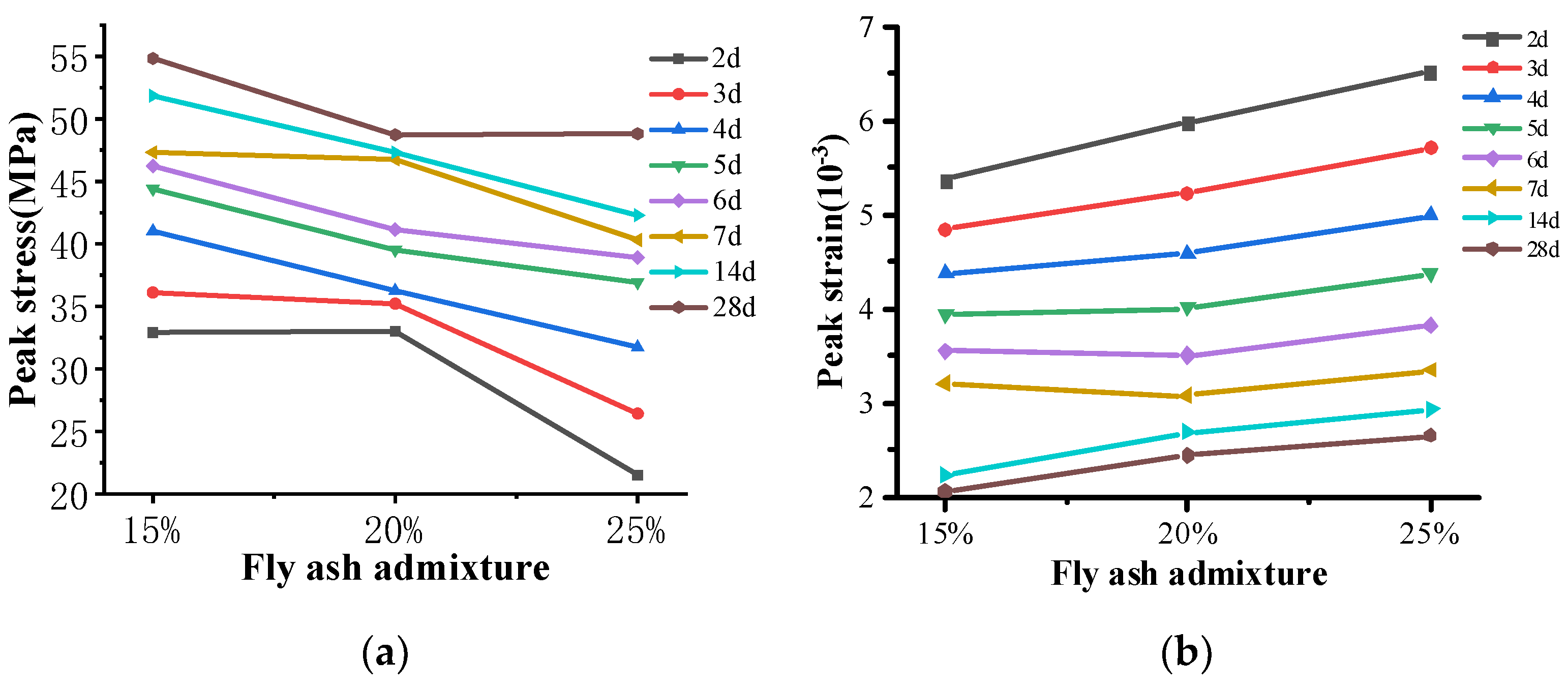
3.3. Effects of Fly Ash Admixture
4. Modeling of the Constitutive of Early Age Manufactured Sand Concrete
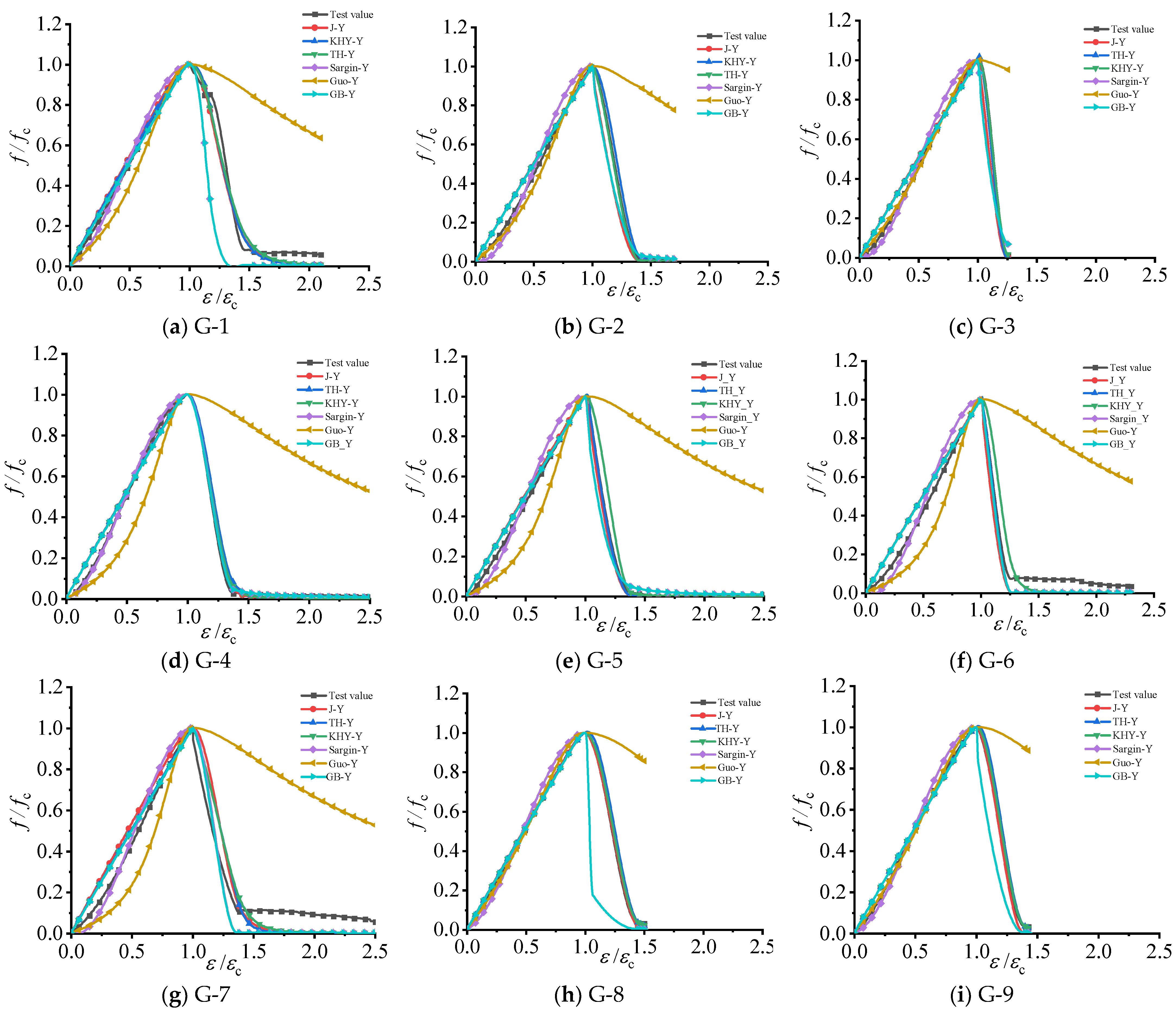
4.1. Fitting Analysis with the Existing Models
4.2. Stress–Strain Curve Parameters Concerning Different Variables
4.2.1. Elastic Modulus
- (1)
- t → ∞, Ec tends to a certain value;
- (2)
- t → 0, Ec → 0;
- (3)
- dE/dt decreases as the age t changes;
- (4)
- Ec = c × e^(−d/t), d > 0, c is generally the modulus of elasticity at age 28d.
4.2.2. Peak Stress
- (1)
- When t tends to 0, the peak stress also tends to 0;
- (2)
- When the age t tends to infinity, the peak stress should gradually converge to a certain value;
- (3)
- The growth rate of the function decreases with age, that is, t tends to infinity, and the derivative of y tends to 0;
- (4)
- t → 0, y → 0.
4.2.3. Peak Strain
- a.
- The linear regression form assumes a directly proportional relationship between peak strain and strength, ;
- b.
- The power function regression form assumes a non-linear relationship between peak strain and strength, where the trend is influenced by power, ;
- c.
- The exponential regression form considers a complex exponential function between peak strain and strength, .
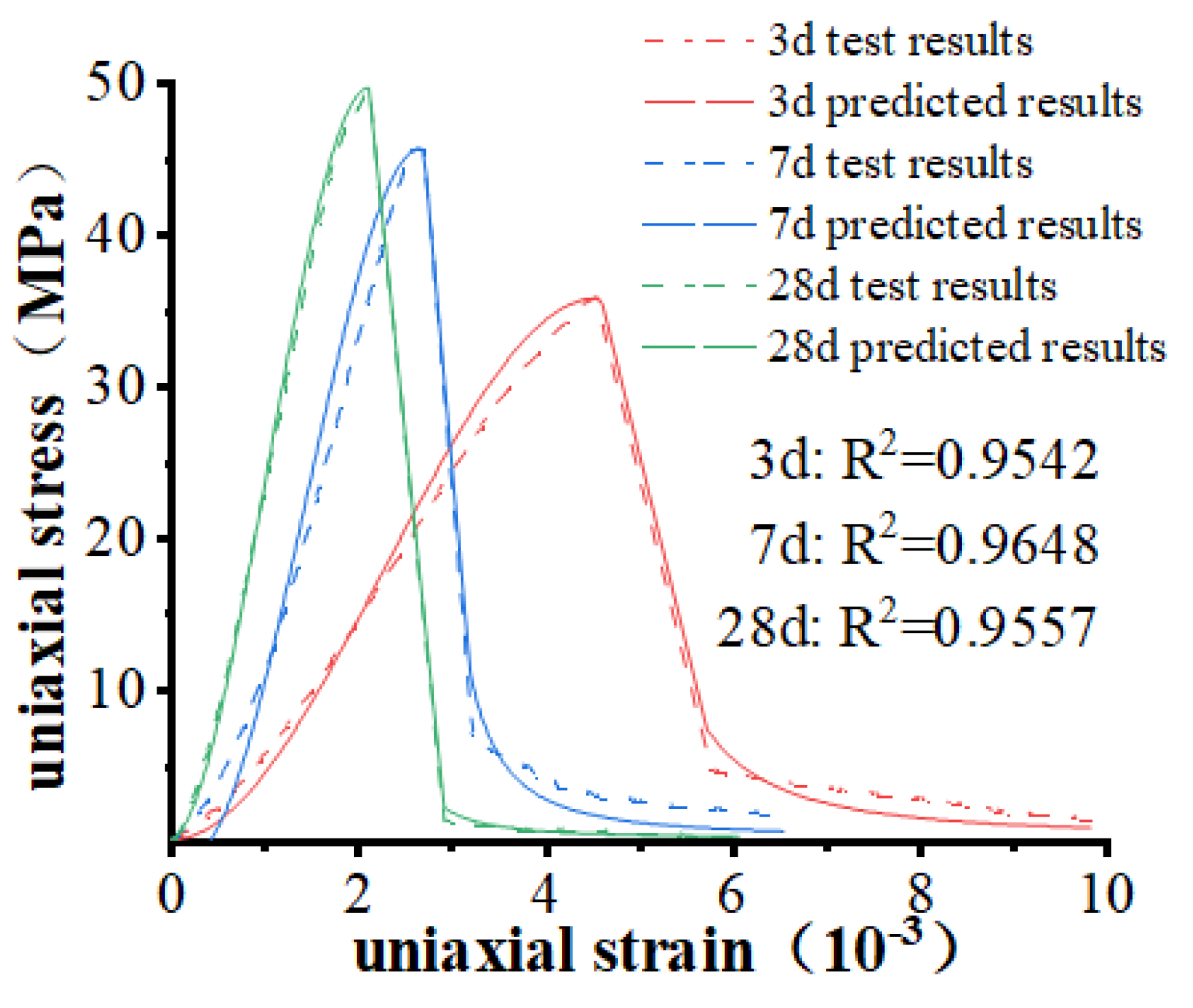
4.3. Constitutive Model of Early Age Manufactured Sand Concrete
5. Application of the Constitutive Model
5.1. Build Finite Element Model
5.1.1. Basic Assumptions
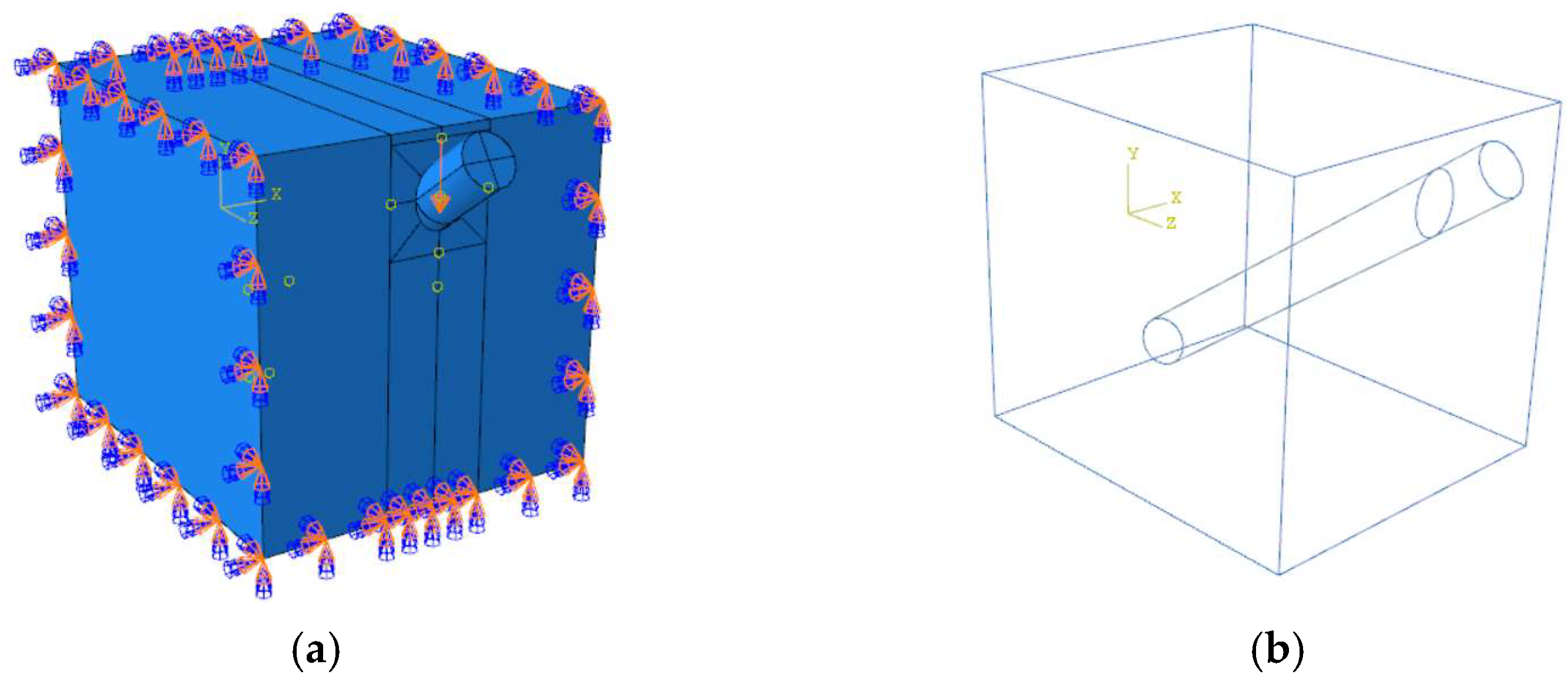
5.1.2. Finite Element Model
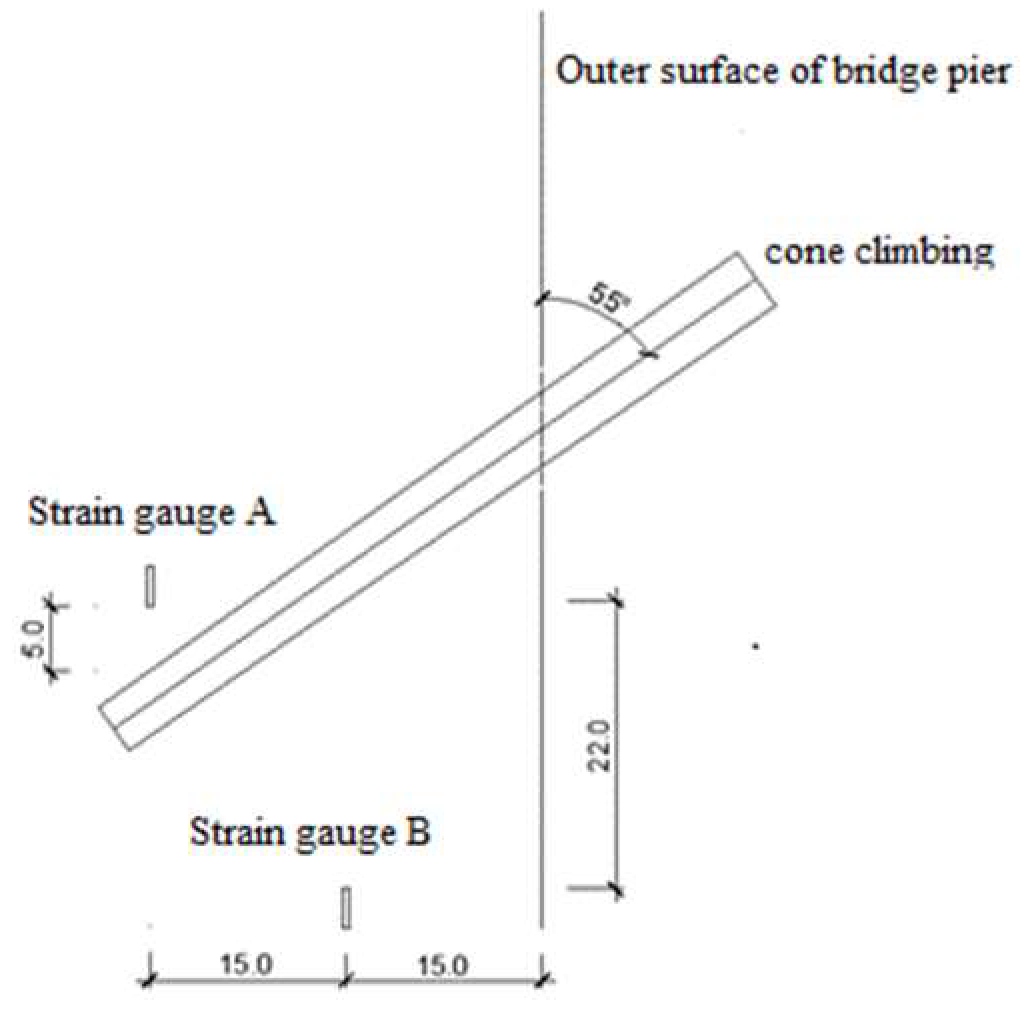
5.2. On-Site Monitoring Program
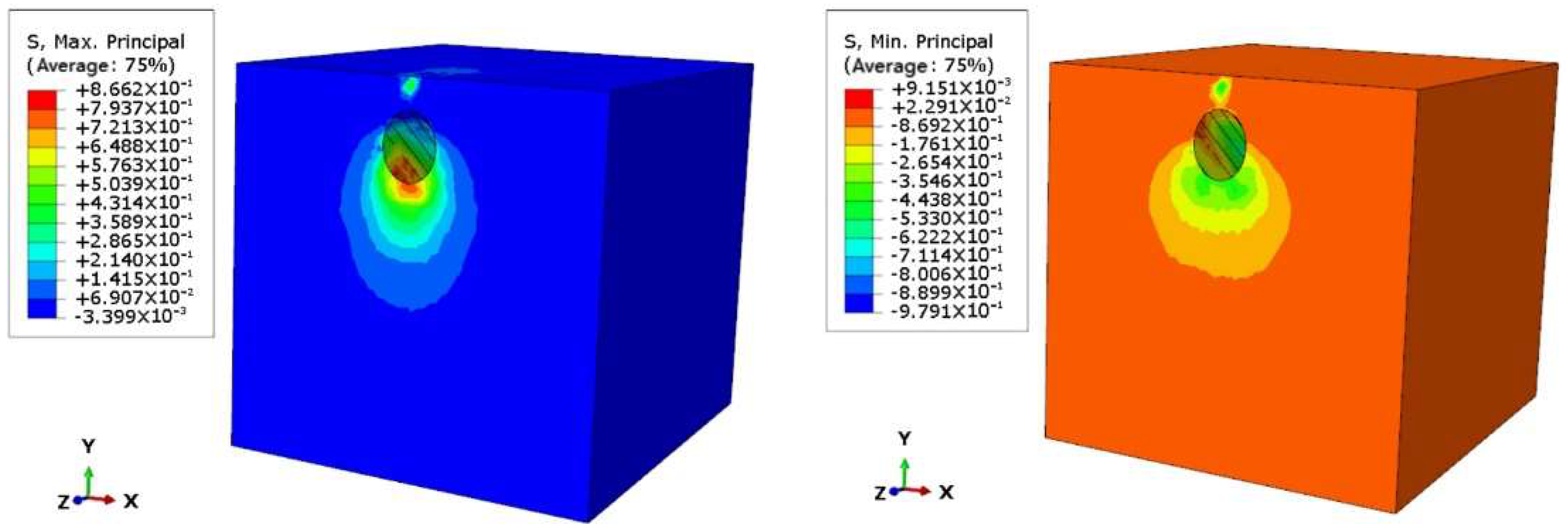
5.3. Analysis of Finite Element Model Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, X.; Liu, M.; Liu, X. Study on mechanical properties and carbon emission of desert sand and manufactured sand concrete. J. Civ. Eng. 2022, 55, 23–30. [Google Scholar]
- Xiao, C.; Guo, Y.; Li, B.; Zhou, M.; Li, B.; Liu, Z.; Zhou, J. Coupled effects of the content and methylene blue value (MBV)of microfines on the performance of manufactured sand concrete. Constr. Build. Mater. 2020, 240, 17953. [Google Scholar]
- Shen, W.; Liu, Y.; Wang, Z.; Cao, L.; Wu, D.; Wang, Y.; Ji, X. Influence of manufactured sand’s characteristics on its concrete performance, Constr. Build. Mater. 2018, 172, 574–583. [Google Scholar] [CrossRef]
- Shen, W.; Yang, Z.; Cao, L. Characterization of manufactured sand: Particle shape, surface texture and behavior in concrete. Constr. Build. Mater. 2016, 114, 595–601. [Google Scholar] [CrossRef]
- Deng, C.; Yan, J.; Ye, X. Research on the effect of manufactured sand admixture on mechanical properties and volume stability of concrete. New Build. Mater. 2018, 45, 42–46. [Google Scholar]
- Zhang, M.H. Microstructure, crack propagation, and mechanical properties of cement pastes containing high volumes of fly ashes. Cem. Concr. Res. 1995, 25, 165–1178. [Google Scholar] [CrossRef]
- De la Varga, I.; Spragg, R.P.; Di Bella, C.; Castro, J.; Bentz, D.P.; Weiss, J. Fluid transport in high volume fly ash mixtures with and without internal curing. Cem. Concr. Compos. 2014, 45, 102–110. [Google Scholar] [CrossRef]
- Juang, C.; Kuo, W. Properties and Mechanical Strength Analysis of Concrete Using Fly Ash, Ground Granulated Blast Furnace Slag and Various Superplasticizers. Buildings 2023, 13, 1644. [Google Scholar] [CrossRef]
- Wu, H.; Hu, R.; Yang, D.; Ma, Z. Micro-macro characterizations of mortar containing construction waste fines as replacement of cement and sand: A comparative study. Constr. Build. Mater. 2023, 383, 131328. [Google Scholar] [CrossRef]
- Zhang, M.; Xu, J.; Li, M.; Yuan, X. Influence of Stone Powder Content from Manufactured Sand Concrete on Shrinkage, Cracking, Compressive Strength, and Penetration. Buildings 2023, 13, 1833. [Google Scholar] [CrossRef]
- Ma, Z.; Shen, J.; Wang, C.; Wu, H. Characterization of sustainable mortar containing high-quality recycled manufactured sand crushed from recycled coarse aggregate. Cem. Concr. Compos. 2022, 132, 104629. [Google Scholar] [CrossRef]
- Gao, Y.; Ren, X.; Zhang, J. Proposed constitutive law of uniaxial compression for concrete under deterioration effects. Bull. Chin. Ceram. Soc. 2020, 13, 2048. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Wang, G.; Yang, S. Experimental study on mechanical properties and stress-strain principal relationship of desert sand concrete. J. Appl. Mech. 2019, 36, 1131–1137+1261. [Google Scholar]
- Ju, G.; Li, Z.; Wang, W. Experimental study on axial compression performance of sand concrete in Gurbantunggut desert. Concrete 2019, 4, 33–36. [Google Scholar]
- Gao, Y.; He, Z.; Song, L. Influence of manufactured sand mixing rate on mechanical properties of plastic concrete. People’s Yellow River 2019, 41, 148–151+157. [Google Scholar]
- Chen, Z.; Qin, Y.; Liu, G. Experimental study on the principal relationship of manufactured sand concrete after high temperature. Concrete 2013, 12, 72–74+86. [Google Scholar]
- Xie, K.; Liu, Z.; Gai, B.; Zhu, M.; Xin, Y. Experimental study on stress-strain of manufactured sand concrete. Silic. Bull. 2020, 39, 3823–3831. [Google Scholar]
- Xie, K.; Liu, Z.; Gai, B.; Xin, Y.; Zhu, M. Ontogenetic relationships and mechanical properties of concrete with manufactured sand of different lithologies. J. Archit. Civ. Eng. 2021, 38, 99–106. [Google Scholar]
- JGJ 55-2011; Design of Ordinary Concrete Proportions. Ministry of Housing and Urban Rural Development of the People’s Republic of China: Beijing, China, 2011. Available online: https//www.doc88.com/p-1166129088978.html (accessed on 3 August 2023).
- Guo, Z.; Shi, X. Principles and Analysis of Reinforced Concrete; Tsinghua University Press: Beijing, China, 2003. [Google Scholar]
- Xu, Z.; Yuan, Q.; Yang, Z. Mechanical properties of early-age concrete and its uniaxial principal structure model. J. SUT 2015, 5, 92–96. [Google Scholar]
- Liu, S.; Yan, P. Effect of limestone powder on the filling effect of cement slurry and pore structure of mortar. J. Chin. Ceram. Soc. 2008, 36, 5. [Google Scholar]
- Carreira, D.J.; Chu, K. Stress-strain relationship for plain concrete in compression. J. Am. Concr. Inst. 1985, 82, 797–804. [Google Scholar]
- Wee, T.; Chin, M.; Mansur, M. Stress-Strain Relationship of High-Strength Concrete in Compression. J. Mater. Civ. Eng. 1996, 8, 70–76. [Google Scholar] [CrossRef]
- Yang, K.; Mun, J.; Cho, M. Stress-Strain Model for Various Unconfined Concretes in Compression. ACI Struct. J. 2014, 111, 819–826. [Google Scholar] [CrossRef]
- Sargin, M. Stress-Strain Relationship for Concrete and the Analysis of Structural Concrete Sections. Master’s Thesis, University of Waterloo, Waterloo, ON, Canada, 1971. [Google Scholar]
- GB 50010-2010; Code for the Design of Concrete Structures. China Architecture & Building Press: Beijing, China, 2015.
- Guo, Z.; Zhang, X.; Zhang, D. Experimental study of the full stress-strain curve of concrete. J. Build. Struct. 1982, 3, 1–12. [Google Scholar]
- Zhang, W.; Ye, J.; Bai, Z.; Li, X. Intersection queue length estimation method based on networked vehicle trajectory data. Chin. J. Highw. 2022, 35, 216–225. [Google Scholar]
- Samani, A.; Attard, M. A stress–strain model for uniaxial and confined concrete under compression. Eng. Struct. 2012, 41, 335–349. [Google Scholar] [CrossRef]
- Zhang, Y. Experimental Study on the Macroscopic Constitutive Relationship of Reinforced Concrete in Axial Compression. Master’s Thesis, Chongqing Jiaotong University, Chongqing, China, 2013. [Google Scholar]
- Xu, J. Research on the Whole-Process Analysis Method of Hollow Slab Beams Based on the Unified Constitutive of Steel Reinforcement. Master’s Thesis, Chongqing Jiaotong University, Chongqing, China, 2014. [Google Scholar]






| Project | Density (g·cm−3) | Specific Surface Area (cm2·g−1) | Setting Time (min) | Flexural Strength (MPa) | Compressive Strength (MPa) | |
|---|---|---|---|---|---|---|
| Initial Setting Time | Final Setting Time | 3d | 3d | |||
| Technical indicators | 3.1 | 3450 | 204 | 272 | 6.5 | 33.4 |
| Group | Water-to-Binder Ratio | Fly Ash Admixture | Sand Rate | Coarse Aggregate Proportioning 10~20 mm:5~10 mm | Water Consumption (kg) | Super-Plasticizer Amount (%) |
|---|---|---|---|---|---|---|
| G-1 | 0.32 | 15% | 42% | 6:4 | 165 | 1.2 |
| G-2 | 0.32 | 20% | 42% | 6:4 | 165 | 1.2 |
| G-3 | 0.32 | 25% | 42% | 6:4 | 165 | 1.2 |
| G-4 | 0.34 | 15% | 42% | 6:4 | 165 | 1.2 |
| G-5 | 0.34 | 20% | 42% | 6:4 | 165 | 1.2 |
| G-6 | 0.34 | 25% | 42% | 6:4 | 165 | 1.2 |
| G-7 | 0.36 | 15% | 42% | 6:4 | 165 | 1.2 |
| G-8 | 0.36 | 20% | 42% | 6:4 | 165 | 1.2 |
| G-9 | 0.36 | 25% | 42% | 6:4 | 165 | 1.2 |
| Work Conditions | Evaluation Indicators | J-Y | TH-Y | KHY-Y | Sargin-Y | Guo-Y | GB-Y |
|---|---|---|---|---|---|---|---|
| G-1 | R2 | 0.9884 | 0.9692 | 0.9824 | 0.9162 | 0.6771 | 0.8750 |
| MAE | 0.1076 | 0.0973 | 0.0973 | 0.1209 | 2.0090 | 0.8584 | |
| MSE | 0.0004 | 0.0004 | 0.0004 | 0.0005 | 1.1955 | 0.4010 | |
| G-2 | R2 | 0.9817 | 0.9831 | 0.9833 | 0.9548 | 0.7608 | 0.9182 |
| MAE | 0.6295 | 0.2110 | 0.3915 | 0.3066 | 2.3495 | 0.7706 | |
| MSE | 0.0586 | 0.0082 | 0.0243 | 0.0175 | 1.6118 | 0.0872 | |
| G-3 | R2 | 0.9819 | 0.9836 | 0.9838 | 0.9973 | 0.6197 | 0.8810 |
| MAE | 0.1278 | 0.1252 | 0.1358 | 0.1211 | 3.1258 | 0.8574 | |
| MSE | 0.0006 | 0.0006 | 0.006 | 0.0005 | 2.0452 | 0.4007 | |
| G-4 | R2 | 0.9907 | 0.9907 | 0.8908 | 0.9917 | 0.6987 | 0.8916 |
| MAE | 0.1031 | 0.1014 | 0.0998 | 0.0986 | 3.8832 | 0.6899 | |
| MSE | 0.0004 | 0.0004 | 0.004 | 0.0004 | 2.2508 | 0.0247 | |
| G-5 | R2 | 0.9925 | 0.9943 | 0.9944 | 0.9954 | 0.6817 | 0.9213 |
| MAE | 0.1164 | 0.1359 | 0.1236 | 0.0998 | 3.8563 | 0.2754 | |
| MSE | 0.0005 | 0.0006 | 0.0006 | 0.0004 | 2.2487 | 0.0091 | |
| G-6 | R2 | 0.9580 | 0.9596 | 0.8635 | 0.9591 | 0.6742 | 0.9046 |
| MAE | 0.1308 | 0.1412 | 0.2356 | 0.1339 | 3.7981 | 0.8962 | |
| MSE | 0.0006 | 0.0006 | 0.0083 | 0.0006 | 2.1585 | 0.0844 | |
| G-7 | R2 | 0.9314 | 0.9410 | 0.8465 | 0.9486 | 0.6758 | 0.8740 |
| MAE | 0.2402 | 0.2185 | 0.2397 | 0.1225 | 3.6596 | 0.9698 | |
| MSE | 0.0086 | 0.0081 | 0.0084 | 0.0006 | 2.0983 | 0.4088 | |
| G-8 | R2 | 0.9979 | 0.9986 | 0.9987 | 0.9936 | 0.8813 | 0.8958 |
| MAE | 0.0985 | 0.0998 | 0.0956 | 0.1003 | 1.1875 | 1.1981 | |
| MSE | 0.0004 | 0.0004 | 0.0004 | 0.0004 | 0.6352 | 0.6392 | |
| G-9 | R2 | 0.9930 | 0.9925 | 0.9913 | 0.9962 | 0.8898 | 0.8917 |
| MAE | 0.1005 | 0.0972 | 0.1082 | 0.0975 | 1.1275 | 1.1382 | |
| MSE | 0.0004 | 0.0004 | 0.0004 | 0.0004 | 0.6163 | 0.6197 | |
| Average value | R2 | 0.9795 | 0.9792 | 0.9483 | 0.9775 | 0.7288 | 0.8948 |
| MAE | 0.1832 | 0.1364 | 0.1701 | 0.1335 | 2.7864 | 0.8348 | |
| MSE | 0.0078 | 0.0022 | 0.0049 | 0.0024 | 1.6511 | 0.2972 |
| Fitting the Model | ||||||
|---|---|---|---|---|---|---|
| Parameters | a | b | a | b | a | b |
| 0.2359 | 0.006 | 21.639 | −1.1078 | 14.353 | 0.0338 | |
| Goodness-of-fit R2 | 0.8019 | 0.8479 | 0.9056 | |||
| Relative Location | Data | 3d | 4d | 5d |
|---|---|---|---|---|
| (Strain gauge A) | Measured value (με) | −28.4 | −33.6 | −46.4 |
| Simulated values (με) | −30.6 | −35.8 | −42.4 | |
| Difference values (%) | 7.6 | 6.5 | 9.4 | |
| (Strain gauge B) | Measured value (με) | 8.5 | 9.7 | 27.6 |
| Simulated values (με) | 9.3 | 10.6 | 29.3 | |
| Difference values (%) | 9.4 | 9.2 | 6.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pu, G.; Xiong, H.; Li, N.; Liu, B. Investigation of Uniaxial Compression Stress–Strain Relationship of Early Age Manufactured Sand Concrete and Its Application. Buildings 2023, 13, 2187. https://doi.org/10.3390/buildings13092187
Pu G, Xiong H, Li N, Liu B. Investigation of Uniaxial Compression Stress–Strain Relationship of Early Age Manufactured Sand Concrete and Its Application. Buildings. 2023; 13(9):2187. https://doi.org/10.3390/buildings13092187
Chicago/Turabian StylePu, Guangning, Huaiyu Xiong, Ning Li, and Bin Liu. 2023. "Investigation of Uniaxial Compression Stress–Strain Relationship of Early Age Manufactured Sand Concrete and Its Application" Buildings 13, no. 9: 2187. https://doi.org/10.3390/buildings13092187
APA StylePu, G., Xiong, H., Li, N., & Liu, B. (2023). Investigation of Uniaxial Compression Stress–Strain Relationship of Early Age Manufactured Sand Concrete and Its Application. Buildings, 13(9), 2187. https://doi.org/10.3390/buildings13092187







