Blast-Resistance and Damage Behavior of Underwater Explosion for Concrete Gravity Dam Considering Concrete Strength Partition

Abstract

The consequences of dam damage caused by explosions, wars, and terrorist attacks are extremely serious, and they can cause casualties among downstream residents. Studying the damage behaviors of dams is a prerequisite for improving their anti-knock performance. Researchers view the dam as homogeneous for research; but in reality, the concrete strength of the dam decreases from bottom to top. The partitioning of dam concrete strength can meet the different functional and economic requirements of a concrete gravity dam (referred to as concrete strength partition gravity dam (CSPGD)). Therefore, CSPGD shows a more complex dynamic performance and failure characteristics under the impact load of an underwater explosion. First, by investigating the current status of anti-knock research on CSPGDs, a fully coupled finite element numerical model for an underwater explosion of CSPGD was established. Considering the initial stress such as the self-weight of the dam, the upstream reservoir hydrostatic pressure, and the uplift pressure of the dam foundation during the service period, the anti-knock performance of CSPGD was studied. The results showed that the interface of CSPGD had a strain rate effect under the action of blast load, and it was easy to produce tensile failure at a low strain rate. In addition, the dynamic response and damage characteristics under different explosion scenarios such as explosive charge weight (w), detonation depth (D), and standoff distance (R) were further studied. The dam crest was always a weak anti-knock part, and the foundation anti-sliding stability was also very important to dam safety. Therefore, it was proposed and suggested to use the crack length of the dam crest and dam foundation to evaluate the overall anti-knock capacity of CSPGD. The study also found that the detonation depth affected the response time of dam damage and had a significant impact on the anti-knock performance of CSPGD.

1. Introduction

In recent years, there have been many explosion accidents caused by military and terrorist activities around the world, which seriously threaten the safety of government buildings [1], ships [2], bridges [3], high dams [4,5], and other important infrastructure. More and more attention has been paid to the dynamic response and protective performance of these structures under blast loads [6,7,8]. As an important civil building, water conservancy dams have become the focus of military strikes [9] due to their significant political and economic benefits. The release of flood water will cause a series of chain reactions downstream once the dam breaks, causing serious disasters [4,10]. Therefore, it is very important to grasp the failure mechanism of dams under blast loads.

Many scholars have carried out research on the dynamic response and damage mode of dams under blast shock loads. The United States once carried out a nuclear effect test on a dam in Colorado and obtained a lot of precious data [11]. Vanadit-Ellis [12] reported a model test on the damage effects of an underwater explosion on a concrete gravity dam using a centrifuge and obtained the failure mode of dam damage under the impact load of an underwater explosion. Real and accurate data could be obtained through the on-site explosion test. Huang et al. [13,14,15,16] studied the failure modes and effects of the bubble pulse of a homogeneous concrete gravity dam subject to near-field underwater explosion and scaled the failure of a concrete gravity dam subject to underwater explosion through centralized testing and numerical simulation. They explored the damage modes of homogeneous concrete dams and proposed a method for establishing a scaled model. At present, the field test conditions are very limited due to the disadvantages of high cost, difficult data collection, and possible personal injury. With the rapid development of computer hardware and software, numerical simulation has gradually become mainstream to study the response and damage of dams under the action of blast load, and it has been proven to be reliable [17,18]. Since the destructive effect of an explosion shock wave propagating in water is much stronger than that in the air [4], the underwater explosion has the greatest damage potential to concrete gravity dams, and the current research also mainly focuses on the overall response and damage mode of the dam. Yu [19] established a fully coupled underwater explosion model using the ALE algorithm, analyzed the dynamic response of the dam under the action of underwater contact explosion, and summarized the distribution of dam damage. Linsbauer [20] established a reservoir water-dam model to study the dynamic response and stability of a concrete gravity dam (with cracks on the upstream surface) under the impact load of an explosion at the bottom of the reservoir. Wang [4,21] established an underwater explosion dam model by the coupled Eulerian–Lagrangian method, studied the dynamic response and damage model, and proposed a dam damage prediction model.

So far, many studies have revealed the dynamic response of concrete gravity dams under blast shock loads from different perspectives, but these studies treat gravity dams as homogeneous concrete dams [22,23,24,25]. However, in order to meet the functional and economic requirements of different parts of the dam during the actual construction process, concrete dam materials with different strengths were often used for different parts based on the functional requirements. The mechanical properties of dam-building materials are different under the action of external loads [26], which may also lead to differences in the overall impact resistance of the dam, and the damage mode under explosion impact loads may be more complicated. In addition, some studies believe that the dam crest is the weakest part of the entire dam structure [4], and it is unreasonable to only use the local damage degree of the dam crest to define the anti-knock capability of the whole concrete gravity dam. The dam failure caused by foundation anti-sliding instability was more serious than the dam crest damage. Therefore, more attention should be given to the foundation damage status, and a more reasonable damage assessment strategy should be established considering the dam foundation stability.

In addition, dam pressure mainly arises from self-weight, upstream hydrostatic pressure, and uplift pressure of the foundation during dam operation. These three factors were important for the design of dam slip stability. In previous studies, the initial stress field was usually ignored.

The main purpose was to study the effect of underwater explosion on the damage characteristics and structural dynamic response of a CSPGD considering the initial stress field. In order to achieve the research objective, we used LS-DYNA Version 971 software to establish a fully coupled numerical model of underwater explosion, and the initial stress field caused by self-weight, upstream hydrostatic pressure, and dam foundation uplift pressure was considered. The vulnerability of CSPGDs under different explosion scenarios such as explosive charge weight, detonation depth, and standoff distance was studied, and the damage prediction equation was obtained by fitting. It was suggested to evaluate the blast resistance of the entire CSPGD using the crack penetration ratio of the dam foundation and dam crest.

2. Material Model

2.1. Concrete Material Model

Concrete is a material with high strain and high strain rate under explosive irradiation. Continue surface cap model (CSCM) is mainly used to simulate rock, concrete, and clay media, and the model can describe the response problem of concrete materials under high strain rate conditions. It is a constitutive model based on the superposition principle of pore and crack effects in solid mechanics. The CSCM requires only uniaxial compressive strength to automatically generate relevant parameters. The model combines shear (failure) surface with hardened compaction surface (cap) in the form of a product. The yield function is defined by three stress invariants proposed by Schwer and Murray [27] and Sandler [28]:

$$Y\left(I_1,J_2,J_3\right)=J_2-R{\left(J_3\right)}^2{F}_f^2\left(I_1\right)F_c\left(I_1,k\right)$$

(1)

where $F_f^{}\left(I_1\right)$ is the shear failure surface, $F_c\left(I_1,k\right)$ is the hardened cap, $k$ is the cap hardening parameter and $R\left(J_3\right)$ is the Rubin’s three invariant reduction coefficient [29]. The multiplicative form allows the cap and shear surfaces to combine continuously and smoothly at their intersections.

The shear failure surface $F_f\left(I_1\right)$ is defined as:

$$F_f\left(I_1\right)=\alpha -\lambda {\exp }^{-\beta I_1}+\theta I_1$$

(2)

material constants α, β, λ and θ are determined from triaxial compression test data.

The hardened surface of the cap is expressed as:

$$F_c\left(I_1,k\right)=\{\begin{array}{l}1-\frac{{\left(I_1-L\left(k\right)\right)}^2}{{\left(X\left(k\right)-L\left(k\right)\right)}^2}\begin{array}{cc}& I_1\ge L\left(k\right)\end{array}\\ 1\begin{array}{ccc}& & \begin{array}{ccc}& & \begin{array}{ccc}& \begin{array}{cc}& I_1\le L\left(k\right)\end{array}& \end{array}\end{array}\end{array}\end{array}$$

(3)

$$L\left(k\right)=\{\begin{array}{l}k\begin{array}{cc}& k\ge k_0\end{array}\\ k_0\begin{array}{cc}& k\le k_0\end{array}\end{array}$$

(4)

$$X\left(k\right)=L\left(k\right)+R{F}_f\left(I_1\right)$$

(5)

When $I_1\ge L\left(k\right)$, the ellipse (or cap) is shown in Equation (3). When $I_1=L\left(k\right)$, the shear failure surface intersects the cap at this point. $k_0$ is the value of $I_1$ at the initial intersection of the shear plane and the cap before the cap expands or contracts. When the plastic volume compresses, the cap expands (i.e., $X\left(k\right)$ and $k$ increase), and when the plastic volume expands, the cap contracts (i.e., $X\left(k\right)$ and $k$ decrease). The motion of the cap is governed by the hardening Equation (6):

$${\epsilon }_v^p=W\left[1-{\exp }^{\left(-D_1\left(X-X_0\right)-D_2{\left(X-X_0\right)}^2\right)}\right]$$

(6)

where ${\epsilon }_v^p$ is the plastic volume strain, W is the maximum plastic volume strain and $X_0$ is the initial position of the cap at $k=k_0$. Parameters $X_0$, $R$, $W$, $D_1$ and $D_2$ are determined from hydrostatic compression and uniaxial strain tests.

In addition, the CSCM considers the ductile and brittle damage accumulation of concrete materials [30]. The ductile damage accumulation is determined by plastic strain component, and the brittle damage accumulation is determined by the maximum principal strain.

The formula for calculating the damage plastic stress is:

$${\sigma }_{\mathrm{d}}=(1-d)\sigma$$

(7)

where ${\sigma }_{\mathrm{d}}$ is the non-damage plastic stress, $d$ is the damage factor.

Brittle and ductile damage are shown in Equations (8) and (9):

$$d({\tau }_t)=\frac{0.999}{D}\left[\frac{1+D}{1+D{e}^{-C({\tau }_t-{\tau }_{0t})}}\right]$$

(8)

$$d({\tau }_c)=\frac{d_{\max }}{B}\left[\frac{1+B}{1+B{e}^{-A({\tau }_c-{\tau }_{0c})}}\right]$$

(9)

where ${\tau }_t$ is the energy term of brittle damage, ${\tau }_{0t}$ is the brittle damage threshold, ${\tau }_c$ is the energy term of ductile damage, ${\tau }_{0c}$ is the ductile damage threshold, $d_{\max }$ is the maximum damage value that the material can achieve, parameters $A,B,C$ and $D$ determine the shape of the stress–strain curve.

2.2. Rock Foundation HJC Model

The rock foundation was hard granite, its mechanical properties were similar to concrete and under the action of near-field explosion, it had obvious strain-rate-related characteristics. The HJC model [31,32] comprehensively considers the effects of strain rate, damage degree, and damage softening on the constitutive relationship of materials. It can better describe the problems of large deformation, high strain rate, and damage of materials, including yield equation, damage evolution equation, and equation of state [32]. The parameters of the HJC model are shown in

Table 1. The parameters of rock foundation in HJC model [31,32].

Fundamental Parameters	Value	Strength Surface	Value	Damage Parameters	Value	EOS Parameters	Value
Density ${\rho }_0$ (kg/m3)	2800	$A$	0.79	$D_1$	0.04	Crushing pressure $p_c$ (MPa)	16
Shear modulus $G$ (Gpa)	16.7	$B$	1.60	$D_2$	1.0	Crushing volumetric strain ${\mu }_c$	0.001
Compressive strength $f_c^{’}$ (Mpa)	150	$N$	0.61	$e_{f\min }$	0.01	Locking pressure $p_1$ (Mpa)	800
$f_s$	0.004	$C$	0.007	$T$ (Mpa)	7.00	Locking volumetric strain ${\mu }_1$	0.10
		${\dot{\epsilon }}_0$	0.01			$K_1$ (Mpa)	85
		${\sigma }_{\max }^{*}$	7.00			$K_2$ (Mpa)	−171
						$K_3$ (Mpa)	208

.

2.3. JWL Equation of State

In the prediction and calculation of detonation performance, the equation of state of explosive detonation products is a function of pressure, specific volume, and temperature. The high-energy explosive uses a high explosive burn model, and the explosion pressure is described by JWL’s [33] equation of state:

$$P=A\left(1-\frac{\omega }{R_{1}V}\right)e^{-R_{1}V}+B\left(1-\frac{\omega }{R_{2}V}\right)e^{-R_{2}V}+\frac{\omega E}{V}$$

(10)

where P is the detonation pressure, E is the internal energy per unit volume of detonation, V is the relative volume, $A$, $B$, $R_1$, $R_2$, and $\omega$ are constants. The parameter values of the high-energy explosive material model are: $\rho$ = 1630 kg/m³, D = 6950 m/s, $P_{c-J}$ = 21 GPa, A = 373 GPa, B = 3.74 GPa, $R_1$ = 4.15, $R_2$ = 0.9, $\omega$ = 0.35, $E_0$ = 7 GJ/m³, $V_0$ = 1.00.

2.4. Equation of State for Water

When explosives explode in water, their pressure is much greater than the static pressure of the surrounding water medium, resulting in shock waves and bubble pulsation. Water is described by Gruneisen equation of state [33], which defines the relationship between pressure and volume for compressed materials. Its expression is:

$$P=\frac{{\rho }_{0}C\mu \left[1+\left(1-\frac{{\gamma }_0}{2}\right)\mu -\frac{a}{2}{\mu }^2\right]}{{\left[1-\left(S_1-1\right)\mu -S_2\frac{{\mu }^2}{\mu +1}-S_3\frac{{\mu }^3}{{\left(\mu +1\right)}^2}\right]}^2}+\left({\gamma }_0+a\mu \right)E$$

(11)

where $C$, $S_1$, $S_2$, and $S_3$ are constants, ${\rho }_0$ is the initial density, ${\gamma }_0$ is the Gruneisen coefficient, $a$ is the first-order volume correction to ${\gamma }_0$, $E$ is the internal energy per unit volume, $\mu =\rho {\rho }_0^{-1}-1$. The parameters of the water body model are as follows: ${\rho }_0$ = 1025 kg/m³, $C$ = 1480 m/s, $a$ = 0, $S_1$ = 2.56, $S_2$ = 1.986, $S_3$ = 1.2268, ${\gamma }_0$ = 0.35, $E$ = 1.89 MJ/m³.

2.5. Equation of State for Air

When explosives explode in air, they instantly transform into high-temperature and high-pressure explosive products. Explosion products expand in air, resulting in the formation of sparse waves within explosion products. At the same time, the explosive products strongly compress air, forming shock waves in air. The air is described by the Mat_Null material model and the linear polynomial equation of state [33], which is expressed as:

$$P=C_0+C_1\mu +C_2{\mu }^2+C_3{\mu }^3+\left(C_4+C_5\mu +C_6{\mu }^2\right)E$$

(12)

where $C_0~C_6$ are constant constants, $E$ is the internal energy per unit volume, $\mu =\rho {\rho }_0^{-1}-1$, $\rho$, and ${\rho }_0$ are the current and initial air densities, respectively. The parameters of the air model are as follows: ${\rho }_0$ = 1.293 kg/m³, $C_0=C_1=C_2=C_3=C_6=0$, $C_4=C_5=0.401$, $V_0$ = 1.0, $E$ = 0.25 MJ/m³.

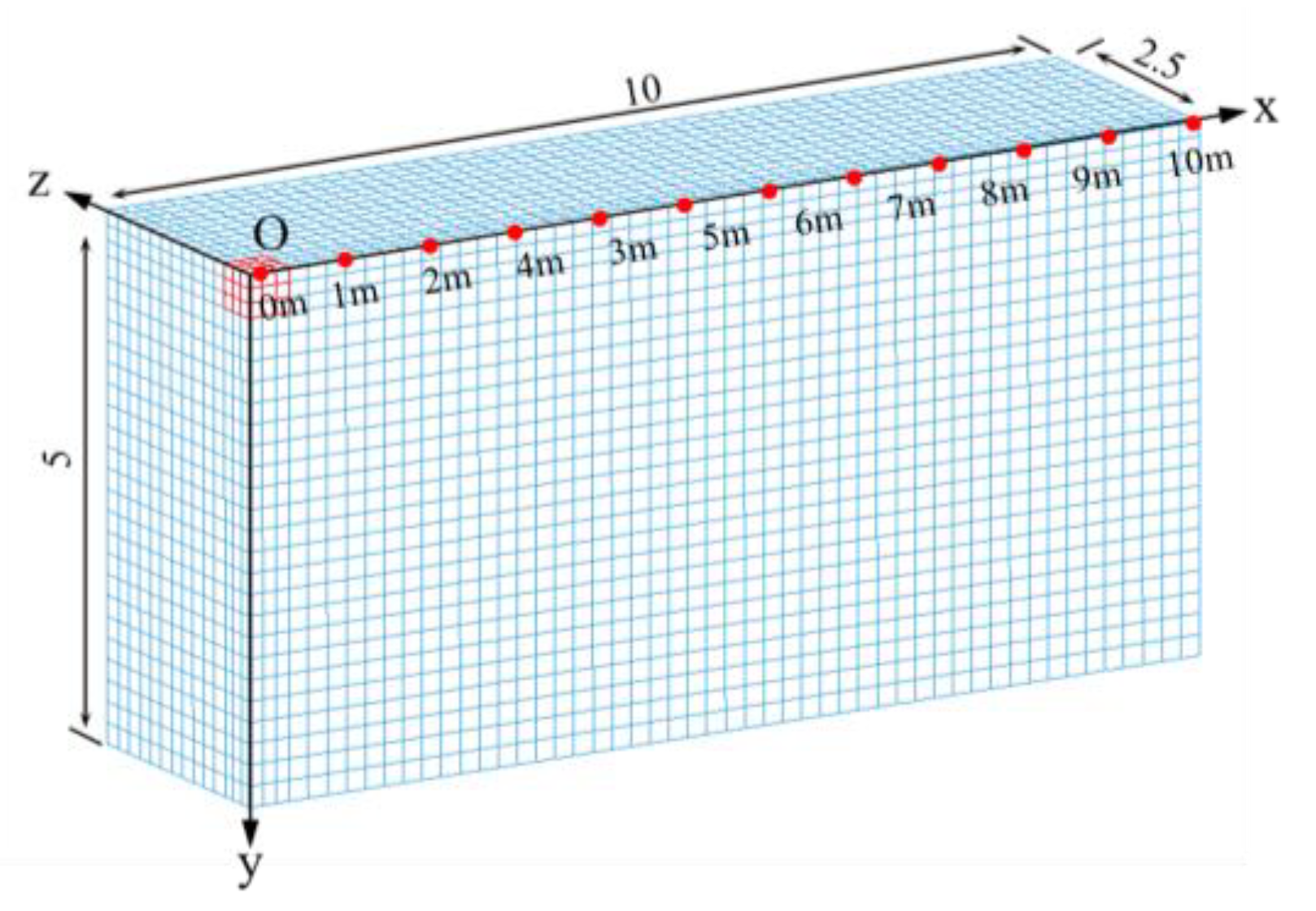
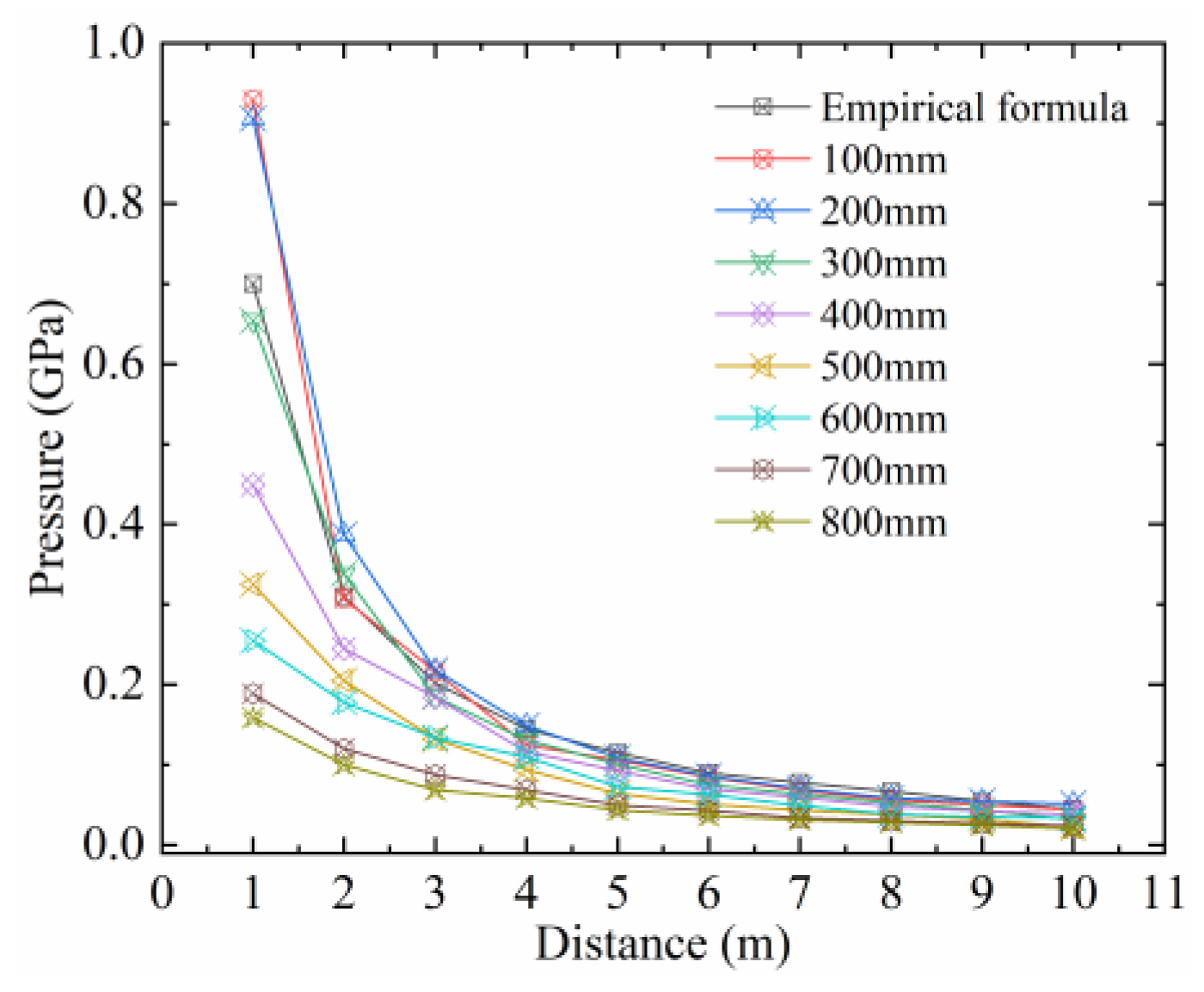
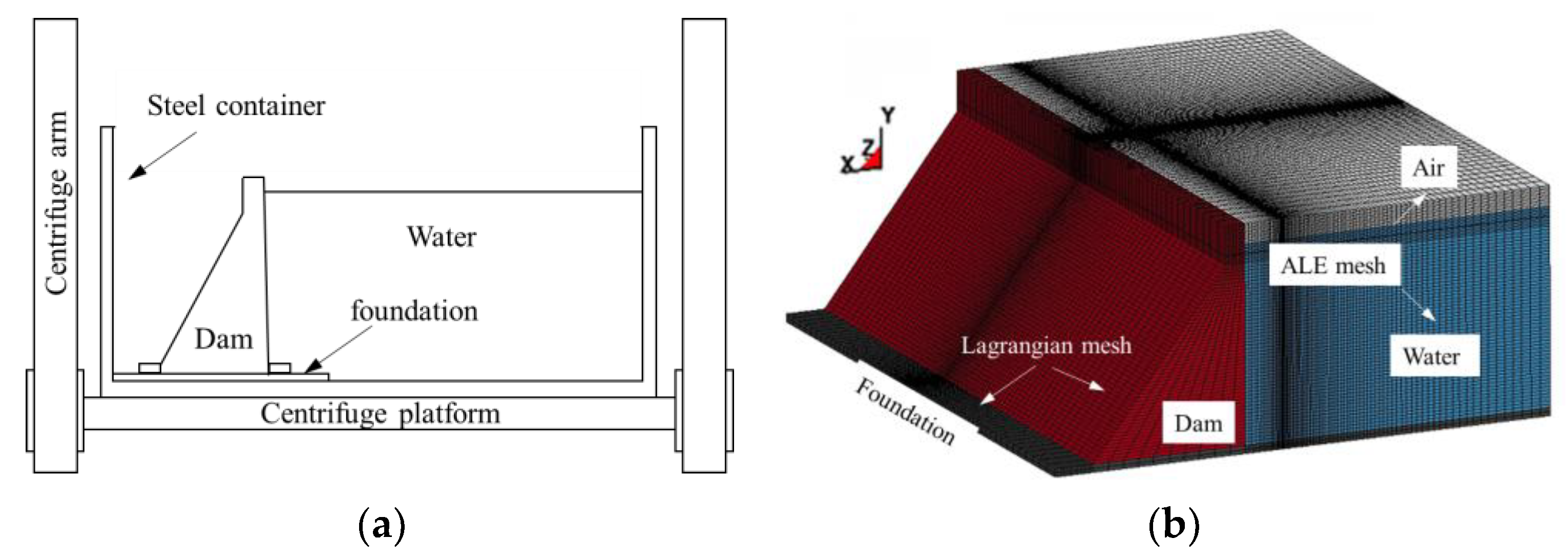
3. Validation of the Fully Coupled Aerial Explosion Model

3.1. Numerical Model Validation

The element mesh size could affect building damage area after explosion and overpressure peak value near blast center. To analyze the size effect of 3D model element mesh under impact load, the element mesh size was taken as 100~800 mm and the increment was 100 mm. The calculated results were compared with the empirical formula of Cole [34] to verify the reliability of numerical model.

A numerical model of underwater explosion (shown in Figure 1) was established, and the 1/8 model was selected to study the law of free propagation of shock waves in water by symmetry. The model range was 10 m × 5 m × 2.5 m, and the TNT weight was 1000 kg. The symmetry plane was set as symmetry boundary and the other cut surfaces were set as transmission boundary. The cubic explosive charge was located at point O at the coordinate x = y = z = 0 m. Figure 2 shows the target points of pressure–distance curve. As can be seen from Figure 2, the agreement between numerical and experimental results was consistent. When a large-sized element mesh was used to simulate near-burst distance, the difference between calculated results and empirical values was obvious. The calculation results of small-sized elements mesh were closer to empirical values in both the near and far explosive center distances.

3.2. Validation of the Fully Coupled Aerial Explosion Model

The dynamic response of structures and their failures under blast shock loads was a complex physical process. The coupled Lagrangian–Eulerian method [35,36,37,38] fully combined the advantages of Lagrangian method and Eulerian method in the finite element analysis technology, which could effectively describe the dynamic interaction of fluid–structure interaction and large deformation problems. To verified that the fully coupled model could accurately simulate the response and damage of concrete structures under blast loads. According to [12], a full coupled numerical model validation of gravity dam was conducted using scaled physical model tests by Vanadit Ellis and Davis [12]. As shown in Figure 3a, the scaled model of the concrete gravity dam in the experiment consisted of eight dam monoliths with a size of 152 cm × 40 cm (length × Width). There was a transition joint between the dam monoliths. There was literature indicating that friction connections need to be set between dam monoliths [39] and the friction coefficient in the dam monoliths was taken as 0.7. The TNT weight and detonation depth were set to 8 g and 0.025 m underwater, respectively, with standoff distances of 0.10 m, 0.15 m, and 0.20 m. We established a dam-foundation-water-air-TNT fully coupled model, as shown in Figure 3b, gradually densifying the mesh of explosives, reservoir water, and the dam elements in the model to ensure calculation accuracy. The whole model consisted of 722,936 solid elements. Eulerian mesh for air, water, and TNT. Lagrangian mesh for dam and foundation. Setting transmission boundary conditions at the model truncation point to avoid shock wave reflection.

When the unit damage factor of calculation result was greater than 0.75, it was generally considered that macroscopic damage generated in this area. When the unit damage factor was greater than 0.99, it was considered that the part had penetrating failure. A large number of crack damage areas appeared on the concrete [40]. Figure 4 shows the failure modes of the dams obtain from numerical simulation and physical model tests. The numerical simulation results were highly similar to the physical model test results as shown in Figure 4a–c, verifying the effectiveness of the numerical simulation method.

In addition, from the results of physical model tests and numerical simulation tests, it can be found that the transverse joints of the dam can limit the propagation of explosion shock waves between adjacent dam monoliths, manifested as discontinuous failure. The dam monolith failure mainly occurred in a single dam monolith closest to the explosion source. To simplify the calculation, a single dam monolith was used for research in the following text.

4. Analysis of Anti-Knock Performance of CSPGD

4.1. Description of Analysis Model

Concrete gravity dams relied on their own gravity to maintain stability and were mainly destroyed by a single dam monolith [12,41] under explosion loads. Taking a concrete gravity dam monolith as a research object, shown in Figure 5, the dam height was 114 m, the top width was 20 m, the bottom width was 112.5 m, the toe of slope was ψ = 55°, the thickness of a single dam monolith was 15 m, and the upstream water depth was 100 m. According to the functional requirements, there were three kinds of building materials with different strengths from the dam foundation to the dam crest: RI, RII, and RIII. The standard values of compressive strength were 40 MPa, 35 Mpa, and 30 MPa. The dam was built on solid granite and the joint surface was stable. The dam foundation uplift pressure reduction coefficient was taken as 0.25, and the influence of corridor system on the structure was not considered. The distance from detonation position to upstream dam surface was 10 m, 15 m, 20 m, 25 m, 30 m, and 35 m. The distance from detonation position to reservoir bottom was D = 10 m, 30 m, 60 m, and 80 m. The TNT weight was 250 kg, 500 kg, 750 kg, 1000 kg, 2000 kg, and 3000 kg. The characteristics of shock dynamic response of CSPGD structures was analyzed. The schematic diagram of dam cross-section, detonation position, and target points (P₁, P₂, P₃) are shown in Figure 5.

To establish a fully coupled finite element model of a gravity dam monolith, as shown in Figure 6, take one side of the dam’s symmetry plane as the research object to reduce the amount of calculation and calculation time. The model included five material models including symmetrical dam monolith, rock foundation, TNT, reservoir water, and air. The model was extended by two times the dam height along horizontal sides and downward and the thickness along the dam axis was taken as 7.5 m. The TNT mesh size was 100 mm [42] and the meshes away from the TNT gradually increased. The unit size in the middle and upper part of the dam was 300 mm [9], which gradually increased along the direction of the dam bottom. All meshes were connected by common nodes. A full constraint was set at the truncation at the bottom of rock foundation, a symmetric boundary was set on symmetry plane, and the truncation surface was set as a non-reflection boundary condition to simulate a semi-infinite region.

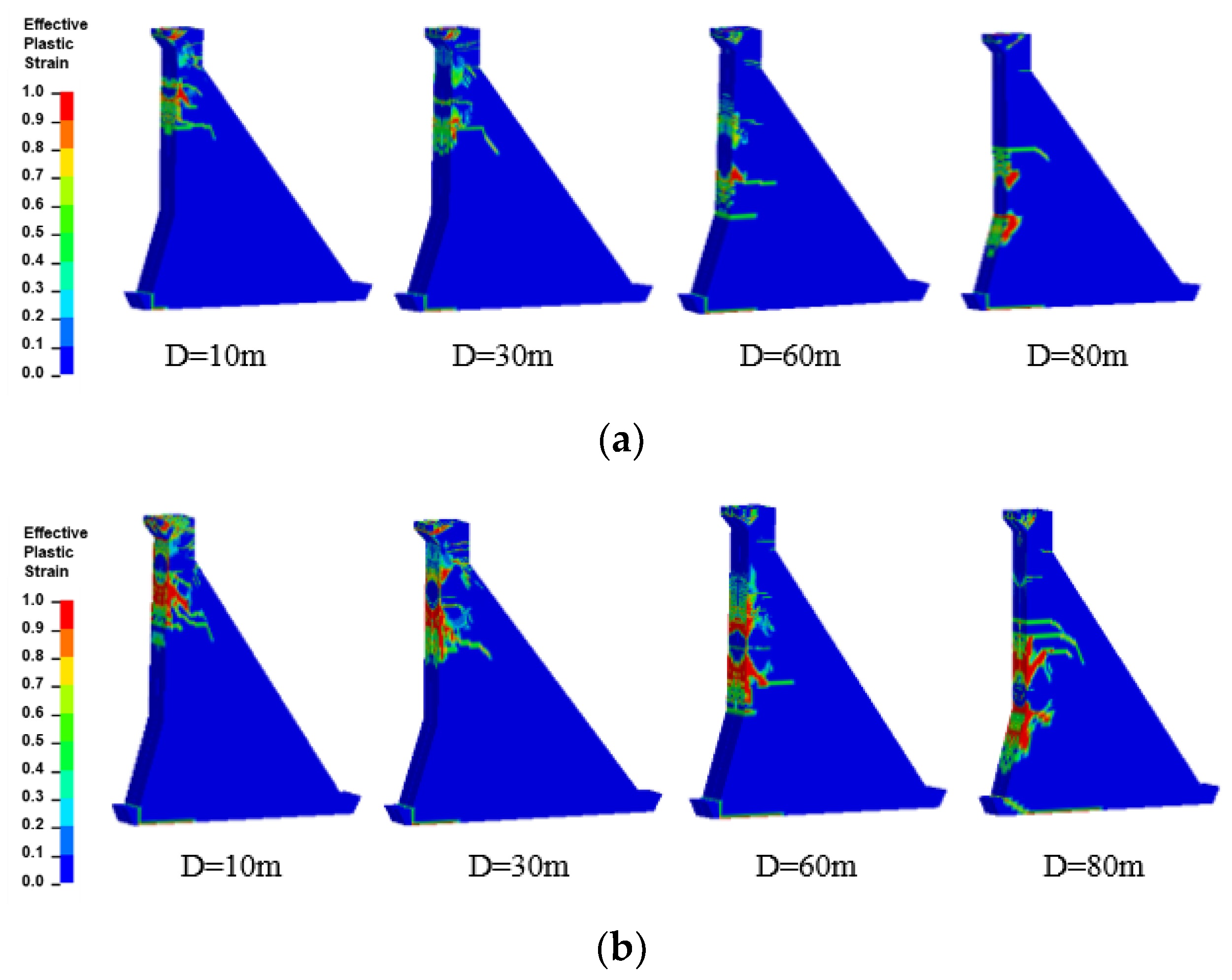
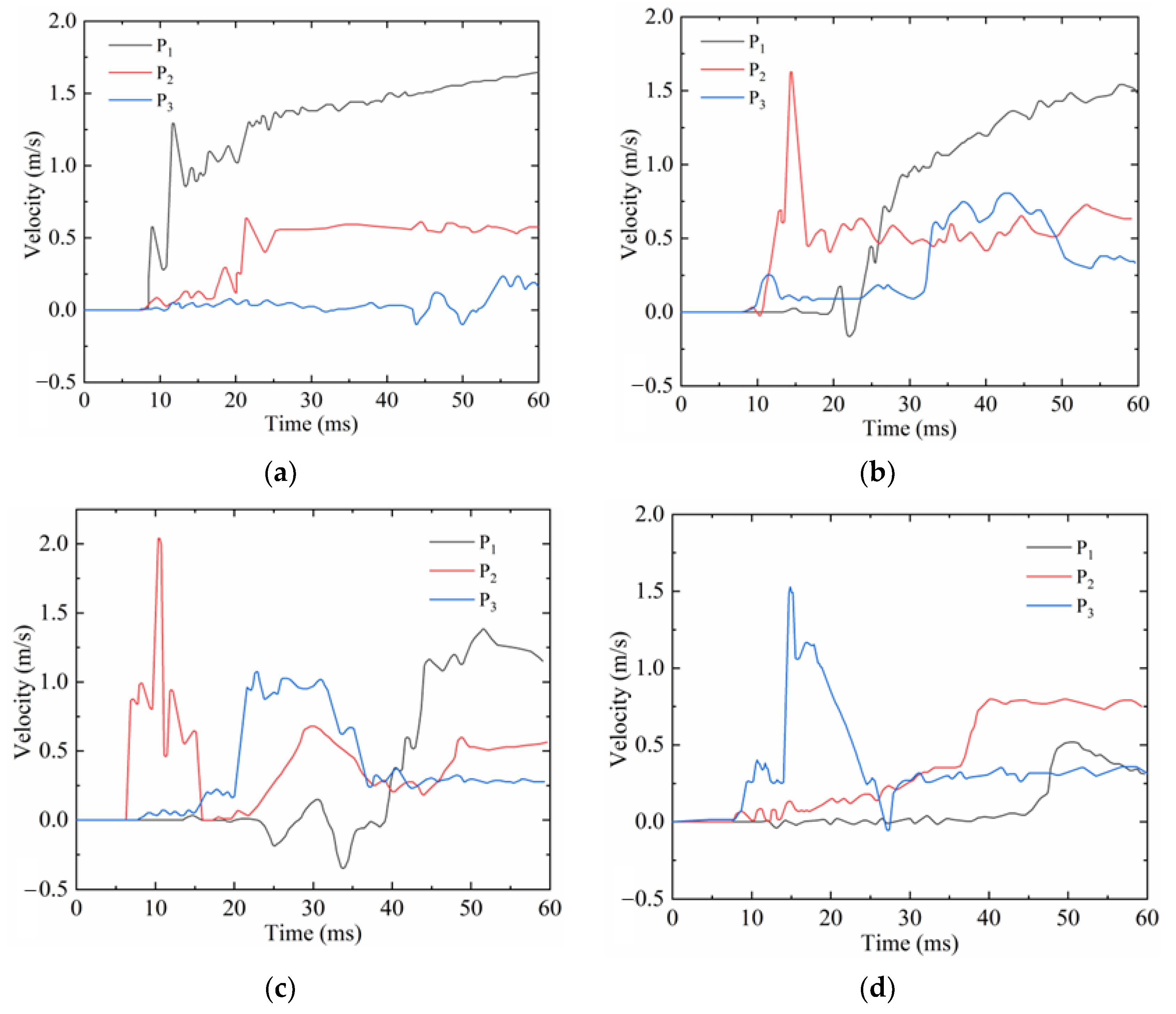
4.2. Effect of Detonation Depth on Destruction Mode

Figure 7 shows the destruction modes of CSPGDs with different initiation depths for w = 250 kg and w = 750 kg (R = 10 m). It can be seen from Figure 7a that when the w = 250 kg, the dam near free water surface was damaged due to the cut-off effect of free water surface. The crest cracks expanded from the upstream surface to dam interior and the blast shock wave caused tension cracks at the interface between RIII and RII, which spread from the upstream surface along the dam interior to the dam toe direction. With the increase in detonation depth, the cracks at the interface of RII and RIII gradually became longer, the length of the tensile cracks downstream of the dam crest gradually became shorter, and the cracks in dam foundation gradually became longer. It is worth noting that the underwater explosion was cratered on the dam’s upstream surface at the center of explosive. In the explosion near the interface of RII and RIII, no cracks were generated between RII and RIII due to the effect of the high strain rate [43]. It can be seen from that when the shock wave propagated from upstream surface to downstream surface, the tensile strength of concrete was much smaller than compressive strength, resulting in certain tensile damage and damage to downstream surface. Tensile damage failure also generated in the dam heel region due to the overall response, while no tensile crack failure generated at the interface between RI and RII.

It can be seen from Figure 7b that when the w = 750 kg, the failure mode was roughly the same as when the w = 250 kg. The underwater explosion shock wave caused serious local damage to the dam upper part and the interface between RII and RIII. Bending failure and punching damages were the cause of in the upstream facing downstream of the dams. The damages extended obliquely to the dam interior and did not penetrate the dam monolith.

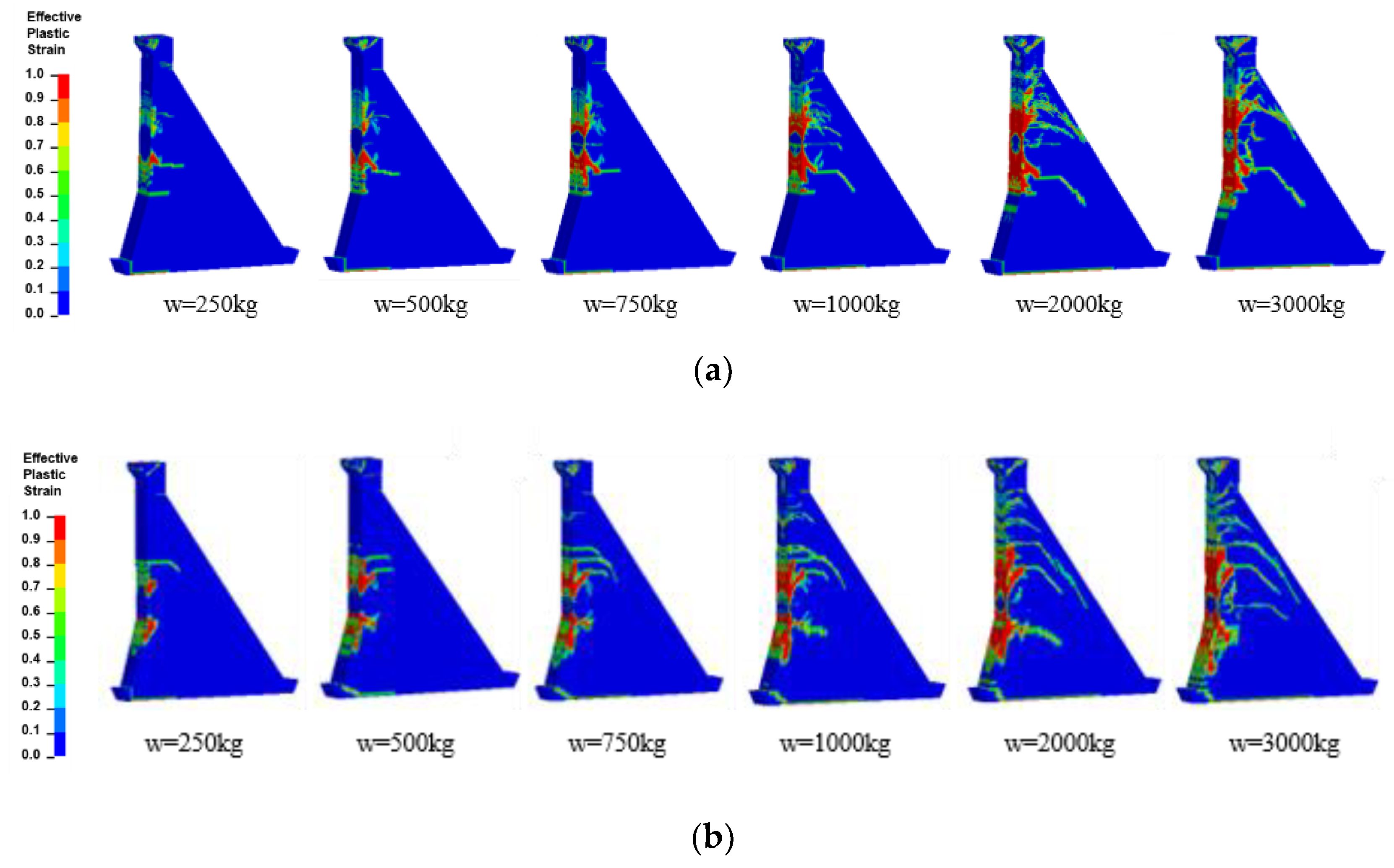
4.3. Effect of TNT Weight on Destruction Mode

Figure 8 shows the dam destruction modes with different TNT weights at D = 60 m and D = 80 m (R = 10 m). It can be seen from Figure 8a that when the D = 60 m, the damage area on upstream surface became larger, and the tensile force generated by blast shock wave caused the cracks to gradually increase and become wider with the increase in TNT weight. The dam crest was always the weakest part for damage. The end of dam internal crack extended to the dam toe, and the dam foundation surface crack gradually became longer until it was completely penetrated. When the w > 750 kg, shear cracks generated at the interface between RIII and RII, which did not penetrate the dam due to overpressure. It can be seen from Figure 8b that the damage range of dam with D = 80 m was similar to that of the D = 60 m. The difference is that the length and number of cracks inside the dam increased sharply (D = 80 m). No cracks were generated at the interface of RI and RII materials. This shows that the dam foundation cracks spread along the interface between RI and rock foundation, and eventually, the penetrating cracks were formed, which led to the instability of the dam.

4.4. Effect of Standoff Distance on Destruction Mode

Figure 9 shows the destruction modes of CSPGD with different standoff distances with w = 500 kg (D = 10 m). It can be seen from Figure 9 that the upstream damage was significantly weakened as the initiation distance increased (R < 35 m), and the length of cracks in dam crest and dam foundation gradually decreased. It is worth noting that the interface of RII and RIII produced tensile cracks in the range of R ≤ 25 m, while the interface of RI and RII did not produce crack failure.

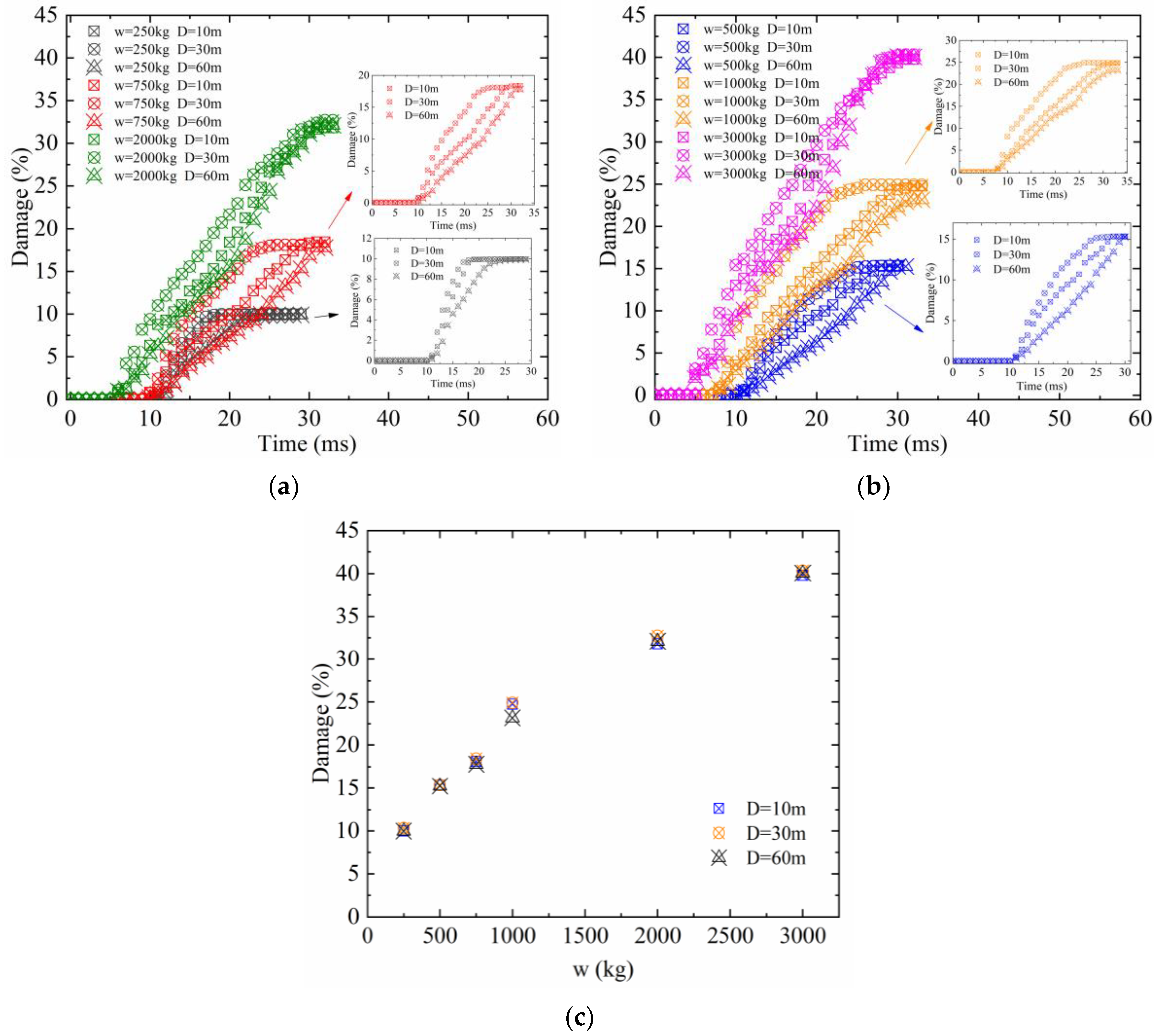
4.5. Effects of Detonation Depth and TNT Weight on Cumulative Damage

The dam’s damaged volume seemed to reflect its anti-knock performance, and we used the dam’s damaged volume to the intact dam monolith volume as dam-damage percentage. Figure 10 shows the damage time history curves of CSPGDs under different TNT weights and detonation depths (R = 10 m). It can be seen from Figure 10 that the dam damages were related to TNT weight. The detonation depth affected the response time of dam damage, as shown in Figure 10a,b. Compared with the dam response time at the detonation depths of D = 10 m and D = 60 m, the dam response duration after explosion shock at D = 30 m was the shortest when the TNT weight was lower (w < 1000 kg). This indicates that the D = 30 m was more sensitive to the dam dynamic mechanical response under blast shock from shown in Figure 10a,b. However, the detonation pressure generated by higher TNT weight (w > 1000 kg) far exceeded the ultimate bearing capacity of dam-building material and the dam damage was more serious. The response duration was not obvious due to large overpressure peak. At the same time, the dam-damage values under different detonation depths gradually approached and the dam-damage value was basically the same after detonation shown in Figure 10c. TNT weights of 250 kg, 500 kg, 750 kg, 1000 kg, 2000 kg, and 3000 kg corresponded to dam-damage approximation values of 10%, 15%, 18%, 25%, 33%, and 40%.

According to Section 4.2 and Figure 10, the detonation depth had a great influence on the dam dynamic response at w = 250 kg and R = 15 m. Figure 11 shows the time–history relationship of horizontal velocity of target points at different initiation depths. After detonation, the target points closest to the blast center reacted rapidly and strongly under the action of detonation products and shock waves, while the reaction farther away from the blast center was slower, as shown in Figure 11. When the detonation depth was small, the horizontal velocity of target point P₁ rose sharply and then rose slowly due to a small horizontal constraint and the larger overall response of the dam shown in Figure 11a. As the initiation depth increased, as shown in Figure 11b,c, the distance and horizontal velocity response time for shock wave to reach the target point P₁ became longer. The horizontal speed of P₂ and P₃ became larger and the response time became shorter. Due to the larger lateral stiffness in the middle and lower parts of the dam, the velocities of P₂ and P₃ dropped rapidly after rising sharply. In addition, due to inertia, the target point P₁ at the top and the target point P₃ at the bottom had obvious negative speeds. The initiation depth continued to increase, as shown in Figure 11d, and the horizontal velocity responses of P₁ and P₂ were relatively small. Because the dam dynamic response was mainly concentrated in a blast zone, resulting in a small overall bending behavior of the dam.

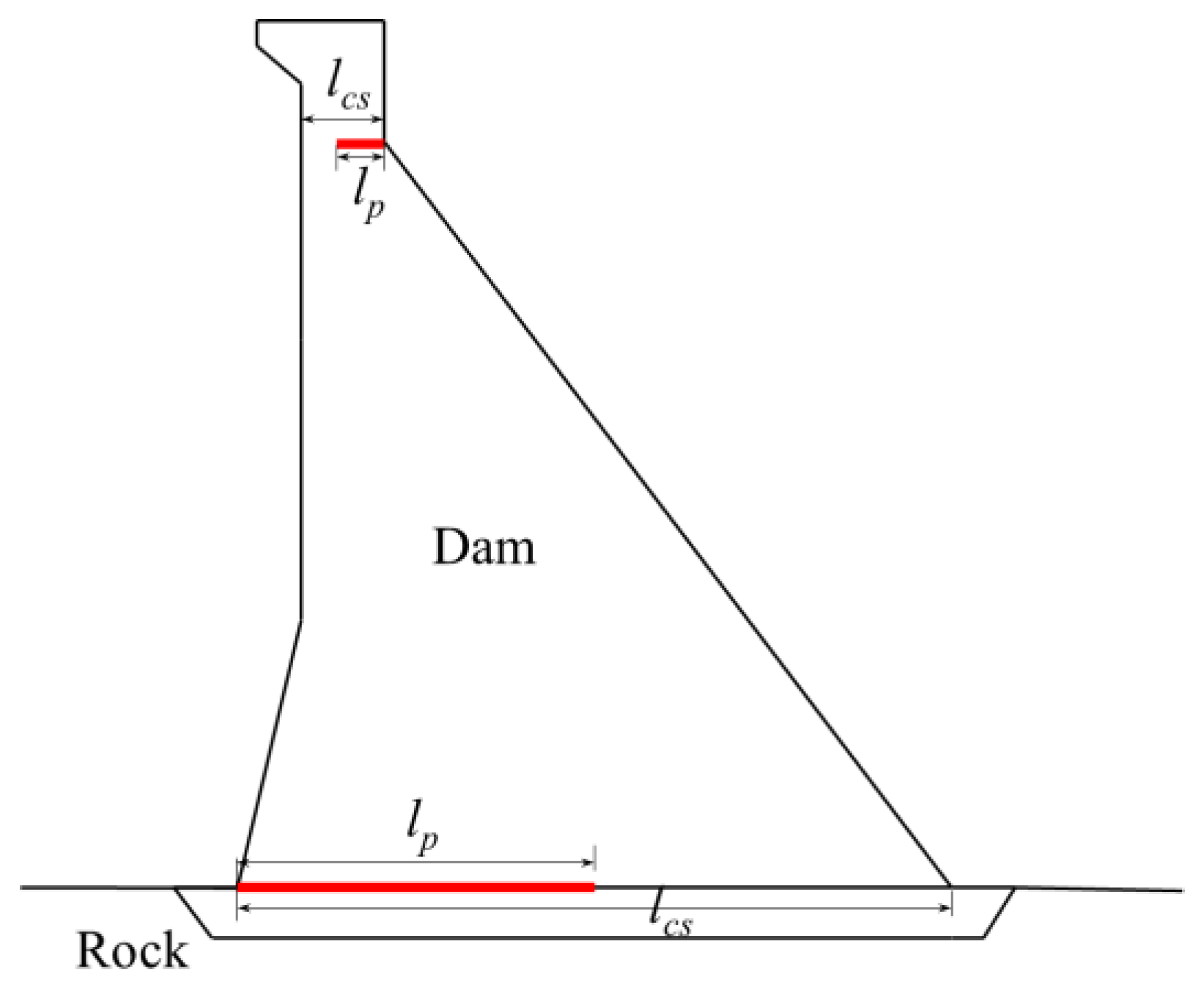
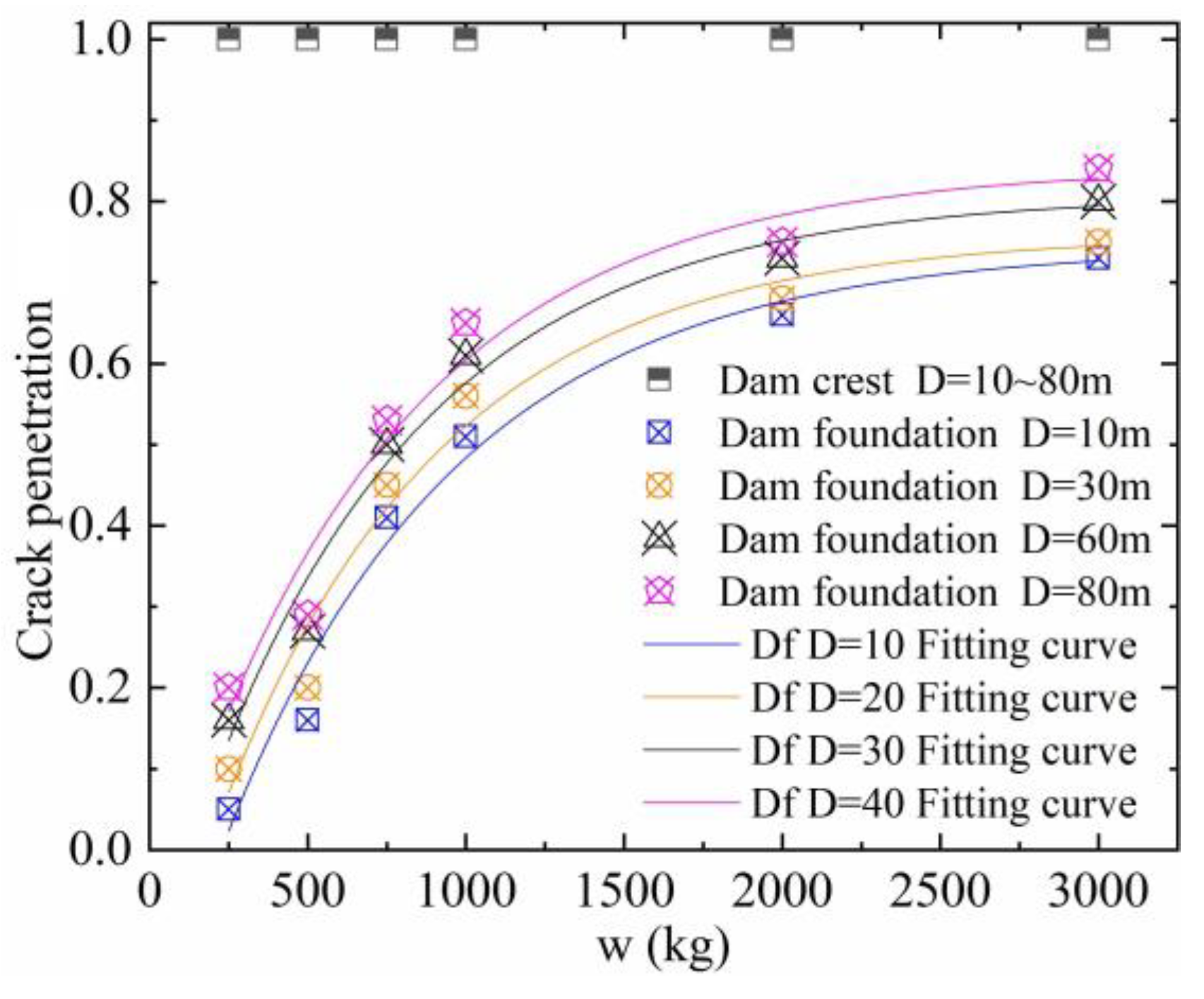
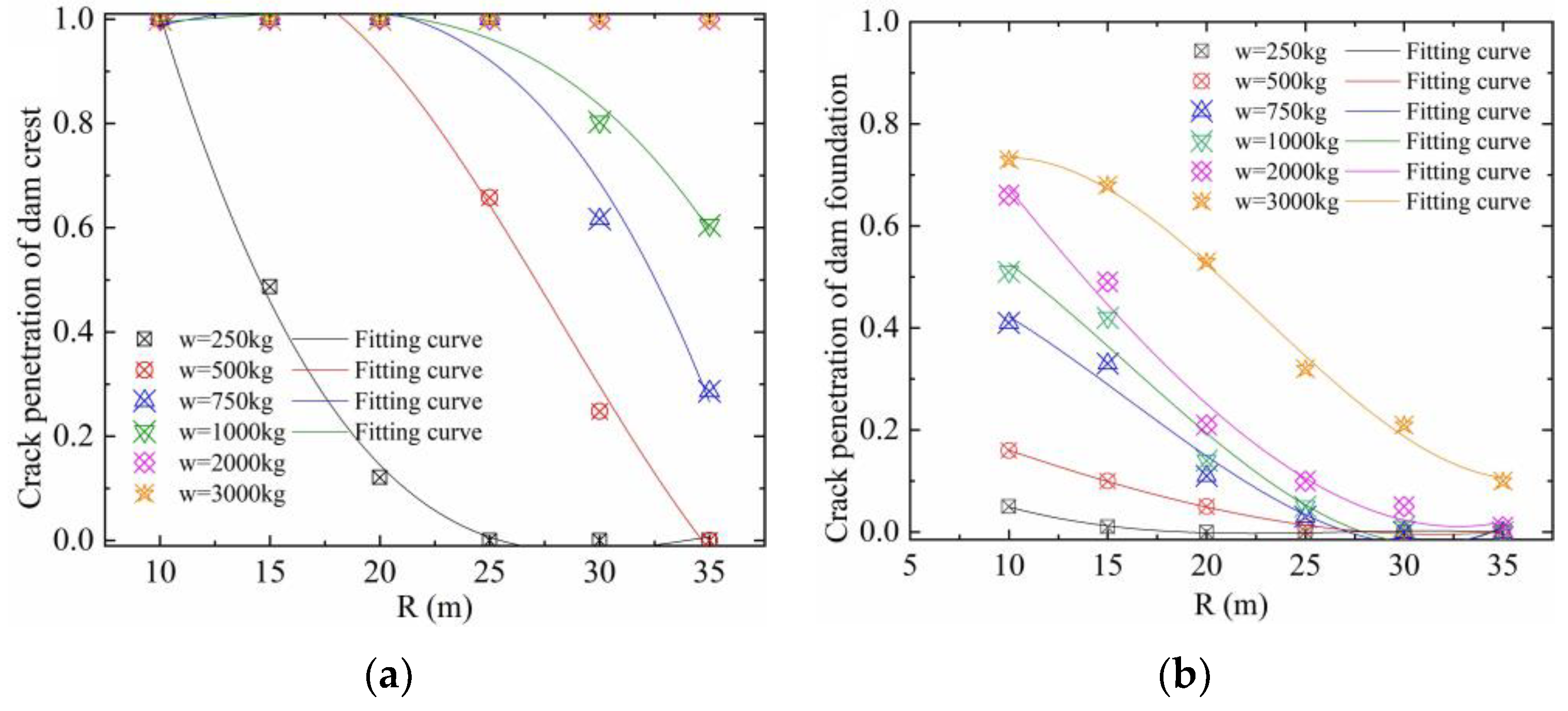
4.6. Relationship between the TNT Weight, Horizontal Initiation Distance, and the Crack Penetration Ratio

In order to describe the relationship between dam crack penetration length and damage degree shown in Figure 12, we defined the ratio of the crack penetration length ($l_p$) to the corresponding section length ($l_{cs}$) as the crack penetration ratio $P_r=l_p/l_{cs}$, the $P_r$ only varies within 0 to 1. It can be seen from Figure 13 that the dam crest failure at different initiation depths (R = 10 m) is always a penetrating crack with the increase in TNT weight. The penetration of the dam foundation cracks increased gradually with the increase in detonation depth and TNT weight. According to the data fitting of TNT weight and dam foundation crack penetration ratio at different detonation depths, the prediction Formula (13) was obtained, and its correlation coefficient is shown in

Table 2. The coefficient of TNT weight and dam foundation crack penetration ratio (R = 10 m).

D/m	m	n	R*2
10	0.2922	1.5702	0.9592
30	0.2796	1.4482	0.9477
60	0.2736	1.3521	0.9551
80	0.2731	1.3172	0.9470

R* is coefficient of variable.

. Figure 14 shows that the crack penetration ratio of the dam crest shown in Figure 14a and the dam foundation from shown in Figure 14b gradually decreased with the increase in initiation distance (D = 10 m). When the standoff distance was less than 20 m, any TNT weight exceeding 250 kg can cause the dam crest to be damaged to varying degrees, and the dam foundation cracks should also be concerned. The predicted relationship between the standoff distance and the dam crest and dam foundation crack penetration ratio under different TNT weights is shown in Equation (14) and the fitting correlation coefficients of the dam foundation and crest are shown in

Table 3. The coefficient of standoff distance and dam foundation crack penetration ratio (D = 10 m).

w/kg	t	s	k	l	R*2
250	−1 × 10−5	0.0011	−0.0279	0.2343	0.9929
500	4 × 10−6	3 × 10−5	−0.0151	0.3043	0.9986
750	4 × 10−5	−0.0021	0.0047	0.5395	0.9753
1000	5 × 10−5	−0.0024	0.0043	0.6762	0.9701
2000	2 × 10−5	−0.0002	−0.0494	1.1700	0.9865
3000	7 × 10−5	−0.005	0.0783	0.3776	0.9962

R* is coefficient of variable.

and

Table 4. The coefficient of standoff distance and dam crest crack penetration ratio (D = 10 m).

w/kg	t	s	k	l	R*2
250	−8 × 10−5	0.0084	−0.2815	3.0638	0.9977
500	0.0001	−0.0102	0.2177	−0.2982	0.9859
750	−7 × 10−5	0.0021	−0.0158	0.9983	0.9725
1000	−4 × 10−5	0.0017	−0.0187	1.0565	0.9796

R* is coefficient of variable.

.

The expressions of TNT weight and dam foundation crack penetration ratio under different blasting depths are as follows:

$$P_r=m\ln w-n$$

(13)

The prediction expressions of standoff distance and dam crest and foundation crack penetration ratio under different TNT weights are as follows:

$$P_r=t{R}^3–s{R}^2+kR+l$$

(14)

4.7. CSPGD Damage Statistics

From the results of Section 4.2 and 4.4, the overall damage area and damage range of the dam including upper dam crest and the lower part of dam body were obviously weakened with the increase in standoff distance. With the increase in detonation depth, the thickness response of the dam closest to the detonation point increased. The damage range of upper dam crest was significantly reduced. The damage scope of the lower part of the dam increased significantly. The penetration of the dam foundation was prone to anti-sliding and instability, and the consequences were more serious. It is worth noting that when the weight of TNT was 250 kg, the penetration cracks were mainly at the dam crest, and the penetration degree of cracks in the dam foundation was small. Dam crest failure was not allowed. Therefore, in order to show the characteristics of the dam failure caused by the cracks at dam crest with a small TNT weight (w = 250 kg), we took the crack penetration of the dam crest as the standard for evaluating the dam failure when the TNT weight was equal to 250 kg. Taking the penetration of the dam foundation cracks as the criterion for evaluating the dam failure when the TNT weight was greater than 250 kg. Based on the theory of plasticity index [44] and literature [40], a large number of numerical calculations were carried out on the dam damage caused by different TNT weights and make statistics on calculation results. The statistical results are shown in Figure 15.

5. Conclusions

This aim of this research was to study the vulnerability effects of underwater explosions of CSPGDs in working condition. A fully coupled water–air–TNT–dam-foundation model was established by LS-DYNA software and the model response and damage rationality were verified. Considering the influence of the initial stress field caused by self-weight, upstream hydrostatic pressure and dam foundation uplift pressure, a fully coupled numerical simulation model of underwater explosive CSPGD was established. The effects of detonation depth, TNT weight, and standoff distance on the blast damage effect of CSPGD were explored.

• The detonation depth had a significant impact on the dam anti-knock performance. When TNT weight and standoff distance remained unchanged, the damage position and horizontal velocity response on upstream surface showed a downward trend with the increase in detonation depth. The dam foundation cracks at the interface between the RI and rock foundation continued to increase, which adversely affected the anti-sliding stability of the dam foundation. The interface between RIII and RII had a strain rate effect and the RIII and RII were prone to tensile cracks under low strain. The detonation depth had no significant effect on the penetration degree of the dam crest crack and the dam crest was always a penetrating crack. At the same time, the detonation depth affected the response time of the dam damage but did not affect the final damage range value.
• The standoff distance affected the dam anti-knock performance. The dam damage caused by a short-range underwater explosion was more serious, and the dynamic response of the dam crest was also more severe than that of a long-distance explosion. In special periods, isolation measures should be taken to avoid underwater explosions near the dams.
• The dam damage degree was evaluated by the crack penetration ratio. According to the calculation results, different detonation depths, standoff distances, and the dam crest and dam foundation crack penetration ratio were fitted. The study found that the crack penetration ratio conformed a logarithmic relationship with TNT weights and conformed a cubic polynomial relationship with standoff distance, which provided a reference for the dam damage prediction under the action of explosion impact.
• By introducing the concept of crack penetration, the dam crest (TNT = 250 kg) and dam foundation (TNT > 250 kg) were used as damage indicators to evaluate the anti-knock performance of the dams with different TNT weights. The dam failure curves were obtained based on the statistical method to count the damage results in all scenarios.