Next Article in Journal
Performance of FRP-Upgraded RC One-Way Ribbed Slabs with an Opening in Flexure Zone
Previous Article in Journal
Cooling Energy Benefits of Increased Green Infrastructure in Subtropical Urban Building Environments
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Buildings
Volume 13
Issue 9
10.3390/buildings13092259
buildings-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Economic Seismic Performance of Buildings with Peer Methodology and Fema P-58

by
Wladimir Ramírez
1,*,
Margarita Mayacela
2,
Luis Contreras
2,
Nestor Iza
3,
Evelin Quishpe
4 and
Leonardo Rentería
5
1
Faculty of Civil and Mechanical Engineering, Technical University of Ambato, Ambato 180207, Ecuador
2
Faculty of Civil and Mechanical Engineering, Research and Development Directorate, Technical University of Ambato, Ambato 180207, Ecuador
3
Engineering Department, Duraciv Cia. Ltd.a., Puyo 160101, Ecuador
4
Material Procurement Department, China CAMC Engineering Co., Ltd., Quito 170201, Ecuador
5
Faculty of Engineering, National University of Chimborazo, Riobamba 060108, Ecuador
*
Author to whom correspondence should be addressed.
Buildings 2023, 13(9), 2259; https://doi.org/10.3390/buildings13092259
Submission received: 13 June 2023 / Revised: 14 July 2023 / Accepted: 11 August 2023 / Published: 6 September 2023
(This article belongs to the Section Building Structures)
Browse Figures
Versions Notes

Abstract

:
The performance-based seismic design pretends to take care of the lives of the occupants and reduce the cost of damage caused by earthquakes. Several ways of estimating damage and economic losses have been developed, but most of them lack objectivity and have great dispersion in the results. In the last decade, the advancement of technology has allowed the appearance of new methodologies, such as the one developed by the Pacific Earthquake Engineering Research Center (PEER methodology). However, the information regarding application and scope is scarce. In the present investigation, the economic seismic performance for a steel building was determined by applying the PEER methodology with different levels of seismic intensity. A multi-family residential model of special moment frames (SMF) was used, and the structure was designed by means of modal analysis. Spectral, incremental dynamic non-linear analysis was performed where the structural response was determined, with the help of the PACT software. The seismic performance, expressed as the repair costs, repair times, deaths, and injuries, was defined. The results obtained indicate that buildings designed with traditional structural standards can be demolished after the action of an earthquake because the repair costs exceed 40% of the replacement cost. Rare and very rare seismic events can cause the total suspension of the service and a considerable number of deaths and injuries.

1. Introduction

Earthquakes are among the most destructive natural disasters, and their incidence is greater when they occur in densely populated urban areas. Earthquakes cause substantial economic losses due to the collapse of structures, repairs of structural elements, non-structural elements, prolonged downtime of the building, and numerous deaths [1,2,3,4]. Non-structural elements are essential for building functionality and represent a significant investment. It is crucial for civil engineers to accurately estimate the cost of earthquake damage before it occurs [5,6].
The objective of a traditional seismic design is to save lives and prevent collapse, and as such, traditional codes and standards do not address the damage control aspects necessary to limit the risks associated with an earthquake and prevent significant economic losses. Recent seismic events have demonstrated that excessive residual drifts following an earthquake can lead to high repair costs, temporary service interruption due to required repairs, or even the total destruction of buildings. For this reason, most codes set limits on this parameter. Research conducted on non-structural elements and contents has shown that the damage they can suffer is related to floor accelerations, a parameter not typically considered in traditional codes [7,8,9].
Among the old methods of estimating damage, there are procedures based on the Mercalli scale, which relate the perceived visible damage in the structure to ground acceleration or soil type and a damage factor [10,11]. There are also maps of ground motion that relate Mercalli intensity to economic losses or losses of human life [12,13]. One of the limitations of these old methods is their subjectivity and the significant dispersion in results.
Since the 1990s, performance-based seismic design, also known as consequence-based design, has emerged. It aims to achieve a reasonable match between the expected consequences and estimated consequences in design [14]. This new approach to structural design sets objectives and damage levels for each level of seismic intensity [5,15,16,17]. In 2012, the Federal Emergency Management Agency (FEMA) published a series of products, including an objective methodology for the probabilistic estimation of economic losses [15]. This methodology involves four steps: estimating seismic hazard through ground intensities or seismic hazard curves; assessing the structural response to ground motion using non-linear analysis; expressing the structural response in terms of drifts and accelerations; and estimating the damage level in structural and non-structural elements and contents using fragility functions.
Fragility functions are used in seismic engineering to calculate the probabilities of different damage states based on seismic responses. Initially developed for nuclear power plants, fragility functions have gradually been implemented for buildings, bridges, structural and non-structural elements, and contents [5,16,17,18].
The seismic fragility of structures can be studied with empirical and analytical models; empirical fragility curves are built from the collected damage data, while analytical models are treated in a probabilistic manner. In the PEER methodology, the estimation of fragility is carried out using probabilistic seismic fragility analysis (PSFA) [19]. The probabilistic models constitute a special case of analysis. The research carried out by Xu-Yang Cao [20] estimates the fragility in the PSFA field for reinforced concrete frames subjected to non-stationary stochastic ground movements with various states of damage without reaching collapse. In this research, classical parametric probabilistic models such as least squares regression (LSR) and maximum likelihood estimation (MLE) are applied, while non-parametric models are simultaneously developed, such as the kernel density estimation (KDE) and Monte Carlo simulation (MCS). The results obtained indicate that the effectiveness, precision, and applicability of each model depends on several factors, such as computational resources, damage levels, seismic intensity, and the number of samples.
The final step is estimating the level of loss, which is expressed probabilistically as a performance function. This procedure, known as the Pacific Earthquake Engineering Research Center (PEER) methodology [21,22], is designed to be flexible and cater to user needs rather than being prescriptive. It results in earthquake-resistant designs that not only focus on human life [23].
The PEER methodology has been incorporated into the freely available PACT software, which collects and stores basic construction information such as the building area, structural system, non-structural systems and components, and structural response parameters including story drifts ratios, accelerations, and residual lateral drifts [24]. Previous studies have used this methodology and software to compare the seismic performance between different structural systems, compare the performance before and after reinforcement, and conduct individual building and regional studies at the city level [7,23,25,26]. The use of this methodology provides estimates of economic losses and other performance parameters such as the number of deaths, which many countries are adopting as indicators of seismic resilience [15,27,28]. These indicators also serve as a common language for decision-making and the transfer of required information between engineers and employers or stockholders.
Achieving the appropriate seismic performance of a building requires coordination between structural, non-structural, and content performance, thus achieving overall seismic performance. In this context, estimating damage and calculating economic losses before earthquakes occur remains a fundamental concern due to the limited information available on the application, scope, and limitations of new methodologies.
This research presents the application of the PEER methodology to calculate the economic seismic performance of a structural steel building, as part of the application PACT software, which is used to create an economic model that includes both structural and non-structural elements. The results are expressed through performance functions in terms of repair costs, repair time, and the number of deaths and injuries. The study demonstrates that economic losses are significant even for conventional levels of seismic intensity, for which the structures are designed. In fact, buildings can be demolished after an earthquake due to the high costs of repair. Furthermore, it is evident that the damage suffered by structural elements is related to story drifts ratios, while the damage to non-structural elements is related to story drifts ratios and floor accelerations.

2. Methodology

For the determination of economic seismic performance, a regular six-story building was used, with a structural system resistant to seismic loads consisting of steel special moment frames with cruciform columns and hot-rolled I-beams. The design of the structural elements was performed using modal spectral analysis consistent with the site-specific recommendations of NEC-15 [29]. Subsequently, incremental non-linear dynamic analyses were conducted to determine the accelerations, story drifts ratios, and residual drifts for each floor under different levels of seismic demand. With the assistance of the PACT software, an economic model was developed, including general building data, structural response, population, repair costs, fragility functions for structural and non-structural elements, and contents. Performance functions were then used to estimate the economic seismic performance in terms of repair costs, repair time, and the number of fatalities and injuries.
The modern approach to calculating economic seismic performance or estimating the economic losses resulting from a seismic event of a certain intensity is based on four steps: estimating seismic hazard; estimating structural response; estimating the level of damage in structural and non-structural elements and contents; and estimating the level of loss. The results are expressed probabilistically as a performance function, and this process is referred to as the PEER methodology. The calculation is performed using Equation (1) [30].
λ D V = ʃ ʃ ʃ G ( D V | D M ) | d G ( D M | E D P ) | | d G ( E D P | I M ) | | d λ ( I M ) |
where IM represents the measures of seismic intensity (design spectrum acceleration), EDP represents the engineering demand or structural response parameters (drifts, accelerations), DM represents the measures of damage (discrete damage states), DV represents the decision variable (economic losses), G(DV/DM) is a conditional complementary cumulative distribution function, and λ is a consequence function [31,32].
For the analysis of the building, a dead load of 6.26 KN/ m 2 was considered for the lower floors and 3.06 KN/ m 2 for the roof, and a live load of 2 KN/ m 2 was considered for all inhabited floors and 0.7 KN/ m 2 for the roof, based on the recommendations of the NEC-15 non-seismic loads chapter [1,2,3,4,33].
Considering the building’s use, an importance factor of I = 1 was adopted. The building was considered regular in both plan and elevation ϕ P = 1 ,   ϕ E = 1 , the seismic response reduction coefficient used was R = 6, as recommended by the same standard in the seismic hazard chapter [29], and the reactive load W was considered as the sum of the dead load and 25% of the live load, resulting in the basal shear being 16% of the reactive load.
V = 0.16   W

2.1. Design of Structural Elements

Modal spectral analysis was performed to determine the demands resulting from the combination of vertical loads and seismic loads. This ensured that the structural elements had sufficient strength and stiffness, satisfying the limit states of strength, serviceability, and dynamic behavior, as recommended by NEC, AISC, and standards [34,35,36,37]. The structural elements were designed with the ETABS software from a three-dimensional model with bar-type elements, and ASTM A36 steel was used while considering probable yield factors and probable stress, as described in the AISC 341-10 standard [35].
Reduced beam section (RBS) connections were used for the beam-column connections following the recommendations of AISC [36]. The design carried out complied with the recommendations of the standards for new steel buildings. The arrangement and dimensions of the structural elements can be seen in Figure 1 and Figure 2 and Table 1.

2.2. Incremental Dynamic Non-linear Analysis

Material non-linearity in the beams and columns was represented through a concentrated plasticity model, following Table 9-6 of the ASCE 41-13 standard [38], and the location of the plastic hinge (Sh) was assigned considering the result of the RBS connection. To evaluate the building, four levels of seismic intensity were used, representing a frequent, occasional, rare, and very rare earthquake [29]. Eleven seismic records were selected from the Pacific Earthquake Engineering Research Center database [39] (See Table 2), and the criteria for the selection of records were based on compatibility with the target spectrum for the city of Puyo, the reverse mode of failure, and a shear wave velocity (Vs30) of less than 180 m/s. The records prior to the analysis were corrected with a cubic baseline correction and trimmed using the intensity area method in a range between 5% and 95%. Figure 3 shows one of the processed seismic records. Finally, the seismic records were scaled to four levels of seismic intensity (0.46 g, 0.723 g, 0.975 g, and 1.887 g) which were expressed as a fraction of gravity (See Figure 4), using the spectral matching methodology in the frequency domain. This ensured that the seismic records matched the target response spectra for each intensity level.
Non-linear dynamic analysis was performed using the direct integration method with a damping ratio of 5% relative to critical damping, The damping of a building depends on several factors, among which are the height of the building, material, structural system, and level of damage in an earthquake. However, for analysis purposes, several standards recommend using a damping of less than or equal to 3 or 5% [29,38,40].
The analysis considered rigid prequalified connections and seismically compact sections with a high ductility and energy dissipation capacity, following the seismic provisions for structural steel buildings suggested by the American Institute of Steel Construction (AISC) [35,36]. The time step intervals ranged from 0.01 to 0.02 s, depending on the number of data points in each seismic record.

2.3. Economic Model

The PACT software, provided by the Federal Emergency Management Agency (FEMA), was used to develop the economic model and subsequently calculate the economic seismic performance and loss estimation. The data considered were as follows:

2.3.1. General Information of the Building

The building has a total area of 2688 m2 distributed over six equal floors. The costs and repair times were determined considering the Ecuadorian market. The maximum number of workers per square foot used to calculate the repair time was 0.001 (1 worker per 1000 square feet), following the recommendations of volume 2 of FEMA P 58 [41].
Taking into account the Ecuadorian market, a budget was made where the replacement cost of the building (construction cost plus demolition) was estimated to be 687.35 USD/m2, the repair cost of the building structure was estimated to be 507.67 USD/m2, and the repair time was estimated to be 1095 days.
The threshold for total loss was set at 0.40, as suggested by volume 1 of FEMA P 58 [15], which states that when the repair cost exceeds 40%, many homeowners prefer to demolish the existing building and replace it with a new one.
The PACT software, which employs the Monte Carlo method, was used to determine the probability of occurrence of the consequences. In the software, 500 realizations were defined to obtain more stable data for repair cost and repair time [42].

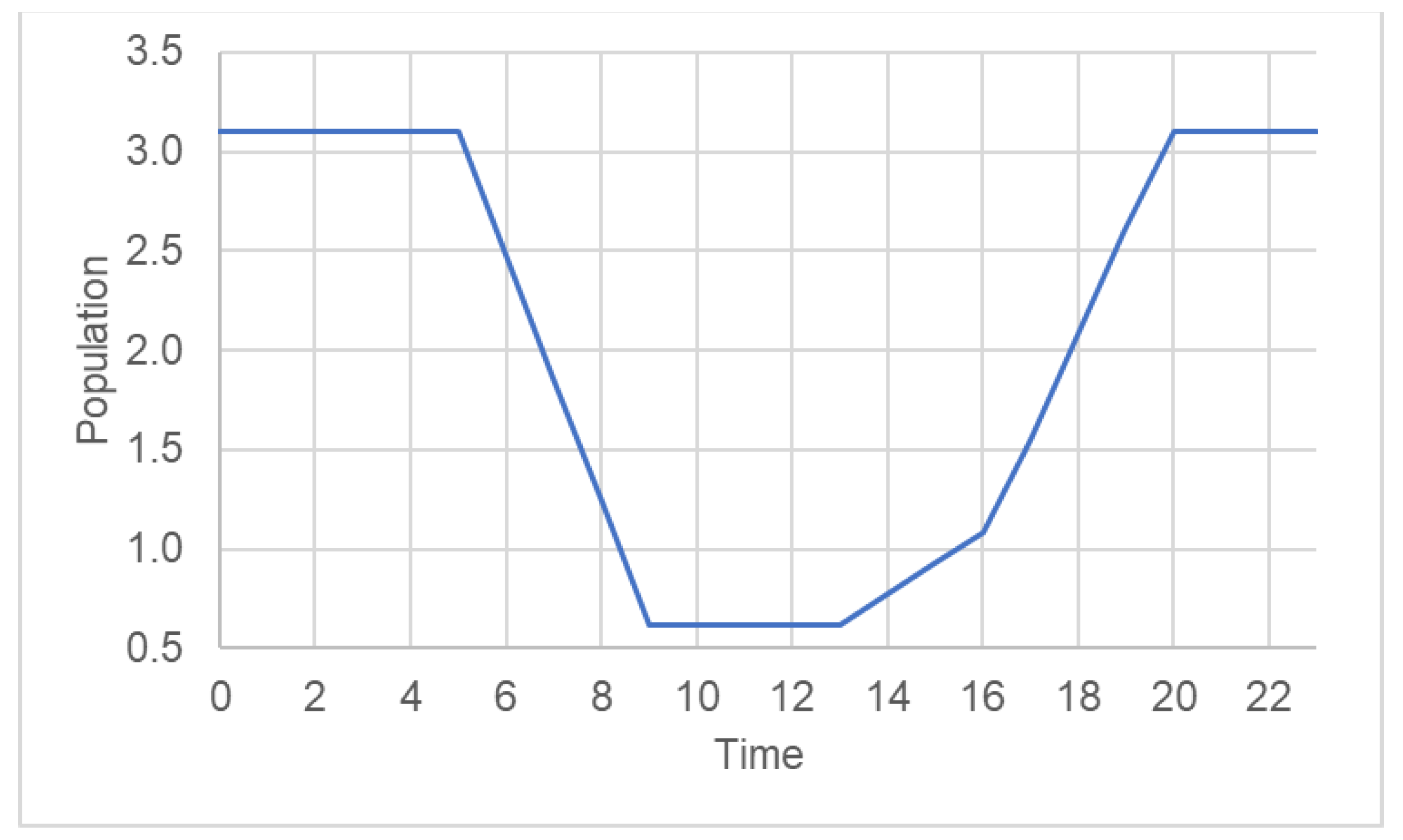
2.3.2. Population Model

To represent the population of the building, a residential model was used, which enabled us to estimate the potential number of victims in the building [15]. The peak number of occupants per 100 square feet was 3.1 with a dispersion of 0.2. From Monday to Friday, the peak occurred between 0:00–5 AM and 20:00–23:00 PM (see Figure 5), while on Saturdays and Sundays, the peak occurred between 0:00–8 AM and 22:00–23:00 PM.

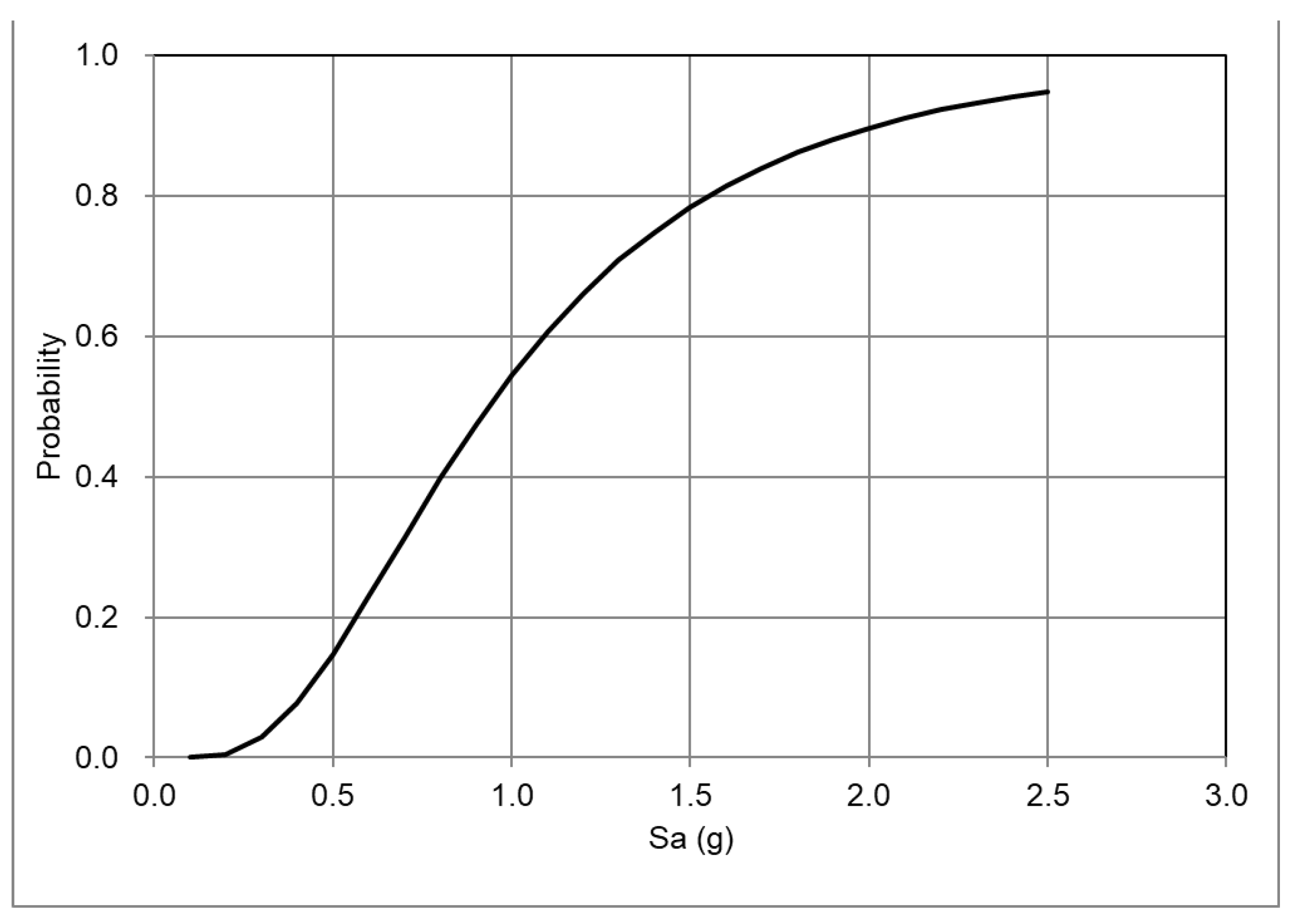
2.3.3. Fragility Functions

To estimate the expected economic losses due to structural damage in non-structural elements and components, fragility functions were used, which indicate the probability of damage that an element may suffer, given a structural response parameter [43,44]. The parameters assigned were story drifts ratios and floor accelerations (see Figure 6).
From the PACT program database [24], elements with their respective fragility curves were selected, as defined in FEMA P-58 [41], and each element is assigned a code, as shown in Table 3 and Figure 7.
The quantities of structural elements were estimated based on plans, while non-structural elements were estimated according to Table F5 of FEMA P-58 Volume 1 [15]. This table provides values at 10th, 50th, and 90th percentiles, and these quantities are based on the information obtained from the analysis of 3000 buildings.
These tables were programmed in the FEMA P58 Volume 3.3 Normative Quantity Estimation Tool by entering the floor area and occupancy of each floor into a spreadsheet, so that the quantities for the building were obtained.

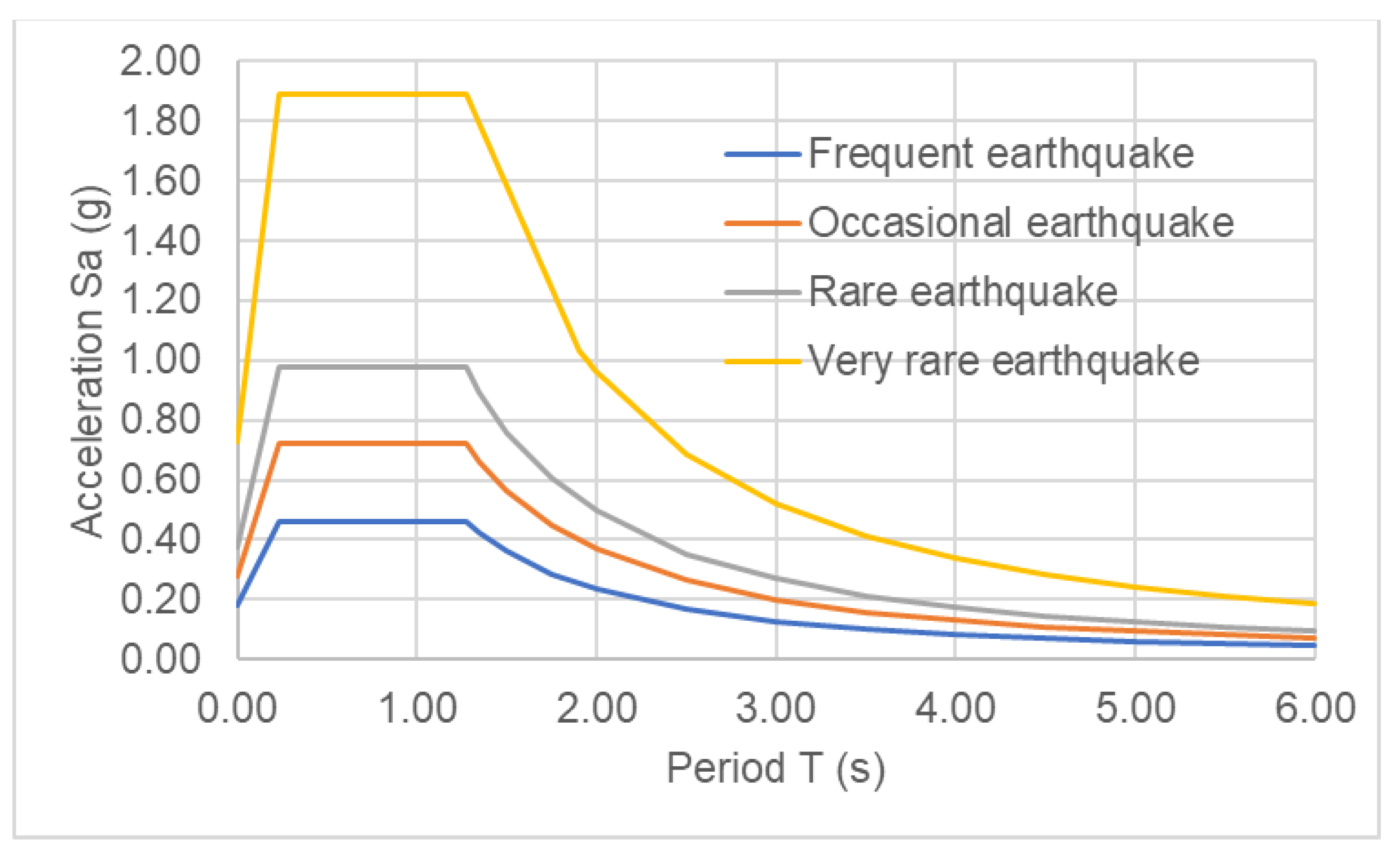
2.4. Collapse Fragility Curve of the Building

The collapse fragility curve indicates the probability of the structure collapsing at a given level of seismic intensity (see Figure 8) [45,46,47]. The structural collapse was detected with the maximum lateral deformation for which the analysis model presented numerical instability, as recommended in volume 1 of FEMA P-58 [15].
Using the “Collapse Fragility Tool”, the collapse fragility was defined by using the four levels of seismic intensity defined earlier. Twenty-two analyses were performed for each intensity level, obtaining the number of collapses for each level.
To construct the collapse fragility curve, an average acceleration Sa of 0.935 g was obtained using a dispersion of 0.6 for well-configured regular buildings, as recommended by [15,41]. A potential collapse mode was assumed, assuming the total collapse on all floors in the first mode, with a 90% probability of fatality and 10% probability of survival with injuries. Subsequently, the potential casualties for each intensity level were assessed.

3. Analysis and Discussion of Results

With the story drifts ratios and floor accelerations obtained from the non-linear dynamic analysis for each level of seismic intensity, for the two main directions of the building, 500 realizations were made with a dispersion of 0.6 in the PACT program. The economic performance functions were obtained for the four levels of seismic intensity: frequent seismic event, occasional seismic event, rare seismic event, and very rare seismic event.

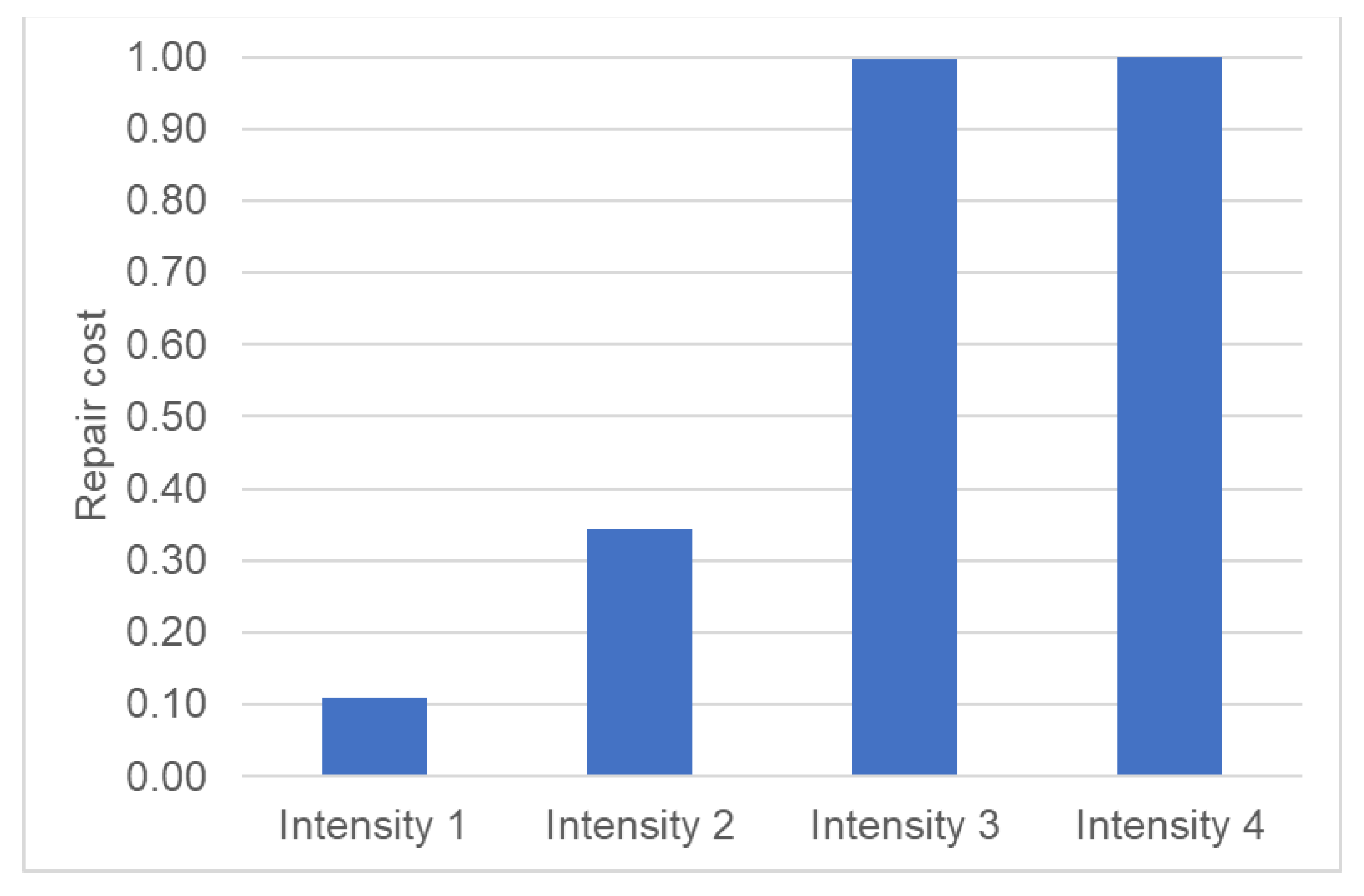
3.1. Repair Costs

The repair cost was determined by the fragility functions of each structural and non-structural component used, which are associated with story drifts ratios or floor accelerations [41].
Figure 9 shows the economic performance function of the building for the four intensity levels, which expresses the probability of having a certain value of repair cost or economic loss expressed as a fraction of the replacement cost of the building.
It can be observed that if design intensity 1 occurs, there is a probability of less than 86% that the repair cost will be 1, meaning that the repair cost is equal to the replacement cost of the building, which is $1,841,408.93 USD. If design intensity 2 occurs, there is a probability of less than 56% that the repair cost will be 100% of the replacement cost. For design intensity 3, there is a probability of less than 42% that the repair cost will be 100% of the replacement cost. Finally, for design intensity 4, there is a probability of less than 6% that the repair cost will be 100% of the replacement cost.
Similarly, taking design intensity 4 as an example, there is a probability of more than 94% that the repair costs will be equal to the replacement cost.
In many cases, average economic losses are analyzed, which correspond to a probability of 50%. Figure 10 shows the repair costs generated by each level of seismic intensity expressed as a fraction of the replacement cost for a probability of 50%. As the seismic intensity increases, the repair costs increase from 11% for intensity level 1 to 34% for intensity level 2. As the seismic intensity further increases, the floor accelerations and story drifts ratios increase, resulting in a higher number of damaged elements for intensity levels 3 and 4. It was determined that structural collapse occurred, and the repair cost is equal to the total estimated cost initially estimated for the building replacement. The increase in the repair cost caused by the increase in seismic intensity is composed of two parts: the first part is due to the repair cost of the structure, which is ambiguously described in the design philosophy of conventional codes, and the second part corresponds to the costs of non-structural elements, which are not considered by conventional codes and have been estimated using the PEER methodology [29,41,42].

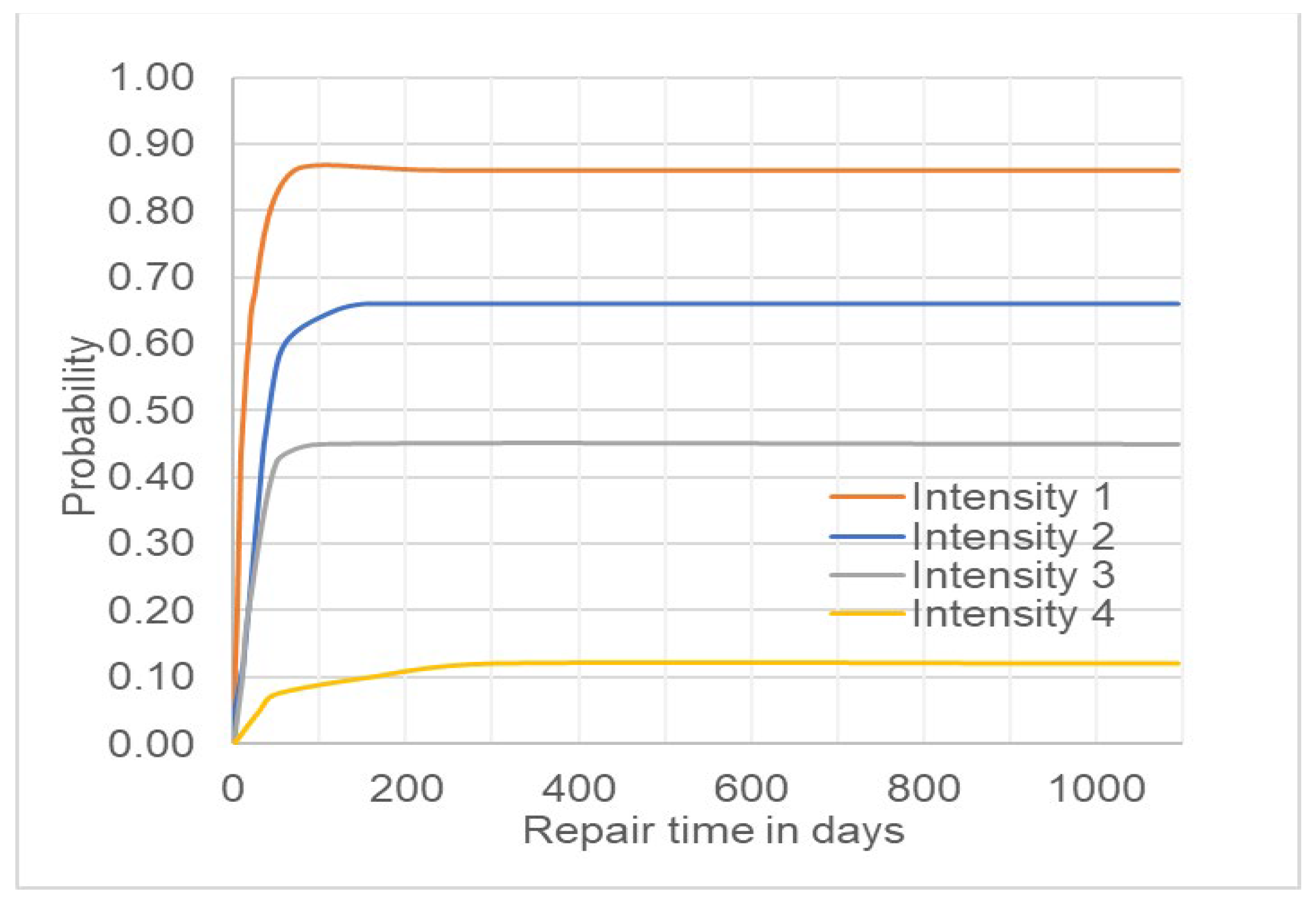
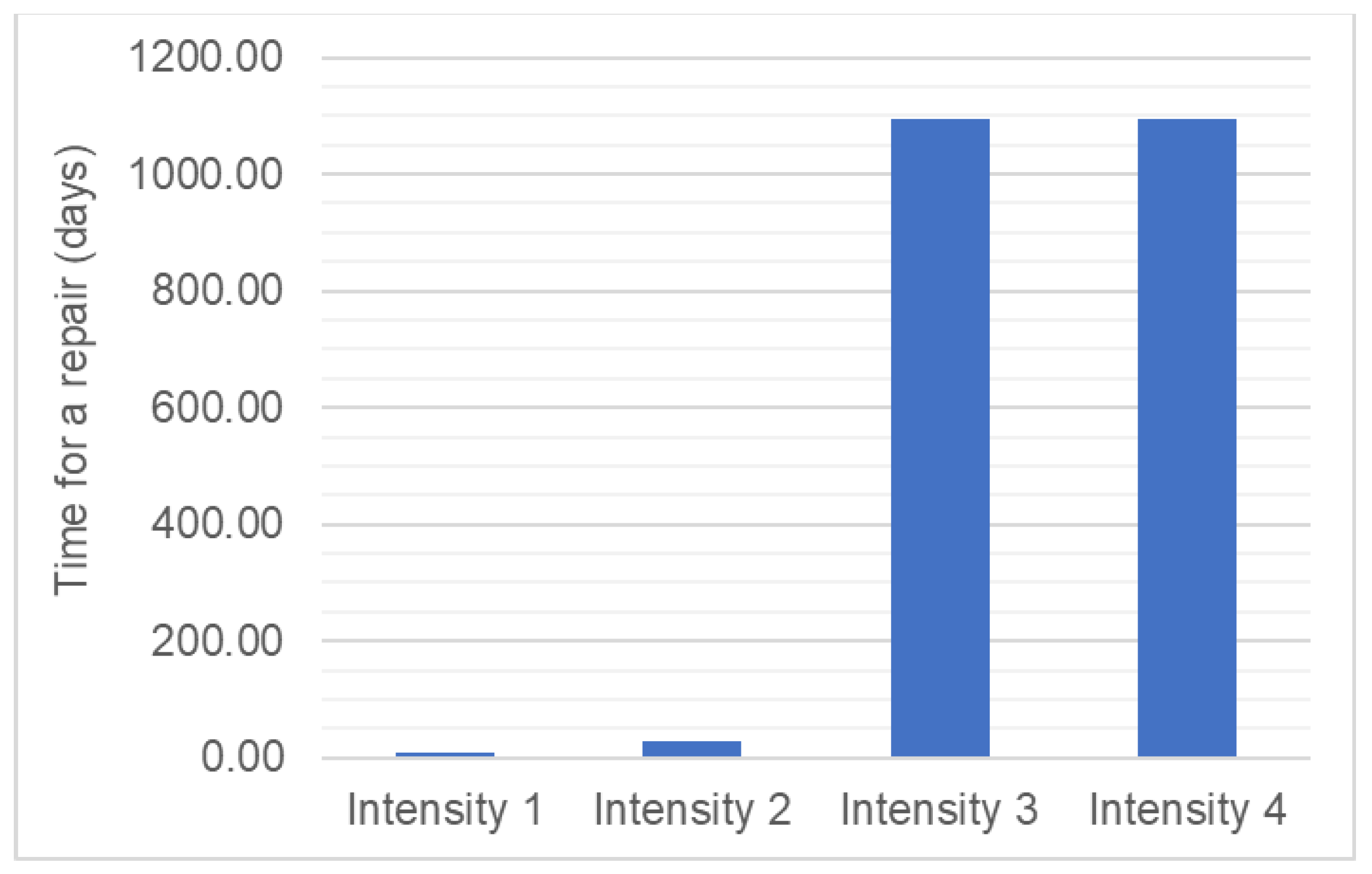
3.2. Repair Time

In Figure 11, the building performance function can be observed, which expresses the probability of having a specific value for the repair time, expressed in days. It can be observed that for design intensity 1, there is a probability lower than 86% that the repair time will be 1095 days, which is the estimated total time for repair and demolition. If design intensity 2 occurs, there is a probability lower than 66% that the repair time will be 1095 days. For design intensity 3, there is a probability lower than 45%, and similarly, if design intensity 4 occurs, there is a probability lower than 12% that the repair time will be 1095 days. Similarly, taking design intensity 4 as an example, it can be indicated that there is a probability higher than 88% that the repair time will be 1095 days.
In Figure 12, the average repair times generated by each seismic intensity level can be observed, and are expressed in days for a 50% probability. As the seismic intensity increases, the repair times rise from 10 days for design intensity level 1 to 28 days for design intensity level 2. For intensity levels 3 and 4, the repair times increase up to 1095 days due to structural collapse. These repair times are considered with all activities working in parallel. For design intensity levels 1 and 2, where there is no collapse, the suspension of service does not represent a significant cost compared to the project cost, as it is a residential building. However, for design intensity levels 3 and 4, the building practically ceases to function and represents a total loss. Repair time is a parameter not included in conventional standards [29,37,40,48].

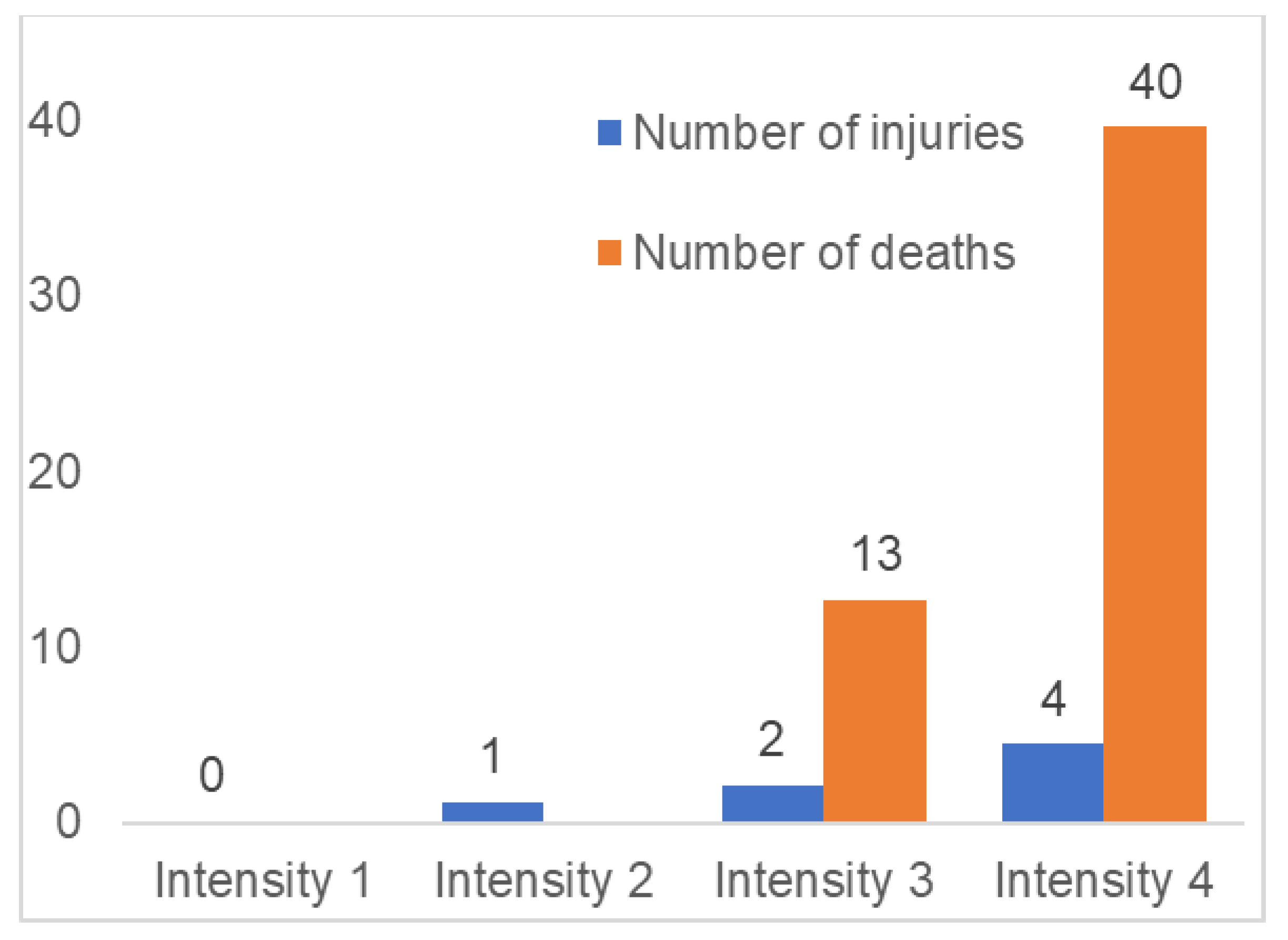
3.3. Number of Deaths and Injuries

Using the collapse fragility curve and the population model of the structure, the probable number of deaths and injuries was determined for each seismic intensity level (see Figure 13). In the first two intensity levels, no deaths were found. In intensity levels 3 and 4, 13 and 40 deaths, respectively, occurred due to structural collapse at these intensity levels.
The number of injuries occurred from the second level of seismic intensity onwards, with one injury for intensity level 2, two injuries for intensity level 3, and four injuries for intensity level 4. It can be observed that as the seismic intensity increases, the number of victims also increases. Additionally, it was determined that most victims were caused by the detachment of the false ceiling. The number of deaths and injuries is a factor that can lead to the structure being deemed unsafe [41].
The structural design of the building was carried out using the design base earthquake represented by seismic intensity level 3. Based on the results obtained in terms of costs and repair times, it is identified that the conventional design methodology for special moment frames in high-seismicity zones does not adequately meet the expectations of modern society. Economic losses for a rare earthquake (475-year return period) and a very rare earthquake (2500-year return period) can be close to or exceed 40% of the building replacement cost, resulting in the total loss of the project and the need for demolition. Similarly, the results of deaths and injuries for different levels of seismic intensity show that the life-saving philosophy expressed in conventional design standards is not achieved, as this philosophy only focuses on the structure itself and does not consider the influence of non-structural elements and contents that can also cause severe health damage and death to the occupants, similar to the results obtained in other research studies [25,49,50].

4. Conclusions

Using incremental dynamic non-linear analysis, the structural response in terms of floor accelerations and story drifts ratios was analyzed for a six-story steel building. By employing the PEER methodology with the assistance of the PACT program, an economic model was created, allowing us to determine the seismic performance and economic implications of the building for four levels of seismic intensity.
Worldwide Ecuador is considered a country with high seismic risk, but in the literature, no research has been found that considers the seismic hazard of Ecuador with the PEER methodology. The present investigation exposes relevant information on indicators of seismic resilience (repair costs, time repair, number of deaths and injuries) that will serve as scientific support to improve design standards and traditional construction practices in several countries around the world.
The results of the number of deaths and injuries indicate that the conventional design methodology and philosophy are not sufficient to meet the objective of saving the lives of the occupants, given that for medium and high seismic intensities represented by rare and very rare earthquakes, several deaths were registered. In the same way, for low intensities (occasional earthquake) and high intensities, there were few injuries registered. The results of the repair costs indicate that the conventional methodology does not provide an adequate procedure to minimize the risk of economic losses either, since for medium and high seismic intensities, the repair costs were close to or exceeded 40% of the replacement cost, which suggests that buildings designed according to traditional structural standards may be demolished after an earthquake due to the high repair costs.
Economic loss costs consist of the direct costs of repair plus the costs for loss of functionality over time. The results expressed in repair time showed that for medium and high seismic intensities, the repair time is equal to the replacement time of the structure, which suggests that the traditional design standards currently used in most countries do not comply with seismic resilience.
The methodology used allowed for the evaluation of the probability of structural and non-structural components being damaged due to seismic action. It was determined that damage to structural elements is related to story drifts ratios, while damage to non-structural elements is related to both story drifts ratios and floor accelerations. This reflects the need for current building codes to include limits on floor acceleration values, not only on story drifts ratios, as has been done so far. This approach achieves better seismic performance and improved design of non-structural elements. Likewise, it was evident that as the seismic intensity increases, economic losses increase due to the damage suffered by the elements.
The studies carried out in this research correspond to a specific type of structural system. For future investigations, it is recommended to analyze different structural systems and different levels of damping and non-structural elements and contents.
Based on the results of this research, it has been identified that the PEER methodology and PACT software present some limitations. For instance, economic seismic behavior is calculated with consequences that occur inside the building and does not consider external agents, such as damage to the access roads that can cause the loss of the functionality of the building. Earthquakes can also cause fires, spills of dangerous substances, and other effects that are not contemplated in the methodology.

Author Contributions

Conceptualization, M.M. and W.R.; methodology, M.M. and W.R.; validation, N.I., M.M. and L.C.; formal analysis, L.C., M.M. and W.R.; investigation, E.Q., M.M., L.R. and E.Q.; writing—original draft preparation, W.R.; writing—review and editing, M.M., W.R. and L.C.; visualization, E.Q., L.C., L.R. and N.I.; supervision, M.M. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the Technical University of Ambato, Research and Development Directorate, Research Project PFICM27 “Aplicación de vibración ambiental para el estudio de la frecuencia natural de estructuras de edificación de hormigón armado existentes en la zona urbana del cantón Latacunga”.

Data Availability Statement

The data presented in this study are available upon request from the corresponding author.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Fierro, E.A.; Miranda, E.; Perry, C.L. Behavior of Nonstructural Components in Recent Earthquakes. In AEI 2011: Building Integrated Solutions–Proceedings of the AEI 2011 Conference; American Society of Civil Engineers: Reston, VI, USA, 2011; pp. 369–377. [Google Scholar] [CrossRef]
  2. Miranda, E.; Mosqueda, G.; Retamales, R. Desempeño de componentes no estructurales durante el terremoto del 27 de febrero de 2010 en Chile. Terremoto 2012, 28, S453–S471. [Google Scholar] [CrossRef]
  3. Guha-Sapir, D.; Vos, F.; Below, R.; Ponserre, S. Annual Disaster Statistical Review 2010: The Numbers and Trends; Centre for Research on the Epidemiology of Disasters, Catholic University of Lovaina: Brussels, Belgium, 2011. [Google Scholar]
  4. Guha-Sapir, D.; Vos, F.; Below, R.; Ponserre, S. Annual Disaster Statistical Review 2011: The Numbers and Trends; Centre for Research on the Epidemiology of Disasters, Catholic University of Lovaina: Brussels, Belgium, 2012. [Google Scholar]
  5. Ramirez, C.M.; Lignos, D.G.; Miranda, E.; Kolios, D. Fragility functions for pre-Northridge welded steel moment-resisting beam-to-column connections. Eng. Struct. 2012, 45, 574–584. [Google Scholar] [CrossRef]
  6. Taghavi, S.; Miranda, E. Response Assessment of Nonstructural Building Elements; Pacific Earthquake Engineering Research Center, University of California Berkeley: Berkeley, CA, USA, 2003. [Google Scholar]
  7. Nobahar, E.; Asgarian, B.; Mercan, O.; Soroushian, S. A post-tensioned self-centering yielding brace system: Development and performance-based seismic analysis. Struct. Infrastruct. Eng. 2021, 17, 392–412. [Google Scholar] [CrossRef]
  8. Bommer, J.; Bray, J.; Kyriazis, P.; Yasuda, G.S. Perspectives on European Earthquake Engineering and Seismology; Ansal, A., Ed.; Springer Science+Business Media: New York, NY, USA, 2014; Volume 1. [Google Scholar] [CrossRef]
  9. Del Vecchio, C.; Di Ludovico, M.; Pampanin, S.; Prota, A. Repair Costs of Existing RC Buildings Damaged by the L’Aquila Earthquake and Comparison with FEMA P-58 Predictions. Earthq. Spectra 2018, 34, 237–263. [Google Scholar] [CrossRef]
  10. Algermissen, S.T.; Steinbrugge, K.V. Seismic Hazard and Risk Assessment: Some Case Studies. Geneva Pap. Risk Insur. 1984, 9, 8–26. [Google Scholar] [CrossRef]
  11. McCann, M.W.; Sauter, F.; Shah, H.C. A technical note on PGA-intensity relations with applications to damage estimation. Bull. Seismol. Soc. Am. 1980, 70, 631–637. [Google Scholar] [CrossRef]
  12. Böse, M.; Sokolov, V.; Wenzel, F. Shake Map Methodology for Intermediate-Depth Vrancea (Romania) Earthquakes. Earthq. Spectra 2009, 25, 497–514. [Google Scholar] [CrossRef]
  13. Wald, D.J.; Quitoriano, V.; Heaton, T.H.; Kanamori, H.; Scrivner, C.W.; Worden, C.B. TriNet “ShakeMaps”: Rapid Generation of Peak Ground Motion and Intensity Maps for Earthquakes in Southern California. Earthq. Spectra 1999, 15, 537–555. [Google Scholar] [CrossRef]
  14. Comartin, C.; Niewiarowski, R.; Rojahn, C. Seismic Evaluation and Retrofit of Concrete Buildings ATC-40; Applied Technology Council: Redwood City, CA, USA, 1996. [Google Scholar]
  15. Mahoney, M.; Hanson, R.D. Seismic Performance Assessment of Buildings Volume 1-Methodology Second Edition Prepared for Federal Emergency Management Agency. Available online: https://www.atcouncil.org/docman/fema/246-fema-p-58-1-seismic-performance-assessment-of-buildings-volume-1-methodology-second-edition/file (accessed on 4 April 2023).
  16. Kennedy, R.P.; Ravindra, M.K. Seismic fragilities for nuclear power plant risk studies. Nucl. Eng. Des. 1984, 79, 47–68. [Google Scholar] [CrossRef]
  17. Akkar, S.; Sucuoǧlu, H.; Yakut, A. Displacement-based fragility functions for low- And mid-rise ordinary concrete buildings. Earthq. Spectra 2005, 21, 901–927. [Google Scholar] [CrossRef]
  18. Choe, D.-E.; Gardoni, P.; Rosowsky, D.; Haukass, T. Probabilistic capacity models and seismic fragility estimates for RC columns subject to corrosion. Reliab. Eng. Syst. Saf. 2008, 93, 383–393. [Google Scholar] [CrossRef]
  19. Yazdanpanah, O.; Mohebi, B.; Kazemi, F.; Mansouri, I.; Jankowski, R. Development of fragility curves in adjacent steel moment-resisting frames considering pounding effects through improved wavelet-based refined damage-sensitive. Mech. Syst. Signal Process. 2022, 173, 109038. [Google Scholar] [CrossRef]
  20. Cao, X.Y.; Feng, D.C.; Li, Y. Assessment of various seismic fragility analysis approaches for structures excited by non-stationary stochastic ground motions. Mech. Syst. Signal Process. 2023, 186, 109838. [Google Scholar] [CrossRef]
  21. Bozorgnia, Y.; Bertero, V.V. (Eds.) Earthquake Engineering: From Engineering Seismology to Performance-Based Engineering; CRC Press: Boca Raton, FL, USA, 2004. [Google Scholar] [CrossRef]
  22. Miranda, E. Use of probability-based measures for automated damage assessment. Struct. Des. Tall Spec. Build. 2006, 15, 35–50. [Google Scholar] [CrossRef]
  23. Jarrett, J.A.; Judd, J.P.; Charney, F.A. Comparative evaluation of innovative and traditional seismic-resisting systems using the FEMA P-58 procedure. J. Constr. Steel Res. 2015, 105, 107–118. [Google Scholar] [CrossRef]
  24. John, A.; Martin y Associates, Inc.; Naeim, F.; Hagie, S. PACT; Federal Emergency Management Agency: Redwood, CA, USA, 2018. [Google Scholar]
  25. Del Gobbo, G.M.; Williams, M.S.; Blakeborough, A. Seismic performance assessment of Eurocode 8-compliant concentric braced frame buildings using FEMA P-58. Eng. Struct. 2018, 155, 192–208. [Google Scholar] [CrossRef]
  26. Zeng, X.; Lu, X.; Yang, T.Y.; Xu, Z. Application of the FEMA-P58 methodology for regional earthquake loss prediction. Nat. Hazards 2016, 83, 177–192. [Google Scholar] [CrossRef]
  27. Zareian, F.; Krawinkler, H. Simplified Performance-Based Earthquake Engineering, Stanford University, California, USA, 2006. Available online: https://search.proquest.com/openview/2f1029b572bba391c1056c8b98822974/1?pq-origsite=gscholar&cbl=18750&diss=y (accessed on 4 April 2023).
  28. Aslani, H. Probabilistic Earthquake Loss Estimation and Loss Disaggregation in Buildings, Stanford University, California, USA, 2005. Available online: https://search.proquest.com/openview/e0b374032cd05de724e28c31e4e7d333/1?pq-origsite=gscholar&cbl=18750&diss=y (accessed on 4 April 2023).
  29. Ministerio de Desarrollo Urbano y Vivienda (MIDUVI). NEC-SE-DS; Ministerio de Desarrollo Urbano y Vivienda (MIDUVI): Quito, Ecuador, 2014. [Google Scholar]
  30. Comartin, C.D.; Niewiarowski, R.W.; Freeman, S.A.; Turner, F.M. Seismic Evaluation and Retrofit of Concrete Buildings: A Practical Overview of the ATC 40 Document. Earthq. Spectra 2000, 16, 241–261. [Google Scholar] [CrossRef]
  31. Cremen, G.; Baker, J.W. Quantifying the benefits of building instruments to FEMA P-58 rapid post-earthquake damage and loss predictions. Eng. Struct. 2018, 176, 243–253. [Google Scholar] [CrossRef]
  32. Papadopoulos, A.N.; Vamvatsikos, D.; Kazantzi, A.K. Development and application of FEMA P-58 compatible story loss functions. Earthq. Spectra 2019, 55, 95–112. [Google Scholar] [CrossRef]
  33. Ministerio de Desarrollo Urbano y Vivienda (MIDUVI). NEC-SE-CG; Ministerio de Desarrollo Urbano y Vivienda (MIDUVI): Quito, Ecuador, 2014. [Google Scholar]
  34. Ministerio de Desarrollo Urbano y Vivienda (MIDUVI). NEC-SE-AC; Ministerio de Desarrollo Urbano y Vivienda (MIDUVI): Quito, Ecuador, 2014. [Google Scholar]
  35. American Institute of Steel Construction. Seismic Provisions for Structural Steel Buildings; American Institute of Steel Construction: Chicago, IL, USA, 2010. [Google Scholar]
  36. American Institute of Steel Construction. Prequalified Connections for Special and Intermediate Steel Moment Frames for Seismic Applications; American Institute of Steel Construction: Chicago, IL, USA, 2011. [Google Scholar]
  37. American Society of Civil Engineers. Minimum Design Loads for Buildings and Other Structures (ASCE/SEI 7-10); American Society of Civil Engineers: Reston, VI, USA, 2010. [Google Scholar]
  38. ASCE American Society of Civil Engineers, Structural Engineering Institute. Seismic Evaluation and Retrofit of Existing Buildings; ASCE American Society of Civil Engineers, Structural Engineering Institute: Reston, VI, USA, 2014. [Google Scholar]
  39. Pacific Earthquake Engineering Research Center. Base de datos de Movimiento Terrestre PEER—Centro PEER. Available online: https://ngawest2.berkeley.edu/ (accessed on 9 March 2023).
  40. Gobierno De La Ciudad De México. Normas Técnicas Complementarias Para Diseño Por Sismo (NTC 2020); México, 2020. Available online: https://www.studocu.com/es-mx/document/universidad-autonoma-metropolitana/gramatica-normativa/normas-tecnicas-complementarias-para-el-diseno-por-sismo-9-de-junio-de-2020/17584908 (accessed on 4 April 2023).
  41. Mahoney, M.; Hanson, R.D. FEMA P-58-2/Seismic Performance Assessment of Buildings Volume 2-Implementation Guide, 2nd ed.; Federal Emergency Management Agency: Redwood City, CA, USA, 2018. [Google Scholar]
  42. Cardone, D.; Perrone, G. Damage and Loss Assessment of Pre-70 RC Frame Buildings with FEMA P-58. J. Earthq. Eng. 2016, 21, 23–61. [Google Scholar] [CrossRef]
  43. Cremen, G.; Baker, J.W. Improving FEMA P-58 non-structural component fragility functions and loss predictions. Bull. Earthq. Eng. 2019, 17, 1941–1960. [Google Scholar] [CrossRef]
  44. Xu, Z.; Zhang, H.; Lu, X.; Xu, Y.; Zhang, Z.; Li, Y. A prediction method of building seismic loss based on BIM and FEMA P-58. Autom Constr. 2019, 102, 245–257. [Google Scholar] [CrossRef]
  45. Majdi, A.; Vacareanu, R. Evaluation of Seismic Damage to Iraqi Educational Reinforced Building Using FEMA P-58 Methodology. Earth Environ. Sci. 2021. [Google Scholar] [CrossRef]
  46. Ramanathan, K.; Padgett, J.E.; DesRoches, R. Temporal evolution of seismic fragility curves for concrete box-girder bridges in California. Eng. Struct. 2015, 97, 29–46. [Google Scholar] [CrossRef]
  47. Shinozuka, M.; Feng, M.Q.; Kim, H.-K.; Kim, S.-H. Nonlinear Static Procedure for Fragility Curve Development. J. Eng. Mech. 2000, 126, 1287–1295. [Google Scholar] [CrossRef]
  48. Ministerio de Ambiente, Vivienda y Desarrollo Territorial. Reglamento Colombiano de Construcción Sismo Resistente (NSR-10); Bogotá, Colombia, 2010. Available online: https://www.andi.com.co/Uploads/Reglamento_colombiano_construccion_sismo_resistente_636536179523160220.pdf (accessed on 4 April 2023).
  49. Hwang, S.-H.; Lignos, D.G. Earthquake-induced loss assessment of steel frame buildings with special moment frames designed in highly seismic regions. Earthq. Eng. Struct. Dyn. 2017, 46, 2141–2162. [Google Scholar] [CrossRef]
  50. Beheshti Aval, S.B.; Kouhestani, H.S.; Mottaghi, L. Effectiveness of two conventional methods for seismic retrofit of steel and RC moment resisting frames based on damage control criteria. Earthq. Eng. Eng. Vib. 2017, 16, 537–555. [Google Scholar] [CrossRef]
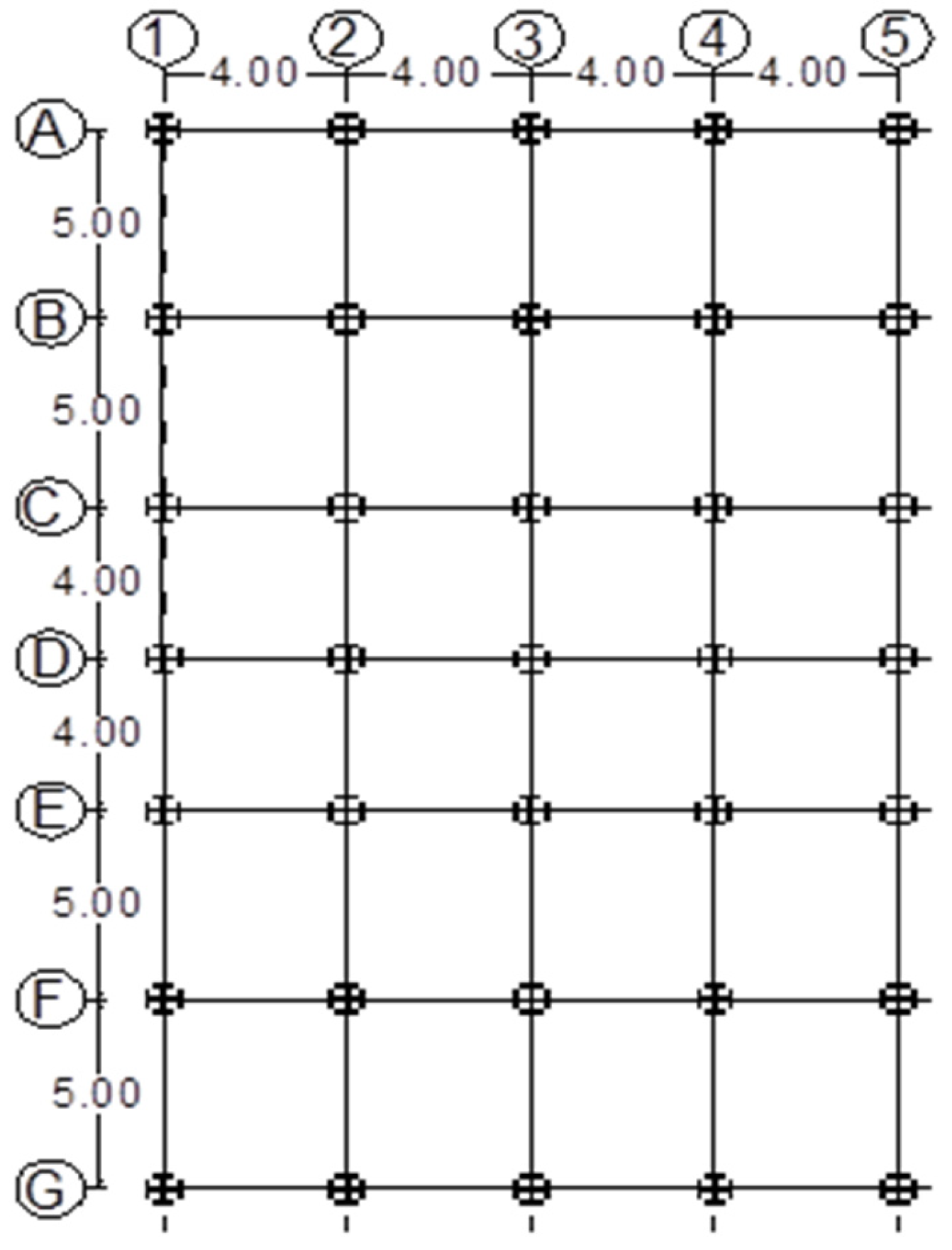
Buildings 13 02259 g001
Figure 1. Floor view of the building. Where A–G are the horizontal axes and 1–5 are the vertical axes.
Figure 1. Floor view of the building. Where A–G are the horizontal axes and 1–5 are the vertical axes.
Buildings 13 02259 g001
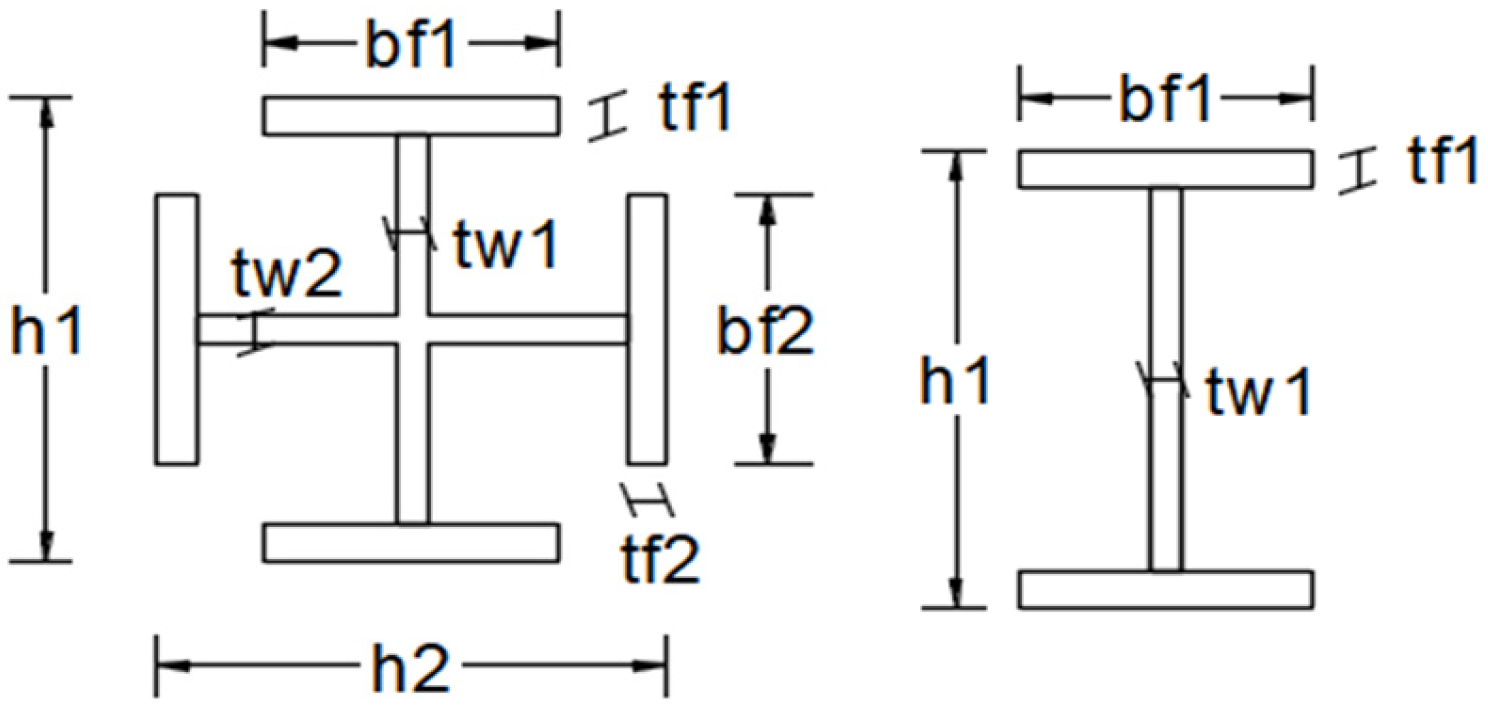
Buildings 13 02259 g002
Figure 2. Sections of structural elements.
Figure 2. Sections of structural elements.
Buildings 13 02259 g002
Buildings 13 02259 g003
Figure 3. Cropped Accelerogram Coalinga326, X component, Acceleration (g) vs. Time (s).
Figure 3. Cropped Accelerogram Coalinga326, X component, Acceleration (g) vs. Time (s).
Buildings 13 02259 g003
Buildings 13 02259 g004
Figure 4. Seismic intensity levels.
Figure 4. Seismic intensity levels.
Buildings 13 02259 g004
Buildings 13 02259 g005
Figure 5. Residential population model on Monday-Friday (adapted from [24]).
Figure 5. Residential population model on Monday-Friday (adapted from [24]).
Buildings 13 02259 g005
Buildings 13 02259 g006
Figure 6. Story drifts ratio for one direction.
Figure 6. Story drifts ratio for one direction.
Buildings 13 02259 g006
Buildings 13 02259 g007
Figure 7. Steel beam-column connection fragility function (Adapted from [24]).
Figure 7. Steel beam-column connection fragility function (Adapted from [24]).
Buildings 13 02259 g007
Buildings 13 02259 g008
Figure 8. Collapse fragility curve.
Figure 8. Collapse fragility curve.
Buildings 13 02259 g008
Buildings 13 02259 g009
Figure 9. Repair costs for four intensity levels.
Figure 9. Repair costs for four intensity levels.
Buildings 13 02259 g009
Buildings 13 02259 g010
Figure 10. Repair costs at 50% probability for four intensity levels.
Figure 10. Repair costs at 50% probability for four intensity levels.
Buildings 13 02259 g010
Buildings 13 02259 g011
Figure 11. Total repair time for four intensity levels.
Figure 11. Total repair time for four intensity levels.
Buildings 13 02259 g011
Buildings 13 02259 g012
Figure 12. Repair time for four intensity levels.
Figure 12. Repair time for four intensity levels.
Buildings 13 02259 g012
Buildings 13 02259 g013
Figure 13. Number of injuries and deaths for all intensity levels.
Figure 13. Number of injuries and deaths for all intensity levels.
Buildings 13 02259 g013
Table 1. Structural elements used.
Table 1. Structural elements used.
Dimensions (mm)
TypeLocationtf1tw1h1bf1tf2tw2h2bf2
Column cross 600 × 5001st floor, 2nd floor, 3rd floor30.015.5600.0300.028.014.5500.0300.0
Column cross 500 × 4004th floor, 5th floor, 6th floor24.013.5400.0300.028.014.5500.0300.0
Beam IPE 3601st floor, 2nd floor, 3rd floor12.78.0360.0170.0
Beam IPE 3304th floor, 5th floor11.57.5330.0160.0
Beam IPE 3006th Floor10.77.1300.0150.0
Table 2. Seismic records.
Table 2. Seismic records.
EarthquakeYearSeasonMagnitude (Mw)Fault TypeVs30 (m/s)
“Coalinga-01”1983“Parkfield—Cholame 2WA”6.36Reverse173.02
“Coalinga-01”1983“Parkfield—Fault Zone 1”6.36Reverse178.27
“Northridge-01”1994“Carson—Water St”6.69Reverse160.58
“Chi-Chi_ Taiwan-03”1999“CHY047”6.20Reverse169.52
“Niigata_ Japan”2004“NIG011”6.63Reverse149.97
“Niigata_ Japan”2004“NIG013”6.63Reverse174.55
“Chuetsu-oki_ Japan”2007“NIG010”6.80Reverse173.09
“Chuetsu-oki_ Japan”2007“NIG013”6.80Reverse174.55
“Iwate_ Japan”2008“AKT016”6.90Reverse158.16
“Iwate_ Japan”2008“MYG006”6.90Reverse146.72
“Iwate_ Japan”2008“MYG007”6.90Reverse166.75
Table 3. Elements with defined fragility functions.
Table 3. Elements with defined fragility functions.
ElementTypeCode
Steel beam-column connection one directionStructural elementB1035.001
Steel beam-column connection in both directionsStructural elementB1035.011
Interior plaster wallNon-structural elementC1011.001a
Exterior wall of panelsNon-structural elementB2011.001b
Plaster ceilingNon-structural elementC3032.001a
Steel drinking water pipeNon-structural elementD2021.011a
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Ramírez, W.; Mayacela, M.; Contreras, L.; Iza, N.; Quishpe, E.; Rentería, L. Economic Seismic Performance of Buildings with Peer Methodology and Fema P-58. Buildings 2023, 13, 2259. https://doi.org/10.3390/buildings13092259

AMA Style

Ramírez W, Mayacela M, Contreras L, Iza N, Quishpe E, Rentería L. Economic Seismic Performance of Buildings with Peer Methodology and Fema P-58. Buildings. 2023; 13(9):2259. https://doi.org/10.3390/buildings13092259

Chicago/Turabian Style

Ramírez, Wladimir, Margarita Mayacela, Luis Contreras, Nestor Iza, Evelin Quishpe, and Leonardo Rentería. 2023. "Economic Seismic Performance of Buildings with Peer Methodology and Fema P-58" Buildings 13, no. 9: 2259. https://doi.org/10.3390/buildings13092259

APA Style

Ramírez, W., Mayacela, M., Contreras, L., Iza, N., Quishpe, E., & Rentería, L. (2023). Economic Seismic Performance of Buildings with Peer Methodology and Fema P-58. Buildings, 13(9), 2259. https://doi.org/10.3390/buildings13092259

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop