Performance of FRP-Upgraded RC One-Way Ribbed Slabs with an Opening in Flexure Zone
Abstract
:1. Introduction
2. Experimental Program
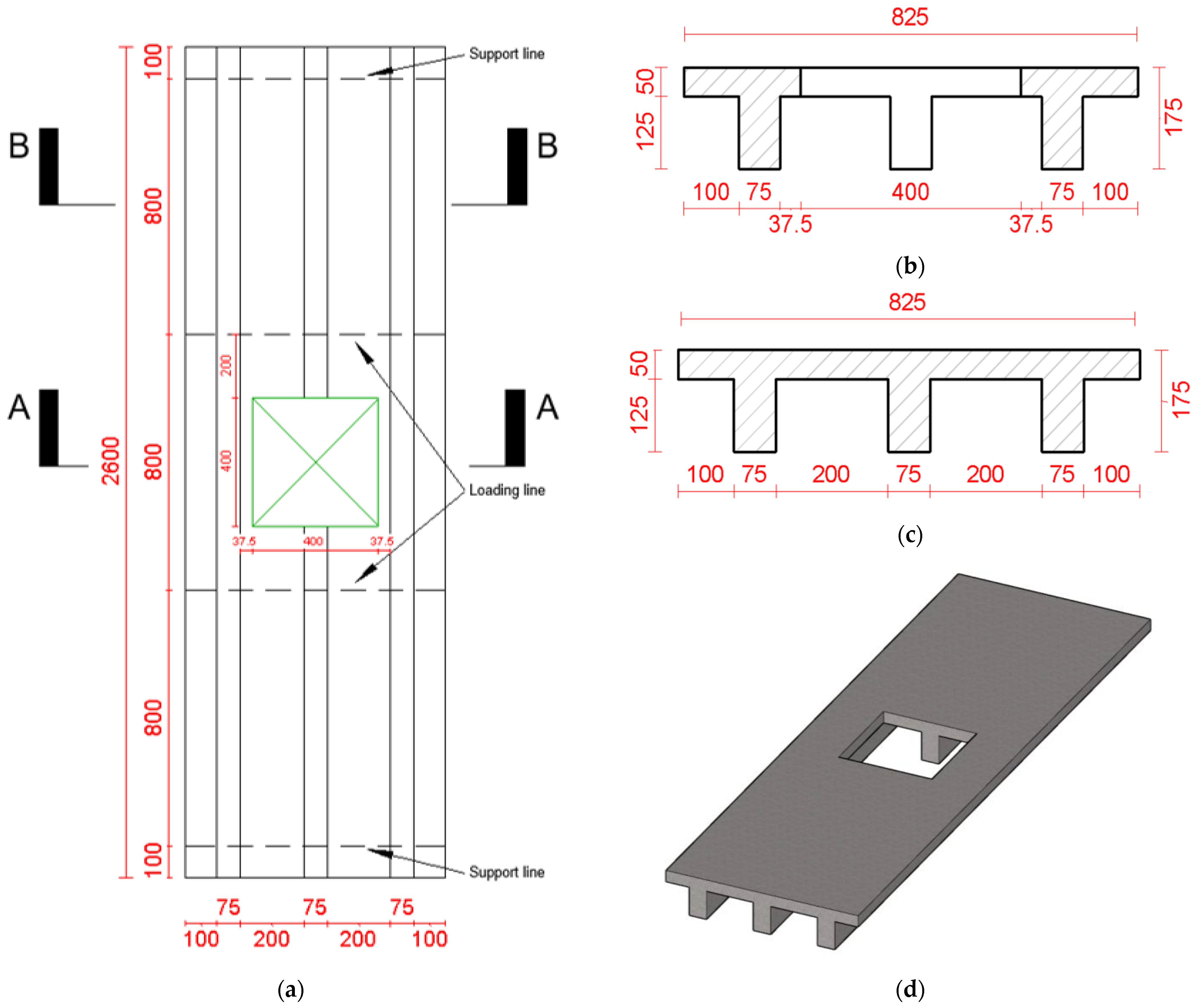
2.1. Test Matrix
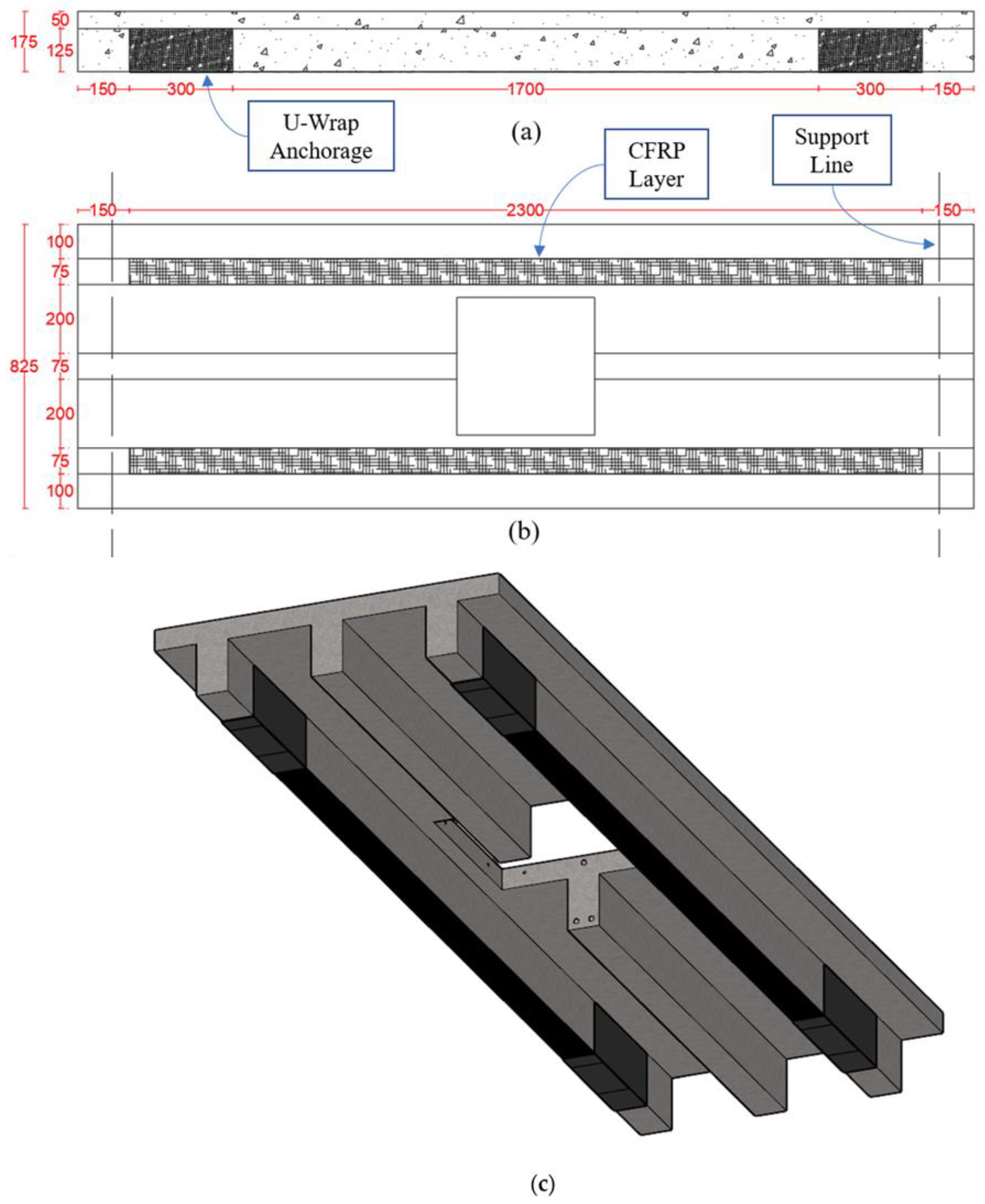
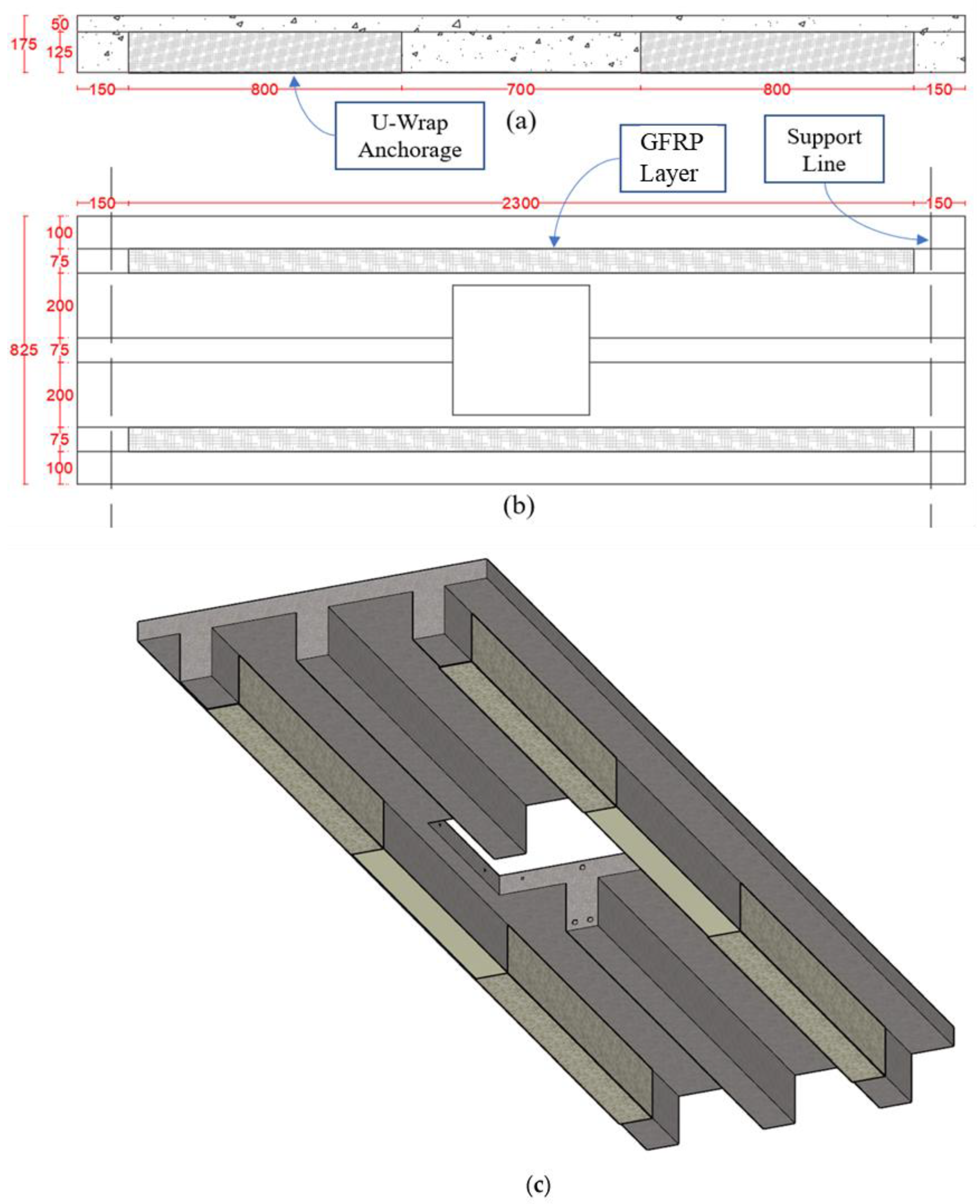
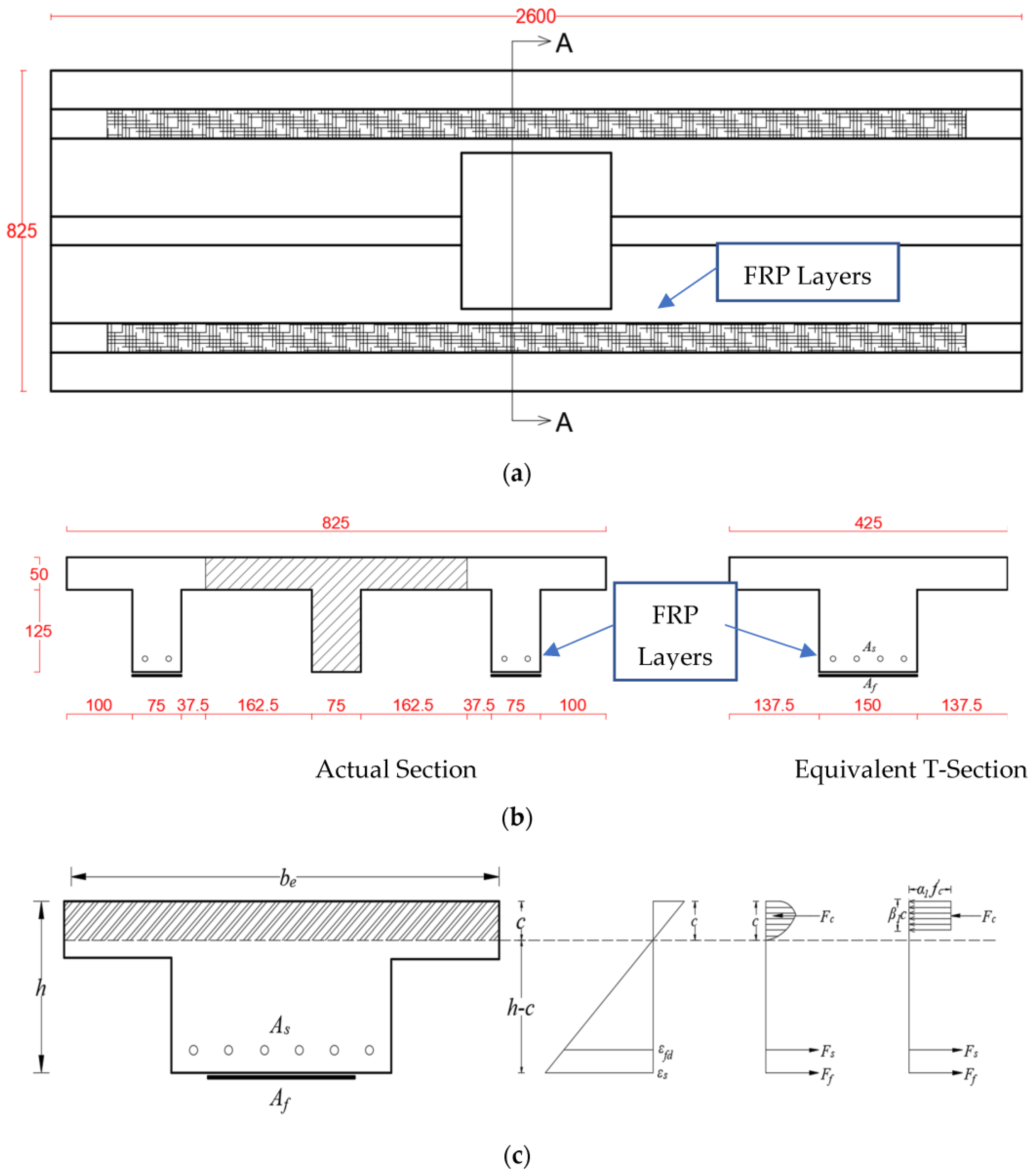
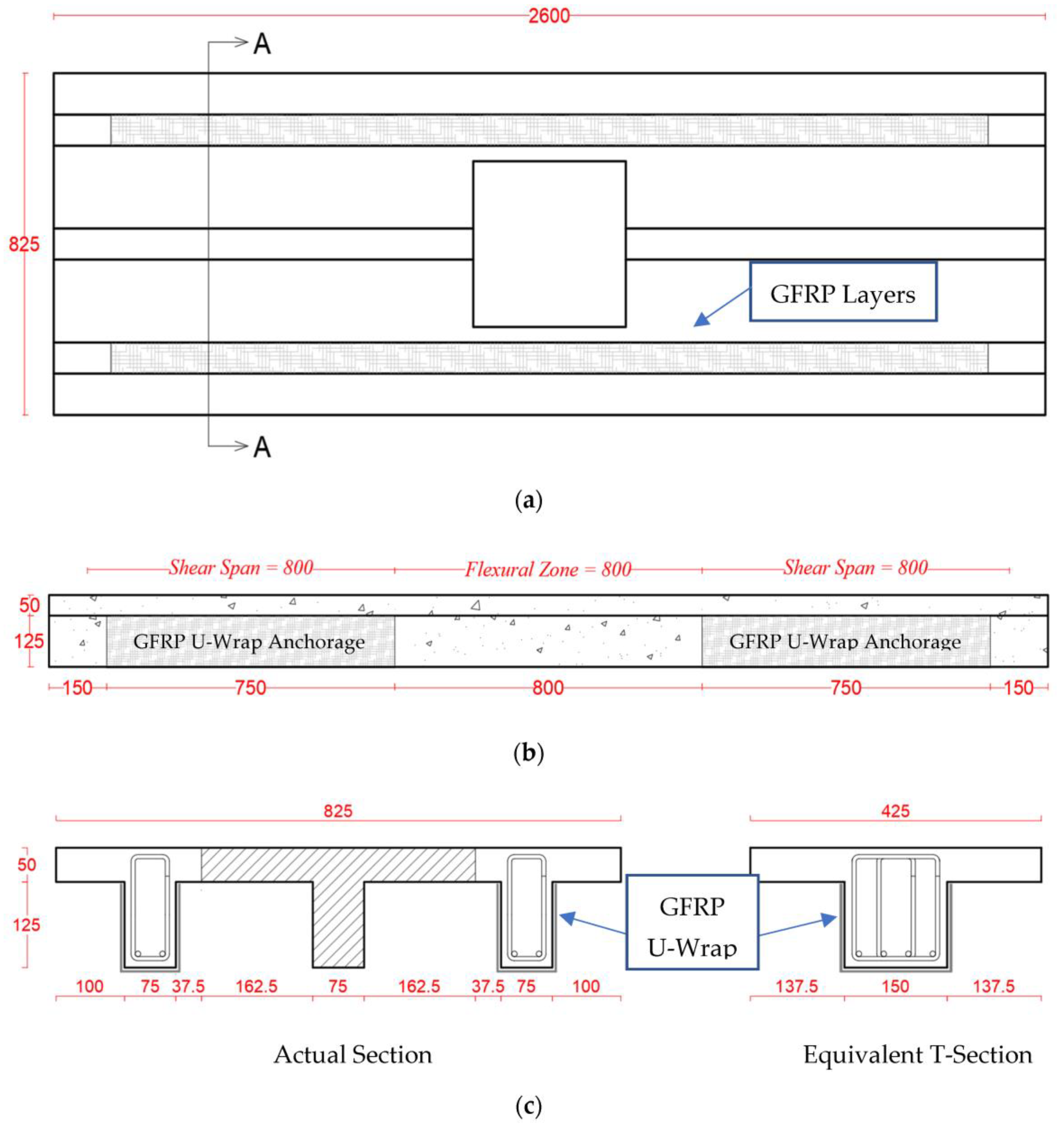
2.2. Strengthening Schemes
2.3. Properties of Constituent Materials
2.4. Preparation of Slab Specimens
2.5. Test Setup
3. Results and Discussion
3.1. Failure Modes
3.1.1. Control Specimen without Opening (S-C)
3.1.2. Control Specimen with Flexure Opening (S-FO-C)
3.1.3. CFRP-Strengthened Specimen (S-FO-S1)
3.1.4. CFRP-Strengthened Specimen (S-FO-S2)
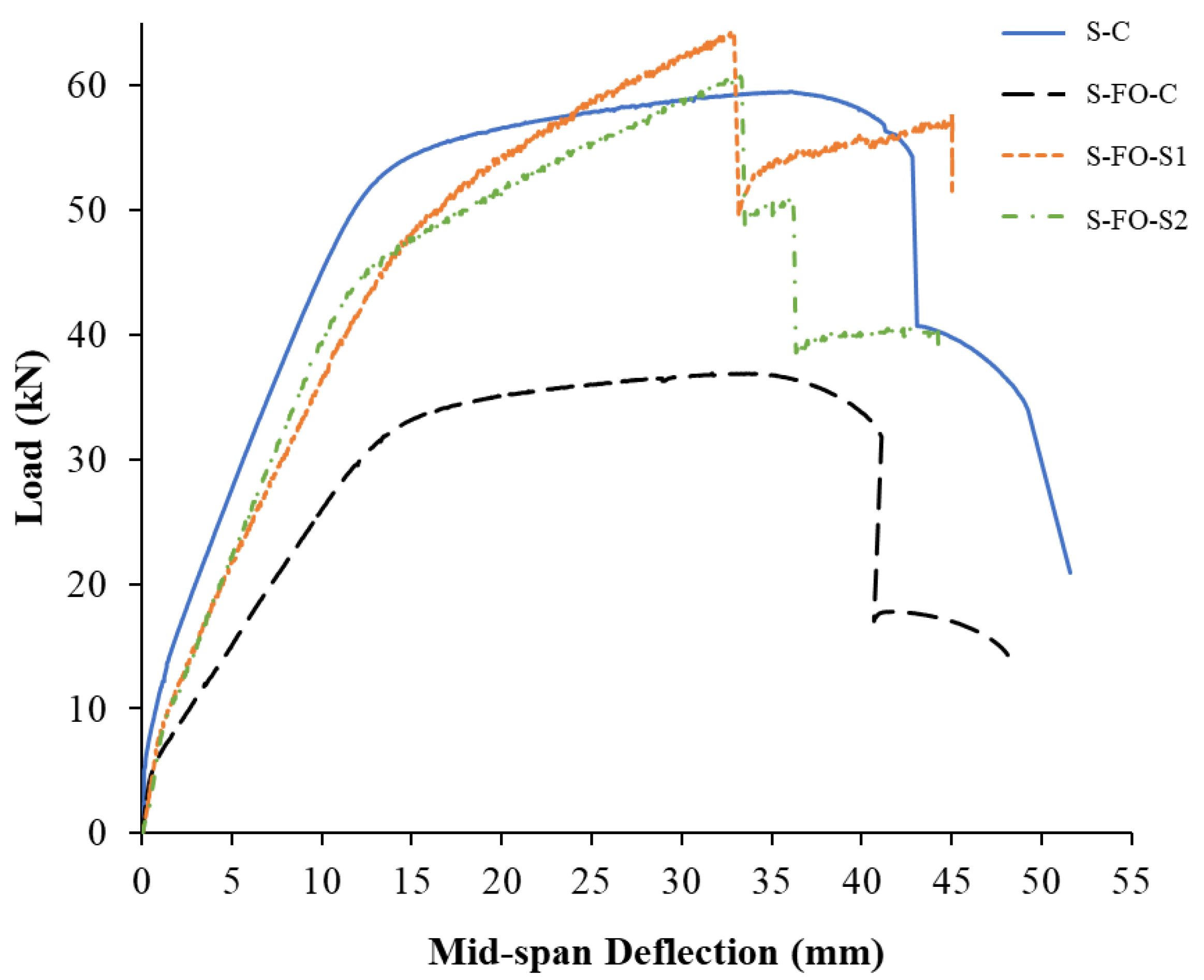
3.2. Relationships of Load versus Mid-Span Deflection
3.2.1. Control Specimen without Opening (S-C)
3.2.2. Control Specimen with Flexure Opening (S-FO-C)
3.2.3. CFRP-Strengthened Specimen (S-FO-S1)
3.2.4. GFRP-Strengthened Specimen (S-FO-S2)
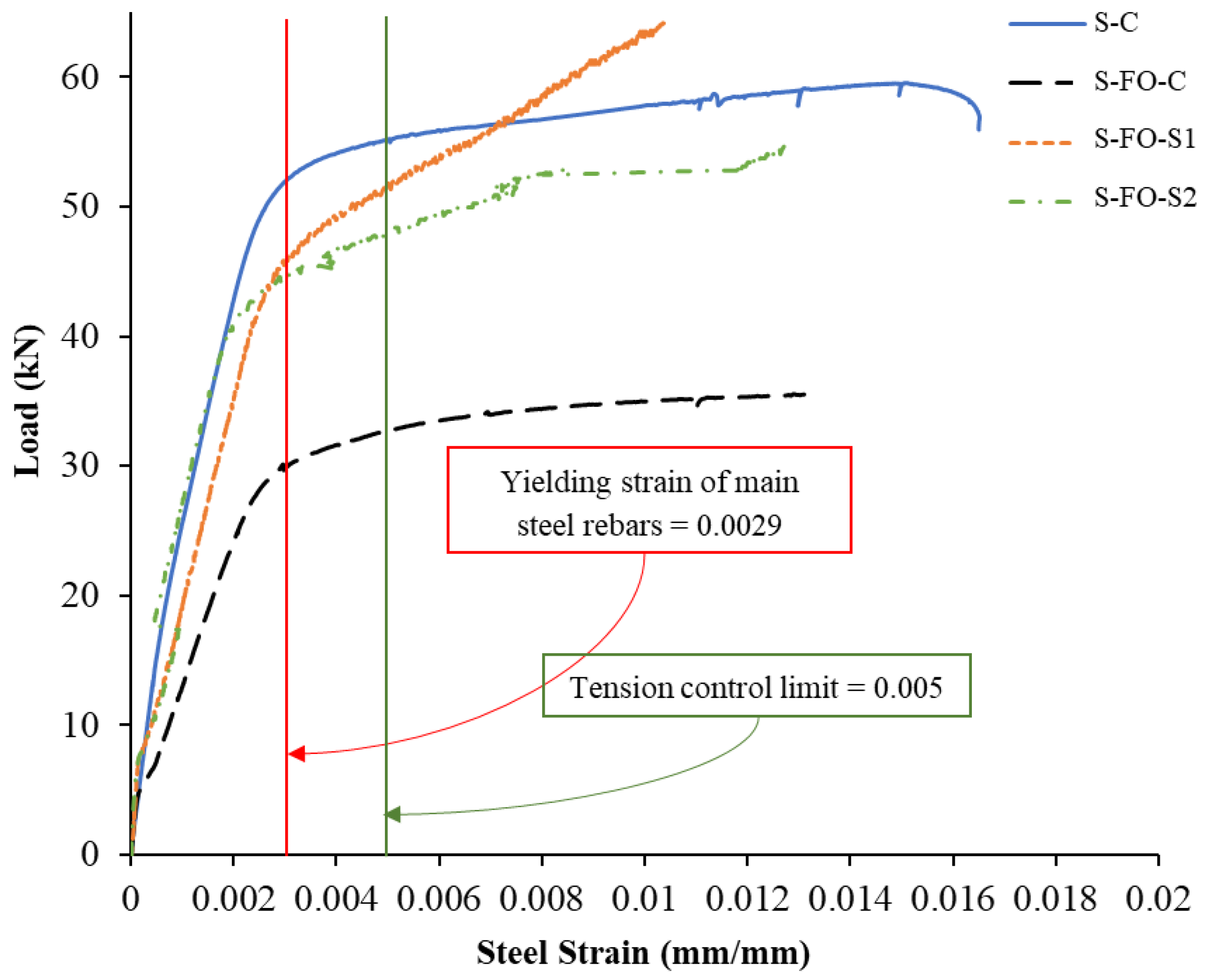
3.3. Relationships of Load versus Strain
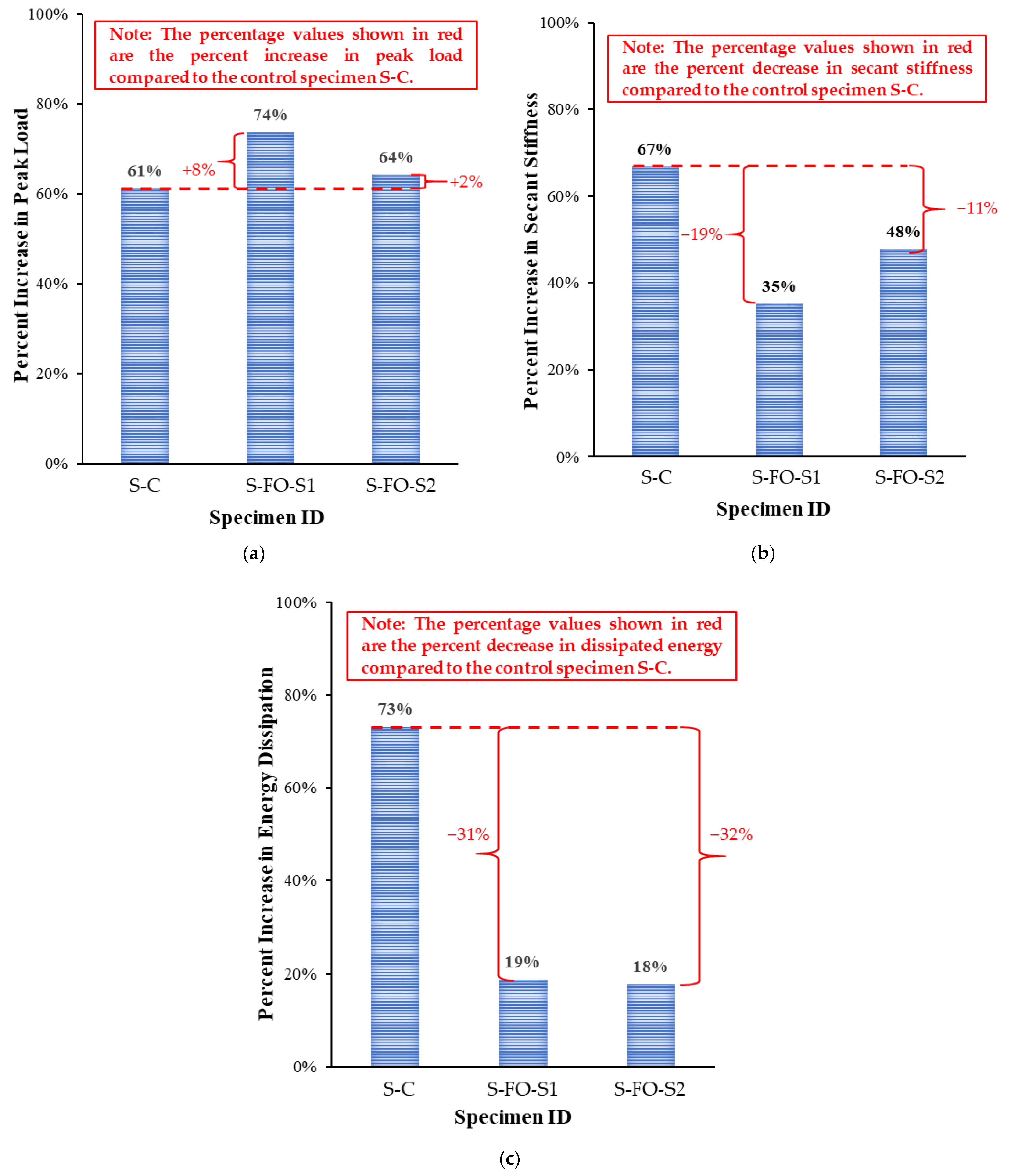
3.4. Comparison of Experimental Results
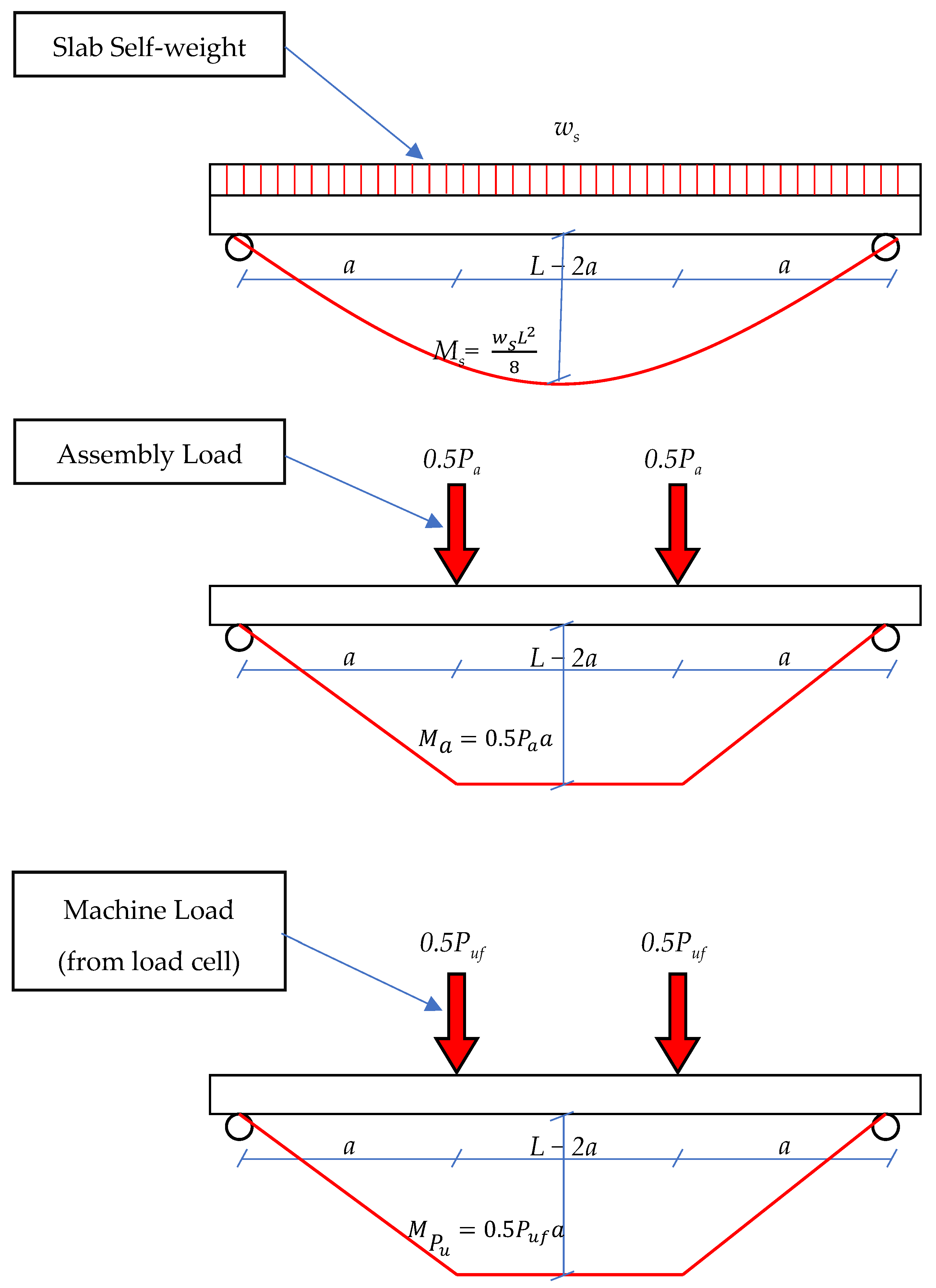
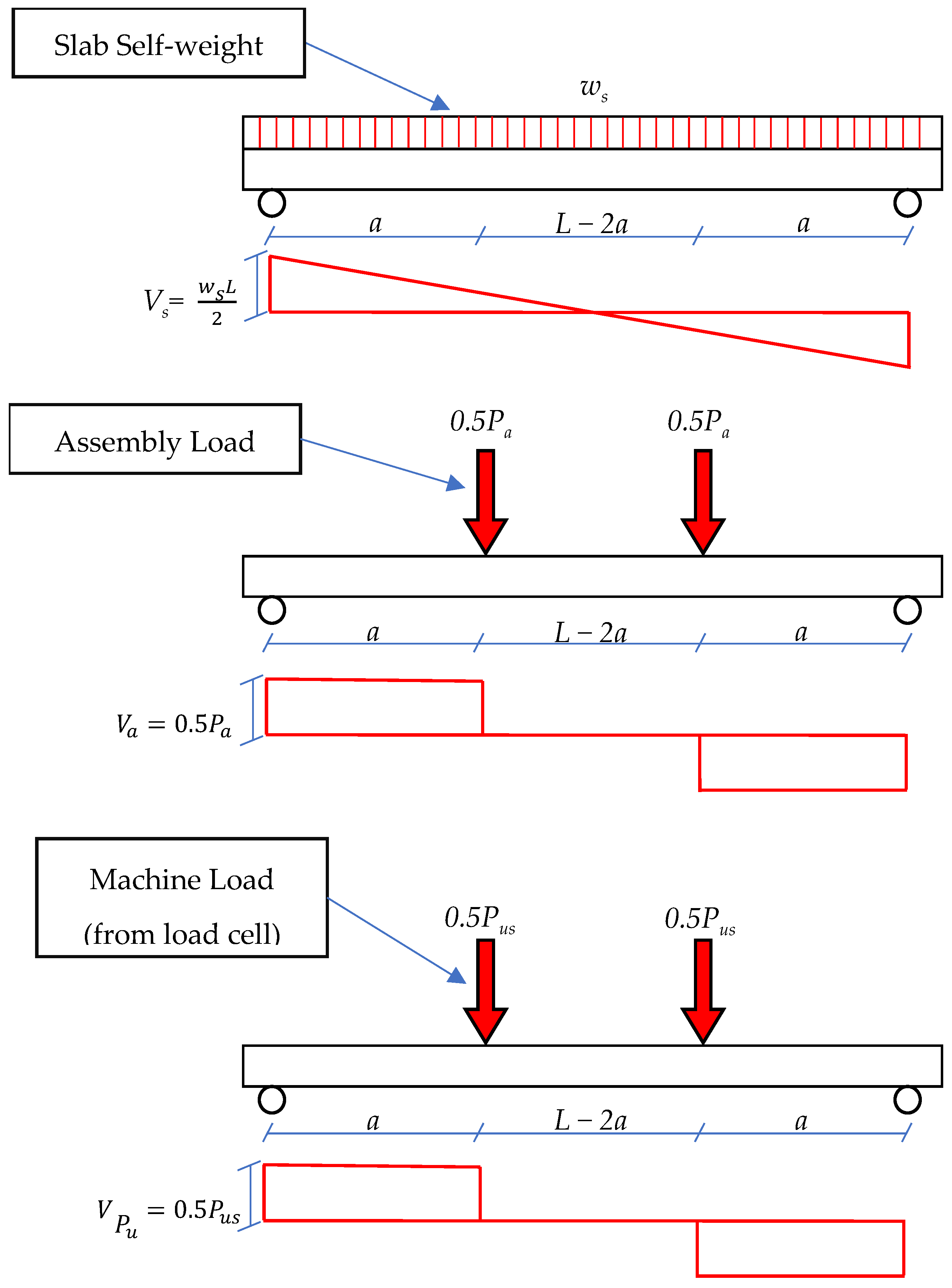
4. Analytical Modeling
4.1. Control Specimen without Opening (S-C)
4.1.1. Calculation of Flexural Capacity
4.1.2. Calculation of Shear Capacity
4.2. Control Specimen with Flexure Opening (S-FO-C)
4.3. FRP-Strengthened Specimens S-FO-S1 and S-FO-S2
4.3.1. Calculation of Flexural Capacity
4.3.2. Calculation of Shear Capacity
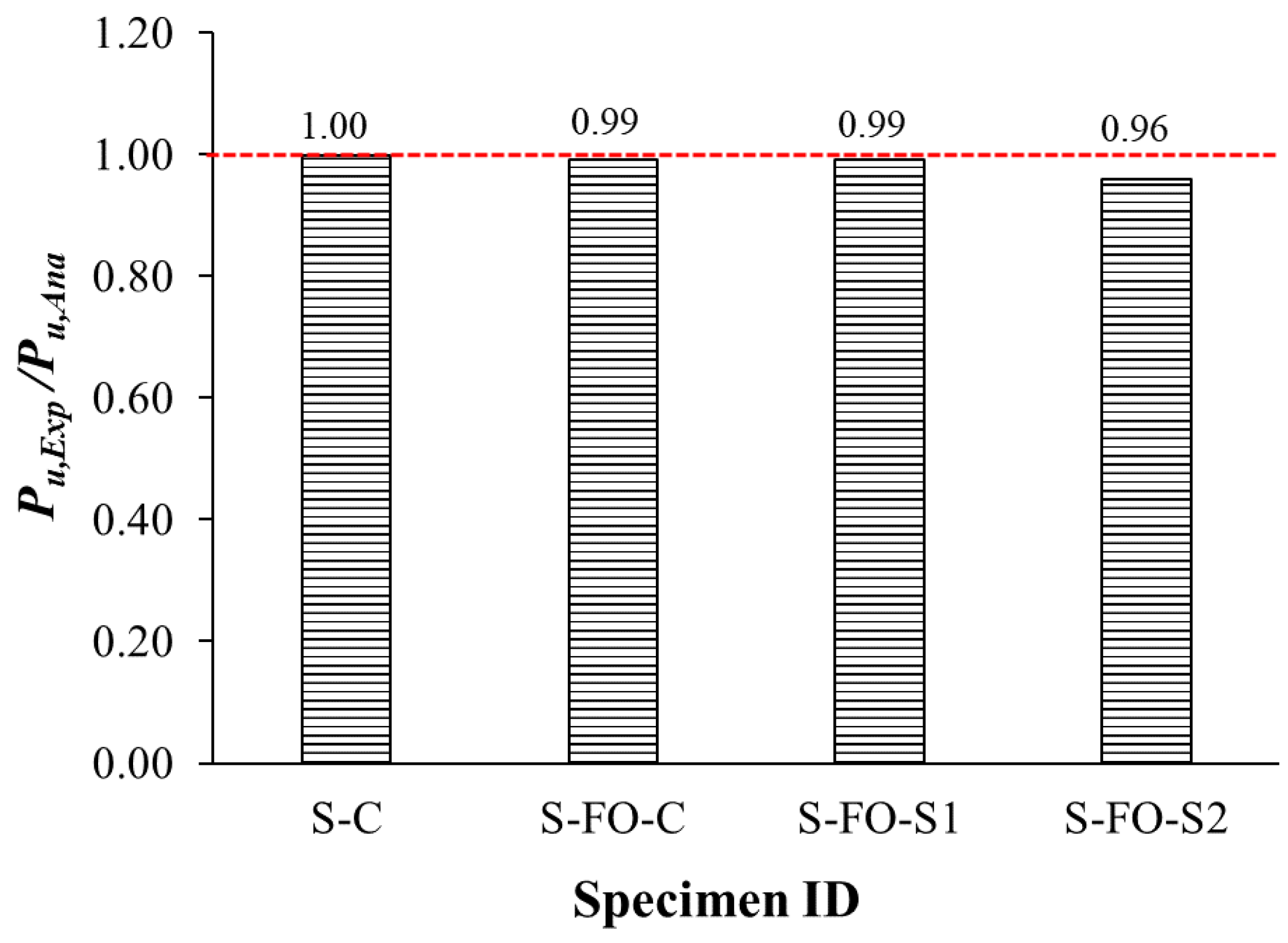
4.4. Experimental versus Analytical Peak Loads
5. Conclusions
- Both control specimen without opening and control slab with flexure opening were found to have common failure modes, which are flexure failure by fracture of steel rebars followed by crushing of concrete on the compression zone. The failure of both strengthened specimens was due to rupture in the FRP sheets combined with concrete cover delamination, and it was followed by fracture of bottom tension rebars of ribs and then crushing of concrete on the compression zone.
- The presence of a single opening in the peak-moment region (flexure opening) reduced the slab capacity by about 38% compared with the specimen without an opening. This is attributed to the cutting of the middle rib in the peak-moment region, and hence, the flexural capacity of the specimen was for two ribs only.
- Strengthening of slabs using CFRP and GFRP composite sheets not only fully restored the load-carrying capacity but also slightly enhanced the load-carrying capacity by 8% and 2%, respectively, compared to the control slab without opening.
- Strengthening schemes S1 and S2 revealed an enhancement in stiffness by 35% and 48%, respectively, in comparison with the unstrengthened slab with an opening. However, the stiffness was not restored with respect to the control slab without opening, and it decreased by 19% and 11%, respectively. Also, strengthening schemes S1 and S2 revealed an increase in the energy dissipated in slab failure by 19% and 18%, respectively, compared with the unstrengthened specimen with an opening. Nevertheless, the dissipated energy was not fully restored in comparison with the control slab without opening, and it decreased by 31% and 32%, respectively.
- Simplified analytical models were suggested in this research for computing the ultimate load of both unstrengthened and strengthened slabs. The models considered all possible flexural and shear failure modes at the critical sections. The analytical procedure predicted the ultimate load of the specimens very well, with prediction errors not exceeding 4%.
- Although the adopted strengthening schemes were efficient enough to restore the load-carrying capacity of ribbed slab having flexure opening located in the maximum-moment region, there is a need to assess the effectiveness of these schemes when the openings are cut in the shear zone.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hadjazi, K.; Sereir, Z.; Amziane, S. Creep response of intermediate flexural cracking behavior of reinforced concrete beam strengthened with an externally bonded FRP plate. Int. J. Solids Struct. 2016, 94, 196–205. [Google Scholar] [CrossRef]
- Barris, C.; Sala, P.; Gómez, J.; Torres, L. Flexural behaviour of FRP reinforced concrete beams strengthened with NSM CFRP strips. Compos. Struct. 2020, 241, 112059. [Google Scholar] [CrossRef]
- Elsanadedy, H.M.; Abbas, H.; Almusallam, T.H.; Al-Salloum, Y.A. Hybrid UHPC/NSM CFRP strips vs. traditional systems for flexural upgrading of RC beams–Experimental and FE study. Compos. Struct. 2020, 261, 113291. [Google Scholar] [CrossRef]
- Zhang, F.; Gao, L.; Wu, Y.F.; Liu, J. Flexural design of reinforced concrete structures strengthened with hybrid bonded FRP. Compos. Struct. 2021, 269, 113996. [Google Scholar] [CrossRef]
- Askar, M.K.; Hassan, A.F.; Al-Kamaki, Y.S. Flexural and shear strengthening of reinforced concrete beams using FRP composites: A state of the art. Case Stud. Constr. Mater. 2022, 17, e01189. [Google Scholar] [CrossRef]
- Hadi, S. Full-scale experimental evaluation of flexural strength and ductility of reinforced concrete beams strengthened with various FRP mechanisms. Structures 2022, 43, 1160–1176. [Google Scholar] [CrossRef]
- Al-Salloum, Y.A.; Siddiqui, N.A.; Elsanadedy, H.M.; Abadel, A.A.; Aqel, M.A. Textile reinforced mortar (TRM) versus FRP as strengthening material of seismically deficient RC beam-column joints. ASCE J. Compos. Constr. 2011, 15, 875–1002. [Google Scholar] [CrossRef]
- Almusallam, T.; Al-Salloum, Y.; Elsanadedy, H.; Alshenawy, A.; Iqbal, R. Behavior of FRP-Strengthened RC Beams with Large Rectangular Web Openings in Flexure Zones: Experimental and Numerical Study. Int. J. Concr. Struct. Mater. 2018, 12, 47. [Google Scholar] [CrossRef]
- Elsanadedy, H.M.; Al-Salloum, Y.A.; Almusallam, T.H.; Alshenawy, A.O.; Abbas, H. Experimental and numerical study on FRP-upgraded RC beams with large rectangular web openings in shear zones. Constr. Build. Mater. 2019, 194, 322–343. [Google Scholar] [CrossRef]
- fib bulletin 14. In Externally Bonded FRP Reinforcement for RC Structures; Technical Report prepared by the Working Party EBR of Task Group 9.3; International Federation for Structural Concrete: Lausanne, Switzerland, 2001.
- Modrea, A.; Vlase, S.; Calin, M.R.; Peterlicean, A. The influence of dimensional and structural shifts of the elastic constant values in cylinder fiber composites. J. Optoelecton. Adv. Mater. 2013, 15, 278–283. [Google Scholar]
- Teodorescu-Draghicescu, H.; Vlase, S.; Scutaru, L.; Serbina, L.; Calin, M.R. Hysteresis effect in a three-phase polymer matrix composite subjected to static cyclic loadings. Optoelectron. Adv. Mater-Rapid Commun. 2011, 5, 273–277. [Google Scholar]
- Zhu, Y.; Zhang, Y.; Hussein, H.H.; Chen, G. Flexural strengthening of reinforced concrete beams or slabs using ultra-high performance concrete (UHPC): A state of the art review. Eng. Struct. 2020, 205, 110035. [Google Scholar] [CrossRef]
- Baig, Z.I.; Alsayed, S.H.; Abbas, H. Punching of slab–column connections strengthened using external steel shear bolts. Mag. Concr. Res. 2016, 68, 55–68. [Google Scholar] [CrossRef]
- Zheng, X.; Wan, B.; Huang, P.; Huang, J. Experimental study of hybrid strengthening technique using carbon fiber laminates and steel plates for reinforced concrete slabs. Constr. Build. Mater. 2019, 210, 324–337. [Google Scholar] [CrossRef]
- Kim, H.Y.; You, Y.J.; Ryu, G.S.; Koh, K.T.; Ahn, G.H.; Kang, S.H. Flexural strengthening of concrete slab-type elements with textile reinforced concrete. Materials 2020, 13, 2246. [Google Scholar] [CrossRef] [PubMed]
- El-Mandouh, M.A.; Elsamak, G.; Rageh, B.O.; Hamoda, A.; Abdelazeem, F. Experimental and numerical investigation of one-way reinforced concrete slabs using various strengthening systems. Case Stud. Constr. Mater. 2023, 18, e01691. [Google Scholar] [CrossRef]
- Zainal, S.I.; Hejazi, F.; Mafaileh, A.M. Strengthening of Reinforced Concrete slabs using macro and micro synthetic fibers. Structures 2023, 51, 1579–1590. [Google Scholar] [CrossRef]
- Vasquez, A.; Karbhari, V. Fiber reinforced polymer composite strengthening of concrete slabs with cutouts. ACI Struct. J. 2003, 100, 665–673. [Google Scholar]
- Tan, K.; Zhao, H. Strengthening of opening in one-way reinforced concrete slabs using carbon fiber-reinforced polymer systems. ASCE J. Compos. Constr. 2004, 8, 393–401. [Google Scholar] [CrossRef]
- Smith, S.T.; Kim, S.J. Strengthening of one-way spanning RC slabs with cutouts using FRP Composites. Constr. Build. Mater. 2009, 23, 1578–1590. [Google Scholar] [CrossRef]
- Seliem, H.M.; Seracino, R.; Sumner, E.A.; Smith, S.T. Case study on the restoration of flexural capacity of continuous one-way RC slabs with cutouts. ASCE J. Compos. Constr. 2011, 15, 992–998. [Google Scholar] [CrossRef]
- Anil, Ö.; Kaya, N.; Arslan, O. Strengthening of one-way RC slab with opening using CFRP strips. Constr. Build. Mater. 2013, 48, 883–893. [Google Scholar] [CrossRef]
- Floruţ, S.C.; Sas, G.; Popescu, C.; Stoian, V. Tests on reinforced concrete slabs with cut-out openings strengthened with fibre-reinforced polymers. Compos. Part B-Eng. 2014, 66, 484–493. [Google Scholar] [CrossRef]
- Victor, J.M.; Syed, S. Analytical study on strengthening of waffle slab with opening using CFRP sheets and stiffening ribs. Int. Res. J. Eng. Technol. 2016, 3, 239–243. [Google Scholar]
- Shehab, H.K.; Eisa, A.S.; El-Awady, K.A. Strengthening of cutouts in existing one-way spanning R. C. flat slabs using CFRP sheets. Int. J. Concr. Struct. Mater. 2017, 11, 327–341. [Google Scholar] [CrossRef]
- Mahlis, M.; Shoeib, A.E.; Elnaby, S.A.; Sherif, A. The effect of cutting openings on the behavior of two-way solid loaded slabs. Structures 2018, 16, 137–149. [Google Scholar] [CrossRef]
- Eskandarinadaf, A.; Esfahani, M.R. Strengthening of two-way RC slabs with central opening. KSCE J. Civ. Eng. 2019, 23, 1228–1235. [Google Scholar] [CrossRef]
- Golham, M.A.; Al-Ahmed, A.H. Behavior of GFRP reinforced concrete slabs with openings strengthened by CFRP strips. Results Eng. 2023, 18, 101033. [Google Scholar] [CrossRef]
- Choi, Y.; Park, I.H.; Kang, S.G.; Cho, C.G. Strengthening of RC slabs with symmetric openings using GFRP composite beams. Polymers 2013, 5, 1352–1361. [Google Scholar] [CrossRef]
- ACI 440.2R-17; Guide for the Design and Construction of Externally Bonded FRP Systems for Strengthening Concrete Structures. American Concrete Institute: Farmington Hills, MI, USA, 2017.
- ASTM C39/C39M; Standard Test Method for Compressive Strength of Cylindrical. ASTM: West Conshohocken, PA, USA, 2018.
- ASTM E8/E8M; Standard Test Methods for Tension Testing of Metallic Materials. ASTM: West Conshohocken, PA, USA, 2016.
- ASTM D3039/D3039M; Standard Test Method for Tensile Properties of Polymer Matrix Composite Materials. ASTM: West Conshohocken, PA, USA, 2017.
- Almusallam, T.H.; Elsanadedy, H.M.; Al-Salloum, Y.A. Effect of longitudinal steel ratio on behavior of RC beams strengthened with FRP composites—Experimental and FE study. ASCE J. Compos. Constr. 2014, 19, 486. [Google Scholar] [CrossRef]
- Elsanadedy, H.M.; Abbas, H.; Al-Salloum, Y.A.; Almusallam, T.H. Prediction of intermediate crack debonding strain of externally bonded FRP laminates in RC beams and one-way slabs. ASCE J. Compos. Constr. 2014, 18, 04014008. [Google Scholar] [CrossRef]
- NZS 4203; Code of Practice for General Structural Design and Design Loadings for Buildings 1. New Zealand Standard (NZS): Wellington, New Zealand, 1992.
- ACI 318-19; Building Code Requirements for Structural Concrete and Commentary. American Concrete Institute: Detroit, MI, USA, 2019.












| Specimen ID | Opening Presence | No. of Openings and Location | Strengthening | No. of Specimens |
|---|---|---|---|---|
| S-C | None | None | Control | 1 |
| S-FO-C | Yes | Single–Mid-span | Control | 1 |
| S-FO-S1 | Yes | Single–Mid-span | Scheme-1: CFRP sheets | 1 |
| S-FO-S2 | Yes | Single–Mid-span | Scheme-2: GFRP sheets | 1 |
| Concrete | ||
|---|---|---|
| Average compressive strength after 28 days | 38 MPa | |
| 40 MPa | ||
| Steel reinforcement | ||
| Bar diameter | Yield strength | Ultimate strength |
| Ø 6 mm | 400 MPa | 447 MPa |
| Ø 8 mm | 580 MPa | 629 MPa |
| FRP composite system | ||
| CFRP | GFRP | |
| Elastic modulus of FRP laminates | 70 GPa | 25 GPa |
| Fracture strain | 0.015 | 0.0168 |
| Ultimate tensile strength | 1126.6 MPa | 422 MPa |
| Thickness per layer | 0.6 mm | 0.56 mm |
| Specimen ID | Pcr (kN) | Py (kN) | Pu (kN) | Δcr (mm) | Δy (mm) | Δpu (mm) | Δu (mm) | ks (kN/mm) | Eu (kN.mm) | μΔ |
|---|---|---|---|---|---|---|---|---|---|---|
| S-C | 5.1 | 51.6 | 59.6 | 0.1 | 12.5 | 36.4 | 43.1 | 4.12 | 2136 | 3.4 |
| S-FO-C | 4.6 | 30.1 | 36.9 | 0.4 | 12.2 | 31.7 | 41.1 | 2.47 | 1234 | 3.4 |
| S-FO-S1 | 7.3 | 45.9 | 64.2 | 0.8 | 13.7 | 32.7 | 33.2 | 3.34 | 1465 | 2.4 |
| S-FO-S2 | 7.6 | 44.9 | 60.7 | 1.0 | 12.3 | 33.1 | 33.6 | 3.65 | 1451 | 2.7 |
| Specimen ID | Strain in Bottom Steel Rebars at Peak Load | Peak Strain in Bottom Steel Rebars | Peak Strain in FRP Sheets |
|---|---|---|---|
| S-C | 0.0156 | 0.0168 | - |
| S-FO-C | 0.0131 | 0.0132 | - |
| S-FO-S1 | 0.0104 | 0.0134 | 0.0103 |
| S-FO-S2 | 0.0128 | 0.0144 | 0.0144 |
| Specimen ID | Pu,Exp (kN) | Puf,Ana (kN) | Pus,Ana (kN) | Pu,Ana (kN) | Pu,Exp/Pu,Ana |
|---|---|---|---|---|---|
| S-C | 59.6 | 59.7 | 183.5 | 59.7 | 1.00 |
| S-FO-C | 36.9 | 37.2 | 119.8 | 37.2 | 0.99 |
| S-FO-S1 | 64.2 | 64.7 | 119.8 | 64.7 | 0.99 |
| S-FO-S2 | 60.7 | 63.3 | 185.6 | 63.3 | 0.96 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Al Kallas, A.; Elsanadedy, H.; Abbas, H.; Almusallam, T.; Al-Salloum, Y. Performance of FRP-Upgraded RC One-Way Ribbed Slabs with an Opening in Flexure Zone. Buildings 2023, 13, 2260. https://doi.org/10.3390/buildings13092260
Al Kallas A, Elsanadedy H, Abbas H, Almusallam T, Al-Salloum Y. Performance of FRP-Upgraded RC One-Way Ribbed Slabs with an Opening in Flexure Zone. Buildings. 2023; 13(9):2260. https://doi.org/10.3390/buildings13092260
Chicago/Turabian StyleAl Kallas, Amjad, Hussein Elsanadedy, Husain Abbas, Tarek Almusallam, and Yousef Al-Salloum. 2023. "Performance of FRP-Upgraded RC One-Way Ribbed Slabs with an Opening in Flexure Zone" Buildings 13, no. 9: 2260. https://doi.org/10.3390/buildings13092260
APA StyleAl Kallas, A., Elsanadedy, H., Abbas, H., Almusallam, T., & Al-Salloum, Y. (2023). Performance of FRP-Upgraded RC One-Way Ribbed Slabs with an Opening in Flexure Zone. Buildings, 13(9), 2260. https://doi.org/10.3390/buildings13092260






