Review on the Prediction and Control of Structural Vibration and Noise in Buildings Caused by Rail Transit
Abstract
:1. Introduction
2. Measurement Methods
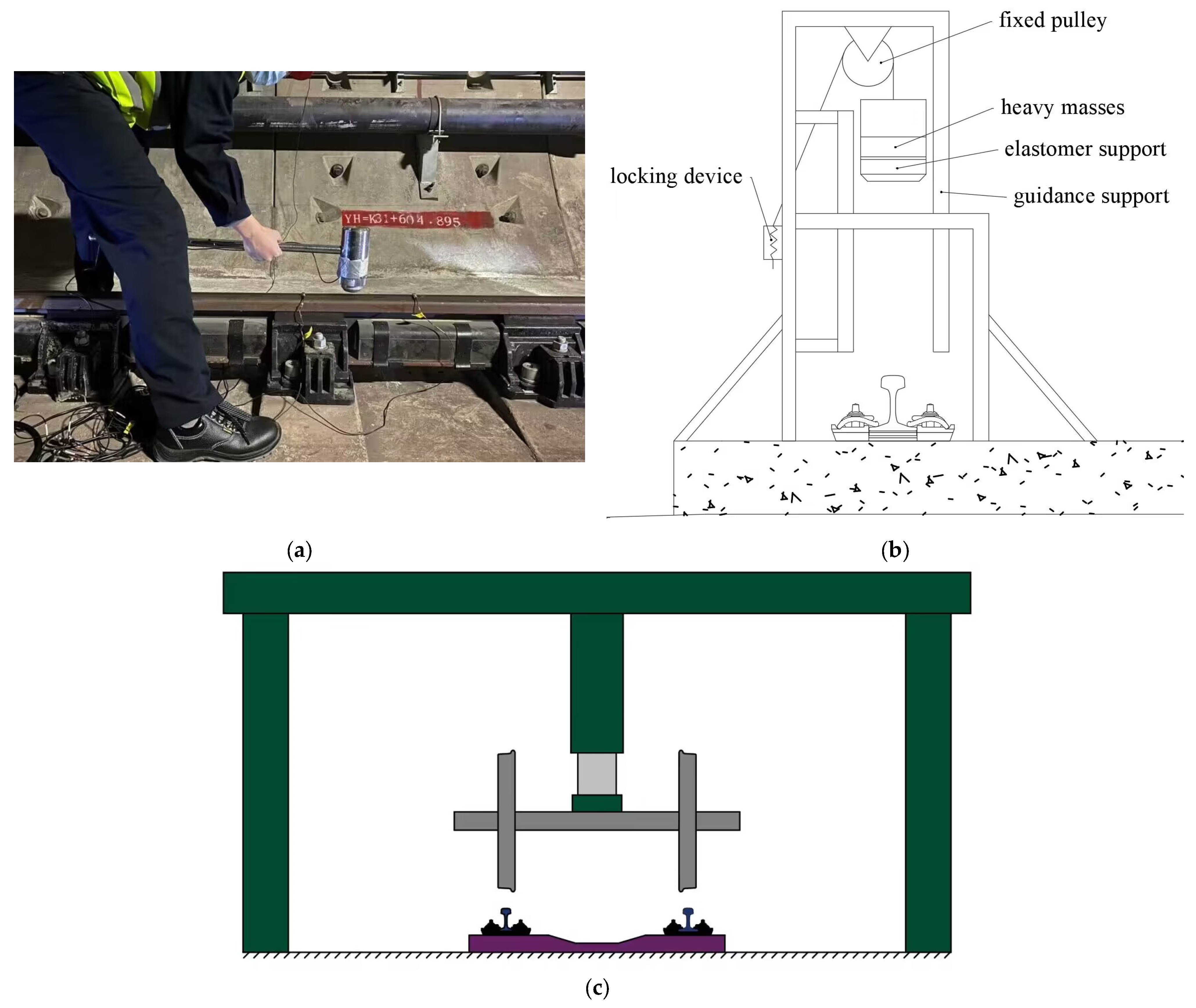
2.1. Fixed-Point Excitation Measurement
2.2. Real-Vehicle Measurement
3. Modelling and Prediction Methods
3.1. Physical Model
- (1)
- Wheel–rail excitation source prediction
- (2)
- Soil layer propagation path modelling
- (a)
- Semi-analytical method (transfer matrix method)
- (b)
- FEM–BEM
- (c)
- FEM–IEM
- (d)
- 2.5D FEM–BEM
- (3)
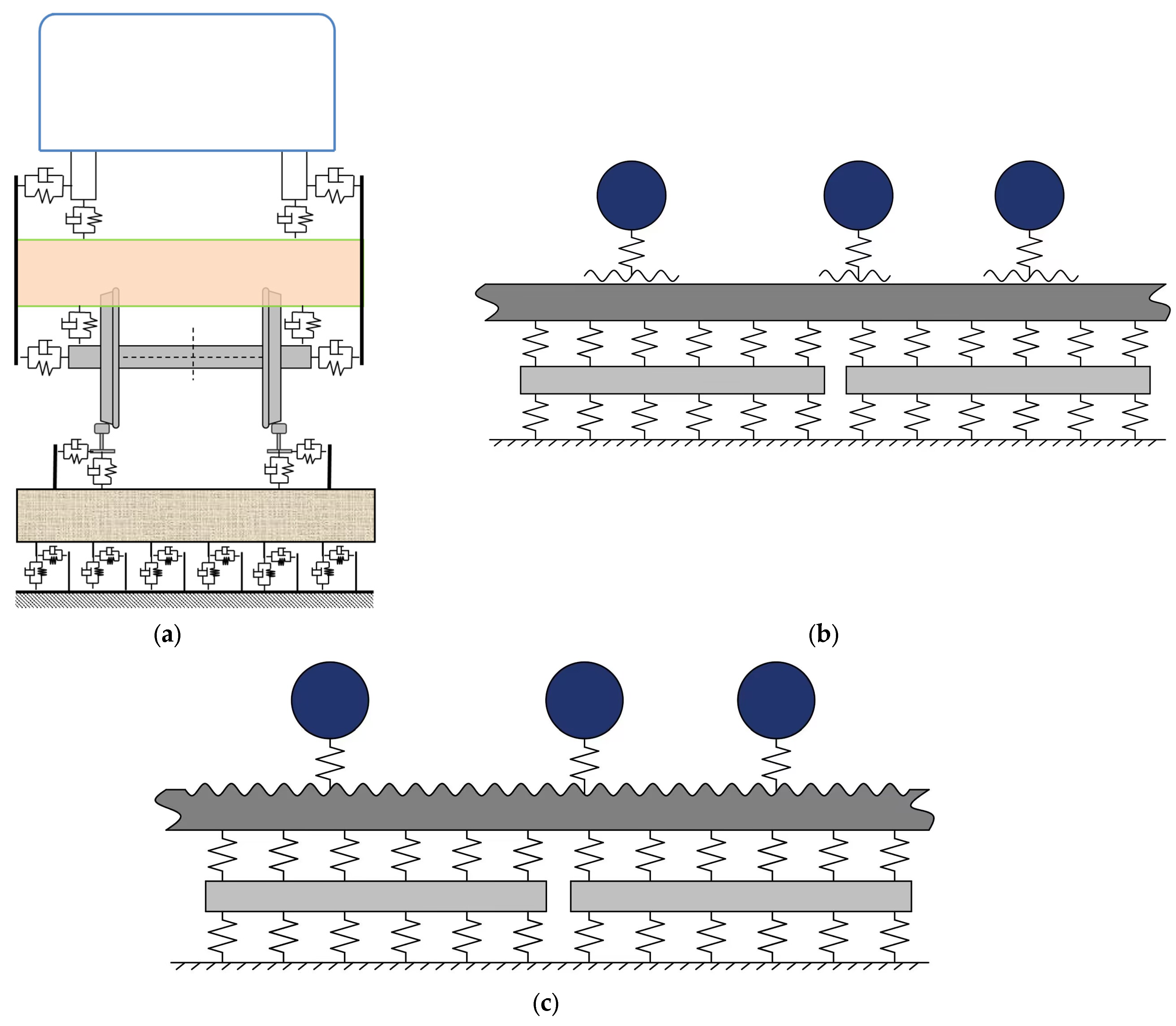
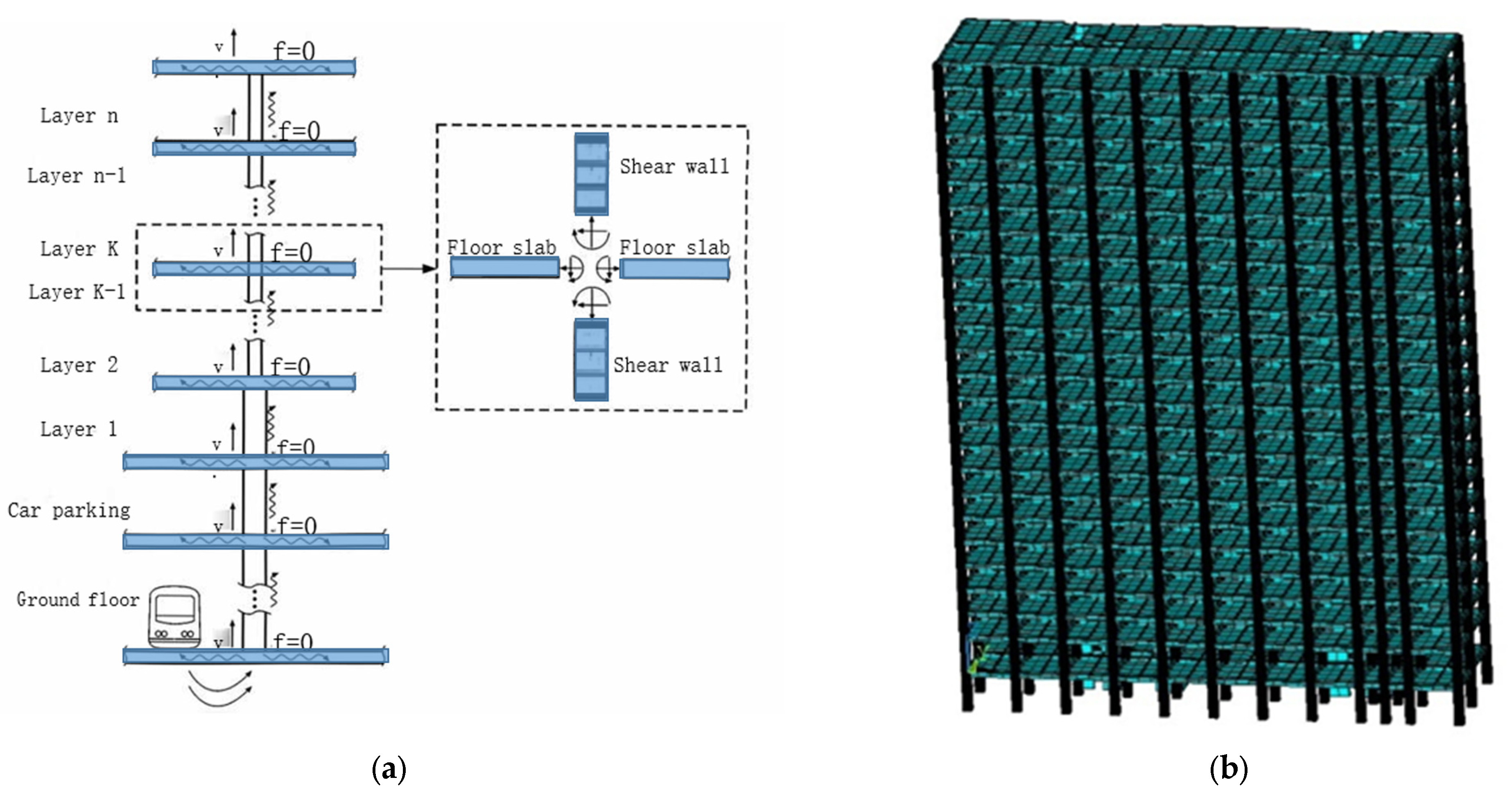
- Modelling of building structures and coupling with soils
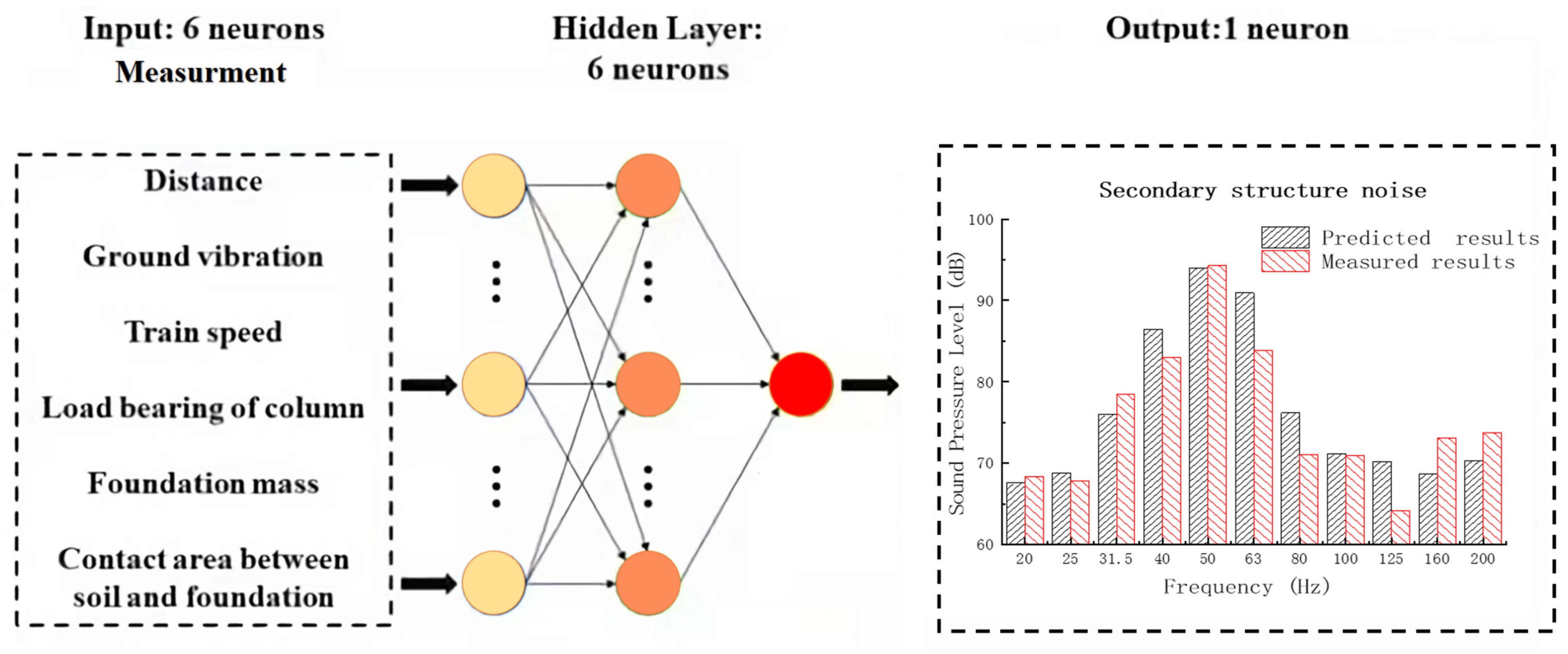
3.2. Data-Driven Model
4. Control Measures
4.1. Excitation Source Control
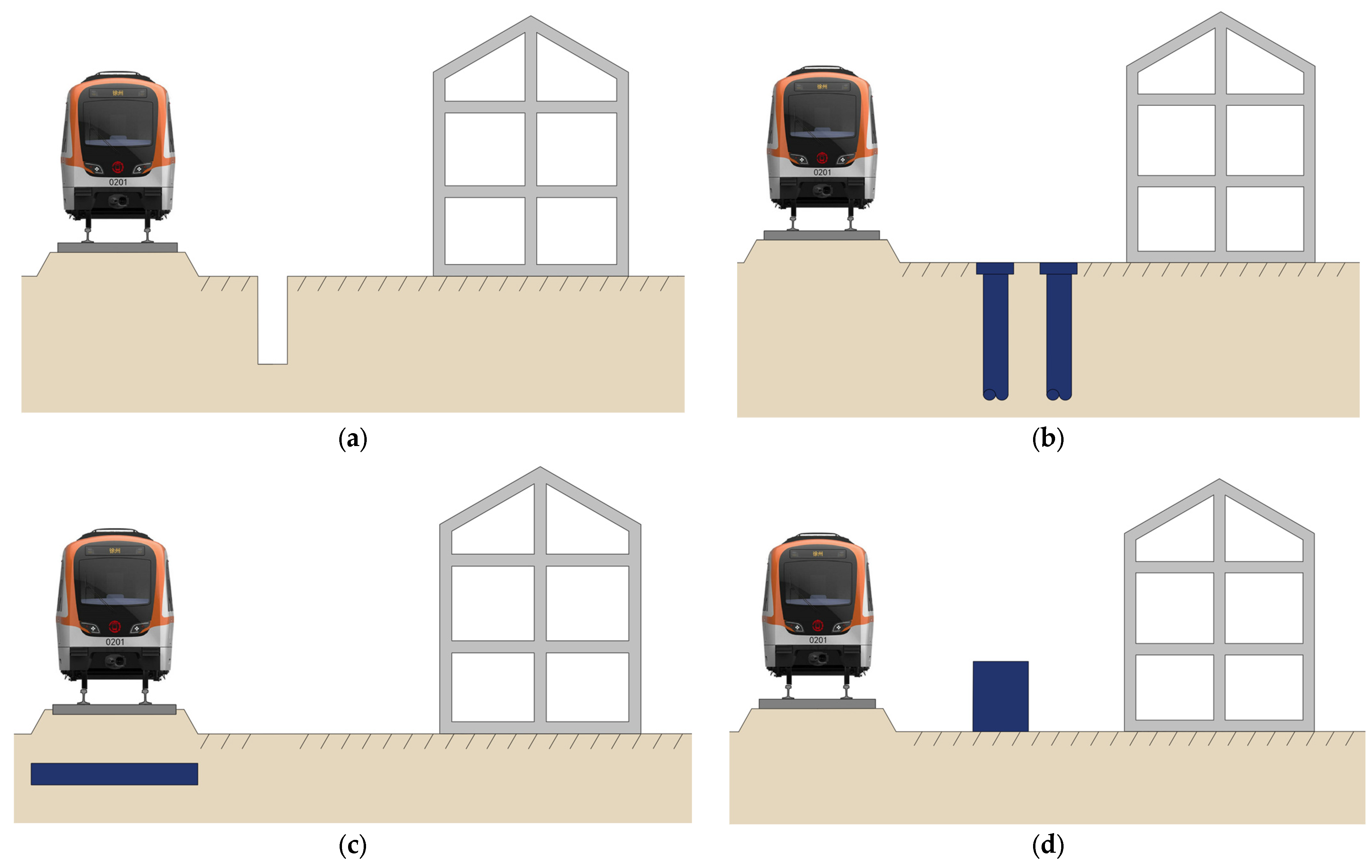
4.2. Propagation Path Control
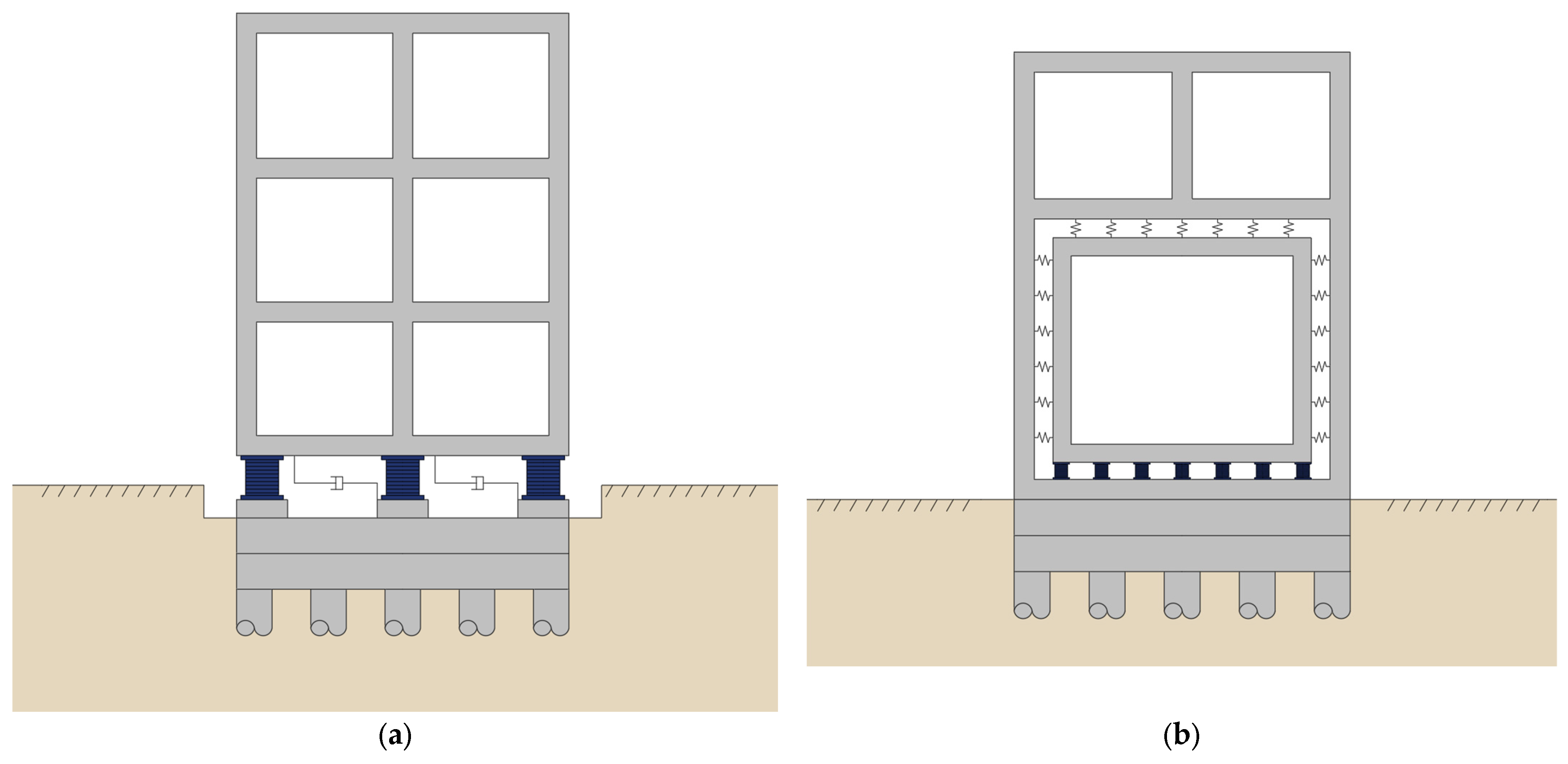
4.3. Receiver Control
5. Conclusions
- (1)
- Since the vehicle–track system is mutually coupled, the introduction of vibration-damping measures will affect the train load to some extent. Laboratory tests are challenged to simulate the vibration and noise reduction situation when the actual train load passes, which could lead to overestimating the vibration damping performance and insertion loss of damping products.
- (2)
- Within 30 m of the subway line, the primary frequencies of environmental vibrations and secondary structural noise induced by trains generally fall between 30 to 80 Hz. Nonetheless, certain segments or structures may exhibit structural resonances or parameter excitations that result in primary frequencies below 30 Hz. Furthermore, as the distance from the central axis of the subway increases, the dominant vibration frequency tends to shift towards lower frequencies.
- (3)
- Field testing is the most direct method to reflect the characteristics of environmental vibration and secondary structural noise in rail transportation, as well as to test the vibration damping and noise reduction performance of damping products. However, it is influenced by various factors, which makes it difficult to achieve single-variable control. It also exhibits a strong random nature, which hinders in-depth mechanistic research. Therefore, reproducibility should be ensured when using field data.
- (4)
- Due to the intricate nature and complexity of structural vibration noise in buildings, the potential of data-driven models remains substantial. However, the fundamental laws that such phenomenon adheres to, along with factors like sample size and the hypothesis testing of the data, still require further investigation.
- (5)
- The principle of low-stiffness fasteners lies in enhancing the system damping ability to achieve a reduction in the amplitude of wheel–rail P2 forces. Therefore, when designing low-stiffness fasteners, special attention should be given to the damping coefficient of the fasteners, and the sole use of low-stiffness fasteners should be avoided to prevent the spread of rail corrugation.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Shen, X.; Wei, H.; Lie, T.T. Management and utilization of urban rail transit regenerative braking energy based on the bypass DC loop. IEEE Trans. Transp. Electrif. 2020, 7, 1699–1711. [Google Scholar] [CrossRef]
- Sheng, X. A review on modelling ground vibrations generated by underground trains. Int. J. Rail Transp. 2019, 7, 241–261. [Google Scholar] [CrossRef]
- Thompson, D.J.; Kouroussis, G.; Ntotsios, E. Modelling, simulation and evaluation of ground vibration caused by rail vehicles. Veh. Syst. Dyn. 2019, 57, 936–983. [Google Scholar] [CrossRef]
- Qiu, Y.; Zou, C.; Wu, J.; Shen, Z.; Zhong, Z. Building vibration measurements induced by train operation on concrete floor. Constr. Build. Mater. 2023, 394, 132283. [Google Scholar] [CrossRef]
- Sheng, X.; Li, M.; Jones, C.J.C.; Thompson, D.J. Using the Fourier-series approach to study interactions between moving wheels and a periodically supported rail. J. Sound Vib. 2007, 303, 873–894. [Google Scholar] [CrossRef]
- He, Y.; Wang, X.; Han, J.; Xiao, X.; Sheng, X. Study on the influence of resilient wheels on vibration and acoustic radiation characteristics of suburban railway concrete box girder bridges. Appl. Acoust. 2022, 187, 108529. [Google Scholar] [CrossRef]
- Ouakka, S.; Verlinden, O.; Kouroussis, G. Railway ground vibration and mitigation measures: Benchmarking of best practices. Railw. Eng. Sci. 2022, 30, 1–22. [Google Scholar] [CrossRef]
- Licitra, G.; Fredianelli, L.; Petri, D.; Vigotti, M.A. Annoyance evaluation due to overall railway noise and vibration in Pisa urban areas. Sci. Total Environ. 2016, 568, 1315–1325. [Google Scholar] [CrossRef]
- Leventhall, H.G. Low frequency noise and annoyance. Noise Health 2004, 6, 59–72. [Google Scholar]
- Petri, D.; Licitra, G.; Vigotti, M.A.; Fredianelli, L. Effects of exposure to road, railway, airport and recreational noise on blood pressure and hypertension. Int. J. Environ. Res. Public Health 2021, 18, 9145. [Google Scholar] [CrossRef]
- Möhler, U. Community response to railway noise: A review of social surveys. J. Sound Vib. 1988, 120, 321–332. [Google Scholar] [CrossRef]
- Bein, T.; Bös, J.; Herold, S.; Mayer, D.; Melz, T.; Thomaier, M. Smart interfaces and semi-active vibration absorber for noise reduction in vehicle structures. Aerosp. Sci. Technol. 2008, 12, 62–73. [Google Scholar] [CrossRef]
- Gürgen, S.; Sofuoğlu, M.A. Smart polymer integrated cork composites for enhanced vibration damping properties. Compos. Struct. 2021, 258, 113200. [Google Scholar] [CrossRef]
- Wang, B.; Kari, L. Modeling and vibration control of a smart vibration isolation system based on magneto-sensitive rubber. Smart Mater. Struct. 2019, 28, 065026. [Google Scholar] [CrossRef]
- Bunn, F.; Zannin, P.H.T. Assessment of railway noise in an urban setting. Appl. Acoust. 2016, 104, 16–23. [Google Scholar] [CrossRef]
- Sadeghi, J.; Vasheghani, M.; Khajehdezfuly, A. Propagation of structure-borne noise in building adjacent to subway lines. Constr. Build. Mater. 2023, 401, 132765. [Google Scholar] [CrossRef]
- Schock, R.W.; Paulson, W.E. A survey of shock and vibration environments in the four major modes of transportation. Shock Vib. Bull. 1965, 35, 1–19. [Google Scholar]
- Degrande, G.; Schevenels, M.; Chatterjee, P.; Velde, W.V.D.; Hölscher, P.; Hopman, V.; Wang, A.; Dadkah, N. Vibrations due to a test train at variable speeds in a deep bored tunnel embedded in London clay. J. Sound Vib. 2006, 293, 626–644. [Google Scholar] [CrossRef]
- Xu, Q.Y.; Ou, X.; Au, F.T.K.; Lou, P.; Xiao, Z.C. Effects of track irregularities on environmental vibration caused by underground railway. Eur. J. Mech.-A/Solids 2016, 59, 280–293. [Google Scholar] [CrossRef]
- Fujikake, T. A prediction method for the propagation of ground vibration from railway trains on level tracks with welded rails. J. Sound Vib. 1986, 128, 524–527. [Google Scholar] [CrossRef]
- Licitra, G.; Artuso, F.; Bernardini, M.; Moro, A.; Fidecaro, F.; Fredianelli, L. Acoustic Beamforming Algorithms and Their Applications in Environmental Noise. Curr. Pollut. Rep. 2023, 1–24. [Google Scholar] [CrossRef]
- Kanka, S.; Fredianelli, L.; Artuso, F.; Fidecaro, F.; Licitra, G. Evaluation of Acoustic Comfort and Sound Energy Transmission in a Yacht. Energies 2023, 16, 808. [Google Scholar] [CrossRef]
- Barré, S.; Ortiz, N.M. Room impulse response measurement and delay-and-sum beamforming, application to room and building acoustics. Proc. Euronoise 2015, 2015, 161–166. [Google Scholar]
- Ortiz, N.M.; Barré, S.; Vonrhein, B. The Acoustic Camera as a valid tool to gain additional information over traditional methods in architectural acoustics. Energy Procedia 2015, 78, 122–127. [Google Scholar] [CrossRef]
- Wang, C.; Lei, X.; Liu, W.; Si, P. Prediction Method of Ground Vibration Caused by High-Speed Railway Based on the Formula from the Federal Transportation Administration. J. Transp. Eng. Part A Syst. 2023, 149, 04023090. [Google Scholar] [CrossRef]
- Kouroussis, G.; Mouzakis, H.P.; Vogiatzis, K.E. Structural impact response for assessing railway vibration induced on buildings. Mech. Ind. 2017, 18, 803. [Google Scholar] [CrossRef]
- Lei, X. Methods for predicting the ambient vibration and noise resulting from rail transit. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2020, 234, 1054–1067. [Google Scholar] [CrossRef]
- Dong, H.; Li, Z.; Gao, L. A railway isolator to preserve the fundamental frequency analysis and test. J. Rubber Res. 2020, 23, 101–109. [Google Scholar] [CrossRef]
- Liu, W.; Liang, R.; Zhang, H.; Wu, Z.; Jiang, B. Deep learning based identification and uncertainty analysis of metro train induced ground-borne vibration. Mech. Syst. Signal Process. 2023, 189, 110062. [Google Scholar] [CrossRef]
- Zhai, W.; He, Z.; Song, X. Prediction of high-speed train induced ground vibration based on train-track-ground system model. Earthq. Eng. Eng. Vib. 2010, 9, 545–554. [Google Scholar] [CrossRef]
- Hao, Y.; Qi, H.; Liu, S.; Nian, V.; Zhang, Z. Study of noise and vibration impacts to buildings due to urban rail transit and mitigation measures. Sustainability 2022, 14, 3119. [Google Scholar] [CrossRef]
- Zou, C.; Wang, Y.; Wang, P.; Guo, J. Measurement of ground and nearby building vibration and noise induced by trains in a metro depot. Sci. Total Environ. 2015, 536, 761–773. [Google Scholar] [CrossRef] [PubMed]
- Qu, S.; Yang, J.; Zhu, S.; Zhai, W.; Kouroussis, G.; Zhang, Q. Experimental study on ground vibration induced by double-line subway trains and road traffic. Transp. Geotech. 2021, 29, 100564. [Google Scholar] [CrossRef]
- Zou, C.; Wang, Y.; Moore, J.A.; Sanayei, M. Train-induced field vibration measurements of ground and over-track buildings. Sci. Total Environ. 2017, 575, 1339–1351. [Google Scholar] [CrossRef] [PubMed]
- Colaço, A.; Castanheira-Pinto, A.; Costa, P.A.; Ruiz, J.F. Combination of experimental measurements and numerical modelling for prediction of ground-borne vibrations induced by railway traffic. Constr. Build. Mater. 2022, 343, 127928. [Google Scholar] [CrossRef]
- Xing, M.; Wang, P.; Zhao, C.; Wu, X.; Kang, X. Ground-borne vibration generated by high-speed train viaduct systems in soft-upper/hard-lower rock strata. J. Cent. South Univ. 2021, 28, 2140–2157. [Google Scholar] [CrossRef]
- Ju, S.H.; Lin, H.T. Experimentally investigating finite element accuracy for ground vibrations induced by high-speed trains. Eng. Struct. 2008, 30, 733–746. [Google Scholar] [CrossRef]
- Ju, S.H.; Lin, H.T.; Chen, T.K. Studying characteristics of train-induced ground vibrations adjacent to an elevated railway by field experiments. J. Geotech. Geoenviron. Eng. 2007, 133, 1302–1307. [Google Scholar] [CrossRef]
- Chen, Y.; Feng, Q.; Liu, Q.; Jiang, J. Experimental study on the characteristics of train-induced vibration in a new structure of metro depot. Environ. Sci. Pollut. Res. 2021, 28, 41407–41422. [Google Scholar] [CrossRef]
- Tao, Z.; Wang, Y.; Sanayei, M.; Moore, J.A.; Zou, C. Experimental study of train-induced vibration in over-track buildings in a metro depot. Eng. Struct. 2019, 198, 109473. [Google Scholar] [CrossRef]
- Liang, R.; Ding, D.; Liu, W.; Sun, F.; Cheng, Y. Experimental study of the source and transmission characteristics of train-induced vibration in the over-track building in a metro depot. J. Vib. Control 2023, 29, 1738–1751. [Google Scholar] [CrossRef]
- Krylov, V.V. Generation of ground vibrations by superfast trains. Appl. Acoust. 1995, 44, 149–164. [Google Scholar] [CrossRef]
- Krylov, V.; Ferguson, C. Calculation of low-frequency ground vibrations from railway trains. Appl. Acoust. 1994, 42, 199–213. [Google Scholar] [CrossRef]
- Madshus, C.; Kaynia, A.M. High-speed railway lines on soft ground: Dynamic behaviour at critical train speed. J. Sound Vib. 2000, 231, 689–701. [Google Scholar] [CrossRef]
- Thompson, D. Railway Noise and Vibration: Mechanisms, Modelling and Means of Control; Elsevier: Amsterdam, The Netherlands, 2008. [Google Scholar]
- Zhai, W.; Xia, H.; Cai, C.; Gao, M.; Li, X.; Guo, X.; Zhang, N.; Wang, K. High-speed train–track–bridge dynamic interactions–Part I: Theoretical model and numerical simulation. Int. J. Rail Transp. 2013, 1, 3–24. [Google Scholar] [CrossRef]
- Zhai, W.; Wang, K.; Cai, C. Fundamentals of vehicle-track coupled dynamics. Veh. Syst. Dyn. 2009, 47, 1349–1376. [Google Scholar] [CrossRef]
- Sheng, X.; Jones, C.J.C.; Petyt, M. The Fourier Transformed Stationary and Moving Dynamic Flexibility Matrices of a Layered Ground; Institute of Sound and Vibration Research: Southampton, UK, 1999. [Google Scholar]
- Chua, K.H.; Balendra, T.; Lo, K.W. Groundborne vibrations due to trains in tunnels. Earthq. Eng. Struct. Dyn. 1992, 21, 445–460. [Google Scholar] [CrossRef]
- Li, Q.; Li, W.Q.; Wu, D.J.; Song, X.D. A combined power flow and infinite element approach to the simulation of medium-frequency noise radiated from bridges and rails. J. Sound Vib. 2016, 365, 134–156. [Google Scholar] [CrossRef]
- Zhang, X.; Li, X.; Hao, H.; Wang, D.; Li, Y. A case study of interior low-frequency noise from box-shaped bridge girders induced by running trains: Its mechanism, prediction and countermeasures. J. Sound Vib. 2016, 367, 129–144. [Google Scholar] [CrossRef]
- Sheng, X.; Jones, C.J.C.; Petyt, M. Ground vibration generated by a harmonic load acting on a railway track. J. Sound Vib. 1999, 225, 3–28. [Google Scholar] [CrossRef]
- Baeza, L.; Ouyang, H. A railway track dynamics model based on modal substructuring and a cyclic boundary condition. J. Sound Vib. 2011, 330, 75–86. [Google Scholar] [CrossRef]
- Baeza, L.; Fayos, J.; Roda, A.; Insa, R. High frequency railway vehicle-track dynamics through flexible rotating wheelsets. Veh. Syst. Dyn. 2008, 46, 647–659. [Google Scholar] [CrossRef]
- Sheng, X.; Jones, C.J.C.; Thompson, D.J. Ground vibration generated by a harmonic load moving in a circular tunnel in a layered ground. J. Low Freq. Noise Vib. Act. Control 2003, 22, 83–96. [Google Scholar] [CrossRef]
- Auersch, L. The excitation of ground vibration by rail traffic: Theory of vehicle-track-soil interaction and measurements on high-speed lines. J. Sound Vib. 2005, 284, 103–132. [Google Scholar] [CrossRef]
- Connolly, D.; Giannopoulos, A.; Forde, M.C. Numerical modelling of ground borne vibrations from high speed rail lines on embankments. Soil Dyn. Earthq. Eng. 2013, 46, 13–19. [Google Scholar] [CrossRef]
- Sheng, X.; Jones, C.J.C.; Thompson, D.J. Modelling ground vibration from railways using wavenumber finite-and boundary-element methods. Phys. Eng. Sci. 2005, 461, 2043–2070. [Google Scholar] [CrossRef]
- Sheng, X.; Jones, C.J.C.; Thompson, D.J. Prediction of ground vibration from trains using the wavenumber finite and boundary element methods. J. Sound Vib. 2006, 293, 575–586. [Google Scholar] [CrossRef]
- Khandelwal, M.; Singh, T.N. Evaluation of blast-induced ground vibration predictors. Soil Dyn. Earthq. Eng. 2007, 27, 116–125. [Google Scholar] [CrossRef]
- Kaynia, A.M.; Madshus, C.; Zackrisson, P. Ground vibration from high-speed trains: Prediction and countermeasure. J. Geotech. Geoenviron. Eng. 2000, 126, 531–537. [Google Scholar] [CrossRef]
- Lysmer, J.; Kuhlemeyer, R.L. Finite dynamic model for infinite media. J. Eng. Mech. Div. 1969, 95, 859–877. [Google Scholar] [CrossRef]
- Yang, Y.B.; Kuo, S.R.; Hung, H.H. Frequency-independent infinite elements for analysing semi-infinite problems. Int. J. Numer. Methods Eng. 1996, 39, 3553–3569. [Google Scholar] [CrossRef]
- Auersch, L. The effect of critically moving loads on the vibrations of soft soils and isolated railway tracks. J. Sound Vib. 2008, 310, 587–607. [Google Scholar] [CrossRef]
- Fiala, P.; Degrande, G.; Augusztinovicz, F. Numerical modelling of ground-borne noise and vibration in buildings due to surface rail traffic. J. Sound Vib. 2007, 301, 718–738. [Google Scholar] [CrossRef]
- Andersen, L.; Nielsen, S.R.K. Reduction of ground vibration by means of barriers or soil improvement along a railway track. Soil Dyn. Earthq. Eng. 2005, 25, 701–716. [Google Scholar] [CrossRef]
- El Kacimi, A.; Woodward, P.K.; Laghrouche, O.; Medero, G. Time domain 3D finite element modelling of train-induced vibration at high speed. Comput. Struct. 2013, 118, 66–73. [Google Scholar] [CrossRef]
- Sheng, X.; Jones, C.; Thompson, D. Moving Green’s functions for a layered circular cylinder of infinite length. ISVR Tech. Memo. 2002, 885, 1–34. [Google Scholar]
- Galvín, P.; François, S.; Schevenels, M.; Bongini, E.; Degrande, G.; Lombaert, G. A 2.5 D coupled FE-BE model for the prediction of railway induced vibrations. Soil Dyn. Earthq. Eng. 2010, 30, 1500–1512. [Google Scholar] [CrossRef]
- Huang, J.; Yuan, T.; Peng, L.; Yu, J.; Ding, Z. Model test on dynamic characteristics of invert and foundation soils of high-speed railway tunnel. Earthq. Eng. Eng. Vib. 2015, 14, 549–559. [Google Scholar] [CrossRef]
- Wang, F.T.; Tao, X.X.; Zheng, X. Inversion of excitation source in ground vibration from urban railway traffic. Sci. China Technol. Sci. 2012, 55, 950–959. [Google Scholar] [CrossRef]
- Colaço, A.; Costa, P.A.; Amado-Mendes, P.; Calcada, R. Vibrations induced by railway traffic in buildings: Experimental validation of a sub-structuring methodology based on 2.5 D FEM-MFS and 3D FEM. Eng. Struct. 2021, 240, 112381. [Google Scholar] [CrossRef]
- Sanayei, M.; Moore, J.A.; Brett, C.R. Measurement and prediction of train-induced vibrations in a full-scale building. Eng. Struct. 2014, 77, 119–128. [Google Scholar] [CrossRef]
- Arcos, R.; Soares, P.J.; Costa, P.A.; Godinho, L. An experimental/numerical hybrid methodology for the prediction of railway-induced ground-borne vibration on buildings to be constructed close to existing railway infrastructures: Numerical validation and parametric study. Soil Dyn. Earthq. Eng. 2021, 150, 106888. [Google Scholar] [CrossRef]
- Sadeghi, J.; Vasheghani, M. Safety of buildings against train induced structure borne noise. Build. Environ. 2021, 197, 107784. [Google Scholar] [CrossRef]
- Yang, Y.B.; Ge, P.; Li, Q.; Liang, X.; Wu, Y. 2.5 D vibration of railway-side buildings mitigated by open or infilled trenches considering rail irregularity. Soil Dyn. Earthq. Eng. 2018, 106, 204–214. [Google Scholar] [CrossRef]
- Nagy, A.B.; Fiala, P.; Márki, F.; Augusztinovicz, F.; Degrande, G.; Jacobs, S.; Brassenx, D. Prediction of interior noise in buildings generated by underground rail traffic. J. Sound Vib. 2006, 293, 680–690. [Google Scholar] [CrossRef]
- Liang, R.; Liu, W.; Li, W.; Wu, Z. A traffic noise source identification method for buildings adjacent to multiple transport infrastructures based on deep learning. Build. Environ. 2022, 211, 108764. [Google Scholar] [CrossRef]
- Li, X.; Chen, Y.; Zou, C.; Wu, J.; Shen, Z.; Chen, Y. Building coupling loss measurement and prediction due to train-induced vertical vibrations. Soil Dyn. Earthq. Eng. 2023, 164, 107644. [Google Scholar] [CrossRef]
- Zhang, Y.; Yuen, K.V. Time-frequency fusion features-based incremental network for smartphone measured structural seismic response classification. Eng. Struct. 2023, 278, 115575. [Google Scholar] [CrossRef]
- Zhang, Y.; Yuen, K.V. Crack detection using fusion features-based broad learning system and image processing. Comput. Aided Civ. Infrastruct. Eng. 2021, 36, 1568–1584. [Google Scholar] [CrossRef]
- Nelson, J.T. Recent developments in ground-borne noise and vibration control. J. Sound Vib. 1996, 193, 367–376. [Google Scholar] [CrossRef]
- Grassie, S.L. Rail irregularities, corrugation and acoustic roughness: Characteristics, significance and effects of reprofiling. J. Rail Rapid Transit 2012, 226, 542–557. [Google Scholar] [CrossRef]
- Mirza, A.A.; Frid, A.; Nielsen, J.; Jones, C. Ground vibration induced by railway traffic-the influence of vehicle parameters. Notes Numer. Fluid Mech. Multidiscip. Des. 2012, 118, 259–266. [Google Scholar]
- Kouroussis, G.; Verlinden, O.; Conti, C. On the interest of integrating vehicle dynamics for the ground propagation of vibrations: The case of urban railway traffic. Veh. Syst. Dyn. 2010, 48, 1553–1571. [Google Scholar] [CrossRef]
- He, Y.; Zhou, Q.; Xu, F.; Sheng, X.; He, Y.; Han, J. An investigation into the effect of rubber design parameters of a resilient wheel on wheel-rail noise. Appl. Acoust. 2023, 205, 109259. [Google Scholar] [CrossRef]
- Wilson, G.P.; Saurenman, H.J.; Nelson, J.T. Control of ground-borne noise and vibration. J. Sound Vib. 1983, 87, 339–350. [Google Scholar] [CrossRef]
- Johansson, A.; Nielsen, J.; Bolmsvik, R.; Karlström, A.; Lundén, R. Under sleeper pads-Influence on dynamic train-track interaction. Wear 2008, 265, 1479–1487. [Google Scholar] [CrossRef]
- Xin, T.; Ding, Y.; Wang, P.; Gao, L. Application of rubber mats in transition zone between two different slab tracks in high-speed railway. Constr. Build. Mater. 2020, 243, 118219. [Google Scholar] [CrossRef]
- Liang, L.; Li, X.; Yin, J.; Wang, D.; Gao, W.; Guo, Z. Vibration characteristics of damping pad floating slab on the long-span steel truss cable-stayed bridge in urban rail transit. Eng. Struct. 2019, 191, 92–103. [Google Scholar] [CrossRef]
- Adam, D.; Vogel, A.; Zimmermann, A. Ground improvement techniques beneath existing rail tracks. Proc. Inst. Civ. Eng. Ground Improv. 2007, 11, 229–235. [Google Scholar] [CrossRef]
- Peplow, A.T.; Kaynia, A.M. Prediction and validation of traffic vibration reduction due to cement column stabilization. Soil Dyn. Earthq. Eng. 2007, 27, 793–802. [Google Scholar] [CrossRef]
- Coulier, P.; François, S.; Degrande, G.; Geert, L. Mitigation of railway induced vibrations using stiff wave barriers. In Proceedings of the 6th International Symposium on Environmental Vibration, Shanghai, China, 8–10 November 2013; Gao, G.Y., Ed.; Department of Civil Engineering: Ghent, Belgium, 2013; pp. 1–34. [Google Scholar]
- Zoccali, P.; Cantisani, G.; Loprencipe, G. Ground-vibrations induced by trains: Filled trenches mitigation capacity and length influence. Constr. Build. Mater. 2015, 74, 1–8. [Google Scholar] [CrossRef]
- François, S.; Schevenels, M.; Thyssen, B.; Borgions, J.; Degrande, G. Design and efficiency of a composite vibration isolating screen in soil. Soil Dyn. Earthq. Eng. 2012, 39, 113–127. [Google Scholar] [CrossRef]
- Takemiya, H.; Fujiwara, A. Wave propagation/impediment in a stratum and wave impeding block (WIB) measured for SSI response reduction. Soil Dyn. Earthq. Eng. 1994, 13, 49–61. [Google Scholar] [CrossRef]
- Jones, C.J.C. Use of numerical models to determine the effectiveness of anti-vibration systems for railways. Inst. Civ. Eng. Transp. 1994, 105, 43–51. [Google Scholar] [CrossRef]
- Hemsworth, B. Reducing groundborne vibrations: State-of-the-art study. J. Sound Vib. 2000, 231, 703–709. [Google Scholar] [CrossRef]
- Fiala, P.; Gupta, S.; Degrande, G.; Augusztinovicz, F. A parametric study on countermeasures to mitigate sub-way traffic induced vibration and noise in buildings. In Proceedings of the ISMA2008 International Conference on Noise and Vibration Engineering, Leuven, Belgium, 15–17 September 2008; Friswell, M.I., Flores, E., Eds.; Railway Dynamics and Ground Vibrations: Leuven, Belgium, 2008; pp. 2751–2764. [Google Scholar]
- Chen, Z.; Peng, S.; Zeng, D.; He, Q.; Tang, J.; Zhang, M. Basement Design for Vibration Reduction of High-Rise Buildings under Metro Operation. KSCE J. Civ. Eng. 2023, 27, 1732–1750. [Google Scholar] [CrossRef]
- Lavassani, S.H.H.; Shangapour, S.; Homami, P.; Gharehbaghi, V.; Farsangi, E.N.; Yang, T.Y. An innovative methodology for hybrid vibration control (MR+TMD) of buildings under seismic excitations. Soil Dyn. Earthq. Eng. 2022, 155, 107175. [Google Scholar] [CrossRef]
- Kaiyu, J.; Jian, W.; Minjie, W.; Chunzheng, D.; Binzhou, C. Forming and machining technology for metamaterials. In Proceedings of the 2022 IEEE MTT-S International Microwave Workshop Series on Advanced Materials and Processes for RF and THz Applications (IMWS-AMP), Guangzhou, China, 27–29 November 2022; pp. 1–3. [Google Scholar]
- Zhang, J.; Yao, D.; Peng, W.; Wang, R.; Li, J.; Guo, S. Optimal design of lightweight acoustic metamaterials for low-frequency noise and vibration control of high-speed train composite floor. Appl. Acoust. 2022, 199, 109041. [Google Scholar] [CrossRef]
- Dai, H.; Zhang, X.; Zheng, Y.; Pei, W.; Zhou, R.; Liu, R.; Gong, Y. Review and prospects of metamaterials used to control elastic waves and vibrations. Front. Phys. 2022, 10, 1179. [Google Scholar] [CrossRef]
- Gao, N.; Zhang, Z.; Deng, J.; Guo, X.; Cheng, B.; Hou, H. Acoustic metamaterials for noise reduction: A review. Adv. Mater. Technol. 2022, 7, 2100698. [Google Scholar] [CrossRef]
- Ning, S.; Yang, F.; Luo, C.; Liu, Z.; Zhuang, Z. Low-frequency tunable locally resonant band gaps in acoustic metamaterials through large deformation. Extrem. Mech. Lett. 2020, 35, 100623. [Google Scholar] [CrossRef]
- Liu, Y.F.; Huang, J.K.; Li, Y.G.; Shi, Z.F. Trees as large-scale natural metamaterials for low-frequency vibration reduction. Constr. Build. Mater. 2019, 199, 737–745. [Google Scholar] [CrossRef]
- Kaewunruen, S.; Martin, V. Life cycle assessment of railway ground-borne noise and vibration mitigation methods using geosynthetics, metamaterials and ground improvement. Sustainability 2018, 10, 3753. [Google Scholar] [CrossRef]








Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, Y.; Zhang, Y.; Yao, Y.; He, Y.; Sheng, X. Review on the Prediction and Control of Structural Vibration and Noise in Buildings Caused by Rail Transit. Buildings 2023, 13, 2310. https://doi.org/10.3390/buildings13092310
He Y, Zhang Y, Yao Y, He Y, Sheng X. Review on the Prediction and Control of Structural Vibration and Noise in Buildings Caused by Rail Transit. Buildings. 2023; 13(9):2310. https://doi.org/10.3390/buildings13092310
Chicago/Turabian StyleHe, Yuanpeng, Yang Zhang, Yuyang Yao, Yulong He, and Xiaozhen Sheng. 2023. "Review on the Prediction and Control of Structural Vibration and Noise in Buildings Caused by Rail Transit" Buildings 13, no. 9: 2310. https://doi.org/10.3390/buildings13092310
APA StyleHe, Y., Zhang, Y., Yao, Y., He, Y., & Sheng, X. (2023). Review on the Prediction and Control of Structural Vibration and Noise in Buildings Caused by Rail Transit. Buildings, 13(9), 2310. https://doi.org/10.3390/buildings13092310






