Modified (Spherical and Cylindrical) Permeation Diffusion Model Considering Deep Bed Filtration Effect
Abstract
:1. Introduction
2. Macroscopic Filtration Model
2.1. Macroscopic Filtration Model
2.2. Influence of Filtration Effect
2.2.1. Slurry Density and Viscosity
2.2.2. Permeability
3. Permeation Diffusion Model Considering Filtration Effect
3.1. Modeling
3.2. The Relation between Slurry Diffusion Radius and Time
3.3. Analytical Solution for a Spherical (Cylindrical) Permeation Model Based on the Linear Filtration Law
3.3.1. Analytical Solution for Cement Volume Fraction and Porosity
3.3.2. Analytical Solution for Pressure Gradient
3.4. Numerical Solution for Infiltration Model Based on Nonlinear Filtration Law
4. Engineering Application
4.1. Project Overview
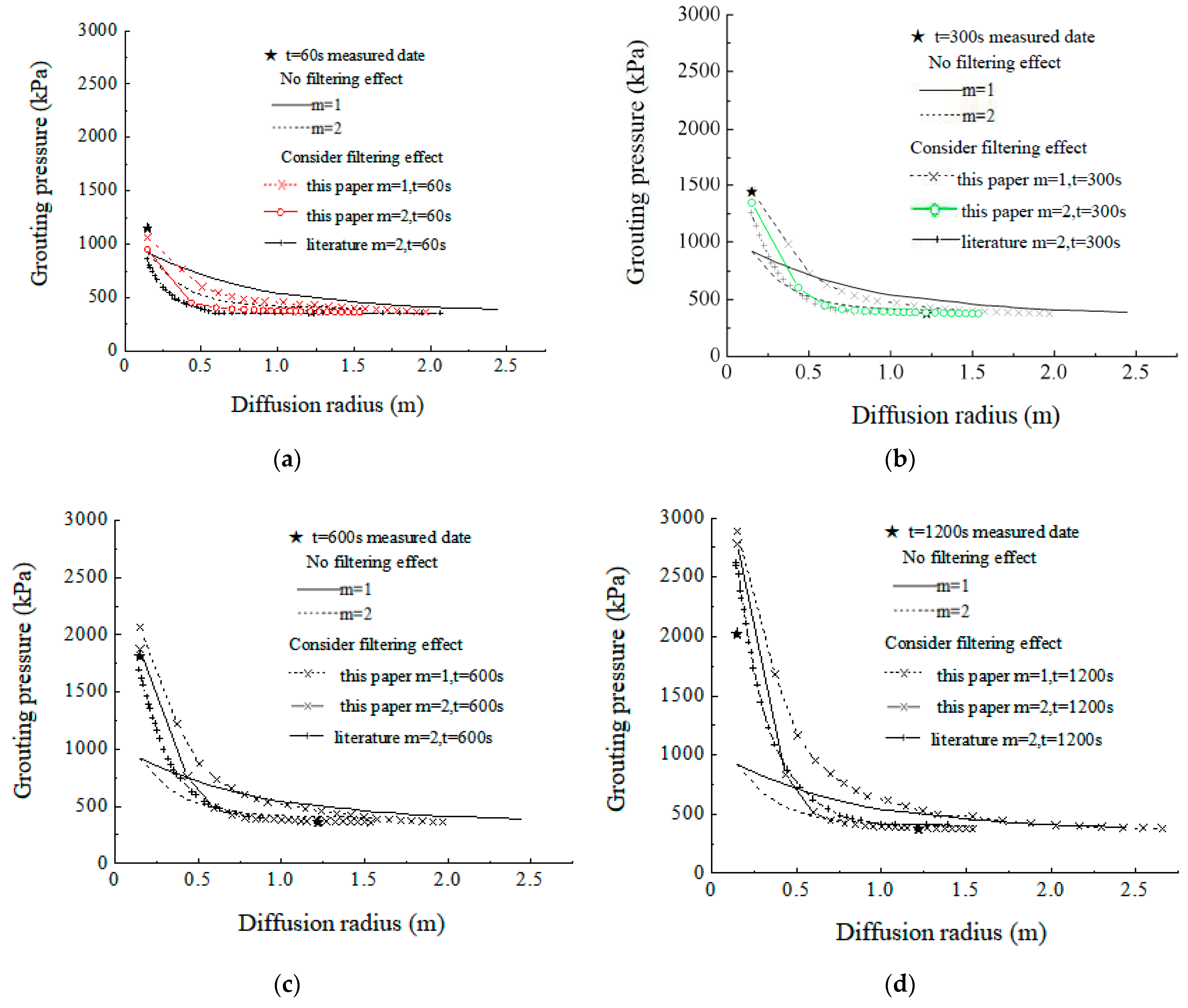
4.2. Result Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Saada, Z.; Canou, J.; Dormieux, L.; Dupla, J.C. Evaluation of elementary filtration properties of a cement grout injected in a sand. Can. Geotech. J. 2006, 43, 1273–1289. [Google Scholar] [CrossRef]
- Chupin, O.; Saiyouri, N.; Hicher, P.Y. The effects of filtration on the injection of cement-based grouts in sand columns. Transp. Porous Media 2008, 72, 227–240. [Google Scholar] [CrossRef]
- Raffle, J.F.; Greenwood, D.A. The relation between the rheological characteristics of grouts and their capacity to permeate soil. In Proceedings of the 5th International Conference on Soil Mechanics and Foundation Engineering, Paris, France, 17–22 July 1961; Volume 2, pp. 789–794. [Google Scholar]
- Lombad, G. The hole of the cohesion in cement grouting of rock. In Proceedings of the Fifteen Congress Large Dams, Lausanne, Switzerland, 24–30 June 1985. [Google Scholar]
- Li, S.; Liu, R.; Zhang, Q.S.; Sun, Z.Z.; Zhang, X.; Zhu, M.T. Research on C-S slurry diffusion mechanism with time-dependent behavior of viscosity. Chin. J. Rock Mech. Eng. 2013, 32, 2415–2421. [Google Scholar]
- Bouchelaghem, F.; Vulliet, L. Mathematical and numerical filtration–advection–dispersion model of miscible grout propagation in saturated porous media. Int. J. Numer. Anal. Methods Geomech. 2001, 25, 1195–1227. [Google Scholar] [CrossRef]
- Maghous, S.; Saada, Z.; Dormieux, L.; Canou, J.; Dupla, J. A model for in situ grouting with account for particle filtration. Comput. Geotech. 2007, 34, 164–174. [Google Scholar] [CrossRef]
- Saada, Z.; Canou, J.; Dormieux, L.; Dupla, J.C.; Maghous, S. Modelling of cement suspension flow in granular porous media. Int. J. Numer. Anal. Methods Geomech. 2005, 29, 691–711. [Google Scholar] [CrossRef]
- Kim, Y.S.; Whittle, A.J. Particle Network Model for Simulating the Filtration of a Microfine Cement Grout in Sand. J. Geotech. Geoenviron. Eng. 2009, 135, 224–236. [Google Scholar] [CrossRef]
- Wang, X.; Cheng, H.; Yao, Z.; Rong, C.; Huang, X.; Liu, X. Theoretical Research on Sand Penetration Grouting Based on Cylindrical Diffusion Model of Tortuous Tubes. Water 2022, 14, 1028. [Google Scholar] [CrossRef]
- Zhao, X.; Yang, Z.; Meng, X.; Wang, S.; Li, R.; Xu, H.; Wang, X.; Ye, C.; Xiang, T.; Xu, W.; et al. Study on Mechanism and Verification of Columnar Penetration Grouting of Time-Varying Newtonian Fluids. Processes 2023, 11, 1151. [Google Scholar] [CrossRef]
- Yang, Z.; Hou, K.; Liang, W.; Chen, Y.; Yang, B. Study of diffusion parameters of Newtonian fluid based on column-hemispherical penetration grouting. Rock Soil Mech. 2014, 35, 17–24. [Google Scholar]
- Huang, F.; Lyu, J.; Gao, H.; Wang, G. Modified Maag’s Spherical Diffusion Model of Vacuum Penetration Grouting. Math. Probl. Eng. 2018, 2018, 1758651. [Google Scholar] [CrossRef]
- Fang, K.; Xia, T.; Bao, L. Cement grout dispersion considering filtration in gravel. Chin. J. Rock Mech. Eng. 2013, 32, 1443–1448. [Google Scholar]
- Ye, F.; Gou, C.; Liu, Y.; Sun, H. Half-spherical surface diffusion model of shield tunnel back-filled grouts. J. Tongji Univ. Nat. Sci. 2012, 40, 1789–1794. [Google Scholar]
- Wu, Y.; Ren, G.; Zhang, X.; Zhao, C.; Zhao, C. Spherical Permeation Grouting Model of a Power-Law Fluid Considering the Soil Unloading Effect. Int. J. Geomech. 2024, 24, 04023266. [Google Scholar] [CrossRef]
- Ding, Y.; Yang, Z.Q.; Yang, Y.; Zhu, Y.Y.; Guo, Y.F.; Zhang, J.; Chen, X.G. Study on Penetration Grouting Mechanism Based on Newton Fluid of Time-Dependent Behavior of Rheological Parameters. Shock. Vib. 2020, 2020, 8811028. [Google Scholar] [CrossRef]
- Kim, J.; Lee, I.; Jang, J.; Choi, H. Groutability of cement-based grout with consideration of viscosity and filtration phenomenon. Int. J. Numer. Anal. Methods Geomech. 2009, 33, 1771–1797. [Google Scholar] [CrossRef]
- Tien, C.; Payatakes, A.C. Advances in deep bed filtration. AIChE J. 1979, 25, 737–759. [Google Scholar] [CrossRef]
- Tarafdar, S.; Dey, A.; Gupta, B.S. A multiple state stochastic model for deep-bed filtration. Chem. Eng. Technol. 1992, 15, 44–50. [Google Scholar] [CrossRef]
- Kuang, J.; Zan, Y.; Wang, J. Theory and Project Example of Grout in Geotechnical Engineering; Science Press: Beijing, China, 2001; pp. 49–52. [Google Scholar]

| Parameter | Initial Water–Cement Ratio | Initial Cement Volume Fraction | Initial Grouting Radius | Initial Grouting Rate | Initial Porosity | Initial Permeability | Filtration Coefficient | Permeability Coefficient Test Parameter |
|---|---|---|---|---|---|---|---|---|
| Value | 0.7 | 0.32 | 0.15 | 0.015 | 0.385 | 0.0005 | 0.00029 | −34 |
| Diffusion Radius (m) | t = 60 s | t = 300 s | t = 600 s | t = 1200 s | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| m = 1 | m = 2 | Measured Data | m = 1 | m = 2 | Measured Data | m = 1 | m = 2 | Measured Data | m = 1 | m = 2 | Measured Data | |
| 0.2 | 932 | 932 | 1195 | 932 | 932 | 1428 | 932 | 932 | 1826 | 932 | 932 | 2000 |
| 0.5 | 735 | 556 | — | 735 | 556 | — | 735 | 556 | — | 735 | 556 | — |
| 1.2 | 531 | 422 | 417 | 531 | 422 | 417 | 531 | 422 | 417 | 531 | 422 | 417 |
| 2.0 | 462 | — | — | 462 | — | — | 462 | — | — | 462 | — | — |
| 2.5 | 443 | — | — | 443 | — | — | 443 | — | — | 443 | — | — |
| Diffusion Radius (m) | t = 60 s | t = 300 s | t = 600 s | t = 1200 s | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| No Filtering Effect | Consider Filtering Effect | No Filtering Effect | Consider Filtering Effect | No Filtering Effect | Consider Filtering Effect | No Filtering Effect | Consider Filtering Effect | |||||||||
| m = 1 | m = 2 | m = 1 | m = 2 | m = 1 | m = 2 | m = 1 | m = 2 | m = 1 | m = 2 | m = 1 | m = 2 | m = 1 | m = 2 | m = 1 | m = 2 | |
| 0.2 | 932 | 932 | 1123 | 939 | 932 | 932 | 1425 | 1358 | 932 | 932 | 2080 | 1843 | 932 | 932 | 2860 | 2786 |
| 0.5 | 735 | 556 | 596 | 439 | 735 | 556 | 750 | 542 | 735 | 556 | 935 | 682 | 735 | 556 | 1187 | 765 |
| 1.2 | 531 | 422 | 438 | 419 | 531 | 422 | 441 | 420 | 531 | 422 | 486 | 422 | 531 | 422 | 549 | 425 |
| 2.0 | 462 | — | 412 | — | 462 | — | 425 | — | 462 | — | 443 | — | 462 | — | 468 | — |
| 2.5 | 443 | — | 1123 | 939 | 443 | — | — | — | 443 | — | — | — | 443 | — | — | — |
| Diffusion Radius (m) | t = 60 s | t = 300 s | t = 600 s | t = 1200 s | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| m = 1 | m = 2 | Literature (m = 2) | m = 1 | m = 2 | Literature (m = 2) | m = 1 | m = 2 | Literature (m = 2) | m = 1 | m = 2 | Literature (m = 2) | |
| 0.2 | 1123 | 939 | 938 | 1425 | 1358 | 1302 | 2080 | 1843 | 1819 | 2860 | 2786 | 2636 |
| 0.5 | 596 | 439 | 430 | 750 | 542 | 500 | 935 | 682 | 609 | 1187 | 765 | 750 |
| 1.2 | 438 | 419 | 419 | 441 | 420 | 420 | 486 | 422 | 422 | 549 | 425 | 426 |
| 2.0 | 412 | — | 412 | 425 | — | — | 443 | — | — | 468 | — | — |
| 2.5 | 1123 | 939 | — | — | — | — | — | — | — | — | — | — |
| Diffusion Radius (m) | t = 60 s | t = 300 s | t = 600 s | t = 1200 s | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| m = 1 | m = 2 | Measured Data | m = 1 | m = 2 | Measured Data | m = 1 | m = 2 | Measured Data | m = 1 | m = 2 | Measured Data | |
| 0.2 | 1123 | 939 | 1195 | 1425 | 1358 | 1428 | 2080 | 1843 | 1826 | 2860 | 2786 | 2000 |
| 0.5 | 596 | 439 | — | 750 | 542 | — | 935 | 682 | — | 1187 | 765 | — |
| 1.2 | 438 | 419 | 417 | 441 | 420 | 417 | 486 | 422 | 417 | 549 | 425 | 417 |
| 2.0 | 412 | — | — | 425 | — | — | 443 | — | — | 468 | — | — |
| 2.5 | 1123 | 939 | — | — | — | — | — | — | — | — | — | — |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, L.; Li, J.; Zhang, R.; Qin, S.; Dong, Y.; Wu, J. Modified (Spherical and Cylindrical) Permeation Diffusion Model Considering Deep Bed Filtration Effect. Buildings 2024, 14, 124. https://doi.org/10.3390/buildings14010124
Song L, Li J, Zhang R, Qin S, Dong Y, Wu J. Modified (Spherical and Cylindrical) Permeation Diffusion Model Considering Deep Bed Filtration Effect. Buildings. 2024; 14(1):124. https://doi.org/10.3390/buildings14010124
Chicago/Turabian StyleSong, Liang, Jun Li, Rongtang Zhang, Shipeng Qin, Yiqie Dong, and Jie Wu. 2024. "Modified (Spherical and Cylindrical) Permeation Diffusion Model Considering Deep Bed Filtration Effect" Buildings 14, no. 1: 124. https://doi.org/10.3390/buildings14010124
APA StyleSong, L., Li, J., Zhang, R., Qin, S., Dong, Y., & Wu, J. (2024). Modified (Spherical and Cylindrical) Permeation Diffusion Model Considering Deep Bed Filtration Effect. Buildings, 14(1), 124. https://doi.org/10.3390/buildings14010124







