Behavior of FRP-Retrofitted Wall-like RC Columns after Preloading to Simulate In-Service Conditions
Abstract
:1. Introduction
2. Experimental Campaign
2.1. Experimental Matrix
2.2. Material Properties
2.3. Preparation and Testing Setup of Columns
3. Discussion of Experimental Findings
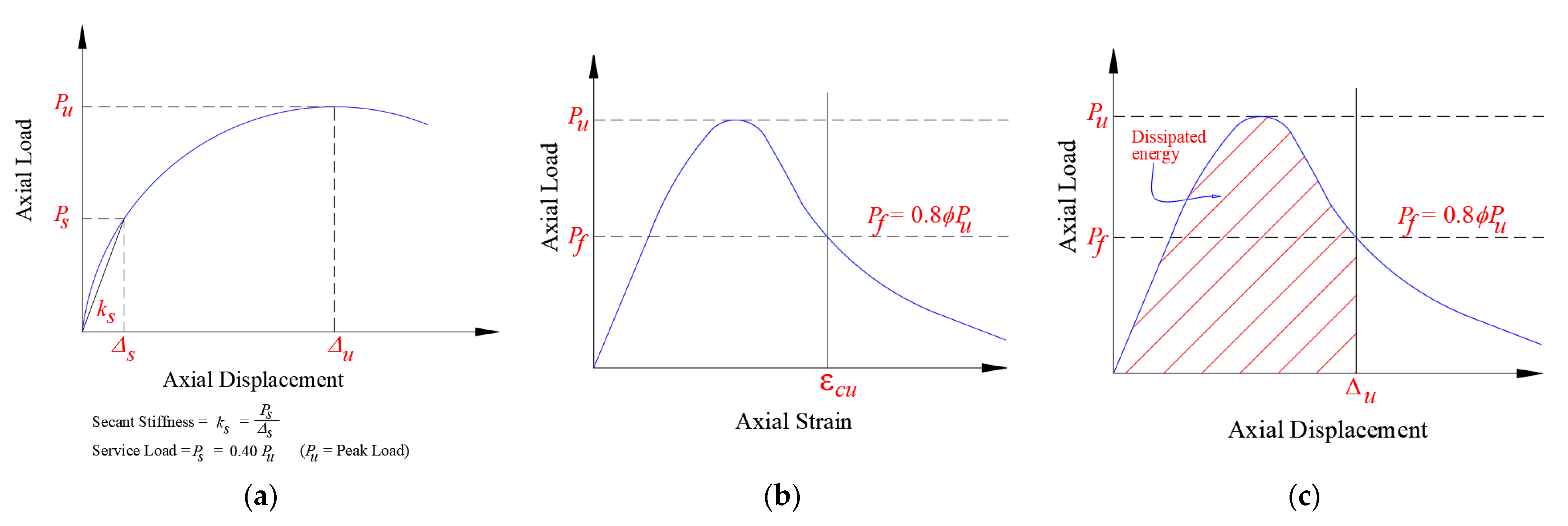
3.1. Key Experimental Parameters
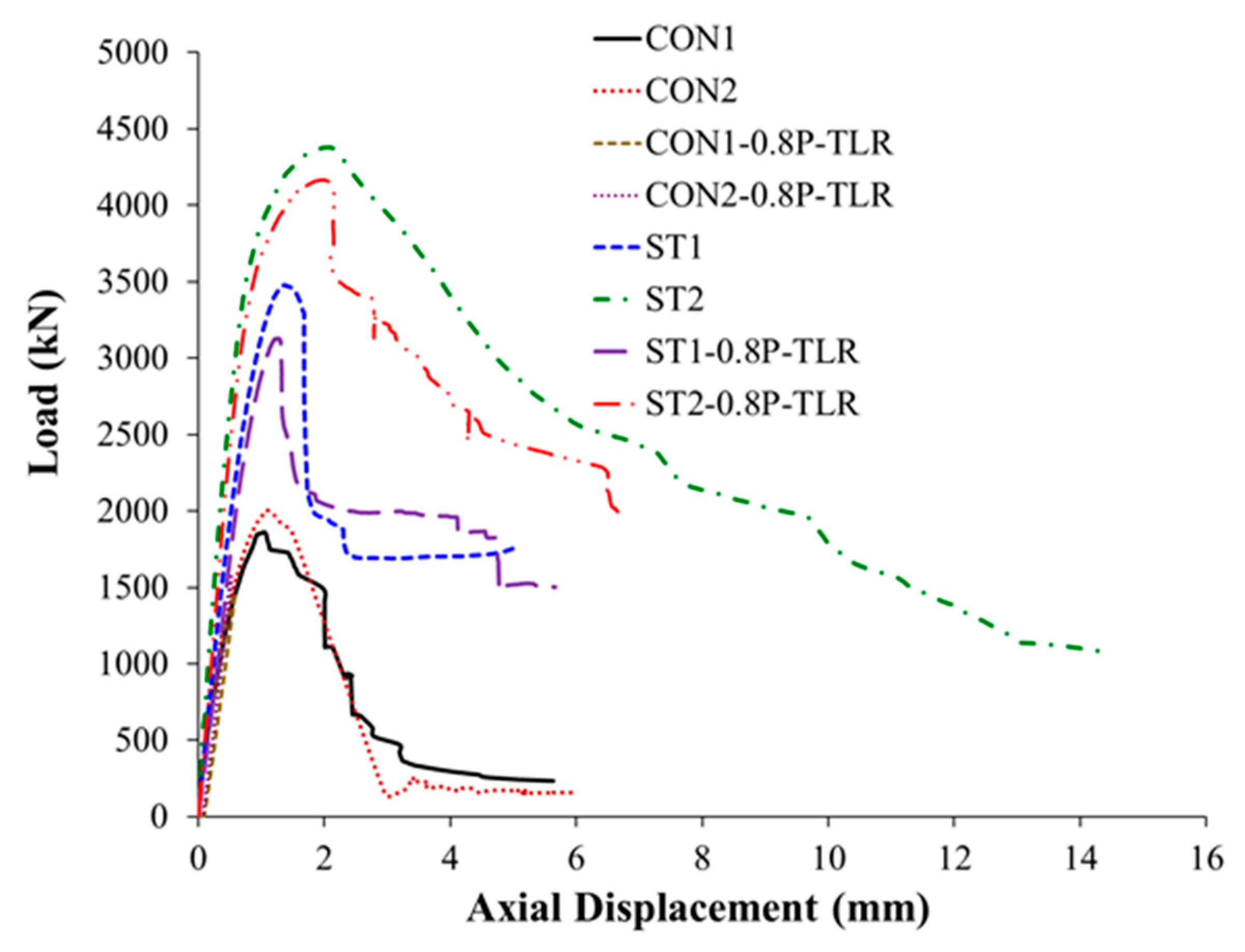
3.2. Load-Displacement Plots
3.3. Control Specimens
3.4. Upgraded Specimen ST1-0.8P-TLR
3.5. Upgraded Specimen ST2-0.8P-TLR
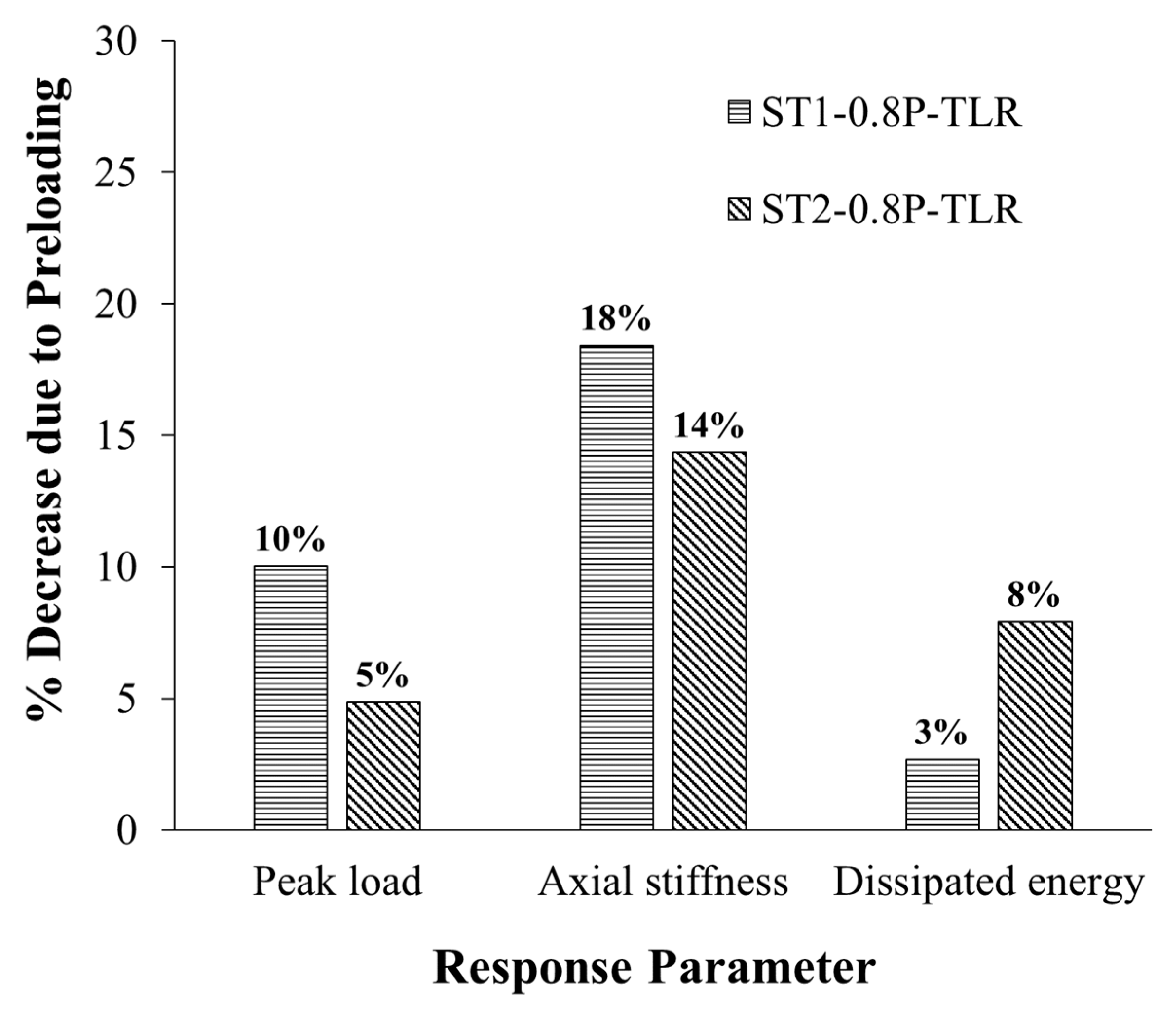
3.6. Effect of Preloading
4. Finite Element Analysis
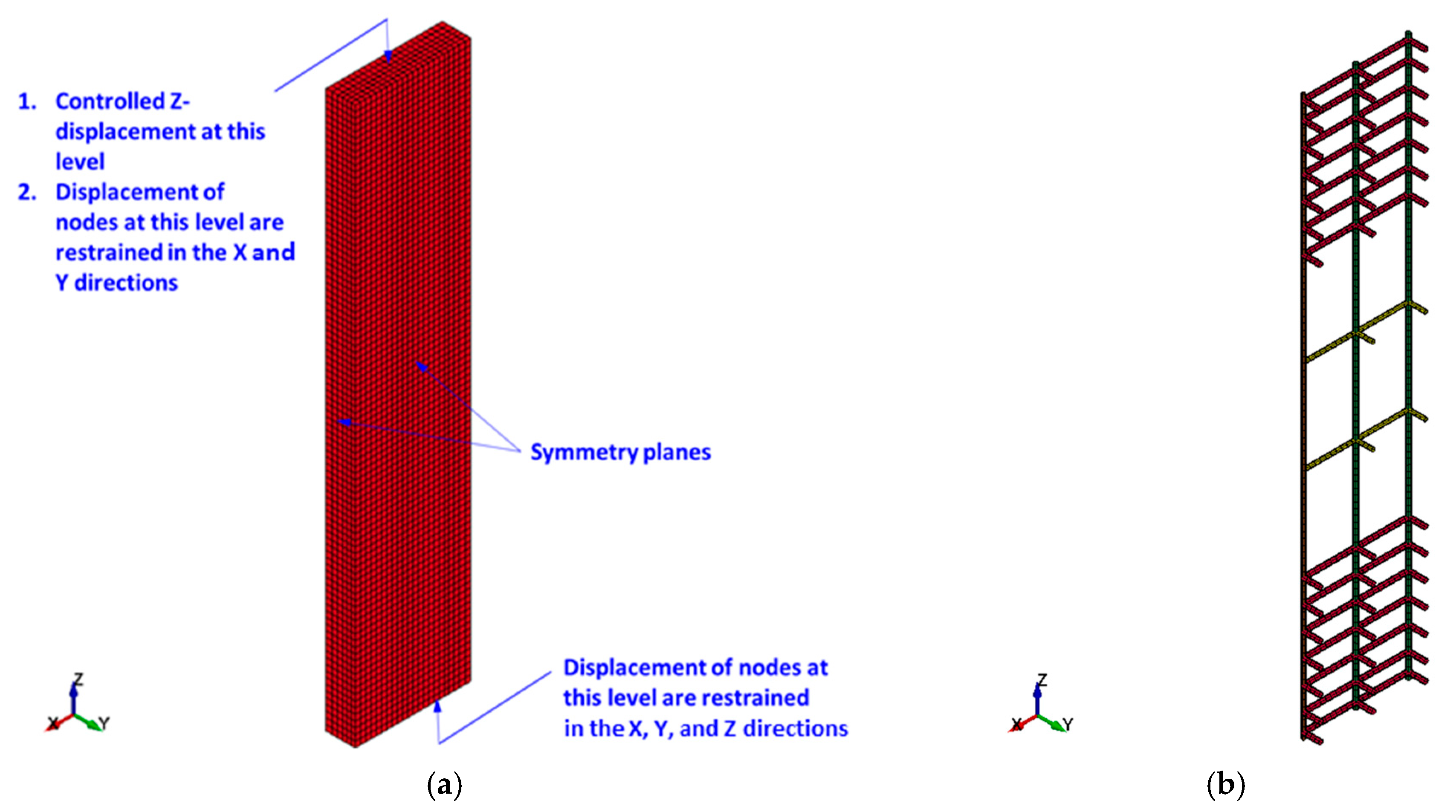
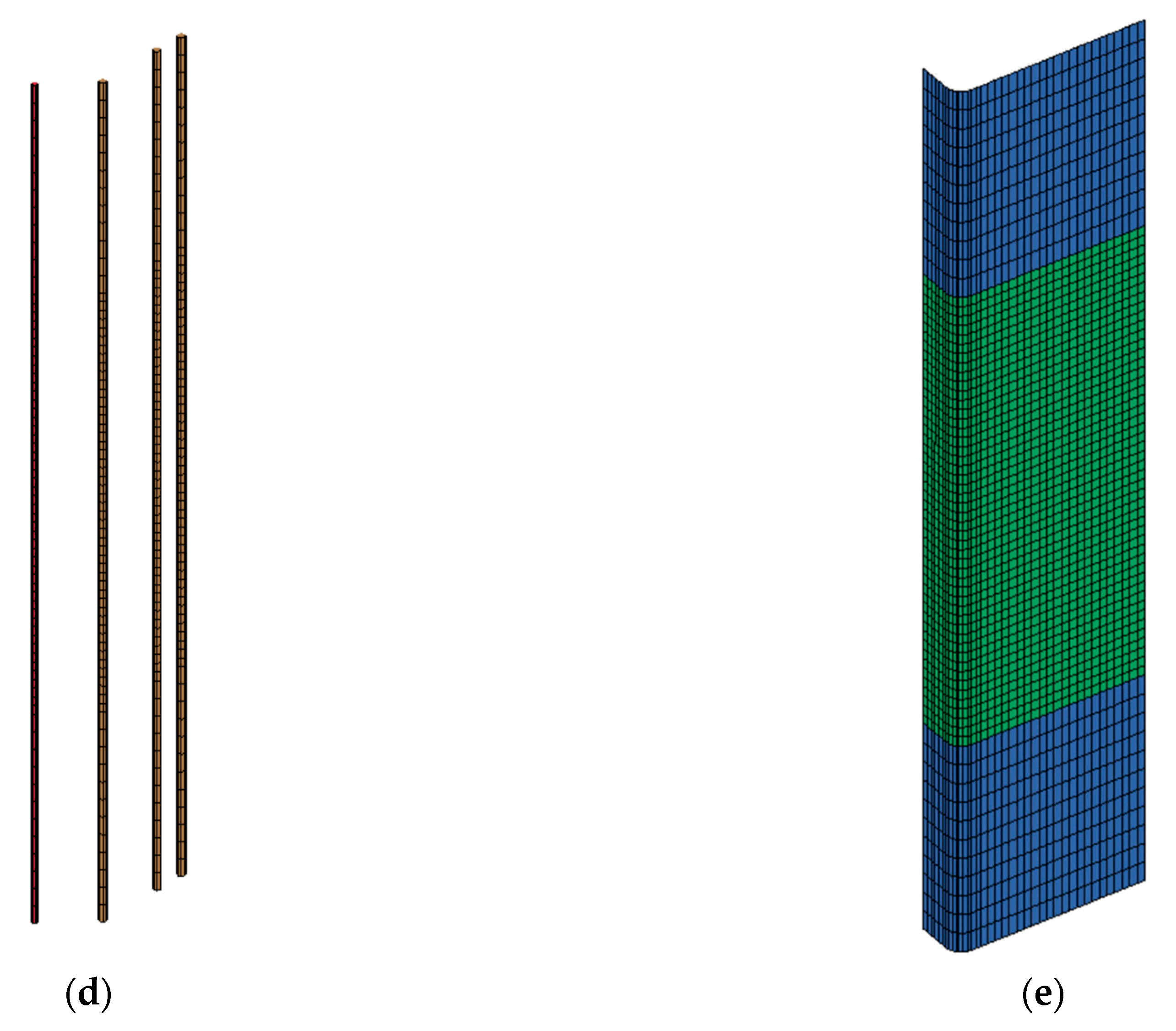
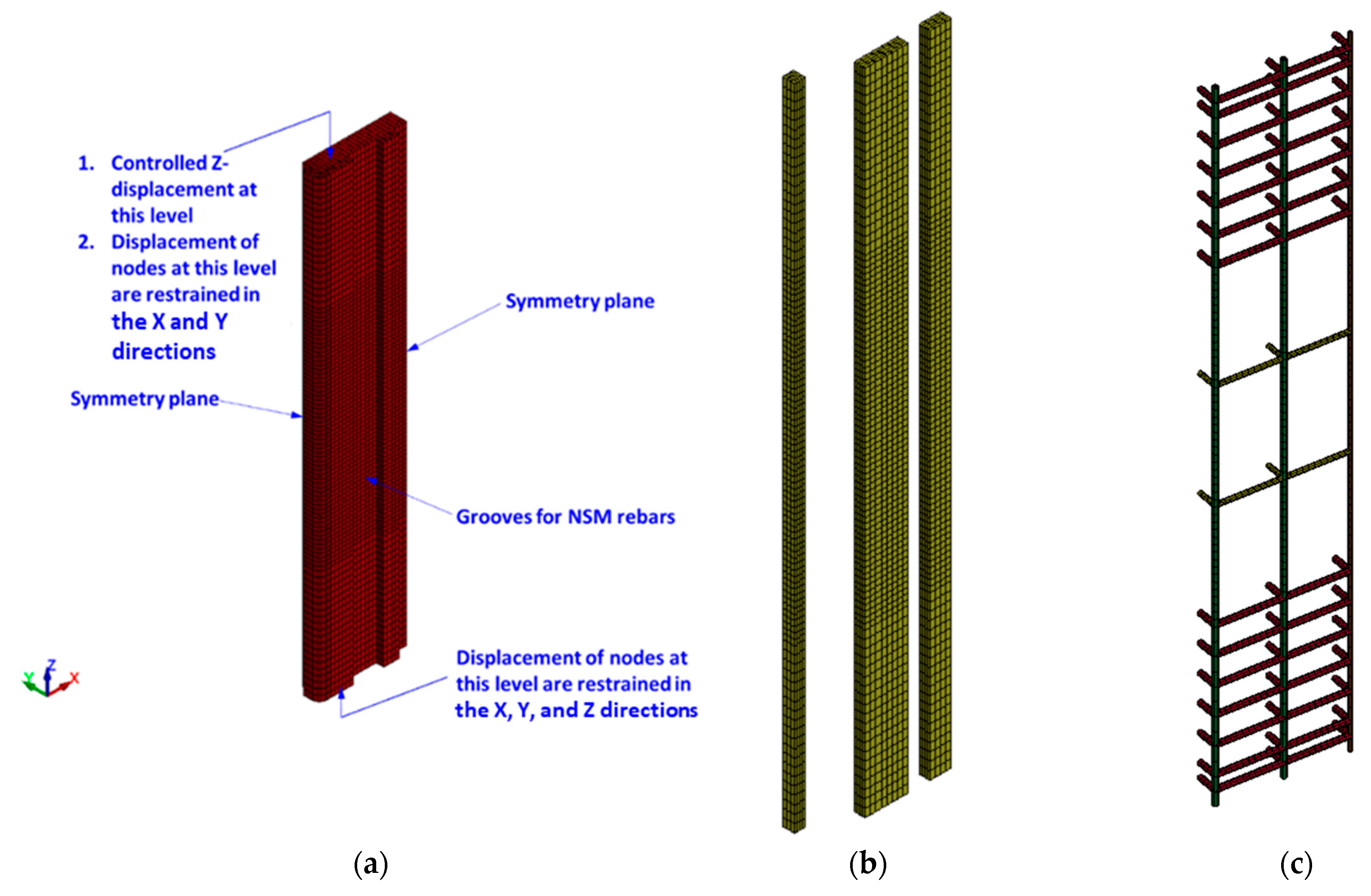
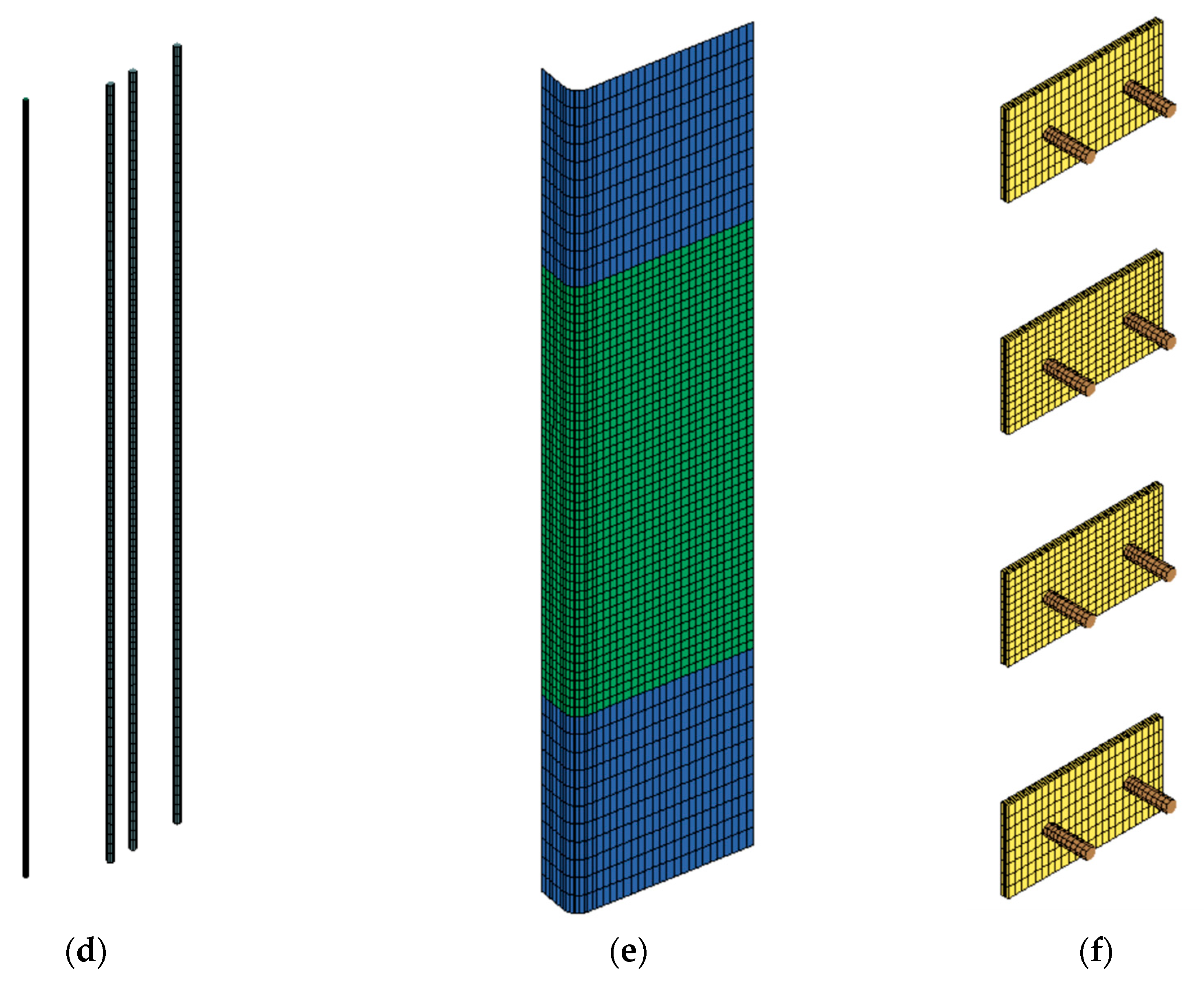
4.1. Mesh and Geometry
4.2. Material Modeling
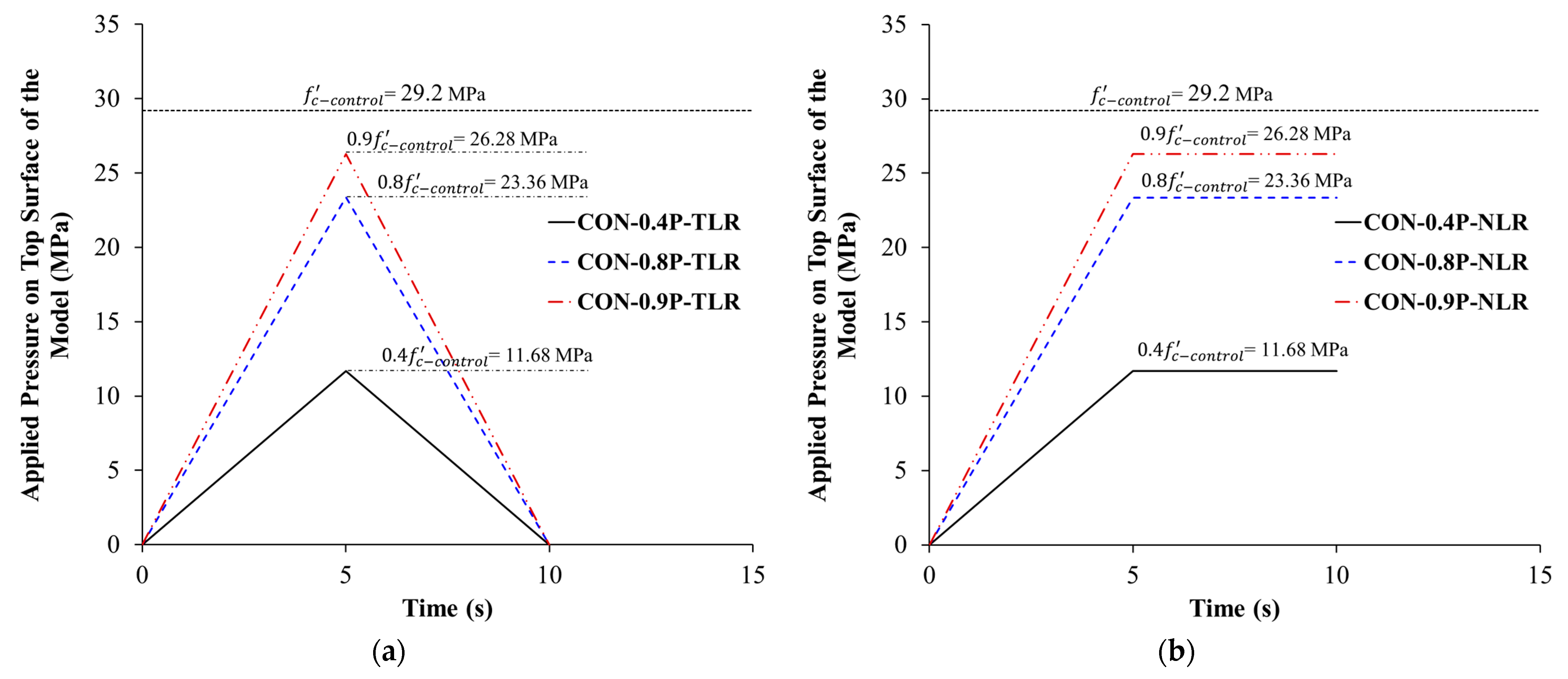
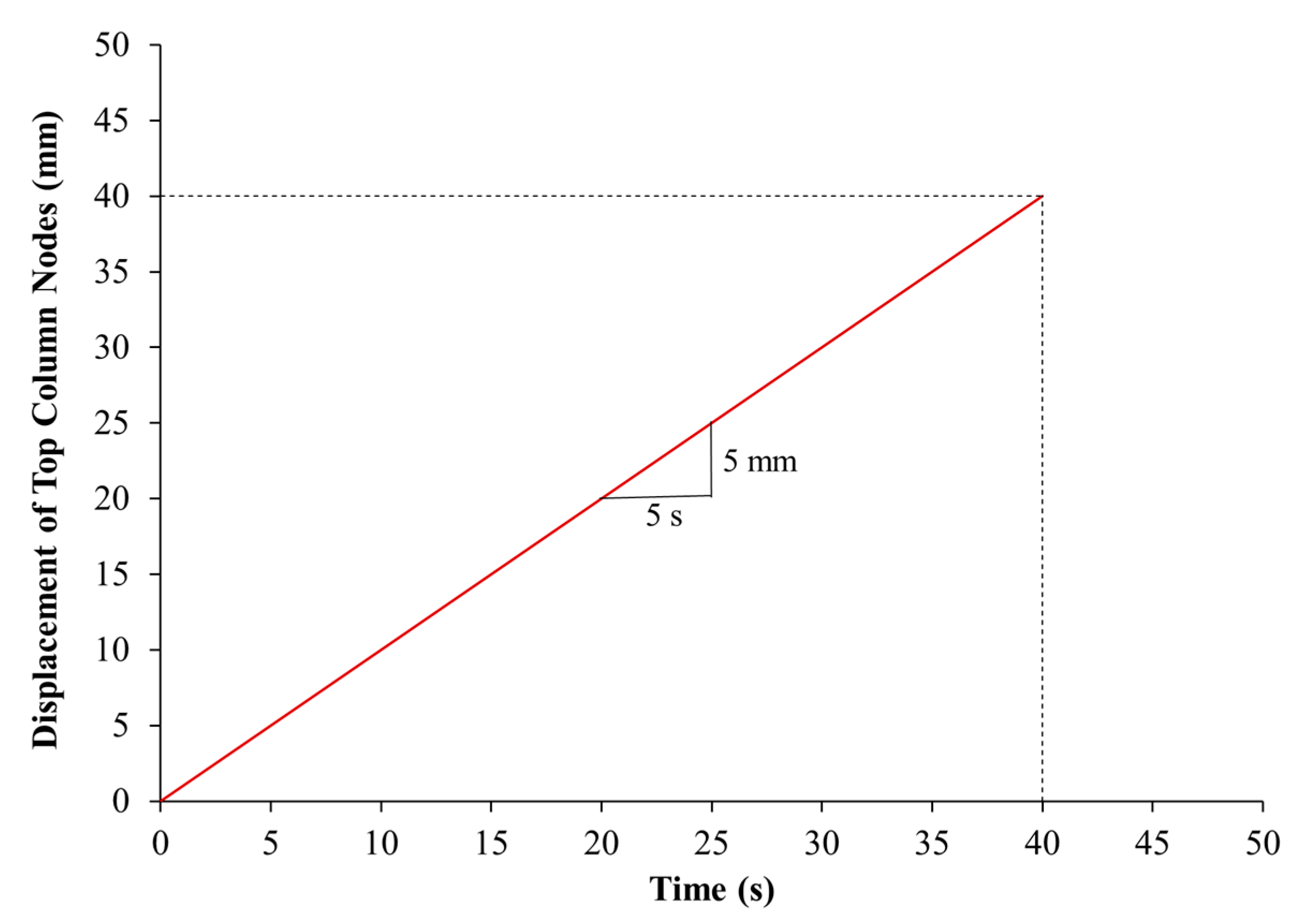
4.3. Boundary Conditions and Analysis Strategy
4.4. Finite Element Results
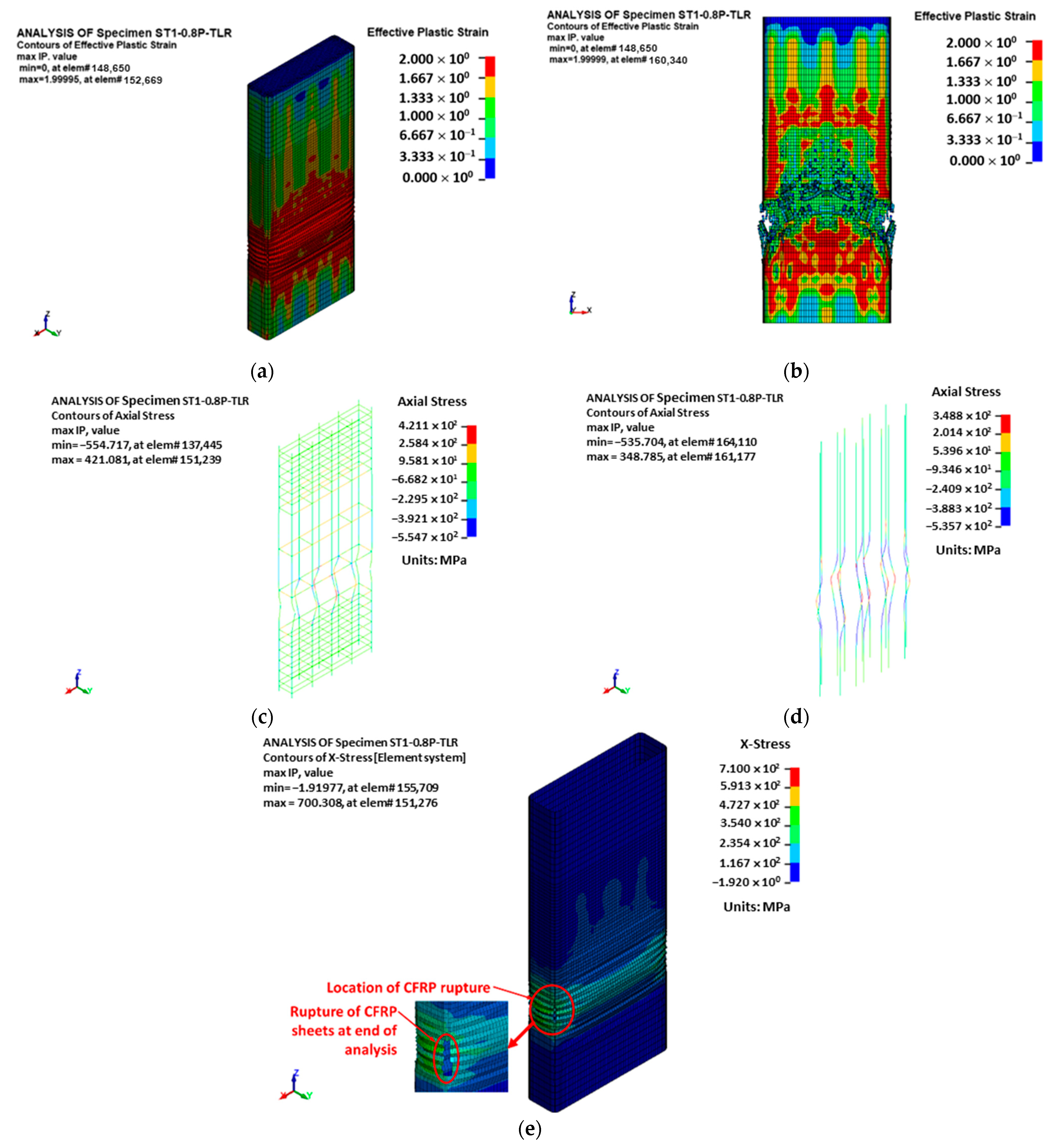
4.4.1. Failure Pattern
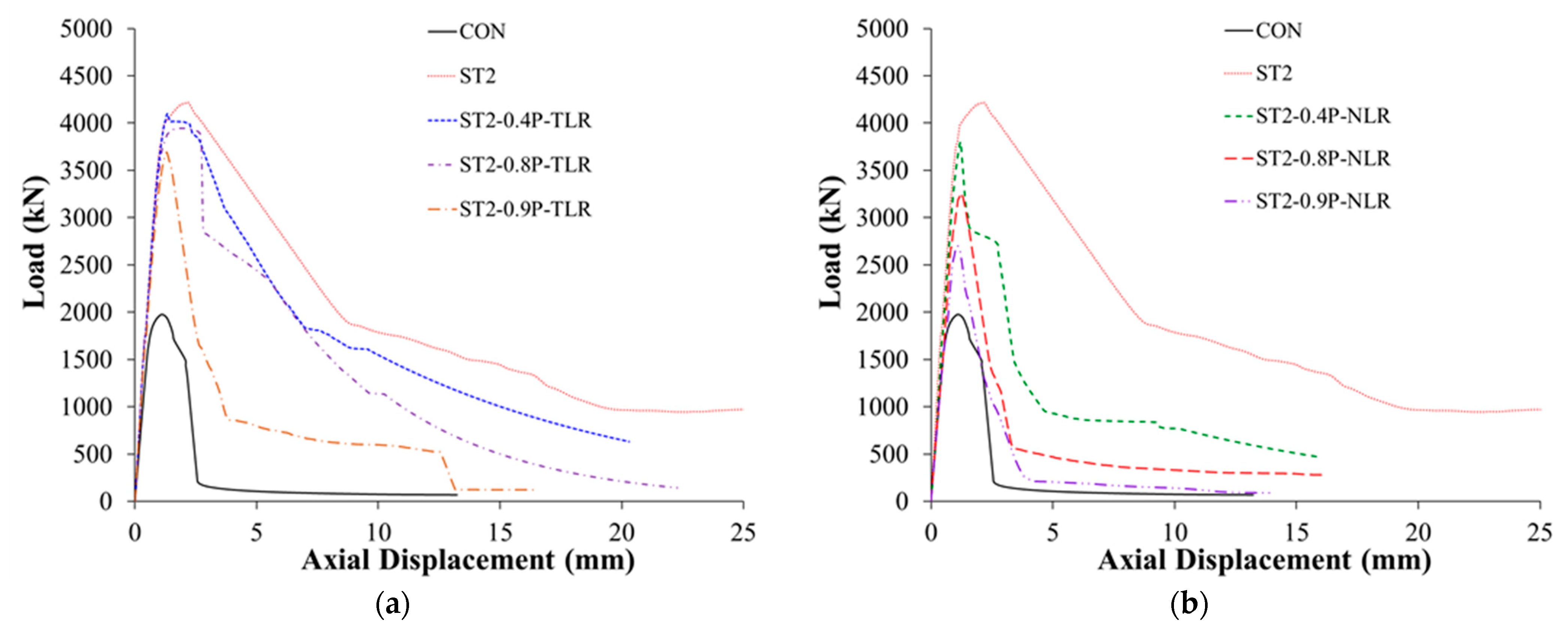
4.4.2. Load-Displacement Plots
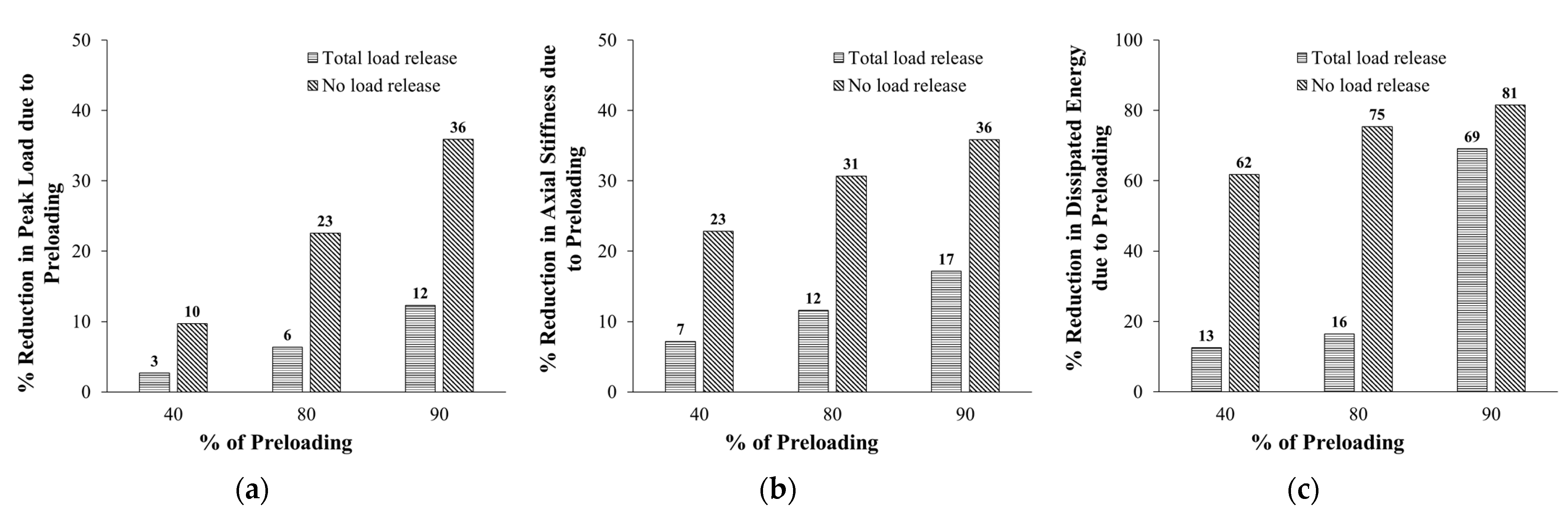
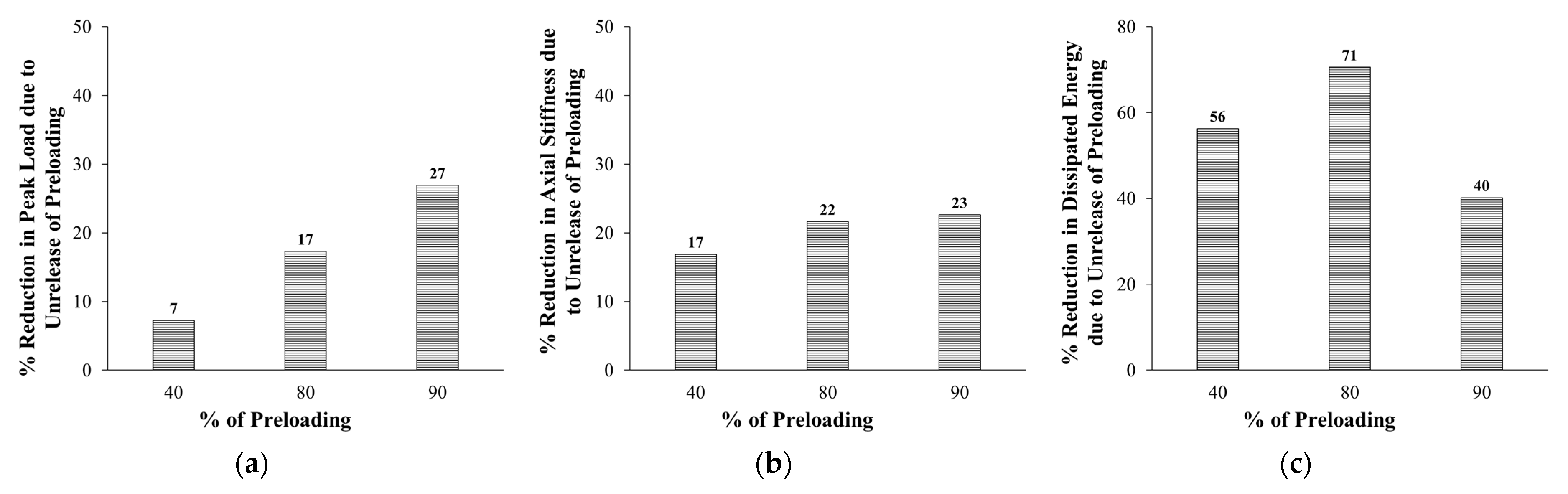
5. Parametric Study
6. Conclusions
- The failure of the upgraded columns in the two studied retrofitting configurations began with the FRP sheets’ bulging, caused by the expansion of the column cross-section, as well as the NSM and main rebars’ buckling. Ultimately, the upgraded columns failed due to the fracture of the FRP sheets.
- In practical scenarios where the unstrengthened column is preloaded to 80% of its peak load and then fully unloaded, the testing campaign proved the efficiency of the two studied schemes in improving the axial load-displacement characteristics of the columns. However, the second scheme was considerably superior to the first one due to the extra confinement provided by the bolted steel plates. This scheme improved the peak load, stiffness, and dissipated energy by 115%, 75%, and 524%, respectively.
- The performed FE analysis accurately assessed the load versus axial displacement behavior of the examined wall-like columns. This affirms the appropriateness of the utilized constitutive models for steel, concrete, and FRP materials. These verified models can be applied in future studies to explore RC wall-like columns with different aspect ratios and under conditions of eccentric loading.
- The conducted parametric study proved that for all response parameters of wall-like columns, as the percent of preloading increased, the percent increase due to strengthening decreased, and the decrease in the case of no load release is significantly more than the case of total load release. For the worst-case scenario of unrelease of the preloading, as the percent of preloading increased from zero to 90%, the percent increase in peak load, stiffness, and dissipated energy due to strengthening was significantly reduced from 113% to 37%, 57% to 1%, and 551% to 21%, respectively.
- From the parametric study carried out in this research, it was found that even with the worst-case scenario of unstrengthened RC wall-like columns preloaded with 90% of their axial resistance without releasing the load, their strengthening using the second scheme was efficient at enhancing the load-displacement response. Compared with the unstrengthened column, the upgrading scheme in such a case improved the peak load and dissipated energy, respectively, by 37% and 21%; however, it almost retained the axial secant stiffness of the column.
- The conclusions derived above are limited to RC wall-like columns with a depth-to-width ratio not exceeding 4. The findings of this study are also limited to wall-like columns fabricated from normal-strength concrete. For wall-like columns with a sectional aspect ratio exceeding 4 or fabricated from high-strength concrete, experimental research is needed.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bett, B.J.; Klingner, R.E.; Jisra, J.O. Lateral load response of strengthened and repaired reinforced concrete columns. ACI Struct. J. 1988, 85, 499–508. [Google Scholar]
- Rodriguey, M.; Park, R. Seismic load tests on reinforced concrete columns strengthened by jacketing. ACI Struct. J. 1994, 91, 150–159. [Google Scholar]
- Campione, G. Load carrying capacity of RC compressed columns strengthened with steel angles and strips. Eng. Struct. 2012, 40, 457–465. [Google Scholar] [CrossRef]
- Khalifa, E.S.; Al-Tersawy, S.H. Experimental and analytical behavior of strengthened reinforced concrete columns with steel angles and strips. Int. J. Adv. Struct. Eng. 2014, 6, 6. [Google Scholar] [CrossRef]
- Tarabia, A.M.; Albakry, H.F. Strengthening of RC columns by steel angles and strips. Alex. Eng. J. 2014, 53, 615–626. [Google Scholar] [CrossRef]
- Abdel-Hay, A.S.; Fawzy, Y.A.G. Behavior of partially defected R.C columns strengthened using steel jackets. HBRC J. 2015, 11, 194–200. [Google Scholar] [CrossRef]
- Shan, Z.; Chen, L.; Liang, K.; Su, R.K.L.; Xu, Z. Strengthening design of RC columns with direct fastening steel jackets. Appl. Sci. 2021, 11, 3649. [Google Scholar] [CrossRef]
- Shan, Z.; Guo, Q.; Liang, K.; Ji, X.; Chen, L.; Li, L.; Xu, Z. Design approach and its optimization for bolted steel plate strengthened RC beams considering the effect of connection bolt slip. In Structures; Elsevier: Amsterdam, The Netherlands, 2023; Volume 57, p. 105045. [Google Scholar]
- Chen, L.; Liang, K.; Shan, Z. Experimental and theoretical studies on bond behavior between concrete and FRP bars with different surface conditions. Compos. Struct. 2023, 309, 116721. [Google Scholar] [CrossRef]
- Stanciu, M.D.; Drăghicescu, H.T.; Roșca, I.C. Mechanical Properties of GFRPs Exposed to Tensile, Compression and Tensile–Tensile Cyclic Tests. Polymers 2021, 13, 898. [Google Scholar] [CrossRef]
- Wu, J.; Zhu, Y.; Li, C. Experimental Investigation of Fatigue Capacity of Bending-Anchored CFRP Cables. Polymers 2023, 15, 2483. [Google Scholar] [CrossRef]
- Xian, G.; Guo, R.; Li, C. Combined effects of sustained bending loading, water immersion and fiber hybrid mode on the mechanical properties of carbon/glass fiber reinforced polymer composite. Compos. Struct. 2022, 281, 115060. [Google Scholar] [CrossRef]
- Elsanadedy, H.; Alaoud, L.; Abbas, H.; Almusallam, T.; Al-Salloum, Y. Externally bonded CFRP composites versus steel stirrups for the confinement of substandard lap spliced GFRP bars in RC beams. Compos. Struct. 2023, 306, 116602. [Google Scholar] [CrossRef]
- Tan, K.H. Strength enhancement of rectangular RC columns using FRP. J. Compos. Constr. ASCE 2002, 6, 175–183. [Google Scholar] [CrossRef]
- Hosny, A.; Shaheen, H.; Abdelrahman, A.; Elafandy, T. Uniaxial tests on rectangular columns strengthened with CFRP. In Proceedings of the Third Middle East Symposium on Structural Composites for Infrastructure Applications, Aswan, Egypt, 14–17 December 2002. [Google Scholar]
- Tanwongsval, S.; Maalej, M.; Paramasivam, P. Strengthening of RC wall-like columns with FRP under sustained loading. Mater. Struct. 2003, 36, 282–290. [Google Scholar] [CrossRef]
- Maalej, M.; Tanwongsval, S.; Paramasivam, P. Modelling of rectangular RC columns strengthened with FRP. Cem. Concr. Compos. 2003, 25, 263–276. [Google Scholar] [CrossRef]
- Prota, A.; Manfredi, G.; Cosenza, E. Ultimate behavior of axially loaded RC wall-like columns confined with GFRP. Compos. Part B 2006, 37, 670–678. [Google Scholar] [CrossRef]
- De Luca, A.; Nardone, F.; Lignola, G.P.; Prota, A.; Nanni, A. Wall-like reinforced concrete columns externally confined by means of glass FRP laminates. Adv. Struct. Eng. 2013, 16, 593–603. [Google Scholar] [CrossRef]
- Alsayed, S.H.; Almusallam, T.H.; Ibrahim, S.M.; Al-Hazmi, N.M.; Al-Salloum, Y.A.; Abbas, H. Experimental and numerical investigation for compression response of CFRP strengthened shape modified wall-like RC column. Constr. Build. Mater. 2014, 63, 72–80. [Google Scholar] [CrossRef]
- Triantafillou, T.C.; Choutopoulou, E.; Fotaki, E.; Skorda, M.; Stathopoulou, M.; Karlos, K. FRP confinement of wall-like reinforced concrete columns. Mater. Struct. Mater. Constr. 2016, 49, 651–664. [Google Scholar] [CrossRef]
- Abbas, H.; Ibrahim, S.M.; Al-Hazmi, N.; Elsanadedy, H.; Almusallam, T.; Al-Salloum, Y. Axial Compression Behavior of Wall-like Reinforced Concrete Columns Retrofitted Using Different FRP Schemes. Buildings 2022, 13, 26. [Google Scholar] [CrossRef]
- Al-Salloum, Y.; Abbas, H.; Elsanadedy, H.; Siddiqui, N.; Almusallam, T. Compression behavior of RC wall-like columns strengthened using NSM/CFRP system without shape modification. In Structures; Elsevier: Amsterdam, The Netherlands, 2023; Volume 57, p. 105158. [Google Scholar]
- Elsanadedy, H.; Abbas, H.; Almusallam, T.; Al-Salloum, Y. Performance of Concentrically Loaded RC Wall-like Columns Upgraded with Innovative Hybrid NSM/CFRP System. Polymers 2023, 15, 378. [Google Scholar] [CrossRef]
- Elsanadedy, H.; Abbas, H.; Siddiqui, N.; Almusallam, T.; Al-Salloum, Y. Hybrid Steel/NSM/GFRP System versus GFRP Wrapping for Upgrading RC Wall-like Columns. Polymers 2023, 15, 1886. [Google Scholar] [CrossRef]
- Mander, J.B.; Priestley, M.J.; Park, R. Theoretical stress-strain model for confined concrete. J. Struct. Eng. 1988, 114, 1804–1826. [Google Scholar] [CrossRef]
- Wang, Y.C.; Resrepo, J.I. Investigations of concentrically loaded reinforced concrete columns confined with glass fiber-reinforced polymer jackets. ACI Struct. J. 2001, 98, 377–385. [Google Scholar]
- Saatcioglu, M.; Razvi, S.R. Strength and ductility of confined concrete. J. Struct. Eng. 1992, 118, 590–607. [Google Scholar] [CrossRef]
- Yalcim, C.; Saatcioglu, M. Inelastic analysis of reinforced concrete columns. Comput. Struct. 2000, 77, 539–555. [Google Scholar] [CrossRef]
- ASTM C39/C39M-21; Standard Test Method for Compressive Strength of Cylindrical Concrete Specimens. ASTM: West Conshohocken, PA, USA, 2021.
- ASTM E8/E8M-22; Standard Test Methods for Tension Testing of Metallic Materials. ASTM: West Conshohocken, PA, USA, 2022.
- ASTM D3039/D3039M; Standard Test Method for Tensile Properties of Polymer Matrix Composite Materials. ASTM: West Conshohocken, PA, USA, 2014.
- ACI 440.2R-17; Guide for the Design and Construction of Externally Bonded FRP Systems for Strengthening Concrete Structures. American Concrete Institute: Detroit, MI, USA, 2017.
- ASTM A370–16; Standard Test Methods and Definitions for Mechanical Testing of Steel Products. American Society for Testing and Materials: West Conshohocken, PA, USA, 2016.
- ACI 318-19; ACI Committee 318; American Concrete Institute. Building Code Requirements for Structural Concrete (ACI 318-19): An ACI Standard: Commentary on Building Code Requirements for Structural Concrete (ACI 318R-19), an ACI Report. American Concrete Institute: Farmington Hills, MI, USA, 2019.
- Livermore Software Technology Corporation (LSTC). LS-DYNA Keyword User’s Manual Vol. 1–3, Version R11; LSTC: Livermore, CA, USA, 2018. [Google Scholar]
- Belytschko, T.B.; Tsay, C.S. Explicit algorithms for non-linear dynamics of shells. J. Appl. Mech. Appl. Mech. Div. ASME 1981, 48, 209–231. [Google Scholar]
- Malvar, L.J.; Crawford, J.E.; Wesevich, J.W.; Simons, D. A plasticity concrete material model for DYNA 3D. Int. J. Impact Eng. 1997, 19, 847–873. [Google Scholar] [CrossRef]
- Malvar, L.J.; Crawford, J.E.; Morrill, K.B. K&C concrete material model Release III—Automated generation of material input. In K&C Technical Report TR-99-24-B1; Report to the Defense Nuclear Agency: Fort Belvoir, VA, USA, 2000. [Google Scholar]
- Magallanes, J.M.; Wu, Y.; Malvar, L.J.; Crawford, J.E. Recent improvements to release III of the K&C concrete model. In Proceedings of the 11th International LS-DYNA Users Conference, Dearborn, MI, USA, 6–8 June 2010. [Google Scholar]
- Chang, F.K.; Chang, K.Y. A progressive damage model for laminated composites containing stress concentration. J. Compos. Mater. 1987, 21, 834–855. [Google Scholar] [CrossRef]
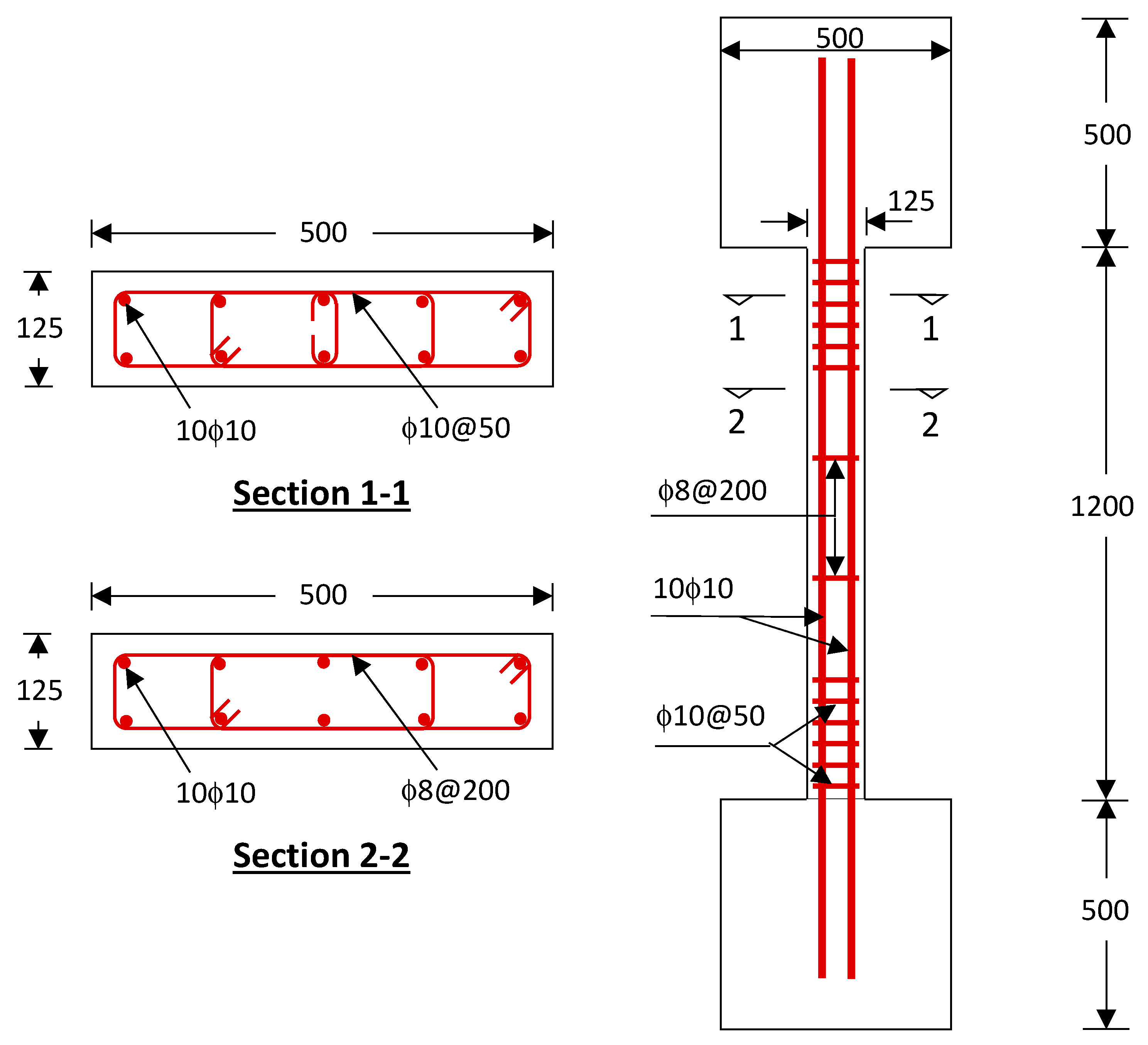
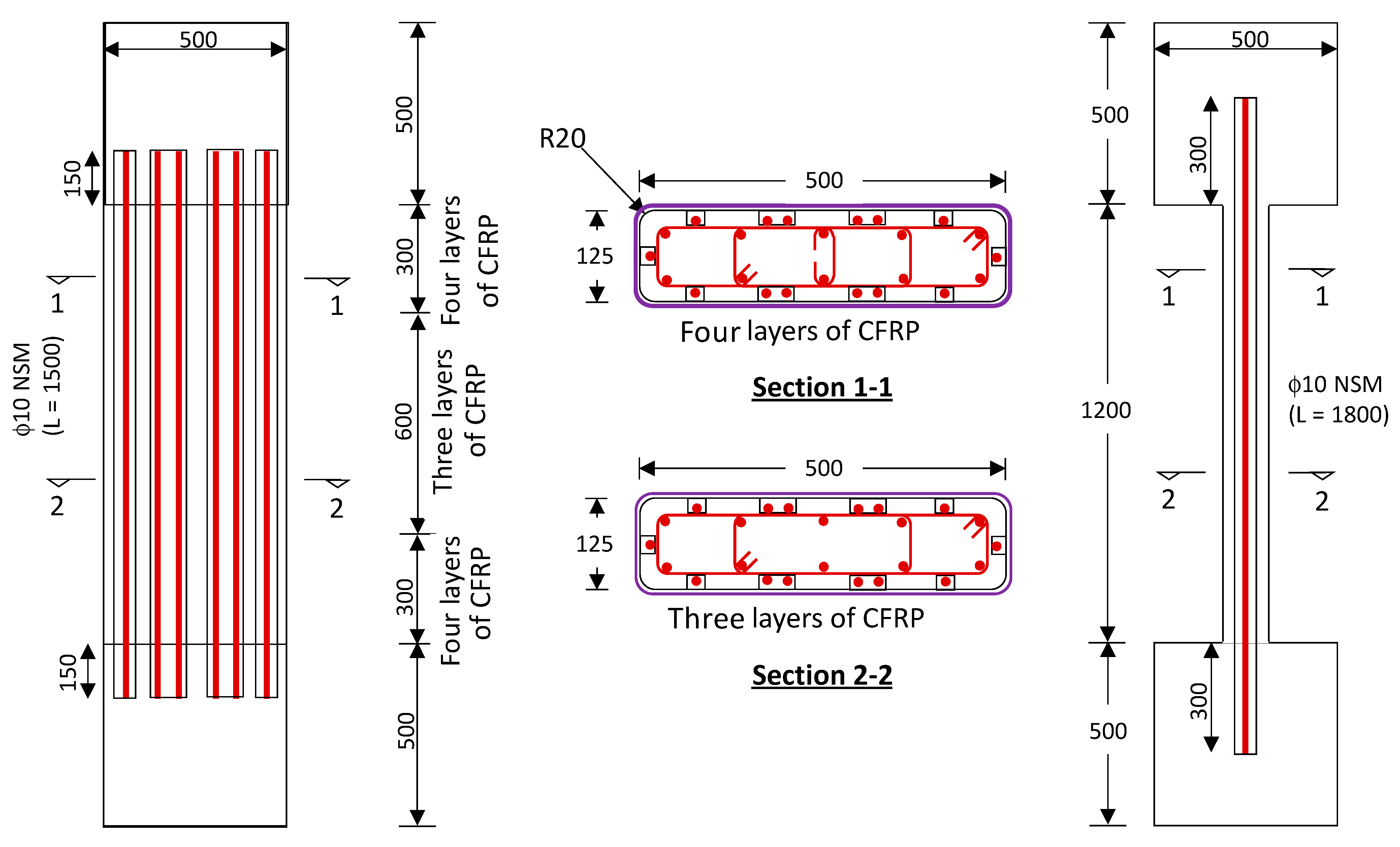
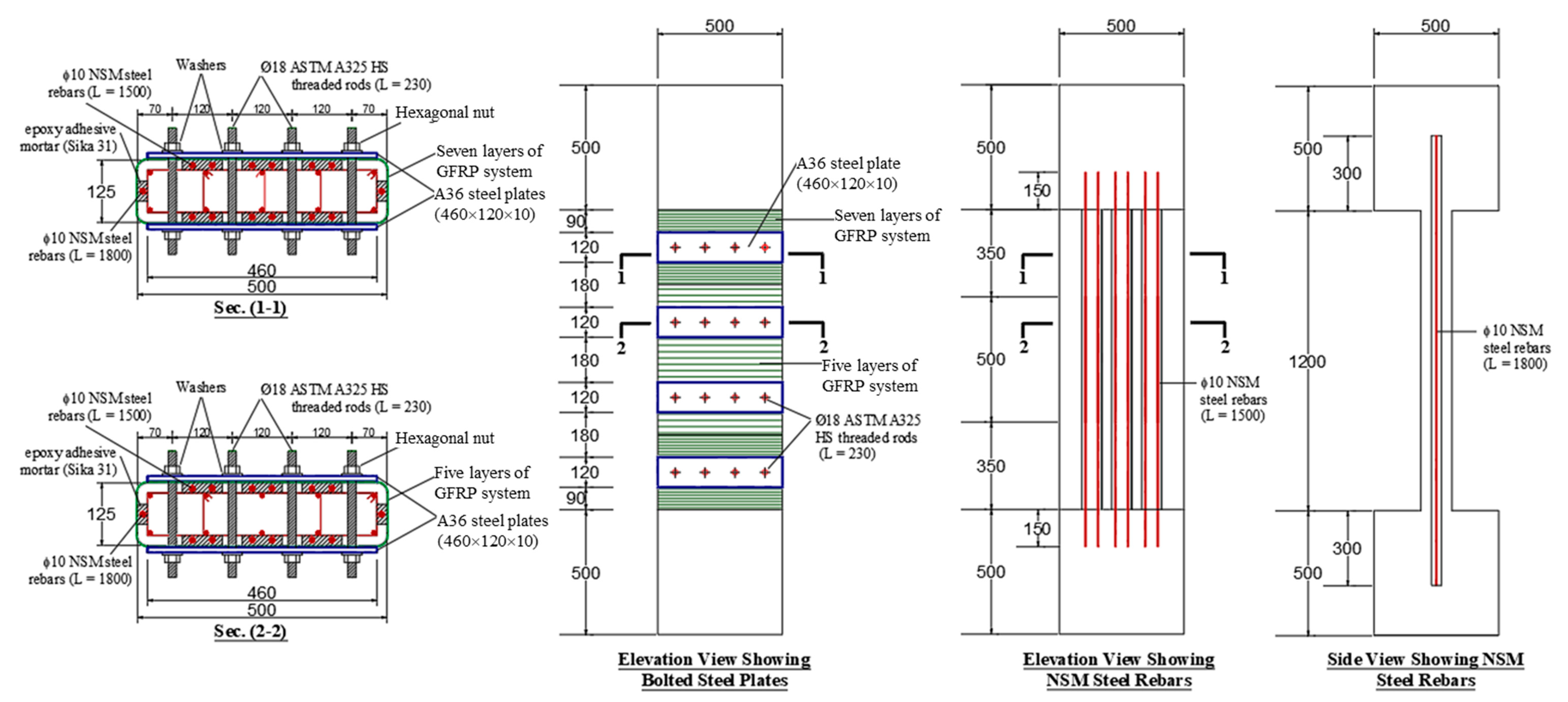










| Specimen ID | Strengthening Scheme | Loading Condition | No. of Casted Specimens | No. of Tested Specimens | Notes |
|---|---|---|---|---|---|
| CON1 and CON2 | Unstrengthened to be used as control specimen | Loaded up to failure | 2 | 2 | Tested in Refs. [24,25] |
| ST1 | Strengthened using first scheme (externally bonded CFRP layers combined with connected NSM steel rebars) | Loaded up to failure | 1 | 1 | Tested in Ref. [24] |
| CON1-0.8P-TLR | Unstrengthened | Loaded up to 80% of the average peak load of specimens CON1 and CON2, and the load was then totally released | 1 | 1 | Tested in this study |
| ST1-0.8P-TLR | It is the same as specimen CON1-0.8P-TLR and was strengthened after preloading using first scheme | Loaded up to failure | - | 1 | Tested in this study |
| ST2 | Strengthened using second scheme (externally bonded GFRP layers + bolted steel plates + connected NSM steel rebars) | Loaded up to failure | 1 | 1 | Tested in Ref. [25] |
| CON2-0.8P-TLR | Unstrengthened | Loaded up to 80% of the average peak load of specimens CON1 and CON2, and the load was then totally released | 1 | 1 | Tested in this study |
| ST2-0.8P-TLR | It is the same as specimen CON2-0.8P-TLR and was strengthened after preloading using second scheme | Loaded up to failure | - | 1 | Tested in this study |
| Total No. of columns | 6 | 8 | |||
| Concrete | ||||
|---|---|---|---|---|
| Model No. | 72R3 | |||
| Model type | Concrete damage | |||
| Compressive strength (MPa) | 29.2 ± 3.4 | |||
| Poisson’s ratio | 0.2 | |||
| Maximum size of aggregate | 10 mm | |||
| Epoxy mortar | ||||
| Model No. | 72R3 | |||
| Model type | Concrete damage | |||
| Compressive strength | 65 MPa | |||
| Poisson’s ratio | 0.2 | |||
| Maximum size of aggregate | 5 mm | |||
| Steel rebars, threaded rods, and plates | ϕ8 rebars | ϕ10 rebars | ϕ18 threaded rods | Plates |
| Model No. | 24 | |||
| Model type | Piecewise linear plasticity | |||
| Yield strength (MPa) | 548 ± 7.1 | 531 ± 6.3 | 711 ± 8.7 | 230 ± 8.0 |
| Poisson’s ratio | 0.3 | 0.3 | 0.3 | 0.3 |
| Elastic modulus (GPa) | 200 | 200 | 200 | 200 |
| Tangent modulus (MPa) | 86.37 ± 6.6 | 133.75 ± 9.9 | 0 | 0 |
| Plastic strain at failure | 9.72% | 9.73% | 6.64% | 19.89% |
| FRP material | CFRP sheets | GFRP sheets | ||
| Model No. | 54–55 | |||
| Model type | Enhanced composite damage | |||
| Layer thickness | 1.3 mm | 1.3 mm | ||
| Tensile modulus in fiber dir. (Gpa) | 71.46 | 20.9 | ||
| Tensile modulus in transverse dir. (Gpa) | 3.59 | 1.05 | ||
| Tensile strength in fiber dir. (MPa) | 710 ± 7.7 | 253 ± 6.9 | ||
| Tensile strength in transverse dir. (MPa) | 71 | 25.3 | ||
| Specimen ID | Outputs | Service Load (kN) | Displacement at Service Load (mm) | Yield Load (kN) | Displacement at Yield Load (mm) | Max. Load (kN) | Displacement at Max. Load (mm) | Ultimate Displacement (mm) | Axial Stiffness at Service Load (kN/mm) | Dissipated Energy at Ultimate State (kN·mm) |
|---|---|---|---|---|---|---|---|---|---|---|
| CON1 | EXP | 745 | 0.27 | 1846 | 0.93 | 1862 | 1.05 | 2.01 | 2810 | 2866 |
| FE | 790 | 0.25 | 1969 | 1.04 | 1974 | 1.09 | 2.15 | 3158 | 3220 | |
| EXP/FE | 0.94 | 1.06 | 0.94 | 0.89 | 0.94 | 0.96 | 0.93 | 0.89 | 0.89 | |
| CON2 | EXP | 802 | 0.29 | 1919 | 0.93 | 2006 | 1.11 | 1.97 | 2815 | 3157 |
| FE | 790 | 0.25 | 1969 | 1.04 | 1974 | 1.09 | 2.15 | 3158 | 3220 | |
| EXP/FE | 1.02 | 1.14 | 0.97 | 0.89 | 1.02 | 1.02 | 0.92 | 0.89 | 0.98 | |
| ST1 | EXP | 1391 | 0.34 | 3223 | 1.06 | 3478 | 1.37 | 1.72 | 4092 | 4212 |
| FE | 1475 | 0.37 | 3491 | 1.18 | 3686 | 1.40 | 1.75 | 4020 | 4343 | |
| EXP/FE | 0.94 | 0.93 | 0.92 | 0.89 | 0.94 | 0.98 | 0.98 | 1.02 | 0.97 | |
| CON1-0.8P-TLR | EXP | 774 | 0.27 | NY | NY | 1463 | 0.59 | 0.59 | 2865 | 503 |
| FE | 790 | 0.25 | NY | NY | 1600 | 0.56 | 0.56 | 3158 | 461 | |
| EXP/FE | 0.98 | 1.08 | - | - | 0.91 | 1.05 | 1.05 | 0.91 | 1.09 | |
| ST1-0.8P-TLR | EXP | 1252 | 0.38 | 2975 | 1.06 | 3129 | 1.27 | 2.08 | 3338 | 4099 |
| FE | 1360 | 0.37 | 3281 | 1.17 | 3400 | 1.28 | 1.88 | 3698 | 4052 | |
| EXP/FE | 0.92 | 1.02 | 0.91 | 0.91 | 0.92 | 0.99 | 1.10 | 0.90 | 1.01 | |
| ST2 | EXP | 1751.5 | 0.31 | 3647 | 0.84 | 4379 | 2.06 | 5.11 | 5743 | 20,396 |
| FE | 1684.8 | 0.34 | 3753 | 1.03 | 4212 | 2.20 | 6.25 | 4954 | 20,967 | |
| EXP/FE | 1.04 | 0.90 | 0.97 | 0.82 | 1.04 | 0.94 | 0.82 | 1.16 | 0.97 | |
| CON2-0.8P-TLR | EXP | 774 | 0.27 | NY | NY | 1573 | 0.53 | 0.53 | 2919 | 460 |
| FE | 790 | 0.25 | NY | NY | 1600 | 0.56 | 0.56 | 3158 | 461 | |
| EXP/FE | 0.98 | 1.06 | - | - | 0.98 | 0.95 | 0.95 | 0.92 | 1.00 | |
| ST2-0.8P-TLR | EXP | 1666 | 0.34 | 3527 | 0.89 | 4166 | 1.98 | 6.50 | 4919 | 18,781 |
| FE | 1577 | 0.36 | 3665 | 1.08 | 3943 | 2.00 | 6.24 | 4380 | 17,516 | |
| EXP/FE | 1.06 | 0.94 | 0.96 | 0.82 | 1.06 | 0.99 | 1.04 | 1.12 | 1.07 |
| Specimen ID | Outputs | Max. Average Concrete Compressive Strength (MPa) | Max. Actual Concrete Compressive Strength (MPa) | Axial Strain in Concrete at Max. Stress | Ultimate Axial Strain in Concrete | Axial Strain in Vertical Steel Bars at Max. Load | Axial Strain in NSM Bars at Max. Load | Max. Horizontal Strain in FRP Sheets | Max. Horizontal Strain in Steel Plates |
|---|---|---|---|---|---|---|---|---|---|
| CON1 | EXP | 29.8 | 23.4 | 0.0026 | 0.0050 | 0.0034 | - | - | - |
| FE | 31.6 | 25.2 | 0.0027 | 0.0054 | 0.0033 | - | - | - | |
| EXP/FE | 0.94 | 0.93 | 0.96 | 0.93 | 1.04 | - | - | - | |
| CON2 | EXP | 32.1 | 25.74 | 0.0028 | 0.0049 | 0.0031 | - | - | - |
| FE | 31.6 | 25.23 | 0.0027 | 0.0054 | 0.0033 | - | - | - | |
| EXP/FE | 1.02 | 1.02 | 1.02 | 0.92 | 0.95 | - | - | - | |
| ST1 | EXP | 56.0 | 41.1 | 0.0034 | 0.0043 | 0.0038 | NA | NA | - |
| FE | 59.0 | 44.6 | 0.0035 | 0.0044 | 0.0038 | 0.0033 | −0.0099 | - | |
| EXP/FE | 0.95 | 0.92 | 0.98 | 0.98 | 1.00 | - | - | - | |
| CON1-0.8P-TLR | EXP | 23.4 | 17.0 | 0.0015 | 0.0015 | 0.0022 | - | - | - |
| FE | 25.6 | 19.2 | 0.0014 | 0.0014 | 0.0022 | - | - | - | |
| EXP/FE | 0.91 | 0.88 | - | - | 0.97 | - | - | - | |
| ST1-0.8P-TLR | EXP | 50.3 | 35.3 | 0.0032 | 0.0052 | 0.0038 | 0.0030 | 0.0085 | - |
| FE | 54.4 | 39.8 | 0.0032 | 0.0047 | 0.0035 | 0.0027 | 0.0098 | - | |
| EXP/FE | 0.93 | 0.89 | 0.99 | 1.10 | 1.10 | 1.10 | 0.86 | - | |
| ST2 | EXP | 70.45 | 56.05 | 0.0051 | 0.0128 | 0.0114 | 0.0124 | 0.0144 | 0.0034 |
| FE | 67.39 | 53.29 | 0.0055 | 0.0156 | 0.0123 | 0.0137 | 0.0121 | 0.0038 | |
| EXP/FE | 1.05 | 1.05 | 0.94 | 0.82 | 0.93 | 0.91 | 1.19 | 0.89 | |
| CON2-0.8P-TLR | EXP | 25.2 | 18.7 | 0.0013 | 0.0013 | 0.0018 | - | - | - |
| FE | 25.6 | 19.2 | 0.0014 | 0.0014 | 0.0022 | - | - | - | |
| EXP/FE | 0.98 | 0.98 | 0.95 | 0.95 | 0.81 | - | - | - | |
| ST2-0.8P-TLR | EXP | 67.02 | 52.52 | 0.0049 | 0.0163 | 0.0107 | 0.0078 | 0.0123 | NA |
| FE | 63.09 | 48.83 | 0.0050 | 0.0156 | 0.0098 | 0.0074 | 0.0121 | 0.0036 | |
| EXP/FE | 1.06 | 1.08 | 0.99 | 1.04 | 1.09 | 1.06 | 1.02 | - |
| Specimen ID | Strengthening Scheme | Loading Condition | Notes |
|---|---|---|---|
| CON | Unstrengthened to be used as control specimen | Loaded up to failure | Modeled in Ref. [25] |
| CON-0.4P-TLR | Unstrengthened | Loaded up to 40% of the peak load of specimen CON, and the load was then totally released | Modeled in this study |
| CON-0.4P-NLR | Unstrengthened | Loaded up to 40% of the peak load of specimen CON, and the load was not released | S/A |
| CON-0.8P-TLR | Unstrengthened | Loaded up to 80% of the peak load of specimen CON, and the load was then totally released | S/A |
| CON-0.8P-NLR | Unstrengthened | Loaded up to 80% of the peak load of specimen CON, and the load was not released | S/A |
| CON-0.9P-TLR | Unstrengthened | Loaded up to 90% of the peak load of specimen CON, and the load was then totally released | S/A |
| CON-0.9P-NLR | Unstrengthened | Loaded up to 90% of the peak load of specimen CON, and the load was not released | S/A |
| ST2 | Strengthened using second scheme (externally bonded GFRP layers + bolted steel plates + connected NSM steel rebars) | Loaded up to failure | Modeled in Ref. [25] |
| ST2-0.4P-TLR | It is the same as specimen CON-0.4P-TLR, and it will be strengthened after preloading using second scheme | S/A | Modeled in this study |
| ST2-0.4P-NLR | It is the same as specimen CON-0.4P-NLR, and it will be strengthened after preloading using second scheme | S/A | S/A |
| ST2-0.8P-TLR | It is the same as specimen CON-0.8P-TLR, and it will be strengthened after preloading using second scheme | S/A | S/A |
| ST2-0.8P-NLR | It is the same as specimen CON-0.8P-NLR, and it will be strengthened after preloading using second scheme | S/A | S/A |
| ST2-0.9P-TLR | It is the same as specimen CON-0.9P-TLR, and it will be strengthened after preloading using second scheme | S/A | S/A |
| ST2-0.9P-NLR | It is the same as specimen CON-0.9P-NLR, and it will be strengthened after preloading using second scheme | S/A | S/A |
| Specimen ID | Yield Load (kN) | Displacement at Yield Load (mm) | Max. Load (kN) | Displacement at Max. Load (mm) | Ultimate Displacement (mm) | Axial Stiffness at Service Load (kN/mm) | Dissipated Energy at Ultimate State (kN·mm) | Ultimate Axial Strain in Concrete (Microstrain) | Axial Strain in Vertical Steel Bars at Max. Load (Microstrain) |
|---|---|---|---|---|---|---|---|---|---|
| CON | 1969 | 1.04 | 1974 | 1.09 | 2.15 | 3158 | 3220 | 5378 | 3276 |
| CON-0.4P-TLR | NY | NY | 800 | 0.25 | 0.25 | 3158 | 100 | 627 | 527 |
| CON-0.4P-NLR | NY | NY | 800 | 0.25 | 0.25 | 3158 | 100 | 627 | 527 |
| CON-0.8P-TLR | NY | NY | 1600 | 0.56 | 0.56 | 3158 | 461 | 1395 | 2227 |
| CON-0.8P-NLR | NY | NY | 1600 | 0.56 | 0.56 | 3158 | 461 | 1395 | 2227 |
| CON-0.9P-TLR | NY | NY | 1800 | 0.67 | 0.67 | 3158 | 685 | 1681 | 2534 |
| CON-0.9P-NLR | NY | NY | 1800 | 0.67 | 0.67 | 3158 | 685 | 1681 | 2534 |
| ST2 | 3753 | 1.03 | 4212 | 2.20 | 6.25 | 4954 | 20,967 | 15,622 | 12,269 |
| ST2-0.4P-TLR | 3847 | 1.11 | 4100 | 1.34 | 6.07 | 4598 | 18,344 | 15,170 | 94,980 |
| ST2-0.4P-NLR | 3375 | 0.96 | 3803 | 1.22 | 3.13 | 3823 | 8018 | 7826 | 7785 |
| ST2-0.8P-TLR | 3665 | 1.08 | 3943 | 2.00 | 6.24 | 4380 | 17,516 | 15,593 | 9795 |
| ST2-0.8P-NLR | 2922 | 0.97 | 3262 | 1.25 | 2.40 | 3433 | 5157 | 6001 | 3998 |
| ST2-0.9P-TLR | 3350 | 1.01 | 3693 | 1.31 | 2.62 | 4105 | 6486 | 6546 | 7476 |
| ST2-0.9P-NLR | 2570 | 0.93 | 2700 | 1.09 | 2.10 | 3177 | 3881 | 5249 | 5697 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Elsanadedy, H.; Abbas, H.; Almusallam, T.; Al-Salloum, Y. Behavior of FRP-Retrofitted Wall-like RC Columns after Preloading to Simulate In-Service Conditions. Buildings 2024, 14, 61. https://doi.org/10.3390/buildings14010061
Elsanadedy H, Abbas H, Almusallam T, Al-Salloum Y. Behavior of FRP-Retrofitted Wall-like RC Columns after Preloading to Simulate In-Service Conditions. Buildings. 2024; 14(1):61. https://doi.org/10.3390/buildings14010061
Chicago/Turabian StyleElsanadedy, Hussein, Husain Abbas, Tarek Almusallam, and Yousef Al-Salloum. 2024. "Behavior of FRP-Retrofitted Wall-like RC Columns after Preloading to Simulate In-Service Conditions" Buildings 14, no. 1: 61. https://doi.org/10.3390/buildings14010061
APA StyleElsanadedy, H., Abbas, H., Almusallam, T., & Al-Salloum, Y. (2024). Behavior of FRP-Retrofitted Wall-like RC Columns after Preloading to Simulate In-Service Conditions. Buildings, 14(1), 61. https://doi.org/10.3390/buildings14010061






