Improved Projection Pursuit Model to Evaluate the Maturity of Healthy Building Technology in China

Abstract

The development of healthy building technology has become a major trend in the global construction industry, especially in China, owing to accelerating urbanization and increasing health awareness among residents. However, an effective evaluation framework to quantify and evaluate the maturity of healthy building technology is lacking. This paper proposes a novel maturity evaluation model for healthy building technology. After analyzing the Driver–Pressure–State–Impact–Response (DPSIR) framework for asserting the maturity of healthy building in China, it constructs an evaluation indicator system, comprising five and twenty-seven first- and second-class indicators, respectively. Subsequently, this paper constructs an improved projection pursuit model based on border collie optimization. The model obtains evaluation results by mining evaluation data, thus overcoming the limitations of traditional evaluation models in dealing with complex data. The empirical research results demonstrate that China is in the optimization stage in terms of the level of maturity of healthy building technology. The weight of impact is as high as 0.2743, which is the most important first-level indicator. Strict green energy utilization policy requirements are the most important secondary indicator, with a weight of 0.0513. Notably, the model is more advanced than other algorithms. In addition, this paper offers some countermeasures and suggestions to promote healthy building in China. Developing and applying this model can promote and popularize healthy building technology in China and even the globe and contribute to a healthier and more sustainable living environment.

1. Introduction

Healthy building has become an important aspect of the global construction industry during the past 40 years due to a focus on sustainable development, with the goal of healthy and comfortable living and working environments. For example, the office building at 425 Park Avenue, New York, USA, is the first WELL-certified healthy building. It is designed to improve 11 parameters to ensure the well-being of tenants.

China is promoting the development of healthy buildings. The Green Building Action Plan was issued by the State Council of China. The number of healthy building projects in China is expected to be close to 1500 by 2025, with a total GDP of 46.6 billion. However, healthy buildings are relatively rare in China compared to developed countries (such as the United States and France). China has developed healthy building evaluation systems, but few studies investigated actual projects, and managers (e.g., government policy-makers, architects, and building operators) lack decision support. The purpose of this paper is to provide this support.

A healthy building means that managers comprehensively consider the impact of a building on human health and the environment during the building’s lifecycle. The building is designed to improve the physical and mental health of residents [1]. The maturity of a healthy building refers to its comprehensive performance and effectiveness in promoting residents’ physical and mental health and improving overall quality of life during the design, construction, and operation of a building project. This concept involves many factors such as the materials used in buildings, internal environmental controls, and sustainable utilization of natural resources, which reflects the close relationship between the built environment and public health as well as its progress level. Healthy buildings require mature technologies and management concepts. A maturity evaluation is a multi-attribute evaluation problem [2]. The maturity evaluation of the healthy buildings in China includes the following: (1) establishing a scientific and practical indicator system, (2) calculating accurate indicator weights, and (3) developing a fair and accurate evaluation model.

Research on healthy buildings has made significant achievements recently. To the best of the authors’ knowledge, no studies have investigated the maturity of healthy buildings. Most focused on an evaluation of healthy buildings.

Lee et al. [3] put forward a qualitative indoor environment assessment method to evaluate the health performance of buildings. Small [4] analyzed the failures of healthy buildings and concluded that an interdisciplinary approach, including experts in architecture and medicine, is required to develop healthy buildings. Loftness et al. [5] summarized the technical measures needed to develop healthy buildings, providing a basis for our research. Paine and Thompson [6] investigated environmental indicators affecting healthy buildings from an urban planning perspective. Gherscovici and Mayer [7] summarized the latest research on the effects of healthy buildings on residents’ back and neck pain. Serano and Li [8] studied the relationship between the built environment and residents’ health, emphasizing that healthy buildings should improve people’s lives and work. Wang et al. [9] summarized healthy building development in China in recent years but did not analyze the maturity of healthy buildings. Na et al. [10] focused on healthy building management in Korea, considering how it could be improved within a given cost range. Mao et al. [11] obtained 80 indicators affecting healthy buildings from a questionnaire survey. However, too many indicators were unsuitable for practical applications. In addition, the authors did not explain the relationship between the indicators, which is required to determine the factors influencing the performance of healthy buildings.

Shao et al. [12] used the analytic hierarchy process (AHP) to calculate the weights of healthy building indicators in the Taiwan Province in China. For the convenience of reading,

Table A1. An abbreviation list.

Abbreviation	Standard Expression
AHP	analytic hierarchy process
CFDs	computational fluid dynamics
MCDM	multi-criteria decision-making
PPM	projection pursuit mode
GAs	genetic algorithms
PSO	particle swarm optimization
BCO	border collie optimization
DPSIR	Driver–Pressure–State–Impact–Response
EEA	European Environment Agency
ACO	colony optimization
SA	simulated annealing
GJO	golden jackal optimization
WOA	walrus optimization algorithm
AOA	arithmetic optimization algorithm

of this manuscript summarizes all the abbreviations in this paper. Chen et al. [13] identified the main factors affecting healthy buildings based on the grounded theory and obtained the indices’ importance values based on the survey results. The AHP and questionnaire surveys are subjective weight calculation methods because they are influenced by expert opinions. Gong et al. [14] used the AHP and entropy weight method to calculate the indicator weights of a healthy building in Quanzhou, China. The entropy weight method is affected by data variability and may result in unreasonable weights in complex problems such as the evaluation of the maturity of healthy building technology [15]. It is a classic risk to set weights through AHP, but in recent years, scholars seem to prefer quantitative methods of data mining to determine indicator weights.

Saadatjoo et al. [16] used computational fluid dynamics (CFDs) to simulate and analyze the ventilation in healthy buildings. This method is suitable for analyzing ventilation but not for the other properties of healthy buildings. Lee et al. [3] constructed a healthy building evaluation model based on a performance tree. Most of these methods require setting the membership degree of parameters determined by experts in advance to obtain accurate evaluation results, and it is difficult to extract sufficient information. Many factors affect the performance of smart buildings, and a sufficiently large data set is required. Choosing an evaluation method suitable for evaluating multiple attributes and extracting sufficient data from the evaluation indicator are challenging.

The projection pursuit model (PPM) is a novel data mining algorithm. It obtains the weights and evaluation results by mining the evaluation data. This method is in-creasingly used for multi-attribute evaluations of complex systems, such as sugarcane plantations [17] and construction safety risks [18]. Zhu et al. [18] used the PPM to pro-ject high-dimensional data into a low-dimensional space to analyze multiple attributes and evaluate construction safety risk. Zhao et al. [17] evaluated a sugarcane plantation and found that the PPM retained sufficient data information. Liu et al. [19] demon-strated that the PPM was highly suitable for evaluating the complex relationships be-tween variables and for dealing with diverse data types. In addition, the optimal pro-jection direction must be determined in the PPM to ensure accurate results. Optimiza-tion problems can be complex, and traditional methods may not provide the global op-timal solution or have low computational efficiency. Border collie optimization (BCO) imitates the border collie’s approach to herding sheep [20]. It divides the population into sheep-dogs and sheep, and simulates herding, ensuring a global optimum solution.

This paper proposes a novel maturity evaluation model for healthy buildings in China, providing the following contributions:

(1)

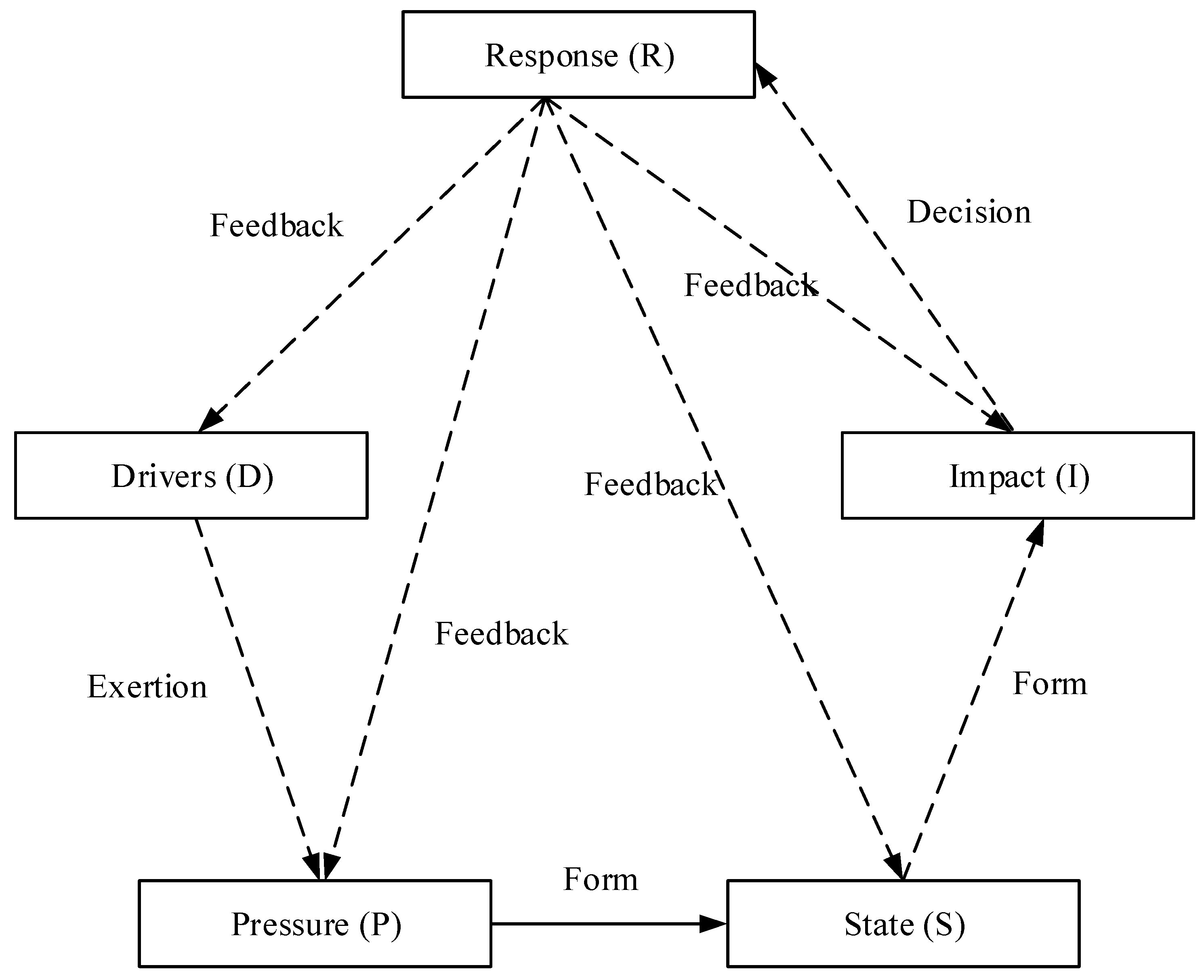
We use the Driver–Pressure–State–Impact–Response framework (DPSIR) to construct a novel indicator system for evaluating the maturity of healthy buildings in China. This framework comprehensively identifies factors influencing the application and promotion of healthy buildings in China and reveals the logical relationship between the indicators.

(2)

A maturity evaluation model for healthy buildings in China is established using a BCO-improved PPM. The model uses BCO to select the best projection direction of the PPM and derives the indicator weights and evaluation levels from the maturity evaluation data. This model combines the powerful data extraction capacity of the PPM and the BCO’s ability to obtain a global optimum solution, providing a new tool for healthy building managers.

(3)

Several strategies are recommended to promote healthy buildings in China. The proposed method provides new insights for managers and scholars and balances the economic and environmental benefits of healthy buildings.

The remainder of this article is structured as follows. Section 2 describes the methods used, including the evaluation indicator system and evaluation model for the maturity of healthy buildings in China. Section 3 provides the results and the application of the model to several healthy building projects in China. Section 4 is the discussion. Section 5 summarizes this paper and presents the limitations.

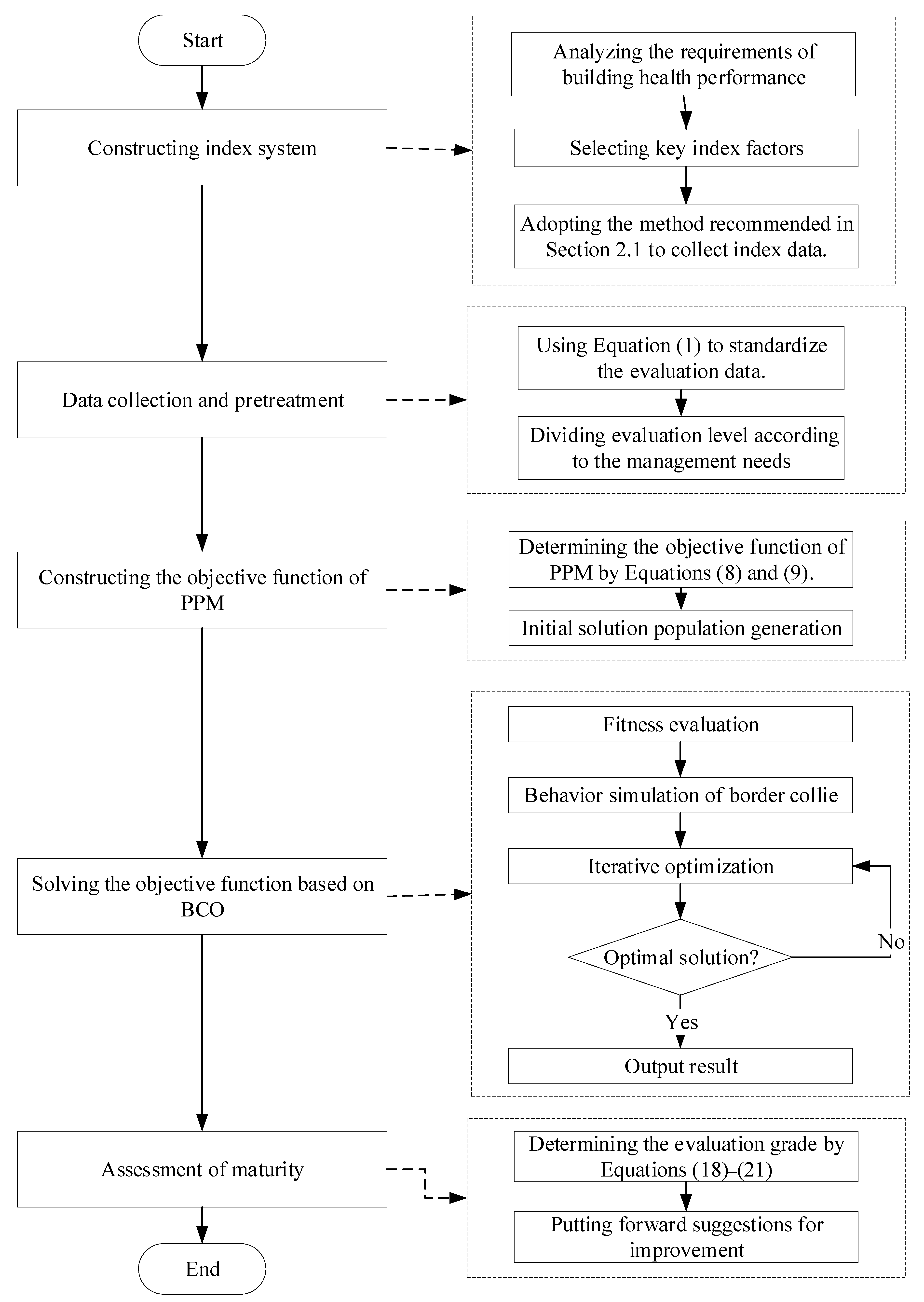
2. Materials and Methods

2.1. The Proposed Indicator System Based on the DPSIR

The European Environment Agency (EEA) proposed the DPSIR based on the PSR model in 1997. This framework describes the interaction and feedback mechanisms, among other factors. It has been widely used for assessing the sustainable development of complex systems [21]. The DPSIR considers the following five aspects:

(1)

Drivers. They are the driving force in promoting healthy buildings. Examples include the public’s increasing demand for a healthy living and working environment, the government’s policy support for healthy buildings, and the rising price of traditional energy.

(2)

Pressure. This refers to the potential obstacles to promoting healthy buildings. Examples include the high construction and operating costs of healthy buildings, the few environmental protection measures, a lack of low-carbon building materials, and a lack of citizen knowledge of healthy buildings.

(3)

State. This refers to the state of healthy buildings, such as the existing technology used, the number, the durability, the stability, and the comfort of existing healthy buildings.

(4)

Impact. This refers to the social and environmental benefits of healthy buildings. Examples include improvements in residents’ satisfaction, improvements in the environment, and the economic benefits to the individuals and enterprises in healthy buildings.

(5)

Response. This refers to the measures taken by employees to promote healthy buildings. Examples include improvements in technology, research, development, and publicity.

The logical relationship among the factors in the DPSIR is dynamic and cyclic, with many interactions [22]. For example, when few environmentally friendly and low-carbon building materials are available (high pressure), policy-makers can implement stronger drivers, and the healthy building industry will respond by increasing technology research and development. As a result, more environmentally friendly and low-carbon building materials are developed, improving the number of healthy buildings (state), the environment (impact), and sustainable development (driver). The DPSIR for assessing the maturity of healthy buildings in China is shown in Figure 1.

A preliminary analysis of the influencing factors was conducted using the United States WELL building standard, the United States Fitwel standard, the Nine Foundations of a Healthy Building (Harvard University), Healthy Building: A Guide for the Construction and Renovation of Healthy Buildings for Developers and Contractors (France), and China’s Assessment Standard for Green Building (GB/T 50378-2019). A literature review was conducted, searching for the keyword “smart building”. The indicator system is listed in

Table 1. Indicator system for evaluating healthy buildings in China using the DPSIR.

Primary Indices	Secondary Indices	Ref.
$\mathrm{Drivers}: D$	Urbanization ratio: $D_1$	[22]
	Enhancement of public health awareness: $D_2$	[11]
	Strict green energy utilization policy requirements: $D_3$	[22]
	Increased policy support for healthy buildings: $D_4$	[22,23]
$\mathrm{Pressure}: P$	Increased construction costs: $P_1$	[11,24]
	Increased operating costs: $P_2$	[11,24]
	Lack of healthy building technology: $P_3$	[22,23]
	Lack of experience in healthy building management: $P_4$	[11]
	Lack of environmentally friendly materials: $P_5$	[11,25]
	Citizens’ insufficient understanding of healthy buildings: $P_6$	[1]
$\mathrm{State}: S$	Proportion of existing healthy buildings: $S_1$	[22]
	Proportion of healthy building management system: $S_2$	[9]
	Proportion of environmentally friendly materials: $S_3$	[1,25]
	Safety of existing healthy buildings: $S_4$	[11,26]
	Comfort of existing healthy buildings: $S_5$	[22,27]
$\mathrm{Impact}: I$	Improving citizens’ satisfaction with healthy buildings: $I_1$	[11,26]
	Environmental improvement: $I_2$	[22,28]
	Reduction of energy consumption: $I_3$	[1,26]
	Promotion of building‘s market value: $I_4$	[11,26]
	Increases in building rent: $I_5$	[9,26]
	Improvement of residents’ health: $I_6$	[22,27,29]
	Increased jobs: $I_7$	[1]
$\mathrm{Response}: R$	Higher technology research and development expenses: $R_1$	[11,23]
	Strengthening citizens’ perceptions: $R_2$	[9]
	Increased economic benefits of healthy buildings: $R_3$	[11,24]
	Reduced investment risk of the owner: $R_4$	[1,30]
	Strengthening the implementation of healthy building standards: $R_5$	[11]

.

In Table 1, $P_1$, $P_2$, $P_3$, $P_4$, $P_5,$ and $P_6$ are the cost indicators. The smaller the indicator score, the greater the promotion of healthy buildings. The other indicators are benefit indicators. The larger the indicator score, the greater the promotion of healthy buildings. $D_1$, $P_1$, $P_2$, $S_1$, $S_3$, $I_3$, $I_5$, $R_1$, and $R_3$ are the quantitative indicators, and the rest are the qualitative indicators. The maturity assessment of healthy buildings in China is a complex multi-attribute problem.

See Appendix B for the definition of secondary indicators and their impact on healthy building engineering.

Extreme value normalization was used to preprocess the data. The initial evaluation indicator data set was $\left\{x_{ij}|i=1,\cdots ,n;j=1,\cdots ,m\right\}$, where $x_{ij}$ is the $j$-th indicator value of the $i$-th evaluation object, $n$ is the number of objects to be evaluated, and $m$ is the number of secondary indices.

The normalized data set $\left\{x_{ij}^{\mathrm{*}}\right\}$ is obtained by Equation (1) [31]:

$$x_{ij}^{*}=\left\{\begin{array}{cc}{\displaystyle \frac{x_{ij}-\mathrm{m}\mathrm{i}\mathrm{n}\left\{x_j\right\}}{\max \left\{x_j\right\}-\mathrm{m}\mathrm{i}\mathrm{n}\left\{x_j\right\}}}& if benefit indicator\\ {\displaystyle \frac{\max \left\{x_j\right\}-x_{ij}}{\max \left\{x_j\right\}-\mathrm{m}\mathrm{i}\mathrm{n}\left\{x_j\right\}}}& if cost indicator\end{array}\right.,$$

(1)

where $\mathrm{m}\mathrm{a}\mathrm{x}\left\{x_j\right\}$ and $\mathrm{m}\mathrm{i}\mathrm{n}\left\{x_j\right\}$ are the maximum and minimum values of the $j$-th indicator, respectively. For the convenience of reading,

Table A2. Mathematical variable list.

Mathematical Variable	Meaning	Location of Appearance
$x_{ij}^{*}$	normalized evaluation data	Equation (1)
$x_{ij}$	original evaluation data	Equation (1)
$z_i$	required maturity evaluation value	Equation (2)
$a\left(j\right)$	$\mathrm{square} \mathrm{root} \mathrm{of} \mathrm{the} \mathrm{weight} \mathrm{of} \mathrm{the} j$-th indicator	Equation (2)
$S_z$	$\mathrm{the} \mathrm{standard} \mathrm{deviation} \mathrm{of} \mathrm{the} \mathrm{projection} \mathrm{value} z_i$	Equation (3)
$D_Z$	$\mathrm{the} \mathrm{local} \mathrm{density} \mathrm{of} z_i$	Equation (3)
$\mathbf{Q}\left(a\right)$	projection function of PPM	Equation (3)
$E_z$	$\mathrm{the} \mathrm{average} \mathrm{projection} \mathrm{value} \mathrm{of} \mathrm{the} \mathrm{sequence} \left\{z_i\right\}$	Equation (4)
$R$	the window radius of the local density	Equation (5)
$U$	a unit step function	Equation (5)
$r_{ik}$	$\mathrm{the} \mathrm{distance} \mathrm{between} z_i$$\mathrm{and} z_k$	Equation (6)
$V_f\left(t+1\right)$	$\mathrm{the} \mathrm{speeds} \mathrm{of} \mathrm{the} \mathrm{lead} \mathrm{dog} \mathrm{at} \mathrm{time} t+1$	Equation (10)
$V_f\left(t\right)$	$\mathrm{the} \mathrm{speeds} \mathrm{of} \mathrm{the} \mathrm{lead} \mathrm{dog} \mathrm{at} \mathrm{time} t$	Equation (10)
${Acc}_f\left(t\right)$	$\mathrm{the} \mathrm{acceleration} \mathrm{of} \mathrm{the} \mathrm{lead} \mathrm{dog} \mathrm{at} \mathrm{time} t$	Equation (10)
${Pop}_f\left(t\right)$	$\mathrm{the} \mathrm{position} \mathrm{of} \mathrm{the} \mathrm{lead} \mathrm{dog} \mathrm{at} \mathrm{time} t$	Equation (10)
$V_{sg}\left(t+1\right)$	the speed at which the sheep move due to the lead dog’s actions	Equation (11)
${Pop}_{sg}\left(t\right)$	$\mathrm{the} \mathrm{optimum} \mathrm{sheep} \mathrm{position} \mathrm{at} \mathrm{time} t$	Equation (11)
${\theta }_1$, ${\theta }_2$	random angles	Equation (12)
$V_{le}\left(t+1\right)$	$\mathrm{the} \mathrm{velocity} \mathrm{of} \mathrm{the} \mathrm{left} \mathrm{dog} \mathrm{at} \mathrm{time} t+1$	Equation (13)
${Acc}_{le}\left(t\right)$	$\mathrm{the} \mathrm{acceleration} \mathrm{of} \mathrm{the} \mathrm{left} \mathrm{dog} \mathrm{at} \mathrm{time} t$	Equation (13)
$d$	the dimension of the problem to be optimized	Equation (15)
$\mathrm{A}\mathrm{v}\mathrm{g}$	the average function	Equation (15)
${Pop}_f\left(t+1\right)$	$\mathrm{the} \mathrm{position} \mathrm{of} \mathrm{the} \mathrm{lead} \mathrm{dog} \mathrm{at} \mathrm{time} t+1$	Equation (16)
${Pop}_{le}\left(t+1\right)$	$\mathrm{the} \mathrm{position} \mathrm{of} \mathrm{the} \mathrm{left} \mathrm{dog} \mathrm{at} \mathrm{time} t+1$	Equation (16)
${Pop}_{ri}\left(t+1\right)$	$\mathrm{the} \mathrm{position} \mathrm{of} \mathrm{the} \mathrm{right} \mathrm{dog} \mathrm{at} \mathrm{time} t+1$	Equation (16)
$d_{ij}$	$\mathrm{the} \mathrm{distance} \mathrm{between} \mathrm{the} i$$-\mathrm{th} \mathrm{sample} \mathrm{and} \mathrm{the} j$-th sample	Equation (18)
$L_t$	the squared sum of differences	Equation (19)
$x_{it}$	$i$$-\mathrm{th} \mathrm{sample} \mathrm{in} \mathrm{class} G_t$	Equation (19)
$n_t$	$\mathrm{the} \mathrm{number} \mathrm{of} \mathrm{samples} \mathrm{in} \mathrm{class} G_t$	Equation (19)
${\overline{x}}_t$	$\mathrm{the} \mathrm{center} \mathrm{of} \mathrm{gravity} \mathrm{of} \mathrm{class} G_t$	Equation (19)
$L$	the sum of squares	Equation (20)

of this manuscript summarizes all the mathematical variables in this paper.

2.2. The Proposed Evaluation Model Based on BCO-Improved PPM

(1)

The projection indicator function is $\mathbf{Q}\left(a\right).$

The evaluation indicator system with the 27 indicators has the projection directions $a=\left\{a\left(1\right),\cdots ,a\left(j\right),\cdots ,a\left(27\right)\right\}$. A one-dimensional projection value is obtained, i.e., the required maturity evaluation value $z_i$ [17] is as follows:

$$z_i={\sum }_{j=1}^{27}a\left(j\right)·x_{ij}^{*},$$

(2)

where $i=1,\cdots ,n$.

In the PPM, the optimal projection direction $a^{\mathrm{*}}$ ensures that the projected value $z_i$ has a high local density and is globally dispersed. The projection function $\mathbf{Q}\left(a\right)$ is defined as [17,32,33,34] follows:

$$\mathbf{Q}\left(a\right)=S_z\ast D_Z,$$

(3)

where $S_z$ is the standard deviation of the projection value $z_i$, and $D_Z$ is the local density of $z_i$.

Optimizing the projection direction is actually necessary to find the best projection index in a certain sense, which is generally closely related to the practical problems. When the data are diversified and complicated, there may be many projection directions, but the best projection direction must be the one that can clearly spread the data into the most meaningful and valuable projection direction.

The main reason “$z_i$ is finally dispersed and highly dense” is that when the PPM is applied to a multi-attribute rating, we hope that the data sets belonging to different evaluation grades can be dispersed as much as possible, while the data sets belonging to the same evaluation grade can be concentrated as much as possible. This was proven mathematically in this manuscript where the PPM was applied to the multi-attribute evaluations.

$S_z$ and $D_Z$ are calculated are as follows [18]:

$$S_z=\sqrt{{\sum }_{i=1}^n{\displaystyle \frac{{\left(z_i-E_z\right)}^2}{n-1}}},$$

(4)

$$D_Z={\sum }_{i=1}^n{\sum }_{k=1}^n\left(R-r_{ik}\right)·U\left(R-r_{ik}\right),$$

(5)

$$r_{ik}=\left|z_i-z_k\right|,$$

(6)

$$U\left(R-r_{ik}\right)=\left\{\begin{array}{cc}1& if R-r_{ik}\ge 0\\ 0& if R-r_{ik}<0\end{array}\right.,$$

(7)

where $E_z$ is the average projection value of the sequence $\left\{z_i\right\}$, $R$ is the window radius of the local density, which is generally ${0.1S}_z$, $r_{ik}$ is the distance between $z_i$ and $z_k$, and $U\left(R-r_{ik}\right)$ is a unit step function.

(2)

The objective function is as follows.

The optimum projection direction is determined by maximizing the projection indicator function [17]:

$$\mathrm{m}\mathrm{a}\mathrm{x}\mathbf{Q}\left(a\right)=S_z\ast D_Z.$$

(8)

The sum of the global weights of the secondary indicators should be 1 in the multi-attribute evaluations. Therefore, the objective function (Equation (8)) must meet the following constraint [18]:

$$\mathrm{s}.\mathrm{t}.{\sum }_{j=1}^{27}{\left(a\left(j\right)\right)}^2=1.$$

(9)

Since it is difficult to solve Equation (8) using the evaluation data, meta-heuristic optimization is typically used.

(3)

BCO is used to solve the objective function.

BCO is a novel meta-heuristic optimization algorithm that imitates sheep herding by border collies. Equation (8) is the objective function of BCO.

Border collies use the following three behaviors to herd sheep:

(1)

Gathering. Border collies control the sheep’s movements from the side and front to gather the animals and move them in a direction.

(2)

Stalking. Border collies track the sheep’s position.

(3)

Eyeing. When sheep leave the herd, the border collie forces them to move in the right direction.

The global optimal solution is for the border collie to herd the sheep back to a specific location.

The BCO algorithm considers three border collies (lead dog, left dog, and right dog). The lead dog is responsible for gathering and has the highest fitness values (${fit}_f$). The left and right dogs have the second and third fitness values (${fit}_{le}$ and ${fit}_{ri}$, respectively). They stalk and guard the sheep. The other population is the sheep, and their fitness value (${fit}_s$) is lower than that of the dogs.

The equation for updating the speed of the three border collies is as follows:

$$\left\{\begin{array}{l}{V}_f\left(t+1\right)=\sqrt{V_f{\left(t\right)}^2+2{Acc}_f\left(t\right)\ast {Pop}_f\left(t\right)}\\ V_{ri}\left(t+1\right)=\sqrt{V_{ri}{\left(t\right)}^2+2{Acc}_{ri}\left(t\right)\ast {Pop}_{ri}\left(t\right)}\\ V_{le}\left(t+1\right)=\sqrt{V_{le}{\left(t\right)}^2+2{Acc}_{le}\left(t\right)\ast {Pop}_{le}\left(t\right)}\end{array}\right.,$$

(10)

where $V_f\left(t+1\right)$ and $V_f\left(t\right)$ are the speeds of the lead dog at time $t+1$ and time $t$, respectively, ${Acc}_f\left(t\right)$ is the acceleration of the lead dog at time $t$, and ${Pop}_f\left(t\right)$ is the position of the lead dog at time $t$. The definitions of the other variables are similar, but the variables have different subscripts representing different border collies.

According to the border collies’ behaviors, the speed of the sheep is updated as follows:

(1)

Gathering.

$$V_{sg}\left(t+1\right)=\sqrt{V_f{\left(t+1\right)}^2+2{Acc}_f\left(t\right)\ast {Pop}_{sg}\left(t\right)},$$

(11)

where $V_{sg}\left(t+1\right)$ is the speed at which the sheep move due to the lead dog’s actions, and ${Pop}_{sg}\left(t\right)$ is the optimum sheep position at time $t$.

(2)

Stalking.

$$\left\{\begin{array}{l}{V}_s\left(t+1\right)={\displaystyle \frac{V_s^1\left(t+1\right)+V_s^2\left(t+1\right)}{2}}\\ V_s^1\left(t+1\right)=\sqrt{{\left(V_{ri}\left(t+1\right)tan{\theta }_1\right)}^2+2{Acc}_{ri}\left(t\right)\ast {Pop}_{ri}\left(t\right)}\\ V_s^2\left(t+1\right)=\sqrt{{\left(V_{le}\left(t+1\right)tan{\theta }_2\right)}^2+2{Acc}_{le}\left(t\right)\ast {Pop}_{le}\left(t\right)}\end{array}\right.,$$

(12)

where ${\theta }_1$ and ${\theta }_2$ are random angles.

(3)

Eyeing.

$$V_{se}\left(t+1\right)=\left\{\begin{array}{cc}\sqrt{V_{le}{\left(t+1\right)}^2-2{Acc}_{le}\left(t\right)\ast {Pop}_{sg}\left(t\right)}& if {fit}_{le}\le {fit}_{ri}\\ \sqrt{V_{ri}{\left(t+1\right)}^2+2{Acc}_{ri}\left(t\right)\ast {Pop}_{sg}\left(t\right)}& if {fit}_{le}>{fit}_{ri}\end{array}\right.,$$

(13)

where $V_{le}\left(t+1\right)$ is the velocity of the left dog at time $t+1$, and ${Acc}_{le}\left(t\right)$ is the acceleration of the left dog at time $t$. The parameters of the right dog are the same with different subscripts.

The acceleration of all populations is as follows:

$${Acc}_i(t+1)={\displaystyle \frac{V_i\left(t+1\right)-V_i\left(t\right)}{{Time}_i\left(t\right)}},$$

(14)

where $i\in \left\{f,le,ri,sg,ss,se\right\}$.

The update method for the average time is as follows:

$${Time}_i\left(t+1\right)=\mathrm{A}\mathrm{v}\mathrm{g}{\sum }_{i=1}^d{\displaystyle \frac{V_i\left(t+1\right)-V_i\left(t\right)}{{Acc}_i(t+1)}},$$

(15)

where $d$ is the dimension of the problem to be optimized, and $\mathrm{A}\mathrm{v}\mathrm{g}$ is the average function.

The displacement of the dogs is updated as follows:

$$\left\{\begin{array}{l}{Pop}_f\left(t+1\right)=V_f\left(t+1\right)·{Time}_f\left(t+1\right)+{\displaystyle \frac{{Acc}_f\left(t+1\right)+{Time}_f{\left(t+1\right)}^2}{2}}\\ {Pop}_{le}\left(t+1\right)=V_{le}\left(t+1\right)·{Time}_{le}\left(t+1\right)+{\displaystyle \frac{{Acc}_{le}\left(t+1\right)+{Time}_{le}{\left(t+1\right)}^2}{2}}\\ {Pop}_{ri}\left(t+1\right)=V_{ri}\left(t+1\right)·{Time}_{ri}\left(t+1\right)+{\displaystyle \frac{{Acc}_{ri}\left(t+1\right)+{ Time}_{ri}{\left(t+1\right)}^2}{2}}\end{array}\right.,$$

(16)

where ${Pop}_f\left(t+1\right)$ is the position of the lead dog at time $t+1$, ${Pop}_{le}\left(t+1\right)$ is the position of the left dog at time $t+1$, and ${Pop}_{ri}\left(t+1\right)$ is the position of the right dog at time $t+1$.

The location of the sheep is updated as follows:

$$\left\{\begin{array}{l}{Pop}_{sg}\left(t+1\right)=V_{sg}\left(t+1\right)·{Time}_{sg}\left(t+1\right)+{\displaystyle \frac{{Acc}_{sg}\left(t+1\right)+{Time}_{sg}{\left(t+1\right)}^2}{2}}\\ {Pop}_{ss}\left(t+1\right)=V_{ss}\left(t+1\right)·{Time}_{ss}\left(t+1\right)+{\displaystyle \frac{{Acc}_{ss}\left(t+1\right)+{Time}_{ss}{\left(t+1\right)}^2}{2}}\\ {Pop}_{se}\left(t+1\right)=V_{se}\left(t+1\right)·{Time}_{se}\left(t+1\right)+{\displaystyle \frac{{Acc}_{se}\left(t+1\right)+{Time}_{se}{\left(t+1\right)}^2}{2}}\end{array}\right..$$

(17)

(4)

Cluster analysis of the results using the squared sum of the differences.

The optimal projection value $\left\{z_i^{\mathrm{*}}\right\}$ is derived by using the optimal projection direction $a^{\mathrm{*}}$ in Equation (2), providing the evaluation results for the city or province. The arithmetic average of the optimum projection value $\left\{z_i^{\mathrm{*}}\right\}$ is the evaluation value of the maturity of healthy building technology in China.

The Euclidean distance and squared sum of differences were used to analyze the factors influencing the maturity of healthy building technology.

The Euclidean distance is the distance between two points in two-dimensional and three-dimensional spaces. It is expressed as follows:

$$d_{ij}=\sqrt{{\sum }_{k=1}^p{\left(x_{ik}-x_{jk}\right)}^2},$$

(18)

where $d_{ij}$ represents the distance between the $i$-th sample and the $j$-th sample. Ward’s method for calculating the squared sum of differences is a mature method for determining the local optimum. The $n$ samples are clustered into $k$ classes: $\left\{G_1,G_2,\cdots ,G_k\right\}$.

The squared sum of the differences $L_t$ in class $G_t$ is as follows:

$$L_t={\sum }_{i=1}^{n_t}{\left(x_{it}-{\overline{x}}_t\right)}^{`}\left(x_{it}-{\overline{x}}_t\right),$$

(19)

where $x_{it}$ represents the $i$-th sample in class $G_t$, $n_t$ is the number of samples in class $G_t$, and ${\overline{x}}_t$ is the center of gravity of class $G_t$.

The sum of the squares in class $L$ is as follows:

$$L={\sum }_{i=1}^k{\sum }_{i=1}^{n_t}{\left(x_{it}-{\overline{x}}_t\right)}^{`}\left(x_{it}-{\overline{x}}_t\right).$$

(20)

If classes $G_p$ and $G_q$ are merged into $G_r$, the equation for calculating the distance between class $G_k$ and the new class $G_r$ is as follows:

$$D_w^2\left(k,r\right)={\displaystyle \frac{n_p+n_k}{n_r+n_k}}{D}_w^2\left(k,p\right)+{\displaystyle \frac{n_q+n_q}{n_r+n_k}}{D}_w^2\left(k,p\right)-{\displaystyle \frac{n_k}{n_r+n_k}}{D}_w^2\left(p,q\right).$$

(21)

This method was used to classify the evaluation values, and SPSS software v26.0 was used to compare the samples’ $z_i^{\mathrm{*}}$ values. The more similar the values, the more likely they are to fall into the same class.

2.3. The Implementation of the Proposed Model

The evaluation model proposed in this paper was used to evaluate the maturity of healthy building applications in China. The core innovation of this model is its improved ability to deal with complex data and nonlinear characteristics. Building on the research results in Section 2.1 and Section 2.2, this section introduces the stepwise realization of the model.

Step 1: Determine the evaluation indicator system. The main requirements of the evaluation model are determined by conducting a demand analysis of the building’s health performance. Using the demand analysis results, select the key indicators to measure the maturity of the building health application. Notably, managers should directly use the indicator system established in Section 2.1 or add or delete the secondary indicators in the indicator system presented in Table 1.

Step 2: Data collection and pretreatment. According to the determined evaluation indicator system, collect the relevant data on actual construction projects. It is worth noting that the data acquisition of qualitative indicators should be scientifically and comprehensively investigated by a questionnaire. To eliminate the influence between different dimensional indicators, adopt Equation (1) to standardize the evaluation data. In addition, based on management needs, divide the evaluation grades of the application proficiency and all of the secondary indicators.

Step 3: Construct the projection pursuit model (PPM). From the evaluation data obtained in Step 2, construct the initial projection pursuit model using Equation (2). Determine the objective function of the initial projection pursuit model according to Equations (8) and (9). The calculation method of each variable in the objective function is based on Equations (4)–(7). The model evaluates the application maturity of a healthy building by establishing a mathematical relationship between the evaluation data from all secondary indicators and the maturity evaluation grade.

Step 4: Solve the objective function based on BCO. This involves the following steps: (1) Generation of initial solution population. Generate the initial solution population using the BCO algorithm. Each solution represents a potential projection direction. (2) Fitness evaluation. Evaluate the fitness of each solution, that is, its effectiveness in evaluating the health maturity of buildings. (3) Behavior simulation of a border collie. Simulate a border collie’s behavior, including tracking, driving, and updating the position of sheep, to optimize the solution group and determine the optimal projection direction. Different types of border collies and sheep adopt different formulas for updating speed and position. (4) Iterative optimization. Obtain the optimal solution by iteration until the termination condition is met (such as the maximum number of iterations or the improvement of the solution is less than a certain threshold).

Step 5: Maturity evaluation and analysis. This involves the following steps: (1) Square each element in the optimal projection vector that is optimized using BCO, which is the objective weight of each secondary indicator. (2) Use the Euclidean distance and square sum of deviations algorithm (Equations (18)–(21)) to describe the difference between the research object and the preset evaluation grade. (3) Obtain the final evaluation result based on the difference between the research object and the preset evaluation grade. (4) Based on the evaluation results, identify the advantages and disadvantages of the building health application and suggest improvements.

By performing the above steps, the model can not only accurately evaluate the maturity of the building health application but also guide the specific optimization for the building’s design and management, thus promoting healthy building applications. The flow chart of the proposed model is shown in Figure 2.

It is worth mentioning that the methodology proposed in this manuscript still has the following supplements. The core idea of the evaluation model developed in this paper is to use the PPM to mine the structural characteristics of the evaluation data to obtain the evaluation results. However, in the process of using the PPM, its evaluation results are influenced by the best projection direction. Therefore, this paper uses BCO, a novel meta-heuristic optimization algorithm, to find the best projection direction of the PPM. In addition, in order to describe the evaluation results in more detail, this paper uses the Euclidean distance and square sum of deviations algorithm to analyze the differences between the evaluation results and the evaluation grades.

3. Case Study

3.1. Data Source and Preprocessing

This paper collected the evaluation data for all secondary indicators based on the data collection method presented in Section 2.1. The indicators can be divided into qualitative and quantitative indicators based on their characteristics. Qualitative indicators are mainly obtained by a questionnaire survey. Therefore, Section 3.1 mainly includes two parts: (1) Obtaining qualitative index data based on a questionnaire survey. (2) Obtaining quantitative index data based on a field investigation and other methods. In addition, this section also reveals the questionnaire survey process of collecting qualitative index data in detail, so that readers can understand the research details of this manuscript in more detail.

(1) Qualitative indicators were obtained through a questionnaire survey. The main steps for administering the questionnaire survey were as follows.

Step 1: Design the questionnaire. The purpose, target group, and the type of information to be collected were determined. The content of the questionnaire was compiled based on the characteristics of the secondary indicators, and the scoring rules of these indicators were clearly defined [35]. Experts in the field reviewed and pretested the draft questionnaire to ensure its accuracy, relevance, and comprehensibility.

Step 2: Sample selection. According to the research purpose and target accuracy of this paper, no less than 20 invited experts were required for each questionnaire (empirical data). Considering the scarcity of experts in the field of healthy building in China, this study utilized a targeted invitation instead of a random sampling to achieve the survey object.

Step 3: Data collection. To ensure that the questionnaire survey was efficient, this paper collected data by filling out paper questionnaires and collecting them on the spot.

Step 4: Data analysis. The data obtained based on the questionnaire survey were imported into SPSS 19.0 software, and a descriptive statistical analysis (frequency, percentage, average, etc.) and inferential statistical analysis (t-test, variance analysis, regression analysis, etc.) were conducted. Notably, all the questionnaire results must pass the consistency test.

Step 5: Results report. The average score of the qualitative indicator scored by 20 experts was taken as the indicator score. Considering that different experts have different expert weights, this paper adopted the following methods to calculate the average value of the indicator [36].

$$w_j={\displaystyle \frac{N_j}{{\sum }_{j=1}^{20}{N}_j}},$$

(22)

where $w_j$ represents the expert weight of the $j$ th expert, $N_j$ represents the number of healthy building projects that the $j$ th expert participated in, and 20 represents the 20 experts who participated in this questionnaire. Notably, the more experts who participated in healthy building, the higher the weight of the experts.

$$x_i={\sum }_{j=1}^{20}{w}_j{x}_i^j,$$

(23)

where $x_i^j$ represents the score of the $j$ th expert on the $i$ th qualitative indicator, and $x_i$ is the final score of the $i$ th qualitative indicator.

Before the questionnaire survey, it was necessary to divide the evaluation grades of each indicator. In this paper, the application maturity of healthy building in China was divided into five levels: the enlightenment stage (I), development stage (II), optimization stage (III), maturity stage (IV), and innovation stage (V). Stage I indicates that healthy building practitioners in China have begun to pay attention to the concept of healthy building, but a systematic methodology has not been actualized. Stage II indicates that the healthy building industry in China has formed a set of guiding principles for the design, construction, operation, and maintenance of healthy buildings, and some of them have been applied in practice. Stage III indicates that health building practitioners in China have fully integrated the concept of healthy building into the design, construction, operation, and maintenance of healthy buildings, and its effect on promoting the health of users has been pronounced. Stage IV means that the health factors are fully considered in the design, construction, operation, and maintenance of healthy buildings in China. Stage V indicates that healthy buildings in China are beginning to lead the new trend of healthy building globally.

At present, scholars have neither unified nor clarified the classification of the application maturity of healthy building [37,38]. The grade division of each secondary indicator is given in detail according to the above-mentioned evaluation equivalence division principle, the definition of each secondary indicator, and the actual context of the case, as listed in

Table 2. Evaluation grading and indicator score of secondary indicators.

Indicator	I	II	III	IV	V	Score
$D_1$	$\left[0,\left.60\%\right)\right.$	$\left[60\%,\left.70\%\right)\right.$	$\left[70\%,\left.80\%\right)\right.$	$\left[80\%,\left.90\%\right)\right.$	$\left[90\%,100\%\right]$	66.8%
$D_2$	$\left[0,\left.20\right)\right.$	$\left[20,\left.40\right)\right.$	$\left[40,\left.60\right)\right.$	$\left[60,\left.80\right)\right.$	$\left[\mathrm{80,100}\right]$	57.7021
$D_3$	$\left[0,\left.20\right)\right.$	$\left[20,\left.40\right)\right.$	$\left[40,\left.60\right)\right.$	$\left[60,\left.80\right)\right.$	$\left[\mathrm{80,100}\right]$	39.5745
$D_4$	$\left[0,\left.20\right)\right.$	$\left[20,\left.40\right)\right.$	$\left[40,\left.60\right)\right.$	$\left[60,\left.80\right)\right.$	$\left[\mathrm{80,100}\right]$	45.5426
$P_1$	$\left[\mathrm{10,100}\right]$	$\left[-10,\left.10\right)\right.$	$\left[-50,\left.-10\right)\right.$	$\left[-100,\left.-50\right)\right.$	$\left[-2000,-100\right]$	12.83
$P_2$	$\left[\mathrm{50,500}\right]$	$\left[-50,\left.50\right)\right.$	$\left[-100,\left.-50\right)\right.$	$\left[-200,\left.-100\right)\right.$	$\left[-5000,-200\right]$	19.625
$P_3$	$\left[0,\left.20\right)\right.$	$\left[20,\left.40\right)\right.$	$\left[40,\left.60\right)\right.$	$\left[60,\left.80\right)\right.$	$\left[\mathrm{80,100}\right]$	45.4894
$P_4$	$\left[0,\left.20\right)\right.$	$\left[20,\left.40\right)\right.$	$\left[40,\left.60\right)\right.$	$\left[60,\left.80\right)\right.$	$\left[\mathrm{80,100}\right]$	44.1489
$P_5$	$\left[0,\left.20\right)\right.$	$\left[20,\left.40\right)\right.$	$\left[40,\left.60\right)\right.$	$\left[60,\left.80\right)\right.$	$\left[\mathrm{80,100}\right]$	45.5319
$P_6$	$\left[0,\left.20\right)\right.$	$\left[20,\left.40\right)\right.$	$\left[40,\left.60\right)\right.$	$\left[60,\left.80\right)\right.$	$\left[\mathrm{80,100}\right]$	56.1383
$S_1$	$\left[0,\left.2\%\right)\right.$	$\left[2\%,\left.5\%\right)\right.$	$\left[5\%,\left.10\%\right)\right.$	$\left[10\%,\left.60\%\right)\right.$	$\left[60\%,100\%\right]$	1.36%
$S_2$	$\left[0,\left.20\right)\right.$	$\left[20,\left.40\right)\right.$	$\left[40,\left.60\right)\right.$	$\left[60,\left.80\right)\right.$	$\left[\mathrm{80,100}\right]$	54.7234
$S_3$	$\left[0,\left.20\%\right)\right.$	$\left[20\%,\left.40\%\right)\right.$	$\left[40\%,\left.60\%\right)\right.$	$\left[60\%,\left.80\%\right)\right.$	$\left[80\%,100\%\right]$	40%
$S_4$	$\left[0,\left.20\right)\right.$	$\left[20,\left.40\right)\right.$	$\left[40,\left.60\right)\right.$	$\left[60,\left.80\right)\right.$	$\left[\mathrm{80,100}\right]$	36.5319
$S_5$	$\left[0,\left.20\right)\right.$	$\left[20,\left.40\right)\right.$	$\left[40,\left.60\right)\right.$	$\left[60,\left.80\right)\right.$	$\left[\mathrm{80,100}\right]$	52.7447
$I_1$	$\left[0,\left.20\right)\right.$	$\left[20,\left.40\right)\right.$	$\left[40,\left.60\right)\right.$	$\left[60,\left.80\right)\right.$	$\left[\mathrm{80,100}\right]$	49.3191
$I_2$	$\left[0,\left.20\right)\right.$	$\left[20,\left.40\right)\right.$	$\left[40,\left.60\right)\right.$	$\left[60,\left.80\right)\right.$	$\left[\mathrm{80,100}\right]$	57.9574
$I_3$	$\left[0,\left.10\right)\right.$	$\left[10,\left.20\right)\right.$	$\left[20,\left.50\right)\right.$	$\left[50,\left.100\right)\right.$	$\left[\mathrm{100,1000}\right]$	20.15
$I_4$	$\left[0,\left.20\right)\right.$	$\left[20,\left.40\right)\right.$	$\left[40,\left.60\right)\right.$	$\left[60,\left.80\right)\right.$	$\left[\mathrm{80,100}\right]$	52.9574
$I_5$	$\left[0,\left.5\%\right)\right.$	$\left[5\%,\left.10\%\right)\right.$	$\left[10\%,\left.20\%\right)\right.$	$\left[20\%,\left.40\%\right)\right.$	$\left[40\%,100\%\right]$	7.58%
$I_6$	$\left[0,\left.20\right)\right.$	$\left[20,\left.40\right)\right.$	$\left[40,\left.60\right)\right.$	$\left[60,\left.80\right)\right.$	$\left[\mathrm{80,100}\right]$	43.2340
$I_7$	$\left[0,\left.20\right)\right.$	$\left[20,\left.40\right)\right.$	$\left[40,\left.60\right)\right.$	$\left[60,\left.80\right)\right.$	$\left[\mathrm{80,100}\right]$	46.4574
$R_1$	$\left[0,\left.1\right)\right.$	$\left[1,\left.5\right)\right.$	$\left[5,\left.10\right)\right.$	$\left[10,\left.20\right)\right.$	$\left[\mathrm{20,1000}\right]$	3.98
$R_2$	$\left[0,\left.20\right)\right.$	$\left[20,\left.40\right)\right.$	$\left[40,\left.60\right)\right.$	$\left[60,\left.80\right)\right.$	$\left[\mathrm{80,100}\right]$	37.8085
$R_3$	$\left[0,\left.1\right)\right.$	$\left[1,\left.5\right)\right.$	$\left[5,\left.10\right)\right.$	$\left[10,\left.20\right)\right.$	$\left[\mathrm{20,1000}\right]$	4.2
$R_4$	$\left[0,\left.20\right)\right.$	$\left[20,\left.40\right)\right.$	$\left[40,\left.60\right)\right.$	$\left[60,\left.80\right)\right.$	$\left[\mathrm{80,100}\right]$	48.5000
$R_5$	$\left[0,\left.20\right)\right.$	$\left[20,\left.40\right)\right.$	$\left[40,\left.60\right)\right.$	$\left[60,\left.80\right)\right.$	$\left[\mathrm{80,100}\right]$	49.9149

. For the case study, this paper considered the Ant A Space (http://healthybuildinglabel.com/newsinfo/6873319.html (accessed on 1 May 2024)) and Yinchuan Yunshang Yuehai Project (http://healthybuildinglabel.com/newsinfo/6817006.html (accessed on 1 May 2024)).

From Table 2, the units of measurement for $P_1$,$P_2$, $I_3$, $R_1$, and $R_3$ are millions of RMB, millions of RMB/year, tons of standard coal/year, millions of RMB, and millions of RMB, respectively. The V values of $P_1$, $P_2$, $I_3$, and $R_1$ were replaced by −2000, −5000, 1000, and 1000, respectively.

The personal information of the 20 experts who participated in the survey is presented in

Table 3. Personal information of experts who participated in the survey.

No.	Degree	Professional Title	Number of Participants in Healthy Buildings	Work Years	Work Unit
(1)	Master	Associate senior	5	10	Supervision
(2)	Bachelor	Senior	7	22	Design
(3)	Doctoral	Senior	4	24	University
(4)	Master	Associate senior	6	8	Construction
(5)	Doctoral	Senior	4	23	University
(6)	Master	Associate senior	4	25	Supervision
(7)	Doctoral	Senior	5	26	University
(8)	Master	Associate senior	3	10	Design
(9)	Master	Senior	4	21	Construction
(10)	Bachelor	Senior	5	16	Construction
(11)	Doctoral	Senior	3	12	University
(12)	Bachelor	Senior	5	27	Operating
(13)	Master	Associate senior	3	14	Supervision
(14)	Master	Senior	5	28	Design
(15)	Bachelor	Associate senior	4	18	Operating
(16)	Doctoral	Senior	6	23	University
(17)	Master	Associate senior	5	12	Supervision
(18)	Bachelor	Senior	4	15	Design
(19)	Doctoral	Senior	5	11	Construction
(20)	Master	Senior	7	27	Construction

.

As listed in Table 3, all the experts who participated in the survey had a high level of education, and six experts had doctoral degrees (30%). All experts had professional titles of associate senior or senior. The average work experience of the 20 experts was 18.6 years, and they were from different sectors in the healthy building industry. Therefore, the experts are intimately familiar with healthy building.

Notably, the number of healthy building projects that the 20 experts were involved in is small, mainly owing to healthy building being a recent development in China, and to the engineering practice of healthy building being in its infancy. This represents a limitation of this paper.

The results of the questionnaire survey were collected and sorted, and Cronbach’s α of all items was greater than 0.7, that is, it passed the reliability test [39]. The scores of all the qualitative indicators were obtained by substituting the results of this questionnaire into Equations (22) and (23), as listed in Table 2.

(2) Quantitative indicators were obtained by field investigation or consulting statistical data.

Qualitative evaluation data are in the last column of Table 2, and quantitative data are given in

Table 4. Calculation process or data source of quantitative indicator data.

Indicator	Calculation Process or Data Source
$D_1$	China national bureau of statistics (https://www.stats.gov.cn/sj/ndsj/, accessed on 1 May 2024).
$P_1$	The added value of the construction cost of the two cases selected in this paper is 52.89 and −27.23, respectively, with an average of 12.83.
$P_2$	The added value of operating costs of the two cases selected in this paper is −23.5 and −15.75, respectively, with an average of 19.625.
$S_1$	In 2022, the new building area in China was 9.05 billion square meters, of which the building area with a healthy building logo was 123 million square meters, 1.23/90.5 = 1.36%.
$S_3$	Chinese building materials network (https://www.cnprofit.com/index.html, accessed on 1 May 2024)
$I_3$	The reduction of energy consumption for the two cases selected in this paper are 16.80 and 23.50, respectively, with an average of 20.15.
$I_5$	The building rental rate of 10 healthy buildings is predicted, and the average value is 7.58%.
$R_1$	The technical research and development expenses of many healthy building enterprises in China were investigated, and the average value was 3.98.
$R_3$	The predicted values of economic rewards for the two cases selected in this paper are 2.57 and 5.83, respectively, with an average of 4.2.

. The combination of these two types of data is the evaluation data used in this case analysis.

3.2. Evaluating the Maturity of Healthy Building Technology in China

(1)

Constructing a projection indicator function

The normalized research data ${\mathbf{X}}_1$ can be obtained by introducing the data in Table 2 into Equation (1). ${\mathbf{X}}_1$ is substituted into Equations (8) and (9) to construct the projection indicator function $\mathbf{Q}\left(a\right)$. To improve the stability of the prediction model, this paper randomly selected 200 data points from each preset evaluation grade to form the data set ${\mathbf{X}}_2$.

The projection indicator function $\mathbf{Q}\left(a\right)$ constructed in this paper is a high-dimensional nonlinear problem with constraints. This study utilized BCO to determine the optimal solution of the projection indicator function.

(2)

BCO was used to solve the objective function

${\mathbf{X}}_1$ and ${\mathbf{X}}_2$ were substituted into a self-compiled program that was developed based on MATLAB 2021A for calculations. The algorithm setting of BCO is relatively simple, and the related program was from https://github.com/Tulika-opt/Border-Collie-Optimization (accessed on 1 May 2024). In this study, the population size was 20, and the upper limit of iteration was 1000 [20].

Table 5. Partial iterative calculation process of BCO algorithm.

Iterations	$\mathbf{Fitness} \mathbf{of} \mathit{k}-1$	$\mathbf{Fitness} \mathbf{of} \mathit{k}$	Precision	Find the Optimal Solution?
70	23.485604827	23.485234212	0.000370615 > 0.0001	No
71	23.485234212	23.485234223	1.1 × 10−8 < 0.0001	Yes
72	23.485234223	23.485234221	2 × 10−9 < 0.0001	Yes
1000	23.485234223	23.485234223	0 < 0.0001	Yes

tracks in detail the calculation process of the BCO algorithm.

As presented in Table 5, the BCO algorithm achieved convergence accuracy in the 71st optimization and achieved the best projection vector. Recalculation was conducted 100 times, and BCO found the best projection vector after 72.57 generations of optimization on average. In the 100 repeat calculations, the best BCO performance obtained the best projection vector in the 68th generation.

(3)

Weight calculation of indicators

To reduce the calculation error, the elements in the optimal projection direction of the 100 calculation results were averaged. The normalized result was the final optimal projection direction, as listed in

Table 6. Weight calculation results.

Indicator	Optimal Projection Vector	Weight	Ranking	Indicator	Optimal Projection Vector	Weight	Ranking
$D$	-	0.1635	5	$S_2$	0.2126	0.0452	3
$P$	-	0.1935	2	$S_3$	0.1819	0.0331	19
$S$	-	0.1860	3	$S_4$	0.1716	0.0295	22
$I$	-	0.2743	1	$S_5$	0.2070	0.0429	10
$R$	-	0.1827	4	$I_1$	0.2126	0.0452	4
$D_1$	0.1510	0.0228	26	$I_2$	0.2111	0.0446	7
$D_2$	0.2119	0.0449	5	$I_3$	0.2005	0.0402	12
$D_3$	0.2264	0.0513	1	$I_4$	0.2231	0.0498	2
$D_4$	0.2110	0.0445	8	$I_5$	0.1772	0.0314	20
$P_1$	0.1861	0.0346	17	$I_6$	0.2090	0.0437	9
$P_2$	0.1682	0.0283	24	$I_7$	0.1397	0.0195	27
$P_3$	0.1532	0.0235	25	$R_1$	0.1969	0.0388	13
$P_4$	0.1842	0.0339	18	$R_2$	0.1929	0.0372	14
$P_5$	0.1686	0.0284	23	$R_3$	0.2023	0.0409	11
$P_6$	0.2117	0.0448	6	$R_4$	0.1884	0.0355	15
$S_1$	0.1882	0.0354	16	$R_5$	0.1740	0.0303	21

. Squaring the values of the 27 elements in the best projection direction yielded the objective weight of each secondary indicator [18]. The weights of the secondary indicators under each primary indicator were summed to obtain the weight calculation result of each primary indicator. The weight calculation results are listed in Table 6.

Table 6 reveals that the Impact($I$) is the most important first-level indicator, and its weight is as high as 0.2743. The weight order of the five first-level indicators was $I$ > $P$ > $S$ > $R$ > $D$. This finding contradicts most research results obtained using the DPSIR framework [40,41,42,43]. At present, the mainstream academic view holds that $D$ or $S$ is the most important first-level indicator for most sustainability systems. This difference in the results may be attributed to different first-level indicators being included in the different numbers of second-level indicators. Therefore, this paper calculated the average indicator weight of each first-level indicator by dividing the weight of the first-level indicator by the number of second-level indicators included in this indicator. The order of the average indicator weight of the first-level indicators was $D$ (0.0409) > $S$ (0.0392) > $I$ (0.0372) > $R$ (0.0365) > $P$ (0.0323). Taken from this perspective, the calculation results of this paper do not conflict with the mainstream calculation results.

In addition, this paper adopted an objective weight calculation method based on the data structure characteristics. This method involves first calculating the weight of the secondary indicators and then directly synthesizing the weight of the primary indicators based on the calculation results of the secondary indicators. However, the mainstream practice is to use the subjective weight calculation method, in which the weight of the first-level indicators is first calculated, after which the weight of the second-level indicators is then comprehensively obtained. This may also explain the conflicting results.

Among the secondary indicators, $D_3$ (strict green energy utilization policy requirements) had the largest weight. This suggests that with the intensification of global climate change and environmental deterioration, the demand for green energy in the construction industry is increasing. The strictness of the policy reflects the importance attached to the environmental protection standards of the construction industry and ensures sustainable progress in the development of construction technology. Moreover, in China, government policies have a more pronounced role in guiding industrial development. The Chinese Municipal Government proposed that “lucid waters and lush mountains are invaluable assets” and formulated corresponding environmental protection objectives and measures. A strict green energy utilization policy is key to realizing these macrostrategies.

$I_7$ (Increased jobs) had the smallest weight, only 0.0195. This suggests that although increasing related jobs is an important part of the maturity of healthy building technology, other factors are prioritized when evaluating the maturity of healthy building technology. Specifically, with the development of automation and intelligent technology, the implementation of building technology may increasingly rely on high-tech equipment and systems rather than traditional manpower. This technological change may lead to a relative decrease in the demand for traditional construction-related jobs. Therefore, when evaluating the technical maturity of a healthy building, the added weight of the related jobs will be smaller.

(4)

Determination of evaluation grade

After 100 repeated calculations, the best projection value of the promotion maturity of healthy building in China was 1.0082 (average of the 100 calculations). Notably, 1000 sets of preset data (${\mathbf{X}}_2$) were scattered between 0.0239 and 2.0687. The clustering distribution of these data can be obtained by inserting them into Equations (18)–(22) in turn, as listed in

Table 7. Cluster analysis of the results.

Evaluation Grade	Cluster Distribution
I	0.0239–0.5324
II	0.5754–0.8952
III	0.9872–1.2577
IV	1.3587–1.6874
V	1.8572–2.0687

.

The clustering results in Table 7 reveal that the promotion maturity of healthy building in China is III. In recent years, the government of China and the construction industry have taken a series of policy measures, which have significantly promoted healthy building practices, hence the result. China has adopted green and healthy building as its future development direction and issued a series of promotion policies at the national level. For example, both the 13th Five-Year Plan and the 14th Five-Year Plan clearly outline energy saving, emission reduction, and green building as development goals. The Ministry of Housing and Urban–Rural Development of China has issued several standards and guidelines related to green buildings and healthy buildings, such as the “Evaluation Criteria for Green Buildings” and “Design Guidelines for Healthy Houses”, which provide specific technical guidance for the design and construction of healthy buildings. In addition, with the improvement of residents’ living standards and the enhancement of health awareness, the public demand for healthy, comfortable, and environmentally friendly housing in China is rising. This urges developers and builders to adopt more healthy building concepts in architectural design and construction. In recent years, numerous green building demonstration projects have been undertaken in China’s big cities, such as Beijing, Shanghai, and Shenzhen. These projects usually include the application of various healthy building technologies, such as optimizing natural lighting, improving indoor air quality, and using building materials with high energy efficiency.

The above case analysis results demonstrate that the model proposed in this paper can effectively evaluate and predict the maturity of healthy buildings in China. The model proposed in this paper successfully identified the key factors that affect technology maturity and presents evaluation results that are realistic. These results not only provide definitive indicators for the construction industry in China to evaluate and improve its level of technical implementation but also assist policy-makers in formulating relevant healthy building standards and policies.

4. Discussion

This section discusses the calculation performance and calculation details of the model proposed in this paper. In addition, this section presents suggestions that decision-makers can implement to promote healthy building in China.

4.1. Comparison of Computational Performance of Different Optimization Algorithms

This paper adopts BCO, a novel meta-heuristic optimization algorithm, to improve the projection pursuit model, which is one of its main contributions. To verify the capability of the BCO algorithm in improving the projection pursuit method, this paper compares the computational performance of several classical algorithms and the latest optimization algorithms in improving the projection pursuit model. These optimization algorithms include the GA [44], PSO [45], ant colony optimization (ACO) [46], simulated annealing (SA) [47], golden jackal optimization, (GJO) [48], the walrus optimization algorithm (WOA) [49,50], and the arithmetic optimization algorithm (AOA) [51]. GJO, the WOA, and the AOA are recent meta-heuristic optimization algorithms. The calculation parameter setting and calculation principle behind each optimization algorithm can be obtained from the corresponding references.

To ensure fairness in comparing the algorithm’s performance, all the optimization algorithms were run for 100 epochs in the same computer environment, and the average of the 100 calculation results was taken as the final calculation result, as listed in

Table 8. Computational performance of different algorithms.

Algorithm	Means	Standard Deviations	Minimum Values	Maximum Values	Minimum Time (seconds)
BCO	1.0082	1.2234 × 10−6	1.0079	1.0083	122.83
GA	1.0067	6.4149 × 10−4	1.0028	1.0079	653.59
PSO	1.0092	2.1067 × 10−4	1.0067	1.0103	290.48
ACO	1.0083	3.1161 × 10−5	1.0071	1.0095	171.60
SA	1.0106	2.3135 × 10−5	1.0093	1.0114	268.06
GJO	1.0081	7.2723 × 10−5	1.0074	1.0096	327.08
WOA	1.0083	1.2496 × 10−5	1.0075	1.0094	230.12
AOA	1.0084	4.8272 × 10−5	1.0076	1.0090	141.37

.

Table 8 reveals that the average values of the eight algorithms are very close, which indicates that they correctly identified the optimal solution. The standard deviation of BCO was the smallest: only 1.2234 × 10⁻⁶. This represents only 0.19% of that of the GA (with the largest standard deviation). Regarding the average convergence speed, BCO was also markedly superior to the other algorithms. Compared with the GA, PSO, ACO, SA, GJO, the WOA, and the AOA, BCO was 530.76 s (81.21%), 167.65 s (57.71%), 48.77 s (28.42%), 145.23 s (54.18%), and 2000 s faster, respectively. These calculation results prove the suitability of the BCO algorithm for improving the projection pursuit method.

In addition, compared with traditional meta-heuristic optimization algorithms (GAs, PSO, ACO, and SA), the novel meta-heuristic optimization algorithms (GJO, the WOA, the AOA, and BCO) all exhibited better computational performance.

4.2. Comparative Analysis of Different Evaluation Methods

The maturity of healthy building technology is typically multi-attributed. At present, the mainstream research methods to calculate the indicator weight are AHP and the entropy weight method. Then, the fuzzy comprehensive evaluation, the gray correlation method, and other methods based on fuzzy mathematics are used to determine the evaluation grade. An evaluation of the applicability of these methods to this study are described as follows:

(1)

AHP: In this study, AHP was greatly influenced by subjective judgment. When using AHP to calculate the indicator weight, different expert groups often arrive at markedly different weight calculation results. Moreover, the indicator system constructed in this paper is extensive, and passing the consistency test using AHP is difficult. For example, the author tried to use AHP to calculate the weights of seven secondary indicators under $I$ and passed the consistency test after three questionnaires.

(2)

Entropy weight method: The calculation principle of the entropy weight method involves reflecting the degree of dispersion of the data itself. Therefore, this method requires high quality data. This limits its applicability to evaluating the maturity of healthy building technology. In this paper, the entropy weight method was used to calculate the weight of each indicator, but the calculation results were completely different from the evaluation data used.

(3)

Fuzzy comprehensive evaluation: This method is also a classic subjective evaluation method, so it is also easily influenced by experts’ subjective judgment. Selecting different expert groups and different membership functions will often produce different results.

(4)

Gray correlation analysis: This method is used to evaluate the similarity between data sequences. However, in the research on evaluating the maturity of healthy building technology, the attributes of different indicator data are completely different, which greatly restricts the application of this method to the field of healthy building.

Noticeably, each method has its own unique application scenarios. However, these classical methods are not applicable in this study. The core idea behind the projection pursuit method is to project high-dimensional data into a low-dimensional space, which can comprehensively reflect the characteristics of multi-dimensional data based on the internal structure and distribution of data.

This case study demonstrates that the model can evaluate the maturity of healthy building technology. This section further analyzes the sensitivity of the projection pursuit method to proficiency evaluation data. In this section, the evaluation data of multiple indicators are randomly varied by 5–10%, as listed in

Table 9. Sensitivity analysis of projection pursuit method to proficiency evaluation data.

Case		Optimal Projection Vector	Evaluation Results
Number of Changing Indicators	Amplitude of Variation
0	0	1.0082	III
1	$\pm 5\mathrm{\%}$	1.0085	III
1	$\pm 10\mathrm{\%}$	1.0056	III
3	$\pm 5\mathrm{\%}$	1.0076	III
3	$\pm 10\mathrm{\%}$	1.0050	III
5	$\pm 5\mathrm{\%}$	1.0091	III
5	$\pm 10\mathrm{\%}$	1.0015	III
7	$\pm 5\mathrm{\%}$	1.0031	III
7	$\pm 10\mathrm{\%}$	1.0055	III
9	$\pm 5\mathrm{\%}$	1.0023	III
9	$\pm 10\mathrm{\%}$	1.0019	III

.

Table 9 demonstrates that the model proposed in this paper can still give the evaluation results very stably even when the evaluation data changes markedly. However, obtaining stable calculation results from the traditional qualitative method is difficult, and, even when the expert group changes, very different conclusions can be arrived at. This is the biggest advantage of the quantitative evaluation model proposed in this paper over the traditional qualitative evaluation method.

4.3. Countermeasures and Suggestions for Promoting Healthy Building in China

According to the evaluation results in Section 3.2, China has made some progress in promoting healthy building, but a gap in expectations persists. Therefore, according to the evaluation results, this section puts forward some countermeasures and suggestions to promote the promotion of healthy building in China. Considering that $D_3$ (strict green energy utilization policy requirements), $I_4$ (promotion of the building’s market value), and $S_2$ (promotion of a healthy building management system) are the most critical factors affecting the promotion of healthy building in China, this paper makes the following suggestions to promote development in this field:

(1)

Strengthen policy guidance and legislation. This paper demonstrates that the strictness of green energy policy is an important factor in promoting the development of healthy building. The government should further improve the policy system related to healthy building, especially in the use and management of green energy. It should formulate forward-looking policies, such as providing incentives, including tax incentives and subsidies, to encourage the construction industry to adopt sustainable energy and green building materials. Meanwhile, the implementation of policies should be strengthened to ensure that all construction projects can follow the latest healthy building standards.

(2)

Enhance the market appeal of healthy buildings. The market value of buildings directly affects the popularity of healthy building technology. Therefore, public awareness of the value of healthy building can be improved through education and publicity, and the advantages of healthy building in improving living quality, energy savings and emission reductions, and long-term economic benefits can be capitalized upon. In addition, the government should cooperate with industry organizations to develop a standard model for evaluating the return on investment in healthy building, thereby attracting more investors and developers to healthy building projects.

(3)

Optimize the utilization and integration of a healthy building management system. Considering how little the existing healthy building management system has been utilized, it is crucial to promote its use. The development and adoption of integrated management platforms should be encouraged, which can monitor the energy use of buildings, indoor environmental quality, and other related health indicators in real time. Improving the usability and interoperability of the system can promote the acceptance of the technology and reduce operating costs.

5. Conclusions

In this study, an improved projection pursuit model was developed to evaluate the maturity of healthy building technology in China. Through empirical research, this paper not only identified the key factors affecting the maturity of healthy building technology but also demonstrated the applicability and effect of the model in China. The main conclusions of this paper are as follows:

(1)

This study constructed a DPSIR framework to evaluate the maturity of healthy building technology in China and explained in detail how the five dimensions of driving force, pressure, state, influence, and response affect the maturity of healthy building technology in China. Accordingly, an evaluation indicator system with five first-class indicators and 27 second-class indicators was constructed, which provides a reference for research in this field.

(2)

A projection pursuit method based on BCOwas developed. This model used the powerful data exploration ability of the projection pursuit model to identify the key indicators and determine the evaluation grade from the data structure characteristics of the evaluation data, and it had the advantages of strong objectivity and applicability. In addition, the model had the advantages of a fast BCO convergence and stable calculation.

(3)

The case study revealed the current situation of healthy building technology development in China: it is in the development stage. According to the weight calculation results, strict green energy utilization policy requirements, the promotion of the building’s market value, and the promotion of a healthy building management system were the most critical factors affecting the promotion of healthy building in China. Their indicator weights are 0.0513, 0.0498 and 0.0452, respectively. Even when the nine evaluation data changed significantly, the model proposed in this paper still gave the evaluation results very stably. Empirical research demonstrated that the projection pursuit model can effectively identify and evaluate the key progresses and bottlenecks of healthy building technology.

This paper provides a scientific and systematic tool for monitoring and promoting the development of healthy building technology in China. This can provide data support for policy-makers in formulating relevant building policies, strategic guidance for the construction industry in inculcating healthy building practices, and, ultimately, the formation of a healthier and more sustainable building environment.

The main limitations of this paper are as follows: (1) China’s healthy buildings are in the initial stage, and the number of healthy building projects undertaken by the 20 experts invited to the survey was small. More experts can be invited to participate in surveys and engineering practices in the future. (2) In the future, a more unified evaluation indicator system for decision-makers can be constructed.