Verification and Validation of Modeling of Fluid–Solid Interaction in Explosion-Resistant Designs Using Material Point Method
Abstract
1. Introduction
2. Computational Procedure
2.1. Governing Equations
2.2. Discretization Scheme
2.3. Constitutive Equations
2.3.1. Fluids
2.3.2. Explosives
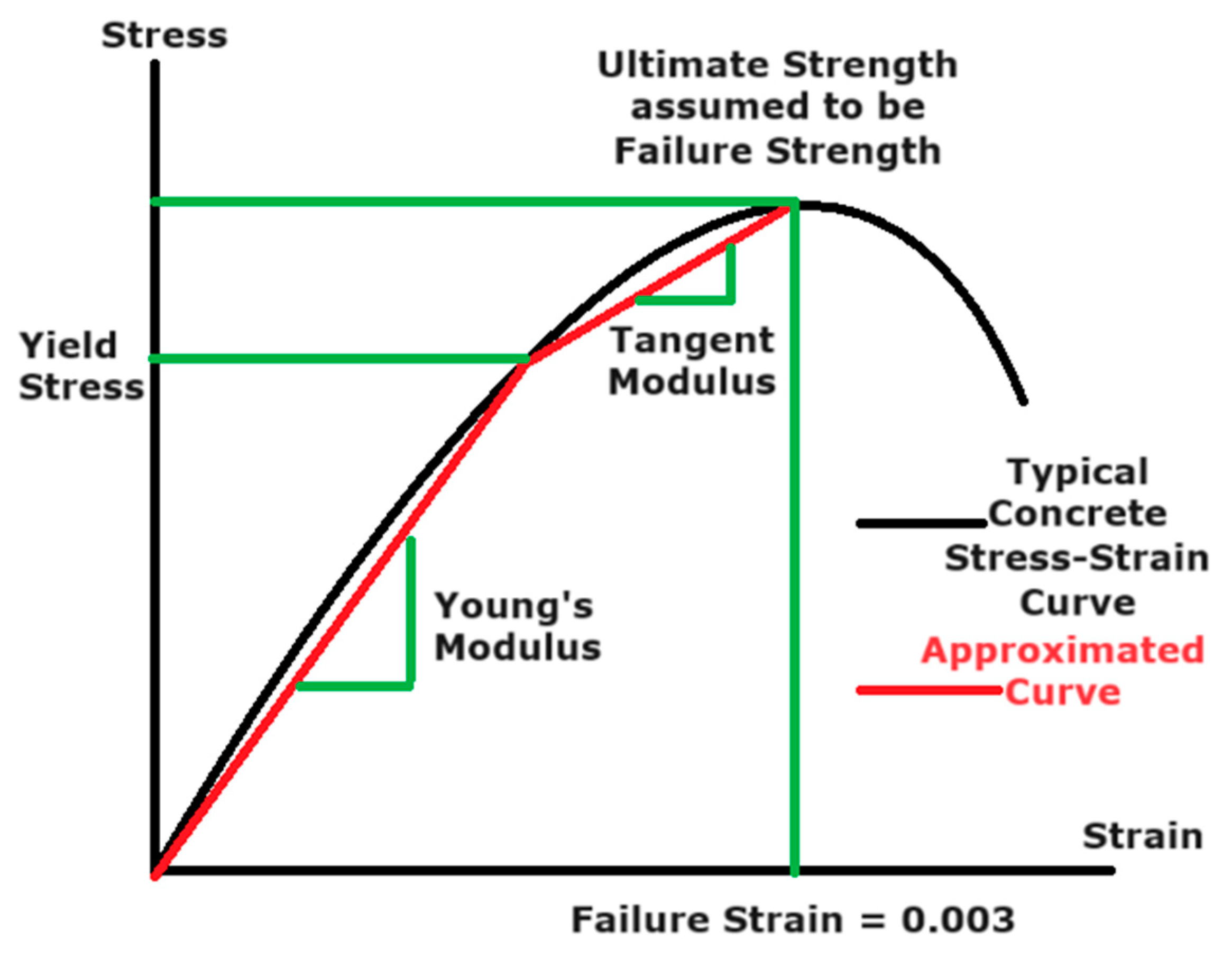
2.3.3. Solids
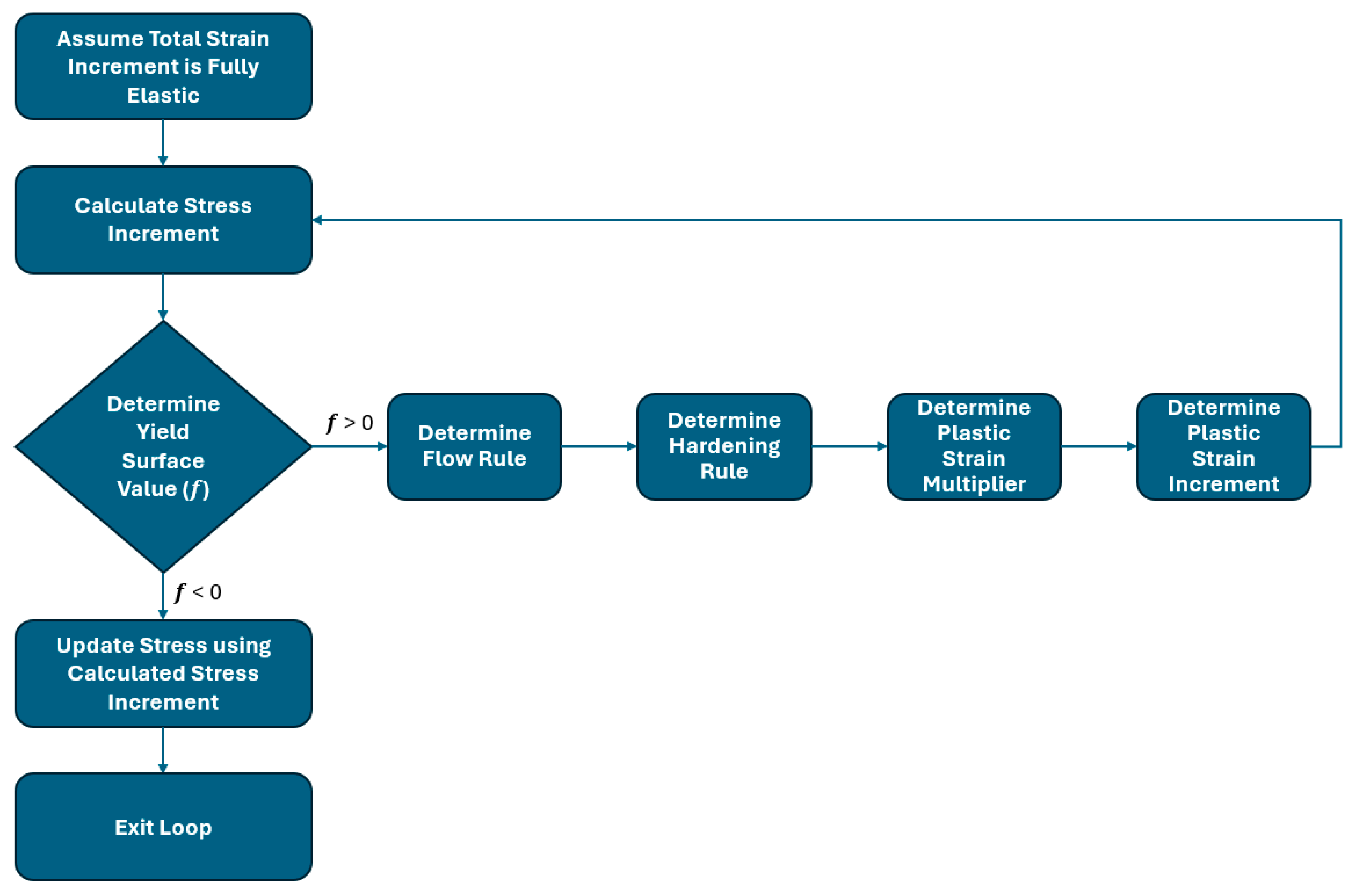
Single-Step Integration Scheme
Iterative Newton–Raphson Integration Scheme
- In each time step, the calculations are performed only if the state of stress, total strain, elastic strain, plastic strain, and internal variables from the previous time step () are available. Accordingly, in the first iterative loop ( = 0) within a specific time step (), the current state is determined so that and . If the iteration loop > 0, then the stress is obtained so that , in which the superscript denotes the inelastic strain.
- Check if yielding occurs by evaluating the yield surface. If yielding does not occur, then the solution is converged, and the stress value is the one obtained in the previous step. If yielding occurs, then the flow rule and incremental stress need to be evaluated.
- Using the Newton–Raphson method, determine the sub-increment of the parameter, that is so that , where .
- The flow rule and updated plastic modulus are evaluated in this step, as detailed in Ref. [40].
- The internal variables and current state of the strain are determined as , .
- The calculation is repeated until the solution is converged for the next time step.
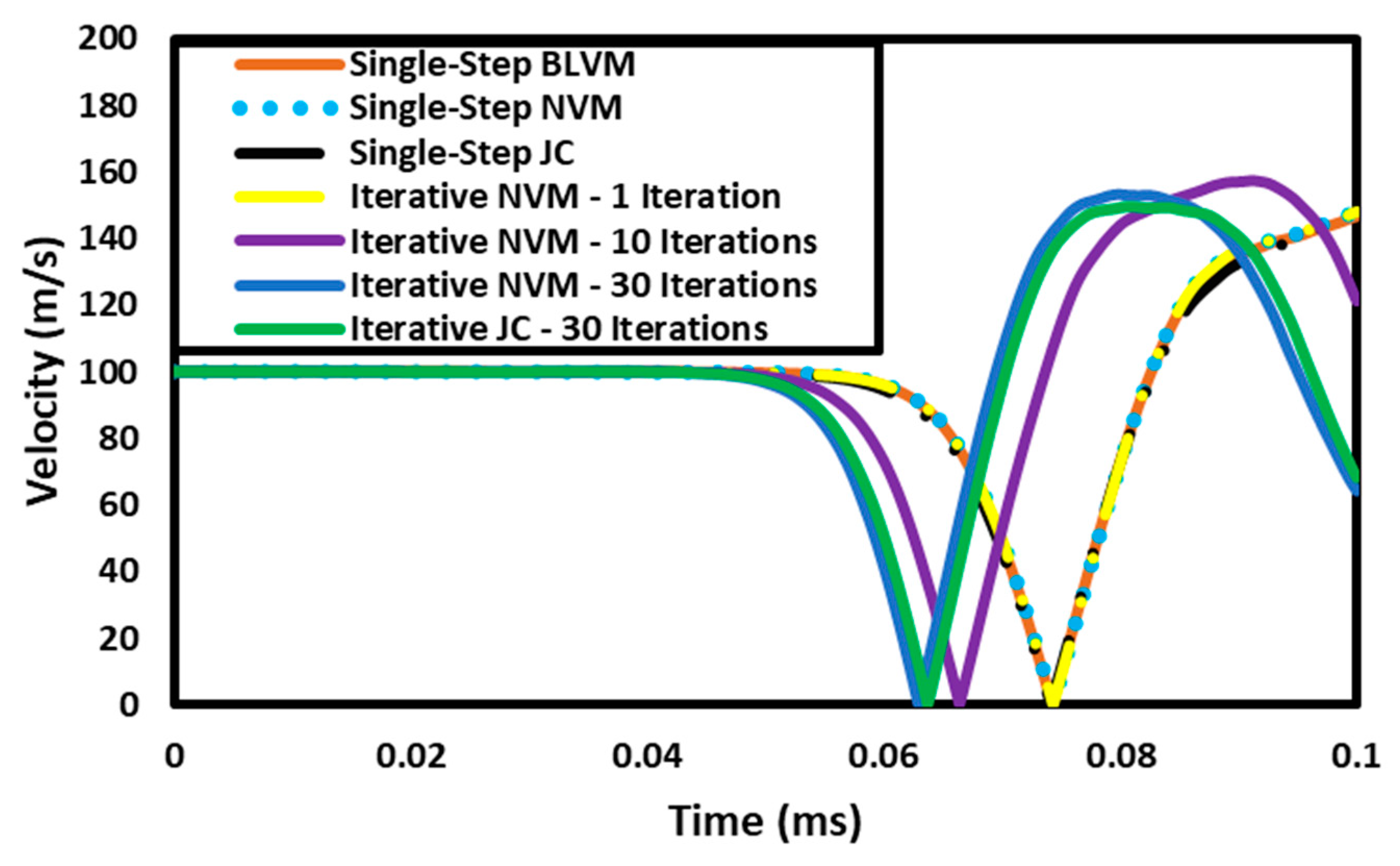
Evaluation of Integration Schemes
3. Results (Case Studies)
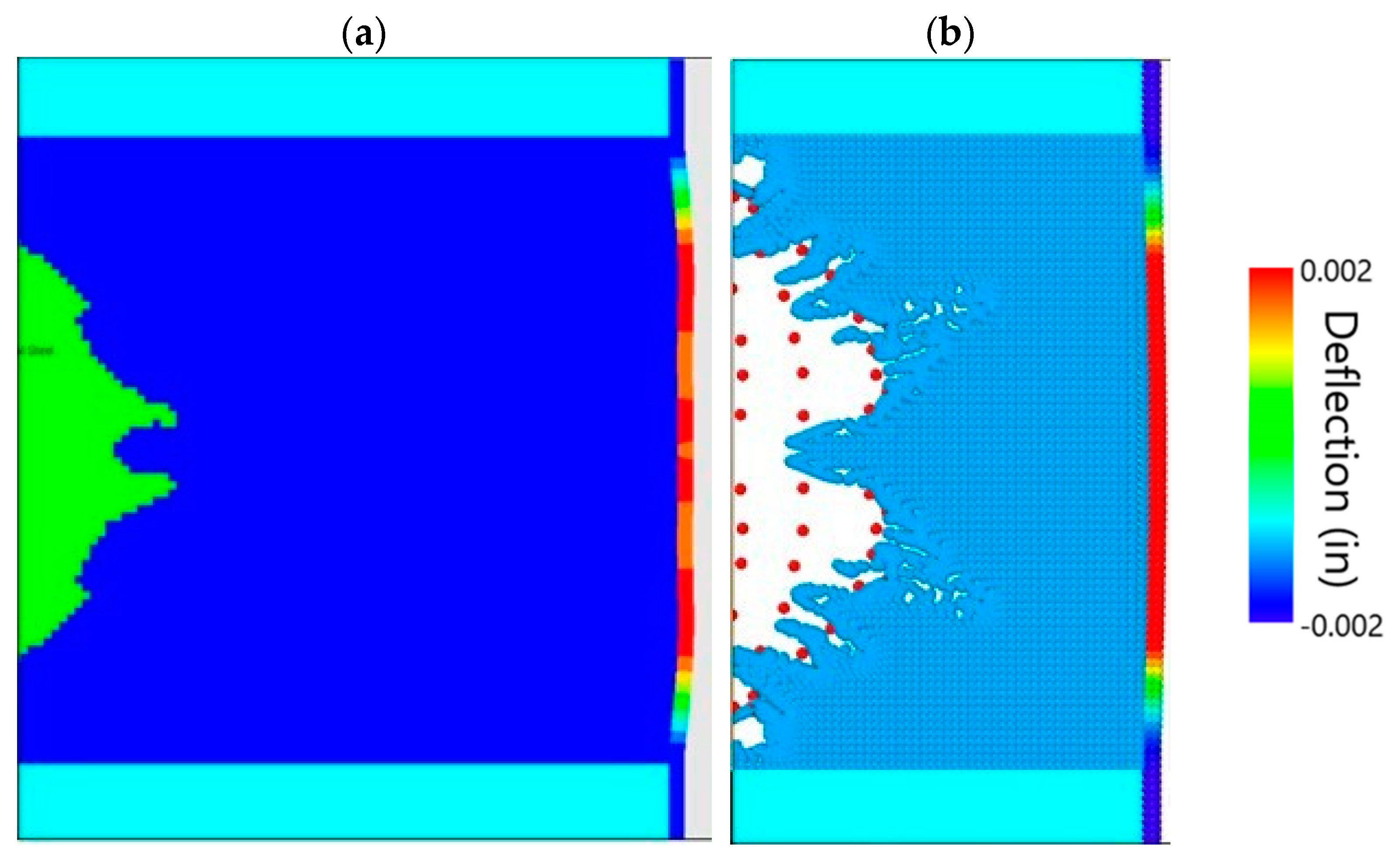
- The first case study is designed to show how the MPM captures fragmentation and damage in a typical confined explosion event, which also demonstrates the comparison between the FEM and MPM in simulating the FSI.
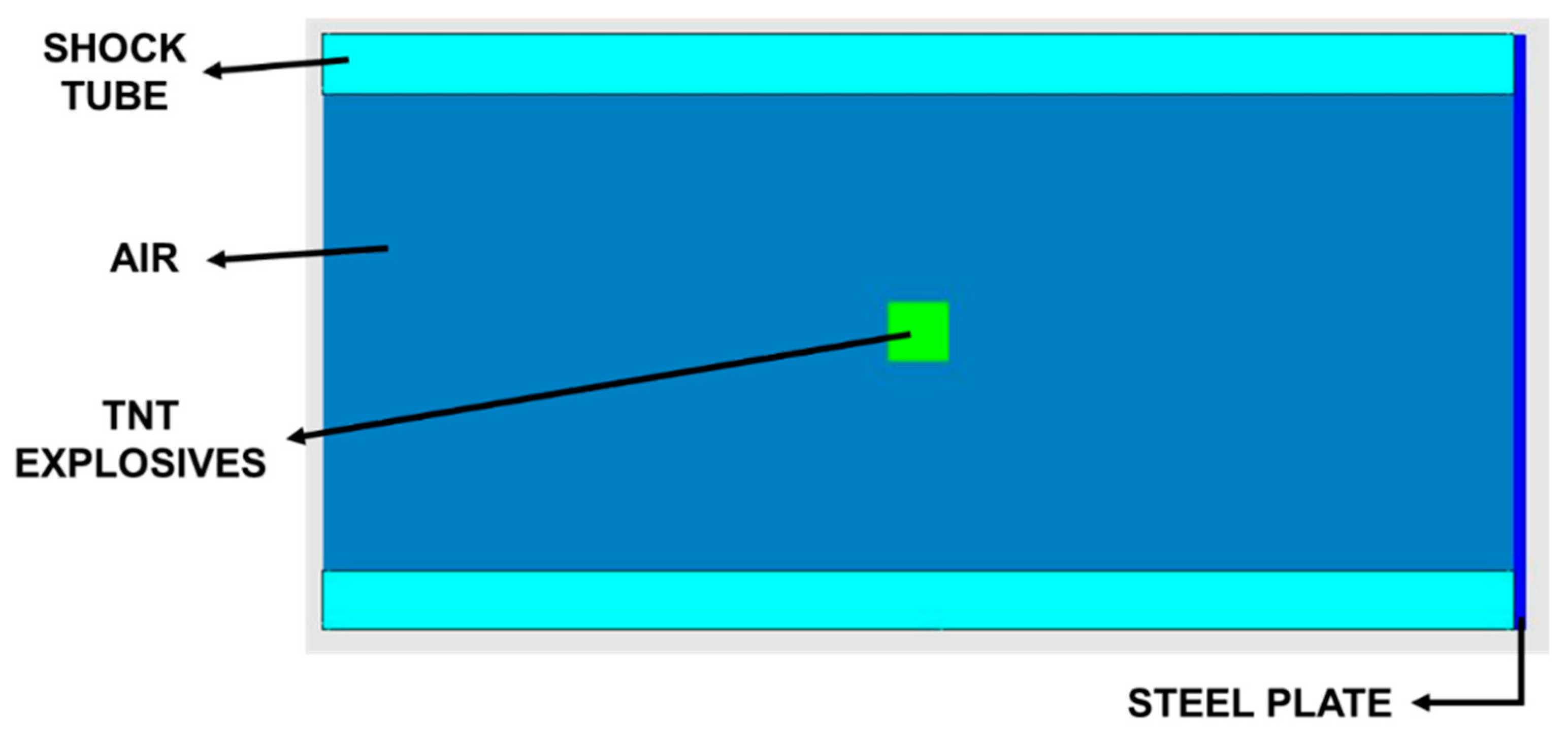
- The second case study is designed to compare, qualitatively, the MPM’s ability to capture the shock tube response against an actual shock tube test.
- Since the second case study validates the MPM solution to be qualitatively consistent with the experiment, the MPM model will be used in the third case study to build an FEM model that captures the physics as simulated by the MPM. This FEM model is needed to be scaled up to model large-scale experiments whenever feasible.
- The fourth case study involves the development of an FEM model that is validated against experimental results. This FEM model is then scaled down and used to validate a corresponding MPM model. Such an approach enables the integration of MPM with FEM in a single computational domain for evaluating large-scale explosion-resistant scenarios.
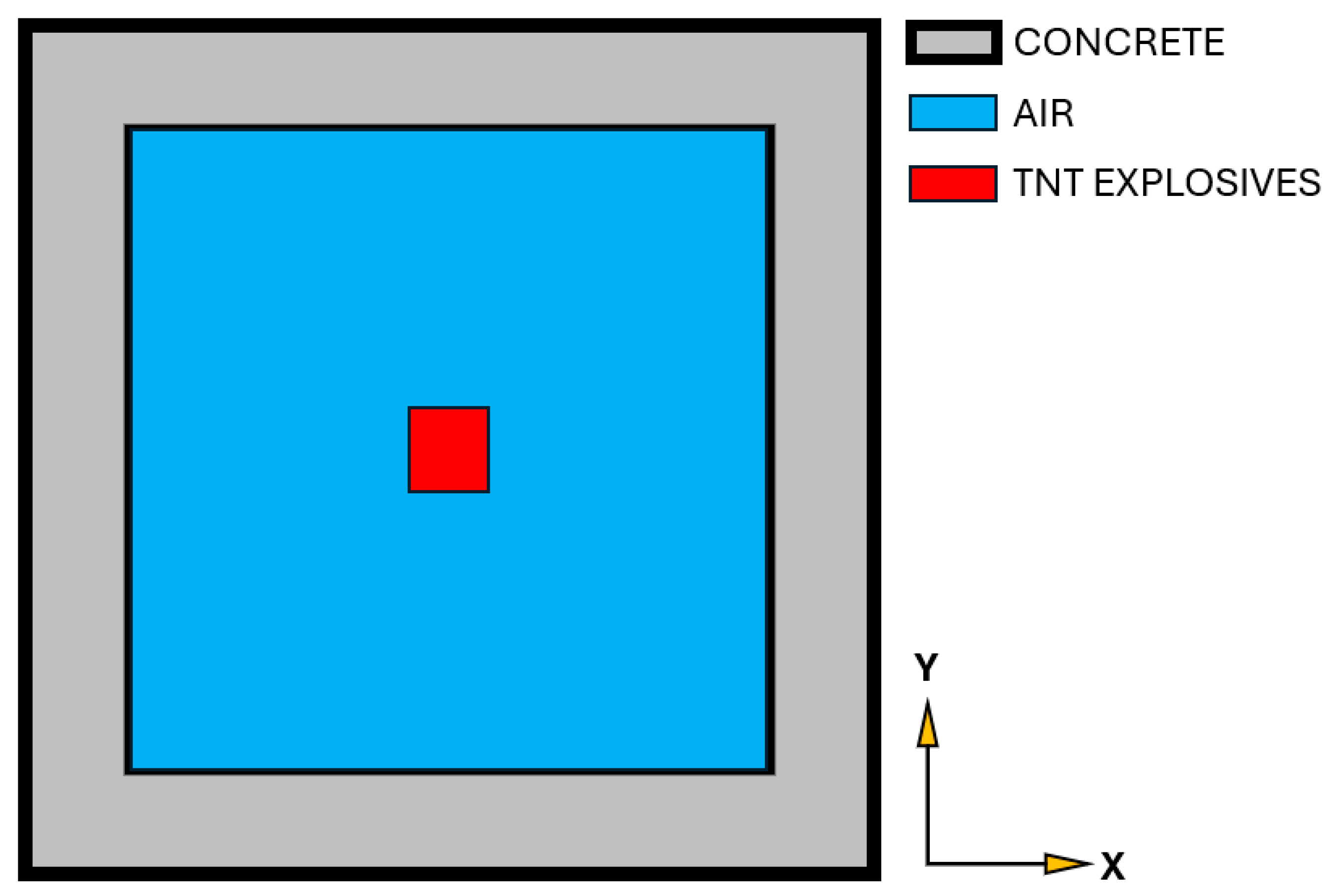
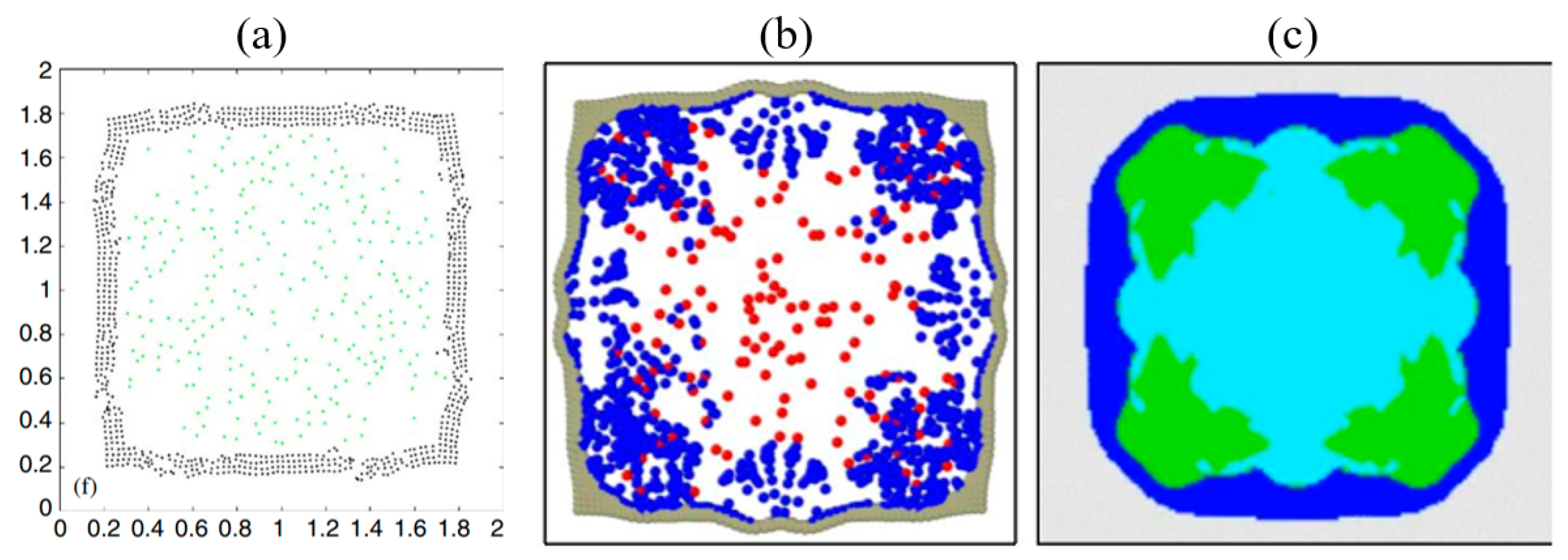
3.1. First Case Study
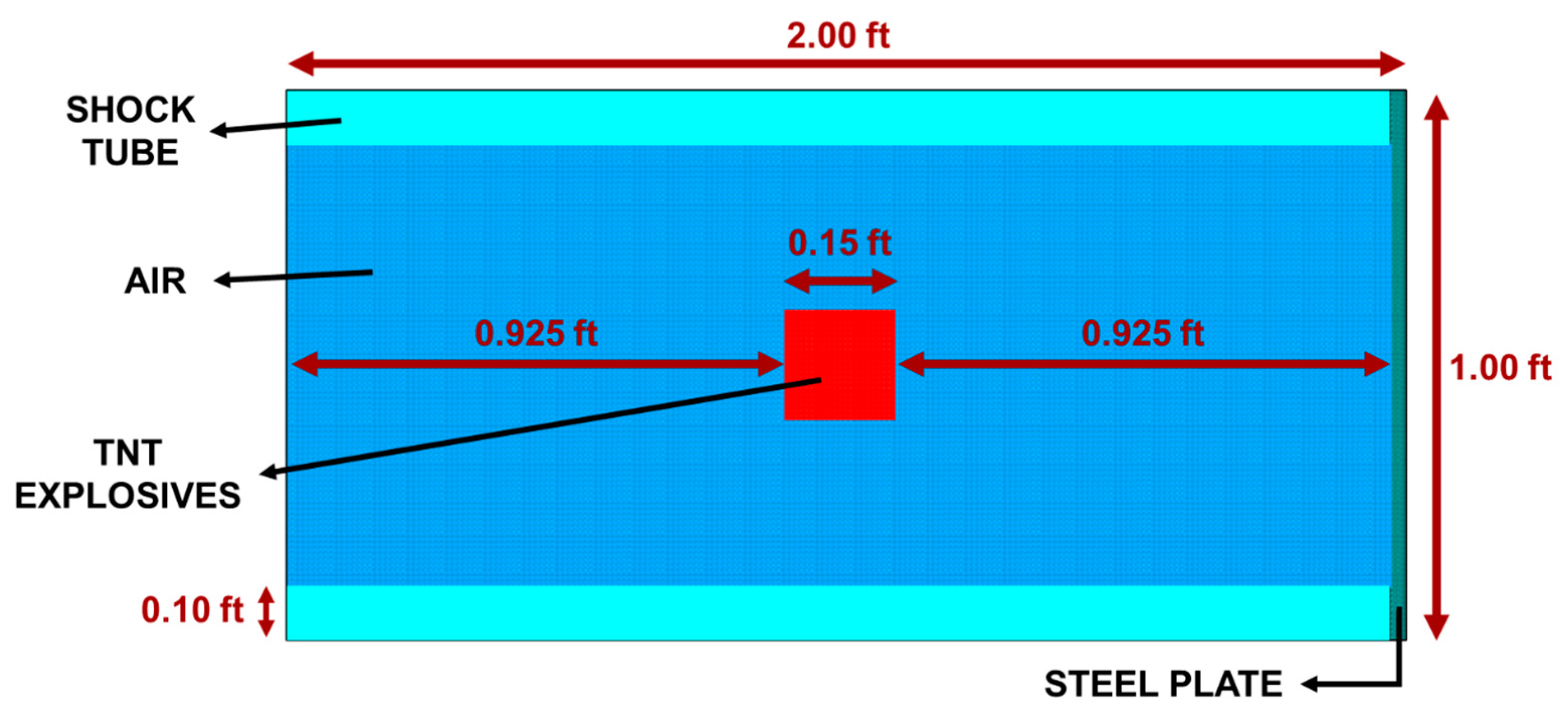
3.1.1. Computational Model Setup
3.1.2. Constitutive Laws
Concrete Box
Ambient Air
TNT Explosives
3.1.3. Results
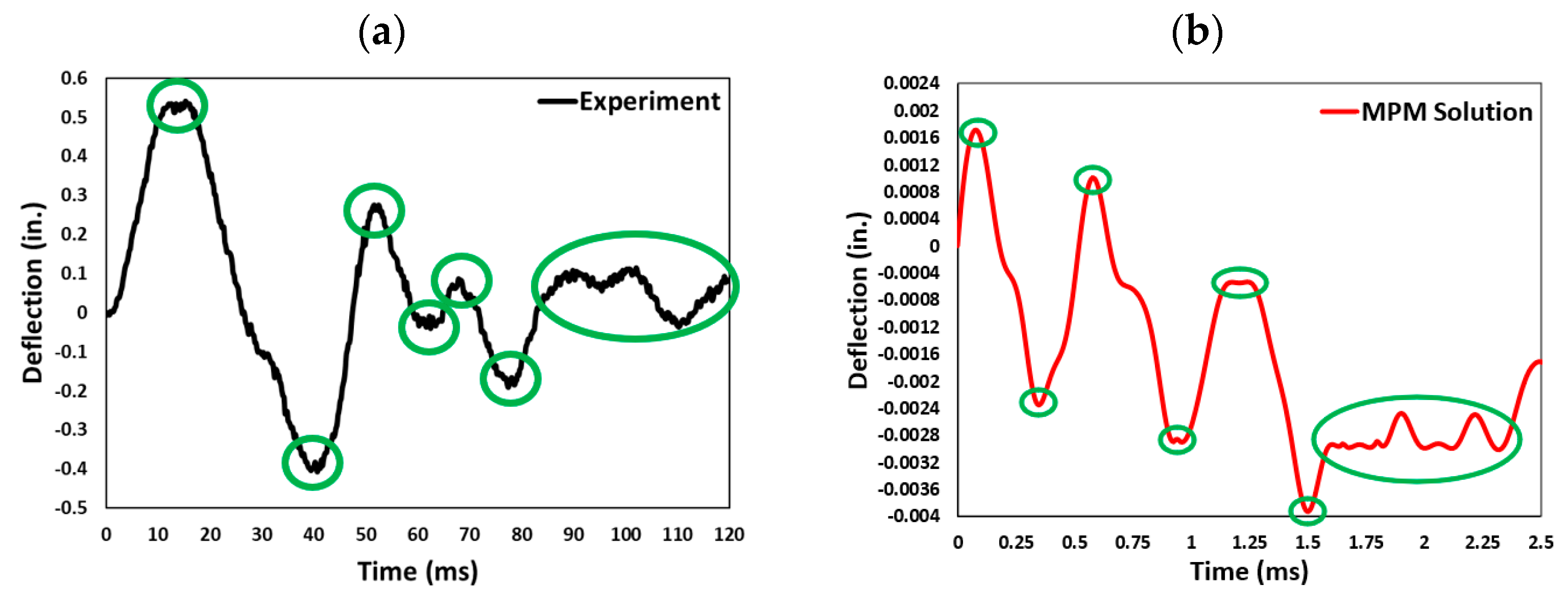
3.2. Second Case Study
3.2.1. Overview of the Experiment
3.2.2. Computational Model Setup
3.2.3. Constitutive Laws
Steel Plate
3.2.4. Results
3.3. Third Case Study
3.3.1. Computational Model Setup
3.3.2. Constitutive Laws
3.3.3. Results
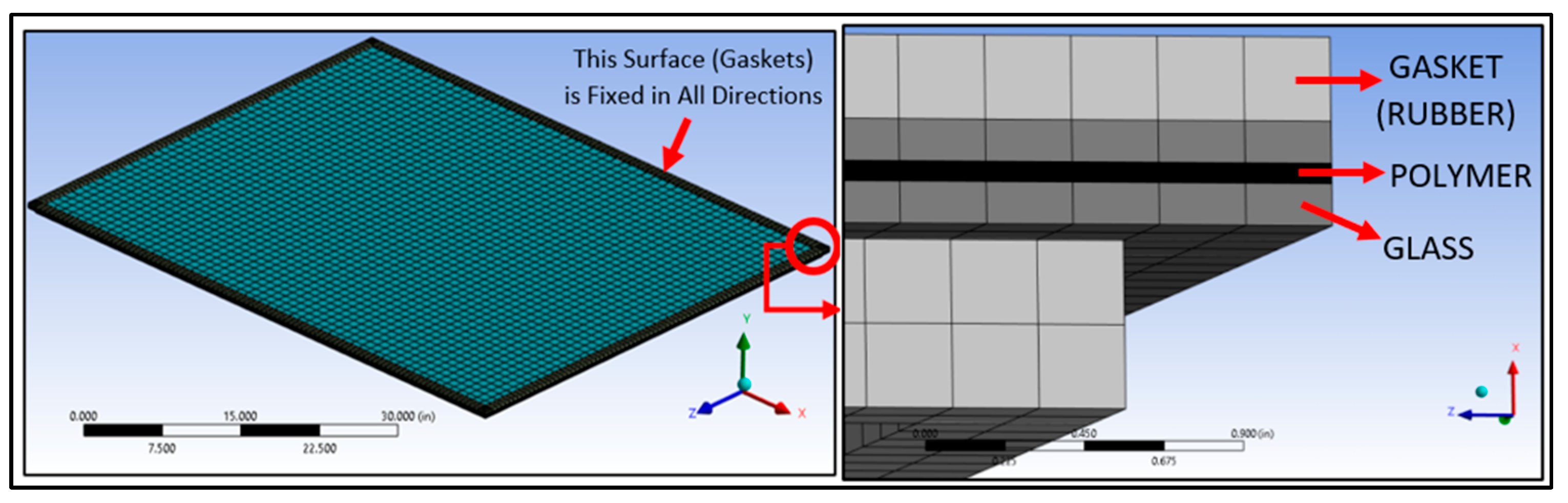
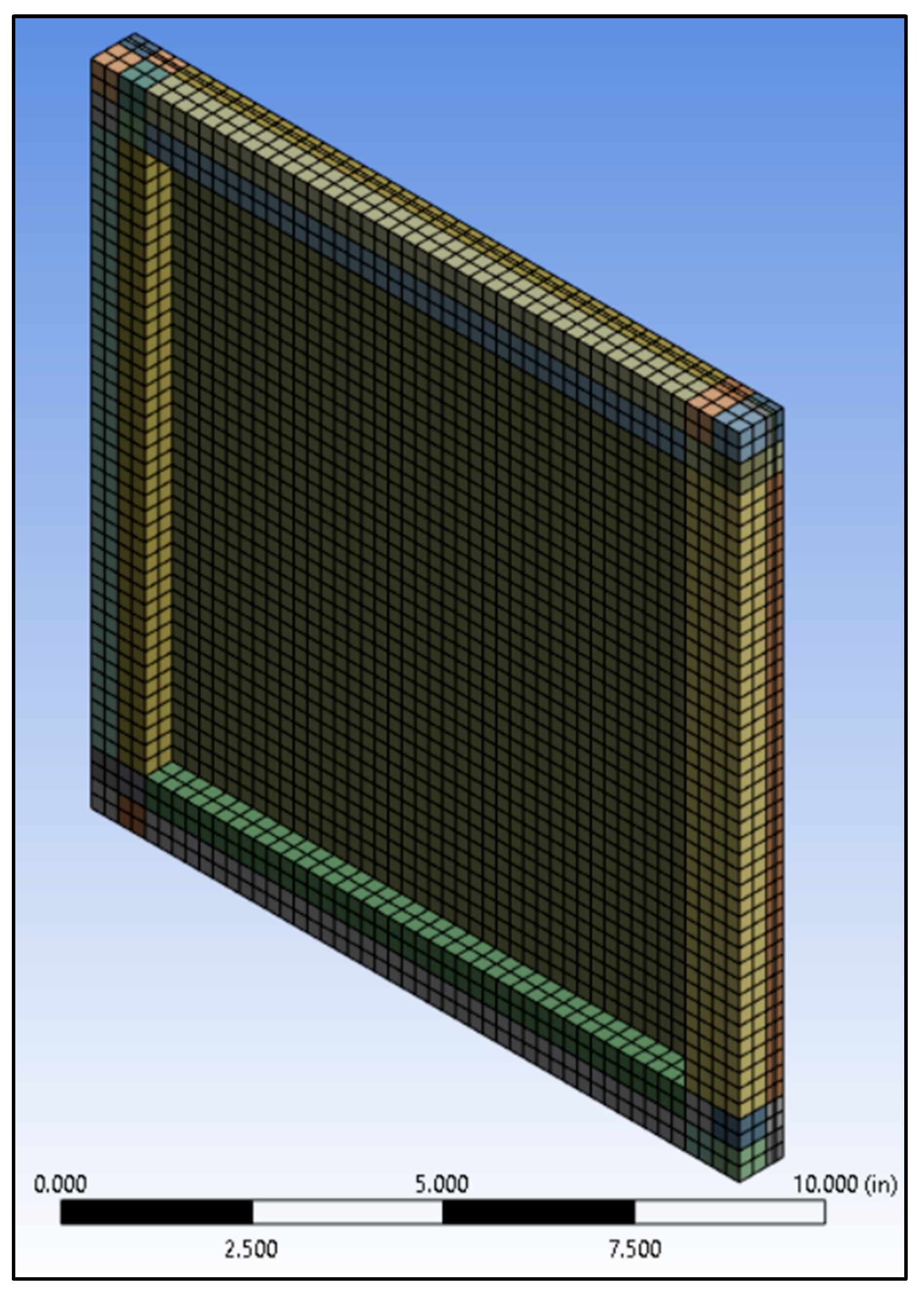
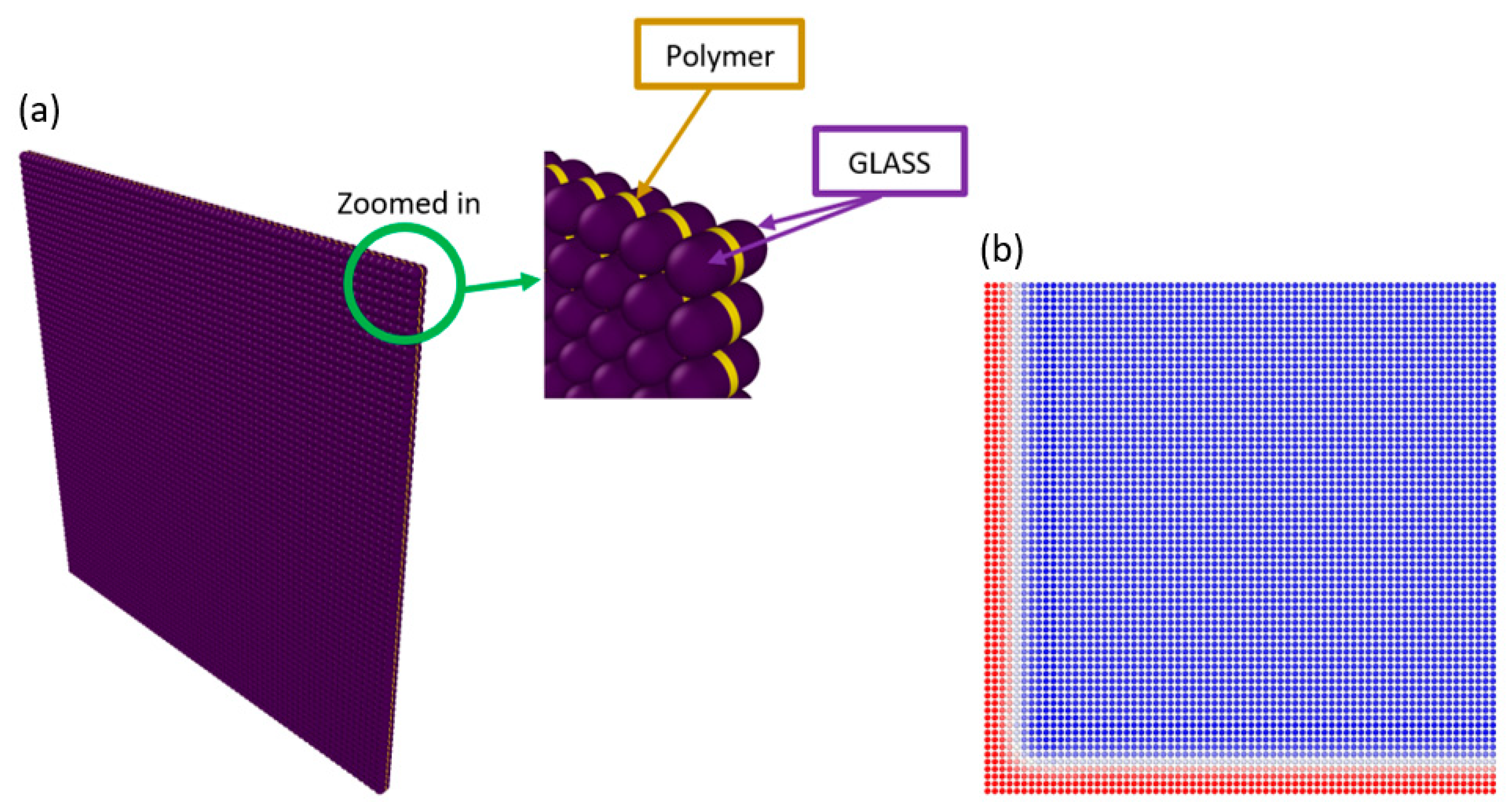
3.4. Fourth Case Study
3.4.1. Overview of the Experimental Test Setup
3.4.2. Computational Model Setup
Large-Scale FEM Model
Small-Scale FEM Model
MPM Model
3.4.3. Constitutive Laws
Glass
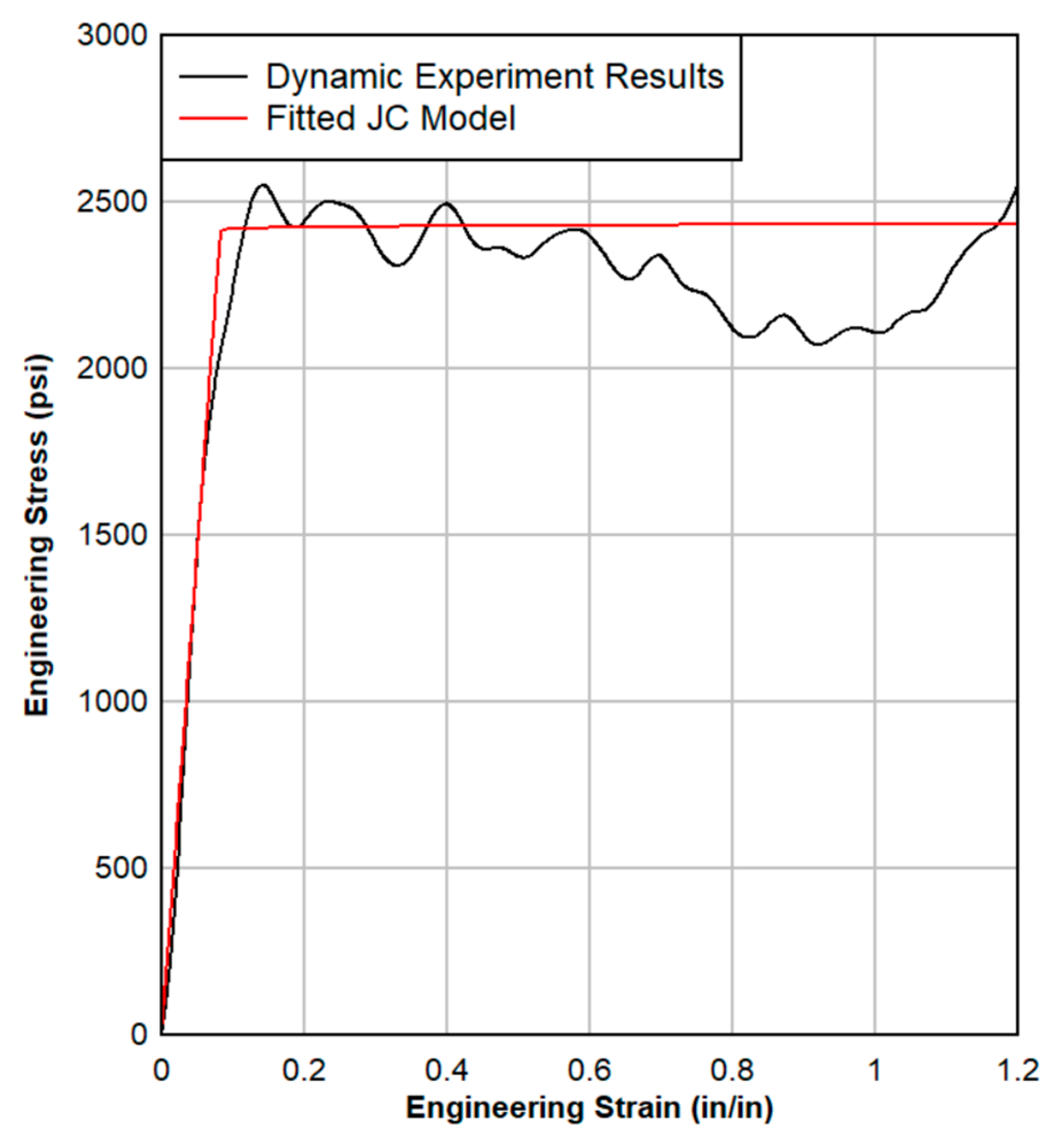
Polymeric Interlayer
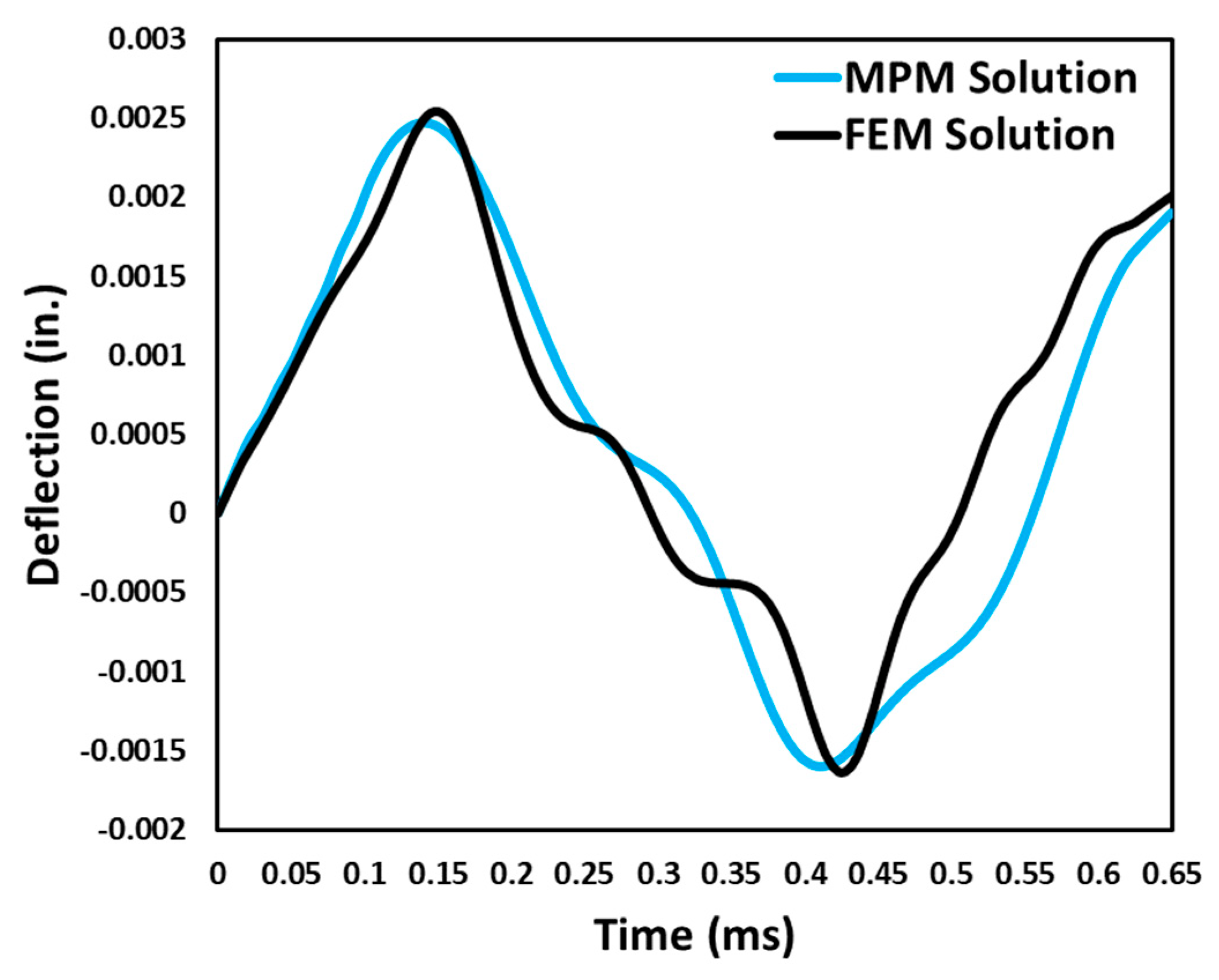
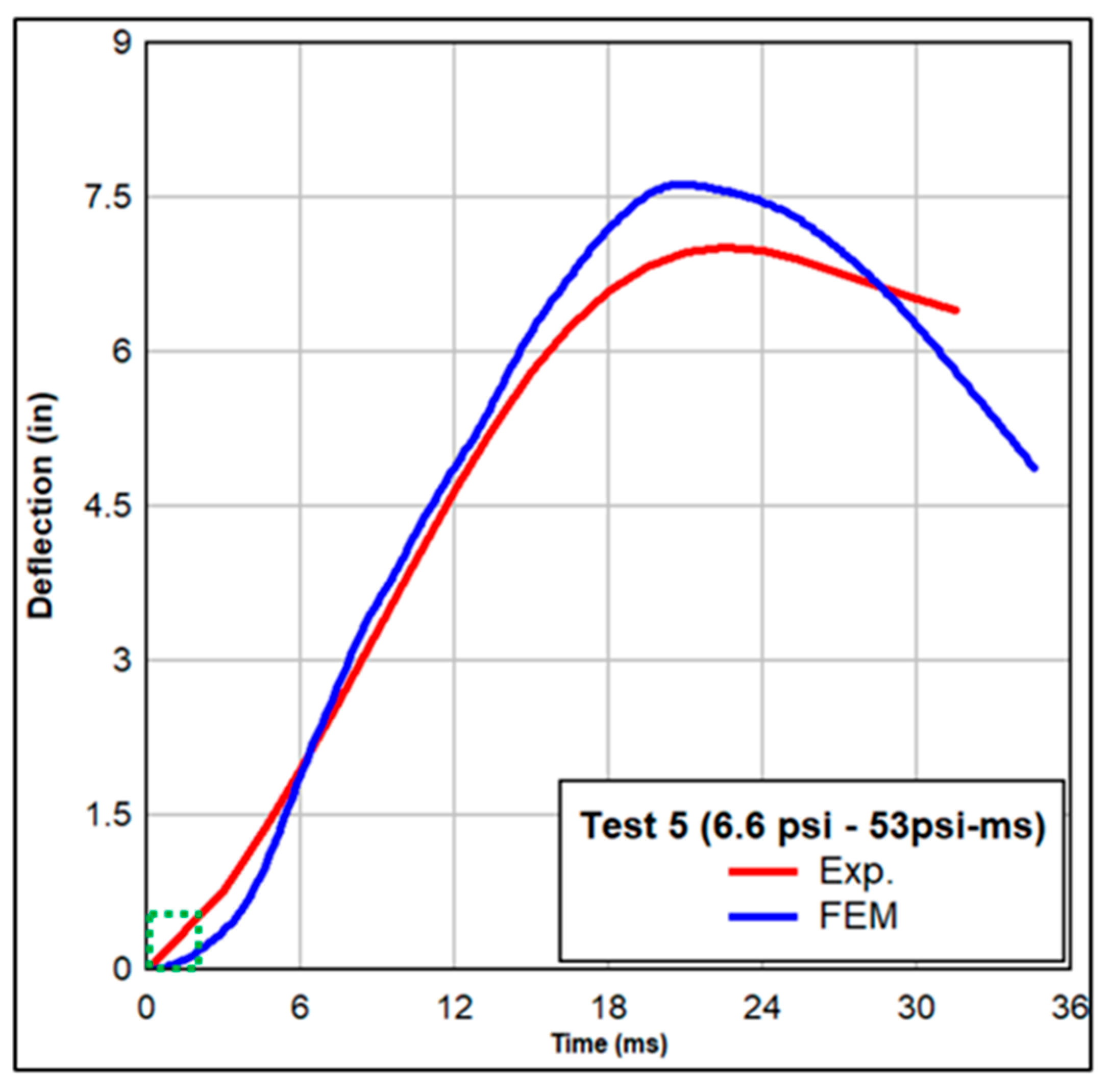
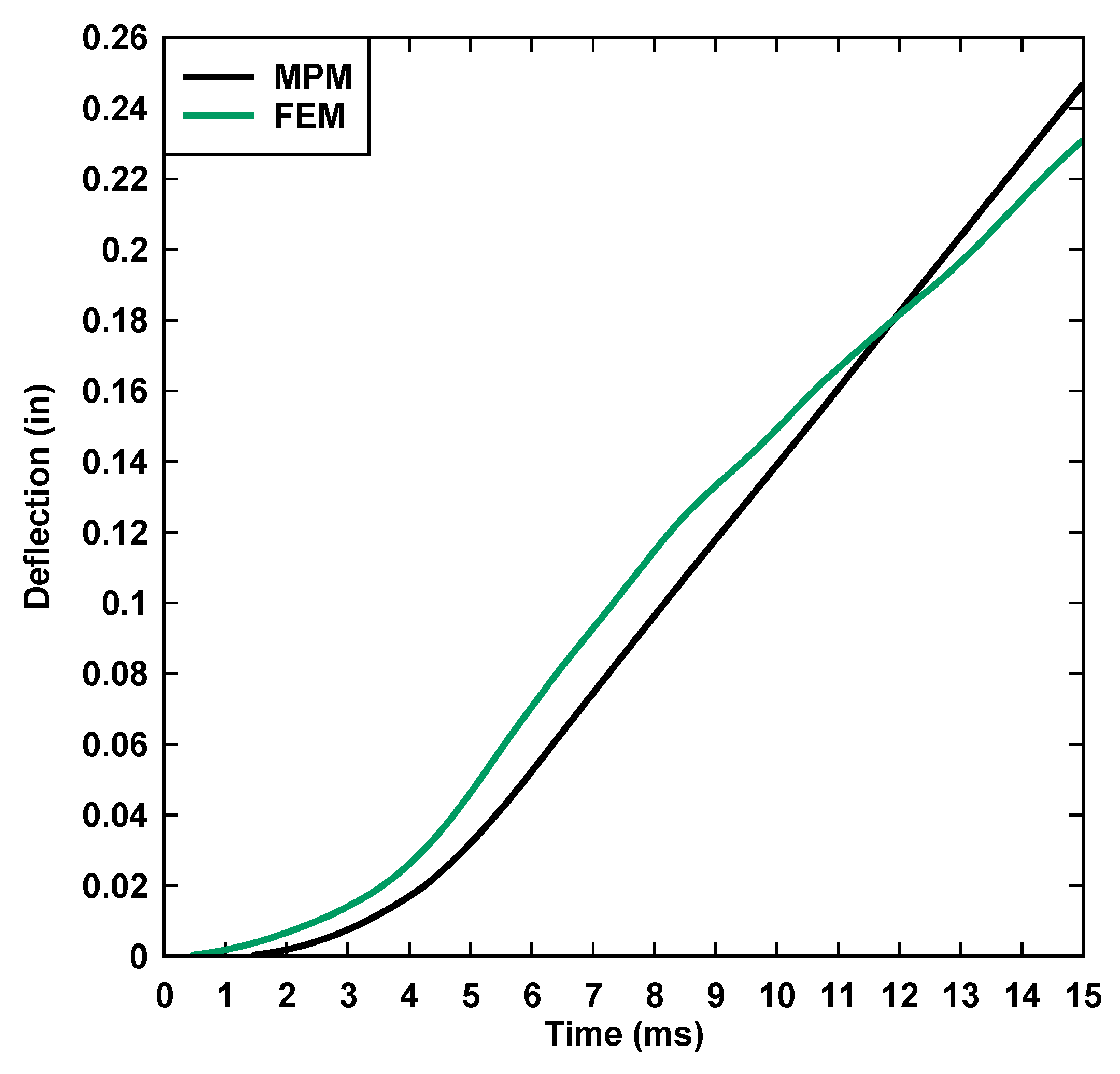
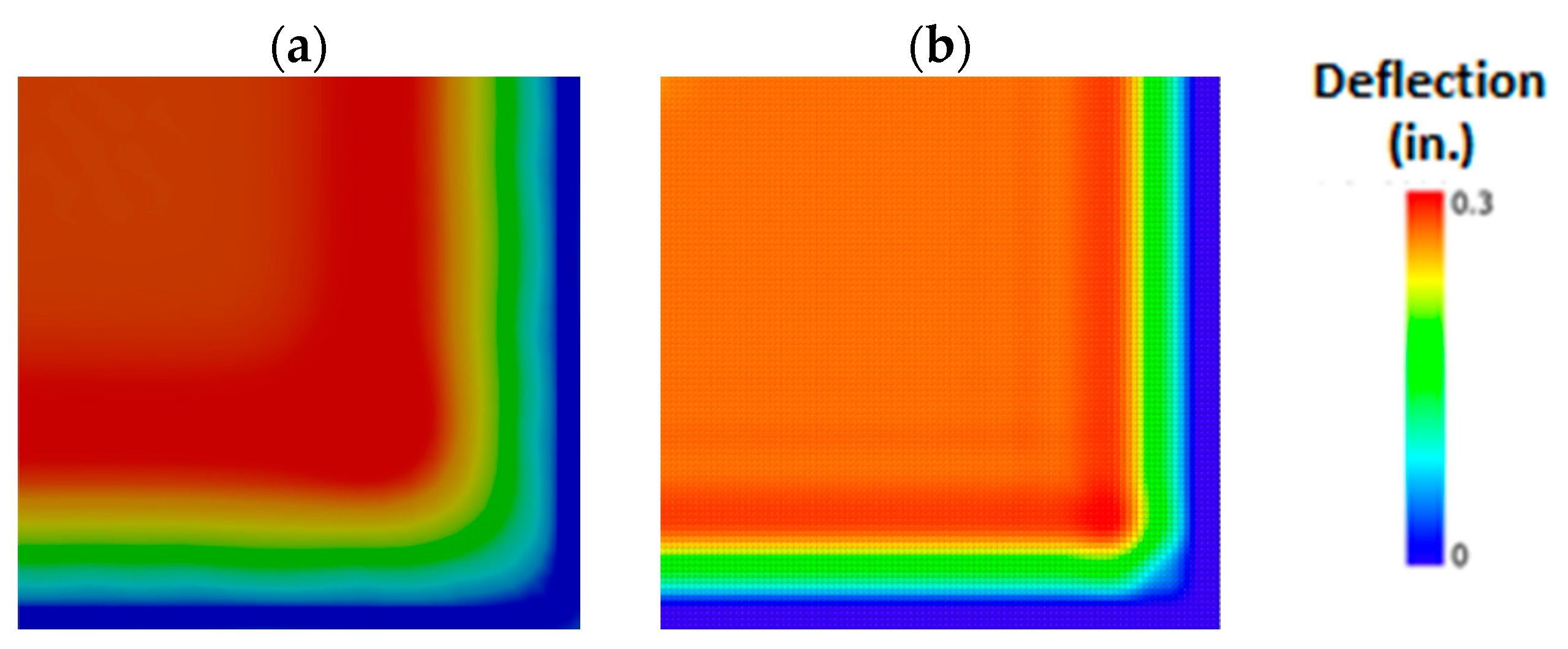
3.4.4. Results
Validation of the Large-Scale FEM Model Against Experiments
Verification of the MPM Model against the Scaled-Down FEM Model
4. Summary and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Momeni, M.; Bedon, C. Review on Glass Curtain Walls under Different Dynamic Mechanical Loads: Regulations, Experimental Methods and Numerical Tools; IntechOpen: London, UK, 2024. [Google Scholar] [CrossRef]
- Momeni, M.; Demetriou, D.; Papadakis, L.; Bedon, C.; Petrou, M.F.; Nicolaides, D. Damage investigation of blast loaded UHPFRC panels with optimized mixture design using advanced material models. Results Eng. 2024, 23, 102518. [Google Scholar] [CrossRef]
- Larcher, M.; Arrigoni, M.; Bedon, C.; Van Doormaal, A.; Haberacker, C.; Hüsken, G.; Millon, O.; Saarenheimo, A.; Solomos, G.; Thamie, L.; et al. Design of Blast-Loaded Glazing Windows and Facades: A Review of Essential Requirements towards Standardization. Adv. Civ. Eng. 2016, 2016, 2604232. [Google Scholar] [CrossRef]
- Saffarini, M.H. Atomistic Thermo-Mechanical Description of the Deformation Behavior, Scaling Laws, and Constitutive Modeling of Nanoporous Gold. 2021. Available online: https://digitalcommons.lsu.edu/gradschool_dissertations/5568 (accessed on 5 January 2023).
- Saffarini, M.H.; Voyiadjis, G.Z.; Ruestes, C.J. Scaling laws for nanoporous metals under uniaxial loading. J. Mater. Res. 2021, 36, 2729–2741. [Google Scholar] [CrossRef]
- Saffarini, M.H.; Voyiadjis, G.Z. Atomistic-Continuum Constitutive Modeling Connection for Gold Foams under Compression at High Strain Rates: The Dislocation Density Effect. Metals 2023, 13, 652. [Google Scholar] [CrossRef]
- Jin, H.J.; Weissmüller, J.; Farkas, D. Mechanical response of nanoporous metals: A story of size, surface stress, and severed struts. MRS Bull. 2018, 43, 35–42. [Google Scholar] [CrossRef]
- Cooper, P.W. Explosives Engineering; VCH Publishers Inc.: New York, NY, USA, 1996. [Google Scholar]
- Zukas, J.A.; Walters, W.P. Explosive Effects and Applications; Springer: New York, NY, USA, 1998. [Google Scholar]
- Alsayed, S.H.; Elsanadedy, H.M.; Al-Zaheri, Z.M.; Al-Salloum, Y.A.; Abbas, H. Blast response of GFRP-strengthened infill masonry walls. Constr. Build. Mater. 2016, 115, 438–451. [Google Scholar] [CrossRef]
- Nawar, M.; Salim, H.; Lusk, B.; Kiger, S. Numerical Simulation and Verification of Curtain Wall Systems under Shock Pressure. Pract. Period. Struct. Des. Constr. 2014, 19, 04014008. [Google Scholar] [CrossRef]
- Chen, Z.; Schreyer, H.L. On nonlocal damage models for interface problems. Int. J. Solids Struct. 1994, 31, 1241–1261. [Google Scholar] [CrossRef]
- Hirt, C.W.; Amsden, A.A.; Cook, J.L. An arbitrary Lagrangian–Eulerian computing method for all flow speeds. J. Comput. Phys. 1974, 14, 227–253. [Google Scholar] [CrossRef]
- Abedini, M.; Mutalib, A.; Raman, S.; Akhlaghi, E. Modeling the effects of high strain rate loading on RC columns using Arbitrary Lagrangian Eulerian (ALE) technique. Rev. Int. Métodos Numér. Cálc. Diseño Ing. 2018, 34, 24. [Google Scholar] [CrossRef]
- Nomura, T.; Hughes, T.J.R. An arbitrary Lagrangian–Eulerian fnite element method for interaction of fluid and a rigid body. Comput. Methods Appl. Mech. Eng. 1992, 95, 115–138. [Google Scholar]
- Von Estorff, O.; Firuziaan, M. Coupled BEM/FEM approach for nonlinear soil/structure interaction. Eng. Anal. Bound. Elem. 2000, 24, 715–725. [Google Scholar] [CrossRef]
- Baum, J.D. Fluid–structure interaction for structural failure assessment. In Proceedings of the Eighth Annual Conference of Computational Fluid Dynamics, Montreal, QC, Canada, 11–13 June 2000. [Google Scholar]
- Fairlie, G. The numerical simulation of high explosives using AUTODYN-2D & 3D. In Proceedings of the Explo ’98, London, UK, 28–29 September 1998. [Google Scholar]
- Zhang, X.; Chen, Z.; Liu, Y. The Material Point Method: A Continuum-Based Particle Method for Extreme Loading Cases; Academic Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Sulsky, D.; Chen, Z.; Schreyer, H.L. A particle method for history-dependent materials. Comput. Methods Appl. Mech. Eng. 1994, 118, 179–196. [Google Scholar] [CrossRef]
- Wu, Y.; Cai, X.-C. A fully implicit domain decomposition-based ALE framework for three-dimensional fluid–structure interaction with application in blood flow computation. J. Comput. Phys. 2014, 258, 524–537. [Google Scholar] [CrossRef]
- Basting, S.; Quaini, A.; Čanić, S.; Glowinski, R. Extended ALE method for fluid–structure interaction problems with large structural displacements. J. Comput. Phys. 2017, 331, 312–336. [Google Scholar] [CrossRef]
- Soares, D., Jr.; Von Estorff, O.; Mansur, W.J. Efficient non-linear solid–fluid interaction analysis by interactive BEM/FEM coupling. Int. J. Numer. Methods Eng. 2005, 64, 1416–1431. [Google Scholar] [CrossRef]
- Elleithy, W.M.; Al-Gahtani, H.; El-Gebeily, M.A. Iterative coupling of BE and FE methods in elastostatics. Eng. Anal. Bound. Elem. 2001, 25, 685–695. [Google Scholar] [CrossRef]
- Chen, Z.; Hu, W.; Shen, L.; Xin, X.; Brannon, R. An evaluation of the MPM for simulating dynamic failure with damage diffusion. Eng. Fract. Mech. 2002, 69, 1873–1890. [Google Scholar] [CrossRef]
- Brackbill, J.U.; Ruppel, H.M. FLIP: A method for adaptively zoned, particle-in-cell calculations of fluid flows in two dimensions. J. Comput. Phys. 1986, 65, 314–343. [Google Scholar] [CrossRef]
- Brackbill, J.U.; Kothe, D.B.; Ruppel, H.M. FLIP: A low-dissipation, particle-in-cell method for fluid flow. Comput. Phys. Commun. 1988, 48, 25–38. [Google Scholar] [CrossRef]
- Hu, W.; Chen, Z. Model-based simulation of the synergistic effects of blast and fragmentation on a concrete wall using the MPM. Int. J. Impact Eng. 2006, 32, 2066–2096. [Google Scholar] [CrossRef]
- Li, J.G.; Hamamoto, Y.; Liu, Y.; Zhang, X. Sloshing impact simulation with material point method and its experimental validations. Comput. Fluids 2014, 103, 86–99. [Google Scholar] [CrossRef]
- Sulsky, D.; Zhou, S.-J.; Schreyer, H.L. Application of a particle-in-cell method to solid mechanics. Comput. Phys. Commun. 1995, 87, 236–252. [Google Scholar] [CrossRef]
- Sulsky, D.; Schreyer, H.L. Axisymmetric form of the material point method with applications to up-setting and Taylor impact problems. Comput. Methods Appl. Mech. Eng. 1996, 139, 409–429. [Google Scholar] [CrossRef]
- Gan, Y.; Sun, Z.; Chen, Z.; Zhang, X.; Liu, Y. Enhancement of the material point method using B-spline basis functions. Int. J. Numer. Methods Eng. 2018, 113, 411–431. [Google Scholar] [CrossRef]
- Kakouris, E.G.; Triantafyllou, S.P. Phase-Field Material Point Method for dynamic brittle fracture with isotropic and anisotropic surface energy. Comput. Methods Appl. Mech. Eng. 2019, 357, 112503. [Google Scholar] [CrossRef]
- Moutsanidis, G.; Long, C.C.; Bazilevs, Y. IGA-MPM: The Isogeometric Material Point Method. Comput. Methods Appl. Mech. Eng. 2020, 372, 113346. [Google Scholar] [CrossRef]
- Tao, J.; Zhang, H.; Zheng, Y.; Chen, Z. Development of generalized interpolation material point method for simulating fully coupled thermomechanical failure evolution. Comput. Methods Appl. Mech. Eng. 2018, 332, 325–342. [Google Scholar] [CrossRef]
- Available online: https://geomechanics.berkeley.edu/research/comp-geo/mpm/ (accessed on 25 December 2023).
- Hu, W.; Chen, Z. A multi-mesh MPM for simulating the meshing process of spur gears. Comput. Struct. 2003, 81, 1991–2002. [Google Scholar] [CrossRef]
- York, A.R., II; Sulsky, D.; Schreyer, H.L. Fluid–membrane interaction based on the material point method. Int. J. Numer. Methods Eng. 2000, 48, 901–924. [Google Scholar] [CrossRef]
- Chen, W.-F.; Han, D.-J. Plasticity for Structural Engineers; J. Ross Publishing: Plantation, FL, USA, 1987. [Google Scholar]
- Chen, Z.; Schreyer, H.L. Formulation and Computational Aspects of Plasticity and Damage Models with Application to Quasi-Brittle Materials; Sandia National Lab.: Albuquerque, NM, USA, 1995. [Google Scholar] [CrossRef]
- He, G.; Dou, Y.; Guo, X.; Liu, Y. Effects of Grain Size on Ballistic Response of Copper Materials. In Proceedings of the ASME International Mechanical Engineering Congress and Exposition, Pittsburgh, PA, USA, 9–15 November 2018. IMECE2017-70585. [Google Scholar] [CrossRef]
- Lusk, B.; Perry, K.; Lusk, S. Predictability of a high explosives shock tube for testing blast resistant windows. Blasting Fragm. 2010, 4, 75–90. [Google Scholar]
- Idriss, J.S.; Lowak, M.J.; Wesevich, J.W.; Montoya, J.R.; Skrzyeki, S.M. Laminated Glass Response Validation and Modeling—Task 2: Dynamic Testing (Project No. 01-02697-002-12) Performed by Baker Engineering and Risk Consultants. Inc. for the U.S. Army Corps of Engineers Protective Design Center, contracted by National Institute of Building Sciences. 2013. [Google Scholar]
- Physical Properties of Glass|Saint Gobain Building Glass UK, (n.d.). Available online: https://www.saint-gobain-glass.co.uk/en-gb/architects/physical-properties (accessed on 7 March 2023).
- Elbelbisi, A.; Elsisi, A.; Saffarini, M.H.; Salim, H.; Chen, Z. Enhanced Blast Response Simulation of LG Panels Using an Elasto-Damage Model with the Finite Element Method. Buildings 2023, 13, 3025. [Google Scholar] [CrossRef]
- Hooper, P.A.; Sukhram, R.A.M.; Blackman, B.R.K.; Dear, J.P. On the Blast Resistance of Laminated Glass. Int. J. Solids Struct. 2012, 49, 899–918. [Google Scholar] [CrossRef]



| Case Study ID | Overall Objective | Designed Problem |
|---|---|---|
| 1 | Show the MPM strength in capturing FSI involving damage evolution as compared with the FEM. | Concrete box containing explosives |
| 2 | Build an MPM model of the shock tube test and validate it qualitatively against the experiment. | Shock tube test |
| 3 | Scale Up (Bottom-Up) approach Establish an FEM model using the validated MPM model from the second case study to simulate an actual shock tube test. | Shock tube test |
| 4 | Scale Down (Top-Down) Approach Develop an FEM model for a problem that does not involve FSI or fragmentation. The model is then scaled down to be used as a basis to verify the corresponding MPM model. | Laminated Glass Panel subjected to blast. |
| Density (kg/m3) | Young’s Modulus (GPa) | Tangent Modulus (GPa) | Poisson’s Ratio | Yield Strength (MPa) |
|---|---|---|---|---|
| 2300 | 25 | 6.25 | 0.18 | 15 |
| Density (kg/m3) | 1.225 |
| Specific Heat Constant Pressure (J/ kg K) | 1006.4 |
| (GPa) | (GPa) | (MJ/m3) | (kg/m3) | |||
|---|---|---|---|---|---|---|
| 373.8 | 3.747 | 4.15 | 0.9 | 0.35 | 6000 | 1630 |
| Sample | Dimensions |
|---|---|
| Outer ply (blast side) | 0.125 in. annealed |
| Interlayer | 0.06 in, PVB |
| Inner ply | 0.125 in. annealed |
| Measured average blast loading | |
| Pressure (psi) | 6.6 |
| Property | Value |
|---|---|
| Density (lb/in3) | 0.0397 |
| Young’s modulus, psi | 27,400 |
| Poisson ratio | 0.495 |
| Elastic limit, psi | 2400 |
| Failure strain | 1.20 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Saffarini, M.H.; Chen, Z.; Elbelbisi, A.; Salim, H.; Perry, K.; Bowman, A.L.; Robert, S.D. Verification and Validation of Modeling of Fluid–Solid Interaction in Explosion-Resistant Designs Using Material Point Method. Buildings 2024, 14, 3137. https://doi.org/10.3390/buildings14103137
Saffarini MH, Chen Z, Elbelbisi A, Salim H, Perry K, Bowman AL, Robert SD. Verification and Validation of Modeling of Fluid–Solid Interaction in Explosion-Resistant Designs Using Material Point Method. Buildings. 2024; 14(10):3137. https://doi.org/10.3390/buildings14103137
Chicago/Turabian StyleSaffarini, Mohammed H., Zhen Chen, Ahmed Elbelbisi, Hani Salim, Kyle Perry, Andrew L. Bowman, and Stephen D. Robert. 2024. "Verification and Validation of Modeling of Fluid–Solid Interaction in Explosion-Resistant Designs Using Material Point Method" Buildings 14, no. 10: 3137. https://doi.org/10.3390/buildings14103137
APA StyleSaffarini, M. H., Chen, Z., Elbelbisi, A., Salim, H., Perry, K., Bowman, A. L., & Robert, S. D. (2024). Verification and Validation of Modeling of Fluid–Solid Interaction in Explosion-Resistant Designs Using Material Point Method. Buildings, 14(10), 3137. https://doi.org/10.3390/buildings14103137







