Progressive Failure of Water-Resistant Stratum in Karst Tunnel Construction Using an Improved Meshfree Method Considering Fluid–Solid Interaction
Abstract
1. Introduction
2. Method
2.1. Constitutive Model of Rock
2.2. Constitutive Model of Fluid
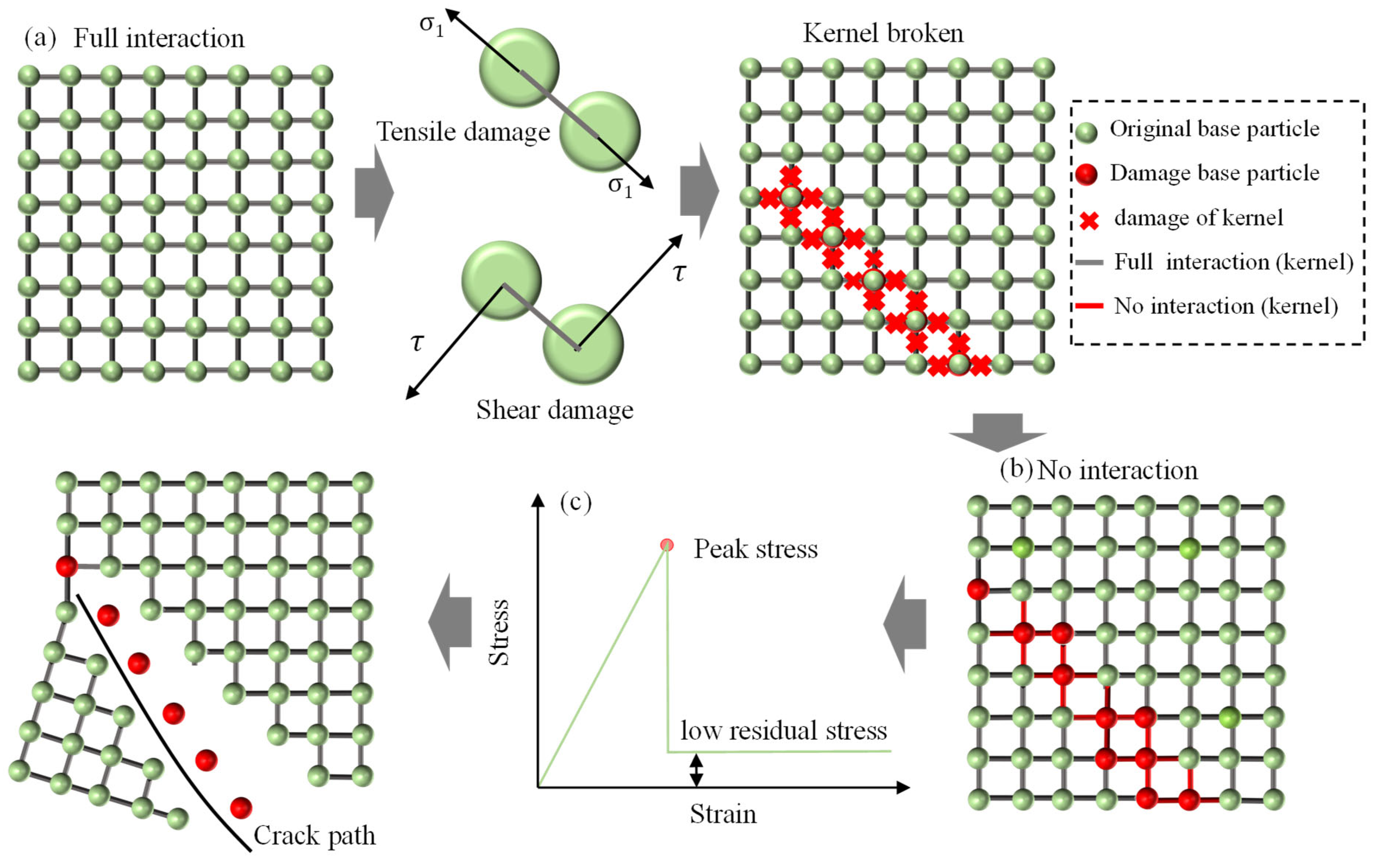
2.3. Cracking Strategy of Rock
2.4. Contact Algorithm of Rock
2.5. Fluid–Solid Interaction Scheme
3. Validation Example
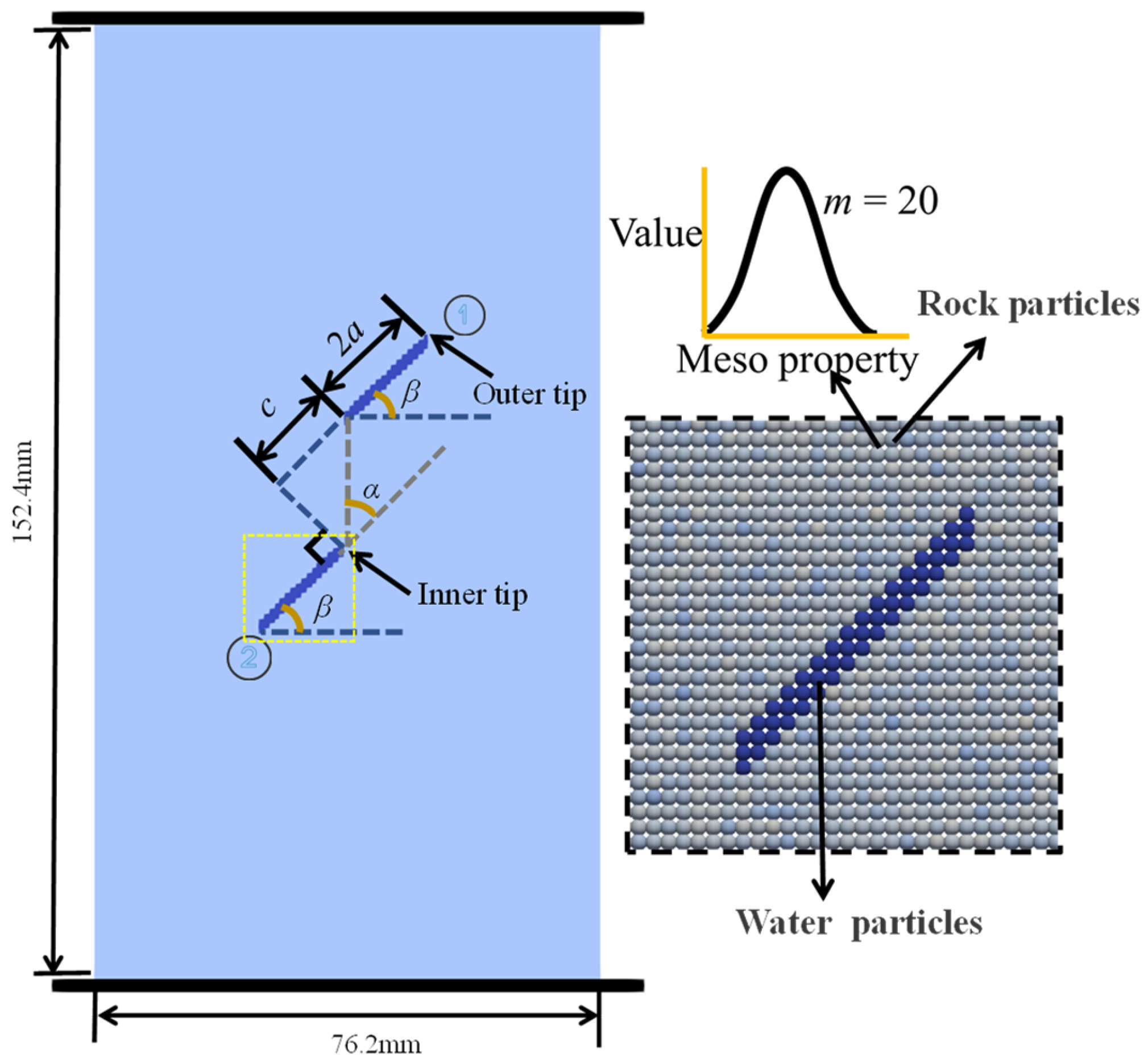
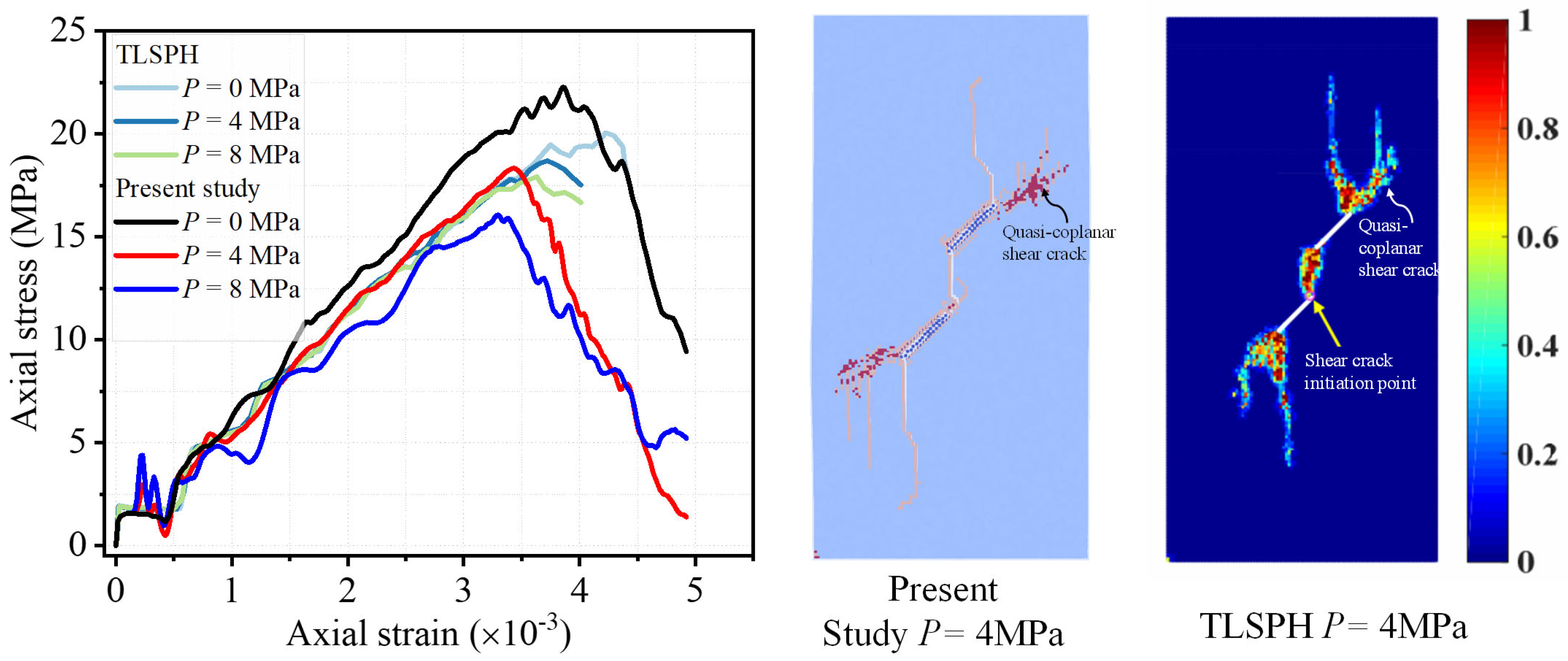
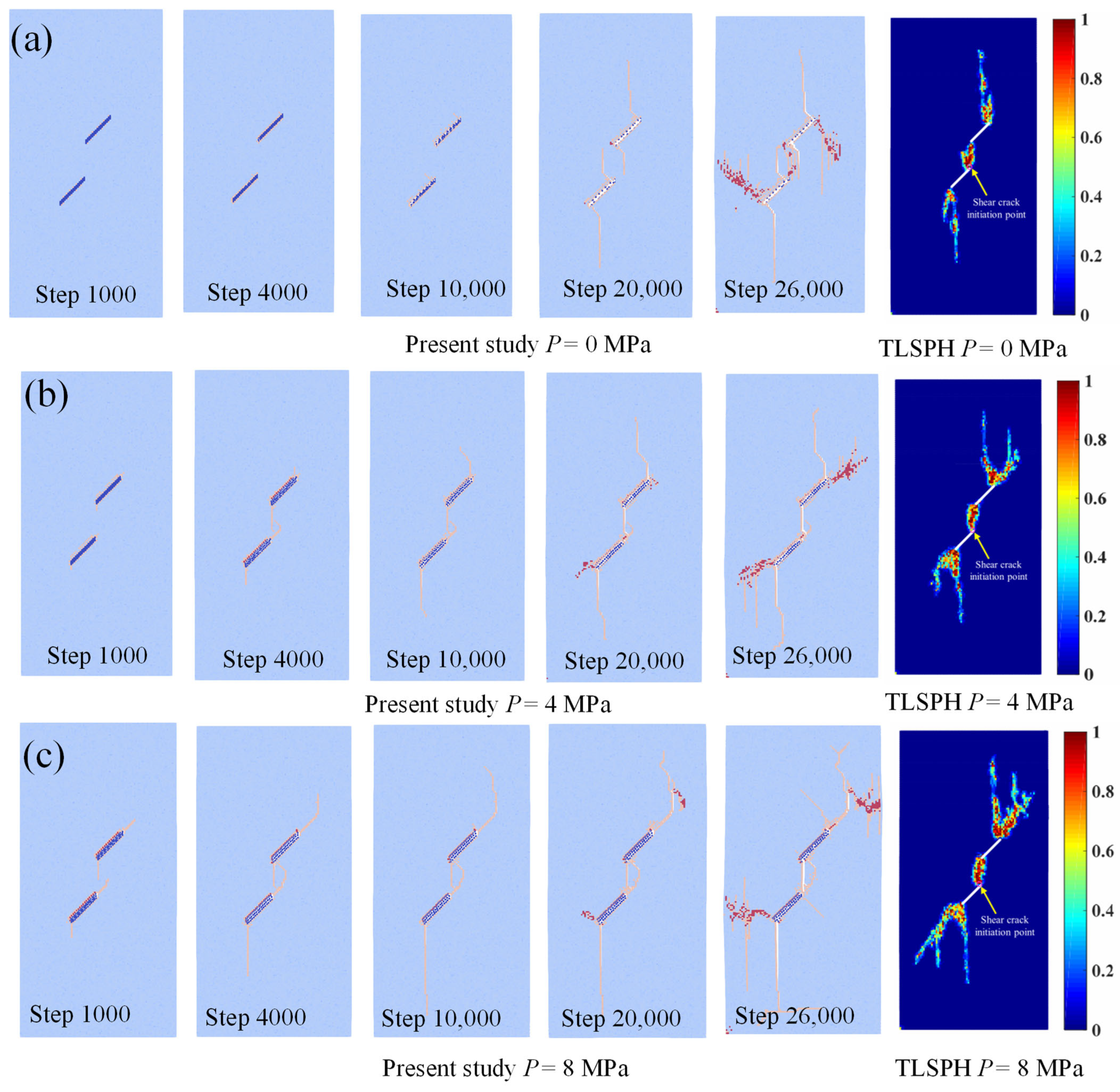
Hydraulic Fracturing of Two Pre-Existing Flawed Rocks
4. Numerical Simulation of the Karst Tunnel
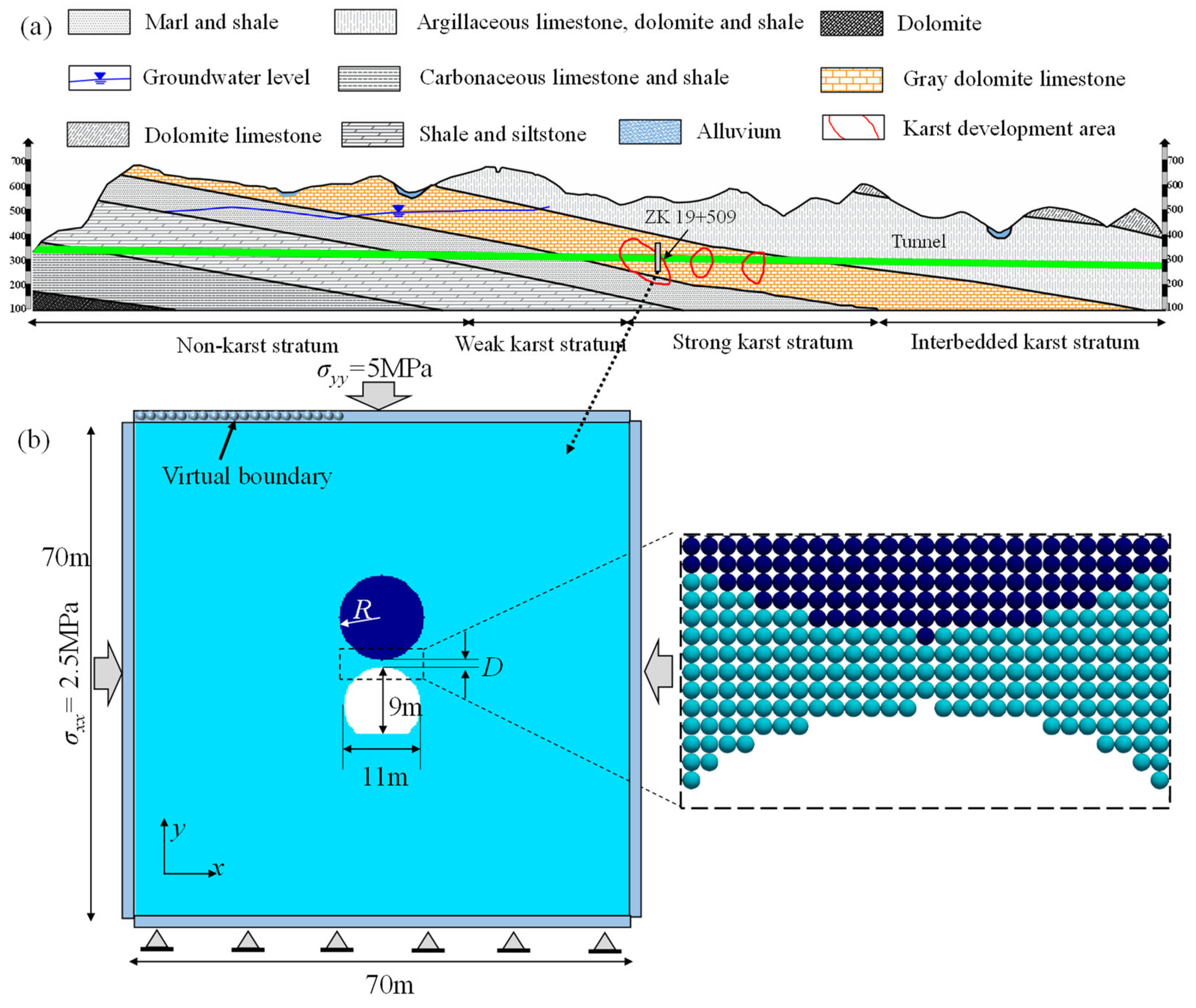
4.1. Engineering Background
4.2. Computation Model and Parameters
4.3. Calculation Results and Analysis
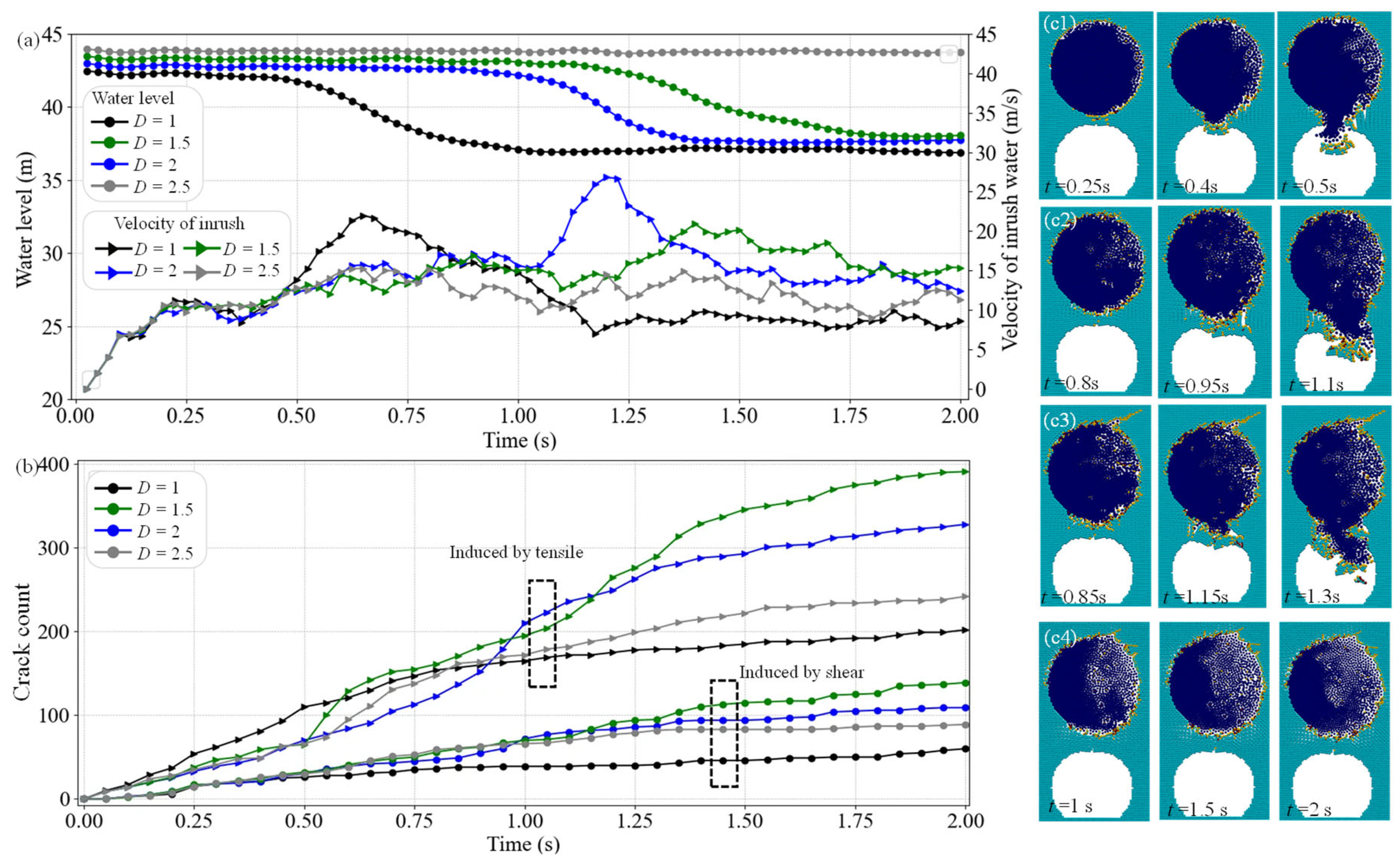
General Inrush Behaviour
4.4. Influence of the Thickness of Water-Resistant Rock
4.5. Influence of the Different Strengths of the Rock Mass
4.6. Influence of Different Radii of Karst Caves
5. Discussion
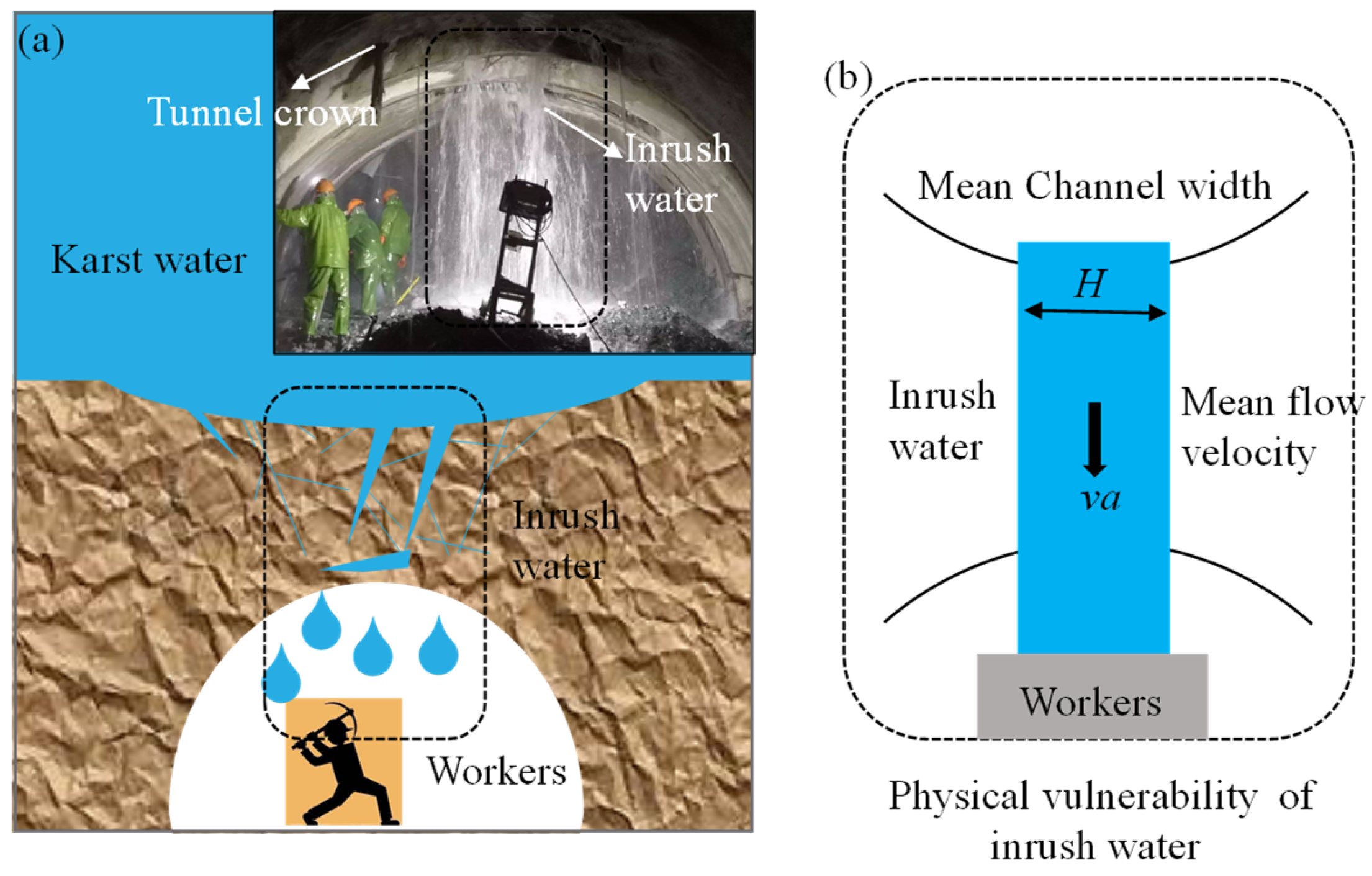
5.1. Physical Vulnerability Induced by Inrush in Karst Areas
5.2. Advantages and Limitations of Method
6. Conclusions
- (1)
- The improved SPH method explicitly simulates progressive failure involving the loss of material continuity and brittle fracture characteristics without re-meshing. Moreover, a two-phase adaptive adjacent algorithm considering the DPs can faithfully capture the FSI and hydraulic fracturing;
- (2)
- The evolution of water inrush in the Jigongling karst tunnel calculated by the SPH method is divided into the equilibrium stage, hydraulic fracturing, local inrush accompanied by the complete failure of the water-resistant wall, overall inrush and stable inrush stages;
- (3)
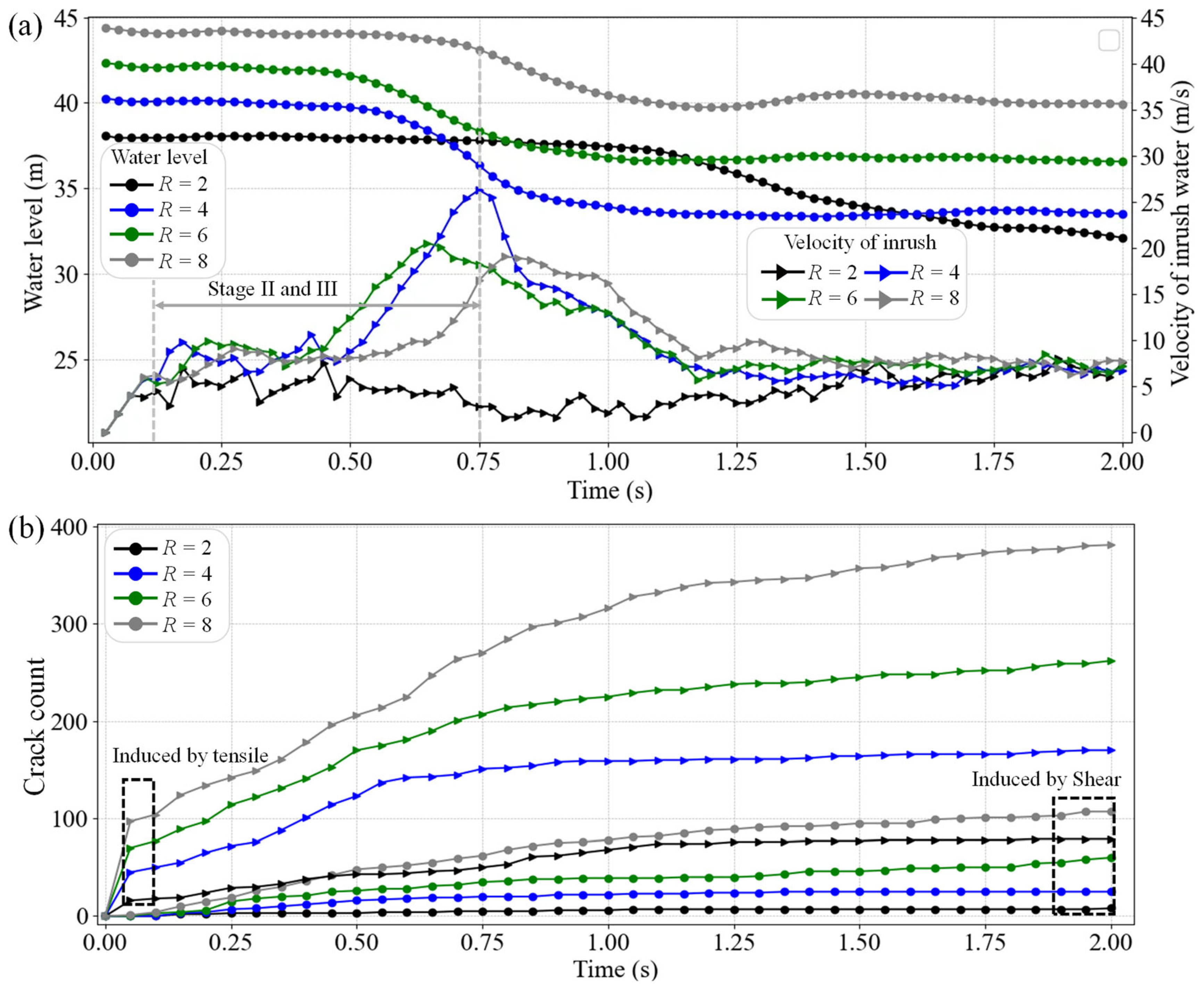
- With increasing thickness and strength of the water-resistant wall, the possibility of water/mud inrush in the tunnel decreases, and a drop in the water level and increase in the flow velocity have a delayed effect during stages III–IV; however, such a delayed effect is less affected by karst cave radii. As the strength of the rock decreases, the peak inrush velocity increases in stage II due to hydraulic fracturing. In addition, as karst cave radii increase and the thickness and strength of rock decrease, tensile and shear cracks in rock significantly increase in stages II–III;
- (4)
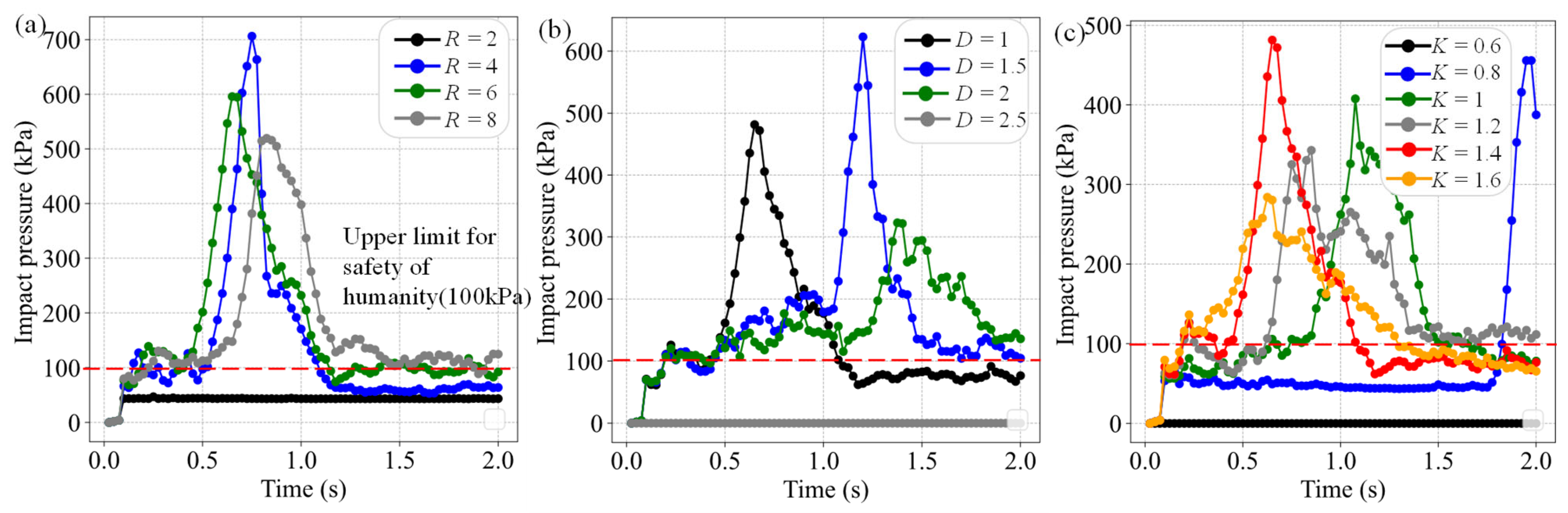
- Once inrush occurs in the Jigongling karst tunnel, the impact pressure during stages III–IV significantly exceeds the upper limit for human safety. In stage V (i.e., stable inrush), the impact pressure significantly decreases and then may be below the upper limit for human safety, which is consistent with the field observations.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhou, Y.; Li, S.C.; Li, L.P.; Zhang, Q.Q.; Shi, S.S.; Song, S.G.; Wang, K.; Chen, D.Y.; Sun, S.Q. New technology for fluid-solid coupling tests of underground engineering and its application in experimental simulation of water inrush in filled-type karst conduit. Chin. J. Geotech. Eng. 2015, 37, 1232–1240. [Google Scholar]
- Pan, D.D.; Li, S.C.; Xu, Z.H.; Li, L.P.; Lu, W.; Lin, P.; Huang, X.; Sun, S.Q.; Gao, C.L. Model tests and numerical analysis for water inrush caused by karst caves filled with confined water in tunnels. Chin. J. Geotech. Eng. 2018, 40, 828–836. [Google Scholar]
- Li, H.; Xu, H.; Li, Z.; Zhang, H.; Zhang, Y.; Chang, T. Study on treatment of fault water gushing in deep roadway. J. Min. Saf. Eng. 2018, 35, 635–641. [Google Scholar]
- Huang, M.L.; Wang, F.; Lu, W.; Tan, Z.S. Numerical study on the process of water inrush in karst caves with hydraulic pressure caused by tunnel excavation. Strateg. Study CAE 2009, 11, 93–96. [Google Scholar]
- Xie, Q.; Cao, Z.L.; Sun, W.C.; Fumagalli, A.; Fu, X.; Wu, Z.H.; Wu, K. Numerical simulation of the fluid-solid coupling mechanism of water and mud inrush in a water-rich fault tunnel. Tunn. Undergr. Space Technol. 2023, 131, 104796. [Google Scholar] [CrossRef]
- Gao, J.Y.; Peng, S.Y.; Chen, G.Q.; Mitani, Y.; Fan, H.Y. Coupled hydro-mechanical analysis for water inrush of fractured rock masses using the discontinuous deformation analysis. Comput. Geotech. 2023, 156, 105247. [Google Scholar] [CrossRef]
- Cui, W.; Tang, Q.W.; Song, H.F. Washout resistance evaluation of fast-setting cement-based grouts considering time-varying viscosity using CFD simulation. Constr. Build. Mater. 2020, 242, 117959. [Google Scholar] [CrossRef]
- Zhang, T.; Gan, Q.; Zhao, Y.X.; Zhu, G.P.; Nie, X.D.; Yang, K.; Li, J.Z. Investigations into mining-induced stress–fracture–seepage field coupling effect considering the response of key stratum and composite aquifer. Rock Mech. Rock Eng. 2019, 52, 4017–4031. [Google Scholar] [CrossRef]
- Pu, H.; Ni, H.Y. Characteristics of water sediment two phase flows in weakly cemented fractured rock mass based on Lattice Boltzmann Method. In Proceedings of the 51st U.S. Rock Mechanics/Geomechanics Symposium, San Francisco, CA, USA, 25–28 June 2017; pp. 1921–1929. [Google Scholar]
- Jin, L.; Zeng, Y.W.; Cheng, T.; Li, J.J. Numerical simulation of mud inrush of tunnels with coupled LBM-DEM. Chin. J. Geotech. Eng. 2021, 43, 1000–1009. [Google Scholar]
- Dave, H.; Herrmann, M.; Kasbaoui, M.H. The volume-filtering immersed boundary method. J. Comput. Phys. 2023, 487, 112136. [Google Scholar] [CrossRef]
- Peng, X.Y.; Liu, J.F.; Cheng, X.; Yu, P.C.; Zhang, Y.B.; Chen, G.Q. Dynamic modelling of soil-rock-mixture slopes using the coupled DDA-SPH method. Eng. Geol. 2022, 307, 106772. [Google Scholar] [CrossRef]
- Fan, H.Y.; Li, L.P.; Chen, G.Q.; Liu, H.L.; Gao, J.Y.; Li, C.Z.; Peng, X.Y.; Zhou, S. Analysis method of the water inrush and collapse in jointed rock mass tunnels: A case study. Eng. Anal. Bound. Elem. 2023, 146, 838–850. [Google Scholar]
- Gao, J.Y.; Fan, H.Y.; Chen, G.Q.; Wang, W.; Zhang, H. Verification of 3D DDA-SPH coupling method and its application in the analysis of geological disasters. Eng. Anal. Bound. Elem. 2024, 158, 68–84. [Google Scholar] [CrossRef]
- Xu, W.J.; Wang, Y.J.; Dong, X.Y. Influence of reservoir water level variations on slope stability and evaluation of landslide tsunami. Bull. Eng. Geol. Environ. 2021, 80, 4891–4907. [Google Scholar] [CrossRef]
- Sun, J.Z.; Zou, L.; Govender, N.; Martínez-Estévez, I.; Crespo, A.J.C.; Sun, Z.; Domínguez, G.M. A resolved SPH-DEM coupling method for analysing the interaction of polyhedral granular materials with fluid. Ocean. Eng. 2023, 287, 115938. [Google Scholar] [CrossRef]
- Nakamichi, Y.; Sugie, S.; Takeyama, T. A coupled MPM–SPH numerical simulation for fully saturated soil. Proc. Lect. Notes Civ. Eng. 2021, 125, 794–801. [Google Scholar]
- Nakamichi, Y.; Sugie, S.; Takeyama, T. Numerical analysis of rain-induced slope failure by using the MPM-SPH coupling method. In Proceedings of the International Conference of the International Association for Computer Methods and Advances in Geomechanics, Turin, Italy, 30 August–2 September 2022; pp. 237–244. [Google Scholar]
- Yang, W.D.; Lv, X.X.; Wang, L.G.; Peng, D.; Chen, X.Z. A DEM–CFD coupling method for modelling two-hole synchronous hydraulic fracturing. Geomech. Geophys. Geo-Energy Geo-Resour. 2023, 9, 6. [Google Scholar] [CrossRef]
- Hassan, E.B.E.; Hoffmann, J.E. Impact of flow direction on the isothermal pressure drop through a packed bed of crushed rock—A DEM-CFD approach. Powder Technol. 2024, 440, 119774. [Google Scholar] [CrossRef]
- Tran, Q.A.; Grimstad, G.; Ghoreishian Amiri, S.A. MPMICE: A hybrid MPM-CFD model for simulating coupled problems in porous media. Application to earthquake-induced submarine landslides. Int. J. Numer. Methods Eng. 2024, 125, e7383. [Google Scholar] [CrossRef]
- Younes, N.; Wautier, A.; Wan, R.; Millet, O.; Nicot, F.; Bouchard, R. DEM-LBM coupling for partially saturated granular assemblies. Comput. Geotech. 2023, 162, 105677. [Google Scholar] [CrossRef]
- Bouchard, R.; Younes, N.; Millet, O.; Wautier, A. Parameter optimization of phase-field-based LBM model for calculating capillary forces. Comput. Geotech. 2024, 172, 106391. [Google Scholar] [CrossRef]
- Gingold, R.A.; Monaghan, J.J. Smoothed particle hydrodynamics: Theory and application to non-spherical stars. Mon. Not. R. Astron. Soc. 1977, 181, 375–389. [Google Scholar] [CrossRef]
- Monaghan, J.J. Simulating Free Surface Flows with SPH. J. Comput. Phys. 1994, 110, 399–406. [Google Scholar] [CrossRef]
- Walhorn, E.; Kölke, A.; Hübner, B.; Dinkler, D. Fluid–structure coupling within a monolithic model involving free surface flows. Comput. Struct. 2005, 83, 2100–2111. [Google Scholar] [CrossRef]
- Fuchs, S.L.; Meier, C.; Wall, W.A.; Cyron, C.J. A novel smoothed particle hydrodynamics and finite element coupling scheme for fluid–structure interaction: The sliding boundary particle approach. Comput. Methods Appl. Mech. Eng. 2021, 383, 113922. [Google Scholar] [CrossRef]
- Hermange, C.; Oger, G.; Le Chenadec, Y.; Le Touzé, D. A 3D SPH–FE coupling for FSI problems and its application to tire hydroplaning simulations on rough ground. Comput. Methods Appl. Mech. Eng. 2019, 355, 558–590. [Google Scholar] [CrossRef]
- O’Connor, J.; Rogers, B.D. A fluid–structure interaction model for free-surface flows and flexible structures using smoothed particle hydrodynamics on a GPU. J. Fluids Struct. 2021, 104, 103312. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, Y.; Qin, Z.; Song, S.G.; Lin, P. Analysis method of water inrush for tunnels with damaged water-resisting rock mass based on finite element method-smooth particle hydrodynamics coupling. Comput. Geotech. 2020, 126, 103725. [Google Scholar] [CrossRef]
- Peng, X.Y.; Yu, P.C.; Cheng, X.; Chen, G.Q.; Zhang, Y.B.; Zhang, H.; Li, C.Z. Dynamic simulation of the water inrush process in tunnel construction using a three-dimensional coupled discontinuous deformation analysis and smoothed particle hydrodynamics method. Tunn. Undergr. Space Technol. 2022, 127, 104612. [Google Scholar] [CrossRef]
- Ji, S.Y.; Chen, X.D.; Liu, L. Coupled DEM-SPH method for interaction between dilated polyhedral particles and fluid. Math. Probl. Eng. 2019, 1, 4987801. [Google Scholar] [CrossRef]
- Chakraborty, S.; Shaw, A. A pseudo-spring based fracture model for SPH simulation of impact dynamics. Int. J. Impact Eng. 2013, 58, 84–95. [Google Scholar] [CrossRef]
- Yu, S.Y.; Ren, X.H.; Zhang, J.X.; Wang, H.J.; Sun, Z.H. An improved form of smoothed particle hydrodynamics method for crack propagation simulation applied in rock mechanics. Int. J. Min. Sci. Technol. 2021, 31, 421–428. [Google Scholar] [CrossRef]
- Mu, D.R.; Zhang, D.Y.; Tang, A.P.; Qu, H.G.; Li, Z.M. Numerical simulation of rock thermal fracture considering friction effect in the framework of smooth particle hydrodynamics based on total Lagrangian formula. Rock Mech. Rock Eng. 2022, 55, 1663–1685. [Google Scholar] [CrossRef]
- Xia, C.Z.; Shi, Z.M.; Liu, M.M.; Li, B.; Yu, S.B.; Xue, J.F. Dynamic analysis of field-scale rockslides based on three-dimensional discontinuous smoothed particle hydrodynamics: A case study of Tangjiashan rockslide. Eng. Geol. 2024, 336, 107558. [Google Scholar] [CrossRef]
- Peng, C.; Wang, S.; Wu, W.; Yu, H.S.; Wang, C.; Chen, J.Y. LOQUAT: An open-source GPU-accelerated SPH solver for geotechnical modeling. Acta Geotech. 2019, 14, 1269–1287. [Google Scholar] [CrossRef]
- Gray, J.P.; Monaghan, J.J. Numerical modelling of stress fields and fracture around magma chambers. J. Volcanol. Geotherm. Res. 2004, 135, 259–283. [Google Scholar] [CrossRef]
- Gharehdash, S.; Barzegar, M.; Palymskiy, I.B.; Fomin, P.A. Blast induced fracture modelling using smoothed particle hydrodynamics. Int. J. Impact Eng. 2020, 135, 103235. [Google Scholar] [CrossRef]
- Abdelrazek, A.M.; Kimura, I.; Shimizu, Y. Simulation of the erosion and seepage failure around sheet pile using two-phase WC-SPH method. J. Jpn. Soc. Civ. Eng. 2016, 72, I_495–I_504. [Google Scholar] [CrossRef]
- Xia, C.Z.; Shi, Z.M.; Li, B. A modified SPH framework of for simulating progressive rock damage and water inrush disasters in tunnel constructions. Comput. Geotech. 2024, 167, 106042. [Google Scholar] [CrossRef]
- Zhou, X.P.; Zhao, Y.; Qian, Q.H. A novel meshless numerical method for modeling progressive failure processes of slopes. Eng. Geol. 2015, 192, 139–153. [Google Scholar] [CrossRef]
- Zhou, X.P.; Wang, Y.T.; Qian, Q.H. Numerical simulation of crack curving and branching in brittle materials under dynamic loads using the extended non-ordinary state-based peridynamics. Eur. J. Mech. A-Solids 2016, 60, 277–299. [Google Scholar] [CrossRef]
- Zhou, X.P.; Xiao, N. Analyzing fracture properties of the 3D reconstructed model of porous rocks. Eng. Fract. Mech. 2018, 189, 175–193. [Google Scholar] [CrossRef]
- Yu, S.Y.; Ren, X.H.; Zhang, J.X.; Wang, H.J.; Sun, Z.H.; Zhou, Y. Numerical simulation on the stability of rock slope based on an improved SPH Method. J. Mt. Sci. 2021, 18, 1937–1950. [Google Scholar] [CrossRef]
- Yu, S.Y.; Yu, J.; Sun, Z.H.; Zhu, C.H.; Yang, J. Numerical investigation and experimental study on fracture processes of central flawed sandstone Brazilian discs. Int. J. Solids Struct. 2023, 262–263, 112054. [Google Scholar] [CrossRef]
- Xia, C.Z.; Shi, Z.M.; Li, B. A revisit of disaster process of Vajont rockslide using a coupled discontinuous smooth particle hydrodynamics (CDSPH) method. Landslides 2024, 21, 197–216. [Google Scholar] [CrossRef]
- Sheikh, B.; Qiu, T.; Ahmadipur, A. Comparison of SPH boundary approaches in simulating frictional soil–structure interaction. Acta Geotech. 2021, 16, 2389–2408. [Google Scholar] [CrossRef]
- Ganesh, K.V.; Patra, P.K.; Travis, K.P. Multiscale modeling of impact through molecular dynamics and smooth particle hydrodynamics. Phys. A Stat. Mech. Its Appl. 2022, 593, 126903. [Google Scholar] [CrossRef]
- Mu, D.R.; Tang, A.P.; Qu, H.G.; Wang, J.J. An extended hydro-mechanical coupling model based on smoothed particle hydrodynamics for simulating crack propagation in rocks under hydraulic and compressive loads. Materials 2023, 16, 1572. [Google Scholar] [CrossRef]
- Zhu, C.W.; Peng, C.; Wu, W. Applications of micropolar SPH in geomechanics. Acta Geotech. 2021, 16, 2355–2369. [Google Scholar] [CrossRef]
- Chakraborty, S.; Islam, M.R.I.; Shaw, A.; Ramachandra, L.S.; Reid, S.R. A computational framework for modelling impact induced damage in ceramic and ceramic-metal composite structures. Compos. Struct. 2017, 164, 263–276. [Google Scholar] [CrossRef]
- Shaw, A.; Reid, S.R.; Roy, D.; Chakraborty, S. Beyond classical dynamic structural plasticity using mesh-free modelling techniques. Int. J. Impact Eng. 2015, 75, 268–278. [Google Scholar] [CrossRef]
- Gao, C.L.; Li, L.P.; Zhou, Z.Q.; Li, Z.H.; Cheng, S.; Wang, L.G.; Zhang, D.S. Peridynamics simulation of water inrush channels evolution process due to rock mass progressive failure in karst tunnels. Int. J. Geomech. 2021, 21, 04021028. [Google Scholar] [CrossRef]
- Xu, Z.H.; Lin, P.; Xing, H.L.; Pan, D.D.; Huang, X. Hydro-mechanical coupling response behaviors in tunnel subjected to a water-filled karst cave. Rock Mech. Rock Eng. 2021, 54, 3737–3756. [Google Scholar] [CrossRef]
- Kazerani, T.; Zhao, J. Micromechanical parameters in bonded particle method for modelling of brittle material failure. Int. J. Numer. Anal. Methods Geomech. 2010, 34, 1877–1895. [Google Scholar] [CrossRef]
- Li, S.C.; Bu, L.; Shi, S.S.; Li, L.P.; Zhou, Z.Q. Prediction for water inrush disaster source and CFD-based design of evacuation routes in karst tunnel. Int. J. Geomech. 2022, 22, 05022001. [Google Scholar] [CrossRef]
- Iverson, R.M. The physics of debris flows. Rev. Geophys. 1997, 35, 245–296. [Google Scholar] [CrossRef]
- Kang, H.S.; Kim, Y.T. The physical vulnerability of different types of building structure to debris flow events. Nat. Hazards 2016, 80, 1475–1493. [Google Scholar] [CrossRef]
- Zhang, J.; Wen, W. Construction technology for the Dazhushan tunnel in a high-pressure fault with abundant water. Mod. Tunn. Technol. 2018, 55, 160–166. [Google Scholar]
- Arrighi, C.; Oumeraci, H.; Castelli, F. Hydrodynamics of pedestrians’ instability in floodwaters. Hydrol. Earth Syst. Sci. 2017, 21, 515–531. [Google Scholar] [CrossRef]
- Bi, J.; Zhou, X.P. Numerical simulation of zonal disintegration of the surrounding rock masses around a deep circular tunnel under dynamic unloading. Int. J. Comput. Methods 2015, 12, 1550020. [Google Scholar] [CrossRef]
- Yu, S.Y.; Ren, X.H.; Zhang, J.X.; Wang, H.J.; Sun, Z.H. An improved smoothed particle hydrodynamics method and its application in rock hydraulic fracture modelling. Rock Mech. Rock Eng. 2021, 54, 6039–6055. [Google Scholar] [CrossRef]
- Mu, D.R.; Wen, A.H.; Zhu, D.Q.; Tang, A.P.; Nie, Z.; Wang, Z.Y. An improved smoothed particle hydrodynamics method for simulating crack propagation and coalescence in brittle fracture of rock materials. Theor. Appl. Fract. Mech. 2022, 119, 103355. [Google Scholar] [CrossRef]
- Xia, C.Z.; Shi, Z.M.; Zheng, H.C.; Wu, X.H. Kernel broken smooth particle hydrodynamics method for crack propagation simulation applied in layered rock cells and tunnels. Undergr. Space 2023, 10, 55–75. [Google Scholar] [CrossRef]
- Vacondio, R.; Mignosa, P.; Pagani, S. 3D SPH numerical simulation of the wave generated by the Vajont rockslide. Adv. Water Resour. 2013, 59, 146–156. [Google Scholar] [CrossRef]
- Liu, L.; Li, S.; Zheng, M.; Wang, D.; Chen, M.; Zhou, J.; Yan, T.; Shi, Z. Inverting the rock mass P-wave velocity field ahead of deep buried tunnel face while borehole drilling. Int. J. Min. Sci. Technol. 2024, 34, 681–697. [Google Scholar] [CrossRef]
- Liu, L.; Li, S.; Zheng, M.; Wang, Y.; Shen, J.; Shi, Z.; Xia, C.; Zhou, J. Identification of rock discontinuities by coda wave analysis while borehole drilling in deep buried tunnels. Tunn. Undergr. Space Technol. 2024, 153, 105969. [Google Scholar] [CrossRef]




| Parameters | Rock Matrix | Water |
|---|---|---|
| Density (kg/m3) | 2650 | 1000 |
| Normal stiffness (GPa/m) | 0.2 | – |
| Friction coefficient | tan (35°) | – |
| Particle spacing (m) | 8 × 10−3 | 8 × 10−3 |
| Boundary particle spacing (m) | 8 × 10−3 | 8 × 10−3 |
| Number of IPs | 18,000 | 50 |
| Kernel function | B-spline | B-spline |
| Kernel smoothing length (m) | 0.7 × 10−3 | 0.7 × 10−3 |
| DP radius (m) | 0.8 × 10−3 | – |
| SPH time step (s) | 5 × 10−8 | 5 × 10−8 |
| δ–SPH coefficient | – | 0.1 |
| Shape parameter, mshape | 20 | – |
| Artificial viscosity parameter | 2 | 2 |
| Artificial viscosity parameter | 4 | 4 |
| Artificial stress parameter e | 0.3 | 0.3 |
| Artificial stress parameter n | 4 | 4 |
| Parameters | Rock Matrix | Water |
|---|---|---|
| Density (kg/m3) | 2500 | 1000 |
| Normal stiffness (MPa/m) | 9.6 | – |
| Friction coefficient | tan (30°) | – |
| Particle spacing (m) | 0.2 | 0.2 |
| Boundary particle spacing (m) | 0.2 | 0.2 |
| Number of IPs | 70,500 | 1512 |
| Kernel function | B–spline | B–spline |
| Kernel smoothing length (m) | 0.2 | 0.3 |
| DP radius (m) | 0.2 | – |
| SPH time step (s) | 1 × 10−4 | 1 × 10−4 |
| δ–SPH coefficient | – | 0.1 |
| Shape parameter, mshape | 20 | – |
| Artificial viscosity parameter | 2 | 2 |
| Artificial viscosity parameter | 4 | 4 |
| Artificial stress parameter e | 0.3 | 0.3 |
| Artificial stress parameter n | 4 | 4 |
| Scenario | Thickness of Water-Resistant Rock D (m) | Strength Reduction Factor of Water-Resistant Rock K | Karst Cave Radius R (m) |
|---|---|---|---|
| I | 1 | 1.4 | 2/4/6/8 |
| II | 1/1.5/2/2.5 | 1.4 | 6 |
| III | 1 | 0.6/0.8/1/1.2/1.4/1.6 | 6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, Y.; Xia, C.; Shi, Z.; Lu, G.; Liu, L.; Liu, M. Progressive Failure of Water-Resistant Stratum in Karst Tunnel Construction Using an Improved Meshfree Method Considering Fluid–Solid Interaction. Buildings 2024, 14, 3140. https://doi.org/10.3390/buildings14103140
Zhou Y, Xia C, Shi Z, Lu G, Liu L, Liu M. Progressive Failure of Water-Resistant Stratum in Karst Tunnel Construction Using an Improved Meshfree Method Considering Fluid–Solid Interaction. Buildings. 2024; 14(10):3140. https://doi.org/10.3390/buildings14103140
Chicago/Turabian StyleZhou, Yuanyuan, Chengzhi Xia, Zhenming Shi, Guangyin Lu, Liu Liu, and Maomao Liu. 2024. "Progressive Failure of Water-Resistant Stratum in Karst Tunnel Construction Using an Improved Meshfree Method Considering Fluid–Solid Interaction" Buildings 14, no. 10: 3140. https://doi.org/10.3390/buildings14103140
APA StyleZhou, Y., Xia, C., Shi, Z., Lu, G., Liu, L., & Liu, M. (2024). Progressive Failure of Water-Resistant Stratum in Karst Tunnel Construction Using an Improved Meshfree Method Considering Fluid–Solid Interaction. Buildings, 14(10), 3140. https://doi.org/10.3390/buildings14103140






