A Survey of Data-Driven Construction Materials Price Forecasting
Abstract
:1. Introduction
2. Research Methodology
3. Results and Analysis
3.1. Causal Modeling
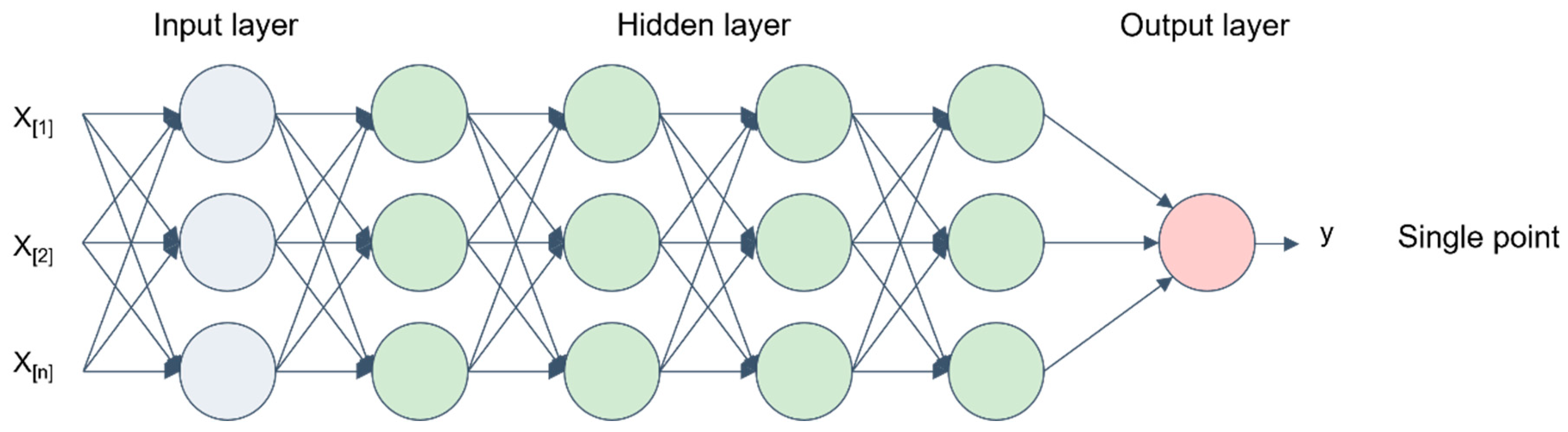
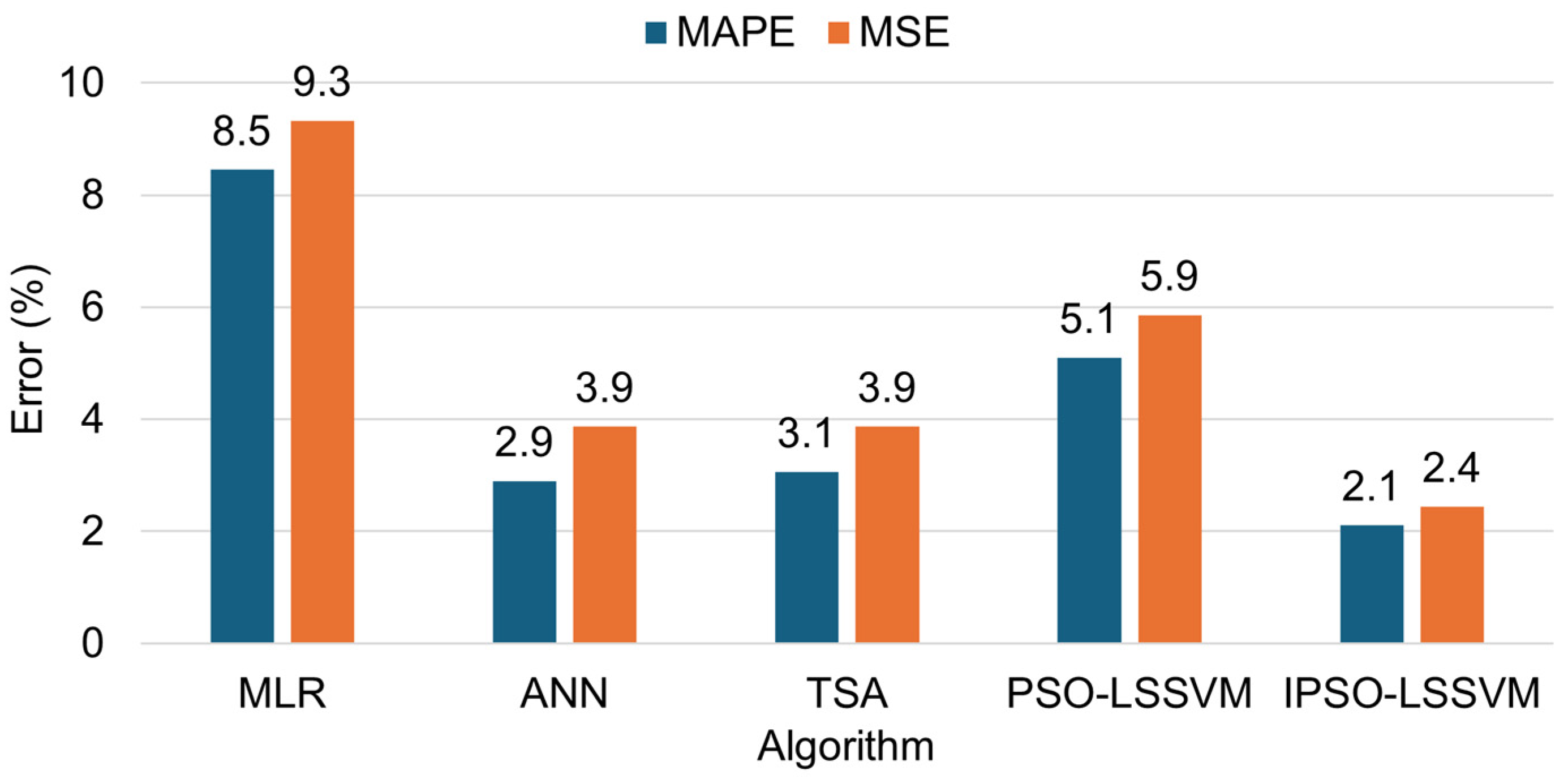
3.1.1. Point Prediction
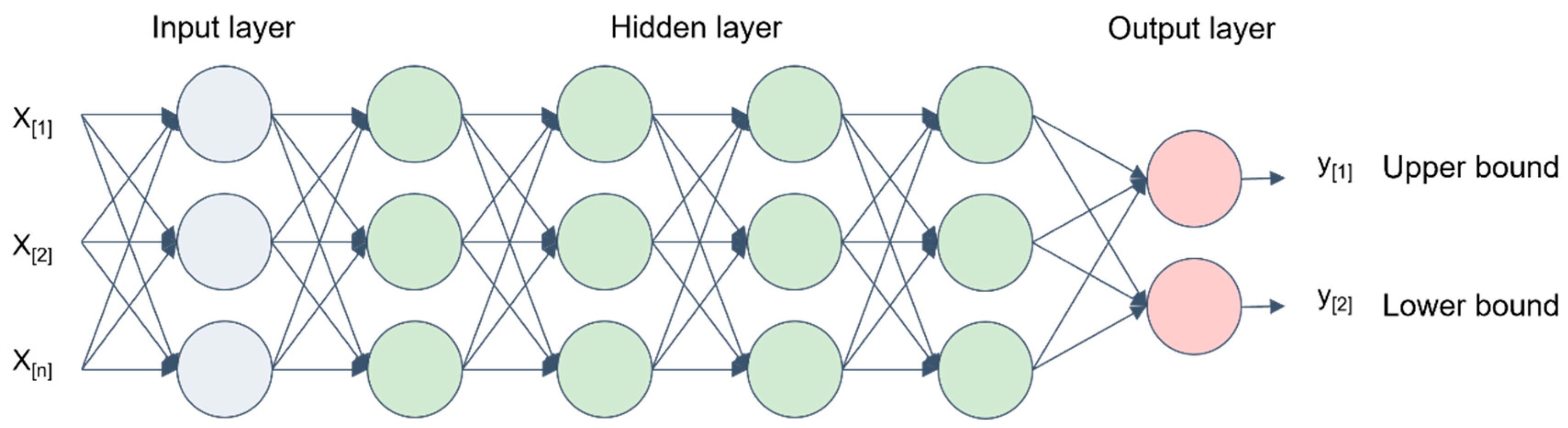
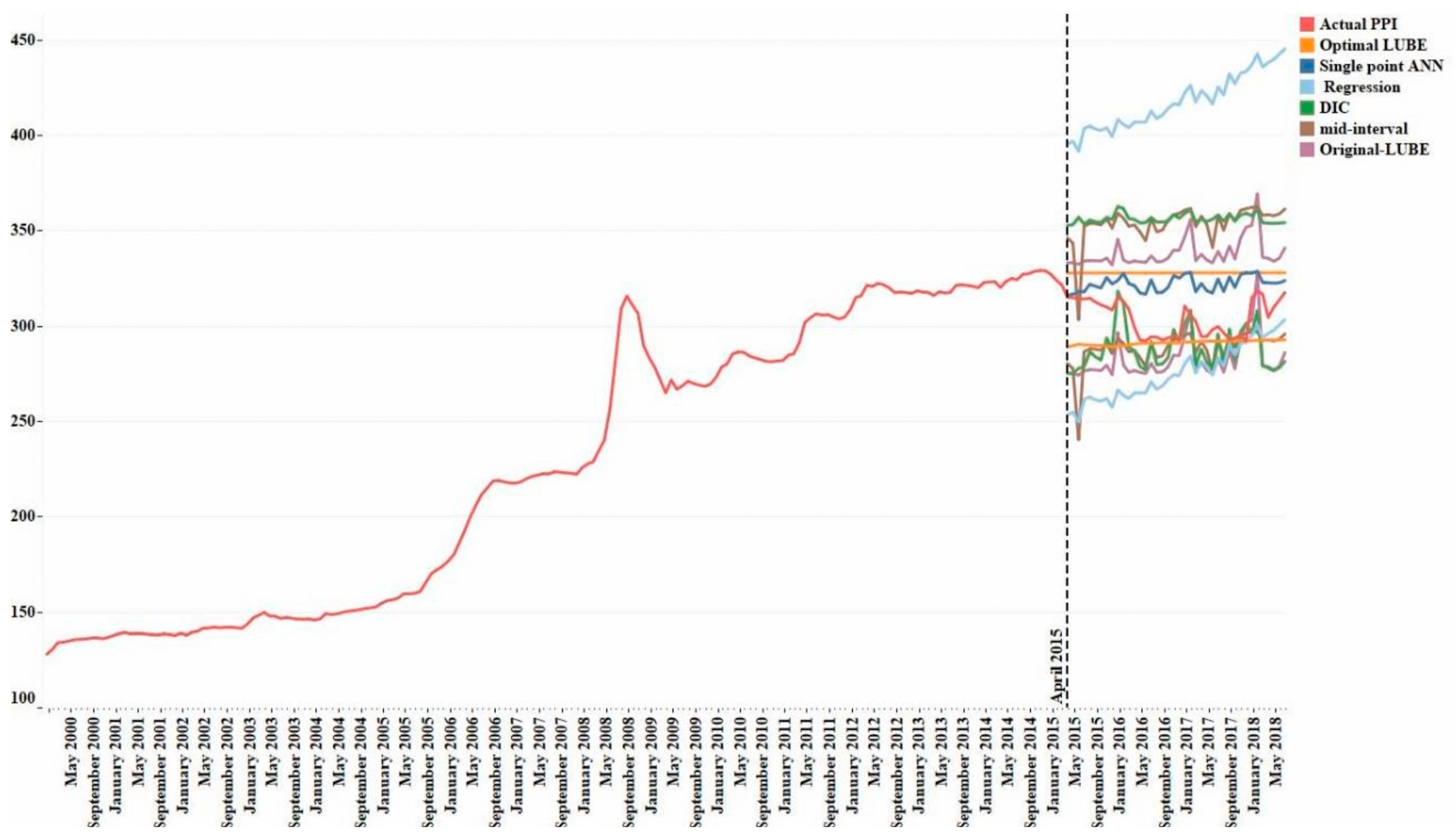
3.1.2. Interval Prediction
3.2. Time-Series Analysis
3.2.1. Univariate Time-Series Analysis
- Develop a conditional mean function.
- Conduct heteroscedasticity testing on the residuals of the mean function to assess the statistical significance of volatility.
- Employ ARCH/GARCH models if heteroscedasticity is present.
- Validate the ARCH/GARCH model by conducting heteroscedasticity testing on its residuals.
- Measure conditional volatility using the established ARCH/GARCH model.
- Evaluate the model’s performance by comparing estimated volatilities with realized volatilities.
- Perform out-of-sample forecasting for conditional volatility.
3.2.2. Multivariate Time-Series Analysis
3.3. Monte Carlo Simulation
4. Summary and Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Mirzadeh, I.; Birgisson, B. Accommodating Energy Price Volatility in Life Cycle Cost Analysis of Asphalt Pavements. J. Civ. Eng. Manag. 2015, 22, 1001–1008. [Google Scholar] [CrossRef]
- Abdul Nabi, M.; Chammout, B.; El-adaway, I.H.; Assaad, R.H.; Assaf, G. Investigating Price Fluctuation Transmission among Construction Materials. In Proceedings of the Construction Research Congress, Des Moines, IA, USA, 20–23 March 2024; American Society of Civil Engineers: Des Moines, IA, USA, 2024; pp. 339–349. [Google Scholar]
- Mack, J.W. Accounting for Material-Specific Inflation Rates in Life-Cycle Cost Analysis for Pavement Type Selection. Transp. Res. Rec. 2012, 2304, 86–96. [Google Scholar] [CrossRef]
- Musarat, M.A.; Alaloul, W.S.; Liew, M.S.; Maqsoom, A.; Qureshi, A.H. Investigating the Impact of Inflation on Building Materials Prices in Construction Industry. J. Build. Eng. 2020, 32, 101485. [Google Scholar] [CrossRef]
- Bilec, M.M.; Marriott, J.; Padilla, M.F.; Snyder, M. Market Analysis of Construction Materials with Recommendations for the Future of the Industry; University of Pittsburgh: Pittsburgh, PA, USA, 2010. [Google Scholar]
- Lee, C.; Lee, E.-B. Prediction Method of Real Discount Rate to Improve Accuracy of Life-Cycle Cost Analysis. Energy Build. 2017, 135, 225–232. [Google Scholar] [CrossRef]
- Cardinal, K.M.; Khalafalla, M.; Rueda-Benavides, J.A. Development of a Stochastic Risk Assessment Protocol for Analyzing the Impact of Fluctuations in Crude Oil and Fuel Prices on Asphalt Prices in the State of Alabama. In Proceedings of the Construction Research Congress, Des Moines, IA, USA, 20–23 March 2024; American Society of Civil Engineers: Des Moines, IA, USA, 2024; pp. 196–206. [Google Scholar]
- Cardinal, K.M.; Khalafalla, M.; Rueda-Benavides, J. Protocol to Assess the Impact of Crude Oil Price Fluctuations on Future Asphalt Prices. Transp. Res. Rec. 2021, 2675, 294–305. [Google Scholar] [CrossRef]
- Akanni, P.O.; Oke, A.E.; Omotilewa, O.J. Implications of Rising Cost of Building Materials in Lagos State Nigeria. SAGE Open 2014, 4, 215824401456121. [Google Scholar] [CrossRef]
- Elfahham, Y. Estimation and Prediction of Construction Cost Index Using Neural Networks, Time Series, and Regression. Alex. Eng. J. 2019, 58, 499–506. [Google Scholar] [CrossRef]
- Ng, S.T.; Cheung, S.O.; Martin Skitmore, R.; Lam, K.C.; Wong, L.Y. Prediction of Tender Price Index Directional Changes. Constr. Manag. Econ. 2000, 18, 843–852. [Google Scholar] [CrossRef]
- Olatunji, O.A. The Impact of Oil Price Regimes on Construction Cost in Nigeria. Constr. Manag. Econ. 2010, 28, 747–759. [Google Scholar] [CrossRef]
- Meglin, R.; Kytzia, S.; Habert, G. Uncertainty, Variability, Price Changes and Their Implications on a Regional Building Materials Industry: The Case of Swiss Canton Argovia. J. Clean. Prod. 2022, 330, 129944. [Google Scholar] [CrossRef]
- Chaitongrat, T.; Janthachai, K.; Kusonkhum, W.; Boonchai, P.; Ikhwali, M.F.; Khotdee, M. Comparing Data Mining Methods for Predicting Cost Construction Projects: A Case Study of Cost Management Datasets from Thailand. J. Infras. Policy Dev. 2024, 8, 2801. [Google Scholar] [CrossRef]
- Mahdavian, A.; Shojaei, A.; Salem, M.; Yuan, J.S.; Oloufa, A.A. Data-Driven Predictive Modeling of Highway Construction Cost Items. J. Constr. Eng. Manag. 2021, 147, 04020180. [Google Scholar] [CrossRef]
- Kim, C.; Khan, G.; Nguyen, B.; Hoang, E.L. Development of a Statistical Model to Predict Materials’ Unit Prices for Future Maintenance and Rehabilitation in Highway Life Cycle Cost Analysis; Mineta Transportation Institute: San Jose, CA, USA, 2020. [Google Scholar]
- Lee, C.-Y.; Chou, B.-J.; Huang, C.-F. Data Science and Reinforcement Learning for Price Forecasting and Raw Material Procurement in Petrochemical Industry. Adv. Eng. Inform. 2022, 51, 101443. [Google Scholar] [CrossRef]
- Wang, Q.K.; Mei, T.T.; Guo, Z.; Kong, L.W. Building Material Price Forecasting Based on Multi-Method in China. In Proceedings of the 2018 IEEE International Conference on Industrial Engineering and Engineering Management (IEEM), Bangkok, Thailand, 16–19 December 2018; IEEE: Bangkok, Thailand, 2018; pp. 1826–1830. [Google Scholar]
- Bassioni, H.A.; Elmasry, M.I.; Ragheb, A.M. Time Series Analysis for the Prediction of RC Material Components Prices in Egypt. In Proceedings of the 28th Annual ARCOM Conference, Edinburgh, UK, 3–5 September 2012; Association of Researchers in Construction Management: Edinburgh, UK, 2012; pp. 381–390. [Google Scholar]
- Deb, C.; Zhang, F.; Yang, J.; Lee, S.E.; Shah, K.W. A Review on Time Series Forecasting Techniques for Building Energy Consumption. Renew. Sustain. Energy Rev. 2017, 74, 902–924. [Google Scholar] [CrossRef]
- Hwang, S. Dynamic Regression Models for Prediction of Construction Costs. J. Constr. Eng. Manag. 2009, 135, 360–367. [Google Scholar] [CrossRef]
- Ashuri, B.; Lu, J. Time Series Analysis of ENR Construction Cost Index. J. Constr. Eng. Manag. 2010, 136, 1227–1237. [Google Scholar] [CrossRef]
- Hwang, S. Time Series Models for Forecasting Construction Costs Using Time Series Indexes. J. Constr. Eng. Manag. 2011, 137, 656–662. [Google Scholar] [CrossRef]
- Joukar, A.; Nahmens, I. Volatility Forecast of Construction Cost Index Using General Autoregressive Conditional Heteroskedastic Method. J. Constr. Eng. Manag. 2016, 142, 04015051. [Google Scholar] [CrossRef]
- Cao, Y.; Ashuri, B.; Baek, M. Prediction of Unit Price Bids of Resurfacing Highway Projects through Ensemble Machine Learning. J. Comput. Civ. Eng. 2018, 32, 04018043. [Google Scholar] [CrossRef]
- Akintoye, A.; Bowen, P.; Hardcastle, C. Macro-Economic Leading Indicators of Construction Contract Prices. Constr. Manag. Econ. 1998, 16, 159–175. [Google Scholar] [CrossRef]
- Ashuri, B.; Shahandashti, S.M.; Lu, J. Empirical Tests for Identifying Leading Indicators of ENR Construction Cost Index. Constr. Manag. Econ. 2012, 30, 917–927. [Google Scholar] [CrossRef]
- Chen, H.L. Using Financial and Macroeconomic Indicators to Forecast Sales of Large Development and Construction Firms. J. Real Estate Finan. Econ. 2010, 40, 310–331. [Google Scholar] [CrossRef]
- Ernest, K.; Theophilus, A.-K.; Amoah, P.; Emmanuel, B.B. Identifying Key Economic Indicators Influencing Tender Price Index Prediction in the Building Industry: A Case Study of Ghana. Int. J. Constr. Manag. 2019, 19, 106–112. [Google Scholar] [CrossRef]
- Ahmadu, H.A.; Ibrahim, Y.M.; Abdulrahman, R.S.; Jibril, U.S.; Yamusa, M.A. Developing Machine Learning Prediction Models for Construction Material Prices in Nigeria. ATBU J. Environ. Technol. 2023, 16, 22–42. [Google Scholar]
- Cao, M.-T.; Cheng, M.-Y.; Wu, Y.-W. Hybrid Computational Model for Forecasting Taiwan Construction Cost Index. J. Constr. Eng. Manag. 2015, 141, 04014089. [Google Scholar] [CrossRef]
- Faghih, S.A.M.; Kashani, H. Forecasting Construction Material Prices Using Vector Error Correction Model. J. Constr. Eng. Manag. 2018, 144, 04018075. [Google Scholar] [CrossRef]
- Ng, S.T.; Cheung, S.O.; Skitmore, M.; Wong, T.C.Y. An Integrated Regression Analysis and Time Series Model for Construction Tender Price Index Forecasting. Constr. Manag. Econ. 2004, 22, 483–493. [Google Scholar] [CrossRef]
- Shahandashti, S.M.; Ashuri, B. Highway Construction Cost Forecasting Using Vector Error Correction Models. J. Manag. Eng. 2016, 32, 04015040. [Google Scholar] [CrossRef]
- Shahandashti, S.M.; Ashuri, B. Forecasting Engineering News-Record Construction Cost Index Using Multivariate Time Series Models. J. Constr. Eng. Manag. 2013, 139, 1237–1243. [Google Scholar] [CrossRef]
- Shiha, A.; Dorra, E.M.; Nassar, K. Neural Networks Model for Prediction of Construction Material Prices in Egypt Using Macroeconomic Indicators. J. Constr. Eng. Manag. 2020, 146, 04020010. [Google Scholar] [CrossRef]
- Hosny, S.; Elsaid, E.; Hosny, H. Prediction of Construction Material Prices Using ARIMA and Multiple Regression Models. Asian J. Civ. Eng. 2023, 24, 1697–1710. [Google Scholar] [CrossRef]
- Jiang, H.; Xu, Y.; Liu, C. Construction Price Prediction Using Vector Error Correction Models. J. Constr. Eng. Manag. 2013, 139, 04013022. [Google Scholar] [CrossRef]
- Zhou, H.; Zhao, J.H. Analysis on Factors to Cause the Price Change of Building Materials. Adv. Mater. Res. 2013, 683, 668–671. [Google Scholar] [CrossRef]
- Ramadan, M. Development and Prediction of a Construction Price Index in Egypt. Master’s Thesis, American University in Cairo, New Cairo, Egypt, 2023. [Google Scholar]
- Wong, J.M.W.; Ng, S.T. Forecasting Construction Tender Price Index in Hong Kong Using Vector Error Correction Model. Constr. Manag. Econ. 2010, 28, 1255–1268. [Google Scholar] [CrossRef]
- Oladipo, F.; Oni, O. Review of Selected Macroeconomic Factors Impacting Building Material Prices in Developing Countries—A Case of Nigeria. Ethiop. J. Environ. Stud. Manag. 2012, 5, 131–137. [Google Scholar] [CrossRef]
- Chakraborty, D.; Elhegazy, H.; Elzarka, H.; Gutierrez, L. A Novel Construction Cost Prediction Model Using Hybrid Natural and Light Gradient Boosting. Adv. Eng. Inform. 2020, 46, 101201. [Google Scholar] [CrossRef]
- Mir, M.; Kabir, H.M.D.; Nasirzadeh, F.; Khosravi, A. Neural Network-Based Interval Forecasting of Construction Material Prices. J. Build. Eng. 2021, 39, 102288. [Google Scholar] [CrossRef]
- Lowe, D.J.; Emsley, M.W.; Harding, A. Predicting Construction Cost Using Multiple Regression Techniques. J. Constr. Eng. Manag. 2006, 132, 750–758. [Google Scholar] [CrossRef]
- Afolabi, A.O.; Abimbola, O. Application of Machine Learning in Cement Price Prediction through a Web-Based System. IJECE 2022, 12, 5214. [Google Scholar] [CrossRef]
- Issa, R.R.A. Application of Artificial Neural Networks to Predicting Construction Material Prices. In Proceedings of the Computing in Civil and Building Engineering (2000), Stanford, CA, USA, 4 August 2000; American Society of Civil Engineers: Stanford, CA, USA, 2000; pp. 1129–1132. [Google Scholar]
- Williams, T.P. Predicting Changes in Construction Cost Indexes Using Neural Networks. J. Constr. Eng. Manag. 1994, 120, 306–320. [Google Scholar] [CrossRef]
- Wilmot, C.G.; Mei, B. Neural Network Modeling of Highway Construction Costs. J. Constr. Eng. Manag. 2005, 131, 765–771. [Google Scholar] [CrossRef]
- Shiha, A. Prediction of Construction Material Prices Using Macroeconomic Indicators: A Neural Networks Model; American University in Cairo: New Cairo, Egypt, 2019. [Google Scholar]
- Marzouk, M.; Amin, A. Predicting Construction Materials Prices Using Fuzzy Logic and Neural Networks. J. Constr. Eng. Manag. 2013, 139, 1190–1198. [Google Scholar] [CrossRef]
- Ouyang, H.; Zhang, X.; Hu, C. Application Research on the Artificial Neural Network in the Building Materials Price Prediction. In the 19th International Conference on Industrial Engineering and Engineering Management; Qi, E., Shen, J., Dou, R., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; pp. 167–175. ISBN 978-3-642-38432-5. [Google Scholar]
- Jha, G.K.; Sinha, K. Time-Delay Neural Networks for Time Series Prediction: An Application to the Monthly Wholesale Price of Oilseeds in India. Neural Comput. Applic. 2014, 24, 563–571. [Google Scholar] [CrossRef]
- Kamaruddin, S.B.A.; Ghani, N.A.M.; Ramli, N.M. Determining the Best Forecasting Model of Cement Price Index in Malaysia. In Proceedings of the 2012 IEEE Colloquium on Humanities, Science and Engineering (CHUSER), Kota Kinabalu, Malaysia, 3–4 December 2012; IEEE: Kota Kinabalu, Malaysia, 2012; pp. 524–528. [Google Scholar]
- Kamaruddin, S.B.A.; Ghani, N.A.M.; Ramli, N.M. Estimating Cement Price Index by Regions in Peninsular Malaysia. In Proceedings of the 2012 International Conference on Statistics in Science, Business and Engineering (ICSSBE), Langkawi, Malaysia, 10–12 September 2012; IEEE: Langkawi, Malaysia, 2012; pp. 1–4. [Google Scholar]
- Tang, B.; Han, J.; Guo, G.; Chen, Y.; Zhang, S. Building Material Prices Forecasting Based on Least Square Support Vector Machine and Improved Particle Swarm Optimization. Archit. Eng. Des. Manag. 2019, 15, 196–212. [Google Scholar] [CrossRef]
- Zhang, J.-L.; Zhang, Y.-J.; Zhang, L. A Novel Hybrid Method for Crude Oil Price Forecasting. Energy Econ. 2015, 49, 649–659. [Google Scholar] [CrossRef]
- Ilbeigi, M.; Ashuri, B.; Joukar, A. Time-Series Analysis for Forecasting Asphalt-Cement Price. J. Manag. Eng. 2017, 33, 04016030. [Google Scholar] [CrossRef]
- Hwang, S.; Park, M.; Lee, H.-S.; Kim, H. Automated Time-Series Cost Forecasting System for Construction Materials. J. Constr. Eng. Manag. 2012, 138, 1259–1269. [Google Scholar] [CrossRef]
- Yao, F.; Zeng, H.; Liu, T.; Wu, Y. Research on Cement Price Fluctuation Prediction Based on EEMD-ARIMA. In Proceedings of the 27th International Symposium on Advancement of Construction Management and Real Estate; Li, J., Lu, W., Peng, Y., Yuan, H., Wang, D., Eds.; Lecture Notes in Operations Research; Springer Nature Singapore: Singapore, 2023; pp. 324–339. ISBN 978-981-9936-25-0. [Google Scholar]
- Ilbeigi, M.; Castro-Lacouture, D.; Joukar, A. Generalized Autoregressive Conditional Heteroscedasticity Model to Quantify and Forecast Uncertainty in the Price of Asphalt Cement. J. Manag. Eng. 2017, 33, 04017026. [Google Scholar] [CrossRef]
- Li, B.; Xin, Q.; Zhang, L. Engineering Cost Prediction Model Based on DNN. Sci. Program. 2022, 2022, 3257856. [Google Scholar] [CrossRef]
- Mao, S.; Tseng, C.-H.; Shang, J.; Wu, Y.; Zeng, X.-J. Construction Cost Index Prediction: A Visibility Graph Network Method. In Proceedings of the 2021 International Joint Conference on Neural Networks (IJCNN), Shenzhen, China, 18 July 2021; IEEE: Shenzhen, China, 2021; pp. 1–6. [Google Scholar]
- Nelson, M.; Hill, T.; Remus, W.; O’Connor, M. Time Series Forecasting Using Neural Networks: Should the Data Be Deseasonalized First? J. Forecast. 1999, 18, 359–367. [Google Scholar] [CrossRef]
- Sezer, O.B.; Gudelek, M.U.; Ozbayoglu, A.M. Financial Time Series Forecasting with Deep Learning: A Systematic Literature Review: 2005–2019. Appl. Soft Comput. 2020, 90, 106181. [Google Scholar] [CrossRef]
- Dong, J.; Chen, Y.; Guan, G. Cost Index Predictions for Construction Engineering Based on LSTM Neural Networks. Adv. Civ. Eng. 2020, 2020, 6518147. [Google Scholar] [CrossRef]
- Kumar Dubey, A.; Kumar, A.; García-Díaz, V.; Kumar Sharma, A.; Kanhaiya, K. Study and Analysis of SARIMA and LSTM in Forecasting Time Series Data. Sustain. Energy Technol. Assess. 2021, 47, 101474. [Google Scholar] [CrossRef]
- Wang, C.; Qiao, J. Construction Project Cost Prediction Method Based on Improved BiLSTM. Appl. Sci. 2024, 14, 978. [Google Scholar] [CrossRef]
- Cao, Y.; Ashuri, B. Predicting the Volatility of Highway Construction Cost Index Using Long Short-Term Memory. J. Manag. Eng. 2020, 36, 04020020. [Google Scholar] [CrossRef]
- Mbah, T.J.; Ye, H.; Zhang, J.; Long, M. Using LSTM and ARIMA to Simulate and Predict Limestone Price Variations. Min. Metall. Explor. 2021, 38, 913–926. [Google Scholar] [CrossRef]
- Lee, C.; Won, J.; Lee, E.-B. Method for Predicting Raw Material Prices for Product Production over Long Periods. J. Constr. Eng. Manag. 2019, 145, 05018017. [Google Scholar] [CrossRef]
- Xu, J.; Moon, S. Stochastic Forecast of Construction Cost Index Using a Cointegrated Vector Autoregression Model. J. Manag. Eng. 2013, 29, 10–18. [Google Scholar] [CrossRef]
- Swei, O.; Gregory, J.; Kirchain, R. Probabilistic Approach for Long-Run Price Projections: Case Study of Concrete and Asphalt. J. Constr. Eng. Manag. 2017, 143, 05016018. [Google Scholar] [CrossRef]
- Swei, O.A. Incorporating Uncertainty in the Life Cycle Cost Analysis of Pavements; Massachusetts Institute of Technology: Cambridge, MA, USA, 2012. [Google Scholar]
- Wang, Y.; Liu, M. Prices of Highway Resurfacing Projects in Economic Downturn: Lessons Learned and Strategies Forward. J. Manag. Eng. 2012, 28, 391–397. [Google Scholar] [CrossRef]
- Back, W.E.; Boles, W.W.; Fry, G.T. Defining Triangular Probability Distributions from Historical Cost Data. J. Constr. Eng. Manag. 2000, 126, 29–37. [Google Scholar] [CrossRef]
- Oshodi, O.; Ejohwomu, O.A.; Famakin, I.O.; Cortez, P. Comparing Univariate Techniques for Tender Price Index Forecasting: Box-Jenkins and Neural Network Model. CEB 2017, 17, 109–123. [Google Scholar] [CrossRef]




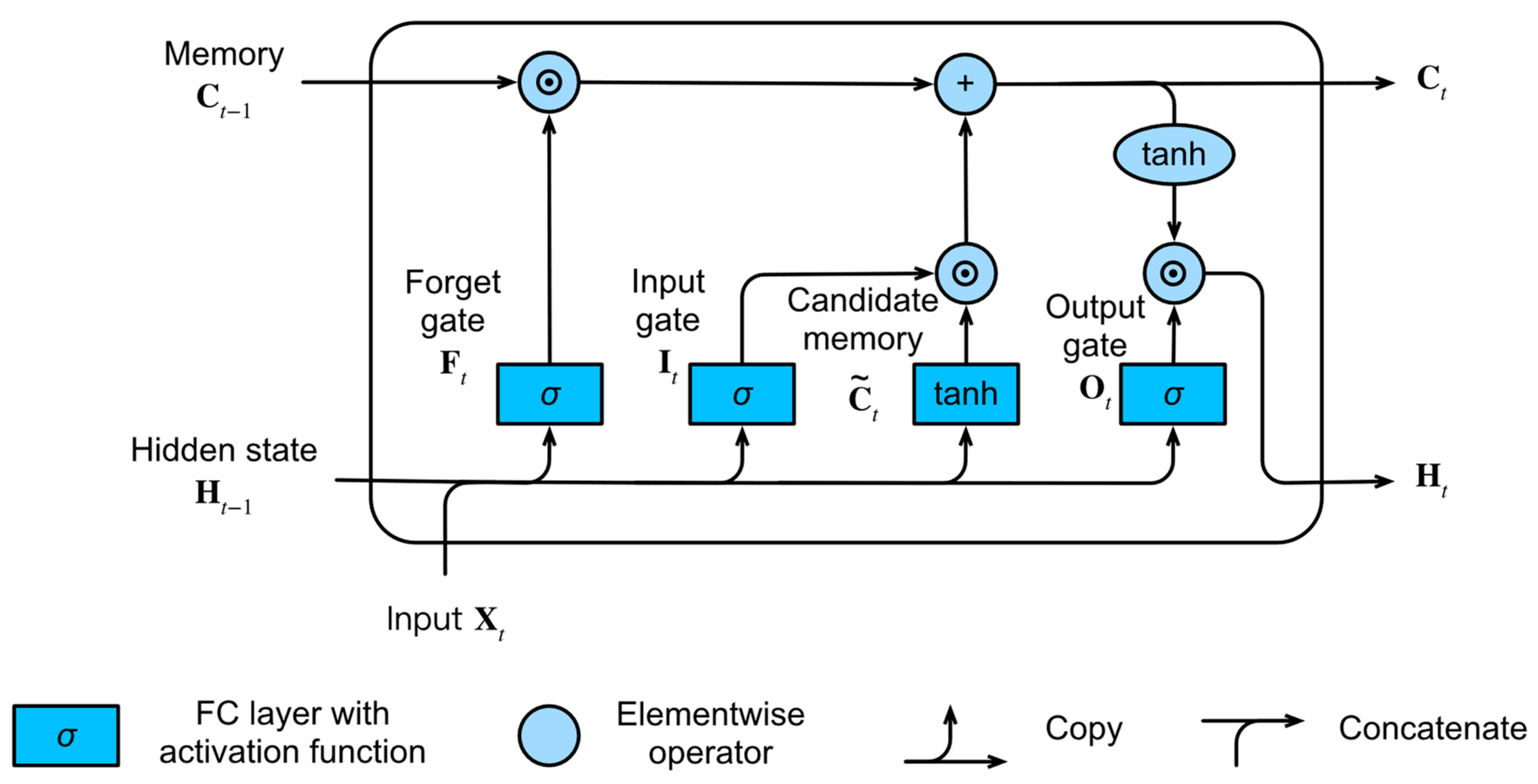
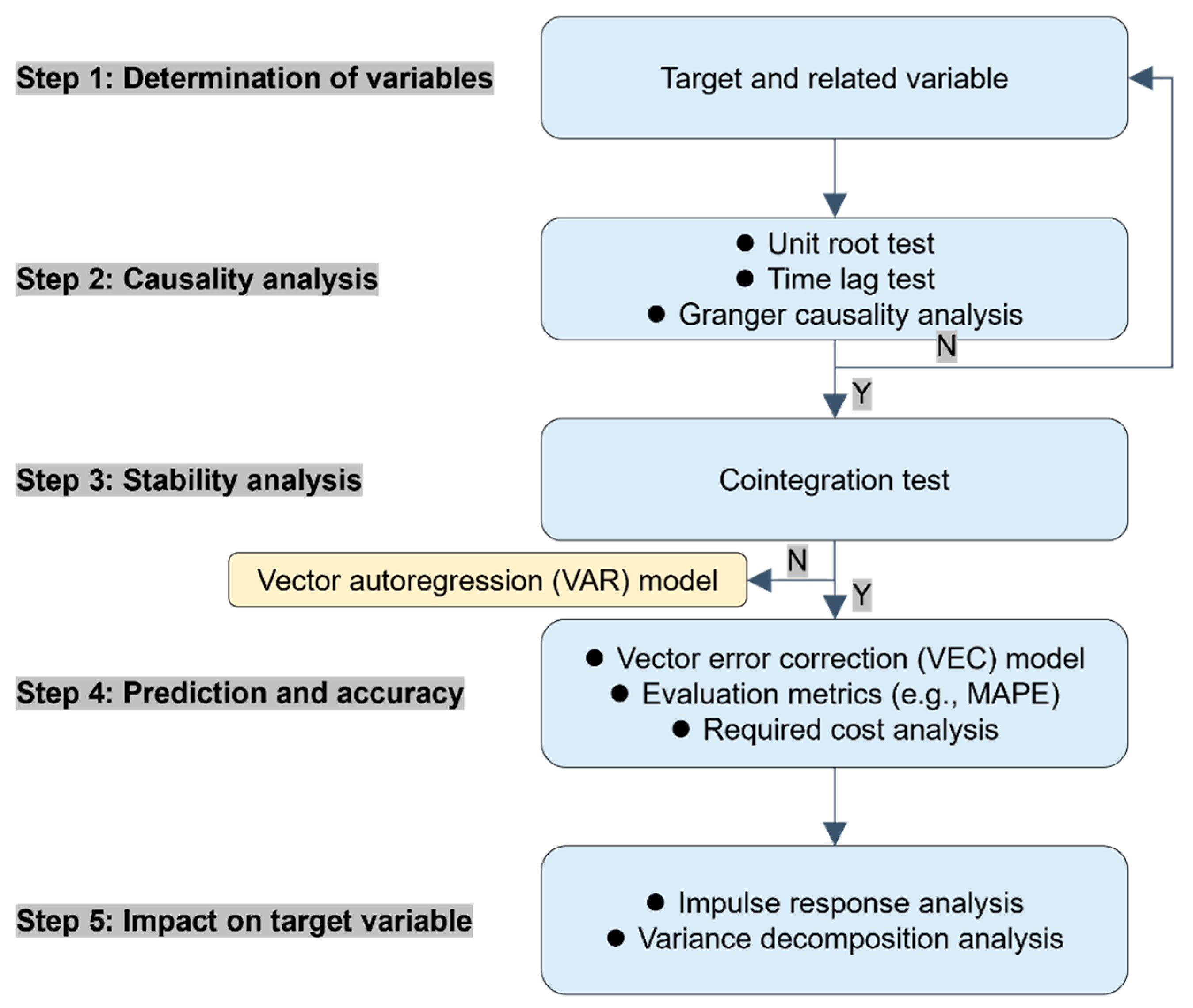

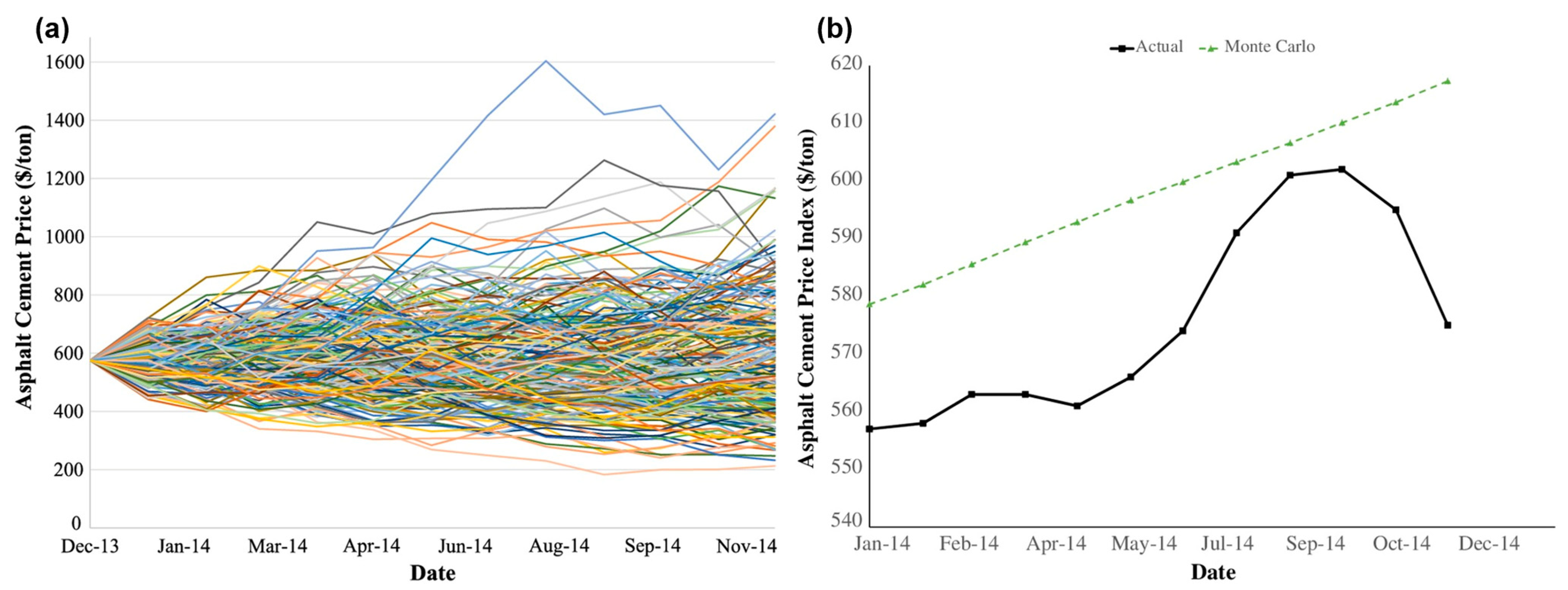
| Economic Indicator | Explained Variable | Country/Region | References |
|---|---|---|---|
| Consumer price index (CPI) | Construction material price; Construction Cost Index; Tender Price Index | United States; Taiwan; Ghana; Hong Kong; Egypt; Nigeria | [11,22,27,29,30,31,32,33,34,35,36] |
| Producer price index (PPI) | Construction material price; Construction Cost Index; Tender Price Index | United States; Australia; Ghana; Egypt | [27,29,36,37,38] |
| Foreign exchange rate | Construction material price; Construction Cost Index; Tender Price Index | Nigeria; Ghana; Hong Kong; Egypt; Nigeria; China | [9,12,29,30,31,36,37,39] |
| Inflation rate | Construction material price; Construction Cost Index; Tender Price Index | United Kingdom; Nigeria; Egypt; China | [12,26,30,37,39] |
| Lending rate | Construction material price; Construction Cost Index; Tender Price Index | Nigeria; Hong Kong; Australia; Ghana; Egypt | [11,12,29,30,31,33,36,38] |
| Money supply (M2)/Monetary policy | Construction material price; Construction Cost Index; Tender Price Index | United States; Hong Kong; United Kingdom; Egypt | [11,26,27,33,37,40] |
| Unemployment rate | Construction material price; Construction Cost Index; Tender Price Index | United States; Hong Kong; United Kingdom; Egypt | [11,26,27,32,33,36,37,38] |
| Employment rate | Construction material price | Egypt | [34,37] |
| Employment in construction | Construction material price; Construction Cost Index | United States | [32,34,35] |
| Gross domestic product (GDP) | Construction material price; Construction Cost Index; Tender Price Index | United States; Hong Kong; Egypt; Nigeria | [11,27,30,36,37,41] |
| GDP-construction | Construction material price; Tender Price Index | Hong Kong; Egypt | [11,37,41] |
| GDP growth rate | Construction Cost Index; Tender Price Index | Hong Kong; Nigeria | [12,33] |
| Implicit GPD deflator | Construction Cost Index; Tender Price Index | United States; Hong Kong | [11,27,35] |
| Crude oil price | Construction Cost Index | Nigeria; United States; Taiwan | [12,27,31] |
| Average hourly earnings | Construction material price; Construction Cost Index | United States | [32,34,35] |
| Foreign reserves | Construction material price | Egypt | [36] |
| Interest rate | Construction material price | Nigeria; Egypt; China | [9,30,37,39] |
| Stock market index | Construction Cost Index; Tender Price Index | United States; Taiwan | [27,31] |
| Balance of payment | Construction material price | Egypt; Nigeria | [37,42] |
| Building cost index | Tender Price Index | Hong Kong | [33,41] |
| Building permits | Construction material price; Construction Cost Index | United States | [32,34,35] |
| Dow Jones industrial average | Construction material price | United States | [27,31,34,35] |
| Export | Construction material price | Egypt; Nigeria | [37,42] |
| External debt | Construction material price | Egypt; Nigeria | [37,42] |
| External reserve | Construction material price | Egypt; Nigeria | [37,42] |
| Housing starts | Construction material price; Construction Cost Index | United States | [32,34,35] |
| Import | Construction material price | Egypt; Nigeria | [37,42] |
| Industrial production | Construction material price | Egypt | [37] |
| National expenditure | Construction material price | Egypt | [28,37] |
| National revenue | Construction material price; Construction Cost Index | United States; Egypt | [27,37] |
| Economic Indicator | Relevance to Construction Material Price |
|---|---|
| Consumer price index (CPI) | CPI changes reflect broader economic conditions that can impact demand, production costs, and, ultimately, material prices within the construction sector. |
| Producer price index (PPI) | PPI reflects changes in the prices received by producers for their output, including materials used in construction, thus impacting the cost structure of construction projects. |
| Foreign exchange rate | Fluctuations in exchange rates can affect the cost of imported materials used in construction, thereby impacting overall material prices in the market. |
| Inflation rate | Higher inflation rates often result in increased production costs, transportation expenses, and demand-driven price pressures, ultimately leading to higher prices for construction materials. |
| Lending rate | Changes in interest rates can impact construction activity, investment decisions, and overall demand for materials, consequently affecting their prices. |
| Money supply (M2)/Monetary policy | Changes in the money supply can affect overall economic activity, including construction demand, which in turn can impact material prices through demand–supply dynamics. |
| Unemployment rate | Higher unemployment may signal decreased demand for construction projects, potentially leading to lower material prices due to reduced demand pressure in the market. |
| Gross domestic product (GDP) | GDP growth reflects overall economic activity, impacting construction demand and investment, thereby influencing material prices through demand-supply dynamics |
| Model | Explanatory Variables | Lag | RMSE | MAE | MAPE |
|---|---|---|---|---|---|
| Univariate ARIMA model | None | (7, 1, 6) | 0.335 | 0.266 | 5.338 |
| Bivariate VEC model | WTI | 4 | 0.109 | 0.091 | 1.780 |
| Multivariate VEC model | CPI, WTI, BP | 4 | 0.117 | 0.103 | 1.951 |
| Multivariate VEC model | CPI, WTI | 8 | 0.082 | 0.062 | 1.205 |
| Forecasting Method | Advantages | Disadvantages | Representative References |
|---|---|---|---|
| Causal modeling | |||
| MLR | Ease of implementation | Accounting for only linear relationship between explanatory variables | [33,37,41,45] |
| ANN | Ability to incorporate complex nonlinear relationships and predict drastic price volatility with sufficient data | Necessity of extensive data collection needed for network training; Intrinsic characteristic of black box | [49,50,77] |
| Time-series analysis | |||
| ARIMA & seasonal ARIMA | Only one variable (i.e., time) is needed for modeling | Inability to include other influencing factors and capture sudden price changes | [23,58] |
| ARCH & GARCH | The ability to capture the time-varying nature of volatility and quantify price volatility risk | Sensitive to the choice of model specifications, including lag orders and distributional assumptions; Computationally intensive | [61] |
| VAR & VEC | The ability to capture the internal structure of price data and achieve Highly accurate forecasting | Difficult implementation; potential failure of forecasting drastic price increase due to inflated market dynamics | [32,73] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Q.; He, P.; Peng, S.; Wang, T.; Ma, J. A Survey of Data-Driven Construction Materials Price Forecasting. Buildings 2024, 14, 3156. https://doi.org/10.3390/buildings14103156
Liu Q, He P, Peng S, Wang T, Ma J. A Survey of Data-Driven Construction Materials Price Forecasting. Buildings. 2024; 14(10):3156. https://doi.org/10.3390/buildings14103156
Chicago/Turabian StyleLiu, Qi, Peikai He, Si Peng, Tao Wang, and Jie Ma. 2024. "A Survey of Data-Driven Construction Materials Price Forecasting" Buildings 14, no. 10: 3156. https://doi.org/10.3390/buildings14103156
APA StyleLiu, Q., He, P., Peng, S., Wang, T., & Ma, J. (2024). A Survey of Data-Driven Construction Materials Price Forecasting. Buildings, 14(10), 3156. https://doi.org/10.3390/buildings14103156







