Impact of Excavation on Adjacent Elevated Bridges and Optimization Analysis of Deformation Control
Abstract
:1. Introduction
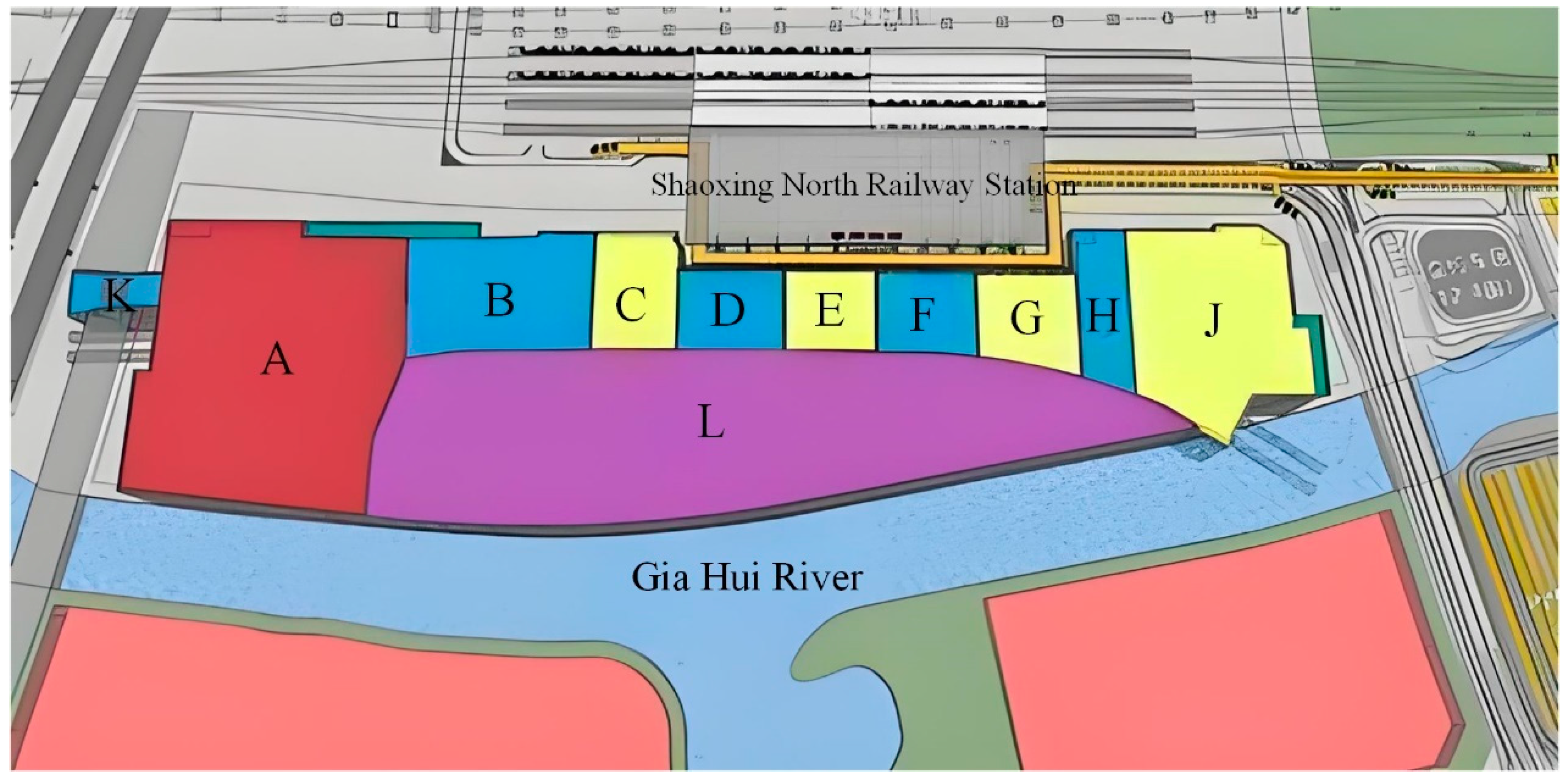
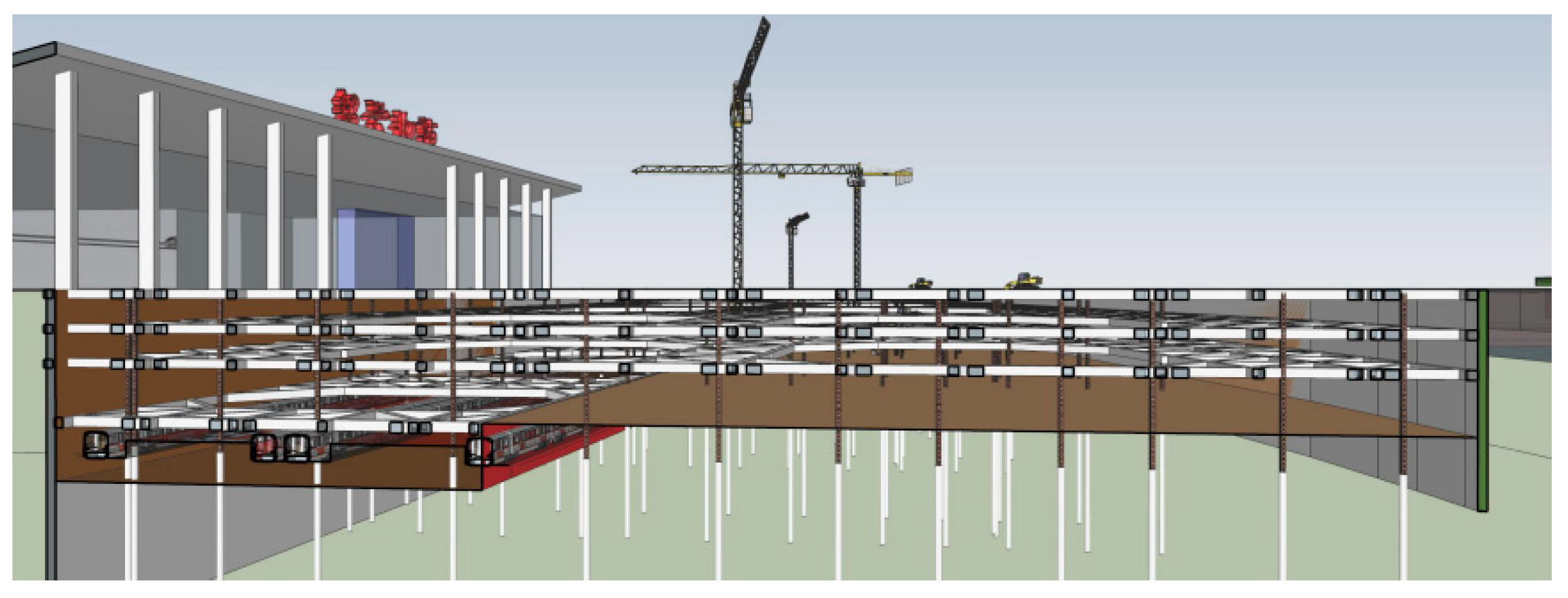
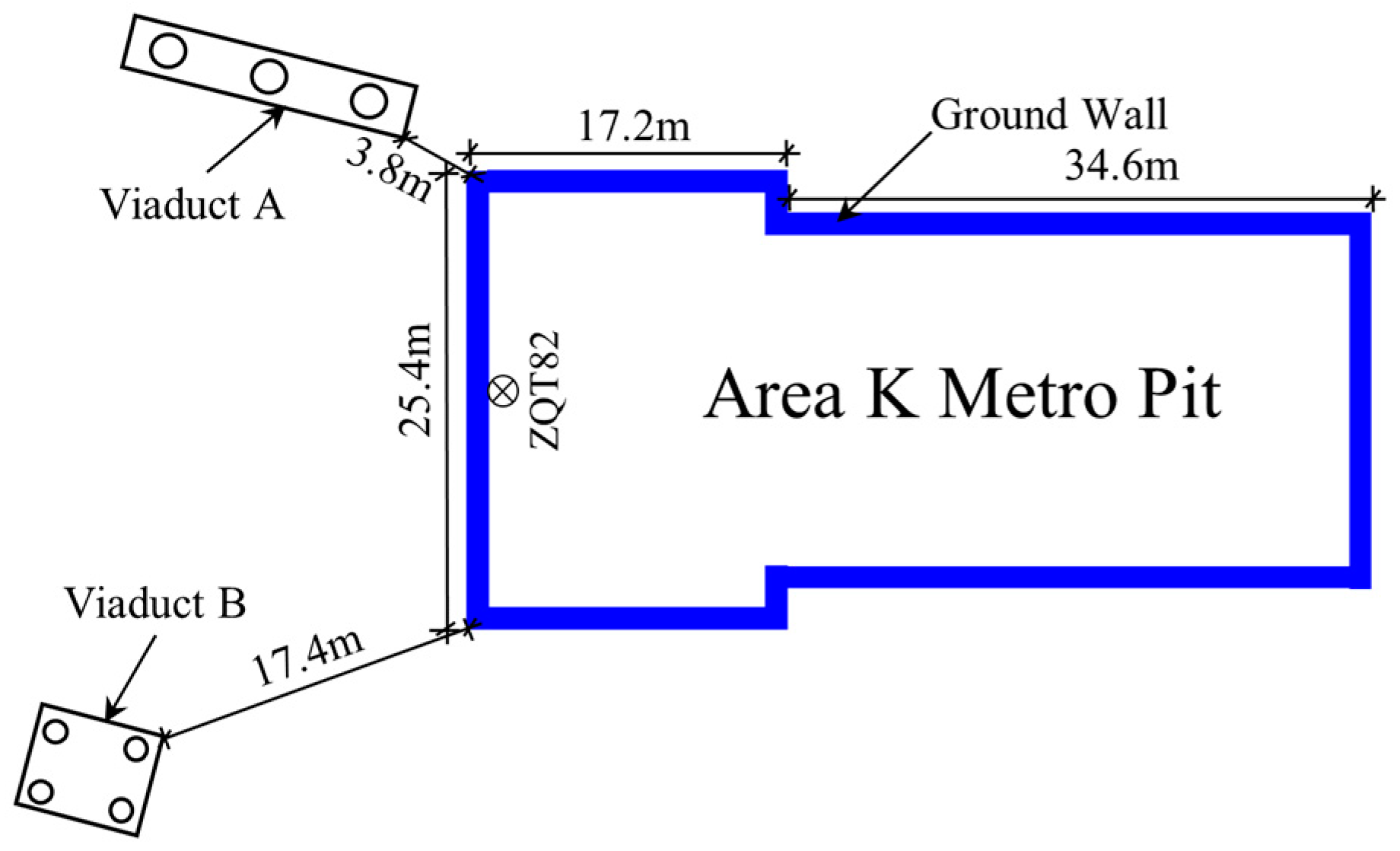
2. Project Overview
2.1. Engineering Background
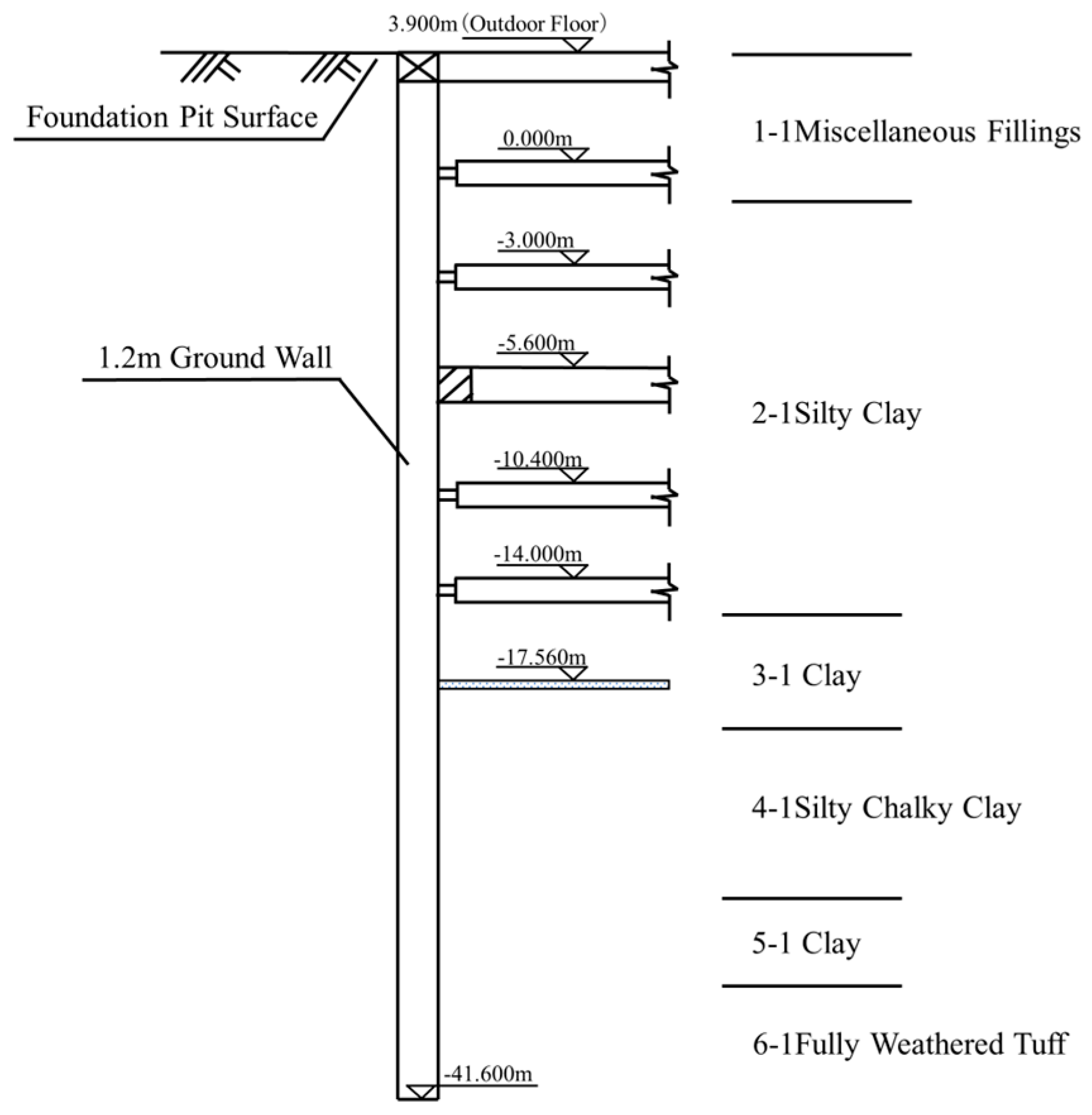
2.2. Hydrogeology
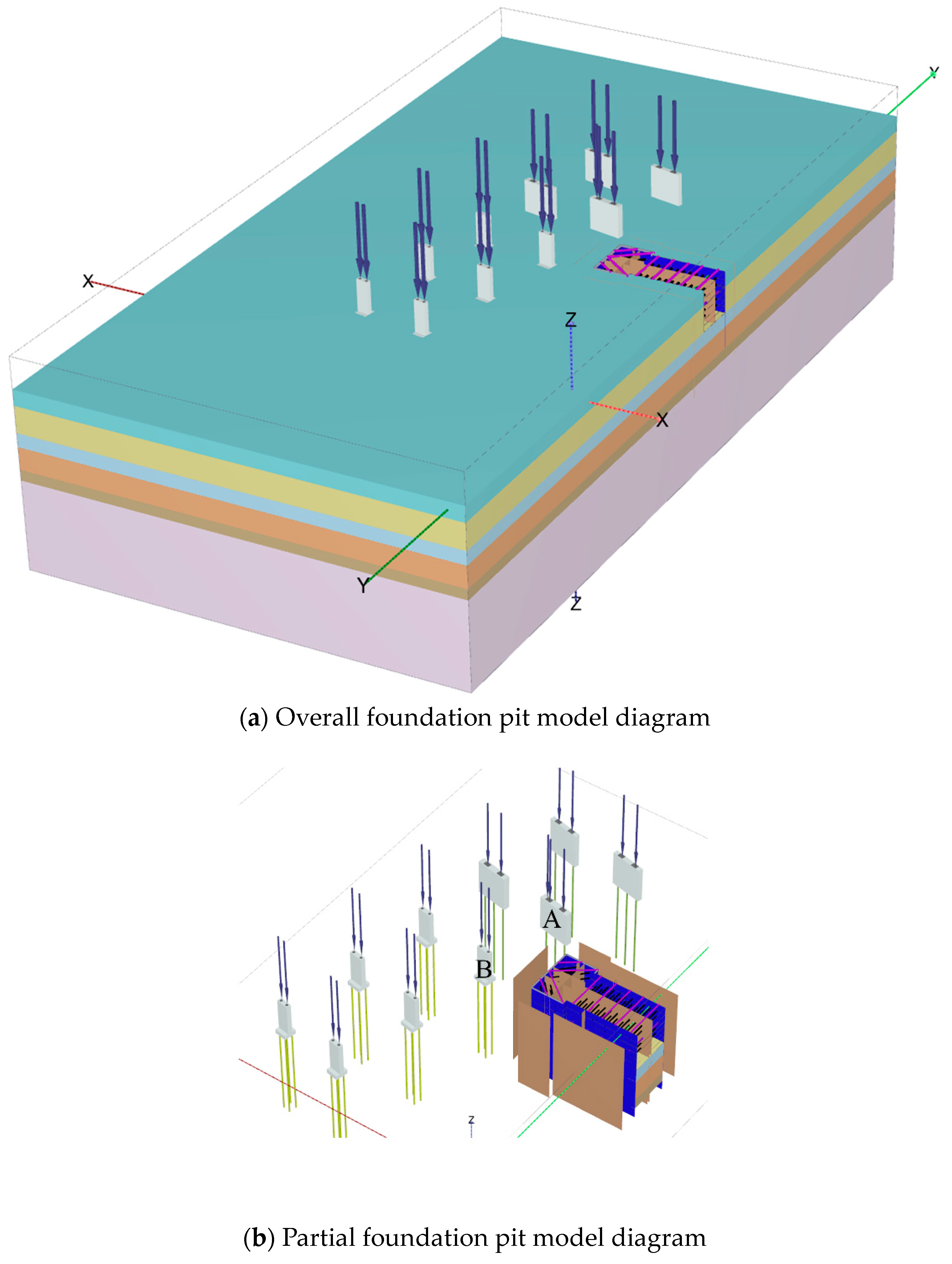
3. Numerical Simulation of Deep Foundation Pit
3.1. Model Establishment
3.2. Selection of Model Parameters
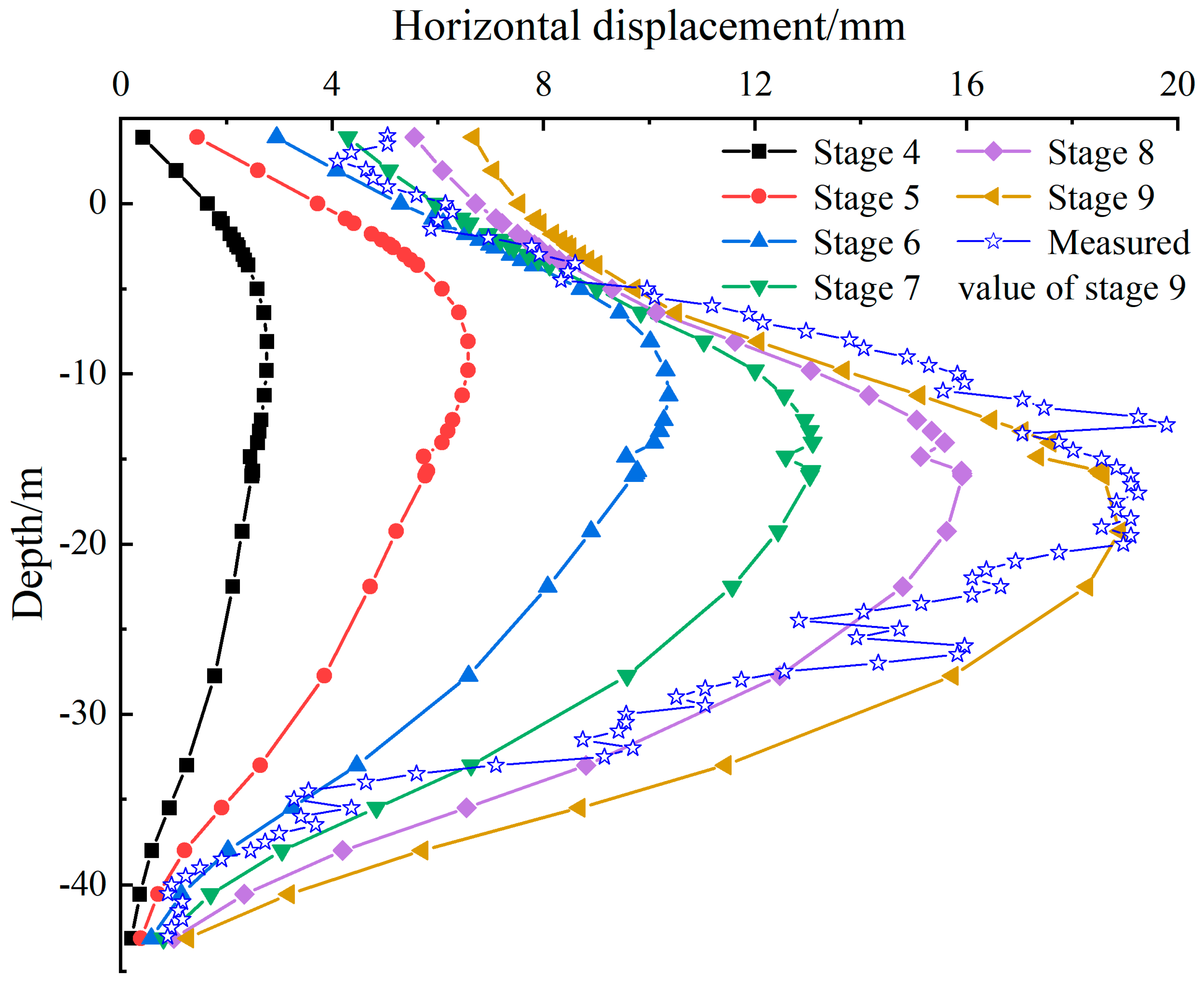
3.3. Validation of Computational Model Suitability
3.4. Numerical Analysis
4. Optimization Study on Deformation Control of Bridge Piers
4.1. Optimization Analysis of Soil Reinforcement around the Foundation Pit
4.2. Optimization Analysis of Soil Reinforcement around the Pier
4.3. Optimization Analysis of Pre-Applied Axial Force
5. Impact of Distance on the Pier
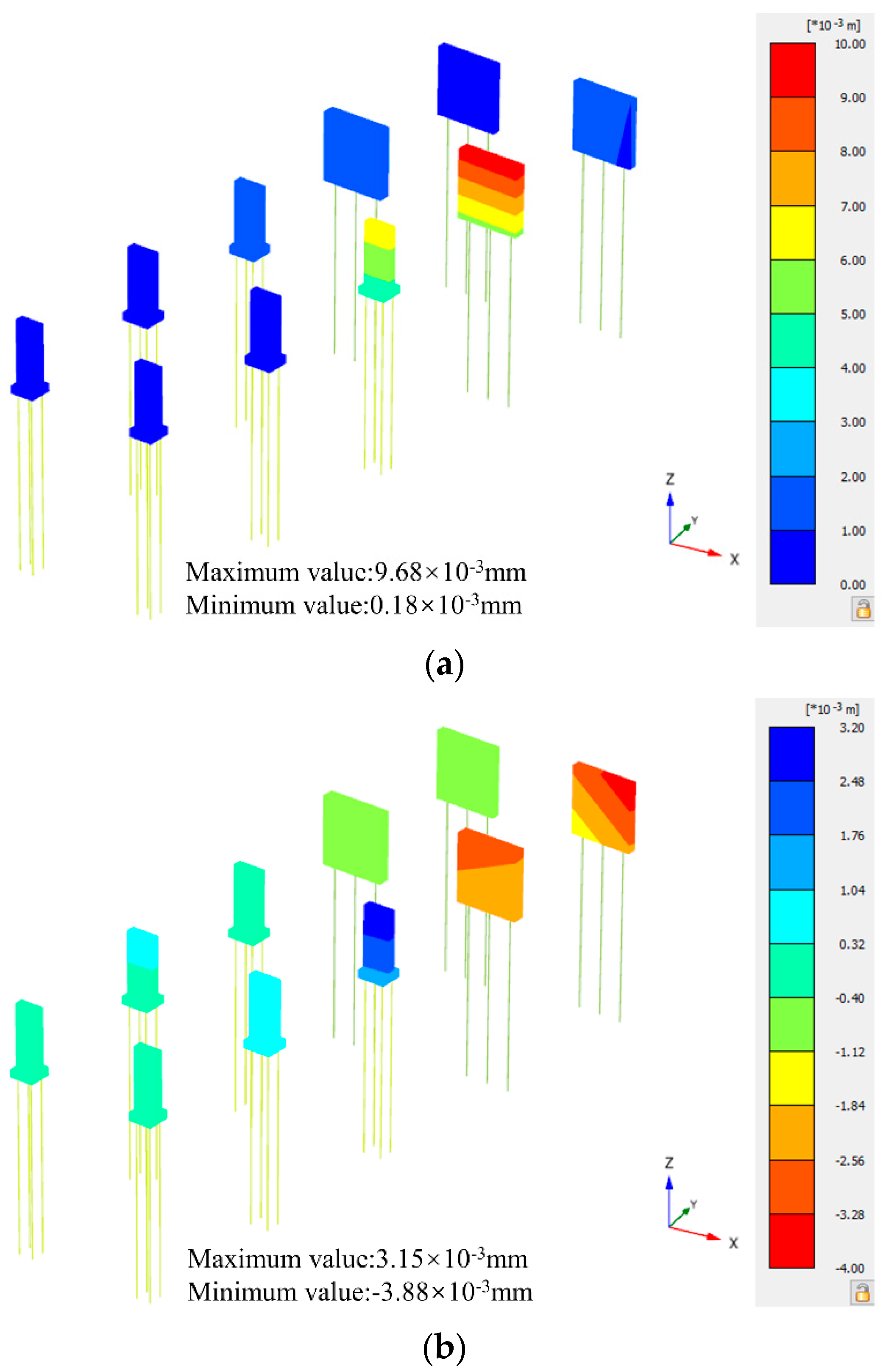
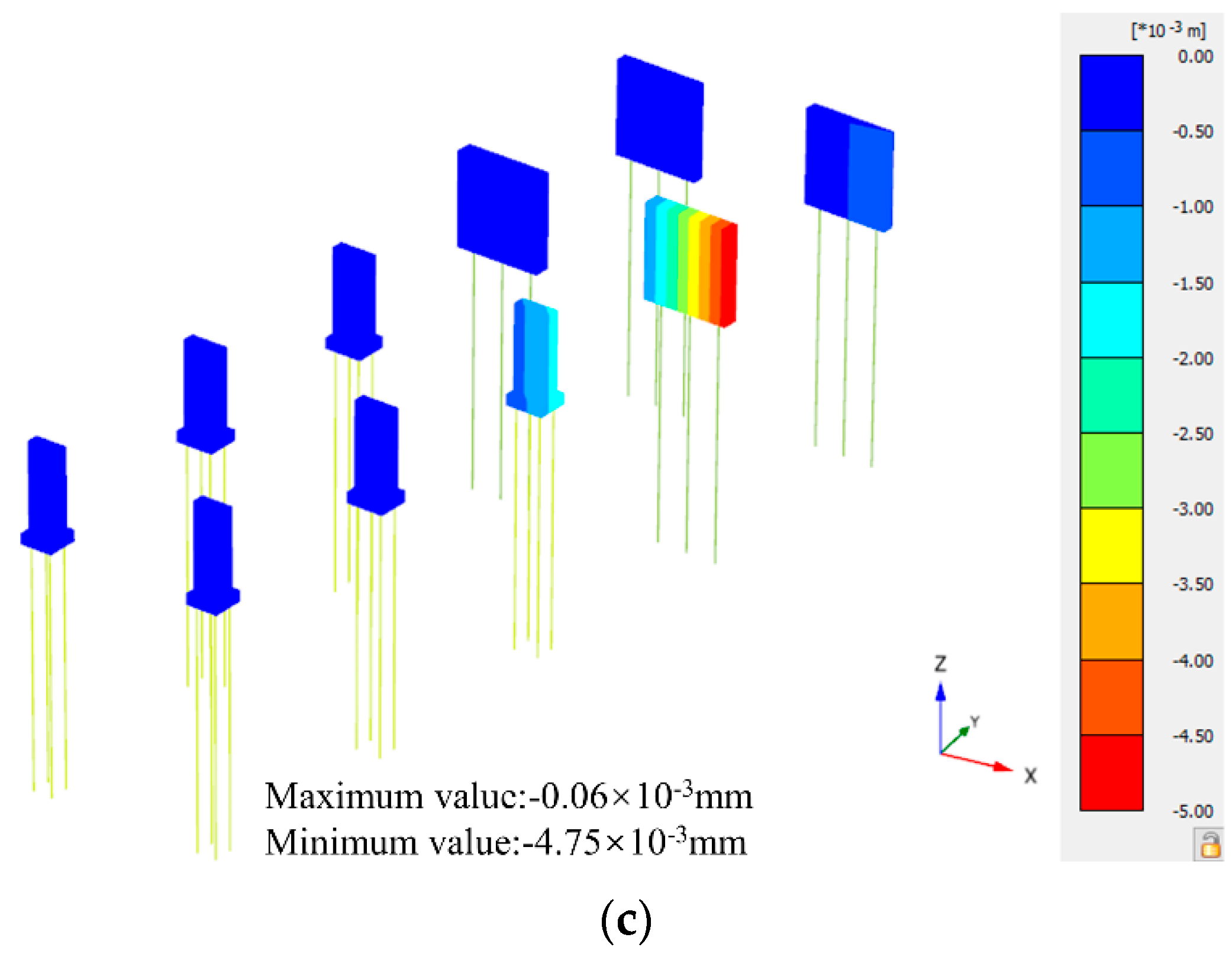
5.1. Analysis of Vertical Displacement of the Elevated Bridge
5.2. Analysis of Horizontal Displacement of the Elevated Bridge in the x-Axis Direction
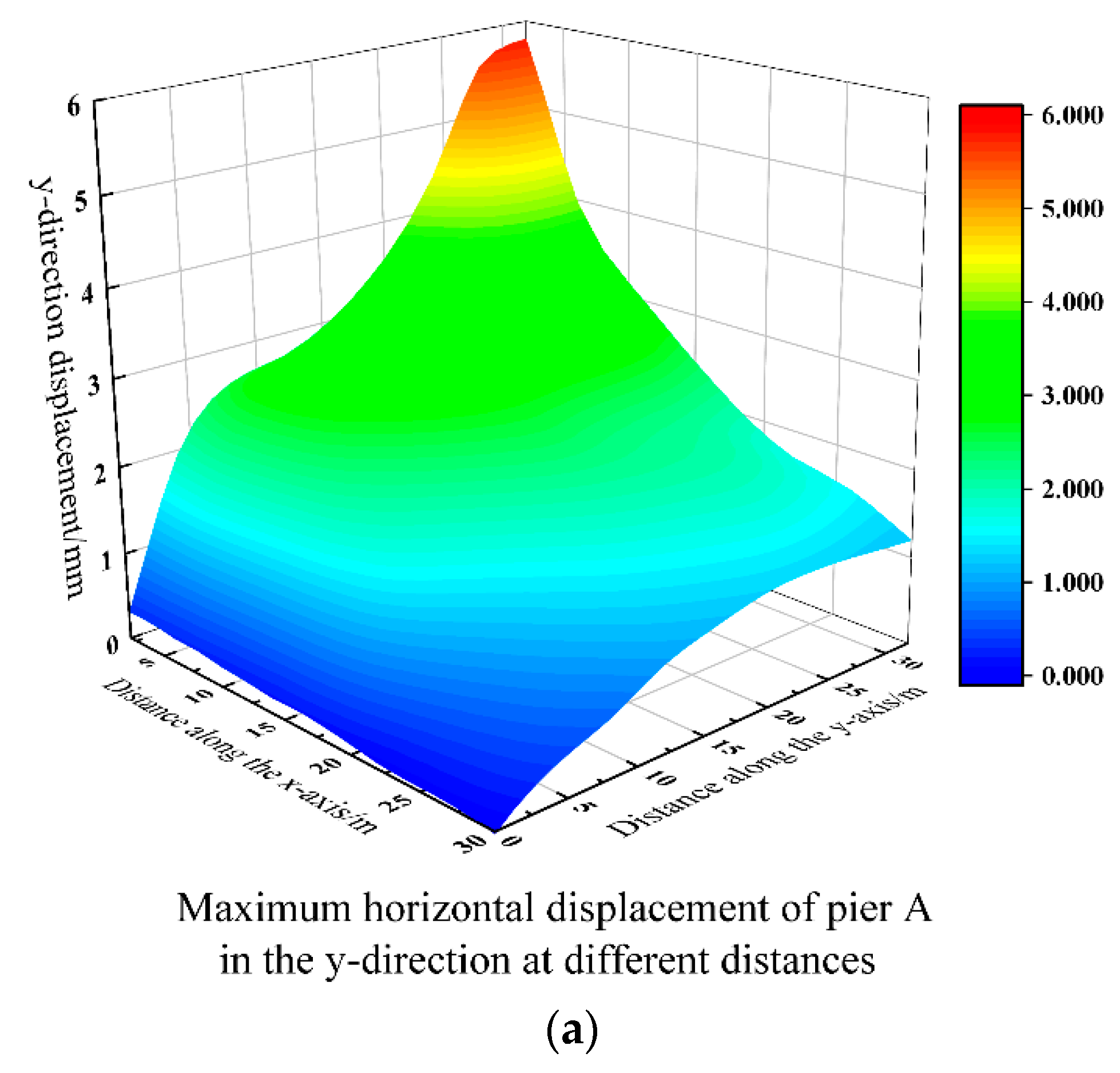
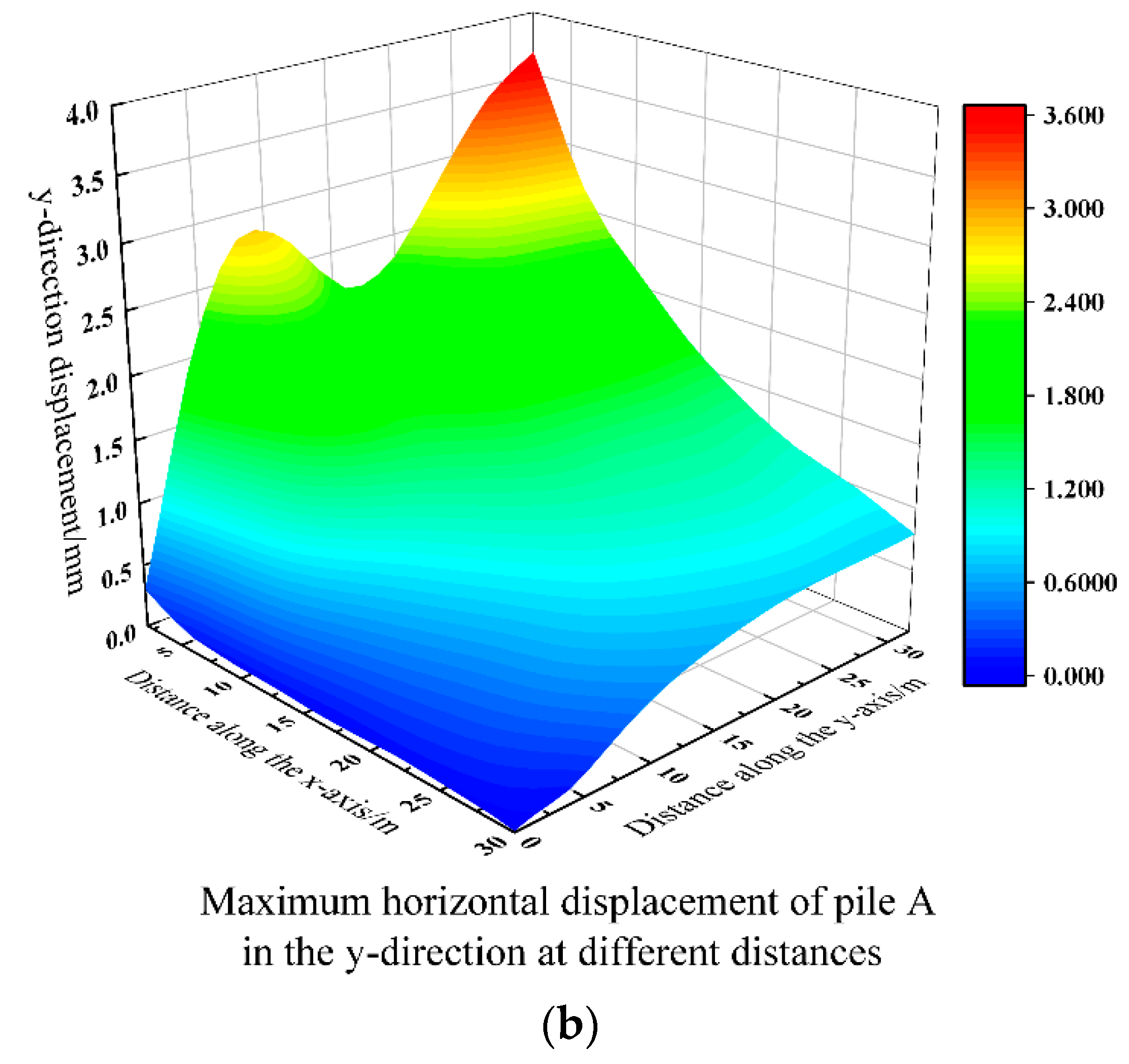
5.3. Analysis of Horizontal Displacement of the Elevated Bridge in the y-Axis Direction
6. Conclusions
6.1. Original Working Condition Simulation
- (1)
- The deformation trend of the bridge pier and bridge pile foundation is consistent: the closer the distance to the foundation pit, the larger the deformation. The maximum deformation of the bridge pier is larger than the maximum deformation of the bridge pile foundation.
- (2)
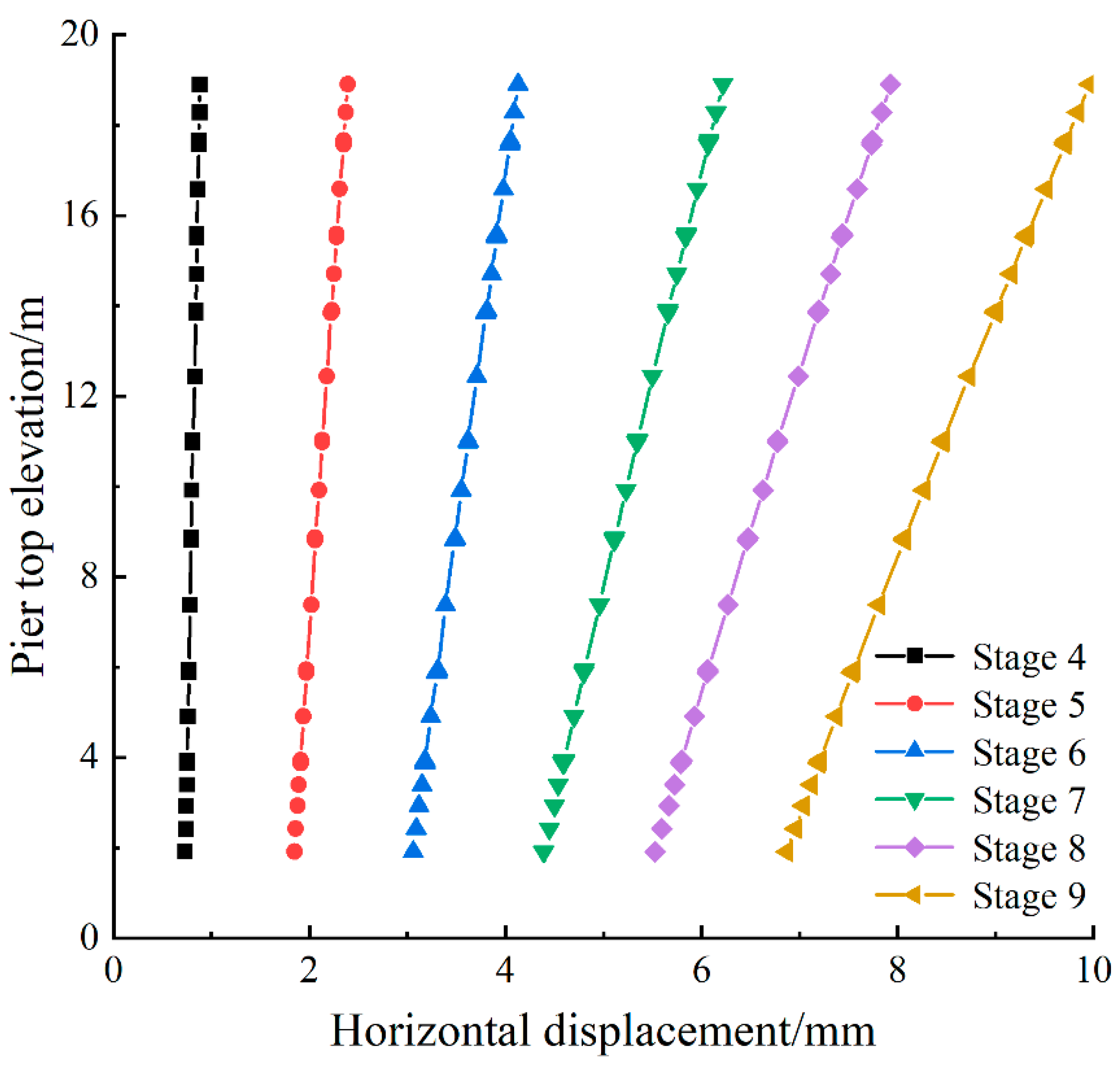
- For elevated Bridge A, the horizontal and vertical displacements of the bridge piers and bridge pile foundations gradually decrease with the increase in distance from the foundation pit. The vertical displacement in the z-axis direction is the most obvious change, with a reduction rate as high as 63.72%~79.49%. The change in the y-axis direction is the second, with a reduction rate of 9.90%~15.70%. The change in the x-axis direction is the least obvious, with a reduction rate of only 1.06%~1.86%.
- (3)
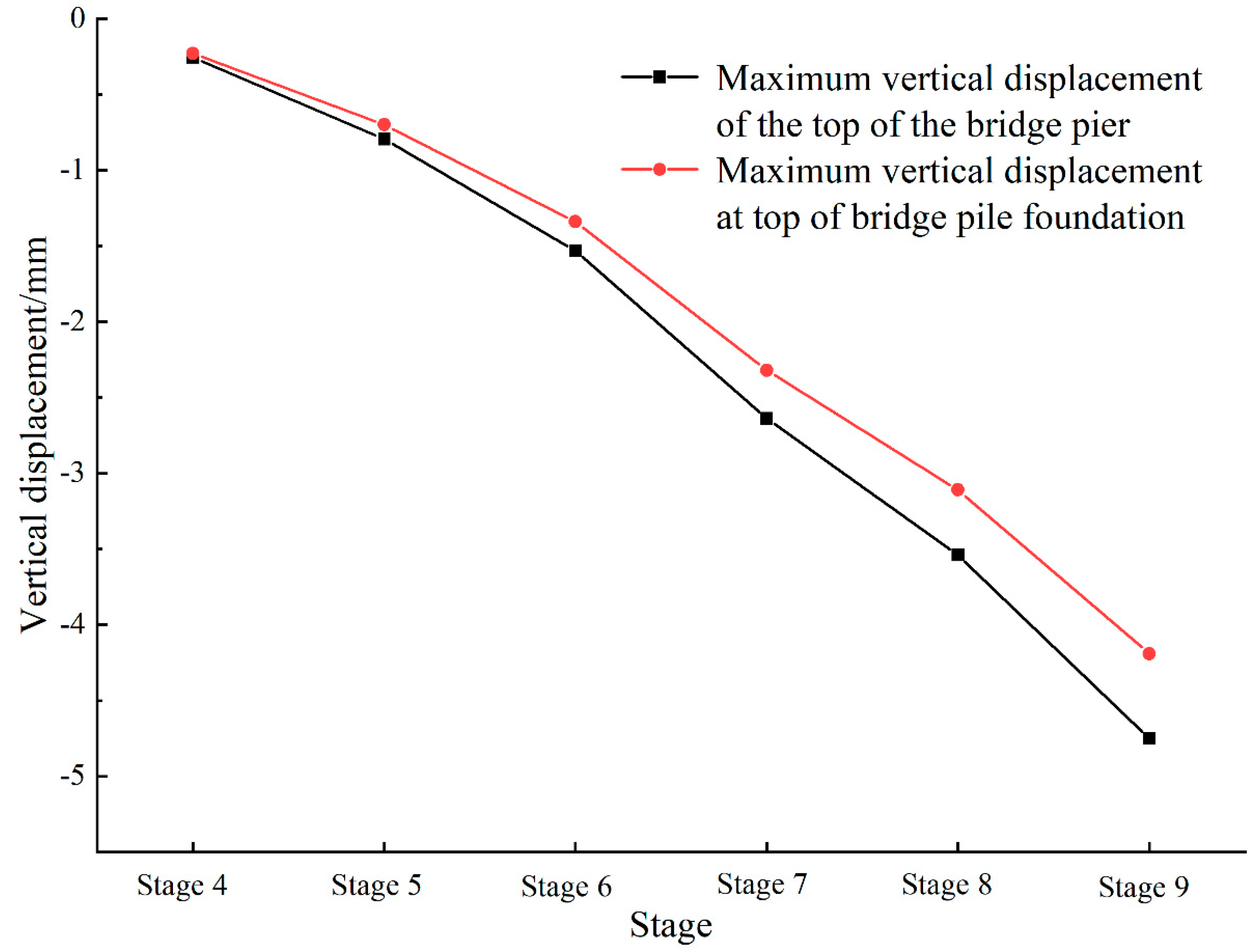
- With the excavation of the foundation pit, the horizontal displacement, vertical displacement, and tilt rate of elevated Bridge A gradually increase with the increase in the excavation depth, in which the maximum horizontal displacement of the bridge pile foundation in the x-axis direction is 5.66 mm; the maximum horizontal displacement in the y-axis direction is 2.03 mm; the maximum vertical displacements of the top of the bridge piers and the top of the bridge pile foundation are 4.75 mm and 4.19 mm, respectively; and the maximum tilt rate of the bridge piers is 0.018%.
6.2. Reinforcement Optimization Analysis
- (1)
- With the increase in the depth of soil reinforcement outside the pit, the vertical displacement and tilt rate of the bridge pier and the bridge pile foundation are gradually reduced, and the deeper the depth of reinforcement, the better the displacement control effect of the elevated bridge.
- (2)
- When the depth of reinforcement is close to the excavation depth, increasing the depth of reinforcement, the control effect of deformation growth is not obvious. It is recommended that the depth of reinforcement is taken as the best excavation depth of the pit in the actual construction, in which using pit peripheral soil reinforcement is better than using the soil around the bridge pier in controlling the deformation.
- (3)
- In controlling the deformation of the surrounding environment caused by the excavation of the foundation pit, the preloaded axial force is the worst, mainly because the preloaded axial force is subjected to the pit angle effect is obvious. Therefore, in the actual construction, the appropriate preloaded axial force should be selected according to the site conditions.
6.3. Influence of Distance on Bridge Piers
- (1)
- The deformation of bridge piers and bridge pile foundations on the whole presents a trend of gradual reduction with the increase in the distance of the viaduct from the pit. The two trends remain consistent.
- (2)
- When the elevated bridge is closer to the foundation pit, it will be affected by the pit angle effect, and the fluctuation of horizontal displacement in the y-axis direction is more significant than the fluctuation of horizontal displacement in the x-axis direction and vertical displacement in the z-axis direction. This indicates that the pit angle effect is more significant to the horizontal displacement in the y-axis direction.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chen, H.; Li, J.; Yang, C.; Wang, X. A theoretical study on ground surface settlement induced by a braced deep excavation. Eur. J. Environ. Civ. Eng. 2020, 24, 1234–1249. [Google Scholar] [CrossRef]
- Lin, Z.; Jiang, Y.; Xiong, Y.; Xu, C.; Guo, Y.; Wang, C.; Fang, T. Analytical solution for displacement-dependent active earth pressure considering the stiffness of cantilever retaining structure in cohesionless soil. Comput. Geotech. 2024, 170, 106258. [Google Scholar] [CrossRef]
- Song, S.; Wang, P.; Yin, Z.; Cheng, Y.P. Micromechanical modeling of hollow cylinder torsional shear test on sand using discrete element method. J. Rock Mech. Geotech. Eng. 2024. [Google Scholar] [CrossRef]
- Wang, P.; Xu, C.; Yin, Z.Y.; Song, S.X.; Xu, C.; Dai, S. A DEM-based Generic Modeling Framework for Hydrate-Bearing Sediments. Comput. Geotech. 2024, 171, 106287. [Google Scholar] [CrossRef]
- Wang, P.; Yin, Z.Y.; Hicher, P.Y.; Cui, Y.J. Micro—Mechanical analysis of one—Dimensional compression of clay with DEM. Int. J. Numer. Anal. Methods Geomech. 2023, 47, 2706–2724. [Google Scholar] [CrossRef]
- Wang, T.; Wang, P.; Yin, Z.Y.; Laouafa, F.; Hicher, P.Y. Hydro-mechanical analysis of particle migration in fractures with CFD-DEM. Eng. Geol. 2024, 335, 107557. [Google Scholar] [CrossRef]
- Delo, G.; Civera, M.; Lenticchia, E.; Miraglia, G.; Surace, C.; Ceravolo, R. Interferometric satellite data in structural health monitoring: An application to the effects of the construction of a subway line in the urban area of Rome. Appl. Sci. 2022, 12, 1658. [Google Scholar] [CrossRef]
- Lei, M.; Lin, D.; Huang, Q.; Wang, X. Research on the construction risk control technology of shield tunnel underneath an operational railway in sand pebble formation: A case study. Eur. J. Environ. Civ. Eng. 2018, 22, 657–673. [Google Scholar] [CrossRef]
- Li, D.; Yan, C. Building deformation prediction based on ground surface settlements of metro-station deep excavation. Adv. Civ. Eng. 2018, 2018, 1–10. [Google Scholar] [CrossRef]
- Zhou, Z.; Ding, H.; Miao, L.; Li, Y. Predictive model for the surface settlement caused by the excavation of twin tunnels. Tunn. Undergr. Space Technol. 2021, 108, 103730. [Google Scholar] [CrossRef]
- Song, D.; Chen, Z.; Dong, L.; Zhou, Q. Monitoring analysis of influence of extra-large complex deep foundation pit on adjacent environment: A case study of Zhengzhou City. China. Geomat. Nat. Hazards Risk 2020, 11, 1165–1178. [Google Scholar] [CrossRef]
- Zhang, D. Influences of deep foundation pit excavation on the stability of adjacent ancient buildings. Buildings 2023, 13, 123–134. [Google Scholar] [CrossRef]
- Xue, H. Research on the control of excavation deformation of super deep foundation pit adjacent to the existing old masonry structure building. Sustainability 2023, 15, 1432. [Google Scholar] [CrossRef]
- Xu, C.J.; Yang, K.F.; Fan, X.Z.; Li, M. Numerical investigation on instability of buildings caused by adjacent deep excavation. J. Perform. Constr. Facil. 2021, 35, 04021065. [Google Scholar] [CrossRef]
- Wang, Q.; Qingtao, W.; Haoyong, Q. Analysis of impact of bilateral deep foundation pit excavation on adjacent existing station. IOP Conf. Ser. Earth Environ. Sci. 2019, 240, 052007. [Google Scholar] [CrossRef]
- Huang, J.; Liu, J.; Guo, K.; Wu, C.; Yang, S.; Luo, M.; Lu, Y. Numerical Simulation Study on the Impact of Deep Foundation Pit Excavation on Adjacent Rail Transit Structures—A Case Study. Buildings 2024, 14, 1853. [Google Scholar] [CrossRef]
- Zhang, X.; Wei, G.; Jiang, C. The study for longitudinal deformation of adjacent shield tunnel due to foundation pit excavation with consideration of the retaining structure deformation. Symmetry 2020, 12, 1507. [Google Scholar] [CrossRef]
- Wang, S.; Wang, W.; Yang, H.; Zhao, J. Study on the influence of adjacent double deep foundation pit excavation sequence on existing tunnel deformation based on HSS constitutive model. Appl. Sci. 2024, 14, 2347. [Google Scholar] [CrossRef]
- Gui, Y.; Zhao, Z.; Qin, X.; Wang, L. Study on deformation law of deep foundation pit with the top-down method and its influence on adjacent subway tunnel. Adv. Civ. Eng. 2020, 2020, 1–15. [Google Scholar] [CrossRef]
- Niu, Y.; Wang, Q.; Ma, F. Study on the influence of foundation pit excavation on the deformation of adjacent subway tunnel in the affected area of fault zones. Sustainability 2023, 15, 2012. [Google Scholar] [CrossRef]
- Liu, J.; Shi, C.; Cao, C.; Zhou, Y. Improved analytical method for pile response due to foundation pit excavation. Comput. Geotech. 2020, 117, 103303. [Google Scholar] [CrossRef]
- Zhong, W.; Huang, N.; Nie, N.; Ding, H.; Gao, F. Study on the Influence of Excavation of Superlarge and Ultra—Deep Foundation Pits on the Pile Foundation of Existing Viaducts. Adv. Civ. Eng. 2023, 2023, 5834958. [Google Scholar] [CrossRef]
- Jiang, Z.; Zhu, S.; Que, X.; Ge, X. Deformation Effects of Deep Foundation Pit Excavation on Retaining Structures and Adjacent Subway Stations. Buildings 2024, 14, 2521. [Google Scholar] [CrossRef]
- Jia, Y.; Shang, Y.; Du, J.; Dang, H. Study on the Control Effect of Pretreatment Measures on the Deformation of Subway Caused by the Excavation of Foundation Pit. In Proceedings of the International Conference on Civil Engineering, Singapore, 24–26 March 2023; Springer Nature Singapore: Singapore, 2023; pp. 683–690. [Google Scholar]
- Feng, S.; Lei, H.; Wan, Y.; Li, W. Influencing factors and control measures of excavation on adjacent bridge foundation based on analytic hierarchy process and finite element method. Front. Struct. Civ. Eng. 2021, 15, 789–799. [Google Scholar] [CrossRef]
- Yang, Y.B.; Chen, C.Y.; Liu, C.; Zhang, Z. Performance of a deep excavation and the influence on adjacent piles: A case history in karst region covered by clay and sand. Undergr. Space 2023, 8, 45–60. [Google Scholar] [CrossRef]
- Yang, Y.; Li, J.; Liu, C.; Wang, S. Influence of deep excavation on adjacent bridge piles considering underlying karst cavern: A case history and numerical investigation. Acta Geotech. 2021, 16, 2453–2471. [Google Scholar] [CrossRef]
- Gu, R.; Zhan, L.; Fang, Y. Model test on the effect of the new undersea tunnel in Macao on the existing Ponte Governador Nobre de Carvalho. Arab. J. Geosci. 2022, 15, 1–14. [Google Scholar] [CrossRef]
- Miao, Y.; Guo, M.; Zhao, X.; Zhang, H. Study on influence of shallow buried tunnel excavation on adjacent bridge piles. Geotech. Geol. Eng. 2023, 41, 3457–3470. [Google Scholar] [CrossRef]
- Huang, J.; Yan, J.; Guo, K.; Yang, X.; Peng, S.; Wu, C. Study on the Impact of Deep Foundation Pit Construction on Nearby Elevated Structures—Case Study. Buildings 2024, 14, 2541. [Google Scholar] [CrossRef]
- DG/TJ08-109-2017; Urban Rail Transit Design Standard. Tongji University Press: Shanghai, China, 2017.
- DBJT08-115-2010; Technical Standards for Safety Protection Areas of Urban Bridges and Tunnels. Tongji University Press: Shanghai, China, 2010.
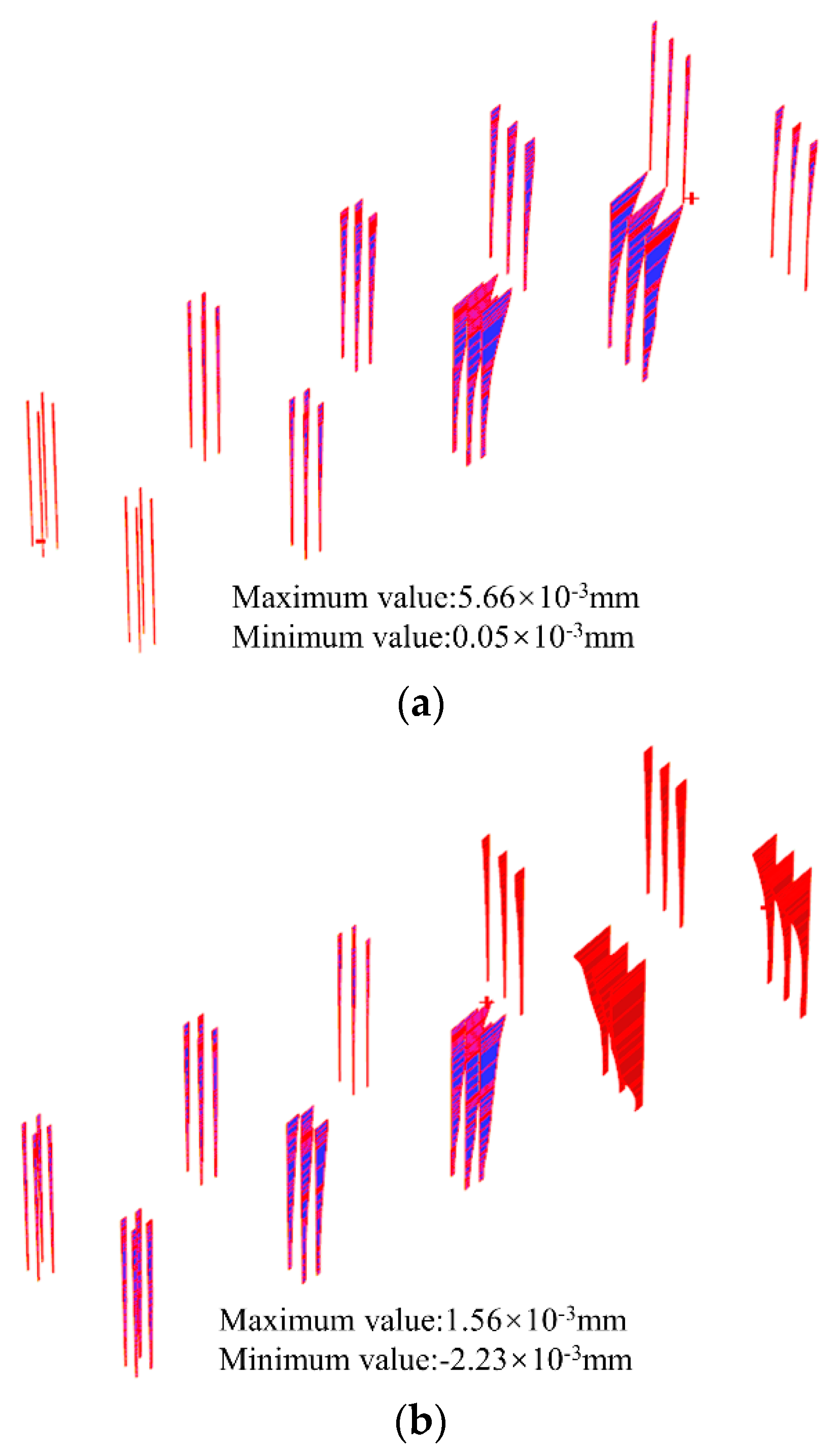
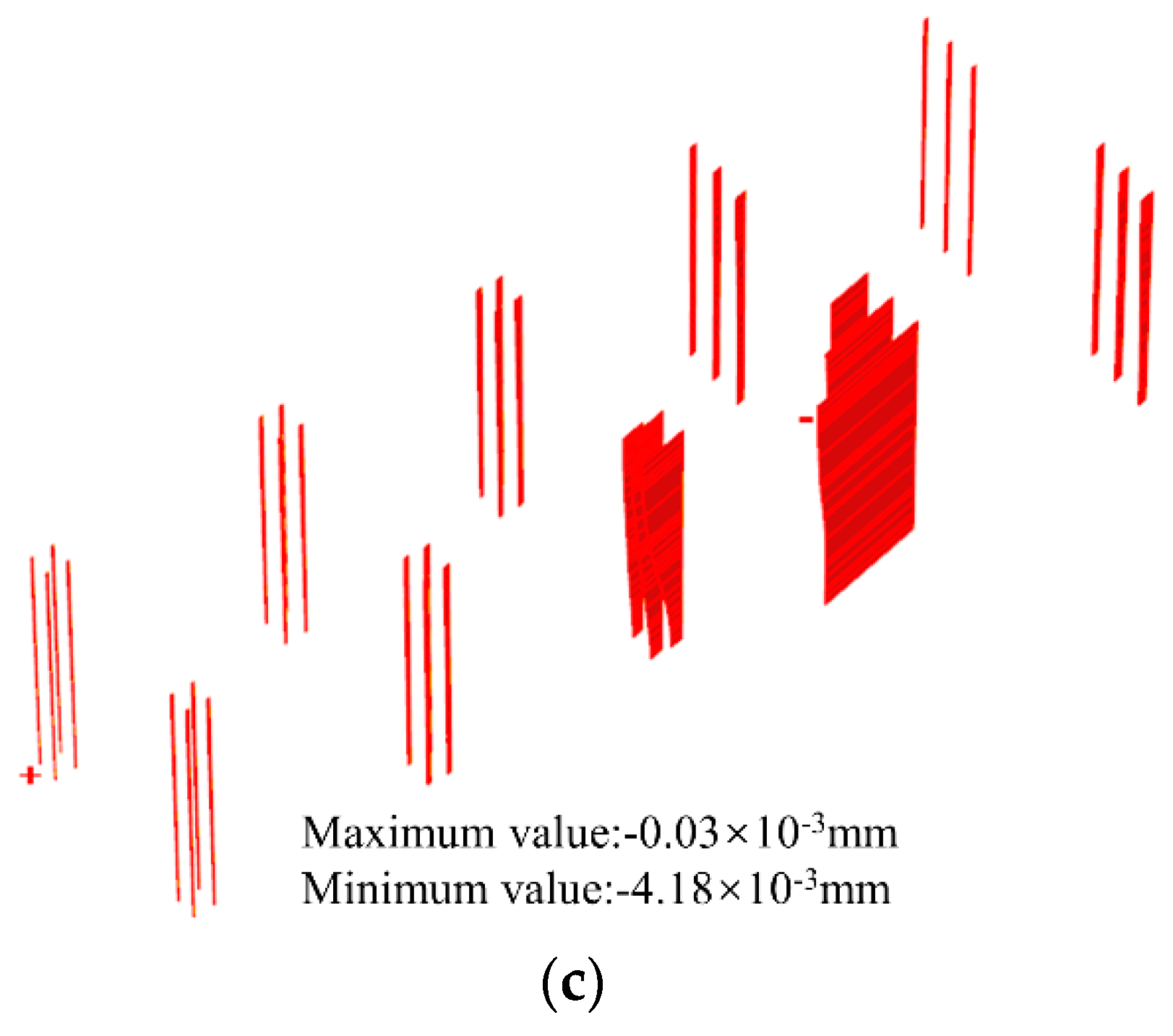



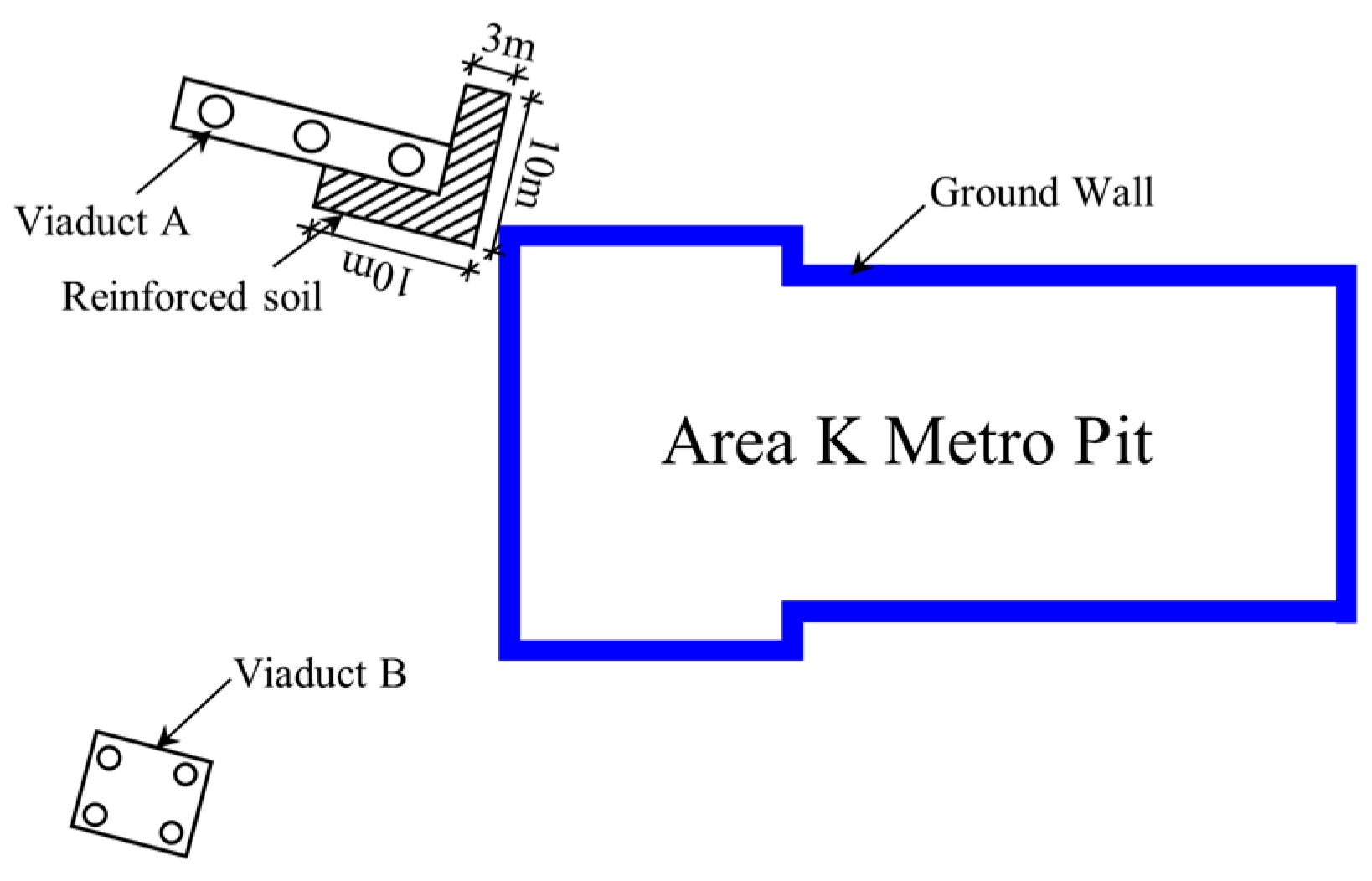

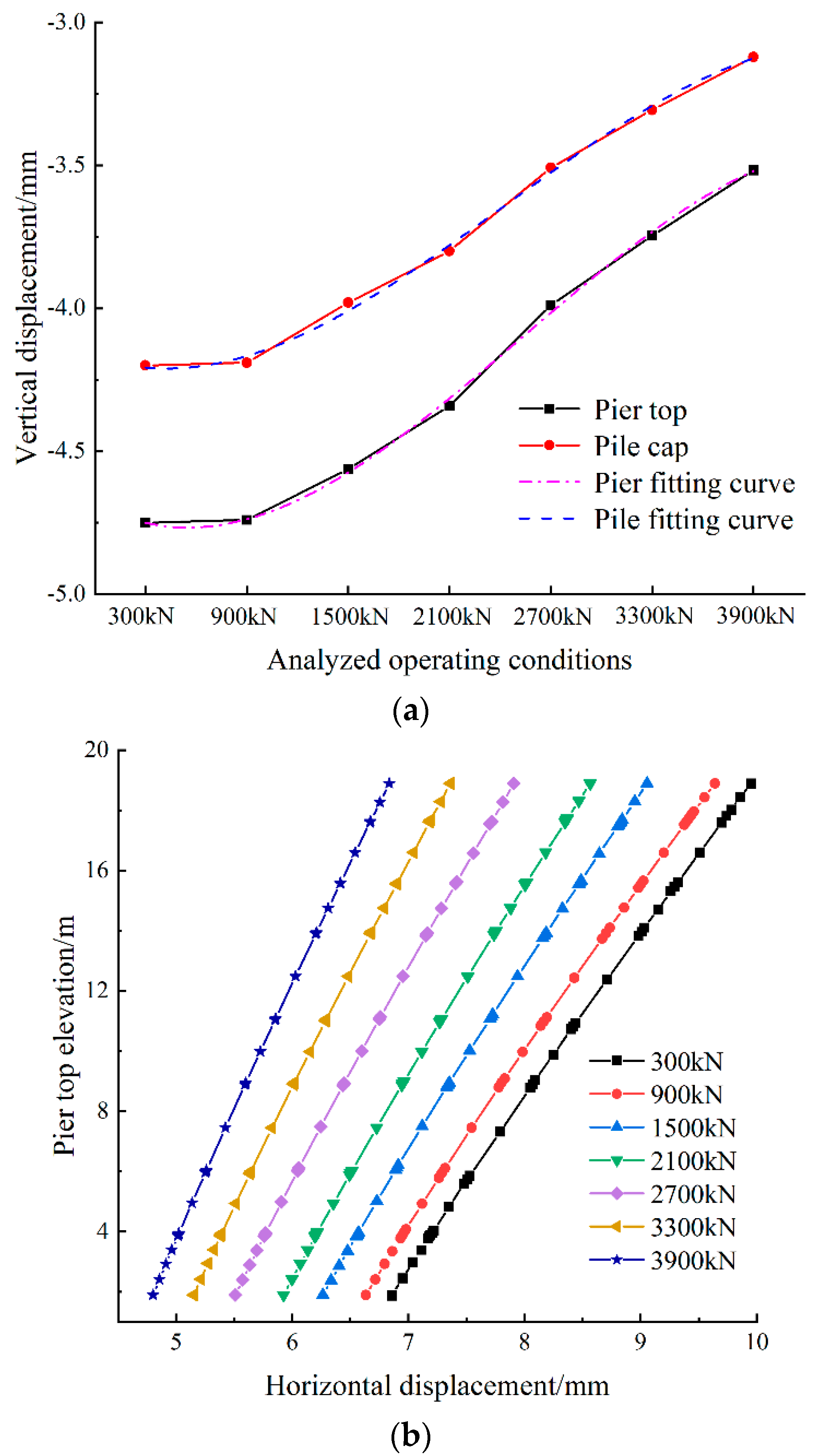
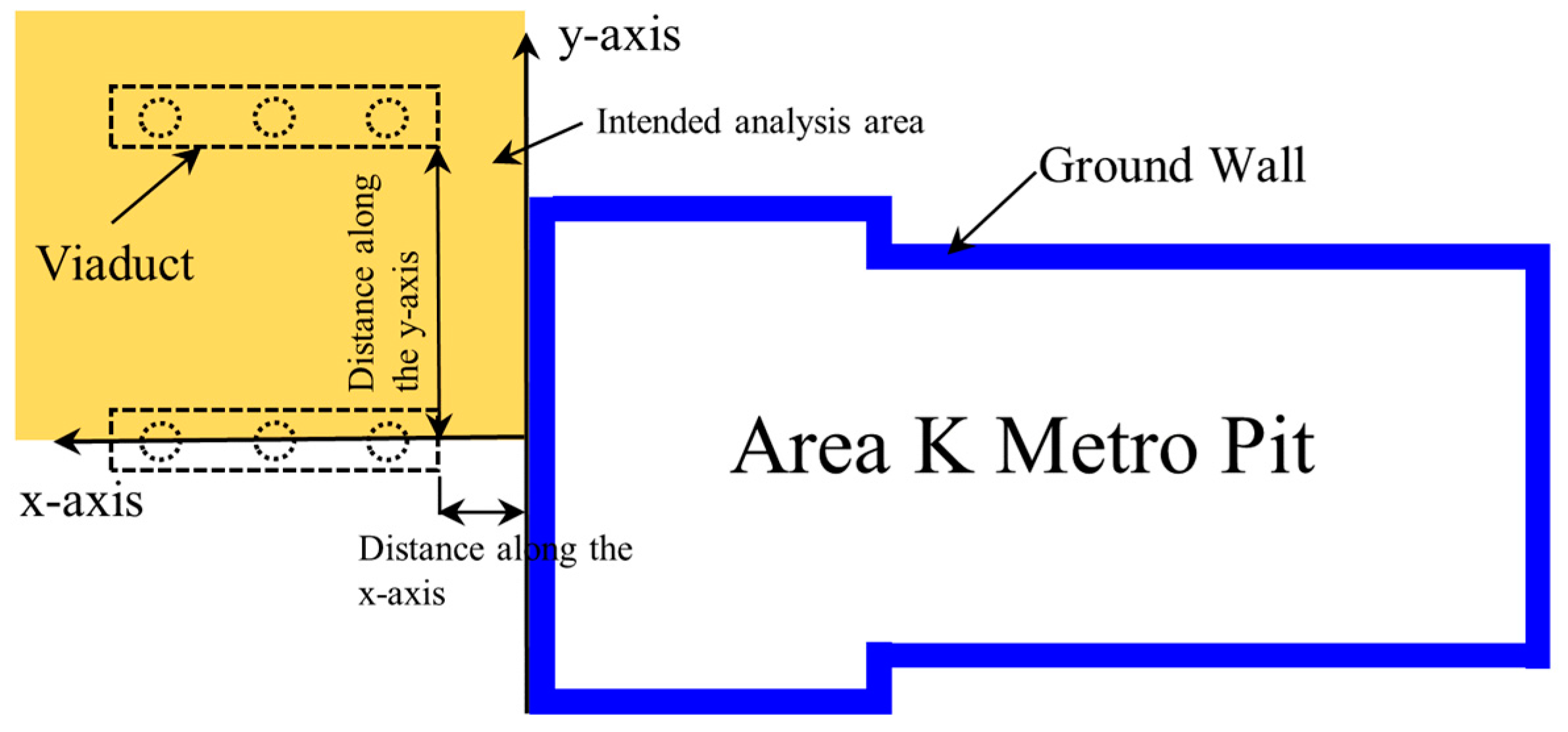



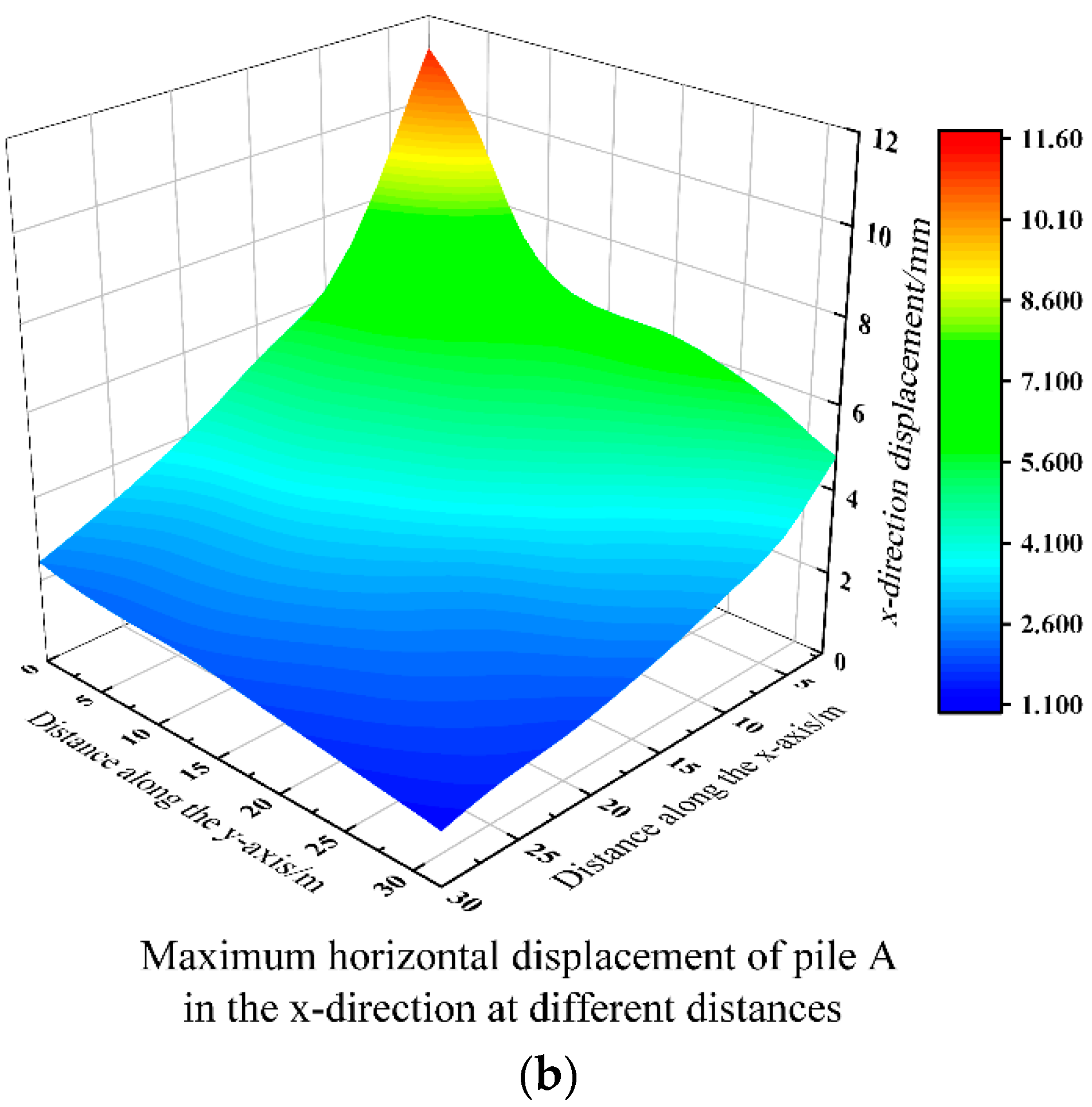

| Structure | Sectional Dimensions (mm) | Elastic Modulus (×103 MPa) | Poisson’s Ratio |
|---|---|---|---|
| Ground wall | 1200 | 31.5 | 0.22 |
| Concrete strut | 900 × 900/1200 × 900 | 33.5 | 0.19 |
| Steel strut | φ609 × 16/φ800 × 16 | 210 | 0.30 |
| Bored pile | φ1300/φ1300 | 31.5 | 0.22 |
| Soil Layer | Name | γ (kN/m3) | c’ (kPa) | φ’ (°) | E50 (MPa) | Eoed (MPa) | Eur (MPa) | G0 (MPa) |
|---|---|---|---|---|---|---|---|---|
| 1-1 | Miscellaneous Fillings | 18.3 | 8.0 | 15.0 | 8.0 | 8.0 | 24.0 | 48.0 |
| 2-1 | Silty Clay | 19.5 | 16.0 | 27.0 | 6.5 | 6.5 | 19.5 | 39.0 |
| 3-1 | Clay | 19.5 | 18.0 | 25.0 | 4.7 | 3.1 | 24.2 | 48.4 |
| 4-1 | Silty Chalky Clay | 17.6 | 15.0 | 24.0 | 3.0 | 3.0 | 9.0 | 18.0 |
| 5-1 | Clay | 18.5 | 18.0 | 25.0 | 4.6 | 4.0 | 23.2 | 46.4 |
| 6-1 | Fully Weathered Tuff | 21.0 | 50.0 | 25.0 | 32.49 | 32.49 | 94.47 | 194.9 |
| Analysis Conditions | Working Condition |
|---|---|
| Stage 1 | Geostatic equilibrium |
| Stage 2 | Diaphragm wall construction |
| Stage 3 | Construction of the first concrete strut (displacement reset) |
| Stage 4 | Excavation 1 (−3.9 m) |
| Stage 5 | Excavation 2 (−6.9 m) |
| Stage 6 | Excavation 3 (−10.3 m) |
| Stage 7 | Excavation 4 (−13.7 m) |
| Stage 8 | Excavation 5 (−16.6 m) |
| Stage 9 | Excavation 6 (−19.6 m) |
| Project Conditions | x Direction/mm | Reduction Rate/% | y Direction/mm | Reduction Rate/% | z Direction/mm | Reduction Rate/% | |
|---|---|---|---|---|---|---|---|
| Pier A top | Max value | 9.65 | 1.86 | 2.93 | 15.70 | 4.73 | 79.49 |
| Min value | 9.47 | 2.47 | 0.97 | ||||
| Pile A top | First pile | 5.66 | 1.06 | 2.02 | 9.90 | 4.19 | 63.72 |
| Second pile | 5.63 | 1.91 | 2.81 | ||||
| Third pile | 5.60 | 1.82 | 1.52 | ||||
| Project | Control Standard |
|---|---|
| Horizontal displacement of diaphragm wall/mm | 39.2 |
| Vertical settlement of elevated bridge/mm | 5.0 |
| Tilt rate of elevated bridge | 1/3500 |
| Analysis Conditions | Condition Description |
|---|---|
| Condition 1 | Current situation simulation (0 m) |
| Condition 2 | Reinforcement depth 5 m |
| Condition 3 | Reinforcement depth 10 m |
| Condition 4 | Reinforcement depth 15 m |
| Condition 5 | Reinforcement depth 20 m |
| Condition 6 | Reinforcement depth 25 m |
| Condition 7 | Reinforcement depth 30 m |
| Analysis Conditions | Condition Description |
|---|---|
| Condition 1 | Current situation simulation (0 m) |
| Condition 2 | Reinforcement depth 5 m |
| Condition 3 | Reinforcement depth 10 m |
| Condition 4 | Reinforcement depth 15 m |
| Condition 5 | Reinforcement depth 20 m |
| Condition 6 | Reinforcement depth 25 m |
| Condition 7 | Reinforcement depth 30 m |
| Analysis Conditions | Condition Description |
|---|---|
| Condition 1 | Current situation simulation (pre-applied axial force of 300 kN) |
| Condition 2 | Pre-applied axial force of 900 kN |
| Condition 3 | Pre-applied axial force of 1500 kN |
| Condition 4 | Pre-applied axial force of 2100 kN |
| Condition 5 | Pre-applied axial force of 2700 kN |
| Condition 6 | Pre-applied axial force of 3300 kN |
| Condition 7 | Pre-applied axial force of 3900 kN |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, J.; Yu, J.; Fang, F.; Lin, G.; Tang, X.; Ding, H.; Xu, C. Impact of Excavation on Adjacent Elevated Bridges and Optimization Analysis of Deformation Control. Buildings 2024, 14, 3197. https://doi.org/10.3390/buildings14103197
Wu J, Yu J, Fang F, Lin G, Tang X, Ding H, Xu C. Impact of Excavation on Adjacent Elevated Bridges and Optimization Analysis of Deformation Control. Buildings. 2024; 14(10):3197. https://doi.org/10.3390/buildings14103197
Chicago/Turabian StyleWu, Jiangpeng, Junping Yu, Fuguan Fang, Gang Lin, Xiaolin Tang, Haibin Ding, and Changjie Xu. 2024. "Impact of Excavation on Adjacent Elevated Bridges and Optimization Analysis of Deformation Control" Buildings 14, no. 10: 3197. https://doi.org/10.3390/buildings14103197
APA StyleWu, J., Yu, J., Fang, F., Lin, G., Tang, X., Ding, H., & Xu, C. (2024). Impact of Excavation on Adjacent Elevated Bridges and Optimization Analysis of Deformation Control. Buildings, 14(10), 3197. https://doi.org/10.3390/buildings14103197





