Finite Element Analysis of Perforated Prestressed Concrete Frame Enhanced by Artificial Neural Networks
Abstract
1. Introduction
2. Finite Element Methods Enhanced by Artificial Neural Networks
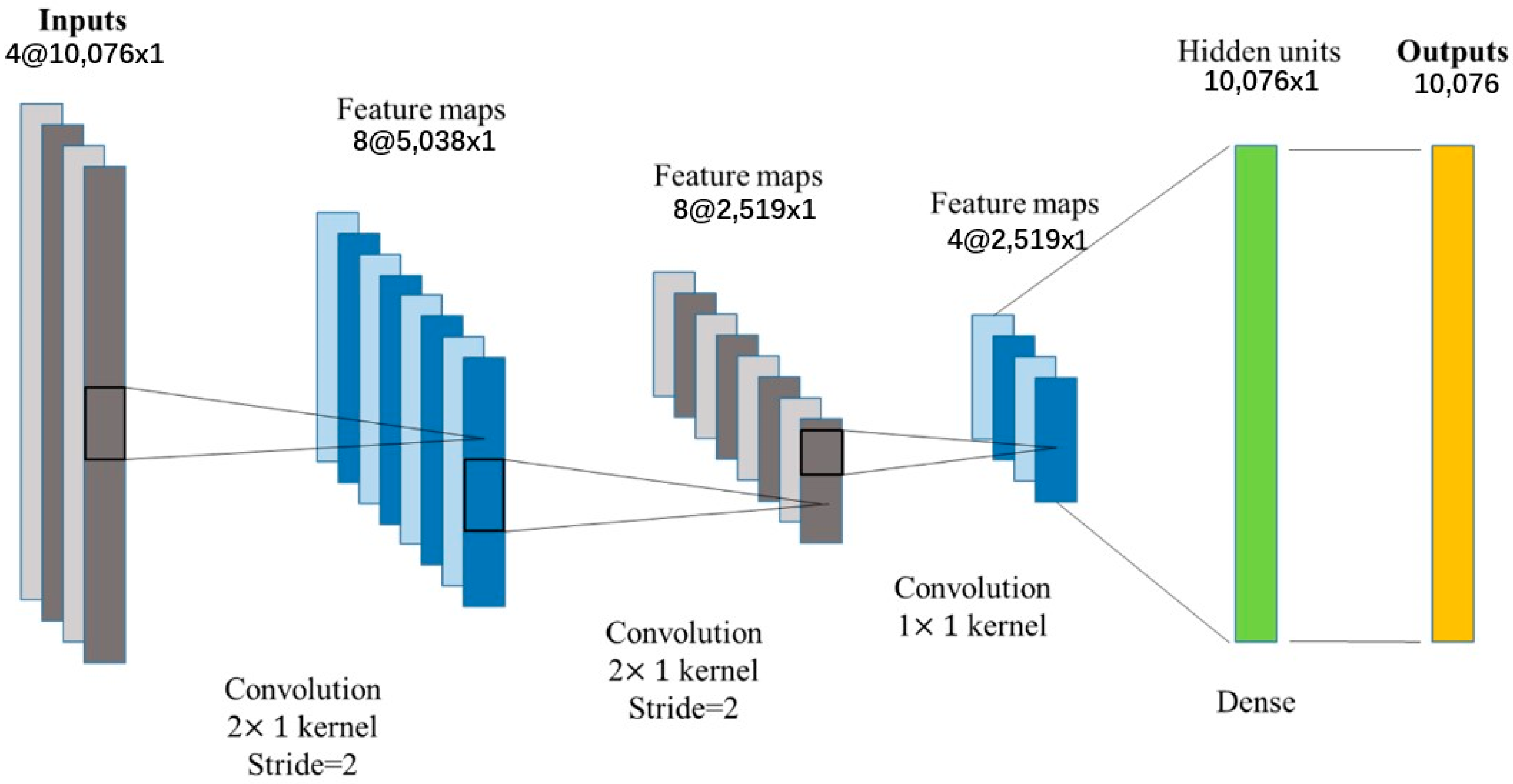
2.1. Surrogate-Based Finite Element Methods
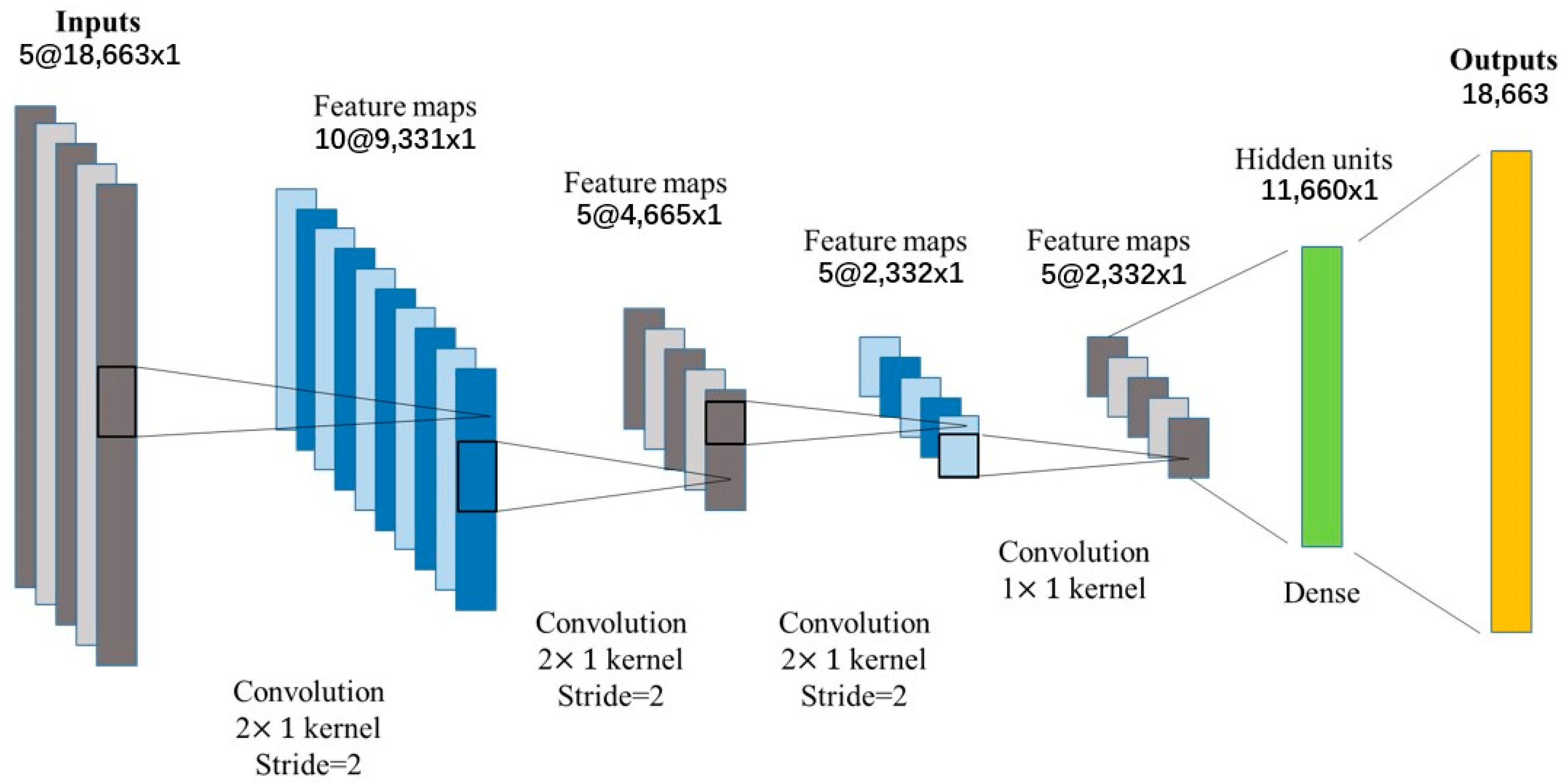
2.2. Artificial Neural Networks
3. Verifications
4. Numerical Examples
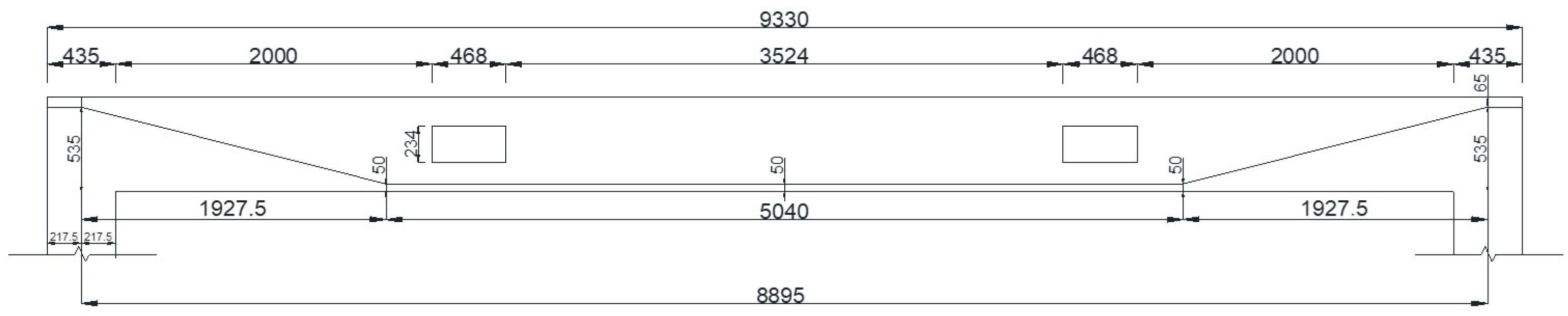
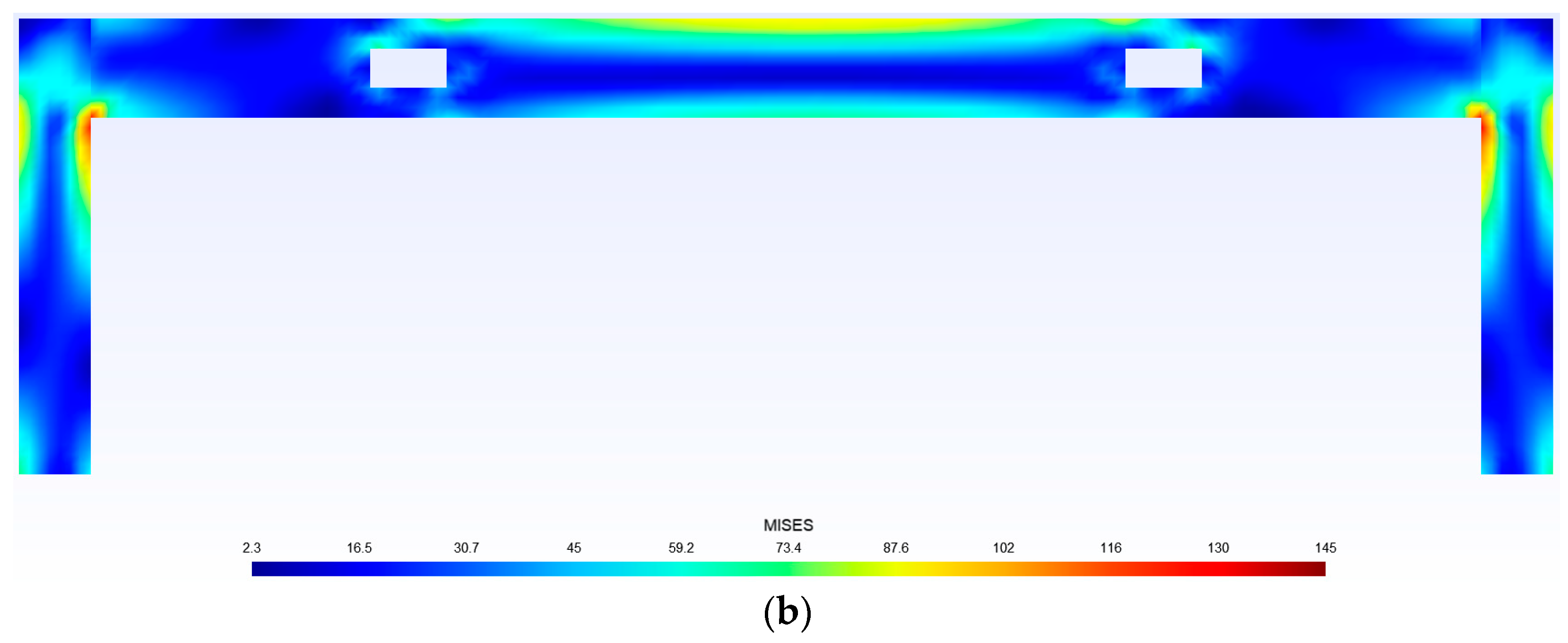
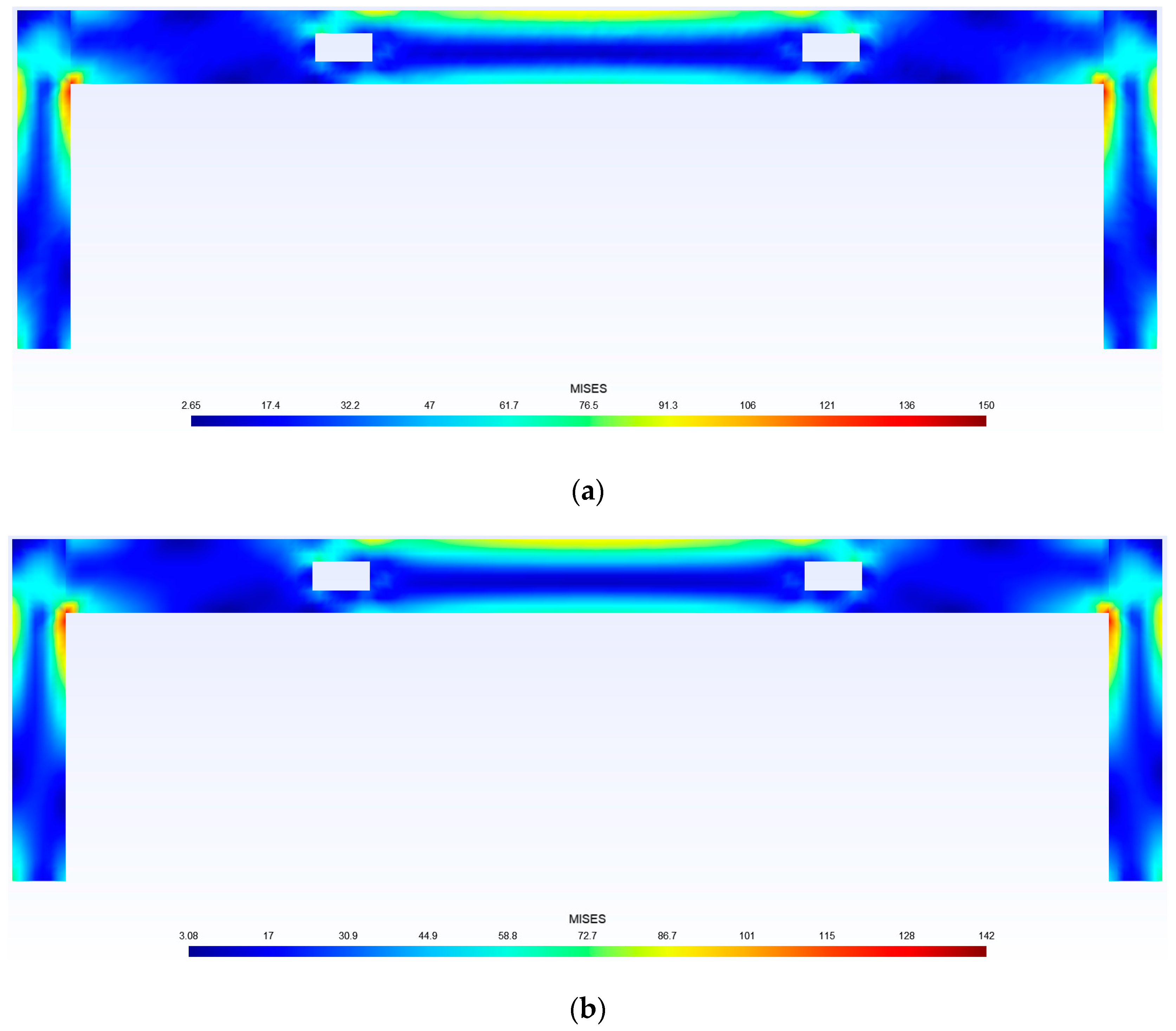
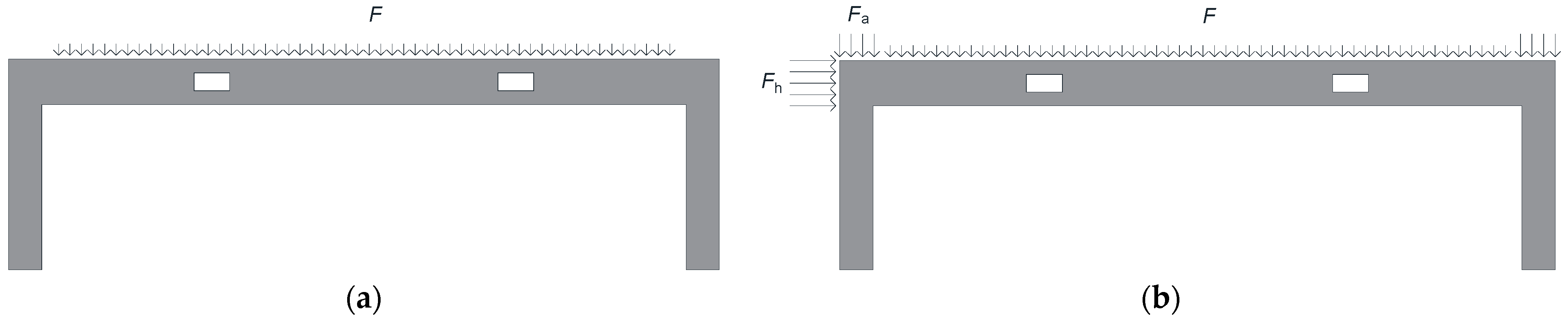
4.1. The Perforated Prestressed Concrete Frame
4.2. Numerical Experiments for Frames with Different Distances between Openings
4.3. Numerical Experiments for Perforated Prestressed Concrete under Different Loadings
5. Conclusions
- (1)
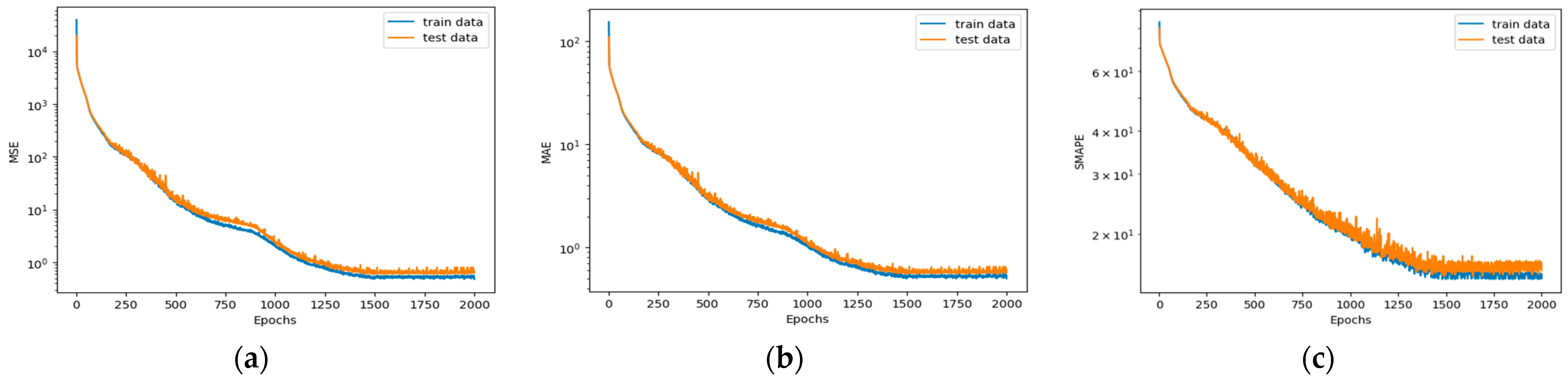
- When using a linear regression model to predict the displacement and stress fields of prestressed concrete simply supported by beams with an open hole and a constant total stiffness matrix, the final SMAPE is less than 1%, and the differences in various indicators between the training and testing datasets are small.
- (2)
- When only changing the opening position, for each type of opening position of the beam, 2000 samples were generated for training by changing the stress levels of each node on the top surface and the tension control stress of the prestressed reinforcement. The SMAPE of the final predicted displacement field and stress field are both less than 5%. When both the opening position and the reinforcement area are changed simultaneously, there is only one sample for each total stiffness matrix. The SMAPE of the final predicted displacement field and stress field is also less than 5%.
- (3)
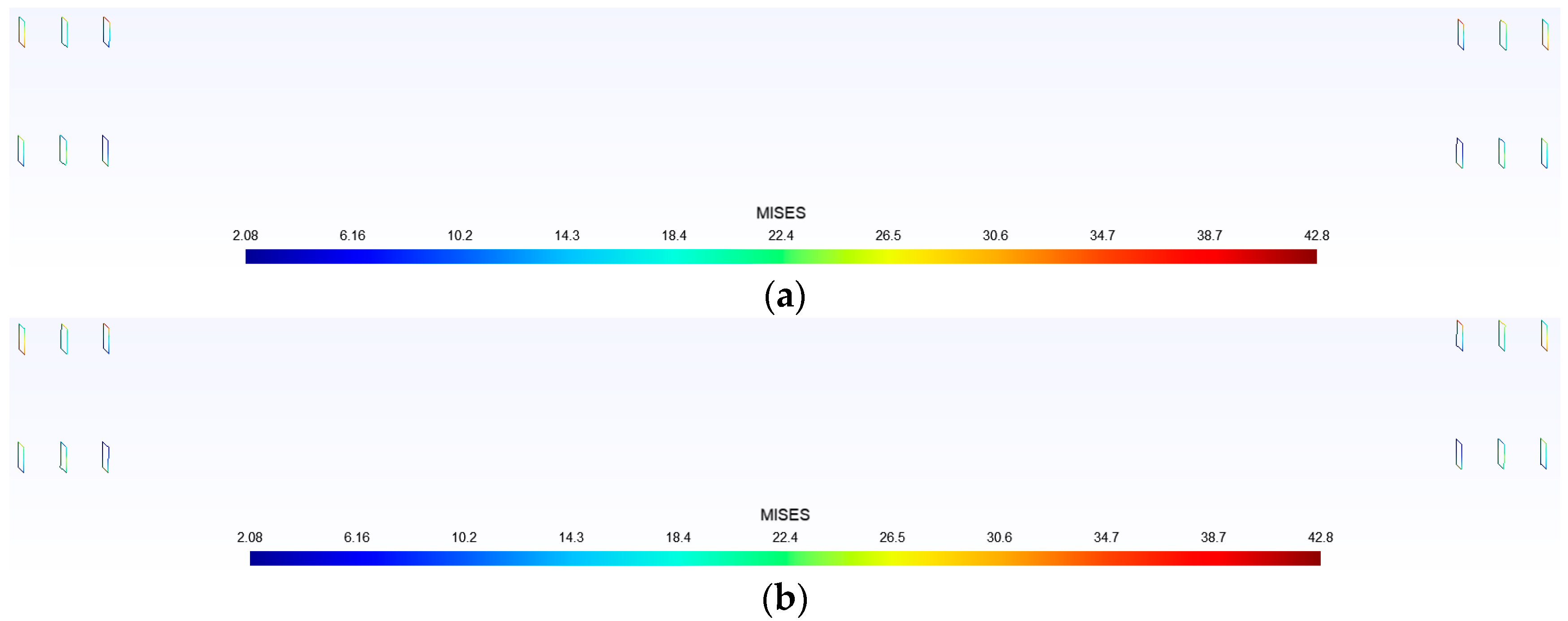
- Due to the vertical displacement of each node of the frame column under a vertical load being close to zero, the SMAPE value is relatively high. However, for the vertical displacement field and stress field of the frame beam, the SMAPE is less than 5%, indicating high prediction accuracy.
- (4)
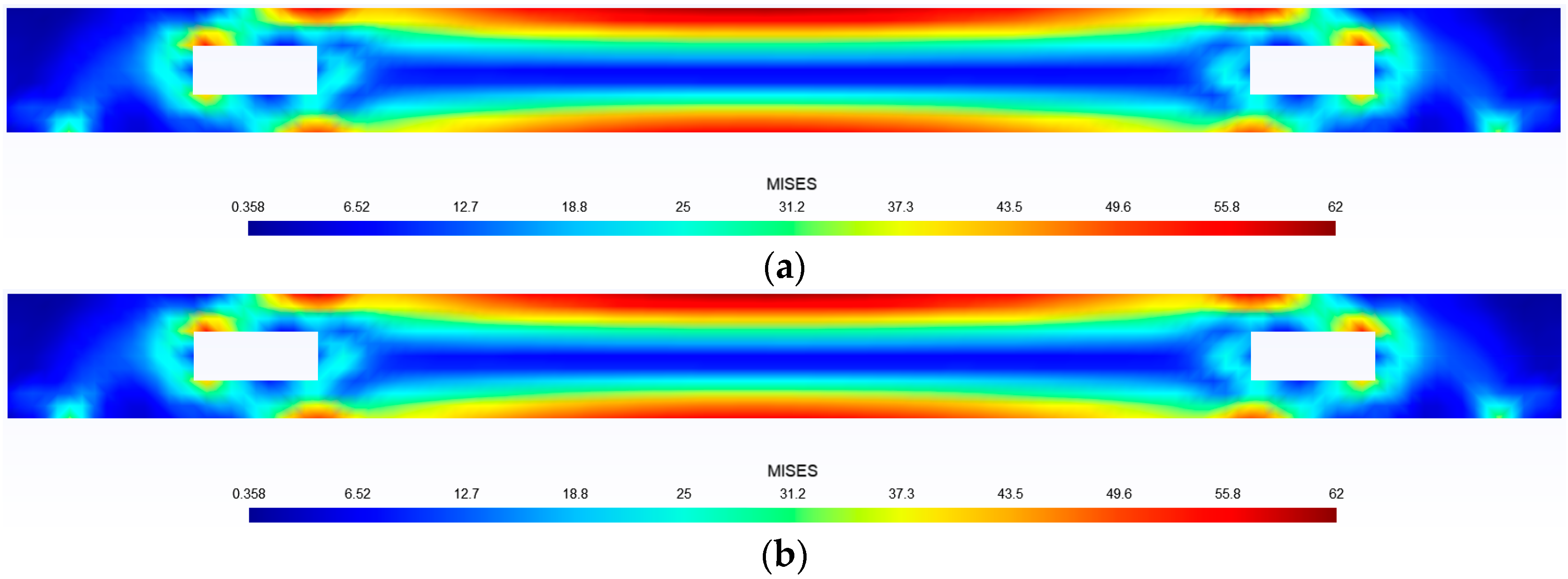
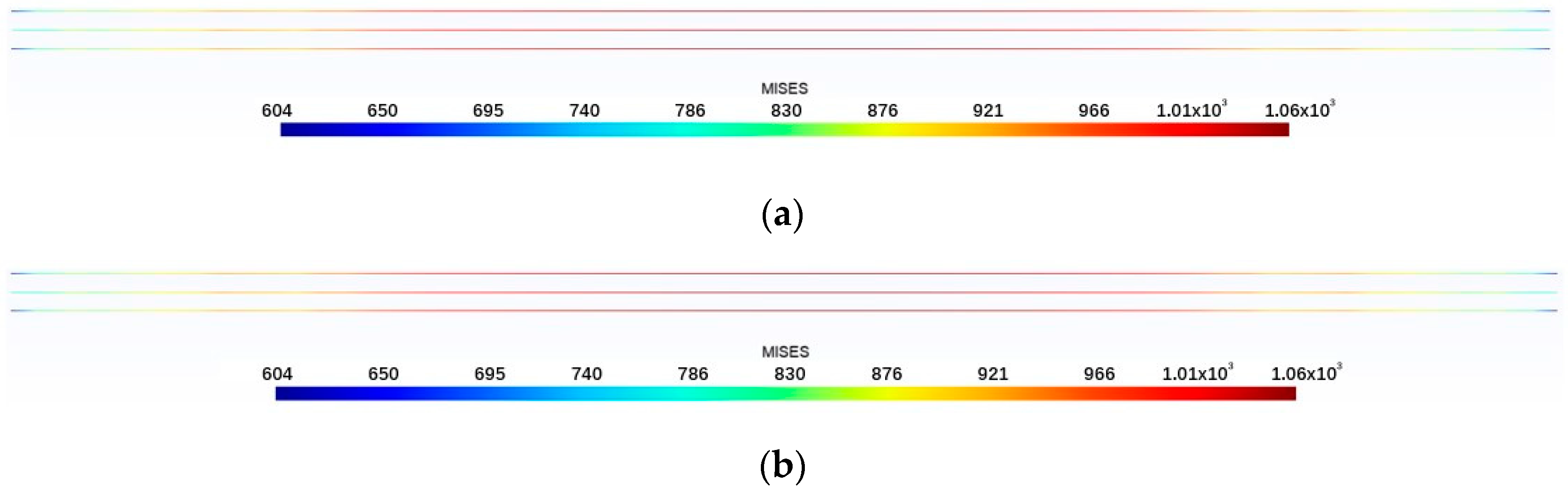
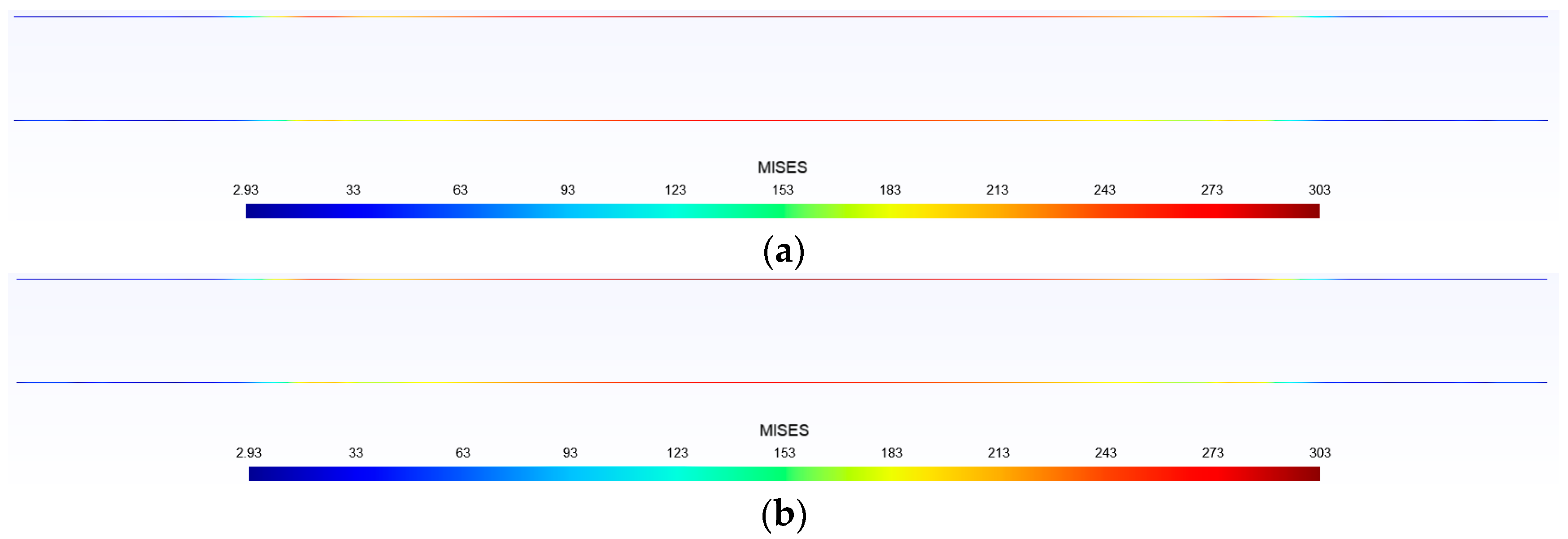
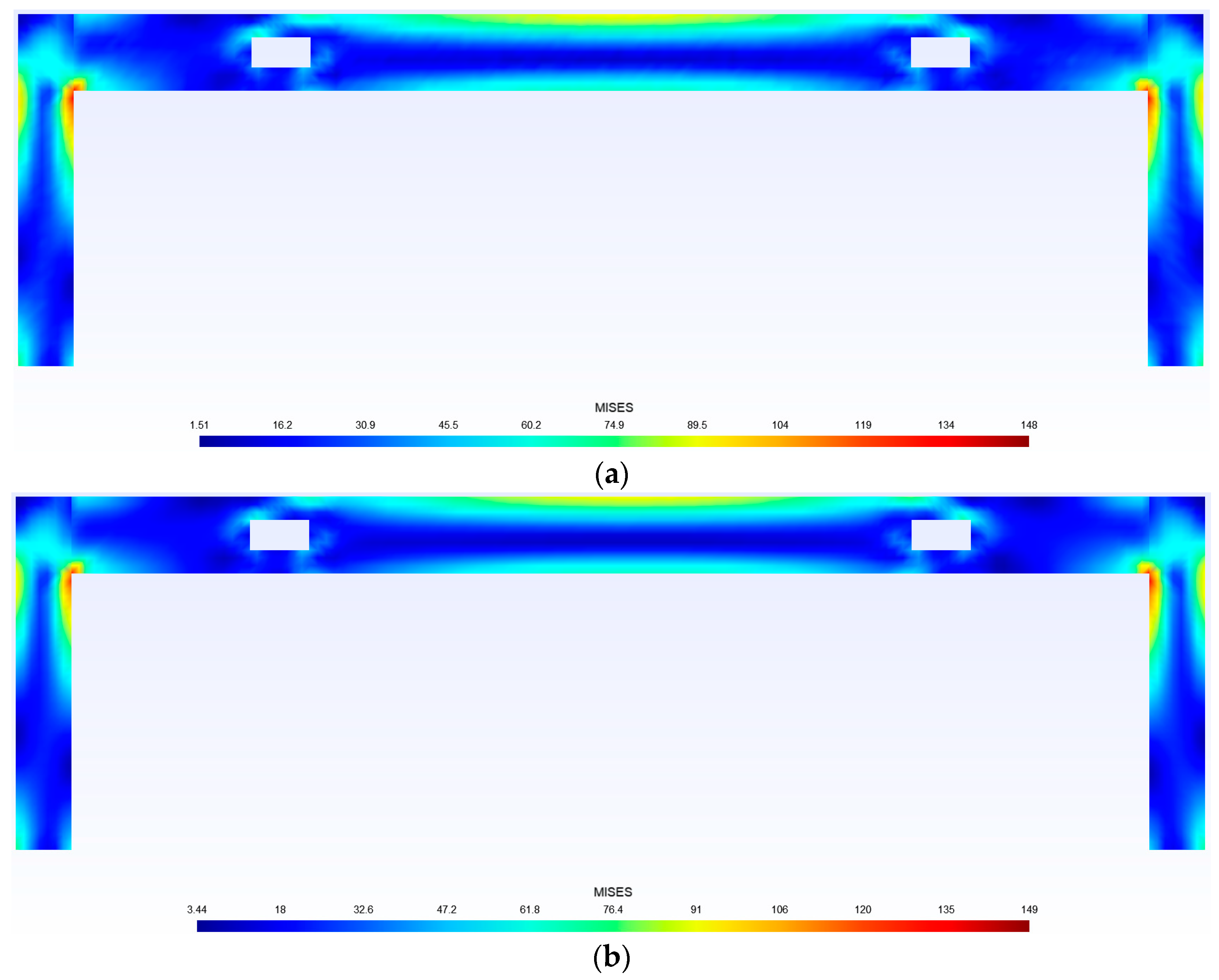
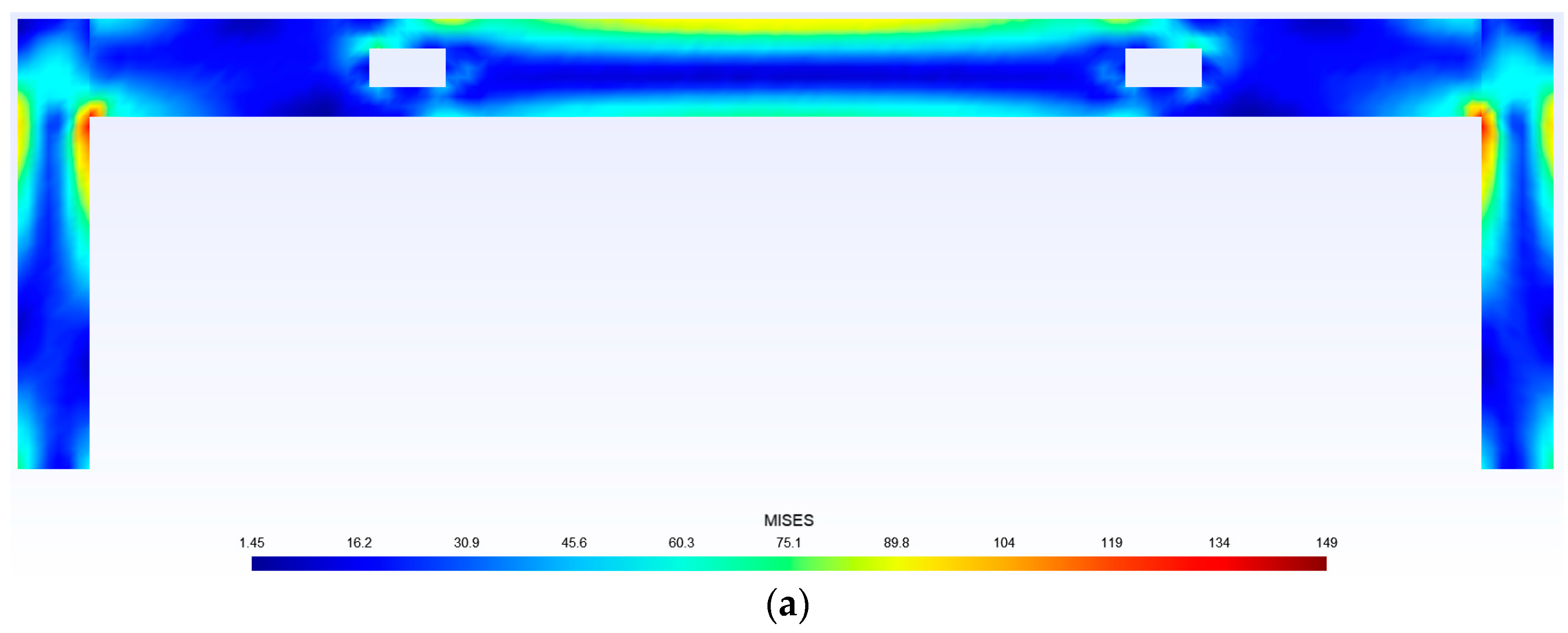
- Compared with the results of a finite element analysis, the relative error is larger at areas with lower stress values. However, most cases have a relative error of less than 5% in areas with high stress values. Therefore, it is feasible to use trained deep learning models for predictions.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Khatir, A.; Capozucca, R.; Khatir, S.; Magagnini, E. Vibration-based crack prediction on a beam model using hybrid butterfly optimization algorithm with artificial neural network. Front. Struct. Civ. Eng. 2022, 16, 976–989. [Google Scholar] [CrossRef]
- Teng, S.; Chen, G.; Wang, S.; Zhang, J.; Sun, X. Digital image correlation-based structural state detection through deep learning. Front. Struct. Civ. Eng. 2022, 16, 45–56. [Google Scholar] [CrossRef]
- Bolandi, H.; Li, X.; Salem, T.; Boddeti, V.N.; Lajnef, N. Bridging finite element and deep learning: High-resolution stress distribution prediction in structural components. Front. Struct. Civ. Eng. 2022, 16, 1365–1377. [Google Scholar] [CrossRef]
- Lin, M.; Teng, S.; Chen, G.; Lv, J.; Hao, Z. Optimal CNN-based semantic segmentation model of cutting slope images. Front. Struct. Civ. Eng. 2022, 16, 414–433. [Google Scholar] [CrossRef]
- Mai, H.-V.T.; Nguyen, M.H.; Trinh, S.H.; Ly, H.-B. Optimization of machine learning models for predicting the compressive strength of fiber-reinforced self-compacting concrete. Front. Struct. Civ. Eng. 2023, 17, 284–305. [Google Scholar] [CrossRef]
- Hai-Bang, L.; Thuy-Anh, N.; Binh, T.P.; May, H.N. A hybrid machine learning model to estimate self-compacting concrete compressive strength. Front. Struct. Civ. Eng. 2022, 16, 990–1002. [Google Scholar]
- Sun, G.; Shi, J.; Deng, Y. Predicting the capacity of perfobond rib shear connector using an ANN model and GSA method. Front. Struct. Civ. Eng. 2022, 16, 1233–1248. [Google Scholar] [CrossRef]
- Javanmardi, R.; Ahmadi-Nedushan, B. Optimal design of double-layer barrel vaults using genetic and pattern search algorithms and optimized neural network as surrogate model. Front. Struct. Civ. Eng. 2023, 17, 378–395. [Google Scholar] [CrossRef]
- Zhi, P.; Wu, Y.C.; Qi, C.; Zhu, T.; Wu, X.; Wu, H.Y. Surrogate-based physics-informed neural networks for elliptic partial differential equations. Mathematics 2023, 11, 2723. [Google Scholar] [CrossRef]
- Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J. Comput. Phys. 2018, 378, 686–707. [Google Scholar] [CrossRef]
- Raissi, M.; Yazdani, A.; Karniadakis, G.E. Hidden fluid mechanics: Learning velocity and pressure fields from flow visual-izations. Science 2020, 367, 1026–1030. [Google Scholar] [CrossRef] [PubMed]
- Pang, G.; D’elia, M.; Parks, M. nPINNs: Nonlocal physics-informed neural networks for a parametrized nonlocal universal Laplacian operator. Algorithms and applications. J. Comput. Phys. 2020, 422, 109760. [Google Scholar] [CrossRef]
- Yang, L.; Meng, X.; Karniadakis, G.E. B-PINNs: Bayesian physics-informed neural networks for forward and inverse PDE problems with noisy data. J. Comput. Phys. 2021, 425, 109913. [Google Scholar] [CrossRef]
- Cui, T.; Fox, C.; O’Sullivan, M.J. Bayesian calibration of a large-scale geothermal reservoir model by a new adaptive delayed acceptance Metropolis Hastings algorithm. Water Resour. Res. 2011, 47, W10521. [Google Scholar] [CrossRef]
- Jagtap, A.D.; Karniadakis, G.E. Extended physics-informed neural networks (XPINNs): A generalized space-time domain decomposition based deep learning framework for nonlinear partial differential equations. Commun. Comput. Phys. 2021, 28, 2002–2041. [Google Scholar] [CrossRef]
- Leung, W.T.; Lin, G.; Zhang, Z. NH-PINN: Neural homogenization-based physics-informed neural network for multiscale problems. J. Comput. Phys. 2022, 470, 111539. [Google Scholar] [CrossRef]
- Chandrasegaran, S.K.; Ramani, K.; Sriram, R.D. The evolution, challenges, and future of knowledge representation in product design systems. Comput.-Aided Des. 2013, 45, 204–228. [Google Scholar] [CrossRef]
- Fang, J.; Sun, G.; Qiu, N. On design optimization for structural crashworthiness and its state of the art. Struct. Multidiscip. Optim. 2017, 55, 1091–1119. [Google Scholar] [CrossRef]
- Bhosekar, A.; Ierapetritou, M. Advances in surrogate based modeling, feasibility analysis, and optimization: A review. Comput. Chem. Eng. 2018, 108, 250–267. [Google Scholar] [CrossRef]
- Schmidt, J.; Marques, M.R.G.; Botti, S. Recent advances and applications of machine learning in solid-state materials science. Comput. Mater. 2019, 5, 83. [Google Scholar] [CrossRef]
- Abueidda, D.W.; Almasri, M.; Ammourah, R. Prediction and optimization of mechanical properties of composites using convolutional neural networks. Compos. Struct. 2019, 227, 111264. [Google Scholar] [CrossRef]
- Niekamp, R.; Niemann, J.; Schröder, J. A surrogate model for the prediction of permeabilities and flow through porous media: A machine learning approach based on stochastic Brownian motion. Comput. Mech. 2023, 71, 563–581. [Google Scholar] [CrossRef]
- Gholizadeh, S.; Seyedpoor, S.M. Shape optimization of arch dams by metaheuristics and neural networks for frequency constraints. Sci. Iran. 2011, 18, 1020–1027. [Google Scholar] [CrossRef]
- Gholizadeh, S. Performance-based optimum seismic design of steel structures by a modified firefly algorithm and a new neural network. Adv. Eng. Softw. 2015, 81, 50–65. [Google Scholar] [CrossRef]
- Ranković, V.; Novaković, A.; Grujović, N. Predicting piezometric water level in dams via artificial neural networks. Neural Comput. Appl. 2014, 24, 1115–1121. [Google Scholar] [CrossRef]
- Liang, L.; Liu, M.; Martin, C. A deep learning approach to estimate stress distribution: A fast and accurate surrogate of finite-element analysis. J. R. Soc. Interface 2018, 15, 20170844. [Google Scholar] [CrossRef]
- Oishi, A.; Yagawa, G. Computational mechanics enhanced by deep learning. Comput. Methods Appl. Mech. Eng. 2017, 327, 327–351. [Google Scholar] [CrossRef]
- Kennedy, J.; Abdalla, H. Static response of prestressed girders with openings. J. Struct. Div. Amesican Sociaty Civ. Eng. 1992, 118, 488–504. [Google Scholar] [CrossRef]
- Abdalla, H.; Kennedy, J. Design against cracking at openings in prestressed concrete beams. J. Prestress. Concr. 1995, 40, 60–75. [Google Scholar] [CrossRef]
- Abdalla, H.; Kennedy, J.; Fellow, A. Design of prestressed concrete beams with openings. J. Struct. Eng. 1995, 121, 890–898. [Google Scholar] [CrossRef]
- Cai, J.; Wang, Y.; Chen, Q. Calculation of shear capacity of reinforced concrete simply supported beam with abdominal openings. J. Archit. Struct. 2014, 35, 149–155. (In Chinese) [Google Scholar]
- Huang, D.; Hou, L.; Cai, J. Experimental study on columns of large steel structure factory buildings with abdominal openings. Ind. Archit. 2012, 42, 128–132. (In Chinese) [Google Scholar]

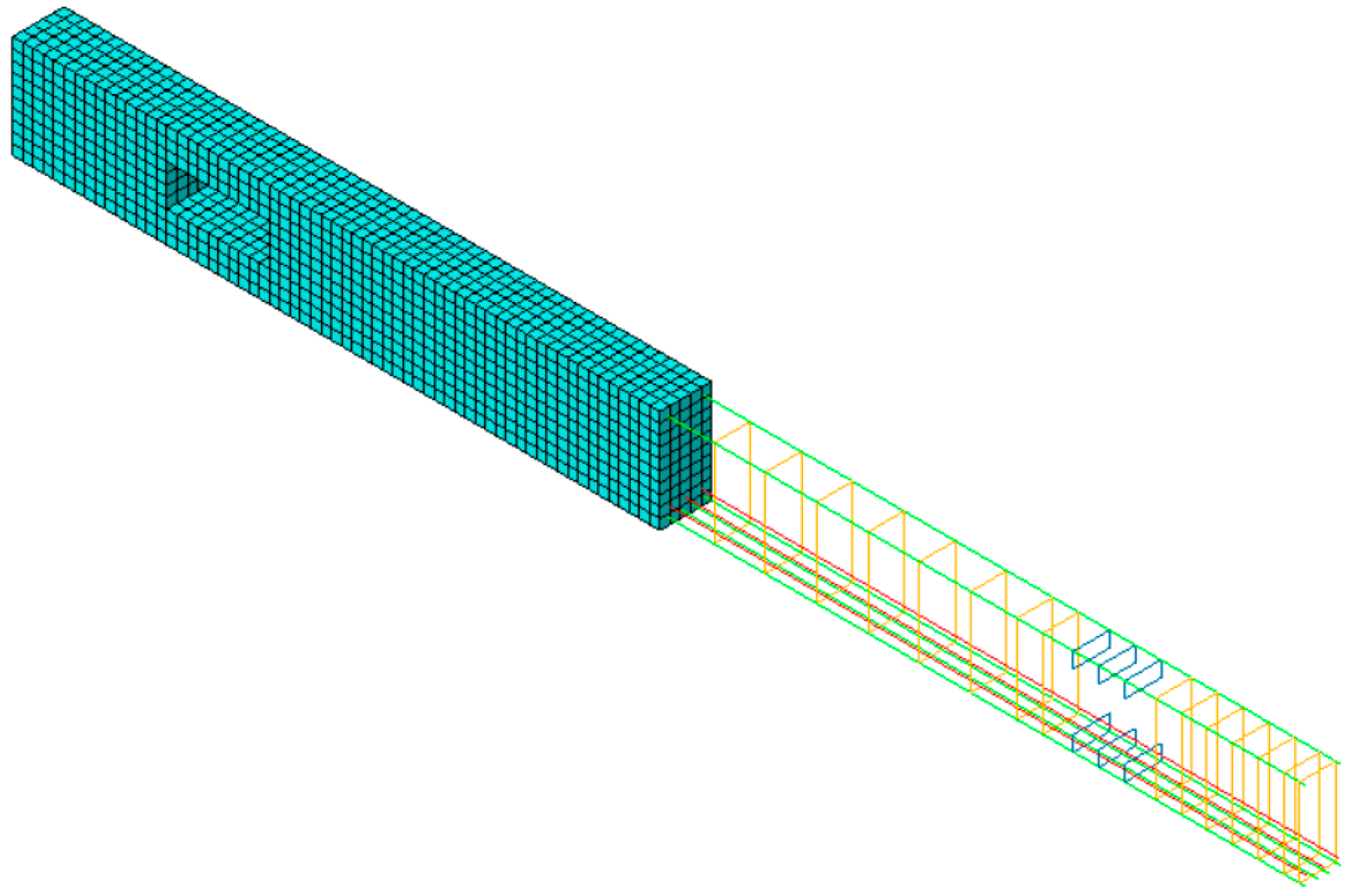





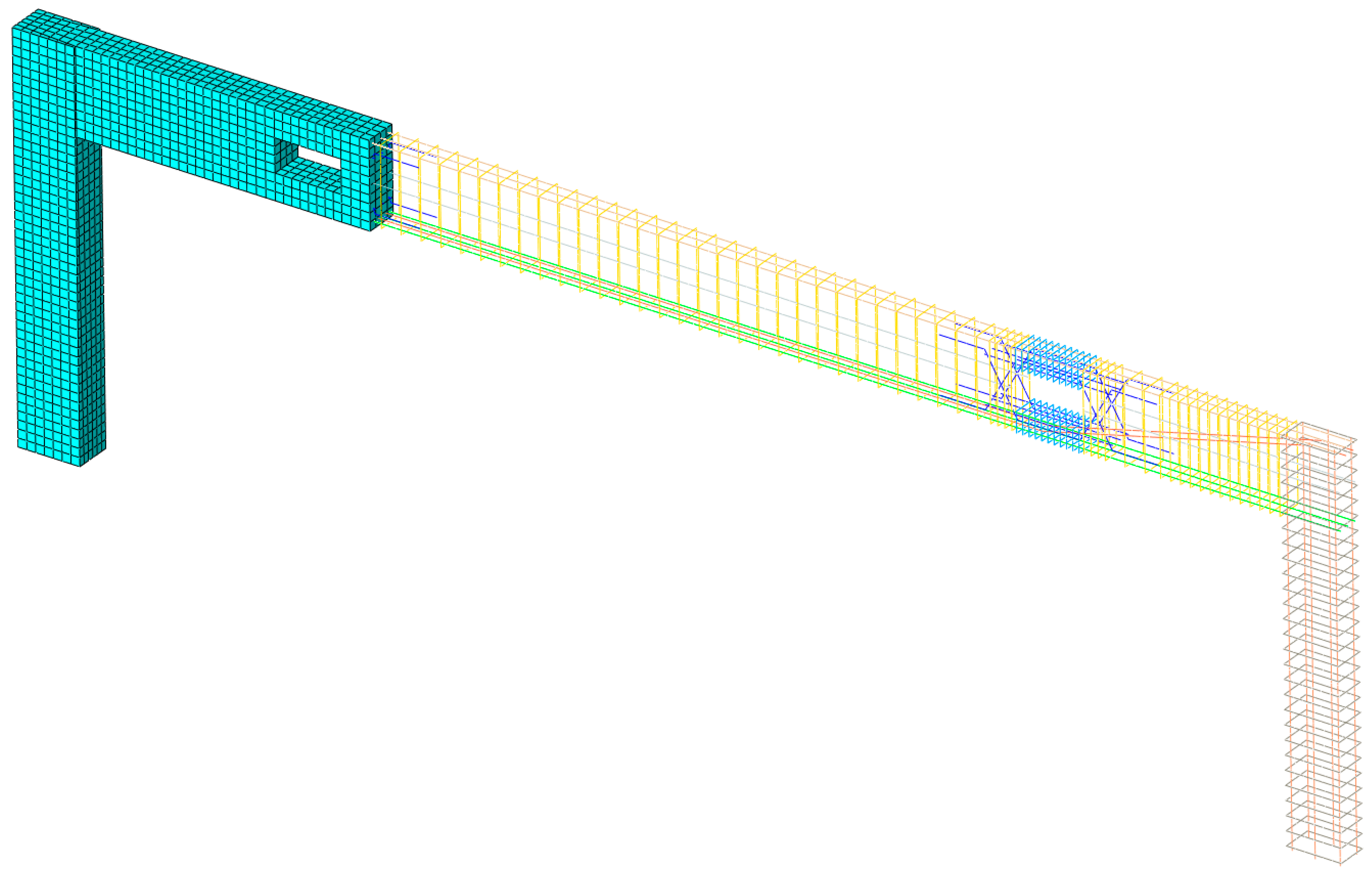



| Element Style | Number of Elements | Number of Nodes | |
|---|---|---|---|
| Concrete | C3D8R | 5850 | 7992 |
| Longitudinal bar | T3D2 | 750 | 756 |
| Prestressed bar | T3D2 | 375 | 378 |
| Beam stirrup | T3D2 | 806 | 806 |
| Chord stirrup | T3D2 | 144 | 144 |
| Total | - | 7925 | 10,076 |
| Element Style | Number of Elements | Number of Nodes | |
|---|---|---|---|
| Concrete | C3D8R | 9208 | 12,699 |
| Prestress bar | T3D2 | 316 | 318 |
| Beam longitudinal bar | T3D2 | 465 | 468 |
| Twisted bar in beam | T3D2 | 276 | 282 |
| Beam stirrup | T3D2 | 1848 | 1848 |
| Beam chord stirrup | T3D2 | 440 | 440 |
| Beam suspension bar | T3D2 | 264 | 264 |
| Beam reinforcement bars | T3D2 | 180 | 192 |
| Column longitudinal bar | T3D2 | 552 | 564 |
| Column stirrup | T3D2 | 1120 | 1120 |
| Total | - | 15,134 | 18,663 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, Y.; Chen, J.; Zhu, P.; Zhi, P. Finite Element Analysis of Perforated Prestressed Concrete Frame Enhanced by Artificial Neural Networks. Buildings 2024, 14, 3215. https://doi.org/10.3390/buildings14103215
Wu Y, Chen J, Zhu P, Zhi P. Finite Element Analysis of Perforated Prestressed Concrete Frame Enhanced by Artificial Neural Networks. Buildings. 2024; 14(10):3215. https://doi.org/10.3390/buildings14103215
Chicago/Turabian StyleWu, Yuching, Jingbin Chen, Peng Zhu, and Peng Zhi. 2024. "Finite Element Analysis of Perforated Prestressed Concrete Frame Enhanced by Artificial Neural Networks" Buildings 14, no. 10: 3215. https://doi.org/10.3390/buildings14103215
APA StyleWu, Y., Chen, J., Zhu, P., & Zhi, P. (2024). Finite Element Analysis of Perforated Prestressed Concrete Frame Enhanced by Artificial Neural Networks. Buildings, 14(10), 3215. https://doi.org/10.3390/buildings14103215







