Rib Alignment Control of Long-Span Arch Bridge in Cable-Stayed Buckle by Multi-Objective Optimization
Abstract
1. Introduction
2. Method and Theory of Cable-Stayed Buckle
2.1. General Solution of Initial Cable Tension and Hoisting Cable Force
2.2. Arch Rib Alignment Control Method Based on Multi-Objective Optimization
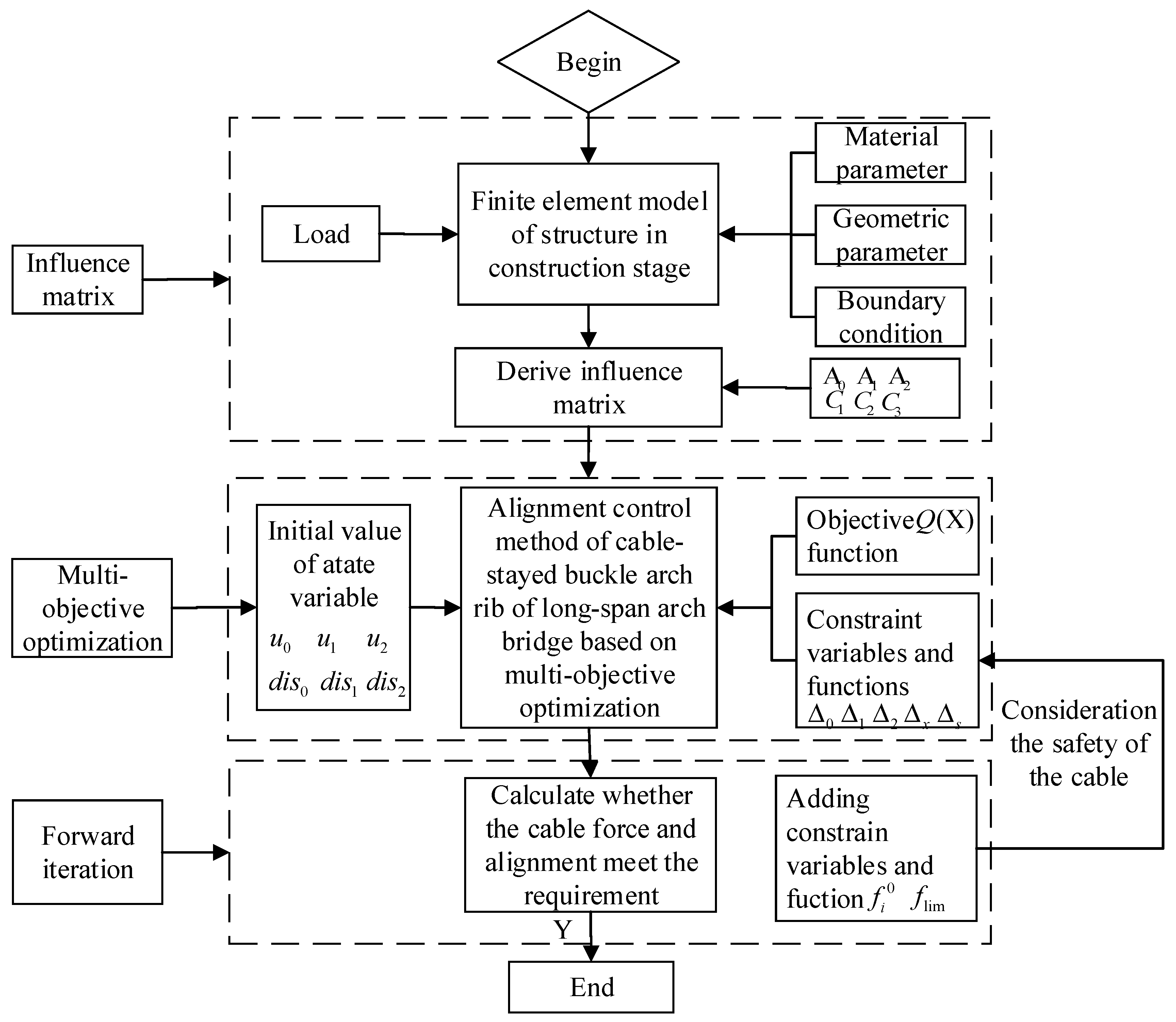
3. Calculation Steps of Arch Rib Alignment Control Based on Multi-Objective Optimization
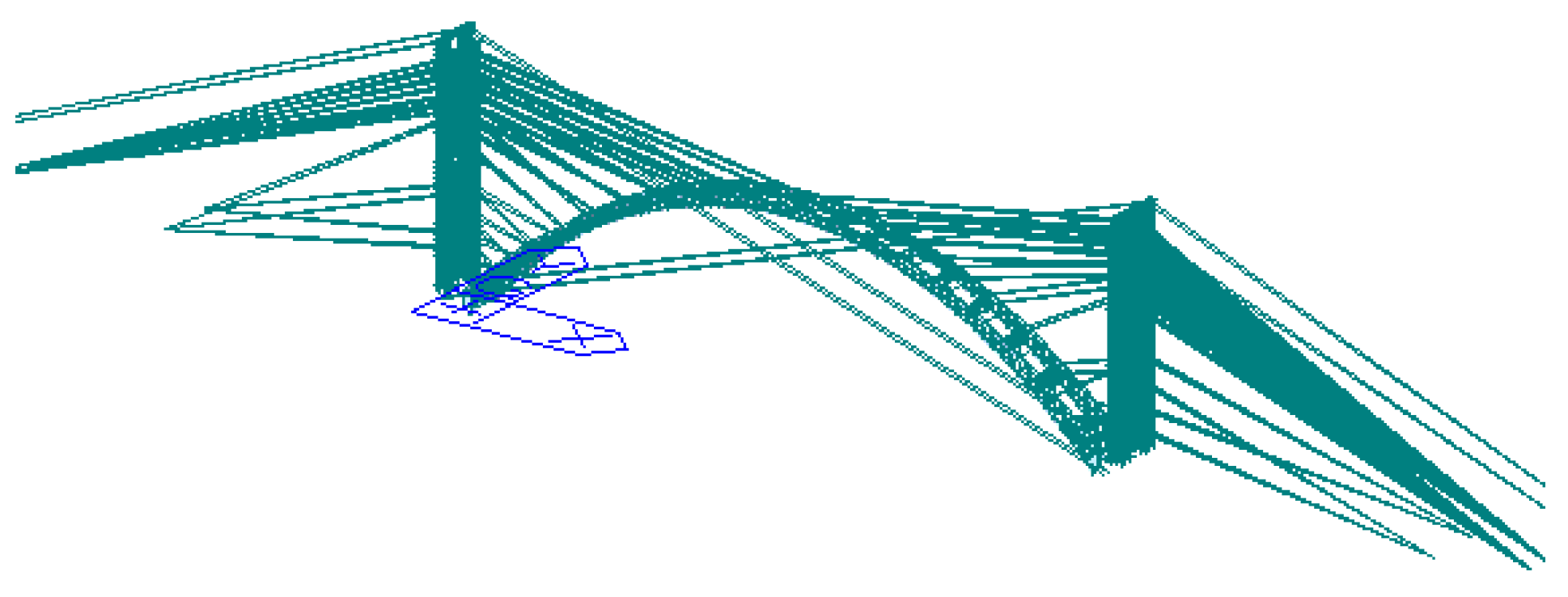
4. Engineering Applications
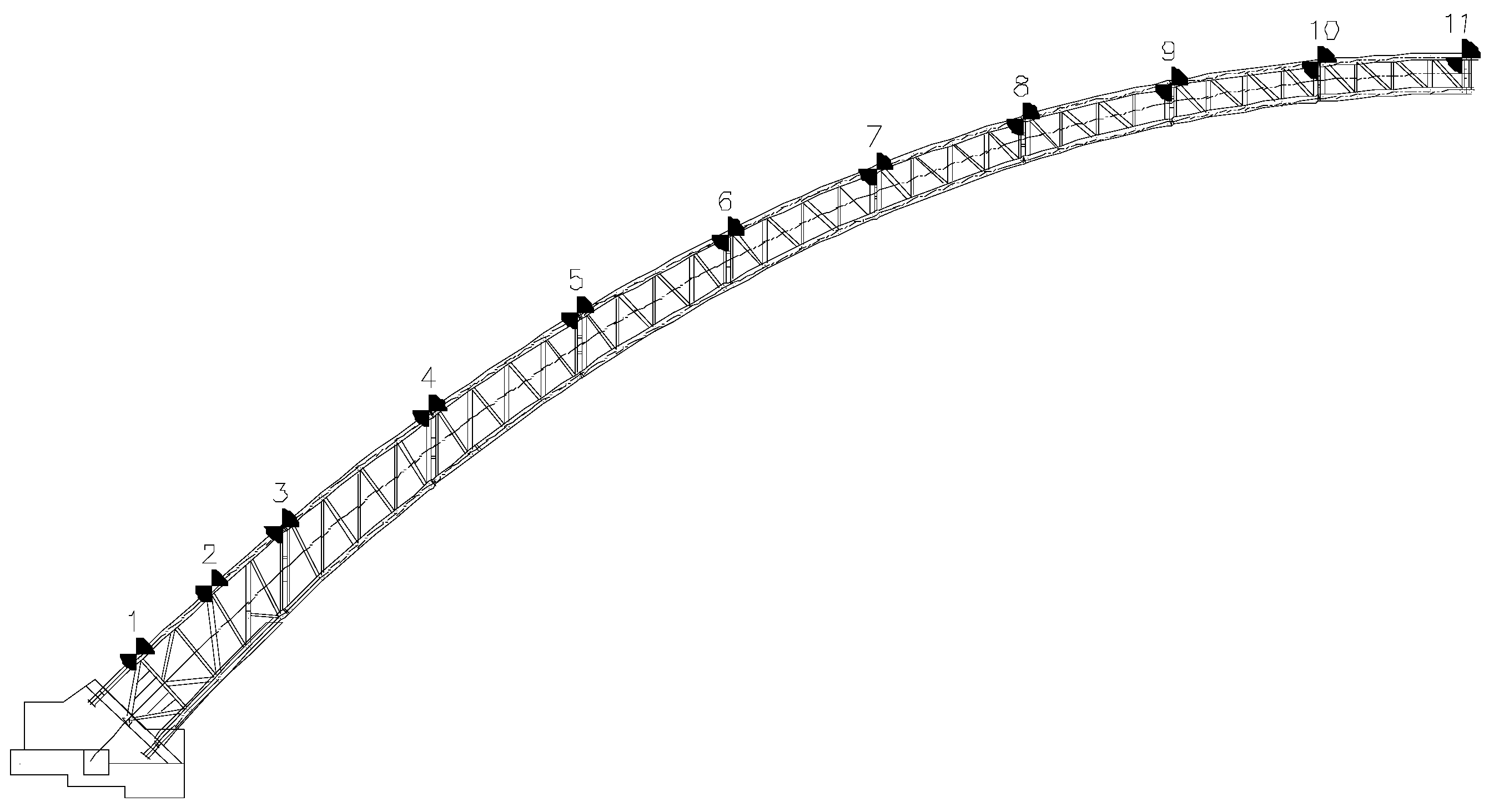
4.1. Engineering Overview and Calculation Model Acquisition
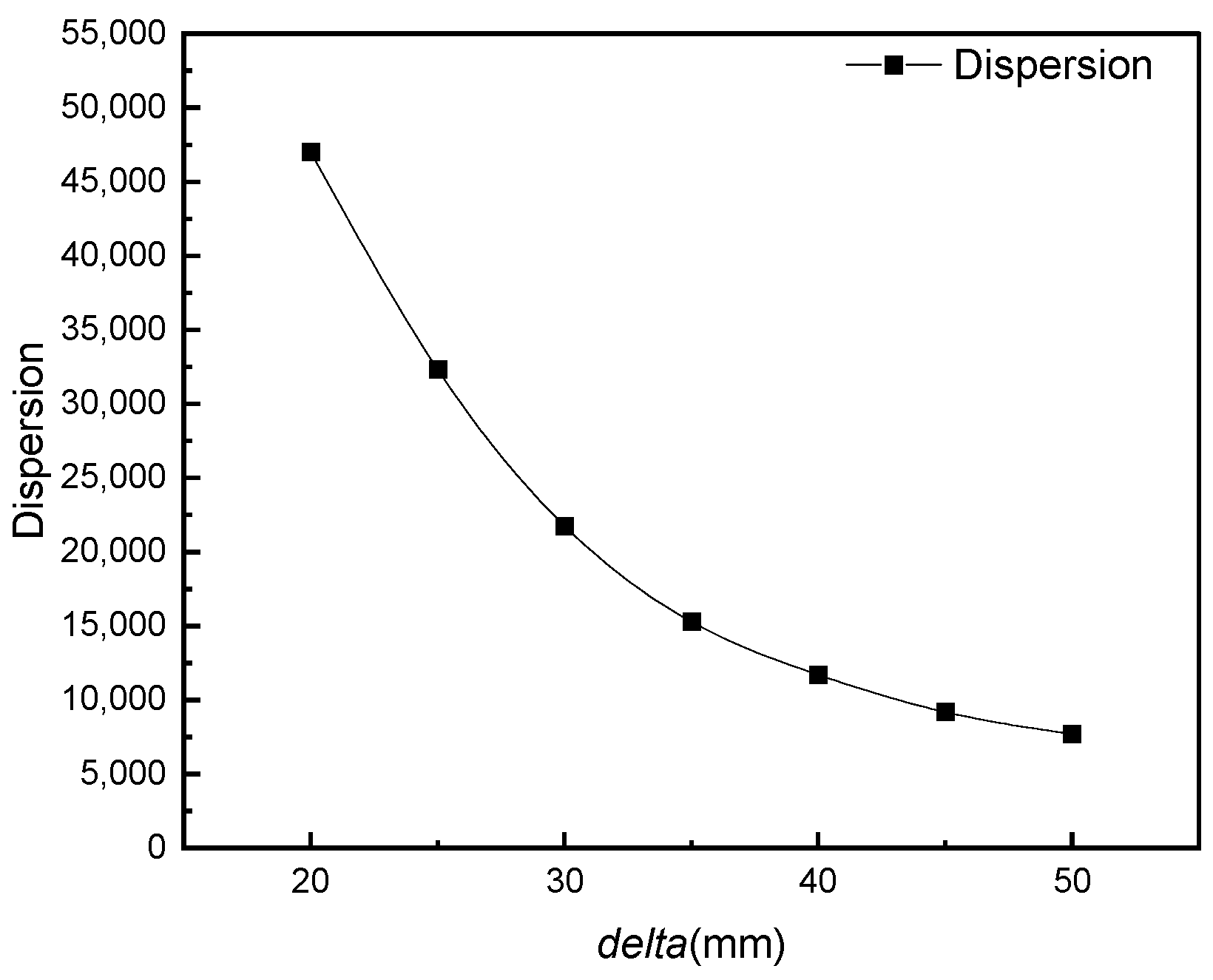
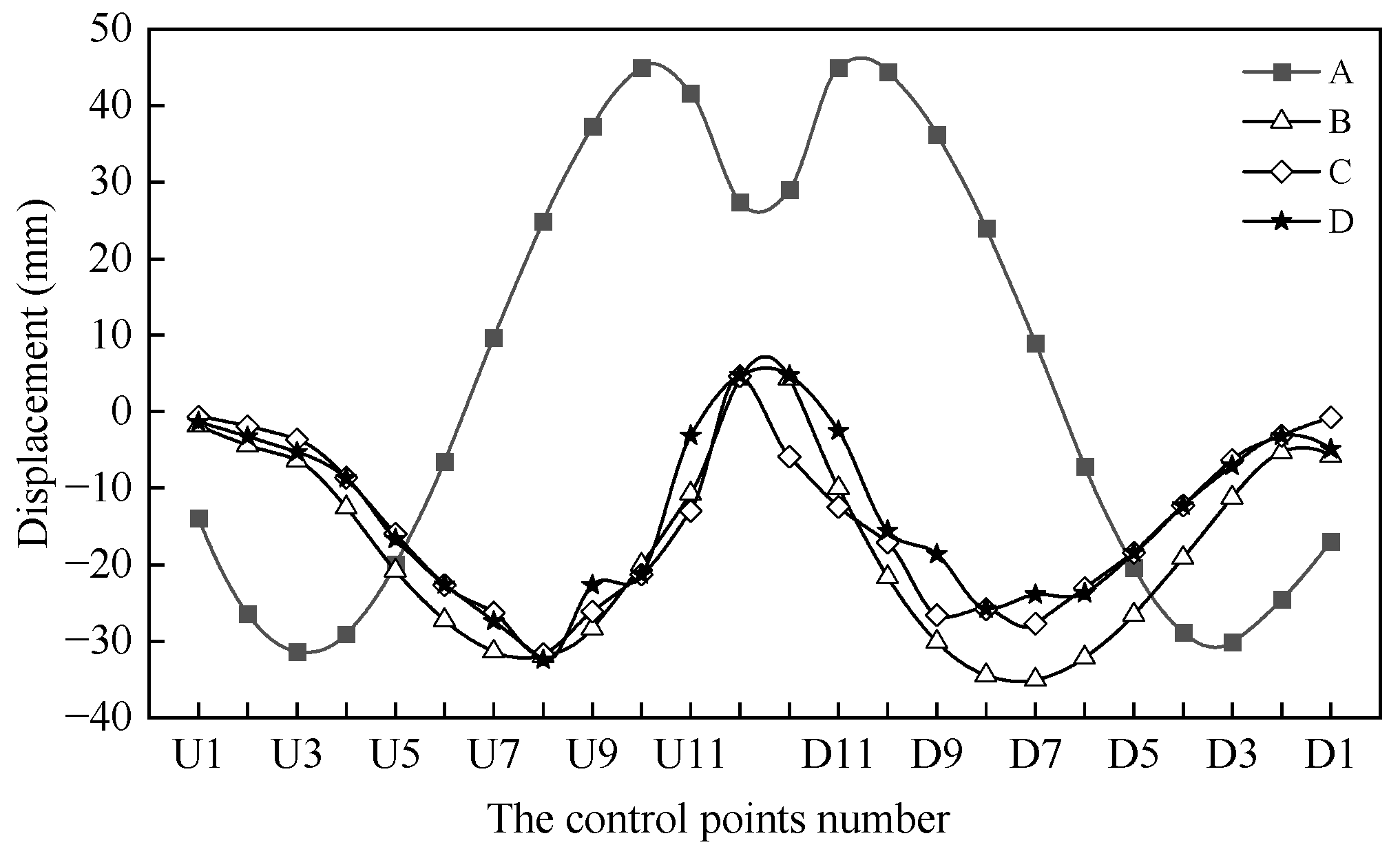
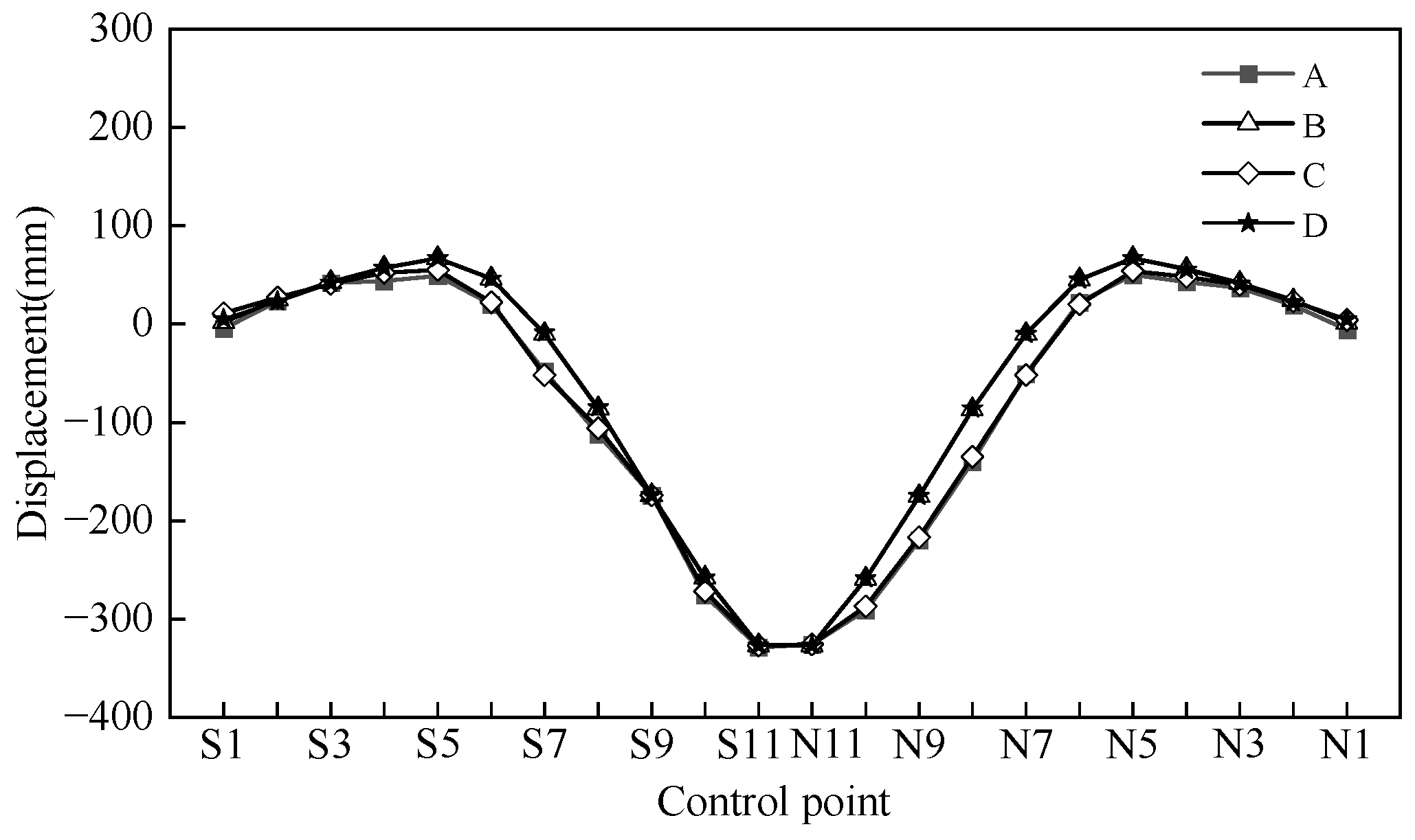
4.2. Results of Arch Rib Alignment Based on Multi-Objective Optimization
4.3. Solution Results
4.4. In Situ Measurement Comparison
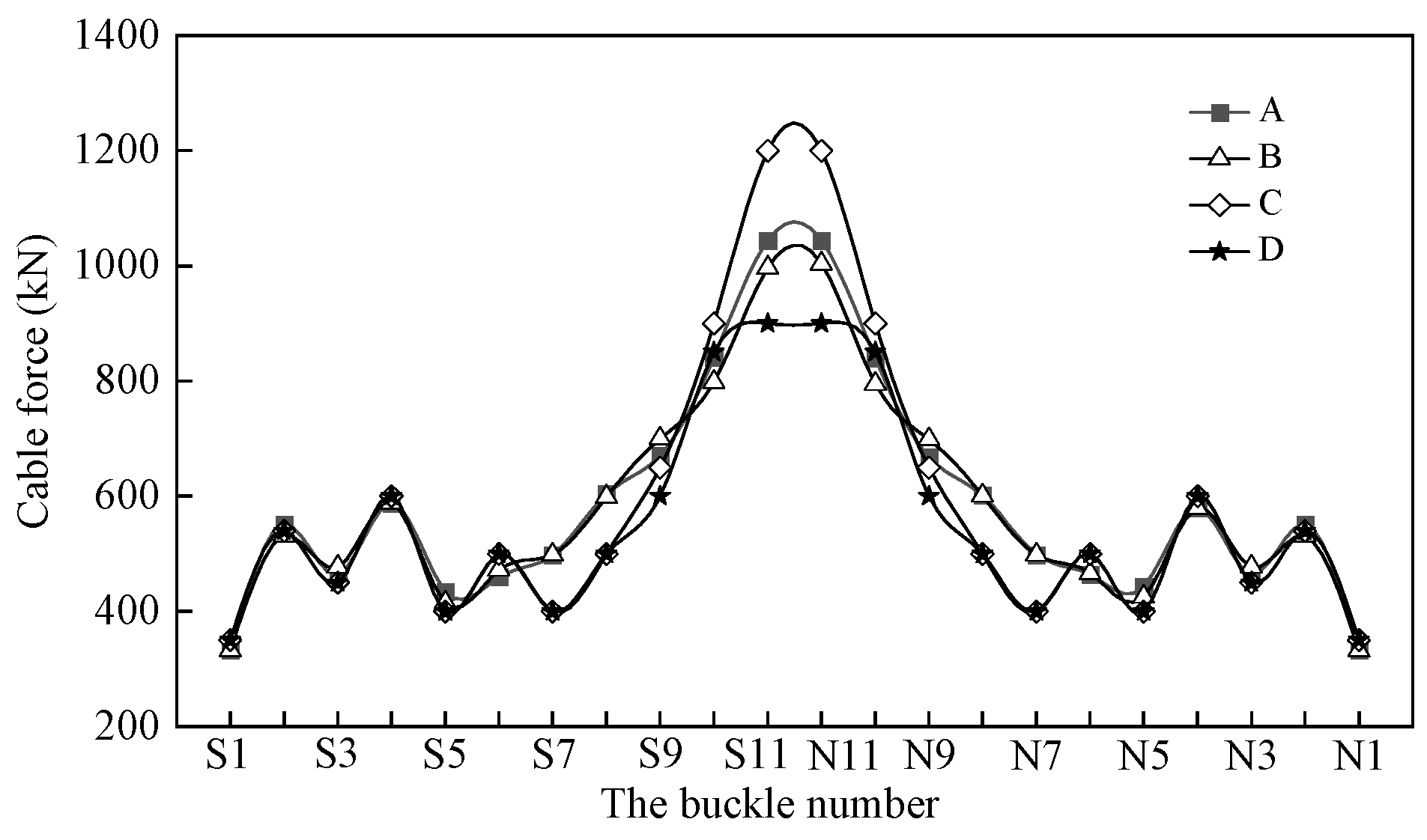
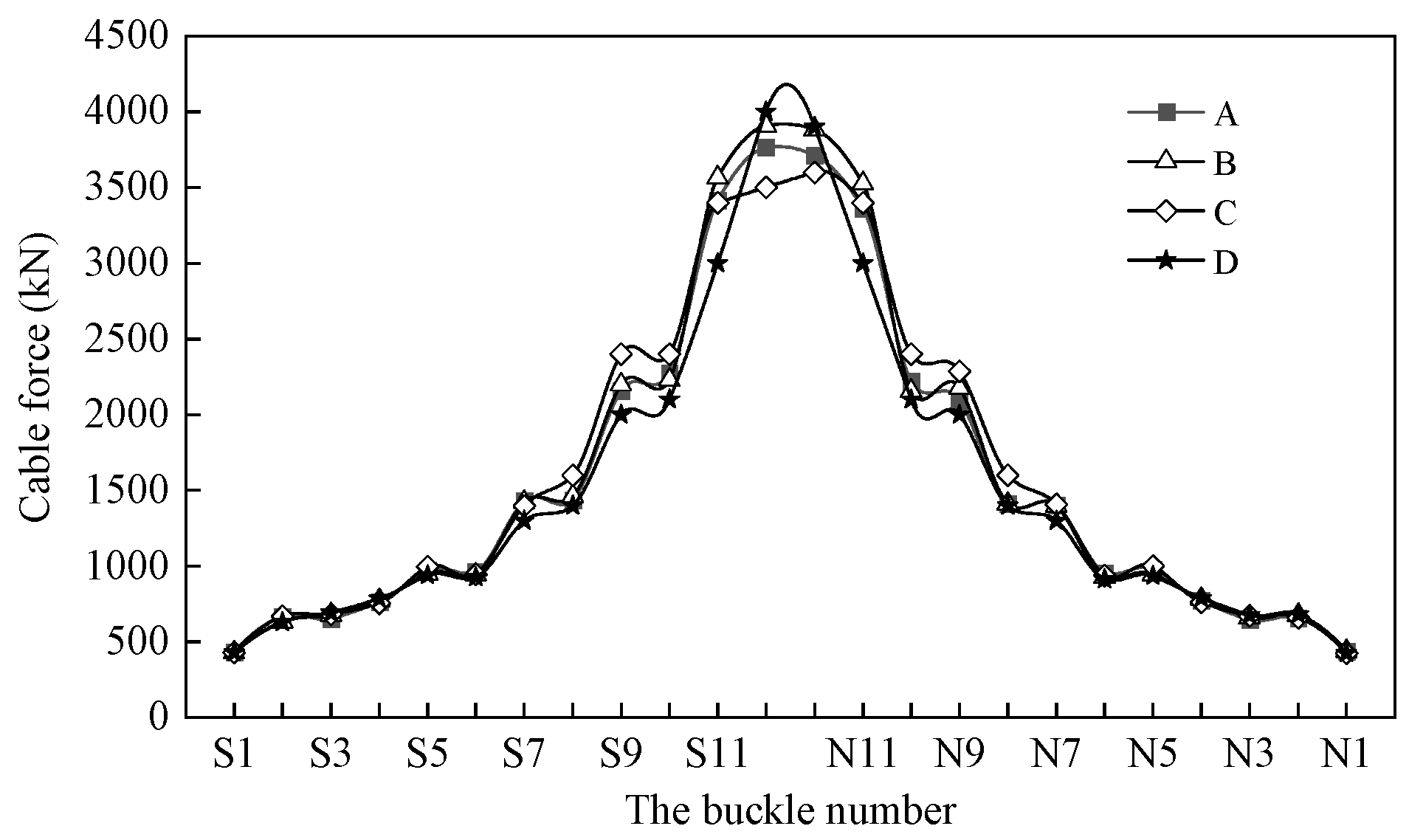
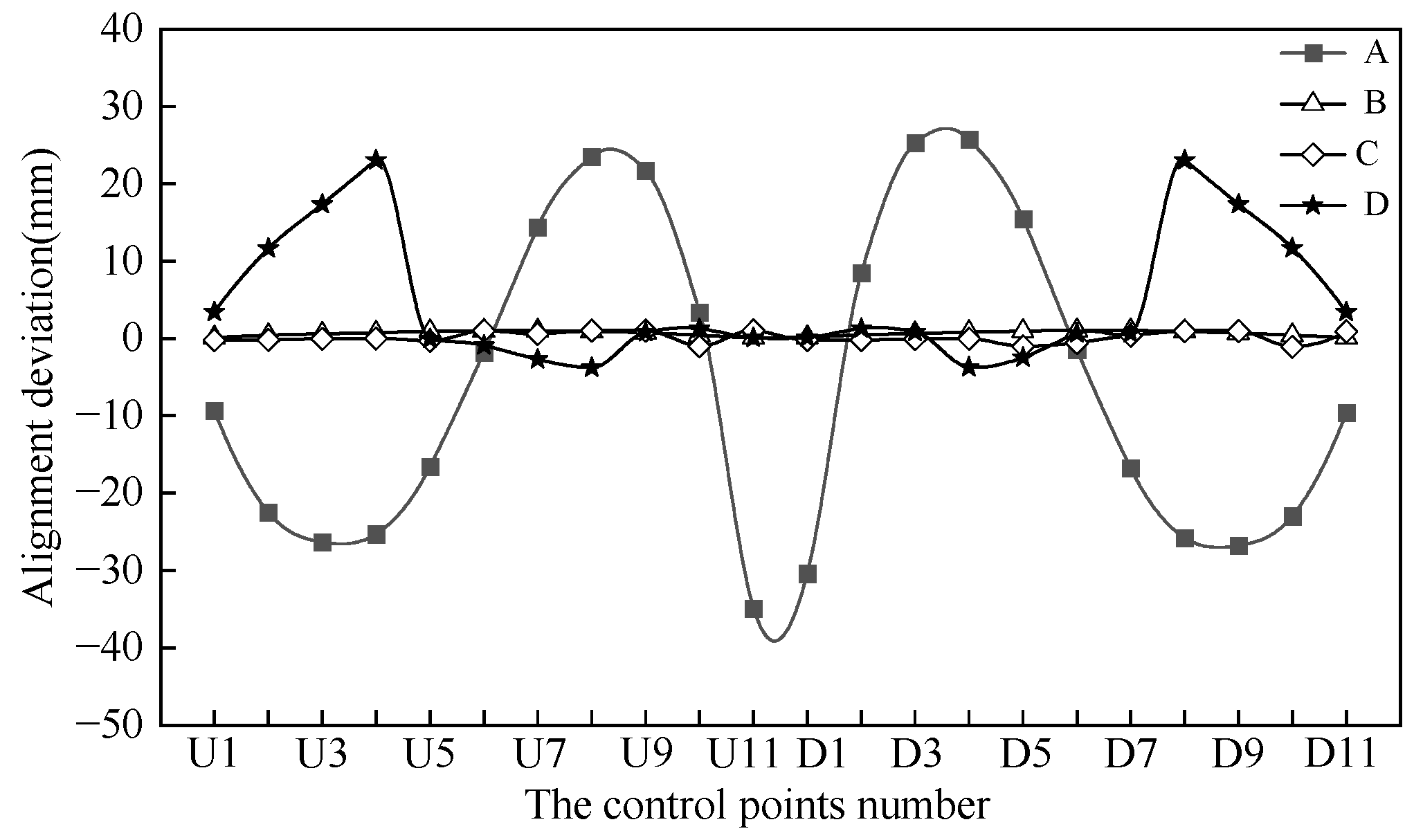
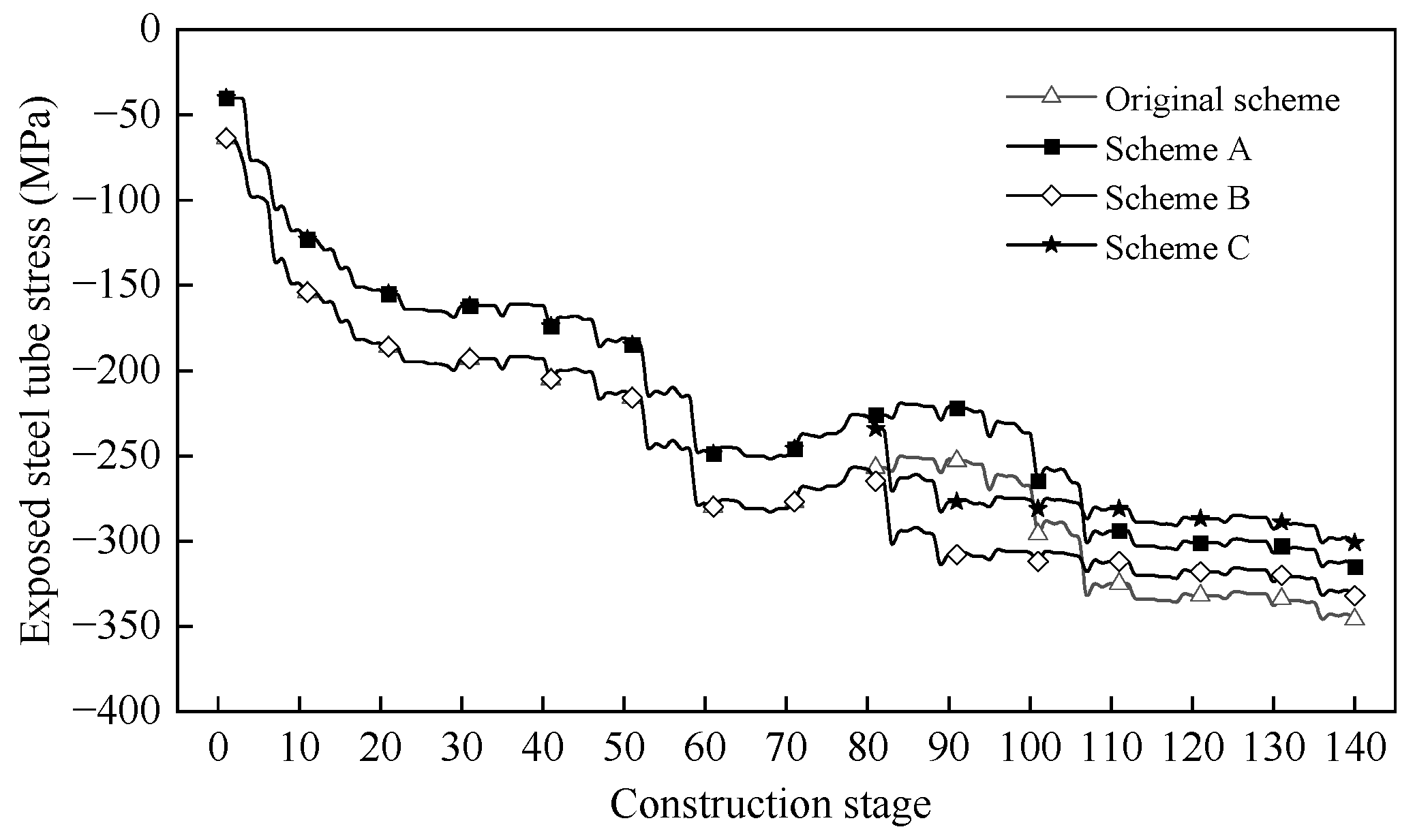
5. Comparative Analysis of Each Optimization Scheme
6. Conclusions
- (1)
- The multi-objective cable force optimization method is an efficient and convenient approach for iterative calculation and engineering applications. It can analyze the relationship between delta and optimization dispersion to determine the difference between actual and target displacement after cable closure under the action of the bare arch.
- (2)
- In constructing cable-stayed buckle long-span arch bridges, arch rib alignment, cable force uniformity, and safety are considered comprehensively. Optimizing the alignment of cable force during construction ensures that the cable force is uniform and meets specification requirements, effectively overcoming the traditional manual cable adjustment and cable force inhomogeneity issues.
- (3)
- The alignment deviation in the construction process could affect the cable force. Still, the multi-objective cable force optimization method can ensure precision during arch segment installation, and the arch/bridge completion states meet specification requirements.
- (4)
- The control cross-sectional stress of exposed steel tube in rigid skeleton arch bridge is related to the installation method and the concrete casting scheme. To achieve a good stress control effect, selecting the appropriate construction scheme to reduce construction risk is necessary.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhao, R.; Zhang, Z. A Summary of Development of Concrete-Filled Steel Tube Framed Arch Bridges in China. Bridge Constr. 2016, 46, 45–50. [Google Scholar]
- Fan, Y.; Xin, J.; Yang, L. Optimization method for the length of the outsourcing concrete working plane on the main arch rib of a rigid-frame arch bridge based on the NSGA-II algorithm. Structures 2024, 59, 105767. [Google Scholar] [CrossRef]
- Tao, T.; Wang, H. Simulation of multivariate ergodic stochastic processes using adaptive spectral sampling and non-uniform fast Fourier transform. Probabilistic Eng. Mech. 2024, 77, 103669. [Google Scholar] [CrossRef]
- Tao, T.; Wang, H. Efficient buffeting analysis of long-span bridges under non-stationary winds: A 2D interpolation enhanced approach. J. Sound Vib. 2023, 559, 117754. [Google Scholar] [CrossRef]
- Yao, X.; Li, C.; Wang, L.; Yu, M.; Zhuo, X.; Hao, T.; Wang, X. A Practical Approach to Alignment and Error Feedback Control for Long-Span Arch Bridges. Buildings 2024, 14, 1995. [Google Scholar] [CrossRef]
- Zhou, Q.; Feng, P.; Zhou, J.; Xin, J.; Wang, J. Analysis of concrete emptying in concrete-filled steel tube arch bridge under uneven temperature field. J. Bridge Constr. 2024, 54, 103–109. [Google Scholar] [CrossRef]
- Mou, T.; Fan, B.; Zhao, Y.; Li, S. Application and Development of Steel Pipe Concrete Bridges in China. Highway 2017, 62, 161–165. [Google Scholar]
- Zhou, Y.; Wang, Y.; Zhou, J. Arch calculation and control method of 500 m class steel pipe arch bridge. China Highw. 2022, 35, 60–72. [Google Scholar] [CrossRef]
- Li, Y.; Li, Y.; Li, J. The calculation method of the whole process cable force optimization of the long-span concrete-filled steel tube arch bridge constructed by cable-stayed suspension method. Prog. Build. Steel Struct. 2019, 21, 33–39. [Google Scholar] [CrossRef]
- Xie, K.; Wang, H.; Guo, X.; Zhou, J. Study on the safety of the concrete pouring process for the main truss arch structure in a long-span concrete-filled steel tube arch bridge. Mech. Adv. Mater. Struct. 2021, 28, 731–740. [Google Scholar] [CrossRef]
- Xu, Y.; Shen, C.; Zhu, Y.; Wang, C. Improved Iteration Algorithm for Determination of Tension of Fastening Stays for Cantilever Construction of Arch Bridge. Bridge Constr. 2016, 46, 65–69. [Google Scholar]
- Zhang, J.; Zheng, J.; Xiao, R. Optimization Calculation and Analysis of Concrete Filled Steel Tube Arch Bridge Hoisting Process. China J. Highw. Transp. 2005, 2, 40–44. [Google Scholar] [CrossRef]
- Zhen, J.; Wang, J.; Feng, Z.; Han, Y.; Qin, D. Test on vacuum auxiliary filling technology of concrete-filled steel tube arch section. China Highw. J. 2014, 27, 44–50. [Google Scholar] [CrossRef]
- Han, Y. Test and application of vacuum assisted filling of concrete in tubular arch bridge. Bridge Constr. 2015, 45, 19–25. [Google Scholar]
- Zhou, D.; Deng, N.; Shi, T. Test and numerical simulation analysis of large scale hydration temperature field of concrete-filled steel tube arch bridge. J. Guangxi Univ. 2021, 46, 51–59. [Google Scholar] [CrossRef]
- Sun, J.; Xie, J. Simulation analysis of the hydration heat of large diameter CFST arch and its effects on loading age. Appl. Therm. Eng. 2019, 150, 482–491. [Google Scholar] [CrossRef]
- Zhou, Q.; Zhou, J.; Zhang, J.; Zhang, L. Self-regulating loading pouring method of long span CFST arch bridge. J. Harbin Inst. Technol. 2020, 52, 82–89. [Google Scholar] [CrossRef]
- Zheng, J.; Wang, J. Chinese steel tube concrete arch bridge. Engineering 2018, 4, 306–331. [Google Scholar] [CrossRef]
- Qin, D.; Zheng, J.; Du, H.; Han, Y.; Zheng, J.; Wei, L. Optimization Calculation Method for Stayed-Buckle Cable Force under One-Time Tension by Fastening Stay Method and Its Application. China Railw. Sci. 2020, 41, 52–60. [Google Scholar]
- Han, Y.; Qin, D.; Zheng, J. Optimization calculation method for CFST arch bridge cable-stayed suspension construction. Highway 2018, 63, 100–104. [Google Scholar]
- Zhou, J.; Liu, J.; Zhou, W.; Yan, R.; Yan, T. Analysis of the influence of temperature changes on the pre lifting value of cable-stayed buckle and the main arch ring shape of steel tube concrete arch bridges. J. China Foreign Highw. 2017, 37, 62–66. [Google Scholar] [CrossRef]
- Chen, B.; Wei, J.; Zhou, J.; Liu, J.P. Application of concrete-filled steel tube arch bridges in China: Current status and prospects. China Civ. Eng. J. 2017, 50, 50. [Google Scholar]
- Yu, M.; Deng, N.; Wang, L.; Hao, T.; Zhang, Z. Study on Sunshine Temperature Effect in Concrete-filled Steel Tubes Arch Rib of Extra-Large Arch Bridge. Highw. Eng. 2021, 46, 99–104. [Google Scholar] [CrossRef]
- Liu, X.; Zhou, G.; Qiu, Y. Optimal Polynomial Time-varying Parameters Discrete Grey Model and Its Applications. Stat. Decis. 2022, 38, 31–36. [Google Scholar]
- Li, X.; Wang, C. STI prediction based on metabolic GM (1, 1) Copula BP neural network. Stat. Decis. 2021, 37, 158–161. [Google Scholar] [CrossRef]
- Vasques, J.F.; Gonalves, R.G.D.J.; Silva-Junior, A.J.D.; Martins, R.S.; Gubert, F.; Mendez-Otero, R. Gangliosides in nervous system development, regeneration, and pathologies. Neural Regen. Res. 2023, 18, 81–86. [Google Scholar] [CrossRef]
- Li, C.; Huang, J.; Li, X. Consider the sunshine temperature field of concrete-filled steel tube arch. Sino-Foreign Highw. 2020, 40, 102–107. [Google Scholar]




| Segment | The Target Displacement After Cable Closure | The Actual Displacement After Cable Closure | The Actual Displacement of the Current Tension Segment | The Actual Displacement of the Current Transverse Brace Segment | Relative Error of Actual Displacement to Target |
|---|---|---|---|---|---|
| 1 | −5 | −14 | 0 | −11 | −9 |
| 2 | −15 | −38 | 8 | −32 | −23 |
| 3 | −23 | −49 | 9 | −44 | −26 |
| 4 | −33 | −58 | 106 | −54 | −25 |
| 5 | −54 | −71 | −11 | −80 | −17 |
| 6 | −77 | −79 | 25 | −87 | −2 |
| 7 | −100 | −86 | −97 | −180 | 14 |
| 8 | −119 | −95 | −51 | −207 | 24 |
| 9 | −137 | −115 | −191 | −292 | 22 |
| 10 | −152 | −149 | −84 | −353 | 3 |
| 11 | −162 | −197 | −322 | −329 | −35 |
| Segment | The Target Displacement After Cable Closure | The Actual Displacement After Cable Closure | The Actual Displacement of the Current Tension Segment | The Actual Displacement of the Current Transverse Brace Segment | Percentage of Error Between Actual Displacement and Target Displacement |
|---|---|---|---|---|---|
| 1 | −6 | −20 | −5 | −15 | −14 |
| 2 | −14 | −41 | −14 | −35 | −27 |
| 3 | −28 | −59 | −31 | −53 | −31 |
| 4 | −56 | −85 | −59 | −69 | −29 |
| 5 | −98 | −118 | −105 | −152 | −20 |
| 6 | −150 | −156 | −156 | −180 | −6 |
| 7 | −208 | −199 | −216 | −302 | 9 |
| 8 | −270 | −245 | −277 | −347 | 25 |
| 9 | −333 | −295 | −339 | −434 | 38 |
| 10 | −384 | −339 | −388 | −490 | 45 |
| 11 | −415 | −374 | −417 | −464 | 41 |
| 12 | −423 | −395 | −420 | −506 | 28 |
| Stage | Construction Stage Content |
|---|---|
| CS1 | Install 12 segment rigid skeleton |
| CS2-CS6 | Install cable closure segment and transverse braces |
| CS7 | Dismantle cable |
| CS8 | Dismantle interim transverse brace |
| CS9-CS24 | Casting and activating concrete in the tube |
| CS25-CS26 | Casting and activating permanent transverse braces |
| CS27-CS62 | Bottom concrete encasement stage |
| CS63-CS68 | Activate bottom stiffness |
| CS69-CS110 | Web concrete encasement stage |
| CS111-CS115 | Activate web stiffness |
| CS115-CS144 | Top plate concrete encasement stage |
| The Optimization Scheme | Optimization Stage | Optimization Content |
|---|---|---|
| A | Rigid skeleton installation stage | Optimize the cable closure scheme |
| B | Concrete encasement casting stage | Optimize the web casting sequence |
| C | Rigid skeleton installation stage Concrete encasement casting stage | Optimize the sequence of cable closure and web casting at the same time |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, M.; Yao, X.; Wang, L.; Hao, T.; Deng, N. Rib Alignment Control of Long-Span Arch Bridge in Cable-Stayed Buckle by Multi-Objective Optimization. Buildings 2024, 14, 3281. https://doi.org/10.3390/buildings14103281
Yu M, Yao X, Wang L, Hao T, Deng N. Rib Alignment Control of Long-Span Arch Bridge in Cable-Stayed Buckle by Multi-Objective Optimization. Buildings. 2024; 14(10):3281. https://doi.org/10.3390/buildings14103281
Chicago/Turabian StyleYu, Mengsheng, Xinyu Yao, Longlin Wang, Tianzhi Hao, and Nianchun Deng. 2024. "Rib Alignment Control of Long-Span Arch Bridge in Cable-Stayed Buckle by Multi-Objective Optimization" Buildings 14, no. 10: 3281. https://doi.org/10.3390/buildings14103281
APA StyleYu, M., Yao, X., Wang, L., Hao, T., & Deng, N. (2024). Rib Alignment Control of Long-Span Arch Bridge in Cable-Stayed Buckle by Multi-Objective Optimization. Buildings, 14(10), 3281. https://doi.org/10.3390/buildings14103281







