Abstract
Modeling and simulation have been extensively used to solve a wide range of problems in structural engineering. However, many simulations require significant computational resources, resulting in exponentially increasing computational time as the spatial and temporal scales of the models increase. This is particularly relevant as the demand for higher fidelity models and simulations increases. Recently, the rapid developments in artificial intelligence technologies, coupled with the wide availability of computational resources and data, have driven the extensive adoption of machine learning techniques to improve the computational accuracy and precision of simulations, which enhances their practicality and potential. In this paper, we present a comprehensive survey of the methodologies and techniques used in this context to solve computationally demanding problems, such as structural system identification, structural design, and prediction applications. Specialized deep neural network algorithms, such as the enhanced probabilistic neural network, have been the subject of numerous articles. However, other machine learning algorithms, including neural dynamic classification and dynamic ensemble learning, have shown significant potential for major advancements in specific applications of structural engineering. Our objective in this paper is to provide a state-of-the-art review of machine learning-based modeling in structural engineering, along with its applications in the following areas: (i) computational mechanics, (ii) structural health monitoring, (iii) structural design and manufacturing, (iv) stress analysis, (v) failure analysis, (vi) material modeling and design, and (vii) optimization problems. We aim to offer a comprehensive overview and provide perspectives on these powerful techniques, which have the potential to become alternatives to conventional modeling methods.
1. Introduction
Machine learning (ML) is a key artificial intelligence technology that has started to impact almost every scientific and engineering field in significant ways [1]. It holds the potential to become a game-changing technology within structural engineering disciplines, using tools such as image recognition [2], multi-object tracking [3], multi-target regression [4], thermal infrared stress identification [5], and engineering stress prediction [6]. The basic assumption regarding ML is that computers are able to detect and quantify complex patterns in data and identify embedded relations between different variables by means of generic algorithms [1,7]. The pattern detection and subsequent relation extraction from the data is achieved even if the underlying physical model is unknown [1]. Furthermore, using automated learning, ML algorithms can keep evolving with a continuous stream of data, which enables continuous improvement [8]. Typically, an ML system comprises three main components: (i) inputs, which include datasets containing images, signals, or features; (ii) the ML algorithm; and (iii) the output [9]. In the context of ML, data and datasets become the main ingredients [7]. In practice, a dataset consists of multiple data points that each characterize an object of the study, while a data point describes a collection of features, either measured or identified. Features are either categorical, ordinal, or numerical [10], and each feature is stored in a vector and counted as a dimension in the feature space. Thus, increasing the number of features increases the dimensionality of the space, which could also improve the accuracy of the algorithm [11]. However, this also complicates the problem and might require the application of dimension-reduction methods to make the problem computationally feasible [1].
ML algorithms can be classified into the following three broad categories:
- Supervised machine learning (SML), including various neural network models [12], support vector machine [13], random forest [14], statistical regression [15], fuzzy classifiers [16], and decision trees [17].
- Unsupervised machine learning (UML), such as different clustering algorithms including competitive learning [18], k-means and hierarchical clustering [19], and deep Boltzmann machine [20].
- Reinforcement machine learning (RML), which encompasses R-learning [21], Q-learning [22], and temporal difference learning [23].
The decision to use a specific ML category depends on the perceived benefits for a given scenario. SML is often chosen when labeled training data is available, allowing the algorithm to learn from input–output pairs in order to make predictions and classifications on new, unseen data [24]. SML is widely used in structural health monitoring applications and material characterization. In contrast, UML is often used when large amounts of unlabeled data are available for the training process. The objective in such cases would be to discover hidden patterns in the data. UML is used for exploratory data analysis, anomaly detection, and clustering data based on similar structures of features [25]. This leads to uncovering insights and aids in dimension reduction. RML is the least commonly used category of ML algorithms in structural engineering. RML uses an agent to learn how to make sequential decisions in an environment to maximize a reward signal [26]. This category of ML can be used in structural control applications by learning optimal control algorithms. The main advantage of RML is its ability to optimize actions in dynamic environments and learn complex strategies through interaction with the environment. These methods and their various applications will be elaborated upon in the following subsection.
The remainder of the paper is organized as follows. In the following subsections, we will briefly review the three categories of ML. Then, a section is dedicated to the applications of each category. Section 2 will present applications of SML; Section 3 will present applications of UML, while applications of RML are surveyed in Section 4. Concluding remarks are presented in Section 5.
1.1. Supervised Machine Learning
Currently, SML stands out as a prevalent sub-branch in the field. Typically, it operates on the principle of learning by example. The term “supervised” stems from the concept that these algorithms undergo training with oversight, akin to having a guiding instructor overseeing the process [27]. During the training phase, input data is paired with predetermined outputs [28]. The algorithm then scrutinizes the data to identify patterns linking the inputs to the outputs. Post-training, the algorithm can process new, unseen inputs and forecast the corresponding outputs based on the identified patterns [29]. Fundamentally, an SML algorithm can be expressed succinctly as follows [30]:
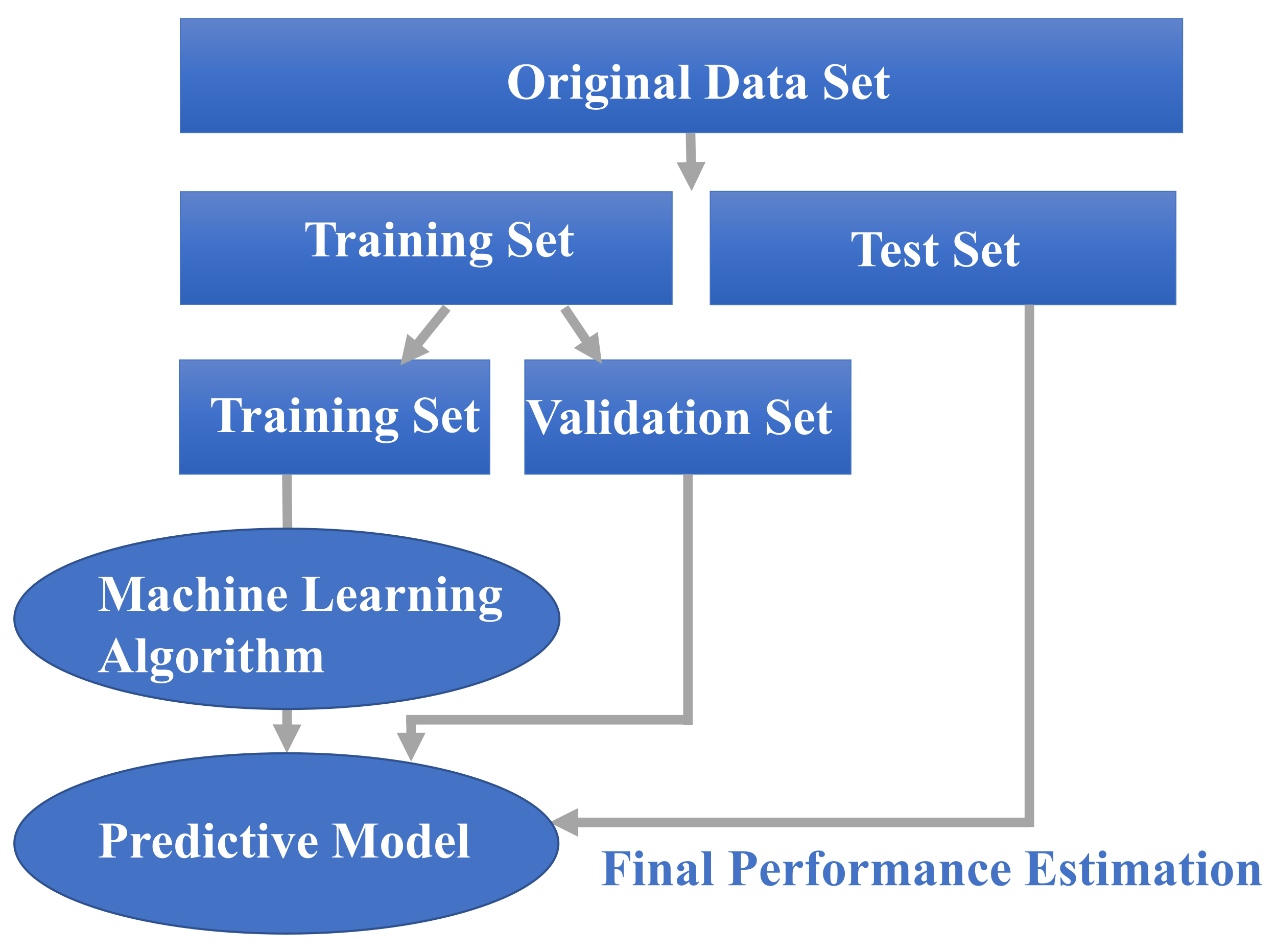
where y represents the predicted output, which is determined by a mapping function assigning a class to an input value x. This function, linking input features to predicted outputs, is generated by the ML model through its training process [31]. Most SML models are trained and evaluated using the same basic process [32], as shown in Figure 1. Note that in the workflow shown in Figure 1, data preparation is one of the most challenging and time-consuming tasks. In this step, all necessary data is collected from various sources, preprocessed, and split into training and test sets [33]. The actual model is built in the next step using various types of SML algorithms. The model is then trained iteratively by feeding it with the training set of data. In each iteration, the model aims to become increasingly accurate by decreasing a predefined error criterion. Training is stopped when a certain number of finite iterations is reached or when predefined stopping criteria are met [34]. In the final step, the trained model is evaluated against the test data to determine its performance and find ways to improve it. It should be noted that the whole process is repeated multiple times until satisfactory results are observed in the model evaluation stage [35].
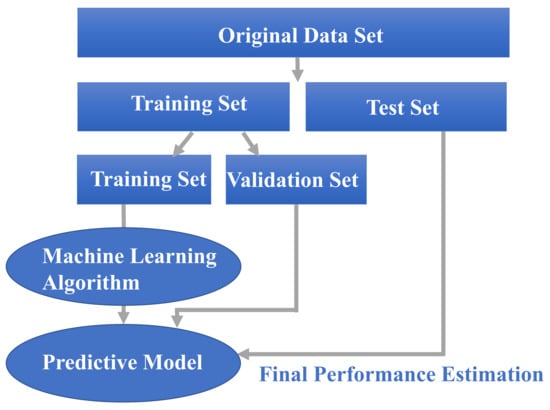
Figure 1.
Schematic of SML process.
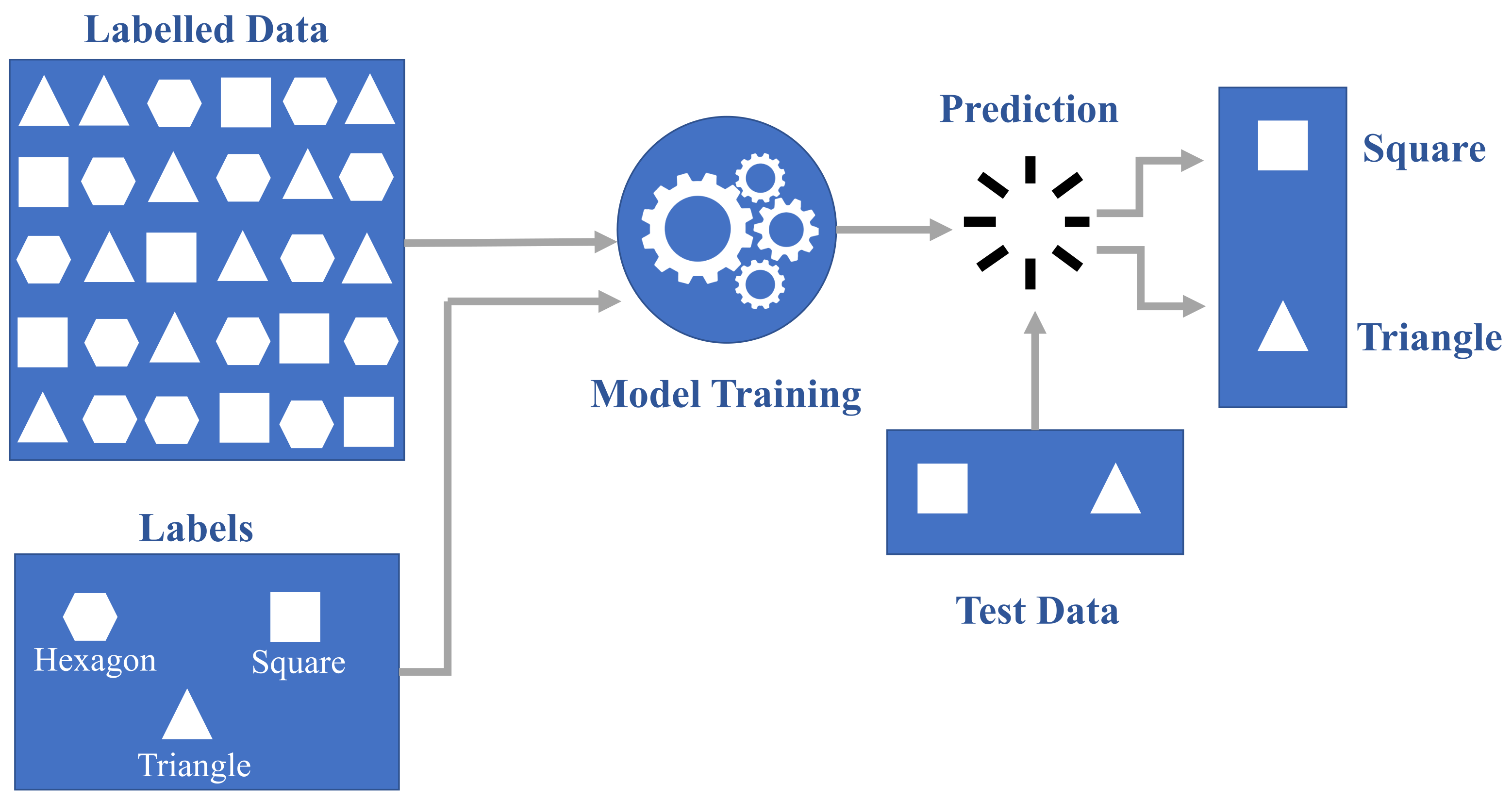
SML comprises two primary types: classification and regression [36]. In the training phase, a classification algorithm is presented with data points already assigned to specific categories. Its task is to assign an input value to the appropriate category, aligning with the provided training data [37]. An illustrative example of classification is shape identification, where the algorithm is tasked with finding features to associate them with shape categories. Hence, the algorithm creates a mapping function as shown in Figure 2. The second most popular SML approach is the regression model. Regression algorithms are used for continuous variables if there is a correlation between inputs and outputs [38]. Different types of regression algorithms can be used in SML, including the regression tree, linear, Bayesian linear, polynomial, and nonlinear regression [39]. The linear regression algorithm produces a vector of coefficients that are then used to define the model [40], and the decision tree produces a tree of if-then statements with specific values assigned to the tree branches. The neural network, along with the optimization algorithm, comprises a trained model, i.e., weights and biases assigned to the nodes of a network so that the output is evaluated by applying a number of numerical evaluations [41].
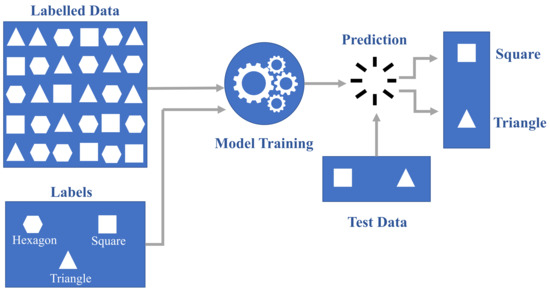
Figure 2.
Schematic of SML classification process.
For both regression and classification, SML can be described by a matrix of input features . Thus, the ith sample has the following vector of values [42]:
such that if is the label associated with the ith sample, the training data are reformulated in pairs, and the entire training data can be represented as [25]:
where is the dimensional feature space and is the label space. For the learning process, a model called hypothesis h is assumed as:
In the next step, the squared loss error function is calculated as [25]:
During the final step, the model undergoes iterative training to optimize in order to minimize the error . In the case of neural networks, backpropagation is employed throughout the training process to compute and assess the gradients necessary for optimization using algorithms such as gradient descent [43] or adaptive moment estimation (Adam) optimizers. The Adam technique combines the principles of momentum optimization [44] and root-mean-square propagation (RMSProp) [45], maintaining exponentially decaying averages of past gradients and past squared gradients.
1.2. Unsupervised Machine Learning
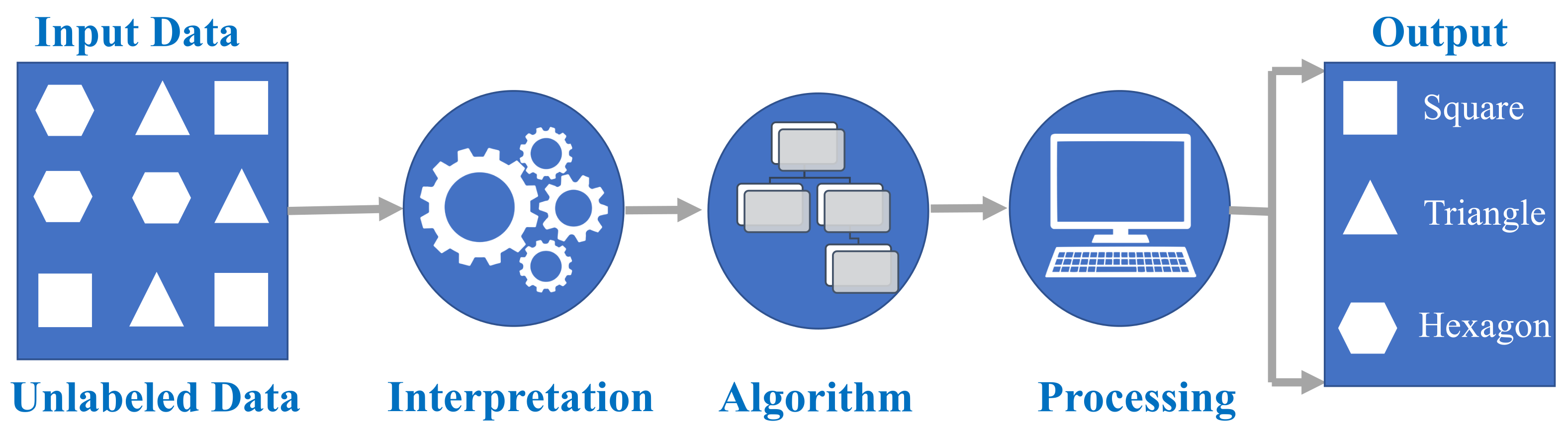
UML commences with unlabeled data and aims to uncover unknown patterns that facilitate a new, more condensed, or comprehensive representation of the contained information [46]. Unlike SML, UML cannot be directly applied to regression or classification problems since the input data lacks predefined outputs. Its objective is to unveil the inherent structure of the dataset, group the data based on similarities, and represent the dataset in a compressed format, as depicted in Figure 3. Here, the input data are unlabeled, meaning they lack categorization, and corresponding outputs are absent. Consequently, the unlabeled input is used to train the machine learning model. Initially, the model scrutinizes the raw data to unveil any latent patterns, followed by the application of suitable algorithms like k-means clustering [46] to forecast data behavior.
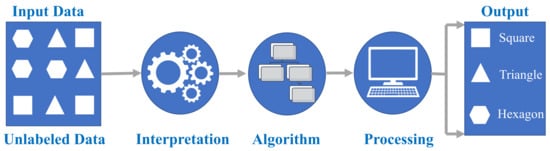
Figure 3.
Schematic of UML classification process.
In general, UML models serve three primary tasks: association, clustering, and dimensionality reduction. Mathematically, this approach quantifies dissimilarity or distance between two data points x and using a real number determined by a distance function , which must satisfy certain conditions [47]:
- i.
- ,
- ii.
- ,
- iii.
- .
Subsequently, the data points are arranged into a specified number of clusters and the centroid of each cluster is then calculated by [48]:
The Sum of Squared Error (SSE) can be used to evaluate the performance of the method as [26]:
We note that the most accurate method is expected to have the smallest error, which can then be reduced by increasing the number of clusters k [49].
1.3. Reinforcement Machine Learning
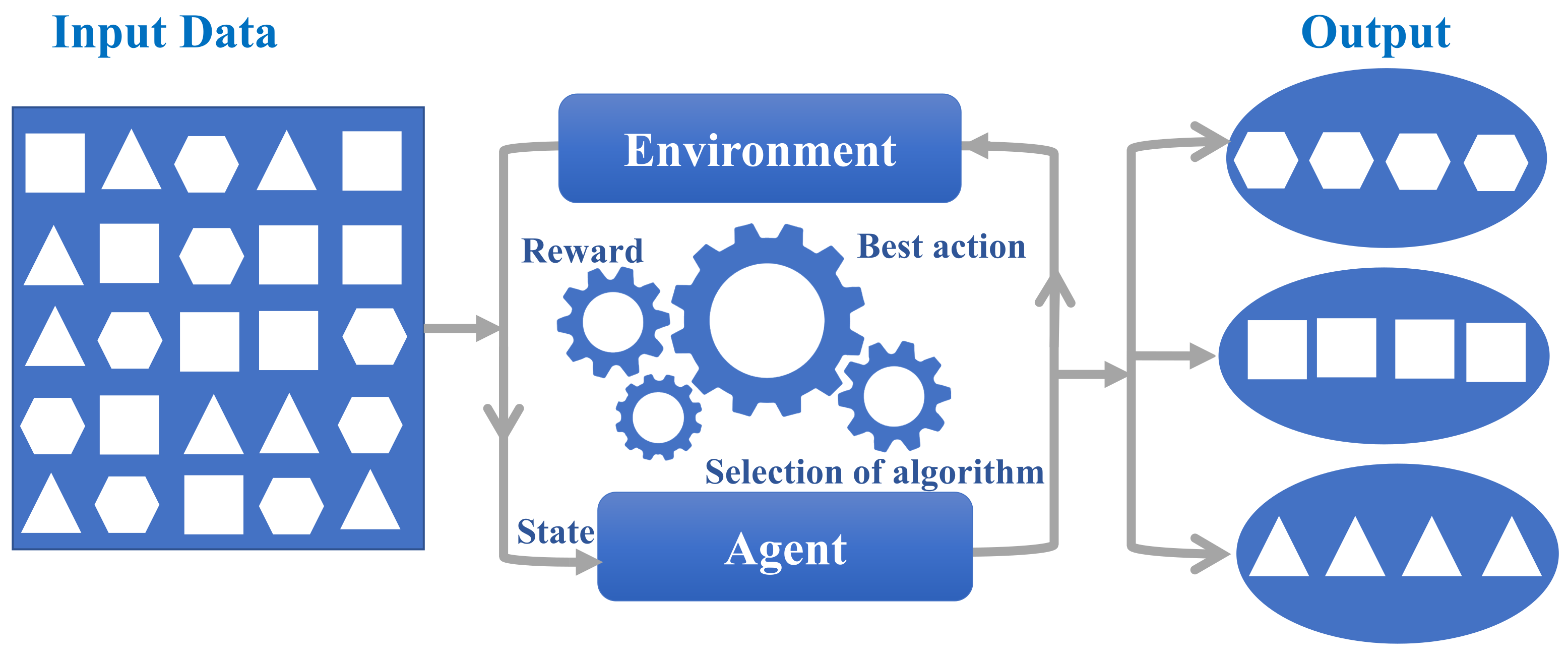
In RML, the algorithm learns to achieve a goal in an uncertain and potentially complex environment, typically using trial and error to come up with a solution to the problem under study [50]. This method learns from an environment with a predefined set of rules and is usually assumed to be deterministic [51]. An RML model interacts with the environment through an agent that has a state in the environment. The agent interacts with the environment through actions, which can change the state of the environment [52]. For each action, the environment yields a new resulting state for the agent and a reward, as shown in Figure 4. The goal of the model is to determine what actions lead to the maximum reward [53]. To this end, RML works by estimating a value for each action. The value is defined as the sum of the immediate reward received by taking an action and the expected value of the new state multiplied by a scaling term [54]. In other words, the value of an action is selected based on how good the next state will be after taking that action, along with the expected future reward from that new state [55]. There are different methods to calculate the value function, such as the Monte Carlo method, temporal difference learning, and gradient descent methods [43].
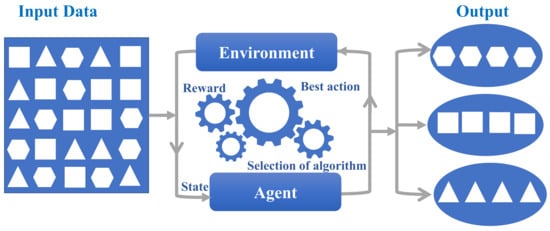
Figure 4.
Schematic of RML classification process.
1.3.1. Monte Carlo Method
The Monte Carlo method updates the value function as [56]:
where V is the value function, is the state at a given time i, is the step size, and is the resulting reward.
1.3.2. Temporal Difference Learning
The temporal difference learning update of the value function is given by [56]:
where is the immediate reward received after taking an action, is the state following the action, and is a scaling term.
1.3.3. Gradient Descent Methods
Gradient descent methods are among the most popular approximators used in RML. In other ML techniques, it is common to learn mappings between inputs and outputs through complex differentiable functions. The same can be carried out to approximate the value function in RML. The function can be updated as follows [43]:
where V is the approximate value function and Q is the updated value estimate given the immediate reward and future state of the action. Note that one needs to define W and specify the variables in terms of i (of Equation (8)).
2. Supervised Machine Learning Applications
Supervised machine learning (SML) algorithms serve as potent predictive tools; however, owing to their complexity, they typically do not provide analytical relationships between input and output data, often being termed as “black box” due to the potential loss of insight into the underlying physics by users. The integration of such approaches with the finite element method (FEM) has recently attracted considerable attention across various research communities. A primary motivation driving this fusion is the aspiration to enhance the balance between numerical precision and computational demand [57].
2.1. Data Requirement and Preprocessing
The primary determinant of the efficacy of SML lies in the dataset utilized for training the SML model [58]. The performance of SML models directly correlates with the quality and relevance of the training data employed [59]. In the SML framework, the data can be either synthetic or real. Real data are either experimental data reported in the literature and laboratory archives [60,61,62,63] or measured (either experimentally or operationally in the field). On the other hand, synthetic data can be generated using numerical models. For instance, finite element analysis is the method often preferred for structural engineering applications [64].
Since its introduction and successful commercialization in the 1950s, the FEM has undergone rapid development. Compared to alternative numerical approaches, the FEM enjoys broader usage across a diverse array of applications, where ample data are available [65]. The simplicity of managing complex geometries and boundary conditions contributes significantly to the widespread adoption of this approach. Moreover, as the finite element mesh is refined, the accuracy of the solutions improves correspondingly. Therefore, the convergence behavior serves as a critical aspect in guaranteeing solution reliability.
A large number of applications in structural mechanics, fluid dynamics, electromagnetics, and various engineering domains rely on FEM for solving boundary value problems. The approximate solutions to the corresponding partial differential equations are computed at discrete points across the computational domain by analyzing the resulting linear algebraic system [65]. For time-domain problems, time-stepping schemes are sometimes necessary for time integration, requiring the solution of the resulting linear system at each time step. The size of these systems can be exceptionally large, ranging from millions to billions of degrees of freedom, and simulation times on cluster machines or supercomputers can vary from hours to days or even weeks. Additionally, even minor adjustments to input parameters necessitate repeating simulations from scratch. Recent advancements in SML algorithms and their successful integration across various domains indicate that, when appropriately selected and trained, these models can significantly enhance conventional methodologies (e.g., the FEM) [65].
The SML algorithm can then learn from the synthetic data to efficiently predict the numerical solutions for new cases [64,66]. However, models developed with synthetic data such as those from finite element analysis are often approximations of real-world scenarios and are liable to underperform in real-world applications where common scenarios involve a large number of variables, substantial uncertainty, and rapid behavioral changes [67]. Hybrid datasets, a combination of synthetic and experimental datasets, have been suggested [67,68] for the purposes of making the models more reliable for real-world applications.
Despite the scalability of linear solvers, finite element models demand substantial computational resources, and aside from the final results, any knowledge gained by the machine during the simulation is lost. Adjusting input parameters even slightly or reproducing studies conducted elsewhere typically necessitates repeating time-consuming analyses from scratch. Conversely, appropriately discretized physical systems yield highly accurate finite element results, which can be utilized alongside input parameters to train SML models [69]. An efficient approach involves training the model on large datasets generated by well-established conventional FEM tools across random fundamental problems [70]. Additionally, training data can be augmented by actual measurements and simulation outcomes for real-world problems shared among users of FEM packages [71]. Notably, when appropriately trained, such models can find utility across a broad spectrum of applications.
2.2. Computational Mechanics
SML has recently found applications in computational mechanics, including the formulation of multiscale elements [65,72], enhancement of traditional elements [73], and development of data-driven solvers [74]. For instance, Capuano and Rimoli [65] employed ML techniques to devise a novel multiscale finite element algorithm known as the smart element, which is noted for its low computational cost. This approach utilizes ML to establish a direct relationship between the computational domain state (outputs) and external forces (inputs), thereby circumventing the complex task of determining the internal displacement field and eliminating the need for numerical iterations. The solution of ordinary differential equations (ODEs) and partial differential equations (PDEs) using neural networks has been investigated in several previous studies [75,76,77], focusing on shallow neural networks and fixed meshes for approximation. With recent advancements in deep learning, there has been a growing interest in the development of unstructured ML-based solutions for ODE and PDE approximation [78,79,80,81,82,83,84]. Many of these methodologies solve ODEs or PDEs by randomly sampling points in the domain, defining a loss function as the summation of residuals for governing equations and boundary conditions, and employing deep neural networks (DNNs) for solution approximation. Saha et al. [85] constructed a hierarchical deep learning neural network by creating structured DNNs. This neural network accepts nodal coordinates as input and generates associated global shape functions with compact support through a neural network whose weights and biases are solely determined by the nodal positions [85].
One of the primary challenges encountered when employing SML approaches is the convergence of approximation errors to acceptable values, which typically necessitates a substantial volume of data. However, acquiring such data for complex models utilizing the FEM can be arduous and costly. To mitigate the data requirements of training ML algorithms, researchers in [86] have developed physics-informed or physics-based learning techniques. The underlying hypothesis posits that encoding information based on the inherent physics of the system can reduce the data necessary for ML algorithm learning. Raissi and Karkiadakis [87] demonstrated that incorporating physics-based information, such as corotational displacements, significantly diminishes the requisite number of training samples. Physics-based ML presents a promising avenue, necessitating the utilization of governing partial differential equations to guide the ML algorithm. Badarinath et al. [88] introduced a surrogate finite element approach leveraging ML to predict the time-varying response of a one-dimensional beam. Various ML models, including decision trees and artificial neural networks (ANNs), were developed and compared in terms of their performance for directly estimating stress distribution across a beam structure. Surrogate finite element models based on ML algorithms demonstrated the ability to accurately estimate the beam response, with ANNs yielding the most precise results. However, Hashemi et al. [89] showed that ML-based surrogate finite element models that use extreme gradient-boosting trees outperform other ML algorithms in predicting the dynamic response of an entire 2D truss structure. Consequently, the efficacy of surrogate models relies not solely on the ML algorithm employed but also on problem conceptualization and approximation. Furthermore, Lu et al. [90] showcased a deep neural operator surrogate model for predicting transient mechanical responses of an interpenetrating phase composite beam comprising aluminum and stainless steel under dynamic loading. The deep neural operator comprises two feedforward neural networks: a trunk net and a branch net, whose matrix product learns the mapping between nonlinear operators. The deep neural operator is deemed robust and potentially capable of yielding extended-time predictions if appropriately trained [90]. Li et al. [91] used graphical neural networks (GNNs) for predicting structural responses (displacement, strain, stress) under dynamic loads. The motivation is that GNNs use an iterative rollout prediction scheme that captures the spatial/temporal dynamics of the structure while being computationally efficient. The approach was implemented to study the structural response of a metal beam, but its scalability has not been demonstrated for larger structures. To account for local nonlinearities in structural systems (e.g., at joints or interfaces), Najera-Flores et al. [92] proposed a data-driven coordinate isolation technique to isolate the nonlinearities and reintroduce their effect as boundary traction. This, coupled with a structure-preserving multi-layer perceptron and boundary measurements only can record the dynamics of the original system.
Finite element solutions depend on domain geometry and material properties, and under specific conditions, solution convergence may degrade due to shear locking [69]. To mitigate locking effects, bending modes can be incorporated according to bending directions, and analytical bending strains can be enforced using an assumed strain method. Optimal bending directions for a given element geometry, material properties, and element deformation are determined to minimize element strain energy. Deep learning is employed to address the time-consuming task of searching for optimal bending directions [93]. This approach offers the advantage of deriving highly accurate finite element solutions even with coarse and severely distorted meshes. Despite its versatility, the FEM can become computationally prohibitive in various scenarios, including problems with discontinuities, singularities, and multiple relevant scales. ML, when combined with numerical solutions, can help alleviate this limitation. For example, Logarzo et al. [94] used ML to homogenize the models of microstructures and produce constitutve laws that can handle nonlinearities and path dependency. The resulting constitutive models could also be integrated into standard FE models and be used to analyze stresses at the level of engineering components. Conversely, Brevis et al. [95] expanded upon the work presented by Mishra [96] through exploring the acceleration of Galerkin-based discretization using ML, specifically the FEM for approximating PDEs. Their objective was to achieve accurate approximations on coarse meshes, effectively resolving quantities of interest.
2.3. Structural Health Monitoring
The structural health monitoring (SHM) process typically entails globally observing a structure or system through measurements, extracting damage-sensitive features from these measurements, and statistically analyzing these features to assess the current state of the structure or system [97]. When continued over a long time period, the SHM process provides updated information on the present state of the structure, taking into account factors such as aging and damage accumulation resulting from the structure’s operational environment. For discrete events such as earthquakes and bombings, SHM can be used for a rapid structural integrity screening [97,98].
SHM for civil infrastructures such as bridges, tunnels, dams, and buildings arose from the need to supplement intermittent structural maintenance and inspections with continuous, online, real-time, and automated systems [99]. Unlike aerospace structures, civil infrastructures are mostly distinct and unique from one another. Thus, a major problem in the SHM of civil infrastructure is the need for long-term evaluation of the structure’s undamaged or healthy state [99]. Other challenges with civil infrastructure damage assessment include the physical size of the structure, variability in operational environments, optimal definition and location of sensors for measurements, identification of damage-sensitive features (especially features sensitive to small damage levels) [97], the ability to differentiate between features sensitive to changes in environmental conditions from those caused by damage, and the development of statistical methods to differentiate between damage and undamaged features [97].
Present-day SHM for civil infrastructures evolved from activities that used to be known as structural monitoring, structural integrity monitoring, or simply monitoring [99]. Today, the aim of SHM for civil infrastructures has broadened to the development of effective and reliable means of acquiring, managing, integrating, and interpreting structural performance indices with the aim of extracting useful information at a minimum cost with less human intervention [99]. SHM for civil infrastructures at its core employs continuous time-dependent data from either physical or parametric models of the structural system measured from vibrations or slowly changing quasi-static effects such as daily thermal changes in the structure [99]. For civil engineering infrastructures, vibration-based damage assessment for bridges and buildings is based on changes in the modal properties of the structure [97,100]. The overarching aim of vibration-based SHM is the monitoring of structural conditions by observing changes to the structural behavior to rapidly and robustly detect structural damage [101]. Initially, there was not much optimism towards real-time component-level damage identification, location, and quantification for civil infrastructures based on vibration studies [99]. Significant progress in civil infrastructure SHM began more as a result of legislation and legal requirements for major construction projects such as dams and bridges [99]. Much research on civil infrastructure SHM today now focuses on component-level or real-time damage monitoring.
The application of ML to SHM may be said to find its root in the acknowledgment that the SHM problem is essentially one of statistical pattern recognition [97]. SHM is a field that is concerned with the process of online-global damage identification. In SHM, damage diagnosis is ranked in an ascending order of difficulty: detection, localization, assessment, and prediction [102]. According to Worden and Manson [102], these levels of the SHM problem can be posed as either a classification, regression, or density estimation ML problem. A structural system is said to be damaged when there are changes in the system that adversely affect its performance. These could be changes in material properties and geometric properties, boundary conditions, and system connectivity [97]. These changes necessitate a comparison between two system states (damaged and undamaged state) for damage identification. The changes are most often recorded as changes in the dynamic response of the structure or system under consideration [97]. Damage may be progressive and occur over a time period, such as fatigue and corrosion, or it may result from independent events such as earthquakes, explosions, or fire. Damage may progress from a material defect to a component failure under certain loading conditions and then to system-level damage. A damaged system still retains functionality, whereas failure occurs when damage progresses to the point of total loss of system functionality.
According to Farrar et al. [103], SHM as a statistical pattern recognition problem can be distilled into the following four steps: operational evaluation, data acquisition, normalization and cleansing, feature selection and information condensation, and statistical model development for feature discrimination. The foremost step, the operational evaluation stage of the process, seeks to define the system’s damage possibilities, operational and environmental conditions for monitoring the system, and possible limitations to monitoring the system [103]. At the statistical model development stage, damage feature discrimination is achieved using supervised learning by means of classification or regression when both damage and undamaged data are available [97]. Supervised ML models are better used to determine the type of damage, the extent of damage, and the remaining useful life of the system [97].
2.3.1. Utilizing Machine Learning
In an early work on ML-based structural health monitoring (SHM), Yeh et al. [104] developed an ML model for diagnosing damage to prestressed concrete piles based on data collated from interviewing several human experts in the field. Advances in computing and sensing devices have created more robust approaches for data collection in damage diagnosis using supervised learning. Supervised ML algorithms have contributed to SHM in buildings [105,106], bridges [107,108,109], and dams [110,111,112,113]. SML algorithms have been used to monitor flow leakages [112], displacements [110], pore pressure [111], and to determine seepage parameters [113] in dams. In [105], derived the first flexural modes of a five-story building from a finite element model, and used them as input to a neural network to determine damage in the structure. The trained neural network outputs the mass and stiffness of the structure, which are used to determine a damage index for the structure. Chang et al. [106] applied the same approach to a seven-story building and to a scaled twin-tower to detect, localize, and appraise damage to the structure.
Recently, transfer learning (TL) has emerged as an important machine learning methodology for SHM. As the name implies, TL is an ML methodology that attempts to transfer knowledge or experiences gained from learning to perform one task to a different but related task [114,115]. Knowledge from a source task is used to improve the training of a related but different target task. The success of a transfer is dependent on the existence of sufficient commonality between the source and target tasks. Generally, it has been recommended as a solution for machine learning applications where data labeling is not achievable and capturing unlabeled data is difficult as well [115]. The learning experience from the source task can be used to reduce the amount of labeled and unlabeled data required for a target task.
One of the challenges for data-driven SHM is the unavailability of labeled damage data due to the difficulties associated with obtaining damage data for large civil infrastructures [116]. Gardner et al. [116] applies heterogeneous TL by means of utilizing labeled damage data over a wide range of damage states from a population of similar structures for data-driven SHM for a structure of interest. This population-based SHM (PBSHM) provides an alternative to SHM unsupervised learning approaches, i.e., novelty detection. The heterogeneous transfer learning is achieved by means of kernelized Bayesian transfer learning (KTBL), which is a supervised learning algorithm that leverages information across multiple datasets to create one generalized classification model. Gosliga et al. [117] also applied PBSHM in the absence of labeled damage data for bridges. Bao et al. [118] combined TL with deep learning approaches. Using data from physics-based (FE-model) and data-driven methods, Gosliga et al. [117] showed that structural condition monitoring can be carried out with limited real-world data. They demonstrated this approach with vibration-based condition identification for steel frame structures with bolted connection damage. Their results showed that TL yielded higher identification accuracies. Tronci et al. [101] also used the concept of TL to detect damage-sensitive features from vibration-based audio datasets of Z24 bridge experimental data. This was carried out to also show that TL can be used to mitigate the unavailability of labeled data for damage assessment [101].
TL can be carried out by means of full model transfer [119] or by transferring a portion of the model [120]. Li et al. [119] applied TL by means of model transfer in combination with deep learning using a convolutional neural network to predict dam behavior. Model transfer is used to reduce training time and improve the performance of the model. Tsialiamanis et al. [120] applied TL by transferring a fixed trained batch of neural network layers trained to localize damage for simpler damage cases to help with feature extraction for difficult cases. TL has also been recommended for SHM of composite structures [121].
Innovative approaches to SHM have been presented by researchers recently. An SHM decision framework applicable to real-world structures to determine whether or not to install vibration-based SHM on a structure has been developed [122]. This framework, in essence, quantifies the value of vibration-based SHM on the basis of the difference in total life-cycle costs and is applicable to a variety of use cases across different time scales. It also covers models for inspection and maintenance decisions throughout a structural life-cycle. The framework uses a Bayesian filter for joint deterioration parameter estimation and structural reliability updating using monitored modal and visual inspection data. Markogiannaki et al. [123] proposed a framework for damage localization and quantification that is model-based rather than data-driven approaches and uses output-only vibration measurements. They use the FE model and FE model updating techniques to obtain the representative numerical model of the structural system.
2.3.2. Digital Twins
The concept of digital twins has been much welcomed by the SHM community. It has been considered a potentially transformative concept in modeling and simulation for engineering applications [100]. A digital twin represents a virtual replica of a system constructed through a combination of algorithms and data. One significant advantage of digital twinning lies in its potential to enhance predictive capabilities. It is envisaged that digital twins will find utility in modeling systems where physics-based models encounter considerable epistemic uncertainty [100]. However, the field of engineering dynamics presents challenges in developing an efficient digital twin [100]. The components necessary for constructing an effective digital twin can be categorized into physics-based modeling, verification and validation, data-enhanced modeling, software integration and management, uncertainty quantification, and output visualization [100]. Wagg et al. [100] showcased the synthesizing process and challenges of the development of an effective digital twin for SHM via the use of a three-story structure. The structural model is deterministically calibrated, validated, and tested to perform as a digital twin. It performs well on test data but fails on new data that introduces non-linearity into the structural model. Improvement in the predictions of the model is observed after data augmentation is introduced into the model by means of a Gaussian process ML. This goes to show the value of data augmentation in the development of digital twins.
2.4. Structural Design and Manufacturing
The structural design process for buildings often consists of decisions on the building shape, the number and connectivity of structural members, and the sizing of these members [124]. ML algorithms have been proposed for the optimization of either one or a combination of these processes. In the design conceptualization stage, the building floor plan largely forms the building shape. Chaillou [125] used a conditional Generative Adversarial Network (cGAN) in a picture-to-picture mapping to generate building floor masterplans. Although this work is currently at the forefront in this domain, it is limited by the discontinuity of structural load-bearing walls from one floor to the next. The output, also being an image file, would require transforming the image outputs into usable design drawings. It should also be emphasized that the work of Chaillou [125] is targeted for use by architects. Ampanavos et al. [126] carried out similar work using a convolution neural network for the development of structural floor layouts in the initial design phase. Rasoulzadeh et al. [127] sought to fully integrate early design stage workflows between architectural, engineering, and construction teams with a 4D sketching interface that comprises geometric modeling, material modeling, and structural analysis modules. The three modules create a framework for reconstructing architectural forms from sketches, predicting the mechanical behavior of materials, and assessing the form and materials based on finite element simulations. It should also be noted that the work in [125,126] is focused on steel frame structures that have a smaller design space (available steel sections) when compared to reinforced concrete structures. Researchers in [124,128,129,130] have focused on reinforced concrete and worked on the layout optimization, sizing, and design of shear walls using several supervised ML algorithms. For example, the work in [131,132] proposed the automation and optimization of building design processes. Researchers have also studied ML applications in prestressed concrete [133], masonary arches [134], estimation of embankment safety loads [135], and steel connection behavior [67].
To produce high-quality and cost-effective structural elements, it is essential to develop the manufacturing and production techniques of these elements. In this context, the cutting force plays a crucial role. Incorrectly selected cutting conditions can lead to intensive stress fields in the cutting zone, resulting in excessive tool wear, diminished accuracy, and a decline in part quality [136]. Furthermore, modeling the milling process has been a significant area of research for many years, driven by the increasingly stringent industrial demands and standards necessary to ensure the quality of manufactured elements. Therefore, research and development efforts are vital to obtaining numerical and statistical approximations of the milling process, aimed at elucidating the phenomena occurring during cutting and predicting manufacturing process quality. It is noteworthy that the majority of milling force models are either analytical [137], empirical [138], or based on finite element analysis [139,140]. Charalampous [141] employed ML in conjunction with finite element models to predict cutting force during the milling process relative to cutting speed. Experimental results from milling investigations were filtered and inputted into ML algorithms to develop reliable predictive models. The study concluded that ML models can accurately estimate the intricate interactions between cutting conditions and resulting cutting forces [141].
ML applications in additive manufacturing have attracted considerable attention from researchers. Jirousek et al. [142] explored the relationship between design parameters of additively manufactured auxetic structures and target properties using machine learning algorithms. Employing Shapley Additive Explanations, the study [142] reveals that strut thickness is the critical parameter affecting the Poisson’s ratio of auxetic structures. The orthotropic mechanical behavior of components poses a challenge in additive manufacturing due to its layer-by-layer fabrication process. Grozav et al. [143] utilize ANNs to predict mechanical properties at various orientation planes of components affected by the layer-by-layer fabrication process. The findings from their research show promise in addressing components prone to orthotropic behavior.
2.5. Stress Analysis
Stress analysis constitutes a cornerstone of structural engineering, representing a dynamic area of research. Numerical analysis methods, such as the FEM, are utilized for stress analysis of intricate structures and systems where obtaining an analytical solution may prove challenging. The finite element analysis (FEA) serves to assess the stress for design, maintenance, and safety of complex structures across various applications, including aerospace, automotive, architecture, and more recently, biomedical engineering [144]. However, dealing with highly nonlinear problems can be a major computational burden for the method. For example, advancements in imaging techniques have facilitated the study of human tissues and organs using biomechanics to develop patient-specific treatment strategies, which has exposed certain limitations for the FEA [69,144,145,146]. In this regard, SML algorithms show strong potential in providing approximate stress analysis results as accurate as those obtained via numerical methods such as the FEM but using significantly fewer computational resources [64,66,88,147,148]. Furthermore, the algorithms presented in [64,66,147] leverage image processing techniques to reduce the computational burden of nonlinear stress analysis using numerical methods. Indeed, it was even possible to achieve stress predictions in real-time using surrogate finite element analysis and SML, as demonstrated in [88]. Such developments clearly reflect the potential SML has in the future for stress analysis.
2.6. Failure Analysis
In recent years, SML-based approaches have garnered significant attention for their capability to reduce the computational burden associated with fatigue assessment. Yan et al. [149] developed an ANN using a dataset comprising numerous crack patterns of reinforced concrete slabs and their corresponding fatigue life. This neural network was utilized to establish a relationship between the fatigue life of bridge decks and the observed surface cracks, enabling quick and quantitative predictions of bridge fatigue life. The study detailed in [149] investigated the fatigue failure reliability of a typical composite steel girder bridge under vehicular overloading conditions. Initially, deterministic simulations were conducted to obtain bridge responses under overloading scenarios, considering overloaded trucks based on axle load and gross weight. To circumvent time-consuming FEA simulations, a feed-forward neural network was trained, validated, and tested. Subsequently, the trained ANN was combined with the Monte Carlo method to predict the fatigue failure probability of steel girder bridges under traffic overloading. Additionally, Reiner et al. [150] developed an ANN surrogate model for simulating progressive damage in fiber-reinforced composites. To address uncertainties and variations in material properties, they incorporated a Markov Monte Carlo Chain as a Bayesian parameter estimator for their input parameters. To overcome the limitations of classical models in estimating fatigue crack growth, interdisciplinary methods are being introduced. Numerical approaches and ML methods are commonly employed and have demonstrated effectiveness. Furthermore, combining numerical approaches with SML algorithms represents an important research direction. For instance, knowledge-based neural networks can be integrated with FEM and optimization algorithms [151].
While numerical approaches typically simulate fatigue crack growth processes alongside classical models, ML methods offer a flexible and alternative approach due to their capability to approximate nonlinear behavior and multivariable learning ability, rendering them promising and advanced methods for such applications [152]. Moreover, various algorithms are employed in data-driven systems within this context, including support vector machine (SVM), genetic algorithms (GAs), ANN, fuzzy logic, neural–fuzzy systems, and particle swarm optimization (PSO) [153]. Using the particle swarm optimization–extreme learning machine (PSO-ELM) algorithm, Yu et al. [154] achieved the evaluation and detection of rail fatigue crack depth with an accuracy exceeding 99.95%. The extreme learning machine is a supervised ML algorithm for training single hidden layer feedforward neural networks (SLFNs) and is noted for its faster convergence compared to conventional neural network algorithms. The remarkable learning and generalization abilities of ML enable it to model internal connections and tendencies from complex or imprecise data. Consequently, ML methods find applications in various facets of fatigue research [155].
In contrast, Zio and Maio [156] utilized the relevance vector machine (RVM) to predict the remaining useful life of a structure. Their application exhibited good agreement with the model-based Bayesian approach for predicting fatigue life in aluminum alloys. However, their study did not assess the method’s applicability to different materials. Meanwhile, Mohanty et al. [157] employed the radial basis function network, an ML algorithm, to model fatigue crack growth. The method demonstrated strong applicability across various aluminum alloys. Nonetheless, a thorough investigation into the differences between different ML algorithms in fatigue crack growth calculation is lacking, making it challenging to determine the most suitable algorithm for fatigue crack growth prediction. The radial basis function network (RBFN) is one such ML algorithm that employs multidimensional spatial interpolation techniques. It can utilize various learning algorithms based on different methods for selecting the center of the activation function. The RBFN can be trained more rapidly than the backpropagation network and is capable of handling nonlinear problems with complex mappings [158,159]. Moreover, it has been shown to be effective for fatigue crack growth under both constant and variable amplitude loadings, as it can predict residual stresses following the shot-peening process using supervised learning supplemented by continuous learning.
2.7. Material Modeling
SML-based material models have been proposed for use within FEM [160]. Hashash et al. [160] formulated the material stiffness matrix from a ML material model for use within FEM. The neural network material model provided a stress–strain relationship from which the implied material stiffness matrix could be extracted. Carneiro et al. [161] trained a ML-based material model to approximate the stress–strain relation that can be obtained from the finite element model of the raw material microstructure or representative volume element (RVE). They analyzed critical macroscopic points where high-fidelity models would be necessary for path-independent materials at large strains. Also, using RVE and deep machine learning, Nikolic et al. [162] modeled temperature-dependent stress–strain hardening curves for material microstructure. The accuracy of ML material models, just like other ML models, depends quantitatively and qualitatively on the provided data [60,160]. In fact, data for developing an ML material model should capture all aspects of the material behavior to be meaningful. SML-based material models, such as those in [161,162,163], approximate material behavior based on the dataset used in developing the model. Oladipo et al. [68] developed an SML model for the design and development of metamaterials based on a hybrid dataset combining numerically simulated results with experimental results. The hybrid dataset is chosen to improve the reliability of the model. They also incorporated Shapley Additive Explanations (SHAPs) to make the SML model interpretable. Long et al. [164] used SML to quantify the effect of structural characteristics of foam structures on their thermal conductivity.
Recently, interest has developed in modeling the behavior of granular materials [165,166,167] using deep learning algorithms such as recurrent neural networks (RNNs) and convolutional neural networks (CNNs). Gang et al. [165] used long short-term memory networks, a class of RNN algorithms, due to the path/history dependency of granular material behavior. Concrete, being a complex material, has attracted the attention of ML researchers from the early days of ANNs [60,61,62,63]. The ML models for predicting the compressive strength of concrete have been quite popular [63,168,169,170,171,172,173,174]. Hakim et al. [168] reported error levels in the strength prediction that are acceptable in concrete technology. Yang et al. [174] used gradient boosting with categorical features support to enhance the prediction of the compressive strength of concrete. Robertson et al. [173] incorporated the thermal history of concrete into the features of the network’s input in addition to the inputs for the mix components. Thermal history is recorded through curing inputs such as specimen maturity, maximum temperature encountered during curing, and the duration of maximum temperature exposure. The study highlights that input analysis revealed strength predictions to be more sensitive to curing inputs compared to mixture inputs [173].
2.8. Optimization Problems
Genetic algorithms (GAs) represent a form of evolutionary algorithms characterized by symbolic optimization. Within genetic programming, binary trees are commonly utilized to depict candidate structures, with diverse hierarchically structured trees constituting the population. Once the evolutionary process commences, it involves selection, crossover, and mutation operations [175]. The symbols and variables at each node can be modified through crossover and mutation. GAs have found extensive application in exploring the relationship between independent and dependent variables, owing to their simple and explicit expressions that offer clear explanations, such as in predicting soil physical indices [176]. Furthermore, they have been advocated as an optimization tool within FEA packages for structural design [177]. However, genetic programming heavily relies on stochastic procedures and operators, and the multitude of potential initial population combinations may become relatively vast [178].
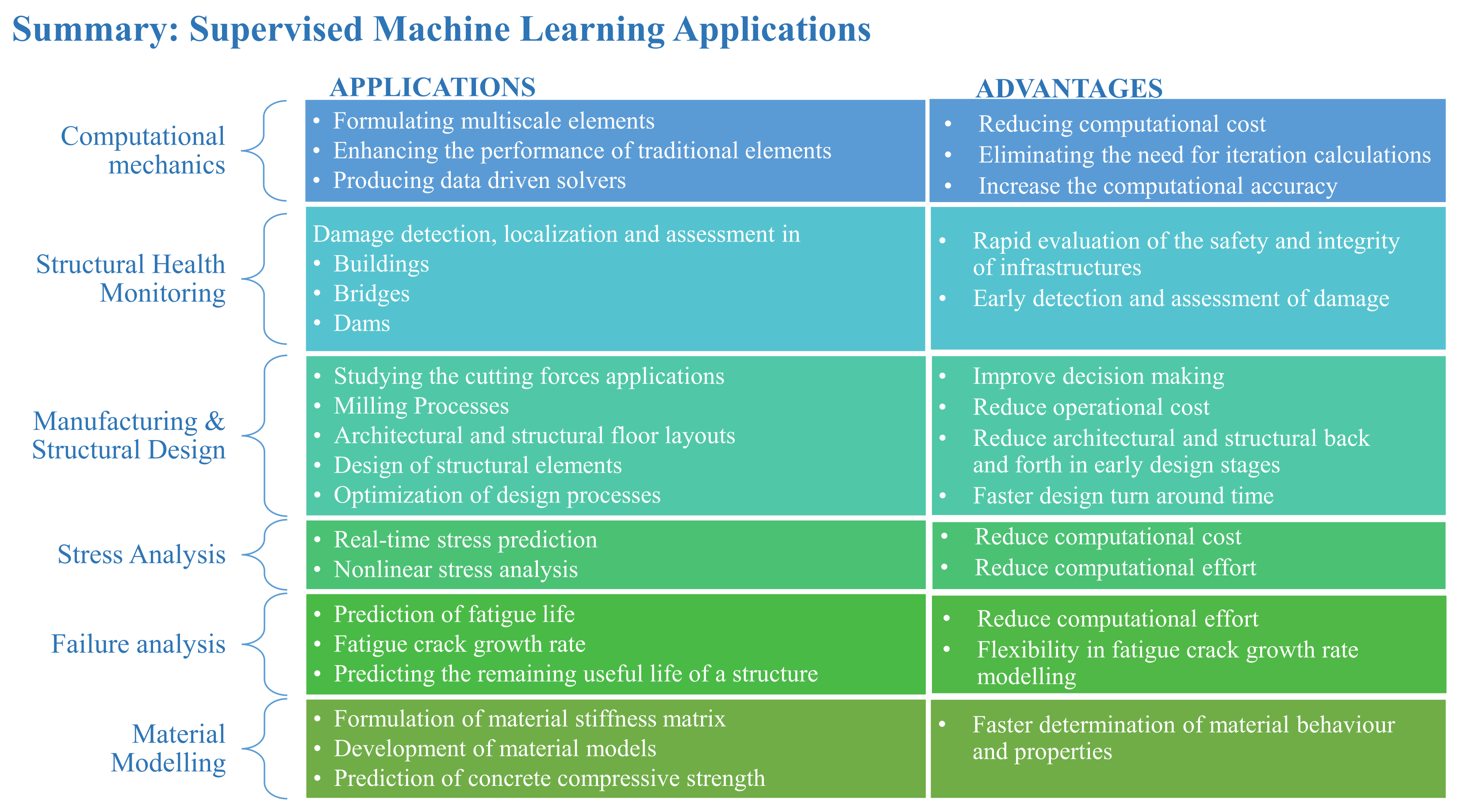
2.9. Summary and Outlook
SML is one of the most widely adopted approaches in ML approaches to structural engineering, particularly in applications involving prediction and classification tasks. This review covers most of the well-known applications using SML as shown in Figure 5.
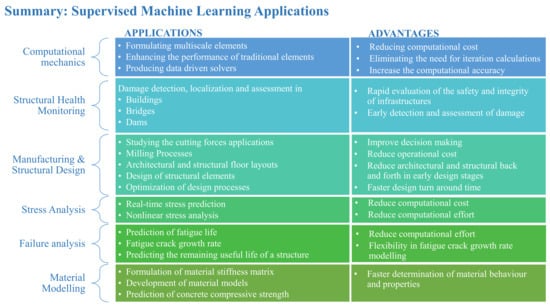
Figure 5.
Summary of SML applications.
SML methods require labeled data, allowing algorithms to learn from input–output pairs and develop a mapping function. Despite its effectiveness, SML faces several challenges. One major limitation is the dependency on high-quality labeled data, which can be both time-consuming and costly to obtain. Furthermore, models developed through SML often exhibit a propensity for overfitting, especially when trained on limited datasets [179]. Additionally, SML techniques can be sensitive to the quality and distribution of training data, leading to inadequate generalization when applied to unseen scenarios. Many existing SML methods operate as “black boxes”, offering little insight into their decision-making processes. This lack of interpretability poses challenges in critical applications where understanding model behavior is essential.
Future research in SML should focus on enhancing model transparency, developing algorithms capable of learning from fewer labeled examples, and improving generalization capabilities across diverse applications in structural engineering.
3. Unsupervised Machine Learning Applications
Unsupervised Machine Learning (UML) is a highly interdisciplinary field that draws upon concepts from statistics, computer science, engineering, optimization theory, and various other scientific and mathematical disciplines. Gharahamani [180] provides a tutorial and overview of UML from a statistical modeling perspective. UML methodologies often draw inspiration from Bayesian principles and information theory. Foundational models within UML encompass state-space models, factor analysis, hidden Markov models, Gaussian mixtures, independent component analysis, principal component analysis, and their respective extensions [180]. The expectation-maximization algorithm is pivotal in this domain, along with fundamental concepts such as graphical models and graphical inference algorithms, which are elaborated on by Le [10]. Moreover, Le [10] provided a concise overview of approximate Bayesian inference techniques, which include methods such as Markov Chain Monte Carlo, variation approximations, expectation propagation, and Laplace approximation.
In general, UML can be especially challenging when working with large sets of data. For example, two prominent techniques in UML, namely Deep Belief Networks (DBNs) and sparse coding, are often too slow for large-scale applications and are thus primarily focused on smaller-scale models [22]. Massively parallel methods have been employed to address these scalability issues [15]. Additionally, the computational capabilities of modern graphics processors surpass those of multi-core central processing units (CPUs), thereby enhancing the applicability of UML methods. General principles for massively parallelizing UML tasks have been developed using graphics processors, and these principles are applied to both DBNs and sparse coding to scale and optimize learning algorithms [22]. Implementations of DBNs have demonstrated speedups of over 70 times compared to dual-core CPU implementations for large models.
Locally linear embedding (LLE) emerges as a UML algorithm that operates without requiring labeled data inputs or feedback from the learning environments. A comprehensive survey of the LLE algorithm, including implementation details, potential applications, extensions, and its relationship to different eigenvector methods used for nonlinear dimensionality reduction and clustering, is provided in [181].
It is noteworthy that UML algorithms may attempt to tackle specific tasks in a more challenging manner than necessary or even address the wrong problem altogether, which is a common criticism. Nonetheless, LLE addresses many of these critiques, distinguishing itself within a novel category of UML algorithms marked by global optimization strategies, straightforward cost functions, and pronounced nonlinear dynamics without strong parametric assumptions [181]. These algorithms are expected to find broad usage across various fields of information processing, particularly as tools to streamline and expedite other machine learning techniques in high-dimensional spaces.
3.1. Cluster Analysis
Cluster analysis, a fundamental method for understanding and learning, organizes data into meaningful groupings based on similarities and characteristics, without using category labels or prior identifiers such as class labels. Data clustering is characterized by the absence of category information and aims to uncover structure within data, with a long history in scientific research [22]. The k-means algorithm, introduced in 1995, stands out as one of the most popular and straightforward clustering algorithms. Building domain-specific search engines represents a significant application of UML. These search engines offer highly accurate results with additional features not available in general web-wide search engines but can be challenging and time-consuming to develop and maintain. To address this challenge, UML techniques have been proposed to automate their creation and maintenance, enabling quick and efficient development with minimal effort and time investment [182]. The emphasis is on topic-directed spreading, such as substring extraction for relevant topics and constructing a hierarchy of browsable topics. By leveraging unlabeled data such as class hierarchies and keywords, the burden on classifiers is reduced. Instead of handling labeled training data, the builder provides a set of keywords for each category, which can serve as a rule for list classification.
Recent advancements in latent class analysis and associated software provide an alternative avenue to conventional clustering methodologies such as k-means, accommodating continuous variables. A comparative evaluation of the two approaches is conducted via data simulations wherein true memberships are identifiable. Parameters conducive to k-means are selected based on assumptions inherent in k-means and discriminant analysis. Typically, clustering techniques do not leverage data pertaining to true group memberships. However, in discriminant analysis, the dataset is initially utilized, serving as a gold standard for subsequent evaluation. Remarkably, this approach yields significant outcomes, with latent class performance aligning closely with actual performance under discriminant analysis, thus blurring the distinction between the two [183].
A novel statistical method, closely linked to latent semantic analysis, has been devised for factor analysis of binary and count data [184]. In contrast, another method employs linear algebra by performing Singular Value Decomposition (SVD) of co-occurrence tables. However, the proposed technique utilizes a generative latent class model for probabilistic mixture decomposition on the dataset. The extracted results offer a more principled approach grounded in solid statistical foundations [184]. This technique incorporates a controlled version concerning temperature and devises maximization algorithms for model fitting, resulting in highly favorable outcomes in practice. Probabilistic latent semantic analysis finds numerous applications in natural language processing, text learning, information retrieval, and machine learning-based applications.
3.2. Data Engineering
UML methods, such as visualization, clustering, outlier detection, or dimension reduction, are commonly employed as an initial step in data mining to glean insights into patterns and relationships within complex datasets [185]. Additionally, clustering can offer preliminary insights into similarity relationships [186], achieved by partitioning observations into groups (clusters) where observations within clusters exhibit greater similarity to each other than to those in other clusters [19]. UML methods also find application in data interpolation techniques, where most extracted data are numerical and can be interpreted as points in numerical space [17]. Indeed, in cases where only a few labeled observations are available, a standard approach for estimating model accuracy is n-fold cross-validation [187]. Maximizing true error, which is the expected error on unseen observations, provides a better estimation of accuracy on an independent hold-out set not revealed to the learning algorithm.
Typically, a UML project commences with the preprocessing of raw multidimensional signals, such as images of faces or spectrograms of speech [19]. The aim of preprocessing is to derive more informative representations of the information in these signals for subsequent operations, including classification, interpolation, visualization, denoising, or outlier detection [17]. In scenarios where prior information is absent, the aforementioned representations must be discovered automatically. This general framework of UML facilitates the exploration of automatic methods that identify unlabeled structures from the statistical regularities of large datasets [188].
In data analysis, it is common for the nature or label of the features in data to be missing or unknown. In such cases, UML algorithms are utilized to explore patterns in the data. Unlike SML, where a desired output is provided to the network, UML tasks entail the network discerning patterns in the input independently. To accomplish these tasks, various UML methods, including frequent pattern detection, clustering, and dimensionality reduction, are employed [7].
3.3. Feature Engineering
One of the primary challenges encountered in developing an automated feature subset selection algorithm for unlabeled data involves determining the number of clusters, coupled with feature selection, as detailed in [47]. Another challenge concerns normalizing the bias of feature selection criteria with respect to dimensionality. Feature subset selection is accomplished using expectation maximization clustering, as elucidated in [189], where two distinct performance criteria are employed to assess candidate feature subsets, namely scatter separability and maximum likelihood. Dy and Brodley [189] furnished proofs regarding the dimensionality biases of these feature criteria and proposed a cross-projection normalization scheme capable of mitigating these biases. Thus, a normalization scheme was essential for the selected feature selection criterion. It is imperative to underscore that the proposed cross-projection criterion normalization scheme effectively mitigates these biases.
The objective of the study presented by Le [10] was to employ UML to construct high-level, class-specific feature detectors from unlabeled images and datasets. This approach is inspired by the neuroscientific hypothesis positing the existence of highly class-specific neurons in the human brain, colloquially referred to as “grandmother neurons”. Contemporary computer vision methodologies typically underscore the importance of labeled data in deriving these class-specific feature detectors. For instance, a large annotated dataset of images containing faces is typically required to train a face detector, often delineated by bounding boxes around the faces. However, in scenarios where labeled data are scarce, significant challenges arise, necessitating large labeled datasets [181].
Cameras that integrate red–green–blue and depth (RGB-D) information provide high-quality synchronized videos for both color and depth, offering an opportunity to enhance object recognition capabilities. However, the challenge of developing features for the color and depth channels of these sensors also intensifies. Liefeng [190] discussed the utilization of hierarchical matching pursuit (HMP) for RGB-D data. Through sparse coding facilitated by HMP, hierarchical feature representations are learned from raw RGB-D data in an unsupervised manner. Extensive experiments across various datasets demonstrate that features acquired through this approach yield superior object detection results when employing linear SVM. These findings are promising, suggesting that current recognition systems could be enhanced without the need for complex manual feature design. Although the architecture of HMP is manually designed, automatically learning such a structure remains a challenging and intriguing endeavor.
Approaches that have not demonstrated efficacy in constructing high-level features often leverage readily available unlabeled data, although they are frequently favored. The research in the realm of UML is extensive, and while this review addresses certain issues and applications, Saul and Roweis [188] observed that no single criterion is universally optimal for all problems. A novel and intriguing perspective is proposed by Dy and Brodley [189], who advocate for hierarchical clustering for feature selection. However, as hierarchical clustering yields dataset groupings at multiple levels, UML techniques can be viewed from the lens of statistical modeling. A coherent framework for learning from data and for interpretation amidst uncertainty is provided through statistics. Numerous statistical models employed for UML can be conceptualized as latent variable models and graphical models, elucidating UML systems for various types of data.
3.4. Structural Health Monitoring
In the absence of damage data, UML models, by means of outlier or novelty detection, are better used to determine the existence and location of damage [97]. Vibration control, damage detection, and localization are some of the key areas of UML in structural health monitoring. Madan [191] used a counter propagation network (CPN) to develop an active controller against the effect of vibrations caused by seismic ground motions on multi-story buildings. The CPN is a feature-sensitive ANN that is self-organizing and self-learning. In the case of SML, a neural network controller is usually trained with known target control forces for known earthquake ground motions, but in practice, it is difficult to know in advance the control forces that can produce the best structural response to an unknown earthquake ground motion. Particularly, without the aid of target or labeled output data, the system learns by exploiting any pattern or structure within the input data, which demonstrates the potential of UML in such applications.
The development of supervised damage detectors is usually faced with the unavailability of damage data for large structures as they cannot be intentionally harmed. For unsupervised damage and anomaly detectors, only undamaged conditions are fed to the detector, and with the use of a suitable algorithm for feature extraction, damage conditions can be classified differently and thus detected [192,193]. Researchers in [192] implemented a nearest neighbor algorithm and in [194], a variational auto-encoder for feature extraction is used. Note that since no labeled data are needed, this approach is regarded as suitable for real-life structural health monitoring [194]. Unsupervised learning has been used as statistical pattern recognition for damage identification and quantification using an autoregressive model [195]. Daneshvar and Hassan [196] also employed autoregressive modeling for feature extraction and then for damage localization using the Kullback–Leibler statistical distance measure. Nevertheless, the method in [196] revealed that it reduces the computational cost of data-driven damage localization when dealing with large vibration data from sensors. Liu et al. [197] used dynamic graph convolutional neural networks and transformer networks in a unified SHM framework. The motivation for using both methods is to overcome the challenge of limited labeled data by analyzing sensor-derived time series data for accurate damage identification. This was coupled with a ‘localization’ score that combines data-driven insights with physics-informed knowledge of structural dynamics. The framework was validated on various structures including a benchmark steel structure. Junges et al. [198] convolutional autoencoders and cGANs for localizing structural damage using Lamb waves without prior feature extraction. The techniques were validated on two full-scale composite wings subjected to impact damage and both methods localized the damage with comparable accuracy.
Eloi et al. [199] proposed an unsupervised TL approach for the SHM of bridges. Using labeled data from FE models as the source domain, they trained classifiers and tested the performance of these classifiers with unlabeled Z-24 bridge monitoring data (target domain). Data from both domains are expected to have similar distributions except for uncertainties in the FE physics-based model of the bridge. Transfer component analysis is the TL method used in this research and it attempts to transform damage-sensitive features from the original space to a latent space where the feature distributions are reduced. Bayane et al. [200] developed five UML algorithms for detecting (in real-time) abrupt changes in bridges. Part of the study was to investigate the impact of sensor location and types on the accuracy of damage detection. Lu et al. [201] proposed using bidirectional long short-term memory networks and a generalized extreme value distribution model to identify and quantify damage in structures. The proposed methodology was validated using data from a numerical steel beam model and a real long-span cable-stayed bridge.
3.5. Structural Design and Manufacturing
Various research studies have proposed systematic frameworks based on data mining to predict the physical quality of intermediate products within interconnected manufacturing processes. Some of these studies delineate data preprocessing and feature extraction components integrated into the inline quality prediction system, while others demonstrate the utilization of a combination of supervised and unsupervised data mining techniques to identify influential operational patterns, promising quality-related features, and production parameters [202].
The steel industry’s production processes are characterized by resource-intensive, complex, and automated interconnected manufacturing operations. Technological and temporal constraints confine product quality assessments to the final production process. Consequently, unnoticed quality deviations traversing the entire value chain can significantly impact failure costs by increasing rejections and interruptions. Hence, novel solutions for continuous quality monitoring are being explored, particularly in a case study on hot rolling mills. The aim is to detect quality deviations at the earliest possible process and in real-time through data mining on distributed measurements across the production chain. Notably, since the product’s quality depends on its processing, the time series of measurements recorded at each production stage may contain quality identification patterns [203]. Furthermore, SML, utilizing quality labels derived from ultrasonic tests, can develop prediction models capable of forecasting the quality-related physical properties of a product even at intermediate production stages [204]. Early defect detection will not only conserve production resources but also promote more sustainable and energy-efficient interconnected manufacturing processes.
Previous works have addressed distributed data mining and its overarching challenges concerning sensor data from interconnected processes [203], as well as the issue of acquiring suitable quality labels [204,205]. Additionally, Konard et al. [204] outlined the deployment of a data storage and acquisition system, along with the initial prediction outcomes based on data collected from the rotary hearth furnace.
3.6. Other Structural Engineering Applications
Recently, work has been devoted to the development of PDE solvers without the use of labeled data [206,207]. Yinhao et al. [207] proposed using physics-constrained deep learning by means of a convolutional encoder–decoder neural network as a PDE solver without the use of labeled data. Junho et al. [206] developed an unsupervised PDE solver adopted from computer vision tasks and requires no training dataset, which they named the unsupervised Legendre–Galerkin neural network. The solver takes input boundary conditions and external forces to output numerical solutions of the PDE. This solver is capable of learning multiple instances of the PDE solutions, unlike most SML solvers, which only predict a single instance of the solution of the PDE for particular initial conditions, boundary conditions, and external forces. Piervincenzo et al. [208] developed a UML algorithm based on outlier analysis for automated fatigue crack detection in structures. In addition, UML in the form of a fuzzy adaptive resonance theory map was used for the prediction of the compressive strength of high-performance concrete [62] and recently in the design optimization of truss structures [209].
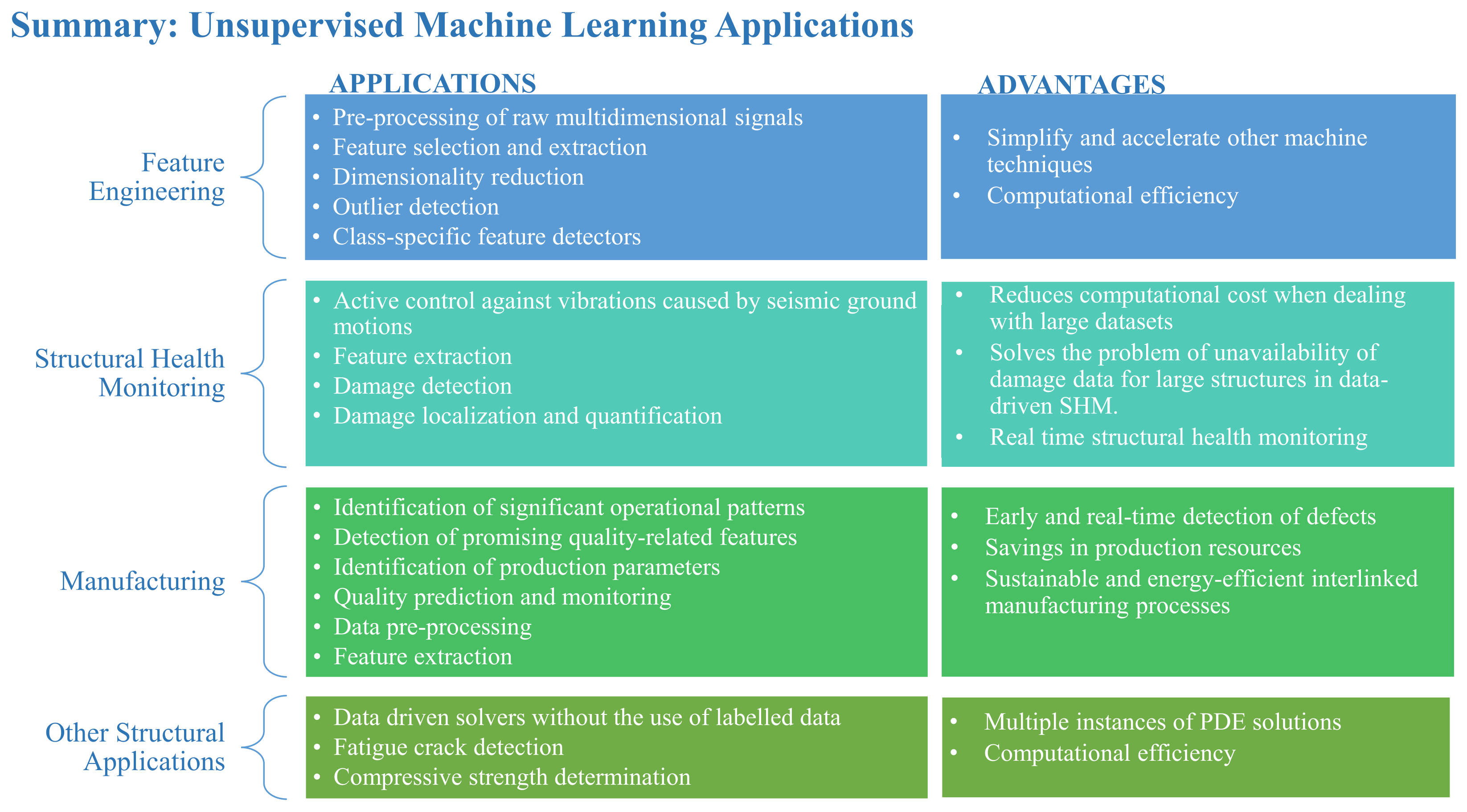
3.7. Summary and Outlook
UML is a valuable tool in structural engineering, enabling the analysis of complex datasets without the need for labeled information. Its applications range from clustering and dimensionality reduction to anomaly detection, all of which aid in understanding structural behaviors and identifying patterns that may not be immediately apparent. The effectiveness of these techniques has been demonstrated in various contexts, including SHM, material characterization, and design optimization as summarized in Figure 6.
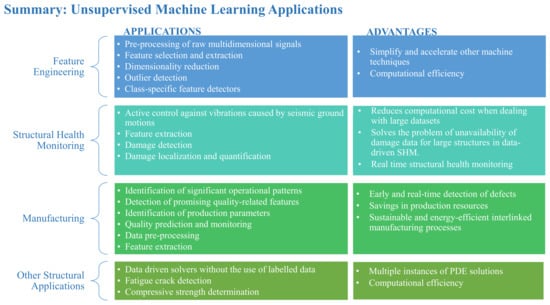
Figure 6.
Summary of UML applications.
Despite the significant advancements in UML methods, several challenges remain. The lack of interpretability in UML algorithms can hinder their adoption in critical applications where understanding the rationale behind decisions is essential. Additionally, the performance of UML models can be sensitive to the underlying assumptions made during the analysis, which may not always align with the complexities of real-world structural systems.
Looking ahead, further research is required to enhance the robustness and reliability of UML techniques in structural engineering. This includes developing methods for better evaluation and validation of UML models, improving algorithms to handle high-dimensional and noisy data, and integrating domain knowledge to guide the learning process. Additionally, advancing interpretability techniques will be crucial for building trust and facilitating the application of UML in practical engineering scenarios.
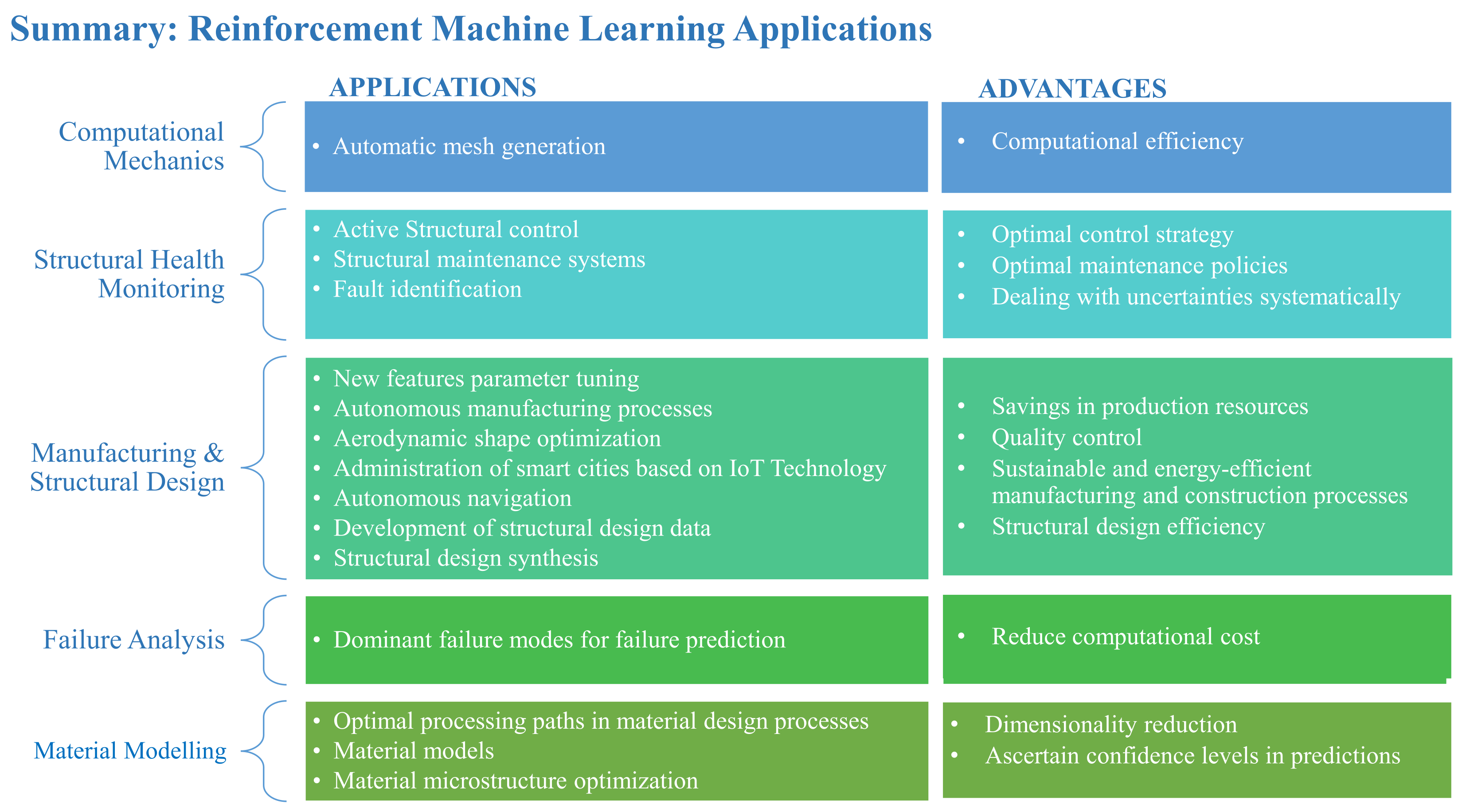
4. Reinforcement Machine Learning Applications
Due to the nature of RML, this class of ML methods is useful for optimization tasks and problems that require a dynamic approach. In most engineering applications, the main goal of RML algorithms is to develop an optimal policy that takes advantage of both the exploratory and exploitative nature of the reinforcement learning paradigm. The agent learns from its previous experiences, using them to maximize its reward, and is also able to develop new solutions by exploring uncharted territory [210]. An agent in a reinforcement learning network adapts quickly to a changing environment, making it very dynamic. The behavior of the agent is often partly deterministic and partly stochastic, making the process of Markov decision an effective formulation for reinforcement learning situations [211]. For complex RML applications that require a lot of training time, especially Markov decision processes (MDPs) that have a large or continuous state, TL has been considered an alternative for speeding up the training time of the reinforcement learning agent [114]. RML has yielded positive results in decision-making and optimization situations involving uncertainties, control, and combinatorial explosion problems as the agent learns from its environment. Popular RML algorithms in research involve the use of Q-learning, adaptive dynamic programming, temporal difference learning, actor–critic reinforcement learning networks, and Monte Carlo simulations [212].
4.1. Data Requirement and Preprocessing
Whereas SML requires high-quality labeled data [213,214] and UML requires large sets of unlabeled data, RML often requires little or no data as an agent learns by trial and error from its experiences in a dynamic environment. An agent can learn from its environment without necessarily having prior knowledge of the environment [211,215]. The data required for reinforcement learning is just enough for the agent to learn how to maximize its long-term reward. Most RML applications are posed as a Markov decision process (MDP) [210,211,212,215], and the MDP is solved when an optimal policy that maximizes the reward function has been found by the agent. In MDPs, models based on free-reinforcement learning algorithms require no knowledge of the reward function or the state-transition probabilities [215], thus reducing the data requirements for model development. It should also be pointed out that data preprocessing techniques depend on the way a problem is formulated in reinforcement learning.
4.2. Computational Mechanics
Mesh generation is an important computational process in the development of accurate, stable, and efficient models for structural analysis. By formulating the mesh generation problem as an MDP, Jie et al. [210] were able to develop a self-learning element extraction system that automatically generates high-quality meshes (quad meshes) in the boundary and interior regions of complex geometries. The proposed meshing algorithm is based on an advantage actor–critic reinforcement learning network. The algorithm is said to be computationally efficient and reduces the time and expertise required for high-quality mesh generation. However, it has been shown that it is difficult to mesh geometries with single-connected domains and boundaries with sharp angles.
4.3. Structural Control
Structural control by means of an RML algorithm has attracted the interest of many researchers. An early work on structural control using reinforcement learning [216] is a case-based algorithm where structural control cases are retrieved and adapted to present control situations based on their past performance. The limitation of this method is that an extensive number of possible control cases need to be prepared for the model. Much more recent RML algorithms formulate the control problem as an MDP [211] or use adaptive dynamic programming [11] or other reinforcement learning methods [217]. RML has become popular for optimal control strategies, especially for complex and nonlinear systems with uncertainties and time variations (e.g., where the structure’s parameters or payload change in time) [215]. It has been used as a control system for the upstream water depth of a canal [218], to suppress transient vibrations in semi-active structures subject to harmonic excitation [219], as a vibration control method for a flexible hinged plate [220], in an Internet-of-Things (IoT)-based bridge structural health monitoring [221], in the structural control of a floating wind turbine [11], and as an active controller for seismic structures [211,217].
The random nature of earthquake disturbances poses systematic uncertainty for the control of structures. Online tuning of an active mass drive system using reinforcement learning has been proposed in [217] for the active control of seismic structures. Arash et al. [217] also incorporated a dynamic state predictor into the reinforcement learning-based controller to accommodate time delay issues. Soheila et al. [211] have further proposed a scalable form of a reinforcement learning-based active control system that is applicable to a variety of control mechanisms, linear and nonlinear response regimes, and several external loadings such as wind, seismic, and other building loads. They also investigated implementation issues such as sensitivity to variations in structural properties and time delays. Reinforcement learning has also been studied for implementation in structural maintenance systems [212,222] and for fault identification [223,224]. An optimal maintenance policy that learns from a bridge’s real historical data [212] and another that seeks to reduce costs [222] have also been developed. A comparative study of several RML algorithms using a baseline dynamic system (a cart-pole) yielded interesting results [215]. An actor–critic policy gradient is shown to converge faster with better stabilization compared to Q-learning in a discrete state-space. In addition, the value-function approximations are demonstrated to have the best performance.
4.4. Structural Design and Manufacturing
RML algorithms are largely applicable in optimization processes while the use of trial-based experiments, physics-based simulations, and surrogate models for the optimization of manufacturing processes is costly, computationally and financially [225]. This is especially true for new features or process parameter tuning. Compared to surrogate models that are case-specific, RML algorithms trained on generic data can be used to develop new non-generic features and process parameters [225]. For large-scale optimization and modeling of autonomic manufacturing processes, they are incorporated as autonomous decision-making systems for robotic operators [226]. The robotic operator learns a behavioral policy that enables it to respond appropriately to variations in its human colleagues and to adapt itself to changes in observations in its environment and its human counterparts. The trained robotic operators are then used to reduce system unpredictability caused by variations in human performance. RML algorithms have been used for general aerodynamic shape optimization in industrial processes without in-depth knowledge of the domain of application [227] and specifically as an aerodynamic shape optimizer for seismic-sensitive structures [228]. They are said to perform better than gradient-based and gradient-free shape optimization methods [227,228].
RML is imperative for the administration of smart cities based on IoT technology [214,221], such as in the optimization of traffic in urban centers. The application of RML algorithms in autonomous navigation has been proposed by several researchers [229,230]. Kevin et al. [230] used Q-learning for offline path planning for autonomous navigation in static environments, and in [229], they studied task and path planning in a constrained but dynamic environment. The work in [229] specifically targeted the assembly and construction of three-dimensional structures using a reinforcement learning trained quadrotor. The optimal policy in [230] is based on path length, safety, and energy consumption while in [229], the optimal path is obtained using a heuristic search method. Structural design, largely being an iterative process, has attracted the application of RML algorithms. Fabian et al. [231] proposed the use of RML for data-driven design automation to overcome the challenges of limited sample and historical design data. They also proposed TL for design tasks using RML. Junhyeon and Rakesh [232] optimized the design of a truss structure using RML. Maximilian and Gordon [233] investigated how to further extend structural design synthesis using deep RML to structural design problems with large state spaces.
4.5. Failure Analysis
Safety assessment often requires the determination of failure modes and stages of components in a structural system. An often-mentioned problem in the optimization of failure prediction using data-driven approaches is that of combinatorial explosion when searching for the dominant failure modes of the structural system [234,235]. Deep RML was applied to combinatorial explosion, posing the failure component selection process as a Markov (sequential) decision process [234,235]. Xiaoshu et al. [234] observed the failure stages and failure components of roof truss and truss bridge structures. They showed that the deep reinforcement approach is computationally efficient and yields a higher accuracy than the Monte Carlo simulation and -unzipping method. The results in [235] show that the proposed method is applicable to failure analysis of actual structures with significantly reduced computational cost.
4.6. Material Modeling and Design
RML has been successfully used in material design optimization problems [213,236] and in dealing with epistemic uncertainty in material models [173]. Johannes et al. [236] employed a deep Q-network with prioritized experience replay to optimize material design processing paths. The optimal processing path yielded a target material structure in the material structure space that delivered a desired set of material properties. Chi-Hua [213] also used Q-learning to optimize the microstructure and material properties of bio-inspired composite materials. The RML algorithm is said to have overcome the high dimensionality problem faced by other optimization methods used in material microstructure design. Due to the “black box” processing nature of ANNs, predictions are usually made without accompanying confidence levels, which can be dangerous for materials with known variability such as concrete [173]. Notice that most of the epistemic uncertainty can occur in a material model due to the unavailability of data on other independent variables that control the material properties. To address this issue, researchers in [173] introduced Bayesian variational inference into an ANN for predicting concrete strength by means of the Monte Carlo dropout method. The Monte Carlo dropout method is incorporated into the model without additional computational cost. The network weights are randomly dropped from the neural network during training and testing [213]. This dropout method introduces model uncertainty into the network. In this manner, the network learns from the uncertainty in its environment (the layers) while making predictions. However, the dropout method in this approach does not allow for extrapolation of results outside the training dataset.
4.7. Summary and Outlook
RML algorithms are suitable for addressing complex optimization problems in structural engineering as summarized in Figure 7. Its capability to adapt to dynamic environments and learn from interactions with them makes RML particularly well suited for applications involving uncertainties, such as structural control and design. The successful implementation of various RML algorithms, including Q-learning and actor–critic methods, has demonstrated their potential to enhance decision-making processes in real-time applications. However, the effectiveness of RML in structural engineering is often limited by the availability of high-quality training data and the computational resources required for extensive training sessions. Additionally, the “black box” nature of many RML algorithms raises concerns about interpretability and the reliability of their predictions, particularly in safety-critical applications.
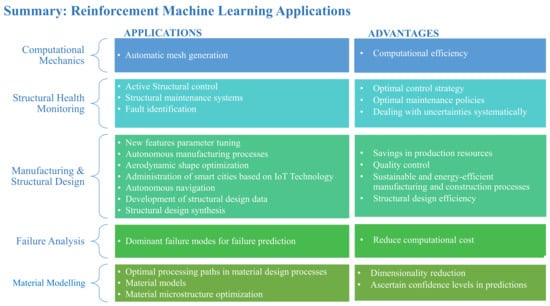
Figure 7.
Summary of RML applications.
There is a need for more research into developing explainable reinforcement learning models that can provide insights into their decision-making processes. Enhancing the robustness of these models against variations in environmental conditions and structural parameters is also crucial. Furthermore, integrating RML with other machine learning paradigms and domain knowledge could facilitate the development of hybrid models that leverage the strengths of each approach.
5. Conclusions
This paper presents a comprehensive review of the applications of machine learning (ML) in structural engineering, examining a diverse array of methodologies and techniques employed to address highly nonlinear problems in this field. The review categorizes the methods into three primary types: supervised machine learning, unsupervised machine learning, and reinforcement machine learning. Each category demonstrates its own strengths: supervised machine learning excels in regression and classification tasks, unsupervised machine learning is adept at clustering and uncovering hidden patterns, and reinforcement machine learning is increasingly favored for automated decision-making applications. Table 1 provides a summary of the applications and methodologies of ML techniques reviewed in this paper.

Table 1.
Summary of ML applications in structural engineering.
Despite the promising advancements in ML for structural engineering applications, several challenges persist, including model reliability, uncertainty quantification, robustness, and interpretability. These challenges, although not the primary focus of this review, represent critical areas for future research aimed at the practical implementation of ML in real-world engineering problems. These challenges and directions for future research were highlighted after surveying the applications of each category of ML methods.
This literature review provides a broad overview of the trends in ML applications within structural engineering, acknowledging the innovative approaches adopted by researchers. The choice of a specific ML method often hinges on the availability of training data; supervised learning is typically preferred when labeled data is accessible, facilitating effective predictions and classifications. In scenarios where unlabeled data is abundant, unsupervised learning techniques play a crucial role in exploratory analysis and anomaly detection. Meanwhile, reinforcement learning stands out for its ability to optimize actions in dynamic environments, making it particularly suitable for structural control applications.
Overall, this review underscores the significance of ML in advancing structural engineering practices, offering insights into how these methods can enhance decision-making, improve model performance, and ultimately contribute to the development of more resilient and efficient structures. Future research should focus on overcoming the existing challenges to maximize the potential of ML in addressing the complexities of real-world structural engineering scenarios.
Funding
The authors gratefully acknowledge the support provided by Qatar University through the internal grant QUCG-CENG-24/25-449, which has significantly facilitated this research.
Acknowledgments
The authors gratefully acknowledge the support provided by Qatar University through Collaborative Grant QUCG-CENG-24/25-449. The findings achieved herein are solely the responsibility of the authors.
Conflicts of Interest
The authors declare that there are no conflicts of interest regarding the publication of this paper.
References
- Zhou, L.; Pan, S.; Wang, J.; Vasilakos, V. Machine learning on big data: Opportunities and challenges. Neurocomputing 2017, 237, 350–361. [Google Scholar] [CrossRef]
- Sui, K.; Lee, W. Image processing analysis and research based on game animation design. J. Vis. Commun. Image Represent. 2019, 64, 94–100. [Google Scholar] [CrossRef]
- Yang, T.; Cappelle, C.; Ruichek, Y.; Bagdouri, M. Multi-object tracking with discriminant correlation filter based deep learning tracker. Integr. Comput.-Aided Eng. 2019, 26, 273–284. [Google Scholar] [CrossRef]
- Syed, F.; Tahir, M.; Rafi, M.; Shahab, M. Features selection for semi-supervised multi-target regression using genetic algorithm. Appl. Intell. 2021, 51, 8961–8984. [Google Scholar] [CrossRef]
- Wang, P.; Bai, X. Regional parallel structural based CNN for thermal infrared face identification. Integr. Comput.-Aided Eng. 2018, 25, 247–260. [Google Scholar] [CrossRef]
- Choppala, S.; Kelmar, T.W.; Chierichetti, M.; Davoudi, F.; Huang, D. Optimal sensor location and stress prediction on a plate using machine learning. In Proceedings of the AIAA SCITECH 2023 Forum, Online, 23–27 January 2023. [Google Scholar]
- Badillo, S.; Banfai, B.; Brizzle, F.; Davy, I.; Hutchinson, L.; Kam-Thong, T.; Polster, J.; Steleret, B.; Zhang, D. An introduction to machine learning. Clin. Pharmacol. Ther. 2020, 107, 871–885. [Google Scholar] [CrossRef] [PubMed]
- Karmaker, S.; Hassan, M.; Smith, M.; Xu, L.; Zhai, C. ACM computing surveys. Knowl. Inf. Syst. 2022, 54, 1–36. [Google Scholar]
- Laisisi, A.; Attoh-Okine, N. Principal components analysis and track quality index: A machine learning approach. Transp. Res. Part C Emerg. Technol. 2018, 91, 230–248. [Google Scholar] [CrossRef]
- Le, Q. Building high-level features using large scale unsupervised learning. In Proceedings of the 2013 IEEE International Conference on Acoustics, Speech and Signal Processing, Vancouver, BC, Canada, 26–31 May 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 8595–8598. [Google Scholar]
- Zhang, J.; Zhao, X.; Wei, X. Reinforcement learning-based structural control of floating wind turbines. IEEE Trans. Syst. Man Cybern. Syst. 2020, 52, 1603–1613. [Google Scholar] [CrossRef]
- Jain, A. Data clustering: 50 years beyond K-means. Pattern Recognit. Lett. 2010, 9, 651–666. [Google Scholar] [CrossRef]
- Zhang, J.; Xiao, M.; Gao, M.; Chu, S. Probability and interval hybrid reliability analysis based on adaptive local approximation of projection outlines using support vector machine. Comput.-Aided Civ. Infrastruct. Eng. 2019, 34, 991–1009. [Google Scholar] [CrossRef]
- Yu, B.; Wang, H.; Shan, W.; Yao, B. Prediction of bus travel time using random forests based on near neighbors. Comput.-Aided Civ. Infrastruct. Eng. 2018, 33, 333–350. [Google Scholar] [CrossRef]
- Shetty, S.; Shetty, S.; Singh, C.; Rao, A. Supervised machine learning: Algorithms and applications. In Fundamental and Methods of Machine and Deep Learning: Algorithms, Tools and Applications; Wiley: Hoboken, NJ, USA, 2022; pp. 1–16. [Google Scholar]
- Abbasi, H.; Bennet, L.; Guann, J.; Unsworth, C. Latent phase detection of hypoxic-ischemic spike transients in the EEG of preterm fetal sheep using reverse biorthogonal wavelets and fuzzy classifier. Int. J. Neural Syst. 2019, 29, 195–212. [Google Scholar] [CrossRef] [PubMed]
- Quinlan, J. Introduction of decision trees. Mach. Learn. 1986, 1, 81–106. [Google Scholar] [CrossRef]
- Lopez-Rubio, E.; Molina-Cabello, E.; Lique-Baena, M.; Dominguez, E. Foreground detection by competitive learning for varying input distributions. Int. J. Neural Syst. 2018, 28, 175–191. [Google Scholar] [CrossRef]
- Chen, Z.; Liu, C. Roadway asset inspection sampling using high-dimensional clustering and locality-sensitivity hashing. Comput.-Aided Civ. Infrastruct. Eng. 2019, 34, 116–129. [Google Scholar] [CrossRef]
- Tramel, W.; Gabrie, M.; Manoel, A.; Caltagirone, F.; Krozakala, F. Deterministic and generalized framework for unsupervised learning with restricted Boltzmann machines. Phys. Rev. 2018, 8, 041006. [Google Scholar] [CrossRef]
- Marugan, A. Applications of reinforcement learning for maintenance of engineering systems:A review. Adv. Eng. Softw. 2023, 183, 103–117. [Google Scholar] [CrossRef]
- Park, J.; Park, J. Enhanced machine learning algorithms: Deep learning, reinforcement learning and Q-learning. J. Inf. Process. Syst. 2020, 16, 1001–1007. [Google Scholar]
- Abdi, J.; Moshiri, B. Application of temporal difference learning rules in short-term traffic flow prediction. Expert Syst. 2015, 32, 49–64. [Google Scholar] [CrossRef]
- Ahmad, T.; Chen, H. Deep learning for multi-scale smart energy forecasting. Energy 2019, 175, 98–112. [Google Scholar] [CrossRef]
- Bishop, C. Pattern Recognition and Machine Learning; Information science and statistics; Springer: New York, NY, USA, 2006. [Google Scholar]
- Andrew, G.; Ritchard, B.; Sutton, S. Reinforcement Learning, 2nd ed.; The MIT Press: Cambridge, MA, USA, 2018. [Google Scholar]
- Jiang, T.; Gradus, J.L.; Rosellini, A. Supervised machine learning: A brief primer. Behav. Ther. 2020, 51, 675–687. [Google Scholar] [CrossRef] [PubMed]
- Singh, A.; Thakur, N.; Sharma, A. A review of supervised machine learning algorithms. Behav. Ther. 2016, 3, 16–32. [Google Scholar]
- Osisanwo, Y.; Akinsola, T.; Awodele, O.; Hinmikaiye, O.; Olakanmi, O.; Akinjobi, J. Supervised machine learning algorithms: Classification and comparison. Int. J. Comput. Trends Technol. 2017, 48, 128–138. [Google Scholar]
- Kotsiantis, B.; Zaharakis, L.; Pintelas, P. Supervised machine learning: A review of classification techniques. Emerg. Artif. Intell. Appl. Comput. Eng. 2007, 160, 3–24. [Google Scholar]
- Belavagi, M.; Muniyal, B. Performance evaluation of supervised machine learning algorithms for the intrusion detection. Procedia Comput. Sci. 2016, 89, 117–123. [Google Scholar] [CrossRef]
- Kim, E.; Kim, W.; Lee, Y. Combination of multiple classifiers for the customers purchase behavior prediction. Decis. Support Syst. 2003, 34, 167–175. [Google Scholar] [CrossRef]
- Huang, J.; Li, Y.; Xie, M. An empirical analysis of data preprocessing for machine learning-based software cost estimation. Inf. Softw. Technol. 2015, 67, 108–127. [Google Scholar] [CrossRef]
- Miseta, T.; Fodor, A.; Vathy-Fogarassy, A. Surpassing early stopping:A novel correlation-based stopping criterion for neural networks. Neurocomputing 2024, 567, 127028. [Google Scholar] [CrossRef]
- Ahmed, U.; Momtaz, R.; Anwar, H.; Shan, A.; Ifran, R.; Nieto, J. Efficient water quality prediction using supervised machine learning. Water 2019, 11, 2210. [Google Scholar] [CrossRef]
- Fernandez, A.; Bella, J.; Dorronsoro, J. Supervised outlier detection for classification and regression. Neurocomputing 2022, 486, 77–92. [Google Scholar] [CrossRef]
- Praveena, M.; Jaiganesh, V. A literature review on supervised machine learning algorithms and boosting process. Int. J. Comput. Appl. 2017, 169, 975–988. [Google Scholar] [CrossRef]
- Jaccard, J.; Wan, C.; Turrisi, R. The detection and interpretation of interaction effects between continuous variables in multiple regression. Multivar. Behav. Res. 1990, 25, 467–478. [Google Scholar] [CrossRef] [PubMed]
- Bahnsen, A.; Aouacha, D.; Ottersten, B. Dependent cost-sensitive decision trees. Expert Syst. Appl. 2015, 42, 6609–6619. [Google Scholar] [CrossRef]
- Maulud, D.; Abdulazez, A. A review on linear regression comprehensive in machine learning. J. Appl. Sci. Technol. Trends 2020, 1, 140–147. [Google Scholar] [CrossRef]
- Utkin, V.; Zhuk, Y. A one-class classification support vector machine model by interval-valued training data. Knowl.-Based Syst. 2017, 120, 43–56. [Google Scholar] [CrossRef]
- Castillo-Botón, C.; Casillas-Pérez, D.; Casanova-Mateo, C.; Ghimire, S.; Cerro-Prada, E.; Gutierrez, P.; Deo, R.; Salcedo-Sanz, S. Machine learning regression and classification methods for fog events prediction. Atmos. Res. 2022, 272, 106157. [Google Scholar] [CrossRef]
- Wojtowytsch, S. Stochastic gradient descent with noise of machine learning type 1:Discrete time analysis. J. Nonlinear Sci. 2023, 33, 45. [Google Scholar] [CrossRef]
- Polyak, B. Some methods of speeding up the convergence of iteration methods. USSR Comput. Math. Math. Phys. 1964, 4, 1–17. [Google Scholar] [CrossRef]
- Peng, Y.; Lee, W. Practical guidelines for resolving the loss divergence caused by the root-mean-aquared propagation optimizer. Appl. Soft Comput. 2024, 153, 13–37. [Google Scholar] [CrossRef]
- Lioyd, S.; Mohsen, M.; Robentrost, P. Quantum algorithms for supervised and unsupervised machine learning. Int. J. Quantuum Phys. 2013, 3, 17–32. [Google Scholar]
- Hofmann, T. Unsupervised learning by probabilistic latent semantic analysis. Int. J. Mach. Learn. 2001, 42, 177–196. [Google Scholar] [CrossRef]
- Sinaga, K.; Yang, M. Unsupervised K-means clustering algorithm. IEEE Access 2020, 8, 80716–80727. [Google Scholar] [CrossRef]
- Mathias, S.; Slager, R. Unsupervised machine learning and band topology. Phys. Rev. Lett. 2020, 124, 226–241. [Google Scholar]
- Einst, D.; Wehenkel, L.; Geurts, P. Trees-based batch mode reinforcement learning. J. Mach. Learn. Res. 2005, 6, 503–2556. [Google Scholar]
- Lin, J. Self improving reactive agents based on reinforcement learning, planning and teaching. J. Mach. Learn. Res. 1992, 8, 293–321. [Google Scholar] [CrossRef]
- Riedmiller, M. Concepts and facilities of a neural reinforcement learning control architecture for technical process control. J. Neural Comput. Appl. 2000, 8, 323–338. [Google Scholar] [CrossRef]
- Agarwal, A.; Kakade, S.; Lee, J.; Mahajen, G. On the theory of policy gradient methods: Optimality, approximation and distribution shift. J. Mach. Learn. Res. 2021, 22, 1–76. [Google Scholar]
- Aswani, A.; Gonzalez, H.; Sastry, S.; Tomlin, G. Probably safe and robust learning-based model predictive control. Automatica 2013, 49, 1216–1226. [Google Scholar] [CrossRef]
- Azar, M.; Munos, R.; Kappen, H. Minimax bounds on the sample, complexity of reinforcement learning with a generative model. Mach. Learn. 2013, 91, 325–349. [Google Scholar] [CrossRef][Green Version]
- Sutton, R.; Andrew, B. Reinforcement learning: An introduction. Robotica 1999, 17, 229–235. [Google Scholar] [CrossRef]
- Ethem, A. Introduction to Machine Learning; MIT Press: Cambridge, MA, USA, 2020. [Google Scholar]
- Ahmed, N.; Atiya, A.; Gayar, N.; El-shishiny, H. An empirical comparison of machine learning models for time series forecasting. Econ. Rev. 2010, 29, 594–621. [Google Scholar] [CrossRef]
- Carbonneau, R.; Lafiamboise, K.; Vaidov, R. Application of machine learning techniques for supply chain demand forecasting. Eur. J. Oper. Res. 2008, 184, 1140–1154. [Google Scholar] [CrossRef]
- Ghaboussi, J.; Garrett, J.; Xiping, W. Knowledge-based modeling of material behavior with neural networks. J. Eng. Mech. 1991, 117, 132–153. [Google Scholar] [CrossRef]
- Yeh, I.C. Modeling concrete strength with augment-neuron networks. J. Mater. Civ. Eng. 1998, 10, 263–268. [Google Scholar] [CrossRef]
- Janusz, K.; Janusz, R.; Artur, D. HPC strength prediction using artificial neural network. J. Comput. Civ. Eng. 1995, 9, 279–284. [Google Scholar]
- Yeh, I.C. Design of high-performance concrete mixture using neural networks and nonlinear programming. J. Comput. Civ. Eng. 1999, 13, 36–42. [Google Scholar] [CrossRef]
- Trent, S.; Renno, J.; Sassi, S.; Mohamed, S. Using image processing techniques in computational mechanics. Comput. Math. Appl. 2023, 136, 1–24. [Google Scholar] [CrossRef]
- Capuano, G.; Rimoli, J.J. Smart finite elements: A novel machine learning. Comput. Methods Appl. Mech. Eng. 2019, 345, 363–381. [Google Scholar] [CrossRef]
- Nashed, M.; Renno, J.; Mohamed, S. Nonlinear analysis of shell structures using image processing and machine learning. Adv. Eng. Softw. 2023, 176, 103392. [Google Scholar] [CrossRef]
- Cabrera, M.; Ninic, J.; Tizani, W. Fusion of experimental and synthetic data for reliable prediction of steel connection behaviour using machine learning. Eng. Comput. 2023, 39, 3993–4011. [Google Scholar] [CrossRef]
- Bolaji, O.; Helio, M.; Krishnan, A.; Sumanta, D. Integrating Experiments, Finite Element Analysis, and Interpretable Machine Learning to Evaluate the Auxetic Response of 3D Printed Re-entrant Metamaterials. J. Mater. Res. Technol. 2023, 25, 1612–1625. [Google Scholar]
- Liang, L.; Liu, M.; Martin, C.; Sun, W. A deep learning approach to estimate stress distribution: A fast and accurate surrogate of finite-element analysis. J. R. Soc. Interface 2018, 15, 20170844. [Google Scholar] [CrossRef] [PubMed]
- Silva, G.; Beber, V.; Pitz, D. Machine learning and finite element analysis: An integrated approach for fatigue lifetime prediction of adhesively bonded joints. Fatigue Fract. Eng. Mater. Struct. 2021, 44, 3334–3348. [Google Scholar] [CrossRef]
- Jokar, M.; Semperlotti, F. Finite element network analysis: A machine learning based computational framework for the simulation of physical systems. Comput. Struct. 2021, 247, 106484. [Google Scholar] [CrossRef]
- Koutsourelakis, S. Stochastic upscaling in soild mechanics: An exercise in machine learning. J. Comput. Phys. 2007, 226, 301–325. [Google Scholar] [CrossRef]
- Oishi, A.; Yagawa, G. Computational mechanics enhanced by deep learning. Comput. Methods Appl. Mech. Eng. 2017, 327, 327–351. [Google Scholar] [CrossRef]
- Kirchdoerfer, T.; Ortiz, M. Data-driven computational mechanics. Comput. Methods Appl. Mech. Eng. 2016, 304, 81–101. [Google Scholar] [CrossRef]
- Lees, H.; Kang, S. Neural algorithm for solving differential equations. J. Comput. Phys. 1990, 91, 110–131. [Google Scholar]
- Meade, J.; Fernandez, A. The numerical solution of linear ordinary differential equations by feedward neural networks. Math. Comput. Model. 1994, 91, 1–25. [Google Scholar] [CrossRef]
- Lagaris, E.; Likas, A.; Fotiadis, I. Artificial neural networks for solving ordinary and partial differential equations. Trans. Neural Netw. 1998, 9, 987–1000. [Google Scholar] [CrossRef] [PubMed]
- Wu, L.; Wang, X.; Xiao, H.; Ling, J. A priori assessment of prediction confidence for data-driven turbulance modeling. Flow Turbul. Combust. 2017, 99, 25–46. [Google Scholar] [CrossRef]
- Xiao, H.; Wu, L.; Wang, H.; Sun, R.; Roy, J. Quantifying and reducing model-form uncertainties in Reynolds averaged Navier-stokes simulations. J. Comput. Phys. 2016, 324, 115–136. [Google Scholar] [CrossRef]
- Weinan, E.; Han, J.; Jentzen, A. Deep learning-based numerical methods for high-dimensional parabolic partial differential equations and backward stochastic differential equations. Commun. Math. Stat. 2017, 5, 349–380. [Google Scholar]
- Berg, J.; Nystorm, K. A unified deep artificial neural network approach to partial differential equations in complex geometries. Neurocomputing 2018, 317, 28–41. [Google Scholar] [CrossRef]
- Trask, N.; Patel, R.; Paul, B.; Atzberger, J. GMLS-Nets: Aframe work for learning from unstructured data. Comput. Sci. 2019, 7, 15–29. [Google Scholar]
- Dufera, T. Deep neural network for system of ordinary differential equatuions: Vectorized algorithm and simulation. Mach. Learn. Appl. 2021, 5, 532–549. [Google Scholar]
- Guo, Y.; Cao, X.; Liu, B.; Gao, M. Solving partial differential equations using deep learning and physical constraints. Appl. Sci. 2020, 10, 5917. [Google Scholar] [CrossRef]
- Saha, S.; Gan, Z.; Cheng, L.; Gao, J.; Kafka, O.; Xie, X.; Li, H.; Tajdari, M.; Kim, H.; Liu, W. Hierarchical deep learning neural network HiDeNN: An artificial intelligence AI framework for computational science and engineering. Comput. Methods Appl. Mech. Eng. 2021, 378, 113452. [Google Scholar] [CrossRef]
- Raissi, M.; Perdikaris, P.; Karniadakis, E. Physics-informed neural networks:Adeep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J. Comput. Phys. 2019, 378, 686–707. [Google Scholar] [CrossRef]
- Raissi, M.; Karniadakis, E. Machine learning of nonlinear partial differential equations. J. Comput. Phys. 2018, 357, 125–141. [Google Scholar] [CrossRef]
- Badarinath, V.; Chierichetti, M.; Kakhki, F. A machine learning approach as a surrogate for a finite element analysis: Status of research and application to one dimensional systems. Sensors 2021, 21, 1654. [Google Scholar] [CrossRef] [PubMed]
- Hashemi, A.; Jang, J.; Beheshti, J. A Machine Learning-Based Surrogate Finite Element Model for Estimating Dynamic Response of Mechanical Systems. IEEE Access 2023, 11, 54509–54525. [Google Scholar] [CrossRef]
- Lu, M.; Mohammadi, A.; Meng, Z.; Meng, X.; Li, G.; Li, Z. Deep neural operator for learning transient response of interpenetrating phase composites subject to dynamic loading. Comput. Mech. 2023, 72, 563–576. [Google Scholar] [CrossRef]
- Li, Q.; Wang, Z.; Li, L.; Hao, H.; Chen, W.; Shao, Y. Machine learning prediction of structural dynamic responses using graph neural networks. Comput. Struct. 2023, 289, 107188. [Google Scholar] [CrossRef]
- Najera-Flores, D.A.; Quinn, D.D.; Garland, A.; Vlachas, K.; Chatzi, E.; Todd, M.D. A structure-preserving machine learning framework for accurate prediction of structural dynamics for systems with isolated nonlinearities. Mech. Syst. Signal Process. 2024, 213, 111340. [Google Scholar] [CrossRef]
- Jung, J.; Jun, H.; Lee, P. Self-updated four-node finite element using deep learning. Comput. Mech. 2022, 69, 23–44. [Google Scholar] [CrossRef]
- Logarzo, H.J.; Capuano, G.; Rimoli, J.J. Smart constitutive laws: Inelastic homogenization through machine learning. Comput. Methods Appl. Mech. Eng. 2021, 373, 113482. [Google Scholar] [CrossRef]
- Brevis, I.; Muga, I.; der Zee, K.V. A machine-learning minimal-residual (ML-MRes) framework for goal-oriented finite element discretizations. Comput. Math. Appl. 2021, 95, 186–199. [Google Scholar] [CrossRef]
- Mishra, S. A machine learning framework for data driven acceleration of computations of differential equations. Math. Eng. 2018, 1, 118–146. [Google Scholar] [CrossRef]
- Farrarand, C.; Worden, K. An introduction to structural health monitoring. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2007, 365, 303–315. [Google Scholar] [CrossRef] [PubMed]
- De Iuliis, M.; Miceli, E.; Castaldo, P. Machine learning modelling of structural response for different seismic signal characteristics: A parametric analysis. Appl. Soft Comput. 2024, 164, 112026. [Google Scholar] [CrossRef]
- Brownjohn, J. Structural health monitoring of civil infrastructure. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2007, 365, 589–622. [Google Scholar] [CrossRef] [PubMed]
- Wagg, J.; Worden, K.; Barthorpe, R.; Gardner, P. Digital twins: State-of-the-art and future directions for modeling and simulation in engineering dynamics applications. ASCE-ASME J. Risk Uncertain. Eng. Syst. Part B Mech. Eng. 2020, 6, 030901. [Google Scholar] [CrossRef]
- Tronci, E.; Beigi, H.; Feng, M.; Betti, R. A transfer learning SHM strategy for bridges enriched by the use of speaker recognition x-vectors. J. Civ. Struct. Health Monit. 2022, 12, 1285–1298. [Google Scholar] [CrossRef]
- Worden, K.; Manson, G. The application of machine learning to structural health monitoring. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2007, 365, 515–537. [Google Scholar] [CrossRef]
- Farrar, C.; Doebling, S.; Nix, D. Vibration–based structural damage identification. Philos. Trans. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 2001, 359, 131–149. [Google Scholar] [CrossRef]
- Yeh, I.C.; Yau-Hwaug, K.; Deh-Shiu, H. Building KBES for diagnosing PC pile with artificial neural network. J. Comput. Civ. Eng. 1993, 7, 71–93. [Google Scholar] [CrossRef]
- González, P.; Zapico, L. Seismic damage identification in buildings using neural networks and modal data. Comput. Struct. 2008, 86, 416–426. [Google Scholar] [CrossRef]
- Chang, C.; Lin, T.; Chang, C. Applications of neural network models for structural health monitoring based on derived modal properties. Measurement 2018, 129, 457–470. [Google Scholar] [CrossRef]
- Soyoz, S.; Feng, Q. Long-term monitoring and identification of bridge structural parameters. Comput.-Aided Civ. Infrastruct. Eng. 2009, 24, 82–92. [Google Scholar] [CrossRef]
- Peng, J.; Zhang, S.; Peng, D.; Liang, K. Application of machine learning method in bridge health monitoring. In Proceedings of the 2017 Second International Conference on Reliability Systems Engineering (ICRSE), Beijing, China, 10–12 July 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 1–7. [Google Scholar]
- Giglioni, V.; Venanzi, I.; Ubertini, F. Supervised machine learning techniques for predicting multiple damage classes in bridges. In Proceedings of the Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series, Long Beach, CA, USA, 12–17 March 2023; Volume 12486, p. 1248617. [Google Scholar]
- Kao, C.; Loh, C. Monitoring of long-term static deformation data of Fei-Tsui arch dam using artificial neural network-based approaches. Struct. Control Health Monit. 2013, 20, 282–303. [Google Scholar] [CrossRef]
- Ranković, V.; Grujović, N.; Divac, D.; Milivojević, N. Development of support vector regression identification model for prediction of dam structural behaviour. Struct. Saf. 2014, 48, 33–39. [Google Scholar] [CrossRef]
- Santillán, D.; Fraile-Ardanuy, J.; Toledo, M.Á. Prediction of gauge readings of filtration in arch dams using artificial neural networks. Tecnol. Cienc. Agua 2014, 5, 81–96. [Google Scholar]
- Song, J.; Yuan, S.; Xu, Z.; Li, X. Fast inversion method for seepage parameters of core earth-rock dam based on LHS-SSA-MKELM fusion surrogate model. Structures 2023, 55, 160–168. [Google Scholar] [CrossRef]
- Taylor, M.; Stone, P. Transfer learning for reinforcement learning domains: A survey. J. Mach. Learn. Res. 2009, 10, 1633–1685. [Google Scholar]
- Zhuang, F.; Qi, Z.; Duan, K.; Xi, D.; Zhu, Y.; Zhu, H.; Xiong, H.; He, Q. A Comprehensive survey on transfer learning. Proc. IEEE 2021, 109, 43–76. [Google Scholar] [CrossRef]
- Gardner, P.; Bull, L.; Dervilis, N.; Worden, K. On the application of Kernelised Bayesian transfer learning to population-based structural health monitoring. Mech. Syst. Signal Process. 2022, 167, 108519. [Google Scholar] [CrossRef]
- Gosliga, J.; Hester, D.; Worden, K.; Bunce, A. On Population-based structural health monitoring for bridges. Mech. Syst. Signal Process. 2022, 173, 108919. [Google Scholar] [CrossRef]
- Bao, N.; Zhang, T.; Huang, R.; Biswal, S.; Su, J.; Wang, Y. A deep transfer learning network for structural condition identification with limited real-world training data. Struct. Control Health Monit. 2023, 8899806. [Google Scholar] [CrossRef]
- Li, Y.; Bao, T.; Gao, Z.; Shu, X.; Zhang, K.; Xie, L.; Zhang, Z. A new dam structural response estimation paradigm powered by deep learning and transfer learning techniques. Struct. Health Monit. 2022, 21, 770–787. [Google Scholar] [CrossRef]
- Tsialiamanis, G.; Wagg, D.; Gardner, P.; Dervilis, N.; Worden, K. On partitioning of an SHM problem and parallels with transfer learning. In Topics in Modal Analysis & Testing, Volume 8: Proceedings of the 38th IMAC, A Conference and Exposition on Structural Dynamics 2020; Springer: Cham, Switzerland, 2021; pp. 41–50. [Google Scholar]
- Azad, M.; Kim, S.; Cheon, Y.; Kim, H. Intelligent structural health monitoring of composite structures using machine learning, deep learning, and transfer learning: A review. Adv. Compos. Mater. 2023, 33, 162–188. [Google Scholar] [CrossRef]
- Kamariotis, A.; Chatzi, E.; Straub, D. A framework for quantifying the value of vibration-based structural health monitoring. Mech. Syst. Signal Process. 2023, 184, 109708. [Google Scholar] [CrossRef]
- Markogiannaki, O.; Arailopoulos, A.; Giagopoulos, D.; Papadimitriou, C. Vibration-based Damage Localization and Quantification Framework of Large-Scale Truss Structures. Struct. Health Monit. 2023, 22, 1376–1398. [Google Scholar] [CrossRef]
- Pizarro, P.; Massone, L. Structural design of reinforced concrete buildings based on deep neural networks. Eng. Struct. 2021, 241, 112377. [Google Scholar] [CrossRef]
- Chaillou, S. Archigan: Artificial intelligence x architecture. In Architectural Intelligence: Selected Papers from the 1st International Conference on Computational Design and Robotic Fabrication (CDRF 2019); Springer: Berlin/Heidelberg, Germany, 2020; pp. 117–127. [Google Scholar]
- Ampanavos, S.; Nourbakhsh, M.; Cheng, C. Structural design recommendations in the early design phase using machine learning. In International Conference on Computer-Aided Architectural Design Futures; Springer: Singapore, 2022; pp. 190–202. [Google Scholar]
- Rasoulzadeh, S.; Senk, V.; Königsberger, M.; Reisinger, J.; Kovacic, I.; Füssl, J.; Wimmer, M. A novel integrative design framework combining 4D sketching, geometry reconstruction, micromechanics material modelling, and structural analysis. Adv. Eng. Informatics 2023, 57, 102074. [Google Scholar] [CrossRef]
- Liao, W.; Lu, X.; Huang, Y.; Zheng, Z.; Lin, Y. Automated structural design of shear wall residential buildings using generative adversarial networks. Autom. Constr. 2021, 132, 103931. [Google Scholar] [CrossRef]
- Zhang, Y.; Mueller, C. Shear wall layout optimization for conceptual design of tall buildings. Eng. Struct. 2017, 140, 225–240. [Google Scholar] [CrossRef]
- Lou, H.; Gao, B.; Jin, F.; Wan, Y.; Wang, Y. Shear wall layout optimization strategy for high-rise buildings based on conceptual design and data-driven tabu search. Comput. Struct. 2021, 250, 106546. [Google Scholar] [CrossRef]
- Chang, K.; Cheng, C. Learning to simulate and design for structural engineering. In Proceedings of the International Conference on Machine Learning, PMLR, Virtual, 13–18 July 2020; pp. 1426–1436. [Google Scholar]
- Preisinger, C.; Heimrath, M. Karamba—A toolkit for parametric structural design. Struct. Eng. Int. 2014, 24, 217–221. [Google Scholar] [CrossRef]
- Khayam, S.; Ajmal, A.; Park, J.; Kim, I.; Park, J. Tendon Stress Estimation from Strain Data of a Bridge Girder Using Machine Learning-Based Surrogate Model. Sensors 2023, 23, 5040. [Google Scholar] [CrossRef] [PubMed]
- Motsa, S.M.; Stavroulakis, G.E.; Drosopoulos, G.A. A data-driven, machine learning scheme used to predict the structural response of masonry arches. Eng. Struct. 2023, 296, 116912. [Google Scholar] [CrossRef]
- Habib, M.; Bashir, B.; Alsalman, A.; Bachir, H. Evaluating the accuracy and effectiveness of machine learning methods for rapidly determining the safety factor of road embankments. Multidiscip. Model. Mater. Struct. 2023, 19, 966–983. [Google Scholar] [CrossRef]
- Skordaris, G.; Bouzakis, K.; Charalampous, P.; Kotsanis, T.; Bouzakis, E.; Bejjani, R. Bias voltage effect on the mechanical properties, adhesion and milling performance of PVD films on cemented carbide inserts. Wear 2018, 404, 50–61. [Google Scholar] [CrossRef]
- Fu, Z.; Yang, W.; Wang, X.; Leopold, J. An analytical force model for ball-end milling based on a predictive machine theory considering cutter runout. Int. J. Adv. Manuf. Technol. 2017, 93, 2061–2069. [Google Scholar]
- Newby, G.; Venkatachalam, S.; Liang, S. Empirical analysis of cutting force constants in Micro-end-milling operations. J. Mater. Process. Technol. 2007, 192, 41–47. [Google Scholar] [CrossRef]
- Man, X.; Ren, D.; Usui, C.; Johnson, T.; Marusich, T. Validation of finite element cutting force prediction for end milling. Procedia CIRP 2012, 1, 663–668. [Google Scholar] [CrossRef]
- Michailidis, N.; Kombogiannis, S.; Charalampous, P.; Maliaris, G.; Stegioudi, F. Computational-experimental investigations of milling porous Aluminimum. CIRP Ann. 2017, 66, 121–124. [Google Scholar] [CrossRef]
- Charalampous, P. Prediction of cutting forces in milling using machine learning algorithms and finite element analysis. J. Mater. Eng. Perform. 2002, 30, 2002–2012. [Google Scholar] [CrossRef]
- Jirousek, O.; Palar, P.; Falta, J.; Dwianto, Y. Design exploration of additively manufactured chiral auxetic structure using explainable machine learning. Mater. Des. 2023, 232, 112128. [Google Scholar]
- Grozav, S.; Sterca, A.; Kočiško, M.; Pollák, M.; Ceclan, V. Artificial Neural Network-Based Predictive Model for Finite Element Analysis of Additive-Manufactured Components. Machines 2023, 11, 547. [Google Scholar] [CrossRef]
- Dwyer, A.; Mathews, B.; Azadani, A.; Ge, L.; Guy, S.; Tseng, E. Migration forces of transcatheter aortic valves in patients with noncalcific aortic insufficiency. J. Thorac. Cardiovasc. Surg. 2009, 138, 1227–1233. [Google Scholar] [CrossRef] [PubMed]
- Aurccio, F.; Conti, M.; Morganti, S.; Reali, A. Simulations of transcather aortic valve implementation: Apatient-specific finite element approach. Comput. Methods Biomech. Biomed. Eng. 2014, 17, 1347–1357. [Google Scholar] [CrossRef] [PubMed]
- Liang, L.; Minliang, L.; John, E.; Wei, S. Synergistic integration of deep neural networks and finite element method with applications of nonlinear large deformation biomechanics. Comput. Methods Appl. Mech. Eng. 2023, 416, 116–218. [Google Scholar] [CrossRef]
- Jiang, H.; Nie, Z.; Yeo, R.; Farimani, A.; Burak, K. Stressgan: A generative deep learning model for two-dimensional stress distribution prediction. J. Appl. Mech. 2021, 88, 051005. [Google Scholar] [CrossRef]
- Kazeruni, M.; Ince, A. Data-driven artificial neural network for elastic plastic stress and strain computation for notched bodies. Theor. Appl. Fract. Mech. 2023, 125, 103917. [Google Scholar] [CrossRef]
- Yan, W.; Deng, L.; Zhang, F.; Li, T.; Li, S. Probabilistic machine learning approach to bridge fatigue failure analysis due to vehicular overloading. Eng. Struct. 2019, 193, 91–99. [Google Scholar] [CrossRef]
- Reiner, J.; Linden, N.; Vaziri, R.; Zobeiry, N.; Kramer, B. Bayesian parameter estimation for the inclusion of uncertainty in progressive damage simulation of composites. Compos. Struct. 2023, 321, 117257. [Google Scholar] [CrossRef]
- Bui, Q.; Tran, V.; Shan, A. Improved knowledge-based neural network (KBNN) model for predicting spring-back angles in metal sheet bending. Int. J. Model. Simul. Sci. Comput. 2014, 5, 135–146. [Google Scholar] [CrossRef]
- Rafiq, Y.; Bugmann, G.; Easterbrook, J. Neural network design for engineering applications. Comuters Struct. 2001, 79, 1541–1552. [Google Scholar] [CrossRef]
- Kan, S.; Tan, C.; Mathew, J. A review on prognostic techniques for non-stationary and non-linear totating systems. Mech. Syst. Signal Process. 2015, 62, 1–20. [Google Scholar] [CrossRef]
- Yu, S.; Qi, S.; Liu, L.; Xu, Q.; Wu, L.; Zeng, W. Application of the Ultrasonic Guided Wave Technique Based on PSO-ELM Algorithm in the Rail Fatigue Crack Assessment. J. Test. Eval. 2023, 51, JTE20220569. [Google Scholar] [CrossRef]
- Cheng, Y.; Huang, L.; Zhou, Y. Artificial neural network technology for the data processing of one-line corrosion fatigue crack growth monitoing. Int. J. Pres. Ves. Pip 1999, 76, 113–116. [Google Scholar] [CrossRef]
- Zio, E.; Maio, D. Fatigue crack growth estimation by relevance vector machine. Expert Syst. Appl. 2012, 39, 10681–10692. [Google Scholar] [CrossRef]
- Mohanty, R.; Mahanta, K.; Mohanty, A.; Thatoi, N. Prediction of constant amplitude fatigue crack growth life of 2024T3 AI alloy with R-ratio effect by GP. Appl. Soft Comput. 2014, 26, 428–434. [Google Scholar] [CrossRef]
- Tan, H.; Bi, H.; Hou, L.; Wong, W. Reliability analysis using radial basis function networks and support vector machines. Comput. Geotech. 2011, 38, 178–186. [Google Scholar] [CrossRef]
- Heng, Y. Intelligent prognostics of machinery health utilising suspended condition monitoring data. Comput. Geotech. 2011, 38, 178–186. [Google Scholar]
- Hashash, Y.; Jung, S.; Ghaboussi, J. Numerical implementation of a neural network based material model in finite element analysis. Int. J. Numer. Methods Eng. 2004, 59, 989–1005. [Google Scholar] [CrossRef]
- Carneiro, A.; Alves, A.; Coelho, R.; Cardoso, J.; Pires, F. A simple machine learning-based framework for faster multi-scale simulations of path-independent materials at large strains. Finite Elem. Anal. Des. 2023, 222, 103956. [Google Scholar] [CrossRef]
- Nikolić, F.; Čanađija, M. Deep Learning of Temperature–Dependent Stress–Strain Hardening Curves. C. R. Mécanique 2023, 351, 151–170. [Google Scholar] [CrossRef]
- Fazily, P.; Yoon, J. Machine learning-driven stress integration method for anisotropic plasticity in sheet metal forming. Int. J. Plast. 2023, 166, 103642. [Google Scholar] [CrossRef]
- Long, C.; Liu, S.; Sun, R.; Lu, J. Impact of structural characteristics on thermal conductivity of foam structures revealed with machine learning. Comput. Mater. Sci. 2024, 237, 112898. [Google Scholar] [CrossRef]
- Gang, M.; Shaoheng, G.; Qiao, W.; YT, F.; Wei, Z. A predictive deep learning framework for path-dependent mechanical behavior of granular materials. Acta Geotech. 2022, 17, 3463–3478. [Google Scholar]
- Mital, U.; José, A. Bridging length scales in granular materials using convolutional neural networks. Comput. Part. Mech. 2022, 9, 221–235. [Google Scholar] [CrossRef]
- Guan, S.; Qu, T.; Feng, Y.T.; Ma, G.; Zhou, W. A machine learning-based multi-scale computational framework for granular materials. Acta Geotech. 2022, 18, 1699–1720. [Google Scholar] [CrossRef]
- Hakim, S.; Noorzaei, J.; Jaafar, M.; Jameel, M.; Mohammadhassani, M. Application of artificial neural networks to predict compressive strength of high strength concrete. Int. J. Phys. Sci. 2011, 6, 975–981. [Google Scholar]
- Al-Janabi, K.; Abdulwahab, A. Modeling of polymer modified-concrete strength with artificial neural networks. Int. J. Civ. Eng. 2008, 10, 47–68. [Google Scholar]
- Kim, J.; Kim, D.; Feng, M.; Yazdani, F. Application of neural networks for estimation of concrete strength. J. Mater. Civ. Eng. 2004, 16, 257–264. [Google Scholar] [CrossRef]
- Kim, K.; Lee, J.; Chang, K. Application of probabilistic neural networks for prediction of concrete strength. J. Mater. Civ. Eng. 2005, 17, 353–362. [Google Scholar] [CrossRef]
- Gupta, R.; kewalramani, A.; Geol, A. Prediction of concrete strength using neural-expert system. J. Mater. Civ. Eng. 2006, 18, 462–466. [Google Scholar] [CrossRef]
- Roberson, M.; Inman, K.; Carey, A.; Howard, I.; Shannon, J. Probabilistic neural networks that predict compressive strength of high strength concrete in mass placements using thermal history. Comput. Struct. 2022, 259, 106707. [Google Scholar] [CrossRef]
- Yang, Y.; Zhang, J.; Huang, F.; Chen, Z.; Qiu, R.; Wu, S. Effect of structural parameters on compression performance of autoclaved aerated concrete: Simulation and machine learning. Constr. Build. Mater. 2024, 423, 135860. [Google Scholar] [CrossRef]
- Korza, R. Genetic Programming: On the Programming of Computers by Natural Selection; MIT Press: Cambridge, MA, USA, 2018; Volume 339, pp. 358–388. [Google Scholar]
- Hein, D.; Udluft, S.; Runkler, A. Interpretable policies for reinforcement learning by genetic programming. Eng. Appl. Artif. Intell. 2018, 76, 158–167. [Google Scholar] [CrossRef]
- Nicholas, A.; Kamran, B.; Zouheir, F. Applicability and viability of a GA based finite element analysis architecture for structural design optimization. Comput. Struct. 2003, 81, 2259–2271. [Google Scholar]
- Hashem, B.; Zahidul, I. Advantages and limitations of genetic algorithms for clustering records. In Proceedings of the 2016 IEEE 11th Conference on Industrial Electronics and Applications (ICIEA), Hefei, China, 5–7 June 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 2478–2483. [Google Scholar]
- Guan, X.; Burton, H. Bias-variance tradeoff in machine learning: Theoretical formulation and implications to structural engineering applications. Structures 2022, 46, 17–30. [Google Scholar] [CrossRef]
- Gharahamani, Z. Unsupervised learning. Adv. Lect. Mach. Learn. 2004, 16, 362–379. [Google Scholar]
- Benyamin, G.; Crowley, M.; Karray, F.; Ghodsi, A. Locally linear embedding. In Elements of Dimensionality Reduction and Manifold Learning; Springer International Publishing: Cham, Switzerland, 2023; Volume 404, pp. 207–247. [Google Scholar]
- Andrew, M.; Kamal, N.; Jason, R.; Kristie, S. A machine learning approach to building domain-specific search engines. In Proceedings of the IJCAI, Stockholm, Sweden, 31 July–6 August 1999; Volume 99, pp. 662–667. [Google Scholar]
- Magidson, J.; Vermunt, J. Latent class models for clustering: A comparison with K-means. Int. Can. J. Mark. Res. 2002, 20, 13–27. [Google Scholar]
- Alcala-Fdez, J.; Sanchez, L.; Garcia, S.; Del-Jesus, M. Software to assess evolutionary algorithms for data mining problems. Soft Comput. 2008, 6, 93–103. [Google Scholar]
- Macqueen, J. Some methods for classification and analysis of multivariate observations. In Proceedings of 5th Berkeley Symposium on Mathematical Statistics and Probability; University of California Press: Berkeley, CA, USA, 1967; Volume 1, pp. 281–297. [Google Scholar]
- John, H.; Langley, P. Estimating continious distributions in Bayesian classifiers. In Proceedings of the 11th Conference on Uncertainty in Artificial Intelligence, Montreal, QC, Canada, 18–20 August 1995; Volume 1, pp. 338–345. [Google Scholar]
- Rakthanmanon, T.; Keogh, J.; Evans, S. MDL-based time series clustering. Knowl. Inf. Syst. 2012, 33, 371–399. [Google Scholar] [CrossRef]
- Saul, L.; Roweis, S. Unsupervised learning of two dimensional manifolds. J. Mach. Learn. Res. 2003, 4, 119–155. [Google Scholar]
- Dy, J.; Brodley, C. Feature selection for unsupervised learning. J. Mach. Learn. Res. 2004, 5, 845–889. [Google Scholar]
- Bo, L.; Ren, X.; Fox, D. Unsupervised feature learning for RGB-D based object recognition. In Proceedings of the Experimental Robotics: The 13th International Symposium on Experimental Robotics, Québec City, QC, Canada, 18–21 June 2012; Springer: Berlin/Heidelberg, Germany, 2013; pp. 387–402. [Google Scholar]
- Madan, A. Vibration control of building structures using self-organizing and self-learning neural networks. J. Sounds Vib. 2005, 287, 759–784. [Google Scholar] [CrossRef]
- Daneshvar, M.; Hassan, S. Unsupervised learning-based damage assessment of full-scale civil structures under long-term and short-term monitoring. Eng. Struct. 2022, 256, 114059. [Google Scholar] [CrossRef]
- García-Macías, E.; Ubertini, F. Integrated SHM systems: Damage detection through unsupervised learning and data fusion. In Structural Health Monitoring Based on Data Science Techniques; Springer: Berlin/Heidelberg, Germany, 2021; pp. 247–268. [Google Scholar]
- Ma, X.; Lin, Y.; Nie, Z.; Ma, H. Structural damage identification based on unsupervised feature-extraction via Variational Auto-encoder. Measurement 2020, 160, 107811. [Google Scholar] [CrossRef]
- Alireza, E.; Hashem, S. An unsupervised learning approach by novel damage indices in structural health monitoring for damage localization and quantification. Struct. Health Monit. 2018, 17, 325–345. [Google Scholar]
- Alireza, E.; Hashem, S.; Stefano, M. Fast unsupervised learning methods for structural health monitoring with large vibration data from dense sensor networks. Struct. Health Monit. 2020, 19, 1685–1710. [Google Scholar]
- Liu, J.; Li, Q.; Li, L.; An, S. Structural damage detection and localization via an unsupervised anomaly detection method. Reliab. Eng. Syst. Saf. 2024, 252, 110465. [Google Scholar] [CrossRef]
- Junges, R.; Rastin, Z.; Lomazzi, L.; Giglio, M.; Cadini, F. Convolutional autoencoders and CGANs for unsupervised structural damage localization. Mech. Syst. Signal Process. 2024, 220, 111645. [Google Scholar] [CrossRef]
- Eloi, F.; Yano, O.; Samuel, D.; Ionut, M.; Mihai, A. Transfer learning to enhance the damage detection performance in bridges when using numerical models. J. Bridge Eng. 2023, 28, 04022134. [Google Scholar]
- Bayane, I.; Leander, J.; Karoumi, R. An unsupervised machine learning approach for real-time damage detection in bridges. Eng. Struct. 2024, 308, 117971. [Google Scholar] [CrossRef]
- Lu, Y.; Tang, L.; Liu, Z.; Zhou, L.; Yang, B.; Jiang, Z.; Liu, Y. Unsupervised quantitative structural damage identification method based on BiLSTM networks and probability distribution model. J. Sound Vib. 2024, 590, 118597. [Google Scholar] [CrossRef]
- Lieber, D.; Stople, M.; Konrad, B.; Deuse, J.; Morik, K. Quality predictions in interlinked manufacturing processes based on supervised and unsupervised machine learning. Procedia CIRP 2013, 7, 193–198. [Google Scholar] [CrossRef]
- Alwood, M.; Cullen, M. Sustainable Materials; UIT Cambridge Ltd.: Cambridge, UK, 2012; Volume 2, pp. 51–54. [Google Scholar]
- Konrad, B.; Lieber, D.; Deuse, J. Striving for zero defect production: Intelligent manufacturing control through data mining in continious rolling mill processes. Robust Manuf. Control 2012, 1, 67–75. [Google Scholar]
- Stolpr, M.; Morik, K. Learning from label proportion by optimizing cluster model selection. Mach. Learn. Knowl. Discov. Databases 2011, 6913, 349–364. [Google Scholar]
- Choi, J.; Kim, N.; Hong, Y. Unsupervised Legendre–Galerkin Neural Network for Solving Partial Differential Equations. IEEE Access 2023, 11, 23433–23446. [Google Scholar] [CrossRef]
- Zhu, Y.; Nicholas, Z.; Phaedon-Stelios, K.; Paris, P. Physics-constrained deep learning for high-dimensional surrogate modeling and uncertainty quantification without labeled data. J. Comput. Phys. 2019, 394, 56–81. [Google Scholar] [CrossRef]
- Piervincenzo, R.; Marcello, C.; Debaditya, D.; Hoon, S.; Kent, H. An unsupervised learning algorithm for fatigue crack detection in waveguides. Smart Mater. Struct. 2009, 18, 025016. [Google Scholar]
- Hau, M.; Qui, L.; Kang, J.; Lee, J. A novel deep unsupervised learning-based framework for optimization of truss structures. Eng. Comput. 2022, 39, 2585–2608. [Google Scholar]
- Pan, J.; Huang, J.; Wang, Y.; Cheng, G.; Zeng, Y. A self-learning finite element extraction system based on reinforcement learning. AI EDAM 2021, 35, 180–208. [Google Scholar] [CrossRef]
- Soheila, E.; Soheil, E.; Debarshi, S.; Shamim, P. Active structural control framework using policy-gradient reinforcement learning. Eng. Struct. 2023, 274, 115122. [Google Scholar]
- Wei, S.; Bao, Y.; Li, H. Optimal policy for structure maintenance: A deep reinforcement learning framework. Struct. Saf. 2020, 83, 101906. [Google Scholar] [CrossRef]
- Yu, C.-H.; Tseng, B.-Y.; Yang, Z.; Tung, C.-C.; Zhao, E.; Ren, Z.-F.; Yu, S.-S.; Chen, P.-Y.; Chen, C.-S.; Buehler, M.J. Hierarchical Multiresolution Design of Bioinspired Structural Composites Using Progressive Reinforcement Learning. Adv. Theory Simul. 2022, 5, 2200459. [Google Scholar] [CrossRef]
- Dhaya, R.; Kanthavel, R.; Fahad, A.; Jayarajan, P.; Mahor, A. Reinforcement learning concepts ministering smart city applications using IoT. In Internet of Things in Smart Technologies for Sustainable Urban Development; Springer: Cham, Switzerland, 2020; pp. 19–41. [Google Scholar]
- Savinay, N.; Nikhil, P.; Rashmi, U.; Koshy, G. Comparison of reinforcement learning algorithms applied to the cart-pole problem. In Proceedings of the 2017 International Conference on Advances in Computing, Communications and Informatics (ICACCI), Udupi, India, 13–16 September 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 26–32. [Google Scholar]
- Bernard, A.; Ian, S. Reinforcement learning for structural control. J. Comput. Civ. Eng. 2008, 22, 133–139. [Google Scholar]
- Arash, K.; Mehdi, S.; Masoud, K. Online control of an active seismic system via reinforcement learning. Struct. Control Health Monit. 2019, 26, e2298. [Google Scholar]
- Kazem, S.; Javad, M. Application of reinforcement learning algorithm for automation of canal structures. Irrig. Drain. 2015, 64, 77–84. [Google Scholar]
- Dominik, P.; ukasz, J. Reinforcement learning-based control to suppress the transient vibration of semi-active structures subjected to unknown harmonic excitation. Comput.-Aided Civ. Infrastruct. Eng. 2022, 38, 1605–1621. [Google Scholar]
- Qiu, Z.-C.; Chen, G.-H.; Zhang, X.-M. Reinforcement learning vibration control for a flexible hinged plate. Aerosp. Sci. Technol. 2021, 118, 107056. [Google Scholar] [CrossRef]
- Yi, L.; Deng, X.; Yang, L.T.; Wu, H.; Wang, M.; Situ, Y. Reinforcement-learning-enabled partial confident information coverage for IoT-based bridge structural health monitoring. IEEE Internet Things J. 2020, 8, 3108–3119. [Google Scholar] [CrossRef]
- Yang, A.; Qiu, Q.; Zhu, M.; Cui, L.; Chen, W.; Chen, J. Condition-based maintenance strategy for redundant systems with arbitrary structures using improved reinforcement learning. Reliab. Eng. Syst. Saf. 2022, 225, 108643. [Google Scholar] [CrossRef]
- Cao, P.; Tang, J. A Reinforcement Learning Hyper-Heuristic in Multi-Objective Single Point Search with Application to Structural Fault Identification. arXiv 2018, arXiv:1812.07958. [Google Scholar]
- Cao, P.; Zhang, Y.; Zhou, K.; Tang, J. A reinforcement learning hyper-heuristic in multi-objective optimization with application to structural damage identification. Struct. Multidiscip. Optim. 2023, 66, 16. [Google Scholar] [CrossRef]
- Zimmerling, C.; Poppe, C.; Stein, O.; Kärger, L. Optimisation of manufacturing process parameters for variable component geometries using reinforcement learning. Mater. Des. 2022, 214, 110423. [Google Scholar] [CrossRef]
- Harley, O.; Ying, L.; Maneesh, K.; Michael, W.; Michael, R. Reinforcement learning for facilitating human–robot-interaction in manufacturing. J. Manuf. Syst. 2020, 56, 326–340. [Google Scholar]
- Jonathan, V.; Jean, R.; Alexander, K.; Hassan, G.; Aurélien, L.; Elie, H. Direct shape optimization through deep reinforcement learning. J. Comput. Phys. 2021, 428, 110080. [Google Scholar]
- Shaopeng, L.; Reda, S.; Teng, W. A knowledge-enhanced deep reinforcement learning-based shape optimizer for aerodynamic mitigation of wind-sensitive structures. Comput.-Aided Civ. Infrastruct. Eng. 2021, 36, 733–746. [Google Scholar]
- Sérgio, D.; Sidney, G.; Cairo, N. Autonomous construction of structures in a dynamic environment using reinforcement learning. In Proceedings of the 2013 IEEE International Systems Conference (SysCon), Orlando, FL, USA, 15–18 April 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 452–459. [Google Scholar]
- Kevin, D.; Oliveira, I.; Daniel, D.; Alexandre, G.; Mário, S.; Alexandre, B. Q-learning based Path Planning Method for UAVs using Priority Shifting. In Proceedings of the 2022 International Conference on Unmanned Aircraft Systems (ICUAS), Dubrovnik, Croatia, 21–24 June 2022; Volume 3, pp. 421–426. [Google Scholar] [CrossRef]
- Fabian, D.; Sebastian, D.; Maximilian, W.; Benjamin, S.; Sandro, W. Reinforcement learning for engineering design automation. Adv. Eng. Inform. 2022, 52, 101612. [Google Scholar]
- Junhyeon, S.; Rakesh, K. Development of an artificial intelligence system to design of structures using reinforcement learning: Proof of concept. In Proceedings of the AIAA Scitech 2021 Forum, Virtual, 11–15 and 19–21 January 2021; p. 1692. [Google Scholar]
- Maximilian, O.; Gordon, W. Design synthesis of structural systems as a Markov decision process solved with deep reinforcement learning. J. Mech. Des. 2023, 145, 061701. [Google Scholar]
- Guan, X.; Xiang, Z.; Bao, Y.; Li, H. Structural dominant failure modes searching method based on deep reinforcement learning. Reliab. Eng. Syst. Saf. 2022, 219, 108258. [Google Scholar] [CrossRef]
- Guan, X.; Sun, H.; Hou, R.; Xu, Y.; Bao, Y.; Li, H. A deep reinforcement learning method for structural dominant failure modes searching based on self-play strategy. Reliab. Eng. Syst. Saf. 2023, 233, 109093. [Google Scholar] [CrossRef]
- Johannes, D.; Lukas, M.; Samuel, Z.; Tarek, I.; Norbert, L.; Dirk, H. Deep reinforcement learning methods for structure-guided processing path optimization. J. Intell. Manuf. 2022, 33, 333–352. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).