Research on the Theoretical Models of FRP-Confined Gangue Aggregate Concrete Partially Filled Steel Tube Columns
Abstract
:1. Introduction
2. Existing Models of CCFFT
2.1. Analysis-Oriented Model for CCFFT
2.1.1. The Axial Stress–Strain Equation of Concrete
2.1.2. Ultimate Stress and Corresponding Strain
2.1.3. The Constitutive Relationship of the Steel Tube
2.1.4. Axial Strain–Lateral Strain Model of Concrete
2.1.5. Generate the Load–Displacement Curve
2.2. Design-Oriented Model for CCFFTs
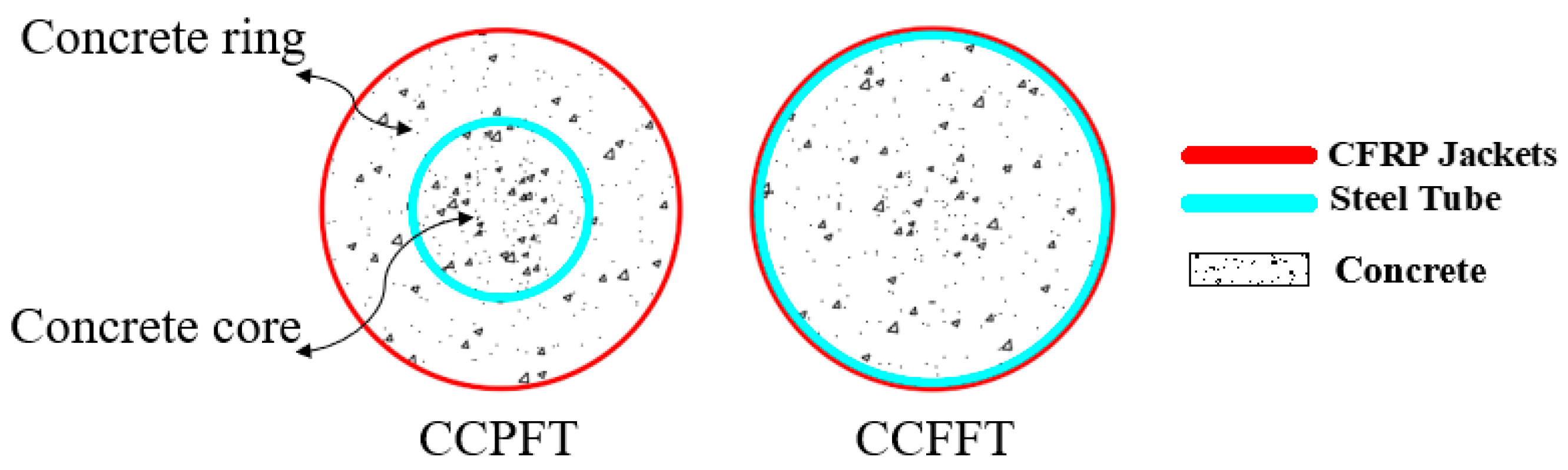
3. Proposal and Establishment of Analysis-Oriented Model of a CGCPFT
3.1. The Stress–Strain Relationship of Gangue Aggregate Concrete Restrained by FRP
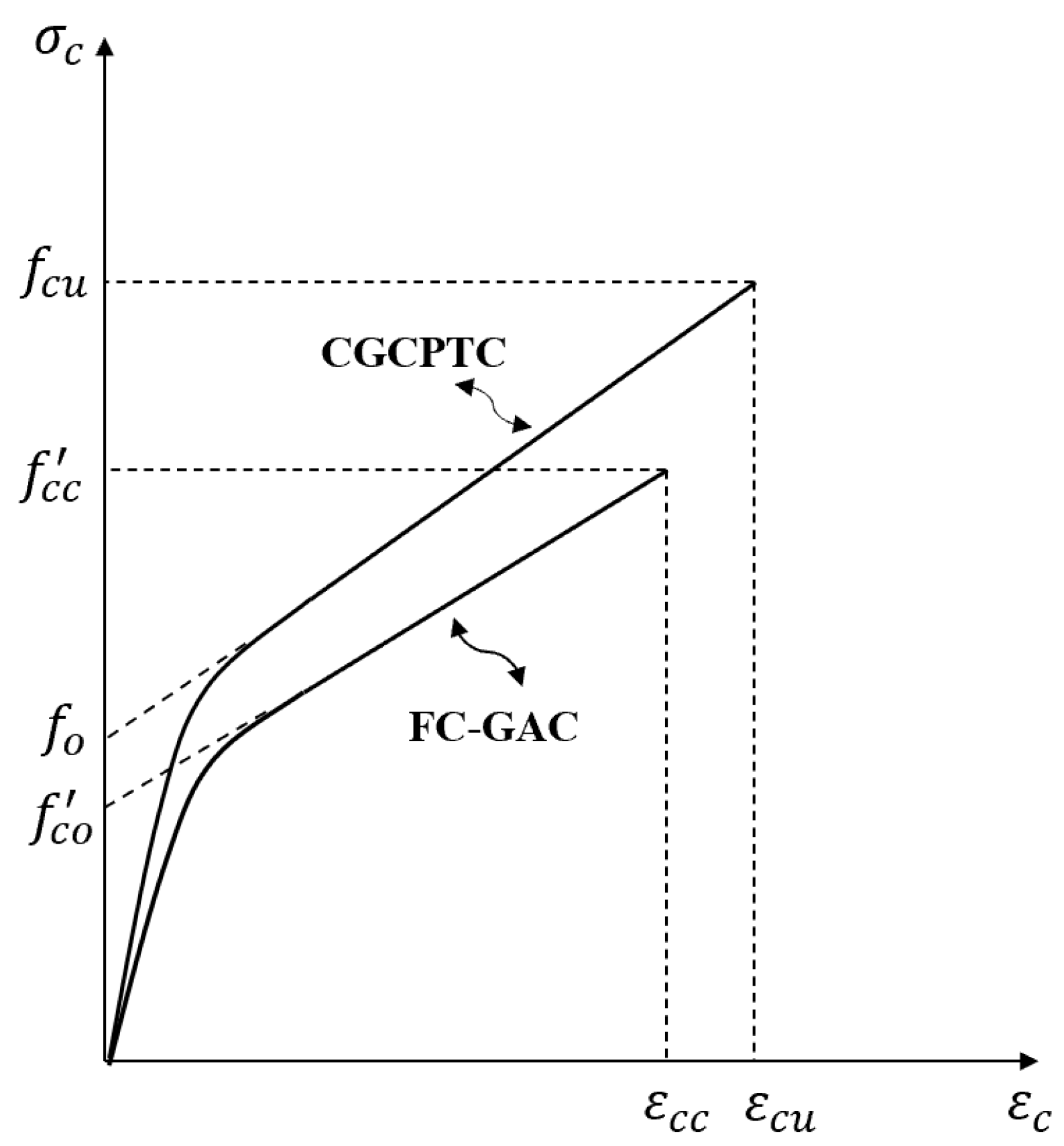
3.1.1. Basic Description
3.1.2. Axial Stress–Strain Equation
3.1.3. Axial Strain–Lateral Strain Equation
3.1.4. Ultimate Stress and Strain
3.2. Discussion on Stress–Strain Model of GAC in CGCPFT
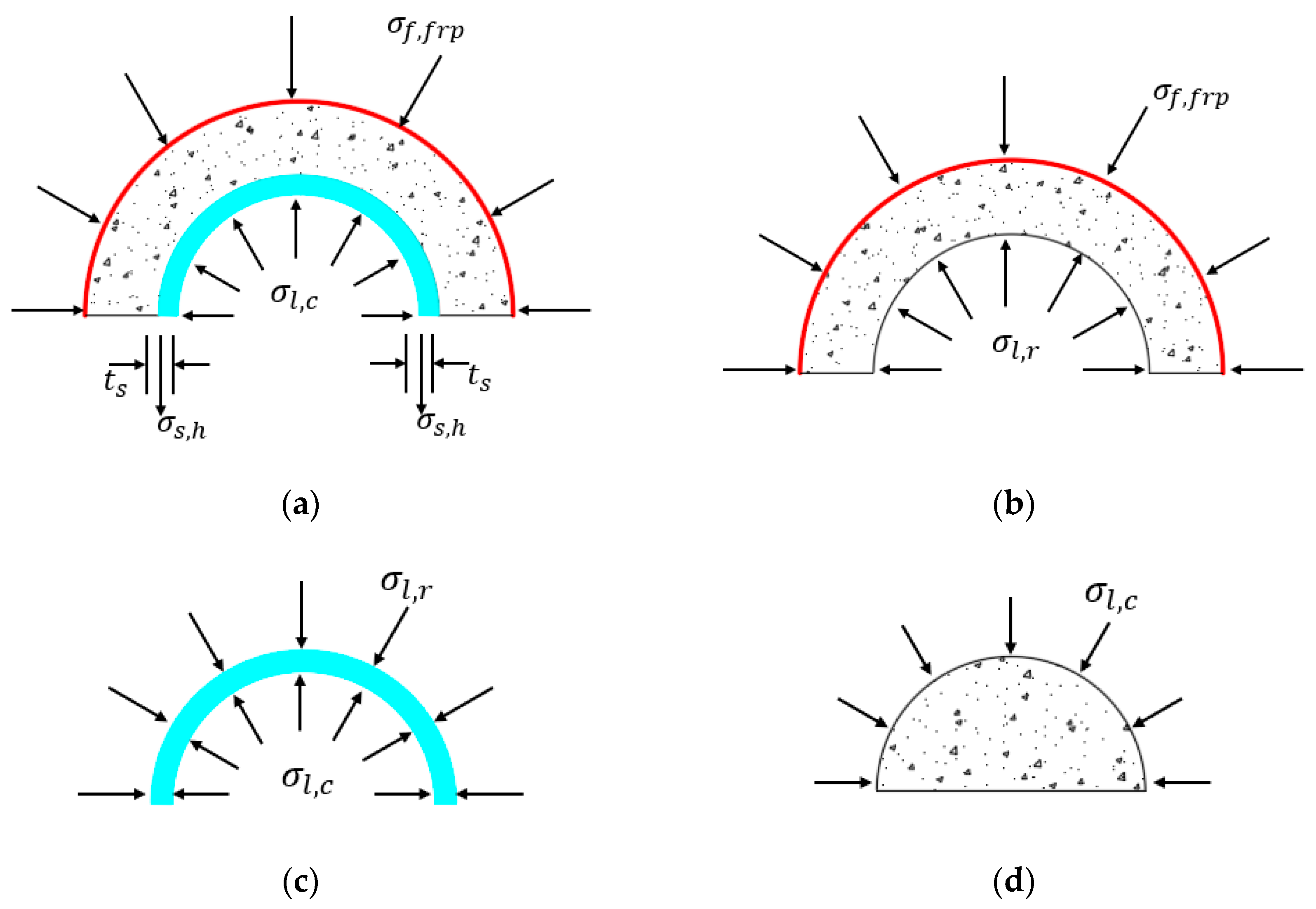
3.2.1. Bond Condition Assumption
3.2.2. Stress–Strain Model of GAC Ring
3.2.3. Stress–Strain Model of GAC Core
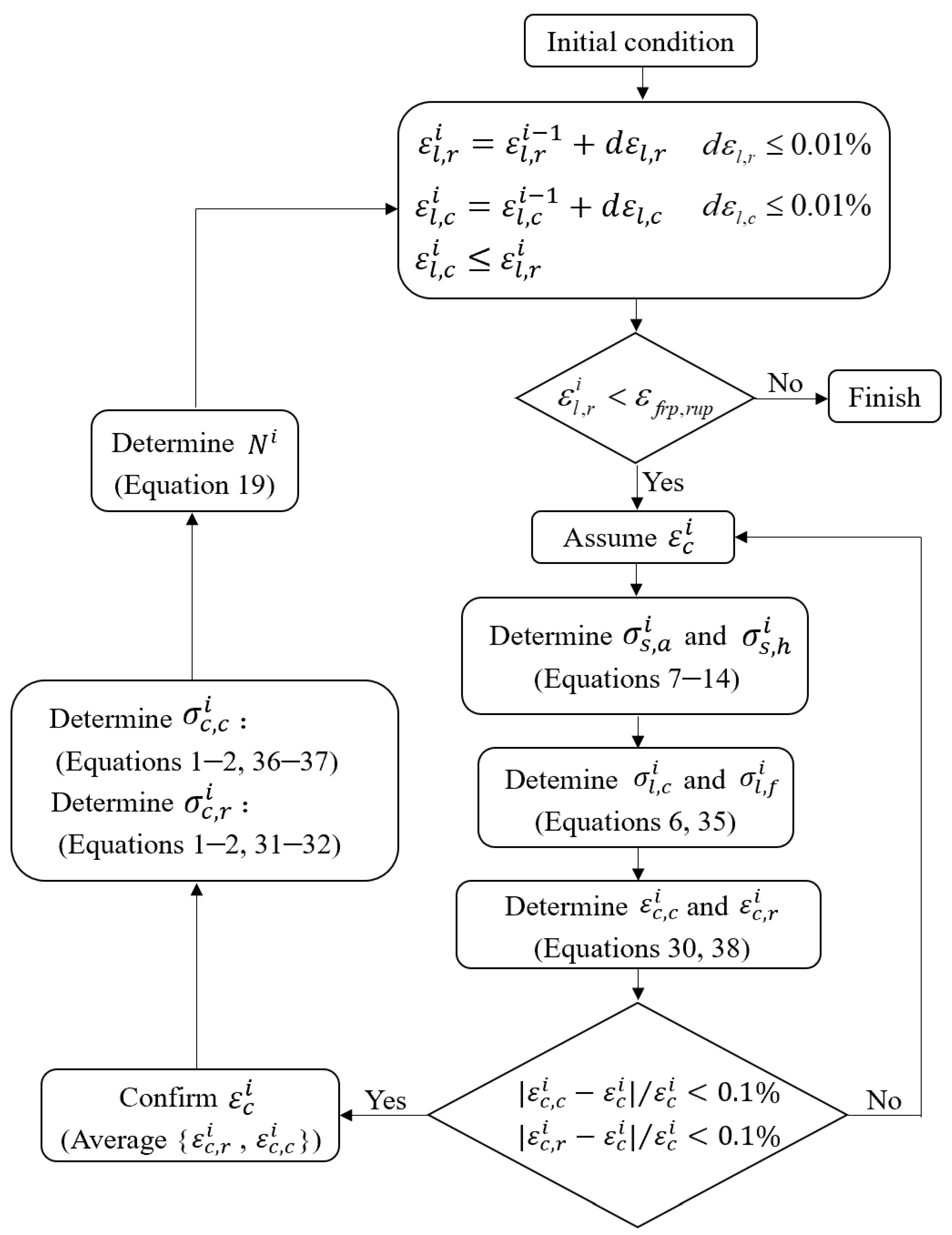
3.3. Generate Axial Load–Displacement Curve
4. Propose the Design-Oriented Model of CGCPFT
4.1. General
4.2. Ultimate Strength
4.3. Ultimate Strain
4.4. Axial Stress–Axial Strain Relationship
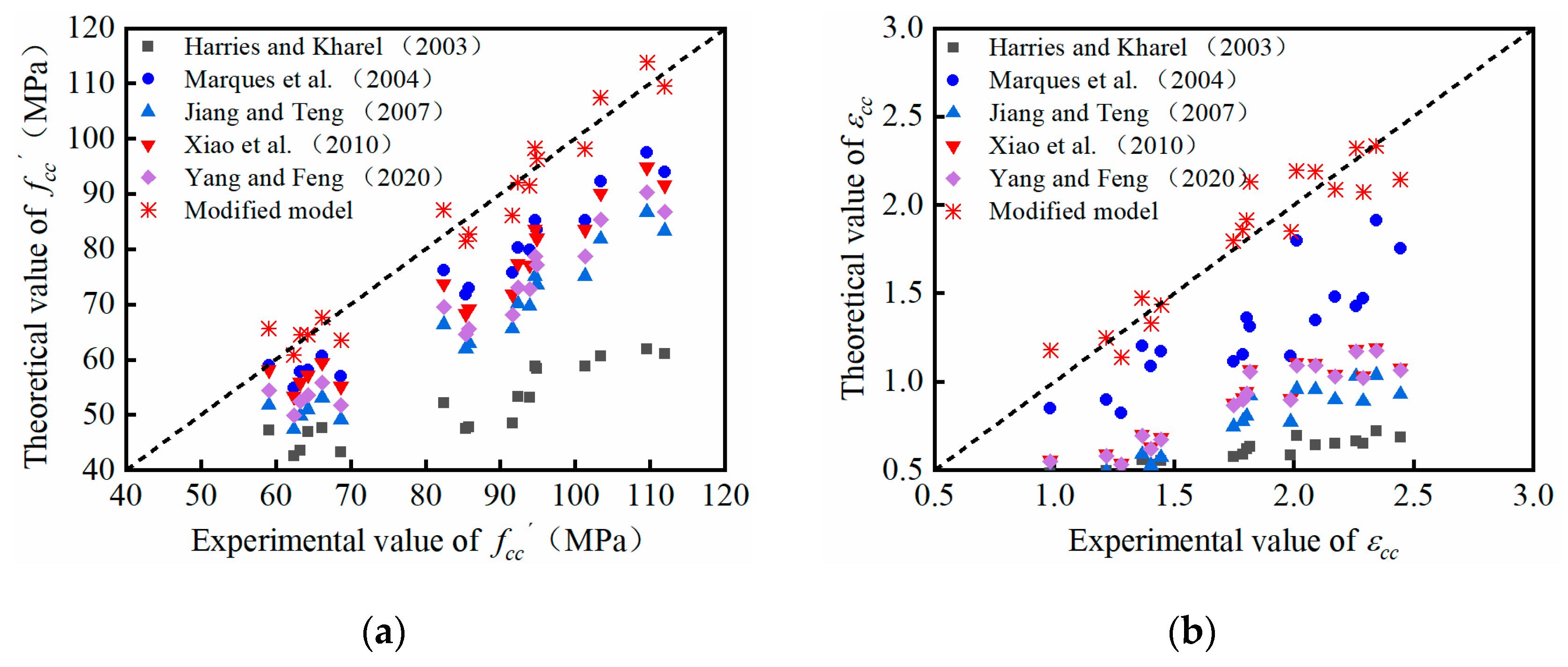
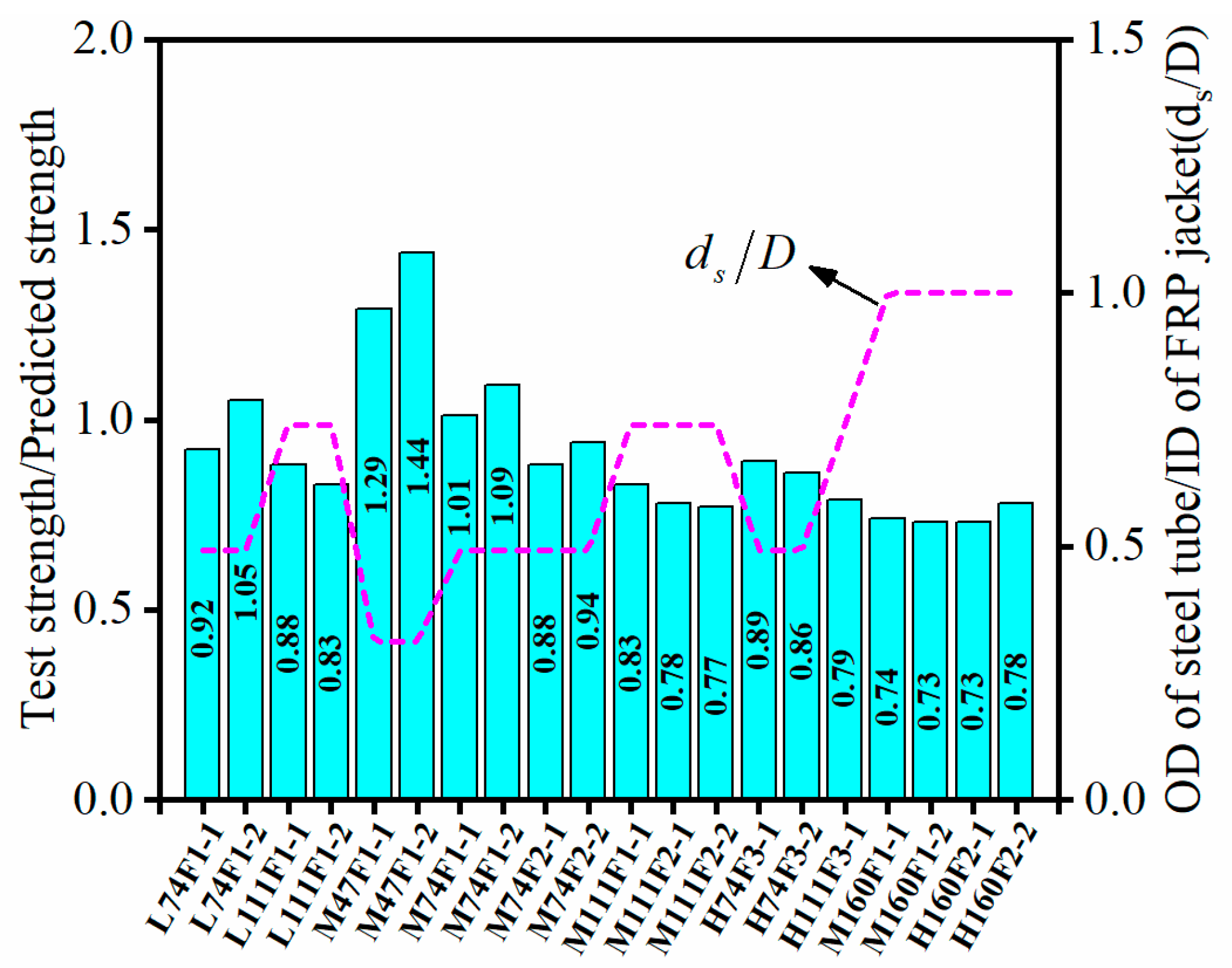
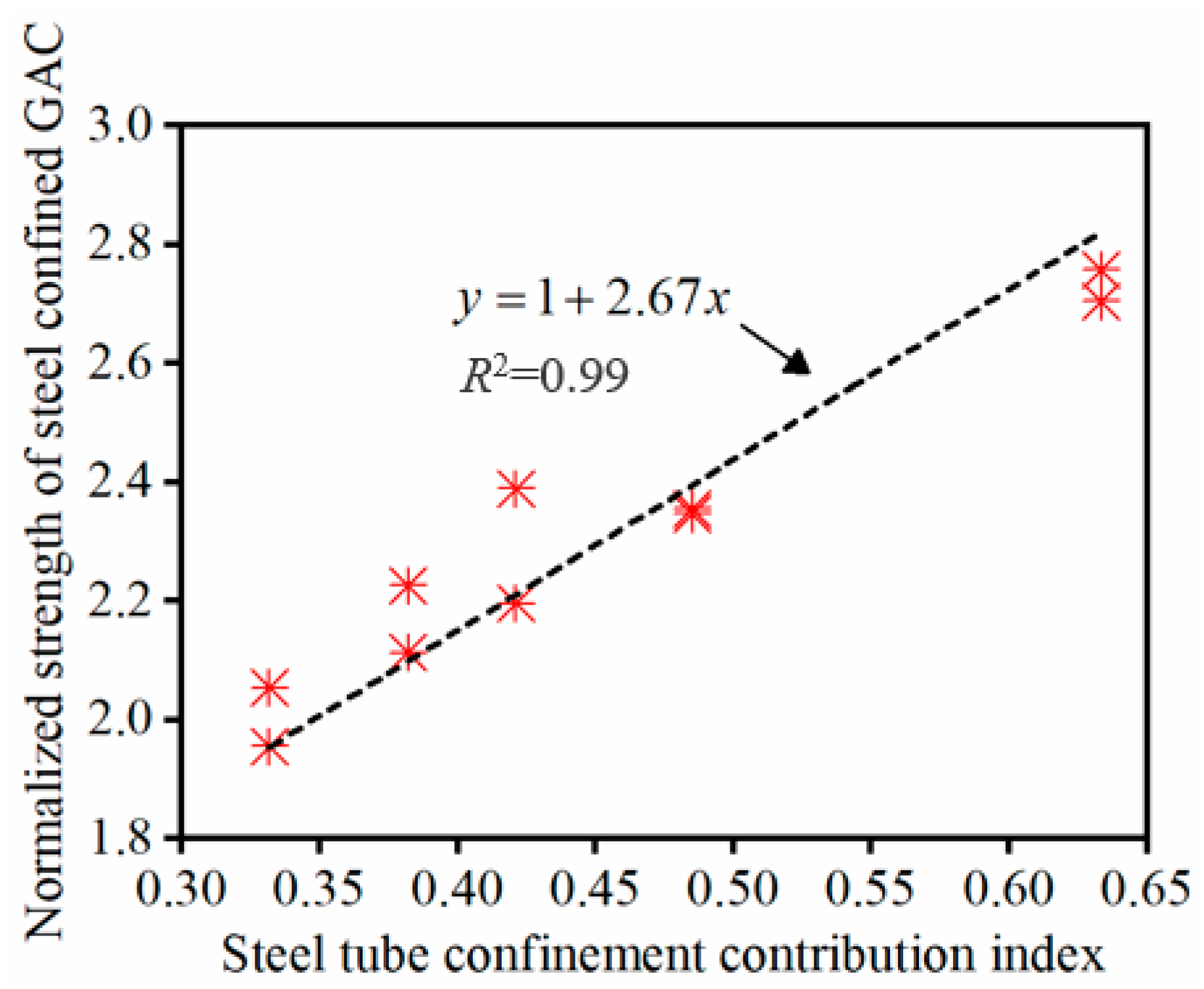
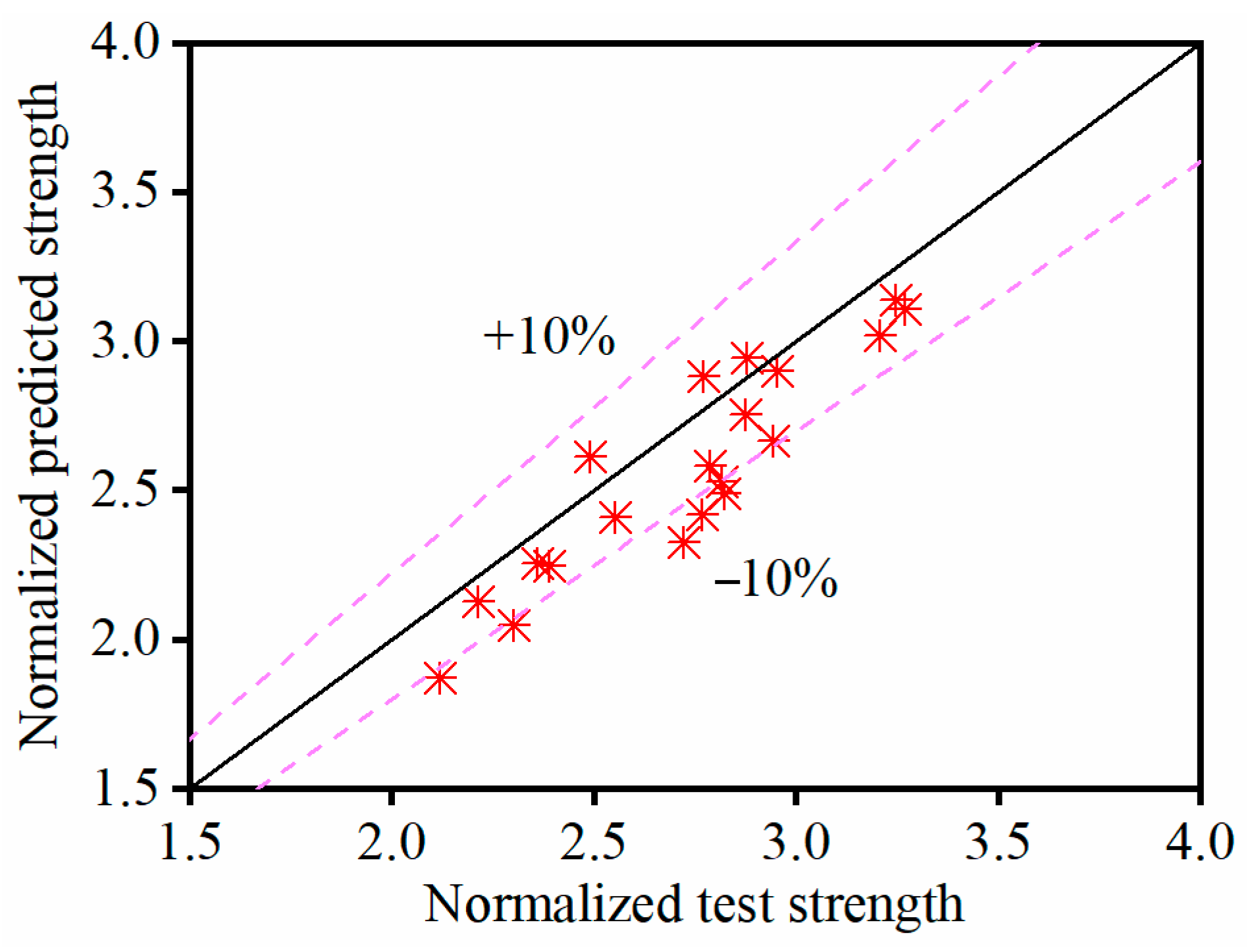
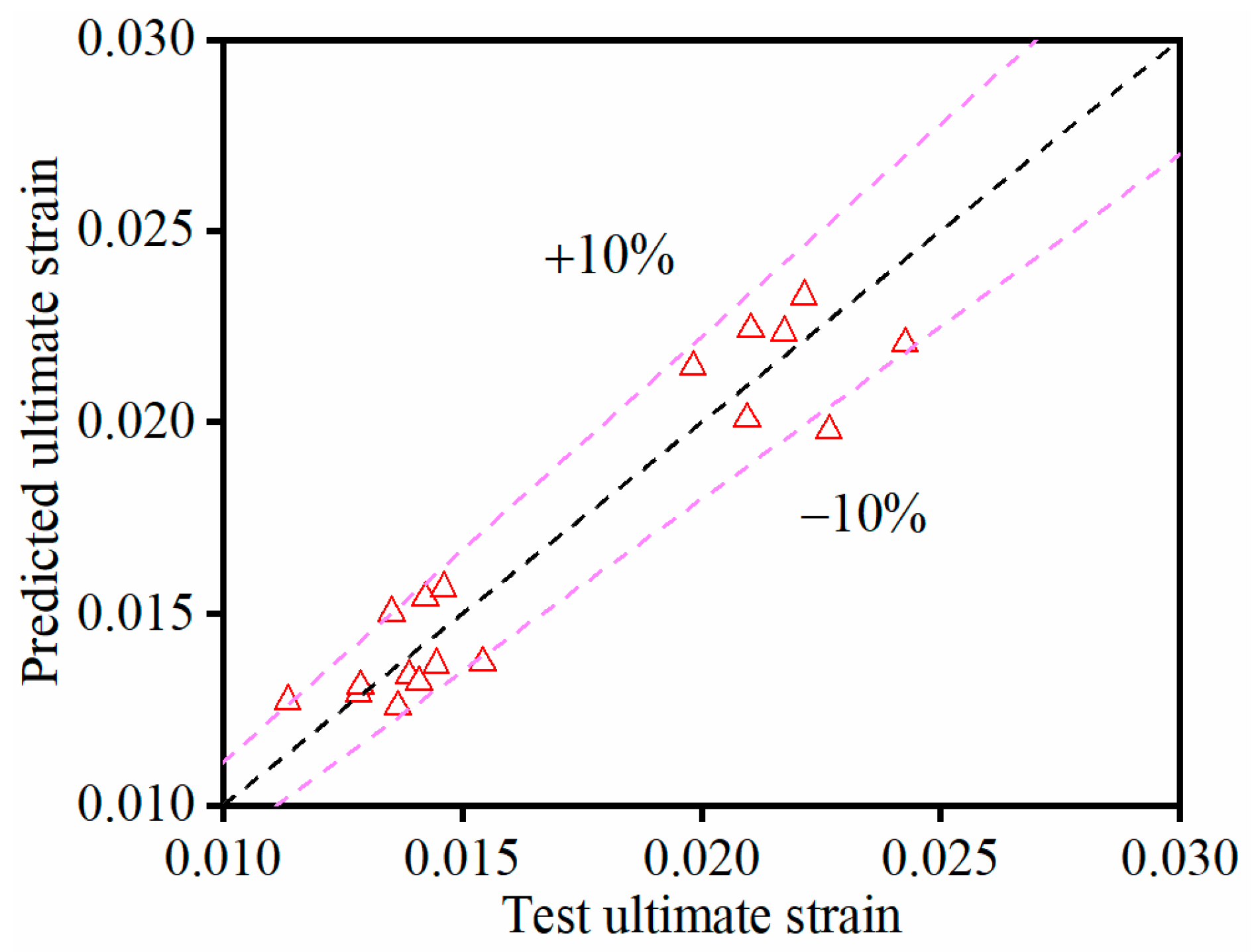
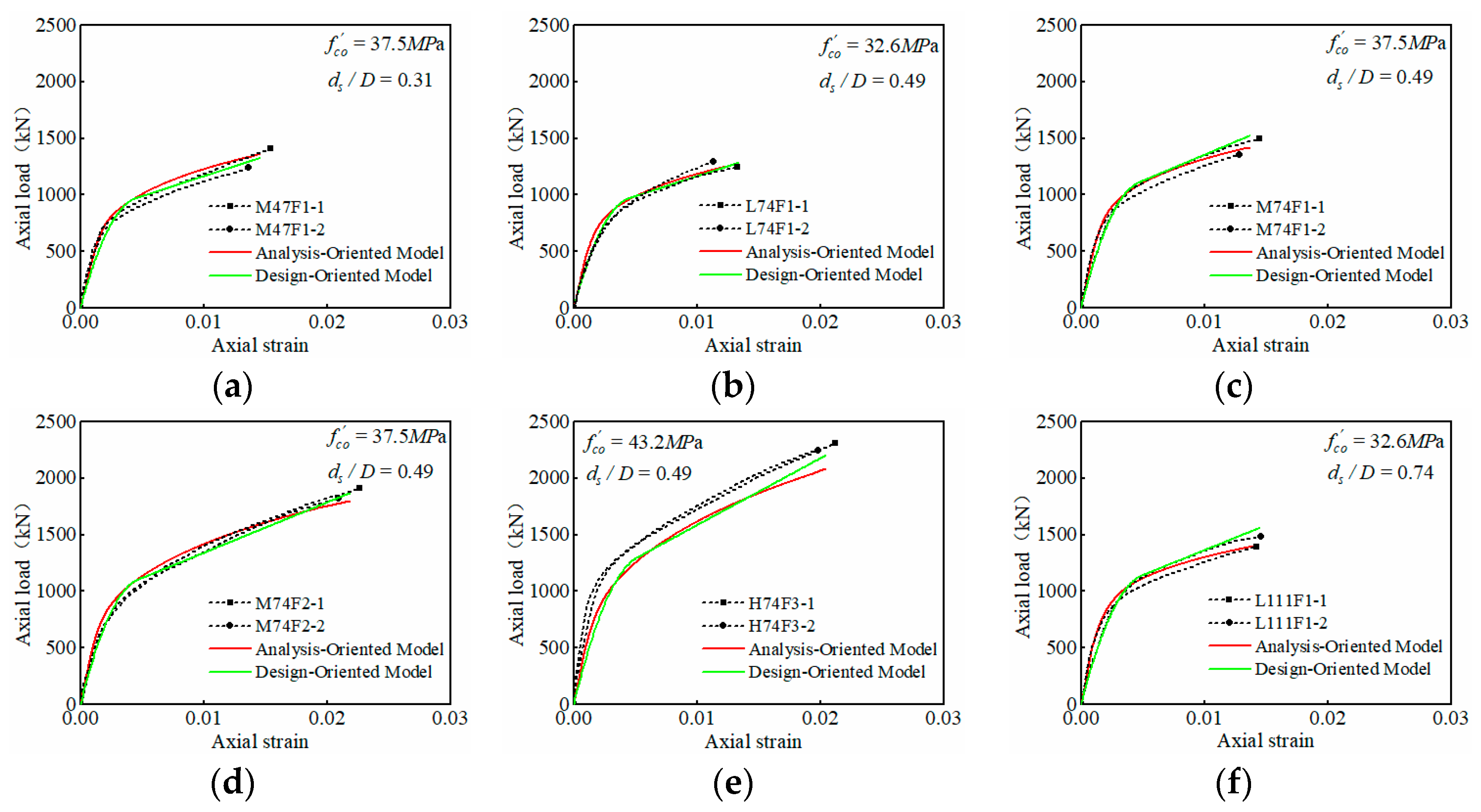
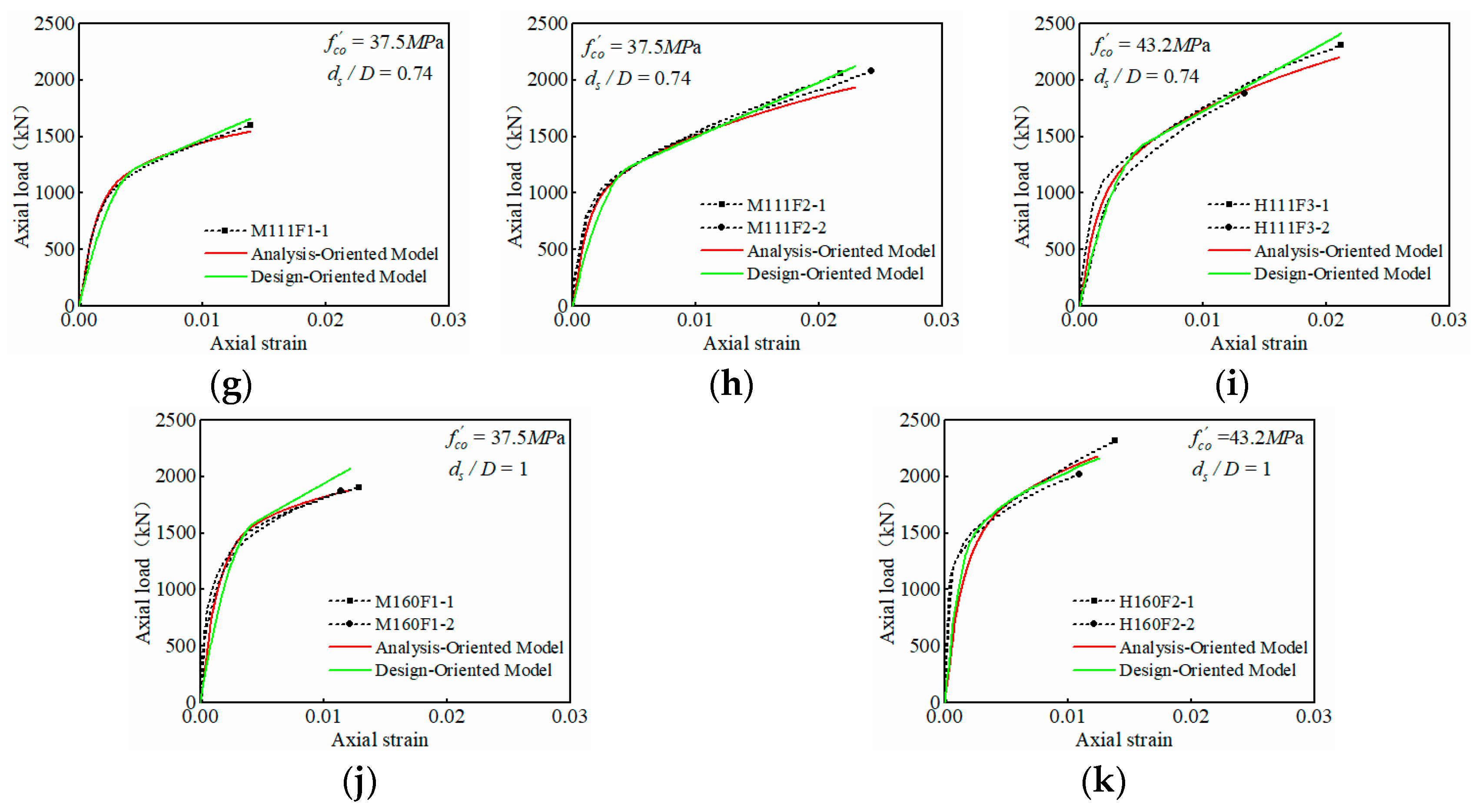
5. Model Validation
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Dong, Z.; Xia, J.; Fan, C.; Cao, J. Activity of calcined coal gangue fine aggregate and its effect on the mechanical behavior of cement mortar. Constr. Build. Mater. 2015, 100, 63–69. [Google Scholar] [CrossRef]
- Zhou, M.; Dou, Y.; Zhang, Y.; Zhang, Y.; Zhang, B. Effects of the variety and content of coal gangue coarse aggregate on the mechanical properties of concrete. Constr. Build. Mater. 2019, 220, 386–395. [Google Scholar] [CrossRef]
- Xian, G.; Bai, Y.; Zhou, P.; Wang, J.; Li, C.; Dong, S.; Guo, R.; Tian, J.; Li, J.; Zhong, J.; et al. Long-term properties evolution and life prediction of glass fiber reinforced thermoplastic bending bars exposed in concrete alkaline environment. J. Build. Eng. 2024, 91, 109641. [Google Scholar] [CrossRef]
- Li, C.; Xian, G. Novel wedge-shaped bond anchorage system for pultruded CFRP plates. Mater. Struct. 2018, 51, 162. [Google Scholar] [CrossRef]
- Zhao, H.; Ren, T.; Remennikov, A. Behaviour of FRP-confined coal reject concrete columns under axial compression. Compos. Struct. 2021, 262, 113621. [Google Scholar] [CrossRef]
- Zhao, H.; Ren, T.; Remennikov, A. Behaviour of FRP-confined coal rejects based backfill material under compression. Constr. Build. Mater. 2020, 268, 121171. [Google Scholar] [CrossRef]
- Teng, J.G.; Lam, L. Behavior and Modeling of Fiber Reinforced Polymer-Confined Concrete. J. Struct. Eng. 2004, 130, 1713–1723. [Google Scholar] [CrossRef]
- Wilt, J.; Liang, R.; GangaRao, H.; Mostoller, J.; NSF I UCRC For Integration Of Composites Into Infrastructure And Constructed Facilities Center. Structural responses of FRP sheet piles under cantilever loading. Sustain. Struct. 2023, 3, 000021. [Google Scholar] [CrossRef]
- Li, Y.; Zhao, X.; Singh, R.R.; Al-Saadi, S. Experimental study on seawater and sea sand concrete filled GFRP and stainless steel tubular stub columns. Thin-Walled Struct. 2016, 106, 390–406. [Google Scholar] [CrossRef]
- Li, Y.-L.; Zhao, X.-L. Hybrid double tube sections utilising seawater and sea sand concrete, FRP and stainless steel. Thin-Walled Struct. 2020, 149, 106643. [Google Scholar] [CrossRef]
- Li, Y.; Zhao, X.; Raman, R.S. Load-strain model for concrete-filled double-skin circular FRP tubes under axial compression. Eng. Struct. 2019, 181, 629–642. [Google Scholar] [CrossRef]
- Li, Y.; Teng, J.; Zhao, X.; Raman, R.S. Theoretical model for seawater and sea sand concrete-filled circular FRP tubular stub columns under axial compression. Eng. Struct. 2018, 160, 71–84. [Google Scholar] [CrossRef]
- Teng, J.-G.; Wang, Z.; Yu, T.; Zhao, Y.; Li, L.-J. Double-tube concrete columns with a high-strength internal steel tube: Concept and behaviour under axial compression. Adv. Struct. Eng. 2018, 21, 1585–1594. [Google Scholar] [CrossRef]
- Yu, T.; Teng, J.G.; Wong, Y.L. Stress-Strain Behavior of Concrete in Hybrid FRP-Concrete-Steel Double-Skin Tubular Columns. J. Struct. Eng. 2010, 136, 379–389. [Google Scholar] [CrossRef]
- Long, Y.-L.; Li, W.-T.; Dai, J.-G.; Gardner, L. Experimental study of concrete-filled CHS stub columns with inner FRP tubes. Thin-Walled Struct. 2018, 122, 606–621. [Google Scholar] [CrossRef]
- Tao, Z.; Han, L.-H.; Zhuang, J.-P. Axial Loading Behavior of CFRP Strengthened Concrete-Filled Steel Tubular Stub Columns. Adv. Struct. Eng. 2007, 10, 37–46. [Google Scholar] [CrossRef]
- Liu, J.; Xu, T.; Guo, Y.; Wang, X.; Chen, Y.F. Behavior of circular CFRP-steel composite tubed high-strength concrete columns under axial compression. Compos. Struct. 2019, 211, 596–609. [Google Scholar] [CrossRef]
- Lu, Y.; Li, N.; Li, S. Behavior of FRP-Confined Concrete-Filled Steel Tube Columns. Polymers 2014, 6, 1333–1349. [Google Scholar] [CrossRef]
- Ding, F.-X.; Lu, D.-R.; Bai, Y.; Gong, Y.-Z.; Yu, Z.-W.; Ni, M.; Li, W. Behaviour of CFRP-confined concrete-filled circular steel tube stub columns under axial loading. Thin-Walled Struct. 2018, 125, 107–118. [Google Scholar] [CrossRef]
- Park, J.; Hong, Y.; Hong, G.; Kim, J.; Choi, S. Design Formulas of Concrete Filled Circular Steel Tubes Reinforced by Carbon Fiber Reinforced Plastic Sheets. Procedia Eng. 2011, 14, 2916–2922. [Google Scholar] [CrossRef]
- Hu, Y.M.; Yu, T.; Teng, J.G. FRP-Confined Circular Concrete-Filled Thin Steel Tubes under Axial Compression. J. Compos. Constr. 2011, 15, 850–860. [Google Scholar] [CrossRef]
- Wei, Y.; Wu, G.; Li, G. Performance of circular concrete-filled fiber-reinforced polymer-steel composite tube columns under axial compression. J. Reinf. Plast. Compos. 2014, 33, 1911–1928. [Google Scholar] [CrossRef]
- Teng, J.; Hu, Y.; Yu, T. Stress–strain model for concrete in FRP-confined steel tubular columns. Eng. Struct. 2013, 49, 156–167. [Google Scholar] [CrossRef]
- Teng, J.G.; Huang, Y.L.; Lam, L.; Ye, L.P. Theoretical Model for Fiber-Reinforced Polymer-Confined Concrete. J. Compos. Constr. 2007, 11, 201–210. [Google Scholar] [CrossRef]
- Zhang, Y.; Wei, Y.; Bai, J.; Zhang, Y. Stress-strain model of an FRP-confined concrete filled steel tube under axial compression. Thin-Walled Struct. 2019, 142, 149–159. [Google Scholar] [CrossRef]
- Wu, Y.-F.; Wei, Y. General Stress-Strain Model for Steel- and FRP-Confined Concrete. J. Compos. Constr. 2015, 19, 04014069. [Google Scholar] [CrossRef]
- Choi, K.-K.; Xiao, Y. Analytical Model of Circular CFRP Confined Concrete-Filled Steel Tubular Columns under Axial Compression. J. Compos. Constr. 2010, 14, 125–133. [Google Scholar] [CrossRef]
- Dong, C.; Kwan, A.; Ho, J. Effects of external confinement on structural performance of concrete-filled steel tubes. J. Constr. Steel Res. 2017, 132, 72–82. [Google Scholar] [CrossRef]
- Zeng, J.-J.; Lv, J.-F.; Lin, G.; Guo, Y.-C.; Li, L.-J. Compressive behavior of double-tube concrete columns with an outer square FRP tube and an inner circular high-strength steel tube. Constr. Build. Mater. 2018, 184, 668–680. [Google Scholar] [CrossRef]
- Lam, L.; Teng, J. Design-oriented stress–strain model for FRP-confined concrete. Constr. Build. Mater. 2003, 17, 471–489. [Google Scholar] [CrossRef]
- Popovics, S. A numerical approach to the complete stress-strain curve of concrete. Cem. Concr. Res. 1973, 3, 583–599. [Google Scholar] [CrossRef]
- Jiang, T.; Teng, J. Analysis-oriented stress–strain models for FRP–confined concrete. Eng. Struct. 2007, 29, 2968–2986. [Google Scholar] [CrossRef]
- Wang, Z.H. Experimental Study and Theoretical Analysis of FRP-Concrete-High Strength Steel Solid Double-tube Columns. Ph.D. Thesis, Zhejiang University, Hangzhou, China, 2017. [Google Scholar]
- Wang, J.; Xia, J.; Chang, H.; Han, Y.; Yu, L. The axial compressive experiment and analytical model for FRP-confined gangue aggregate concrete. Structures 2021, 36, 98–110. [Google Scholar] [CrossRef]
- Teng, J.G.; Jiang, T.; Lam, L.; Luo, Y.Z. Refinement of a Design-Oriented Stress–Strain Model for FRP-Confined Concrete. J. Compos. Constr. 2009, 13, 269–278. [Google Scholar] [CrossRef]
- Ozbakkaloglu, T.; Lim, J.C.; Vincent, T. FRP-confined concrete in circular sections: Review and assessment of stress–strain models. Eng. Struct. 2013, 49, 1068–1088. [Google Scholar] [CrossRef]
- Marques, S.P.C.; Marques, D.C.d.S.C.; da Silva, J.L.; Cavalcante, M.A.A. Model for Analysis of Short Columns of Concrete Confined by Fiber-Reinforced Polymer. J. Compos. Constr. 2004, 8, 332–340. [Google Scholar] [CrossRef]
- Xiao, Q.G.; Teng, J.G.; Yu, T. Behavior and Modeling of Confined High-Strength Concrete. J. Compos. Constr. 2010, 14, 249–259. [Google Scholar] [CrossRef]
- A Harries, K.; Kharel, G. Experimental investigation of the behavior of variably confined concrete. Cem. Concr. Res. 2003, 33, 873–880. [Google Scholar] [CrossRef]
- Yang, J.-Q.; Feng, P. Analysis-oriented models for FRP-confined concrete: 3D interpretation and general methodology. Eng. Struct. 2020, 216, 110749. [Google Scholar] [CrossRef]
- Wang, J.; Xia, J.; Chang, H.; Han, Y.; Yu, L.; Jiang, L. Experimental Study on Axial Compressive Behavior of Gangue Aggregate Concrete Filled FRP and Thin-Walled Steel Double Tubular Columns. Coatings 2021, 11, 1404. [Google Scholar] [CrossRef]
- Che, Y.; Wang, Q.L.; Shao, Y.B. Compressive performances of the concrete filled circular CFRP-steel tube (C-CFRP-CFST). Adv. Steel Constr. 2012, 8, 331–358. [Google Scholar]
- Cha, X.X.; Yu, M.; Zhong, S.T. Study on the consistency of bearing capacity formulas in the “Technical Code for Concrete Filled Steel Tubular Structures”. J. Build. Struct. 2013, 34, 11–20. [Google Scholar]
- Xiong, M.; Lan, Z.; Chen, G.; Lu, Y.; Xu, Z. Behavior of FRP-HSC-steel tubular columns under axial compression: A comparative study. Compos. Struct. 2021, 261, 113566. [Google Scholar] [CrossRef]
- Xiong, M.; Xu, Z.; Chen, G.; Lan, Z. FRP-confined steel-reinforced recycled aggregate concrete columns: Concept and behaviour under axial compression. Compos. Struct. 2020, 246, 112408. [Google Scholar] [CrossRef]




| Models | Peak Strength Models | Corresponding Strain Models |
|---|---|---|
| Harries and Kharel [39] | ||
| Marques et al. [37] | ||
| Jiang and Teng [32] | ||
| Xiao et al. [38] | ||
| Yang and Feng [40] |
| Specimen | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (MPa) | Avg. | (GPa) | Avg. | (%) | Avg. | (mm) | (MPa) | Avg. | (%) | Avg. | (%) | Avg. | Avg. | Avg. | |
| L0-1 | 29.0 | 32.6 | 17.4 | 17.3 | 0.183 | 0.211 | / | / | / | / | / | / | / | / | / |
| L0-2 | 35.7 | 17.3 | 0.214 | / | / | / | / | / | / | ||||||
| L0-3 | 33.1 | 17.1 | 0.235 | / | / | / | / | / | / | ||||||
| L1-1 | / | / | / | / | / | / | 0.167 | 63.3 | 64.8 | 1.367 | 1.406 | 0.917 | 0.862 | 1.988 | 6.672 |
| L1-2 | / | / | / | 0.167 | 62.4 | 1.404 | 0.787 | ||||||||
| L1-3 | / | / | / | 0.167 | 68.7 | 1.446 | 0.881 | ||||||||
| L2-1 | / | / | / | / | / | / | 0.334 | 91.6 | 87.6 | 2.344 | 2.333 | 0.875 | 0.820 | 2.687 | 11.073 |
| L2-2 | / | / | / | 0.334 | 85.4 | 2.444 | 0.779 | ||||||||
| L2-3 | / | / | / | 0.334 | 85.8 | 2.011 | 0.805 | ||||||||
| M0-1 | 37.7 | 37.5 | 20.3 | 20.2 | 0.205 | 0.203 | / | / | / | / | / | / | / | / | / |
| M0-2 | 35.4 | 20.1 | 0.195 | / | / | / | / | / | |||||||
| M0-3 | 39.4 | 20.2 | 0.208 | / | / | / | / | / | |||||||
| M1-1 | / | / | / | / | / | / | 0.167 | 59.1 | 63.2 | 0.983 | 1.160 | 0.756 | 0.766 | 1.685 | 5.723 |
| M1-2 | / | / | / | 0.167 | 66.2 | 1.217 | 0.824 | ||||||||
| M1-3 | / | / | / | 0.167 | 64.3 | 1.280 | 0.717 | ||||||||
| M2-1 | / | / | / | / | / | / | 0.334 | 82.4 | 89.5 | 1.803 | 2.088 | 0.767 | 0.829 | 2.387 | 10.301 |
| M2-2 | / | / | / | 0.334 | 93.9 | 2.29 | 0.855 | ||||||||
| M2-3 | / | / | / | 0.334 | 92.3 | 2.172 | 0.864 | ||||||||
| H0-1 | 43.2 | 43.2 | 21.4 | 21 | 0.205 | 0.209 | / | / | / | / | / | / | / | / | / |
| H0-2 | 44.1 | 20.6 | 0.214 | / | / | / | / | / | |||||||
| H0-3 | 42.4 | 21.0 | 0.209 | / | / | / | / | / | |||||||
| H2-1 | / | / | / | / | / | / | 0.334 | 94.6 | 96.9 | 1.786 | 1.840 | 0.846 | 0.831 | 2.243 | 8.779 |
| H2-2 | / | / | / | 0.334 | 101.3 | 1.987 | 0.841 | ||||||||
| H2-3 | / | / | / | 0.334 | 94.9 | 1.748 | 0.807 | ||||||||
| H3-1 | / | / | / | / | / | / | 0.501 | 109.6 | 108.3 | 2.261 | 2.056 | 0.768 | 0.720 | 2.507 | 9.809 |
| H3-2 | / | / | / | 0.501 | 111.9 | 2.090 | 0.709 | ||||||||
| H3-3 | / | / | / | 0.501 | 103.4 | 1.818 | 0.682 | ||||||||
| Authors | Ultimate Strength Models |
|---|---|
| Wei et al. [22] | |
| Lu et al. [18] | |
| Che et al. [42] | |
| Tao et al. [16] | |
| Park et al. [20] | |
| Dong et al. [28] |
| Specimen | (kN) | ds (mm) | ts (mm) | (MPa) | |
|---|---|---|---|---|---|
| M111-F0-1 | 851 | 111 | 1.8 | 37.5 | 0.485 |
| M111-F0-2 | 854 | 111 | 1.8 | 37.5 | 0.485 |
| M160-F0-1 | 1592 | 160 | 1.8 | 37.5 | 0.382 |
| M160-F0-2 | 1677 | 160 | 1.8 | 37.5 | 0.382 |
| H74-F0-1 | 502 | 74 | 1.8 | 43.2 | 0.634 |
| H74-F0-2 | 512 | 74 | 1.8 | 43.2 | 0.634 |
| H111-F0-1 | 917 | 111 | 1.8 | 43.2 | 0.421 |
| H111-F0-2 | 998 | 111 | 1.8 | 43.2 | 0.421 |
| H160-F0-1 | 1782 | 160 | 2 | 43.2 | 0.332 |
| H160-F0-2 | 1697 | 160 | 2 | 43.2 | 0.332 |
| Specimens | (kN) | (kN) | (%) | (%) | ||
|---|---|---|---|---|---|---|
| L74F1-1 | 576 | 1503 | 2.61 | 0.211 | 1.353 | 6.41 |
| L74F1-2 | 576 | 1293 | 2.24 | 0.211 | 1.136 | 5.38 |
| L111F1-1 | 576 | 1393 | 2.42 | 0.211 | 1.424 | 6.75 |
| L111F1-2 | 576 | 1486 | 2.58 | 0.211 | 1.461 | 6.92 |
| M47F1-1 | 662 | 1409 | 2.13 | 0.203 | 1.543 | 7.60 |
| M47F1-2 | 662 | 1240 | 1.87 | 0.203 | 1.366 | 6.73 |
| M74F1-1 | 662 | 1493 | 2.26 | 0.203 | 1.445 | 7.12 |
| M74F1-2 | 662 | 1356 | 2.05 | 0.203 | 1.284 | 6.33 |
| M74F2-1 | 662 | 1908 | 2.88 | 0.203 | 2.266 | 11.16 |
| M74F2-2 | 662 | 1823 | 2.75 | 0.203 | 2.096 | 10.33 |
| M111F1-1 | 662 | 1597 | 2.41 | 0.203 | 1.389 | 6.84 |
| M111F1-2 b | 662 | / | / | 0.203 | / | / |
| M111F2-1 | 662 | 2057 | 3.11 | 0.203 | 2.173 | 10.70 |
| M111F2-2 | 662 | 2079 | 3.14 | 0.203 | 2.425 | 11.95 |
| H74F3-1 | 763 | 2212 | 2.90 | 0.209 | 2.104 | 10.07 |
| H74F3-2 | 763 | 2244 | 2.94 | 0.209 | 1.983 | 9.49 |
| H111F2-1 a | 763 | 1605 | 2.10 | 0.209 | 0.917 | 4.39 |
| H111F2-2 a | 763 | 1705 | 2.23 | 0.209 | 1.129 | 5.40 |
| H111F3-1 | 763 | 2304 | 3.02 | 0.209 | 2.214 | 10.59 |
| H111F3-2 a | 763 | 1877 | 2.46 | 0.209 | 1.336 | 6.39 |
| M160F1-1 | 754 | 1874 | 2.49 | 0.203 | 1.141 | 5.62 |
| M160F1-2 | 754 | 1906 | 2.53 | 0.203 | 1.288 | 6.34 |
| H160F2-1 a | 868 | 2314 | 2.67 | 0.209 | 1.382 | 6.61 |
| H160F2-2 a | 868 | 2020 | 2.33 | 0.209 | 1.093 | 5.23 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Xia, J.; Sun, C.; Cheng, J.; Zhou, S.; Deng, J. Research on the Theoretical Models of FRP-Confined Gangue Aggregate Concrete Partially Filled Steel Tube Columns. Buildings 2024, 14, 3516. https://doi.org/10.3390/buildings14113516
Wang J, Xia J, Sun C, Cheng J, Zhou S, Deng J. Research on the Theoretical Models of FRP-Confined Gangue Aggregate Concrete Partially Filled Steel Tube Columns. Buildings. 2024; 14(11):3516. https://doi.org/10.3390/buildings14113516
Chicago/Turabian StyleWang, Jian, Junwu Xia, Chuanzhi Sun, Jinsheng Cheng, Shengbo Zhou, and Jibing Deng. 2024. "Research on the Theoretical Models of FRP-Confined Gangue Aggregate Concrete Partially Filled Steel Tube Columns" Buildings 14, no. 11: 3516. https://doi.org/10.3390/buildings14113516
APA StyleWang, J., Xia, J., Sun, C., Cheng, J., Zhou, S., & Deng, J. (2024). Research on the Theoretical Models of FRP-Confined Gangue Aggregate Concrete Partially Filled Steel Tube Columns. Buildings, 14(11), 3516. https://doi.org/10.3390/buildings14113516






