Study on Error Influence Analysis of an Annular Cable Bearing-Grid Structure

Abstract

Manufacturing errors of cable length, external node coordinates and tension force by the passive tension method are inevitable, which will inevitably affect the prestressing of cable bearing-grid structures, while existing studies lack the error analysis of error influences in this area. This paper proposes a method for analyzing random errors in constructing annular cable bearing-grid structures. An error control index and a normal distribution-based random error model, considering the impact of cable and ring beam length errors on cable force, were established afterwards. Taking the roof of the Qatar Education City Stadium as an example, the influence of the length errors of the radial cable, ring cable, and outer pressure ring beam on the structural cable force and stress level was analyzed, and the coupling error effect analysis was carried out. The results show that ring cable force and radial cable force are less affected by the length error of each other’s cables, while they are more affected by the length error of the outer ring beam. Stress levels exhibit greater sensitivity to outer ring beam errors compared to cable length errors. As the error limits of outer ring beam increase, radial and ring cable error ratios and outer ring beam stress errors also rise.

1. Introduction

In contrast to composite structures [1,2] or new structures [3,4], for cable-rod tensioned structures (such as cable domes [5], cable trusses [6], etc.) with cables as the main force-bearing components, the prestress distribution in the cable net can often determine the geometry of the entire structure stiffness and mechanical properties. The construction process of the cable net is the process of establishing the prestress of the structure. In the actual engineering construction process, the manufacturing error of the cable length, the error of the external node coordinates, and the error of the tension force in the cable caused by the passive tension method are inevitable, which will inevitably affect the prestressing of the structure. Therefore, it is necessary to control the construction of the cable-rod tension structure, that is, before construction, the cable length of the structural cable (passive cable and no adjustment cable), the cable force of the active tension cable, and the external connection nodes of the cable network should be addressed. The influence of errors such as coordinates must be analyzed to determine reasonable control indicators. In addition, error impact calculation is required to find the acceptable error limit for each parameter, i.e., uncertainty quantification [7,8].

At present, scholars have conducted a certain degree of research on the error control of cable-rod tension structures. Chen et al. [9] established a mathematical model for the length error of cable-strut tension structural units based on probability and statistics theory, and they pointed out that the construction plan has a significant impact on cable errors. After that, Chen et al. [10] optimized the construction scheme of cable-strut tension structures based on error sensitivity calculations and found that different elements have different error sensitivities. By replacing the selected rods of the shell with passive viscoelastic dampers and applying eigenvalue perturbation techniques and seismic spectrum concepts, Yang et al. [11] analyzed the sensitivity of various topological structures of the mesh shell. Zong et al. [12] proposed an analysis error impact calculation method for the shape accuracy of antenna structures and found that slender cables and high tension levels can improve the overall structural capability to resist the influence of uncertainty on antenna performance. Kong et al. [13] conducted a detailed parameter analysis of a 500 m aperture spherical radio telescope and determined that the deviation in cable blanking length is the most important factor affecting cable force. Hu et al. [14] developed an adaptive Kriging-based method to investigate the global sensitivity of uncertain parameters and discover the influential factors in the manufacturing process of cable-network antennas. Sun et al. [15] conducted a comprehensive study on the random manufacturing errors in the construction process of mesh reflector antennas and analyzed their impact on the surface accuracy of reflectors.

The normal distribution is considered one of the most important distribution functions in error simulation because it is easy to analytically handle and can explicitly solve a large number of problems. The normal distribution is the result of the central limit theorem. The central limit theorem states that the accuracy of approximation increases with the number of repeated observations. In addition, the bell shaped normal distribution helps to model various random variables in a practical way. Wang et al. [16] used an error sensitivity calculation method based on normal distribution to perform single error calculation and multi error coupling calculation on a 500 m aperture spherical radio telescope. Luo et al. [17] proposed the method of multiple random-error effect simulation, considering the effect of active forces of tensioned cables, lengths of passively tensioned cables, and outer node coordinates. Bonizoni et al. [18,19] developed an approximate algorithm for solving the recursive first-order moment problem of tensor training format using perturbation method, and they proved that the recursive fitness and regularity results can hold in Sobolev space value Holder space with mixed regularity. By replacing certain members of the shell with passive viscoelastic dampers and applying eigenvalue perturbation techniques and seismic spectrum concepts, Chen et al. [20] established an element length error model for cable-rod tension structures, derived the basic equations for pre-tension deviation and element length error, and found that the dsds are more sensitive to errors than the rods. A linear quadratic regulator (LQR) based optimal control method for interval uncertainty was proposed [21] to balance the optimal control cost function and minimize state vector fluctuations in spacecraft attitude control. A method for uncertain optimal attitude vibration control was proposed based on interval dimension analysis [22]. Yang et al. [23] treated uncertainty as an interval number and proposed the propagation of uncertain modal coordinates based on non-probability theory. In addition, several published studies [24,25] have elucidated the influence of external pressure ring beams (boundaries) on the internal forces of cable networks.

The annular cable bearing-grid structure used in the Qatar Education City Stadium consists of an upper rigid grid system and a lower cable-rod system. In terms of error control, domestic codes do not have clear structural requirements, and research on construction error control of a new type of tensioned overall structural system of annular cable-supported grid structures is also relatively rare. Therefore, it has certain research value and practical significance to analyze the influence of the error that may occur during the fabrication, construction, and installation of this kind of structure cable net on the stress state of the structure and formulate error control objectives. Taking this project as a case, this paper grasps the influence characteristics of cable length error and peripheral steel ring beam length error on cable force and structural stress level through random error influence analysis and determines a reasonable error control index.

2. Random Error Influence Analysis Method

2.1. Basic Theory

For the general cable-rod space structure, the key control factors of construction are the tension force of the active cable, the length of the cable, and the installation coordinates of the external nodes. According to the form of the cable net and the construction plan, the cables are divided into active cables and passive cables. By tensioning the active cables, prestress is established in the overall structure. According to whether the cable is directly connected with the peripheral structure, it can be divided into the outer cable and the inner cable, and the node connecting the outer cable and the outer structure is the outer node.

In the error analysis, the actual length of the cable, the actual coordinates of the connecting node, and the actual tension of the connecting cable can be expressed as:

$$L=L_0+{\Delta }_L$$

(1)

$$C=C_0+{\Delta }_C$$

(2)

$$T=(1+{\Delta }_T)T_0$$

(3)

where L represents the actual length of the cable; C represents the actual coordinates of the connecting node; T represents the actual tension of the connecting cable; L₀ represents the designed cable length; C₀ represents the design coordinates of the outreach node; and T₀ represents the design tension of the outer cable.

∆_L, ∆_C and ∆_T have the following common characteristics in Equations (1)–(3).

(1)

The sign and magnitude of the error are both uncertain quantities.

(2)

As the number of samples increases, the average value of the error will gradually tend to 0.

(3)

If the number of samples is large enough, the distribution of random errors will also show a certain regularity [8].

For the Qatar Education City Stadium, the error analysis also considers the length error of the external pressure ring beam, that is, the length error of the radial cable is set as ∆_L1, the length error of the ring cable is ∆_L2, and the length error of the ring beam is ∆_C. During the analysis, the influence degree of the independent error factors on the annular cable bearing-grid structure is considered first, then the influence degree of the structure under the action of various error couplings is discussed, and the main influencing factors (sensitivity factors) and secondary influences are obtained.

2.2. Error Distribution Model

By studying a sufficient number of random error samples, the distribution model of random errors can be obtained. Therefore, according to the distribution model of random errors, a sufficient number of error samples can also be randomly generated. If the calculation results of the most unfavorable error samples can meet the requirements of construction, it can be concluded that the effect of random errors on construction is negligible.

Because the three influencing factors, actual cable length (i.e., L), actual coordinates of external nodes (i.e., C), and actual tension forces of external cables (i.e., T), are mutually exclusive and the possibility of positive and negative deviations for each factor is equal, these three errors can be considered to obeys a normal distribution [26], i.e., X~N(μ, σ²), as shown in Figure 1. Among them, X represents the error, N represents the calculation equation of error X, μ is the average, and σ is the standard deviation.

The error distribution function is

$$f(x)={\displaystyle \frac{1}{\sqrt{2\pi \sigma }}}\exp (-{\displaystyle \frac{{(x-\mu )}^2}{2{\sigma }^2}})$$

(4)

Assuming that the maximum allowable error range of X is [X_min, X_max] when the component is fabricated and installed, assume that $P(\left|X^{\prime }\right|\le X_{\max })=99.7\%$, where X_min and X_max represent the minimum and maximum values of the cable length error, respectively. Then, the average value of the error, μ, and the standard deviation of the error, σ, can be obtained according to Equations (5) and (6).

$$\mu ={\displaystyle \frac{X_{\min }+X_{\max }}{2}}$$

(5)

$$\sigma ={\displaystyle \frac{X_{\max }-X_{\min }}{2}}$$

(6)

Generally, when the number of samples is large enough, the mean value µ of the normal distribution is 0, so it can be deduced that the standard deviation σ is 1/3 of the maximum allowable error.

The coupled random error can be expressed in matrix form, as shown in Equation (7).

$$E_{\left(i\right)}=\left[\begin{array}{ccc}{E}_{L\left(i\right)}^{OP}& E_{C\left(i\right)}^{OP}& 0\\ E_{L\left(i\right)}^{IP}& 0& 0\\ E_{L\left(i\right)}^A& E_{C\left(i\right)}^A& E_{T\left(i\right)}^A\end{array}\right]=\left[\begin{array}{ccc}{e}_{l\left(i,1\right)}^{op}& e_{c\left(i,1\right)}^{op}& 0\\ e_{l\left(i,2\right)}^{op}& e_{c\left(i,2\right)}^{op}& 0\\ ⋮& ⋮& ⋮\\ e_{l\left(i,k\right)}^{op}& e_{c\left(i,k\right)}^{op}& 0\\ e_{l\left(i,1\right)}^{ip}& 0& 0\\ e_{l\left(i,2\right)}^{ip}& 0& 0\\ ⋮& ⋮& ⋮\\ e_{l\left(i,m\right)}^{ip}& 0& 0\\ e_{l\left(i,1\right)}^a& e_{c\left(i,1\right)}^a& e_{t\left(i,1\right)}^a\\ e_{l\left(i,2\right)}^a& e_{c\left(i,2\right)}^a& e_{t\left(i,2\right)}^a\\ ⋮& ⋮& ⋮\\ e_{l\left(i,n\right)}^a& e_{c\left(i,n\right)}^a& e_{t\left(i,n\right)}^a\end{array}\right]$$

(7)

Among them: E_(i) is the error matrix of the ith error case of the structure; $E_{L\left(i\right)}^{OP}$ is the column vector of the length error of the external passive cable; $E_{C\left(i\right)}^{OP}$ is the column vector of the installation coordinate error of the external passive cable node; $E_{L\left(i\right)}^{IP}$ is the inner passive cable length error column vector; $E_{L\left(i\right)}^A$ is the column vector of the length error of an active cable; $E_{C\left(i\right)}^A$ is the column vector of the installation coordinate error of an active cable node; $E_{T\left(i\right)}^A$ is the column vector of the tension force error of an active cable; k, m, and n are the numbers of the external passive cables, the internal passive cables, and the active cables, respectively; $e_{l\left(i,j\right)}^{op}$ is the value of the length error of the jth external passive cable under the ith error condition (j = 1, 2, …, k); $e_{c\left(i,j\right)}^{op}$ is the value of the installation coordinate error of the jth external passive cable node under the ith error condition of the structure (j = 1, 2, …, k); $e_{l\left(i,j\right)}^{ip}$ is the value of the jth inner passive cable length error under the ith error condition (j = 1, 2, …, m); $e_{l\left(i,j\right)}^a$ is the value of the jth active cable length error under the ith error condition (j = 1, 2, …, n); $e_{c\left(i,j\right)}^a$ is the value of the installation coordinate error of the jth active cable node under the ith error condition (j = 1, 2, …, n); $e_{t\left(i,j\right)}^a$ is the value of the jth active cable tension error under the ith error condition (j = 1, 2, …, n).

It can be seen from the analysis that the installation coordinate errors of the outer connecting cable nodes can be converted into the additional cable length errors of the outer connecting cables. Therefore, the total cable length error of the outer connecting cable can be defined as:

$$e_{lc\left(i,j\right)}^{op}=e_{l\left(i,j\right)}^{op}+e_{c\left(i,j\right)}^{op} (j=1,2,\dots , k)$$

(8)

where $e_{lc\left(i,j\right)}^{op}$ is the total cable length error of the jth external passive cable of the ith error condition (j = 1, 2, ···, k).

Therefore, Equation (6) can be changed to (k + m + n) × 2 matrix form, such as Equation (9).

$$E_{\left(i\right)}=\left[\begin{array}{cc}{E}_{LC\left(i\right)}^{OP}& 0\\ E_{L\left(i\right)}^{IP}& 0\\ E_{LC\left(i\right)}^A& E_{T\left(i\right)}^A\end{array}\right]=\left[\begin{array}{cc}{E}_{L\left(i\right)}^{OP}+E_{C\left(i\right)}^{OP}& 0\\ E_{L\left(i\right)}^{IP}& 0\\ E_{L\left(i\right)}^A+E_{C\left(i\right)}^A& E_{T\left(i\right)}^A\end{array}\right]=\left[\begin{array}{cc}{e}_{l\left(i,1\right)}^{op}+e_{c\left(i,1\right)}^{op}& 0\\ e_{l\left(i,2\right)}^{op}+e_{c\left(i,2\right)}^{op}& 0\\ ⋮& ⋮\\ e_{l\left(i,k\right)}^{op}+e_{c\left(i,k\right)}^{op}& 0\\ e_{l\left(i,1\right)}^{ip}& 0\\ e_{l\left(i,2\right)}^{ip}& 0\\ ⋮& ⋮\\ e_{l\left(i,m\right)}^{ip}& 0\\ e_{l\left(i,1\right)}^a+e_{c\left(i,1\right)}^a& e_{t\left(i,1\right)}^a\\ e_{l\left(i,2\right)}^a+e_{c\left(i,2\right)}^a& e_{t\left(i,2\right)}^a\\ ⋮& ⋮\\ e_{l\left(i,n\right)}^a+e_{c\left(i,n\right)}^a& e_{t\left(i,n\right)}^a\end{array}\right]$$

(9)

In the Qatar Education City Stadium, all cables are fixed-length cables, so all cables are passive cables while no active cables. In addition, the radial cables are outer cables, and the ring cables are inner cables. The errors considered are the length of the radial cable, the length of the ring cable, and the length of the ring beam, and the coordinate error of the outer joint (the installation coordinates of the surrounding steel structure) is not considered. For the length error of the ring beam, refer to the method of cable length error and introduce it into the structure as the length error of the member. Error types mainly include passive cable length errors, which can be expressed in matrix Equation (10).

$$\begin{array}{cc}{\mathit{E}}_i& ={\left[\begin{array}{cc}{E}_{L,i}^{OP}& E_{L,i}^{IP}\\ E_{C,i}^{OP}& 0\end{array}\right]}^T\hfill \\ & ={\left[\begin{array}{cccccccc}{e}_{L,i,1}^{OP}& e_{L,i,2}^{OP}& \dots & e_{L,j,k}^{OP}& e_{L,i,1}^{IP}& e_{L,i,2}^{IP}& \dots & e_{L,i,m}^{IP}\\ e_{C,i,1}^{OP}& e_{C,i,2}^{OP}& \dots & e_{C,i,k}^{OP}& 0& 0& \dots & 0\end{array}\right]}^T\hfill \end{array}$$

(10)

The specific steps of the error effect analysis are as follows:

(1)

Utilize the normal distribution theory to define the error distribution model of ∆_L1, ∆_L2 and ∆_C.

(2)

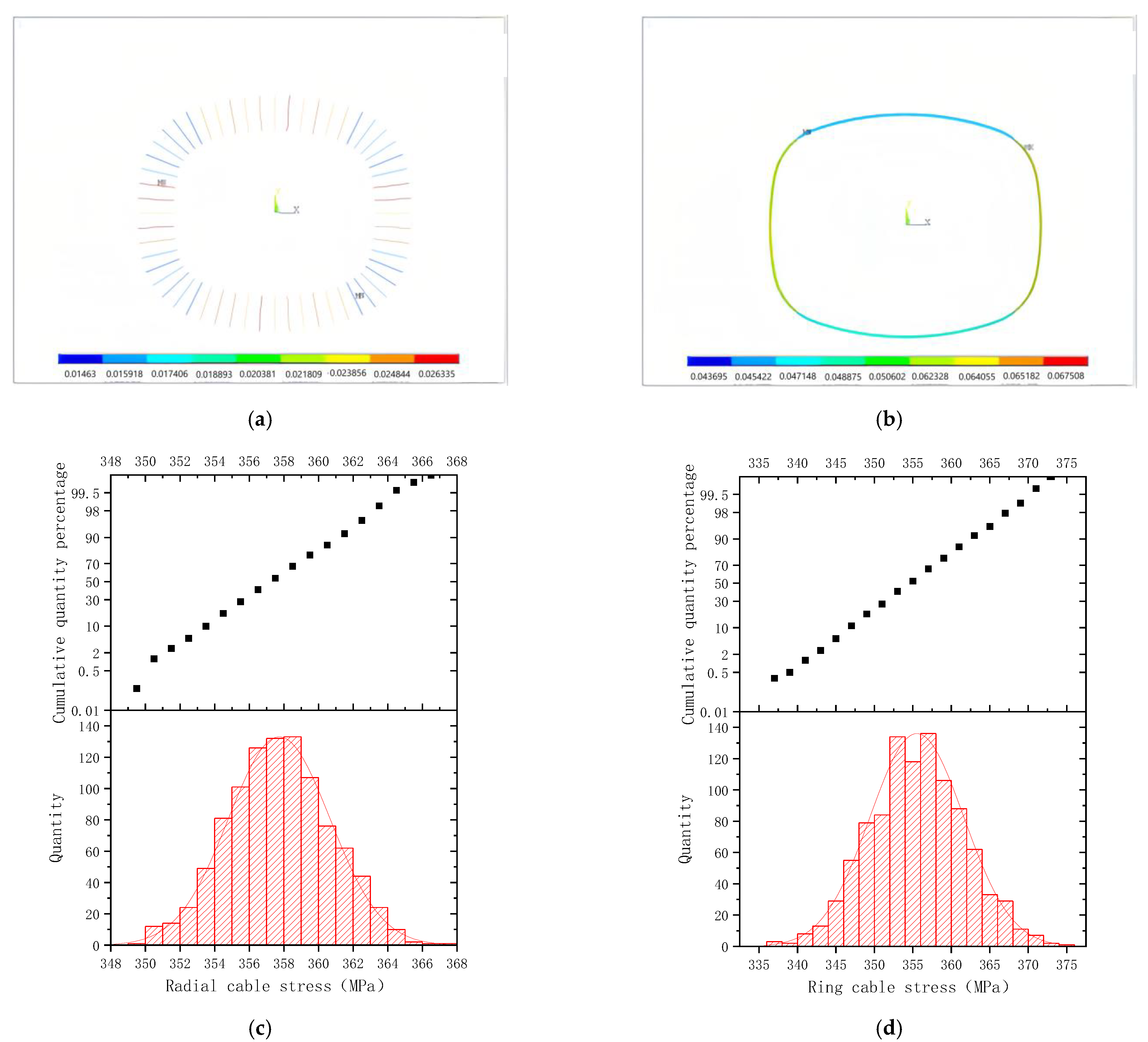
Generate 1000 error samples in random, while each error sample is a calculation error condition of the structure of the Qatar Education City Stadium. Likewise, these 1000 error samples also conform to the normal distribution. Among them, the statistical error distribution of a radial cable, a ring cable, and a ring beam are shown in Figure 2.

(3)

Each generated error case will be introduced into the simulation model and form the calculation case of the defective structure.

(4)

Perform the numerical calculate of each defect condition and obtain the error effect of the simulation model under each condition.

(5)

Compare the cable stress under the non-defect condition and the defect conditions, and obtain the maximum stress error.

(6)

Determine whether the maximum stress error meets the requirements. If it does meet the requirements, the allowable range of the error parameters is set reasonably. Otherwise, adjust the allowable range of the error parameters, and perform steps (1)~(5) again until a reasonable allowable range of the error parameters is obtained.

Through the reasonable allowable range of the various error parameters, the main influencing factors (i.e., sensitive factors) and secondary influencing factors (i.e., nonsensitive factors) are obtained to provide a basis for the construction accuracy control of the Qatar Education City Stadium.

The error limitation of the cable length of the Qatar Education City Stadium adopts American standard code [27], as shown in

Table 1. Error limitations allowed in the ASCE/SEI STANDARD 19-10 specification.

Standard	L0	Error Limitation
ASCE/SEI STANDARD 19-10	≤8.54 m	±2.54 (mm)
	$8.54\mathrm{m}\le L_0\le 36.59\mathrm{m}$	$\pm 0.03\%L_0(\mathrm{mm})$
	>36.59 m	$\pm (\sqrt{L_0(m)}+5)(\mathrm{mm})$

.

3. Analysis and Results

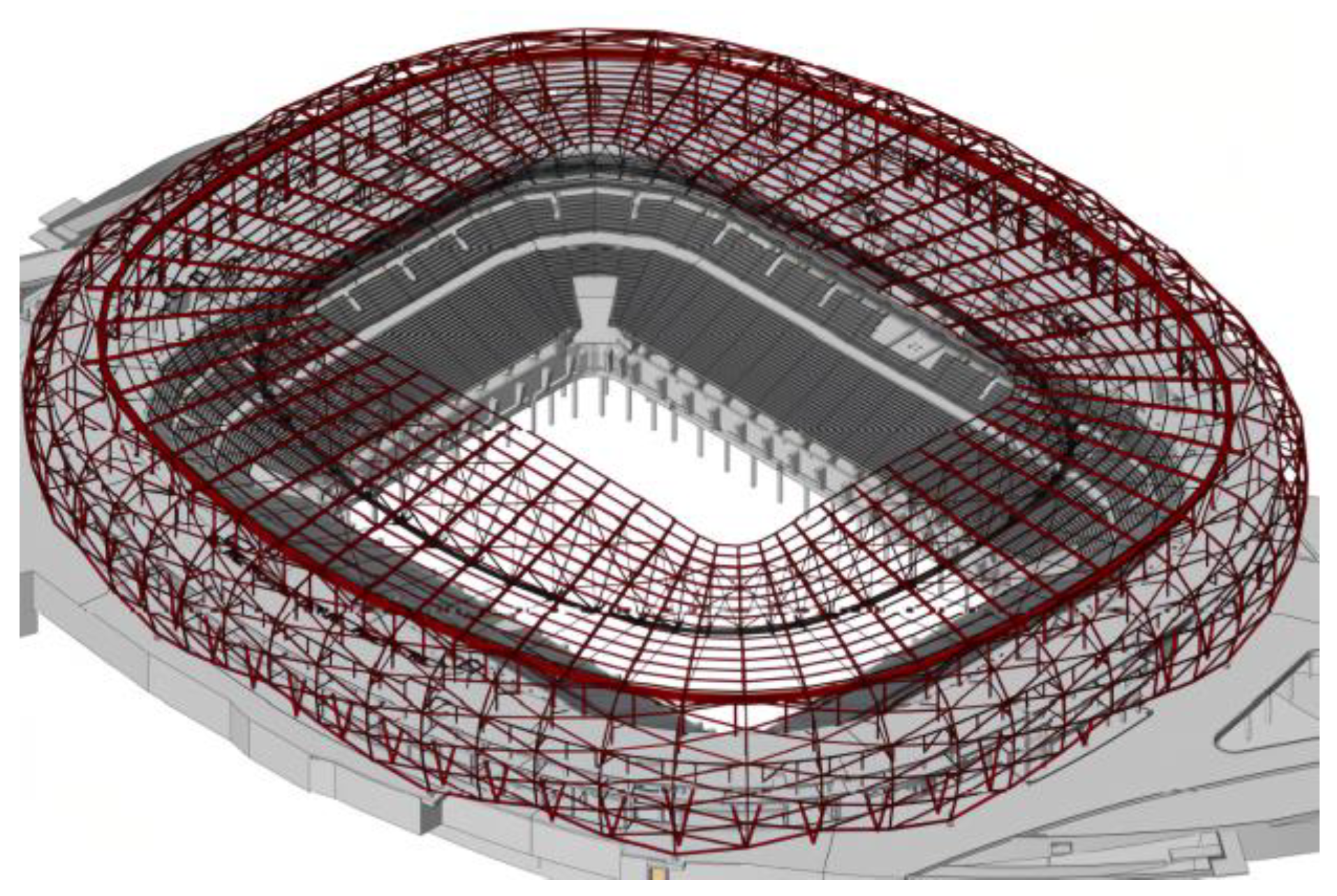
3.1. Project Overview

The roof of the Qatar Education City Stadium is an annular space structure with a long axis of 225 m and a short axis of 196 m on the structural plane, and the maximum cantilever span is 55 m.

According to the requirements of architectural shape, space function, and visual aesthetics, the canopy inside the stadium roof structure adopts an annular spoke-type cable bearing-grid structure. The three-dimensional axonometric of the stadium is shown in Figure 3. The cable-rod system is composed of radial cables, annular ring cables, and struts. The radial cables are arranged in a straight line, with a total of 56 pieces, and projected into a ring. The weight of the upper mesh is balanced by applying prestressing in the radial and annular cables. Sectional and material parameters of members are listed in

Table 2. Sectional and material parameters of members.

Member Name	Section/mm	Elastic Modulus Before Yield/MPa	Yield Strength /MPa
Outer pressure ring beam	1200 × 40	2.06 × 105	420
Radial cable	Φ75~Φ135	1.60 × 105	420
Annular ring cables	8Φ110	1.60 × 105	420
Strut	Φ120 × 15	2.06 × 105	420

.

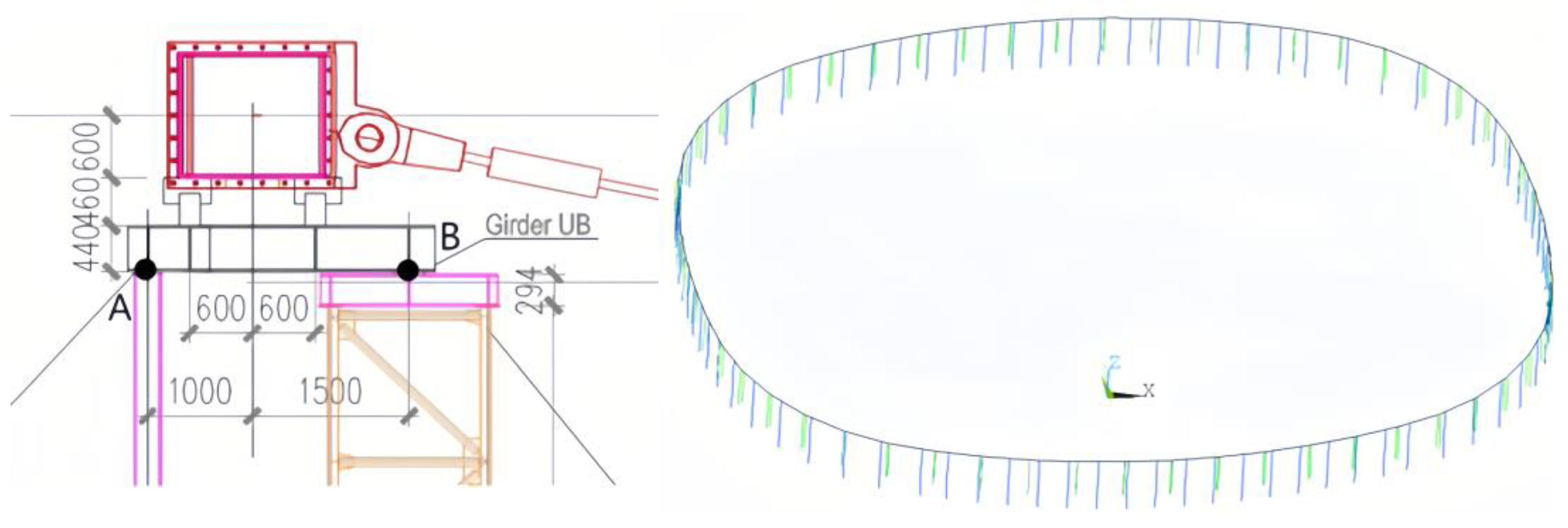
3.2. Analysis Model

The length error analysis of the ring beam and cable system is carried out in ANSYS V12.1 software. The model includes the following components: structural columns (excluding cross braces between columns), additional supports between columns, support frame of the ring beam, external pressure ring beam, radial cables, annular ring cables, and struts. The ANSYS model is shown in Figure 4.

Among them, the ring beam support frame and the cross braces between columns are nonoriginal structural components, which are briefly introduced below.

(1)

Ring beam support frame

During the construction of the structure, to prevent torsion and overturning of the outer pressure ring beam when the cable net is lifted, and to facilitate the construction of the workers, a supporting frame is installed under the ring beam at the tension end of each radial cable. The support frame is established according to the stiffness parameters provided by the design, and the element type adopts LINK10 (compression only). The cross-section of the support frame is square. According to the stress state, the support points of the support frame are mainly divided into inner (B) and outer (A) parts in the radial direction, as shown in Figure 5.

(2)

Cross braces between columns

Due to the weak hoop stiffness of the peripheral structure (structural column, cross braces, external pressure ring beam), the state of hoop instability is easy to trigger during the construction process. Therefore, it is necessary to add additional cross braces between the structural columns to enhance the hoop stiffness of the structure. Due to the different column spacing, the length of diagonal braces vary from 15 m to 18 m. The tentative cross-section is a round steel pipe, which is 355.6 mm in diameter and 6 mm in thickness. The element type of the diagonal brace is set as LINK8 (axial force element), and the specific modeling diagram is shown in Figure 6.

3.3. Overview of Analysis Objects

There are 56 radial cables in this structure, and the inner ring cable bundle are composed of 8 cables, as shown in Figure 7.

Each of the 56 radial cables is an analysis unit, so there are 56 radial cable units. Meanwhile, each unit is set to generate 1000 random error samples, and defects are introduced into the structure to obtain 1000 calculation conditions.

The ring cable has eight cables, and each of them are composed of four segments (i.e., A, B, C, D). The sections and numbers are shown in Figure 7. Therefore, a total of 32 cable segments are considered. The length error is equally divided into each segment of the ring cable, and each segment also generates 1000 random error samples.

The length error of the ring beam is equally applied to each divisions of the ring beam in simulation.

According to the “Technical standard for prestressed steel structures” (JGJ/T 497-2023) “Before completion, the main load-bearing cable force deviation value should be controlled within ±10%”, so [e_fr] takes ±10% [28].

3.4. Load Conditions

In the error analysis calculation, the following load conditions need to be followed.

(1)

Dead load (the self-weight of the structure, considering the magnification factor of 0.15 times)

(2)

Prestressing (including radial cables, ring cables, and external compression ring beams)

(3)

Random errors in the length of the cables and the external pressure ring beam

3.5. Error Combination

According to the error analysis characteristics of the Qatar Education City Stadium, seven error combinations are set. As mentioned above, 1000 working conditions are randomly established for each error combination, and the distribution models all follow normal distribution model. Among them, Combination 1#, 2#, 3# consider the independent error effect, Combination 4# to 8# consider the coupling error effect, and all the error analysis has a 99.7% guarantee rate. The specific error combination statistics table is shown in

Table 3. Error combination statistics [25].

Error Combination	Radial Cable Length Error	Ring Cable Length Error	Length Error of External Pressure Ring Beam
1	${\Delta }_{1L}\le \pm 0.03\%L_0(\mathrm{mm})$	——	——
2	——	${\Delta }_{2L}\le \pm (\sqrt{L_0(m)}+5)(\mathrm{mm})$	——
3	——	——	${\Delta }_C\le \pm 170(\mathrm{mm})$
4	${\Delta }_{1L}\le \pm 0.03\%L_0(\mathrm{mm})$	${\Delta }_{2L}\le \pm (\sqrt{L_0(m)}+5)(\mathrm{mm})$	——
5	${\Delta }_{1L}\le \pm 0.03\%L_0(\mathrm{mm})$	${\Delta }_{2L}\le \pm (\sqrt{L_0(m)}+5)(\mathrm{mm})$	${\Delta }_C\le \pm 42.5(\mathrm{mm})$
6	${\Delta }_{1L}\le \pm 0.03\%L_0(\mathrm{mm})$	${\Delta }_{2L}\le \pm (\sqrt{L_0(m)}+5)(\mathrm{mm})$	${\Delta }_C\le \pm 85(\mathrm{mm})$
7	${\Delta }_{1L}\le \pm 0.03\%L_0(\mathrm{mm})$	${\Delta }_{2L}\le \pm (\sqrt{L_0(m)}+5)(\mathrm{mm})$	${\Delta }_C\le \pm 127.5(\mathrm{mm})$
8	${\Delta }_{1L}\le \pm 0.03\%L_0(\mathrm{mm})$	${\Delta }_{2L}\le \pm (\sqrt{L_0(m)}+5)(\mathrm{mm})$	${\Delta }_C\le \pm 170(\mathrm{mm})$

.

4. Influence Analysis of Independent Error Effect

To analyze the influence of a single error on the structure, three error combinations (i.e., random errors of radial cables within the maximum allowable range, random errors of ring cables within the maximum allowable range, random errors of external pressure ring beam within the maximum allowable range) are simulated. The non-stress length of each radial cable in the Qatar Education City Stadium is approximately 30 m. According to the “Technical Regulations for Prestressed Steel Structures” (CECS 212:2006), when the cable length is 8.54 m < L₀ ≤ 36.59 m, the maximum allowable cable length error is set as E_L = ±0.03% L₀ (mm). When the unstressed length of a single ring cable varies from 112 m to 133 m, the cable length is set as L₀ > 36.59 m, and the maximum allowable cable length error is E_L = $\pm (\sqrt{L_0(m)}+5)$ (mm). The maximum allowable length error of outer ring beam is ±170 mm.

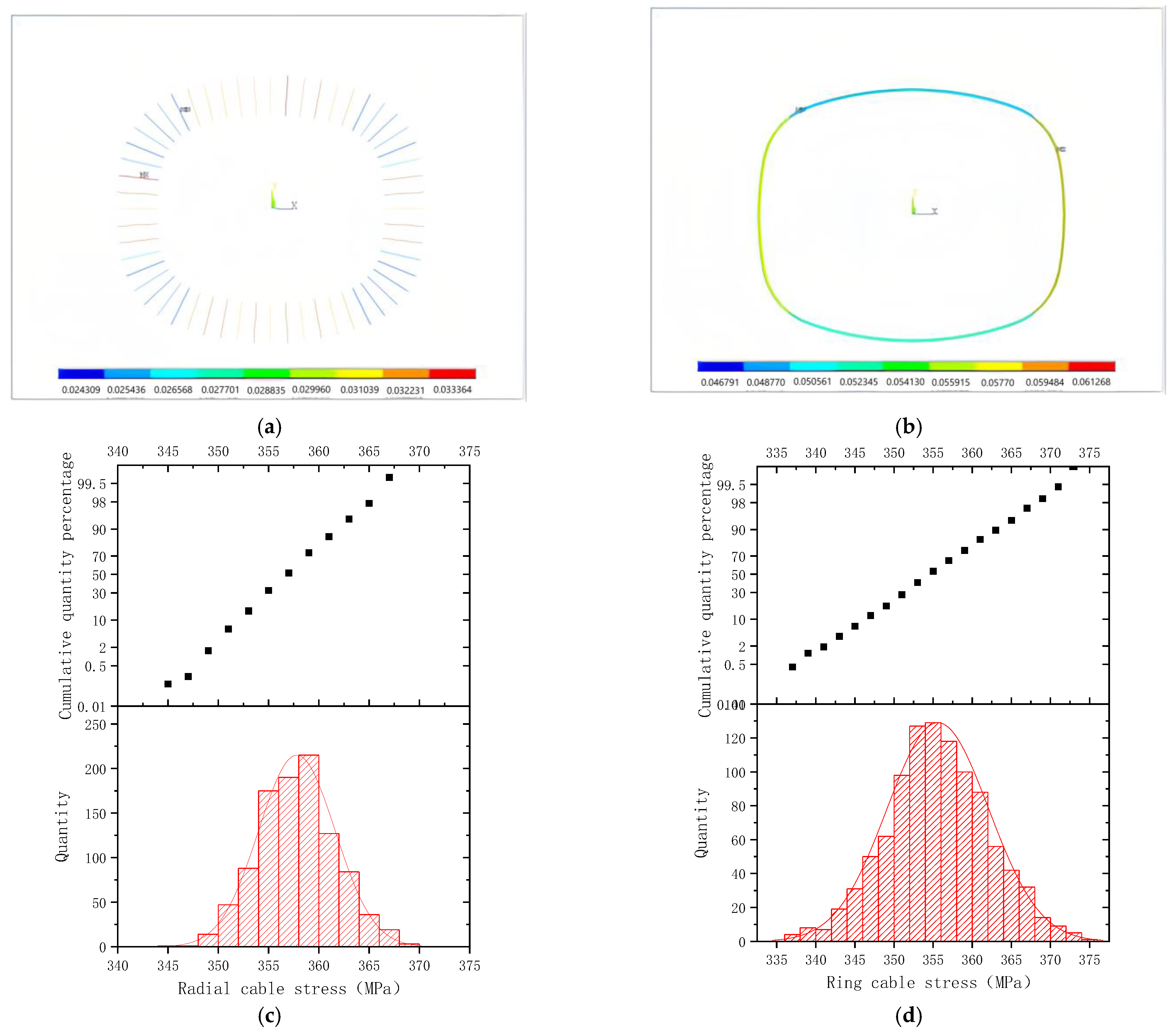
4.1. Radial Cable Length Error

After analyzing 1000 random samples, a radial cable and a ring cable element are selected. When the radial cable length error is the only influence factor, the corresponding cable force error effect diagram is shown in Figure 8. Figure 8 shows that when there is only radial cable length error, the maximum absolute value of the cable force error ratio of the radial cable is 2.722%, and the absolute maximum value of the absolute value of the cable force error ratio of the ring cable is 0.425%. When the radial cable length error is a single factor, the cable force error response of the radial cable is larger than that of the ring cable, but the maximum error ratio is also at a low level.

If the radial cable length error is the only influence factor, the statistics of the influence on the structural stress are shown in

Table 4. The statistics of the influence on the structural stress considering only radial cable length error.

Extreme Value		Maximum Stress Element	Minimum Stress Element
Stress of radial cables/MPa	Theoretical value	378.4	338.8
	Maximum value	388.2	343.9
	Minimum value	368.5	333.7
Stress of ring cables/MPa	Theoretical value	358.1	351.3
	Maximum value	359.6	352.8
	Minimum value	356.6	349.9
Stress of external pressure ring beam/MPa	Theoretical value	−158.1	−82.0
	Maximum value	−160.4	−85.0
	Minimum value	−155.9	−78.9

. Since the external pressure ring beam is compressed, the displayed stress is negative.

4.2. Ring Cable Length Error

After analyzing 1000 random samples, it can be seen from Figure 9 that the absolute value of the cable force error ratio of the radial cable is 0.568%, and the absolute value of the cable force error ratio of the ring cable is 5.774%. If the ring cable length error is the only influence factor, the cable force error of the ring cable is larger than that of the radial cable, while the maximum error ratio is also at a low level.

Figure 9 shows the effect of cable force error with the ring cable length error as the only influence factor.

If the length error of ring cable is the only influence factor, the statistics of the influence on the structural stress are shown in

Table 5. The statistics of the influence on the structural stress considering only ring cable length.

Extreme Value		Maximum Stress Element	Minimum Stress Element
Stress of radial cables/MPa	Theoretical value	378.385	338.824
	Maximum value	380.505	340.727
	Minimum value	376.275	336.931
Stress of ring cables/MPa	Theoretical value	358.108	351.335
	Maximum value	374.34	369.111
	Minimum value	341.665	333.307
Stress of external pressure ring beam MPa	Theoretical value	−158.088	−81.997
	Maximum value	−159.004	−82.459
	Minimum value	−157.178	−81.539

.

4.3. Ring Beam Length Error

After analyzing 1000 random samples, if the length error of the outer pressure ring beam is the only influence factor, the maximum absolute value of the cable force error ratio of the radial cable is 8.332%, and the absolute maximum value of the cable force error ratio of the ring cable is 8.302%. When the length error of the outer pressure ring beam is the only influence factor and the maximum absolute value of the outer pressure ring beam length error is 170 mm, the force error of the radial cable and the ring cable is larger, which is 8.302% and meets the specification that the maximum allowable error varies within 10%. Figure 10 shows the effect of cable force error when the ring beam length error is the only influence factor.

When the ring beam length error is the only influence factor, the statistics of the influence on the structural stress are shown in

Table 6. The statistics of the influence on the structural stress considering only ring beam length.

Extreme Value		Maximum Stress Element	Minimum Stress Element
Stress of radial cables/MPa	Theoretical value	378.385	338.824
	Maximum value	409.605	366.491
	Minimum value	347.048	311.05
Stress of ring cables/MPa	Theoretical value	358.108	351.335
	Maximum value	386.937	380.433
	Minimum value	329.171	322.121
Stress of external pressure ring beam/MPa	Theoretical value	−158.088	−81.997
	Maximum value	−171.56	−89.026
	Minimum value	−144.565	−74.939

.

4.4. Analysis Summary

By analyzing the independent error effects of radial cables, ring cables, and external pressure ring beams, we reached the following conclusions.

If the radial cable length error is the only influence factor, the error response of the radial cable force is more obvious, the maximum ratio is 2.722%, and the error response of the ring cable is 0.425%. If the ring cable length error is the only influence factor, the error response of the ring cable is more obvious, the maximum ratio is 5.744%, and the error response of the radial cable is 0.568%. Else if the length error of the external pressure ring beam is the only influence factor and the maximum allowable length error is set as ±170 mm, the absolute values of the cable force error ratios of the radial cable and the ring cable are relatively larger, which are both close to 8.3%. It can be seen from the comparison that when the only influence factor is the length error of the external pressure ring beam, the cable force errors of the structure are relatively larger.

For the stress error of the external pressure ring beam, it can be seen from the above analysis that if the length error of the external pressure ring beam is the only influence factor, the maximum stress error is 13.5 MPa. If the radial cable length error is the only influence factor, the maximum stress error is 2.4 MPa. Else if the ring cable length error is the only influence factor, the maximum stress error is approximately 1 MPa.

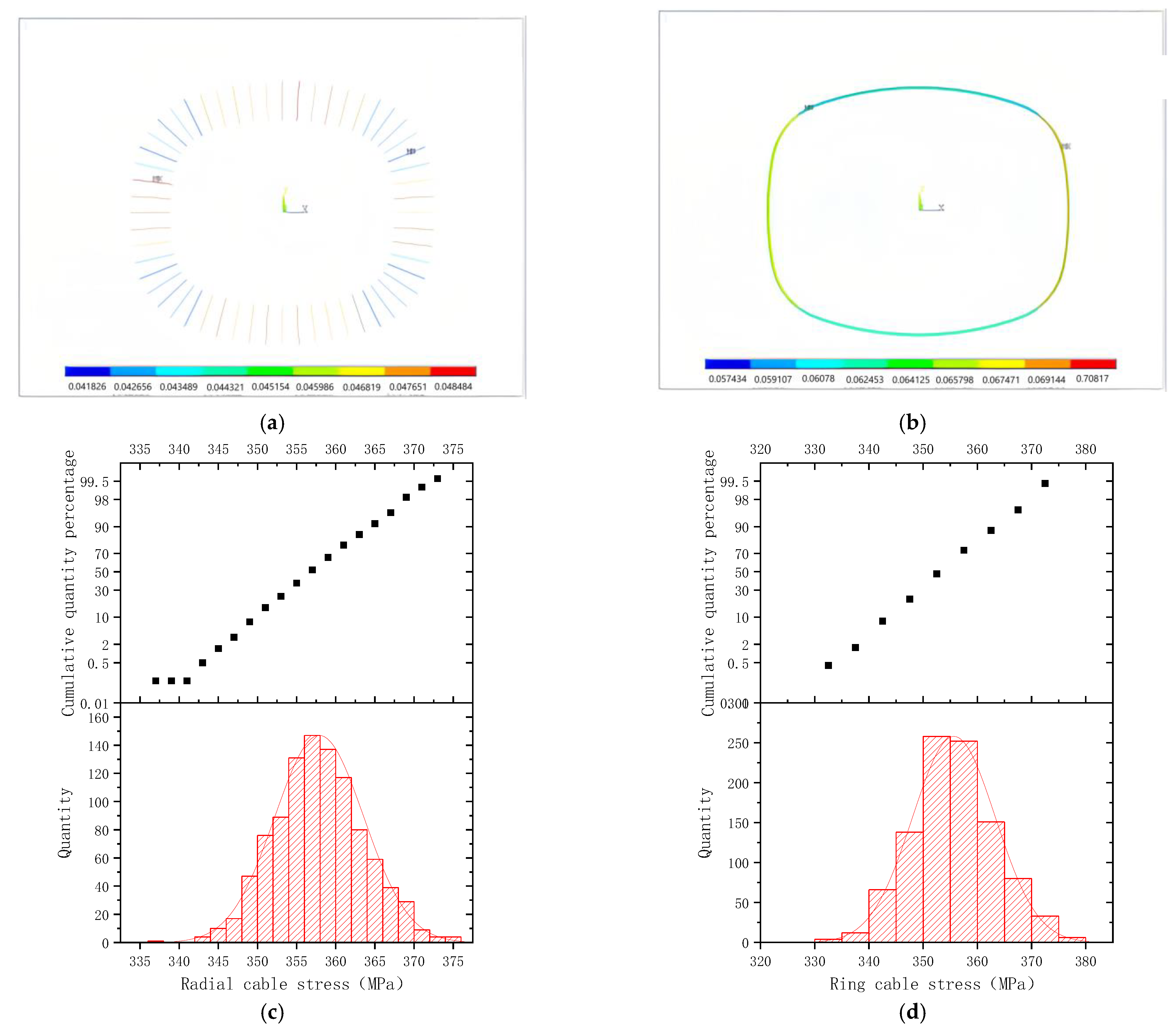
5. Coupling Error Effect Analysis

In addition to the study of the independent error effect, the coupling effect of each error factor cannot be ignored. This study focuses on the coupled analysis of the radial cable length error, the ring cable length error, and the ring beam length error. When determining several coupling error combinations, the appropriate ring beam length error is calculated, and the maximum ring beam length error is set as ±170 mm. The selected values of the ring beam length error for combinations 4# to 8# are 0%, 25%, 50%, 75%, and 100% of the maximum value (i.e., ±170 mm), respectively, as listed in Table 2.

5.1. Combination 4#

In case of error Combination 4#, the maximum value of the cable force error ratio of the radial cable is 2.782%, and the maximum value of the cable force error ratio of the ring cable is 5.924%. The cable force error effect diagram is shown in Figure 11, the statistics of the influence on the structural stress are shown in

Table 7. Statistical table of the influence of Combination 4# coupling errors on structural stress.

Extreme Value		Maximum Stress Element	Minimum Stress Element
Stress of radial cables/MPa	Theoretical value	378.385	338.824
	Maximum value	388.36	344.15
	Minimum value	368.292	333.436
Stress of ring cables/MPa	Theoretical value	358.108	351.335
	Maximum value	374.58	369.673
	Minimum value	341.01	369.673
Stress of external pressure ring beam/MPa	Theoretical value	−158.088	−81.997
	Maximum value	−160.575	−85.024
	Minimum value	−155.705	−78.893

.

5.2. Combination 5#

In the case of Combination 5#, the maximum value of the cable force error ratio of the radial cable is 3.45%, and the maximum value of the cable force error ratio of the ring cable is 6.31%. The cable force error effect diagram is shown in Figure 12, and the statistics of the influence on the structural stress are shown in

Table 8. Statistical table of the influence of Combination 5# coupling errors on structural stress.

Extreme Value		Maximum Stress Element	Minimum Stress Element
Stress of radial cables/MPa	Theoretical value	378.385	338.824
	Maximum value	390.947	347.625
	Minimum value	365.876	330.112
Stress of ring cables/MPa	Theoretical value	358.108	351.335
	Maximum value	375.972	371.056
	Minimum value	339.775	331.504
Stress of external pressure ring beam/MPa	Theoretical value	−158.088	−81.997
	Maximum value	−162.318	−85.556
	Minimum value	−154.035	−78.401

.

5.3. Combination 6#

In the case of Combination 6#, the maximum value of the cable force error ratio of the radial cable is 4.93%, and the maximum value of the cable force error ratio of the ring cable is 7.25%. The cable force error effect diagram is shown in Figure 13, and the statistics of the influence on the structural stress are shown in

Table 9. Statistical table of the influence of Combination 6# coupling errors on structural stress.

Extreme Value		Maximum Stress Element	Minimum Stress Element
Stress of radial cables/MPa	Theoretical value	378.385	338.824
	Maximum value	396.738	353.717
	Minimum value	360.255	324.171
Stress of ring cables/MPa	Theoretical value	358.108	351.335
	Maximum value	379.745	374.694
	Minimum value	336.16	328.023
Stress of external pressure ring beam/MPa	Theoretical value	−158.088	−81.997
	Maximum value	−165.325	−86.713
	Minimum value	−151.102	−77.282

.

5.4. Combination 7#

In the case of Combination 7#, the maximum value of the cable force error ratio of the radial cable is 6.71%, and the maximum value of the cable force error ratio of the ring cable is 8.57%. The cable force error effect diagram is shown in Figure 14, and the statistics of the influence on the structural stress are shown in

Table 10. Statistical table of the influence of Combination 7# coupling errors on structural stress.

Extreme Value		Maximum Stress Element	Minimum Stress Element
Stress of radial cables/MPa	Theoretical value	378.385	338.824
	Maximum value	403.632	360.313
	Minimum value	353.532	317.727
Stress of ring cables/MPa	Theoretical value	358.108	351.335
	Maximum value	384.937	379.749
	Minimum value	331.126	323.126
Stress of external pressure ring beam/MPa	Theoretical value	−158.088	−81.997
	Maximum value	−168.556	−88.157
	Minimum value	−147.945	−75.876

.

5.5. Combination 8#

In the case of Combination 8#, the maximum value of the cable force error ratio of the radial cable is 8.61%, and the maximum value of the cable force error ratio of the ring cable is 10.13%. The cable force error response of the ring cable (i.e., 10.13%) is larger than that of the radial cable (i.e., 8.61%), which has reached the maximum error ratio allowed by the specification of 10%. The cable force error effect diagram is shown in Figure 15, and the statistics of influence on the structural stress are shown in

Table 11. Statistical table of the influence of Combination 8# coupling errors on structural stress.

Extreme Value		Maximum Stress Element	Minimum Stress Element
Stress of radial cables/MPa	Theoretical value	378.385	338.824
	Maximum value	410.94	367.062
	Minimum value	346.397	311.129
Stress of ring cables/MPa	Theoretical value	358.108	351.335
	Maximum value	390.89	385.606
	Minimum value	325.331	317.426
Stress of external pressure ring beam/MPa	Theoretical value	−158.088	−81.997
	Maximum value	−171.853	−89.73
	Minimum value	−144.721	−74.341

.

5.6. Analysis Summary

From the above coupling error effect analysis, the following conclusions were reached.

(1)

With the increase in the maximum allowable value of the length error of the outer pressure ring beam, the error ratio of the radial cable, the error ratio of the ring cable, and the stress error of the outer pressure ring beam also increase. The maximum radial cable force error ratio of Combination 8# is 8.61%, and the maximum cable force error ratio of the ring cable is 10.13%, which has reached the maximum allowable error ratio of 10% in specification. The maximum value of the equivalent stress error of the external pressure ring beam is 13.5 MPa.

(2)

From the calculation and analysis of error combinations 4# to 8#, it can be seen that the maximum cable force error ratio of the ring cable is greater than that of the radial cable, which shows that the sensitivity of the ring cable force to the error is higher than that of the radial cable force.

6. Discussion

6.1. Discussion of Error Effect Analysis

When the only influence factor is the length error of the external pressure ring beam, the stress error of the external pressure ring beam is relatively larger, and the error response is more obvious. It is obvious that the outer pressure ring beam decides the local stiffness of the outer joints in some means. The errors of outer pressure ring beam in radial direction will directly convert into a variable quantity of the length errors of radial or ring cables, while the impact of length errors of other cables should be indirectly transmitted to radial or ring cables through the redistribution of cable forces. In this case, the radial and ring cable force are more sensitive to outer ring beam length errors than to the length errors of other cables.

6.2. Limitations

According to Jin et al. [29], the error in cable cross-sectional area is also an important parameter affecting the forming force of cable structures. In this study, the calculation of error impact was carried out on the premise of knowing the cross-sectional area of all cables in advance, which is applicable to 500 m giant cable-network structures based on relatively more important structural mechanical performance requirements. However, this assumption is not entirely applicable to all cases.

6.3. Advantages and Innovations of the Methods

This paper takes the Qatar Education City Stadium as an example to analyze the construction error of the annular cable bearing-grid structure. The analysis contains two parts, the influence of independent error and the influence of coupled error. The radial cable length error, the ring cable length error, and the length error of outer pressure ring beam were considered as the independent error to perform the independent error analysis, while five different error combinations were conducted to perform the coupling error effect analysis.

This method is practical and helps the main beneficiaries (such as design institutes and manufacturers) make decisions on length error limits, force error limits, and installation error limits for cables and nodes. This calculation method is specifically designed to find the relationship between different error parameters and distinguish the importance of each influencing factor. Therefore, reasonable construction accuracy control indicators can be determined.

In addition, the proposed calculation process and results can be extended to similar cable support structures [30,31] to reduce the impact of errors on structural performance.

7. Conclusions

(1)

The input 1000 random error samples all conform to normal distribution, and the error responses of the structure also conform to the normal distribution.

(2)

In the independent error analysis, if the maximum allowable error of the length of the outer compression ring beam is set as ±170 mm, structural response generated by the independent error of the outer compression ring beam is the most obvious, the absolute values of the cable force error ratios of the radial cable and the ring cable are both close to 8.3%, and the maximum value of the equivalent stress error of the external pressure ring beam is 13.5 MPa.

(3)

When considering the coupling effects of the radial cable, ring cable length error, and external pressure ring beam length error, the resulting cable force error and ring beam stress error are not a linear superposition of the structural response under the independent action of various errors, but a certain discounts occur. Meanwhile, from combinations 4# to 8#, with the increasing length error of the external pressure ring beam, the error response of the structure is becoming increasingly apparent. When the maximum allowable length error of the outer pressure ring beam is set as ±170 mm, the cable force error ratios of the structure reach the maximum allowable error ratio of 10% mentioned in the specification, under the coupling action of the cable force errors of the radial cable and the ring cable.

(4)

It is feasible to use fixed-length cables in the Qatar Education City Stadium project. The control standard for |e_fr| ≤ 10% can be set as ∆_1L ≤ ±0.03%L₀ for radial cable length error, ${\Delta }_{2L}\le \pm (\sqrt{L_0(m)}+5)$ for ring cable length error, and ∆_C ≤ ±170 mm for the length error of the outer pressure ring beam.

(5)

As a natural extension of this study, the error impact analysis method proposed in this study will be used to analyze other types of cable trough structures, such as cable dome, Soteras, cable net, cantilever structure, etc.

Considering the effects of diverse architectural design requirements, small modifications were made to particular support nodes of ANSYS analysis model generated in this study, and the modified analysis model was applied to the construction project and error warning system of the Qatar Education City Stadium.