The Influence of Key Dimensions of the Swivel Hinge on the Mechanical Performance of Bridge Rotary Structure
Abstract
1. Introduction
2. Finite Element Model and Validation
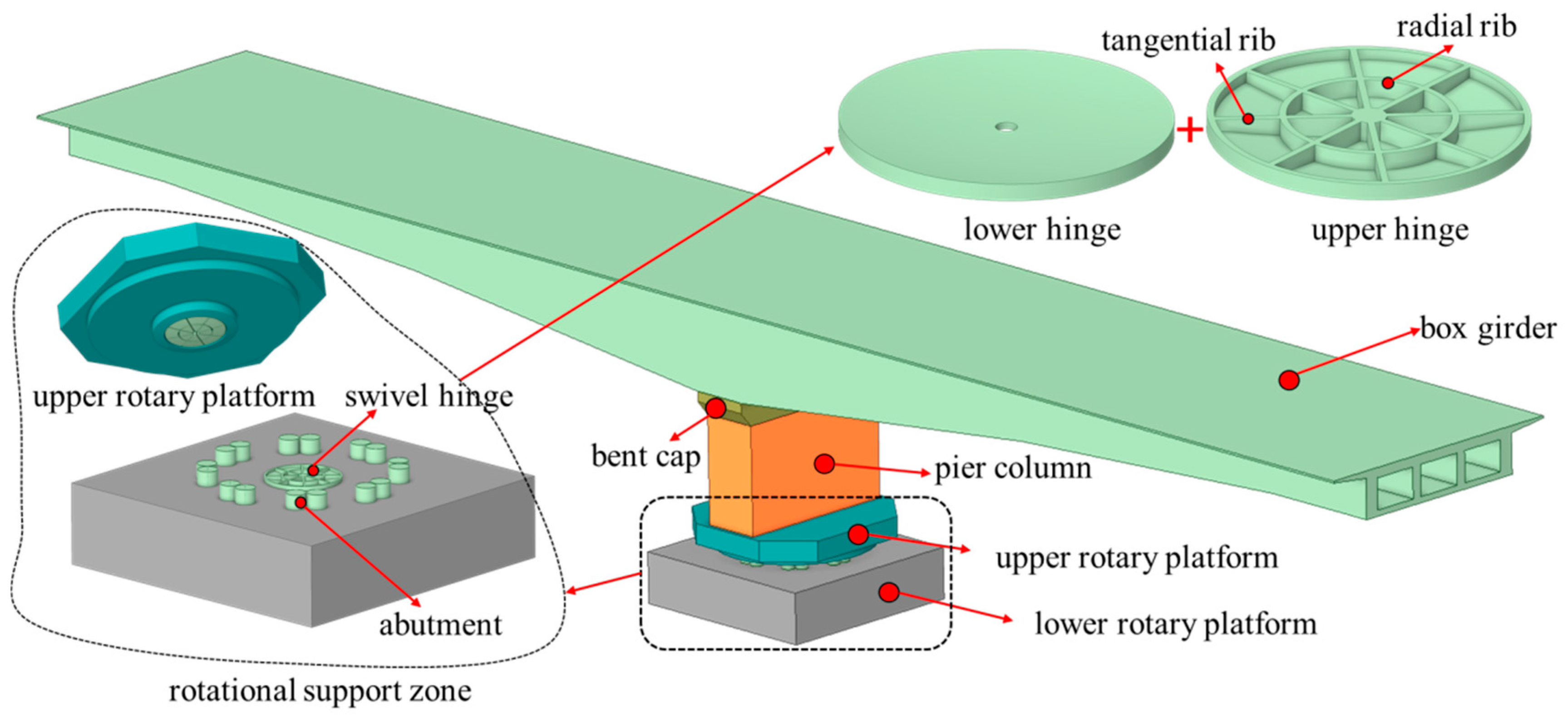
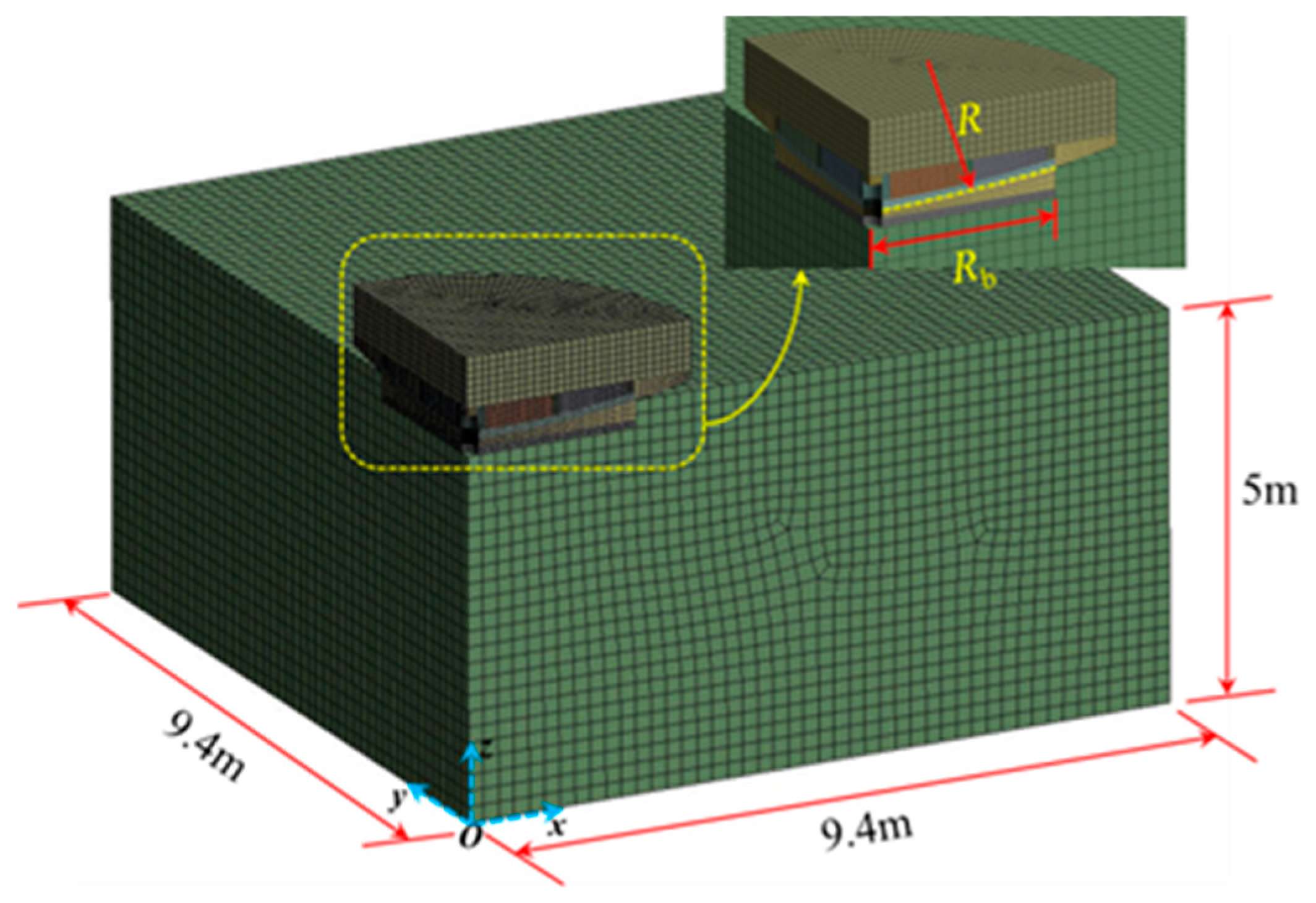
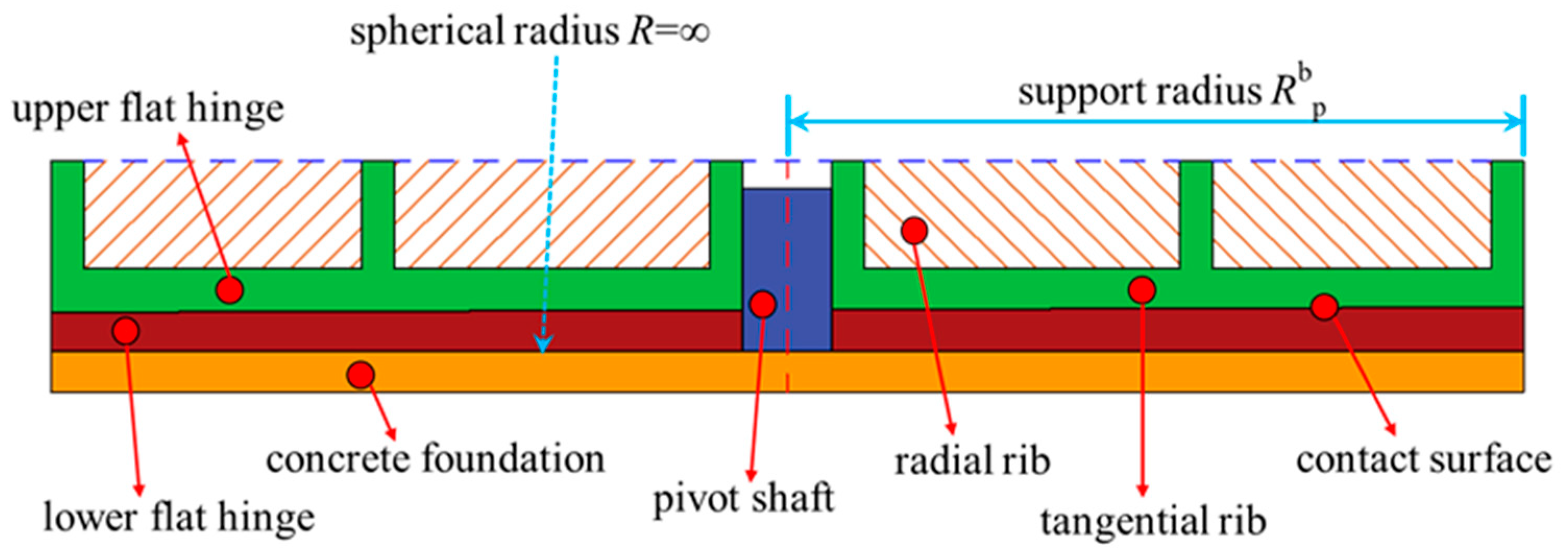
2.1. Model Overview
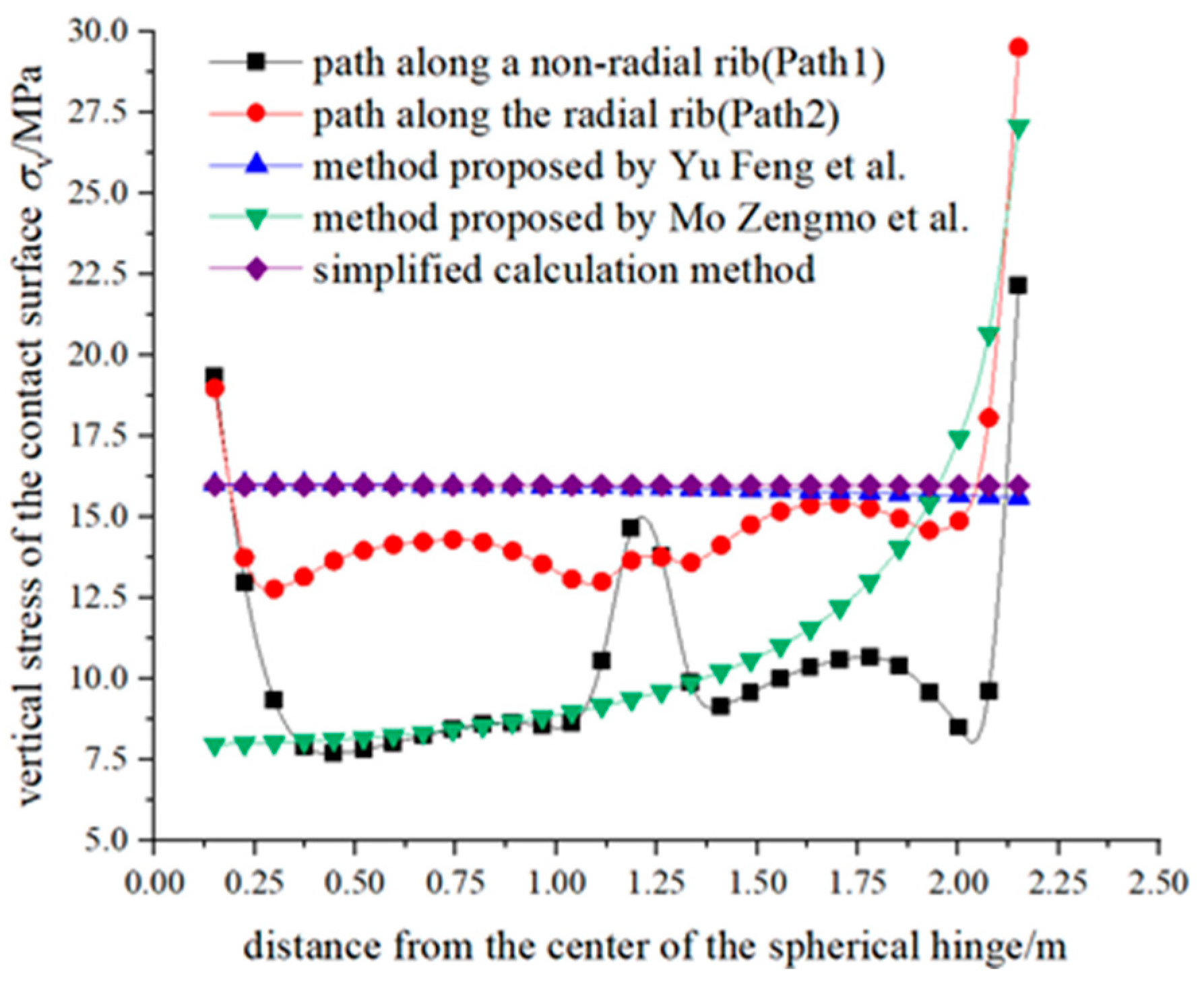
2.2. Model Validation
3. Impact of Spherical Hinge Dimensions on the Anti-Overturning Performance
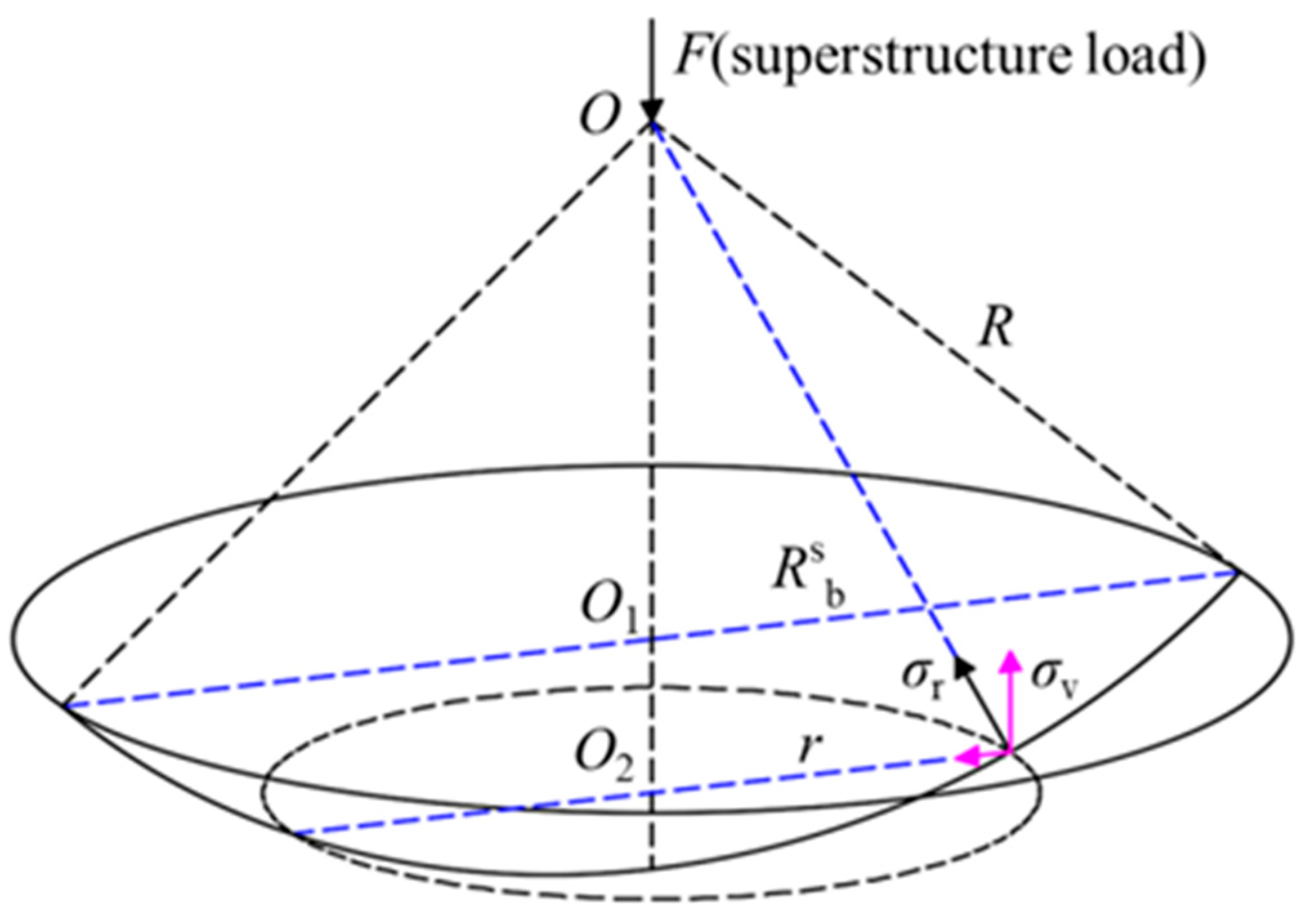
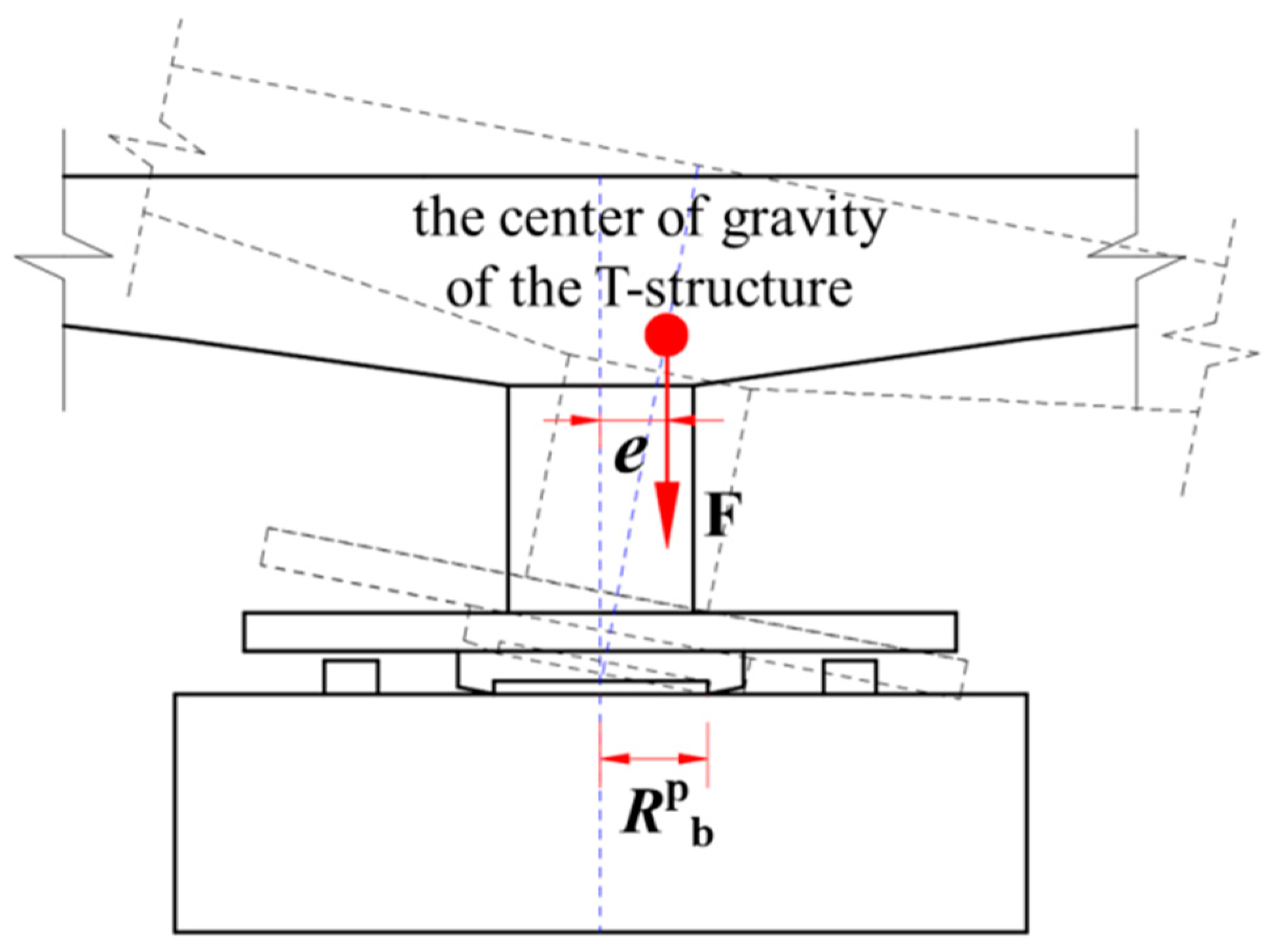
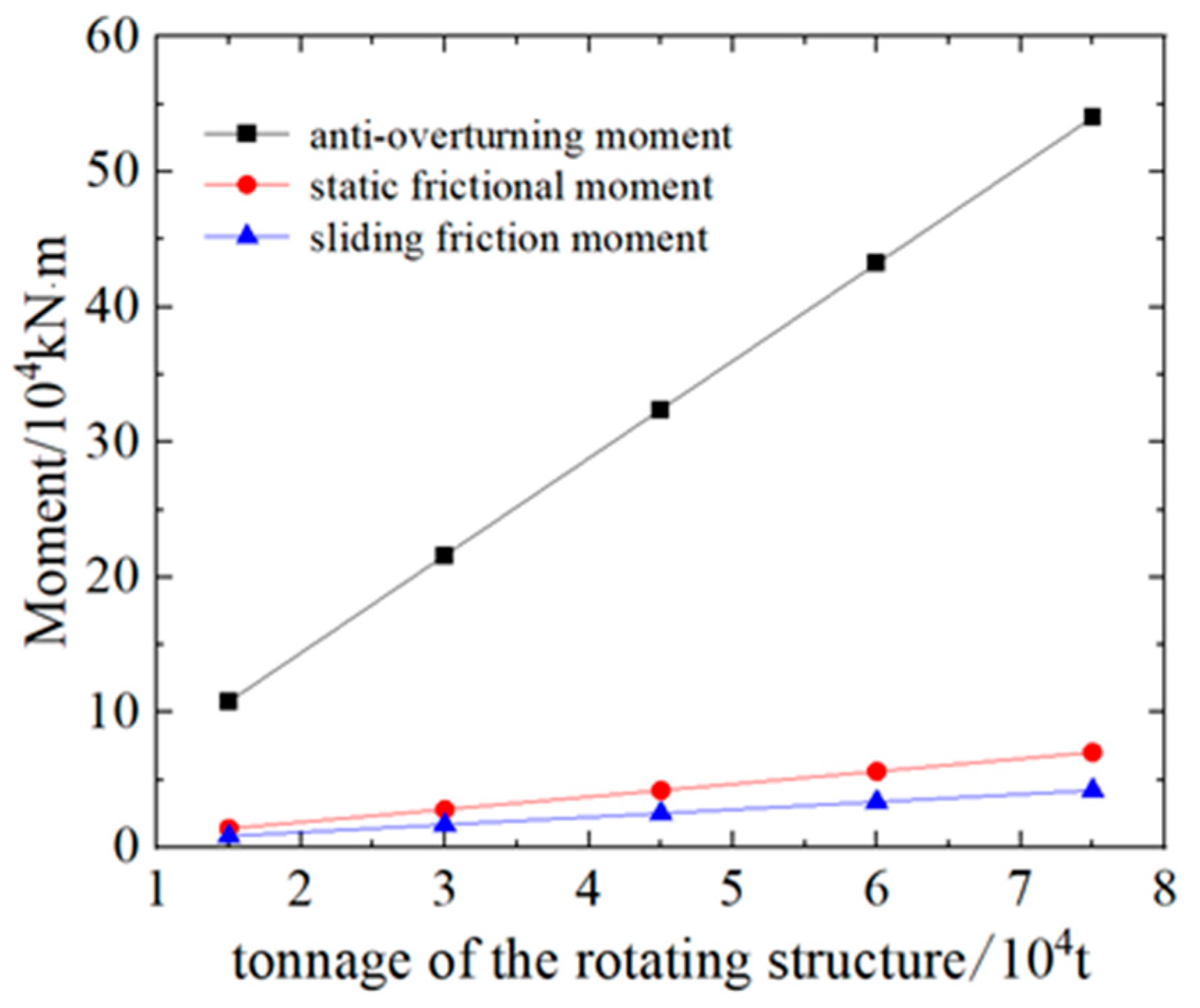
3.1. Theoretical Analysis of Anti-Overturning Performance
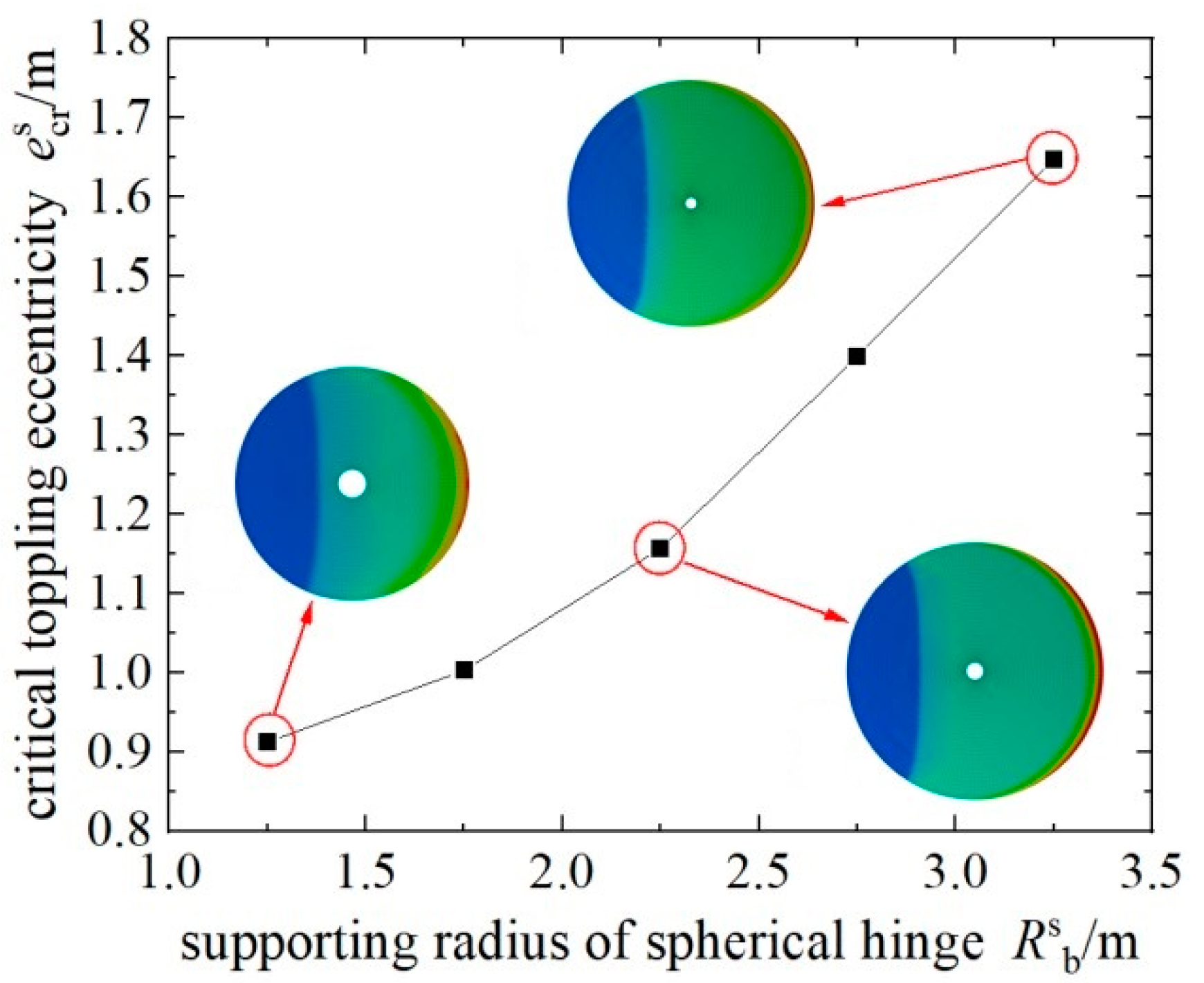
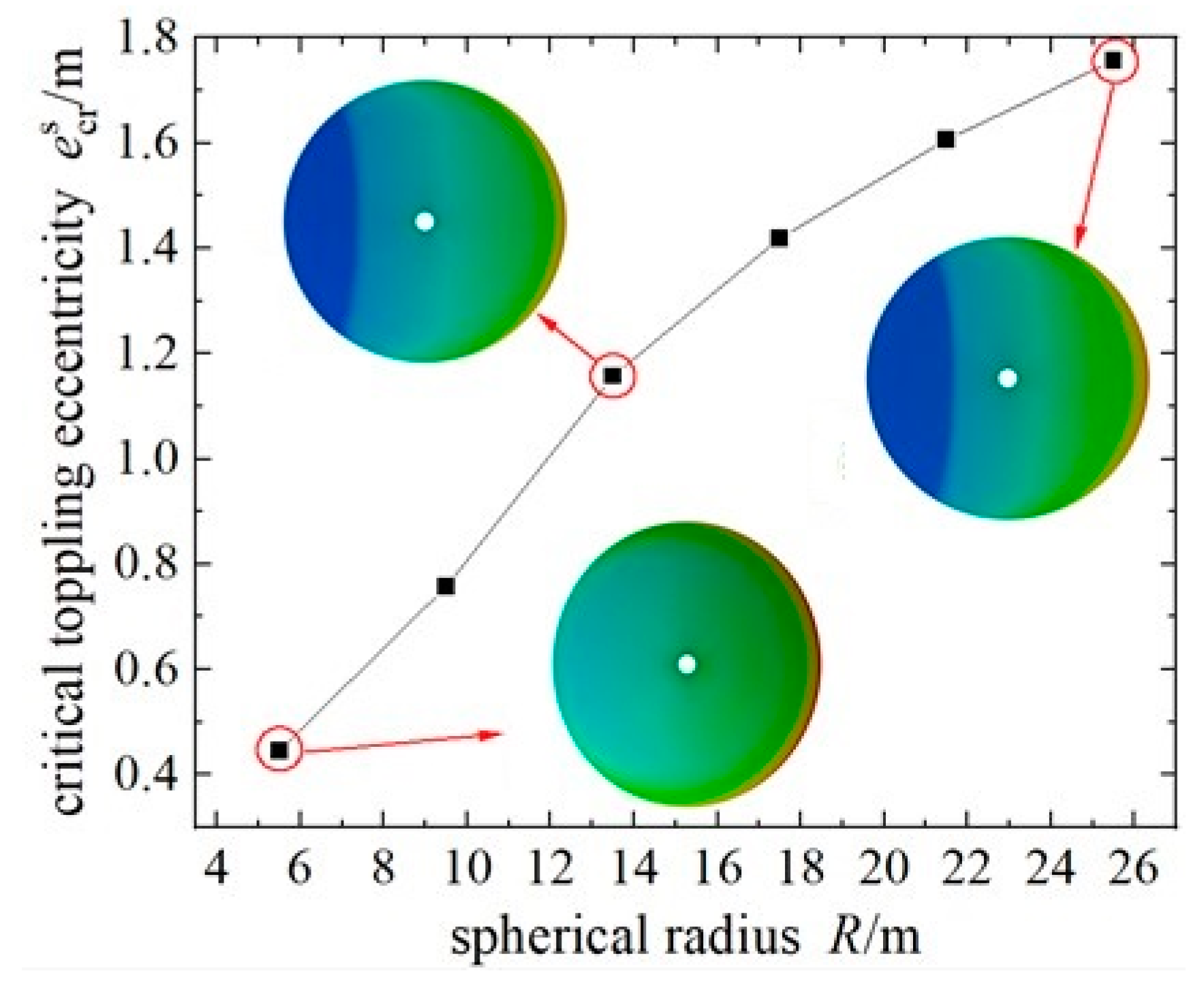
3.2. The Impact of Ball Joint Supporting Radius and Ball Joint Spherical Radius
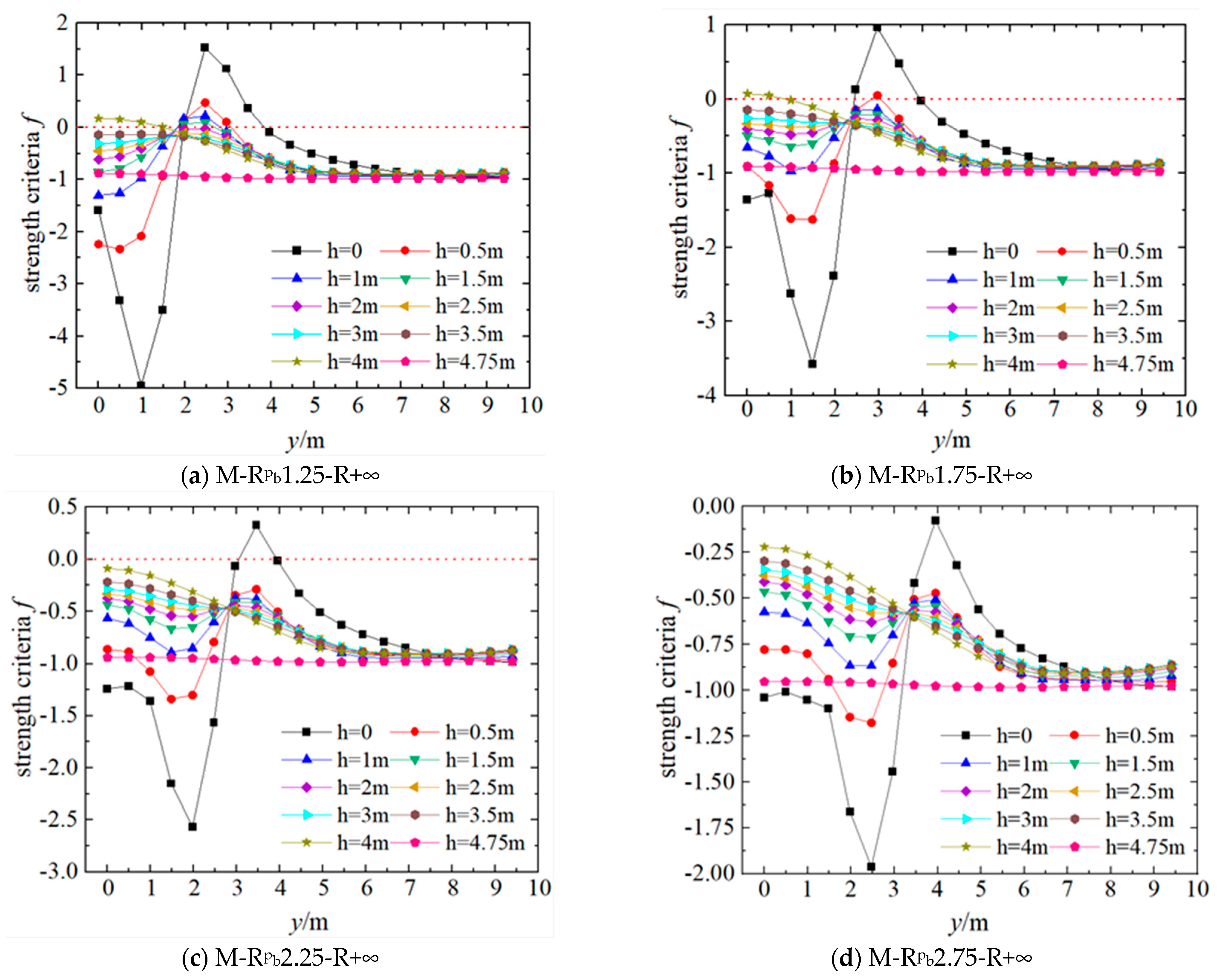
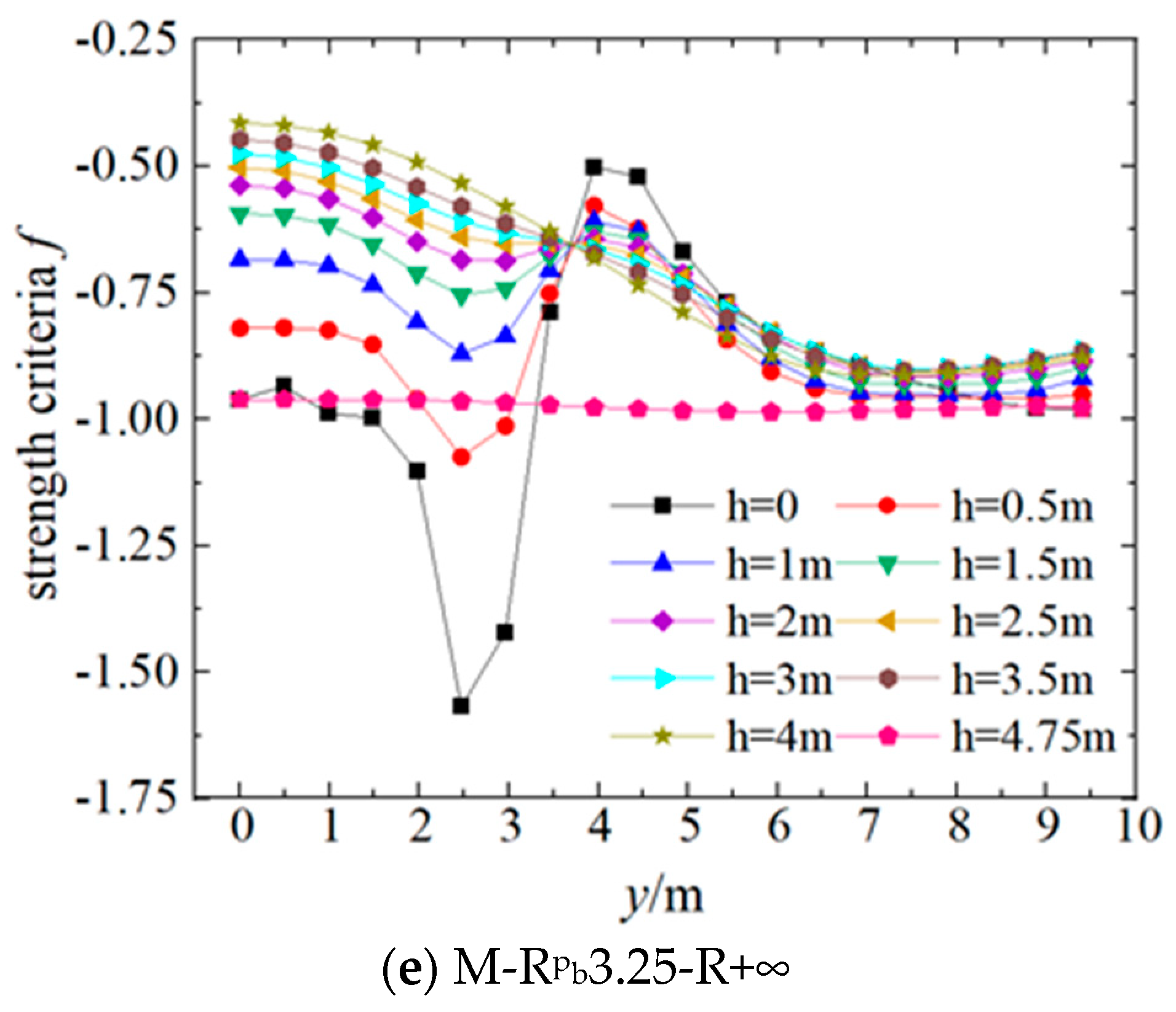
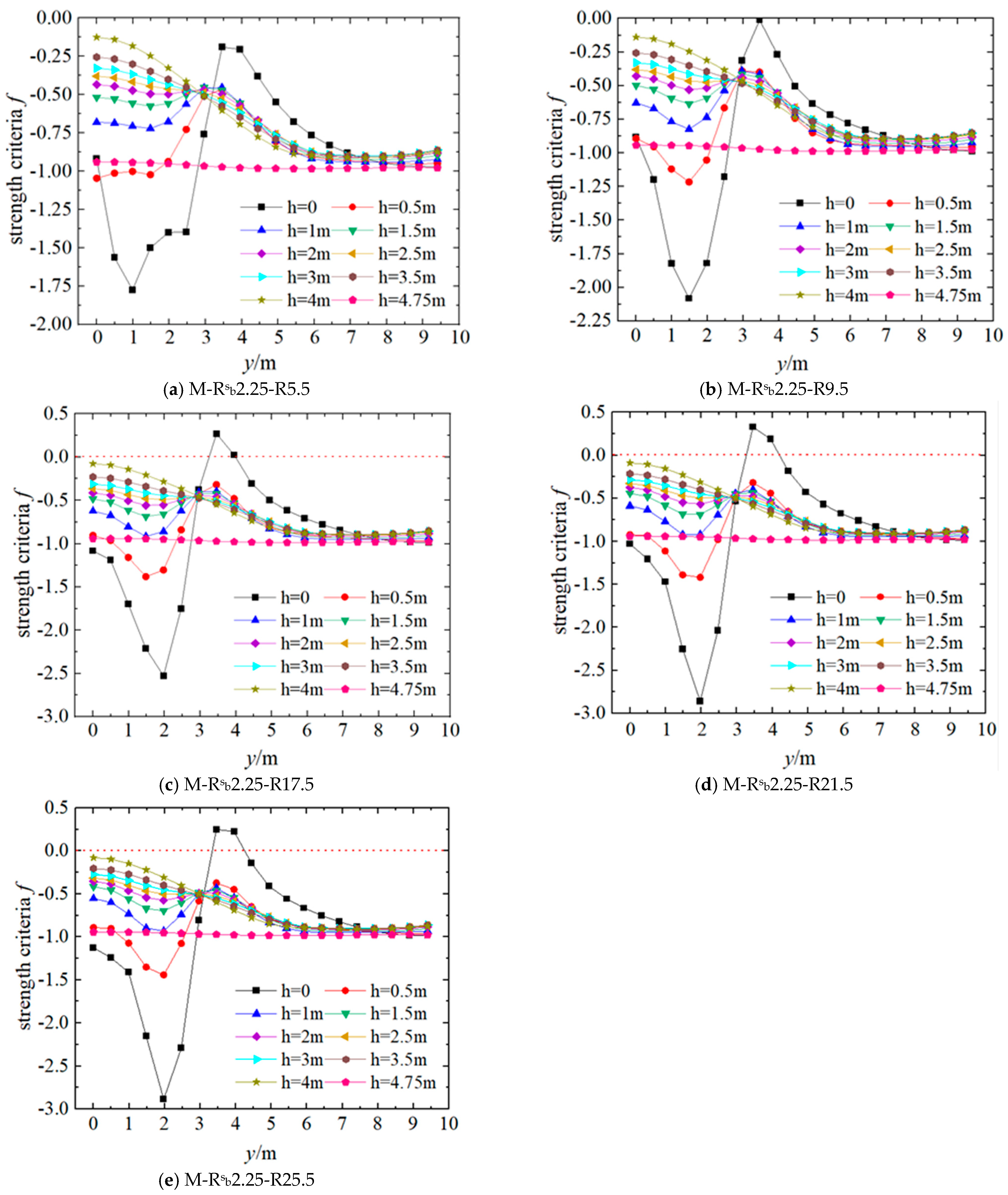
4. The Influence of Hinge Dimensions on the Lower Turntable
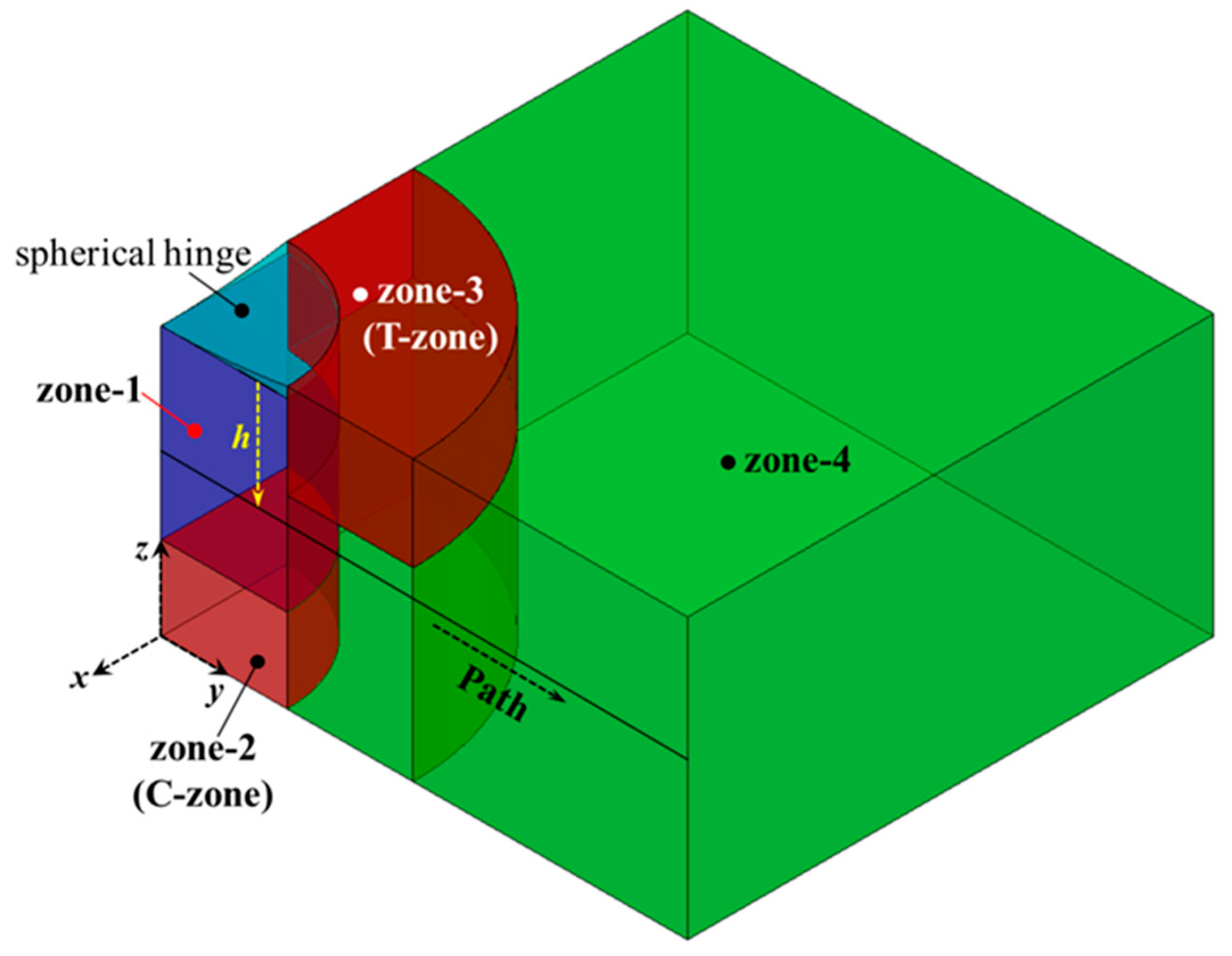
4.1. Local Compression of the Lower Turntable and the Ottosen Strength Criterion
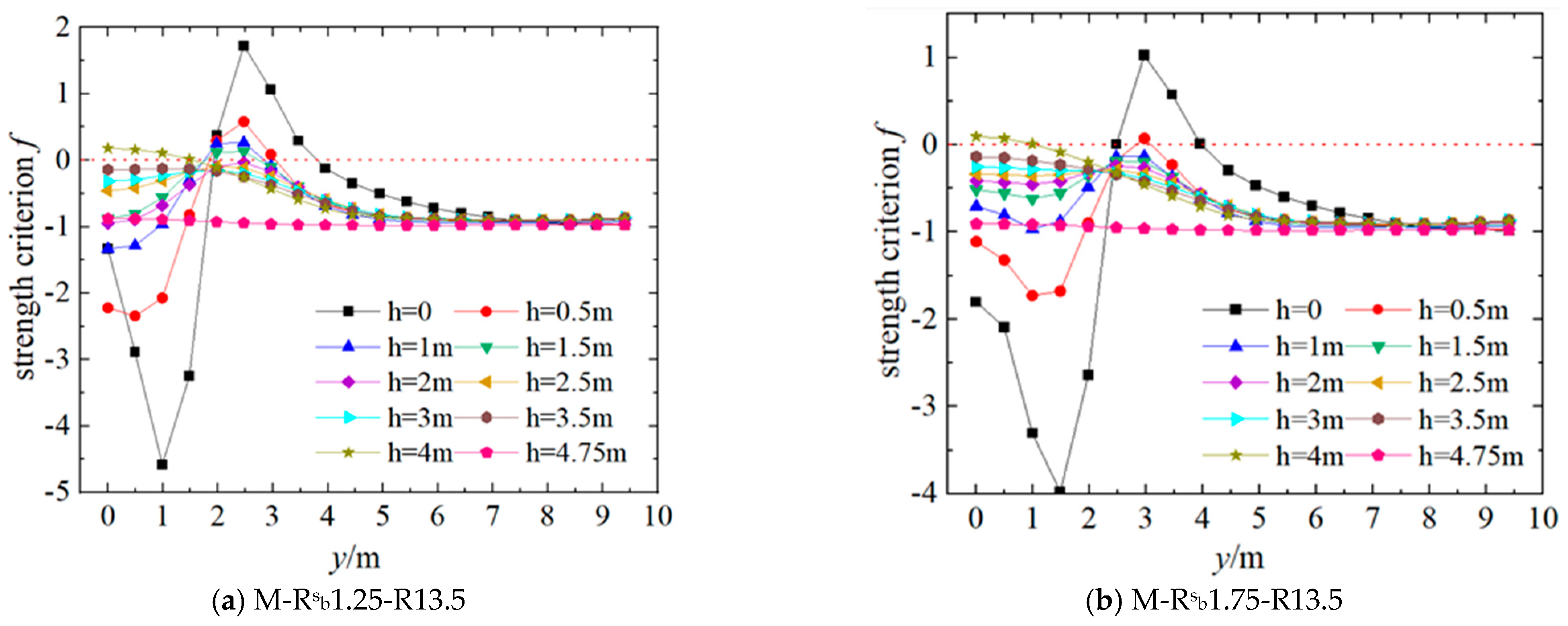
4.2. The Influence of the Support Radius
- (1)
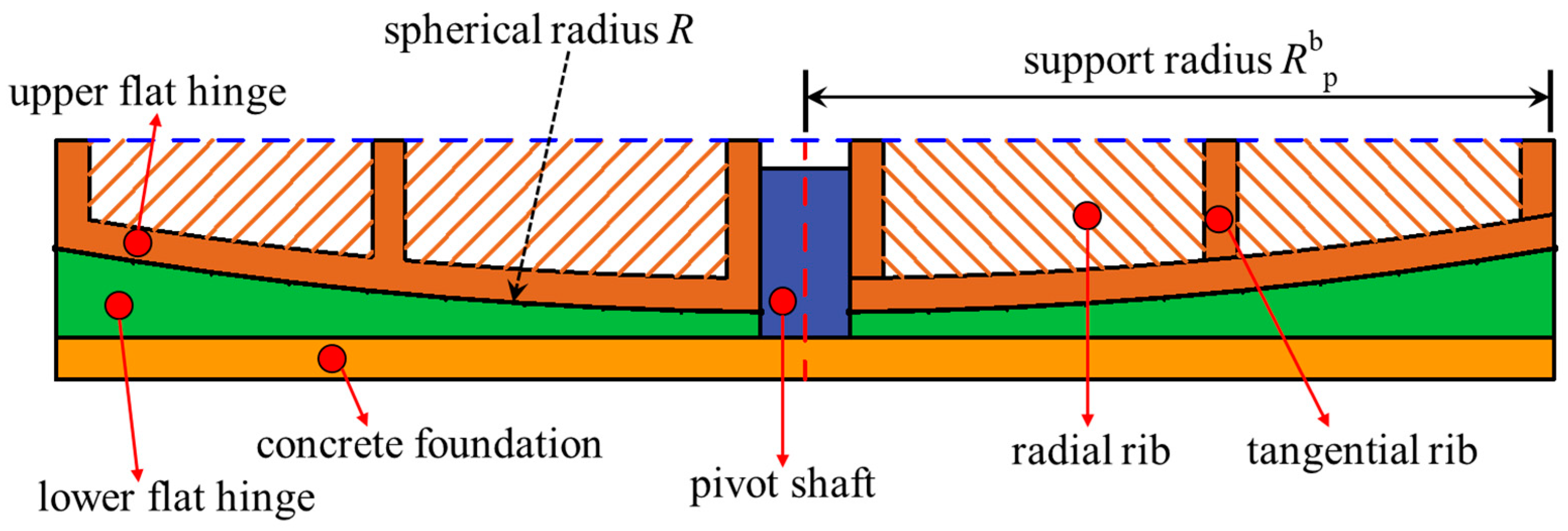
- Spherical Hinge
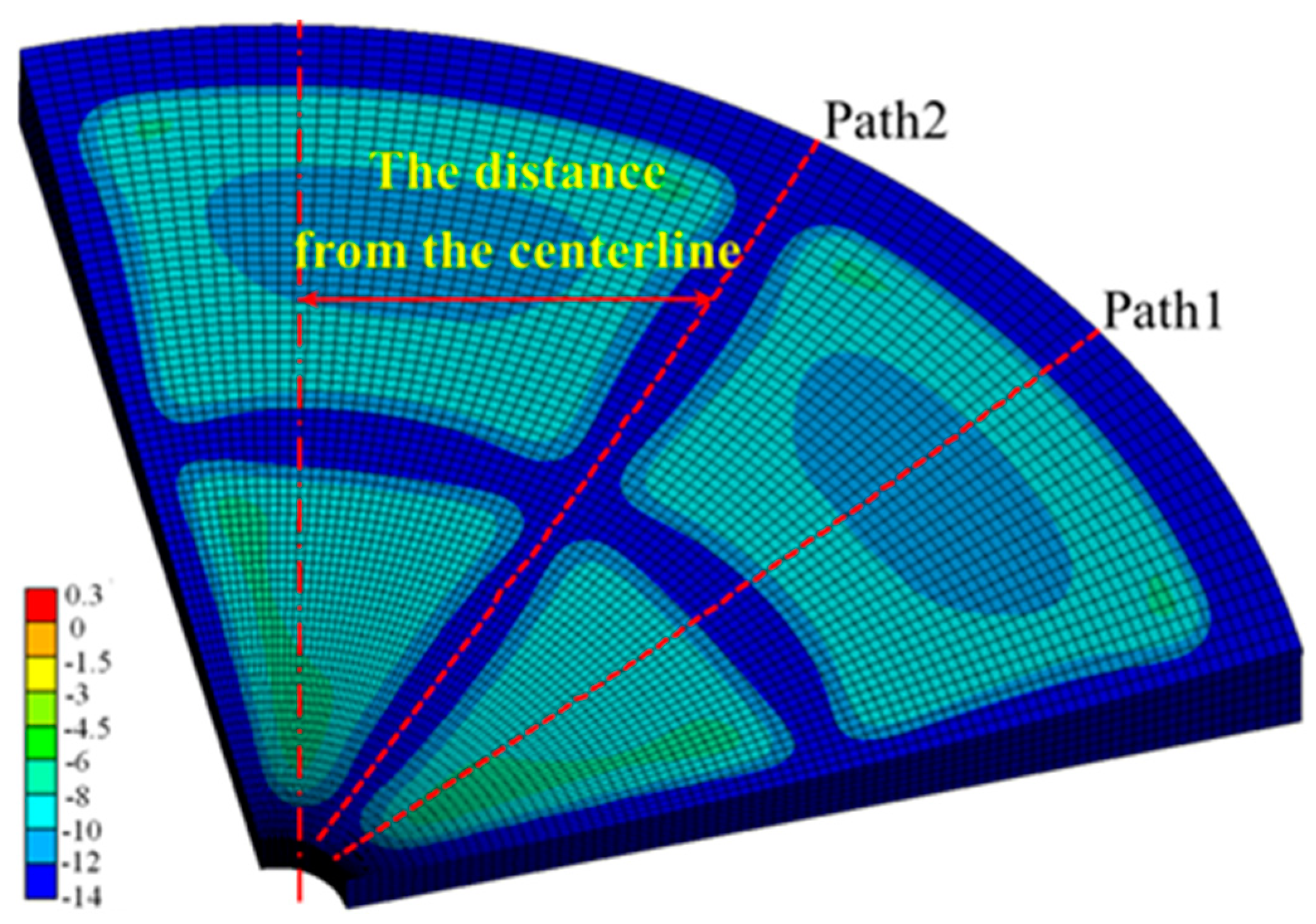
- Zone-1 is under triaxial compressive stress, with minimal difference among the three principal compressive stresses, making it less susceptible to strength failure.
- Zone-2 (C-zone) is prone to primary compressive stress failure.
- Zone-3 (T-zone) is susceptible to primary tensile stress failure.
- Zone-4 experiences minimal stress response due to its distance from the direct-action area of the rotational load, making it less prone to strength failure.
- (2)
- Planar Hinge
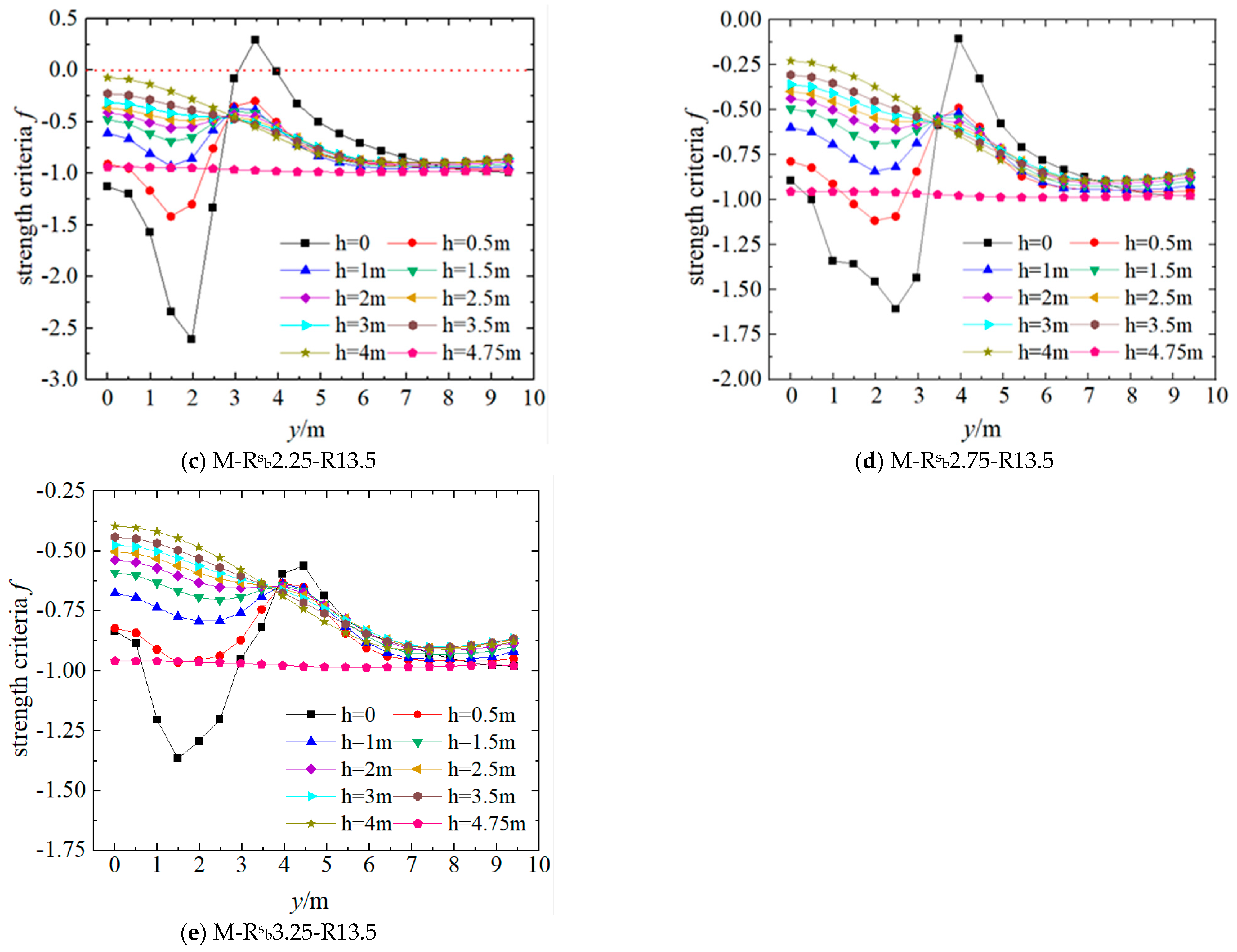
4.3. The Influence of the Spherical Radius
5. Conclusions
- (1)
- The support radius and spherical radius of hinges are two important factors influencing the critical eccentricity of the T-structure against overturning. The critical eccentricity (escr) for the overturning resistance of the T-structure increases with the increase in the support radius (Rb) and the spherical radius (R). With the decrease in Rb, the reduction rate of escr gradually decreases, while the increment of escr gradually decreases with the increase in R. The overturning resistance performance of the T-structure under planar hinges is superior to that observed under spherical hinges.
- (2)
- According to the intensity safety characteristics, the lower turntable can be divided into four areas, Zone-1~Zone-4. In Zone-2(C-zone), with the decrease in hinge bearing radius, there is main compression stress failure; in Zone-3(T-zone), main tensile stress failure may occur; while Zone-1and Zone-4 are not prone to strength failure. The ball hinge radius R has a great influence on Zone-3, and whether the main compressive stress failure occurs in Zone-2 is mainly determined by the rotating hinge bearing radius Rb.
- (3)
- The influence of the spherical radius (R) on the stress and strength safety of the lower turntable is primarily achieved by altering the height (H) from the pivot bottom to the top surface of the lower turntable, with a particularly significant effect on Zone-3. Therefore, whether principal compressive stress failure occurs in this zone is primarily determined by the support radius, with a lesser correlation to the spherical radius of the hinge.
- (4)
- In summary, this paper presents the design range of the support radii (Rb), spherical radii (R), and height (H), as well as the areas where the stress risk needs to be considered in the lower turntable. It provides a sufficient basis for the design of the bridge and guarantees the safety of bridge construction.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
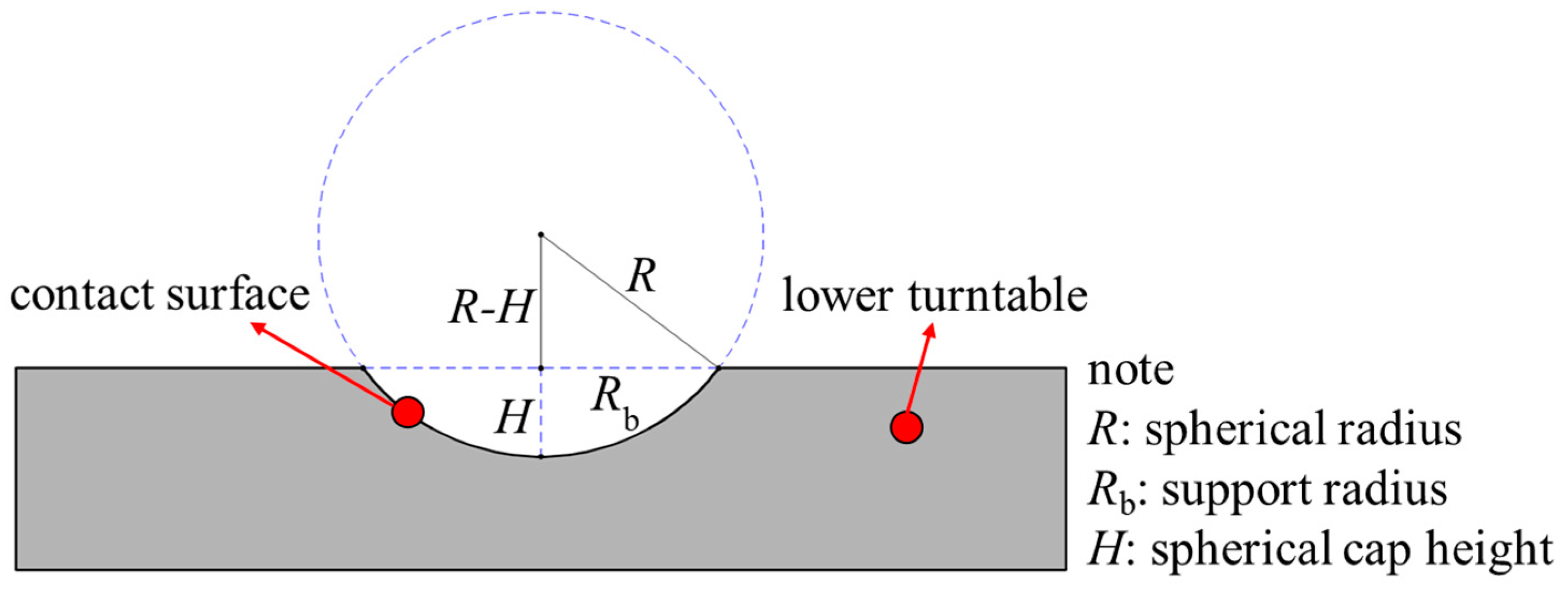
Nomenclature
| Symbol | Definition |
| R | Spherical radius |
| Rb | Supporting radius |
| H | Spherical crown height |
| α | The ratio of radius to height |
| Tsa | The anti-overturning moment produced by the spherical hinge |
| μs | The static friction coefficient |
| σr | The radial stress at any point on the contact surface |
| i, j, and k | Three orthogonal directions |
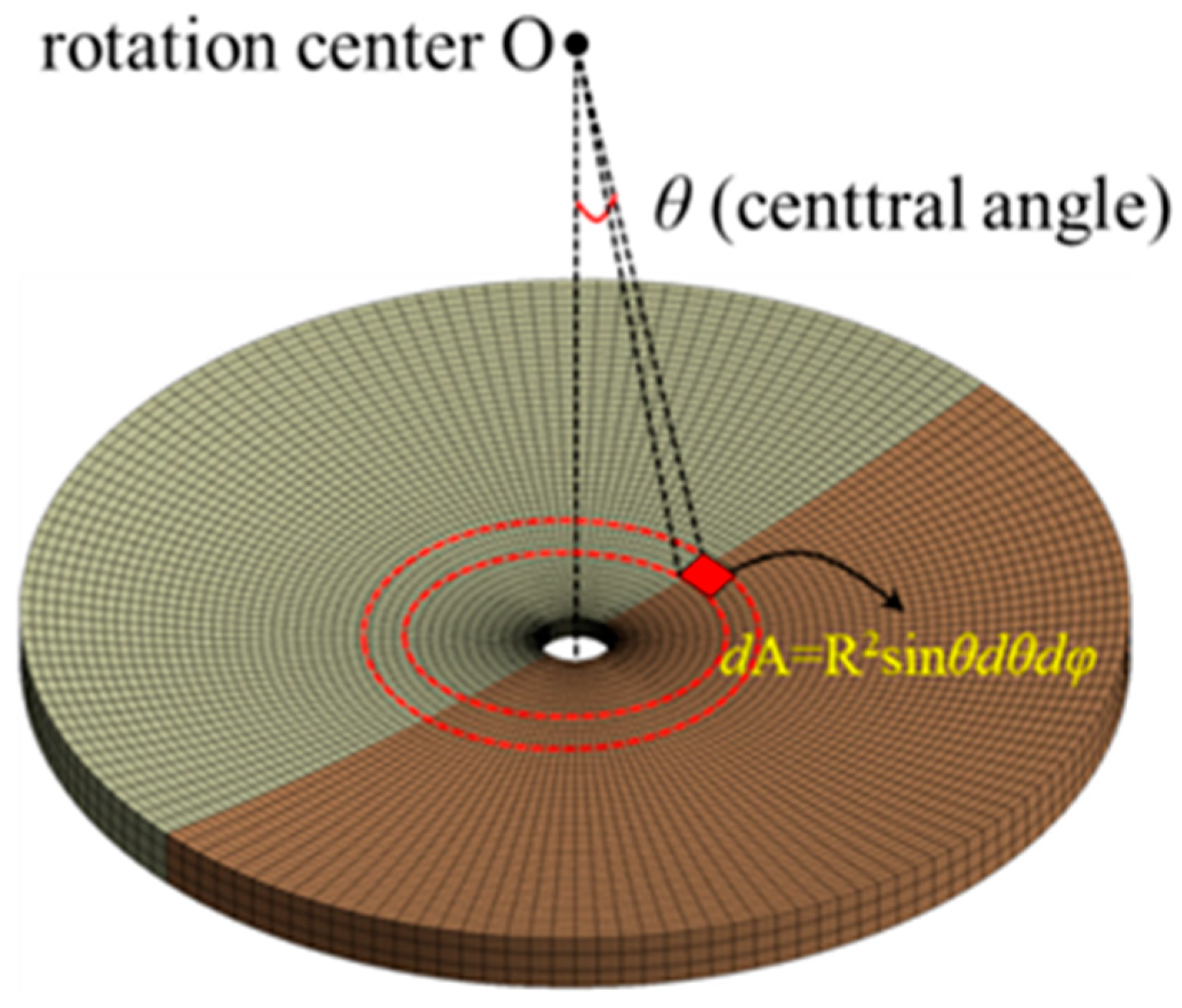
| O | Rotation center |
| θ | Central angle |
| ϕ | The angle between the spherical hinge stress analysis point and the direction of a specific radius |
References
- Wang, L.F.; Wang, E.Q.; Sun, Y.C.; He, D.P.; Ge, J.Y. Mechanical Characteristics of Rotation Construction Process of Ten-Thousand-Ton Cable-Stayed Bridges. J. Transp. Eng. 2015, 15, 52–61. (In Chinese) [Google Scholar]
- Zhang, L.Y. Construction of Bridge Rotation; China Communications Press: Beijing, China, 2002. (In Chinese) [Google Scholar]
- Cheng, F.; Zhang, Q.F.; Wang, J.Q. The development status and prospect of bridge turning construction technology in China. Railw. Stand. Des. 2011, 67–71. [Google Scholar] [CrossRef]
- Li, Q.S. Design of turntable bridge over Bao-Lanzhou Railway on Shi-alkali Highway in Zhongning County. Hunan Commun. Sci. Technol. 2015, 41, 96–101+109. [Google Scholar]
- Huang, S.P.; Tang, Y.; Yuan, Z.X.; Cai, X.P. An Efficient Contact Model for Rotating Mechanism Analysis and Design in Bridge Construction. Balt. J. Road Bridge Eng. 2021, 16, 57–76. [Google Scholar] [CrossRef]
- Ji, J.H.; Han, T.H.; Dong, Z.Q.; Zhu, H.; Wu, G.; Wei, Y.; Soh, C.K. Performance of concrete columns actively strengthened with hoop confinement: A state-of-the-art review. Structures 2023, 54, 461–477. [Google Scholar] [CrossRef]
- Li, C.X.; Li, H.C.; Feng, Z.; Ke, L.; Zhou, J.L.; Yu, S. Local compression behavior of UHPFRC: Experiments and bearing capacity calculation model. Eng. Struct. 2023, 292, 116529. [Google Scholar] [CrossRef]
- Liang, J.H. Design of Balance Weight of Swivel Bridge; Guangdong Water Resources Hydropower: Dongguan, China, 2004; pp. 10–11. [Google Scholar]
- Guo, Y.J.; Li, H.Z.; Cai, H.B. Analysis of ground settlement induced by pipe-jacking construction considering of soil inner diseases. China Civ. Eng. J. 2011, 44, 139–143. [Google Scholar]
- Siwowski, T.; Wysocki, A. Horizontal rotation via floatation as an accelerated bridge construction for long-span footbridge erection: Case study. J. Bridge Eng. 2015, 20, 05014014. [Google Scholar] [CrossRef]
- Yu, F.; Qi, J.N.; Wang, J.Q.; Zhang, W.X.; Zhang, Q.F. Rotation construction of heavy swivel arch bridge for high-speed railway. Structures 2020, 26, 755–764. [Google Scholar]
- Ye, X.W.; Xia, P.S.; Su, Y.H.; Chen, B. Analysis and probabilistic modeling of wind characteristics of an arch bridge using structural health monitoring data during typhoons. Struct. Eng. Mech. 2017, 63, 809–824. [Google Scholar]
- Niu, Y.Z.; Li, H.Y.; Quan, W.; Zhang, L. Research on Horizontal Rotational Joint Types of Ultra-Large-Tonnage Cable-Stayed Bridges. J. Railw. Eng. 2015, 32, 34–39+56. (In Chinese) [Google Scholar]
- Che, X.J.; Zhang, X.D. Anti-overturning in swivel process of large tonnage T-rigid frame bridge. Zhongguo Gonglu Xuebao/China J. Highw. Transp. 2014, 27, 66–72. [Google Scholar]
- Fu, X.C.; Tang, Y.; Cao, W. Comparative Analysis of Planar Joints and Spherical joints in Bridge Rotation Construction. Railw. Constr. 2016, 2016, 35–37. (In Chinese) [Google Scholar]
- Shi, X.; Cao, Z.; Ma, H.; Ruan, X. Failure analysis on a curved girder bridge collapse under eccentric heavy vehicles using explicit finite element method: Case study. J. Bridge Eng. 2018, 23, 05018001. [Google Scholar] [CrossRef]
- Qian, G.F.; Cheng, F.; Wang, J.Q.; Zhang, Q.F. Construction Technology of Ultra-Large-Tonnage Rotating Arch Bridges on Shanghai-Hangzhou High-Speed Railway; China Railway Publishing House: Beijing, China, 2012. (In Chinese) [Google Scholar]
- Liu, S.; Liu, J.; Huang, Y.F.; Zheng, Y.X. Optimization of Swivel Spherical joint Structure Design Based on the Response Surface Method. Sustainability 2023, 15, 10356. [Google Scholar] [CrossRef]
- Wei, S.W. A finite element analysis of the stress of the contact surface of the ball hing of a swing bridge under vertical loads. Traffic Eng. Technol. Natl. Def. 2020, 18, 16–18+76. [Google Scholar]
- Wang, J.W.; Sun, Q.S. Parameter sensitivity analysis of stability of T-shaped rigid frame bridge by adopting swivel construction method. Multidiscip. Model. Mater. Struct. 2020, 16, 1203–1231. [Google Scholar] [CrossRef]
- Fan, B.W. Application Study of Spherical and Flat Bearings in the Design of a 22,400-ton Rotating Bridge. Railw. Eng. Technol. 2020, 2020, 132–134. (In Chinese) [Google Scholar]
- Mo, Z.M.; Huang, S.P.; Wang, W.F. Analysis of Contact Stress of Spherical Hinges in Bridge Rotary Construction. Highway 2021, 66, 184–188. (In Chinese) [Google Scholar]
- Zhang, X.Y.; Wu, H.J.; Li, J.Z.; Pi, A.G.; Huang, F.L. A constitutive model of concrete based on Ottosen yield criterion. Int. J. Solids Struct. 2020, 193–194, 79–89. [Google Scholar]
- China GB 50010-2010; Code for Design of Concrete Structures. Chinese National Standard. China Architecture and Building Press: Beijing, China, 2015. (In Chinese)
- China JTG/T 3650-2020; Technical Specification for Highway Bridges and Culverts. Chinese National Standard. China Communications Press: Beijing, China, 2020. (In Chinese)
- Hossein, N. Probabilistic analysis of strength in retrofitted X-Joints under tensile loading and fire conditions. Buildings 2024, 14, 2105. [Google Scholar] [CrossRef]
- Wei, G.; Zhang, J.; Li, Y.; Tian, W.; An, Y. Investigation on load—Transfer characteristics of spherical hinge structure of swivel bridge based on scale distortion model. Structures 2024, 69, 107565. [Google Scholar]






| Group | Model Number | R/mm | /mm | H/mm | Radius-to-Height Ratio |
|---|---|---|---|---|---|
| 1 | M-1.25-R13.5 | 13,500 | 1250 | 58.0 | 21.6 |
| 2 | M-1.75-R13.5 | 13,500 | 1750 | 113.9 | 15.4 |
| 3 | M-2.25-R13.5 | 13,500 | 2250 | 188.8 | 11.9 |
| 4 | M-2.75-R13.5 | 13,500 | 2750 | 283.1 | 9.7 |
| 5 | M-3.25-R13.5 | 13,500 | 3250 | 397.0 | 8.2 |
| Group | Model Number | R/mm | /mm | H/mm | Radius-to-Height Ratio |
|---|---|---|---|---|---|
| 1 | M-2.25-R5.5 | 5500 | 2250 | 481.3 | 4.7 |
| 2 | M-2.25-R9.5 | 9500 | 2250 | 270.3 | 8.3 |
| 3 | M-2.25-R13.5 | 13,500 | 2250 | 188.8 | 11.9 |
| 4 | M-2.25-R17.5 | 17,500 | 2250 | 145.2 | 15.4 |
| 5 | M-2.25-R21.5 | 21,500 | 2250 | 118.1 | 19.1 |
| 6 | M-2.25-R25.5 | 25,500 | 2250 | 99.5 | 22.6 |
| Group | Model number | R/mm | /mm | H/mm | Radius-to-Height Ratio |
|---|---|---|---|---|---|
| 1 | M-1.25-R+∞ | +∞ | 1250 | 0 | +∞ |
| 2 | M-1.75-R+∞ | +∞ | 1750 | 0 | +∞ |
| 3 | M-2.25-R+∞ | +∞ | 2250 | 0 | +∞ |
| 4 | M-2.75-R+∞ | +∞ | 2750 | 0 | +∞ |
| 5 | M-3.25-R+∞ | +∞ | 3250 | 0 | +∞ |
| Principal Stress /Node Position | h = 0 | h = 4000 mm | ||||
|---|---|---|---|---|---|---|
| N1 | N2 | N3 | N4 | N5 | N6 | |
| σ1 (MPa) | 5.44 | 4.14 | 2.61 | −0.48 | −0.43 | −0.30 |
| σ2 (MPa) | −0.44 | 0.13 | −0.06 | −0.64 | −0.59 | −0.45 |
| σ3 (MPa) | −1.89 | −0.82 | −0.49 | −8.81 | −8.53 | −7.73 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, H.; Yang, Z.; Lu, C.; Li, Z.; Guo, C.; Sha, G. The Influence of Key Dimensions of the Swivel Hinge on the Mechanical Performance of Bridge Rotary Structure. Buildings 2024, 14, 3905. https://doi.org/10.3390/buildings14123905
Wu H, Yang Z, Lu C, Li Z, Guo C, Sha G. The Influence of Key Dimensions of the Swivel Hinge on the Mechanical Performance of Bridge Rotary Structure. Buildings. 2024; 14(12):3905. https://doi.org/10.3390/buildings14123905
Chicago/Turabian StyleWu, Hantao, Zheng Yang, Chunting Lu, Zhongming Li, Chen Guo, and Guohua Sha. 2024. "The Influence of Key Dimensions of the Swivel Hinge on the Mechanical Performance of Bridge Rotary Structure" Buildings 14, no. 12: 3905. https://doi.org/10.3390/buildings14123905
APA StyleWu, H., Yang, Z., Lu, C., Li, Z., Guo, C., & Sha, G. (2024). The Influence of Key Dimensions of the Swivel Hinge on the Mechanical Performance of Bridge Rotary Structure. Buildings, 14(12), 3905. https://doi.org/10.3390/buildings14123905