Numerical Simulation of Backfilling Construction for Underground Reinforced Concrete Grain Silos
Abstract
1. Introduction
2. Engineering Background
3. Finite Element Model
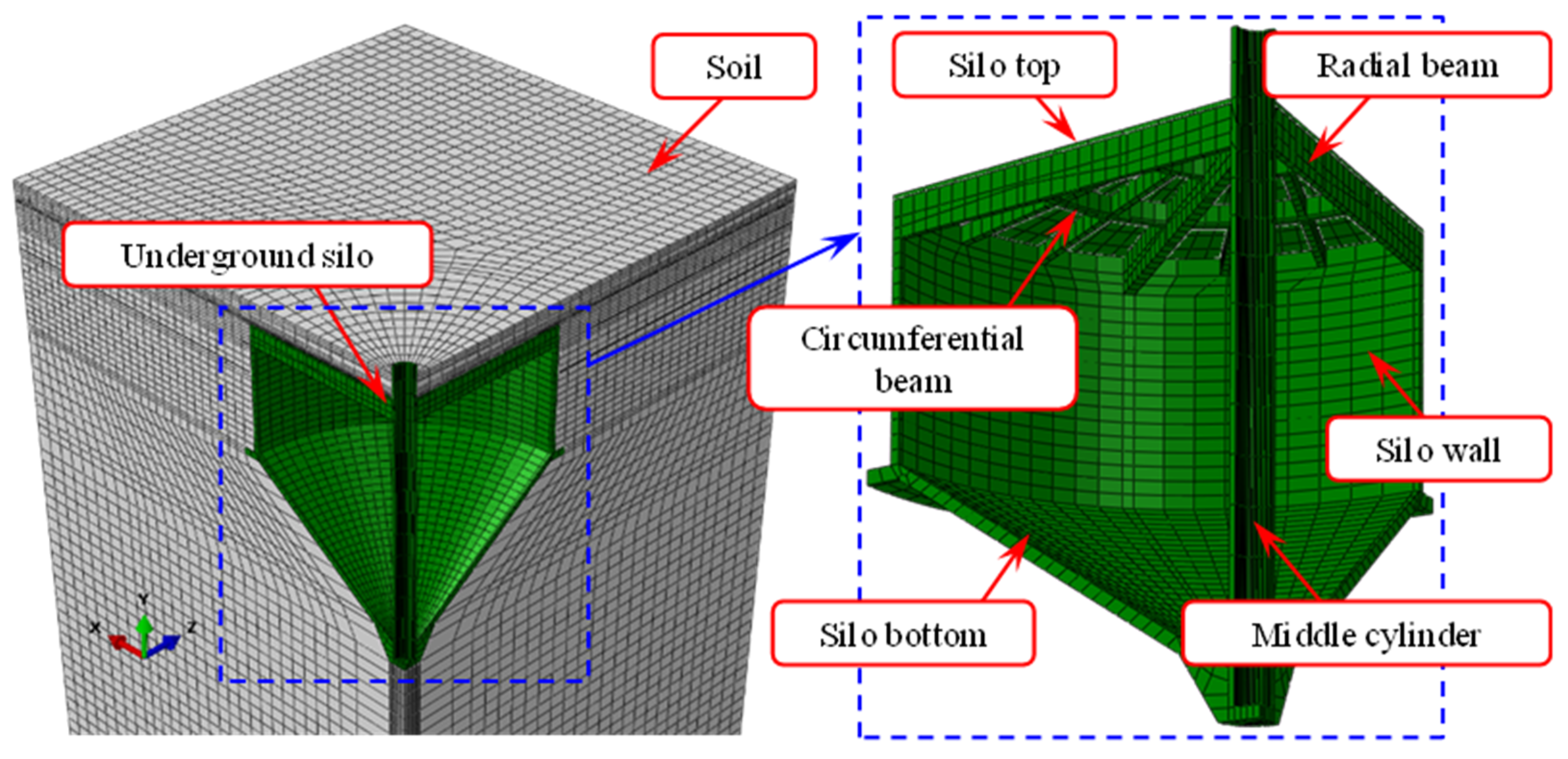
3.1. Construction of FE Model
3.2. Material Properties
3.3. Interaction and Boundary Conditions
4. Results and Discussion
4.1. Silo and Soil Settlement
4.2. Deformation Characteristic
4.2.1. Radial Displacement of Silo Wall
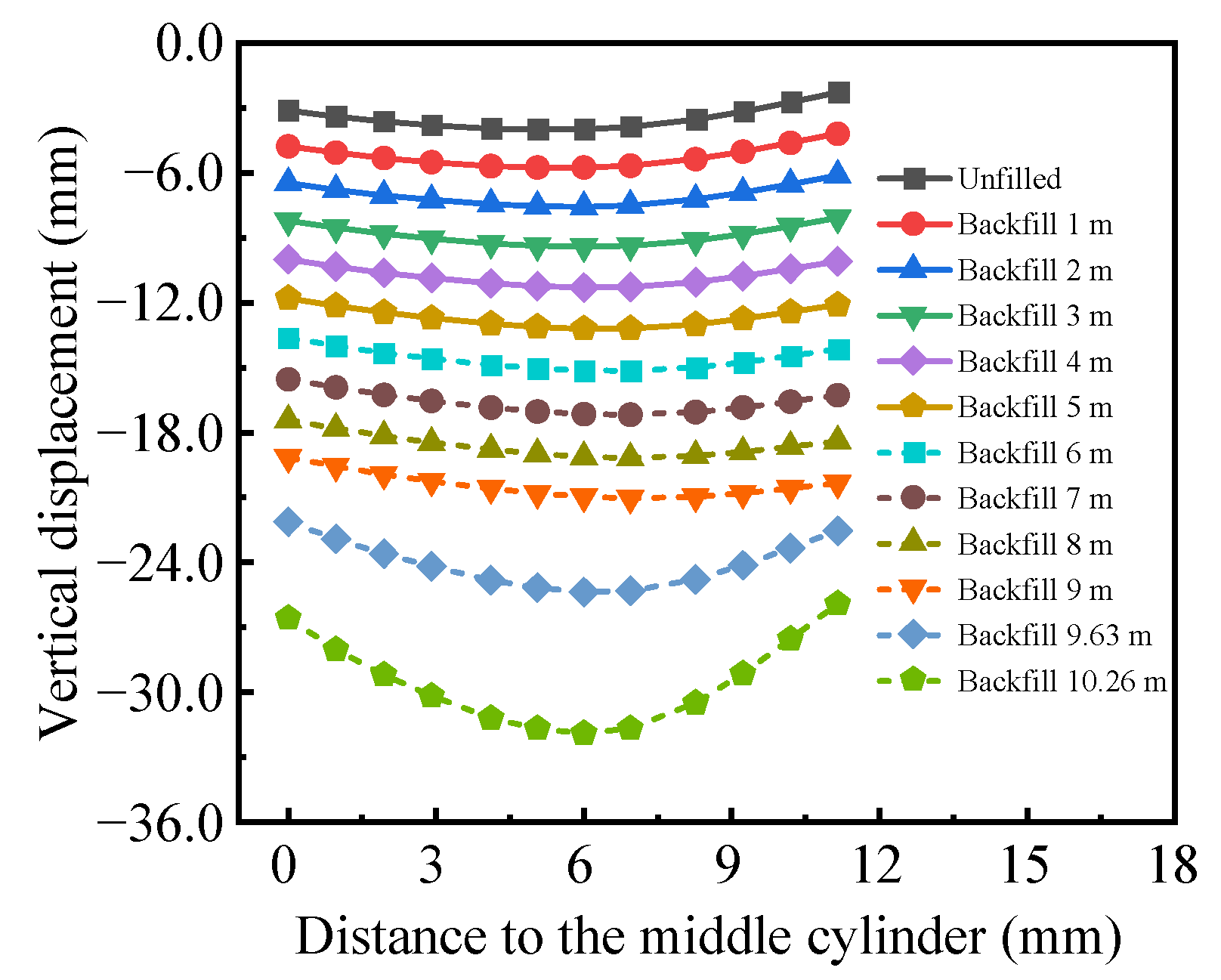
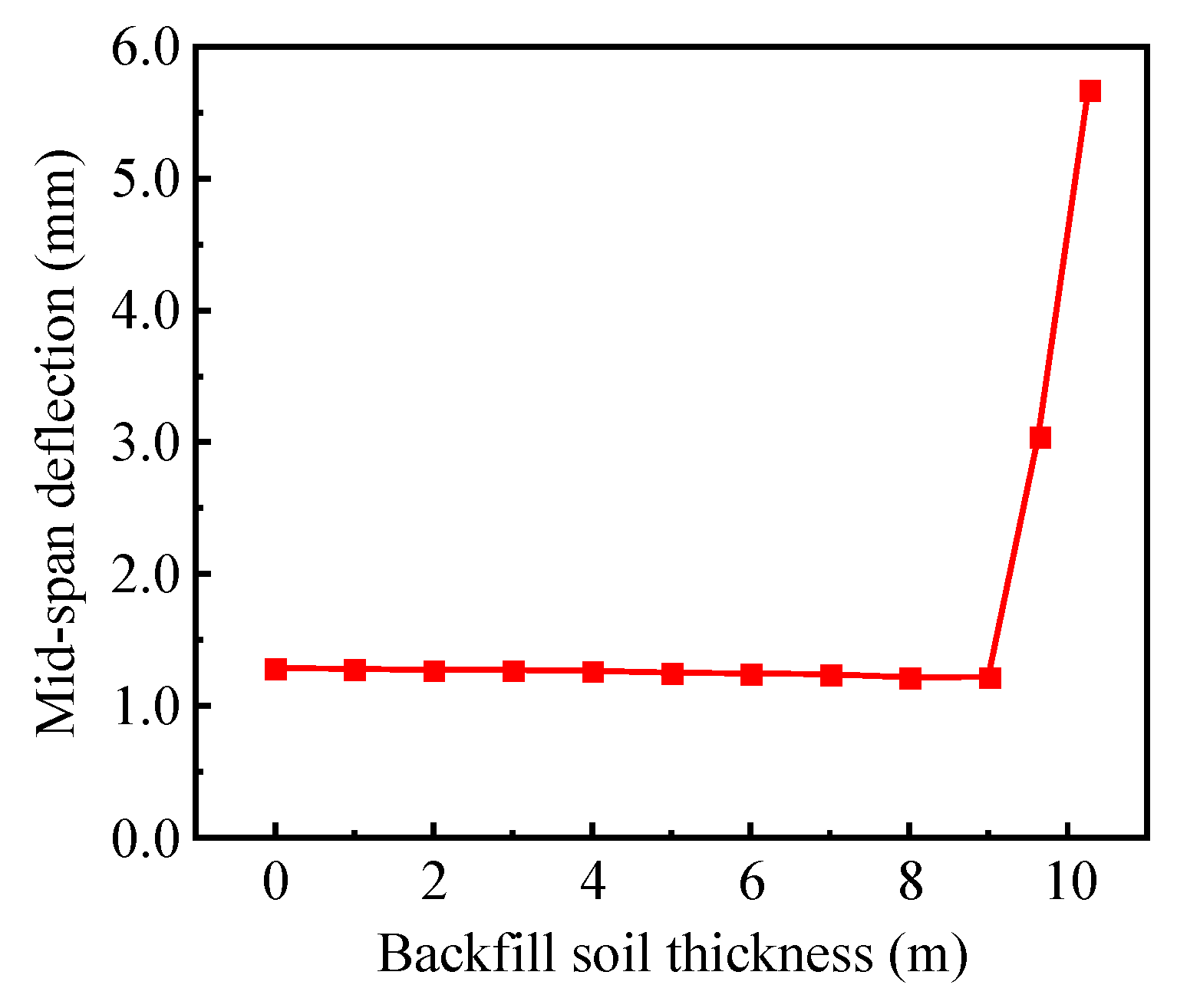
4.2.2. Vertical Displacement of Radial Primary Beam
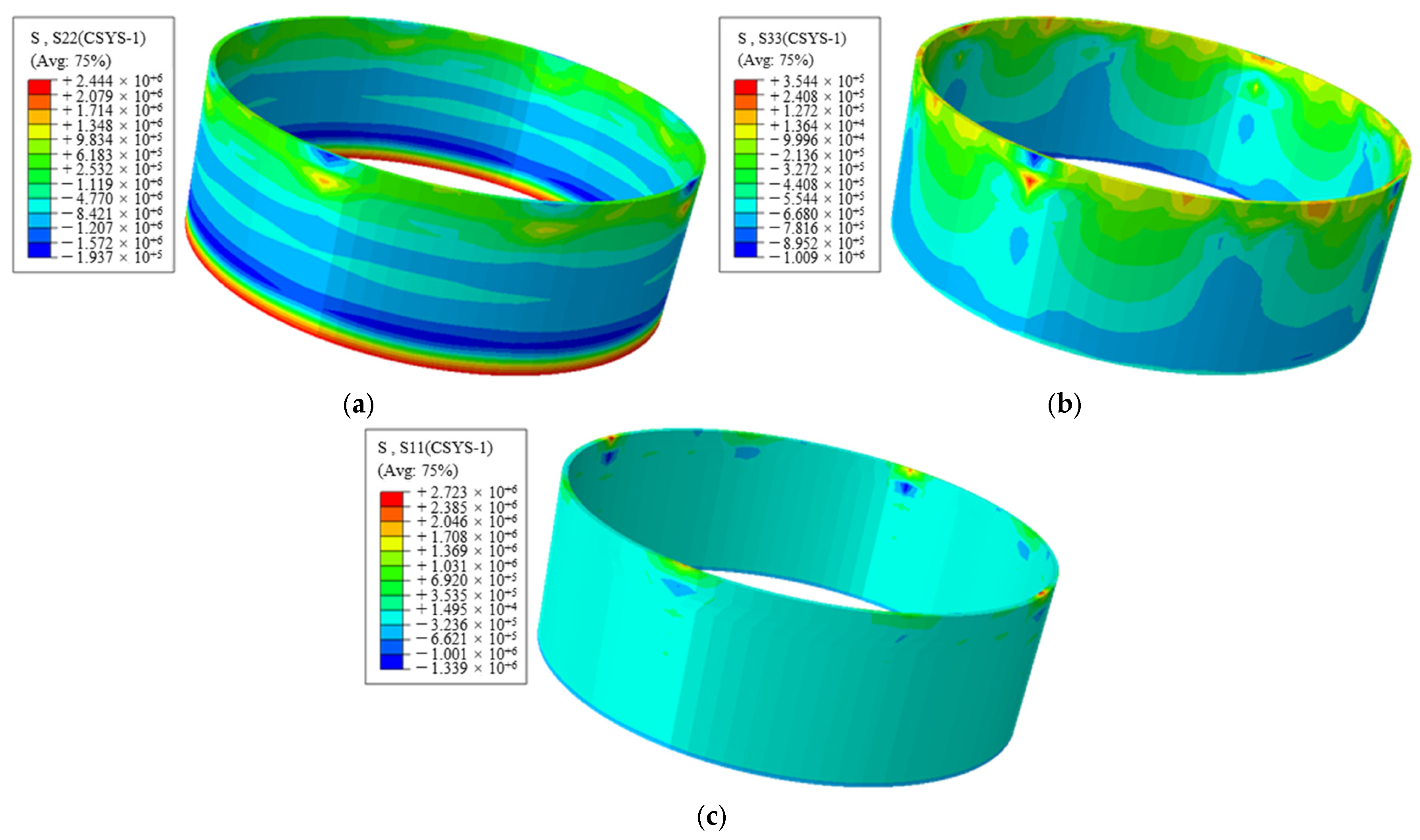
4.3. Stress Distribution
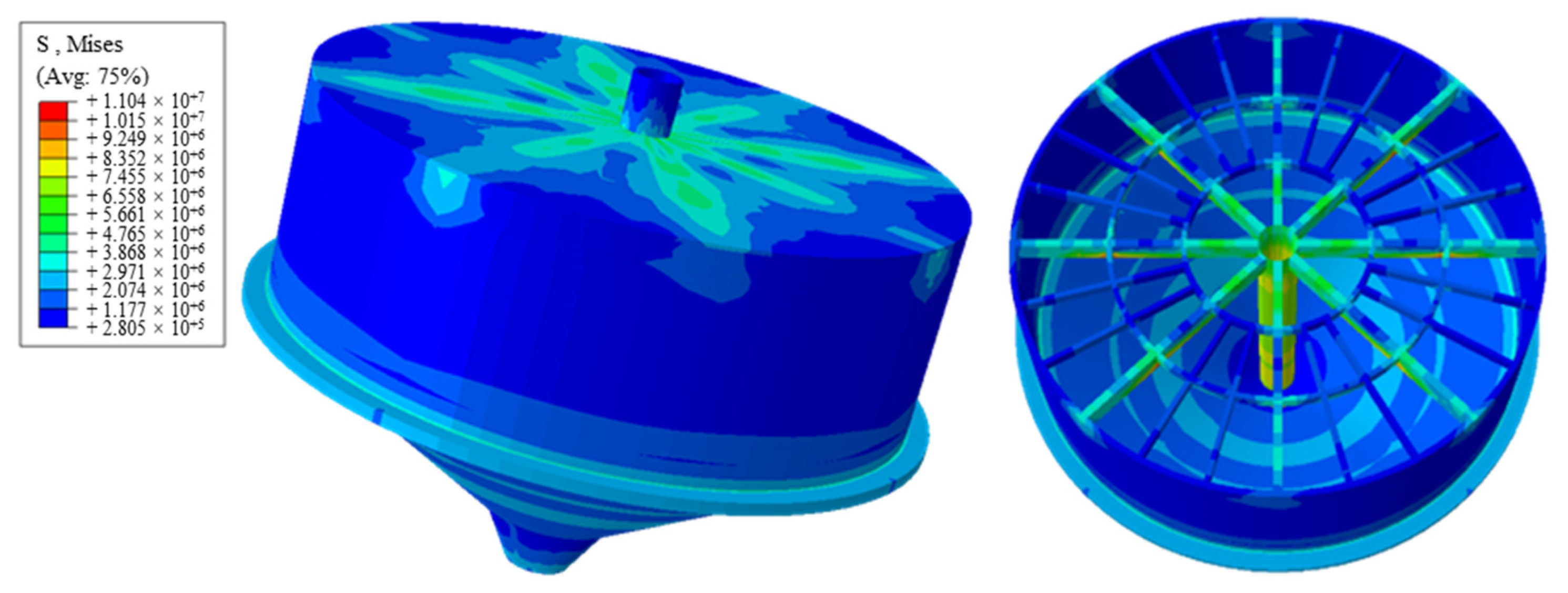
4.3.1. Von Mises Stress Distribution
4.3.2. Normal Stress Distribution of Silo Wall
4.3.3. Normal Stress Distribution of Silo Top
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chen, G.; Hou, J.; Liu, C. A Scientometric Review of Grain Storage Technology in the Past 15 Years (2007–2022) Based on Knowledge Graph and Visualization. Foods 2022, 11, 3836. [Google Scholar] [CrossRef]
- Liu, C.; Chen, G.; Zhou, Y.; Zheng, D.; Zhang, Z. Element tests and simulation of effects of vertical pressure on compression and mildew of wheat. Comput. Electron. Agric. 2022, 203, 107447. [Google Scholar] [CrossRef]
- Cui, H.; Zhang, Q.; Wu, W.; Zhang, H.; Ji, J.; Ma, H. Modeling and Application of Temporal Correlation of Grain Temperature during Grain Storage. Agriculture 2022, 12, 1883. [Google Scholar] [CrossRef]
- Zevgolis, I.E.; Mavrikos, A.A.; Kaliampakos, D.C. Construction, storage capacity and economics of an underground warehousing—Logistics center in Athens, Greece. Tunn. Undergr. Space Technol. 2004, 19, 165–173. [Google Scholar] [CrossRef]
- Valls, A.; Garcia, F.; Ramirez, M.; Benlloch, J. Understanding subterranean grain storage heritage in the Mediterranean region: The Valencian silos (Spain). Tunn. Undergr. Space Technol. 2015, 50, 178–188. [Google Scholar] [CrossRef]
- Yu, H.; Wang, L.; Wang, Z.; Zheng, P. Present condition and outlook for underground silos. J. Henan Univ. Technol. Nat. Sci. Ed. 2008, 29, 79–81. [Google Scholar] [CrossRef]
- Wang, Z.; Chuai, J.; Liu, Y.; Wang, L. Current Situation and New Progresses of Structure Design of Underground Silos. J. Henan Univ. Technol. Nat. Sci. Ed. 2019, 40, 132–138. [Google Scholar] [CrossRef]
- Pan, Y.; Fang, H.; Li, B.; Wang, F. Stability analysis and full-scale test of a new recyclable supporting structure for underground ecological granaries. Eng. Struct. 2019, 192, 205–219. [Google Scholar] [CrossRef]
- Chen, G.; Cui, C.; Fu, Z.; Jin, L. Monitoring analysis on the stress of reinforced concrete underground grain silo. J. Henan Univ. Technol. Nat. Sci. Ed. 2016, 37, 90–95. [Google Scholar] [CrossRef]
- GB50077-2017; Standard for Design of Reinforced Concrete Silos. China Planning Press: Beijing, China, 2015.
- Chen, G.; Yue, L.; Wang, Z.; Wang, H.; Zhang, H. Quasistatic Temperature Field Simulation of Reinforced Concrete Underground Warehouse Grain. J. Chin. Cereals Oils Assoc. 2014, 29, 79–83. [Google Scholar]
- Xiong, X.; Jin, L.; Shi, X.; Guo, H. Study on wall bearing capacity calculation method of reinforced concrete underground granary. J. Henan Univ. Technol. Nat. Sci. Ed. 2015, 36, 95–99. [Google Scholar] [CrossRef]
- Xiong, X.; Jin, L.; Wang, Z. Earth pressure and bearing capacity analysis on the wall of reinforced concrete underground granary. J. Basic Sci. Eng. 2016, 24, 103–114. [Google Scholar] [CrossRef]
- Chen, G.; Cui, C.; Fu, Z.; Jiang, M. Reliability sensitivity analysis of underground silo based on Monte-Carlo stochastic finite element method. J. Henan Univ. Technol. Nat. Sci. Ed. 2017, 38, 86–90+95. [Google Scholar] [CrossRef]
- Liu, H.; Meng, W.; Wang, Z.; Tian, D.; Xu, X.; Liu, X. Buoyancy early warning of underground granary with “2:8 lime soil” backfilling. Trans. Chin. Soc. Agric. Eng. 2019, 35, 299–305. [Google Scholar] [CrossRef]
- Liu, H.; Xu, X.; Zhang, H.; Wang, Z.; Yang, J.; Ma, T. Friction Analysis of Underground Silos during Backfilling. Mod. Food Sci. Technol. 2021, 37, 175–183. [Google Scholar] [CrossRef]
- Chen, G.; Cui, C.; Fu, Z.; Jiang, M. Research on Deformation and Internal Force of Reinforced Concrete Underground Grain Silo Wall. Chin. J. Undergr. Space Eng. 2019, 15, 458–464. [Google Scholar]
- Jin, L.; Liang, X.; Huo, C.; Wang, Z.; Wang, Z. Engineering test and numerical analysis of underground concrete silo. J. Civ. Environ. Eng. 2020, 42, 40–45. [Google Scholar] [CrossRef]
- Chuai, J.; Hou, Z.; Wang, Z.; Wang, L.; Jin, J. Mechanical Properties of the Vertical Joints of Prefabricated Underground Silo Steel Plate Concrete Wall. Adv. Civ. Eng. 2020, 2020, 6643811. [Google Scholar] [CrossRef]
- Zhang, H.; Han, K.; Yang, J.; Chen, L. Experimental and Numerical Investigation of Plastic-Concrete Waterproof Walls of an Underground Granary Subject to Combined Bending Moment and Water Pressure. Buildings 2022, 12, 893. [Google Scholar] [CrossRef]
- Zhang, H.; Pan, C.; Yang, J.; Xi, H. A hydrostatic test study on the waterproofing of an underground ecological granary using a plastic-concrete system. Structures 2022, 44, 58–71. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, H.; Zhou, Y.; Chang, Z. Waterproofing performance of polypropylene-concrete wall of underground silo under combined compressive stress and water pressure. Heliyon 2022, 8, e12074. [Google Scholar] [CrossRef] [PubMed]
- Zhou, L.; Zhu, Z.; Liu, B.; Fan, Y. The effect of radial cracks on tunnel stability. Geomech. Eng. 2018, 15, 721–728. [Google Scholar]
- GB50010-2010; Code for Design of Concrete Structures. China Architecture & Building Press: Beijing, China, 2015.
- Li, G.; Xu, L.; Cheng, G. Reliability analysis for complex large-scale structures based on ANSYS software. Build. Struct. 2002, 5, 58–61. [Google Scholar] [CrossRef]







| Soil Layer | Soil Type | Average Thickness (m) | Accumulated Depth (m) | Moisture Content (%) | Specific Gravity (kN/m3) | Void Ratio | Internal Friction Angle (°) |
|---|---|---|---|---|---|---|---|
| 1 | Silty sand | 1.23 | 1.23 | 21.4 | 20 | 0.540 | 28 |
| 2 | Silty clay | 1.76 | 2.99 | 22.6 | 20.4 | 0.835 | 13.3 |
| 3 | Silt | 1.85 | 4.84 | 22.1 | 20.8 | 0.682 | 24.1 |
| 4 | Silty sand | 5.56 | 10.40 | 21.4 | 20 | 0.540 | 28 |
| 5 | Silt | 1.30 | 11.70 | 24.4 | 21.3 | 0.688 | 25.5 |
| 6 | Silty sand | 6.58 | 18.28 | 21.4 | 20 | 0.540 | 28 |
| 7 | Silt | 1.29 | 19.57 | 23.7 | 20.6 | 0.678 | 26 |
| 8 | Silty sand | 6.88 | 26.45 | 21.4 | 20 | 0.540 | 28 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yue, L.; Chen, G.; Cui, C.; Liu, C.; Zhao, B. Numerical Simulation of Backfilling Construction for Underground Reinforced Concrete Grain Silos. Buildings 2024, 14, 3907. https://doi.org/10.3390/buildings14123907
Yue L, Chen G, Cui C, Liu C, Zhao B. Numerical Simulation of Backfilling Construction for Underground Reinforced Concrete Grain Silos. Buildings. 2024; 14(12):3907. https://doi.org/10.3390/buildings14123907
Chicago/Turabian StyleYue, Longfei, Guixiang Chen, Chenxing Cui, Chaosai Liu, and Boyi Zhao. 2024. "Numerical Simulation of Backfilling Construction for Underground Reinforced Concrete Grain Silos" Buildings 14, no. 12: 3907. https://doi.org/10.3390/buildings14123907
APA StyleYue, L., Chen, G., Cui, C., Liu, C., & Zhao, B. (2024). Numerical Simulation of Backfilling Construction for Underground Reinforced Concrete Grain Silos. Buildings, 14(12), 3907. https://doi.org/10.3390/buildings14123907








