Risk Assessment of Small-Diameter Shield Construction in a Deep Drainage Tunnel Based on an ISM–CRITIC–Cloud Model
Abstract
:1. Introduction
2. Literature Review
3. Methodology
3.1. ISM
3.2. CRITIC Method
3.3. Cloud Model
4. Risk Assessment Model for Small-Diameter Shield Construction in a Deep Drainage Tunnel
4.1. Key Risk Factor Identification Model
4.2. Indicator Weight Calculation Model
4.3. Risk Grade Evaluation Model
5. Engineering Applications
5.1. Project Overview
5.2. Application of Risk Assessment Model
5.2.1. Identification of Key Risk Factors
5.2.2. Calculation of Risk Indicator Weight Value
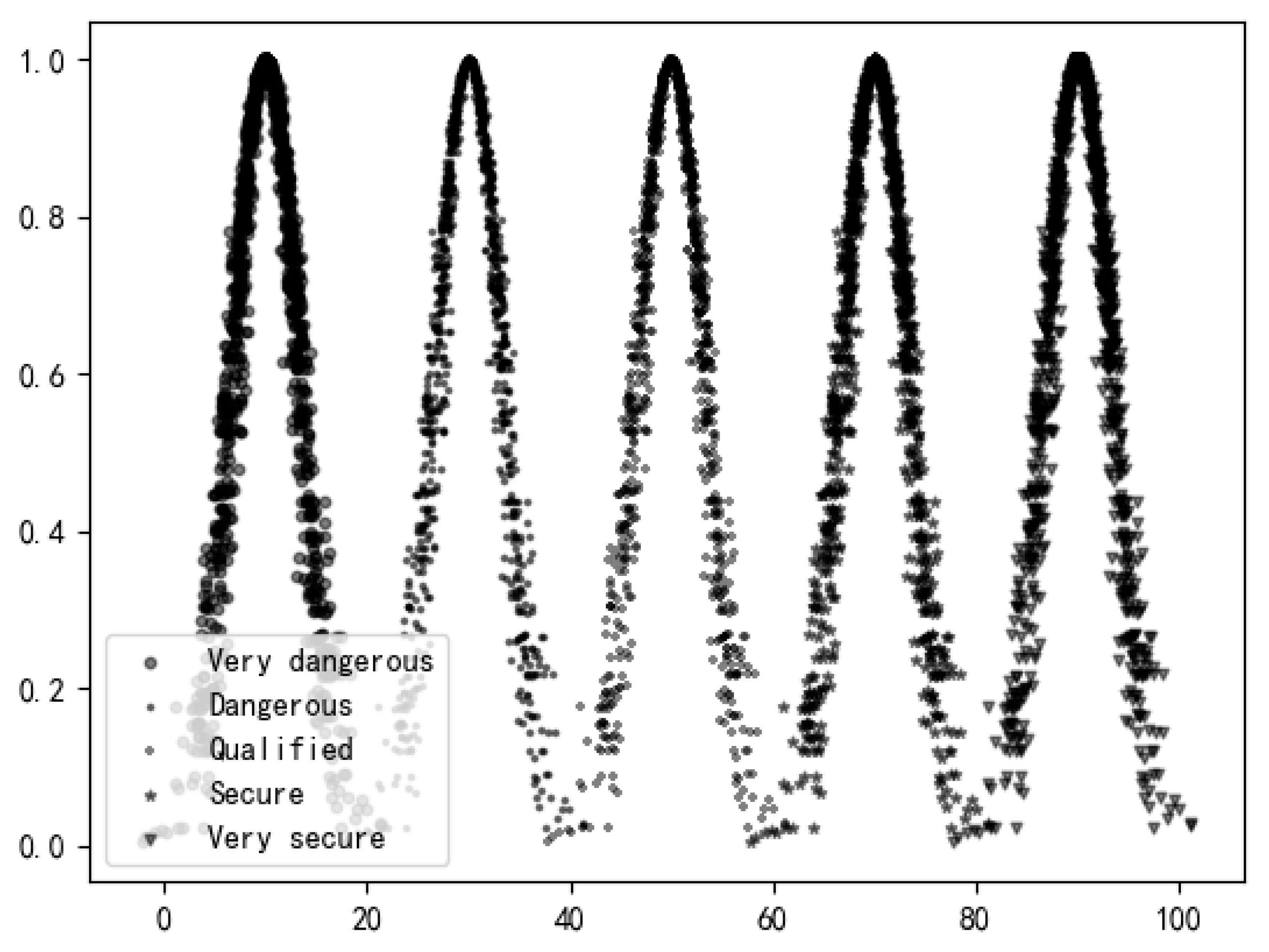
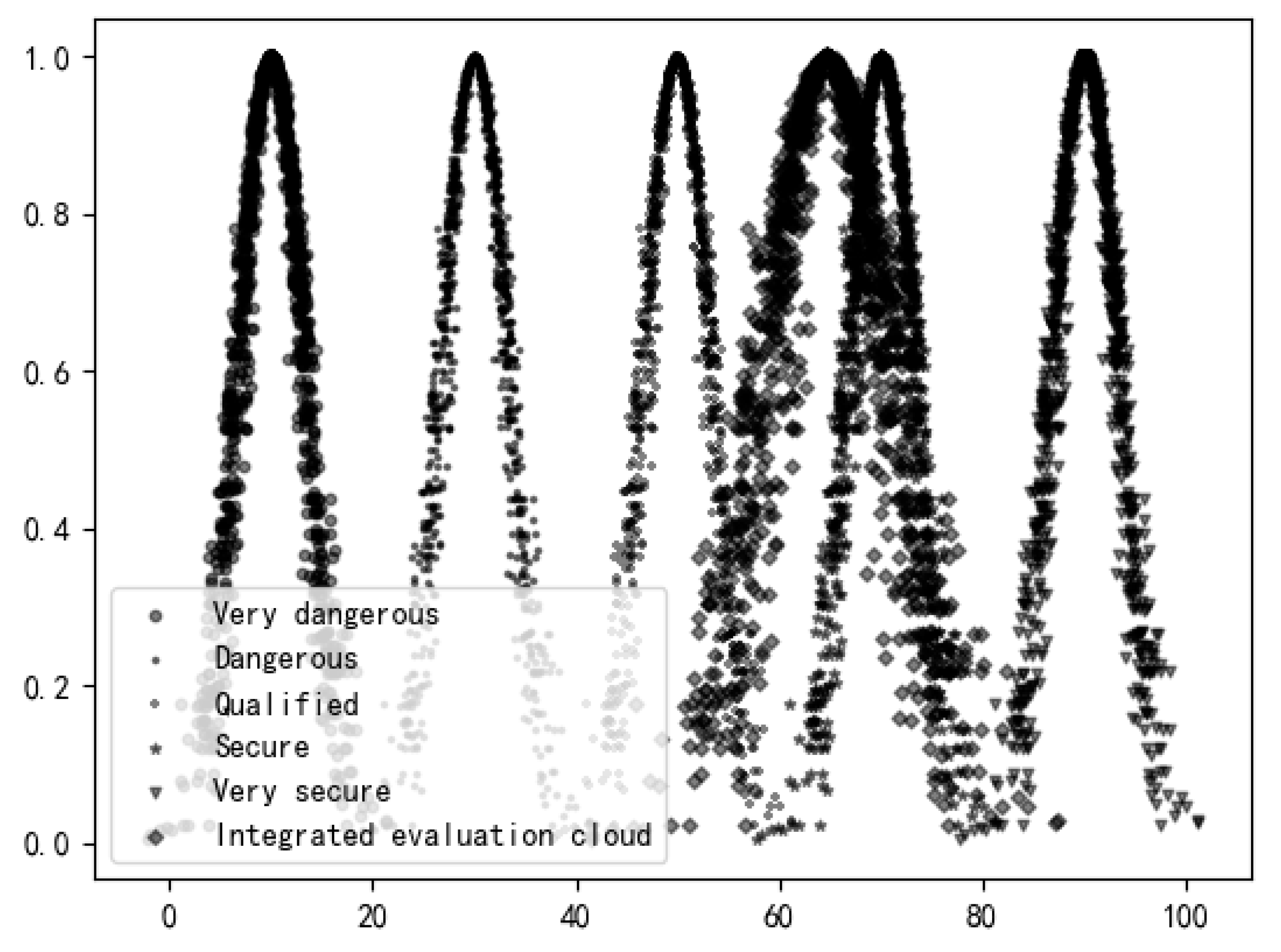
5.2.3. Assessment of Risk Grade
5.3. Analysis of Risk Assessment Results
6. Discussion
6.1. Verification of Model Accuracy
6.2. Implication
6.3. Limitations and Future Research
7. Conclusions
- (1)
- The risk assessment model constructed by combining the ISM, CRITIC and cloud model can solve the ambiguity and uncertainty of the risk assessment of small-diameter shield construction in a deep drainage tunnel, and effectively evaluate the risk level of small-diameter shield construction in a deep drainage tunnel.
- (2)
- The risk assessment model proposed in this study can identify the key risk factors from the numerous risk factors in small-diameter shield construction of deep tunnel drainage, which can not only reduce the interference project and workload of risk assessment, but also provide support for managers’ decision making.
- (3)
- The risk assessment model proposed in this study can rank the importance of the risk factors in small-diameter shield construction of deep tunnel drainage, and provide a theoretical basis for the optimization of resource allocation under the resource constraints of project risk management.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Liao, L.; An, R.D.; Li, J.; Yi, W.M.; Liu, X.F.; Meng, W.K.; Zhu, L. Hydraulic characteristics of stepped spillway dropshafts for urban deep tunnel drainage systems: The case study of Chengdu city. Water Sci. Technol. 2019, 80, 1538–1548. [Google Scholar] [CrossRef]
- Sun, J.Y.; Wu, X.W.; Wang, G.H.; He, J.G.; Li, W.T. The governance and optimization of urban flooding in dense urban areas utilizing deep tunnel drainage systems: A case study of Guangzhou, China. Water 2024, 16, 2429. [Google Scholar] [CrossRef]
- Chung, H.; Park, J.; Kim, B.K.; Kwon, K.; Lee, I.M.; Choi, H. A causal network-based risk matrix model applicable to shield tbm tunneling projects. Sustainability 2021, 13, 4846. [Google Scholar] [CrossRef]
- Xu, N.; Guo, C.R.; Wang, L.; Zhou, X.Q.; Xie, Y. A three-stage dynamic risk model for metro shield tunnel construction. Ksce J. Civ. Eng. 2024, 28, 503–516. [Google Scholar] [CrossRef]
- Wu, H.; Liu, S.; Liu, D.H.; Wang, J.W. Hse risk assessment of major sewage transport tunnel projects at the construction stage based on the structuralentropy weight method and the cloud model. Adv. Civ. Eng. 2020, 2020, 8882903. [Google Scholar] [CrossRef]
- Ding, L.; Sun, Y.J.; Zhang, W.Z.; Bi, G.; Xu, H.Z. Stress monitoring of segment structure during the construction of the small-diameter shield tunnel. Sensors 2023, 23, 8023. [Google Scholar] [CrossRef] [PubMed]
- Hu, K.; Wang, J.W.; Wu, H. Construction safety risk assessment of large-sized deep drainage tunnel projects. Math. Probl. Eng. 2021, 2021, 7380555. [Google Scholar] [CrossRef]
- Ni, H.M.; Li, X.; Huang, J.Q.; Zhou, S.M. Health risk prediction of operational subsea tunnel structure based on Bayesian network. Buildings 2024, 14, 1475. [Google Scholar] [CrossRef]
- Huang, W.; Wu, B. Risk assessment of shield tunnel construction in coastal areas. Pol. J. Environ. Stud. 2024, 33, 2693–2706. [Google Scholar] [CrossRef]
- Guo, D.S.; Meng, F.Y.; Wu, H.N.; Yang, X.X.; Liu, Z. Risk assessment of shield tunneling crossing building based on variable weight theory and cloud model. Tunn. Undergr. Space Technol. 2024, 145, 105593. [Google Scholar] [CrossRef]
- Lin, P.; Xiong, Y.; Xu, Z.H.; Wang, W.Y.; Shao, R.Q. Risk assessment of tbm jamming based on Bayesian networks. Bull. Eng. Geol. Environ. 2022, 81, 47. [Google Scholar] [CrossRef]
- Wu, Z.Q.; Zou, S.L. A static risk assessment model for underwater shield tunnel construction. Sadhana-Acad. Proc. Eng. Sci. 2020, 45, 215. [Google Scholar] [CrossRef]
- Wu, P.; Chen, Q.; Chen, Y.Q.; Chen, S.A.; Zou, J. Ism-micmac based safety risk sources analysis and control measures for underground engineering of urban rail transit projects. J. Eng. Res. 2023, 11, 40–50. [Google Scholar] [CrossRef]
- Sun, J.H.; Wang, W.J.; Xie, L.K. Predicting short-term rockburst using rf-critic and improved cloud model. Nat. Resour. Res. 2024, 33, 471–494. [Google Scholar] [CrossRef]
- Li, J.L.; Yuan, C.; Zhang, B.; Sui, B. Evaluation and application of surrounding rock stability based on the improved weighting multidimensional cloud model. Adv. Civ. Eng. 2021, 2021, 5557477. [Google Scholar] [CrossRef]
- He, K.; Zhu, J.; Wang, H.; Huang, Y.L.; Li, H.J.; Dai, Z.S.; Zhang, J.X.; Stathopoulos, T. Safety risk evaluation of metro shield construction when undercrossing a bridge. Buildings 2023, 13, 2540. [Google Scholar] [CrossRef]
- Meng, G.W.; Ye, Y.C.; Wu, B.; Luo, G.J.; Zhang, X.; Zhou, Z.Q.; Sun, W.T. Risk assessment of shield tunnel construction in karst strata based on fuzzy analytic hierarchy process and cloud model. Shock. Vib. 2021, 2021, 7237136. [Google Scholar] [CrossRef]
- Chen, H.Y.; Yang, S.; Feng, Z.B.; Liu, Y.; Qin, Y.W. Safety evaluation of buildings adjacent to shield construction in karst areas: An improved extension cloud approach. Eng. Appl. Artif. Intell. 2023, 124, 106386. [Google Scholar] [CrossRef]
- Hyun, K.C.; Min, S.; Choi, H.; Park, J.; Lee, I.M. Risk analysis using fault-tree analysis (fta) and analytic hierarchy process (ahp) applicable to shield tbm tunnels. Tunn. Undergr. Space Technol. 2015, 49, 121–129. [Google Scholar] [CrossRef]
- Tang, C.; Shen, C.X.; Zhang, J.J.; Guo, Z. Identification of safety risk factors in metro shield construction. Buildings 2024, 14, 492. [Google Scholar] [CrossRef]
- Yu, R.Z.; Ma, L. Risk evaluation of mega infrastructure construction supply chain in engineering-procurement-construction projects: An integrated fuzzy ahp and fuzzy dematel approach. Eng. Constr. Archit. Manag. 2024; Early Access. [Google Scholar]
- Huang, Z.; Zhang, W.; Sun, H.Y.; Pan, Q.J.; Zhang, J.B.; Li, Y.F. Risk uncertainty analysis in shield tunnel projects. Tunn. Undergr. Space Technol. 2023, 132, 104899. [Google Scholar] [CrossRef]
- Lin, C.J.; Zhang, M.; Li, L.P.; Zhou, Z.Q.; Liu, S.; Liu, C.; Li, T. Risk assessment of tunnel construction based on improved cloud model. J. Perform. Constr. Facil. 2020, 34, 04020028. [Google Scholar] [CrossRef]
- Guo, D.S.; Song, Z.P.; Xu, T.; Zhang, Y.W.; Ding, L.B. Coupling analysis of tunnel construction risk in complex geology and construction factors. J. Constr. Eng. Manag. 2022, 148, 04022097. [Google Scholar] [CrossRef]
- Wang, J.C.; Liu, J.Q.; Wei, Q.; Wang, P. Risk assessment based on combined weighting-cloud model of tunnel construction. Teh. Vjesn. -Tech. Gaz. 2021, 28, 203–210. [Google Scholar]
- Pan, H.Z.; Huang, H.L.Y.; Luo, Z.H.; Wu, C.J.; Yang, S.D. Research on safety risk factors of metro shield tunnel construction in China based on social network analysis. Eng. Constr. Archit. Manag. 2024; ahead-of-print. [Google Scholar] [CrossRef]
- Ou, L.; Chen, Y.; Zhang, J.; Ma, C.S. Dematel-ism-based study of the impact of safety factors on urban rail tunnel construction projects. Comput. Intell. Neurosci. 2022, 2022, 2222556. [Google Scholar] [CrossRef]
- Zheng, W.Q.; Xu, S.X.; Wang, Z.C. Fuzzy comprehensive evaluation of collapse risk in mountain tunnels based on game theory. Appl. Sci. 2024, 14, 5163. [Google Scholar] [CrossRef]
- Krishnan, A.R.; Kasim, M.M.; Hamid, R.; Ghazali, M.F. A modified critic method to estimate the objective weights of decision criteria. Symmetry 2021, 13, 973. [Google Scholar] [CrossRef]
- Wang, Y.C.; Yin, X.; Jing, H.W.; Liu, R.C.; Su, H.J. A novel cloud model for risk analysis of water inrush in karst tunnels. Environ. Earth Sci. 2016, 75, 1450. [Google Scholar] [CrossRef]

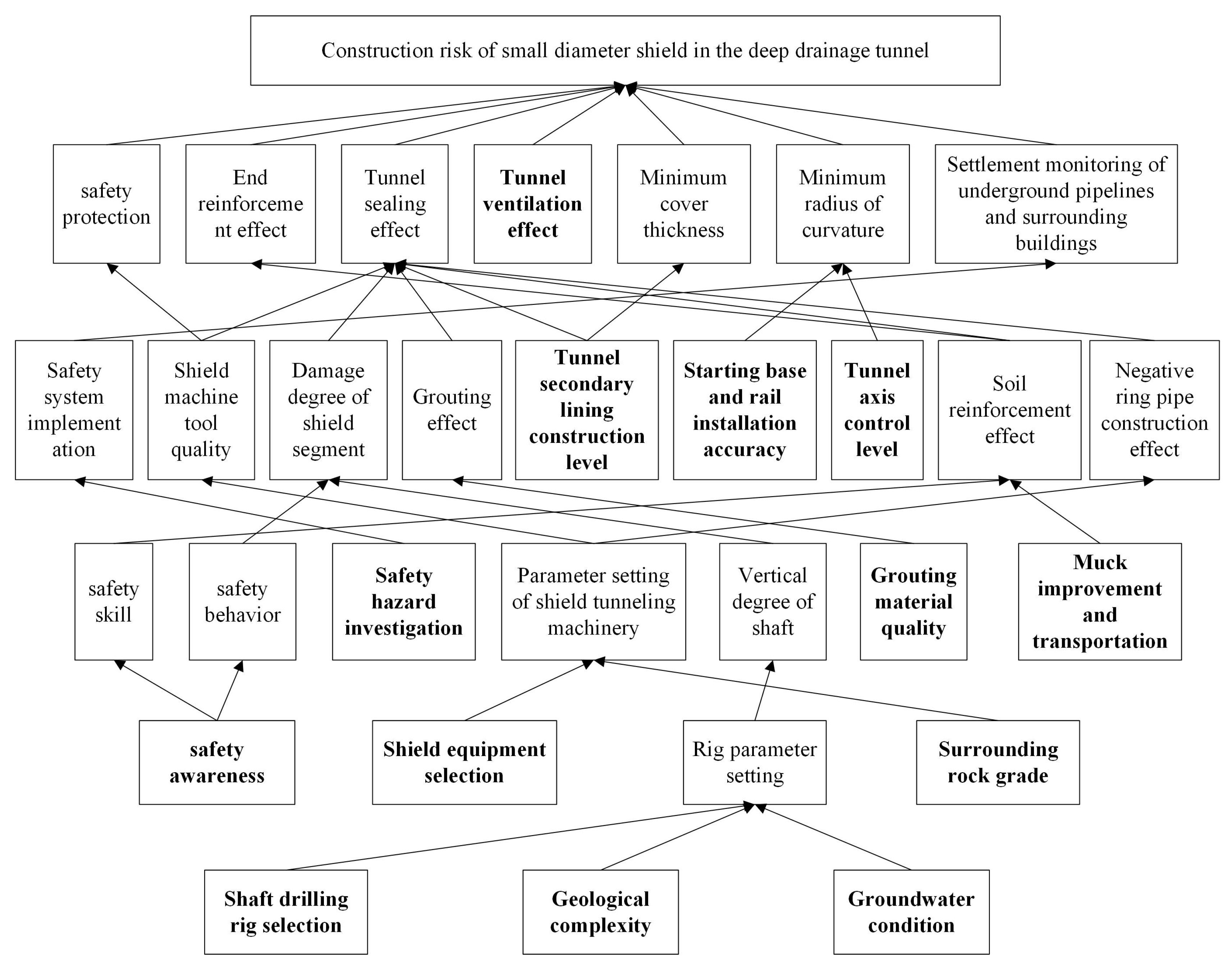
| Number | Risk Factor | Risk Index | Literature Resources |
|---|---|---|---|
| 1 | Personnel and management factors | Safety awareness | Yu and Ma [21] and Huang and Wu [9] |
| 2 | Safety skill | ||
| 3 | Safety protection | ||
| 4 | Safety behavior | ||
| 5 | Safety system implementation | ||
| 6 | Safety hazard investigation | ||
| 7 | Mechanical factor | Shaft drilling rig selection | Hu et al. [7], Guo et al. [10] and Huang et al. [22] |
| 8 | Shield equipment selection | ||
| 9 | Rig parameter setting | ||
| 10 | Parameter setting of shield tunneling machinery | ||
| 11 | Vertical degree of shaft | ||
| 12 | Material factor | Grouting material quality | Chung et al. [3] and Hu et al. [7] |
| 13 | Shield machine tool quality | ||
| 14 | Damage degree of shield segment | ||
| 15 | Muck improvement and transportation | ||
| 16 | Technical factor | Grouting effect | Hu et al. [7], Wu and Zou [12] and Lin et al. [23] |
| 17 | End reinforcement effect | ||
| 18 | Tunnel sealing effect | ||
| 19 | Tunnel secondary lining construction level | ||
| 20 | Starting base and rail installation accuracy | ||
| 21 | Tunnel axis control level | ||
| 22 | Tunnel ventilation effect | ||
| 23 | Soil reinforcement effect | ||
| 24 | Negative ring pipe construction effect | ||
| 25 | Environmental factor | Surrounding rock grade | Guo et al. [24] and Wang et al. [25] |
| 26 | Minimum cover thickness | ||
| 27 | Minimum radius of curvature | ||
| 28 | Geological complexity | ||
| 29 | Groundwater condition | ||
| 30 | Settlement monitoring of underground pipelines and surrounding buildings |
| Number | K1 | K2 | K3 | K4 | K5 | K6 | K7 | K8 | K9 | K10 | K11 | K12 | K13 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Expert 1 | 64 | 70 | 66 | 70 | 70 | 70 | 68 | 66 | 62 | 71 | 64 | 66 | 67 |
| Expert 2 | 70 | 66 | 63 | 71 | 67 | 68 | 73 | 67 | 68 | 65 | 60 | 55 | 61 |
| Expert 3 | 68 | 70 | 66 | 63 | 72 | 56 | 63 | 55 | 64 | 81 | 63 | 61 | 53 |
| Expert 4 | 65 | 71 | 58 | 67 | 52 | 66 | 66 | 57 | 68 | 72 | 64 | 68 | 62 |
| Expert 5 | 63 | 69 | 62 | 58 | 66 | 71 | 71 | 69 | 54 | 70 | 64 | 76 | 59 |
| Expert 6 | 65 | 65 | 71 | 63 | 75 | 63 | 69 | 66 | 58 | 64 | 66 | 69 | 64 |
| Expert 7 | 70 | 66 | 68 | 68 | 71 | 57 | 61 | 51 | 53 | 55 | 65 | 63 | 60 |
| Expert 8 | 64 | 65 | 56 | 71 | 55 | 62 | 60 | 72 | 73 | 67 | 62 | 73 | 64 |
| Expert 9 | 56 | 55 | 66 | 57 | 54 | 55 | 62 | 64 | 63 | 58 | 56 | 64 | 63 |
| Expert 10 | 68 | 71 | 68 | 68 | 66 | 65 | 51 | 67 | 71 | 57 | 63 | 70 | 65 |
| Risk Index | Index Variability | Index Conflict | Information Amount | Weighted Value | Rank |
|---|---|---|---|---|---|
| K1 | 0.843 | 12.272 | 10.349 | 0.076 | 7 |
| K2 | 0.949 | 12.334 | 11.701 | 0.086 | 5 |
| K3 | 0.823 | 12.433 | 10.236 | 0.075 | 9 |
| K4 | 1.179 | 11.723 | 13.816 | 0.102 | 1 |
| K5 | 1.033 | 13.184 | 13.616 | 0.100 | 2 |
| K6 | 0.738 | 12.822 | 9.461 | 0.070 | 11 |
| K7 | 0.527 | 10.486 | 5.527 | 0.041 | 12 |
| K8 | 0.516 | 11.01 | 5.686 | 0.042 | 13 |
| K9 | 0.789 | 13.107 | 10.339 | 0.076 | 7 |
| K10 | 1.059 | 12.201 | 12.925 | 0.095 | 3 |
| K11 | 0.949 | 12.414 | 11.777 | 0.087 | 4 |
| K12 | 0.919 | 11.469 | 10.539 | 0.077 | 6 |
| K13 | 0.919 | 11.013 | 10.12 | 0.074 | 10 |
| Risk Index | Ex | En | He |
|---|---|---|---|
| K1 | 65.3 | 3.71 | 1.833 |
| K2 | 66.8 | 4.261 | 2.215 |
| K3 | 64.4 | 4.662 | 0.291 |
| K4 | 65.6 | 5.364 | 1.584 |
| K5 | 64.8 | 8.372 | 1.674 |
| K6 | 63.3 | 5.891 | 1.164 |
| K7 | 64.4 | 6.267 | 1.452 |
| K8 | 63.4 | 6.818 | 0.941 |
| K9 | 63.4 | 6.768 | 0.952 |
| K10 | 66.0 | 7.771 | 1.843 |
| K11 | 62.7 | 2.532 | 1.351 |
| K12 | 66.5 | 5.891 | 1.571 |
| K13 | 61.8 | 3.559 | 1.618 |
| Comprehensive evaluation cloud | 64.662 | 6.02 | 1.406 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, K.; Wang, J.; Wu, D.; Wang, Y. Risk Assessment of Small-Diameter Shield Construction in a Deep Drainage Tunnel Based on an ISM–CRITIC–Cloud Model. Buildings 2024, 14, 3920. https://doi.org/10.3390/buildings14123920
Hu K, Wang J, Wu D, Wang Y. Risk Assessment of Small-Diameter Shield Construction in a Deep Drainage Tunnel Based on an ISM–CRITIC–Cloud Model. Buildings. 2024; 14(12):3920. https://doi.org/10.3390/buildings14123920
Chicago/Turabian StyleHu, Kai, Junwu Wang, Danhong Wu, and Yingang Wang. 2024. "Risk Assessment of Small-Diameter Shield Construction in a Deep Drainage Tunnel Based on an ISM–CRITIC–Cloud Model" Buildings 14, no. 12: 3920. https://doi.org/10.3390/buildings14123920
APA StyleHu, K., Wang, J., Wu, D., & Wang, Y. (2024). Risk Assessment of Small-Diameter Shield Construction in a Deep Drainage Tunnel Based on an ISM–CRITIC–Cloud Model. Buildings, 14(12), 3920. https://doi.org/10.3390/buildings14123920







