Accurate Dynamic Analysis Method of Cable-Damper System Based on Dynamic Stiffness Method
Abstract
:1. Introduction
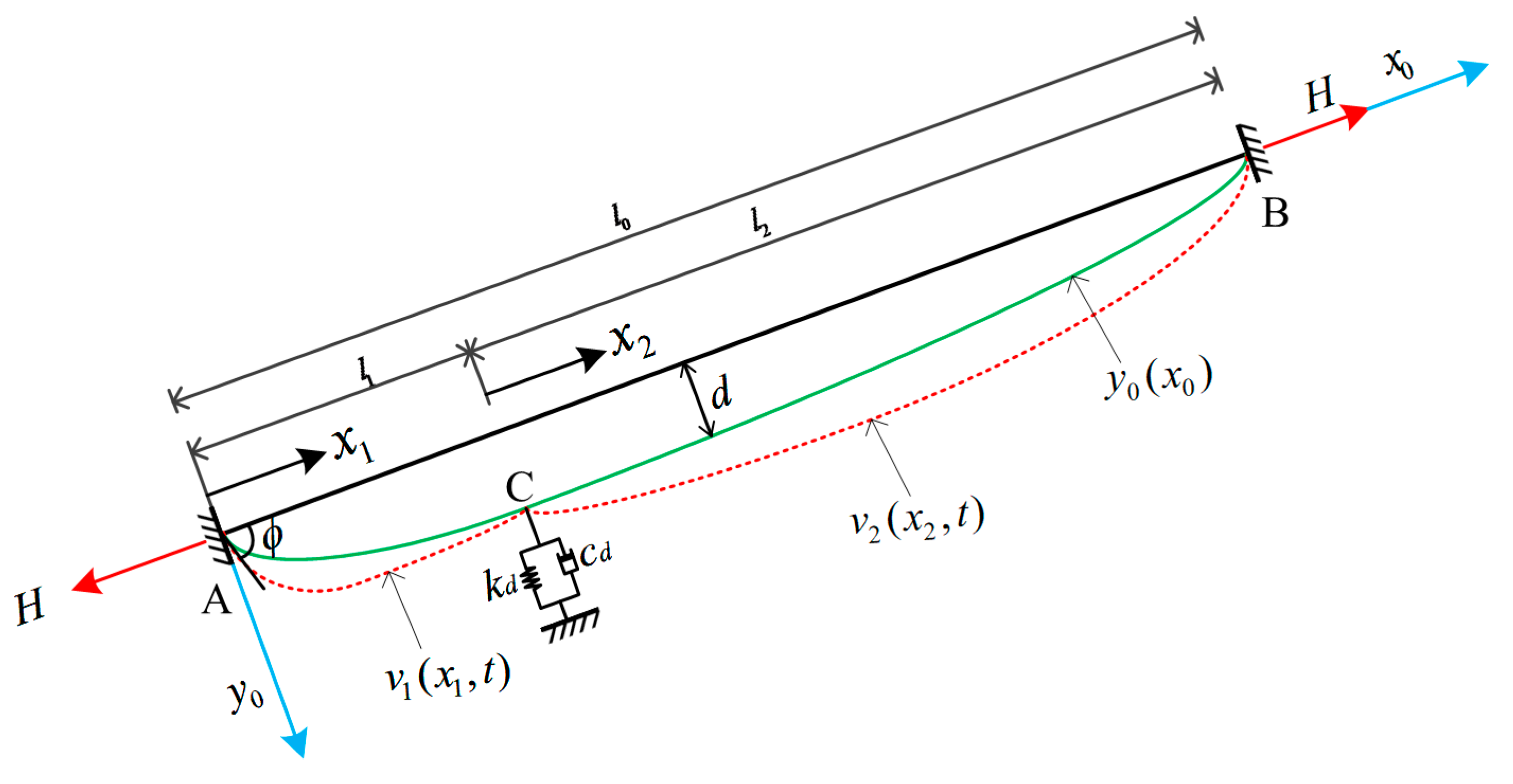
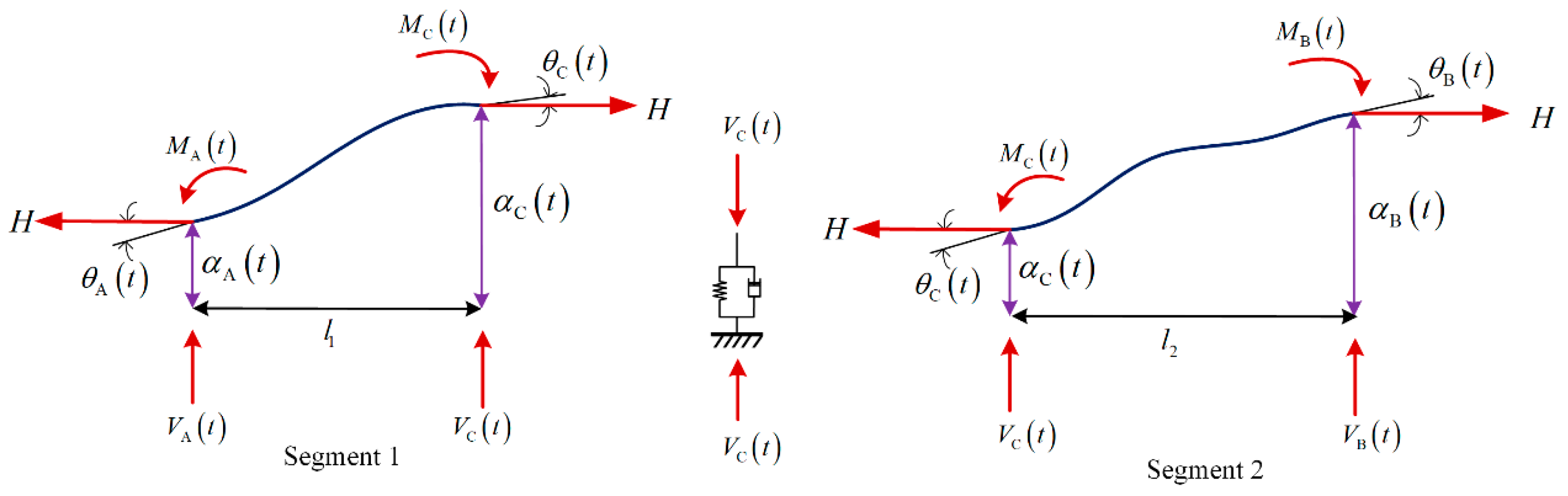
2. Dynamic Analysis Theory of Cable-Damper System
3. Solution of the Frequency Characteristic Equation for the Cable-Damper System
4. Accuracy Verification of the Characteristic Frequency Equation of the Cable-Damper System
4.1. Literature Experimental Verification
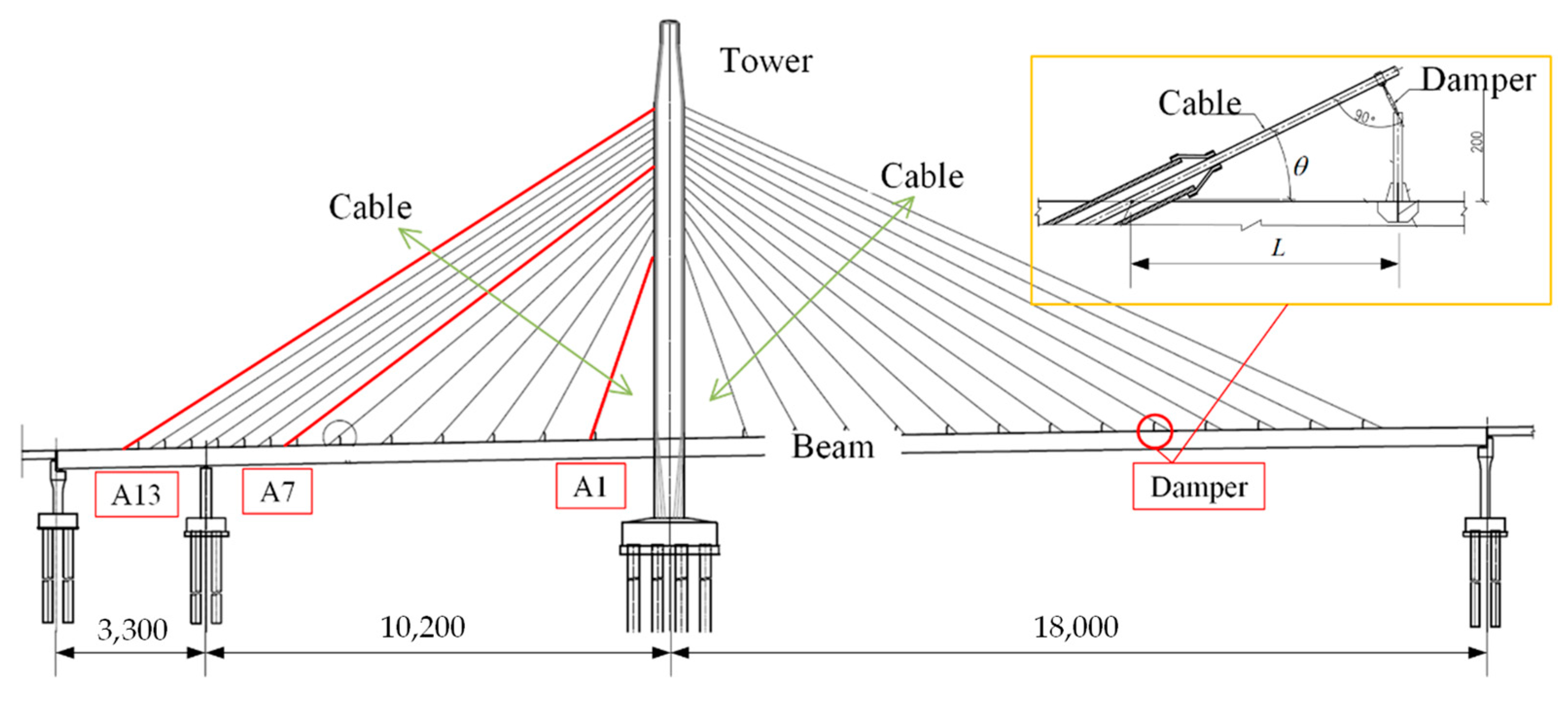
4.2. Real Bridge Data Verification
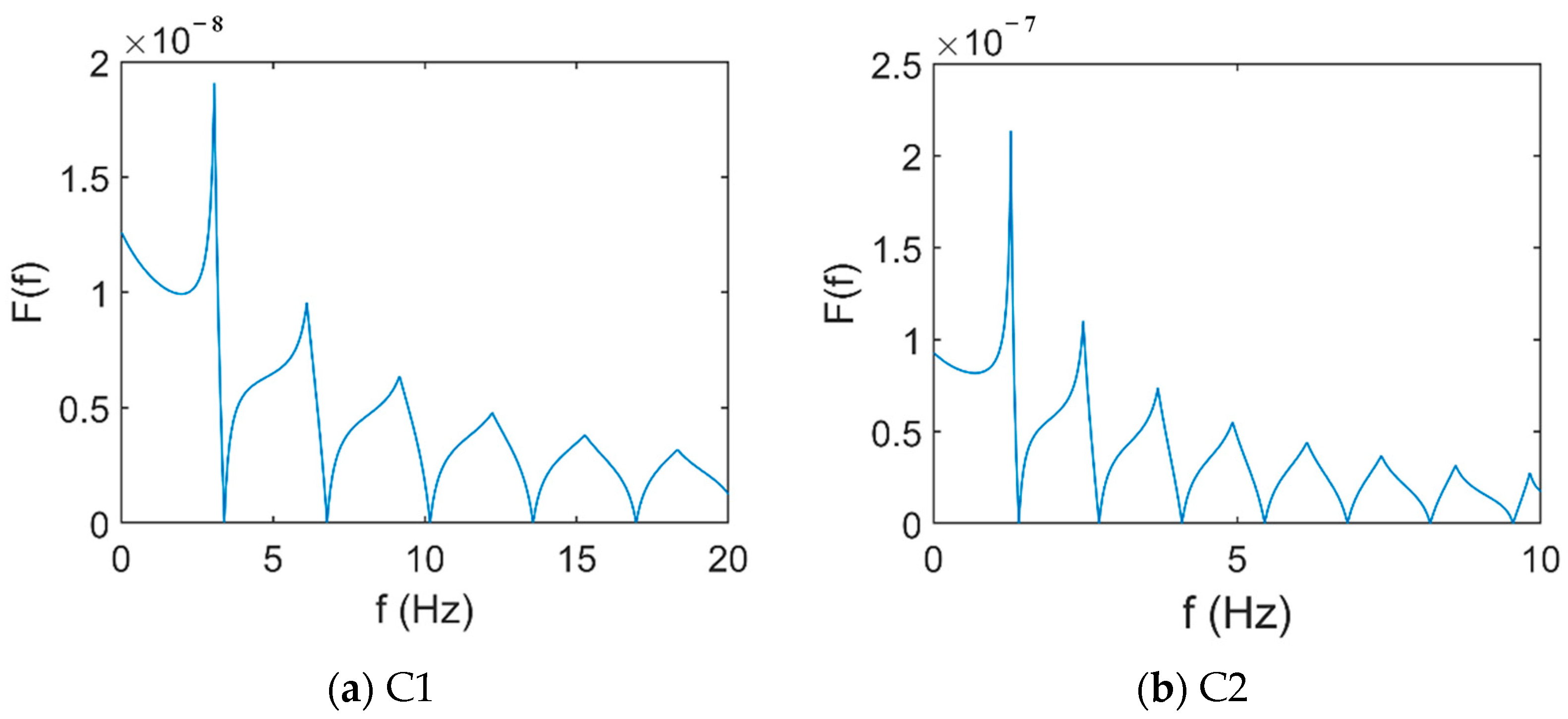
5. Influence of Damper Parameters on Dynamic Characteristics of Cable
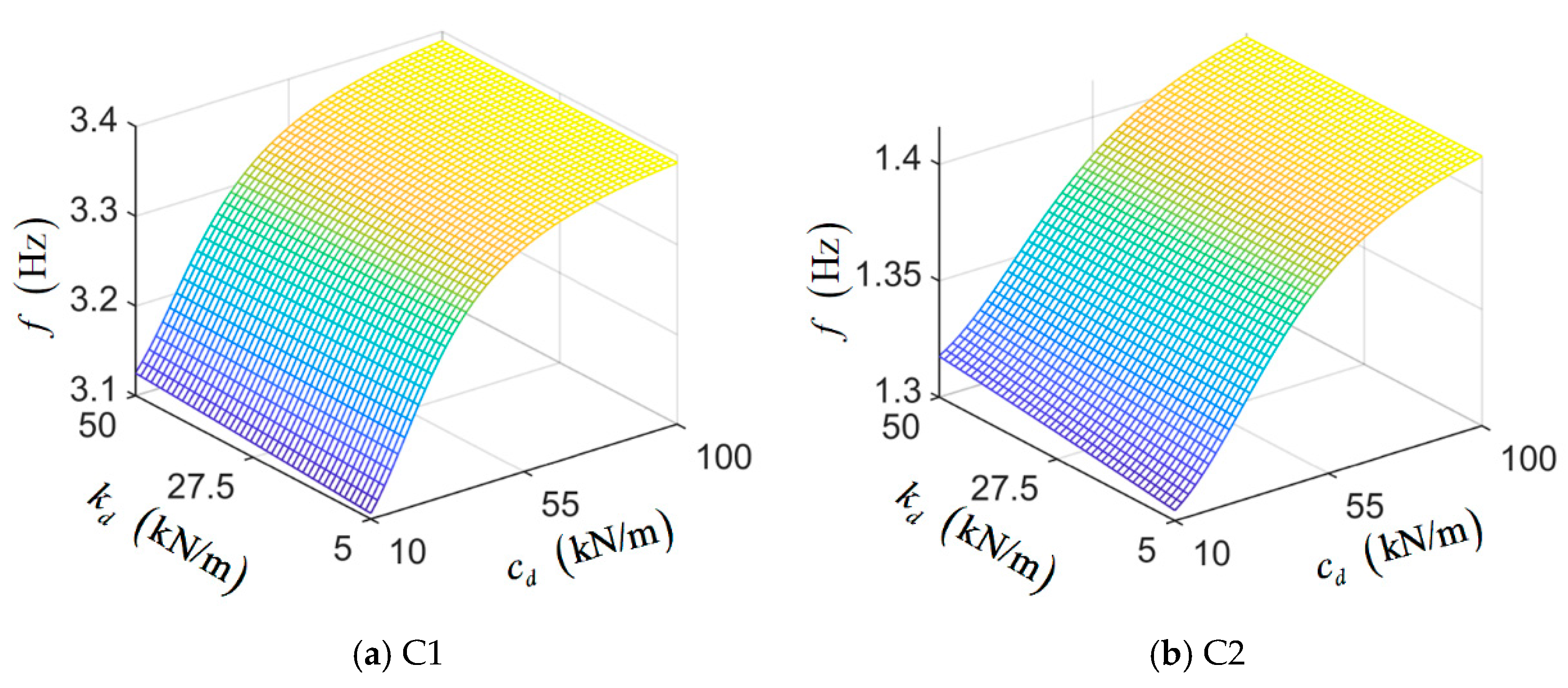
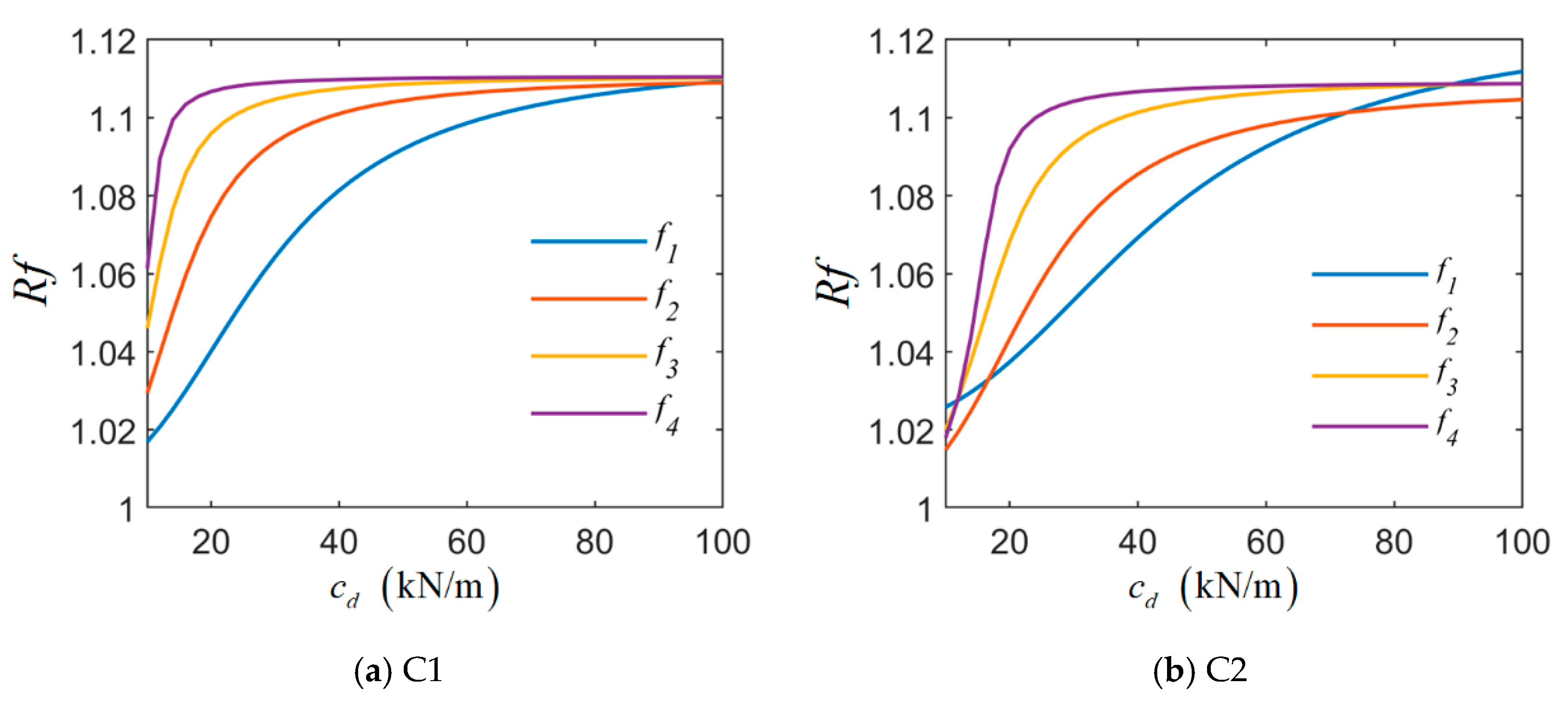
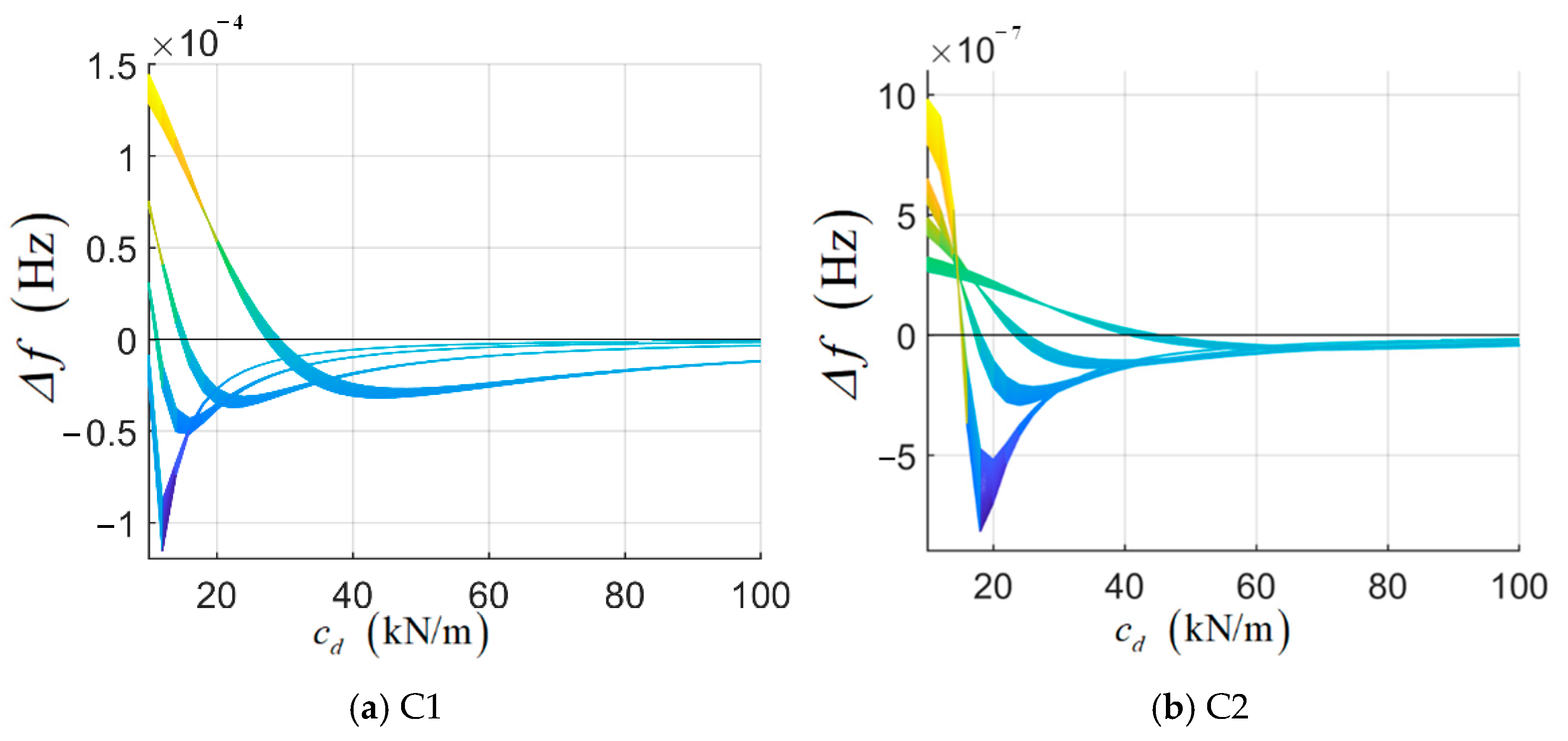
5.1. Influence of Damper Stiffness and Damping Coefficient on Cable Frequency
5.2. Influence of Damper Installation Height on Cable Frequency
6. Discussion
- (1)
- The damping coefficient and installation height of the damper significantly influence the dynamic behavior of the cable, whereas the damper stiffness has a relatively minor effect. The analysis indicates that variations in the damping coefficient and installation height can lead to frequency changes exceeding 10%, with the impact increasing at higher vibration modes. The impact of damper stiffness on frequency is less than 1%; the impact on long cable is greater than that of short cable, and the impact on the first order frequency is higher than the impact on other order frequencies.
- (2)
- As the damping coefficient and installation height of the damper increase, the frequency of each mode of the cable also rises. For different order frequencies, there is an optimal damping coefficient. When the optimal damping coefficient is reached, increasing the damping coefficient has little effect on increasing the cable stiffness. As the order increases, the optimal damping coefficient decreases. When the damper is installed within 0.1 L, the damper’s contribution to the stiffness of the system increases exponentially.
- (3)
- The influence of the damper stiffness on the dynamic characteristics of the cable is affected by the damping coefficient of the damper, and there is a critical damping coefficient. As the cable order increases, the critical damping coefficient decreases. When the damping coefficient is less than the critical coefficient, increasing the damper stiffness will increase the stiffness of the system. When the damping coefficient exceeds the critical damping value, increasing the damper stiffness reduces the overall stiffness of the cable system. However, once the damping coefficient is sufficiently large, the effect of damper stiffness on the dynamic characteristics of the cable becomes negligible, and its influence on the system frequency stabilizes.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Larsen, A.; Larose, G.L. Dynamic Wind Effects on Suspension and Cable-Stayed Bridges. J. Sound Vib. 2015, 334, 2–28. [Google Scholar] [CrossRef]
- Fujino, Y.; Siringoringo, D. Vibration Mechanisms and Controls of Long-Span Bridges: A Review. Struct. Eng. Int. 2013, 23, 248–268. [Google Scholar] [CrossRef]
- Sun, P.; Wang, S.; Wang, D. The Numerical Calculation Method Based on Equivalent Frequency-Independent Time-Domain Damping Model. J. Low Freq. Noise Vib. Act. Control 2022, 41, 1339–1353. [Google Scholar] [CrossRef]
- Wang, S.; He, J.; Fan, J.; Sun, P.; Wang, D. A Time-Domain Method for Free Vibration Responses of an Equivalent Viscous Damped System Based on a Complex Damping Model. Vib. Act. Control. 2023, 42, 1531–1540. [Google Scholar] [CrossRef]
- Fournier, J.A.; Cheng, S. Impact of Damper Stiffness and Damper Support Stiffness on the Efficiency of a Linear Viscous Damper in Controlling Stay Cable Vibrations. J. Bridge Eng. 2014, 19, 04013022. [Google Scholar] [CrossRef]
- Pacheco, B.M.; Fujino, Y.; Sulekh, A. Estimation Curve for Modal Damping in Stay Cables with Viscous Damper. J. Struct. Eng. 1993, 119, 1961–1979. [Google Scholar] [CrossRef]
- Krenk, S. Vibrations of a Taut Cable with an External Damper. J. Appl. Mech. 2000, 67, 772–776. [Google Scholar] [CrossRef]
- Lu, Q.; Sun, Z.; Zhang, W. Nonlinear Parametric Vibration with Different Orders of Small Parameters for Stayed Cables. Eng. Struct. 2020, 224, 111198. [Google Scholar] [CrossRef]
- Krenk, S.; Nielsen, S.R.K. Vibrations of a Shallow Cable with a Viscous Damper. Proc. R. Soc. London. Ser. A Math. Phys. Eng. Sci. 2001, 458, 339–357. [Google Scholar] [CrossRef]
- Main, J.A.; Jones, N.P. Vibration of Tensioned Beams with Intermediate Damper. II: Damper near a Support. J. Eng. Mech. 2007, 133, 379–388. [Google Scholar] [CrossRef]
- Sun, L.; Xu, Y.; Chen, L. Damping Effects of Nonlinear Dampers on a Shallow Cable. Eng. Struct. 2019, 196, 109305. [Google Scholar] [CrossRef]
- Mehrabi, A.B.; Tabatabai, H. Unified Finite Difference Formulation for Free Vibration of Cables. J. Struct. Eng. 1998, 124, 1313–1322. [Google Scholar] [CrossRef]
- Fujino, Y.; Hoang, N. Design Formulas for Damping of a Stay Cable with a Damper. J. Struct. Eng. 2008, 134, 269–278. [Google Scholar] [CrossRef]
- Javanbakht, M.; Cheng, S.; Ghrib, F. Control-Oriented Model for the Dynamic Response of a Damped Cable. J. Sound Vib. 2019, 442, 249–267. [Google Scholar] [CrossRef]
- Zhou, Q.; Nielsen, S.R.K.; Qu, W. Stochastic Response of an Inclined Shallow Cable with Linear Viscous Dampers under Stochastic Excitation. J. Eng. Mech. 2010, 136, 1411–1421. [Google Scholar] [CrossRef]
- Sun, Q.; Zhang, N.; Liu, X. A Dynamic Stiffness Matrix Method for Free Vibrations of Partial-Interaction Composite Beams Based on the Timoshenko Beam Theory. J. Sound Vib. 2022, 520, 116579. [Google Scholar] [CrossRef]
- Banerjee, J.R.; Ananthapuvirajah, A. Free Vibration of Functionally Graded Beams and Frameworks Using the Dynamic Stiffness Method. J. Sound Vib. 2018, 422, 34–47. [Google Scholar] [CrossRef]
- Li, X.; Cheng, Z.; Wang, Z.; Fan, B. Free Vibration of a Taut Cable with a Parallel-Connected Viscous Mass Damper and a Grounded Cross-Tie. J. Low Freq. Noise Vib. Act. Control 2022, 41, 982–995. [Google Scholar] [CrossRef]
- Xu, B.; Dan, D.; Zhao, Y. Frequency-Domain Estimation Method for Vibration-Induced Additional Cable Tension Based on Acceleration Monitoring. J. Vib. Acoust. Trans. ASME 2019, 141, 064502. [Google Scholar] [CrossRef]
- Dan, D.-H.; Xu, B.; Chen, Z.-H. Universal Characteristic Frequency Equation for Cable Transverse Component System and Its Universal Numerical Solution. J. Eng. Mech. 2016, 142, 04015105. [Google Scholar] [CrossRef]
- Furukawa, A.; Suzuki, S.; Kobayashi, R. Tension Estimation Method for Cable with Damper Using Natural Frequencies with Uncertain Modal Order. Front. Built Environ. 2022, 8, 812999. [Google Scholar] [CrossRef]
- Tabatabai, H.; Mehrabi, A.B. Design of Mechanical Viscous Dampers for Stay Cables. J. Bridge Eng. 2000, 5, 114–123. [Google Scholar] [CrossRef]




| Cable | (°) | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| C1 | 30 | 45 | 0.160 | 60 | 2.5 | 1500 | 0.1 | 10 | 20 |
| C2 | 80 | 65 | 0.250 | 36 | 3.5 | 2500 | 0.1 | 10 | 20 |
| Cases | ||||||||
|---|---|---|---|---|---|---|---|---|
| 1 | 377.92 | 61.8 | 4.26 | 3.219 | 0.0286 | 0.15 | 29.3 | 17.9 |
| 2 | 376.75 | 61.8 | 4.26 | 3.219 | 0.0286 | 0.15 | 57.1 | 31.4 |
| 3 | 377.75 | 61.8 | 4.26 | 3.219 | 0.0286 | 0.15 | 84.7 | 52.5 |
| Cases | Order | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|---|
| 1 | Measured value | 2.93 | 5.67 | 8.64 | 11.57 | - | 14.80 | 17.32 | 20.03 |
| This paper | 2.83 | 5.68 | 8.53 | 11.37 | - | 14.23 | 17.03 | 19.91 | |
| Literature | 2.55 | 5.06 | 7.49 | 9.84 | - | 14.48 | 16.88 | 19.33 | |
| Error1 (%) | −3.4% | 0.2% | −1.3% | −1.7% | - | −3.9% | −1.7% | −0.6% | |
| Error2 (%) | −13.0% | −10.8% | −13.3% | −15.0% | - | −2.2% | −2.5% | −3.5% | |
| 2 | Measured value | 2.86 | 5.75 | 8.64 | 11.53 | - | 14.51 | 17.33 | 20.21 |
| This paper | 2.83 | 5.67 | 8.51 | 11.36 | - | 14.21 | 17.03 | 19.88 | |
| Literature | 2.62 | 5.21 | 7.71 | 10.04 | - | 14.47 | 16.86 | 19.33 | |
| Error1 (%) | −0.9% | −1.3% | −1.5% | −1.5% | - | −2.0% | −1.7% | −1.6% | |
| Error2 (%) | −8.4% | −9.4% | −10.8% | −12.9% | - | −0.3% | −2.7% | −4.4% | |
| 3 | Measured value | 2.86 | 5.75 | 8.64 | 11.56 | - | 14.48 | 17.36 | 20.25 |
| This paper | 2.84 | 5.68 | 8.53 | 11.37 | - | 14.22 | 17.06 | 19.91 | |
| Literature | 2.67 | 5.31 | 7.87 | 10.23 | - | 14.50 | 16.88 | 19.38 | |
| Error1 (%) | −0.7% | −1.2% | −1.3% | −1.6% | - | −1.8% | −1.7% | −1.7% | |
| Error2 (%) | −6.6% | −7.7% | −8.9% | −11.5% | - | 0.1% | −2.8% | −4.3% |
| Cable | θ(°) | |||||||
|---|---|---|---|---|---|---|---|---|
| A1 | 55.2 | 52.6 | 0.160 | 69.746 | 2509 | 2348 | 0.065 | 200 |
| A7 | 108.6 | 67.5 | 0.160 | 36.778 | 2007 | 3211 | 0.048 | 1000 |
| A13 | 147.4 | 113.3 | 0.224 | 32.375 | 4627 | 6694 | 0.038 | 2300 |
| Cable | Order | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|---|
| A1 | Measured | 2.170 | 4.294 | 6.348 | 8.759 | 11.044 | 13.471 | 16.269 | 18.884 |
| This paper | 2.167 | 4.256 | 6.458 | 8.725 | 11.090 | 13.568 | 16.178 | 18.937 | |
| Error (%) | −0.1 | −0.9 | 1.7 | −0.4 | 0.4 | 0.7 | −0.6 | 0.3 | |
| A7 | Measured | 1.085 | 2.173 | 3.247 | 4.312 | 5.377 | 6.519 | 7.562 | 8.633 |
| This paper | 1.081 | 2.137 | 3.211 | 4.289 | 5.375 | 6.470 | 7.576 | 8.695 | |
| Error (%) | −0.3 | −1.7 | −1.1 | −0.5 | 0.0 | −0.7 | 0.2 | 0.7 | |
| A13 | Measured | 0.879 | 1.746 | 2.621 | 3.503 | 4.364 | 5.237 | 6.125 | 6.958 |
| This paper | 0.879 | 1.730 | 2.598 | 3.467 | 4.341 | 5.219 | 6.102 | 6.991 | |
| Error (%) | 0.0 | −0.9 | −0.9 | −1.0 | −0.5 | −0.3 | −0.4 | 0.5 |
| Cable | Order 1 | Order 2 | Order 3 | Order 4 |
|---|---|---|---|---|
| C1 | 3.396 | 6.783 | 10.175 | 13.568 |
| Rf | 1.111 | 1.111 | 1.112 | 1.112 |
| C2 | 1.402 | 2.732 | 4.095 | 5.461 |
| Rf | 1.111 | 1.111 | 1.111 | 1.111 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiao, H.; Xu, B.; Jiang, Z.; Cui, C.; Yang, H. Accurate Dynamic Analysis Method of Cable-Damper System Based on Dynamic Stiffness Method. Buildings 2024, 14, 4007. https://doi.org/10.3390/buildings14124007
Jiao H, Xu B, Jiang Z, Cui C, Yang H. Accurate Dynamic Analysis Method of Cable-Damper System Based on Dynamic Stiffness Method. Buildings. 2024; 14(12):4007. https://doi.org/10.3390/buildings14124007
Chicago/Turabian StyleJiao, Hui, Bin Xu, Zhengkai Jiang, Can Cui, and Haoxiang Yang. 2024. "Accurate Dynamic Analysis Method of Cable-Damper System Based on Dynamic Stiffness Method" Buildings 14, no. 12: 4007. https://doi.org/10.3390/buildings14124007
APA StyleJiao, H., Xu, B., Jiang, Z., Cui, C., & Yang, H. (2024). Accurate Dynamic Analysis Method of Cable-Damper System Based on Dynamic Stiffness Method. Buildings, 14(12), 4007. https://doi.org/10.3390/buildings14124007









