Axial Compressive Behavior of Outer Square Inner Circular Spontaneous Combustion Coal Gangue Concrete-Filled Double-Skin Steel Tubular Stub Column
Abstract
:1. Introduction
2. Establishment of Finite Element Model
2.1. Constitutive Model of Materials
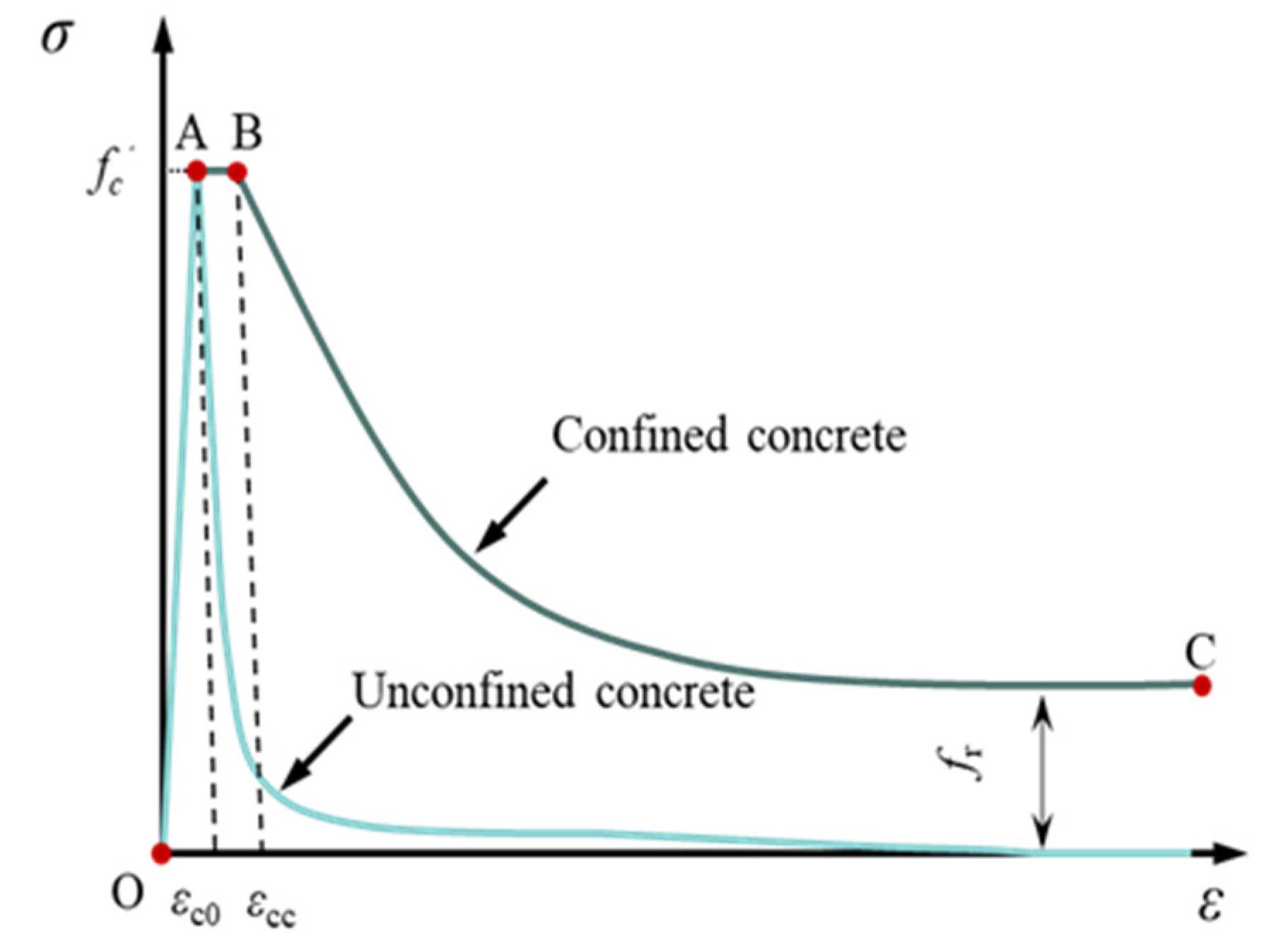
2.1.1. Constitutive Model of Concrete
2.1.2. Constitutive Model of Steel Tube

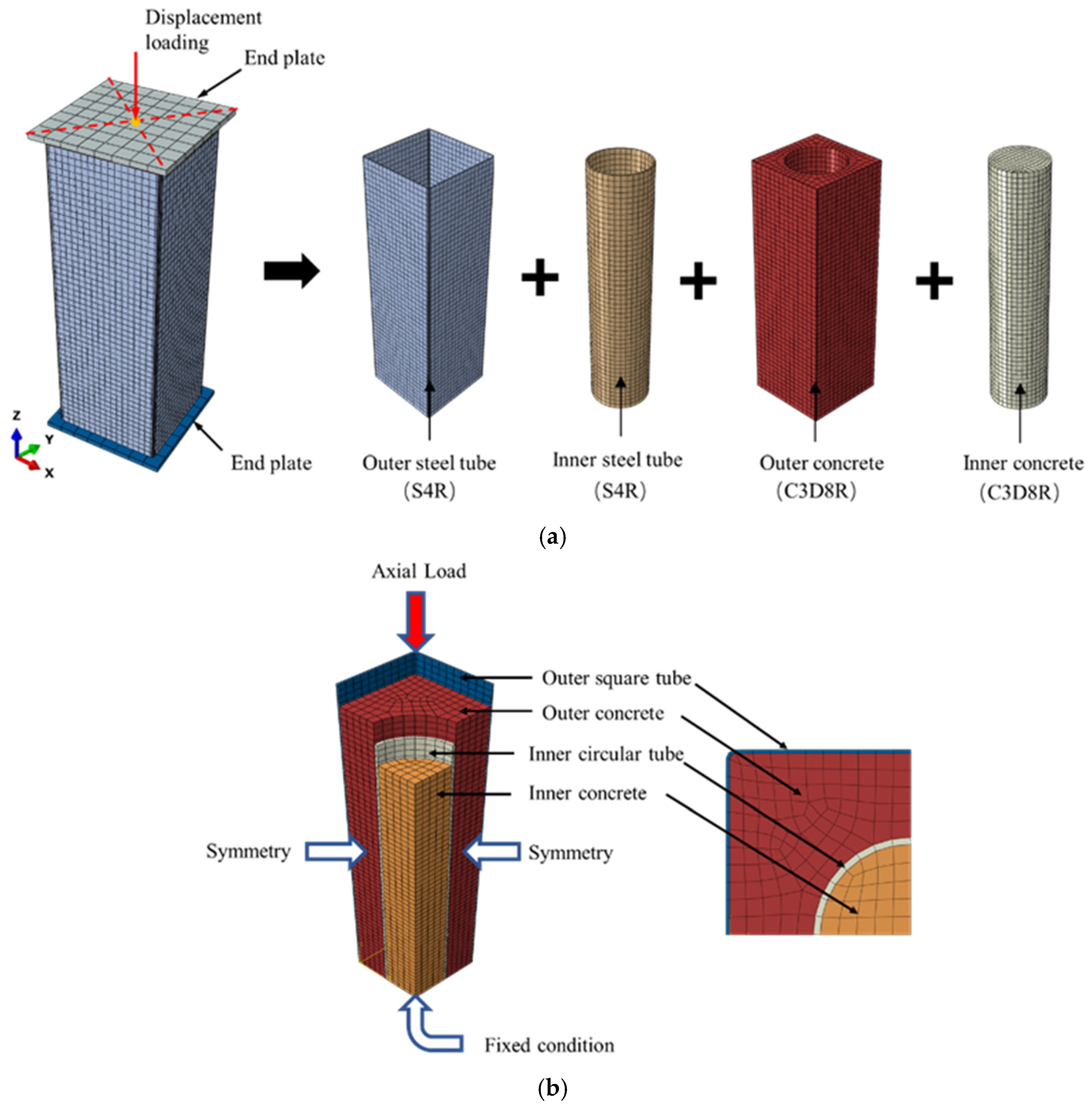
2.2. Element Type, Meshing, and Boundary Conditions
2.3. Definition of Interaction
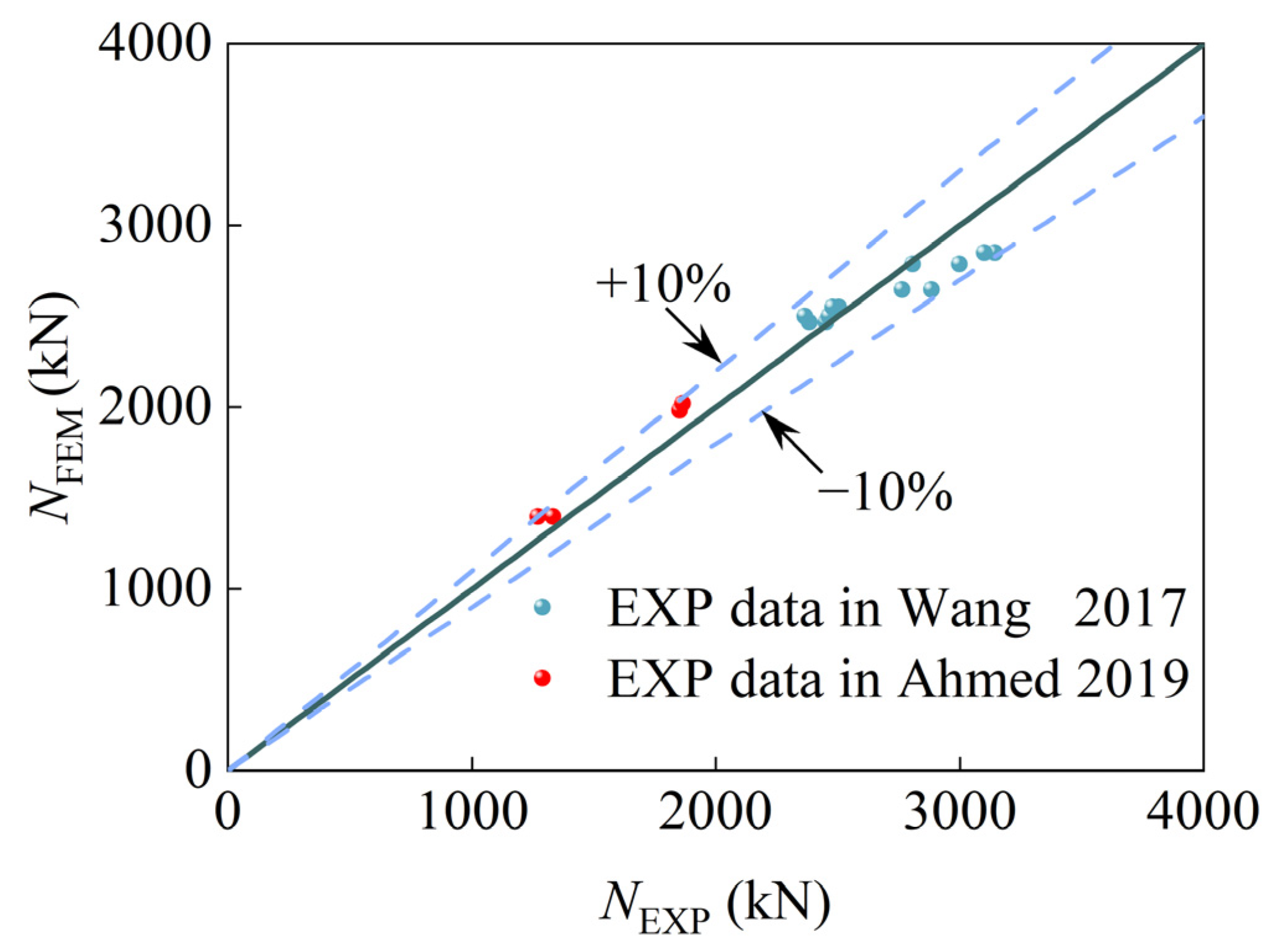
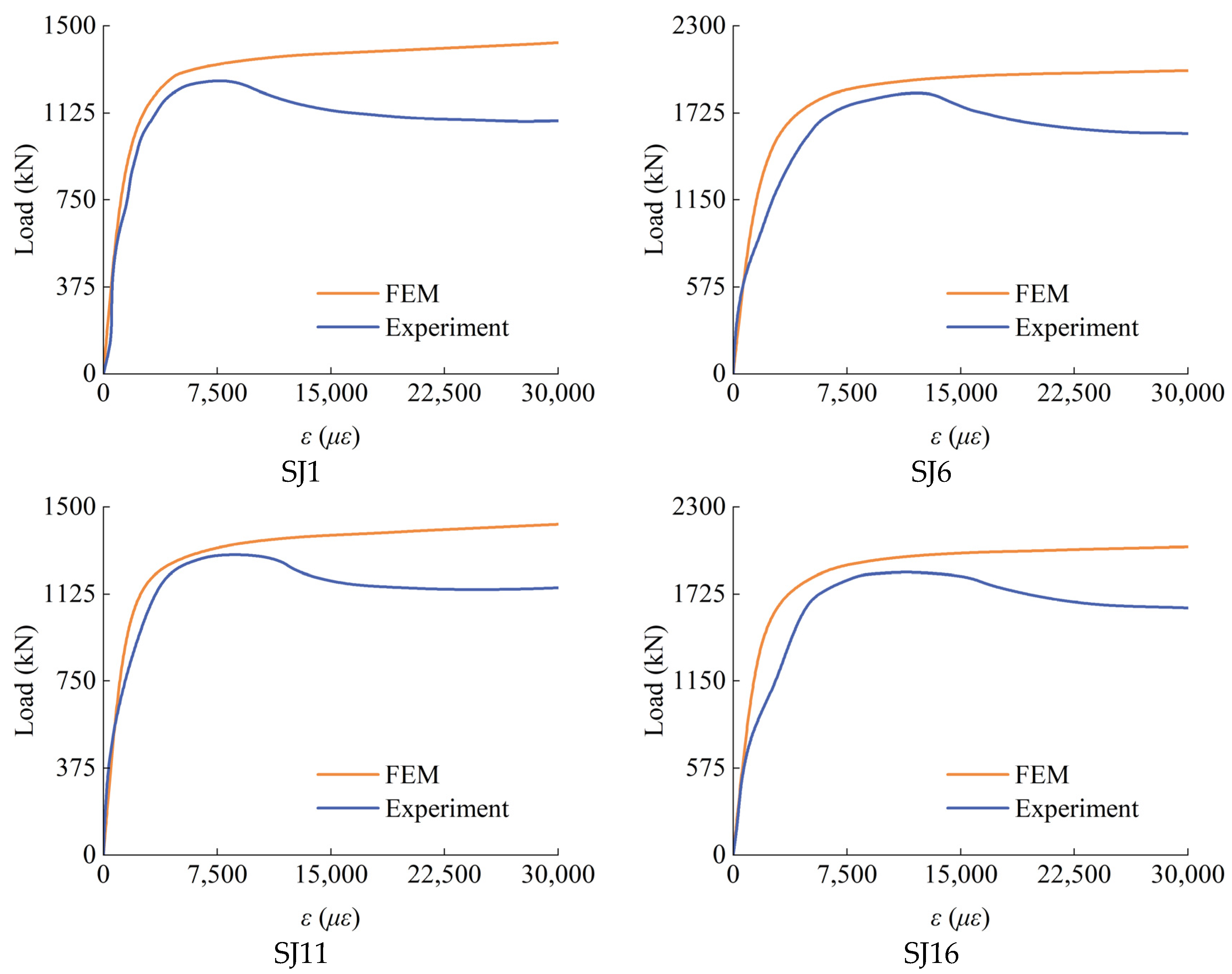
2.4. Validation of Finite Element Model
3. Analysis of Axial Compression Behavior Mechanism of SCGCA-CFST Stub Column
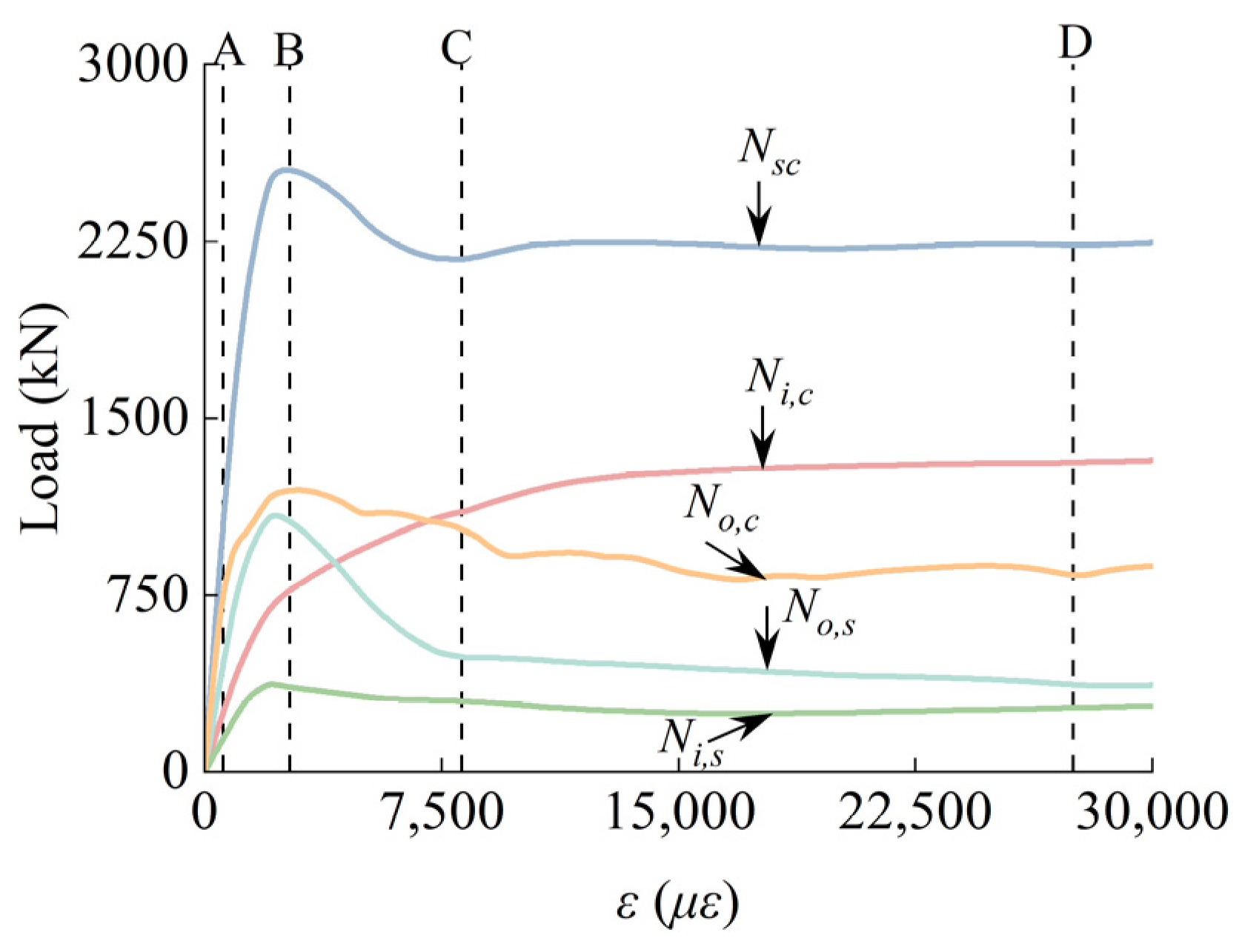
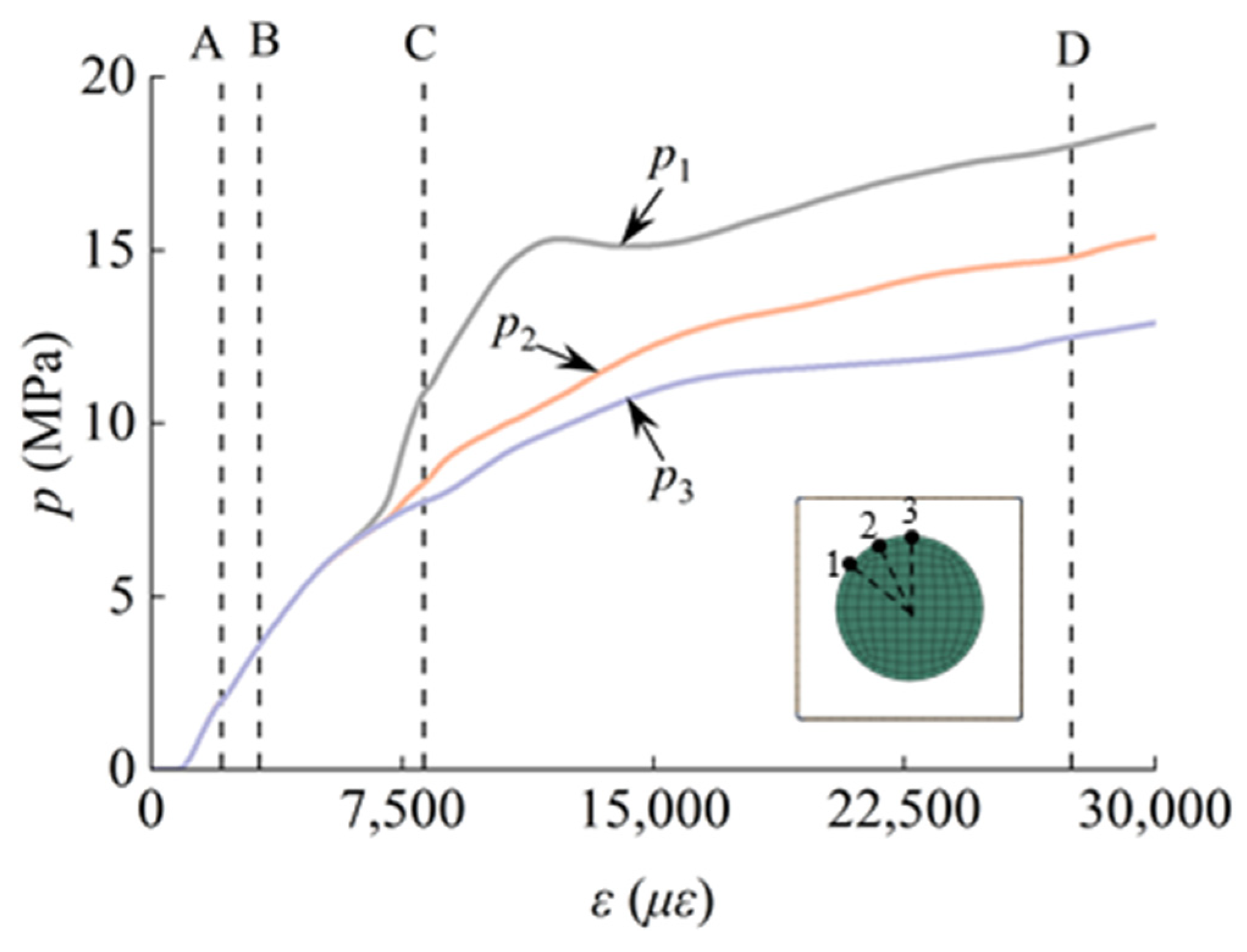
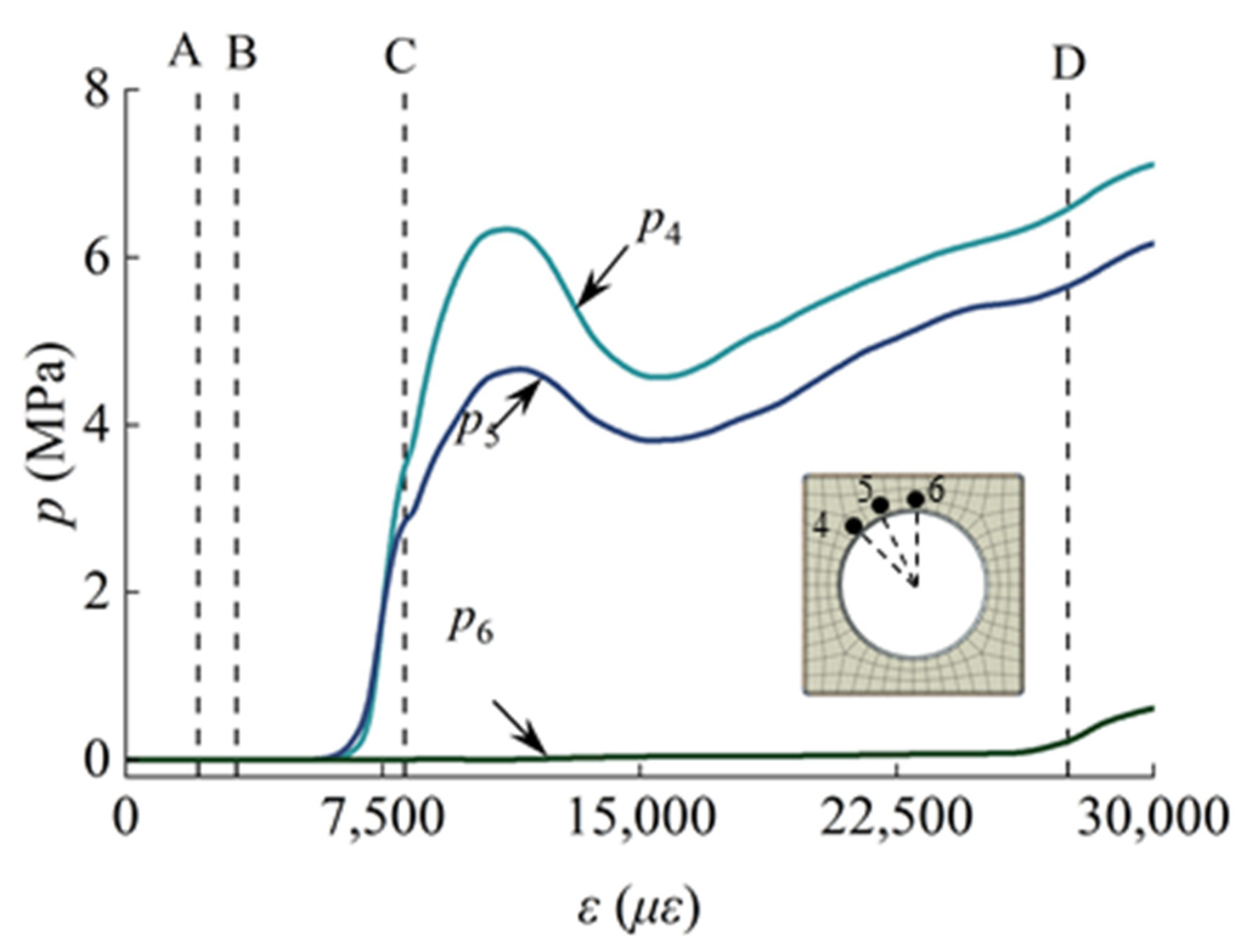
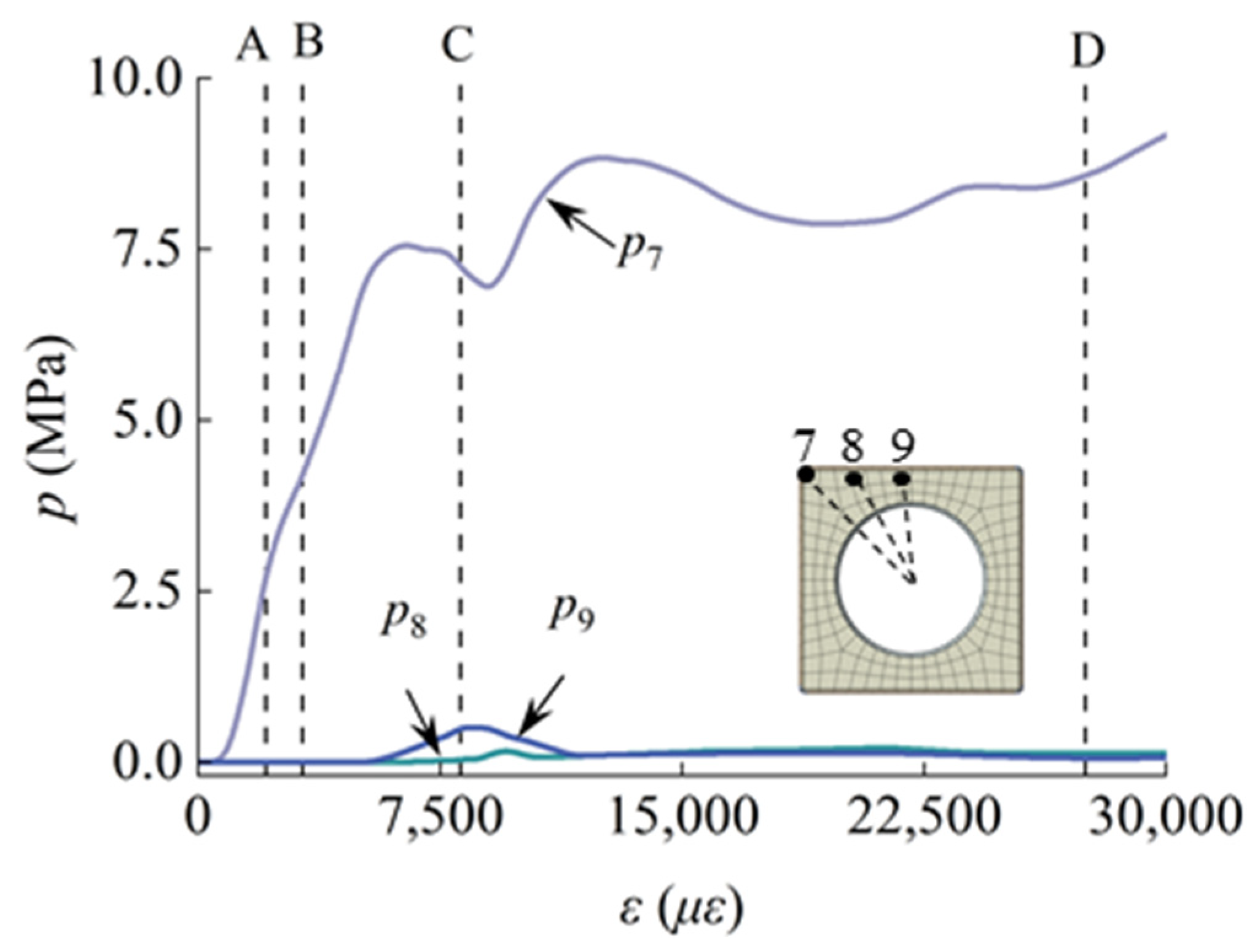
3.1. Relationship Between Load and Strain of Each Part of the Structure During Axial Loading Process
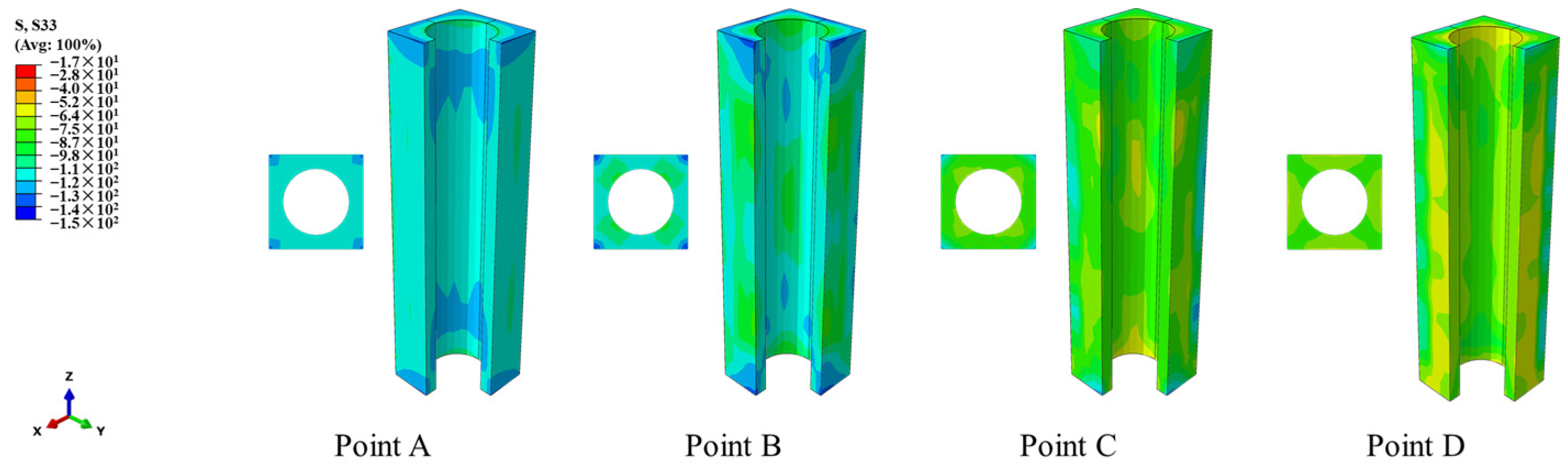
3.2. The Pattern of Longitudinal Stress Distribution Within the Concrete During the Loading Process
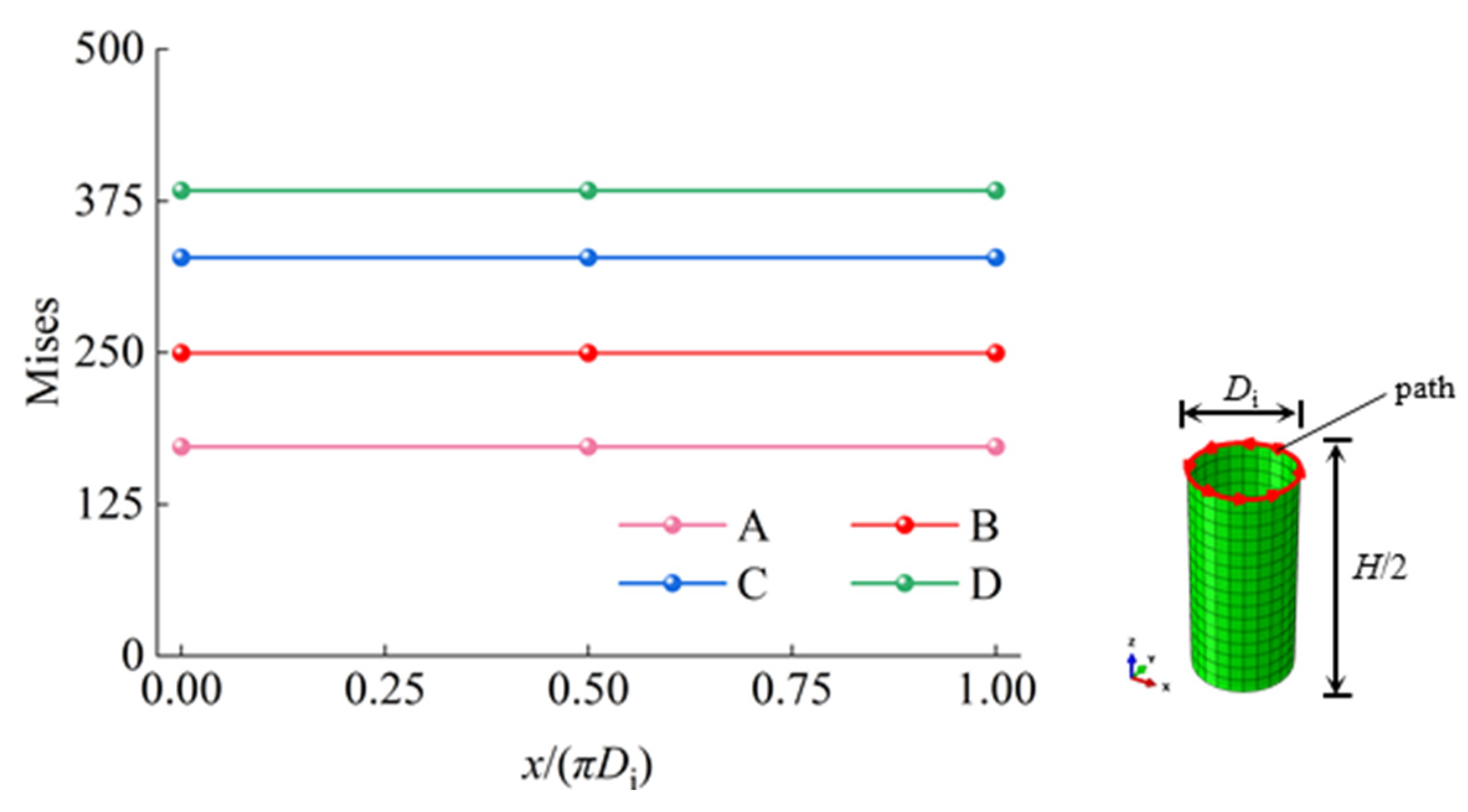
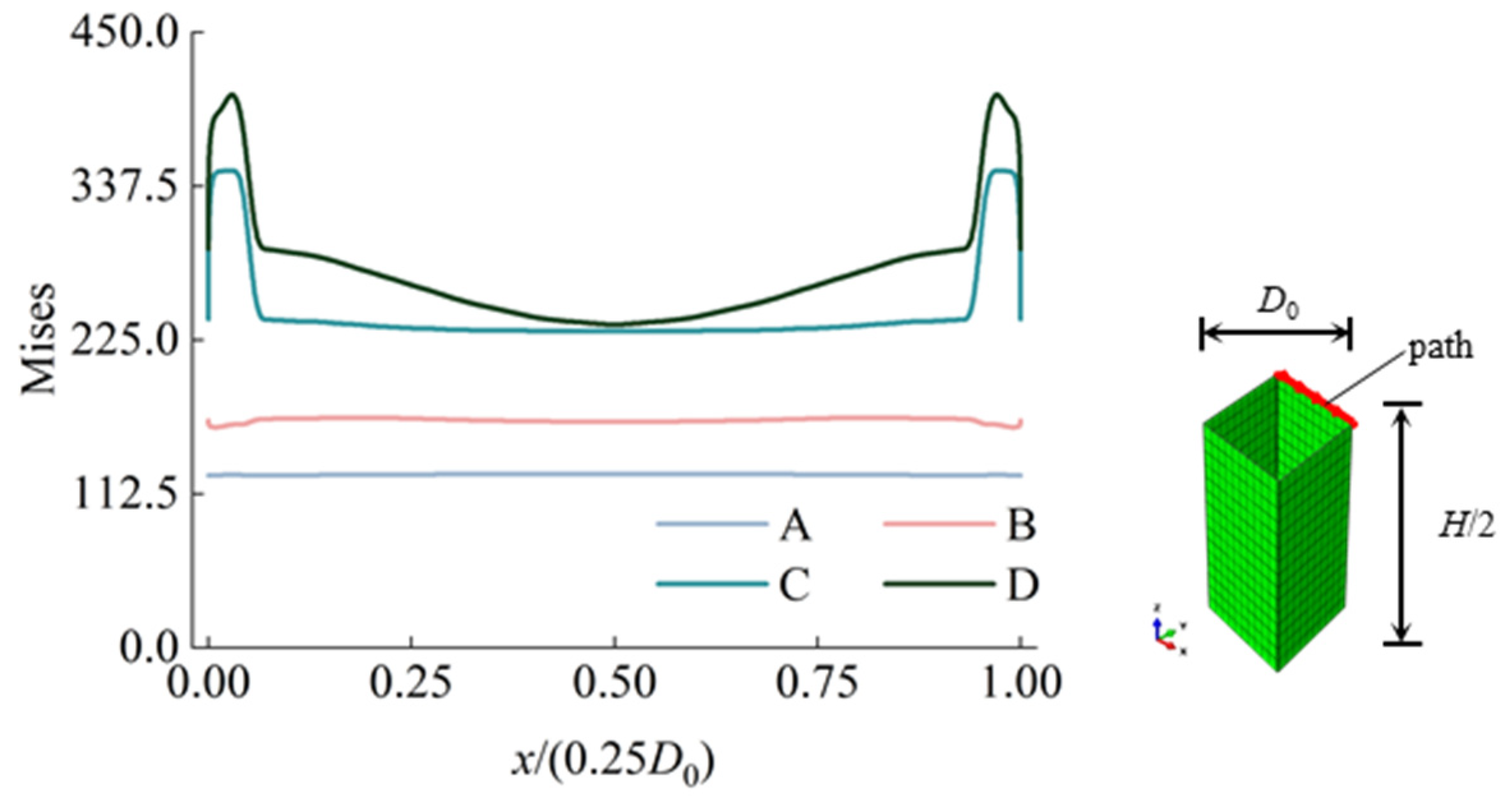
3.3. Mises Stress Distribution of Steel Tube
3.4. Interaction Between Concrete and Steel Tube During Loading Process
4. Prediction of Ultimate Bearing Capacity of SCGCA-CFDST Stub Column
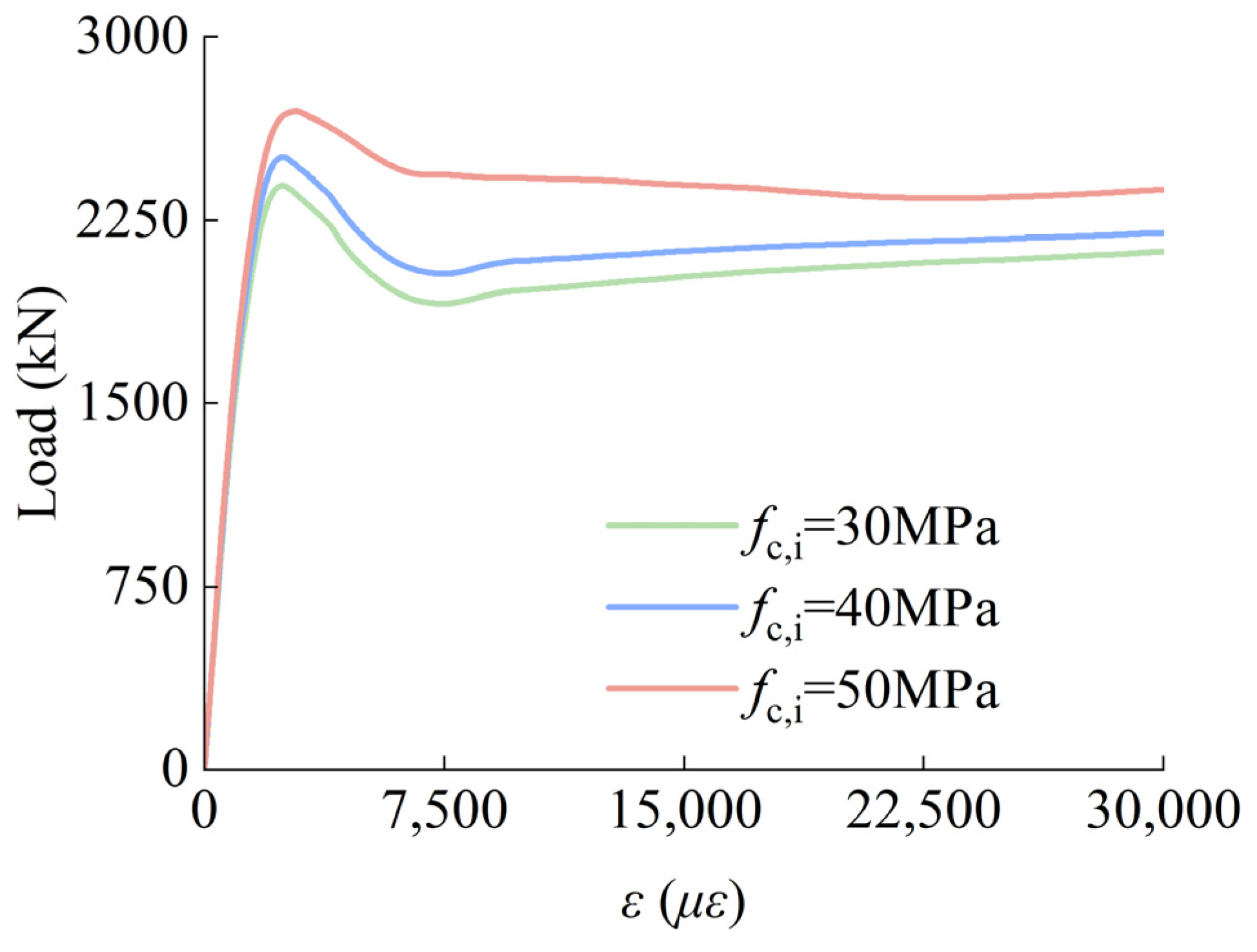
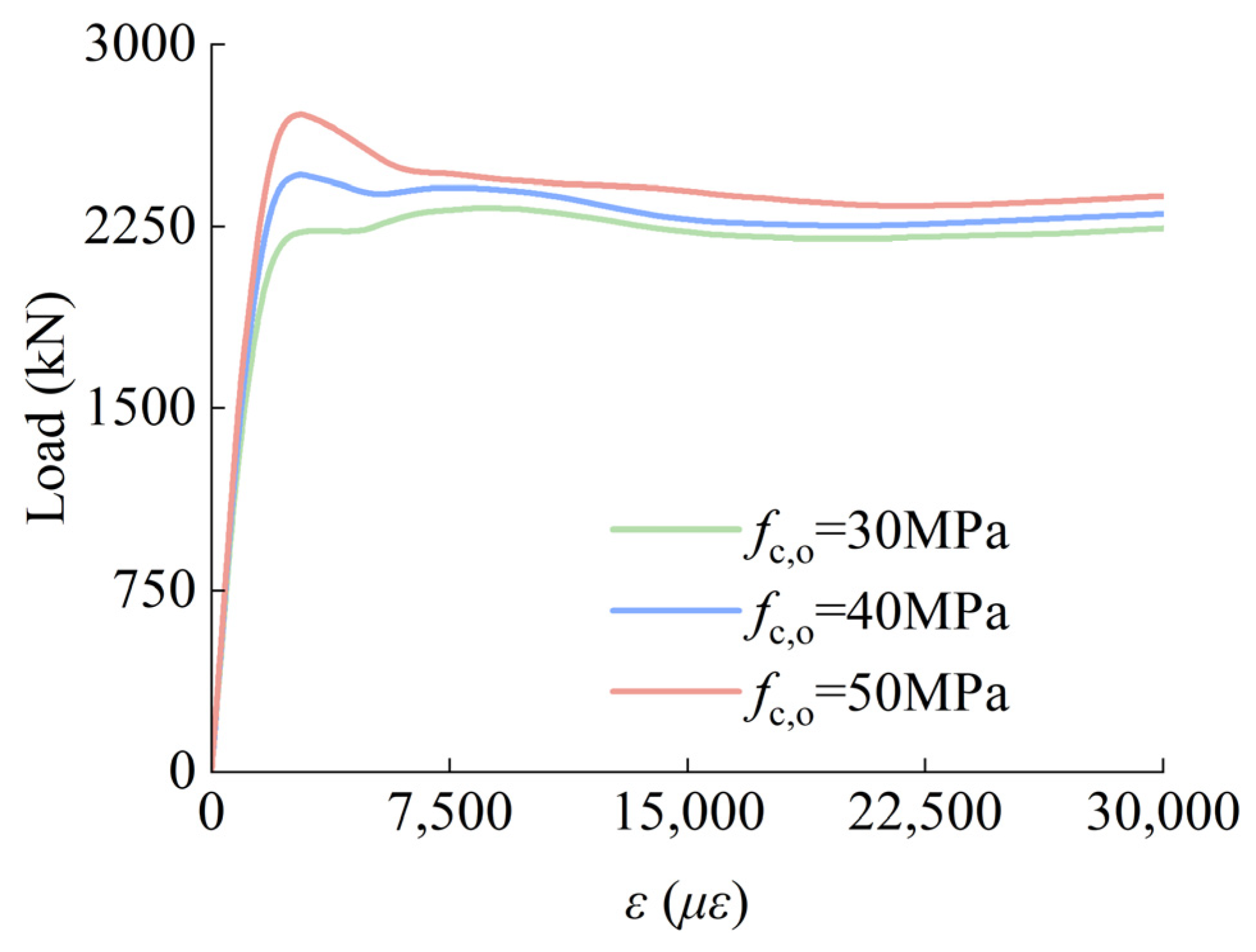
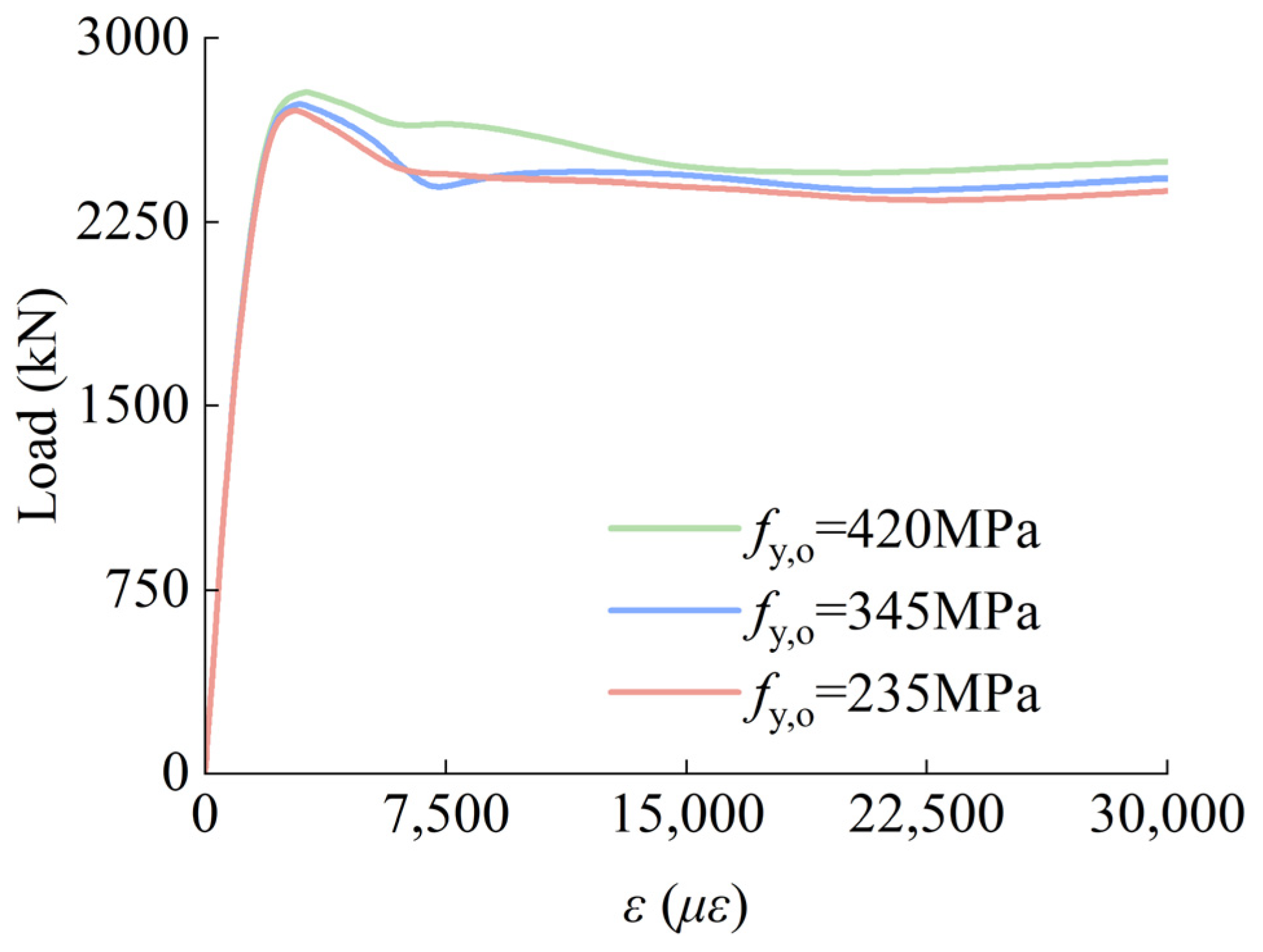
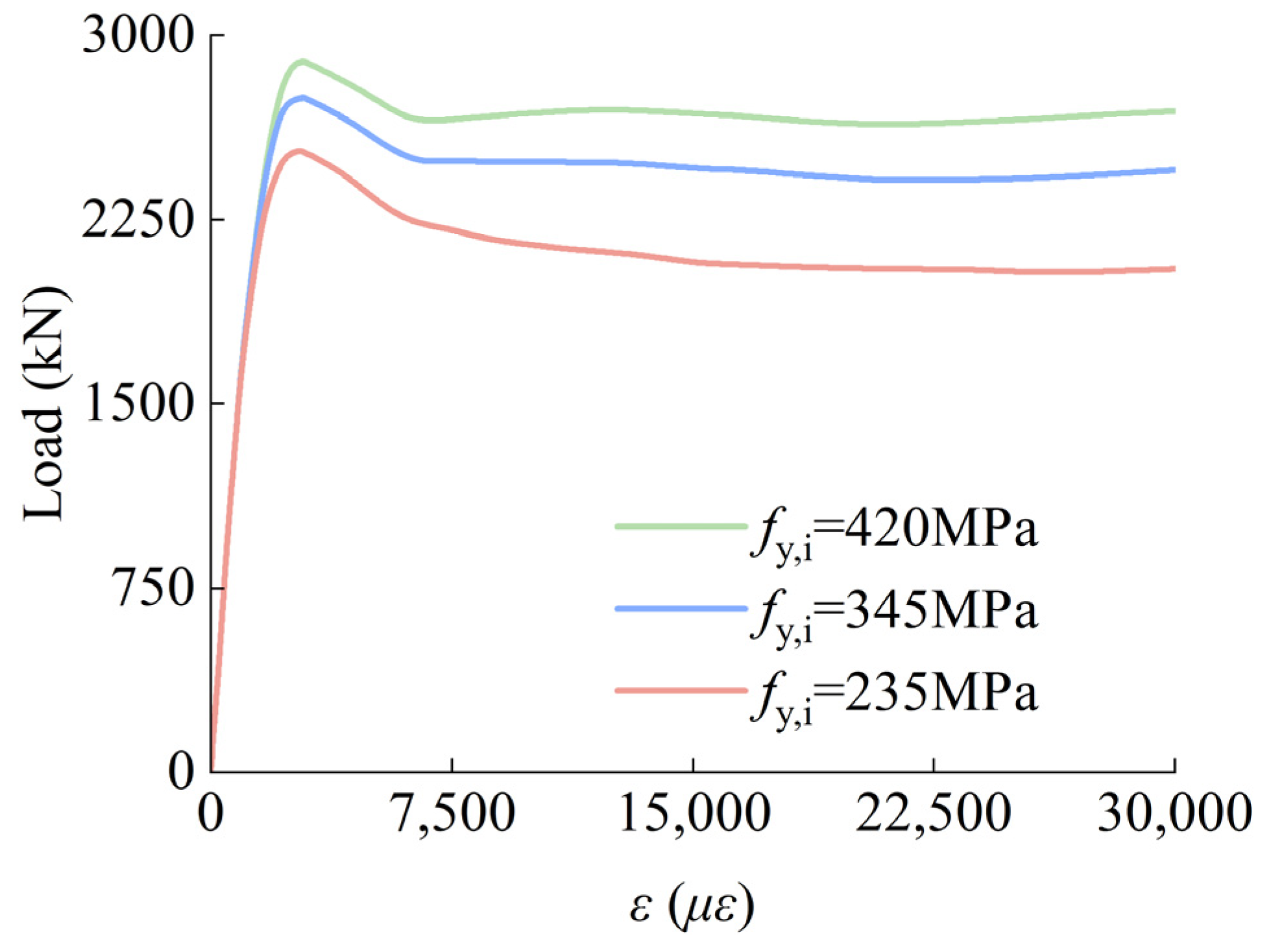
4.1. Parametric Analysis
4.2. Prediction of Ultimate Bearing Capacity
5. Conclusions
- (1)
- Utilizing the constitutive relationship of core concrete made with coarse aggregate derived from spontaneously combusted coal gangue, a finite element analysis model for SCGCA-CFDST stub columns was created. The model was validated against the existing literature, achieving an average absolute error of 2.21%. The average value (μ) and standard deviation (SD) of NFEM/NEXP were 0.99 and 0.061, individually. The outcomes demonstrate the precision of the finite element model presented in this research for predicting the mechanical performance of SCGCA-CFDST stub columns.
- (2)
- Analysis of the typical SCGCA-CFDST stub column’s loading process found that both the outer and inner steel tubes reach the yield state nearly simultaneously. The core SCGCAC’s interaction is significantly higher than that of the sandwiched concrete due to dual-layer confinement from the steel tubes. The outer steel tube enhances the sandwiched concrete’s strength by 3.56 times, less than the 5.41-times increase for the core SCGCAC by the inner steel tube. This suggests that SCGCAC in the core of CFDST offers superior confinement, benefiting engineering applications.
- (3)
- Parametric analysis identified fc,i, fc,o, fy,i, B/to, and D/ti as key factors affecting the SCGCA-CFDST stub column’s load-bearing capacity, with fy,o and D/B having a minor impact. The inner tube’s thickness most significantly influences the load-bearing capacity, increasing it by 42.72%. Finite element analysis validated a formula for calculating the ultimate load-bearing capacity, proving its suitability for predicting SCGCA-CFDST stub columns’ strength.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Aco | Cross-sectional areas for the sandwiched concrete |
| Aci | Cross-Sectional Areas For The Core Coal SCG-CAC |
| Aso | Cross-Sectional Areas For The Outer Steel Tubes |
| Asi | Cross-Sectional Areas For The Outer Inner Tubes |
| Do | All Indicate The Side Length Of The Outer Steel Pipe |
| Di | All Indicate The Side Length Of The Inner Steel Pipe |
| Et | Modulus Of Elasticity Of Steel |
| Ec | Modulus Of Elasticity Of Concrete |
| Compressive Strength Of Concrete Cylinders | |
| Strain | |
| εc0 | Peak Strain Of Unconfined Concrete |
| εcc | Peak Strain Of Confined Concrete |
| Stress | |
| fB | The Confining Pressure Value At Point B |
| fr | Residual Stress |
| fyi | Inner Steel Pipe Yield Strength |
| fyo | Yield Strength Of Outer Steel Pipes |
| ftu | The ultimate tensile strength of the steel tube |
| ti | Inner Steel Pipe Wall Thickness |
| to | The Wall Thickness Of The Outer Steel Pipe |
| Peak Load From The Test | |
| Peak Loads Derived From Finite Element Model | |
| Ac,nominal | Cross-sectional area enclosed by the external steel tube |
| ξo | Constraint Factor |
References
- Jabłońska, B.; Kityk, A.V.; Busch, M.; Huber, P. The Structural and Surface Properties of Natural and Modified Coal Gangue. J. Environ. Manag. 2017, 190, 80–90. [Google Scholar] [CrossRef]
- Li, J.; Wang, J. Comprehensive Utilization and Environmental Risks of Coal Gangue: A Review. J. Clean. Prod. 2019, 239, 117946. [Google Scholar] [CrossRef]
- Cheng, Y.; Hongqiang, M.; Hongyu, C.; Jiaxin, W.; Jing, S.; Zonghui, L.; Mingkai, Y. Preparation and Characterization of Coal Gangue Geopolymers. Constr. Build. Mater. 2018, 187, 318–326. [Google Scholar] [CrossRef]
- Wang, G.; Wei, Y.; Miao, K.; Zheng, K.; Dong, F. Axial Compressive Behavior of Seawater Sea-Sand Coral Aggregate Concrete-Filled Circular FRP-Steel Composite Tube Columns. Constr. Build. Mater. 2022, 315, 125737. [Google Scholar] [CrossRef]
- Zhou, M.; Dou, Y.; Zhang, Y.; Zhang, Y.; Zhang, B. Effects of the Variety and Content of Coal Gangue Coarse Aggregate on the Mechanical Properties of Concrete. Constr. Build. Mater. 2019, 220, 386–395. [Google Scholar] [CrossRef]
- Wang, Q.; Li, Z.; Zhang, Y.; Zhang, H.; Zhou, M.; Fang, Y. Influence of Coarse Coal Gangue Aggregates on Elastic Modulus and Drying Shrinkage Behaviour of Concrete. J. Build. Eng. 2020, 32, 101748. [Google Scholar] [CrossRef]
- Gao, S.; Zhao, G.; Guo, L.; Zhou, L.; Yuan, K. Utilization of Coal Gangue as Coarse Aggregates in Structural Concrete. Constr. Build. Mater. 2021, 268, 121212. [Google Scholar] [CrossRef]
- Qiu, J.; Zhu, M.; Zhou, Y.; Guan, X. Effect and Mechanism of Coal Gangue Concrete Modification by Fly Ash. Constr. Build. Mater. 2021, 294, 123563. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, Q.; Zhou, M.; Fang, Y.; Zhang, Z. Mechanical Properties of Concrete with Coarse Spontaneous Combustion Gangue Aggregate (SCGA): Experimental Investigation and Prediction Methodology. Constr. Build. Mater. 2020, 255, 119337. [Google Scholar] [CrossRef]
- Zhang, T.; Zhu, Q.; Liu, H.; Gao, S. Utilization of Coal Gangue Sand in Structural Concrete as Fine Aggregate towards Sustainable Production. Constr. Build. Mater. 2024, 417, 135264. [Google Scholar] [CrossRef]
- Zhang, Y.; Xu, Q.; Wang, Q.; Zhou, M.; Liu, H.; Guo, H. Axial Compressive Behavior of Circular Concrete-Filled Steel Tube Stub Columns Prepared with Spontaneous-Combustion Coal Gangue Aggregate. J. Build. Eng. 2022, 48, 103987. [Google Scholar] [CrossRef]
- Zhang, N.; Zhao, Z.; Zheng, C. Compression Behavior of GFRP–Coal Gangue Concrete–Steel Tubular Columns. Int. J. Press. Vessels Pip. 2022, 197, 104650. [Google Scholar] [CrossRef]
- Xu, Q.; Zhang, Y.; Liu, H.; Zhou, M.; Wang, Q.; Lin, H. Effect of Spontaneous-Combustion Coal Gangue Aggregate on Axial Performance of Square Concrete-Filled Steel Tube Stub Columns. Structures 2022, 44, 216–235. [Google Scholar] [CrossRef]
- Wang, J.; Chen, J.; Liu, M. Theoretical Model for Spontaneous Combustion Gangue Coarse Aggregate Concrete Filled Steel Tube Stub Columns. J. Constr. Steel Res. 2024, 213, 108353. [Google Scholar] [CrossRef]
- Ci, J.; Ahmed, M.; Tran, V.-L.; Jia, H.; Chen, S. Axial Compressive Behavior of Circular Concrete-Filled Double Steel Tubular Short Columns. Adv. Struct. Eng. 2022, 25, 259–276. [Google Scholar] [CrossRef]
- Hassanein, M.F.; Silvestre, N.; Yan, X.-F. Confinement-Based Direct Design of Circular Concrete-Filled Double-Skin Normal and High Strength Steel Short Columns. Thin-Walled Struct. 2023, 183, 110446. [Google Scholar] [CrossRef]
- Ahmed, M.; Gohari, S.; Sennah, K.; Chen, W.; Liang, Q.Q. Computational Simulation of Nonlinear Inelastic Behavior of Circular Concrete-Filled Stainless-Steel Tubular Short Columns Incorporating Confinement Effects. Eng. Struct. 2023, 274, 115183. [Google Scholar] [CrossRef]
- Yan, X.; Ahmed, M.; Hassanein, M.F.; He, M. Performance Analysis and Design of Circular High-strength Concrete-filled Double-skin Aluminum Tubular Short Columns under Axial Loading. Struct. Concr. 2023, 24, 5677–5696. [Google Scholar] [CrossRef]
- Lin, C.; Zhou, J. Unified Compressive Strength Model for Axially Loaded Circular Composite Short Columns. J. Constr. Steel Res. 2023, 203, 107840. [Google Scholar] [CrossRef]
- Wang, Z.-B.; Tao, Z.; Yu, Q. Axial Compressive Behaviour of Concrete-Filled Double-Tube Stub Columns with Stiffeners. Thin-Walled Struct. 2017, 120, 91–104. [Google Scholar] [CrossRef]
- Ahmed, M.; Liang, Q.Q.; Patel, V.I.; Hadi, M.N.S. Experimental and Numerical Studies of Square Concrete-Filled Double Steel Tubular Short Columns under Eccentric Loading. Eng. Struct. 2019, 197, 109419. [Google Scholar] [CrossRef]
- Zheng, Y.; Tao, Z. Compressive Strength and Stiffness of Concrete-Filled Double-Tube Columns. Thin-Walled Struct. 2019, 134, 174–188. [Google Scholar] [CrossRef]
- Ci, J.; Chen, S.; Jia, H.; Yan, W.; Song, T.; Kim, K.-S. Axial Compression Performance Analysis and Bearing Capacity Calculation on Square Concrete-Filled Double-Tube Short Columns. Mar. Struct. 2020, 72, 102775. [Google Scholar] [CrossRef]
- Liang, Q.Q.; Fragomeni, S. Nonlinear Analysis of Circular Concrete-Filled Steel Tubular Short Columns under Axial Loading. J. Constr. Steel Res. 2009, 65, 2186–2196. [Google Scholar] [CrossRef]
- Samani, A.K.; Attard, M.M. A Stress–Strain Model for Uniaxial and Confined Concrete under Compression. Eng. Struct. 2012, 41, 335–349. [Google Scholar] [CrossRef]
- Binici, B. An Analytical Model for Stress–Strain Behavior of Confined Concrete. Eng. Struct. 2005, 27, 1040–1051. [Google Scholar] [CrossRef]
- Han, L.-H.; Li, W.; Bjorhovde, R. Developments and Advanced Applications of Concrete-Filled Steel Tubular (CFST) Structures: Members. J. Constr. Steel Res. 2014, 100, 211–228. [Google Scholar] [CrossRef]
- Han, L.-H.; Yao, G.-H.; Tao, Z. Performance of Concrete-Filled Thin-Walled Steel Tubes under Pure Torsion. Thin-Walled Struct. 2007, 45, 24–36. [Google Scholar] [CrossRef]
- Elchalakani, M.; Zhao, X.-L.; Grzebieta, R. Tests on Concrete Filled Double-Skin (CHS Outer and SHS Inner) Composite Short Columns under Axial Compression. Thin-Walled Struct. 2002, 40, 415–441. [Google Scholar] [CrossRef]
- Abdel-Rahman, N.; Sivakumaran, K.S. Material Properties Models for Analysis of Cold-Formed Steel Members. J. Struct. Eng. 1997, 123, 1135–1143. [Google Scholar] [CrossRef]
- Liang, H.; Li, W.; Huang, Y.; Lu, Y. Axial Behaviour of CFST Stub Columns Strengthened with Steel Tube and Sandwiched Concrete Jackets. Thin-Walled Struct. 2020, 155, 106942. [Google Scholar] [CrossRef]
- Zhu, Y.; Yang, H.; Gardner, L.; Wan, J. Performance of Reinforced Concrete-Filled Steel Tubular (RCFST) Members Subjected to Transverse Impact Loading. J. Constr. Steel Res. 2022, 188, 107018. [Google Scholar] [CrossRef]
- Qian, J.; Li, N.; Ji, X.; Zhao, Z. Experimental Study on the Seismic Behavior of High Strength Concrete Filled Double-Tube Columns. Earthq. Eng. Eng. Vib. 2014, 13, 47–57. [Google Scholar] [CrossRef]
- Han, L.-H.; He, S.-H.; Liao, F.-Y. Performance and Calculations of Concrete Filled Steel Tubes (CFST) under Axial Tension. J. Constr. Steel Res. 2011, 67, 1699–1709. [Google Scholar] [CrossRef]
- Tao, Z.; Wang, Z.-B.; Yu, Q. Finite Element Modelling of Concrete-Filled Steel Stub Columns under Axial Compression. J. Constr. Steel Res. 2013, 89, 121–131. [Google Scholar] [CrossRef]
- Chen, J.-Y.; Li, W.; Han, L.-H.; Wang, F.-C.; Mu, T.-M. Structural Behaviour of Concrete-Encased CFST Box Stub Columns under Axial Compression. J. Constr. Steel Res. 2019, 158, 248–262. [Google Scholar] [CrossRef]

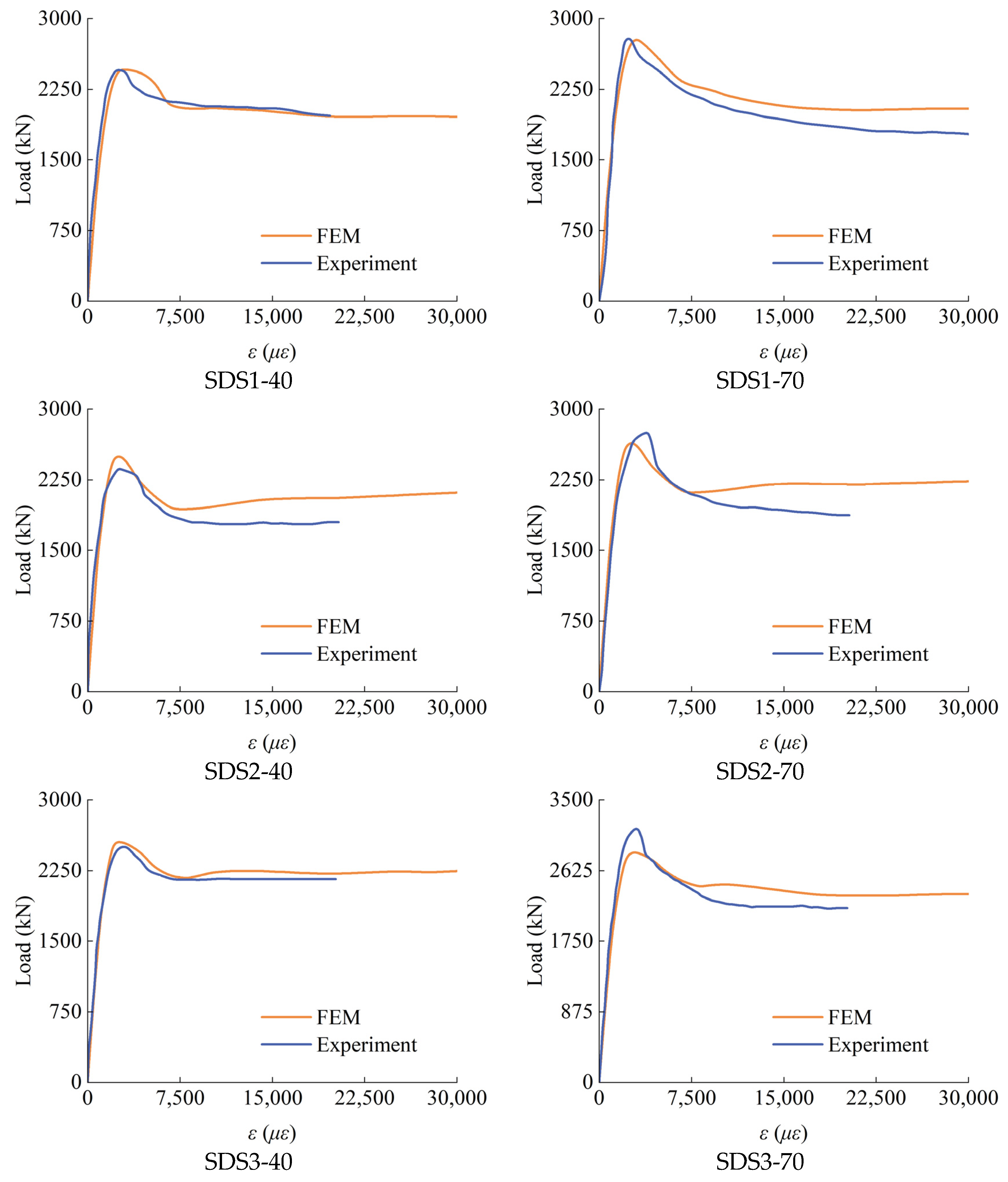





| Specimen | Outer tube | Inner Tube | Concrete | Ultimate Axial Load | Ref. | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SDS1-40a | 200 × 200 × 2.01 | 99.5 | 230 | 136.5 × 1.94 | 70.4 | 492.1 | 42.1 | 42.1 | 2450 | 2467.59 | 0.99 | [20] |
| SDS1-40b | 200 × 200 × 2.01 | 99.5 | 230 | 136.5 × 1.94 | 70.4 | 492.1 | 42.1 | 42.1 | 2383 | 2467.59 | 0.97 | |
| SDS1-70a | 200 × 200 × 2.01 | 99.5 | 230 | 136.5 × 1.94 | 70.4 | 492.1 | 42.1 | 69.8 | 2997 | 2789.48 | 1.07 | |
| SDS1-70b | 200 × 200 × 2.01 | 99.5 | 230 | 136.5 × 1.94 | 70.4 | 492.1 | 42.1 | 69.8 | 2806 | 2789.48 | 1.01 | |
| SDS2-40a | 200 × 200 × 2.01 | 99.5 | 230 | 114.6 × 3.93 | 29.2 | 377.1 | 42.1 | 42.1 | 2366 | 2502.85 | 0.95 | |
| SDS2-40b | 200 × 200 × 2.01 | 99.5 | 230 | 114.6 × 3.93 | 29.2 | 377.1 | 42.1 | 42.1 | 2463 | 2502.85 | 0.98 | |
| SDS2-70a | 200 × 200 × 2.01 | 99.5 | 230 | 114.6 × 3.93 | 29.2 | 377.1 | 42.1 | 69.8 | 2765 | 2648.85 | 1.04 | |
| SDS2-70b | 200 × 200 × 2.01 | 99.5 | 230 | 114.6 × 3.93 | 29.2 | 377.1 | 42.1 | 69.8 | 2884 | 2648.85 | 1.09 | |
| SDS3-40a | 200 × 200 × 2.01 | 99.5 | 230 | 140.1 × 3.78 | 37.1 | 322.4 | 42.1 | 42.1 | 2505 | 2553.24 | 0.98 | |
| SDS3-40b | 200 × 200 × 2.01 | 99.5 | 230 | 140.1 × 3.78 | 37.1 | 322.4 | 42.1 | 42.1 | 2479 | 2553.24 | 0.97 | |
| SDS3-70a | 200 × 200 × 2.01 | 99.5 | 230 | 140.1 × 3.78 | 37.1 | 322.4 | 42.1 | 69.8 | 3144 | 2850.61 | 1.10 | |
| SDS3-70b | 200 × 200 × 2.01 | 99.5 | 230 | 140.1 × 3.78 | 37.1 | 322.4 | 42.1 | 69.8 | 3100 | 2850.61 | 1.09 | |
| SC1 | 125 × 125 × 4 | 31.25 | 360 | 76.1 × 3.2 | 23.8 | 400 | 19.1 | 19.1 | 1269 | 1398.38 | 0.91 | [21] |
| SC6 | 150 × 150 × 5 | 30.00 | 378 | 88.9 × 3.2 | 27.8 | 412 | 19.1 | 19.1 | 1852 | 1983.79 | 0.93 | |
| SC11 | 125 × 125 × 4 | 31.25 | 360 | 76.1 × 3.6 | 21.1 | 353 | 20.6 | 20.6 | 1331 | 1396.49 | 0.95 | |
| SC16 | 150 × 150 × 5 | 30.00 | 378 | 88.9 × 4.0 | 22.2 | 345 | 20.6 | 20.6 | 1865 | 2022.02 | 0.92 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Wang, C.; Gao, Z.; Wei, H.; Hu, Z.; Wang, W. Axial Compressive Behavior of Outer Square Inner Circular Spontaneous Combustion Coal Gangue Concrete-Filled Double-Skin Steel Tubular Stub Column. Buildings 2024, 14, 4064. https://doi.org/10.3390/buildings14124064
Wang J, Wang C, Gao Z, Wei H, Hu Z, Wang W. Axial Compressive Behavior of Outer Square Inner Circular Spontaneous Combustion Coal Gangue Concrete-Filled Double-Skin Steel Tubular Stub Column. Buildings. 2024; 14(12):4064. https://doi.org/10.3390/buildings14124064
Chicago/Turabian StyleWang, Jinli, Chunyuan Wang, Zhe Gao, Haoyan Wei, Zhengping Hu, and Weiwei Wang. 2024. "Axial Compressive Behavior of Outer Square Inner Circular Spontaneous Combustion Coal Gangue Concrete-Filled Double-Skin Steel Tubular Stub Column" Buildings 14, no. 12: 4064. https://doi.org/10.3390/buildings14124064
APA StyleWang, J., Wang, C., Gao, Z., Wei, H., Hu, Z., & Wang, W. (2024). Axial Compressive Behavior of Outer Square Inner Circular Spontaneous Combustion Coal Gangue Concrete-Filled Double-Skin Steel Tubular Stub Column. Buildings, 14(12), 4064. https://doi.org/10.3390/buildings14124064