Theoretical Model for the Stress–Strain Curve of CNT-Reinforced Concrete under Uniaxial Compression
Abstract
:1. Introduction
2. Experiment
2.1. Experimental Program
2.1.1. Materials
2.1.2. Mix Proportions
2.1.3. Specimen Fabrication
2.1.4. Test Procedure
2.2. Results and Discussion
2.2.1. Failure Modes
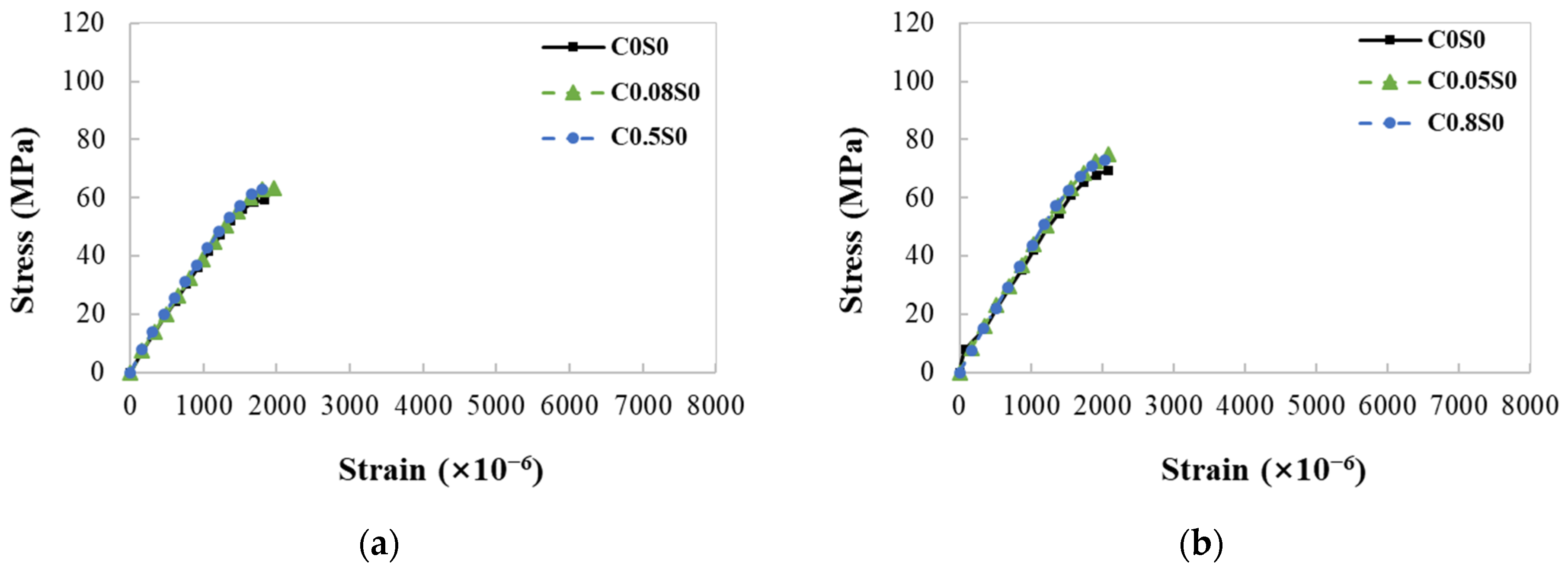
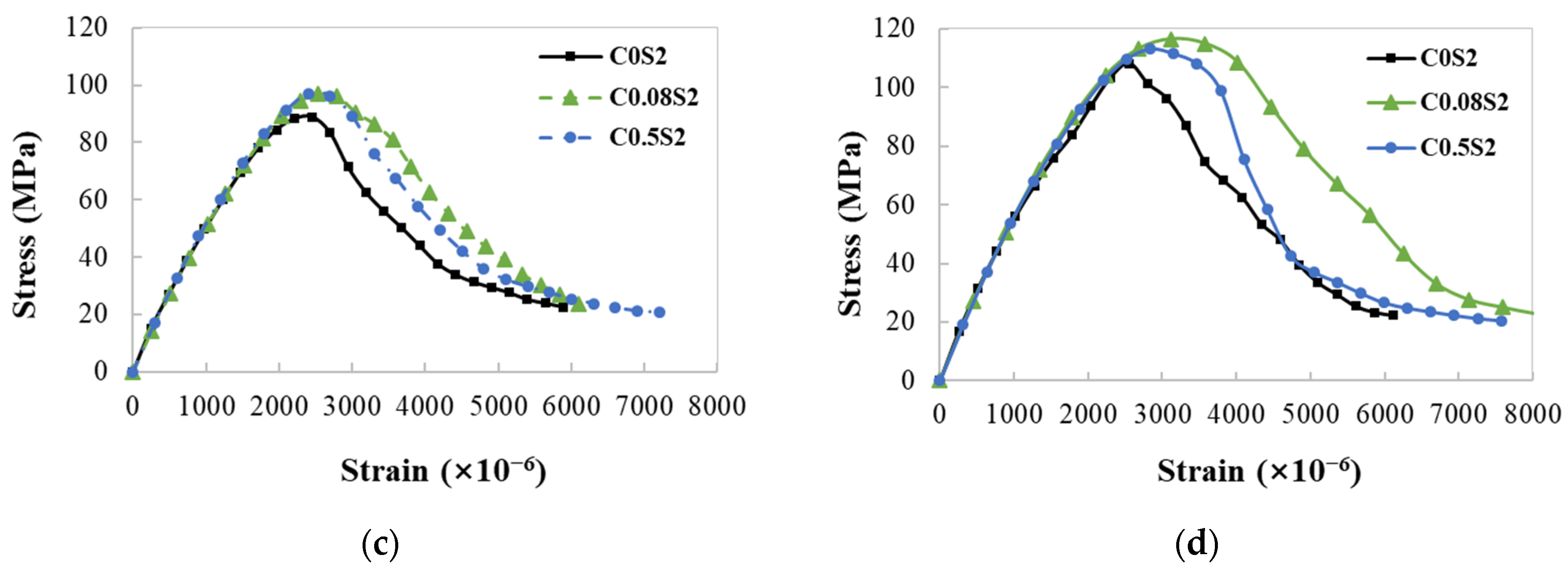
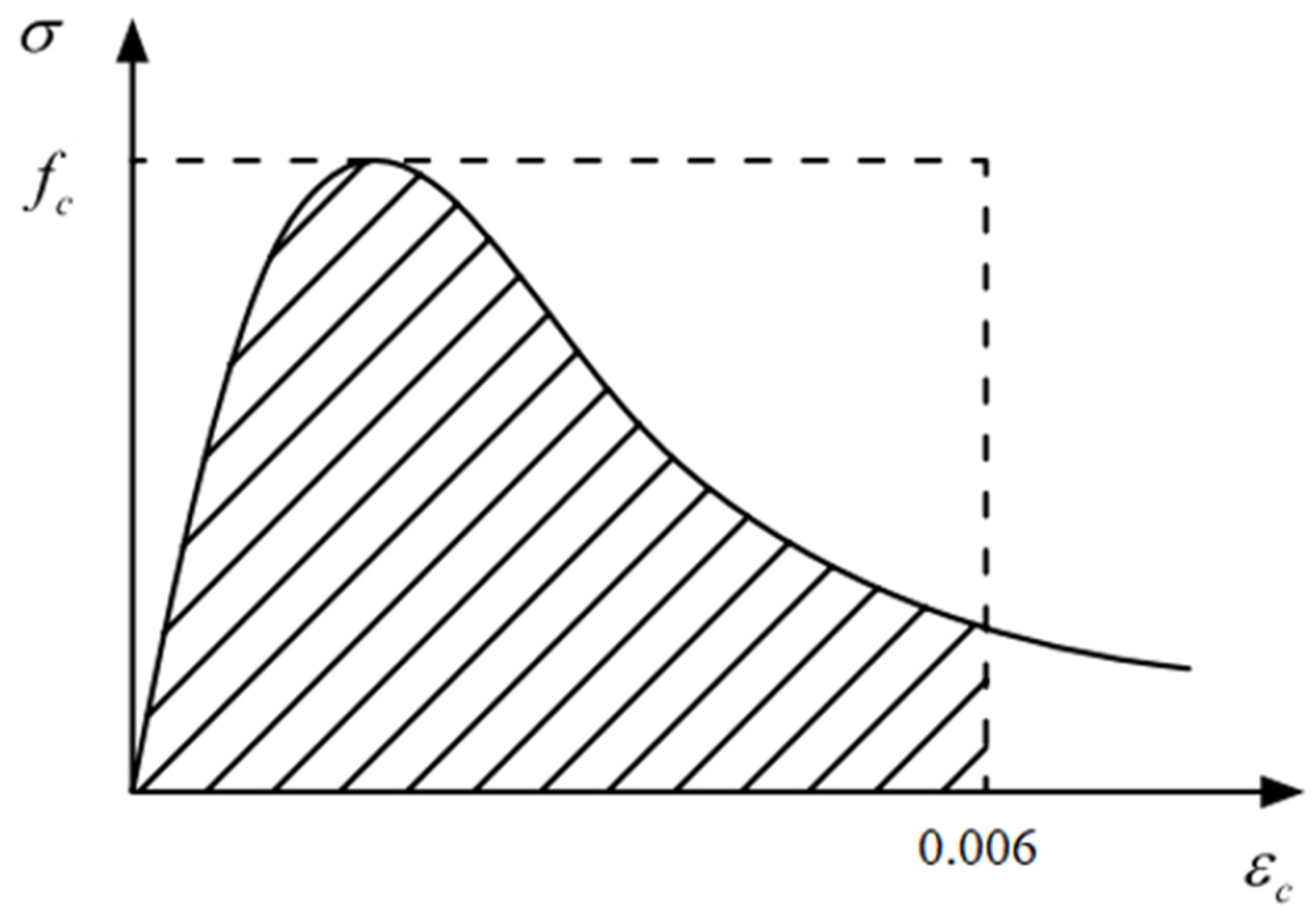
2.2.2. Stress–Strain Curve
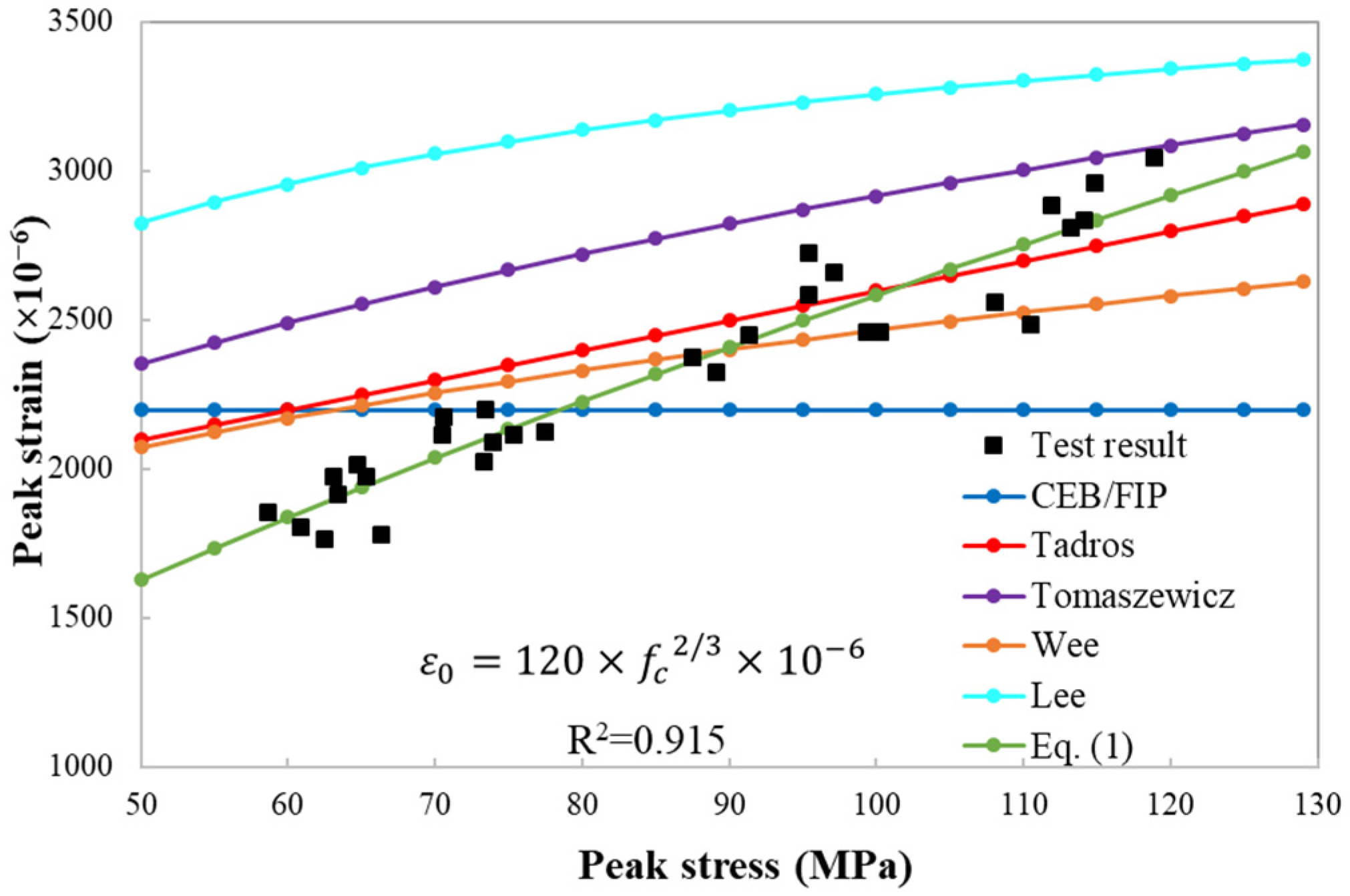
2.2.3. Peak Stress and Peak Strain
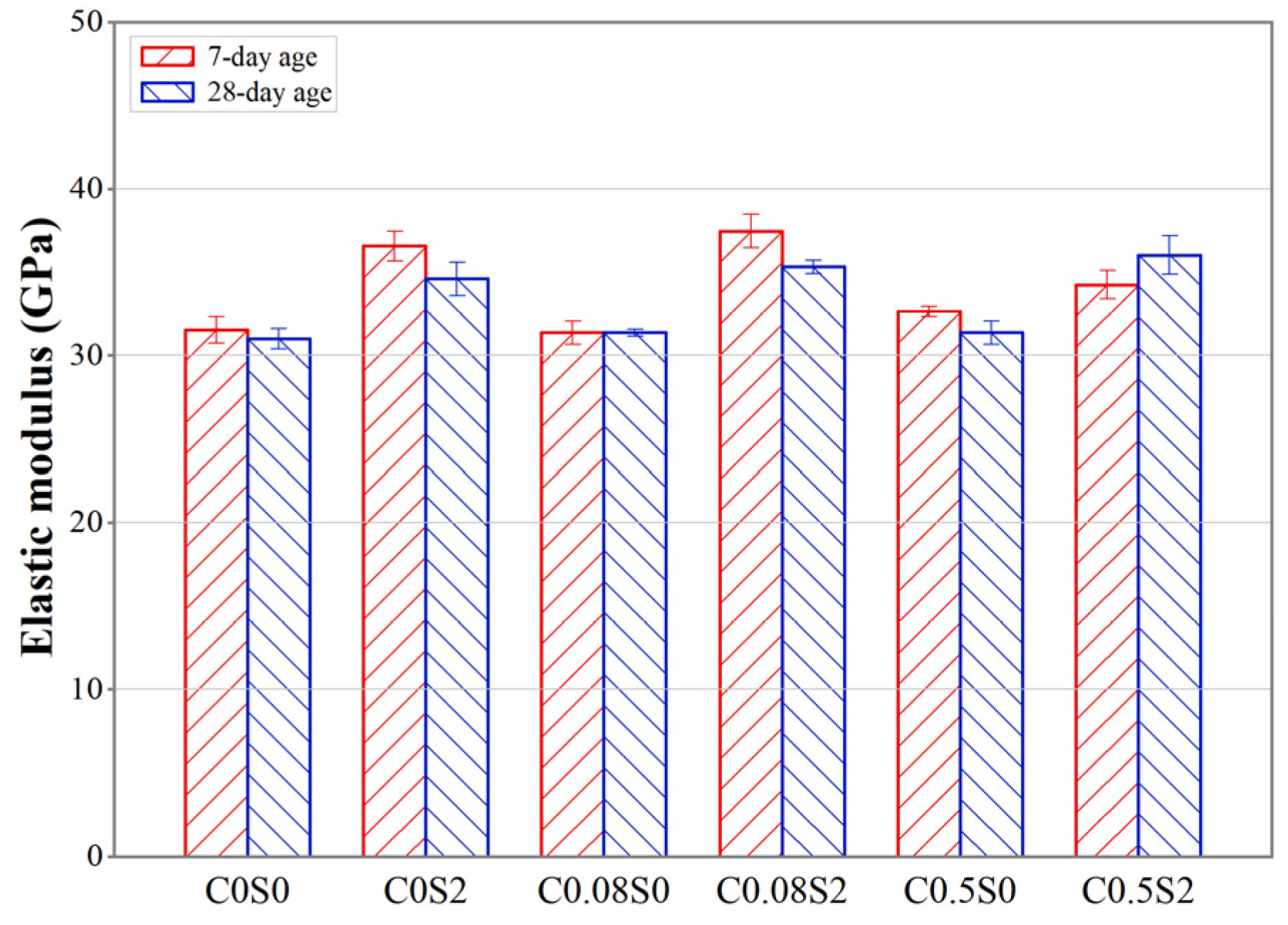
2.2.4. Elastic Modulus
2.2.5. Toughness Index
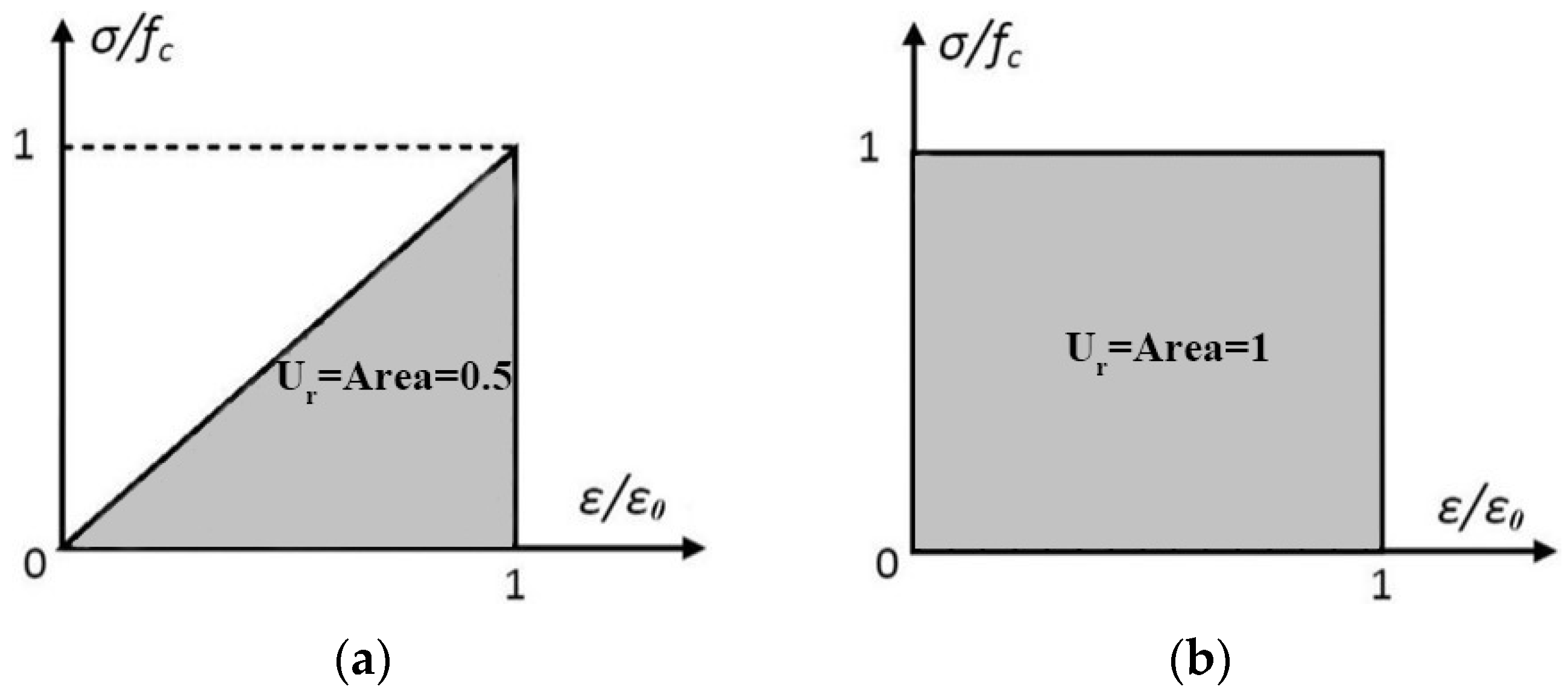
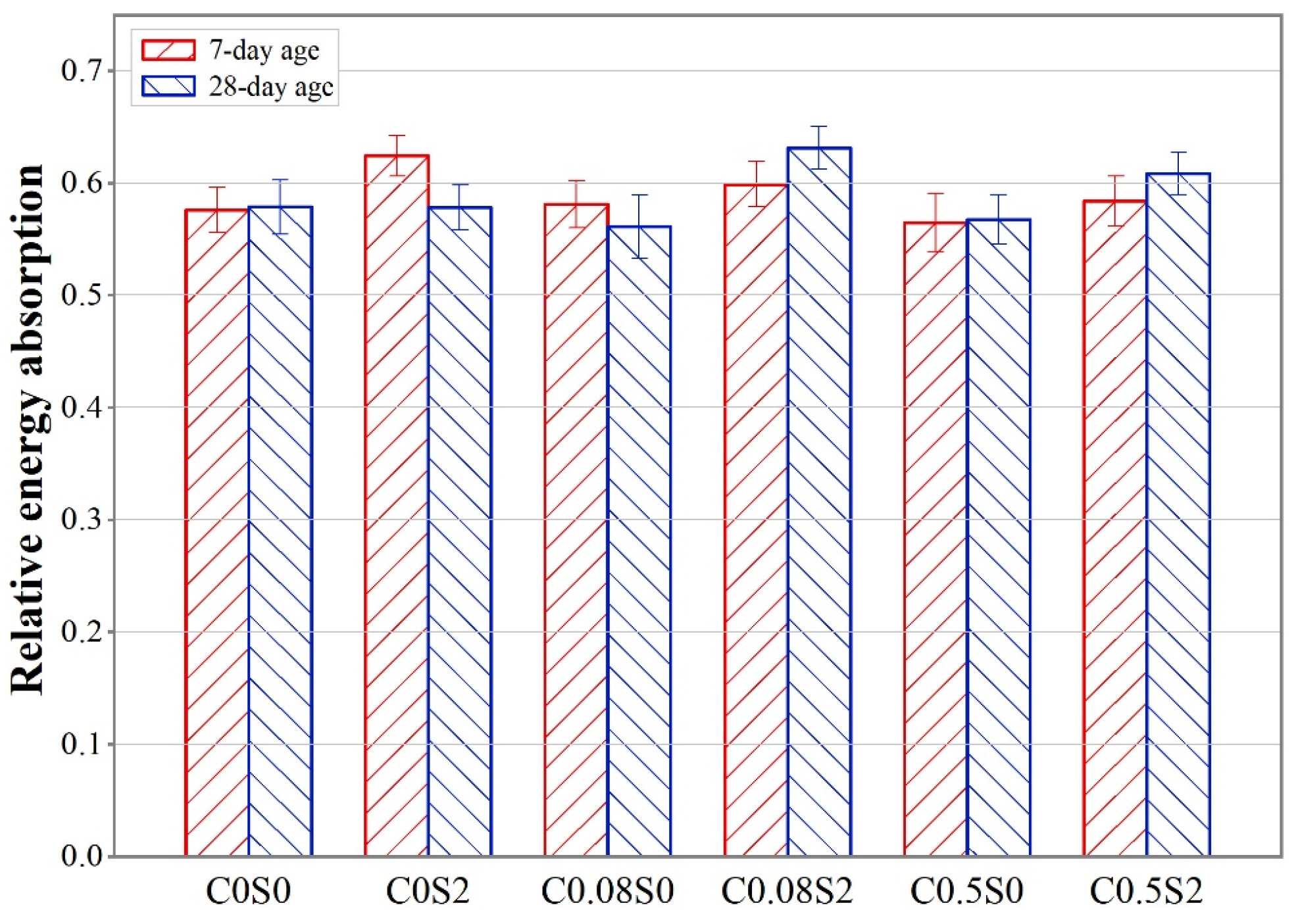
2.2.6. Relative Absorbed Energy
3. Theoretical Models
3.1. Theoretical Model for Peak Strain
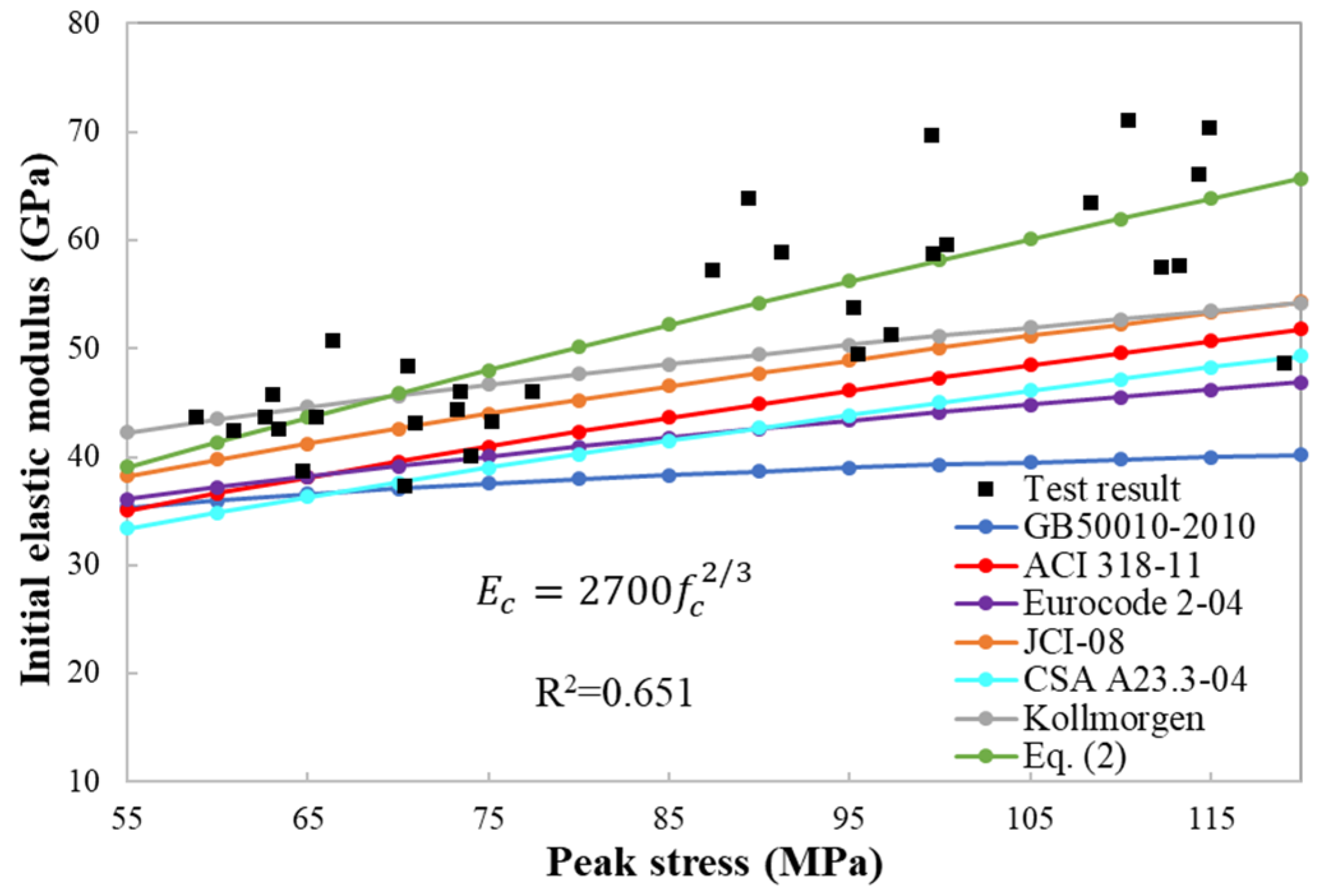
3.2. Theoretical Model for Initial Elastic Modulus
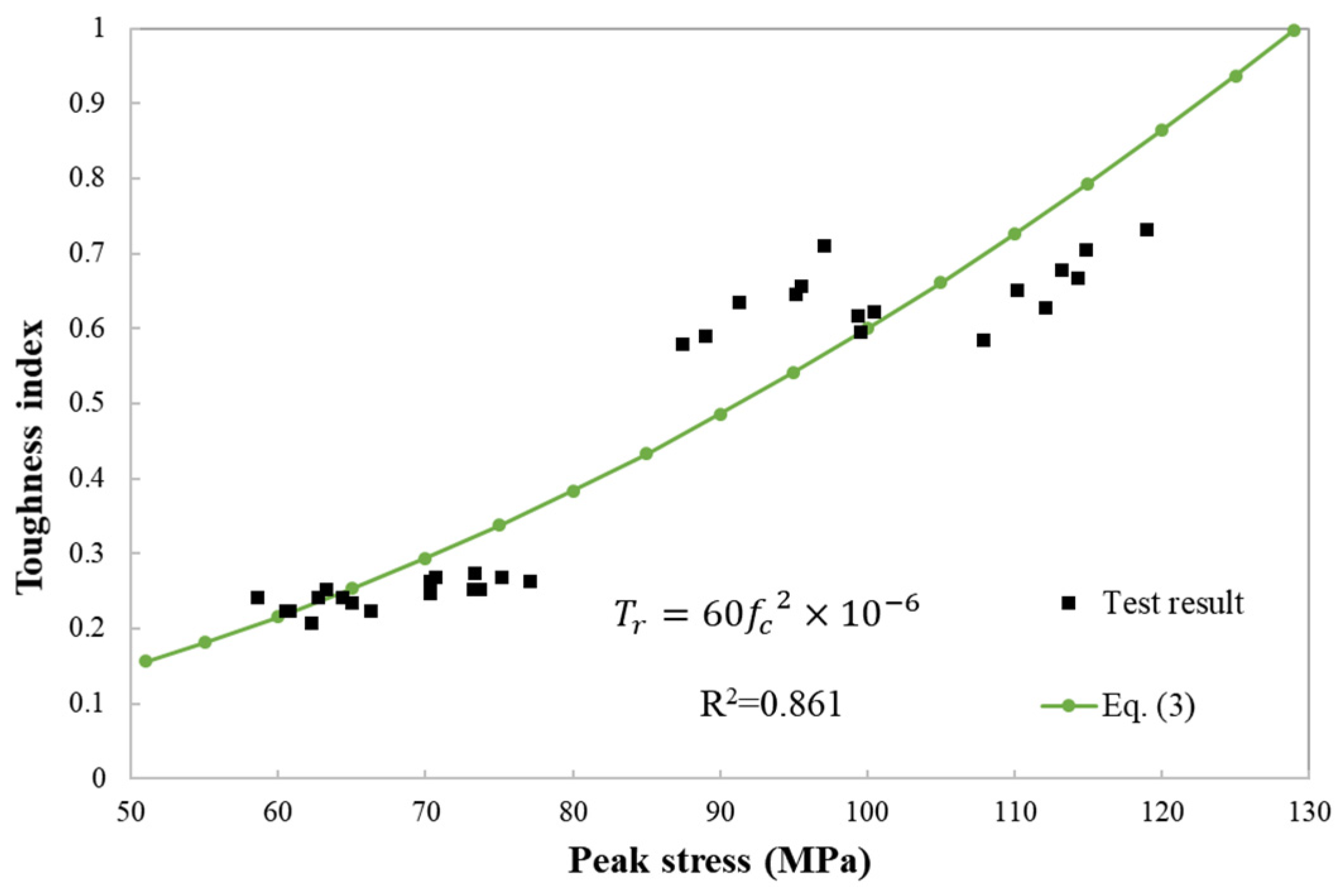
3.3. Theoretical Model for Toughness Index
3.4. Theoretical Model for Relative Absorbed Energy
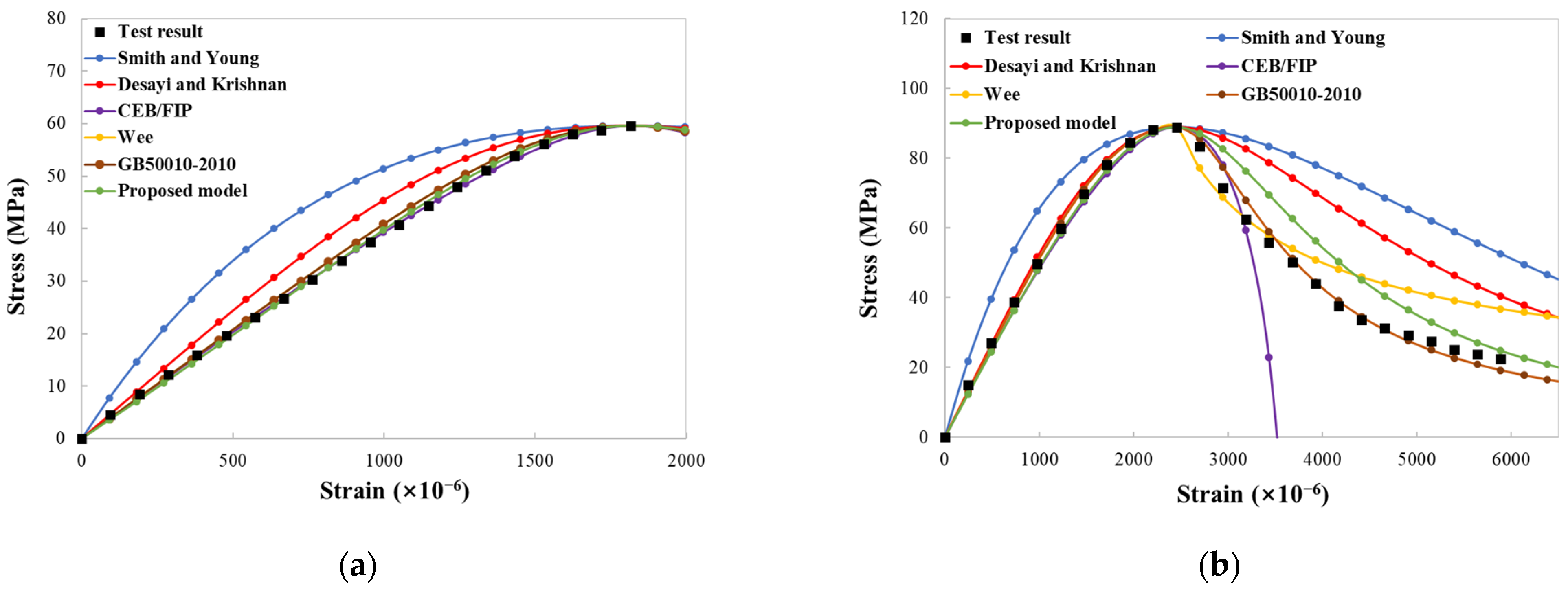
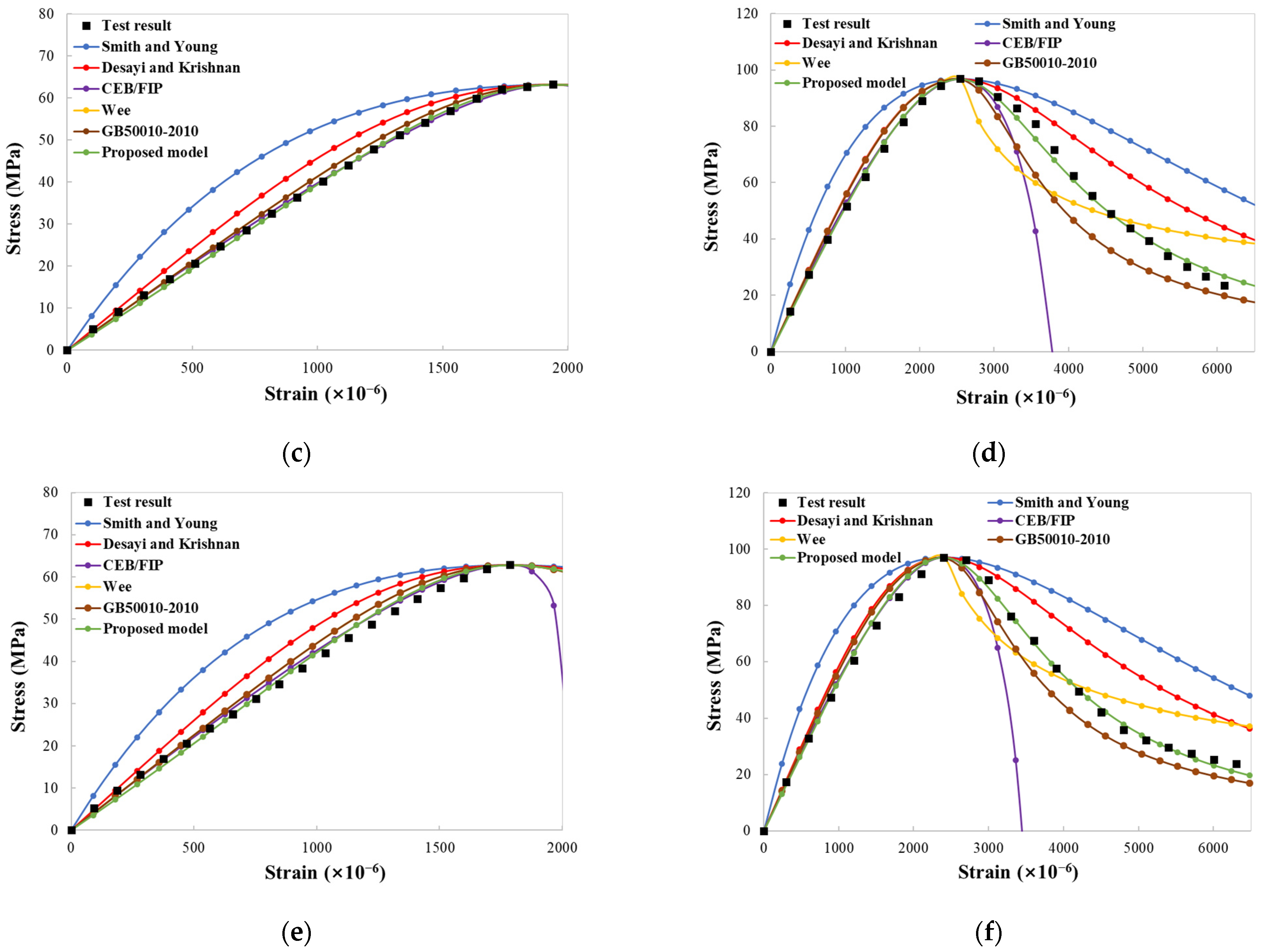
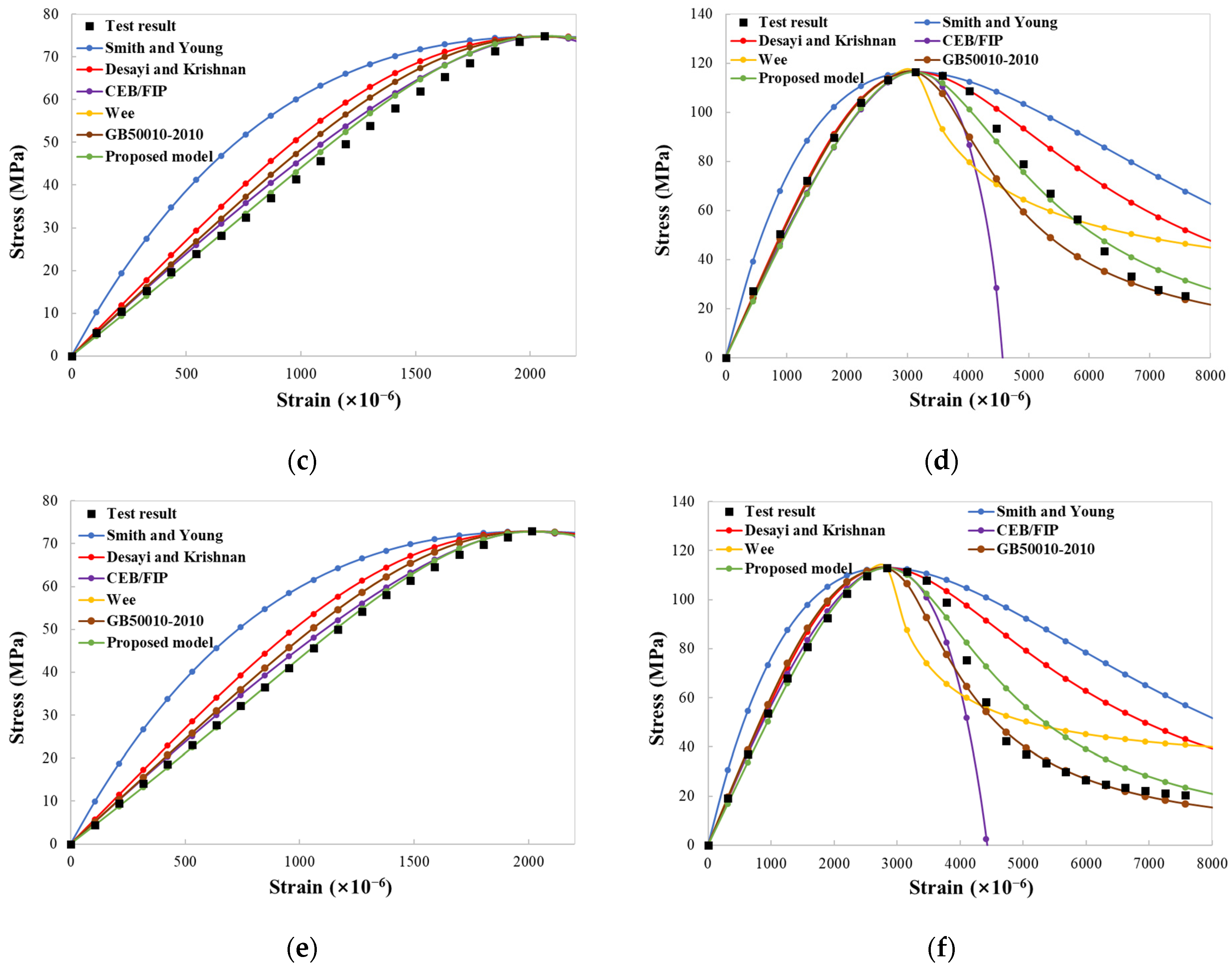
3.5. Theoretical Model for Uniaxial Compressive Stress–Strain Curves
4. Finite Element Analysis
4.1. General
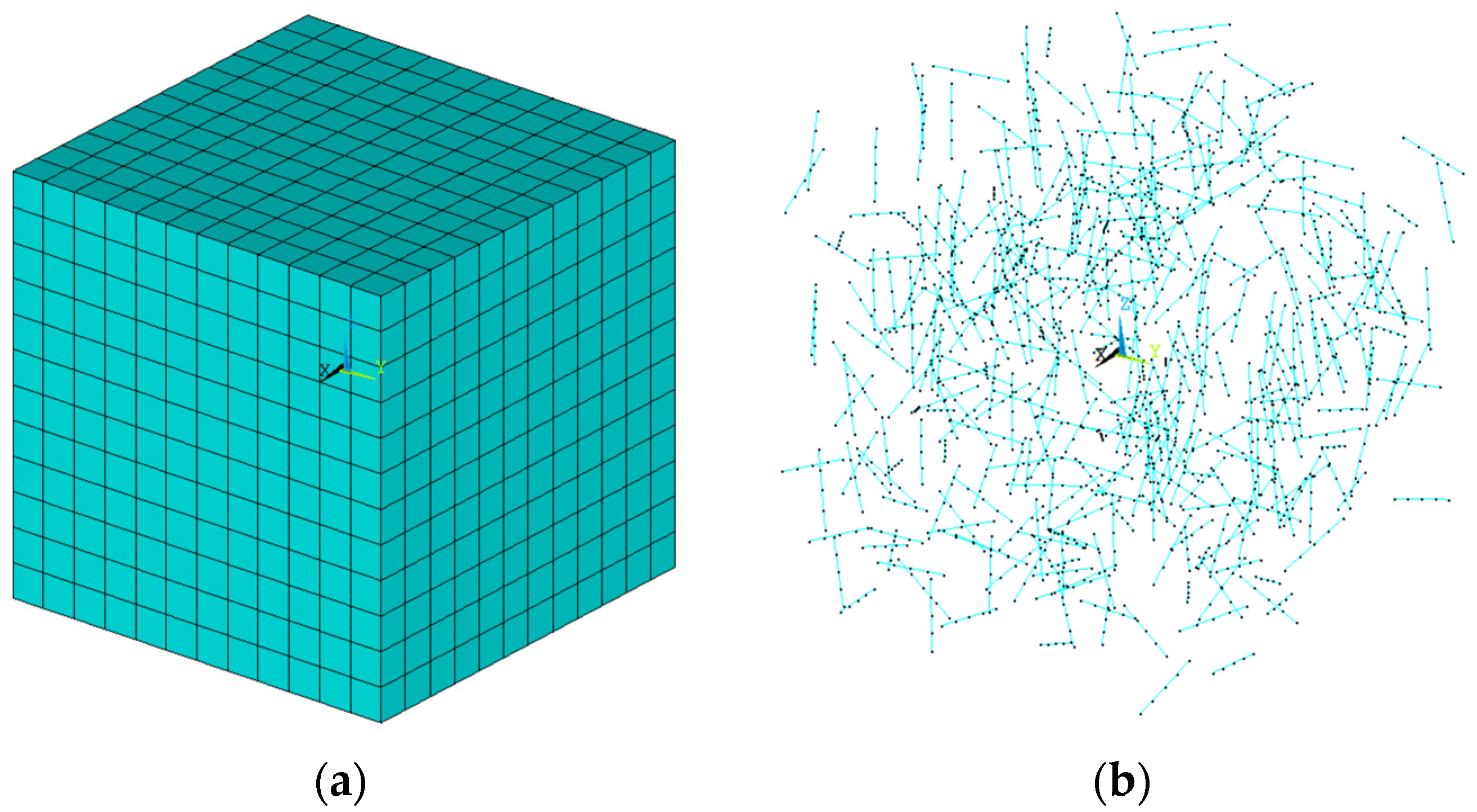
4.2. Modeling of RVE
4.2.1. Geometry and Material Models
4.2.2. Meshing
4.2.3. Constraint and Loading
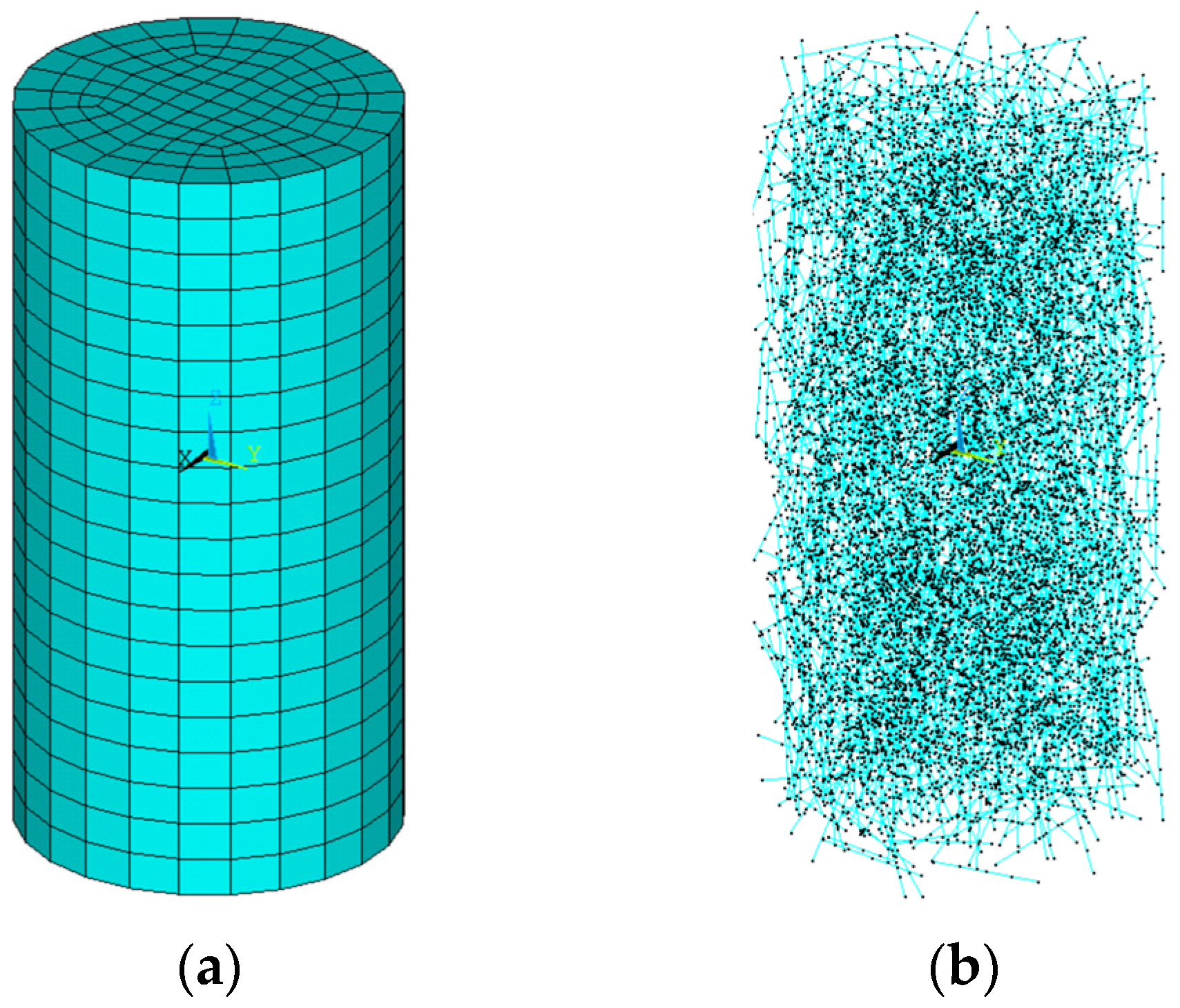
4.3. Modeling of Specimens
4.3.1. Geometry and Material Models
4.3.2. Meshing
4.3.3. Constraints and Loading
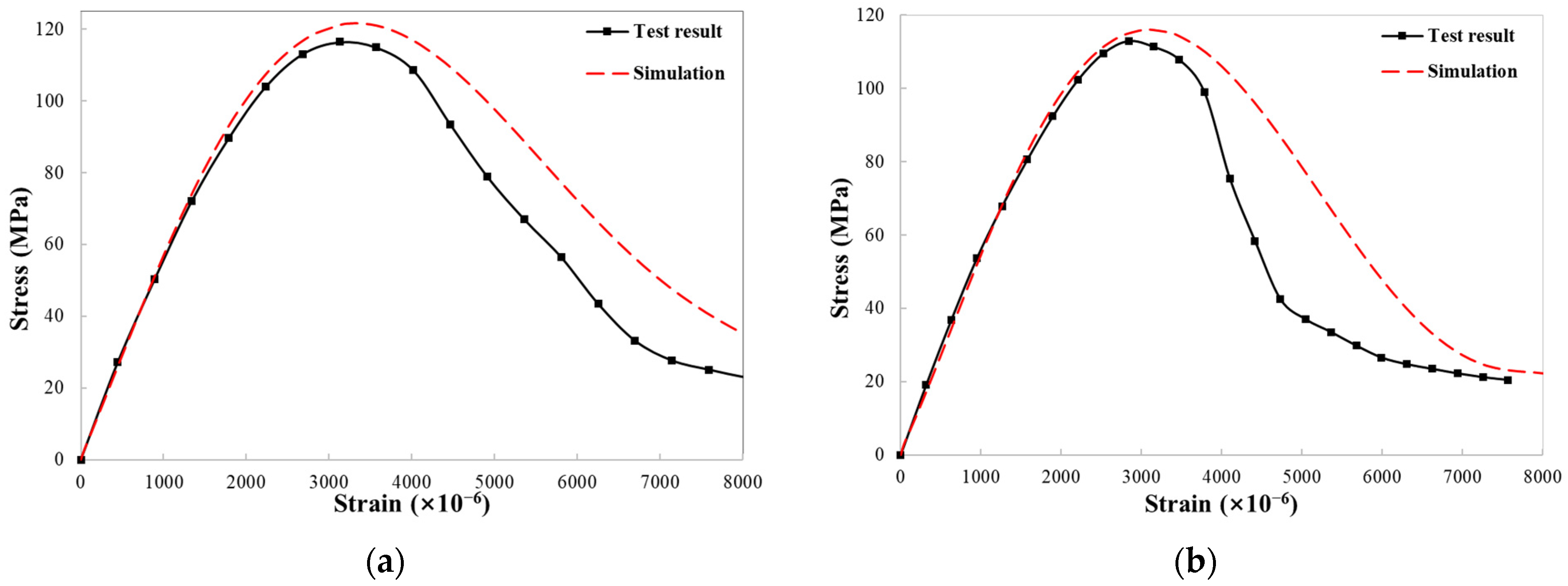
4.4. Results of FEA
4.4.1. Stress–Strain Curve
4.4.2. Crack Development
5. Conclusions
- (1)
- CNT content had little influence on the failure process and elastic modulus. The incorporation of CNTs can enhance the peak stress and peak strain due to CNTs’ bridging effect for nano- and micron-scale cracks, while an excessive CNT content may weaken this effect due to CNTs’ aggregation. Steel fibers can enhance the effect of CNTs on peak stress and peak strain.
- (2)
- In the absence of steel fibers, CNTs had negligible influence on toughness index, while steel fibers can enhance the effect of CNTs on toughness index. Nevertheless, excessive CNTs diminished this enhancement effect.
- (3)
- Steel fibers can increase the peak stress, peak strain, elastic modulus, toughness index and relative absorbed energy of concrete, and can result in ductile failure.
- (4)
- Theoretical models for peak strain, initial elastic modulus, toughness index and relative absorbed energy were established. The models were in good agreement with experiment results.
- (5)
- A theoretical model for the stress–strain curve of CNT-reinforced concrete was developed considering the content of CNTs and steel fibers. The proposed model demonstrated the best fit among the different theoretical models.
- (6)
- Considering the random distribution of CNTs and steel fibers, a simplified FE model was developed using the RVE method. The specimen was divided into two components: steel fibers and RVE with CNTs and cement-based material. There is agreement between the experimental and simulation results. The differences between the FE modelling and the experimental results can be attributed to defects in the test specimens compared with the ideal condition in the simulation. Refined models considering the properties of CNTs at the nanoscale need be further studied for better simulation accuracy.
- (7)
- Due to the high cost of the materials, the mixture proportions considered and tests performed in this study were limited. More tests are needed to study the influence of CNT on concrete properties. Additionally, a simplified FE model was developed, and refined FE models considering properties of CNTs at the nanoscale need be further studied for better simulation accuracy.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yoo, D.Y.; Shin, H.O.; Yang, J.M.; Yoon, Y.S. Material and bond properties of ultra high performance fiber reinforced concrete with micro steel fibers. Compos. Part B Eng. 2014, 58, 122–133. [Google Scholar] [CrossRef]
- Ates, A. Mechanical properties of sandy soils reinforced with cement and randomly distributed glass fibers (GRC). Compos. Part B Eng. 2016, 96, 295–304. [Google Scholar] [CrossRef]
- Hambach, M.; Moeller, H.; Neumann, T.; Volkmer, D. Carbon fiber reinforced cement-based composites as smart floor heating materials. Compos. Part B Eng. 2016, 90, 465–470. [Google Scholar] [CrossRef]
- Shah, S.P.; Ouyang, C. Mechanical behavior of fiber-reinforced cement-based composites. J. Am. Ceram. Soc. 1991, 74, 2727–2738. [Google Scholar] [CrossRef]
- Tyson, B.M.; Abu Al-Rub, R.K.; Yazdanbakhsh, A.; Grasley, Z. Carbon Nanotubes and Carbon Nanofibers for Enhancing the Mechanical Properties of Nanocomposite Cementitious Materials. J. Mater. Civ. Eng. 2011, 23, 1028–1035. [Google Scholar] [CrossRef]
- Pacheco-Torgal, F.; Jalali, S. Nanotechnology: Advantages and drawbacks in the field of construction and building materials. Constr. Build. Mater. 2011, 25, 582–590. [Google Scholar] [CrossRef]
- Makar, J.; Beaudoin, J. Carbon nanotubes and their application in the construction industry. In Proceedings of the 1st International Symposium on Nanotechnology in Construction, Paisley, Scotland, 23–25 June 2003; Bartos, P., Ed.; [Google Scholar]
- Wong, I.S. Effects of Ultra-Low Concentrations of Nanomaterials on the Piezoresistivity of Cementitious Composites. Master’s Thesis, University of California, Berkeley, CA, USA, 2015. [Google Scholar]
- Han, B.; Sun, S.; Ding, S.; Zhang, L.; Yu, X.; Ou, J. Review of nanocarbon-engineered multifunctional cementitious composites. Compos. Part A Appl. Sci. Manuf. 2015, 70, 69–81. [Google Scholar] [CrossRef]
- Onaizi, A.M.; Huseien, G.F.; Lim, N.H.A.S.; Amran, M.; Samadi, M. Effect of nanomaterials inclusion on sustainability of cement-based concretes: A comprehensive review. Constr. Build. Mater. 2021, 306, 124850. [Google Scholar] [CrossRef]
- Jiang, Z.; Sevim, O.; Ozbulut, O.E. Mechanical properties of graphene nanoplatelets-reinforced concrete prepared with different dispersion techniques. Constr. Build. Mater. 2021, 303, 124472. [Google Scholar] [CrossRef]
- Kaushik, B.K.; Goel, S.; Rauthan, G. Future VLSI interconnects: Optical fiber or carbon nanotube—A review. Microelectron. Int. 2007, 24, 53–63. [Google Scholar] [CrossRef]
- Yu, M. Strength and breaking mechanism of multiwalled carbon nanotubes under tensile load. Science 2000, 287, 637–640. [Google Scholar] [CrossRef] [PubMed]
- Walters, D.A.; Ericson, L.M.; Casavant, M.J.; Liu, J.; Colbert, D.T.; Smith, K.A.; Smalley, R.E. Elastic strain of freely suspended single-wall carbon nanotube ropes. Appl. Phys. Lett. 1999, 74, 3803–3805. [Google Scholar] [CrossRef]
- Zhang, P.; Su, J.; Guo, J.; Hu, S. Influence of carbon nanotube on properties of concrete: A review. Constr. Build. Mater. 2023, 369, 13038. [Google Scholar] [CrossRef]
- Jiang, S.; Zhou, D.C.; Zhang, L.Q.; Ouyang, J.; Yu, X.; Cui, X.; Han, B.G. Comparison of compressive strength and electrical resistivity of cementitious composites with different nano- and micro-fillers. Arch. Civ. Mech. Eng. 2018, 18, 60–68. [Google Scholar] [CrossRef]
- Kumar, S.; Kolay, P.; Malla, S.; Mishra, S. Effect of multi-walled carbon nano tubes (CNT) on mechanical strength of cement paste. J. Mater. Civ. Eng. 2012, 24, 84–91. [Google Scholar] [CrossRef]
- Chaipanich, A.; Rianyoi, R.; Nochaiya, T. The effect of carbon nanotubes and silica fume on compressive strength and flexural strength of cement mortars. Mater. Today Proc. 2017, 4, 6065–6071. [Google Scholar] [CrossRef]
- Gillani, S.S.U.; Khitab, A.; Ahmad, S.; Khushnood, R.A.; Ferro, G.A.; Kazmi, S.M.S.; Qureshi, L.A.; Restuccia, L. Improving the mechanical performance of cement composites by carbon nanotubes addition. Procedia Struct. Integr. 2017, 3, 11–17. [Google Scholar] [CrossRef]
- Xu, S.; Liu, J.; Li, Q. Mechanical properties and microstructure of multi-walled carbon nanotube-reinforced cement paste. Constr. Build. Mater. 2015, 76, 16–23. [Google Scholar] [CrossRef]
- Wang, B.; Han, Y.; Liu, S. Effect of highly dispersed carbon nanotubes on the flexural toughness of cement-based composites. Constr. Build. Mater. 2013, 46, 8–12. [Google Scholar] [CrossRef]
- Lourie, O.; Cox, D.; Wagner, H. Buckling and collapse of embedded carbon nanotubes. Phys. Rev. Lett. 1998, 81, 1638. [Google Scholar] [CrossRef]
- Szleifer, I.; Yerushalmi-Rozen, R. Polymers and carbon nanotubes—Dimensionality, interactions and nanotechnology. Polymer 2005, 46, 7803–7818. [Google Scholar] [CrossRef]
- Han, B.G.; Yu, X.; Ou, J.P. Multifunctional and smart carbon nanotube reinforced cement-based materials. In Nanotechnology in Civil Infrastructure: A Paradigm Shift; Springer: Berlin/Heidelberg, Germany, 2011; pp. 1–47. [Google Scholar]
- Lu, Z.; Hou, D.; Meng, L.; Sun, G.; Lu, C.; Li, Z. Mechanism of cement paste reinforced by graphene oxide/carbon nanotubes composites with enhanced mechanical properties. RSC Adv. 2015, 5, 100598–100605. [Google Scholar] [CrossRef]
- Qiu, L.; Yang, X.; Gou, X.; Yang, W.; Ma, Z.; Wallace, G.G.; Li, D. Dispersing Carbon Nanotubes with Graphene Oxide in Water and Synergistic Effects between Graphene Derivatives. Chem.-A Eur. J. 2010, 16, 10653–10658. [Google Scholar] [CrossRef] [PubMed]
- Parveen, S.; Rana, S.; Fangueiro, R. A review on nanomaterial dispersion, microstructure, and mechanical properties of carbon nanotube and nanofiber reinforced cementitious composites. J. Nanomater. 2013, 2013, 3271–3283. [Google Scholar] [CrossRef]
- Nochaiya, T.; Chaipanich, A. Behavior of multi-walled carbon nanotubes on the porosity and microstructure of cement-based materials. Appl. Surf. Sci. 2011, 257, 1941–1945. [Google Scholar] [CrossRef]
- Li, G.Y.; Wang, P.M.; Zhao, X.H. Mechanical behavior and microstructure of cement composites incorporating surface-treated multi-walled carbon nanotubes. Carbon 2005, 43, 1239–1245. [Google Scholar] [CrossRef]
- Musso, S.; Tulliani, J.M.; Ferro, G.; Tagliaferro, A. Influence of carbon nanotubes structure on the mechanical behavior of cement composites. Compos. Sci. Technol. 2009, 69, 1985–1990. [Google Scholar] [CrossRef]
- Abu Al-Rub, R.K.; Ashour, A.I.; Tyson, B.M. On the aspect ratio effect of multi-walled carbon nanotube reinforcements on the mechanical properties of cementitious nanocomposites. Constr. Build. Mater. 2012, 35, 647–655. [Google Scholar] [CrossRef]
- Konsta-Gdoutos, M.S.; Metaxa, Z.S.; Shah, S.P. Highly dispersed carbon nanotube reinforced cement based materials. Cem. Concr. Res. 2010, 40, 1052–1059. [Google Scholar] [CrossRef]
- Luo, J.L.; Duan, Z.D.; Li, H. The influence of surfactants on the processing of multi-walled carbon nanotubes in reinforced cement matrix composites. Phys. Status Solidi A-Appl. Mater. Sci. 2009, 206, 2783–2790. [Google Scholar] [CrossRef]
- Collins, F.; Lambert, J.; Duan, W.H. The influences of admixtures on the dispersion, workability, and strength of carbon nanotube-OPC paste mixtures. Cem. Concr. Compos. 2012, 34, 201–207. [Google Scholar] [CrossRef]
- Cwirzen, A.; Habermehl-Cwirzen, K.; Penttala, V. Surface decoration of carbon nanotubes and mechanical properties of cement/carbon nanotube composites. Adv. Cem. Res. 2017, 29, 65–73. [Google Scholar] [CrossRef]
- ASTM C39/C39M-17; Standard Test Method for Compressive Strength of Cylindrical Concrete Specimens. ASTM International: West Conshohocken, PA, USA, 2017.
- ASTM C31/C31M-03; Standard Practice for Making and Curing Concrete Test Specimens in the Field. ASTM International: West Conshohocken, PA, USA, 2003.
- ASTM C192/C192M-16a; Standard Practice for Making and Curing Concrete Test Specimens in the ASTM Laboratory. ASTM International: West Conshohocken, PA, USA, 2016.
- Jin, L.; Yu, W.X.; Li, D.; Du, X.L. Numerical and theoretical investigation on the size effect of concrete compressive strength considering the maximum aggregate size. Int. J. Mech. Sci. 2021, 192, 106130. [Google Scholar] [CrossRef]
- Tasdemir, M.A.; Tasdemir, C.; Akyüz, S.; Jefferson, A.D.; Lydon, F.D.; Barr, B.I.G. Evaluation of Strains at Peak Stresses in Concrete: A Three-Phase Composite Model Approach. Cem. Concr. Compos. 1998, 20, 301–318. [Google Scholar] [CrossRef]
- Comite Euro-International du Benton (CEB). CEB Model Code 90; Bulletin D’information: Paris, France, 1990; No. 203. [Google Scholar]
- Tadros, G.S. Plastic Rotation of Reinforced Concrete Members Subjected to Bending, Axial Load and Shear. Ph.D. Thesis, ADV DEG, Civil Engineering University of Calgary, Calgary, AB, Canada, 1970. [Google Scholar]
- Tomaszewicz, A. Betongens Arbeidsdiagram; SINTEF Rep. No. STF 65A84605; The Foundation for Industrial and Technical Research: Trondheim, Norway, 1984. [Google Scholar]
- Wee, T.H.; Chin, M.S.; Mansur, M.A. Stress-strain relationship of high-strength concrete in compression. J. Mater. Civ. Eng. 1996, 8, 70–76. [Google Scholar] [CrossRef]
- Lee, I. Complete Stress-Strain Characteristics of High Performance Concrete. Ph.D. Thesis, New Jersey Institute of Technology, Newark, NJ, USA, 2002. [Google Scholar]
- GB 50010-2010; Code for Design of Concrete Structures. National Standard of the People’s Republic of China: Beijing, China, 2010.
- ACI 318-11; Building Code Requirements for Structural Concrete and Commentary, PCA Notes on ACI 318-11: With Design Applications. ACI International: Farmington Hills, MI, USA, 2011.
- Comité Européen de Normalisation. Eurocode 2: Design of Concrete Structures: Part 1-1: General Rules and Rules for Buildings; British Standards Institution: London, UK, 2004. [Google Scholar]
- Japanese Civil Institute. Guidelines for Control of Cracking of Mass Concrete; Japan Concrete Institute: Tokyo, Japan, 2008. [Google Scholar]
- Canadian Standard, CSA, A23.3-04; Design of Concrete Structures. Canadian Standard Association: Toronto, ON, Canada, 2004.
- Kollmorgen, G.A. Impact of Age and Size on the Mechanical Behavior of an Ultra High Performance Concrete. Master’s Thesis, Michigan Technological University, Houghton, MI, USA, 2004. [Google Scholar]
- Nematzadeh, M.; Salari, A.; Ghadami, J.; Naghipour, M. Stress-strain behavior of freshly compressed concrete under axial compression with a practical equation. Constr. Build. Mater. 2016, 115, 402–423. [Google Scholar] [CrossRef]
- Smith, G.M.; Young, L.E. Ultimate theory in flexure by exponential function. ACI J. Proc. 1955, 52, 349–359. [Google Scholar]
- Desayi, P.; Krishnan, S. Equation for the Stress-Strain Curve of Concrete. ACI J. Proc. 1964, 61, 345–350. [Google Scholar]









| Literature | Amount of CNT (% of Cement) | Dispersion Technique | Properties | Increase (%) |
|---|---|---|---|---|
| Jiang et al. [16] | 0.1, 0.5, 1.0 | US 1 | CS 2 | 16.8, 10.0, −3.5 |
| Kumar et al. [17] | 0.5, 0.75, 1.0 | US | CS | 13.7, 1.5, −25.7 |
| STS 3 | 16.7, 4.4, −21.8 | |||
| Chaipanich et al. [18] | 0.5, 1.0 | US | CS | 6.4, 4.1 |
| FS 4 | 2.9, 2.3 | |||
| Gillani et al. [19] | 0.05, 0.1 | ST 5 and US | CS | 19.1, 24.7 |
| STS | 26.0, 18.0 | |||
| Xu et al. [20] | 0.025, 0.05, 0.1 | ST and US | CS | 6.3, 12.7, 14.6 |
| 0.025, 0.05, 0.1, 0.2 | STS | 7.5, 15.0, 30.0, 40.0 | ||
| Wang et al. [21] | 0.05, 0.08, 0.10, 0.12, 0.15 | ST and US | FTI 6 | 31.0, 57.5, 47.1, 31.6, 10.3 |
| Nochaiya et al. [28] | 1.0 | US | TP 7 | 16.0 |
| Li et al. [29] | 0.5 | HMF 8 | CS | 18.9 |
| FS | 25.1 | |||
| TP | 39.2 | |||
| Musso et al. [30] | 0.5 | AS 9 and US | CS | 10.6 |
| Al-Rub et al. [31] | 0.2 | SP 10 and US | FS | 269.0 |
| D 11 | 81.0 | |||
| Konsta-Gdoutos et al. [32] | 0.08 | ST and US | YM 12 | 45.0 |
| FS | 25.0 | |||
| Luo et al. [33] | 0.2 | MS 13, ST and US | CS | 29.5 |
| FS | 35.4 | |||
| Collins et al. [34] | 0.5 | MS, PCA 14 and US | CS | 25.0 |
| Cwirzen et al. [35] | 0.045 | CF 15, PAP 16 and US | CS | 50.0 |
| Average Diameter of Outer Layer (nm) | Average Diameter of Inner Layer (nm) | Average Length (μm) | Surface Area (m2/g) | Loose Bulk Density (g/cm3) | Tapped Bulk Density (g/cm3) |
|---|---|---|---|---|---|
| >50 | 5~15 | 15 | 250~300 | 0.18 | 2.1 |
| Particle Size (μm) | Solvent | Concentration (mg/mL) | pH | Proportion of Single-Layer GO Sheets (%) | Diameter of Single-Layer GO (μm) | Thickness (nm) |
|---|---|---|---|---|---|---|
| <10 μm | water | 4 | 2.2~2.5 | >95 | 0.5~5 | 0.8~12 |
| Length (mm) | Diameter (mm) | Length/ Diameter | Tensile Strength (MPa) | Number of Fibers (/kg) |
|---|---|---|---|---|
| 13 | 0.22 | 60 | 2850 | 224,862 |
| Group | Cement | Silica Fume | Fine Sand | Quartz Powder | Water | Superplasticizer | Accelerator | CNT | GO | Steel Fiber * |
|---|---|---|---|---|---|---|---|---|---|---|
| C0S0 | 100 | 32.5 | 145 | 30 | 24 | 4.3 | 4.2 | 0 | 0 | 0 |
| C0S2 | 100 | 32.5 | 145 | 30 | 24 | 4.3 | 4.2 | 0 | 0 | 2 |
| C0.08S0 | 100 | 32.5 | 145 | 30 | 24 | 4.3 | 4.2 | 0.08 | 0.04 | 0 |
| C0.08S2 | 100 | 32.5 | 145 | 30 | 24 | 4.3 | 4.2 | 0.08 | 0.04 | 2 |
| C0.5S0 | 100 | 32.5 | 145 | 30 | 24 | 4.3 | 4.2 | 0.5 | 0.04 | 0 |
| C0.5S2 | 100 | 32.5 | 145 | 30 | 24 | 4.3 | 4.2 | 0.5 | 0.04 | 2 |
| Literature | Theoretical Model |
|---|---|
| CEB/FIP [41] | |
| Tadros [42] | |
| Tomaszewicz [43] | |
| Wee [44] | |
| Lee [45] |
| Literature | Theoretical Model |
|---|---|
| GB50010–2010 [46] | |
| ACI 318-11 [47] | |
| Eurocode 2-04 [48] | |
| JCI-08 [49] | |
| CSA A23.3-04 [50] | |
| Kollmorgen [51] |
| Literature | Theoretical Model |
|---|---|
| Tasdemir [40] | |
| Nematzadeh [52] |
| Literature | Theoretical Model |
|---|---|
| Smith and Young [53] | |
| Desayi and Krishnan [54] | |
| CEB/FIP [41] | |
| Wee [44] | |
| GB50010-2010 [46] |
| Age (Days) | Group | ||
|---|---|---|---|
| 7 | C0S0 | 1.162 | 0.256 |
| C0S2 | 1.402 | 0.384 | |
| C0.08S0 | 1.239 | 0.235 | |
| C0.08S2 | 1.415 | 0.335 | |
| C0.5S0 | 1.076 | 0.281 | |
| C0.5S2 | 1.320 | 0.371 | |
| 28 | C0S0 | 1.225 | 0.238 |
| C0S2 | 1.218 | 0.412 | |
| C0.08S0 | 1.130 | 0.265 | |
| C0.08S2 | 1.458 | 0.297 | |
| C0.5S0 | 1.153 | 0.258 | |
| C0.5S2 | 1.410 | 0.446 |
| Coefficient | ||||||
|---|---|---|---|---|---|---|
| value | 1.18 | −7.17 | 10.32 | 0.48 | 13.28 | 11.87 |
| Model | 7 Days Old | 28 Days Old | Average | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C0S0 | C0S2 | C0.08 S0 | C0.08 S2 | C0.5S0 | C0.5S2 | C0S0 | C0S2 | C0.08 S0 | C0.08 S2 | C0.5S0 | C0.5S2 | ||
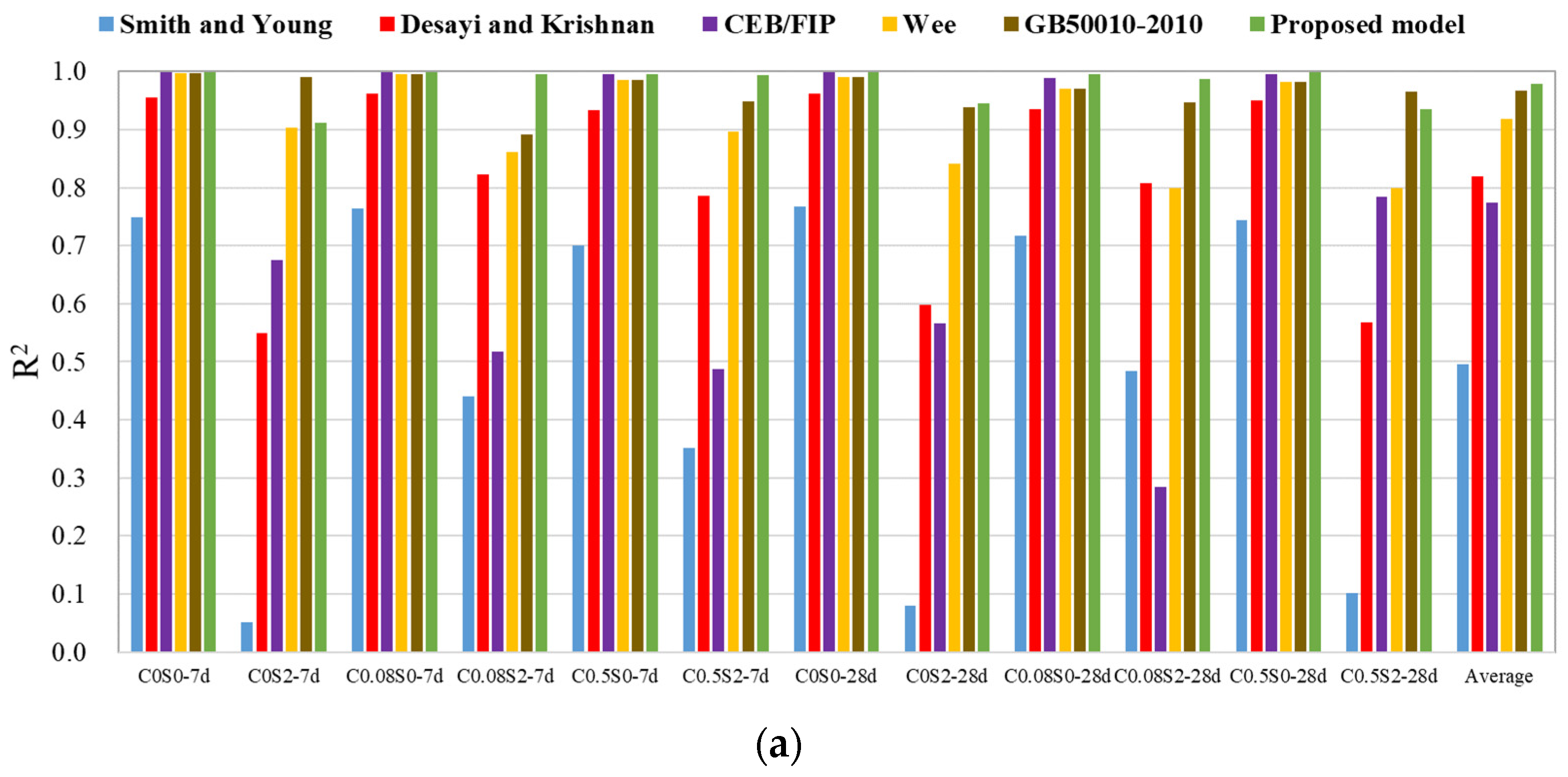
| Smith and Young [53] | 0.748 | 0.052 | 0.764 | 0.440 | 0.701 | 0.352 | 0.767 | 0.079 | 0.717 | 0.484 | 0.744 | 0.101 | 0.496 |
| Desayi and Krishnan [54] | 0.956 | 0.550 | 0.962 | 0.822 | 0.933 | 0.785 | 0.961 | 0.598 | 0.936 | 0.808 | 0.951 | 0.568 | 0.819 |
| CEB/FIP [41] | 0.999 | 0.675 | 0.999 | 0.517 | 0.995 | 0.487 | 0.999 | 0.567 | 0.988 | 0.285 | 0.995 | 0.785 | 0.774 |
| Wee [44] | 0.997 | 0.903 | 0.996 | 0.862 | 0.985 | 0.897 | 0.991 | 0.841 | 0.970 | 0.799 | 0.982 | 0.799 | 0.919 |
| GB50010-2010 [46] | 0.997 | 0.991 | 0.996 | 0.892 | 0.985 | 0.949 | 0.991 | 0.939 | 0.970 | 0.947 | 0.982 | 0.966 | 0.967 |
| Proposed model | 0.999 | 0.912 | 0.999 | 0.995 | 0.995 | 0.991 | 0.999 | 0.945 | 0.995 | 0.987 | 0.999 | 0.935 | 0.979 |
| Model | 7 Days Old | 28 Days Old | Average | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C0S0 | C0S2 | C0.08 S0 | C0.08 S2 | C0.5S0 | C0.5S2 | C0S0 | C0S2 | C0.08 S0 | C0.08 S2 | C0.5S0 | C0.5S2 | ||
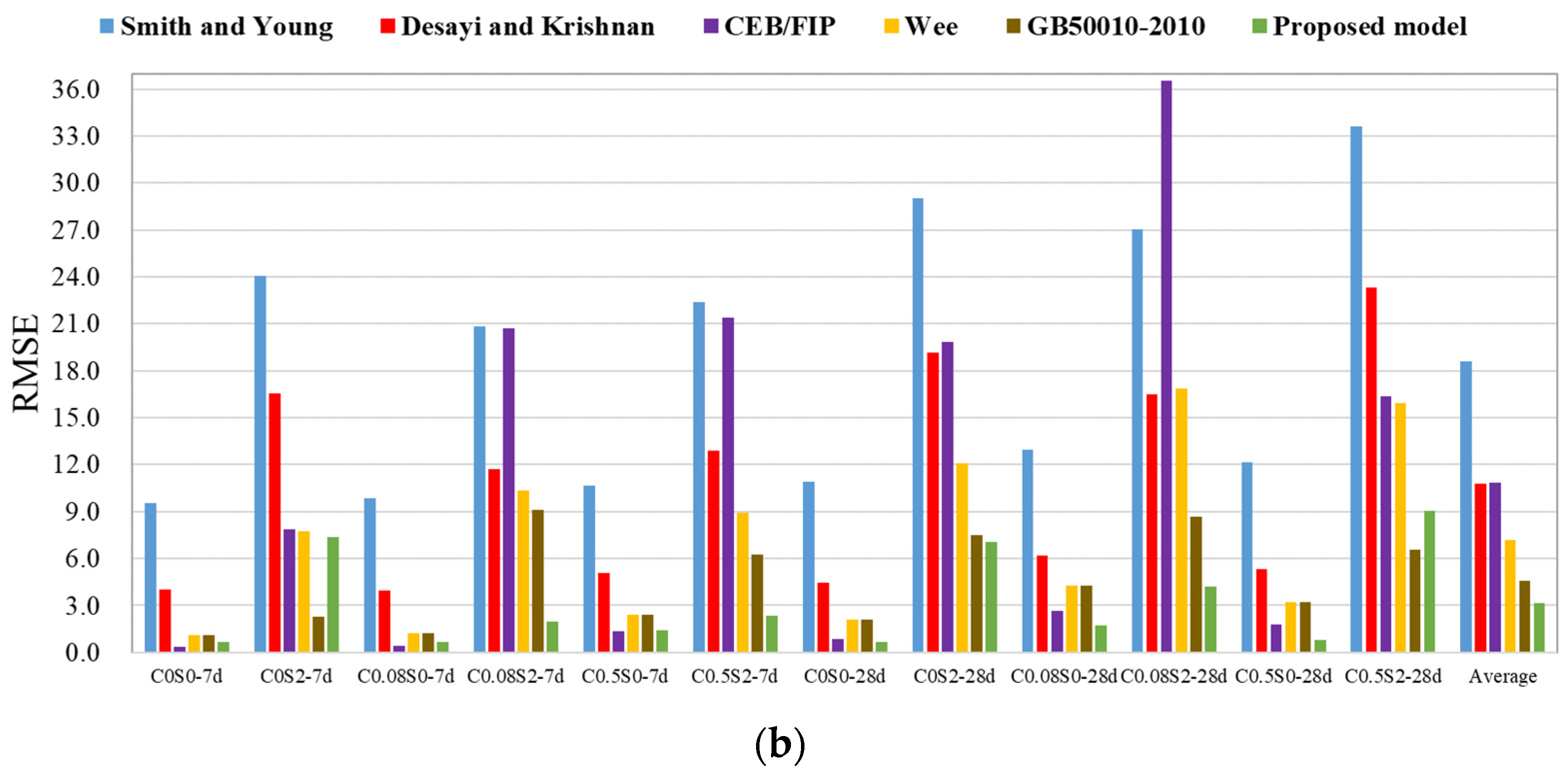
| Smith and Young [53] | 9.54 | 24.06 | 9.85 | 20.81 | 10.68 | 22.41 | 10.90 | 29.02 | 12.97 | 27.06 | 12.14 | 33.64 | 18.59 |
| Desayi and Krishnan [54] | 4.01 | 16.58 | 3.96 | 11.72 | 5.05 | 12.91 | 4.44 | 19.17 | 6.18 | 16.49 | 5.34 | 23.33 | 10.77 |
| CEB/FIP [41] | 0.36 | 7.89 | 0.41 | 20.69 | 1.35 | 21.42 | 0.83 | 19.85 | 2.64 | 36.57 | 1.77 | 16.38 | 10.85 |
| Wee [44] | 1.08 | 7.71 | 1.23 | 10.35 | 2.42 | 8.92 | 2.08 | 12.07 | 4.25 | 16.89 | 3.21 | 15.92 | 7.18 |
| GB50010-2010 [46] | 1.08 | 2.30 | 1.23 | 9.12 | 2.42 | 6.26 | 2.08 | 7.49 | 4.25 | 8.67 | 3.21 | 6.59 | 4.56 |
| Proposed model | 0.65 | 7.34 | 0.66 | 1.98 | 1.42 | 2.36 | 0.66 | 7.07 | 1.75 | 4.22 | 0.78 | 9.06 | 3.16 |
| Model | 7 Days Old | 28 Days Old | Average | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C0S0 | C0S2 | C0.08 S0 | C0.08 S2 | C0.5S0 | C0.5S2 | C0S0 | C0S2 | C0.08 S0 | C0.08 S2 | C0.5S0 | C0.5S2 | ||
| Smith and Young [53] | 0.748 | 0.898 | 0.764 | 0.845 | 0.701 | 0.819 | 0.767 | 0.779 | 0.717 | 0.927 | 0.744 | 0.874 | 0.799 |
| Desayi and Krishnan [54] | 0.956 | 0.997 | 0.962 | 0.985 | 0.933 | 0.973 | 0.961 | 0.954 | 0.936 | 0.999 | 0.951 | 0.991 | 0.967 |
| CEB/FIP [41] | 0.999 | 0.997 | 0.999 | 0.998 | 0.995 | 0.995 | 0.999 | 0.976 | 0.988 | 0.994 | 0.995 | 0.998 | 0.994 |
| Wee [44] | 0.997 | 0.999 | 0.996 | 0.987 | 0.985 | 0.981 | 0.991 | 0.945 | 0.970 | 0.999 | 0.982 | 0.986 | 0.985 |
| GB50010-2010 [46] | 0.997 | 0.999 | 0.996 | 0.987 | 0.985 | 0.981 | 0.991 | 0.945 | 0.970 | 0.999 | 0.982 | 0.986 | 0.985 |
| Proposed model | 0.999 | 0.997 | 0.999 | 0.999 | 0.995 | 0.995 | 0.999 | 0.981 | 0.995 | 0.993 | 0.999 | 0.998 | 0.996 |
| Model | 7 Days Old | 28 Days Old | Average | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C0S0 | C0S2 | C0.08 S0 | C0.08 S2 | C0.5S0 | C0.5S2 | C0S0 | C0S2 | C0.08 S0 | C0.08 S2 | C0.5S0 | C0.5S2 | ||
| Smith and Young [53] | 9.54 | 9.44 | 9.85 | 12.54 | 10.68 | 13.62 | 10.90 | 15.96 | 12.97 | 10.74 | 12.14 | 13.24 | 11.8 |
| Desayi and Krishnan [54] | 4.01 | 1.54 | 3.96 | 3.86 | 5.05 | 5.26 | 4.44 | 7.30 | 6.18 | 1.23 | 5.34 | 3.46 | 4.3 |
| CEB/FIP [41] | 0.36 | 1.72 | 0.41 | 1.38 | 1.35 | 2.33 | 0.83 | 5.29 | 2.64 | 3.05 | 1.77 | 1.61 | 1.89 |
| Wee [44] | 1.08 | 1.08 | 1.23 | 3.66 | 2.42 | 4.43 | 2.08 | 7.94 | 4.25 | 1.36 | 3.21 | 4.39 | 3.09 |
| GB50010-2010 [46] | 1.08 | 1.08 | 1.23 | 3.66 | 2.42 | 4.43 | 2.08 | 7.94 | 4.25 | 1.36 | 3.21 | 4.39 | 3.09 |
| Proposed model | 0.65 | 1.66 | 0.66 | 1.17 | 1.42 | 2.26 | 0.66 | 4.65 | 1.75 | 3.43 | 0.78 | 1.79 | 1.74 |
| Model | 7 Days Old | 28 Days Old | Average | ||||
|---|---|---|---|---|---|---|---|
| C0S2 | C0.08 S2 | C0.5S2 | C0S2 | C0.08 S2 | C0.5S2 | ||
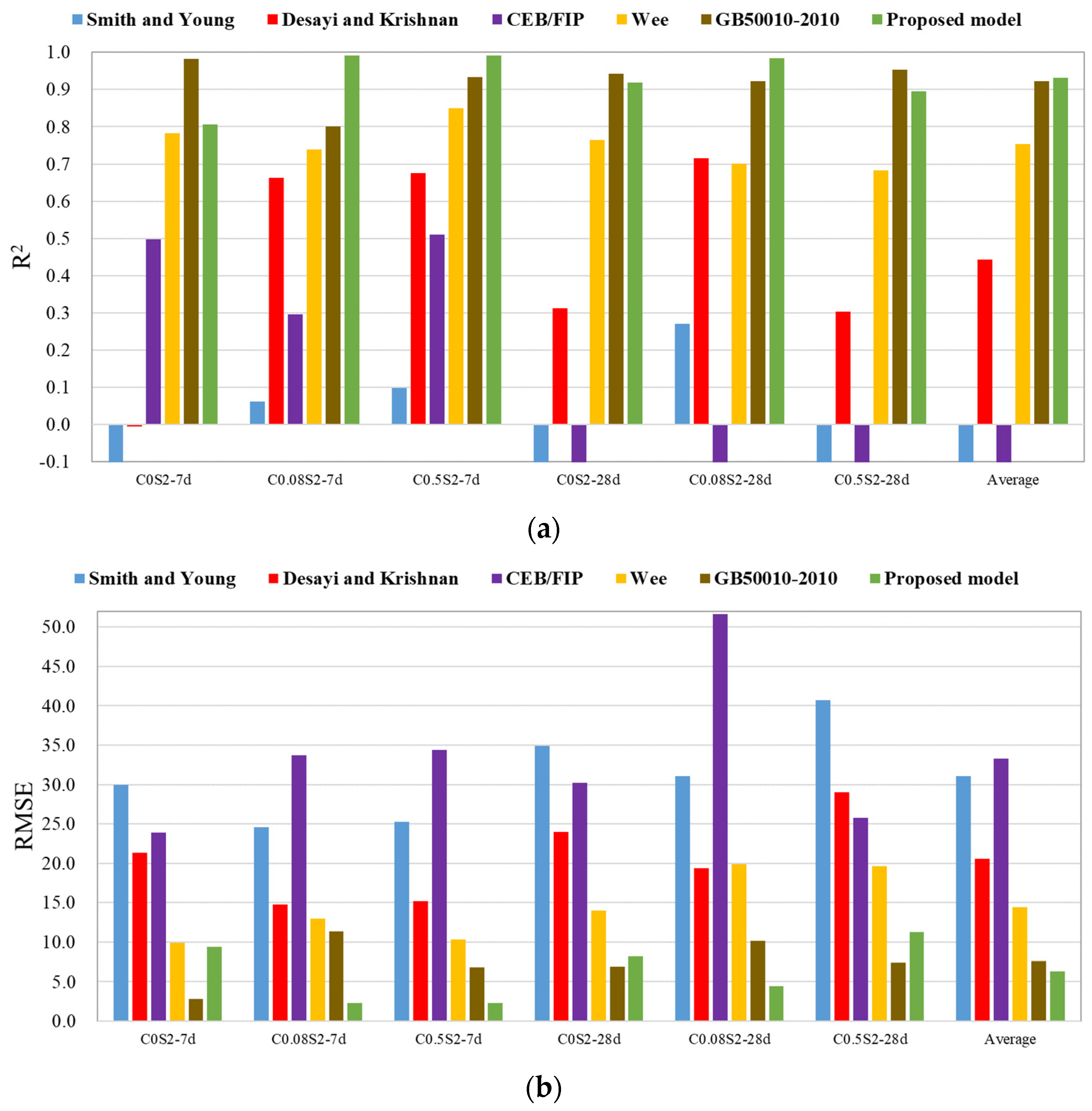
| Smith and Young [53] | −0.981 | 0.062 | 0.097 | −0.458 | 0.271 | −0.371 | −0.230 |
| Desayi and Krishnan [54] | −0.005 | 0.663 | 0.675 | 0.313 | 0.715 | 0.303 | 0.444 |
| CEB/FIP [41] | 0.497 | 0.296 | 0.510 | −2.486 | −17.185 | −0.599 | −3.161 |
| Wee [44] | 0.783 | 0.739 | 0.850 | 0.765 | 0.701 | 0.682 | 0.753 |
| GB50010-2010 [46] | 0.982 | 0.801 | 0.933 | 0.943 | 0.922 | 0.954 | 0.923 |
| Proposed model | 0.807 | 0.991 | 0.992 | 0.919 | 0.985 | 0.896 | 0.932 |
| Model | 7 Days Old | 28 Days Old | Average | ||||
|---|---|---|---|---|---|---|---|
| C0S2 | C0.08 S2 | C0.5S2 | C0S2 | C0.08 S2 | C0.5S2 | ||
| Smith and Young [53] | 29.99 | 24.63 | 25.31 | 34.89 | 31.07 | 40.72 | 31.1 |
| Desayi and Krishnan [54] | 21.36 | 14.77 | 15.18 | 23.95 | 19.42 | 29.04 | 20.62 |
| CEB/FIP [41] | 23.89 | 33.74 | 34.40 | 30.21 | 51.61 | 25.82 | 33.28 |
| Wee [44] | 9.92 | 12.99 | 10.32 | 14.02 | 19.89 | 19.60 | 14.45 |
| GB50010-2010 [46] | 2.82 | 11.35 | 6.88 | 6.88 | 10.17 | 7.47 | 7.59 |
| Proposed model | 9.37 | 2.35 | 2.34 | 8.21 | 4.41 | 11.24 | 6.32 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, P.; Jia, Q.; Li, Z.; Wu, Y.; Ma, Z.J. Theoretical Model for the Stress–Strain Curve of CNT-Reinforced Concrete under Uniaxial Compression. Buildings 2024, 14, 418. https://doi.org/10.3390/buildings14020418
Zhu P, Jia Q, Li Z, Wu Y, Ma ZJ. Theoretical Model for the Stress–Strain Curve of CNT-Reinforced Concrete under Uniaxial Compression. Buildings. 2024; 14(2):418. https://doi.org/10.3390/buildings14020418
Chicago/Turabian StyleZhu, Peng, Qihao Jia, Zhuoxuan Li, Yuching Wu, and Zhongguo John Ma. 2024. "Theoretical Model for the Stress–Strain Curve of CNT-Reinforced Concrete under Uniaxial Compression" Buildings 14, no. 2: 418. https://doi.org/10.3390/buildings14020418
APA StyleZhu, P., Jia, Q., Li, Z., Wu, Y., & Ma, Z. J. (2024). Theoretical Model for the Stress–Strain Curve of CNT-Reinforced Concrete under Uniaxial Compression. Buildings, 14(2), 418. https://doi.org/10.3390/buildings14020418








