Research on an Intelligent Identification Method for Cable-Stayed Force with a Damper Based on Microwave Radar Measurements
Abstract
1. Introduction
2. Working Principle
2.1. Microwave Radar Differential Interferometry Technique
2.2. Microwave Radar Frequency Conversion
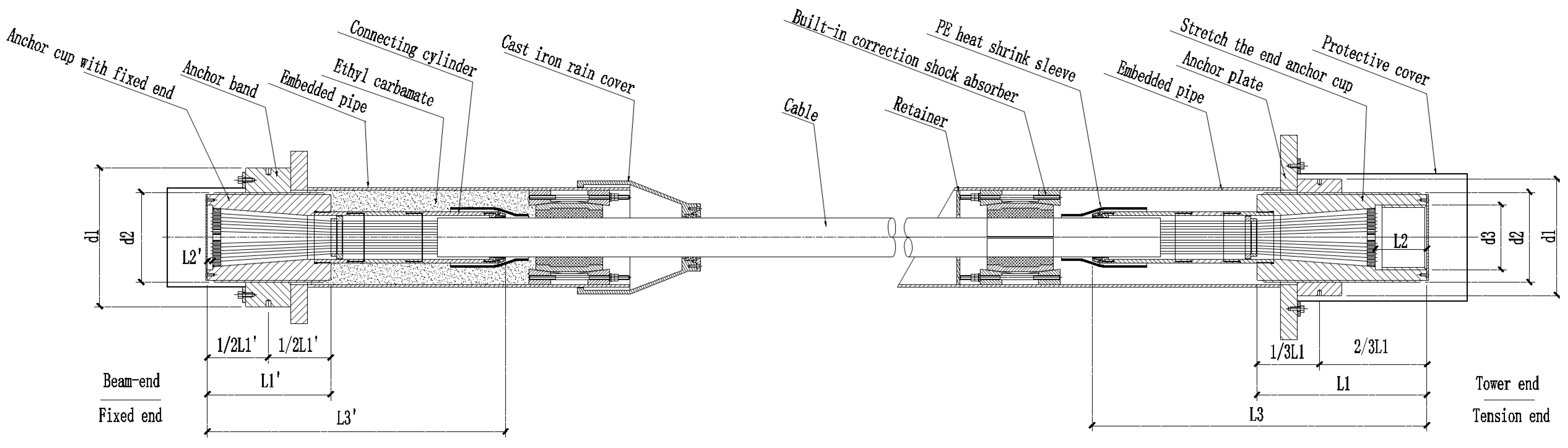
3. Calculation Formula for a Diagonal Cable with a Damper
3.1. Principle
3.2. Boundary Conditions
3.3. Calculation Process
3.4. Consideration of the Correction of Bending Stiffness
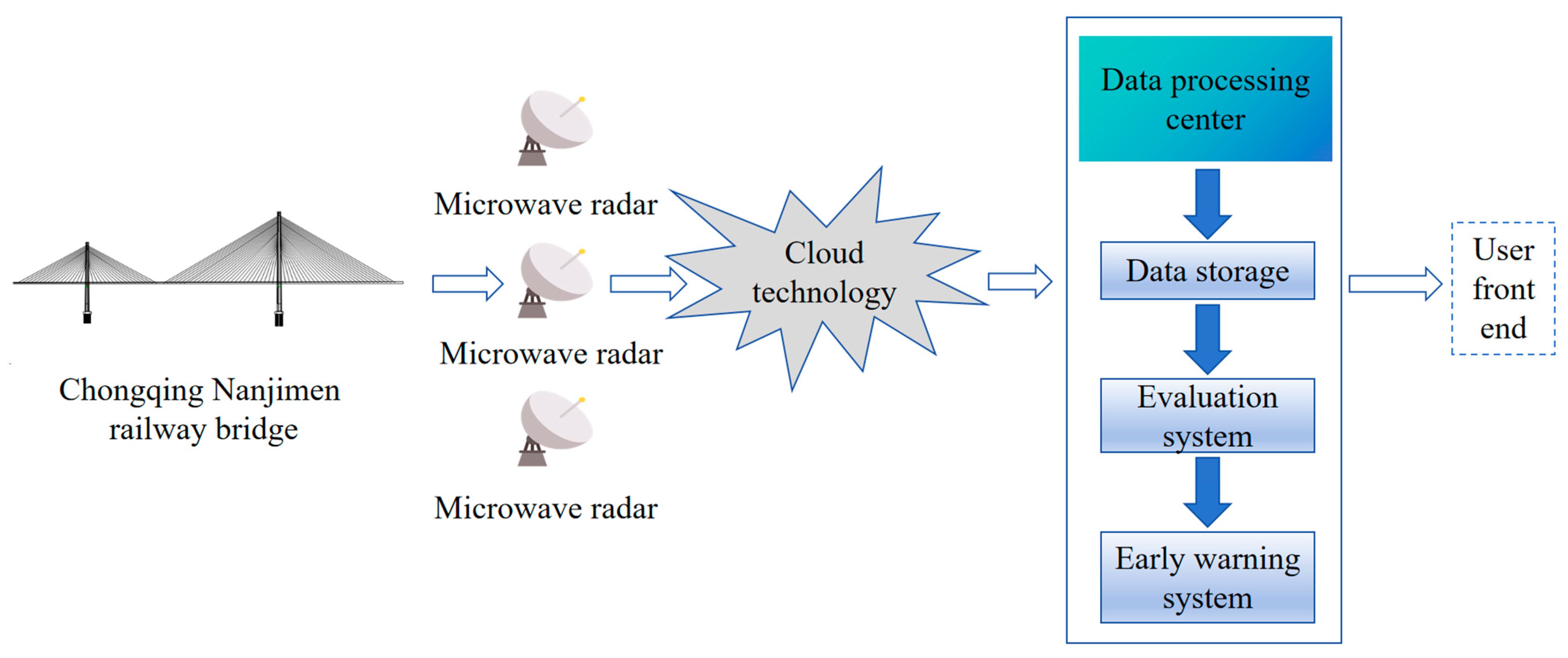
4. Evaluation and Early Warning through Cable Monitoring Based on Cloud Technology
- Sensor and data acquisition and transmission system: First, microwave radar was used to collect the cable vibration data in real time, and then the data were transmitted to the processing, analysis, and storage system through a data acquisition module and data transmission module.
- Data processing, analysis, and storage system: After the data were transmitted to the platform, the calculation formula for the cable force with a damper was used to obtain the monitoring values for professional analysis.
- Evaluation and early warning system: After the monitoring values were obtained, the following evaluation mechanism was established according to the “Technical specification for operation monitoring of urban rail transit facilities Part 2: Bridges (GB/T 39559.2-2020) [S]” [45]:
- 4.
- User front-end: Instructions were issued and data management functions were performed.
5. Engineering Applications
5.1. Project Overview
5.2. Health Monitoring System
5.2.1. System Overview
5.2.2. Microwave Radar Application
5.2.3. GNSS Application
5.2.4. Application of an Environmental Monitoring System
5.3. Application of the Derived Equation for the Calculation of the Cable Force with Dampers
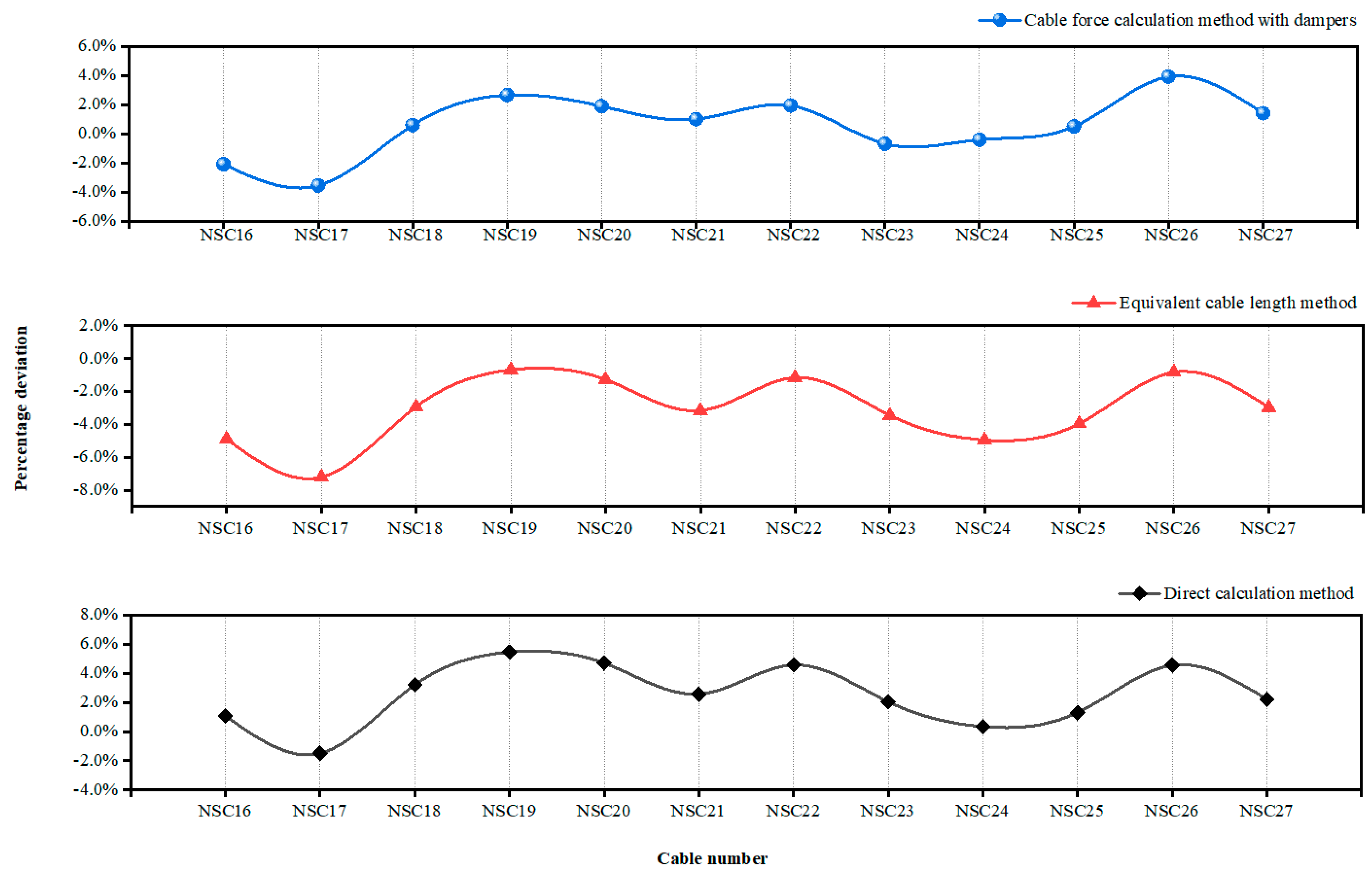
5.3.1. Error Analysis of the Formula for Calculating the Cable Force of a Cable-Stayed Cable with a Damper
5.3.2. Analysis of the Influence of Bending Stiffness on the Calculation
5.4. Intelligent Cloud Platform Application
6. Conclusions and Prospects
6.1. Conclusions
- Measuring the force of a cable with a damper based on microwave radar is an efficient and reliable method. The actual engineering experiments showed that the deviation rate of the cable force measurements was only 0.6% for a cable with a damper over 200 m in length. At the same time, the measurement angle could be freely adjusted, and the measurement penetration was stronger than that of the traditional method. It was proved that the measurement accuracy, efficiency, and applicability of microwave radar for cable force measurement were superior to those of traditional monitoring methods. This has wide application prospects in the field of cable force monitoring for slender cables with dampers.
- Considering the problem of calculating the cable force of cable-stayed cables with dampers, the presented formula is feasible and can effectively improve the accuracy of the calculation of the cable force. Three calculation methods were used to calculate the force of 12 cable-stayed cables with dampers in the mid-span of the north side of the Chongqing Nanjimen Railway Bridge. The maximum cable force error of the calculation formula for the force of a cable-stayed cable with dampers was only 3.9%, which was lower than 7.1% for the direct calculation method and 5.8% for the equivalent cable length method, which proved that the derived calculation formula was reliable, effective, and accurate. It has reference value in the field of cable force calculation for cable-stayed cables with dampers.
- The intelligent cable monitoring platform integrating monitoring, evaluation, and early warning has the functions of real-time monitoring, real-time analysis, and real-time early warning, and it can provide technical support for the scientific management and maintenance of bridges.
- However, microwave radar is susceptible to electromagnetic interference in the environment, resulting in measurement errors. In the presence of occlusions or space constraints, the measurement accuracy will be reduced. Therefore, it should not be used in an environment with strong electromagnetic interference, occlusions, or space restrictions. The measurement distance and frequency should be paid attention to in the measurement process to ensure the penetration of the signal and the accuracy of the measurement results.
6.2. Prospects
- (1)
- The research results in this study showed the achievement of efficient and high-precision measurement of long cables with dampers, but the influence of the cable diameter was not taken into account, and the measurement of short cables with dampers was not studied; further research will be carried out in follow-up work.
- (2)
- The calculation formula for a stayed cable with a damper derived in this study fully considers the influence of the damper, and the calculation results were in line with the expectations, but the influence of the damper was ignored when solving the model. The influence of the damper will be further studied in subsequent work.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Fang, R.; Wu, Y.; Wei, W.; Na, L.; Biao, Q.; Jiang, P.; Yang, Q. An Improved Static Residual Force Algorithm and Its Application in Cable Damage Identification for Cable-Stayed Bridges. Appl. Sci. 2022, 12, 2945. [Google Scholar] [CrossRef]
- Dai, J.; Qin, F.; Geng, J.; Chen, Y. Review on Cable Force Optimization Method for Cable-staved Bridge in Completed Bridge State. China J. Highw. Transp. 2019, 32, 17–37. [Google Scholar]
- Liu, X.; Yi, X.; Wang, B.; Liu, Y. Condition Assessment of Grouped Cable Forces of Cable-Stayed Bridge Using Deflection Data. Buildings 2023, 13, 472. [Google Scholar] [CrossRef]
- Zhou, Y.; Huang, Z.-H.; Wang, Y.; Xiang, Z.-F.; Zhou, J.-T.; Zhang, X.-S. Measurement Method of Stay Cable Force Based on Measured Cable Shape Using Laser Scanning. China J. Highw. Transp. 2021, 34, 91–103. [Google Scholar]
- Wang, S.-R.; Wang, B.; Cheng, C.-S.; Zhou, J.-T.; Qu, J.-Q.; Tan, H. Research on Influencing Factors of Cable Force Measurement Methods Based on Alignment Recognition. China J. Highw. Transp. 2023, 36, 154–165. [Google Scholar]
- Zhang, L.; Qiu, G.; Chen, Z. Structural health monitoring methods of cables in cable-stayed bridge: A review. Measurement 2021, 168, 108343. [Google Scholar] [CrossRef]
- Zhang, Z.-J.; Wang, R.-H.; Zhen, X.-X.; Liu, X.-H. Evaluation of Measurement Methods for Tension of Parallel Steel Strand Stay Cables. Bridge Constr. 2016, 46, 42–47. [Google Scholar]
- Zhang, R.; Yang, Z.; Zhu, X.; Liang, Q.; Xu, R. Practical Formulas to Calculate Suspender Tension Based on Frequency. J. Southwest Jiaotong Univ. 2015, 50, 823–829. [Google Scholar]
- Li, G.-p.; Li, J.-x. Tension Strategy Derived by Non-stress Length of Parallel Steel Strand Stay Cables. China J. Highw. Transp. 2017, 30, 48–56. [Google Scholar]
- Shen, Q.; Yuan, D.-R.; Chen, C.-X. A New Monitoring Device for the Force States of the Pressure Dispersed Anchor Cable. In Proceedings of the 2015 International Conference on Advanced Engineering Materials and Technology, Guangzhou, China, 22–23 August 2015; pp. 836–841. [Google Scholar]
- Liu, X.; Wu, D.; He, C.; Feng, H.; Wu, B. Comparison of AC and pulsed magnetization-based elasto-magnetic methods for tensile force measurement in steel strand. Measurement 2018, 117, 410–418. [Google Scholar] [CrossRef]
- Ji, B.; Cheng, M.; Fu, Z.; Chen, X.; Sun, Y. Influential factors in cable force measurement of cable-stayed bridges based on vibration frequency method. J. Cent. South Univ. (Sci. Technol.) 2015, 46, 2620–2625. [Google Scholar]
- Fang, Z.; Wang, J.-q. Practical Formula for Cable Tension Estimation by Vibration Method. J. Bridge Eng. 2012, 17, 161–164. [Google Scholar] [CrossRef]
- Jo, H.C.; Kim, S.H.; Lee, J.; Sohn, H.-G.; Lim, Y.M. Sag-based cable tension force evaluation of cable-stayed bridges using multiple digital images. Measurement 2021, 186, 110053. [Google Scholar] [CrossRef]
- Liu, X.; Chen, Y.; Hu, H.; Feng, S.; Feng, Z. Measurement method of natural frequencies and tension forces for cables based on elasto-magnetic sensors calibrated by frequencies. AIP Adv. 2022, 12, 015301. [Google Scholar] [CrossRef]
- Liu, H.; Wang, L.; Guo, L.; Zhang, F.; Chen, Z. Intelligent identification of cable force for short and thick building cables based on deep learning. J. Build. Struct. 2023, 44, 204–213. [Google Scholar]
- Wu, W.-H.; Chen, C.-C.; Chen, Y.-C.; Lai, G.; Huang, C.-M. Tension determination for suspenders of arch bridge based on multiple vibration measurements concentrated at one end. Measurement 2018, 123, 254–269. [Google Scholar] [CrossRef]
- Bonopera, M.; Chang, K.-C.; Tullini, N. Vibration of prestressed beams: Experimental and finite-element analysis of post–tensioned thin-walled box-girders. J. Constr. Steel Res. 2023, 205, 107854. [Google Scholar] [CrossRef]
- He, X.-J.; Yang, Y.-C.; Xiao, X.; Wang, J.-J. A vibration frequency method based on finite element equivalent cable length. Bridge Constr. 2016, 46, 40–44. [Google Scholar]
- Tang, S.-H.; Fang, Z. Equivalent cable length calculation method considering influence of intermediate supports. J. Vib. Shock 2013, 32, 82–87. [Google Scholar]
- Wang, X.; Wang, X.; Liang, X.; Zhou, M.; Du, Y. Analysis of suspension cable force of large-span steel tube concrete tied arch bridge. J. Vib. Shock 2023, 42, 306–313. [Google Scholar]
- Gong, J. Design and research of long-span concrete cable-stayed bridge for high-speed railway. J. Railw. Sci. Eng. 2020, 17, 1611–1619. [Google Scholar]
- Sohaib, M. Study on the Influence of Dampers on Cable-Stayed Bridge Cable Force Estimation. Master’s Thesis, Harbin Institute of Technology, Harbin, China, 2019. [Google Scholar]
- Yang, X. Research on Calculation Method and Influencing Factors of Cable Force of Asymmetric Cable-Stayed Bridge. Master’s Thesis, Lanzhou Jiaotong University, Lanzhou, China, 2020. [Google Scholar]
- Liang, X.; Hui, D.; Zhou, J.; Zhong, J.; Yang, J.; Xiao, Y. Construction and application of health monitoring and evaluation system for long-span cable-stayed Bridges. J. China Foreign Highw. 2016, 36, 92–97. [Google Scholar]
- T/CCTAS 68-2023; Technical Specification for the Detection of Bridge Structure Deformation by millimeter Wave Radar (T/CCTAS 68-2023) Group Standard. China Transportation Association: Beijing, China, 2023.
- Wang, J.; Wang, X.; Zhou, Z. Nano millimeter wave radar for bridge cable tension measurement. J. Natl. Univ. Def. Technol. 2022, 44, 118–122. [Google Scholar]
- Wang, T.; Zhang, J.; Jiang, S.; Liu, W.; Chen, Y. Time-varying cable force identification method based on radar vibration measurement technique. J. Vib. Shock 2023, 42, 205–212. [Google Scholar]
- Liu, Y.; Xie, J.-Z.; Tafsirojjaman, T.; Yue, Q.-R.; Tan, C.; Che, G.-J. CFRP lamella stay-cable and its force measurement based on microwave radar. Case Stud. Constr. Mater. 2022, 16, e00824. [Google Scholar] [CrossRef]
- Xu, W.; Du, D.; Kasai, K.; Wang, S. Optimization layout of viscous dampers and its application in retrofitting of a high-rise steel structure. J. Build. Struct. 2022, 43, 32–44. [Google Scholar]
- Duan, Y.-F.; Huang, J.-S.; Deng, N.; Wang, S.-M.; Ying, Z.-G.; He, W. Vector form intrinsic finite element based simulation on parametric vibration of cables. J. Vib. Eng. 2023, 36, 188–195. [Google Scholar]
- Main, J.A.; Jones, N.P. Vibration of tensioned beams with intermediate damper. II: Damper near a support. J. Eng. Mech. 2007, 133, 379–388. [Google Scholar] [CrossRef]
- Jiang, L.L.; Chen, Q.Z. Research on calculation formula of frequency faso force test. Highway 2018, 63, 164–166. [Google Scholar]
- Dan, D.; Zhao, Y.; Yang, T. Vibration measurement based cable trnsion identifcation method for cable-damper system. J. Vib. Shock 2013, 32, 123–127+204. [Google Scholar]
- Huang, W.; Wu, Q.; Chen, B. Force measurement of stay cable considering damper influence. J. Guangxi Univ. (Nat. Sci. Ed.) 2018, 43, 416–424. [Google Scholar]
- Fang, Z.; Zhang, Z.Y. Test of Cable Tension in Cable-stayed Bridges. China J. Highw. Transp. 1997, 1, 51–58. [Google Scholar]
- JGJ297-2013; Technical Specification for Seismic Energy Dissipation of Buildings. Ministry of Housing and Urban-Rural Development of the People’s Republic of China: Beijing, China, 2013.
- JTG/T3650-01-2022; Technical Regulations for Highway Bridge Construction Monitoring. Ministry of Transport of the People’s Republic of China: Beijing, China, 2022.
- Teng, G.; Cao, X.; Gai, W.; Jiang, R. An Experimental Study on Intelligent Bearing System for Bridge Health Monitoring. In Proceedings of the International Conference on Innovative Solutions in Hydropower Engineering and Civil Engineering, Berlin, Germany, 25–27 December 2022; pp. 319–324. [Google Scholar]
- He, Z.; Li, W.; Salehi, H.; Zhang, H.; Zhou, H.; Jiao, P. Integrated structural health monitoring in bridge engineering. Autom. Constr. 2022, 136, 104168. [Google Scholar] [CrossRef]
- Li, X.; Luo, H.; Ding, P.; Chen, X.; Tan, S. Prediction Study on the Alignment of a Steel-Concrete Composite Beam Track Cable-Stayed Bridge. Buildings 2023, 13, 882. [Google Scholar] [CrossRef]
- Sun, L.-M.; Shang, Z.-Q.; Xia, Y. Development and Prospect of Bridge Structural Health Monitoring in the Context of Big Data. China J. Highw. Transp. 2019, 32, 1–20. [Google Scholar]
- Zhou, Y.; Sun, L. Insights into temperature effects on structural deformation of a cable-stayed bridge based on structural health monitoring. Struct. Health Monit. 2018, 18, 778–791. [Google Scholar] [CrossRef]
- Tong, K.; Zhang, H.; Zhao, R.; Zhou, J.; Ying, H. Investigation of SMFL monitoring technique for evaluating the load-bearing capacity of RC bridges. Eng. Struct. 2023, 293, 116667. [Google Scholar] [CrossRef]
- GB/T 39559.2-2020; Specifications for Operational Monitoring of Urban Rail Transit Facilities—Part 2: Bridge. Ministry of Transport of the People’s Republic of China: Beijing, China, 2021.



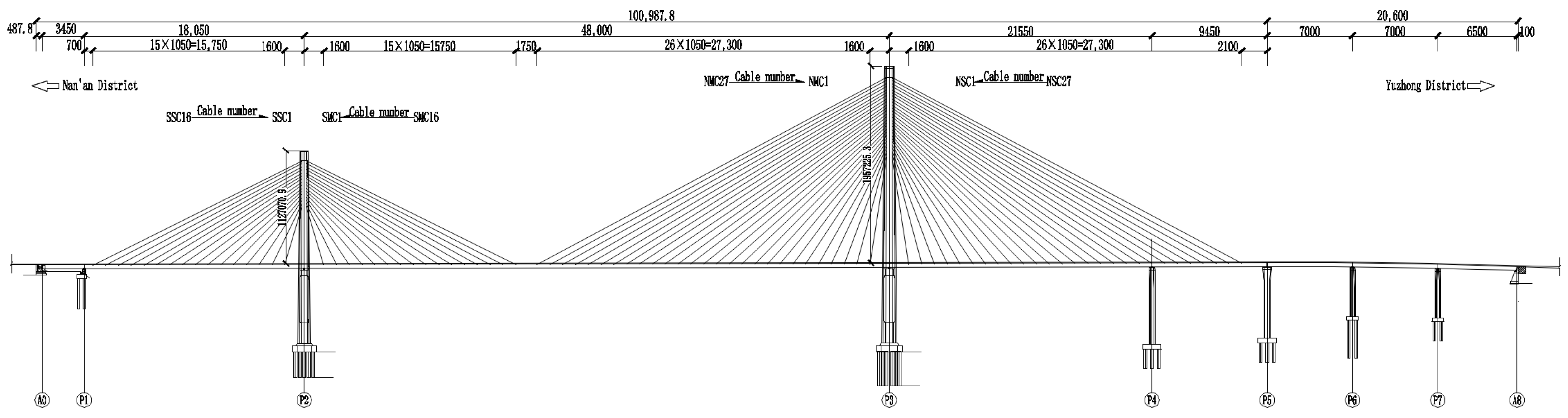
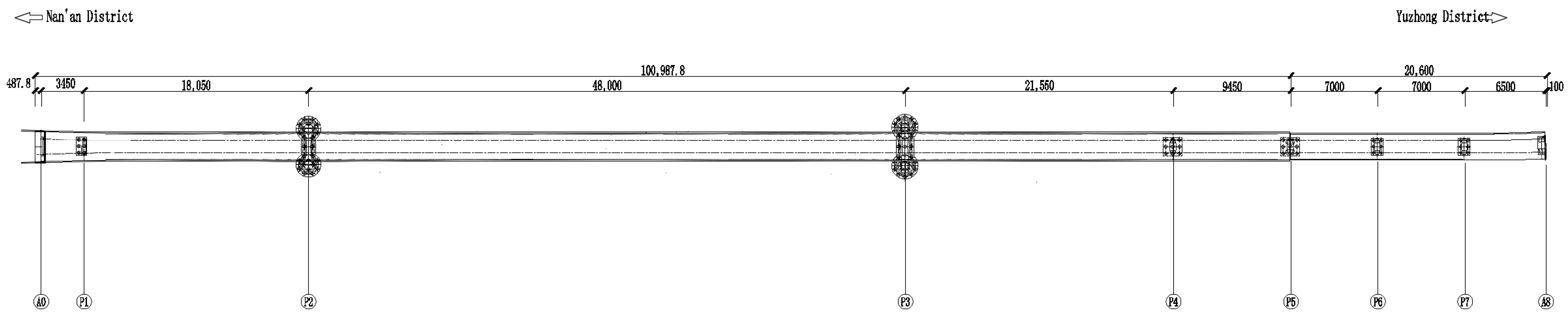


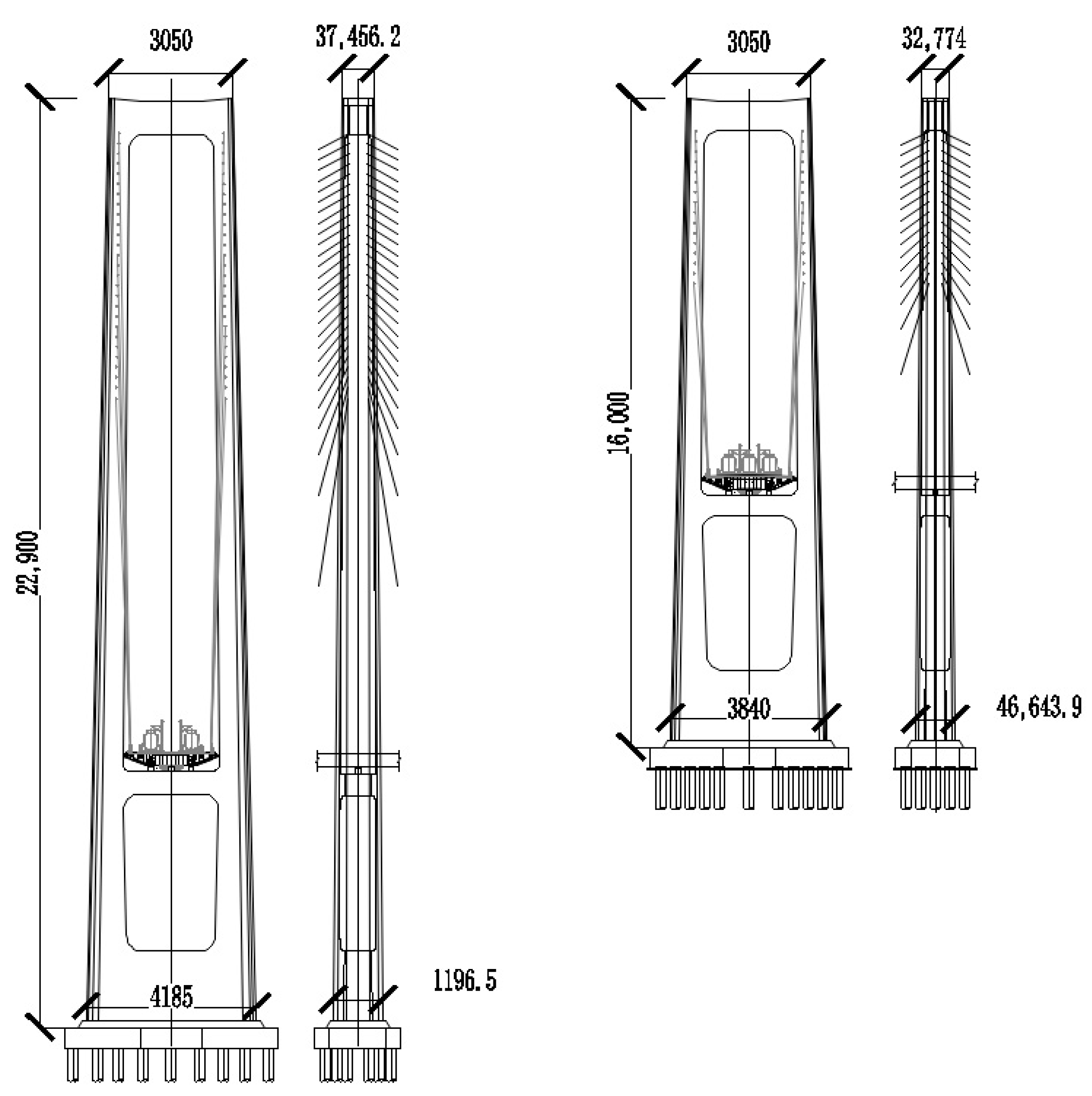
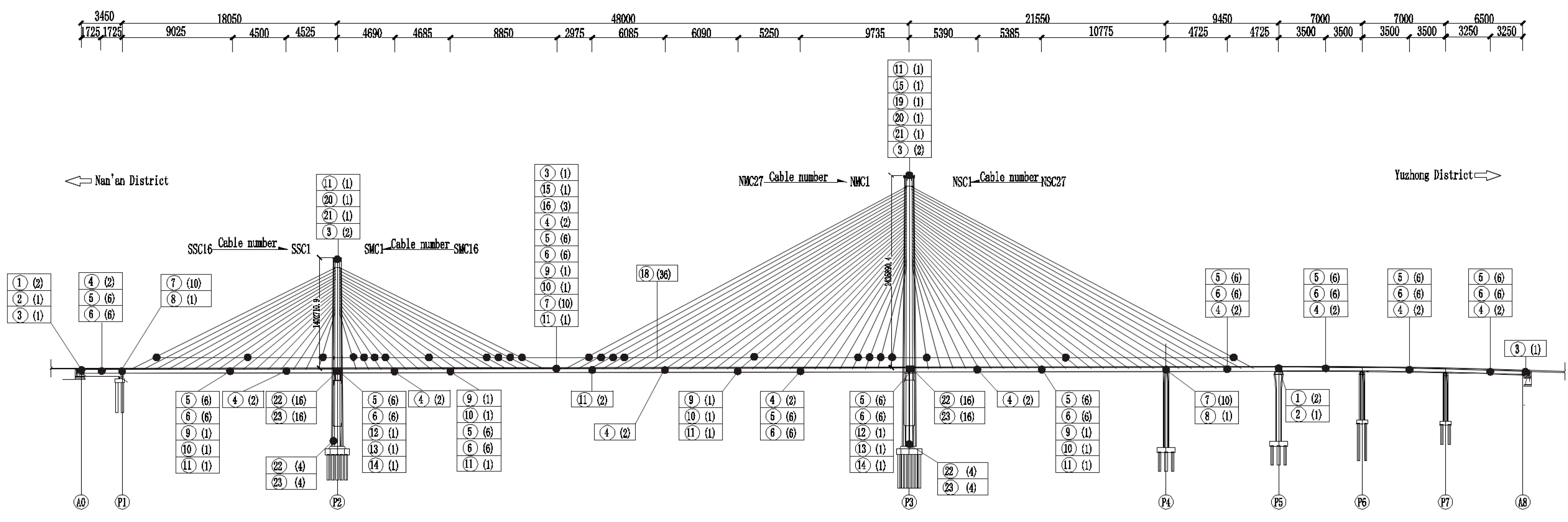





| Monitoring Item | Equipment Category | Monitoring Frequency |
|---|---|---|
| ① | Fiber grating displacement meter | 1 Hz |
| ②, ⑧ | Inclination sensor | 1 Hz |
| ④ | Differential pressure—static level | 1 Hz |
| ⑤, ⑦, ㉒ | Fiber grating strain gauge | 1 Hz |
| ⑥, ⑯, ㉓ | Hygrograph | 1/600 Hz |
| ⑨, ⑩, ⑳, ㉑ | Acceleration sensor | 1/120 Hz |
| ⑪ | GNSS | 1 Hz |
| ⑫, ⑬, ⑭ | Acceleration sensor | 1 Hz |
| ⑮ | Mechanical anemometer | 1 Hz |
| ⑰ | Radar water level gauge | 1/600 Hz |
| ⑱ | Cable force acceleration sensor | 1/120 Hz |
| Transcore pressure sensor | 1/60 Hz | |
| ⑲ | Rain gauge | 1/60 Hz |
| Number | Fundamental Frequency | Theoretical Cable Force S1 (kN) | Measured Cable Force S2 (kN) | |||||
|---|---|---|---|---|---|---|---|---|
| Vibration Frequency Method | Pressure Sensor Method | Microwave Radar Method | Vibration Frequency Method | Pressure Sensor Method | Microwave Radar Method | |||
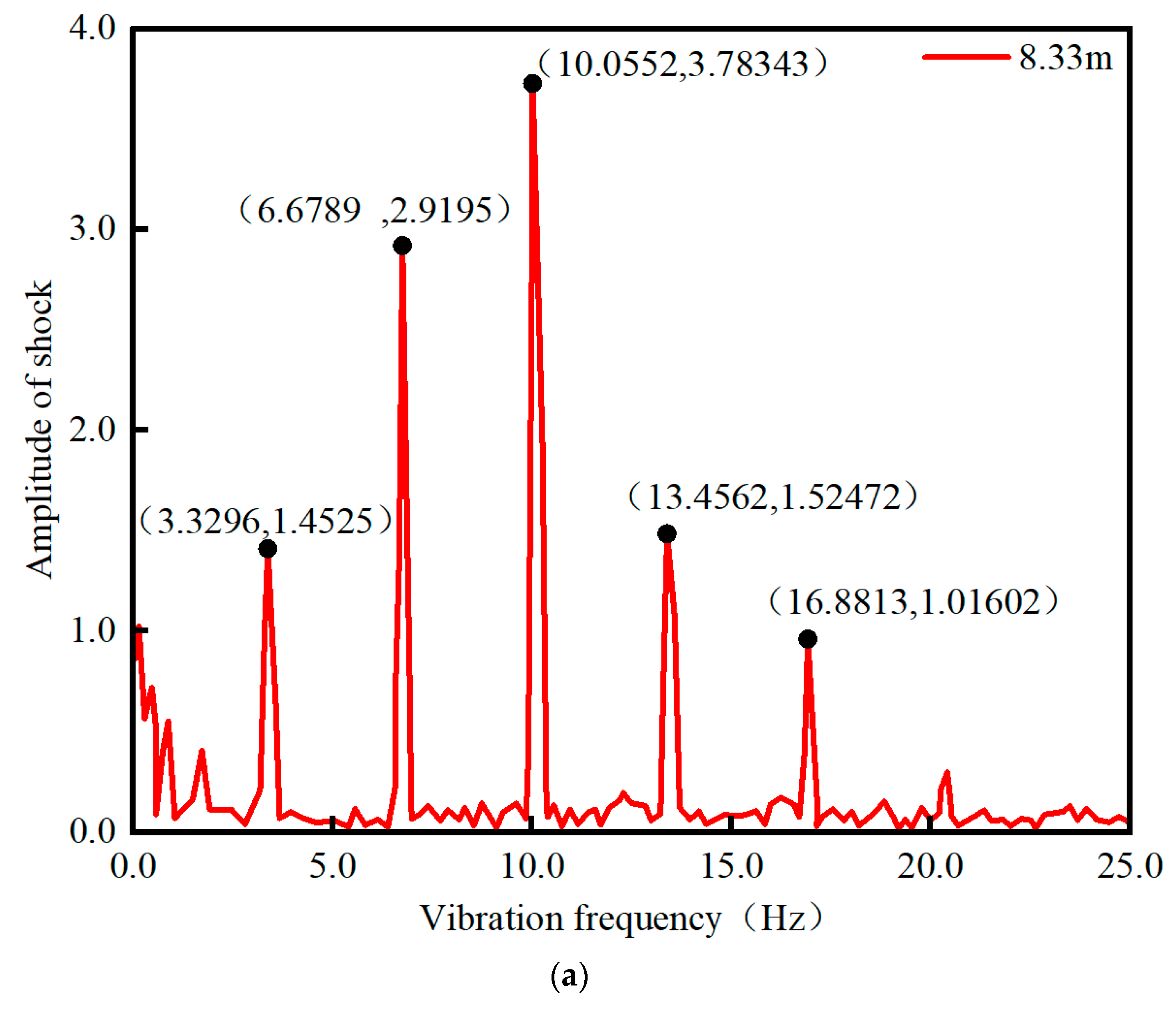
| NMC27 | 0.43 | 6902 | 6550 | 6262 | 6860 | −5.1% | −9.3% | −0.6% |
| Number | Fundamental Frequency | Theoretical Cable Force S1 (kN) | Measured Cable Force S2 (kN) | |||||
|---|---|---|---|---|---|---|---|---|
| Vibration Frequency Method | Pressure Sensor Method | Microwave Radar Method | Vibration Frequency Method | Pressure Sensor Method | Microwave Radar Method | |||
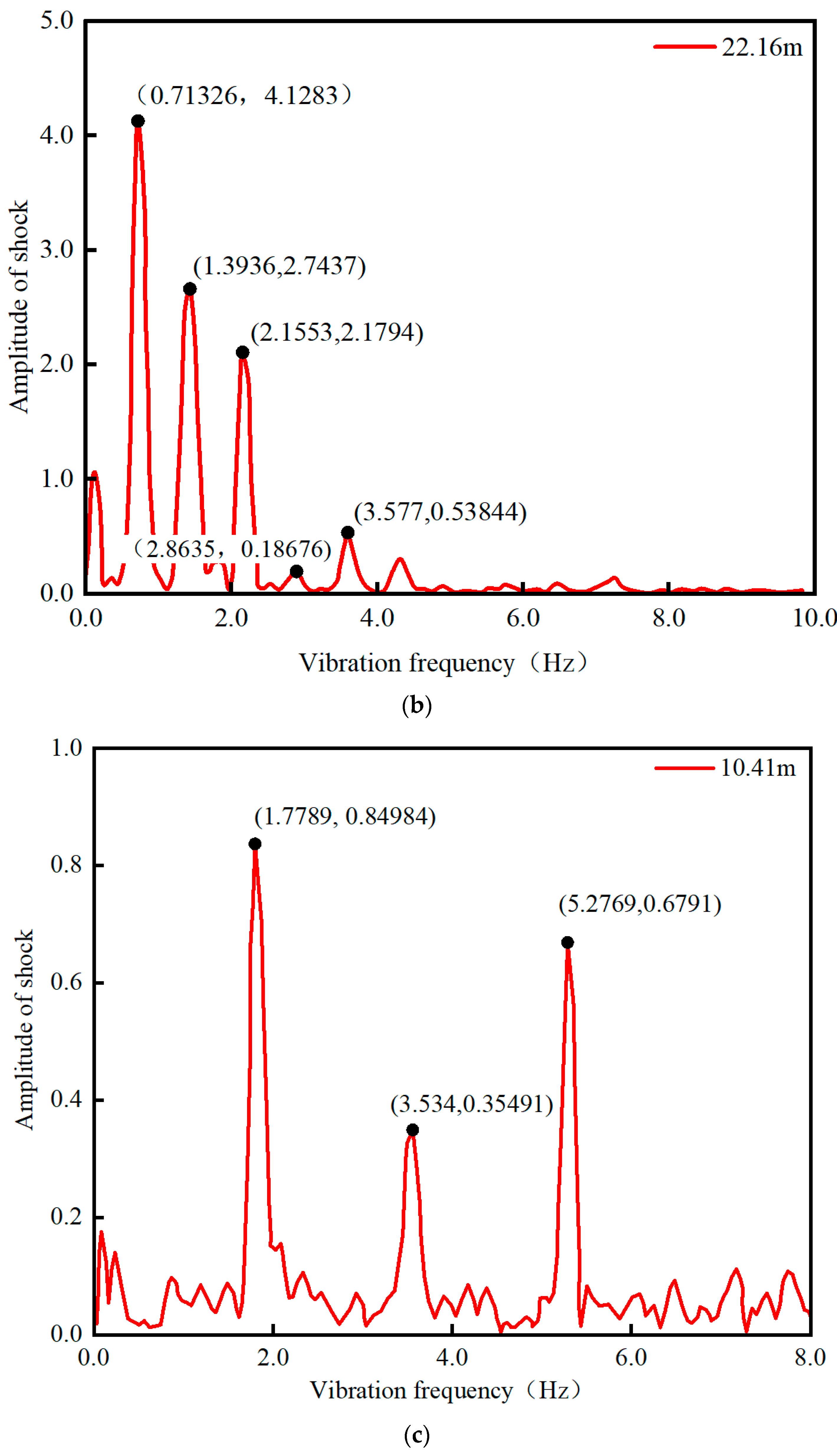
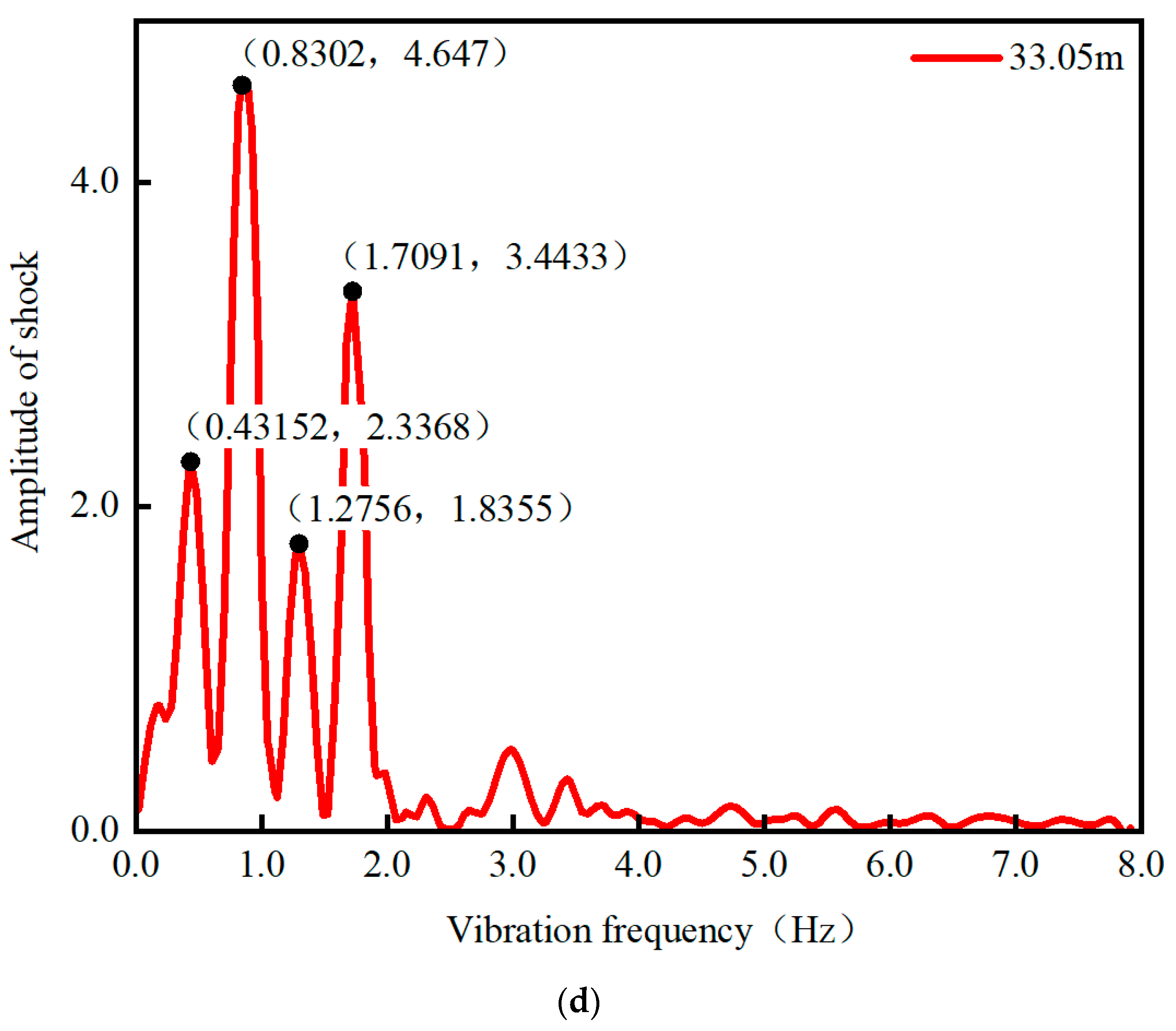
| SMC1 | 3.33 | 4139 | 4010 | 3901 | 4060 | −3.1% | −5.8% | −1.9% |
| SMC16 | 0.71 | 6853 | 6403 | 6302 | 6638 | −6.6% | −8.0% | −3.1% |
| NMC1 | 1.78 | 3695 | 3903 | 3609 | 3804 | 5.6% | −2.3% | 2.9% |
| Project | Vibration Frequency Method | Pressure Sensor Method | Microwave Radar Method |
|---|---|---|---|
| Labor cost | 3–4 people | 3–4 people | 2 people |
| Multi-object measurement | Nonsupport | Nonsupport | Up to 10 cables can be measured simultaneously |
| Precision | The deviation of cable force is large | The cable force deviation is large | Cable force deviation is low |
| Efficiency | One at a time | One at a time | More than 10 at a time |
| Measurement parameter | Frequency | Stress | Displacement |
| Measurement mode | Contact measurement | Contact measurement | Non-contact measurement |
| How tedious the preparation is | A ladder or an elevator is necessary | The sensor must be embedded in advance | Can be directly set up and freely adjusted |
| Penetration characteristic | No | No | Penetrable HDPE/PE sheath |
| Types | Maximum Damping Force (kN) | Maximum Stroke x (mm) | ||
|---|---|---|---|---|
| Linear viscous dampers | 2700 | 0.3 | 3000 | 650 |
| Number | Designed Cable Force (kN) | Actual Calculated Cable Force (kN) | Error Relative to the Theoretical Force | ||||
|---|---|---|---|---|---|---|---|
| Direct Calculation Method | Equivalent Cable Length Method | Cable Force Calculation Method with Dampers | Direct Calculation Method | Equivalent Cable Length Method | Cable Force Calculation Method with Dampers | ||
| NSC16 | 3106 | 3281 | 3086 | 3178 | 5.6% | −0.6% | 2.3% |
| NSC17 | 5075 | 5217 | 4915 | 5109 | 2.8% | −3.2% | 0.7% |
| NSC18 | 5052 | 5366 | 5046 | 5230 | 6.2% | −0.1% | 3.5% |
| NSC19 | 5006 | 5360 | 5047 | 5218 | 7.1% | 0.8% | 4.2% |
| NSC20 | 4370 | 4592 | 4330 | 4469 | 5.1% | −0.9% | 2.3% |
| NSC21 | 5022 | 5136 | 4848 | 5008 | 2.3% | −3.5% | −0.3% |
| NSC22 | 5103 | 5285 | 4995 | 5152 | 3.6% | −2.1% | 1.0% |
| NSC23 | 5124 | 5175 | 4897 | 5037 | 1.0% | −4.4% | −1.7% |
| NSC24 | 5141 | 5115 | 4845 | 5077 | −0.5% | −5.8% | −1.3% |
| NSC25 | 5019 | 5058 | 4795 | 5018 | 0.8% | −4.5% | 0.0% |
| NSC26 | 6406 | 6677 | 6333 | 6636 | 4.2% | −1.1% | 3.6% |
| NSC27 | 5336 | 5454 | 5177 | 5411 | 2.2% | −3.0% | 1.4% |
| Cable Number | Original Cable Length (m) | S (EI = 0 (kN)) | S0 (EI ≠ 0 (kN)) | |
|---|---|---|---|---|
| NSC16 | 208 | 3178 | 3178 | 1.00 |
| NSC17 | 218 | 5109 | 5109 | 1.00 |
| NSC18 | 228 | 5230 | 5230 | 1.00 |
| NSC19 | 238 | 5218 | 5218 | 1.00 |
| NSC20 | 248 | 4469 | 4469 | 1.00 |
| NSC21 | 259 | 5008 | 5008 | 1.00 |
| NSC22 | 269 | 5152 | 5152 | 1.00 |
| NSC23 | 279 | 5037 | 5037 | 1.00 |
| NSC24 | 289 | 5077 | 5077 | 1.00 |
| NSC25 | 300 | 5018 | 5018 | 1.00 |
| NSC26 | 310 | 6636 | 6636 | 1.00 |
| NSC27 | 321 | 5411 | 5411 | 1.00 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Huang, X.; Ding, P.; Wang, Q.; Wang, Q. Research on an Intelligent Identification Method for Cable-Stayed Force with a Damper Based on Microwave Radar Measurements. Buildings 2024, 14, 568. https://doi.org/10.3390/buildings14030568
Li X, Huang X, Ding P, Wang Q, Wang Q. Research on an Intelligent Identification Method for Cable-Stayed Force with a Damper Based on Microwave Radar Measurements. Buildings. 2024; 14(3):568. https://doi.org/10.3390/buildings14030568
Chicago/Turabian StyleLi, Xiaogang, Xiangsheng Huang, Peng Ding, Qiansong Wang, and Qin Wang. 2024. "Research on an Intelligent Identification Method for Cable-Stayed Force with a Damper Based on Microwave Radar Measurements" Buildings 14, no. 3: 568. https://doi.org/10.3390/buildings14030568
APA StyleLi, X., Huang, X., Ding, P., Wang, Q., & Wang, Q. (2024). Research on an Intelligent Identification Method for Cable-Stayed Force with a Damper Based on Microwave Radar Measurements. Buildings, 14(3), 568. https://doi.org/10.3390/buildings14030568





