Investigating the Influence of the Improved Multibody Rope Approach on the Structural Behavior of Dakar Mosque Gridshell Structure
Abstract
:1. Introduction
2. Form-Finding Techniques
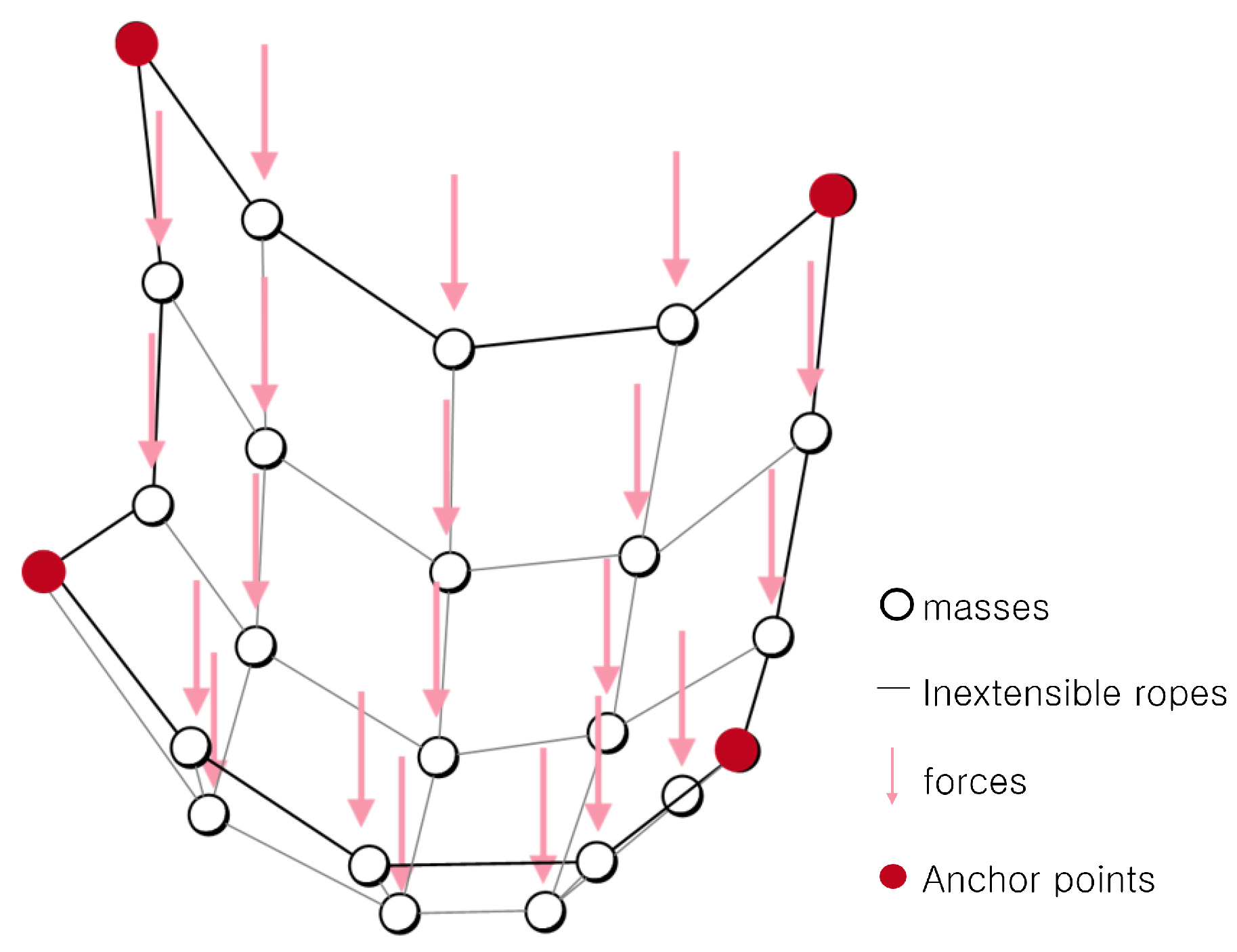
2.1. The Basic MRA Method
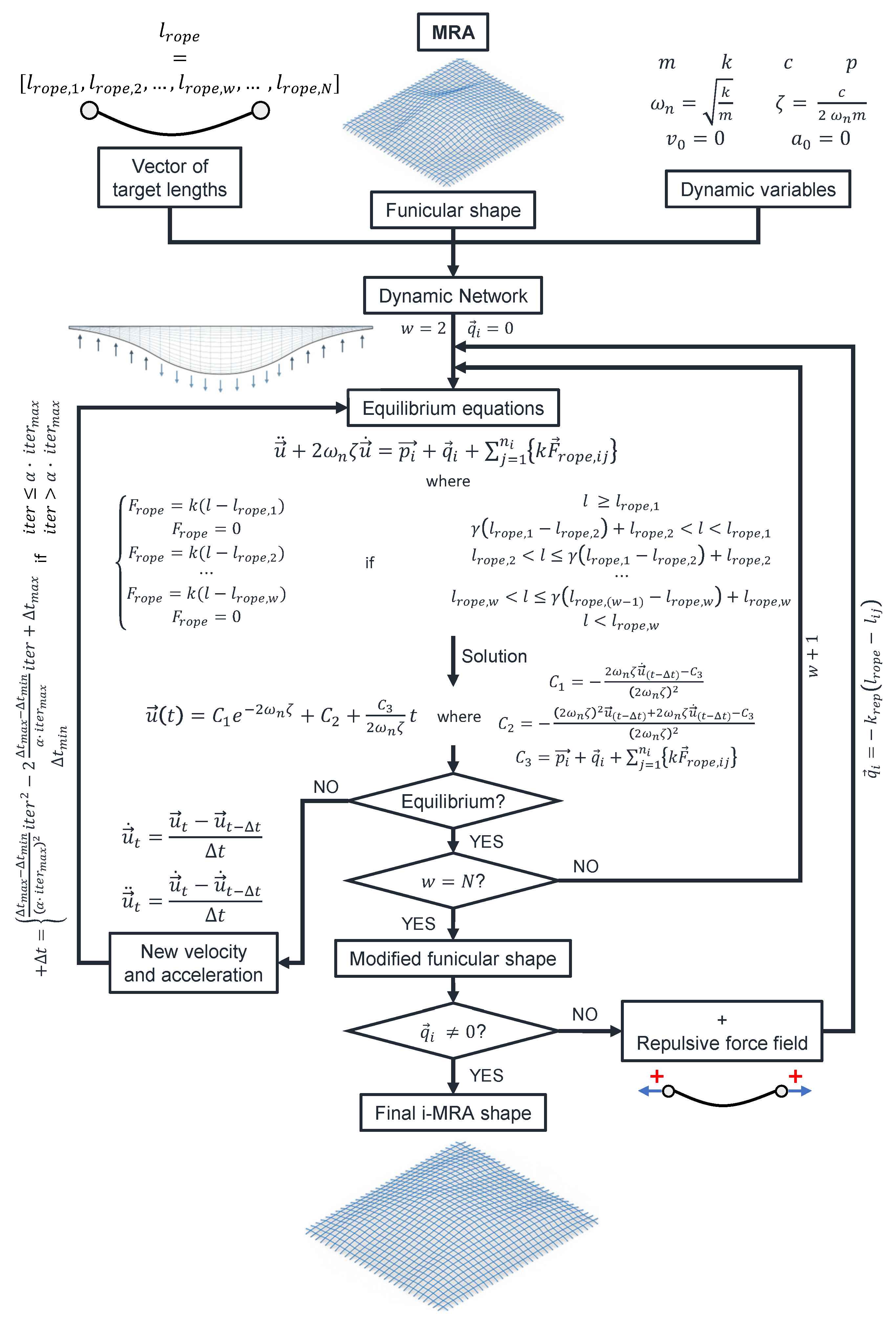
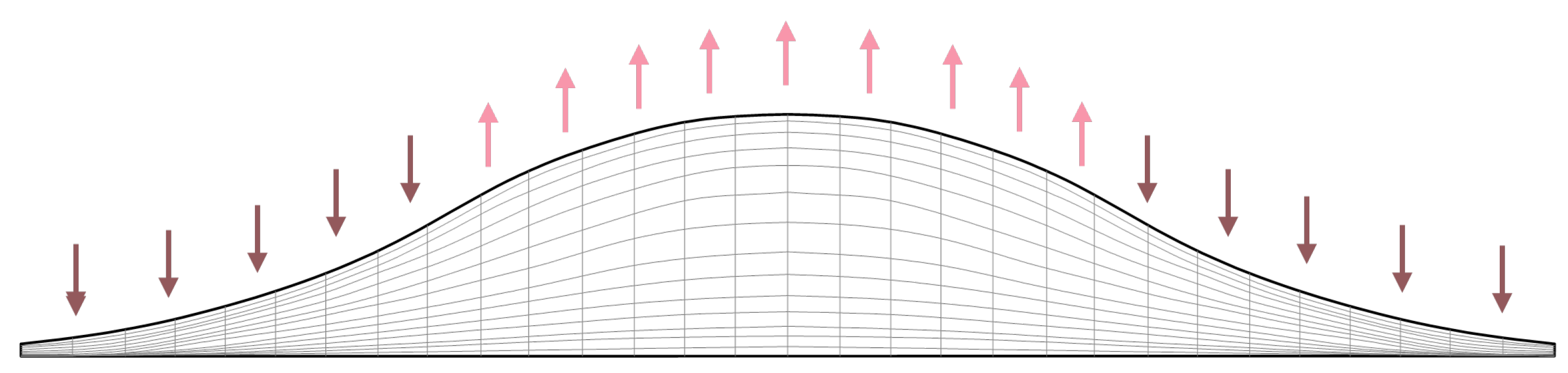
2.2. The Improved MRA Method
3. Geometry of the Dakar Mosque
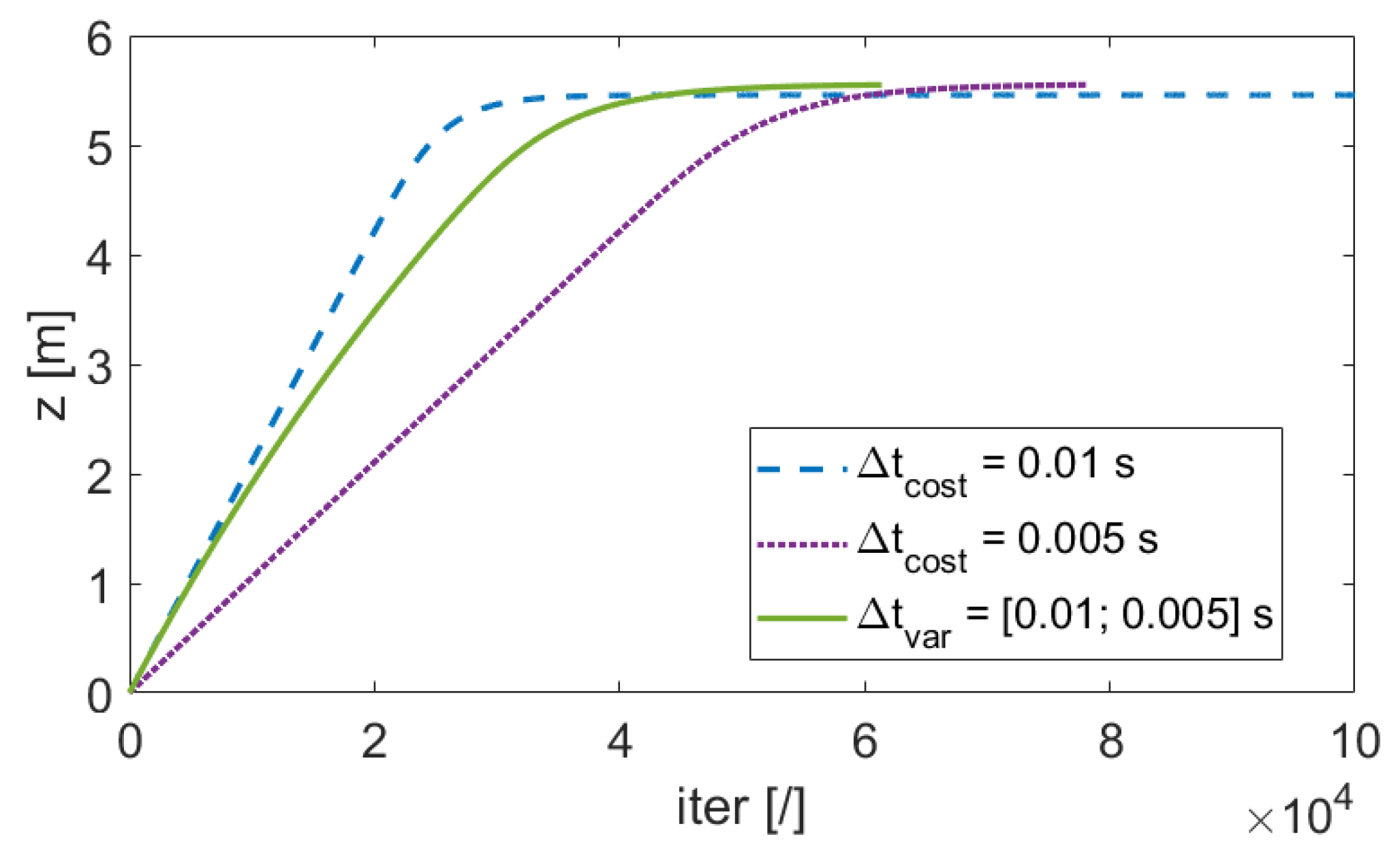
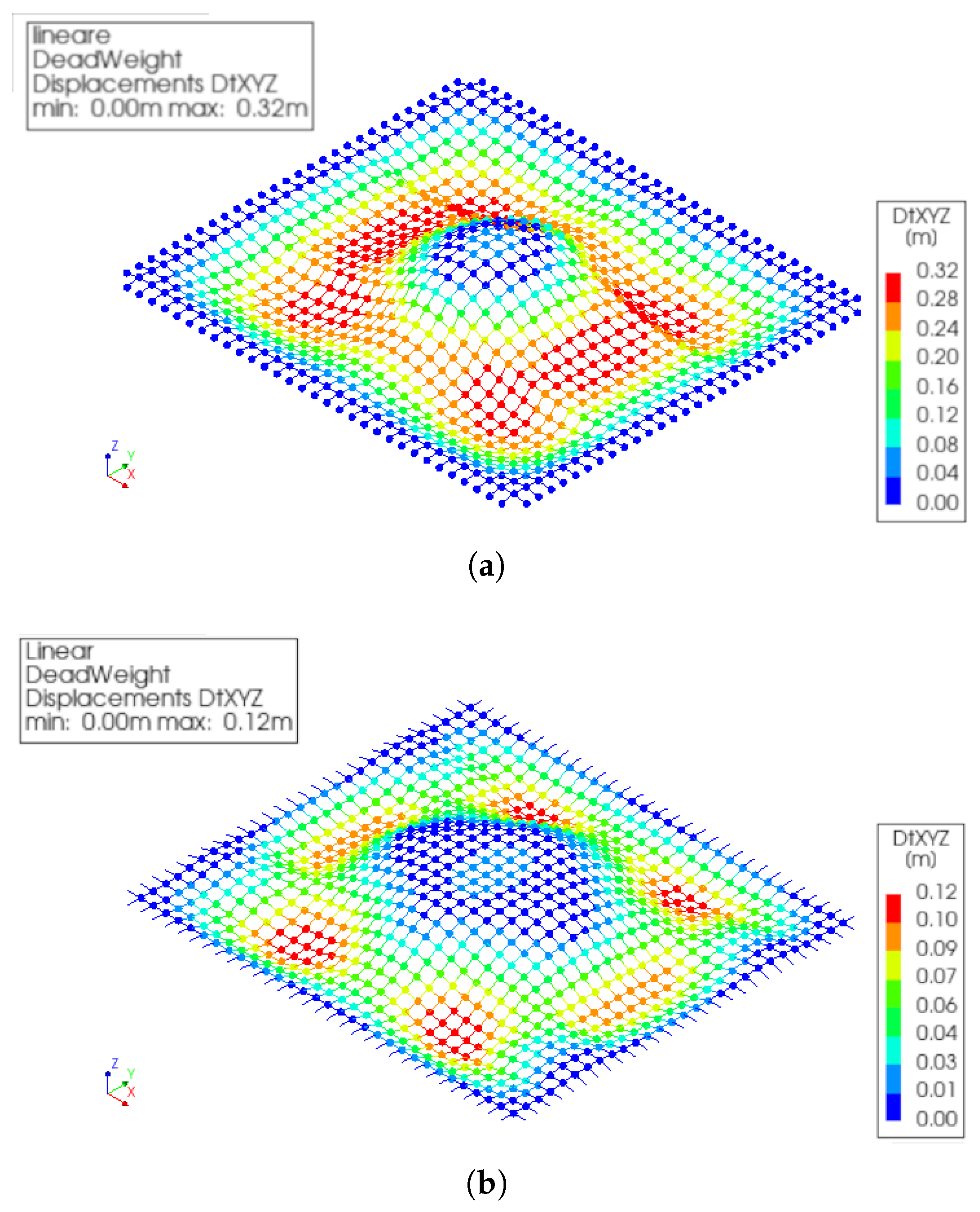
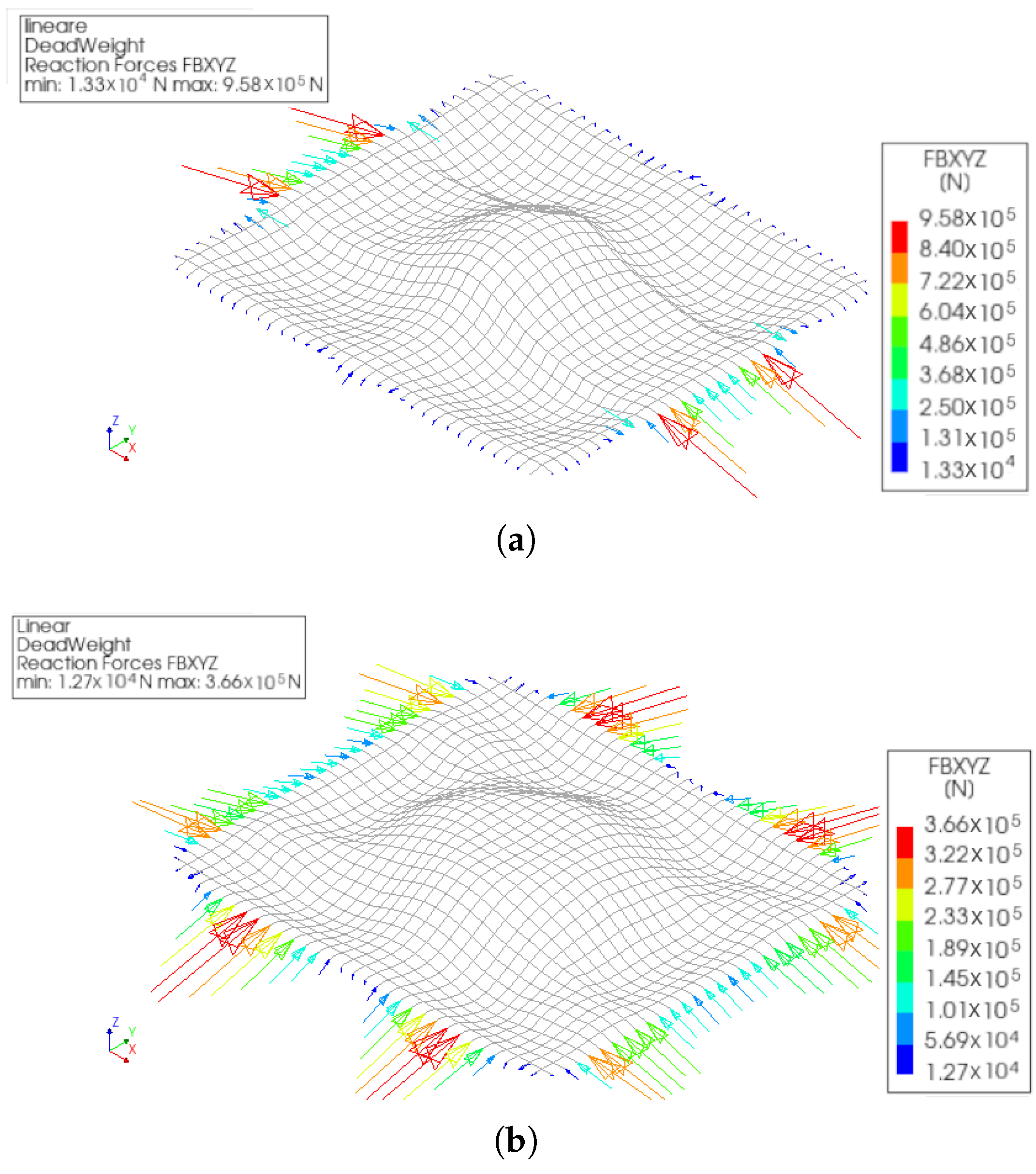
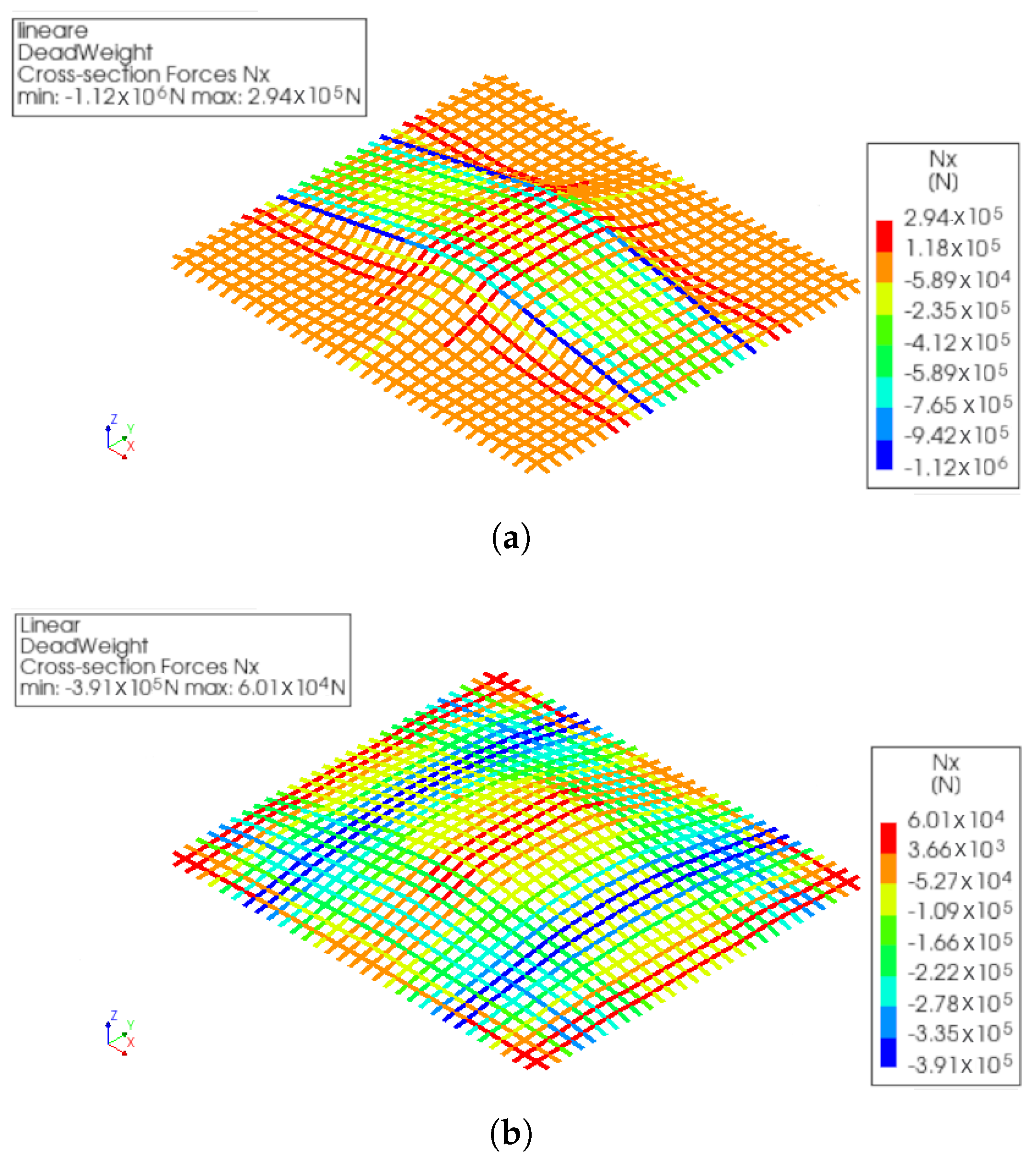
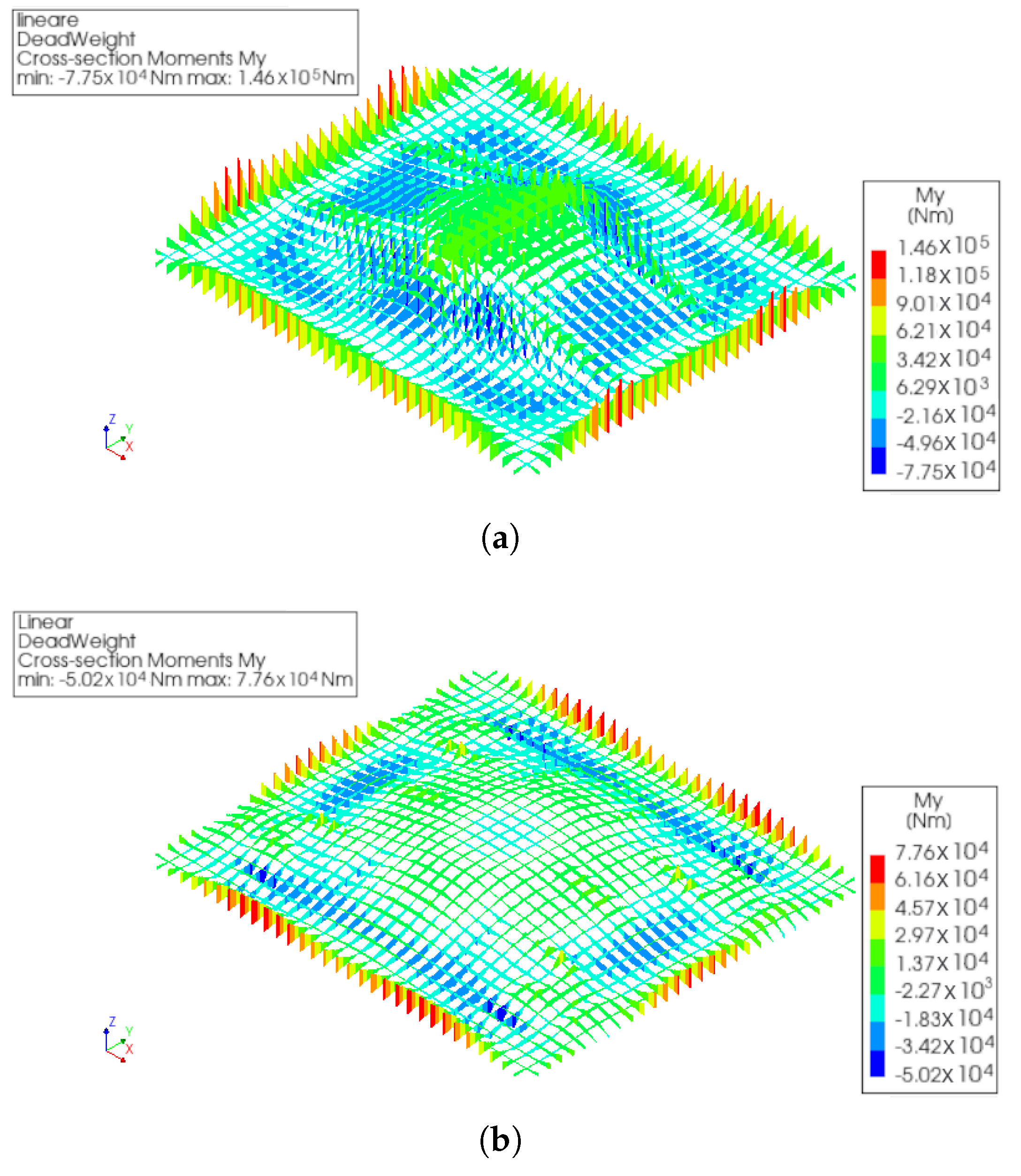
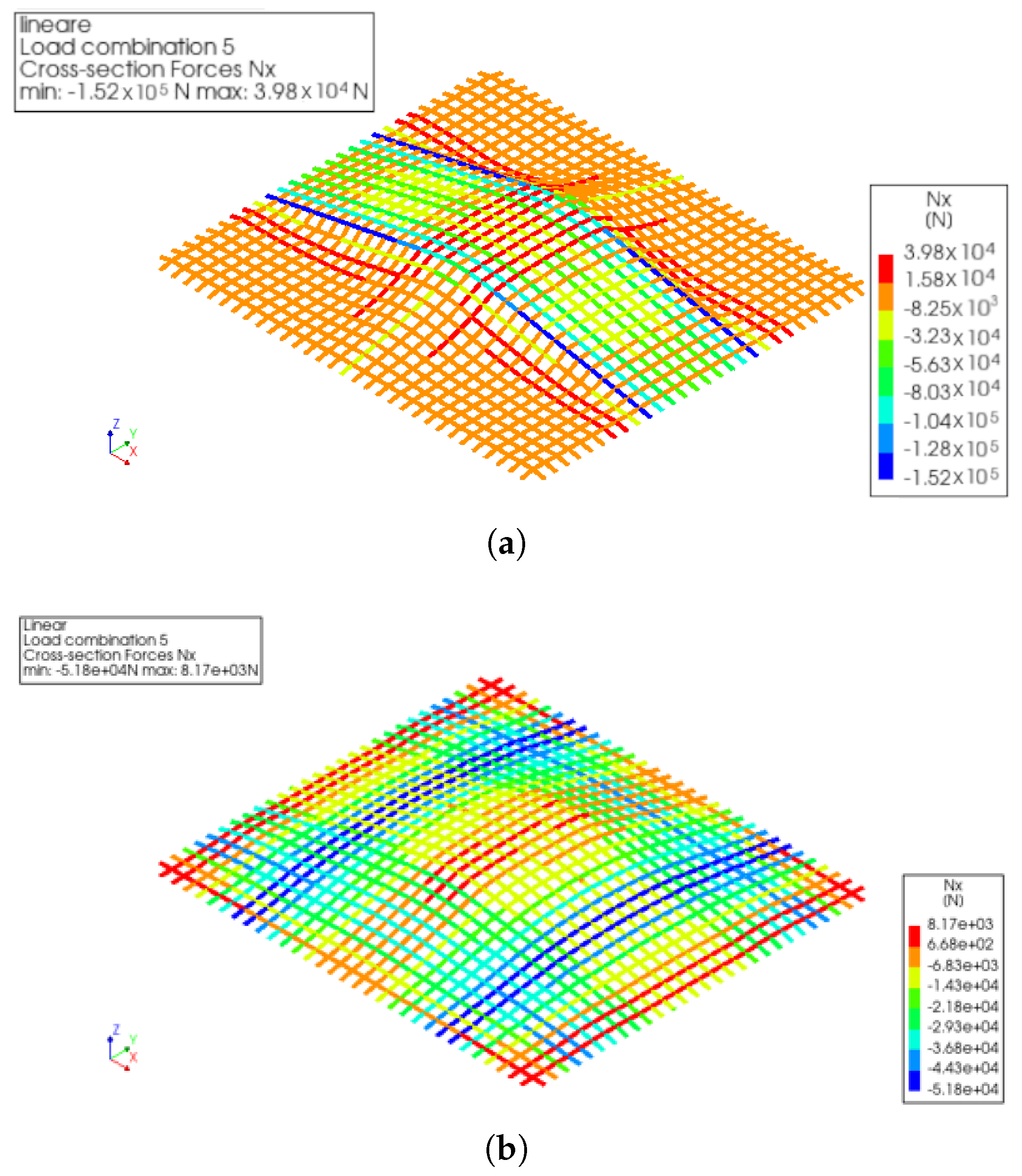
4. Numerical Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Melchiorre, J.; Manuello, A.; Marmo, F.; Adriaenssens, S.; Marano, G. Differential formulation and numerical solution for elastic arches with variable curvature and tapered cross-sections. Eur. J. Mech.-A/Solids 2023, 97, 104757. [Google Scholar] [CrossRef]
- Cucuzza, R.; Rosso, M.M.; Aloisio, A.; Melchiorre, J.; Giudice, M.L.; Marano, G.C. Size and shape optimization of a guyed mast structure under wind, ice and seismic loading. Appl. Sci. 2022, 12, 4875. [Google Scholar] [CrossRef]
- Abbate, E.; Invernizzi, S.; Spanò, A. HBIM parametric modelling from clouds to perform structural analyses based on finite elements: A case study on a parabolic concrete vault. Appl. Geomat. 2022, 14, 79–96. [Google Scholar] [CrossRef]
- Adriaenssens, S.; Block, P.; Veenendaal, D.; Williams, C. Shell Structures for Architecture: Form Finding and Optimization; Routledge: London, UK, 2014. [Google Scholar]
- Marano, G.C.; Rosso, M.M.; Melchiorre, J. Optimization as a Tool for Seismic Protection of Structures. In Proceedings of the World Conference on Seismic Isolation, Turin, Italy, 11–15 September 2022; Springer: Cham, Switzerland, 2022; pp. 100–113. [Google Scholar]
- Rosso, M.M.; Melchiorre, J.; Cucuzza, R.; Manuello, A.; Marano, G.C. Estimation of distribution algorithm for constrained optimization in structural design. In Proceedings of the WCCM-APCOM 2022, Yokohama, Japan, 31 July–5 August 2022; Volume 900. [Google Scholar]
- Happold, E. Philosophy of design with particular respect to buildings. In Structural Engineering: History and Development; CRC Press: Boca Raton, FL, USA, 1997. [Google Scholar]
- Addis, B.; Walker, D. Happold: The Confidence to Build; Taylor & Francis: Abingdon, UK, 2005. [Google Scholar]
- Otto, F.; Hennicke, J.; Matsushita, K. IL10 Gitterschalen; Institut für Leichte Flächentragwerke (IL): Stuttgart, Germany, 1974. [Google Scholar]
- Liddell, I. Frei Otto and the development of gridshells. Case Stud. Struct. Eng. 2015, 4, 39–49. [Google Scholar] [CrossRef]
- Sobek, W.; Blandini, L. The Mansueto Library–Notes on a glazed steel grid shell from design to construction. In Proceedings of the Challenging Glass Conference Proceedings, Delft, The Netherlands, 20–21 May 2010; Volume 2, pp. 179–186. [Google Scholar]
- Fritzsche, K.; van der Sluis, W.; Smits, E.; Bakker, J. Capital C, geometric optimization of a free-form steel gridshell towards planar quadrilateral glass units. In Proceedings of the Challenging Glass Conference Proceedings, Ghent, Belgium, 4 September 2020; Volume 7. [Google Scholar]
- Zhao, C.; Ma, J.; Du, S.; Gu, Y.; Zhou, Y. Mechanical properties of a novel joint of a single-layer aluminum-alloy combined lattice-shell structure. Mater. Tehnol. 2019, 53, 811–819. [Google Scholar] [CrossRef]
- Happold, E.; Wi, L. Timber Lattice Roof for the Mannheim Bundesgartenschau. 1975. Available online: https://pascal-francis.inist.fr/vibad/index.php?action=getRecordDetail&idt=PASCAL7589012232 (accessed on 20 February 2024).
- Harris, R. Design of timber gridded shell structures. Proc. Inst. Civ. Eng.-Struct. Build. 2011, 164, 105–116. [Google Scholar] [CrossRef]
- Collins, M.; Cosgrove, T. A Review of the State of the Art of Timber Gridshell Design and Construction. 2016. Available online: https://www.researchgate.net/profile/Matt-Collins-5/publication/307546000_A_Review_of_the_State_of_the_Art_of_Timber_Gridshell_Design_and_Construction/links/57c7f5e108aec24de04313f1/A-Review-of-the-State-of-the-Art-of-Timber-Gridshell-Design-and-Construction.pdf (accessed on 20 February 2024).
- Chilton, J.; Tang, G. Timber Gridshells: Architecture, Structure and Craft; Routledge: London, UK, 2016. [Google Scholar]
- Douthe, C.; Caron, J.F.; Baverel, O. Gridshell structures in glass fibre reinforced polymers. Constr. Build. Mater. 2010, 24, 1580–1589. [Google Scholar] [CrossRef]
- Baverel, O.; Caron, J.F.; Tayeb, F.; Du Peloux, L. Gridshells in composite materials: Construction of a 300 m2 forum for the solidays’ festival in Paris. Struct. Eng. Int. 2012, 22, 408–414. [Google Scholar] [CrossRef]
- D’Amico, B.; Kermani, A.; Zhang, H.; Pugnale, A.; Colabella, S.; Pone, S. Timber gridshells: Numerical simulation, design and construction of a full scale structure. In Structures; Elsevier: Amsterdam, The Netherlands, 2015; Volume 3, pp. 227–235. [Google Scholar]
- Cabrera Fausto, I.; Fenollosa Forner, E.J.; Llopis-Pulido, V.; Almerich-Chulia, A. Reliability associated with the use of building structural analysis and design software. Arch. e-J. Dissem. Dr. Res. Archit. 2018, 5, 13–37. [Google Scholar]
- Otter, J.R.H.; Cassell, A.C.; Hobbs, R.E.; Poisson. Dynamic relaxation. Proc. Inst. Civ. Eng. 1966, 35, 633–656. [Google Scholar] [CrossRef]
- Kilian, A.; Ochsendorf, J. Particle-spring systems for structural form finding. J. Int. Assoc. Shell Spat. Struct. 2005, 46, 77–84. [Google Scholar]
- Schek, H.J. The force density method for form finding and computation of general networks. Comput. Methods Appl. Mech. Eng. 1974, 3, 115–134. [Google Scholar] [CrossRef]
- Block, P.; Ochsendorf, J. Thrust network analysis: A new methodology for three-dimensional equilibrium. J. Int. Assoc. Shell Spat. Struct. 2007, 48, 167–173. [Google Scholar]
- Manuello, A. Multi-body rope approach for grid shells: Form-finding and imperfection sensitivity. Eng. Struct. 2020, 221, 111029. [Google Scholar] [CrossRef]
- Rian, I.M.; Sassone, M.; Asayama, S. From fractal geometry to architecture: Designing a grid-shell-like structure using the Takagi–Landsberg surface. Comput.-Aided Des. 2018, 98, 40–53. [Google Scholar] [CrossRef]
- Zhao, Z.; Yu, D.; Zhang, T.; Zhang, N.; Liu, H.; Liang, B.; Xian, L. Efficient form-finding algorithm for freeform grid structures based on inverse hanging method. J. Build. Eng. 2022, 46, 103746. [Google Scholar] [CrossRef]
- Huang, W.; Wu, C.; Hu, J.; Gao, W. Weaving structure: A bending-active gridshell for freeform fabrication. Autom. Constr. 2022, 136, 104184. [Google Scholar] [CrossRef]
- Invernizzi, S.; Manuello, A.; Ciaccio, F.; Nicola, P. Design of a modular exhibition structure with additive manufacturing of eco-sustainable materials. Curved Layer. Struct. 2021, 8, 196–209. [Google Scholar] [CrossRef]
- Douthe, C.; Mesnil, R.; Orts, H.; Baverel, O. Isoradial meshes: Covering elastic gridshells with planar facets. Autom. Constr. 2017, 83, 222–236. [Google Scholar] [CrossRef]
- Montagne, N.; Douthe, C.; Tellier, X.; Fivet, C.; Baverel, O. Discrete Voss surfaces: Designing geodesic gridshells with planar cladding panels. Autom. Constr. 2022, 140, 104200. [Google Scholar] [CrossRef]
- Seifi, H.; Javan, A.R.; Xu, S.; Zhao, Y.; Xie, Y.M. Design optimization and additive manufacturing of nodes in gridshell structures. Eng. Struct. 2018, 160, 161–170. [Google Scholar] [CrossRef]
- de Oliveira, I.M.; de Oliveira Pauletti, R.M.; Meneghetti, L.C. Connection system for gridshell structures using parametric modeling and digital fabrication. Autom. Constr. 2020, 109, 102996. [Google Scholar] [CrossRef]
- Fragomeli & Partners. Available online: https://fragomeliandpartners.com/ (accessed on 5 June 2023).
- Bertetto, A.M.; Riberi, F. Form-finding of pierced vaults and digital fabrication of scaled prototype. Curved Layer. Struct. 2021, 8, 210–224. [Google Scholar] [CrossRef]
- Manuello, A.; Melchiorre, J.; Marano, G.C. Improved Multi-Body Rope Approach for Free-form grid Shells. In Proceedings of the Italian Workshop on Shell and Spatial Structures (IWSS 2023), Turin, Italy, 26–28 June 2023. [Google Scholar]
- Melchiorre, J.; Soutiropoulos, S.; Manuello Bertetto, A.; Marano, G.C.; Marmo, F. Grid-Shell Multi-step Structural Optimization with Improved Multi-body Rope Approach and Multi-objective Genetic Algorithm. In Proceedings of the Italian Workshop on Shell and Spatial Structures, Turin, Italy, 26–28 June 2023; Springer: Cham, Switzerland, 2023; pp. 62–72. [Google Scholar]
- Manuello, A.; Melchiorre, J.; Sardone, L.; Marano, G.C. Multi-body Rope Approach for the Form-Finding of Shape Optimized Grid Shell Structures. In Proceedings of the 15th World Congress on Computational Mechanics, Yokohama, Japan, 31 July–5 August 2022. [Google Scholar]
- Cavaliere, I.; Fallacara, G.; Manuello Bertetto, A.; Melchiorre, J.; Marano, G.C. Multy Body Rope Approach and Funicular Prototype for a New Constructive System for Catenary Arches. In Proceedings of the Italian Workshop on Shell and Spatial Structures, Turin, Italy, 26–28 June 2023; Springer: Cham, Switzerland, 2023; pp. 259–268. [Google Scholar]
- Rugino, S. L’experiència del Sagrat a Través dels Llocs Rituals en L’arquitectura; ANUARI d’Arquitectura i Societat: València, Spain, 2021; pp. 198–214. [Google Scholar]
- Llana, D.G.A. La Cota Cero Como Lugar de Intercambio Comunitario; ANUARI d’Arquitectura i Societat: València, Spain, 2023; pp. 124–149. [Google Scholar]
- McNeel, R.; Associates. Rhinoceros 3D, Version 7.0; Robert McNeel & Associates: Seattle, WA, USA, 2023; Available online: https://www.rhino3d.com/ (accessed on 20 February 2024).
- Diana-FEA. Available online: https://dianafea.com/ (accessed on 3 June 2023).
- Melchiorre, J.; Bazzucchi, F.; Manuello Bertetto, A.; Marano, G.C. Postbuckling Echoes of iMRA Introduced Variation in Gridshells Mechanical Behaviour. In Proceedings of the Italian Workshop on Shell and Spatial Structures, Turin, Italy, 26–28 June 2023; Springer: Cham, Switzerland, 2023; pp. 379–389. [Google Scholar]
- Bazzucchi, F.; Manuello, A.; Carpinteri, A. Interaction between different instability phenomena in shallow roofing structures affected by geometrical imperfections. In Proceedings of the IASS Annual Symposia, International Association for Shell and Spatial Structures (IASS), Tokyo, Japan, 26–30 September 2016; Number 17. pp. 1–10. [Google Scholar]
- Bazzucchi, F.; Manuello, A.; Carpinteri, A. Interaction between snap-through and Eulerian instability in shallow structures. Int. J. Non-Linear Mech. 2017, 88, 11–20. [Google Scholar] [CrossRef]
- Bazzucchi, F.; Manuello, A.; Carpinteri, A. Instability load evaluation of shallow imperfection-sensitive structures by form and interaction parameters. Eur. J. Mech.-A/Solids 2017, 66, 201–211. [Google Scholar] [CrossRef]




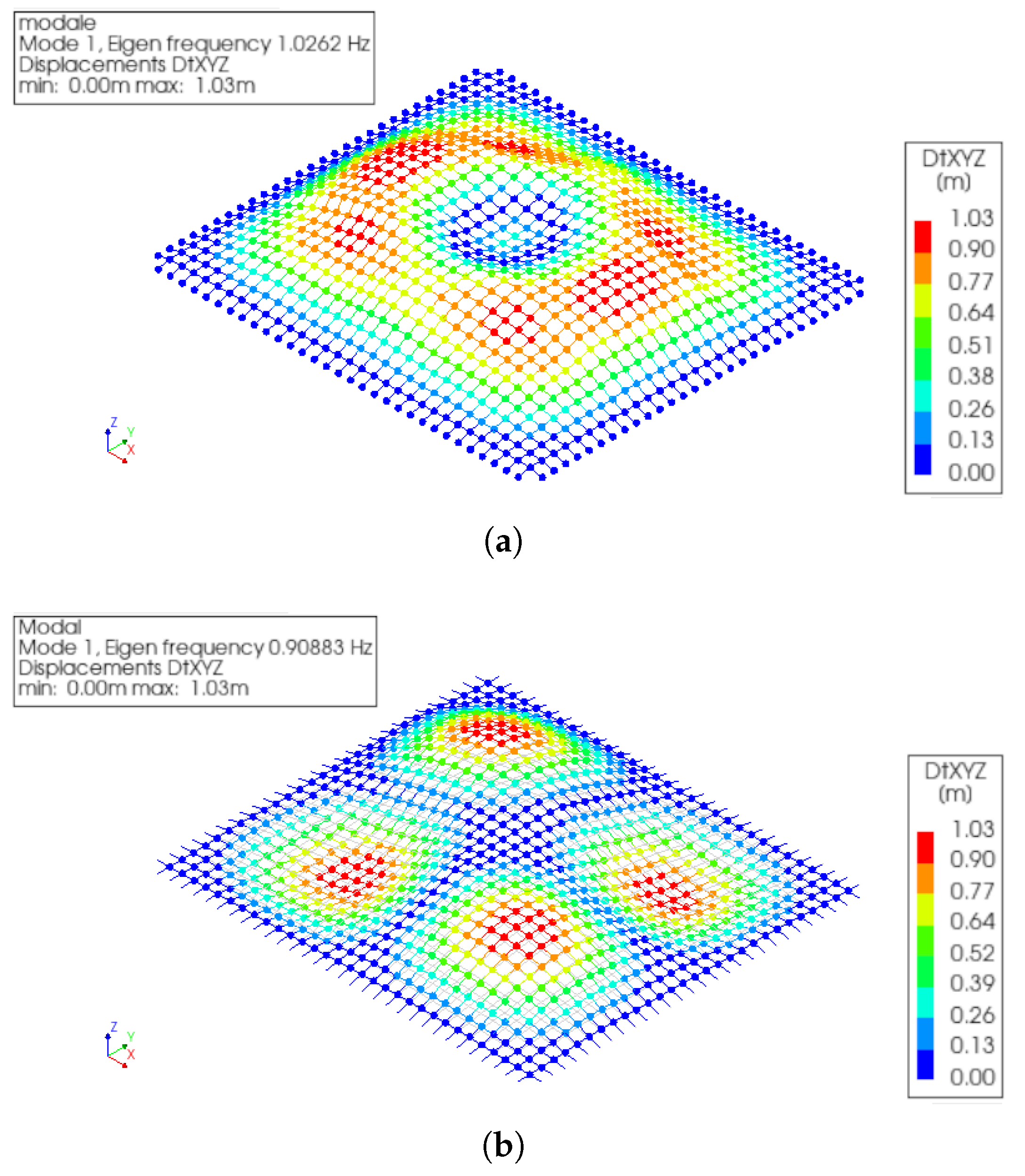
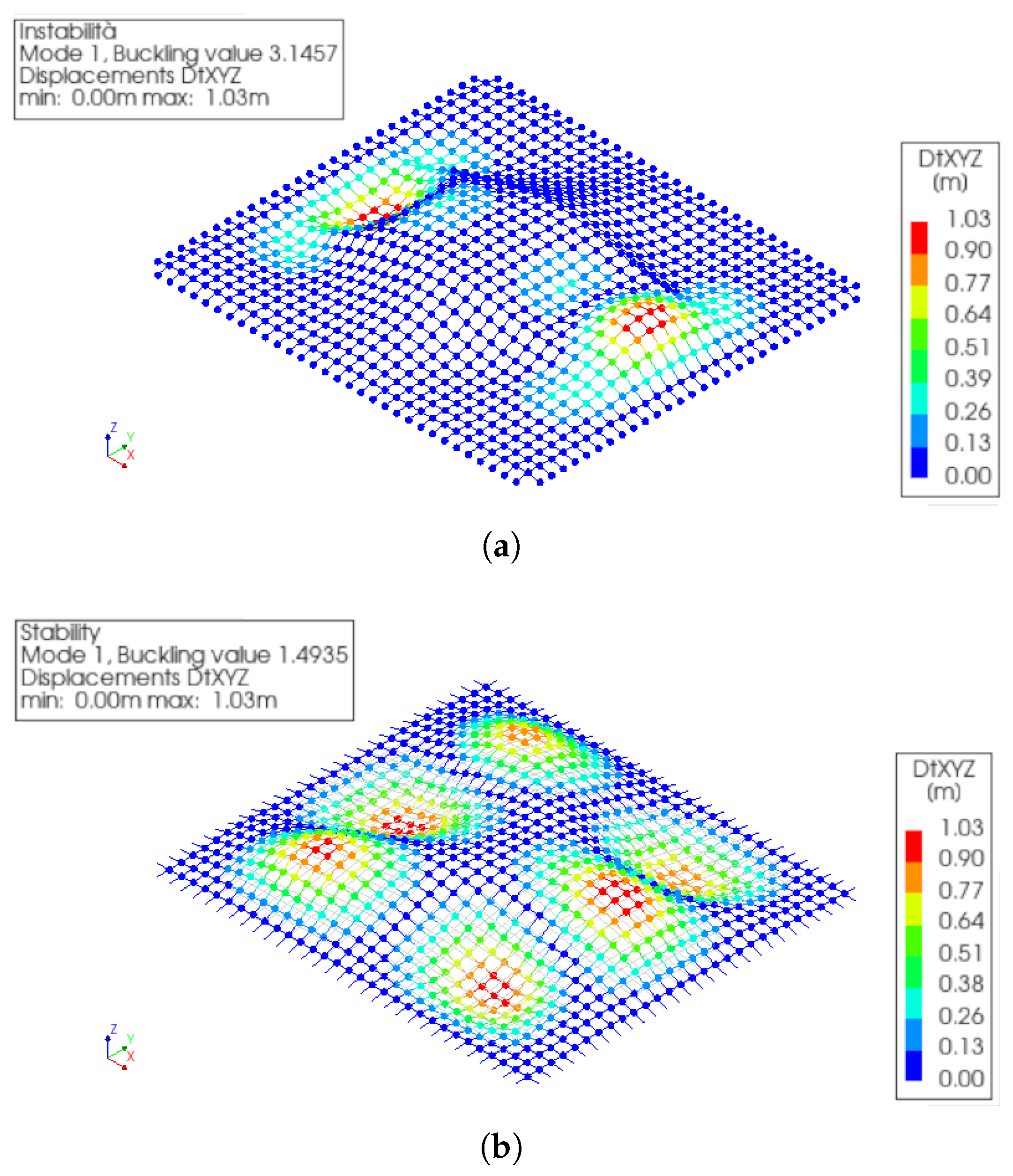
| Mode | MRA | i-MRA | Mode | MRA | i-MRA |
|---|---|---|---|---|---|
| 1 | 1.03 | 0.91 | 11 | 2.11 | 1.85 |
| 2 | 1.07 | 1.06 | 12 | 2.21 | 2.03 |
| 3 | 1.08 | 1.14 | 13 | 2.25 | 2.25 |
| 4 | 1.18 | 1.27 | 14 | 2.52 | 2.26 |
| 5 | 1.81 | 1.52 | 15 | 2.75 | 2.28 |
| 6 | 1.83 | 1.53 | 16 | 2.82 | 2.45 |
| 7 | 1.88 | 1.64 | 17 | 2.89 | 2.73 |
| 8 | 1.92 | 1.72 | 18 | 2.96 | 2.74 |
| 9 | 2.05 | 1.81 | 19 | 3.04 | 2.84 |
| 10 | 2.11 | 1.83 | 20 | 3.06 | 2.85 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Melchiorre, J.; Invernizzi, S.; Manuello Bertetto, A. Investigating the Influence of the Improved Multibody Rope Approach on the Structural Behavior of Dakar Mosque Gridshell Structure. Buildings 2024, 14, 598. https://doi.org/10.3390/buildings14030598
Melchiorre J, Invernizzi S, Manuello Bertetto A. Investigating the Influence of the Improved Multibody Rope Approach on the Structural Behavior of Dakar Mosque Gridshell Structure. Buildings. 2024; 14(3):598. https://doi.org/10.3390/buildings14030598
Chicago/Turabian StyleMelchiorre, Jonathan, Stefano Invernizzi, and Amedeo Manuello Bertetto. 2024. "Investigating the Influence of the Improved Multibody Rope Approach on the Structural Behavior of Dakar Mosque Gridshell Structure" Buildings 14, no. 3: 598. https://doi.org/10.3390/buildings14030598
APA StyleMelchiorre, J., Invernizzi, S., & Manuello Bertetto, A. (2024). Investigating the Influence of the Improved Multibody Rope Approach on the Structural Behavior of Dakar Mosque Gridshell Structure. Buildings, 14(3), 598. https://doi.org/10.3390/buildings14030598








