Influences of Species and Density on the Horizontal Flame Spread Behavior of Densified Wood
Abstract
:1. Introduction
2. Experiments
2.1. Experimental Materials
2.2. Preparation of Densified Wood
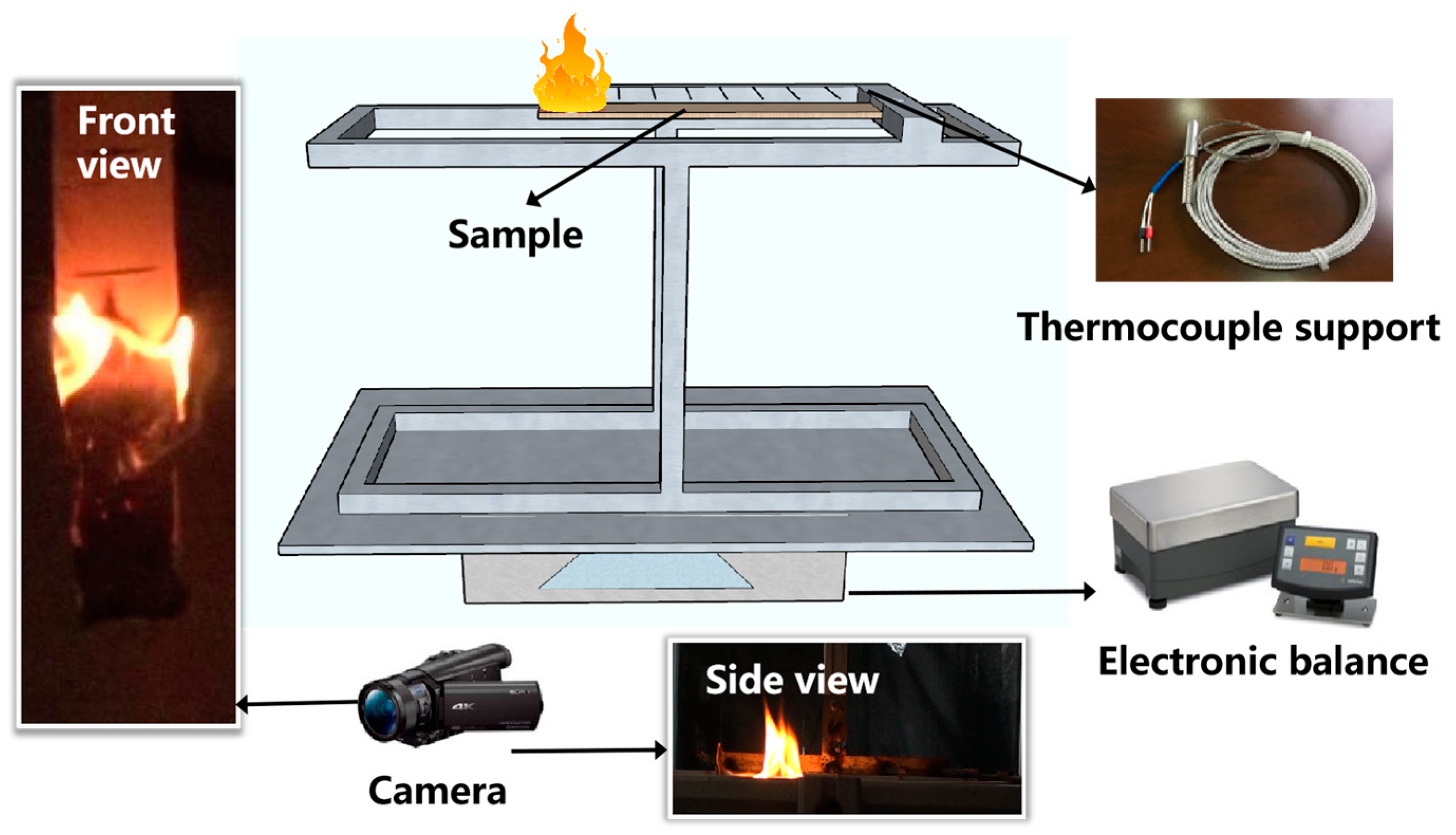
2.3. Experimental Apparatus
3. Results and Discussion
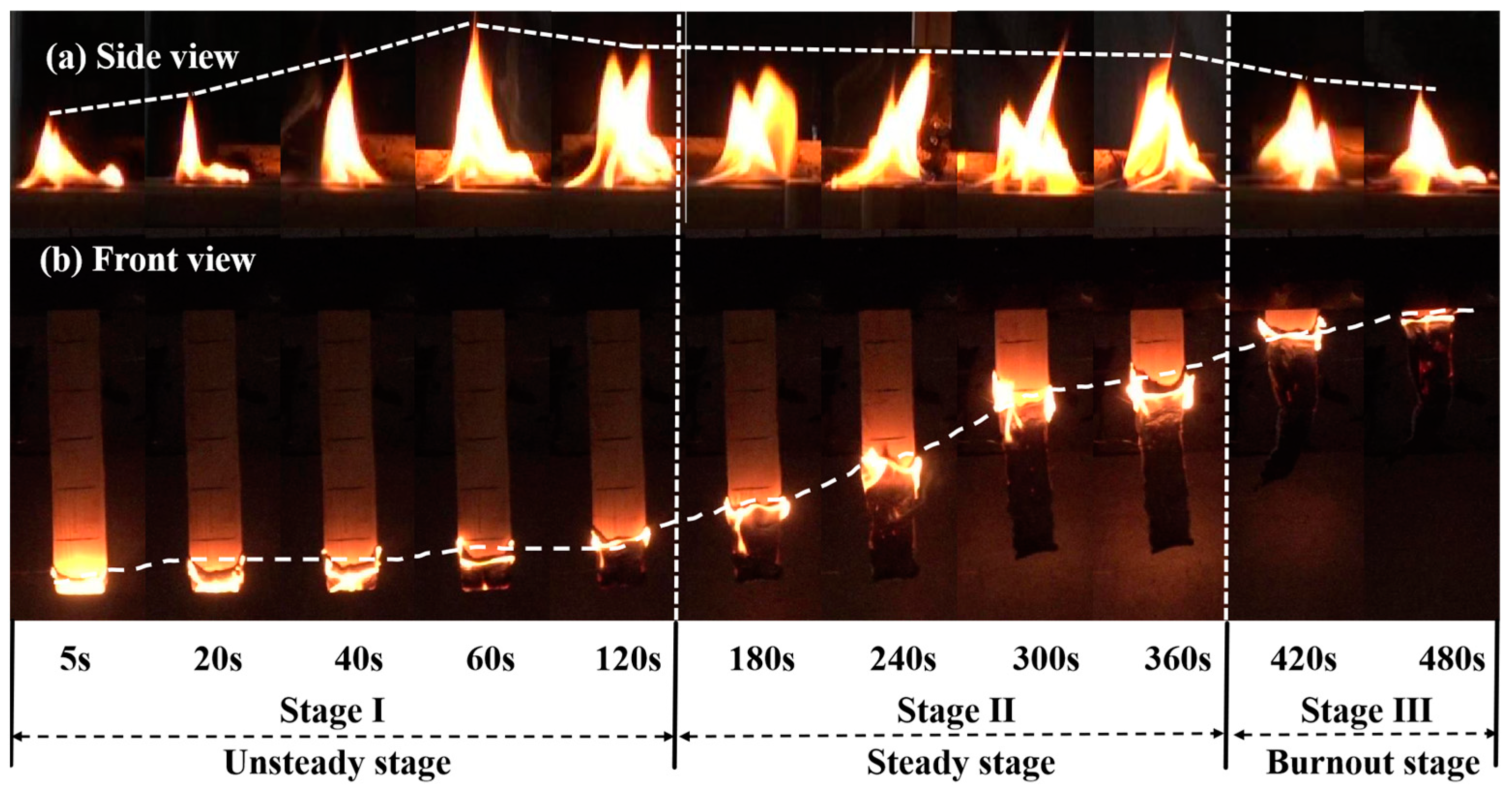
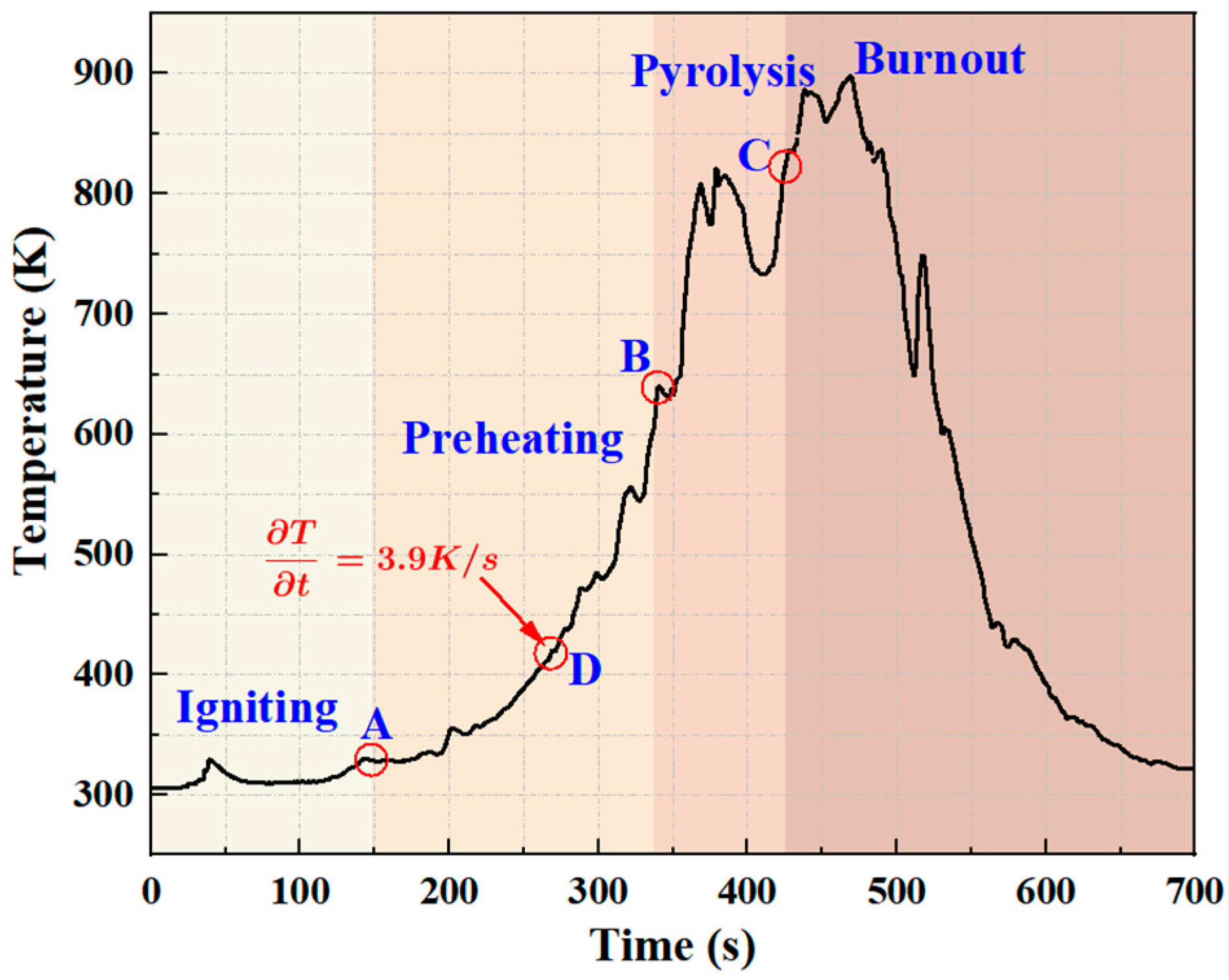
3.1. Typical Flame Form
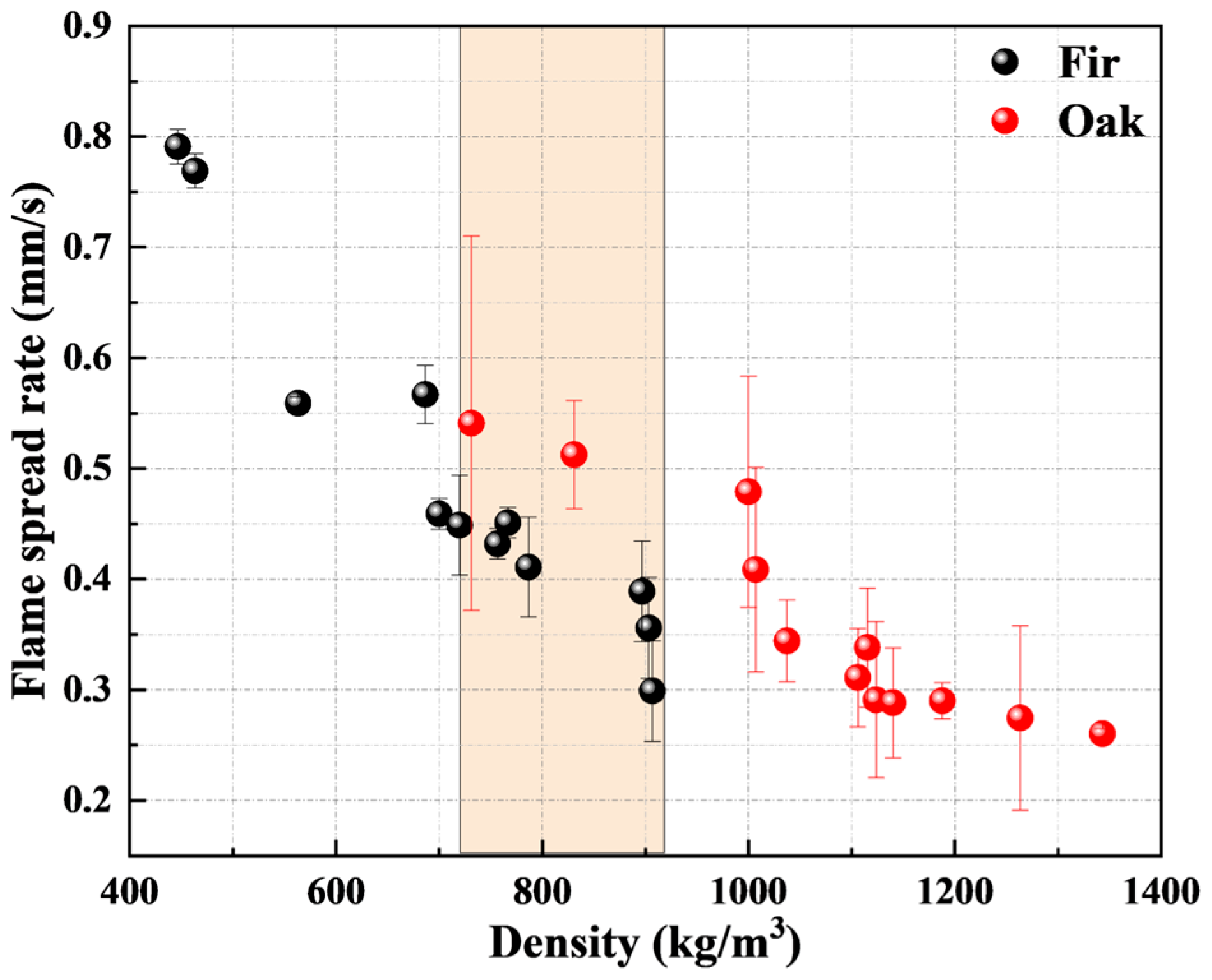
3.2. Flame Spread Rate
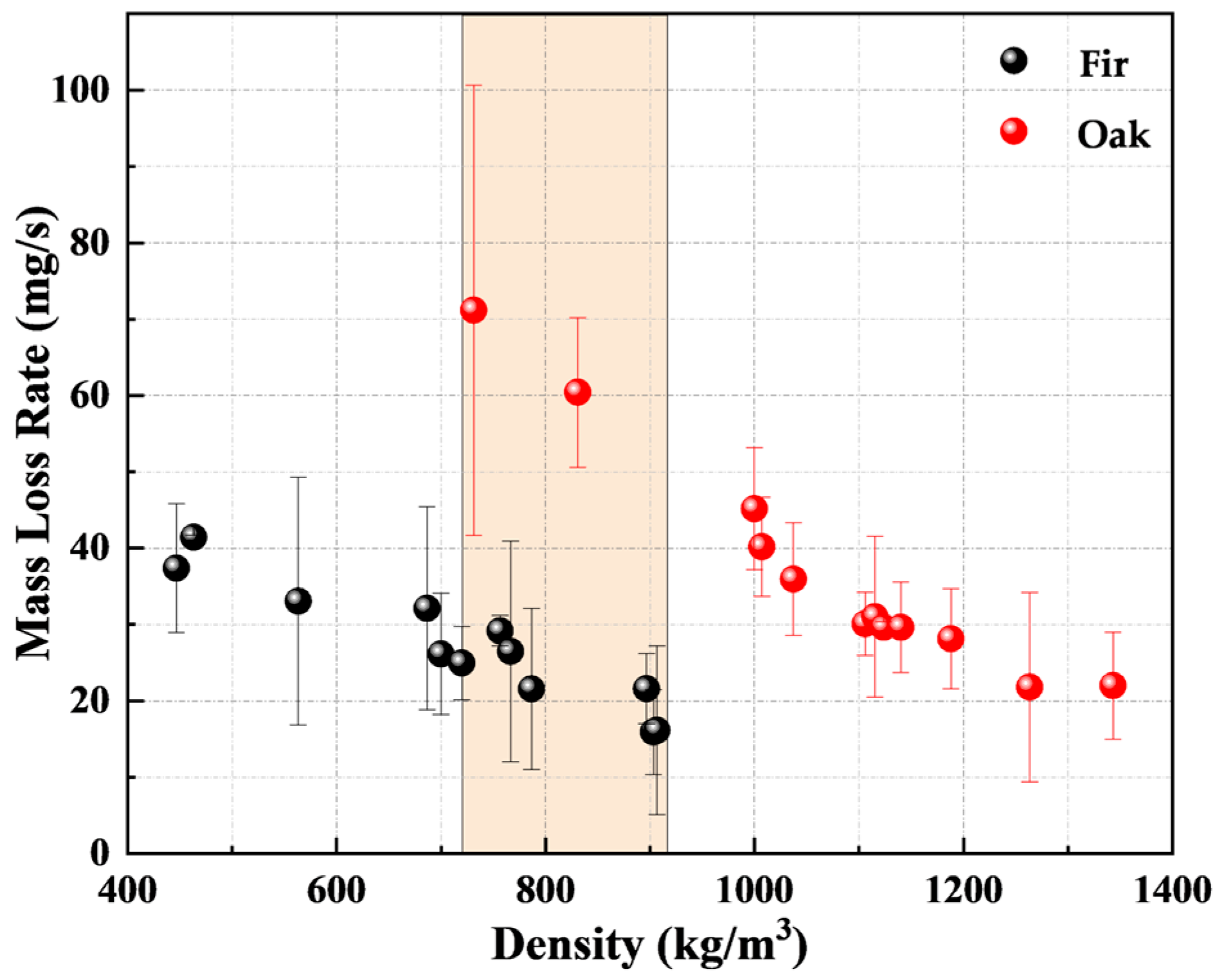
3.3. Mass Loss Rate
3.4. Flame Height
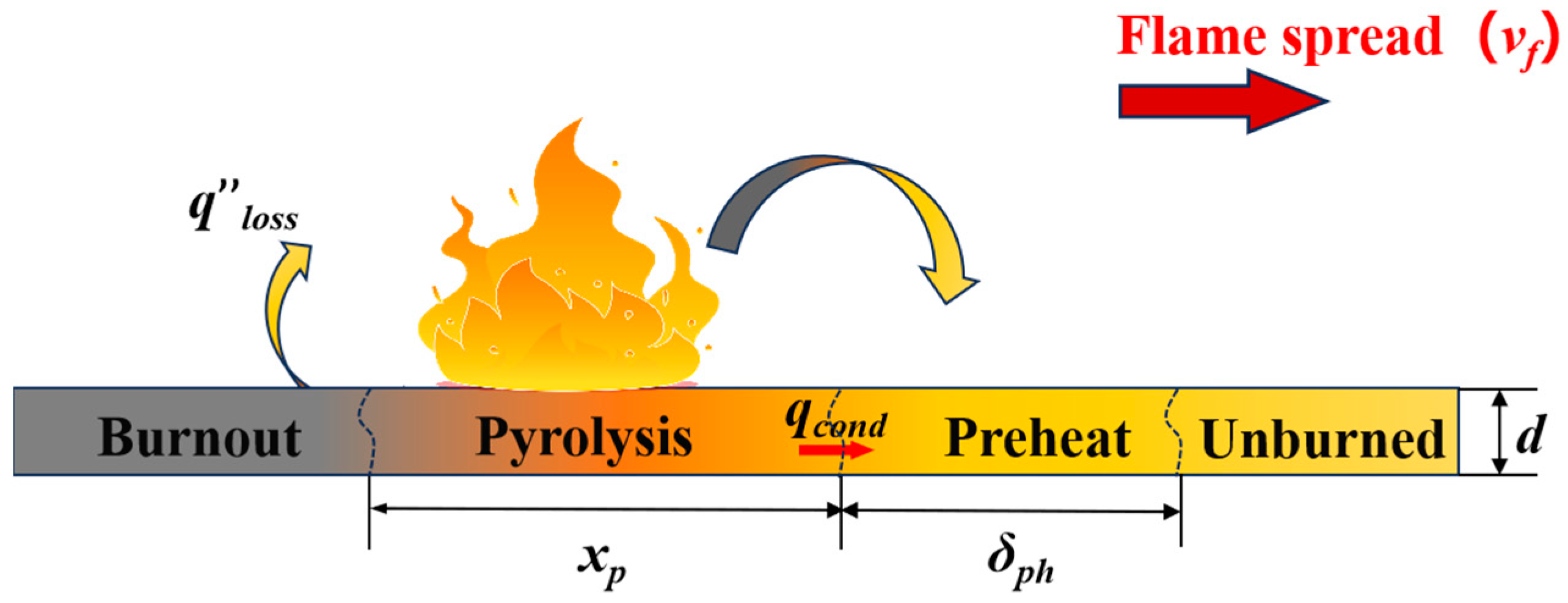
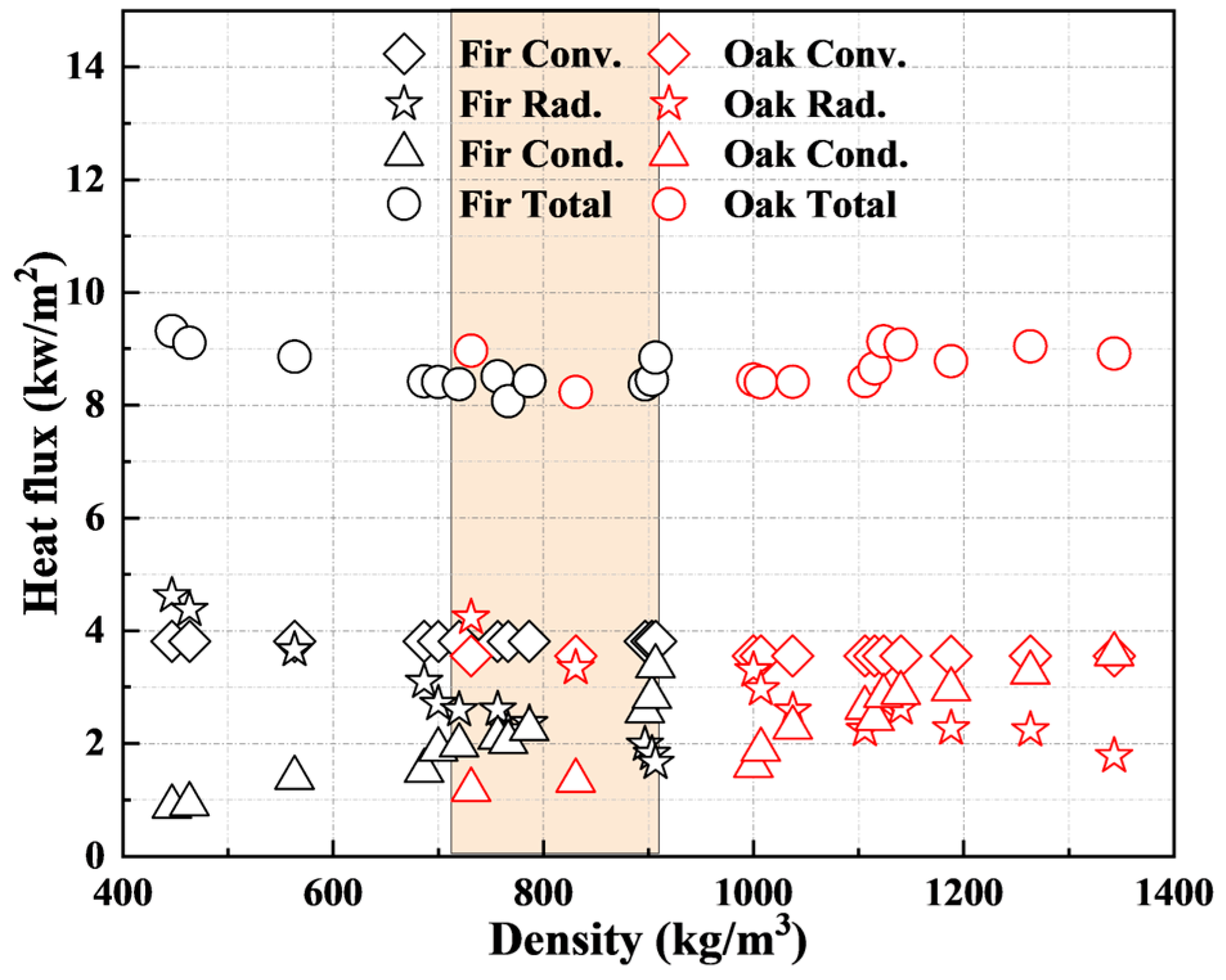
3.5. Heat Transfer Behavior
4. Conclusions
- The flame spread rate was decreased with the increase in wood density. This trend was similar in both densified wood types. Their values were also close at the same density. This indicated that the influence of wood species on flame spread rate was negligible compared to that of wood density.
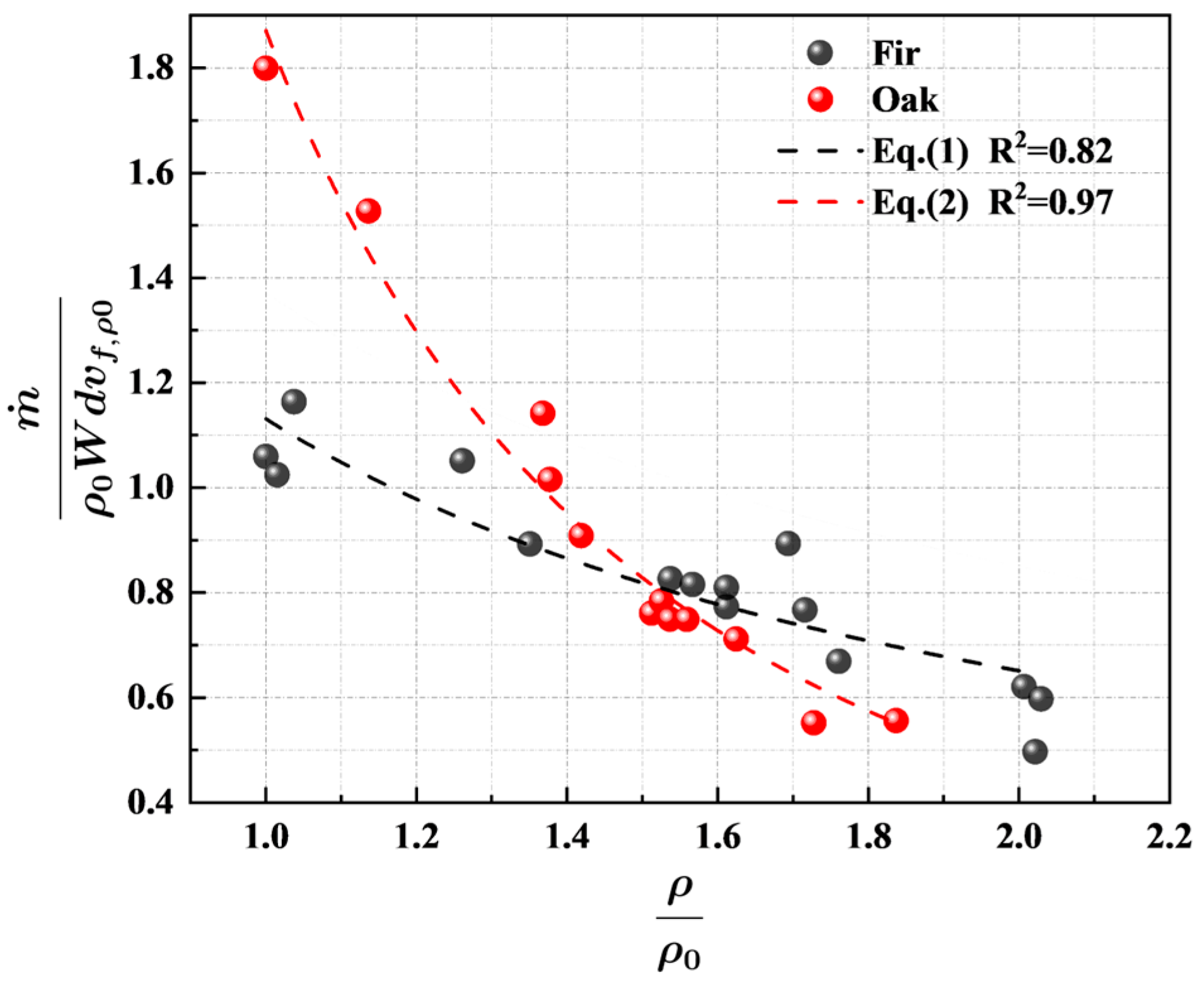
- The mass loss rate of both densified wood types decreased with the increase in wood density due to the enhanced thermal inertia. The densified oak showed a higher mass loss rate than densified fir at the same density due to its lower lignin content (char yield). Correlations between dimensionless mass loss rate and dimensionless density were obtained, which agree with the experiments with an R2 of 0.82 for densified fir and 0.97 for densified oak.
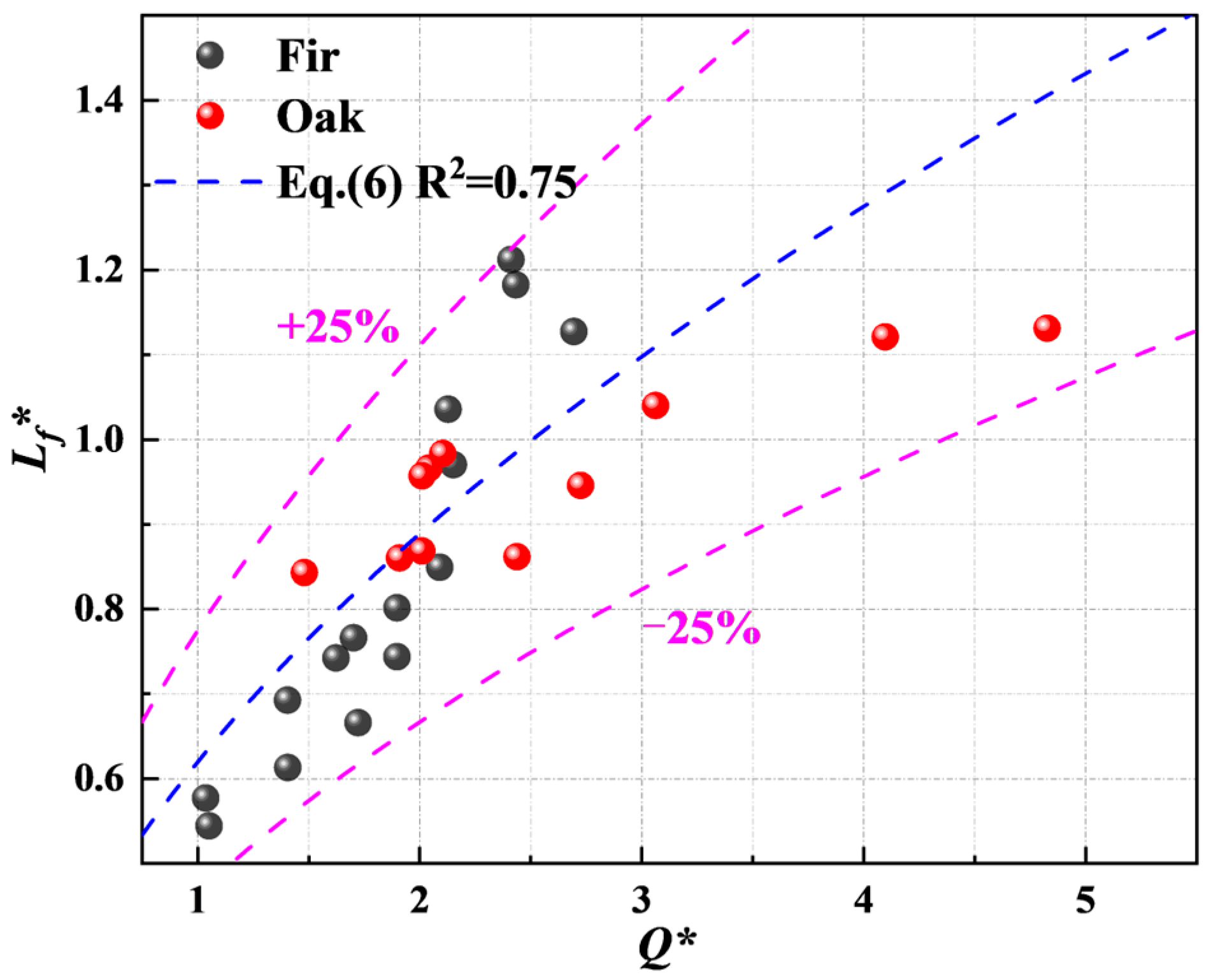
- The flame height of both densified wood types decreased with the increase in wood density. The enhanced density reduced pyrolysis gas production. It formed a condensed char that also reduced the pyrolysis gases release. The densified oak showed a higher flame height than densified fir at the same density since it had a higher mass loss rate. The trend between the and was similar for both densified wood types because their pyrolysis gases were similar.
- As the wood density increased, radiation (and conduction) of densified wood was reduced (and enhanced), while convection remained constant. The densified oak had lower convection than densified fir due to its higher pyrolysis temperature. The densified oak showed lower conduction and higher radiation than densified fir at the same density. Overall, gas-phase heat transfer was dominant in the flame spread of densified wood, but conduction was significant in heat transfer analysis as its contribution could be as high as 70% of gaseous heat transfer.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Parameter | Value (Fir) | Value (Oak) | |
|---|---|---|---|
| Tp | Pyrolysis temperature | 588 K [28] | 600 K [37] |
| kg | Thermal conductivity of air (T = (Tf + Tp)/2) | 0.064 W/(m·K) [41] | 0.0549 W/(m·K) [41] |
| Tchar | Characteristic temperature | 920.5 K | 926.5 K |
| tig | Ignition time (natural wood) | 26.5 s [28] | 57 s [45] |
| cp | Heat capacity of wood | 1.380 kJ/(kg·K) [28] | 1.255 kJ/(kg·K) [35] |
| Heat of combustion of pyrolyzed gases | 12.0 MJ/kg [46] | 15.2 MJ/kg | |
| α | Thermal diffusivity (T = (Tf + Tp)/2) | 1.55 × 10−4 m2/s [41] | 1.09 × 10−4 m2/s [41] |
| Kinematic viscosity (T = (Tf + Tp)/2) | 1.122 × 10−4 m2/s [41] | 0.7637 × 10−4 m2/s [41] | |
| Density of air (T = (Tf + Tp)/2) | 0.367 kg/m3 [41] | 0.4643 kg/m3 [41] | |
| Density of natural wood | 446.67 kg/m3 | 731.20 kg/m3 | |
| Heat capacity of air (T = (Tf + Tp)/2) | 1.131 kJ/(kg·K) [41] | 1.087 kJ/(kg·K) [41] | |
| h | Heat transfer coefficient (T = (Tf + Tp)/2) | 3.69 W/(m2·K) | 3.61 W/(m2·K) |
| ky | Radial thermal conductivity (natural wood) | 0.1589 W/(m·K) | 0.1625 W/(m·K) |
| z | The ratio of volume to surface area | 9.58 × 10−4 m | |
| g | Gravity acceleration | 9.8 m/s2 | |
| σ | Stefan–Boltzmann constant | 5.678 × 10−8 W/(m2·K4) | |
| Tf | Flame temperature | 1253 K | |
| T∞ | Ambient temperature | 300 K | |
| Ts | Initial wood surface temperature | 300 K | |
| β | Thermal expansion coefficient | 1.18 × 10−3 K−1 [41] | |
| θ | Flame tilt angle | 90° | |
| W | Width of wood | 0.05 m | |
| d | Thickness of wood | 0.002 m | |
References
- Chen, C.; Kuang, Y.; Zhu, S.; Burgert, I.; Keplinger, T.; Gong, A.; Li, T.; Berglund, L.; Eichhorn, S.J.; Hu, L. Structure–Property–Function Relationships of Natural and Engineered Wood. Nat. Rev. Mater. 2020, 5, 642–666. [Google Scholar] [CrossRef]
- Bäcklund, K.; Molinari, M.; Lundqvist, P. In Search for Untapped Energy-Saving Potential in Green and Smart Higher Educational Buildings—An Empirical Case Study Involving the Building Occupants. Buildings 2023, 13, 3103. [Google Scholar] [CrossRef]
- Li, T.; Zhai, Y.; He, S.; Gan, W.; Wei, Z.; Heidarinejad, M.; Dalgo, D.; Mi, R.; Zhao, X.; Song, J.; et al. A Radiative Cooling Structural Material. Science 2019, 364, 760–763. [Google Scholar] [CrossRef]
- Fan, C.; Gao, Y.; Li, Y.; Yan, L.; Zhuang, Y.; Zhang, Y.; Wang, Z. A Flame-retardant and Optically Transparent Wood Composite. J. Appl. Polym. Sci. 2022, 139, e52945. [Google Scholar] [CrossRef]
- Tollefson, J. The Wooden Skyscrapers That Could Help to Cool the Planet. Nature 2017, 545, 280–282. [Google Scholar] [CrossRef]
- Namari, S.; Drosky, L.; Pudlitz, B.; Haller, P.; Sotayo, A.; Bradley, D.; Mehra, S.; O’ Ceallaigh, C.; Harte, A.M.; El-Houjeyri, I.; et al. Mechanical Properties of Compressed Wood. Constr. Build. Mater. 2021, 301, 124269. [Google Scholar] [CrossRef]
- Gan, W.; Chen, C.; Wang, Z.; Song, J.; Kuang, Y.; He, S.; Mi, R.; Sunderland, P.B.; Hu, L. Dense, Self-Formed Char Layer Enables a Fire-Retardant Wood Structural Material. Adv. Funct. Mater. 2019, 29, 1807444. [Google Scholar] [CrossRef]
- Yuan, S.; Xiang, K.; Yan, F.; Liu, Q.; Sun, X.; Li, Y.; Du, P. Characteristics and Mechanism of Fire Spread between Full-Scale Wooden Houses from Internal Fires. Buildings 2022, 12, 575. [Google Scholar] [CrossRef]
- Wang, H.; Gong, J.; Wang, H.; Gong, J. A Comparative Study of GA, PSO and SCE Algorithms for Estimating Kinetics of Biomass Pyrolysis. Emerg. Sci. Technol. 2023, 3, 9. [Google Scholar] [CrossRef]
- Kollmann, F.; Cote, W. Solid Wood. In Principles of Wood Science and Technology; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 1968. [Google Scholar]
- Zhou, Y.; Zhou, P.; Bu, R.; Zhang, X.; Chu, T.; Wang, Z. Horizontal Flame Spread Behavior of Densified Wood: Effect of Structural Characteristics. Fuel 2024, 362, 130687. [Google Scholar] [CrossRef]
- Wang, H.; Wang, Z.; Wen, L.; Meng, H.; Wang, W.; Huang, X. The Flame Spread Performance over Discrete Wooden Chips Varying Wood Species. Therm. Sci. Eng. Prog. 2023, 39, 101674. [Google Scholar] [CrossRef]
- Jiang, L.; He, J.-J.; Sun, J.-H. Sample Width and Thickness Effects on Upward Flame Spread over PMMA Surface. J. Hazard. Mater. 2018, 342, 114–120. [Google Scholar] [CrossRef]
- Zhao, L.; Fang, J.; He, X.; Wang, J.; Tao, S.; Zhang, Y. An Analysis of Width Effects on Flame Spread in Conjunction with Concurrent Forced Flow Using a Variable B-Number. Combust. Flame. 2018, 194, 334–342. [Google Scholar] [CrossRef]
- Wang, Q.; Xiao, H.; Wan, W.; Cui, Z.; Zhu, H.; Sun, J. Flame Spread on Inclined Wood Surfaces: Influence of External Heat Flux and Ambient Oxygen Concentration. Combust. Sci. Technol. 2018, 190, 97–113. [Google Scholar] [CrossRef]
- Zhou, J.; Zhu, G.; Gao, Y.; Gao, S.; Chai, G. Experimental Study on the Effects of Width and Self-Extinguishing on the Upward Flame Spread for Linen Fabric. Case Stud. Therm. Eng. 2019, 14, 100500. [Google Scholar] [CrossRef]
- Saito, K.; Williams, F.A.; Wichman, I.S.; Quintiere, J.G. Upward Turbulent Flame Spread on Wood Under External Radiation. J. Heat Transf. 1989, 111, 438–445. [Google Scholar] [CrossRef]
- Fernandez-Pello, A.C.; Ray, S.R.; Glassman, I. Flame Spread in an Opposed Forced Flow: The Effect of Ambient Oxygen Concentration. Symp. Int. Combust. 1981, 18, 579–589. [Google Scholar] [CrossRef]
- Song, J.; Chen, C.; Zhu, S.; Zhu, M.; Dai, J.; Ray, U.; Li, Y.; Kuang, Y.; Li, Y.; Quispe, N.; et al. Processing Bulk Natural Wood into a High-Performance Structural Material. Nature 2018, 554, 224–228. [Google Scholar] [CrossRef]
- Richter, F.; Rein, G. A Multiscale Model of Wood Pyrolysis in Fire to Study the Roles of Chemistry and Heat Transfer at the Mesoscale. Combust. Flame. 2020, 216, 316–325. [Google Scholar] [CrossRef]
- Yi, L.; Zhuang, Y.; Ding, Y.; Gong, J.; Chu, T.; Wang, Z. Influence of Component Fractions and Structure Characteristic on the Combustion Behavior of Densified Wood. Fire Saf. J. 2024, 144, 104086. [Google Scholar] [CrossRef]
- Blasi, C.D.; Wichman, I.S. Effects of Solid-Phase Properties on Flames Spreading over Composite Materials. Combust. Flame 1995, 102, 229–240. [Google Scholar] [CrossRef]
- Kobayashi, Y.; Terashima, K.; Oiwa, R.; Tokoro, M.; Takahashi, S. Opposed-Flow Flame Spread over Carbon Fiber Reinforced Plastic under Variable Flow Velocity and Oxygen Concentration: The Effect of in-Plane Thermal Isotropy and Anisotropy. Proc. Combust. Inst. 2021, 38, 4857–4866. [Google Scholar] [CrossRef]
- Quintiere, J. A Simplified Theory for Generalizing Results from a Radiant Panel Rate of Flame Spread Apparatus. Fire Mater. 1981, 5, 52–60. [Google Scholar] [CrossRef]
- Amaral, S.S.; de Carvalho, J.A., Jr.; Costa, M.A.M.; Neto, T.G.S.; Dellani, R.; Leite, L.H.S. Comparative Study for Hardwood and Softwood Forest Biomass: Chemical Characterization, Combustion Phases and Gas and Particulate Matter Emissions. Bioresour. Technol. 2014, 164, 55–63. [Google Scholar] [CrossRef] [PubMed]
- Hao, H.; Chow, C.L.; Lau, D. Effect of Heat Flux on Combustion of Different Wood Species. Fuel 2020, 278, 118325. [Google Scholar] [CrossRef]
- Chen, Y.; Hao, Y.; Wang, J.; Gao, H.; Liu, G.; Lan, B.; Zhang, Y.; Chen, J. Effect of Ambient Temperature and Wind Speed on Horizontal Flame Spread and Combustion Trace on Typical Decorative Wood Boards. Constr. Build. Mater. 2023, 408, 133597. [Google Scholar] [CrossRef]
- Wang, Z.; Gao, Y.; Zhou, Y.; Fan, C.; Zhou, P.; Gong, J. Pyrolysis and Combustion Behaviors of Densified Wood. Proc. Combust. Inst. 2023, 39, 4175–4184. [Google Scholar] [CrossRef]
- Fan, C.; Gao, Y.; Li, Y.; Yan, L.; Zhu, D.; Guo, S.; Ou, C.; Wang, Z. A Flame-Retardant Densified Wood as Robust and Fire-Safe Structural Material. Wood Sci. Technol. 2023, 57, 111–134. [Google Scholar] [CrossRef]
- Yan, W.G.; Wang, C.J.; Guo, J. One Extended OTSU Flame Image Recognition Method Using RGBL and Stripe Segmentation. Appl. Mech. Mater. 2011, 121–126, 2141–2145. [Google Scholar] [CrossRef]
- Otsu, N. A Threshold Selection Method from Gray-Level Histograms. IEEE Trans. Syst. Man Cybern. 1979, 9, 62–66. [Google Scholar] [CrossRef]
- Zukoski, E.E.; Cetegen, B.M.; Kubota, T. Visible Structure of Buoyant Diffusion Flames. Symp. Int. Combust. 1985, 20, 361–366. [Google Scholar] [CrossRef]
- Hasemi, Y. Experimental Wall Flame Heat Transfer Correlations for the Analysis of Upward Wall Flame Spread. Fire Sci. Technol. 1984, 4, 75–90. [Google Scholar] [CrossRef]
- Gao, Z.H.; Liu, Z.X.; Ji, J.; Fan, C.G.; Li, L.J.; Sun, J.H. Experimental Study of Tunnel Sidewall Effect on Flame Characteristics and Air Entrainment Factor of Methanol Pool Fires. Appl Therm. Eng. 2016, 102, 1314–1319. [Google Scholar] [CrossRef]
- Flity, H.; Jannot, Y.; Terrei, L.; Lardet, P.; Schick, V.; Acem, Z.; Parent, G. Thermal Conductivity Parallel and Perpendicular to Fibers Direction and Heat Capacity Measurements of Eight Wood Species up to 160 °C. Int. J. Therm. Sci. 2024, 195, 108661. [Google Scholar] [CrossRef]
- ISO 13061-1; Physical and Mechanical Properties of Wood—Test Methods for Small Clear Wood Specimens, Part 1: Determination of Moisture Content for Physical and Mechanical Tests. International Organization for Standardization: Geneva, Switzerland, 2017.
- Figueiredo, J.L.; Valenzuela, C.; Bernalte, A.; Encinar, J.M. Pyrolysis of Holm-Oak Wood: Influence of Temperature and Particle Size. Fuel 1989, 68, 1012–1016. [Google Scholar] [CrossRef]
- Leventon, I.T.; Stoliarov, S.I. Evolution of Flame to Surface Heat Flux during Upward Flame Spread on Poly(Methyl Methacrylate). Proc. Combust. Inst. 2013, 34, 2523–2530. [Google Scholar] [CrossRef]
- Beaulieu, P.A.; Dembsey, N.A. Effect of Oxygen on Flame Heat Flux in Horizontal and Vertical Orientations. Fire Saf. J. 2008, 43, 410–428. [Google Scholar] [CrossRef]
- Zhang, Y.; Ji, J.; Li, J.; Sun, J.; Wang, Q.; Huang, X. Effects of Altitude and Sample Width on the Characteristics of Horizontal Flame Spread over Wood Sheets. Fire Saf. J. 2012, 51, 120–125. [Google Scholar] [CrossRef]
- Incropera, F.P.; DeWitt, D.P.; Bergman, T.L.; Lavine, A.S. Fundamentals of Heat and Mass Transfer; Wiley: New York, NY, USA, 2007. [Google Scholar]
- Cai, M.; Chen, S.; Tang, Y.; Li, Q.; An, W. Study on the Influence of Enclosed Vertical Channels on Downward Flame Spread over XPS Thermal Insulation Materials. Case Stud. Therm. Eng. 2019, 14, 100486. [Google Scholar] [CrossRef]
- Quintiere, J.G. Fundamentals of Fire Phenomena; John Wiley & Sons: Hoboken, NJ, USA, 2006. [Google Scholar]
- Rossi, J.-L.; Chetehouna, K.; Collin, A.; Moretti, B.; Balbi, J.-H. Simplified Flame Models and Prediction of the Thermal Radiation Emitted by a Flame Front in an Outdoor Fire. Combust. Sci. Technol. 2010, 182, 1457–1477. [Google Scholar] [CrossRef]
- Shi, L.; Chew, M.Y.L. Experimental Study of Woods under External Heat Flux by Autoignition: Ignition Time and Mass Loss Rate. J. Therm. Anal. Calorim. 2013, 111, 1399–1407. [Google Scholar] [CrossRef]
- Hostikka, S.; Matala, A. Pyrolysis Model for Predicting the Heat Release Rate of Birch Wood. Combust. Sci. Technol. 2017, 189, 1373–1393. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, Y.; Qiu, W.; Zhou, P.; Wang, Z.; Zhang, X.; Mao, X.; Bu, R. Influences of Species and Density on the Horizontal Flame Spread Behavior of Densified Wood. Buildings 2024, 14, 620. https://doi.org/10.3390/buildings14030620
Zhou Y, Qiu W, Zhou P, Wang Z, Zhang X, Mao X, Bu R. Influences of Species and Density on the Horizontal Flame Spread Behavior of Densified Wood. Buildings. 2024; 14(3):620. https://doi.org/10.3390/buildings14030620
Chicago/Turabian StyleZhou, Yang, Wenxi Qiu, Penghui Zhou, Zhengyang Wang, Xiaonan Zhang, Xiangyu Mao, and Rongwei Bu. 2024. "Influences of Species and Density on the Horizontal Flame Spread Behavior of Densified Wood" Buildings 14, no. 3: 620. https://doi.org/10.3390/buildings14030620









