Integrating Combination Weighting of Game Theory and Fuzzy Comprehensive Evaluation for Selecting Deep Foundation Pit Support Scheme
Abstract
1. Introduction
2. Constructing the Decision Model for Deep Foundation Pit Support Scheme
2.1. Determination of Subjective Weight by Analytic Hierarchy Process (AHP)
2.2. Improved Entropy Method for Determining Objective Weights
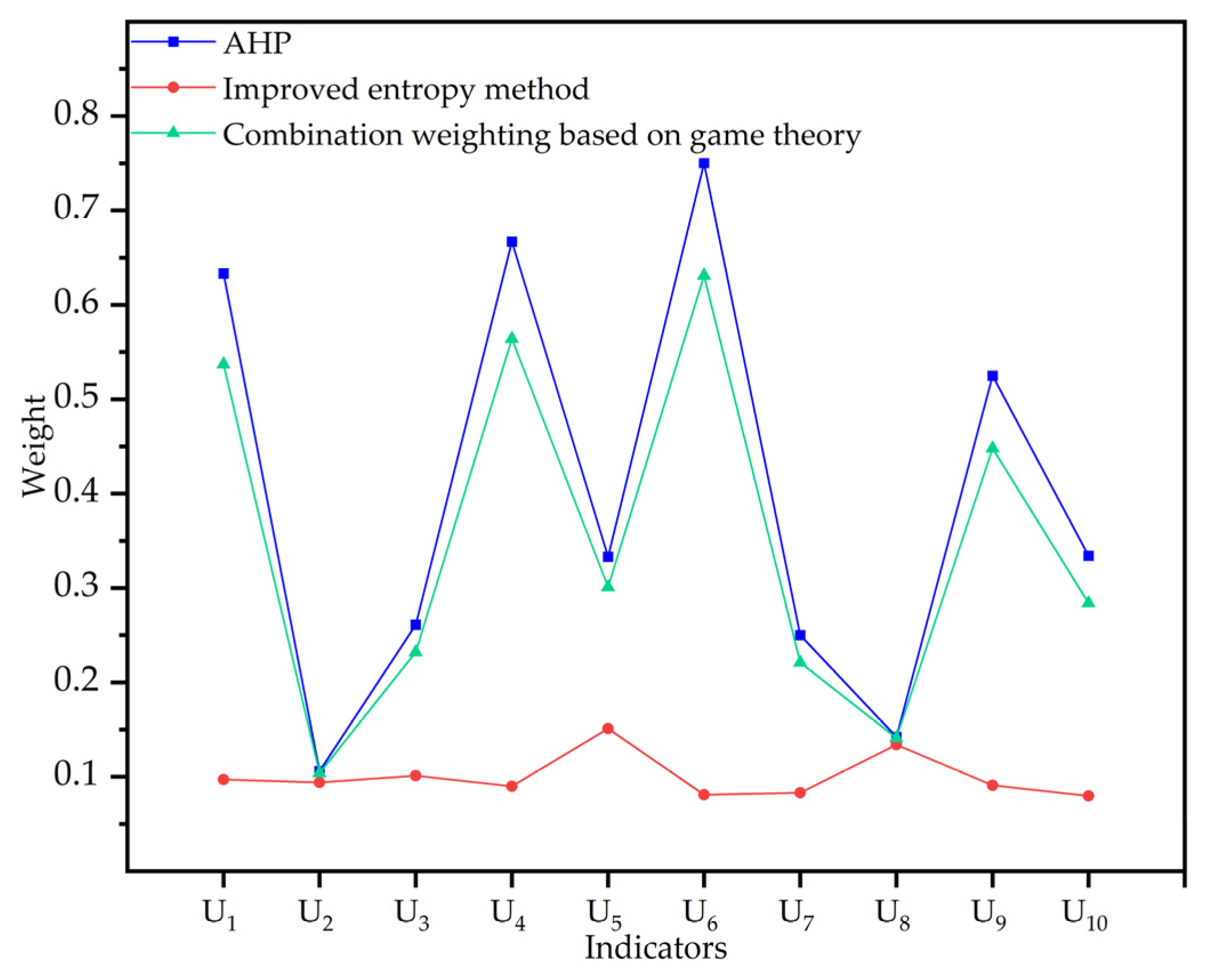
2.3. Modifying the Comprehensive Weight Based on Combination Weighting of Game Theory
2.4. Scheme Optimization Based on Fuzzy Comprehensive Evaluation
3. Case Study and Model Application
3.1. General Situation of Project
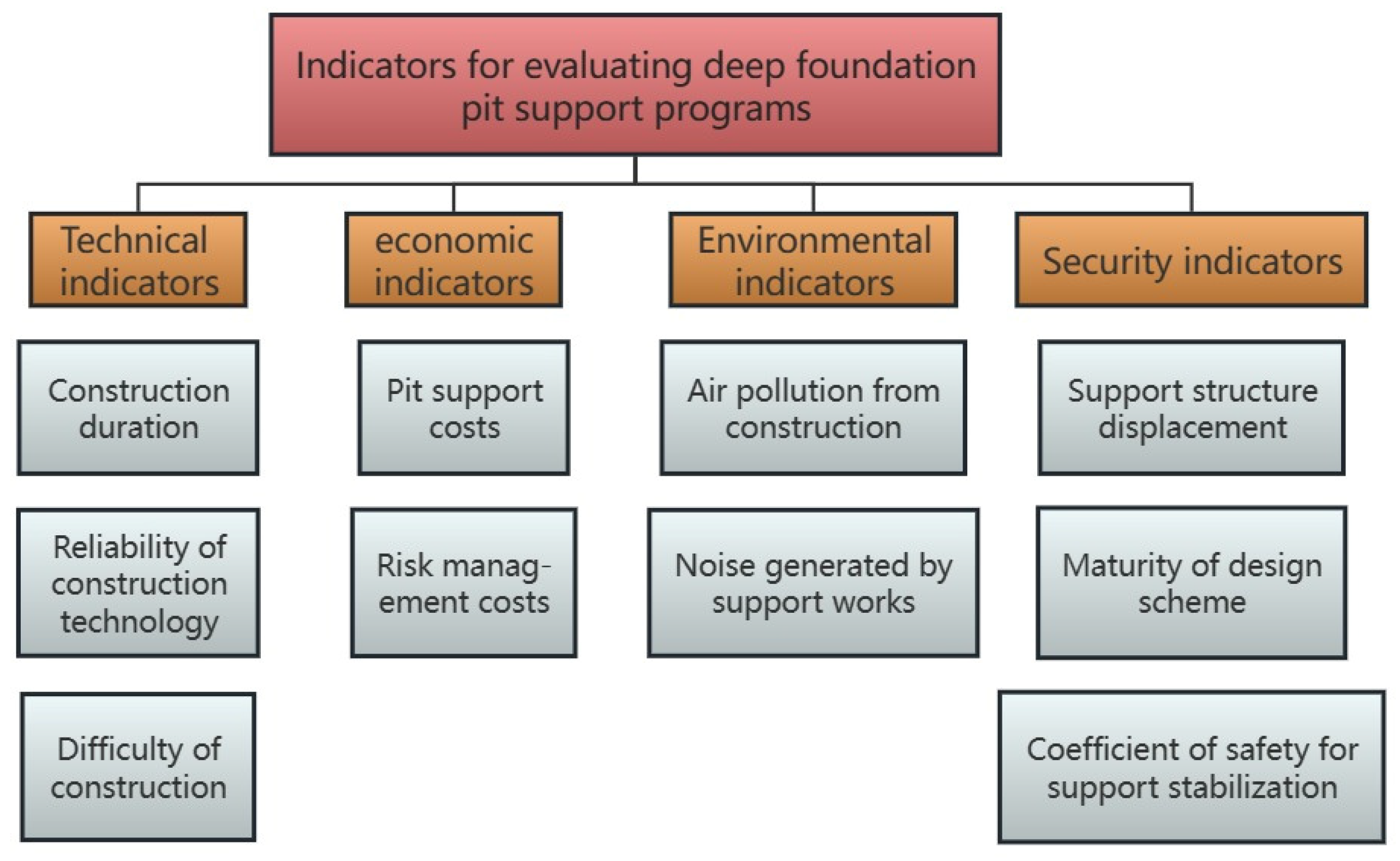
3.2. Construction of Evaluation Index System
3.3. Determination of Deep Foundation Pit Support Scheme
3.4. Verification of the Proposed Foundation Pit Support Scheme
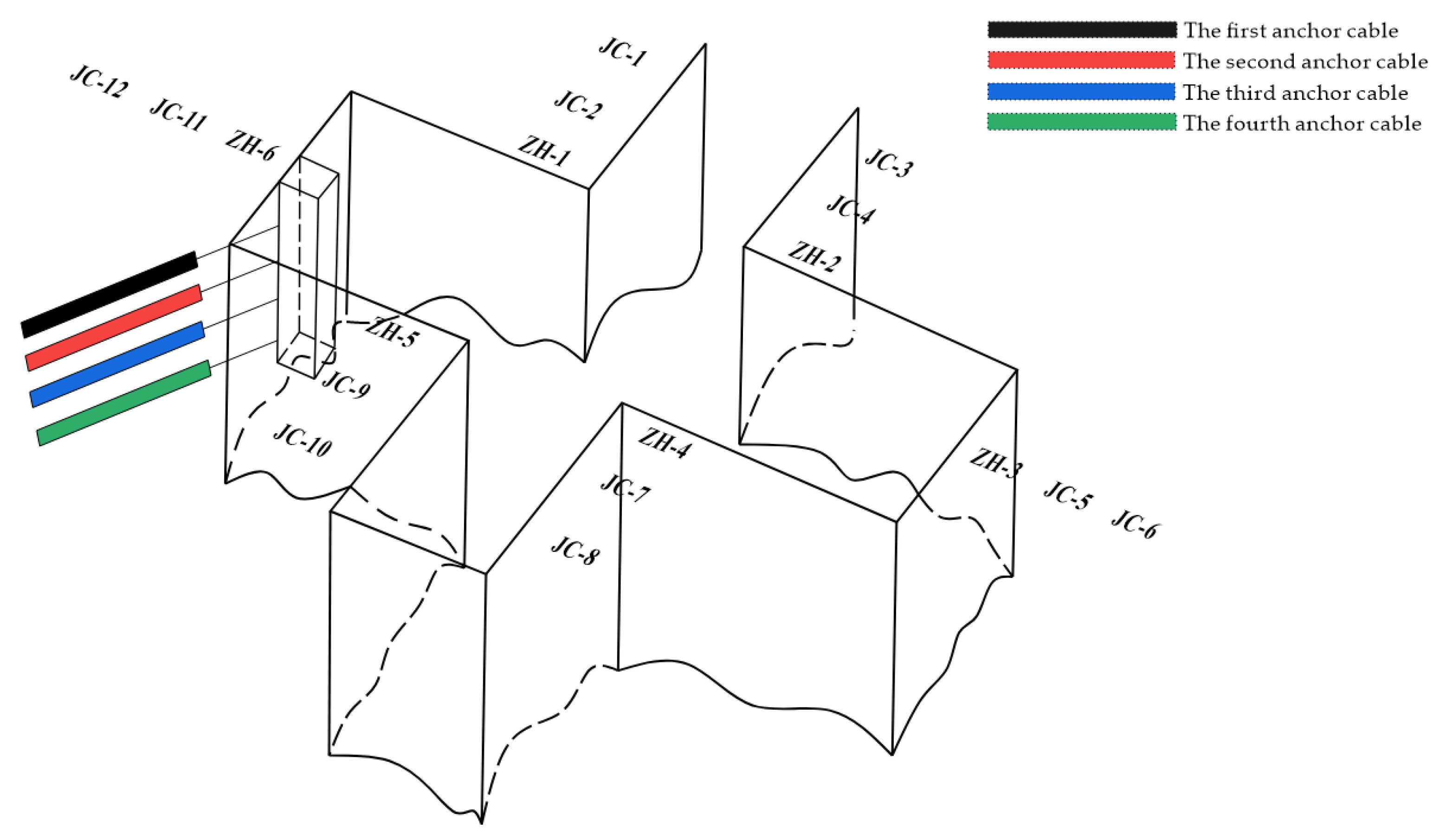
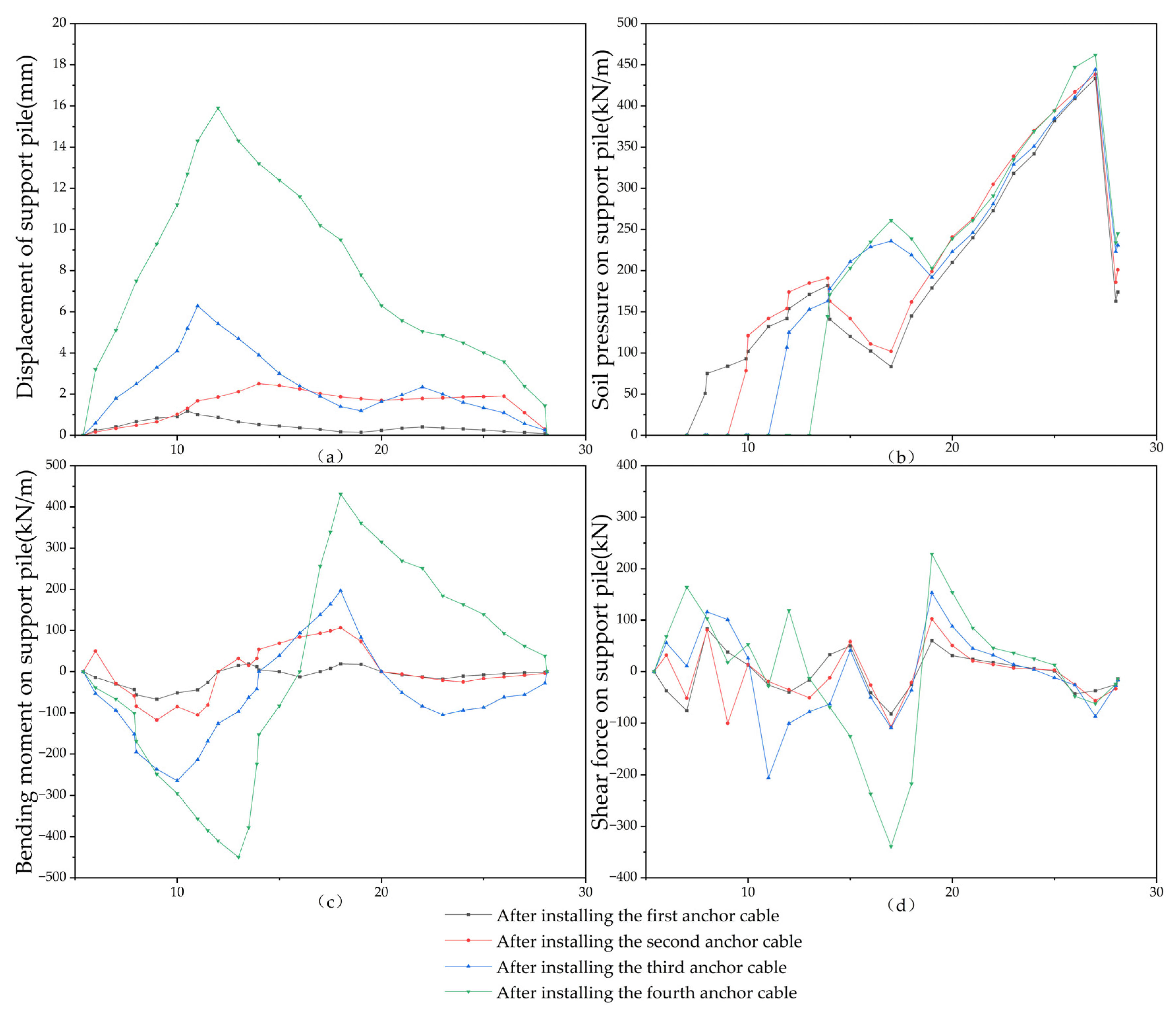
3.4.1. Simulation Calculation of the Proposed Scheme
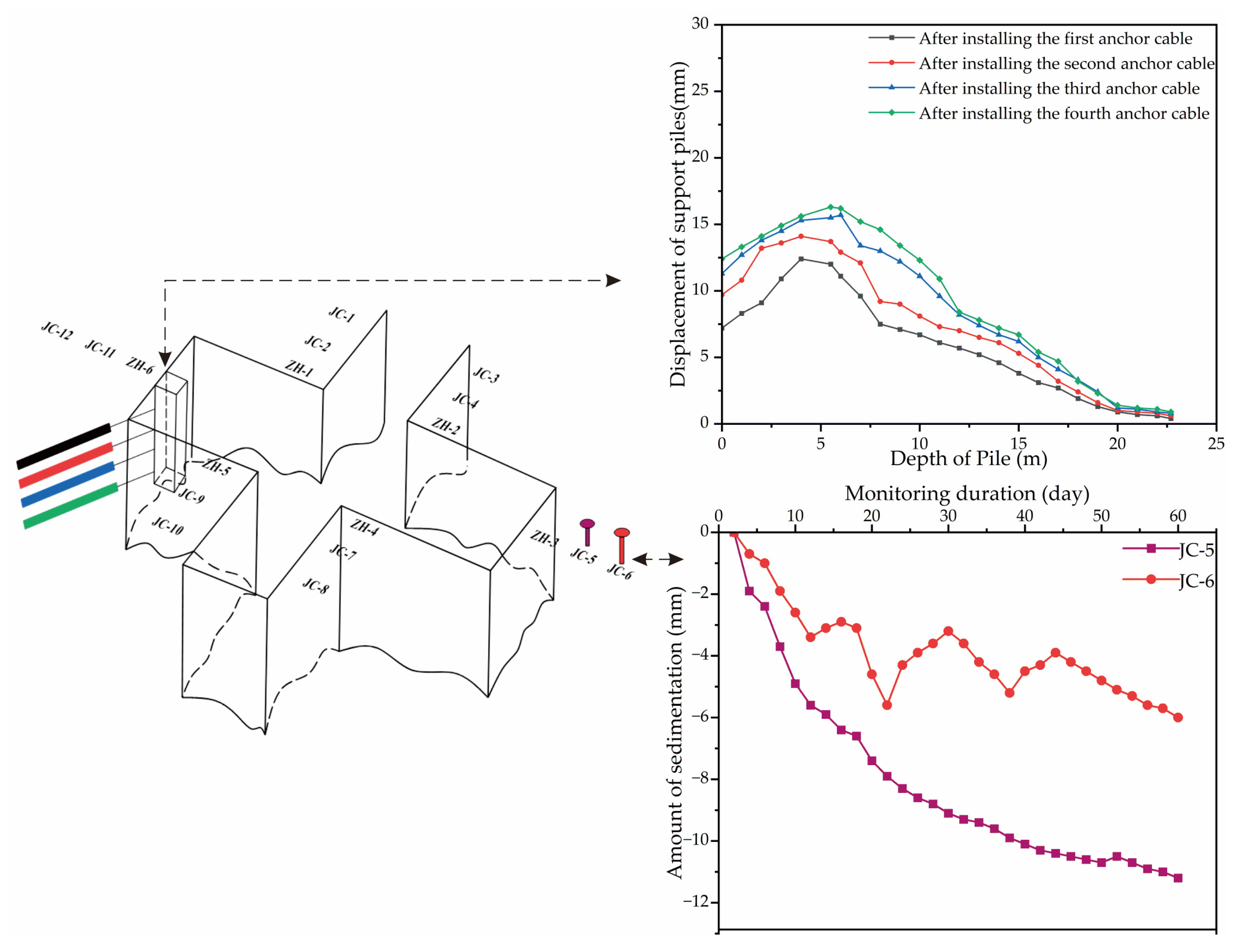
3.4.2. Monitoring Data Analysis of the Proposed Scheme
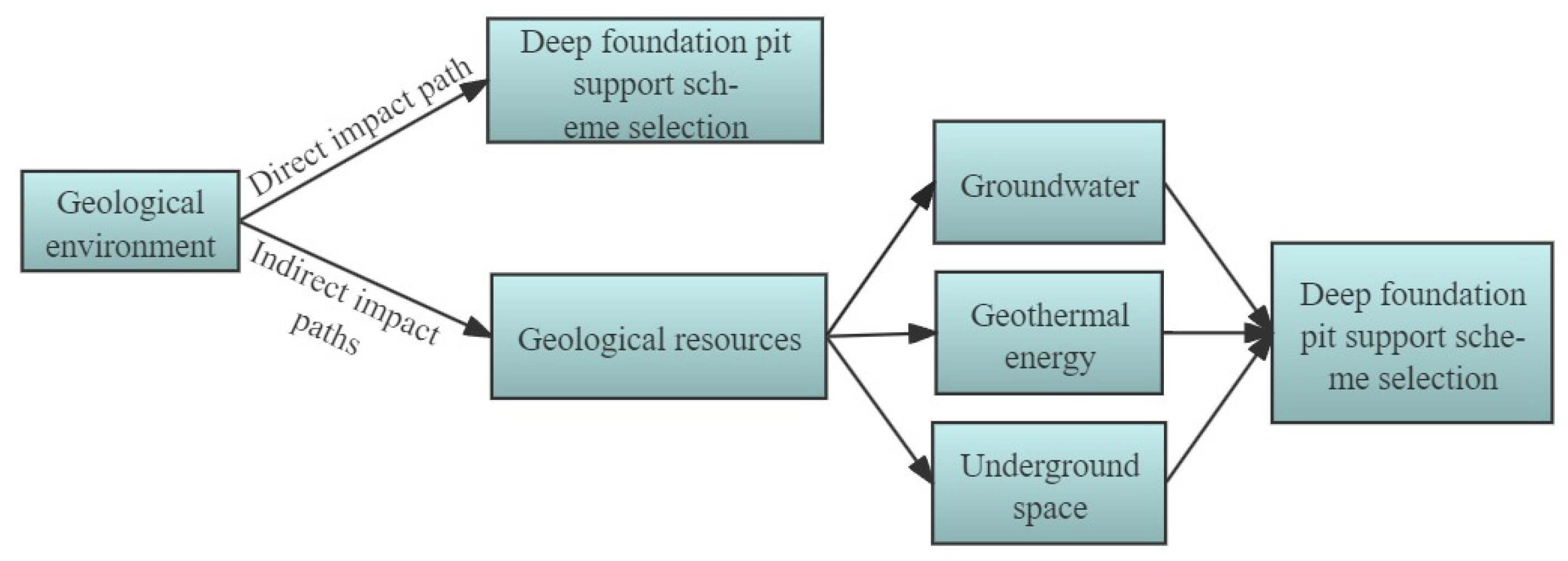
4. Discussion
- 1.
- Direct influence mechanism
- 2.
- Indirect influence mechanism
5. Conclusions
- The subjective and objective weights of the evaluation indexes of the deep foundation pit support scheme are calculated by using the AHP and improved entropy method, respectively, which overcomes the limitations caused by the single method and takes into account the situation that the index data cannot be obtained directly. Then, the comprehensive weight of each index is determined based on the combination weighting of game theory. Compared with the traditional method for obtaining the weight of the scheme evaluation index, the method used in this paper is more objective and scientific in determining the index weight. Finally, the fuzzy comprehensive evaluation method is used to evaluate the scheme. Uncertain decision-making problems such as foundation pit support scheme optimization are effectively dealt with, and a deep foundation pit scheme optimization model is constructed to provide decision support for similar projects.
- The optimization model of deep foundation pit support schemes constructed in this paper is applied to an actual project, and it is determined that the optimal scheme of a city administration corridor project in area A is soil nailing wall + supporting pile + anchor cable. The deformation trend of the supporting pile under different working conditions is simulated, and the calculation results show that the pull-out safety factors of soil nails in the upper part of the foundation pit are all above 6 and the displacement of the supporting pile after installing anchor cables in the lower part meets the design requirements. The coefficient of safety of the supporting structure is 1.61, which is greater than the 1.3 required in the construction safety code, proving the theoretical feasibility and safety of the proposed scheme. Further analysis combined with the actual construction monitoring data shows that the relative error between the actual displacement of the supporting pile and the simulation results is 2.46%, the surface settlement is within the safe range, and the overall supporting structure has a good stability. The accuracy and rationality of the optimization model of the supporting scheme are fully verified.
- By summarizing the advantages, disadvantages, and applicability of the current mainstream optimization methods for deep foundation pit support schemes and comparing the optimization model constructed in this paper, this reflects the applicability and superiority of the model in dealing with insufficient project data, facing fuzzy problems, limited expert experience, and so on. The indirect and direct influence mechanisms of the geological environment on the selection of deep foundation pit support schemes are identified and generalized, and then the influence factors and action path of the selection of support scheme are analyzed. Through the study of geological conditions, the support scheme suitable for the geological environment can be better selected, so as to improve the stability and safety of the project. At the same time, research ideas are provided to establish a framework for the selection of support schemes that can be directly referred to.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, Y.; Rong, S.; Li, H. Research on risk analysis method of super-large deep foundation pit based on dynamic monitoring and fault tree analysis. J. Saf. Sci. Technol. 2023, 19, 89–95. [Google Scholar]
- Gong, X. Some major problems in the development of foundation pit engineering. Chin. J. Geotech. Eng. 2006, 28, 1321–1324. [Google Scholar]
- Liu, B.; Xu, W.; Reddy, K.R. Effects of Demolishing the Deep Excavation Support System Used for Tall Building Construction on Adjacent Metro Line; Modeling and Field Comparison; IFCEE: Dallas, TX, USA, 2015; pp. 1107–1121. [Google Scholar]
- Sun, B.; Zhang, S.; Yang, J. Optimal decision model for the sup-porting scheme of the deep foundation pit based on the prospect theory and BWM. J. Saf. Environ. Eng. 2021, 21, 70–77. [Google Scholar]
- Zheng, S.; Li, S. Improved TOPSIS decision method for optimizing mixed indexes supporting schemes for foundation pit. J. Saf. Sci. China 2014, 24, 98–103. [Google Scholar]
- Tu, B.; Zheng, J.; Ye, S.; Shen, M. Study on excavation response of deep foundation pit supported by SMW piles combined with internal support in soft soil area. Water 2023, 15, 3430. [Google Scholar] [CrossRef]
- He, Y.; Qin, W.; Wang, Y. Optimization of supporting schemes for deep foundation pit based on combined weight and grey Euclid theory. J. Saf. Sci. Technol. 2016, 12, 94–97. [Google Scholar]
- Hefny, A.M.; Sorour, T.M.; Ezzat, M.E. Prediction of the Field Response of Soil-Support Systems in Deep Excavations; Geo-China: Beijing, China, 2016; pp. 141–151. [Google Scholar]
- Issa, U.; Saeed, F.; Miky, Y.; Alqurashi, M.; Osman, E. Hybrid AHP-fuzzy TOPSIS approach for selecting deep excavation support system. Buildings 2022, 12, 295. [Google Scholar] [CrossRef]
- Salimian, S.; Mousavi, S.M.; Tupenaite, L.; Antucheviciene, J. An Integrated Multi-Criteria Decision Model to Select Sustainable Construction Projects under Intuitionistic Fuzzy Conditions. Buildings 2023, 13, 848. [Google Scholar] [CrossRef]
- Temiz, I.; Calis, G. Selection of Construction Equipment by using Multi-criteria Decision Making Methods. Procedia Eng. 2017, 196, 286–293. [Google Scholar] [CrossRef]
- Shahpari, M.; Saradj, M.F.; Pishvaee, S.M.; Piri, S. Assessing the productivity of prefabricated and in-situ construction systems using hybrid multi-criteria decision making method. J. Build. Eng. 2020, 27, 100979. [Google Scholar] [CrossRef]
- Branimir, F.; Ana, H. Multi-Criteria Analysis for the Selection of the Optimal Mining Design Solution—A Case Study on Quarry “Tambura”. Energies 2021, 14, 3200. [Google Scholar]
- Palanikkumar, D.; Upreti, K.; Venkatraman, S.; Suganthi, J.R.; Kannan, S.; Srinivasan, S. Fuzzy Logic for Underground Mining Method Selection. Intell. Autom. Soft Comput. 2022, 32, 1843–1854. [Google Scholar] [CrossRef]
- Ye, W.; Gao, C.; Liu, Z.; Wang, Q.; Su, W. A Fuzzy-AHP-based variable weight safety evaluation model for expansive soil slope. Nat. Hazards 2023, 119, 559–581. [Google Scholar] [CrossRef]
- Jin, L.; Song, B.; Du, X. A modified method for calculating the shear capacity of RC deep flexural members. J. Build. Struct. 2023, 44, 170–182. [Google Scholar]
- Zhou, H.; Cao, P. A fuzzy AHP approach to select supporting schemes for city foundation pit in soft soil. J. Cent. South Univ. (Nat. Sci. Ed.) 2012, 43, 3582–3588. [Google Scholar]
- Jing, W.; Song, S.; Li, Y.; Luo, X. Application of TOPSIS-AISM Interpretation Model in Support Scheme Optimization for Foundation Pit. J. Saf. Environ. Eng. 2023, 30, 76–83. [Google Scholar]
- Wu, Z. Research on the Intelligent Optimization Design Method of Deep Foundation Pit Support. Master’s Thesis, Hunan University, Changsha, China, 2005. [Google Scholar]
- Wei, D. Risk Assessment for Subway Construction Based on Fault Tree Analysis and Analytical Hierarchy Process: A Case Study of Destabilization of Pit Supporting Structure of Tunnel Shaft. Saf. Environ. Eng. 2018, 25, 100–104. [Google Scholar]
- Jiang, Q.; Zhong, S.; Zhu, W. Research on comprehensive risk assessment of forest fire in Beijing-Tianjin-Hebei region. J. Saf. Sci. China 2020, 30, 119–125. [Google Scholar]
- Huang, Y.K.; Xu, S.; Jiang, M.; Li, W. Evaluation for the channel waters navigation safety based on the synthetic weighing of the game theory. J. Saf. Environ. 2021, 21, 2430–2437. [Google Scholar]
- Liu, Z.; Liu, Y.; Xie, R. Identification and fusion of abnormal results in accident reconstruction based on entropy method. China Saf. Sci. J. 2023, 33, 96–104. [Google Scholar]
- Luo, X. Fuzzy Synthetic Evaluation Based on Set-Valued Statistics and Its Application. Math. Pract. Theory 2005, 35, 42–45. [Google Scholar]
- Ma, Y.; Shi, T.; Zhang, W.; Hao, Y.; Huang, J.; Lin, Y. Comprehensive policy evaluation of NEV development in China, Japan, the United States, and Germany based on the AHP-EW model. J. Clean. Prod. 2018, 214, 389–402. [Google Scholar] [CrossRef]
- Wang, G.; Shang, B.; Liu, X.; Li, T.; Qian, C. Study on causes of poisoning and asphyxiation in roadway opening by AHP-entropy weight method. China Saf. Sci. J. 2021, 31, 187–192. [Google Scholar]
- Wei, D.Y.; Du, C.F.; Lin, Y.F.; Chang, B.; Wang, Y. Thermal Environment Assessment of Deep Mine Based on Analytic Hierarchy Process and Fuzzy Comprehensive Evaluation. Case Stud. Therm. Eng. 2020, 19, 100618. [Google Scholar] [CrossRef]
- Wu, X.L.; Hu, F. Analysis of Ecological Carrying Capacity Using A Fuzzy Comprehensive Evaluation method. Ecol. Indic. 2020, 113, 106243. [Google Scholar] [CrossRef]
- Cao, H.; Liu, J. Combinatorial Calculation Model of Active Earth Pressure under Non-limit State and Its Engineering Application. J. Basic Sci. Eng. 2019, 27, 590–601. [Google Scholar]
- Yang, G.; Chen, R. Application of analytic hierarchy process in optimization of deep foundation pit support scheme. J. Shaanxi Univ. Technol. (Nat. Sci. Ed.) 2018, 34, 28–34. [Google Scholar]
- Wei, D.; Li, Y.; Zhang, Y. An Interval Evidential Reasoning-based Approach for Selecting Supporting Scheme for Deep Foundation Pit. J. Highw. Transp. Res. Dev. 2023, 40, 127–134. [Google Scholar]
- Jiang, Y.; Deng, Z.; Wang, D. Research on Supporting Scheme Optimization for Deep Foundation Pit Based on Set Pair Analysis. Chin. J. Undergr. Space Eng. 2016, 12, 131–137. [Google Scholar]
- Zhang, A.; Li, Y.; Zhang, Y. Research on entropy weight-ideal point decision model in foundation pit support scheme selection. Yangtze River 2014, 45 (Suppl. S2), 213–216. [Google Scholar]
- Yuan, W. Application of Improved TOPSIS Model to the Comprehensive Evaluation of Foundation Pit Support Scheme. J. Chang. River Sci. Res. Inst. 2014, 31, 82–86. [Google Scholar]
- Wang, M.; Zhao, K.; Zhu, Q.; Jiang, H.; Jin, J. Decision-making model of supporting schemes of foundation pit based on cumulative prospect theory and connection number. Rock Soil Mech. 2016, 37 (Suppl. S2), 622–628. [Google Scholar]
- Gao, W.; Zhang, Z.; Zhu, J. Optimization of Supporting Plan of Deep Excavation Based on Fuzzy Back Propagation Neural Network. J. Saf. Sci. China 2006, 16, 4–8+1. [Google Scholar]
- He, Y.; Li, C. Optimization of supporting plan for deep foundation pit based on principal component analysis and BP neural network. Sichuan Build. Sci. 2015, 41, 32–35+39. [Google Scholar]
- Zhang, H.; He, Y. A Study of Optimum Seeking Decision for Bracing Schemes of Deep Foundation Pit based on Artificial Neural Network. Constr. Des. Eng. 2004, 5, 69–71. [Google Scholar]
| Matrix Order | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|
| RI | 0 | 0.58 | 0.90 | 1.12 | 1.24 | 1.32 | 1.41 | 1.45 |
| Evaluation Grade | Very Poor | Poor | Ordinary | Good | Very Good |
|---|---|---|---|---|---|
| Point value (C) | 1 | 2 | 3 | 4 | 5 |
| Serial Number | Soil | Soil Thickness (m) | Bulk Density (kN/m3) | Internal Friction Angle (°) | Adhesion (kPa) |
|---|---|---|---|---|---|
| 1 | Miscellaneous fillings | 2.6 | 16.5 | 15.9 | 13.1 |
| 2 | Loess | 2.3 | 18.2 | 25.1 | 6.8 |
| 3 | Powdery Clay | 1.7 | 18.8 | 23.4 | 8.8 |
| 4 | Fine sand | 2.2 | 18.5 | 25 | 7 |
| 5 | Medium coarse sand | 1.3 | 18.9 | 25 | 30 |
| 6 | Silt | 4.5 | 16.1 | 5.6 | 5.2 |
| Indicators | Scheme | Experts | Value | Unitization | |||
|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | ||||
| Reliability of construction technology | I | [70, 80] | [70, 90] | [90, 100] | [70, 80] | 81 | 0.81 |
| II | [70, 80] | [80, 90] | [90, 100] | [80, 90] | 85 | 0.85 | |
| III | [80, 90] | [80, 90] | [90, 100] | [90, 100] | 90 | 0.9 | |
| Degree of construction difficulty | I | [80, 90] | [70, 90] | [70, 90] | [70, 80] | 80.0 | 0.8 |
| II | [70, 80] | [70, 80] | [70, 80] | [60, 70] | 72.5 | 0.725 | |
| III | [60, 80] | [60, 80] | [50, 60] | [70, 80] | 68.3 | 0.683 | |
| Air pollution from construction | I | [70, 80] | [80, 90] | [70, 80] | [80, 100] | 85 | 0.85 |
| II | [80, 90] | [80, 90] | [80, 90] | [90, 100] | 87 | 0.87 | |
| III | [60, 70] | [70, 80] | [70, 80] | [70, 90] | 81 | 0.81 | |
| Maturity of design scheme | I | [70, 80] | [70, 80] | [70, 80] | [60, 70] | 72.5 | 0.725 |
| II | [80, 90] | [80, 90] | [90, 100] | [90, 100] | 90 | 0.9 | |
| III | [70, 80] | [70, 90] | [90, 100] | [70, 80] | 81 | 0.81 | |
| Indicators | Guidelines | Scheme I | Scheme II | Scheme III |
|---|---|---|---|---|
| Technical indicators | Construction duration | 70 | 55 | 45 |
| Reliability of construction technology | 0.81 | 0.85 | 0.90 | |
| Difficulty of construction | 0.80 | 0.725 | 0.683 | |
| Economic indicators | Pit support costs | 303.7 | 263.2 | 223.5 |
| Risk management costs | 12.4 | 13.6 | 23.6 | |
| Environmental indicators | Noise generated by the support works | 85 | 80 | 65 |
| Air pollution caused by construction | 0.85 | 0.87 | 0.81 | |
| Safety indicators | Displacement of pit support | 27 | 32 | 57 |
| Maturity of design scheme | 0.725 | 0.90 | 0.81 | |
| Coefficient of safety of support stabilization | 1.95 | 1.90 | 1.68 |
| Indicators | Evaluation Results | ||||
|---|---|---|---|---|---|
| Very Poor | Poor | Average | Good | Very Good | |
| Construction duration U1 | 2 | 4 | 3 | 1 | 0 |
| Reliability of construction technology U2 | 3 | 2 | 2 | 2 | 1 |
| Difficulty of construction U3 | 3 | 3 | 3 | 1 | 0 |
| Pit support costs U4 | 4 | 3 | 2 | 1 | 0 |
| Risk management costs U5 | 2 | 3 | 3 | 1 | 1 |
| Noise generated by support works U6 | 3 | 2 | 3 | 2 | 0 |
| Air pollution caused by construction U7 | 2 | 4 | 2 | 1 | 1 |
| Displacement of pit support U8 | 0 | 1 | 3 | 3 | 3 |
| Maturity of design scheme U9 | 3 | 2 | 2 | 2 | 0 |
| Coefficient of safety of support stabilization U10 | 0 | 0 | 3 | 5 | 2 |
| Methods | Advantages and Disadvantages | Application | Typical Literature |
|---|---|---|---|
| AHP and fuzzy comprehensive evaluation | Advantages: relatively simple and easy to use, able to consider the hierarchical relationship between multiple factors Disadvantages: relies on the experience of experts, strong subjective factors, there may be the problem that the program selection results do not match the actual project. | It is suitable for simple works, low risk factor, and experienced experts. | [15,17,30] |
| Entropy method | Advantages: the concept of information entropy is taken into account, which is conducive to the comprehensive consideration of the uncertainty and inconsistency of various factors Disadvantages: high data requirements, needs a large amount of data support, in some cases may be affected by data distribution. | It is suitable for projects with more adequate data where uncertainty and information entropy need to be taken into account. | [25,31,32,33] |
| TOPSIS | Advantages: Can make up for the shortcomings of the respective methods to a certain extent, and improve the comprehensiveness and objectivity of decision making. Disadvantages: TOPSIS also has some limitations when dealing with uncertainty, high data volume requirements. | It is suitable for relatively simple and well-structured decision problems, especially when there are relatively sufficient data to provide more credible results for decision making. | [5,18,34] |
| Prospect theory and best–worst method | Advantages: considering the optimal and worst scenarios comprehensively, it helps to reduce the uncertainty of decision making. Disadvantages: need to clarify the optimal and worst scenario, higher requirements for the acquisition and accuracy of information, the calculation process is more complex. | Applicable to decision-making problems that require consideration of different scenarios. | [4,35] |
| Fuzzy neural network | Advantages: able to deal with nonlinear relationships, applicable to the evaluation of complex systems, able to adaptively adjust the model parameters. Disadvantages: high data requirements, needs a large amount of training data, model structure is more complex, poor interpretability. | Suitable for evaluation and prediction of complex support works and projects with adequate data. | [36,37,38] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jin, T.; Zhang, P.; Niu, Y.; Lv, X. Integrating Combination Weighting of Game Theory and Fuzzy Comprehensive Evaluation for Selecting Deep Foundation Pit Support Scheme. Buildings 2024, 14, 619. https://doi.org/10.3390/buildings14030619
Jin T, Zhang P, Niu Y, Lv X. Integrating Combination Weighting of Game Theory and Fuzzy Comprehensive Evaluation for Selecting Deep Foundation Pit Support Scheme. Buildings. 2024; 14(3):619. https://doi.org/10.3390/buildings14030619
Chicago/Turabian StyleJin, Tianlu, Peixing Zhang, Yuanda Niu, and Xiaofeng Lv. 2024. "Integrating Combination Weighting of Game Theory and Fuzzy Comprehensive Evaluation for Selecting Deep Foundation Pit Support Scheme" Buildings 14, no. 3: 619. https://doi.org/10.3390/buildings14030619
APA StyleJin, T., Zhang, P., Niu, Y., & Lv, X. (2024). Integrating Combination Weighting of Game Theory and Fuzzy Comprehensive Evaluation for Selecting Deep Foundation Pit Support Scheme. Buildings, 14(3), 619. https://doi.org/10.3390/buildings14030619





