Comprehensive Numerical Modeling of Prestressed Girder Bridges under Low-Velocity Impact
Abstract
:1. Introduction
- We developed and validated an FE model of a large-scale prestressed girder bridge under impact loads.
- We utilized the dynamic relaxation approach to model large-scale prestressed concrete girders under impact loads.
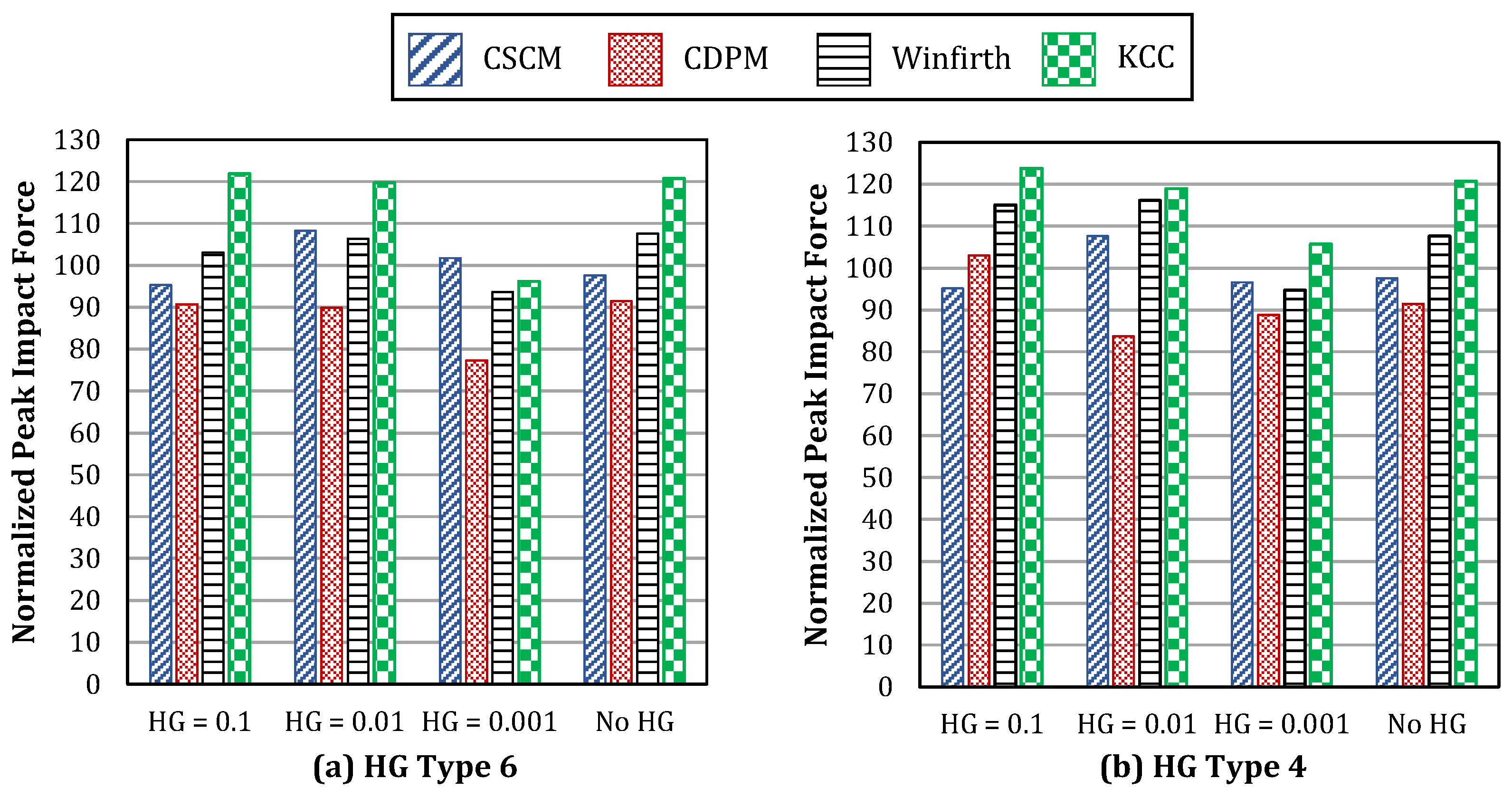
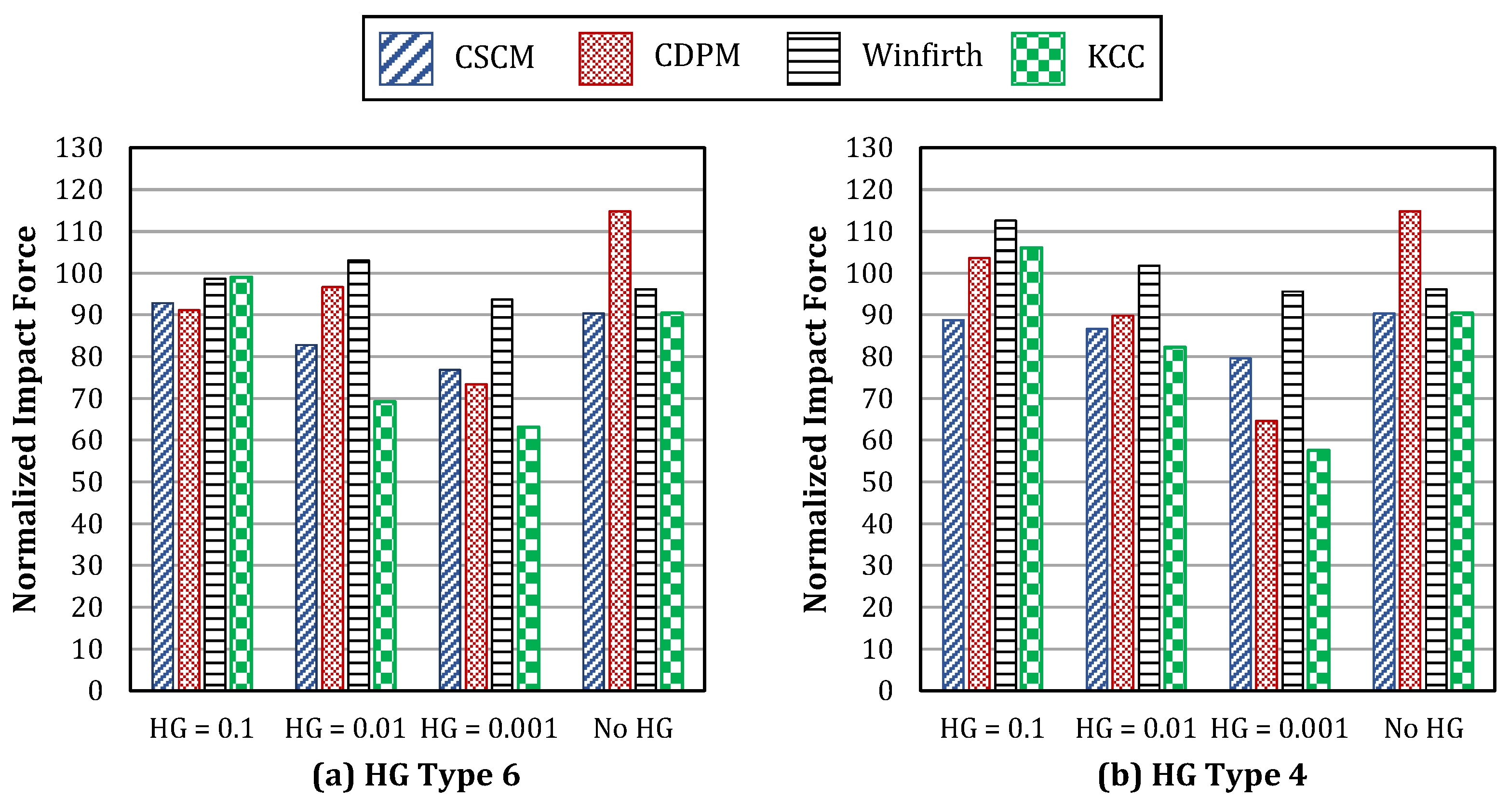
- We compared four different material models and two stiffness-based hourglass types of concrete under impact loads.
- We investigated the effect of different impact parameters, including impact speed, mass, and the effect of prestressing force, on the response of prestressed girder bridges.

2. Research Methodology
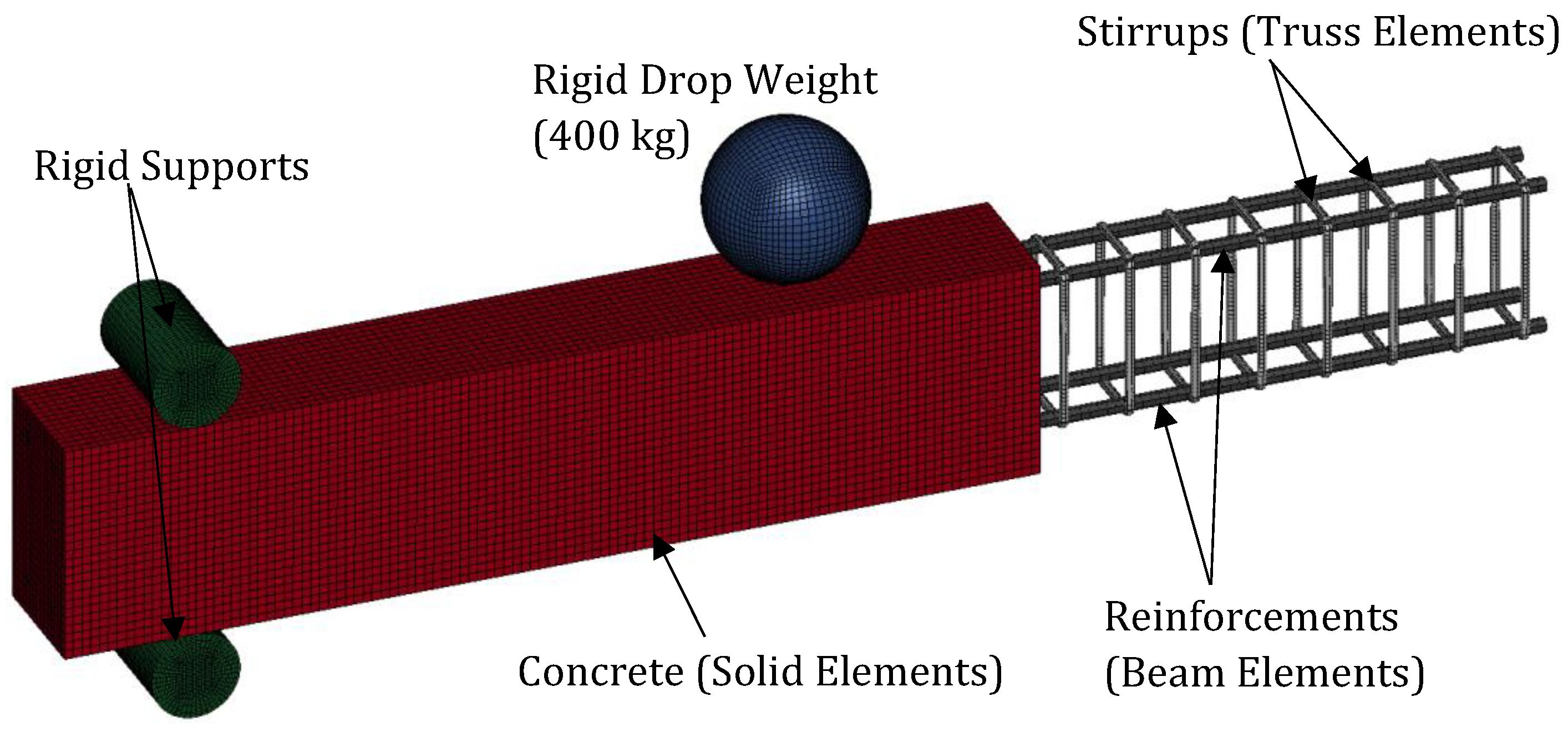
3. Finite Element Modeling
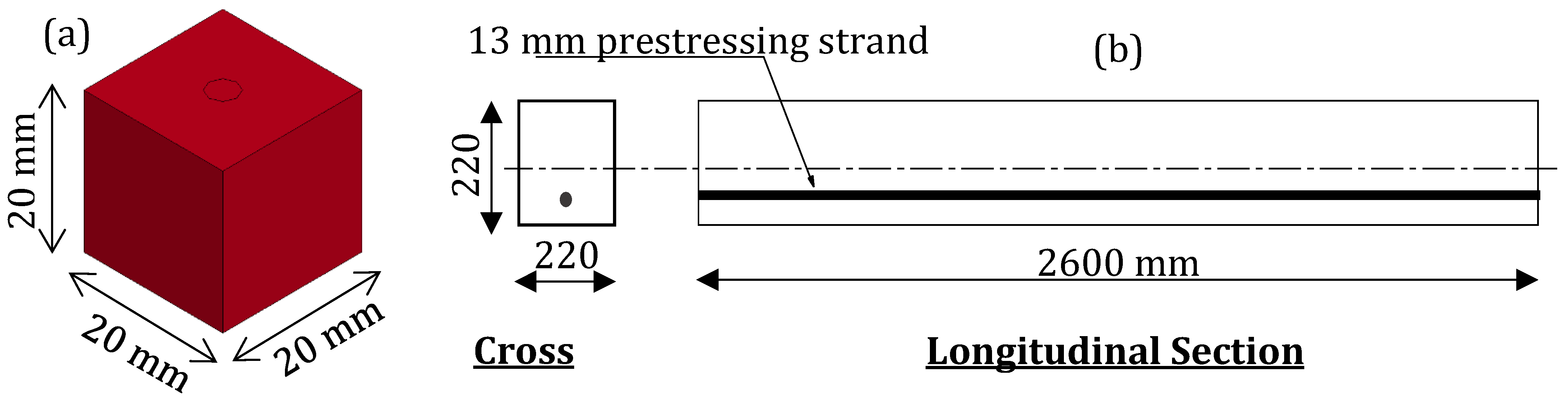
3.1. Modeling of Prestressed Concrete
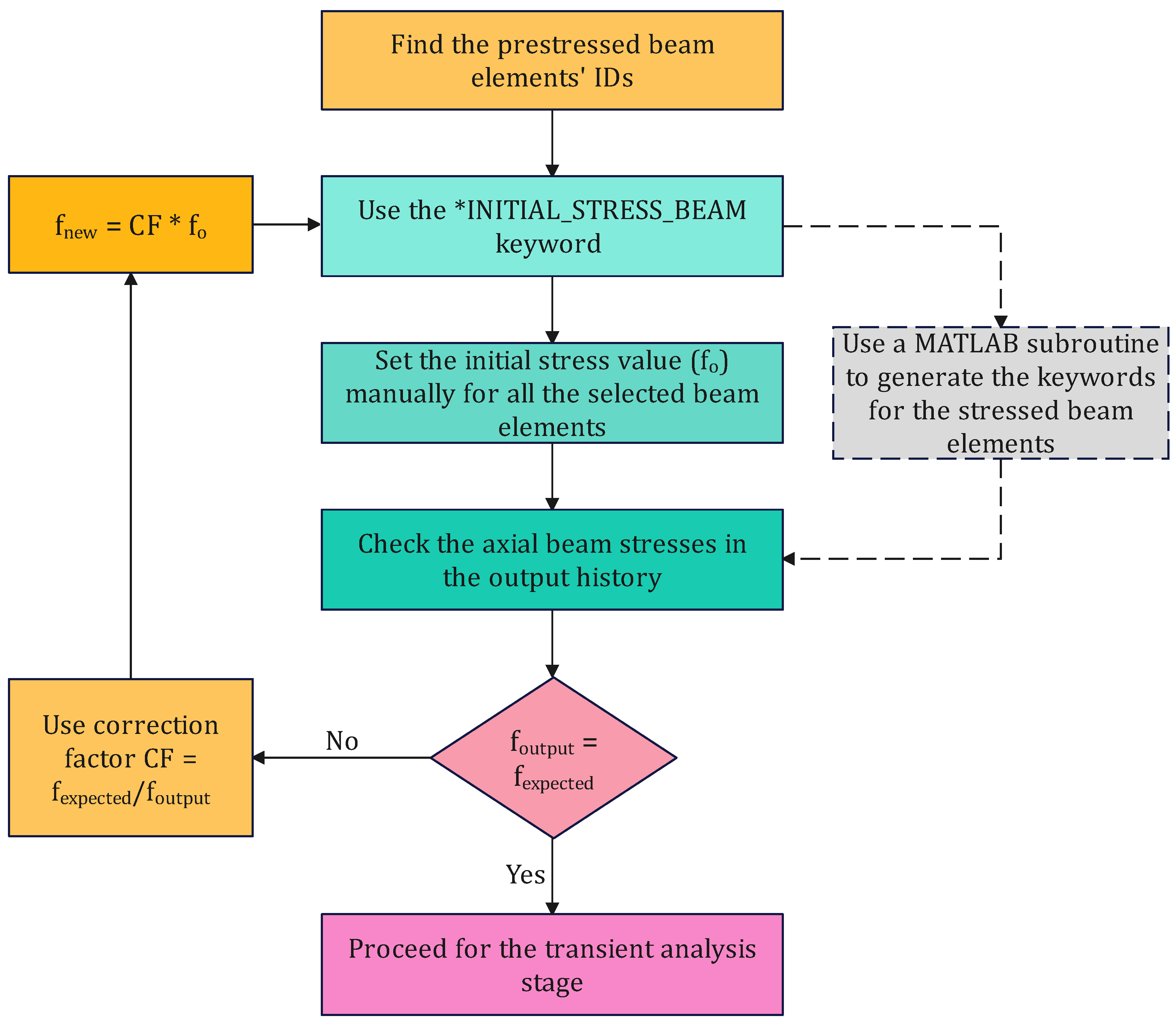
3.1.1. Preloading Step
3.1.2. Coupling
3.2. Constitutive Material Models
3.2.1. Concrete
3.2.2. Steel Reinforcement
3.3. Contacts and Constraints
4. FE Verification and Validation
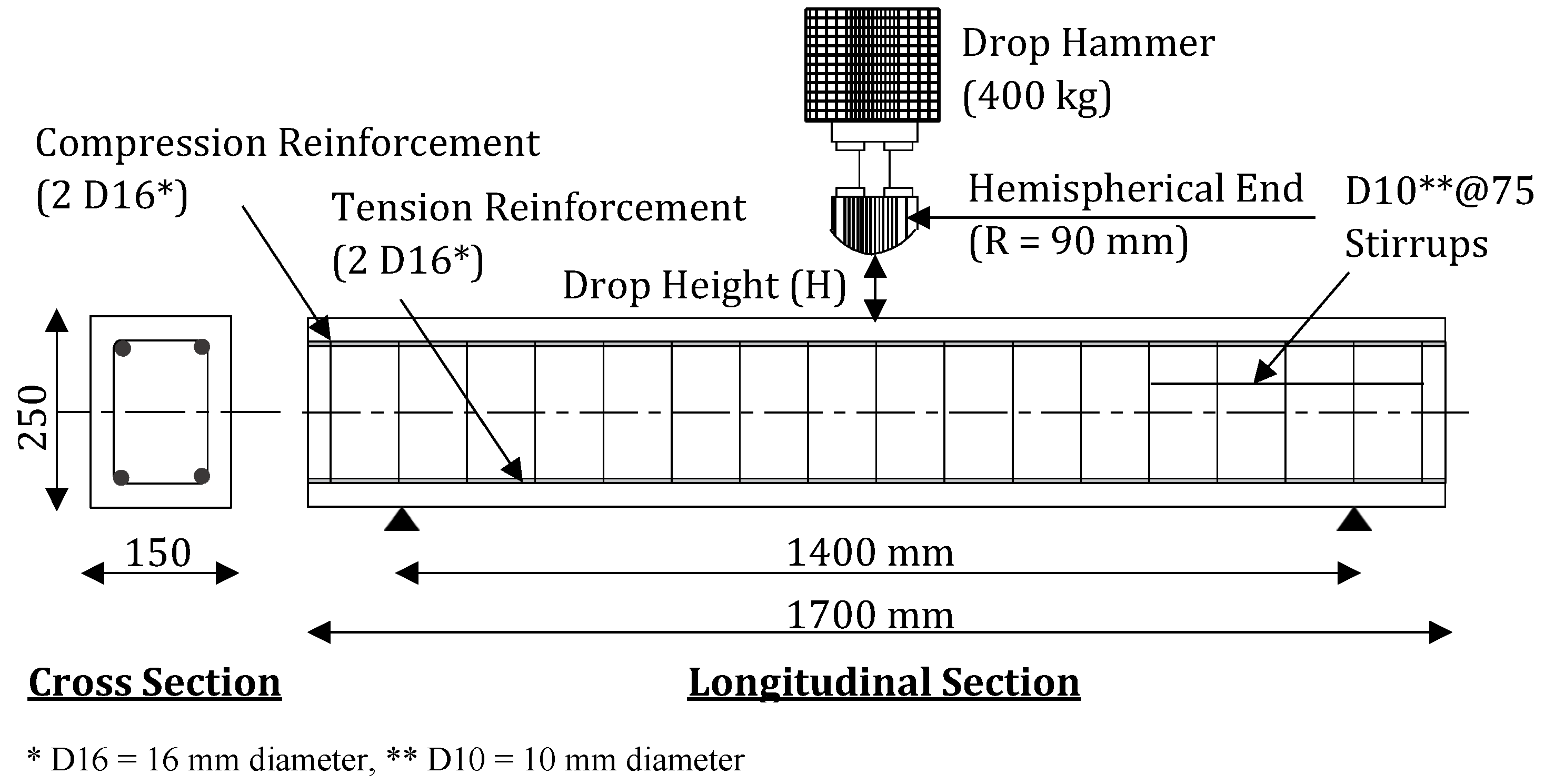
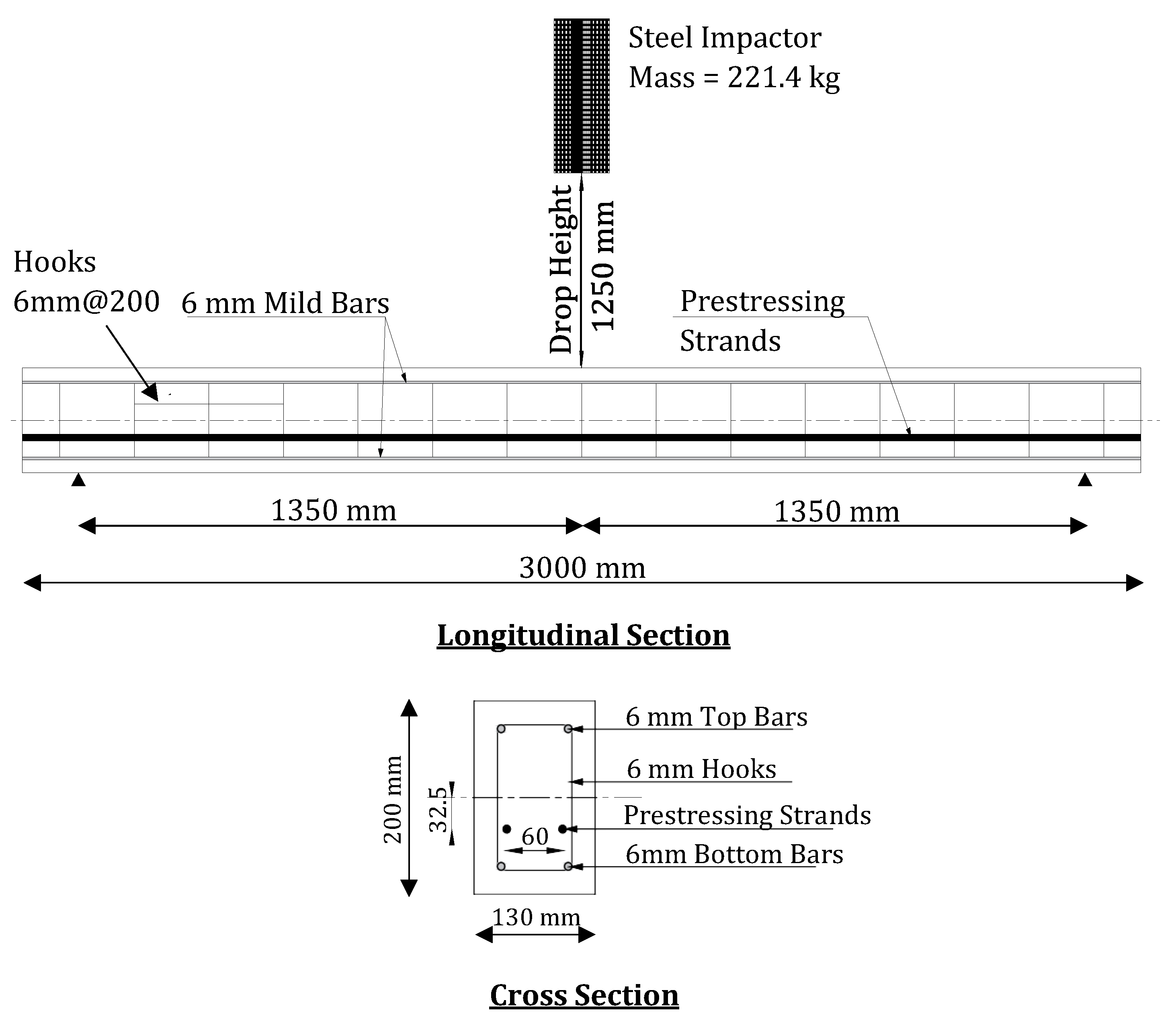
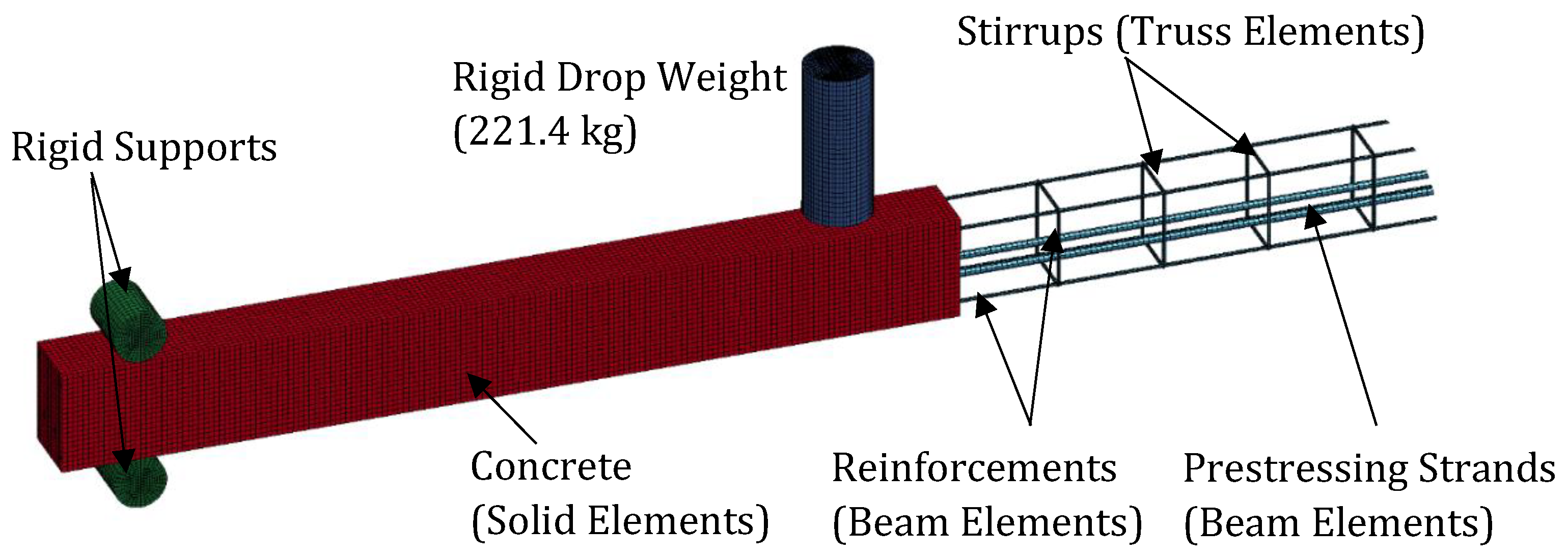
4.1. Impact Testing of a Reinforced Concrete Beam
4.1.1. Experimental Data
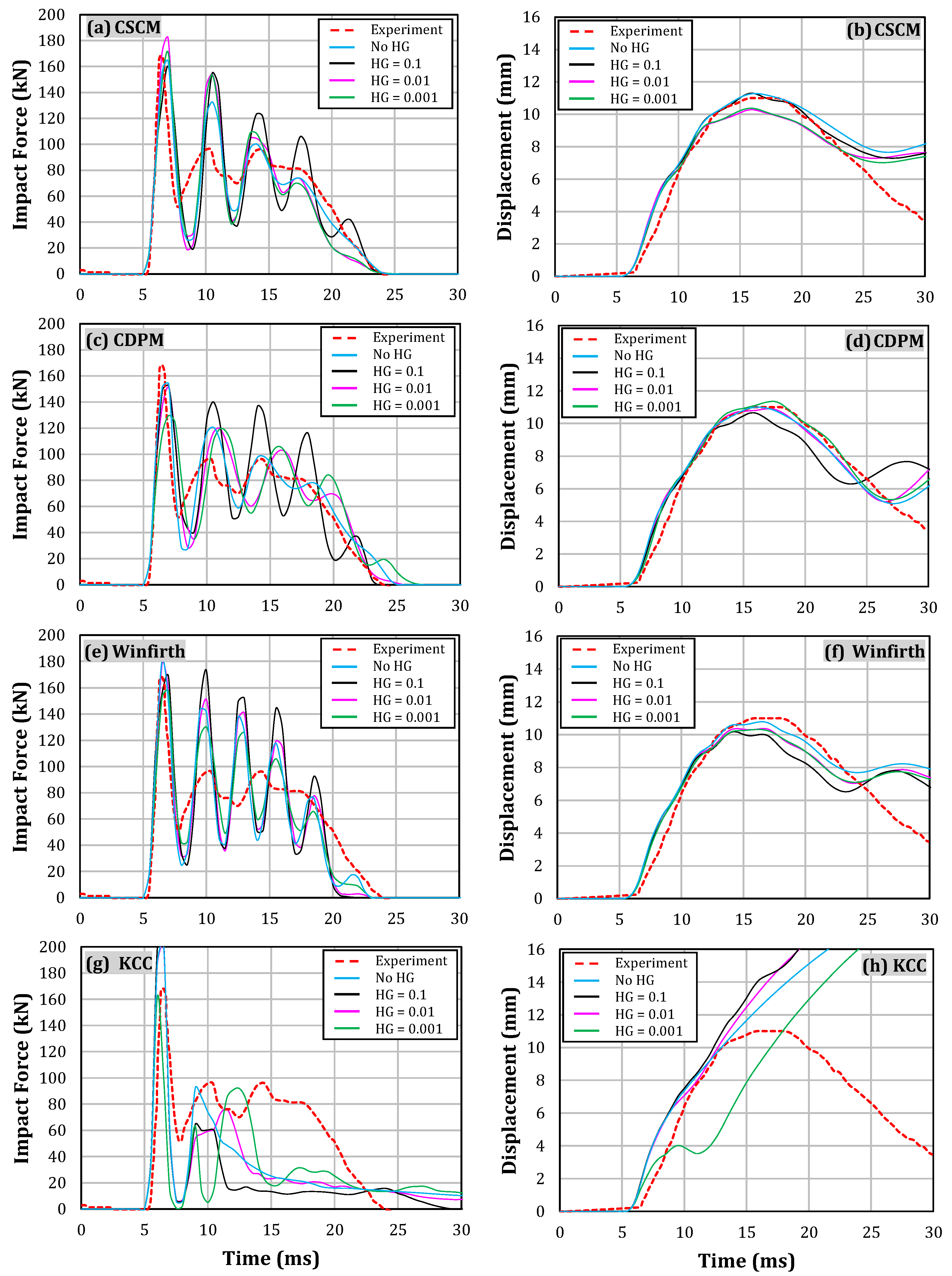
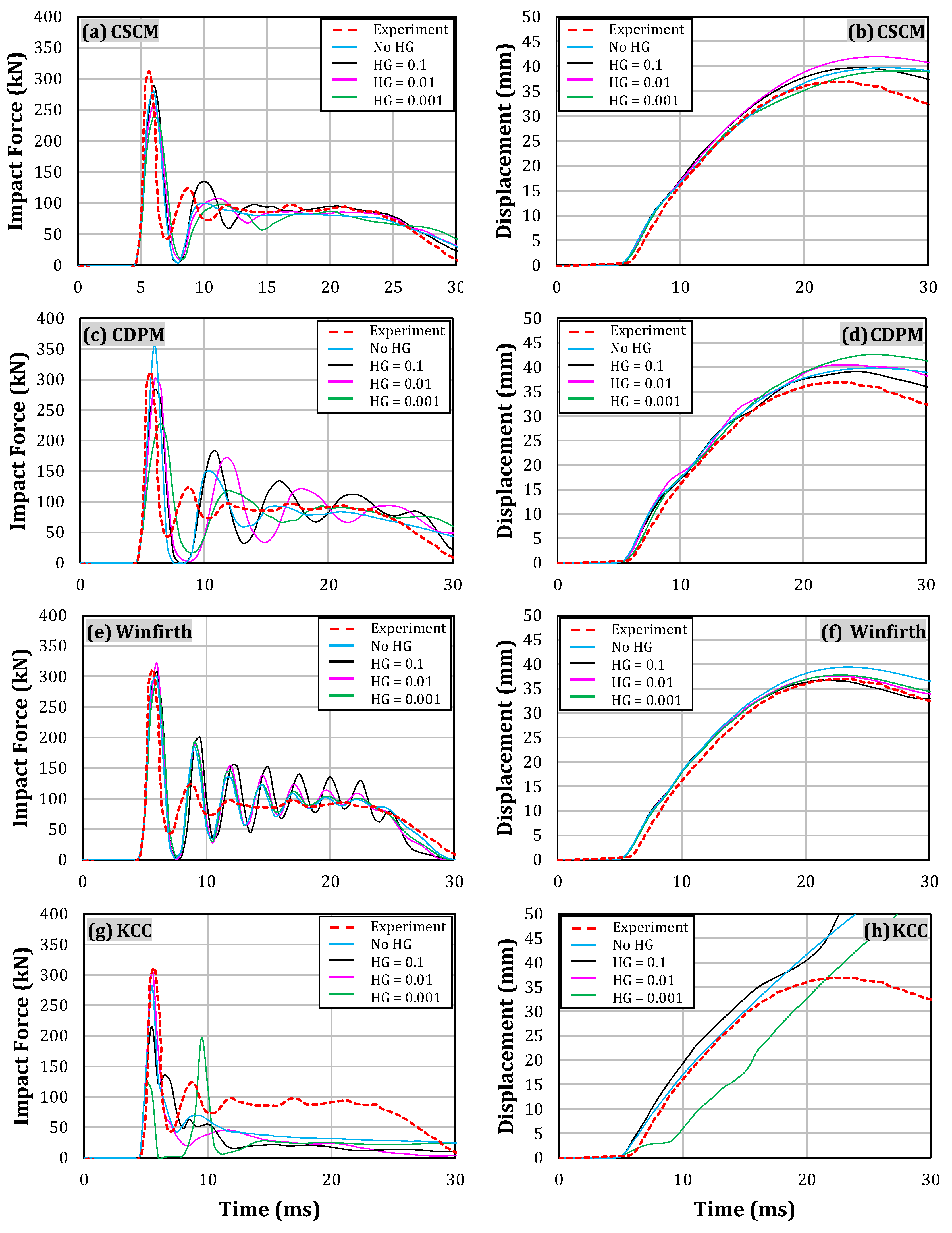
4.1.2. Impact Force and Displacement
4.1.3. Damage Pattern
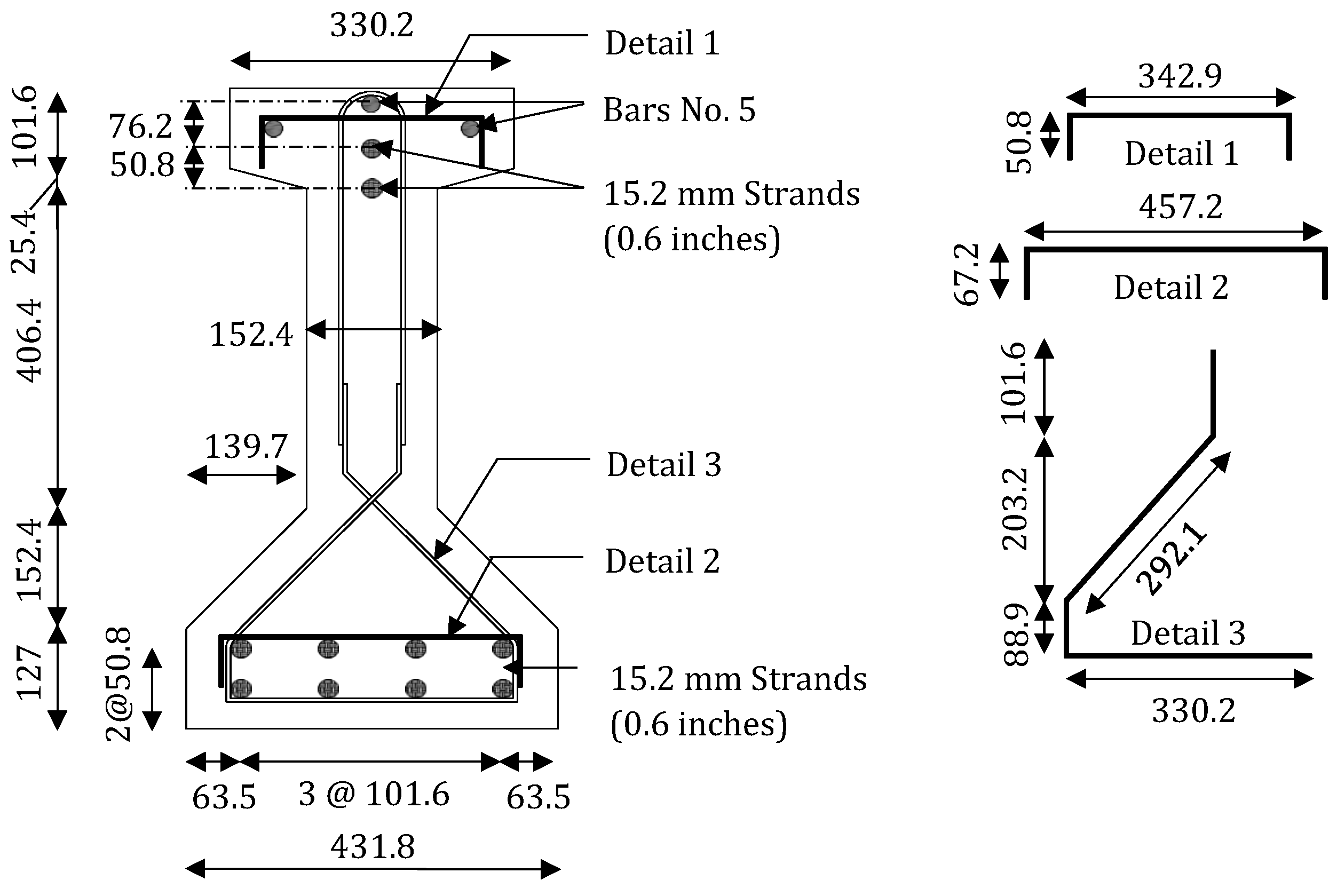
4.2. Impact Testing of a Prestressed Concrete Beam
4.2.1. Experimental Data
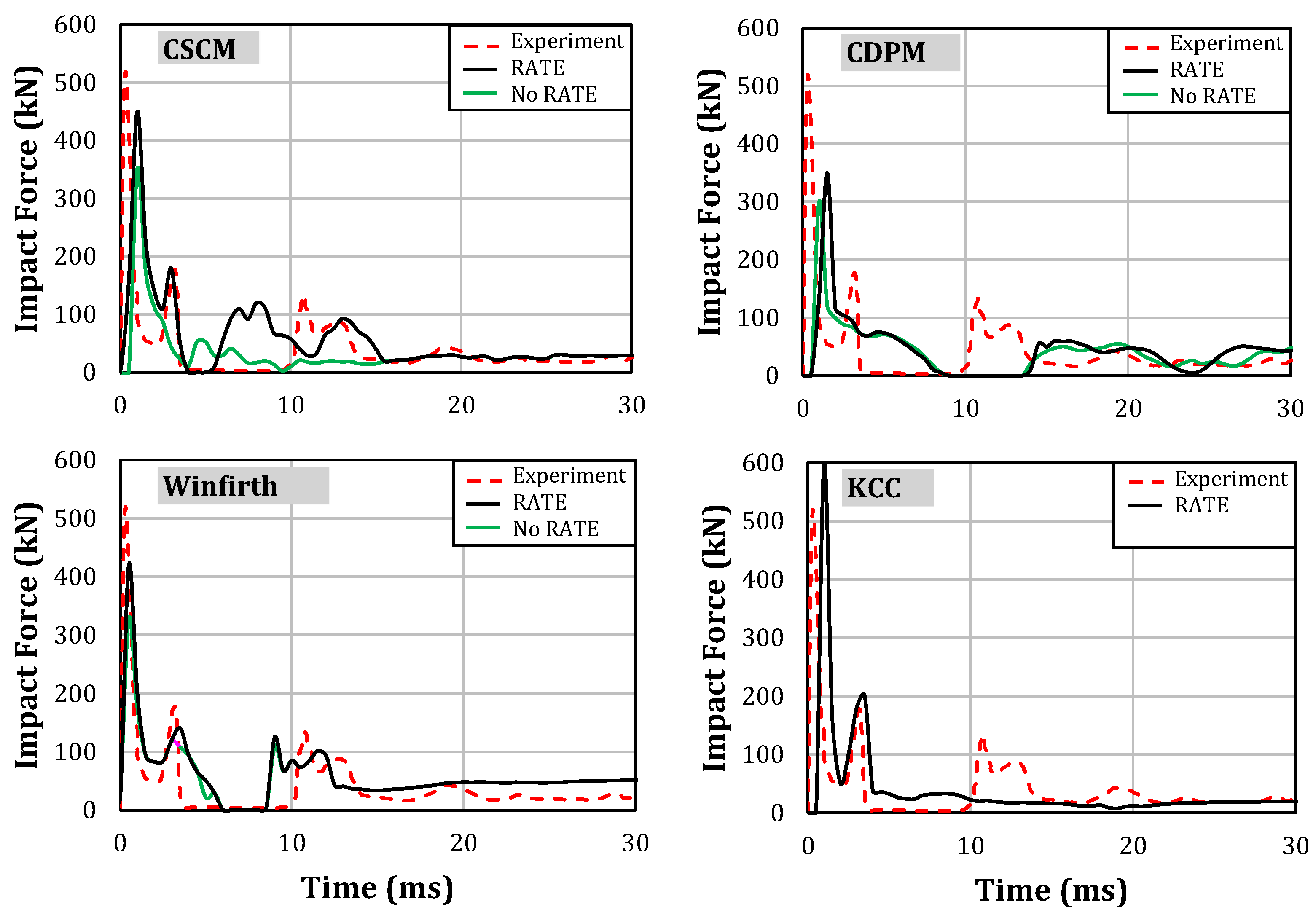
4.2.2. Impact Force and Strain Rate Effect
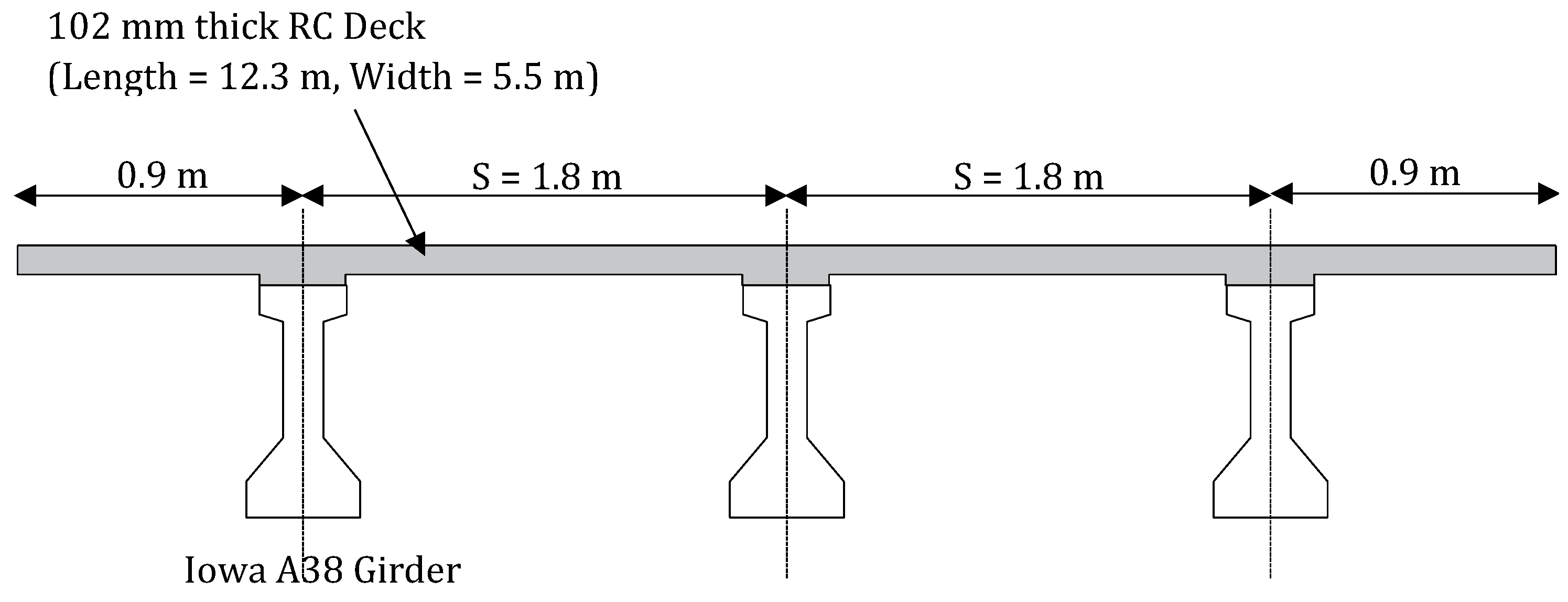
4.3. Static Testing of a Prestressed Girder Bridge
4.3.1. Experimental Data
4.3.2. Load Displacement
5. Impact Study
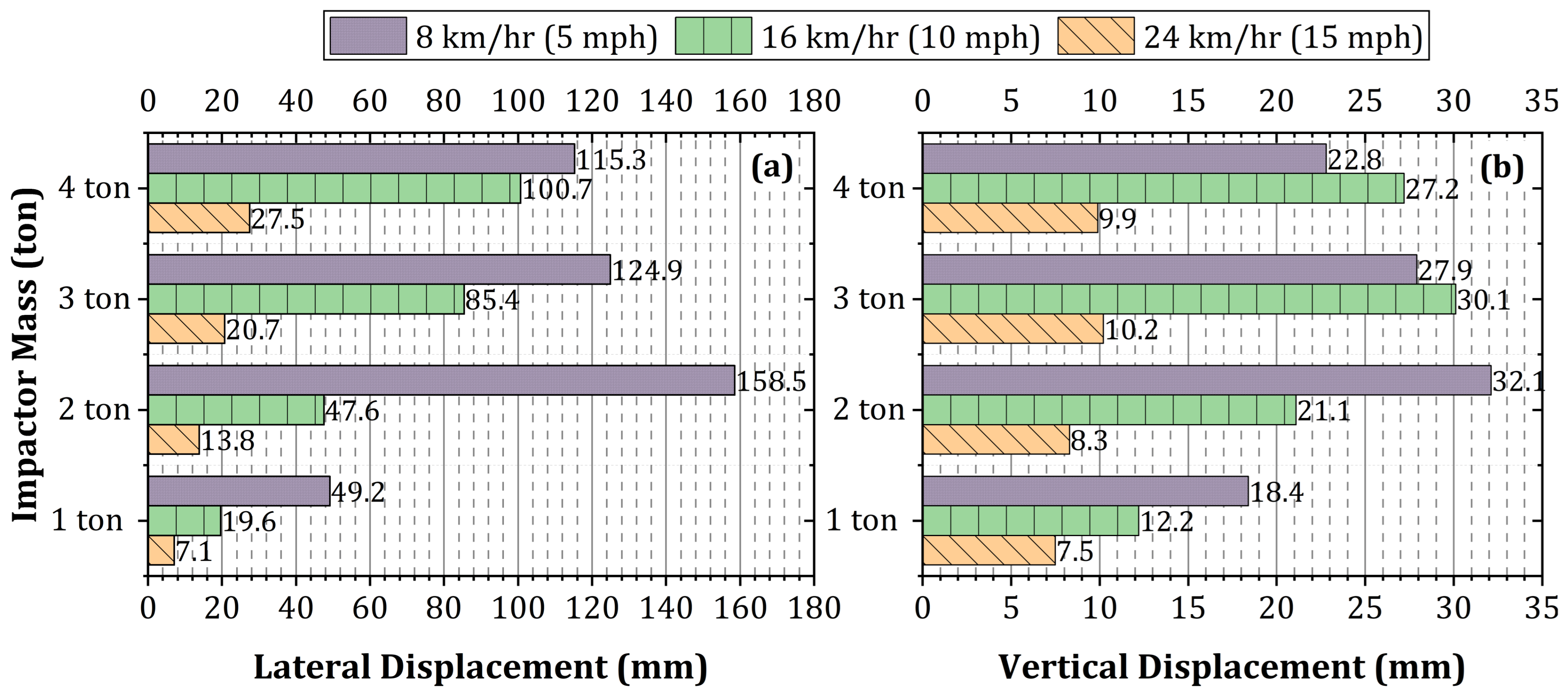
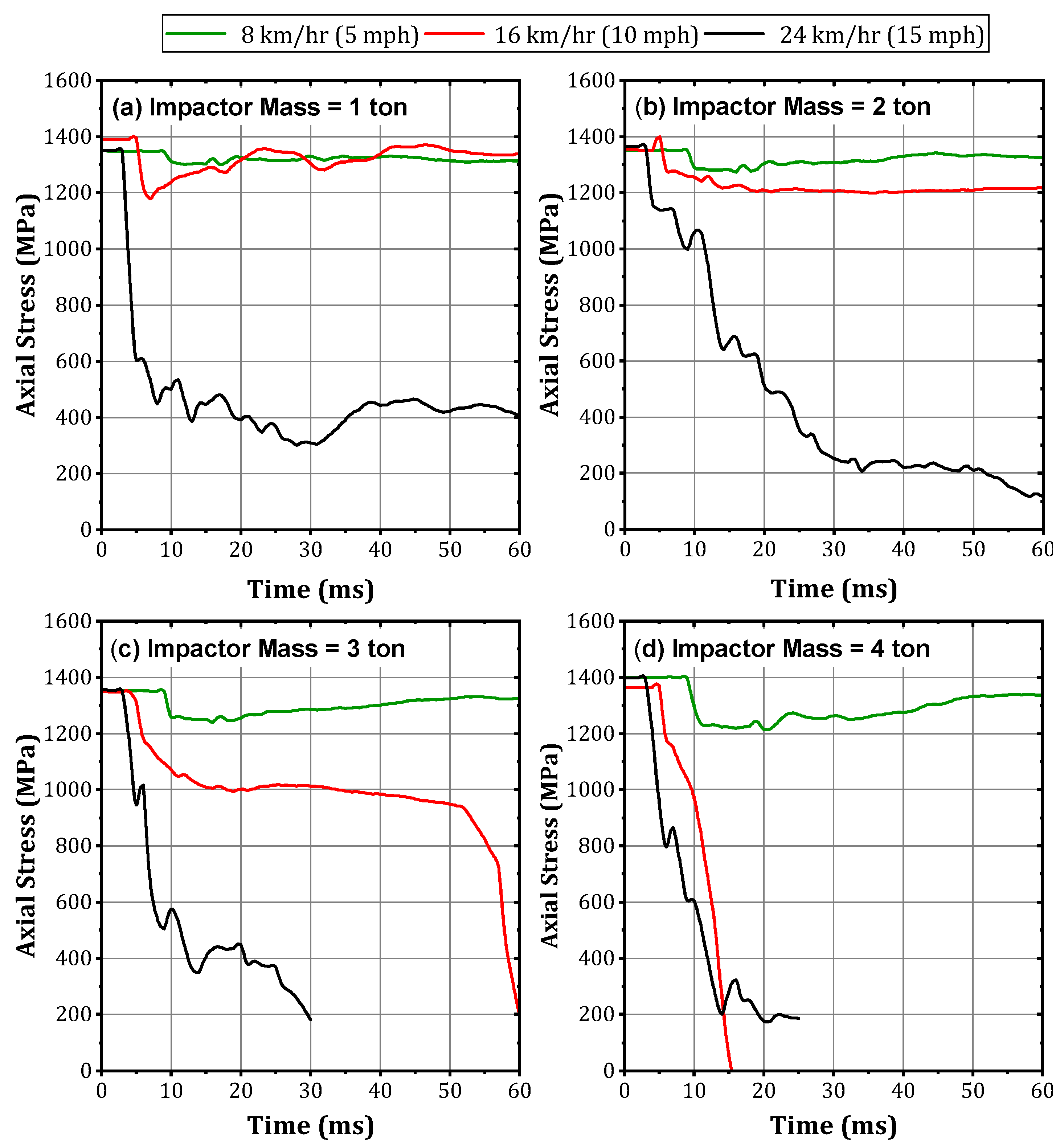
5.1. Impact Speed and Mass
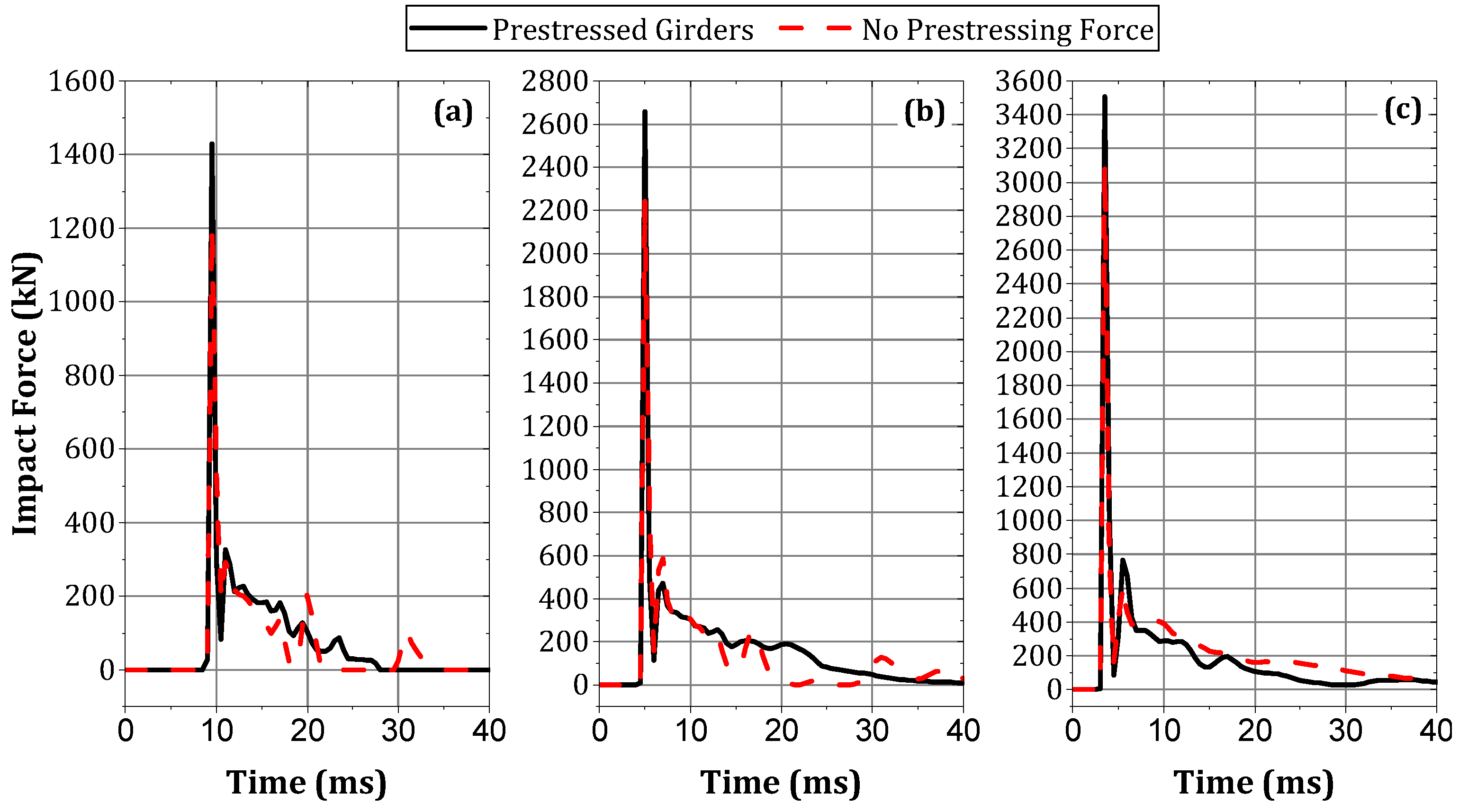
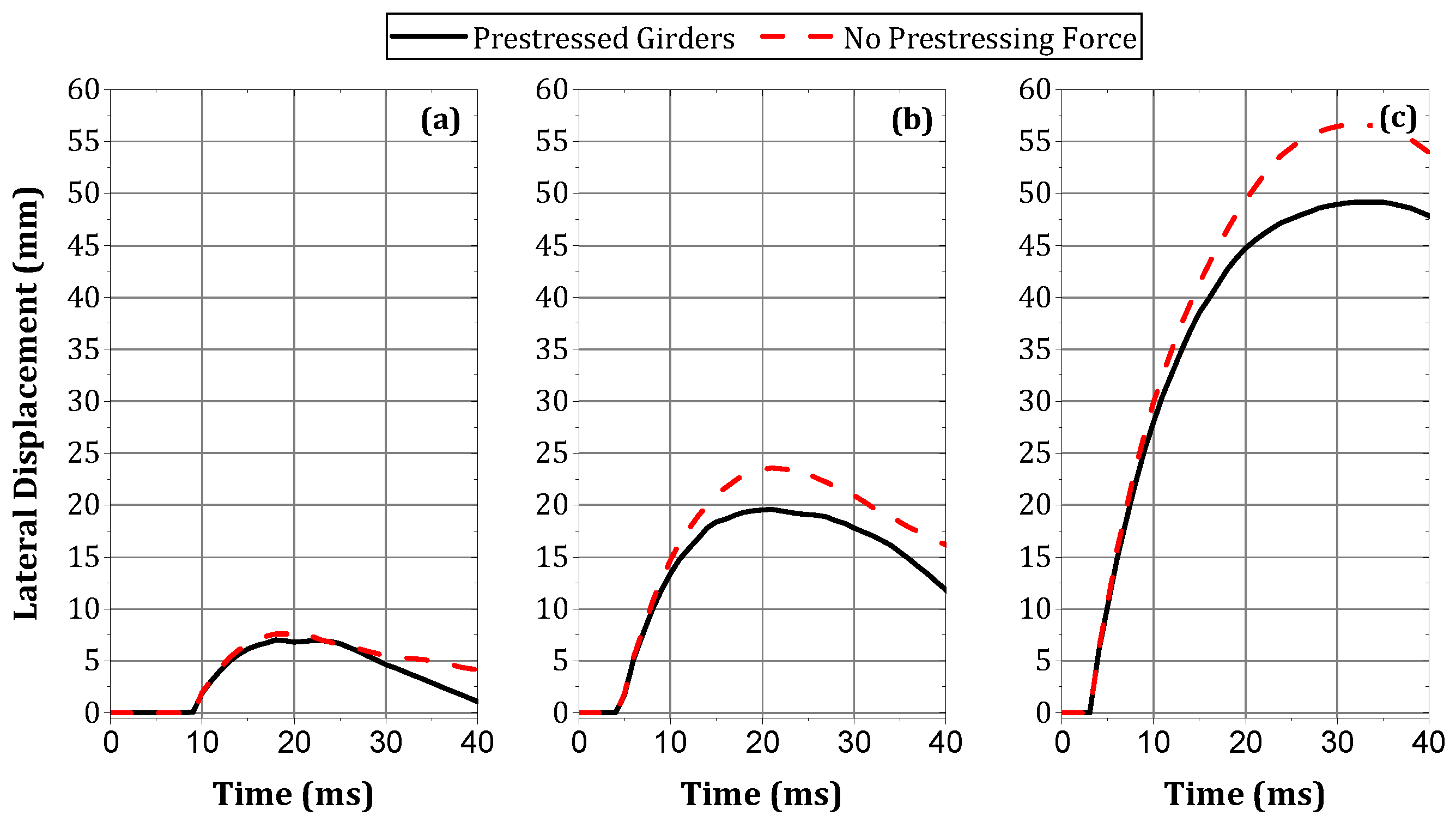
5.2. Prestressing Force
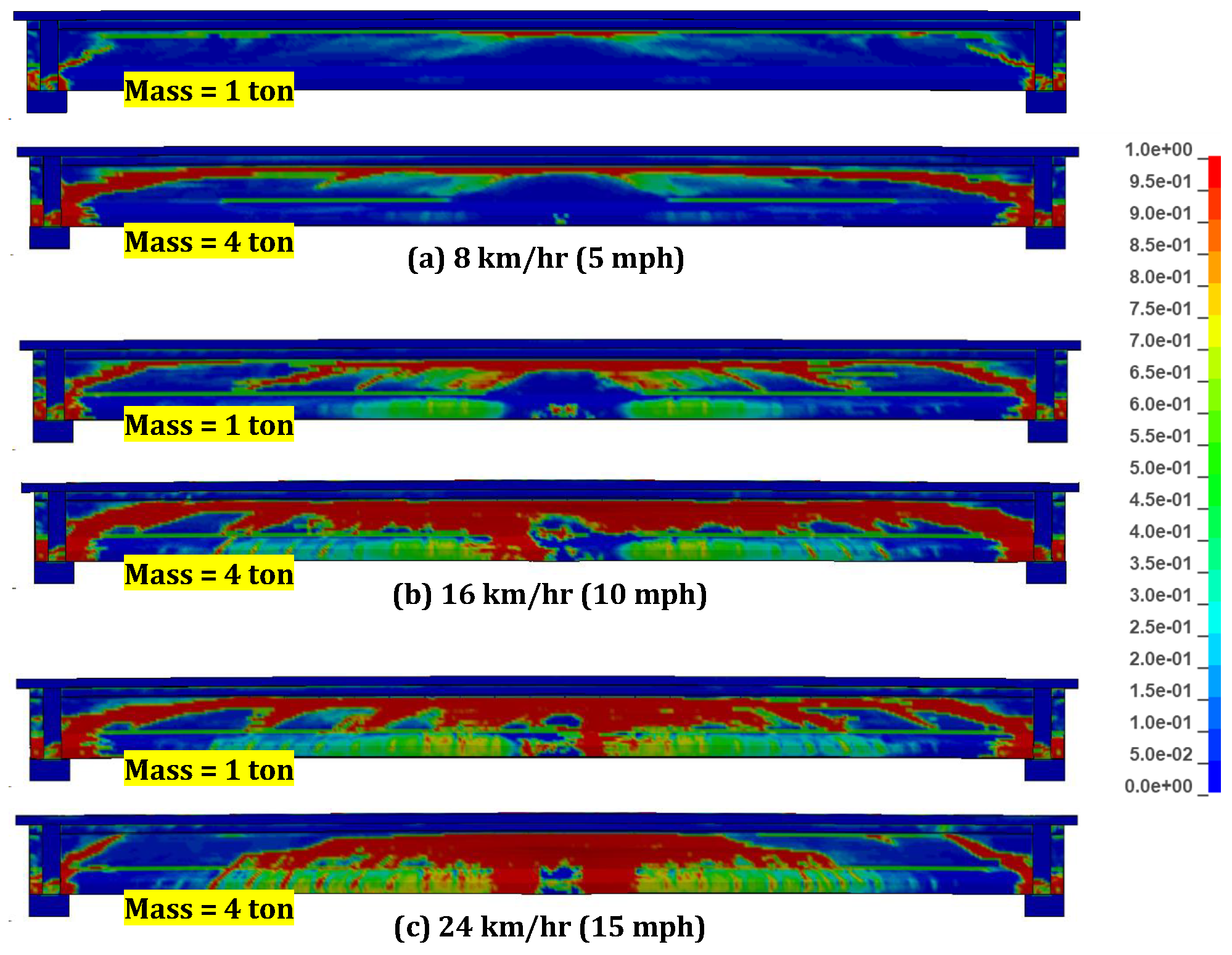
5.3. Damage Pattern
6. Future Works
7. Conclusions
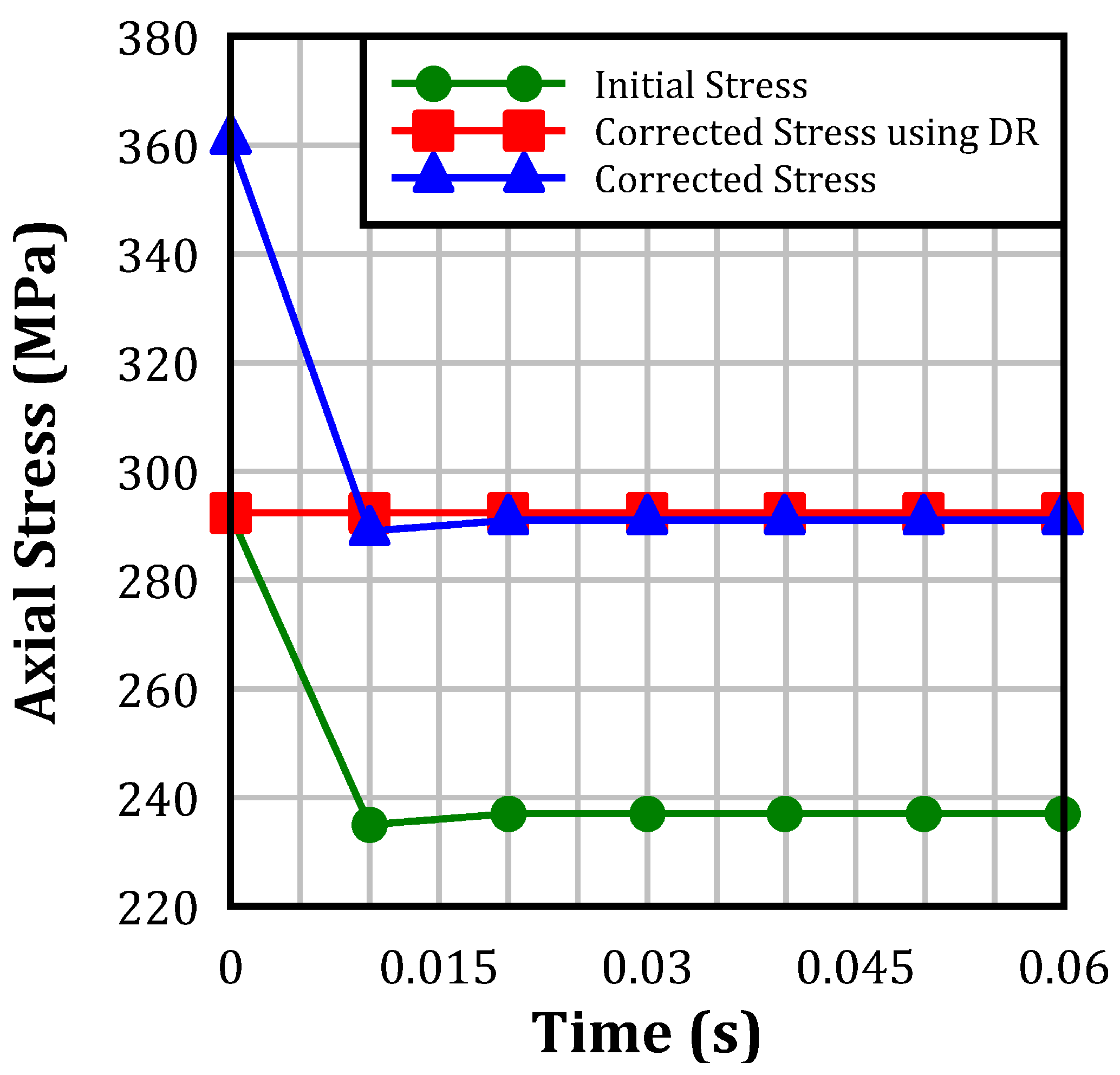
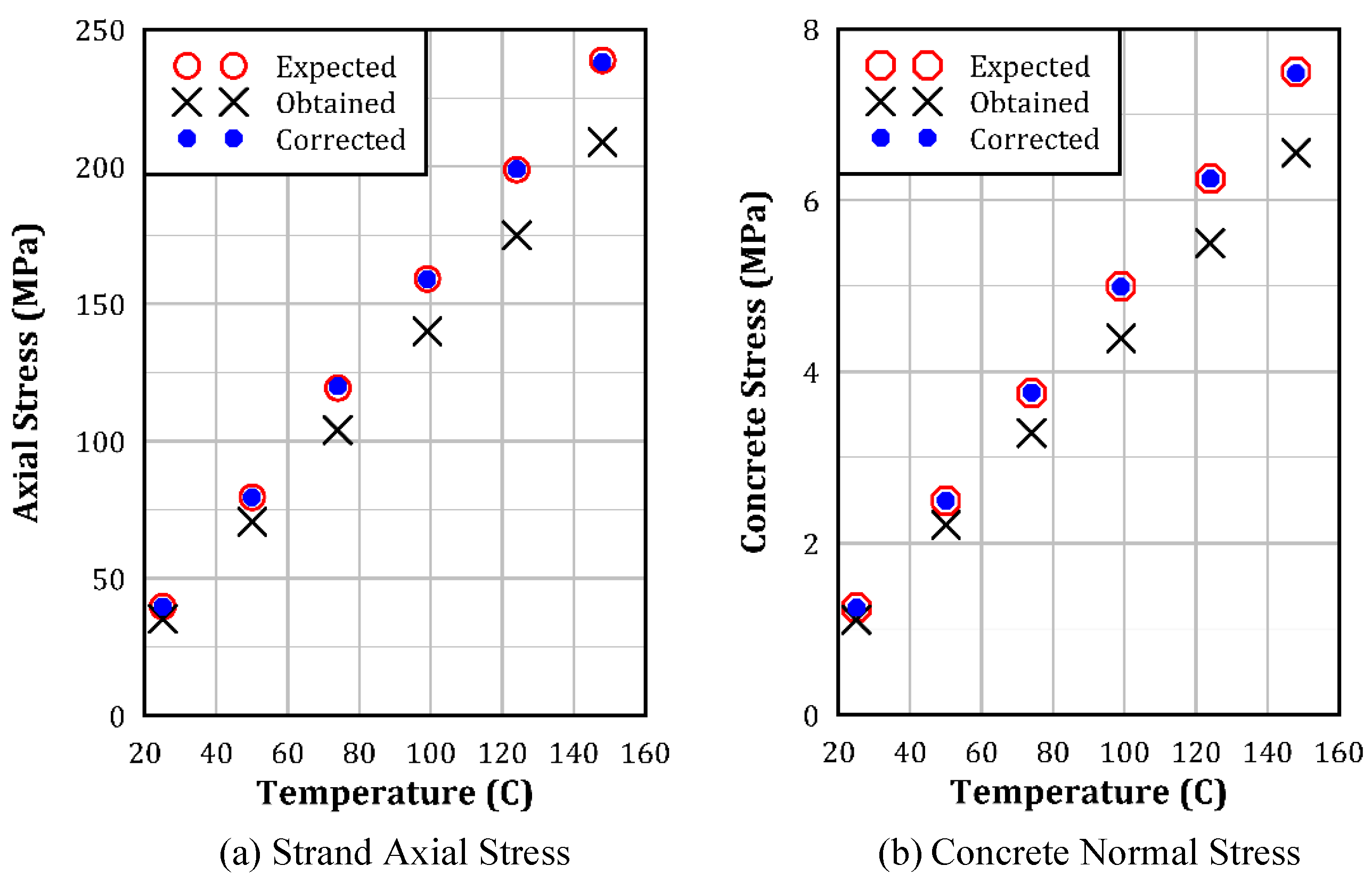
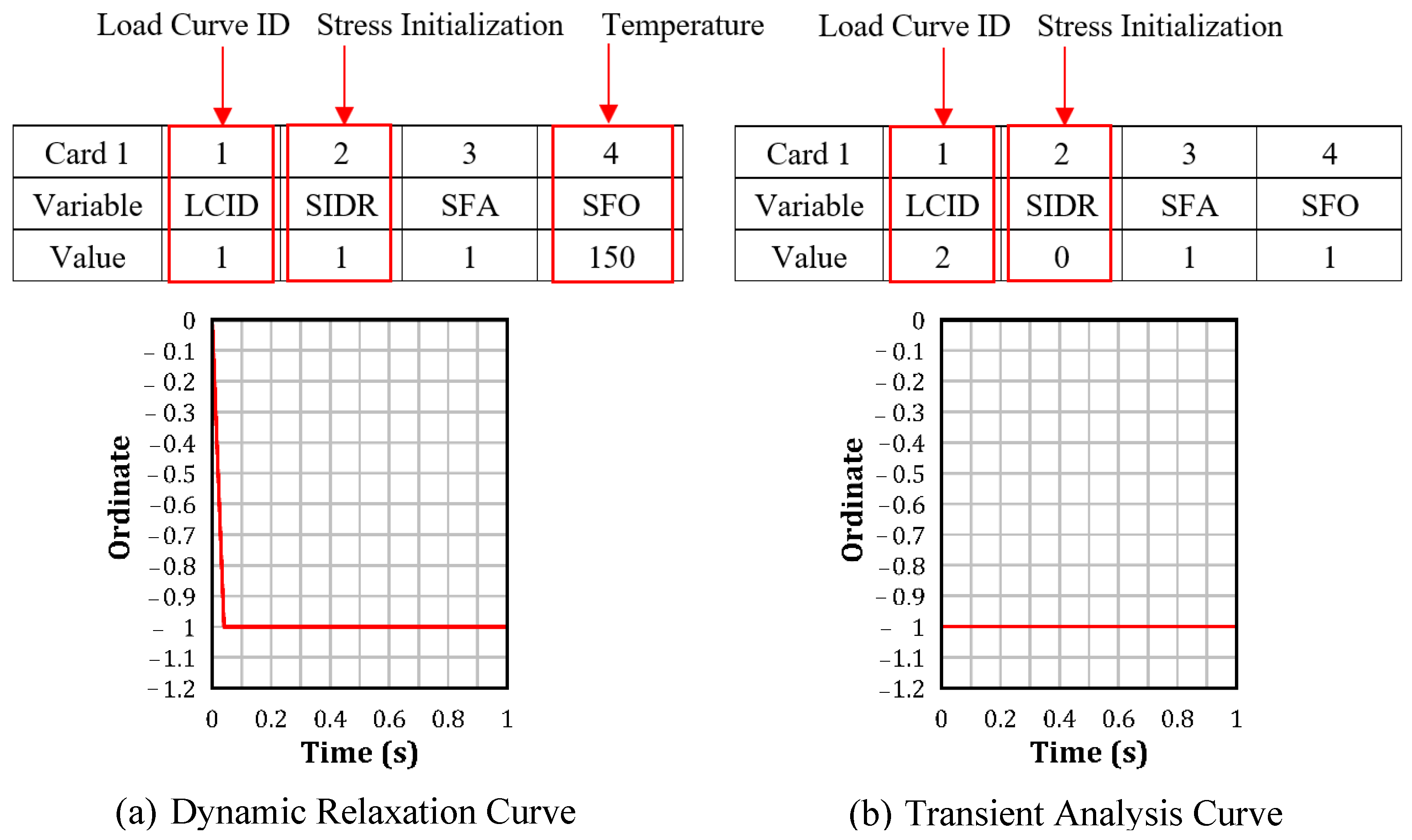
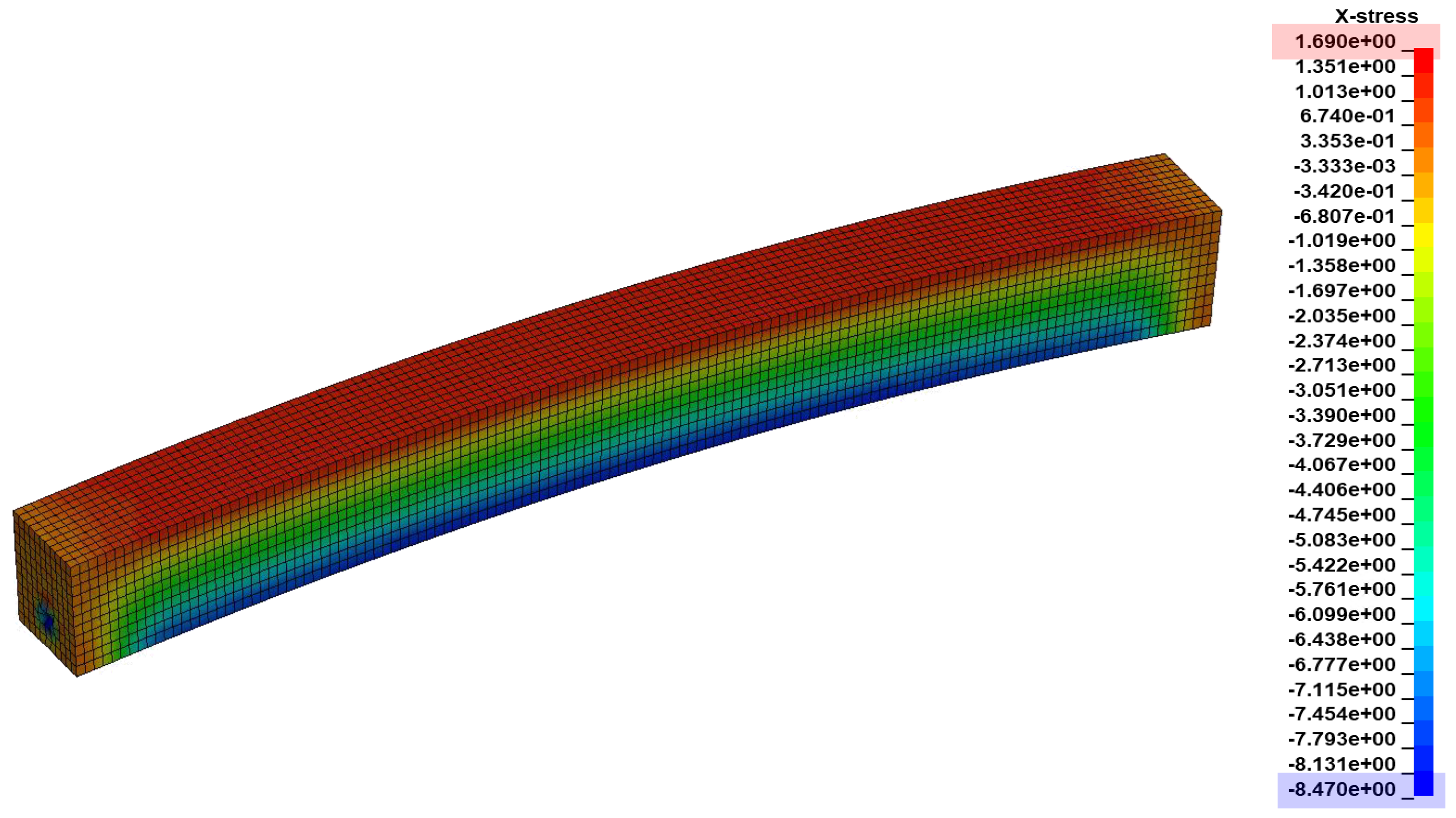
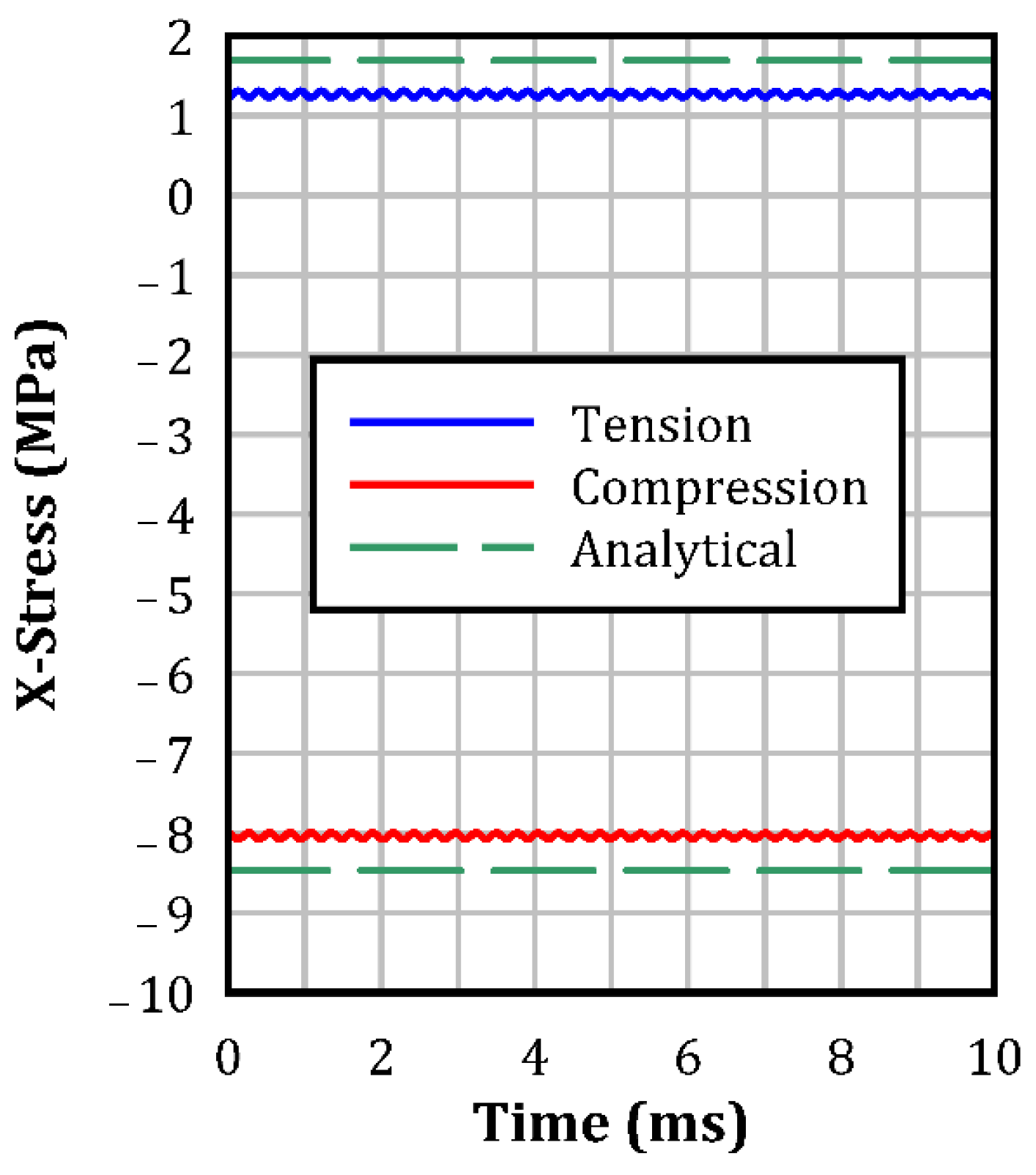
- The three preloading techniques, stress initialization, axial beam force, and temperature-induced shrinkage, could effectively preload the prestressing strands with the desired stress. However, the initial axial force method requires the use of specific spotweld material model and beam elements, which limits its applicability in some instances.
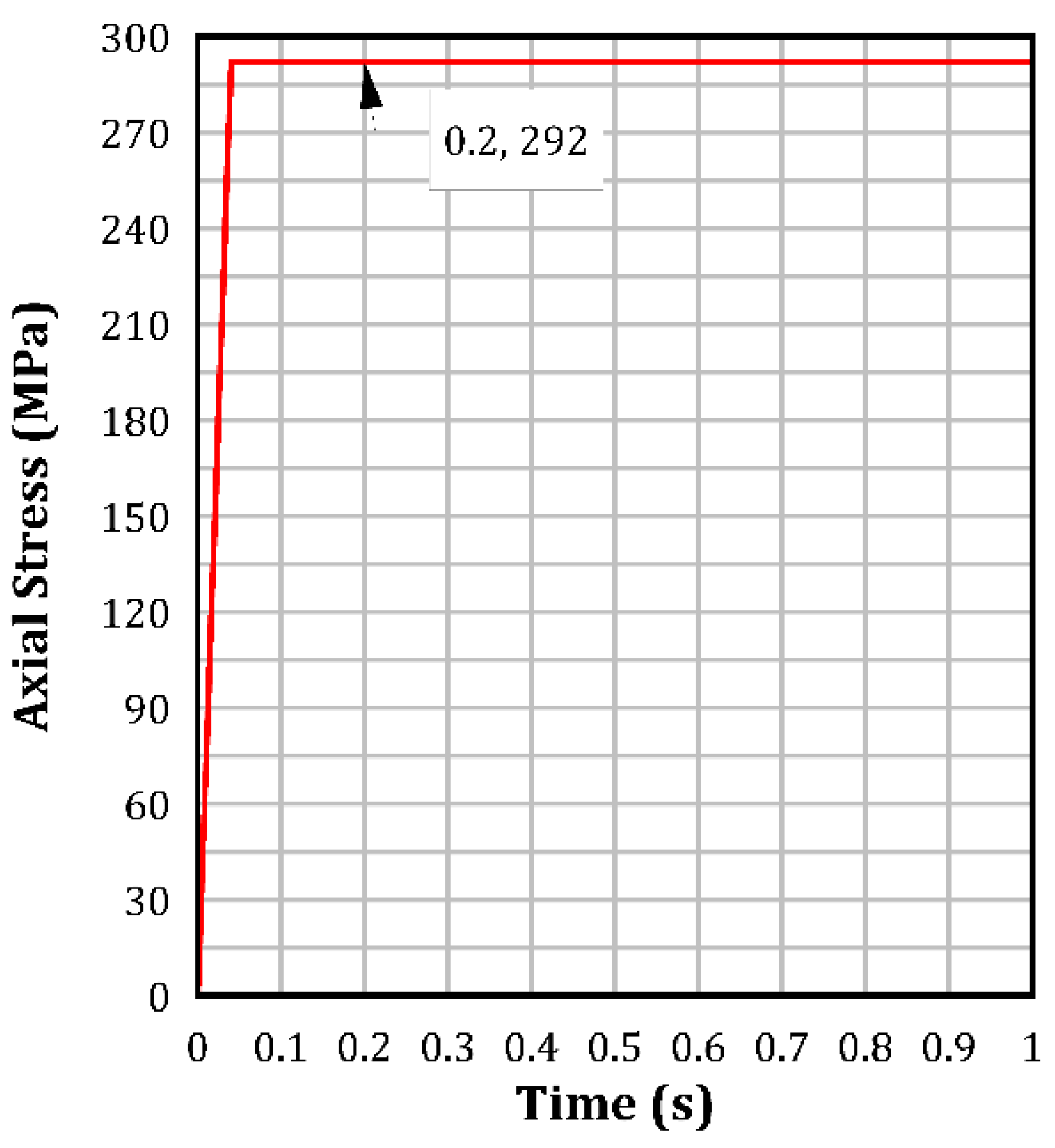
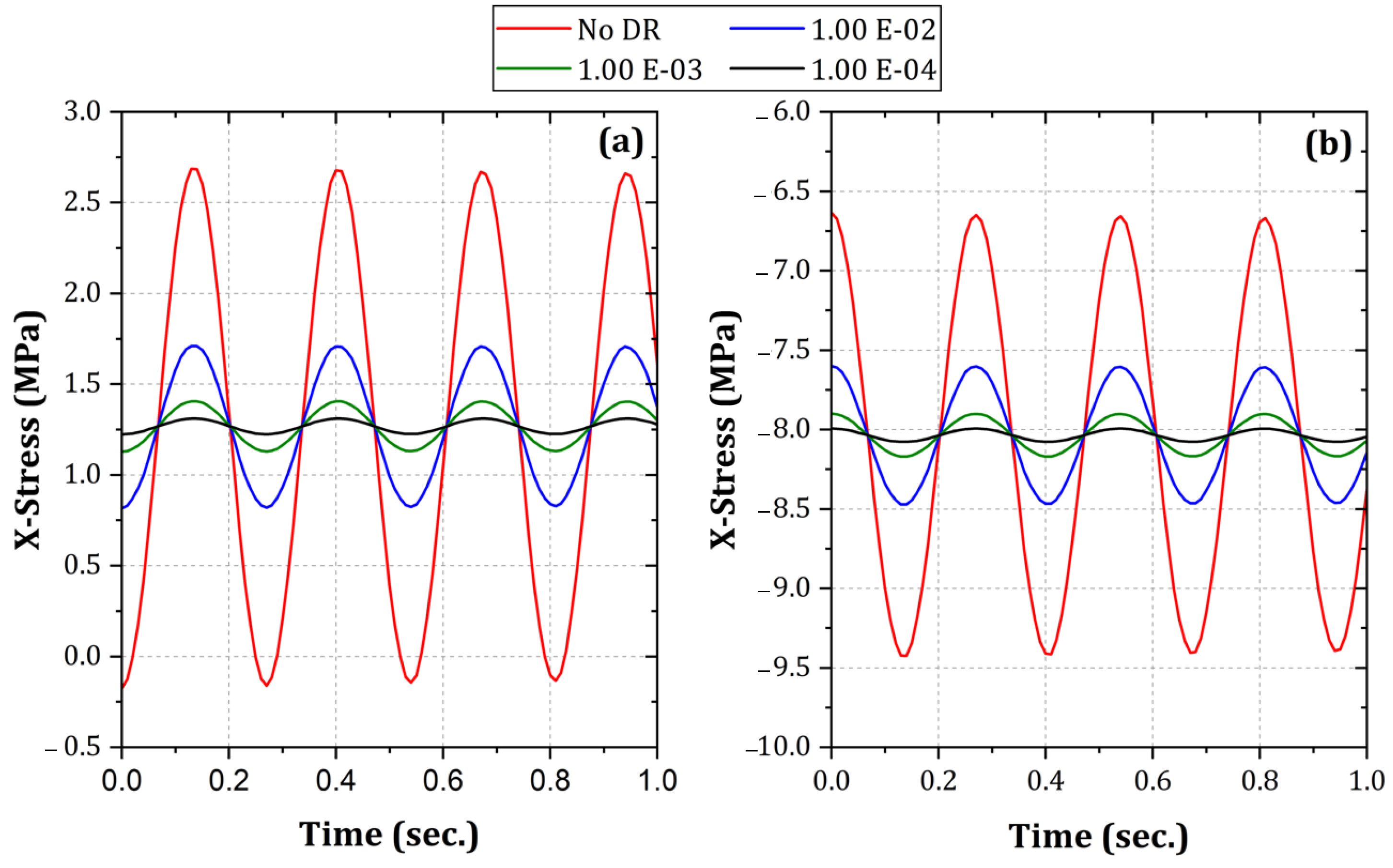
- Utilizing dynamic relaxation within explicit analysis, alongside an appropriate convergence tolerance, is crucial for minimizing the dynamic effect and achieving greater stability, leading to steady-state conditions.
- Among the four material models evaluated, the Continuous Cap Surface Model (CSCM) was the most accurate, with a peak impact force prediction error of less than 8%. Furthermore, the model demonstrated a strong ability to predict crack patterns effectively.
- Impact speed and mass demonstrated a significant influence on the resulting peak impact force experienced by the girder. Higher speeds correspond to greater kinetic energy, leading to increased impact energy transferred to the girder. Similarly, a heavier impactor possesses more momentum, resulting in a greater force applied to the girder upon impact.
- The energy analysis revealed the complex relationship between kinetic energy transmission and internal energy distribution within bridge components. In low-velocity impact scenarios, the impacted girder absorbed approximately 50–60% of the total energy, with the remainder distributed among other bridge components. This underscores the composite nature of the bridge’s response and emphasizes the importance of analyzing the bridge as a whole rather than focusing solely on individual girders.
- The presence of prestressing force showed a significant effect under impact loads, with an increase in the girder’s impact capacity of approximately 16% to 20%.
- The majority of observed damage patterns under impact showed global damage, and the extent of diagonal cracks increased with the increase in impact energy.
- The developed FE model was able to determine the variation in the strands’ prestressing stress, indicating instances of strand severing and cutting.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AASHTO | The American Association of State Highway and Transportation Officials |
| CSCM | Continuous Surface Cap Model |
| CDPM | Concrete Damage Plastic Model |
| DIF | Dynamic Increase Factor |
| DOT | Department of Transportation |
| DR | Dynamic relaxation |
| FE | Finite element |
| FEA | Finte Element Analysis |
| HG | Hourglass |
| IE | Internal energy |
| KCC | Karagozian & Case Concrete |
| KE | Kinetic energy |
| RC | Reinforced concrete |
References
- Agrawal, A.; Xu, X.; Chen, Z. Strikes on low clearance bridges by over-height trucks in New York State. Retrieved Dec. 2013, 5, 2014. [Google Scholar]
- Oppong, K.; Saini, D.; Shafei, B. Characterization of impact-induced forces and damage to bridge superstructures due to over-height collision. Eng. Struct. 2021, 236, 112014. [Google Scholar] [CrossRef]
- Fu, C.C.; Burhouse, J.R.; Chang, G.L. Overheight vehicle collisions with highway bridges. Transp. Res. Rec. 2004, 1865, 80–88. [Google Scholar] [CrossRef]
- Kiakojouri, F.; De Biagi, V.; Marchelli, M.; Chiaia, B. A conceptual note on the definition of initial failure in progressive collapse scenarios. In Structures; Elsevier: Amsterdam, The Netherlands, 2024; Volume 60, p. 105921. [Google Scholar]
- Gsa, U. Progressive Collapse Analysis and Design Guidelines for New Federal Office Buildings and Major Modernization Projects; Guideline Report; The US General Services Administration: Washington, DC, USA, 2003.
- Jiang, H.; Chorzepa, M.G. Evaluation of a new FRP fender system for bridge pier protection against vessel collision. J. Bridge Eng. 2015, 20, 05014010. [Google Scholar] [CrossRef]
- Jiang, H.; Chorzepa, M.G. Case study: Evaluation of a floating steel fender system for bridge pier protection against vessel collision. J. Bridge Eng. 2016, 21, 05016008. [Google Scholar] [CrossRef]
- Tian, L.; Huang, F. Numerical simulation for progressive collapse of continuous girder bridge subjected to ship impact. Trans. Tianjin Univ. 2014, 20, 250–256. [Google Scholar] [CrossRef]
- AASHTO American Association of State Highway and Transportation Officials. Commentary for Vessel Collision Design of Highway Bridges; American Association of State Highway and Transportation Officials: Washington, DC, USA, 1991. [Google Scholar]
- Jiang, H.; Wang, J.; Chorzepa, M.G.; Zhao, J. Numerical investigation of progressive collapse of a multispan continuous bridge subjected to vessel collision. J. Bridge Eng. 2017, 22, 04017008. [Google Scholar] [CrossRef]
- Kasan, J.L.; Harries, K.A. Analysis of eccentrically loaded adjacent box girders. J. Bridge Eng. 2013, 18, 15–25. [Google Scholar] [CrossRef]
- Kishi, N.; Nakano, O.; Matsuoka, K.; Ando, T. Experimental study on ultimate strength of flexural-failure-type RC beams under impact loading. Transactions 2001, 1525. [Google Scholar]
- Tachibana, S.; Masuya, H.; Nakamura, S. Performance based design of reinforced concrete beams under impact. Nat. Hazards Earth Syst. Sci. 2010, 10, 1069–1078. [Google Scholar] [CrossRef]
- Kishi, N.; Mikami, H. Empirical Formulas for Designing Reinforced Concrete Beams under Impact Loading. ACI Struct. J. 2012, 109, 509. [Google Scholar]
- Nghiem, A.; Kang, T.H.K. Drop-Weight Testing on Concrete Beams and ACI Design Equations for Maximum and Residual Deflections under Low-Velocity Impact. ACI Struct. J. 2020, 117, 199. [Google Scholar]
- Xu, X.; Zhang, H.; Du, X.; Liu, Q. Vehicle collision with RC structures: A state-of-the-art review. In Structures; Elsevier: Amsterdam, The Netherlands, 2022; Volume 44, pp. 1617–1635. [Google Scholar]
- Chen, L.; El-Tawil, S.; Xiao, Y. Reduced models for simulating collisions between trucks and bridge piers. J. Bridge Eng. 2016, 21, 04016020. [Google Scholar] [CrossRef]
- Heng, K.; Li, R.; Li, Z.; Wu, H. Dynamic responses of highway bridge subjected to heavy truck impact. Eng. Struct. 2021, 232, 111828. [Google Scholar] [CrossRef]
- Song, J.; Hu, D.; Luo, S.; Liu, W.; Wang, D.; Sun, Q.; Zhang, G. Energy-absorption behavior of metallic hollow sphere structures under impact loading. Eng. Struct. 2021, 226, 111350. [Google Scholar] [CrossRef]
- Cengiz, A.; Gurbuz, T.; Ilki, A.; Aydogan, M. Dynamic and Residual Static Behavior of Axially Loaded RC Columns Subjected to Low-Elevation Impact Loading. Buildings 2023, 14, 92. [Google Scholar] [CrossRef]
- Liu, T.; Chen, L. Numerical simulation of vehicle collision with reinforced concrete piers protected by FRP-foam composites. In Structures Congress 2019; American Society of Civil Engineers: Reston, VA, USA, 2019; pp. 70–81. [Google Scholar]
- Abdelkarim, O.I.; ElGawady, M.A. Performance of bridge piers under vehicle collision. Eng. Struct. 2017, 140, 337–352. [Google Scholar] [CrossRef]
- Wu, M.; Jin, L.; Du, X. Dynamic response analysis of bridge precast segment piers under vehicle collision. Eng. Fail. Anal. 2021, 124, 105363. [Google Scholar] [CrossRef]
- Li, R.; Cao, D.; Wu, H.; Wang, D. Collapse analysis and damage evaluation of typical simply supported double-pier RC bridge under truck collision. In Structures; Elsevier: Amsterdam, The Netherlands, 2021; Volume 33, pp. 3222–3238. [Google Scholar]
- Wang, S.; Lei, Z.; Zhao, J.; Li, Y.; Lei, M.; Liu, Y. A research of similarity design of collision guardrails under the overpass. In Proceedings of the 2011 Second International Conference on Mechanic Automation and Control Engineering, Hohhot, China, 15–17 July 2011; pp. 1903–1906. [Google Scholar]
- Trajkovski, J.; Ambrož, M.; Kunc, R. The importance of friction coefficient between vehicle tyres and concrete safety barrier to vehicle rollover: FE analysis study. Strojniški Vestn. 2018, 64, 1–11. [Google Scholar] [CrossRef]
- Neves, R.R.; Fransplass, H.; Langseth, M.; Driemeier, L.; Alves, M. Performance of some basic types of road barriers subjected to the collision of a light vehicle. J. Braz. Soc. Mech. Sci. Eng. 2018, 40, 274. [Google Scholar] [CrossRef]
- Safari Honar, F.; Broujerdian, V.; Mohammadi Dehcheshmeh, E.; Bedon, C. Nonlinear Dynamic Assessment of a Steel Frame Structure Subjected to Truck Collision. Buildings 2023, 13, 1545. [Google Scholar] [CrossRef]
- Chen, A.; Liu, Y.; Ma, R.; Zhou, X. Experimental and Numerical Analysis of Reinforced Concrete Columns under Lateral Impact Loading. Buildings 2023, 13, 708. [Google Scholar] [CrossRef]
- Raj, A.; Nagarajan, P.; Aikot Pallikkara, S. Application of fiber-reinforced rubcrete for crash barriers. J. Mater. Civ. Eng. 2020, 32, 04020358. [Google Scholar] [CrossRef]
- Kelly, J. The Effects of Impact Loading on Prestressed Concrete Beams. Ph.D. Thesis, Heriot-Watt University, Edinburgh, UK, 2011. [Google Scholar]
- Jing, Y.; Ma, Z.J.; Clarke, D.B. Full-scale lateral impact testing of prestressed concrete girder. Struct. Concr. 2016, 17, 947–958. [Google Scholar] [CrossRef]
- Xu, L.; Lu, X.Z.; Smith, S.T.; He, S. Scaled model test for collision between over-height truck and bridge superstructure. Int. J. Impact Eng. 2012, 49, 31–42. [Google Scholar] [CrossRef]
- Atahan, A.O.; Cansiz, O.F. Impact analysis of a vertical flared back bridge rail-to-guardrail transition structure using simulation. Finite Elem. Anal. Des. 2005, 41, 371–396. [Google Scholar] [CrossRef]
- Xu, L.; Lu, X.; Guan, H.; Zhang, Y. Finite-element and simplified models for collision simulation between overheight trucks and bridge superstructures. J. Bridge Eng. 2013, 18, 1140–1151. [Google Scholar] [CrossRef]
- Oppong, K.; Saini, D.; Shafei, B. Ultrahigh-performance concrete for improving impact resistance of bridge superstructures to overheight collision. J. Bridge Eng. 2021, 26, 04021060. [Google Scholar] [CrossRef]
- Jing, Y.; Zhang, X.; Zhou, Y.; Zhao, Y.; Li, W. Dynamic Response and Impact Force Calculation of PC Box Girder Bridge Subjected to Over-Height Vehicle Collision. Buildings 2023, 13, 495. [Google Scholar] [CrossRef]
- Berton, E.; Bouaanani, N.; Lamarche, C.P.; Roy, N. Finite element modeling of the impact of heavy vehicles on highway and pedestrian bridge decks. Procedia Eng. 2017, 199, 2451–2456. [Google Scholar] [CrossRef]
- Jiang, H.; Chorzepa, M.G. An effective numerical simulation methodology to predict the impact response of pre-stressed concrete members. Eng. Fail. Anal. 2015, 55, 63–78. [Google Scholar] [CrossRef]
- Husain, M.; Yu, J.; Wu, J. Comparisons of different approaches of modelling prestress in concrete members using LS-DYNA and its applications. In Concrete—Innovations in Materials, Design and Structures; The International Federation for Structural Concrete: Krakow, Poland, 2019; pp. 812–819. [Google Scholar]
- Saini, D.; Shafei, B. Concrete constitutive models for low velocity impact simulations. Int. J. Impact Eng. 2019, 132, 103329. [Google Scholar] [CrossRef]
- Thai, D.K.; Kim, S.E. Numerical simulation of pre-stressed concrete slab subjected to moderate velocity impact loading. Eng. Fail. Anal. 2017, 79, 820–835. [Google Scholar] [CrossRef]
- Elbelbisi, A.H.; El-Sisi, A.A.; Hassan, H.A.; Salim, H.A.; Shabaan, H.F. Parametric study on steel–concrete composite beams strengthened with post-tensioned CFRP tendons. Sustainability 2022, 14, 15792. [Google Scholar] [CrossRef]
- El-Belbisi, A. Strengthening of Pre-stressed Steel–Concrete Composite Beams Using Carbon Fiber Tendons–A Parametric Study. Arch. Med. 2018, 4, 1–7. [Google Scholar]
- LSTC Manual; Livermore Software Technology Corporation: Livermore, CA, USA, 1998; Manual.
- Fujikake, K.; Li, B.; Soeun, S. Impact response of reinforced concrete beam and its analytical evaluation. J. Struct. Eng. 2009, 135, 938–950. [Google Scholar] [CrossRef]
- Comite Euro-International du Beton. Concrete Structures under Impact and Impulsive Loading: Synthesis Report; Comite Euro-International du Beton: Lausanne, Switzerland, 1988. [Google Scholar]
- Malvar, L.J.; Crawford, J.E. Dynamic increase factors for concrete. DTIC Doc. 1998, 1, 1–6. [Google Scholar]
- Saini, D.; Shafei, B. Investigation of concrete-filled steel tube beams strengthened with CFRP against impact loads. Compos. Struct. 2019, 208, 744–757. [Google Scholar] [CrossRef]
- Yin, X.; Li, Q.; Xu, X.; Chen, B.; Guo, K.; Xu, S. Investigation of continuous surface cap model (CSCM) for numerical simulation of strain-hardening fibre-reinforced cementitious composites against low-velocity impacts. Compos. Struct. 2023, 304, 116424. [Google Scholar] [CrossRef]
- Gharavi, A.; Asgarpoor, M.; Epackachi, S. Evaluation of plasticity-based concrete constitutive models under monotonic and cyclic loadings. Struct. Des. Tall Spec. Build. 2022, 31, e1919. [Google Scholar] [CrossRef]
- Grassl, P.; Jirásek, M. Damage-plastic model for concrete failure. Int. J. Solids Struct. 2006, 43, 7166–7196. [Google Scholar] [CrossRef]
- Elbelbisi, A.; Elsisi, A.; Saffarini, M.H.; Salim, H.; Chen, Z. Enhanced Blast Response Simulation of LG Panels Using an Elasto-Damage Model with the Finite Element Method. Buildings 2023, 13, 3025. [Google Scholar] [CrossRef]
- Ottosen, N.S. A failure criterion for concrete. J. Eng. Mech. Div. 1977, 103, 527–535. [Google Scholar] [CrossRef]
- Broadhouse, B. DRASTIC: A Computer Code for Dynamic Analysis of Stress Transients in Reinforced Concrete; UKAEA Atomic Energy Establishment: Abingdon, UK, 1986; Report.
- Malvar, L.J.; Crawford, J.E.; Wesevich, J.W.; Simons, D. A plasticity concrete material model for DYNA3D. Int. J. Impact Eng. 1997, 19, 847–873. [Google Scholar] [CrossRef]
- Schwer, L.E.; Malvar, L.J. Simplified concrete modeling with* MAT_CONCRETE_DAMAGE_REL3. In Proceedings of the JRI LS-Dyna User Week, Bamberg, Germany, 20–21 October 2005; pp. 49–60. [Google Scholar]
- Magallanes, J.M.; Wu, Y.; Malvar, L.J.; Crawford, J.E. Recent improvements to release III of the K&C concrete model. In Proceedings of the 11th International LS-DYNA Users Conference, Detroit, MI, USA, 6–8 June 2010; Livermore Software Technology Corporation: Livermore, CA, USA, 2010; Volume 1, pp. 37–48. [Google Scholar]
- LSTC Manual Version 970; LS-DYNA Manual; Livermore Software Technology Corporation: Livermore, CA, USA, 2006.
- Marais, S.; Tait, R.; Cloete, T.; Nurick, G. Material testing at high strain rate using the split Hopkinson pressure bar. Lat. Am. J. Solids Struct. 2004, 1, 219–339. [Google Scholar]
- Schwer, L.E.; Key, S.W.; Pucik, T.; Bindeman, L.P. An assessment of the LS-DYNA hourglass formulations via the 3D patch test. In Proceedings of the 5th European LS-DYNA Users Conference, Birmingham, UK, 25–26 May 2005. [Google Scholar]
- Klaiber, F.; Wipf, T.; Russo, F.; Paradis, R.; Mateega, R. Field/Laboratory Testing of Damaged Prestressed Concrete Girder Bridges; Iowa State University: Ames, IA, USA, 1999. [Google Scholar]
- Abendroth, R.E.; Klaiber, F.W.; Shafer, M.W. Lateral Load Resistance of Diaphragms in Prestressed Concrete Girder Bridges; Technical Report; Iowa State University: Ames, IA, USA, 1991. [Google Scholar]
- Yang, M.; Qiao, P.; McLean, D.I.; Khaleghi, B. Effects of overheight truck impacts on intermediate diaphragms in prestressed concrete bridge girders. PCI J. 2010, 55, 58–78. [Google Scholar] [CrossRef]
- Abendroth, R.E.; Andrawes, B.; Fanous, F. Steel Diaphragms in Prestressed Concrete Girder Bridges; Technical Report; Iowa Department of Transportation: Ames, IA, USA, 2004.




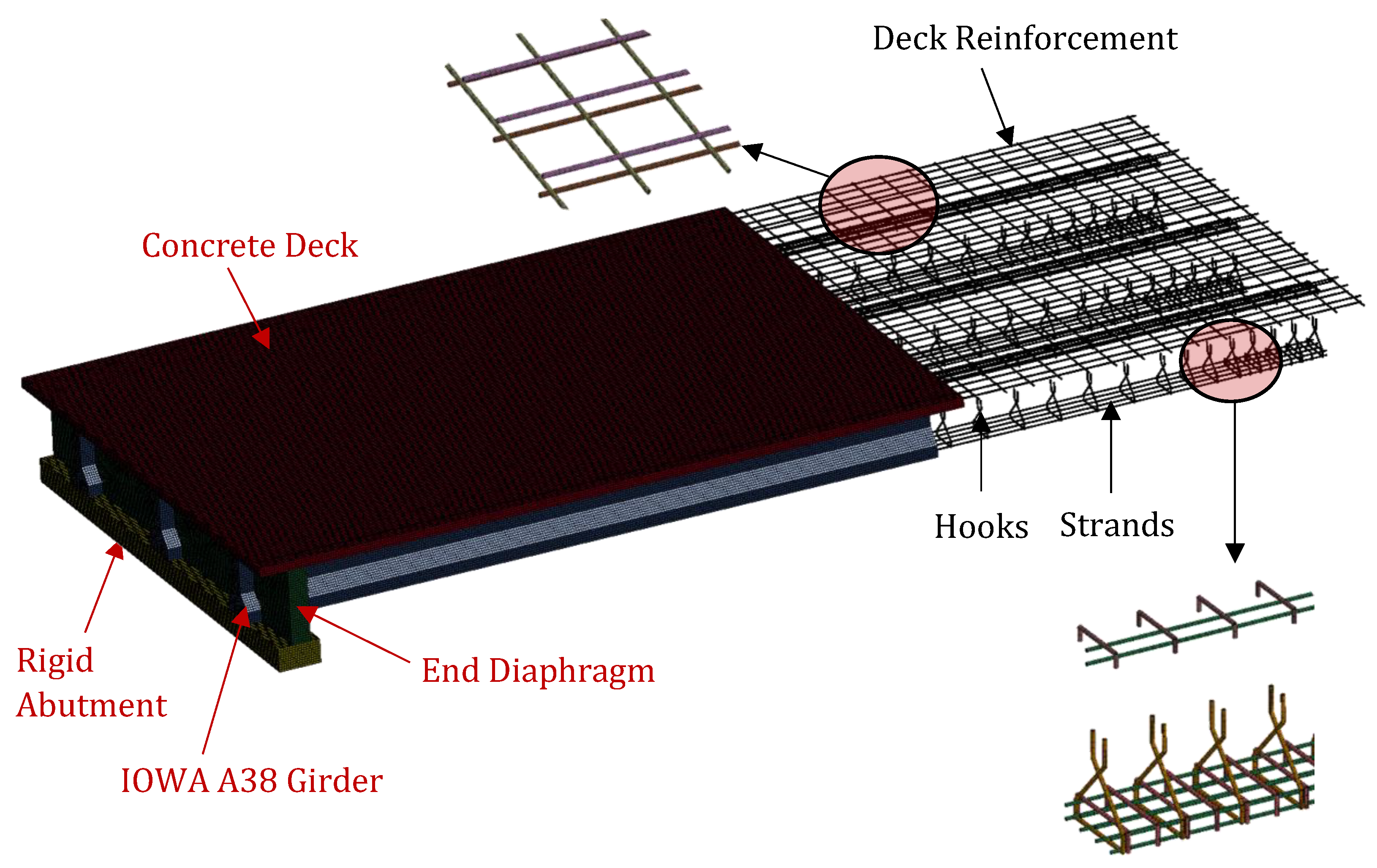
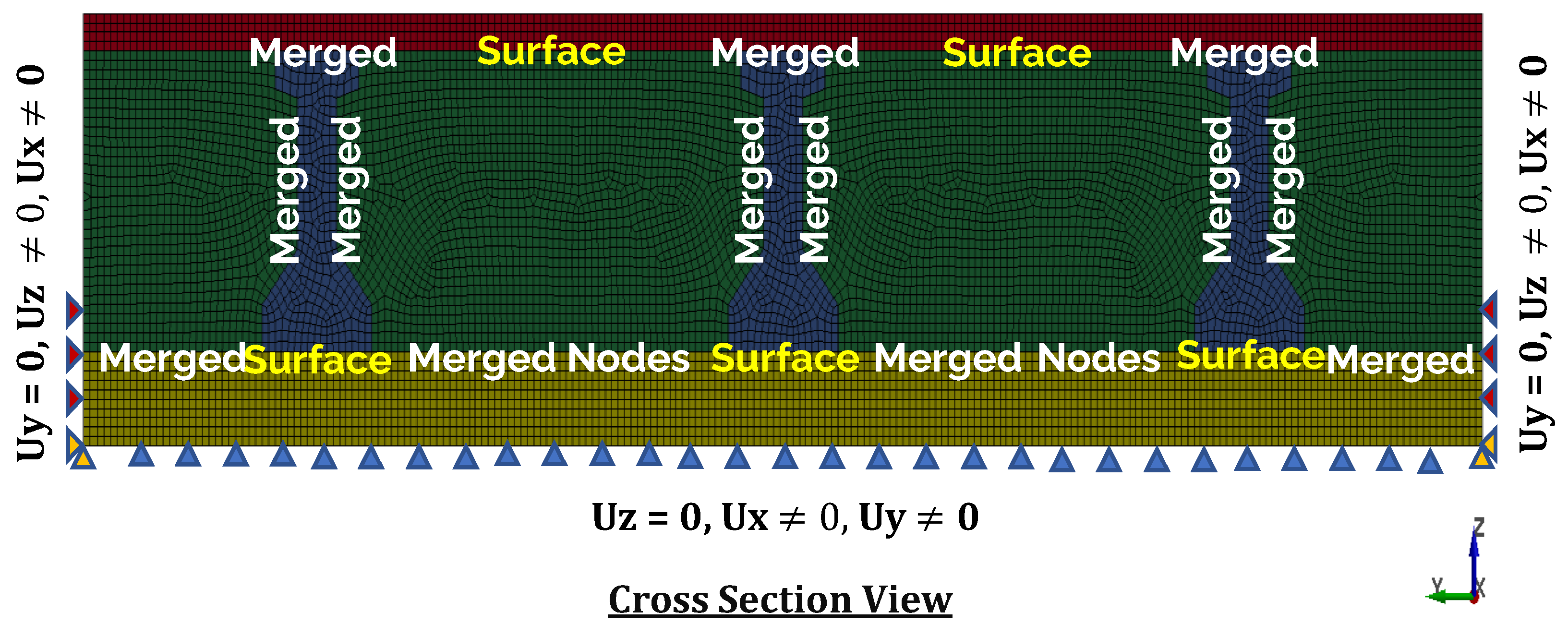

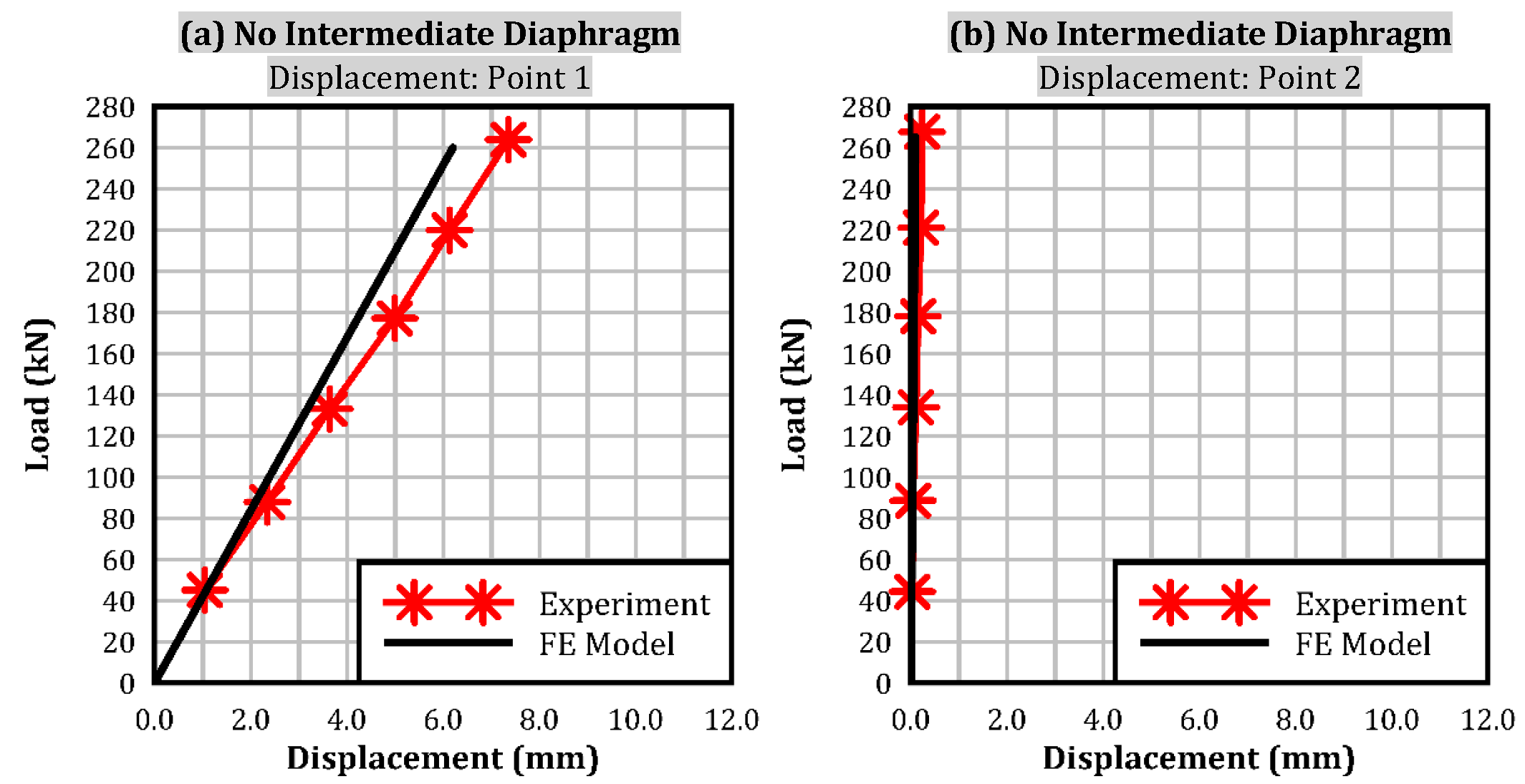

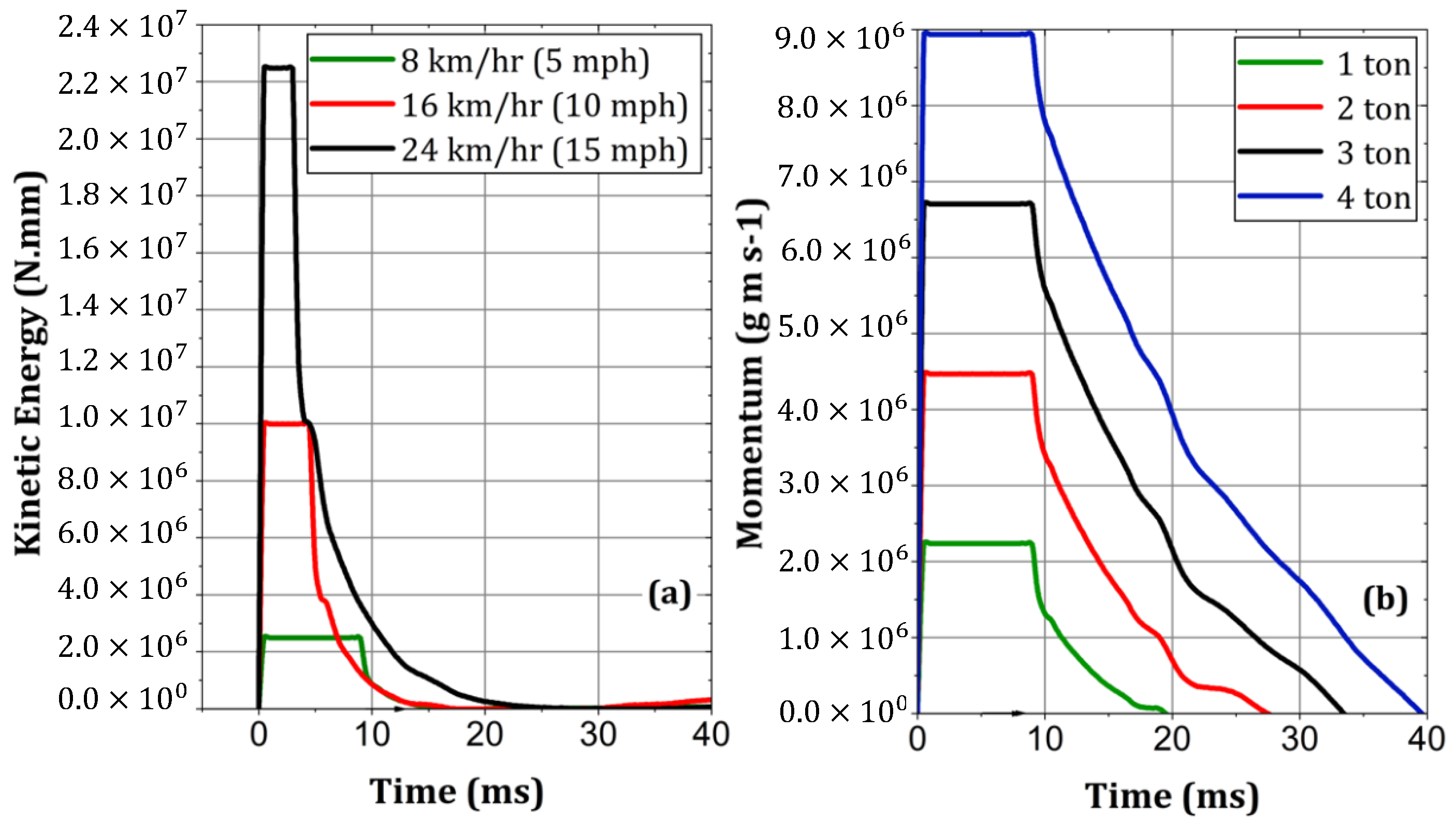

| Parameter | Values |
|---|---|
| Impact speed (3 variables) | 8, 16, and 24 km/h (5, 10, and 15 mph) |
| Impactor mass (4 variables) | 1, 2, 3, and 4 tons |
| Prestressing force (2 variables) | Existing, and No Prestressing Force |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Elshazli, M.T.; Abdulazeez, M.M.; ElGawady, M.; Ibrahim, A. Comprehensive Numerical Modeling of Prestressed Girder Bridges under Low-Velocity Impact. Buildings 2024, 14, 640. https://doi.org/10.3390/buildings14030640
Elshazli MT, Abdulazeez MM, ElGawady M, Ibrahim A. Comprehensive Numerical Modeling of Prestressed Girder Bridges under Low-Velocity Impact. Buildings. 2024; 14(3):640. https://doi.org/10.3390/buildings14030640
Chicago/Turabian StyleElshazli, Mohamed T., Mohanad M. Abdulazeez, Mohamed ElGawady, and Ahmed Ibrahim. 2024. "Comprehensive Numerical Modeling of Prestressed Girder Bridges under Low-Velocity Impact" Buildings 14, no. 3: 640. https://doi.org/10.3390/buildings14030640
APA StyleElshazli, M. T., Abdulazeez, M. M., ElGawady, M., & Ibrahim, A. (2024). Comprehensive Numerical Modeling of Prestressed Girder Bridges under Low-Velocity Impact. Buildings, 14(3), 640. https://doi.org/10.3390/buildings14030640








