Study on the Equivalent Stiffness of a Local Resonance Metamaterial Concrete Unit Cell
Abstract
:1. Introduction
2. Theoretical Model
2.1. One-Dimensional Vibration Theory Model
2.2. Two-Dimensional Vibration Theory Model
2.3. Finite Element Model
2.4. Model Comparison
3. Improved Model and Parameter Analysis
3.1. Improved Model
3.2. Parameter Analysis
3.2.1. Working Condition 1
3.2.2. Working Condition 2
3.2.3. Working Condition 3
4. Discussion
5. Conclusions
- (1)
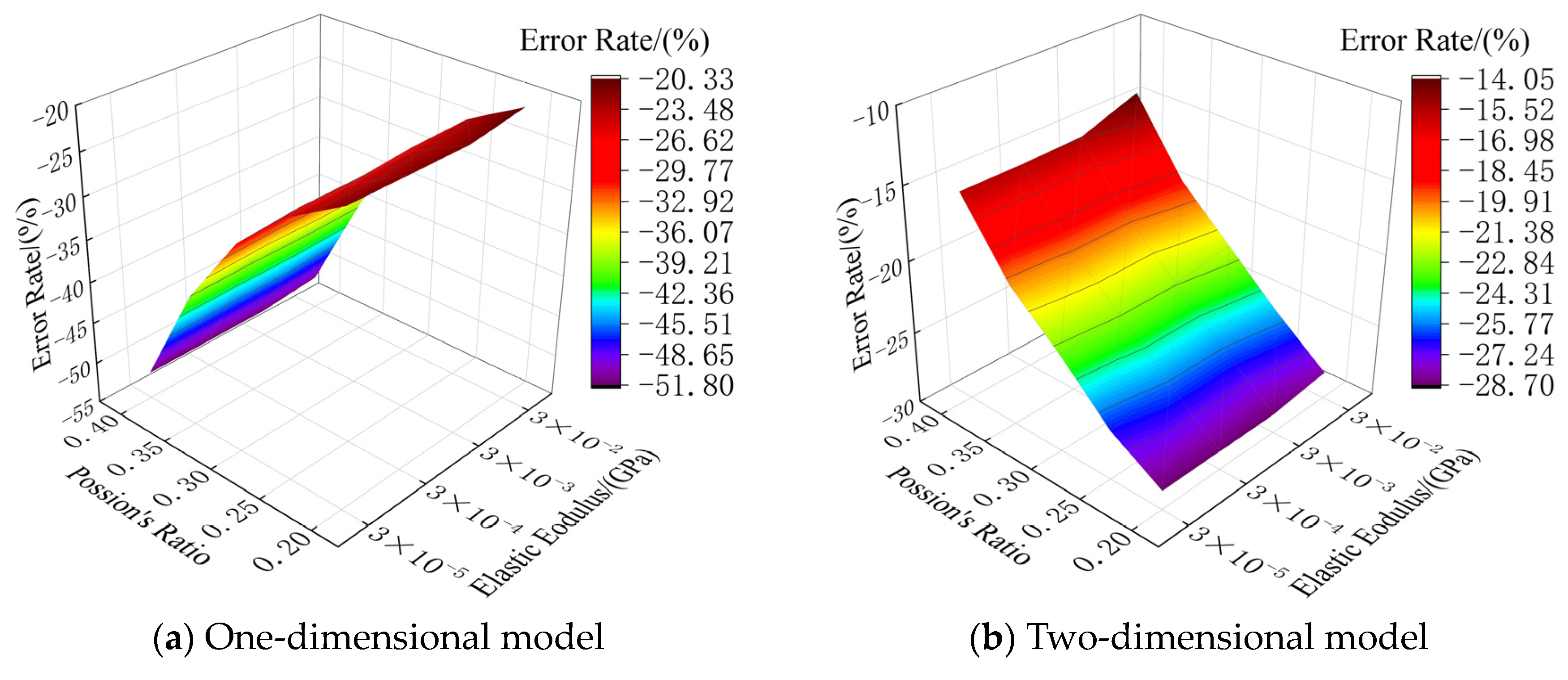
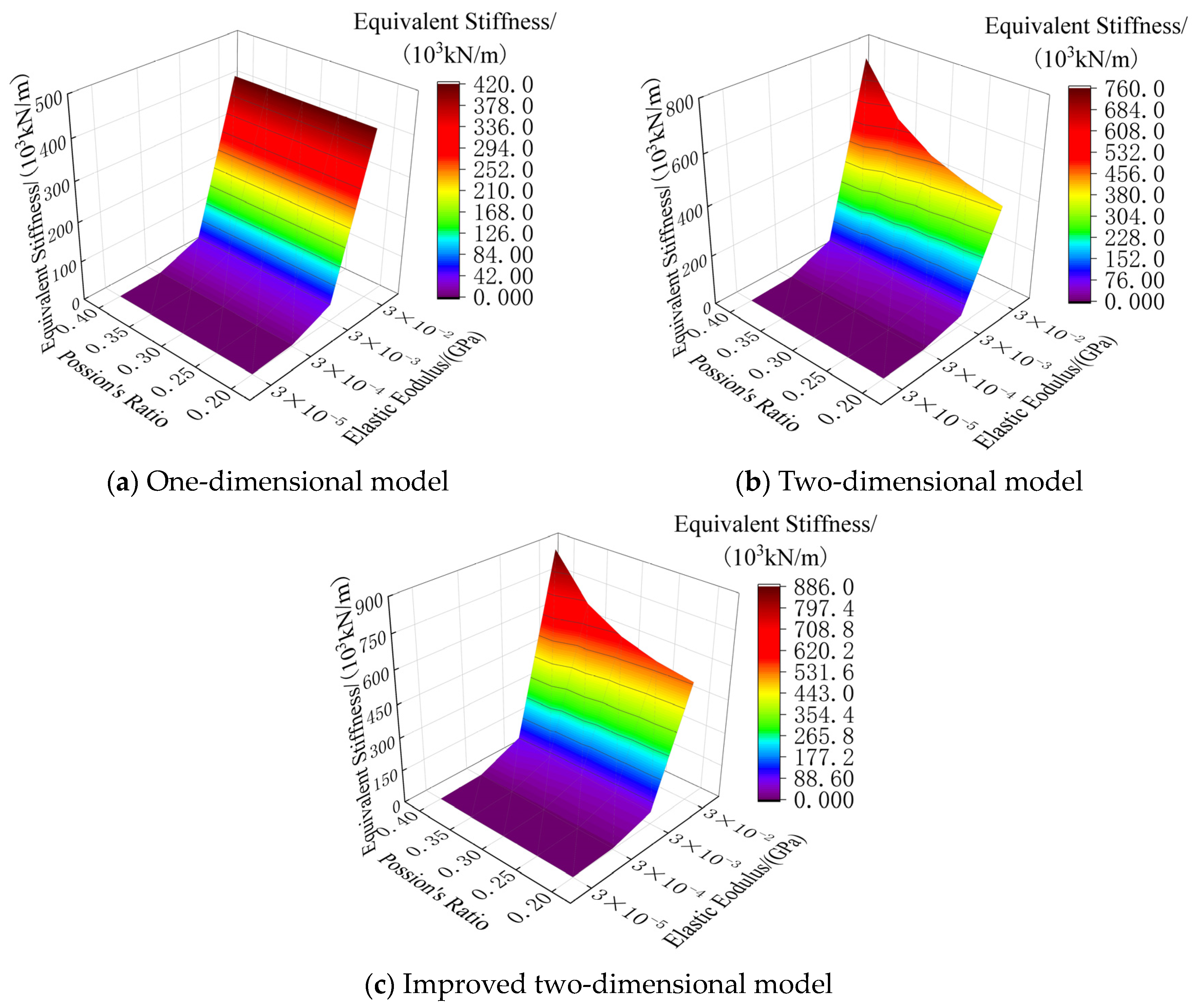
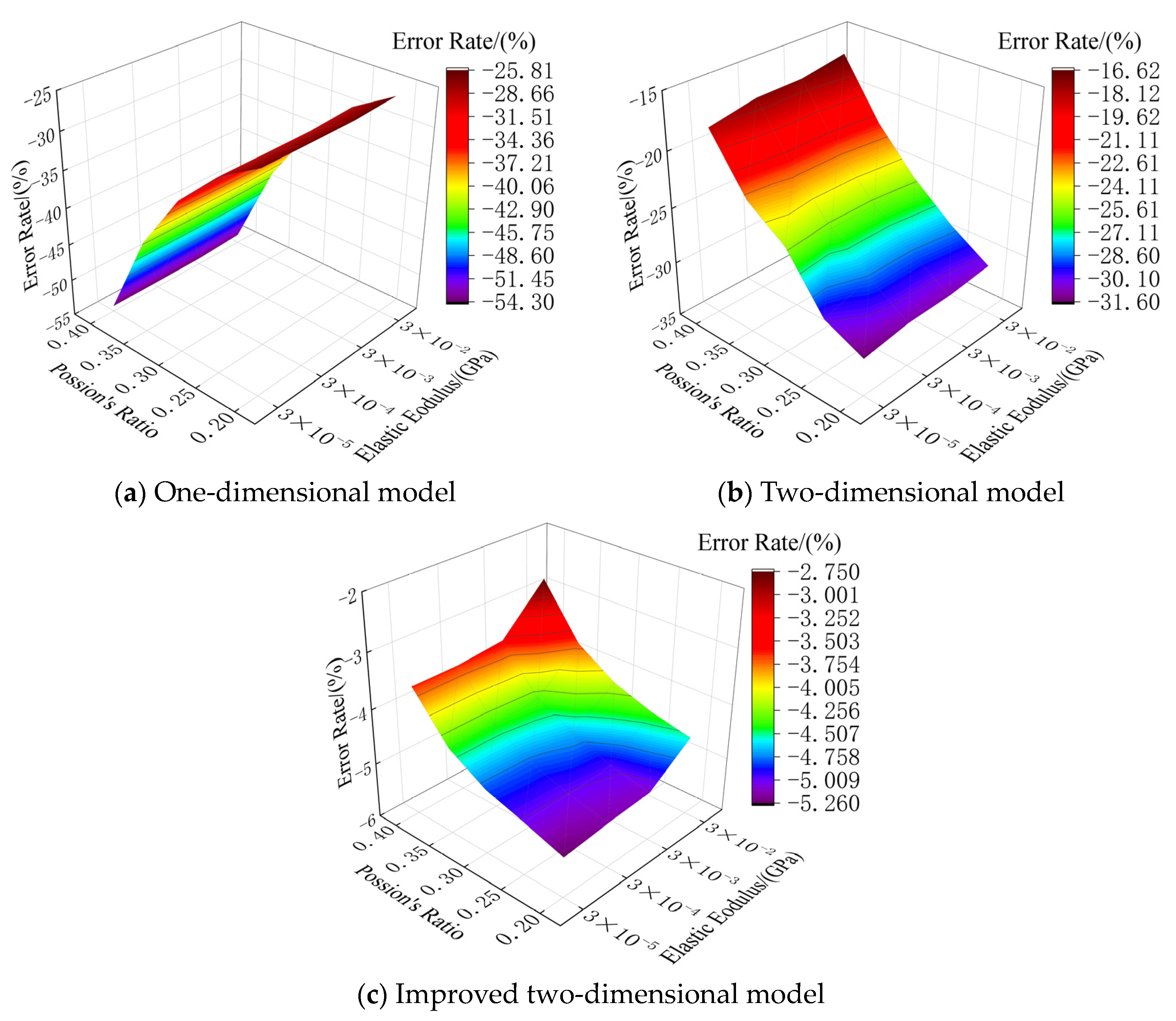
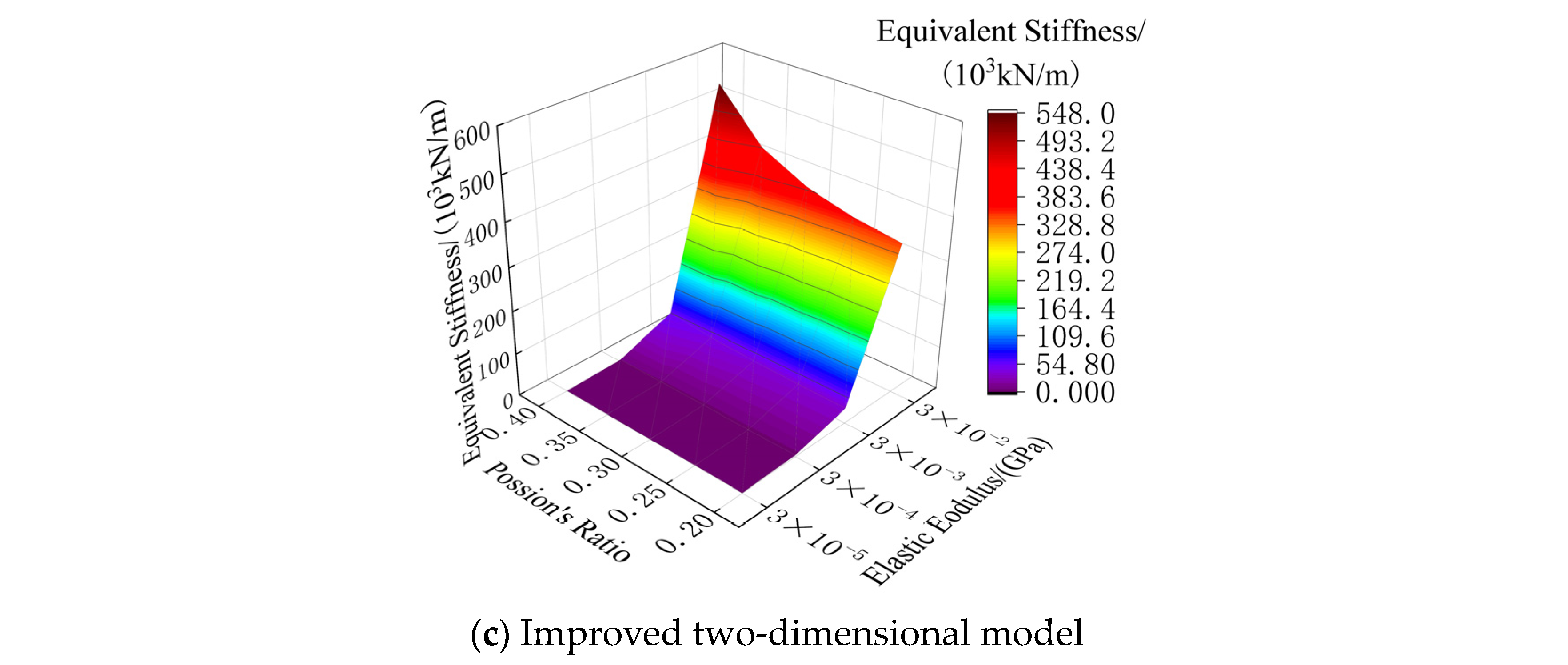
- When the elastic modulus and Poisson’s ratio are constant, the prediction results of the one- and two-dimensional theoretical vibration models and the improved two-dimensional model all decrease with the increase in the coating thickness, while the error rates increase. When the geometric parameters and Poisson’s ratio are constant, the prediction results of the one-and two-dimensional theoretical vibration models and the improved two-dimensional model increase with the increase in the elastic modulus, while the error rates decrease.
- (2)
- When the geometric parameters and elastic modulus of the coating remain unchanged, the prediction results of the one-dimensional vibration-theoretical model remain unchanged, and the error rate increases with the increase in Poisson’s ratio. The prediction results of the two-dimensional vibration theory model and the improved two-dimensional model increase with the increase in Poisson’s ratio, while the error rates decrease.
- (3)
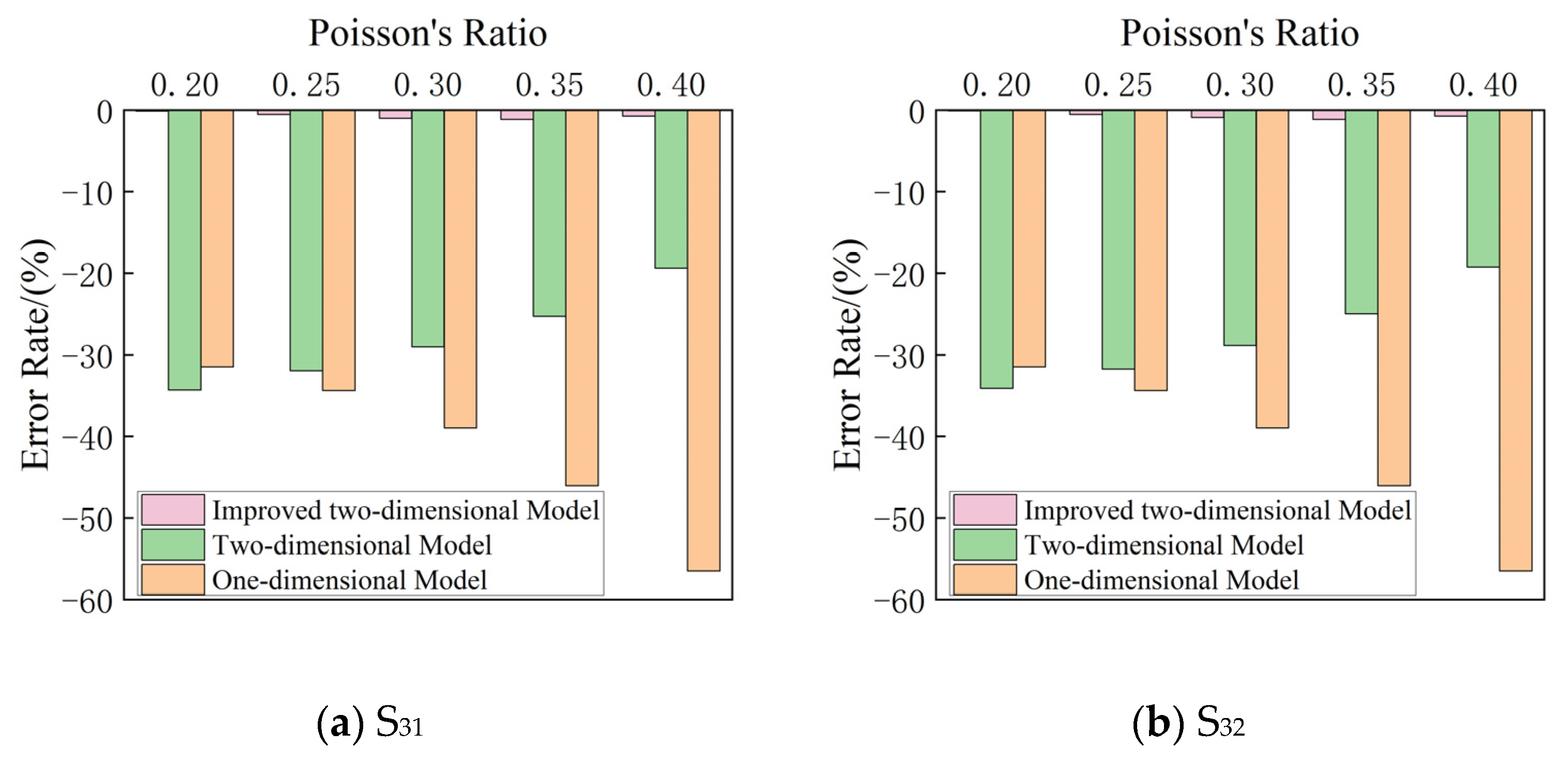
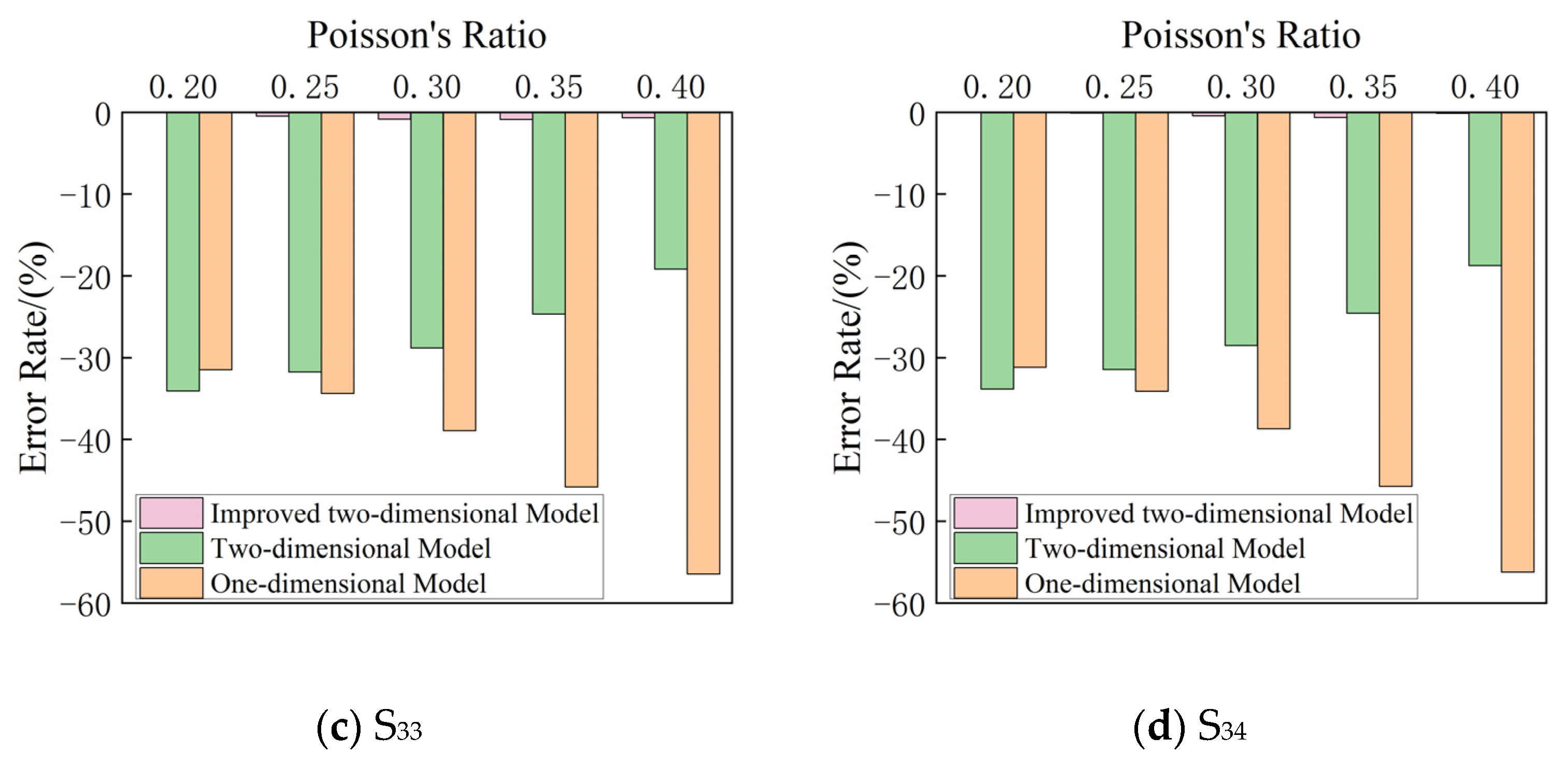
- The one-dimensional theoretical vibration model cannot accurately predict the simulation results; in the research scope of this paper, the error rate is up to −56.49% (the negative sign means that the theoretical result is smaller than the simulation result). The two-dimensional theoretical vibration model is suitable for the case of a large elastic modulus, large Poisson’s ratio and thin coating thickness. In other cases, the error rate of the two-dimensional theoretical vibration model can reach up to −34.28%. The improved two-dimensional theoretical vibration model is applicable to all situations. The absolute value of the error rate of working condition 2 is generally within 5%, and it is generally within 1% for working condition 3. This shows that the improved two-dimensional theoretical vibration model proposed in this paper is more accurate, can better explain the vibration characteristics of the metamaterial concrete unit cell and is more suitable for the prediction of its equivalent stiffness value.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wegener, M. Metamaterials Beyond Optics. Science 2013, 342, 939–940. [Google Scholar] [CrossRef] [PubMed]
- Landy, N.; Smith, D.R. A full-parameter unidirectional metamaterial cloak for microwaves. Nat. Mater. 2013, 12, 25–28. [Google Scholar] [CrossRef] [PubMed]
- Marunin, M.V.; Polikarpova, N.V. Polarization of Acoustic Waves in Two-Dimensional Phononic Crystals Based on Fused Silica. Materials 2022, 15, 8315. [Google Scholar] [CrossRef] [PubMed]
- Li, B.; Tan, K.T.; Christensen, J. Tailoring the thermal conductivity in nanophononic metamaterials. Phys. Rev. B 2017, 95, 144305. [Google Scholar] [CrossRef]
- Wang, Y.-Z.; Li, F.-M.; Wang, Y.-S. Influences of active control on elastic wave propagation in a weakly nonlinear phononic crystal with a monoatomic lattice chain. Int. J. Mech. Sci. 2016, 106, 357–362. [Google Scholar] [CrossRef]
- Banerjee, B.; Nagy, P.B. An Introduction to Metamaterials and Waves in Composites. J. Acoust. Soc. Am. 2012, 131, 1665–1666. [Google Scholar] [CrossRef]
- Al Ba’Ba’A, H.B.; Nouh, M. Mechanics of longitudinal and flexural locally resonant elastic metamaterials using a structural power flow approach. Int. J. Mech. Sci. 2017, 122, 341–354. [Google Scholar] [CrossRef]
- Liu, X.N.; Hu, G.K.; Huang, G.L.; Sun, C.T. An elastic metamaterial with simultaneously negative mass density and bulk modulus. Appl. Phys. Lett. 2011, 98, 251907. [Google Scholar] [CrossRef]
- Li, J.; Chan, C.T. Double-negative acoustic metamaterial. Phys. Rev. E 2004, 70, 055602. [Google Scholar] [CrossRef]
- Xu, C.; Chen, W.; Hao, H.; Pham, T.M.; Li, Z.; Jin, H. Dynamic compressive properties of metaconcrete material. Constr. Build. Mater. 2022, 351, 128974. [Google Scholar] [CrossRef]
- Ansari, M.; Tartaglione, F.; Koenke, C. Experimental Validation of Dynamic Response of Small-Scale Metaconcrete Beams at Resonance Vibration. Materials 2023, 16, 5029. [Google Scholar] [CrossRef] [PubMed]
- Chen, Z.; Wang, G.; Lim, C. Artificially engineered metaconcrete with wide bandgap for seismic surface wave manipulation. Eng. Struct. 2023, 276, 115375. [Google Scholar] [CrossRef]
- Xu, C.; Chen, W.; Hao, H.; Bi, K.; Pham, T.M. Experimental and numerical assessment of stress wave attenuation of metaconcrete rods subjected to impulsive loads. Int. J. Impact Eng. 2021, 159, 104052. [Google Scholar] [CrossRef]
- Li, Q.Q.; He, Z.C.; Li, E.; Cheng, A.G. Design of a multi-resonator metamaterial for mitigating impact force. J. Appl. Phys. 2019, 125, 035104. [Google Scholar] [CrossRef]
- Jin, H.; Chen, W.; Hao, H.; Hao, Y. Numerical study on impact resistance of metaconcrete. Sci. Sin. Phys. Mech. Astron. 2020, 50, 024609. [Google Scholar] [CrossRef]
- Briccola, D.; Cuni, M.; De Juli, A.; Ortiz, M.; Pandolfi, A. Experimental validation of the attenuation properties in the sonic range of metaconcrete containing two types of resonant inclusions. Exp. Mech. 2020, 61, 515–532. [Google Scholar] [CrossRef]
- Li, C.; Qing, H.; Ru, C.Q. On two initial-boundary-value problems for impact dynamics of metaconcrete rods. Eng. Math. 2023, 140, 5. [Google Scholar] [CrossRef]
- Jin, H.; Hao, H.; Hao, Y.; Chen, W. Predicting the response of locally resonant concrete structure under blast load. Constr. Build. Mater. 2020, 252, 118920. [Google Scholar] [CrossRef]
- Jin, H.; Hao, H.; Chen, W.; Xu, C. Effect of enhanced coating layer on the bandgap characteristics and response of metaconcrete. Mech. Adv. Mater. Struct. 2021, 30, 175–188. [Google Scholar] [CrossRef]
- Gao, Y.; Wang, H. Comparative investigation of full bandgap behaviors of perforated auxetic metaconcretes with or without soft filler. Mater. Today Commun. 2024, 38, 108526. [Google Scholar] [CrossRef]
- Xiao, P.; Miao, L.; Zheng, H.; Lei, L. Low frequency vibration reduction bandgap characteristics and engineering application of phononic-like crystal metaconcrete material. Constr. Build. Mater. 2024, 411, 134734. [Google Scholar] [CrossRef]
- Xiong, J.; Ren, F.; Li, S.; Tian, S.; Li, Y.; Mo, J. A study on low-frequency vibration mitigation by using the metamaterial-tailored composite concrete-filled steel tube column. Eng. Struct. 2024, 305, 117673. [Google Scholar] [CrossRef]
- Chen, B.; Zheng, Y.; Dai, S.; Qu, Y. Bandgap enhancement of a piezoelectric metamaterial beam shunted with circuits incorporating fractional and cubic nonlinearities. Mech. Syst. Signal Process. 2024, 212, 111262. [Google Scholar] [CrossRef]
- Bae, M.H.; Oh, J.H. Nonlinear elastic metamaterial for tunable bandgap at quasi-static frequency. Mech. Syst. Signal Process. 2022, 170, 108832. [Google Scholar] [CrossRef]
- Anigbogu, W.; Bardaweel, H. A Comparative Study and Analysis of Layered-Beam and Single-Beam Metamaterial Structures: Transmissibility Bandgap Development. Appl. Sci. 2022, 12, 7550. [Google Scholar] [CrossRef]
- Jian, Y.; Hu, G.; Tang, L.; Xu, J.; Aw, K.C. A generic theoretical approach for estimating bandgap bounds of metamaterial beams. J. Appl. Phys. 2021, 130, 054501. [Google Scholar] [CrossRef]
- Ma, Y.L.; Wang, X.M.; Mei, Y.L. Acoustic Metamaterials Composed of Pre-stressed Oscillator Unit Cells and the Effective Method of Adjusting and Expanding Bandgap. In Advances in Machinery, Materials Science and Engineering Application; License CC BY-NC 4.0; IOS Press: Amsterdam, The Netherlands, 2022. [Google Scholar] [CrossRef]
- Cui, R.; Zhou, J.; Gong, D. Wave-resistance sleeper with locally resonant phononic crystals: Bandgap property and vibration reduction mechanism. AIP Adv. 2021, 11, 035043. [Google Scholar] [CrossRef]
- Carvalho, A.L.L.; Gomes, C.B.F.; dos Santos, J.M.C.; de Miranda, E.J.P., Jr. Effect of Resonant Aggregate Parameters in Metaconcrete Thin Plates on Flexural Bandgaps: Numerical Simulations. Mater. Res. 2023, 26 (Suppl. 1), e20220547. [Google Scholar] [CrossRef]
- Slesarenko, V. Bandgap structure in elastic metamaterials with curvy Bezier beams. Appl. Phys. Lett. 2023, 123, 081702. [Google Scholar] [CrossRef]
- Chen, J.; Qu, Y.; Guo, Z.; Li, D.; Zhang, G. A one-dimensional model for mechanical coupling metamaterials using couple stress theory. Math. Mech. Solids 2023, 28, 2732–2755. [Google Scholar] [CrossRef]
- Zhou, Y.; Ye, L.; Chen, Y. Developing three-dimensional mechanical metamaterials with tailorable bandgaps for impact mitigation. J. Phys. D Appl. Phys. 2024, 57, 195501. [Google Scholar] [CrossRef]
- Zhang, E.; Lu, G.Y.; Yang, H.W.; Lin, S. Band gap characteristics of metamaterial concrete and its attenuation effect on shock wave. Explos. Shock. 2020, 502, 116088. [Google Scholar]
- Han, J.; Lu, G.Y. A study of undamped free vibration characteristics on a metaconcrete unit cell. J. Vib. Shock 2021, 40, 173–178. [Google Scholar] [CrossRef]
- Han, J.; Lu, G.Y.; Zhao, Y.T. A study of damped free vibration characteristics on a metaconcrete unit. J. Vib. Shock 2022, 41, 31. [Google Scholar] [CrossRef]
- Han, J.; Lu, G. Study on damping forced vibration characteristics of metamaconcrete unit cell and optimizing aggregate selection. Constr. Build. Mater. 2024, 421, 135598. [Google Scholar] [CrossRef]
- Bo, Z.; Li, Z. New Analytical Model for Composite Materials Containing Local Resonance Units. J. Eng. Mech. 2011, 137, 1–7. [Google Scholar] [CrossRef]
- Vo, N.H.; Pham, T.M.; Bi, K.; Chen, W.; Hao, H. Stress Wave Mitigation Properties of Dual-meta Panels against Blast Loads. Int. J. Impact Eng. 2021, 154, 103877. [Google Scholar] [CrossRef]
- Vo, N.H.; Pham, T.M.; Bi, K.; Hao, H. Model for analytical investigation on meta-lattice truss for low-frequency spatial wave manipulation. Wave Motion 2021, 103, 102735. [Google Scholar] [CrossRef]
- Yu, J.; Jung, J.; Wang, S. Derivation and Validation of Bandgap Equation Using Serpentine Resonator. Appl. Sci. 2022, 12, 3934. [Google Scholar] [CrossRef]
- Wen, X.S.; Wen, J.H.; Yu, D.L. Phononic Crystal; National Defense Industry Press: Arlington, VA, USA, 2009. [Google Scholar]
- Oyelade, A.O.; Abiodun, Y.O.; Sadiq, M.O. Dynamic behaviour of concrete containing aggregate resonant frequency. J. Comput. Appl. Mech. 2018, 49, 380–385. [Google Scholar] [CrossRef]
- Gao, Y.J.; Fan, H.L.; Zhang, B.; Jin, F.N. Research on the clipping effect of metamaterial wave-absorbing concrete slabs under the action of two-dimensional plane waves. J. Vib. Shock 2018, 37, 39–44. [Google Scholar] [CrossRef]
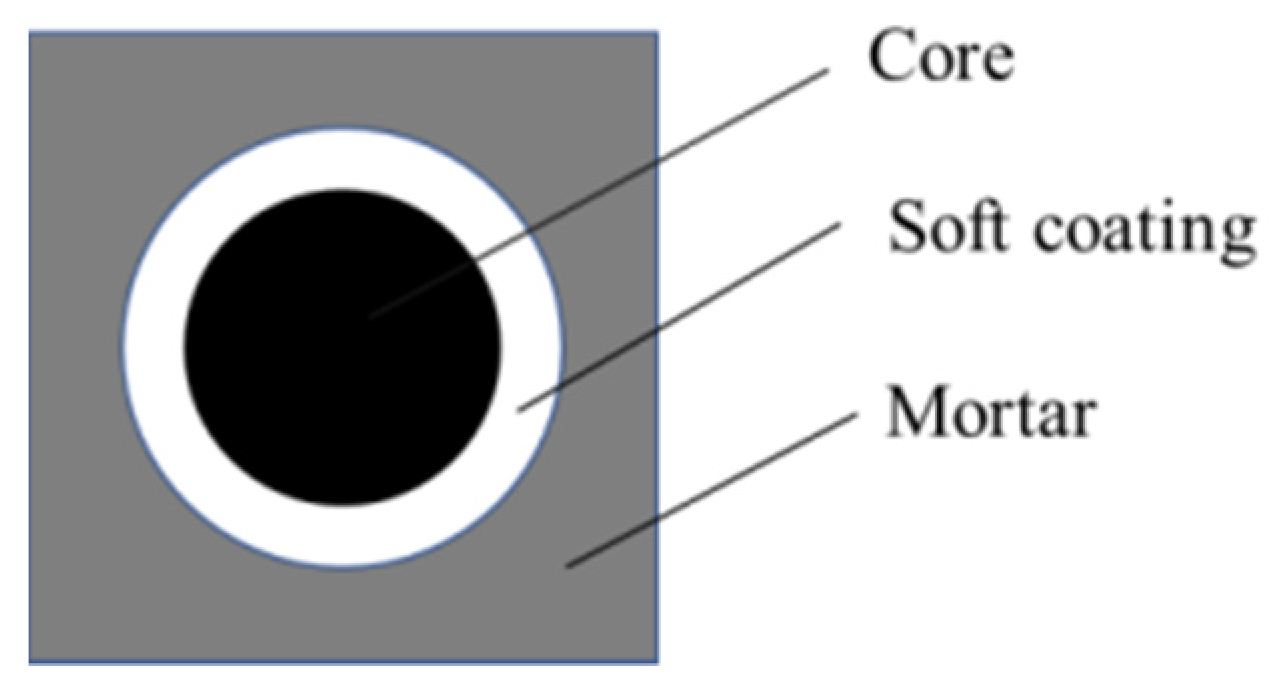
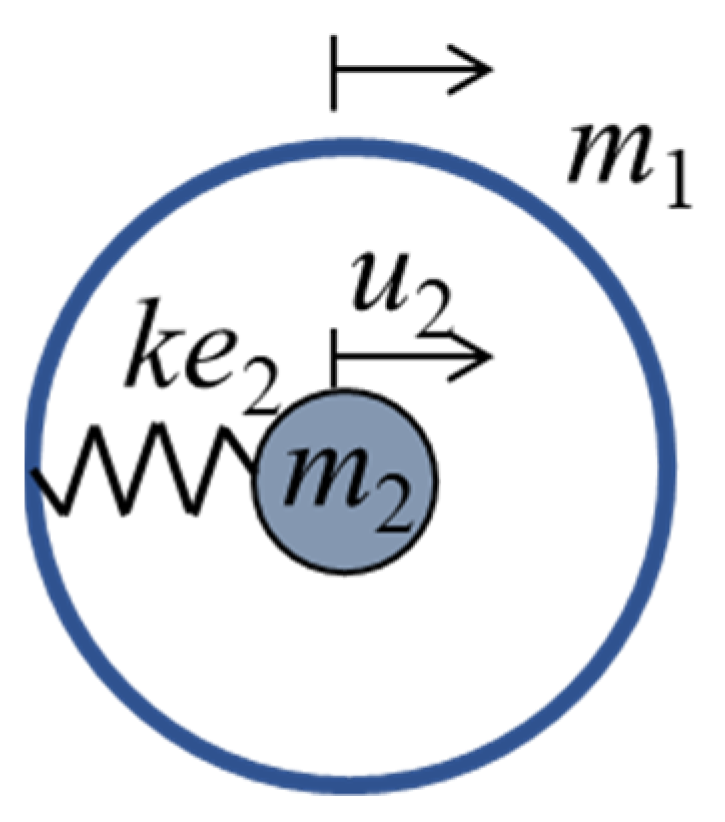
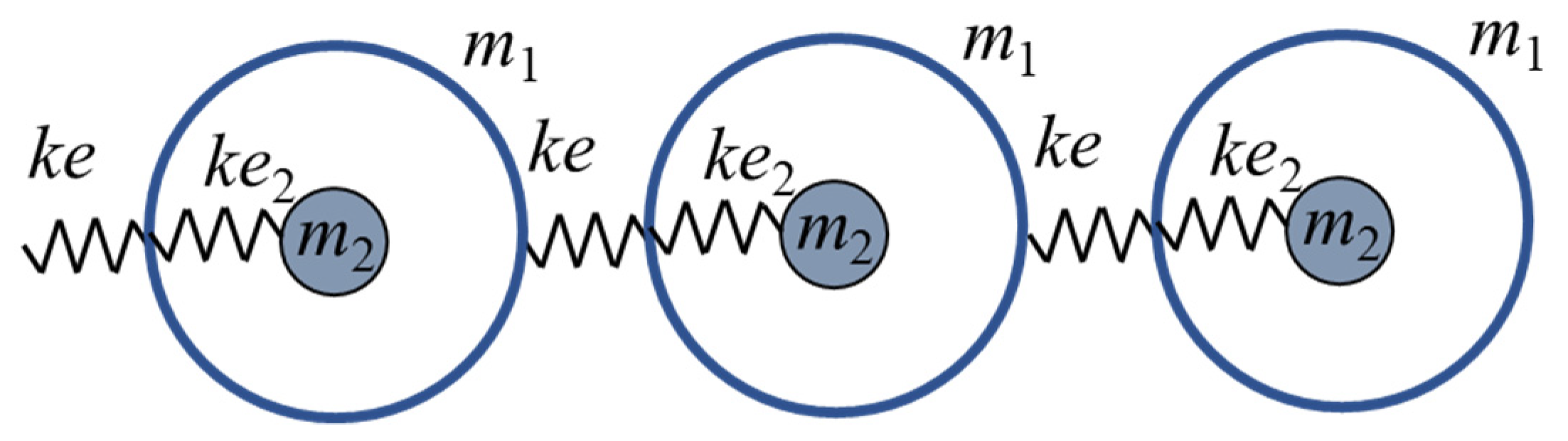


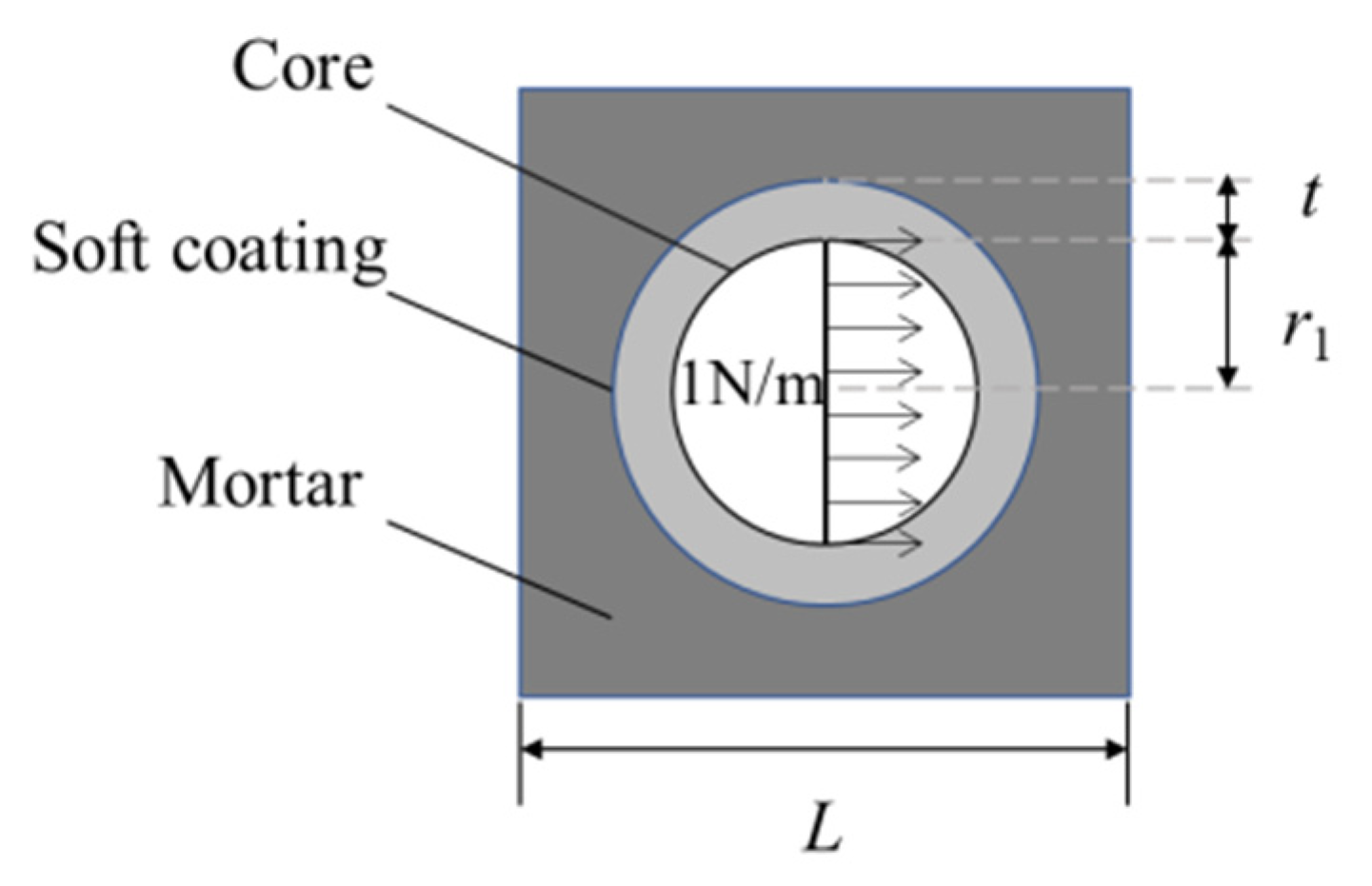
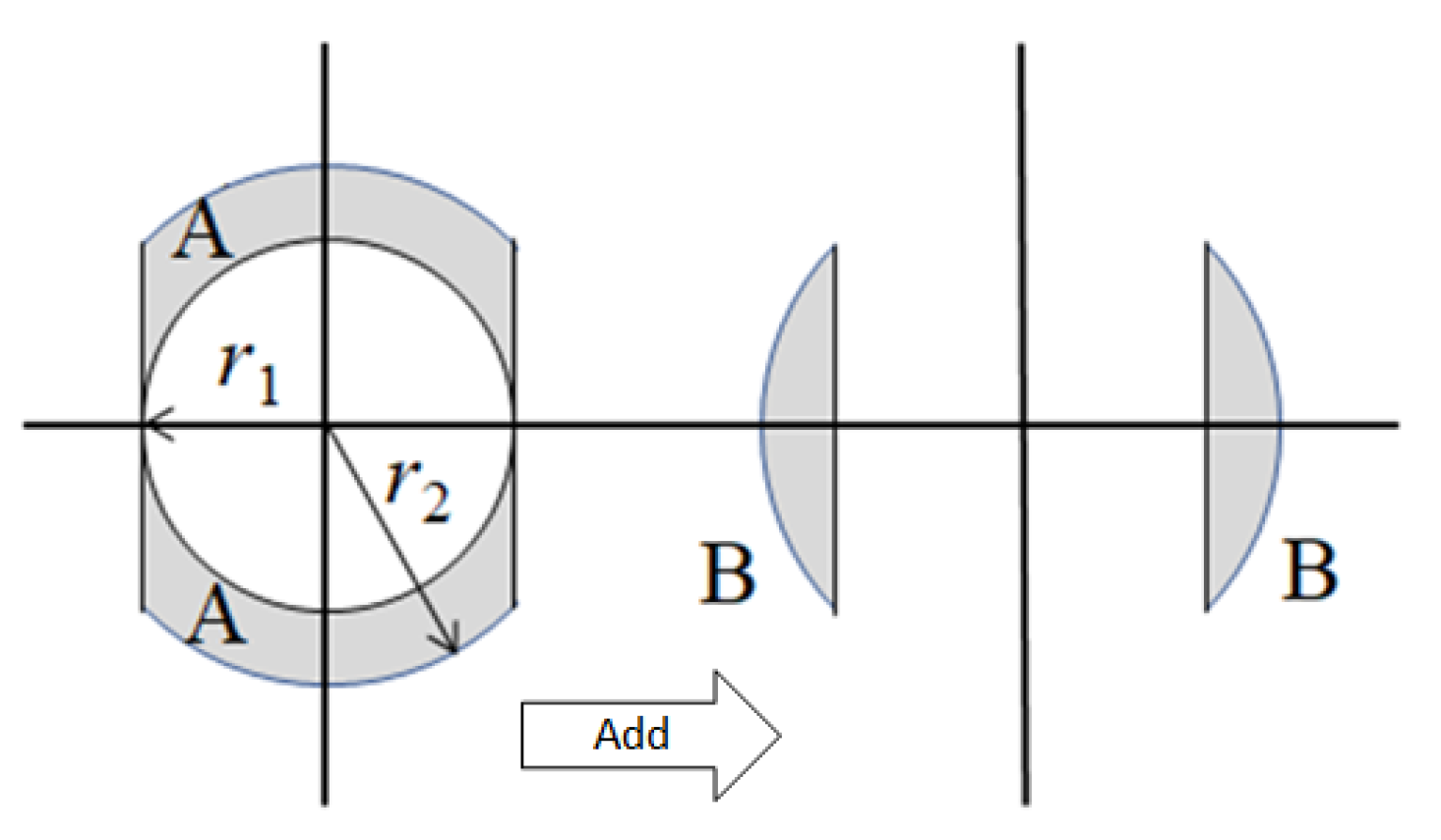






| L (mm) | (mm) | t (mm) | |
|---|---|---|---|
| Basic Model | 20 | 9 | 1 |
| Material | Density (kg/m3) | Modulus of Elasticity (GPa) | Poisson’s Ratio | (GPa) | (GPa) |
|---|---|---|---|---|---|
| Mortar | 2500 | 30 | 0.2 | 8.33 | 12.5 |
| Lead | 11,600 | 16.00 | 0.369 | 42.00 | 14.90 |
| Rubber | 1300 | 0.469 |
| Coating | Equivalent Stiffness (103 kN/m) | ||||
|---|---|---|---|---|---|
| Numerical Simulation | One-Dimensional Model | Error Rate (%) | Two-Dimensional Model | Error Rate (%) | |
| 1 mm rubber | 19.41 | 3.84 | −80.22 | 17.91 | −7.73 |
| 2 mm rubber | 8.59 | 1.68 | −80.44 | 8.08 | −5.94 |
| 3 mm rubber | 4.80 | 0.96 | −80.00 | 4.75 | −1.04 |
| Coating | Equivalent Stiffness (103 kN/m) | ||||||
|---|---|---|---|---|---|---|---|
| Numerical Simulation | One- Dimensional Model | Error Rate (%) | Two-Dimensional Model | Error Rate (%) | Improved Two-Dimensional Model | Error Rate (%) | |
| 1 mm Rubber | 19.41 | 3.84 | −80.22 | 17.91 | −7.73 | 18.58 | −4.28 |
| 2 mm Rubber | 8.59 | 1.68 | −80.44 | 8.08 | −5.94 | 8.55 | −0.47 |
| 3 mm Rubber | 4.80 | 0.96 | −80.00 | 4.75 | −1.04 | 5.13 | 6.88 |
| Parameters | Equivalent Stiffness (103 kN/m) | |||||||
|---|---|---|---|---|---|---|---|---|
| S | Numerical Simulation | One- Dimensional | Error Rate (%) | Two- Dimensional | Error Rate (%) | Improved Two- Dimensional | Error Rate (%) | |
| S11 | 0.20 | 1.22 | 0.96 | −21.31 | 0.87 | −28.69 | 1.08 | −11.48 |
| 0.25 | 1.28 | −25.00 | 0.94 | −26.56 | 1.14 | −10.94 | ||
| 0.30 | 1.38 | −30.43 | 1.06 | −23.19 | 1.25 | −9.42 | ||
| 0.35 | 1.58 | −39.24 | 1.26 | −20.25 | 1.45 | −8.22 | ||
| 0.40 | 1.99 | −51.76 | 1.68 | −15.58 | 1.86 | −6.53 | ||
| S12 | 0.20 | 12.21 | 9.60 | −21.38 | 8.71 | −28.67 | 10.81 | −11.47 |
| 0.25 | 12.78 | −24.88 | 9.41 | −25.91 | 11.43 | −10.56 | ||
| 0.30 | 13.68 | −29.82 | 10.56 | −22.81 | 12.50 | −8.63 | ||
| 0.35 | 15.69 | −38.81 | 12.59 | −19.76 | 14.45 | −7.90 | ||
| 0.40 | 19.90 | −51.75 | 16.81 | −15.57 | 18.61 | −6.48 | ||
| S13 | 0.20 | 122.14 | 96.00 | −21.40 | 87.14 | −28.66 | 108.15 | −11.45 |
| 0.25 | 126.98 | −24.39 | 94.11 | −25.89 | 114.28 | −10.00 | ||
| 0.30 | 136.75 | −29.80 | 105.57 | −22.80 | 124.97 | −8.61 | ||
| 0.35 | 156.86 | −38.80 | 125.87 | −19.76 | 144.55 | −7.85 | ||
| 0.40 | 198.76 | −51.70 | 168.05 | −15.45 | 186.07 | −6.38 | ||
| S14 | 0.20 | 1205.01 | 960.00 | −20.33 | 871.39 | −28.11 | 1081.54 | −10.78 |
| 0.25 | 1259.84 | −23.80 | 941.10 | −25.30 | 1142.84 | −9.29 | ||
| 0.30 | 1355.93 | −29.20 | 1055.72 | −22.14 | 1249.71 | −7.83 | ||
| 0.35 | 1553.40 | −38.20 | 1258.67 | −18.97 | 1445.47 | −6.95 | ||
| 0.40 | 1955.99 | −50.92 | 1680.53 | −14.08 | 1860.66 | −4.87 | ||
| Parameters | Equivalent Stiffness (103 kN/m) | |||||||
|---|---|---|---|---|---|---|---|---|
| S | Numerical Simulation | One- Dimensional | Error Rate (%) | Two- Dimensional | Error Rate (%) | Improved Two- Dimensional | Error Rate (%) | |
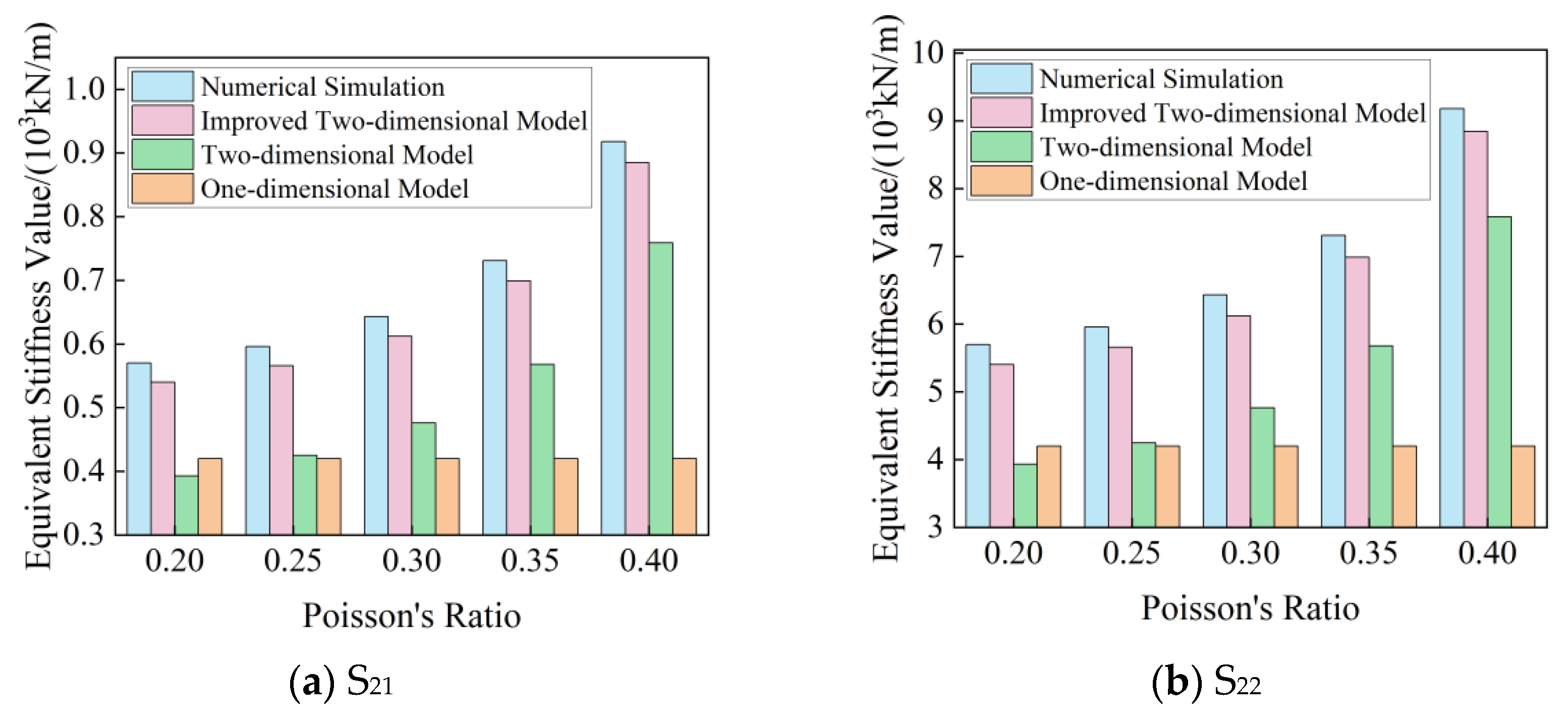
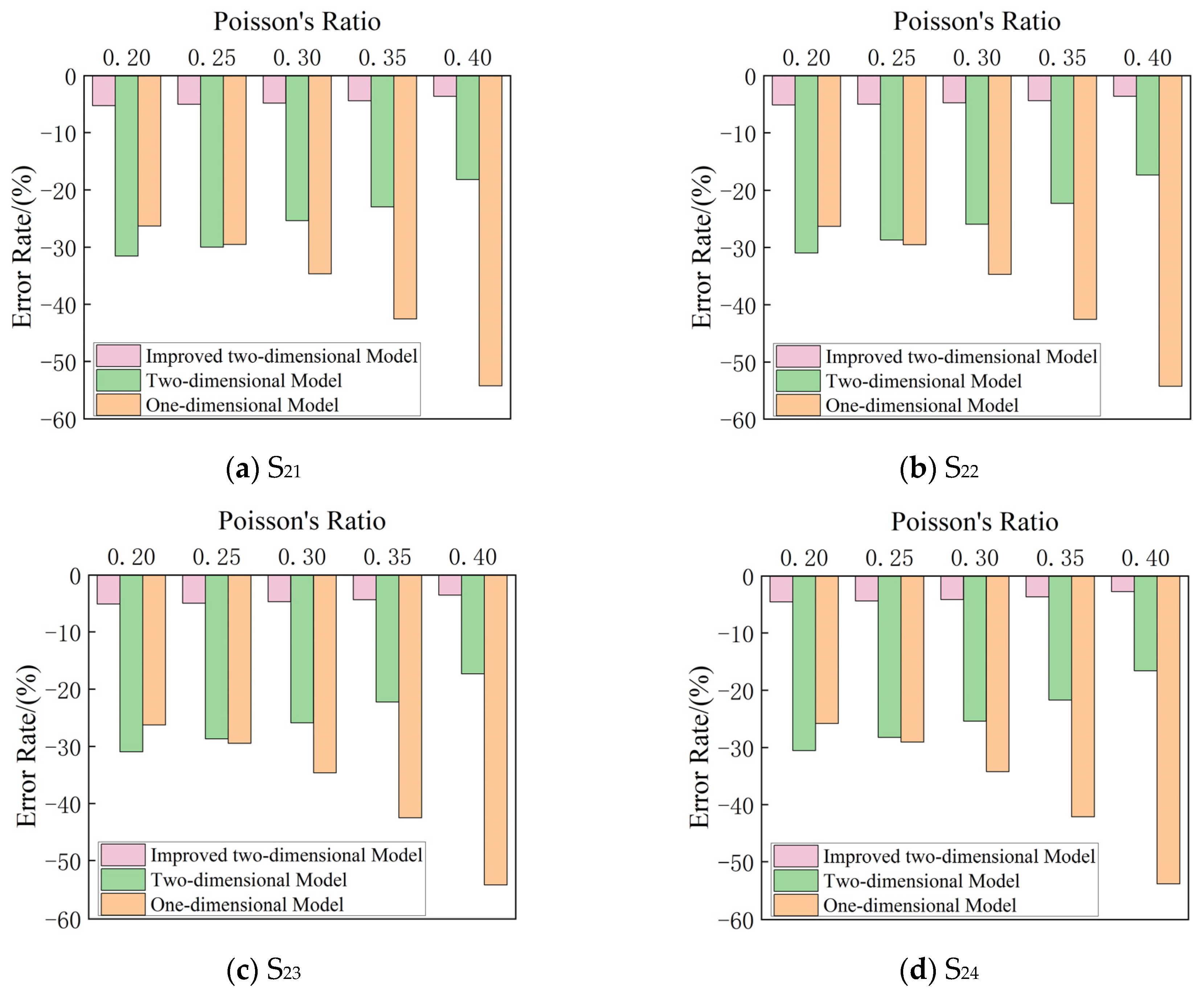
| S21 | 0.20 | 0.570 | 0.42 | −26.32 | 0.393 | −31.58 | 0.540 | −5.26 |
| 0.25 | 0.596 | −29.53 | 0.425 | −30.00 | 0.566 | −5.03 | ||
| 0.30 | 0.643 | −34.68 | 0.476 | −25.35 | 0.612 | −4.82 | ||
| 0.35 | 0.731 | −42.55 | 0.568 | −22.97 | 0.699 | −4.42 | ||
| 0.40 | 0.918 | −54.25 | 0.759 | −18.21 | 0.885 | −3.63 | ||
| S22 | 0.20 | 5.699 | 4.20 | −26.30 | 3.932 | −31.00 | 5.404 | −5.17 |
| 0.25 | 5.959 | −29.52 | 4.247 | −28.73 | 5.660 | −5.02 | ||
| 0.30 | 6.431 | −34.69 | 4.764 | −25.92 | 6.123 | −4.80 | ||
| 0.35 | 7.311 | −42.55 | 5.680 | −22.31 | 6.988 | −4.42 | ||
| 0.40 | 9.178 | −54.24 | 7.584 | −17.38 | 8.845 | −3.63 | ||
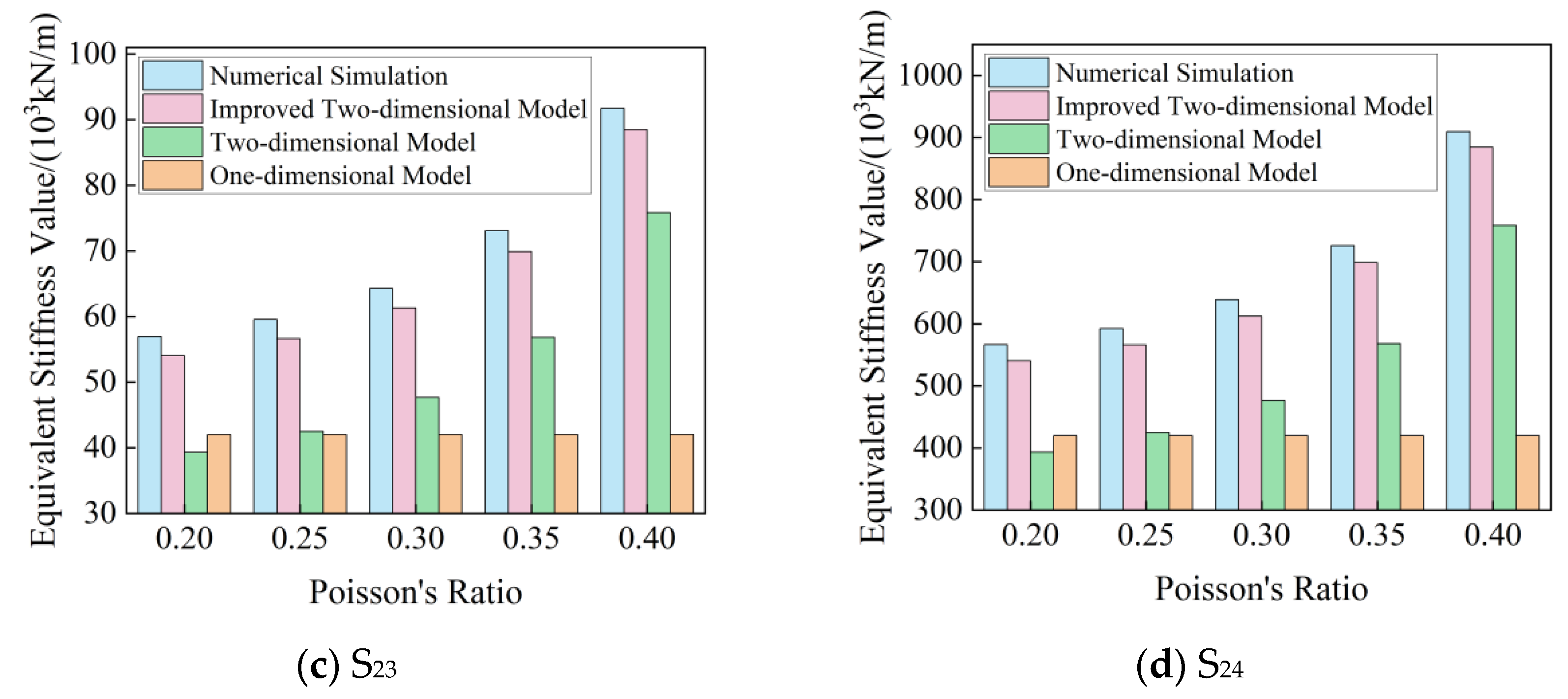
| S23 | 0.20 | 56.95 | 42.00 | −26.25 | 39.32 | −30.96 | 54.04 | −5.11 |
| 0.25 | 59.56 | −29.48 | 42.47 | −28.69 | 56.60 | −4.97 | ||
| 0.30 | 64.27 | −34.65 | 47.64 | −25.88 | 61.26 | −4.68 | ||
| 0.35 | 73.06 | −42.51 | 56.80 | −22.26 | 69.88 | −4.35 | ||
| 0.40 | 91.71 | −54.20 | 75.83 | −17.32 | 88.45 | −3.55 | ||
| S24 | 0.20 | 566.15 | 420.00 | −25.81 | 393.22 | −30.54 | 540.40 | −4.55 |
| 0.25 | 591.98 | −29.05 | 424.68 | −28.26 | 565.97 | −4.39 | ||
| 0.30 | 638.71 | −34.24 | 476.41 | −25.41 | 612.26 | −4.14 | ||
| 0.35 | 725.61 | −42.12 | 567.99 | −21.72 | 698.81 | −3.69 | ||
| 0.40 | 909.55 | −53.82 | 758.36 | −16.62 | 884.51 | −2.75 | ||
| Parameters | Equivalent Stiffness (103 kN/m) | |||||||
|---|---|---|---|---|---|---|---|---|
| S | Numerical Simulation | One- Dimensional | Error Rate (%) | Two- Dimensional | Error Rate (%) | Improved Two- Dimensional | Error Rate (%) | |
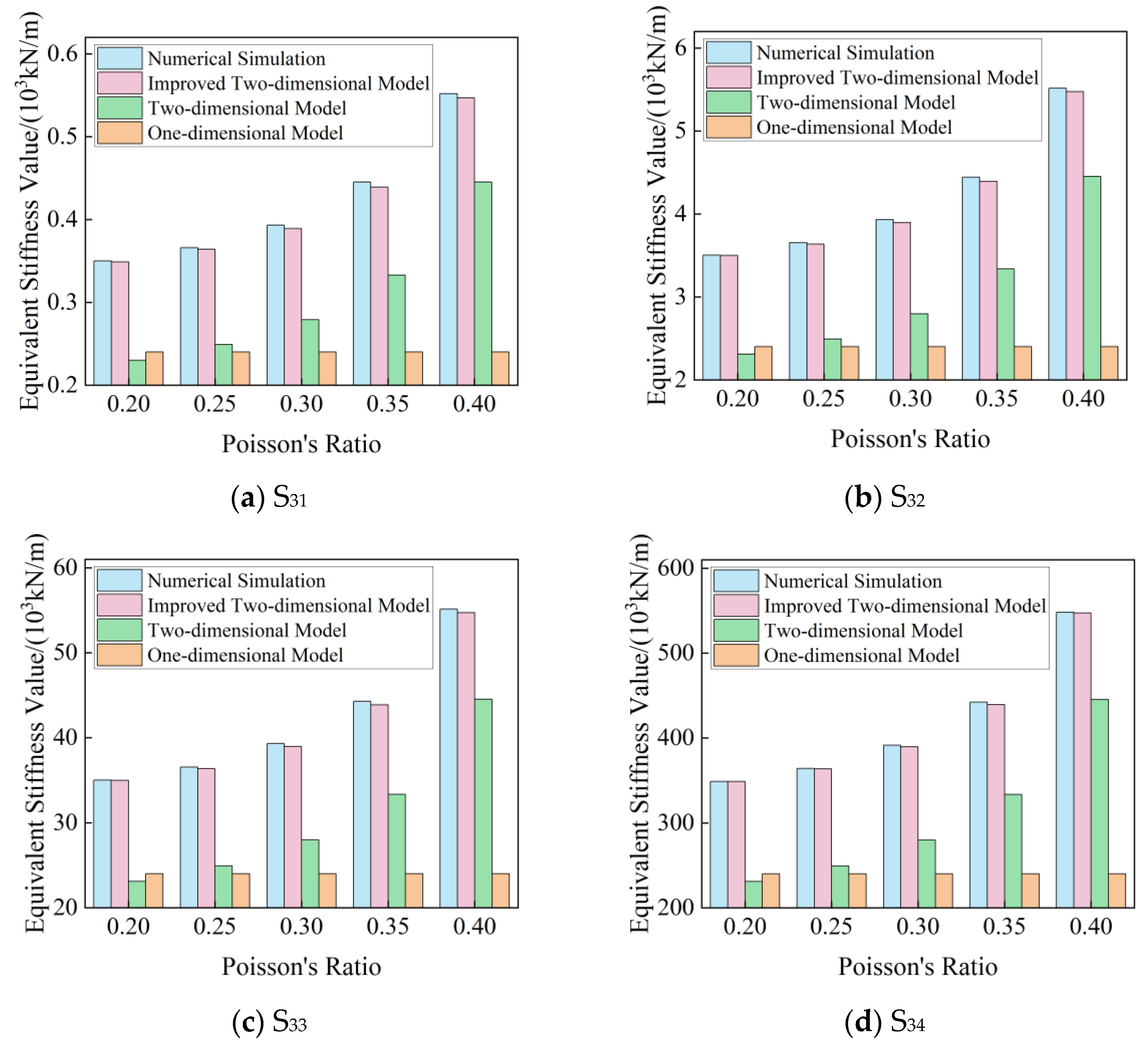
| S31 | 0.20 | 0.350 | 0.24 | −31.51 | 0.230 | −34.28 | 0.349 | −0.14 |
| 0.25 | 0.366 | −34.36 | 0.249 | −31.97 | 0.364 | −0.55 | ||
| 0.30 | 0.393 | −38.97 | 0.279 | −29.01 | 0.389 | −1.02 | ||
| 0.35 | 0.445 | −46.01 | 0.333 | −25.27 | 0.439 | −1.15 | ||
| 0.40 | 0.552 | −56.49 | 0.445 | −19.38 | 0.547 | −0.75 | ||
| S32 | 0.20 | 3.504 | 2.40 | −31.51 | 2.310 | −34.08 | 3.500 | −0.11 |
| 0.25 | 3.656 | −34.36 | 2.494 | −31.78 | 3.636 | −0.55 | ||
| 0.30 | 3.933 | −38.97 | 2.798 | −28.86 | 3.897 | −0.92 | ||
| 0.35 | 4.445 | −46.01 | 3.336 | −24.95 | 4.394 | −1.15 | ||
| 0.40 | 5.515 | −56.49 | 4.454 | −19.24 | 5.474 | −0.74 | ||
| S33 | 0.20 | 35.03 | 24.00 | −31.49 | 23.10 | −34.06 | 35.00 | −0.09 |
| 0.25 | 36.55 | −34.34 | 24.94 | −31.76 | 36.37 | −0.49 | ||
| 0.30 | 39.31 | −38.95 | 27.98 | −28.82 | 38.97 | −0.86 | ||
| 0.35 | 44.28 | −45.80 | 33.36 | −24.66 | 43.89 | −0.88 | ||
| 0.40 | 55.12 | −56.46 | 44.54 | −19.19 | 54.74 | −0.69 | ||
| S34 | 0.20 | 348.91 | 240.00 | −31.21 | 230.97 | −33.80 | 348.89 | −0.01 |
| 0.25 | 364.02 | −34.07 | 249.45 | −31.47 | 363.67 | −0.10 | ||
| 0.30 | 391.46 | −38.69 | 279.83 | −28.52 | 389.66 | −0.46 | ||
| 0.35 | 442.24 | −45.73 | 333.63 | −24.56 | 439.39 | −0.64 | ||
| 0.40 | 548.21 | −56.22 | 445.45 | −18.74 | 547.43 | −0.14 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, H.; Zhang, E.; Lu, G. Study on the Equivalent Stiffness of a Local Resonance Metamaterial Concrete Unit Cell. Buildings 2024, 14, 1035. https://doi.org/10.3390/buildings14041035
Zhao H, Zhang E, Lu G. Study on the Equivalent Stiffness of a Local Resonance Metamaterial Concrete Unit Cell. Buildings. 2024; 14(4):1035. https://doi.org/10.3390/buildings14041035
Chicago/Turabian StyleZhao, Haixiang, En Zhang, and Guoyun Lu. 2024. "Study on the Equivalent Stiffness of a Local Resonance Metamaterial Concrete Unit Cell" Buildings 14, no. 4: 1035. https://doi.org/10.3390/buildings14041035





