Precision of Measurements of Delayed Slip in Structural High-Strength Assemblies by Contact and Optical Methods
Abstract
:1. Introduction
2. Measuring Methods
2.1. LVDT
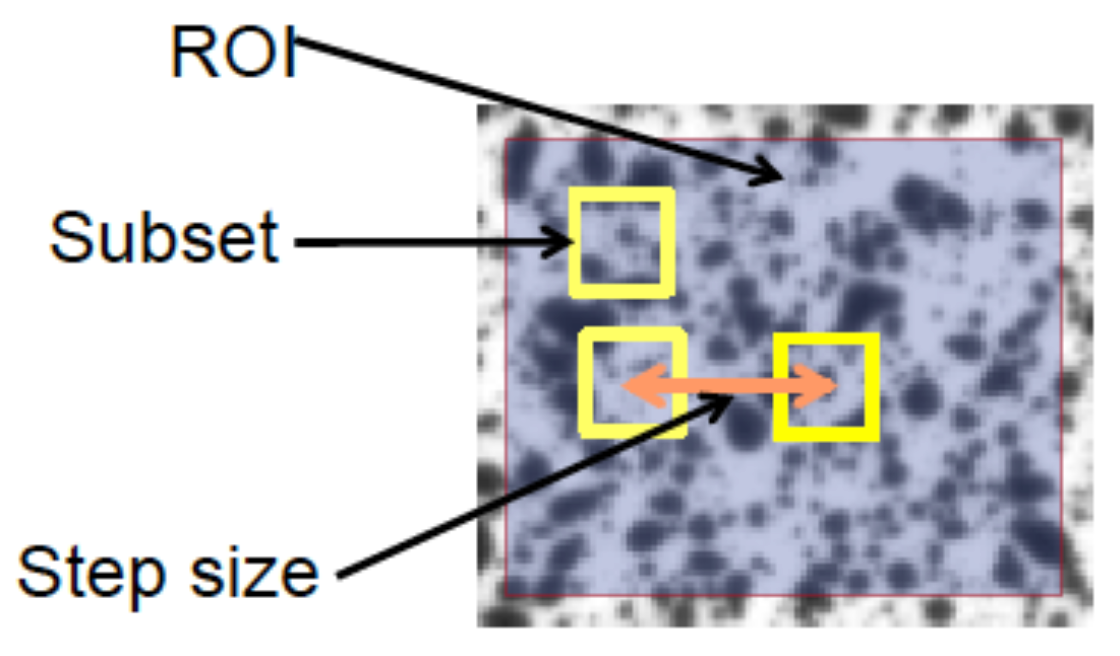
2.2. Digital Image Correlation
3. Experimental Test
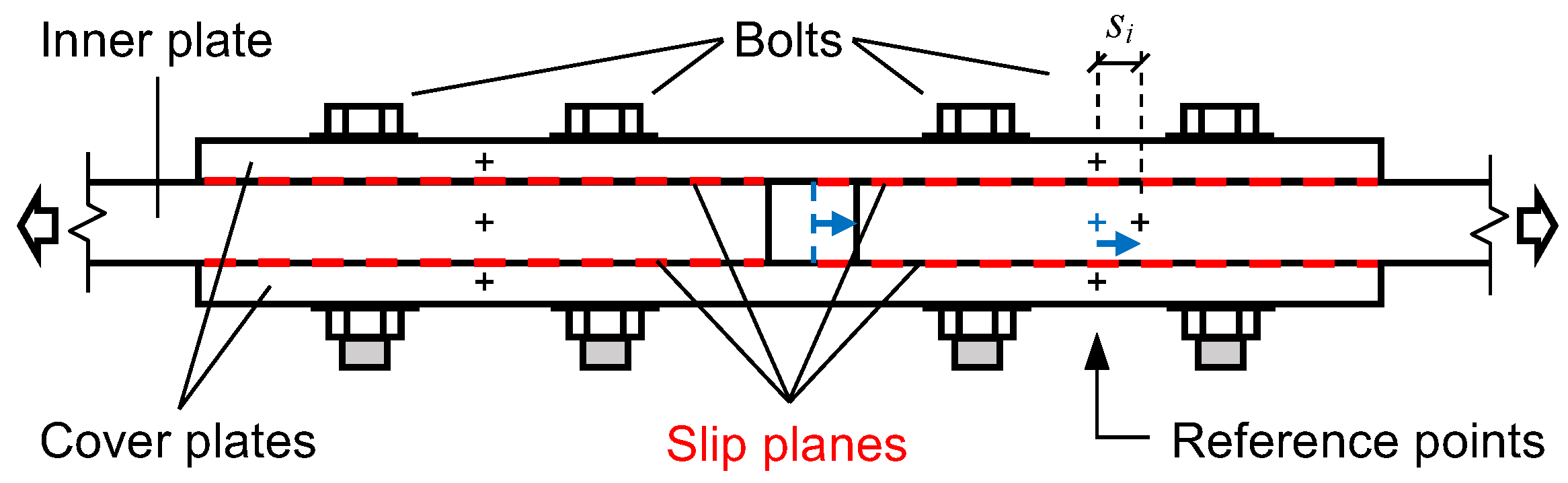
3.1. Specimen
3.2. Slip Measurements
3.2.1. LVDT
3.2.2. DIC
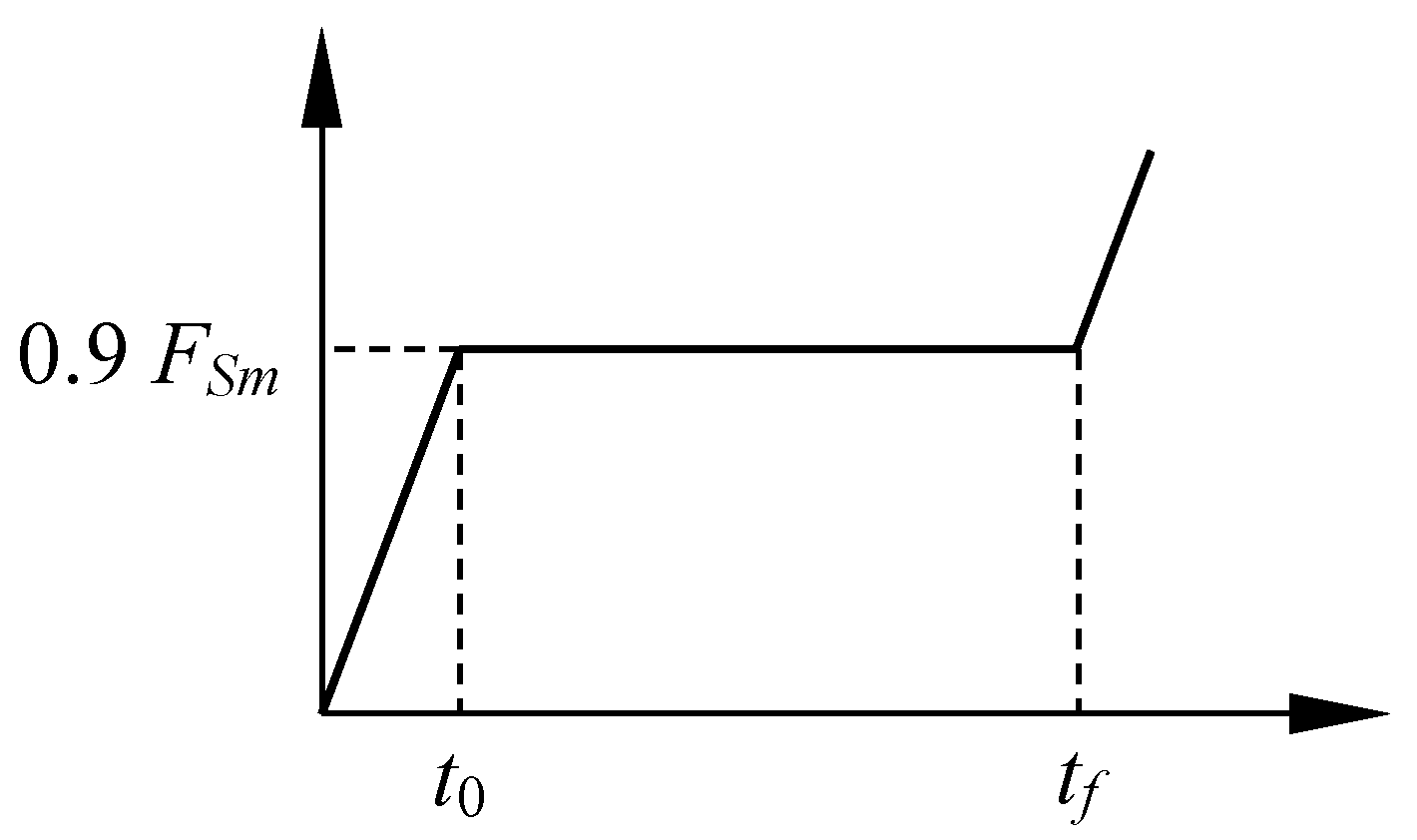
3.3. Experimental Procedure
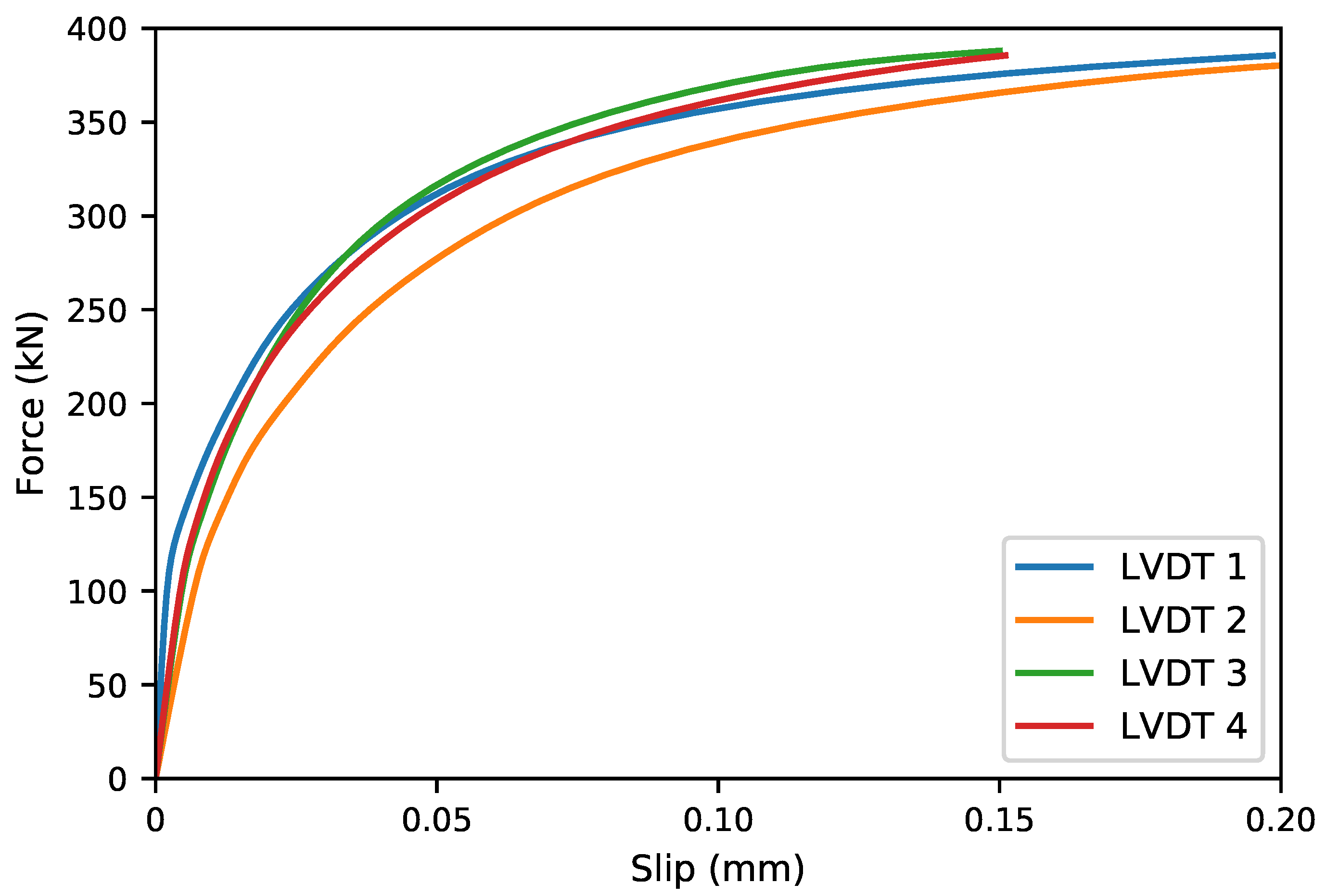
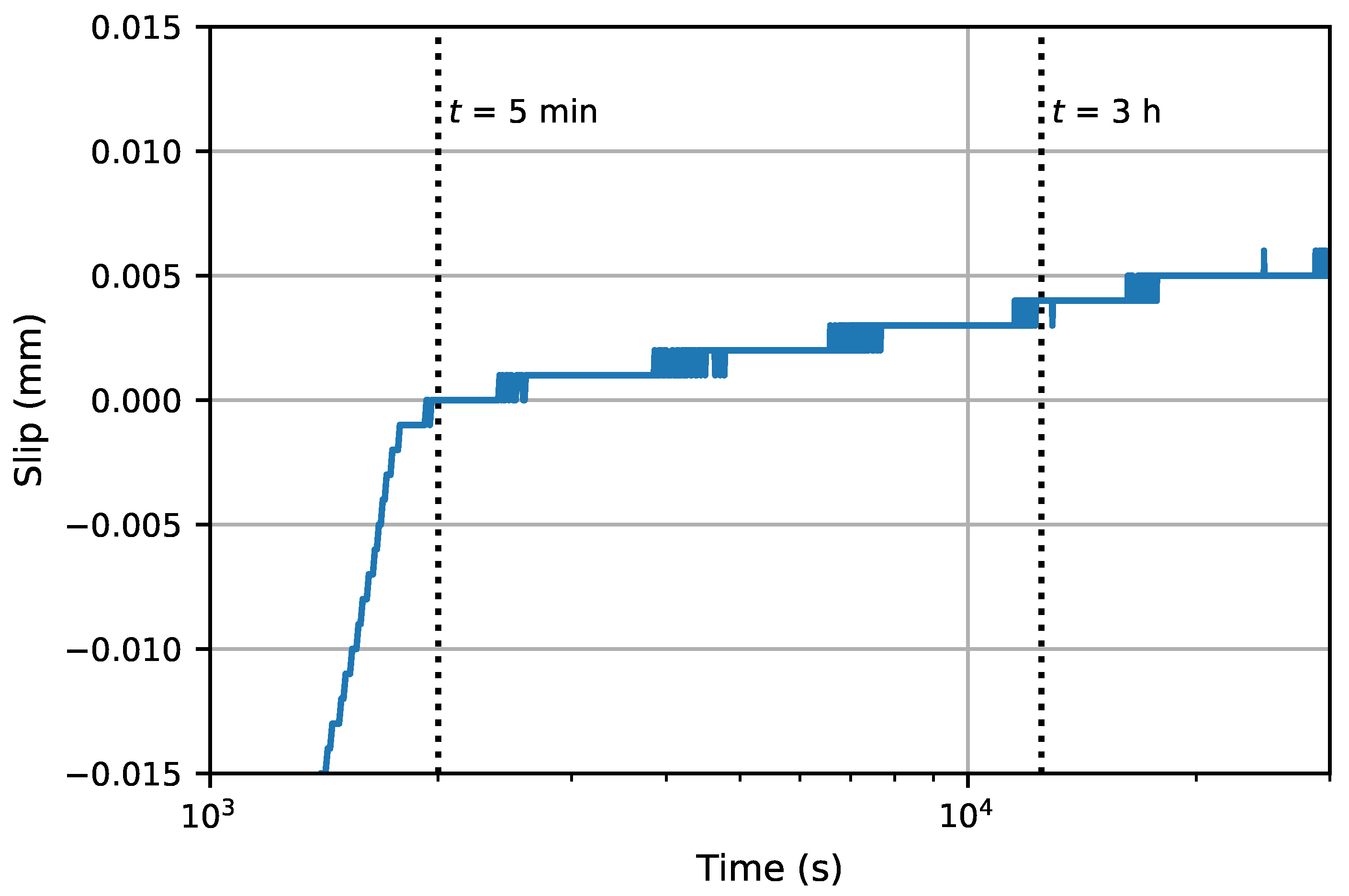
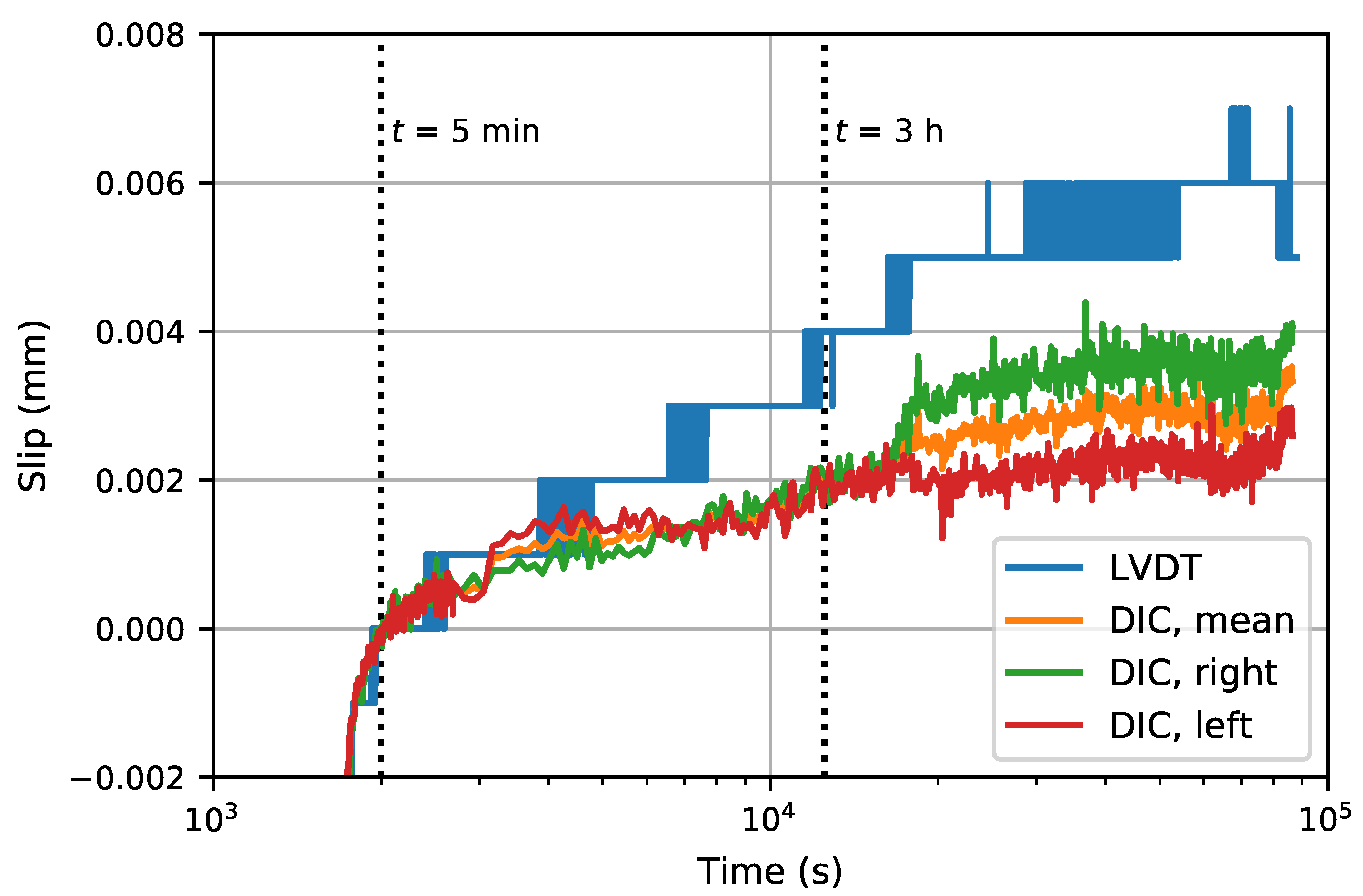
4. Results
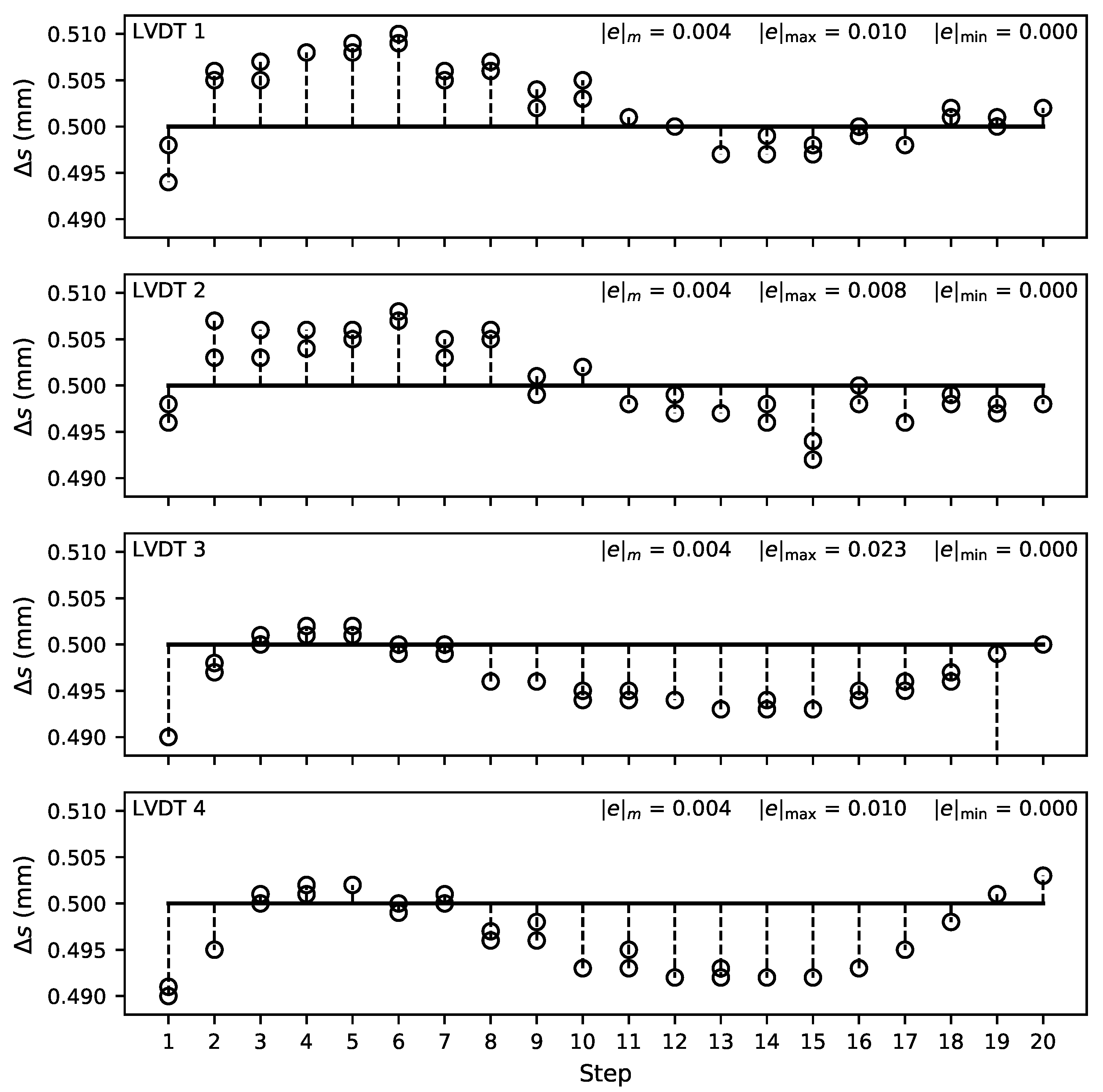
4.1. LVDT Measurement
4.2. DIC Measurement
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Connor, J.J.; Faraji, S. Fundamentals of Structural Engineering, 2nd ed.; Springer: Cham, Switzerland, 2016. [Google Scholar] [CrossRef]
- EN 1090-2:2018; Execution of Steel Structures and Aluminium Structures—Part 2: Technical Requirements for Steel Structures. CEN: Brussels, Belgium, 2018.
- Stranghöner, N.; Afzali, N.; de Vries, P.; Glienke, R.; Ebert, A. Optimization of the test procedure for slip factor tests according to EN 1090-2. Steel Constr. 2017, 10, 267–281. [Google Scholar] [CrossRef]
- Cruz, A.; Simões, R.; Alves, R. Slip factor in slip resistant joints with high strength steel. J. Constr. Steel Res. 2012, 70, 280–288. [Google Scholar] [CrossRef]
- Chen, G.; Zhang, B.; Liu, P.; Ding, H. An Adaptive Analog Circuit for LVDT’s Nanometer Measurement without Losing Sensitivity and Range. IEEE Sens. J. 2015, 15, 2248–2254. [Google Scholar] [CrossRef]
- Felipe-Sesé, L.; Molina-Viedma, A.J.; Pastor-Cintas, M.; López-Alba, E.; Díaz, F.A. Exploiting phase-based motion magnification for the measurement of subtle 3D deformation maps with FP+2D-DIC. Measurement 2022, 195, 111122. [Google Scholar] [CrossRef]
- Shao, Y.; Li, L.; Li, J.; An, S.; Hao, H. Target-free 3D tiny structural vibration measurement based on deep learning and motion magnification. J. Sound Vib. 2022, 538, 117244. [Google Scholar] [CrossRef]
- Scislo, L. Single-Point and Surface Quality Assessment Algorithm in Continuous Production with the Use of 3D Laser Doppler Scanning Vibrometry System. Sensors 2023, 23, 1263. [Google Scholar] [CrossRef]
- Peters, W.H.; Ranson, W.F. Digital imaging techniques in experimental stress-analysis. Opt. Eng. 1982, 21, 427–431. [Google Scholar] [CrossRef]
- Sutton, M.A.; Wolters, W.J.; Peters, W.H.; Ranson, W.F.; McNeill, S.R. Determination of displacements using an improved digital correlation method. Image Vis. Comput. 1983, 1, 133–139. [Google Scholar] [CrossRef]
- Chu, T.C.; Ranson, W.F.; Sutton, M.A.; Peters, W.H. Applications of Digital-Image-Correlation techniques to experimental mechanics. Exp. Mech. 1985, 25, 232–244. [Google Scholar] [CrossRef]
- Sutton, M.A.; Orteu, J.J.; Schreier, H. Image Correlation for Shape, Motion and Deformation Measurements. Basic Concepts, Theory and Applications; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Gencturk, B.; Hossain, K.; Kapadia, A.; Labib, E.; Mo, Y.L. Use of digital image correlation technique in full-scale testing of prestressed concrete structures. Measurement 2014, 47, 505–515. [Google Scholar] [CrossRef]
- Hild, F.; Roux, S. Comparison of local and global approaches to Digital Image Correlation. Exp. Mech. 2012, 52, 1503–1519. [Google Scholar] [CrossRef]
- Pan, K.; Yu, R.C.; Ruiz, G.; Zhang, X.X.; Wu, Z.; de la Rosa, A. The propagation speed of multiple dynamic cracks in fiber-reinforced cement-based composites measured using DIC. Cem. Concr. Compos. 2021, 122, 104140. [Google Scholar] [CrossRef]
- Lu, H.; Cary, P.D. Deformation measurements by digital image correlation: Implementation of a second-order displacement gradient. Exp. Mech. 2000, 40, 393–400. [Google Scholar] [CrossRef]
- Reu, P.L. A realistic error budget for two dimension Digital Image Correlation. In Advancement of Optical Methods in Experimental Mechanics; Conference Proceedings of the Society for Experimental Mechanics Series; Jin, H., Yoshida, S., Lamberti, L., Lin, M.T., Eds.; Springer: Cham, Switzerland, 2016; Volume 3, Chapter 24; pp. 189–193. [Google Scholar] [CrossRef]
- Réthoré, J.; Hild, F.; Roux, S. Shear-band capturing using a multiscale extended digital image correlation technique. Comput. Methods Appl. Mech. Eng. 2007, 196, 5016–5030. [Google Scholar] [CrossRef]
- de Crevoisier, J.; Swiergiel, N.; Champaney, L.; Hild, F. Identification of in situ frictional properties of bolted assemblies with digital image correlation. Exp. Mech. 2012, 52, 561–572. [Google Scholar] [CrossRef]
- Lacey, A.W.; Chen, W.; Hao, H.; Bi, K. Experimental and numerical study of the slip factor for G350-steel bolted connections. J. Constr. Steel Res. 2019, 158, 576–590. [Google Scholar] [CrossRef]
- ISO 5725-1:1994; Accuracy (Trueness and Precision) of Measurement Methods and Results—Part 1: General Principles and Definitions. ISO: Geneva, Switzerland, 2018.
- Menditto, A.; Patriarca, M.; Magnusson, B. Understanding the meaning of accuracy, trueness and precision. Accredit. Qual. Assur. 2007, 12, 45–47. [Google Scholar] [CrossRef]
- Jones, E.M.C.; Iadicola, M.A. (Eds.) A Good Practices Guide for Digital Image Correlation; International Digital Image Correlation Society: Boston, MA, USA, 2018. [Google Scholar] [CrossRef]
- Tian, Q.; Huhns, M.N. Algorithms for subpixel registration. Comput. Vis. Graph. Image Process. 1986, 35, 220–233. [Google Scholar] [CrossRef]
- Schreier, H.W.; Sutton, M.A. Systematic errors in digital image correlation due to undermatched subset shape functions. Exp. Mech. 2002, 42, 303–310. [Google Scholar] [CrossRef]
- Luu, L.; Wang, Z.; Vo, M.; Hoang, T.; Ma, J. Accuracy enhancement of digital image correlation with B-spline interpolation. Opt. Lett. 2011, 36, 3070–3072. [Google Scholar] [CrossRef]
- HajiRassouliha, A.; Taberner, A.J.; Nash, M.P.; Nielsen, P.M.F. Subpixel phase-based image registration using Savitzky-Golay differentiators in gradient-correlation. Comput. Vis. Image Underst. 2018, 170, 28–39. [Google Scholar] [CrossRef]
- Barranger, Y.; Doumalin, P.; Dupré, J.C.; Germaneau, A. Digital Image Correlation accuracy: Influence of kind of speckle and recording setup. In Proceedings of the ICEM 14: 14th International Conference on Experimental Mechanics, Poitiers, France, 4–9 July 2010; EPJ Web of Conferences. Bremand, F., Ed.; EDP Sciences: Les Ulis, France, 2010; Volume 6, p. 31002. [Google Scholar] [CrossRef]
- Bomarito, G.F.; Hochhalter, J.D.; Ruggles, T.J.; Cannon, A.H. Increasing accuracy and precision of digital image correlation through pattern optimization. Opt. Lasers Eng. 2017, 91, 73–85. [Google Scholar] [CrossRef]
- Pan, B.; Yu, L.; Wu, D. High-Accuracy 2D Digital Image Correlation Measurements with Bilateral Telecentric Lenses: Error Analysis and Experimental Verification. Exp. Mech. 2013, 53, 1719–1733. [Google Scholar] [CrossRef]
- Reis, M.; Adorna, M.; Jirousek, O.; Jung, A. Improving DIC accuracy in experimental setups. Adv. Eng. Mater. 2019, 21, 1900092. [Google Scholar] [CrossRef]
- Pan, B.; Li, K. A fast digital image correlation method for deformation measurement. Opt. Lasers Eng. 2011, 49, 841–847. [Google Scholar] [CrossRef]
- Pan, B.; Li, K.; Tong, W. Fast, robust and accurate Digital Image Correlation calculation without redundant computations. Exp. Mech. 2013, 53, 1277–1289. [Google Scholar] [CrossRef]
- Reu, P.L.; Toussaint, E.; Jones, E.; Bruck, H.A.; Iadicola, M.; Balcaen, R.; Turner, D.Z.; Siebert, T.; Lava, P.; Simonsen, M. DIC Challenge: Developing images and guidelines for evaluating accuracy and resolution of 2D analyses. Exp. Mech. 2018, 58, 1067–1099. [Google Scholar] [CrossRef]
- Reu, P.L.; Toussaint, E.; Jones, E.; Bruck, H.; Iadicola, M.; Balcaen, R.; Turner, D.; Siebert, T.; Lava, P.; Simonsen, M.; et al. Update on the 2D-DIC Challenge: Results and Conclusions. In Advancement of Optical Methods & Digital Image Correlation in Experimental Mechanics, Volume 3; Lamberti, L., Lin, M.T., Furlong, C., Sciammarella, C., Reu, P.L., Sutton, M.A., Eds.; Conference Proceedings of the Society for Experimental Mechanics Series; Springer: Berlin/Heidelberg, Germany, 2019; pp. 81–84. [Google Scholar] [CrossRef]
- Dupré, J.C.; Doumalin, P.; Husseini, H.A.; Germaneau, A.; Bremand, F. Displacement discontinuity or complex shape of sample: Assessment of accuracy and adaptation of local DIC approach. Strain 2015, 51, 391–404. [Google Scholar] [CrossRef]



| Precision | Full Range (± Full Scale) [mm] | |||
|---|---|---|---|---|
| 1 (±0.5) | 2 (±1) | 5 (±2.5) | 10 (±5) | |
| 0.10% | 0.001 | 0.002 | 0.005 | 0.01 |
| 0.25% | 0.0025 | 0.005 | 0.0125 | 0.025 |
| 0.50% | 0.005 | 0.01 | 0.025 | 0.05 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ortega, J.J.; Pan, K.; Ruiz, G.; Zhang, X. Precision of Measurements of Delayed Slip in Structural High-Strength Assemblies by Contact and Optical Methods. Buildings 2024, 14, 1046. https://doi.org/10.3390/buildings14041046
Ortega JJ, Pan K, Ruiz G, Zhang X. Precision of Measurements of Delayed Slip in Structural High-Strength Assemblies by Contact and Optical Methods. Buildings. 2024; 14(4):1046. https://doi.org/10.3390/buildings14041046
Chicago/Turabian StyleOrtega, José Joaquín, Kaiming Pan, Gonzalo Ruiz, and Xiaoxin Zhang. 2024. "Precision of Measurements of Delayed Slip in Structural High-Strength Assemblies by Contact and Optical Methods" Buildings 14, no. 4: 1046. https://doi.org/10.3390/buildings14041046
APA StyleOrtega, J. J., Pan, K., Ruiz, G., & Zhang, X. (2024). Precision of Measurements of Delayed Slip in Structural High-Strength Assemblies by Contact and Optical Methods. Buildings, 14(4), 1046. https://doi.org/10.3390/buildings14041046







