Improved FEM Natural Frequency Calculation for Structural Frames by Local Correction Procedure
Abstract
:1. Introduction
2. Natural Frequency Analysis of Some Fundamental Cases Using One Element Per Bar
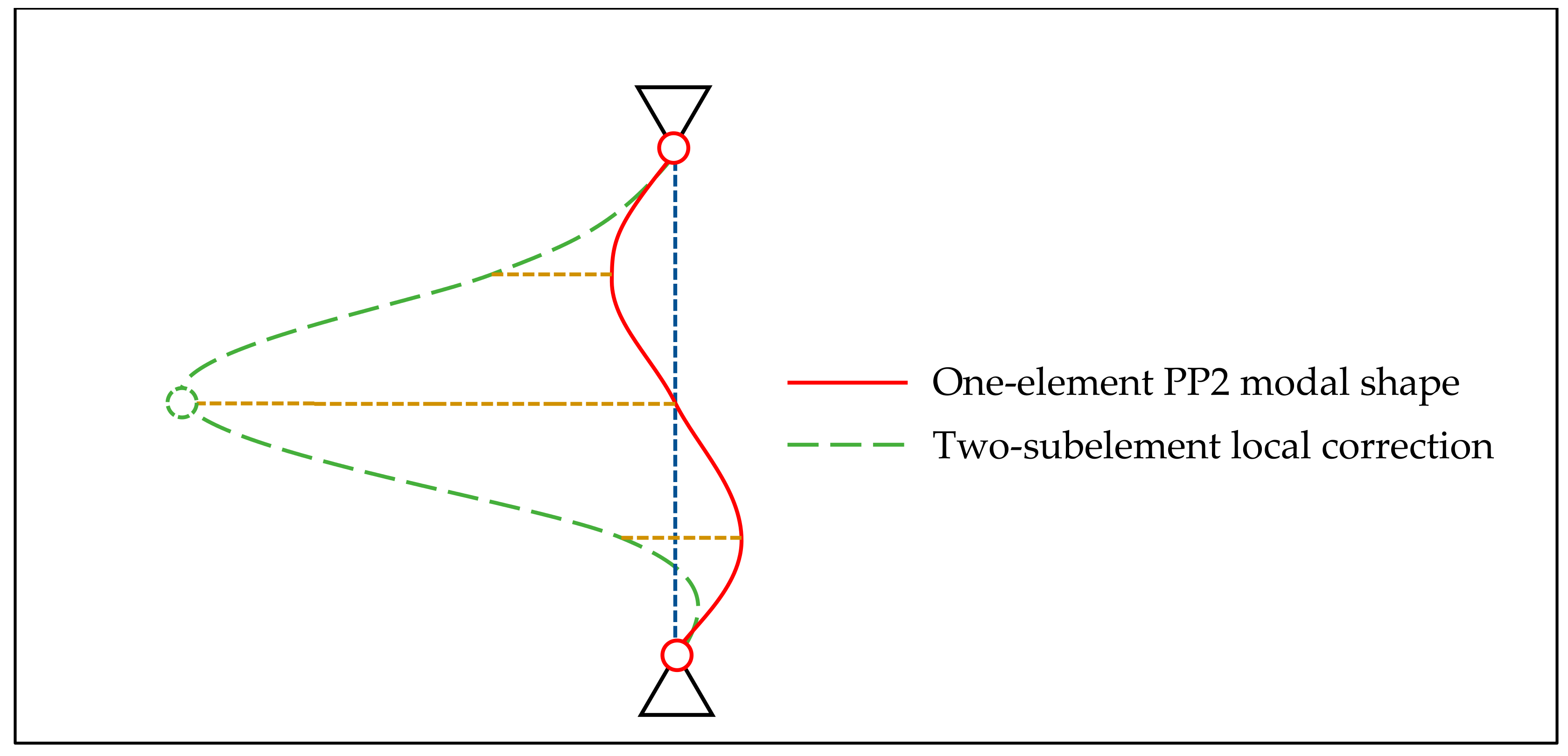
3. Corrected Calculation of Natural Frequencies in Some Fundamental Cases Using One Element Per Bar
| Algorithm 1. Correction of the natural frequency of a one-element bar |
| Evaluate and as 2-subelement refinements of and using Equation (3) |
| Evaluate the projection matrix P with Equation (8) |
| Calculate as the lowest natural frequency in Equation (9) |
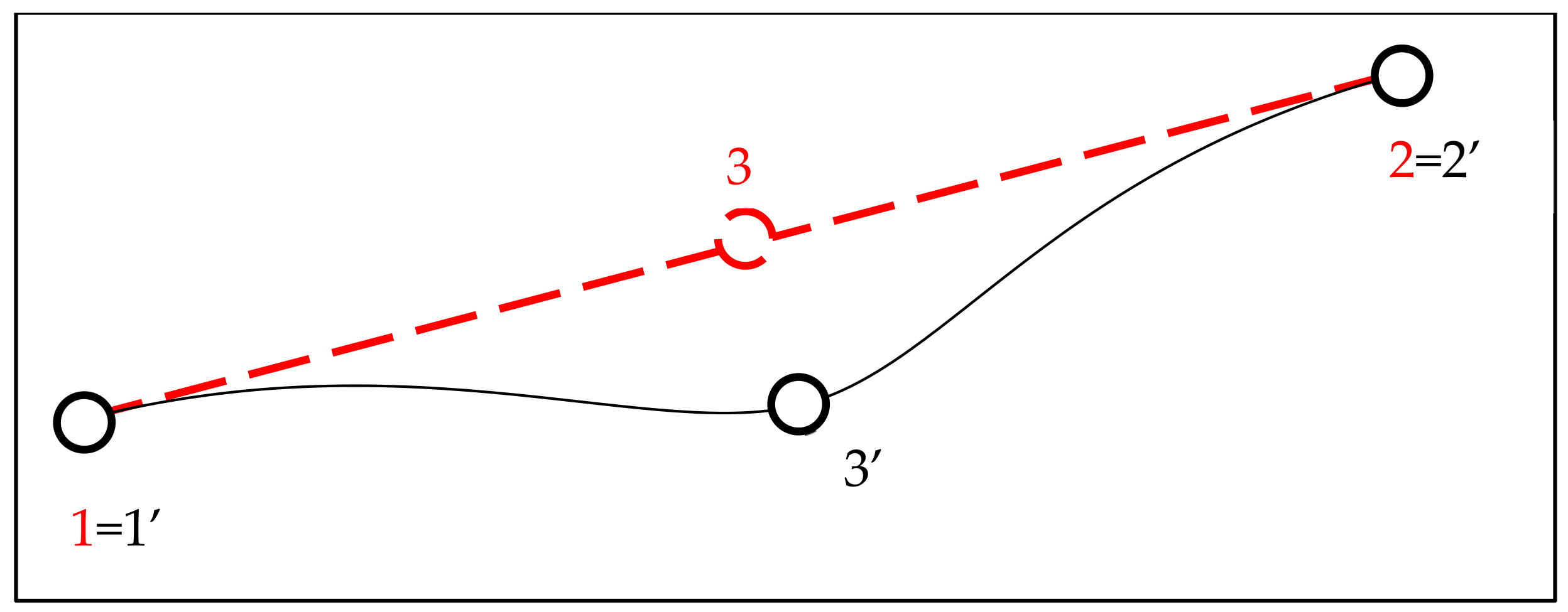
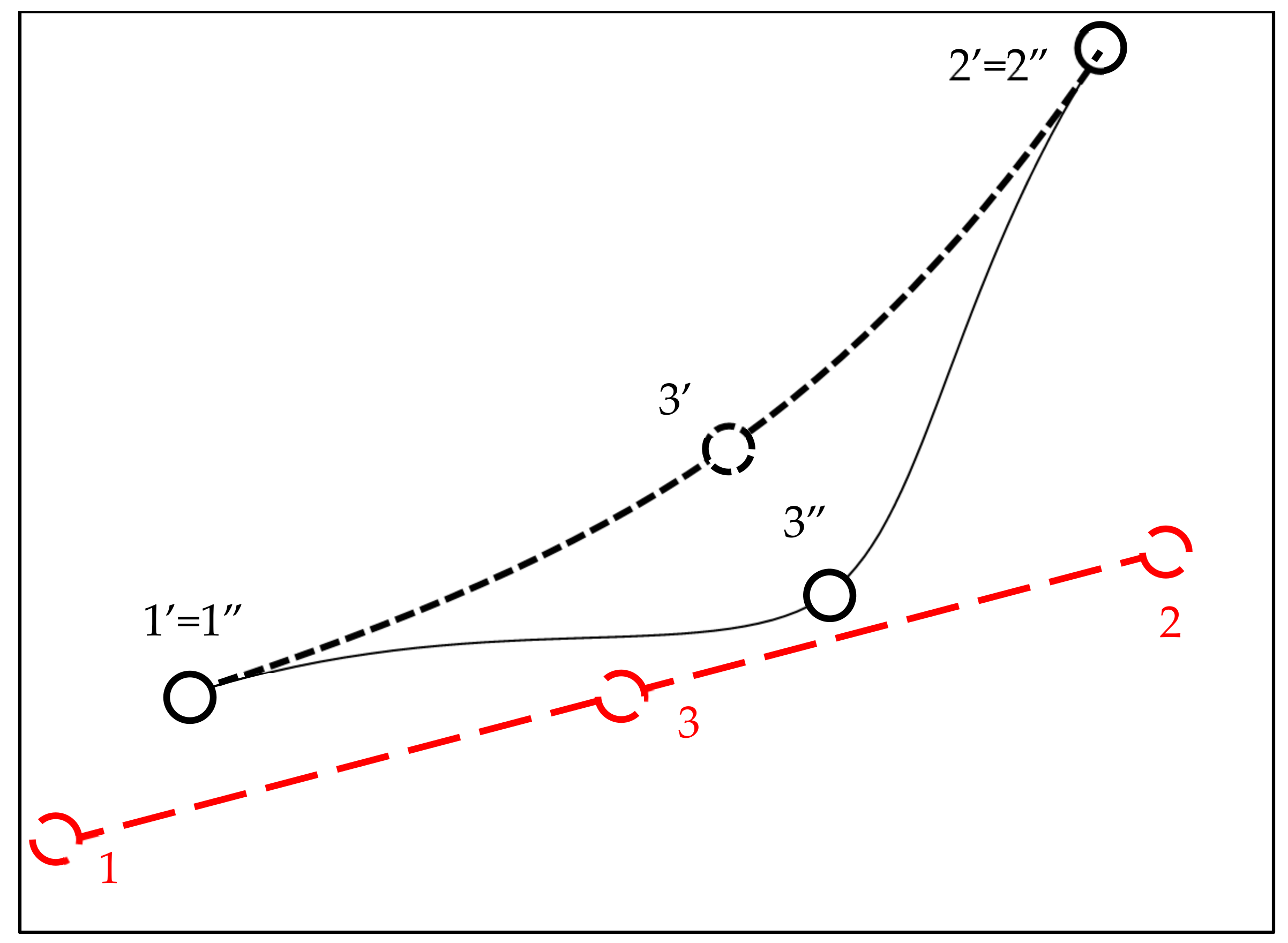
4. Correction of Natural Frequencies for Multiple-Element Structures
- The local element corrections can be combined additively into an overall modal correction.
- When calculating local corrections for an element, the rest of the structure can be sufficiently represented by the frame modal shape and an amplitude variable .
- The corrected natural frequency for the whole frame can be calculated using Rayleigh’s quotient with the corrected modal shape.
- Local corrections for different natural frequencies can be calculated in isolation from each other once the distortion factor has been introduced to solve the override problem.
| Algorithm 2. Computation of the corrected quadratic forms of an element and |
| Overall frame inputs: , Frame element inputs: , , |
| Subelement inputs: |
| Evaluate and as 2-subelement refinements of and using Equation (3) |
| Convert to local element coordinates by the following operations: (: element rotation matrix) |
| Calculate , in Equations (6) and (19) |
| Calculate , in Equations (17) and (18) |
| Obtain as the first eigenvector of Equation (16) |
| Evaluate , by applying Equations (24)–(26) |
| Algorithm 3. Computation of N corrected natural frequencies of whole frame |
| Receive as inputs frame magnitudes , , , , For all elements, receive as inputs one-element magnitudes , , |
| For , , For e = 1.. number of elements , Calculate , with Algorithm 2 End |
| Calculate with Equation (27) Calculate element distortion factor: End If > 100% in an element, split it in half and repeat |
- Axial displacements can be eliminated from the correction procedure on account of their higher stiffness [37].
- In most cases exactly or approximately and needs not be calculated.
- can often be calculated explicitly as a linear expression, and consequently, Equation (6) is unnecessary.
- Equations (17), (18), (25) and (26) can be easily programmed with scalar operations in terms of their constituent parts thereby avoiding matrix/vector operations.
- Using all of the above, the main component of the computational cost is the solution of the local eigenvalue problem which can be obtained with a few iterations of the power method.
5. Results
5.1. 2D Building Portal Frame
5.2. 3D Stand Structure
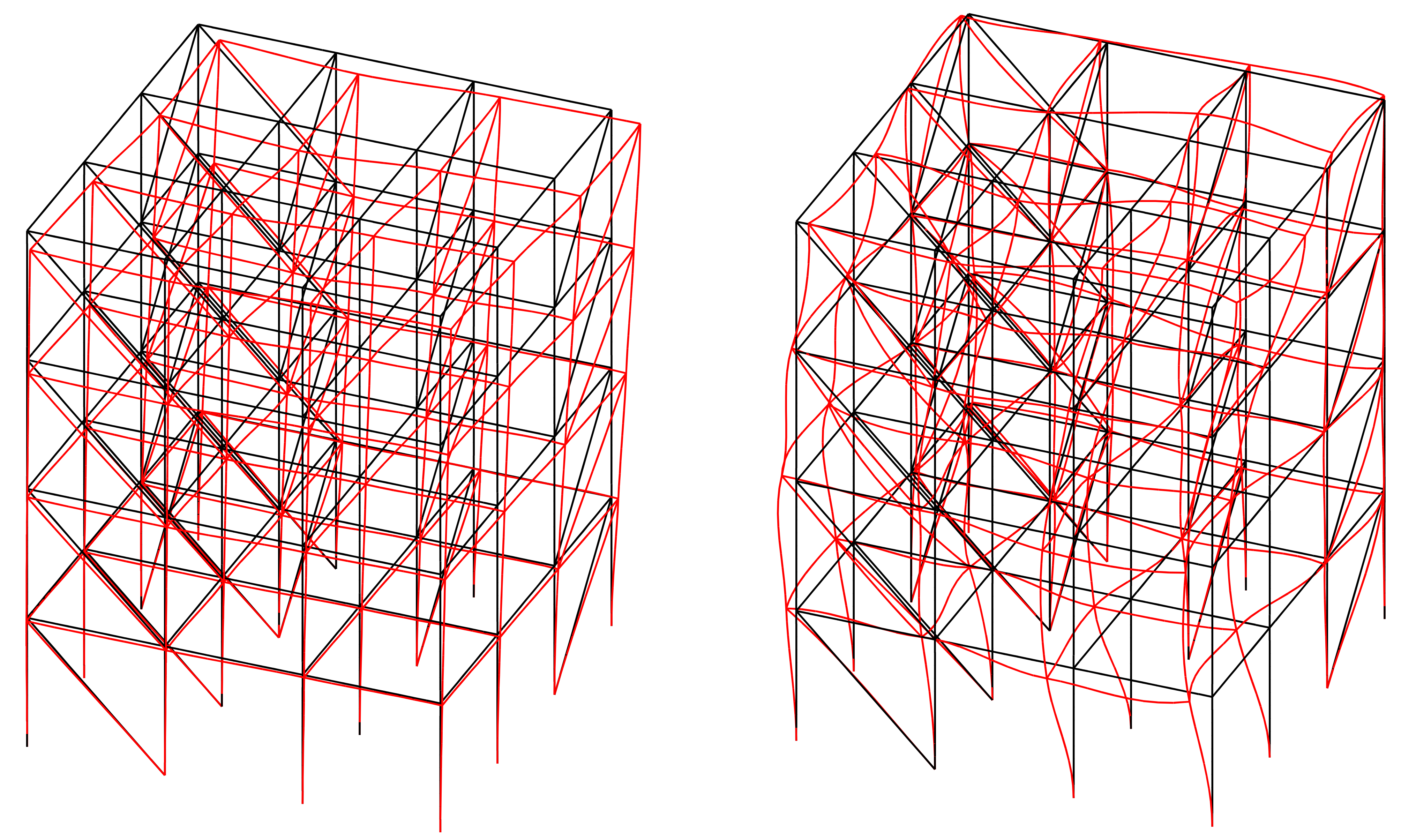
5.3. 3D Building Structure
6. Discussion
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chopra, A.K. Dynamics of Structures: Theory and Applications to Earthquake Engineering, 6th ed.; Pearson: London, UK, 2023. [Google Scholar]
- Spanish Structural Code (Código Estructural); Spanish Ministry of Transport, Mobility and the Urban Agenda (Ministerio de Transportes, Movilidad y Agenda Urbana): Madrid, Spain, 2021.
- EN1993-1-1; Eurocode 3: Design of Steel Structures. European Committee for Standardization: Brussels, Belgium, 2005.
- Staff, American Society of Civil Engineers (ASCE). Minimum Design Loads for Buildings and Other Structures, 3rd ed.; American Society of Civil Engineers: Reston, VA, USA, 2013. [Google Scholar]
- Biswas, P.; Peronto, J. Design and Performance of Tall Buildings for Wind, 1st ed.; American Society of Civil Engineers (ASCE): Reston, VA, USA, 2020. [Google Scholar]
- Petyt, M. Introduction to Finite Element Vibration Analysis, 2nd ed.; Cambridge University Press: Cambridge, UK, 2015. [Google Scholar]
- Zienkiewicz, O.C.; Taylor, R.L.; Zhu, J.Z. The Finite Element Method: Its Basis and Fundamentals; Butterworth-Heinemann: Cambridge, UK, 2013; Volume 3. [Google Scholar]
- Xie, Y.M.; Steven, G.P. Improving finite element predictions of buckling loads of beams and frames. Comput. Struct. 1994, 52, 381–385. [Google Scholar] [CrossRef]
- Mackie, R.I. Improving finite element predictions of modes of vibration. Int. J. Numer. Methods Eng. 1992, 33, 333–344. [Google Scholar] [CrossRef]
- Xie, Y.M.; Steven, G.P. Explicit formulas for correcting finite-element predictions of natural frequencies. Commun. Numer. Methods Eng. 1993, 9, 671–680. [Google Scholar] [CrossRef]
- Babuška, I.; Rheinboldt, W.C. A-posteriori error estimates for the finite element method. Int. J. Numer. Methods Eng. 1978, 12, 1597–1615. [Google Scholar] [CrossRef]
- Babuška, I. Accuracy Estimates and Adaptive Refinements in Finite Element Computations; Wiley: Chichester, UK, 1986. [Google Scholar]
- Zienkiewicz, O.C.; Zhu, J.Z. The superconvergent patch recovery (SPR) and adaptive finite element refinement. Comput. Methods Appl. Mech. Eng. 1992, 101, 207–224. [Google Scholar] [CrossRef]
- Boroomand, B.; Zienkiewicz, O.C. Recovery by equilibrium in patches (REP). Int. J. Numer. Methods Eng. 1997, 40, 137–164. [Google Scholar] [CrossRef]
- Sun, H.; Yuan, S. An improved local error estimate in adaptive finite element analysis based on element energy projection technique. Eng. Comput. 2023, 40, 246–264. [Google Scholar] [CrossRef]
- Wiberg, N.-E.; Abdulwahab, F.; Ziukas, S. Improved element stresses for node and element patches using superconvergent patch recovery. Commun. Numer. Methods Eng. 1995, 11, 619–627. [Google Scholar] [CrossRef]
- Wiberg, N.; Abdulwahab, F. Patch recovery based on superconvergent derivatives and equilibrium. Int. J. Numer. Methods Eng. 1993, 36, 2703–2724. [Google Scholar] [CrossRef]
- Wiberg, N.; Bausys, R.; Hager, P. Improved eigenfrequencies and eigenmodes in free vibration analysis. Comput. Struct. 1999, 73, 79–89. [Google Scholar] [CrossRef]
- Liu, G.R. A generalized gradient smoothing technique and the smoothed bilinear form for Galerkin formulation of a wide class of computational methods. Int. J. Comput. Methods 2008, 5, 199–236. [Google Scholar] [CrossRef]
- Liu, G.R. On G space theory. Int. J. Comput. Methods 2009, 6, 257–289. [Google Scholar] [CrossRef]
- Liu, G.R.; Nguyen-Thoi, T.; Nguyen-Xuan, H.; Lam, K.Y. A node-based smoothed finite element method (NS-FEM) for upper bound solutions to solid mechanics problems. Comput. Struct. 2009, 87, 14–26. [Google Scholar] [CrossRef]
- Liu, G.R.; Nguyen-Thoi, T.; Lam, K.Y. An edge-based smoothed finite element method (ES-FEM) for static, free and forced vibration analyses of solids. J. Sound Vib. 2009, 320, 1100–1130. [Google Scholar] [CrossRef]
- Zienkiewicz, O.C.; De, S.R.; Gago, J.P.; Kelly, D.W. The hierarchical concept in finite element analysis. Comput. Struct. 1983, 16, 53–65. [Google Scholar] [CrossRef]
- Ganesan, N.; Engels, R.C. Hierarchical Bernoulli-Euler beam finite elements. Comput. Struct. 1992, 43, 297–304. [Google Scholar] [CrossRef]
- Tai, C.-Y.; Chan, Y.J. A hierarchic high-order Timoshenko beam finite element. Comput. Struct. 2016, 165, 48–58. [Google Scholar] [CrossRef]
- Hui, Y.; Giunta, G.; Belouettar, S.; Huang, Q.; Hu, H.; Carrera, E. A free vibration analysis of three-dimensional sandwich beams using hierarchical one-dimensional finite elements. Compos. Part B Eng. 2017, 110, 7–19. [Google Scholar] [CrossRef]
- Fried, I.; Chavez, M. Superaccurate finite element eigenvalue computation. J. Sound Vib. 2004, 275, 415–422. [Google Scholar] [CrossRef]
- Fried, I.; Leong, K. Superaccurate finite element eigenvalues via a Rayleigh quotient correction. J. Sound Vib. 2005, 288, 375–386. [Google Scholar] [CrossRef]
- Li, E.; He, Z.C. Development of a perfect match system in the improvement of eigenfrequencies of free vibration. Appl. Math. Model. 2017, 44, 614–639. [Google Scholar] [CrossRef]
- Guddati, M.N.; Yue, B. Modified integration rules for reducing dispersion error in finite element methods. Comput. Methods Appl. Mech. Eng. 2004, 193, 275–287. [Google Scholar] [CrossRef]
- Shang, H.Y.; Machado, R.D.; Abdalla Filho, J.E. Dynamic analysis of Euler–Bernoulli beam problems using the Generalized Finite Element Method. Comput. Struct. 2016, 173, 109–122. [Google Scholar] [CrossRef]
- Hsu, Y.S. Enriched finite element methods for Timoshenko beam free vibration analysis. Appl. Math. Model. 2016, 40, 7012–7033. [Google Scholar]
- Cornaggia, R.; Darrigrand, E.; Le Marrec, L.; Mahé, F. Enriched finite elements and local rescaling for vibrations of axially inhomogeneous Timoshenko beams. J. Sound Vib. 2020, 474, 115228. [Google Scholar] [CrossRef]
- Necib, B.; Sun, C.T. Analysis of truss beams using a high order Timoshenko beam finite element. J. Sound Vib. 1989, 130, 149–159. [Google Scholar] [CrossRef]
- Wang, T.; Mikkola, A.; Matikainen, M.K. An Overview of Higher-Order Beam Elements Based on the Absolute Nodal Coordinate Formulation. J. Comput. Nonlinear Dynam. 2022, 17, 091001. [Google Scholar] [CrossRef]
- Nguyen, T.; Nguyen, N.; Lee, J.; Nguyen, Q. Vibration analysis of thin-walled functionally graded sandwich beams with non-uniform polygonal cross-sections. Compos. Struct. 2021, 278, 114723. [Google Scholar] [CrossRef]
- Urruzola, J.; Garmendia, I. Calculation of Linear Buckling Load for Frames Modeled with One-Finite-Element Beams and Columns. Computation 2023, 11, 109. [Google Scholar] [CrossRef]
- Meirovitch, L. Fundamentals of Vibrations; McGraw-Hill: New York, NY, USA, 2001. [Google Scholar]
- Luo, J.; Huang, M.; Lei, Y. Temperature Effect on Vibration Properties and Vibration-Based Damage Identification of Bridge Structures: A Literature Review. Buildings 2022, 12, 1209. [Google Scholar] [CrossRef]
- Huang, M.; Zhang, J.; Hu, J.; Ye, Z.; Deng, Z.; Wan, N. Nonlinear modeling of temperature-induced bearing displacement of long-span single-pier rigid frame bridge based on DCNN-LSTM. Case Stud. Therm. Eng. 2024, 53, 103897. [Google Scholar] [CrossRef]
- Deng, Z.; Huang, M.; Wan, N.; Zhang, J. The Current Development of Structural Health Monitoring for Bridges: A Review. Buildings 2023, 13, 1360. [Google Scholar] [CrossRef]
- Huang, M.; Ling, Z.; Sun, C.; Lei, Y.; Xiang, C.; Wan, Z.; Gu, J. Two-stage damage identification for bridge bearings based on sailfish optimization and element relative modal strain energy. Struct. Eng. Mech. Int. J. 2023, 86, 715–730. [Google Scholar]
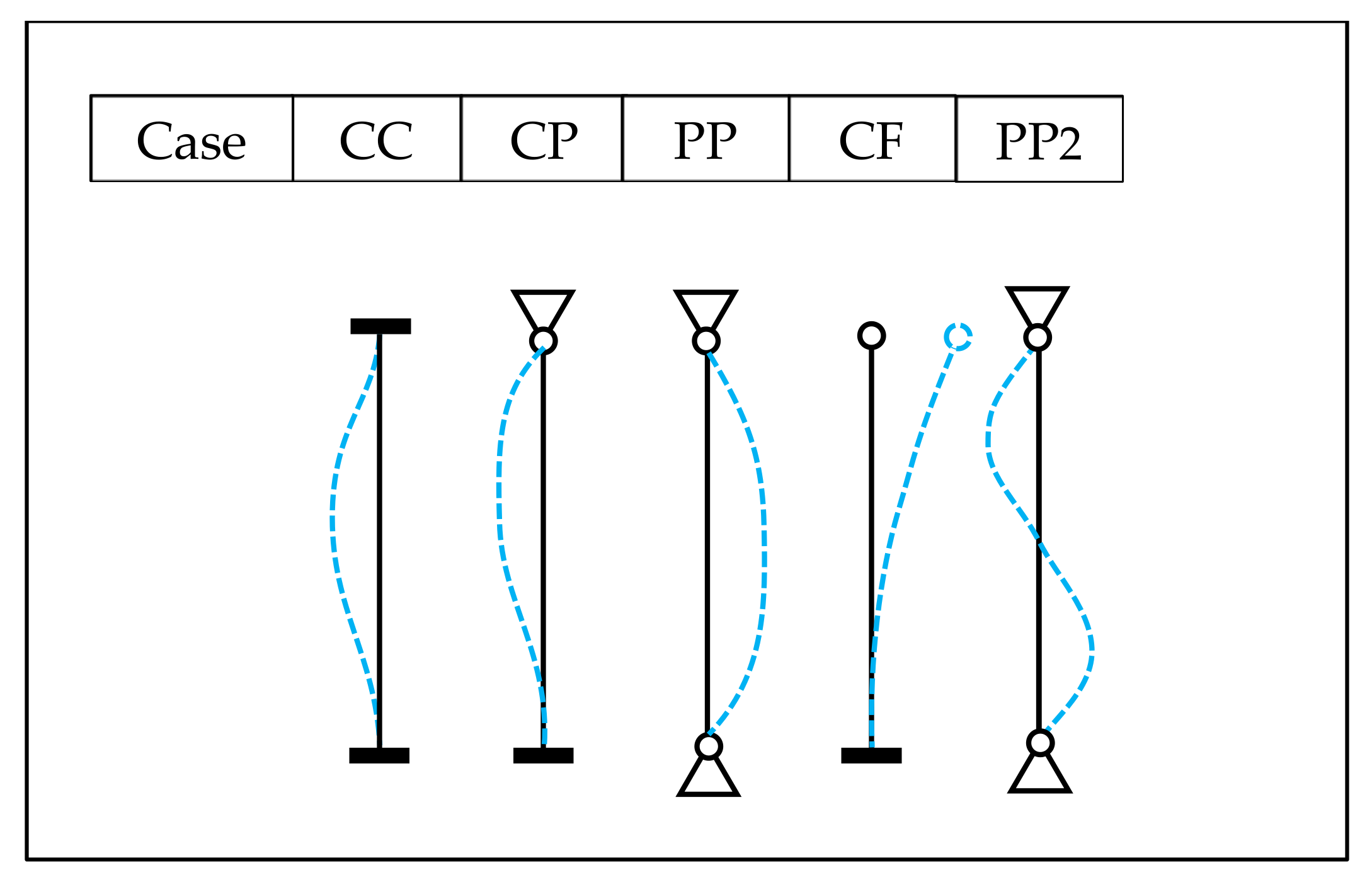


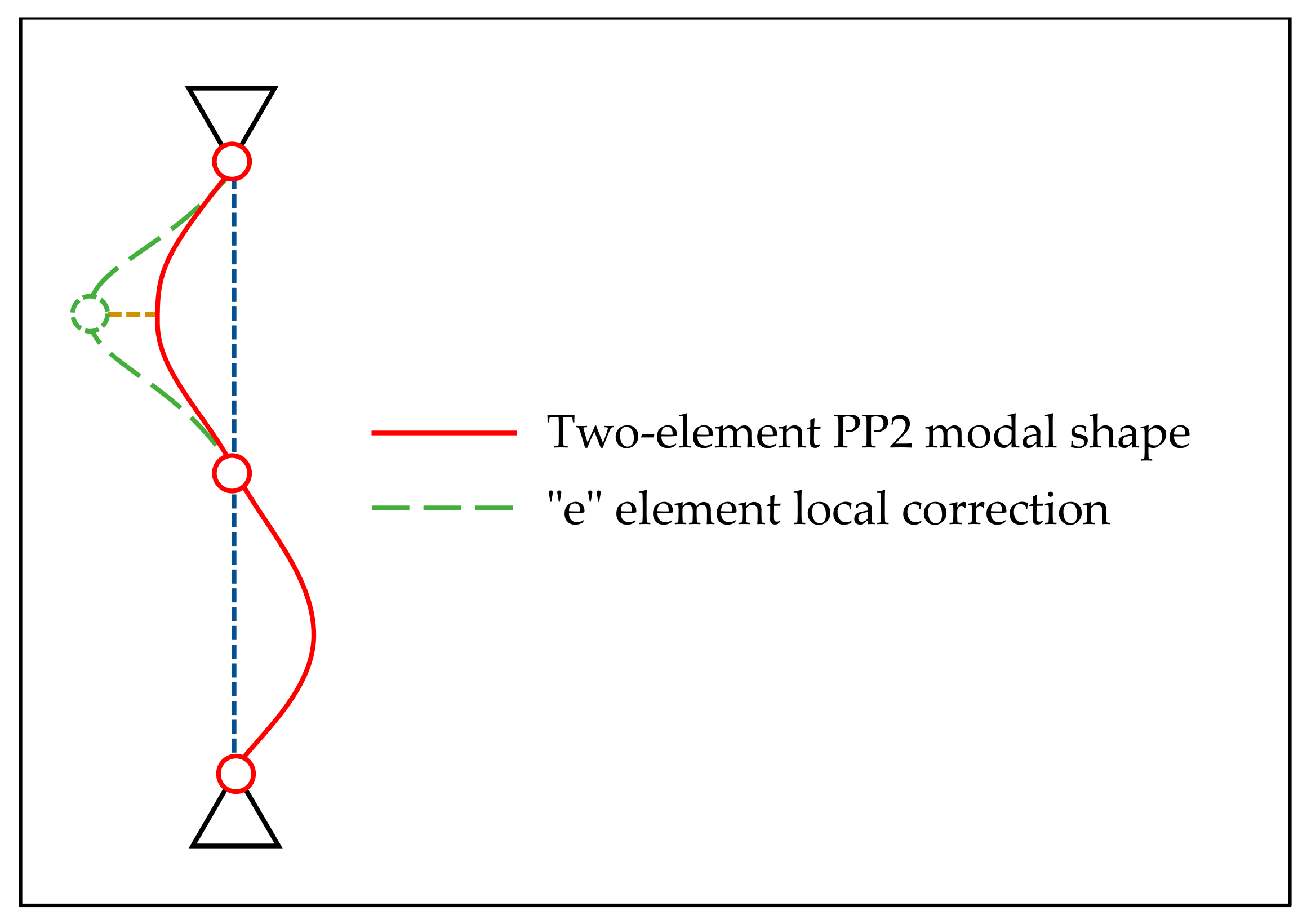
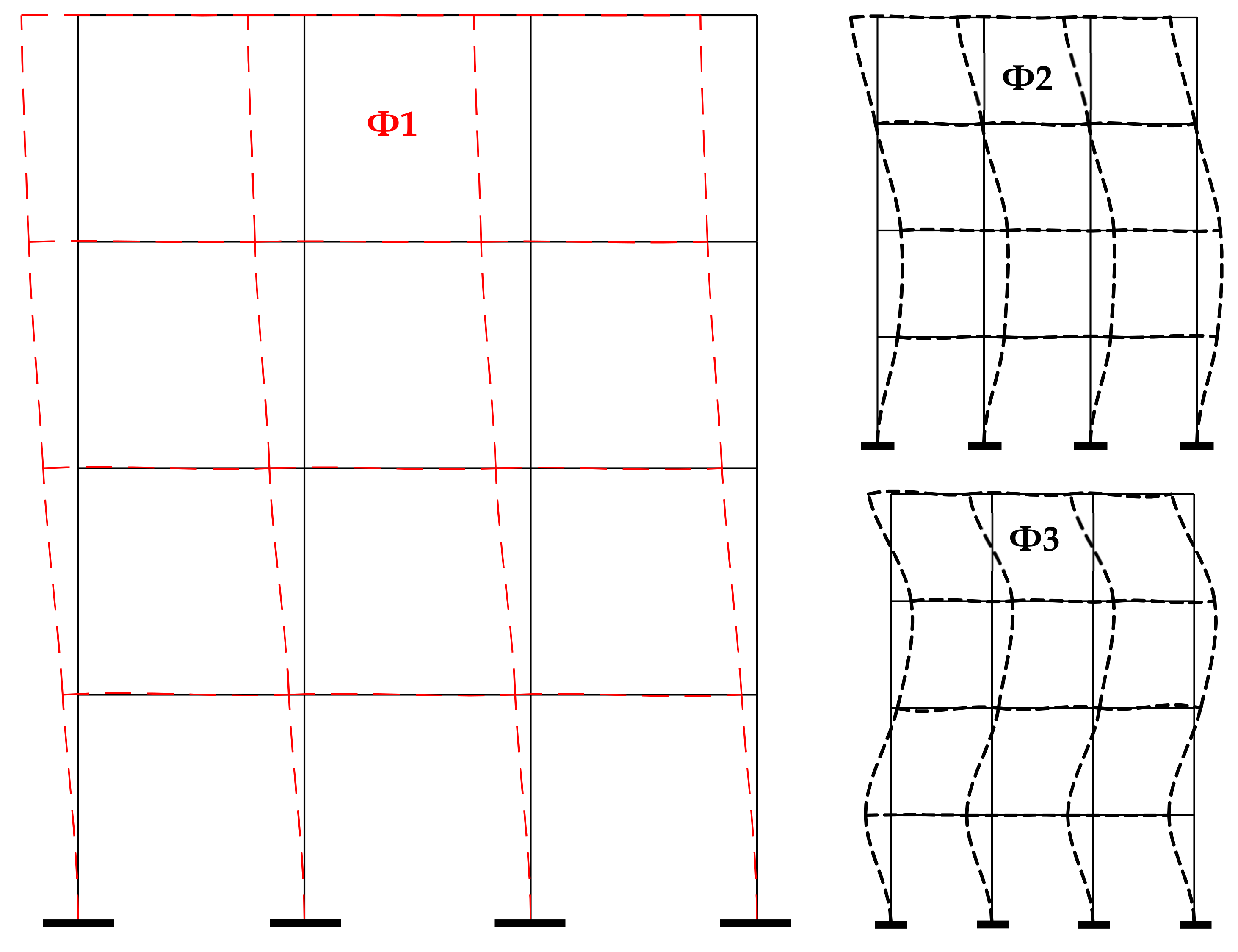


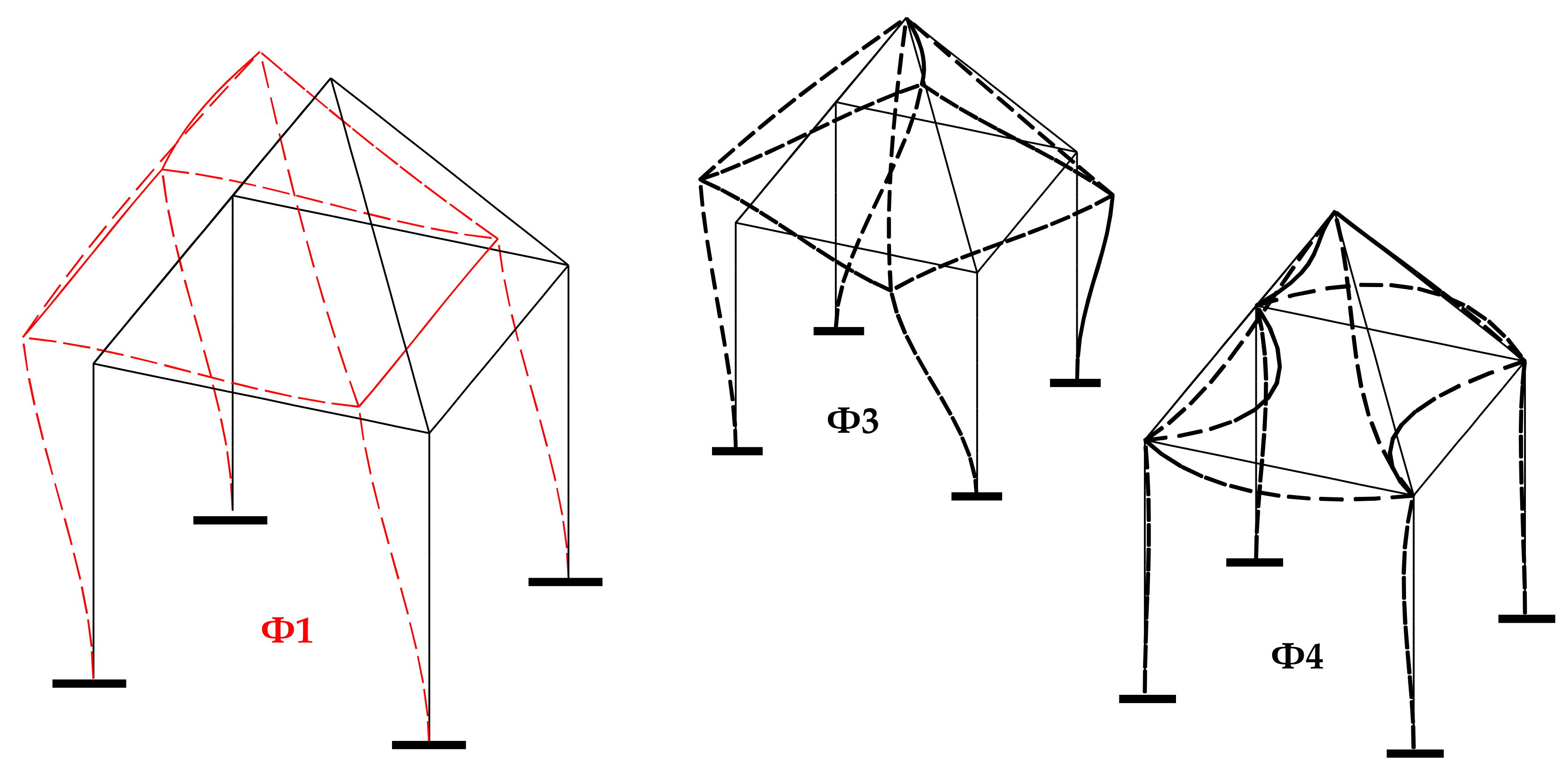
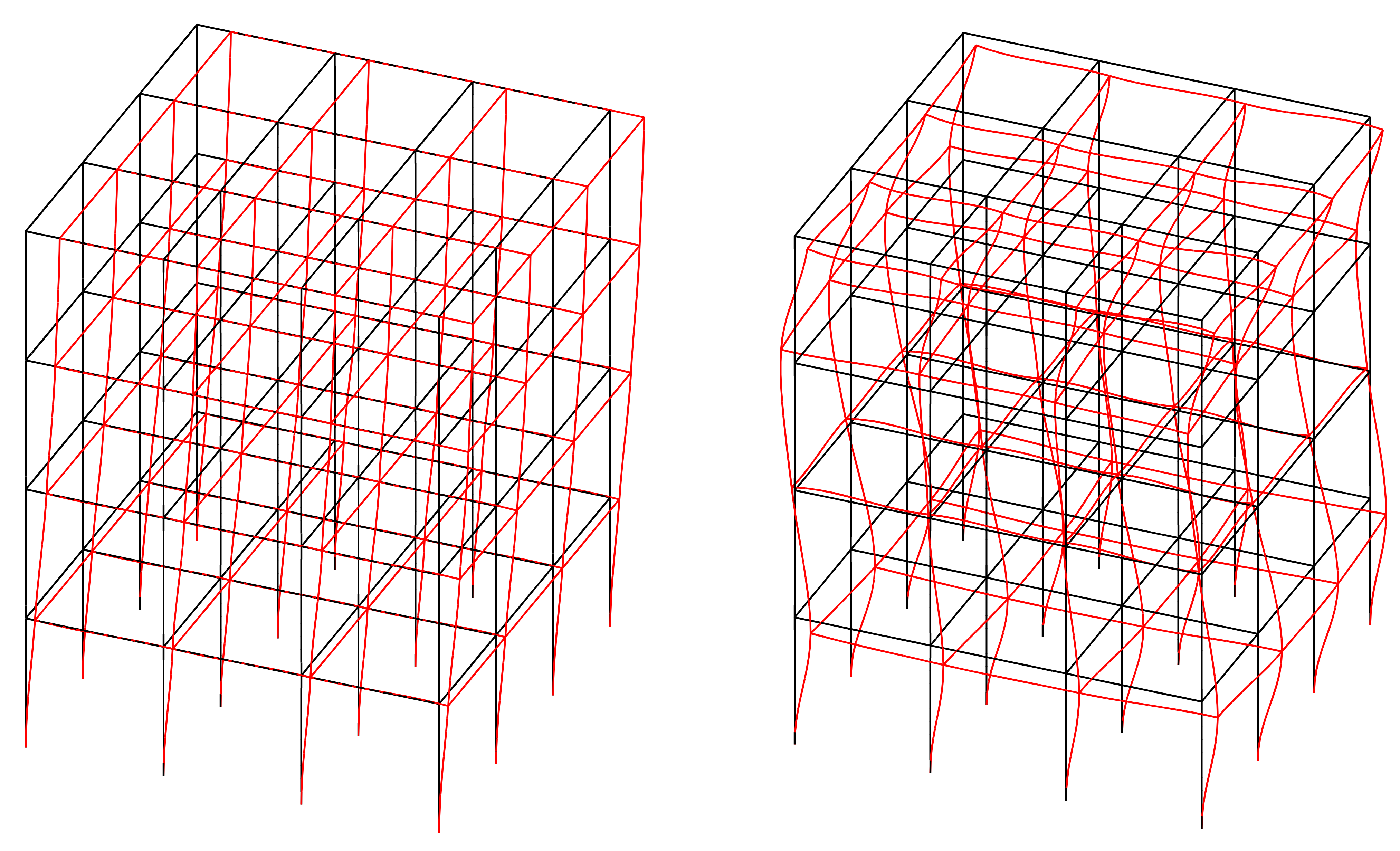
| Nel 2 | CC | CP | PP | CF | PP2 |
|---|---|---|---|---|---|
| 1 | - | 32.92% | 10.99% | 0.48% | 27.14% |
| 2 | 1.62% | 0.93% | 0.39% | 0.05% | 10.98% |
| 3 | 0.41% | 0.20% | 0.08% | 0.01% | 1.17% |
| 4 | 0.13% | 0.06% | 0.03% | 0.00% | 0.38% |
| Nel | CC | CP | PP | CF | PP2 |
|---|---|---|---|---|---|
| 1 | 1.61% | 0.93% | 0.39% | 0.05% | 42.42% |
| Nel | CC | CP | PP | CF | PP2 |
|---|---|---|---|---|---|
| 1 | -% | 211.33% | 49.66% | 1.73% | 1.4 × 1029% |
| Nel | CC | CP | PP | CF | PP2 |
|---|---|---|---|---|---|
| 1 | 1.61% | 0.93% | 0.39% | 0.05% | 42.42% |
| 2 | 0.13% | 0.06% | 0.03% | 0.00% | 0.47% |
| Nel | CC | CP | PP | CF | PP2 |
|---|---|---|---|---|---|
| 1 | -% | 211.33% | 49.66% | 1.73% | 1.4 × 1029% |
| 2 | 6.28% | 2.57% | 1.49% | 0.09% | 55.81% |
| Mode # | Exact 1 ω (rad/s) | 1-Elem. 2 ω (rad/s) | Relative 3 Error (%) | Corrected ω (rad/s) 4 | Relative 5 Error (%) | Distortion Factor γ (%) | Distorted Elements # |
|---|---|---|---|---|---|---|---|
| 1 | 34.88 | 34.89 | 0.02 | 34.88 | 0.00 | 1.14 | 0 |
| 2 | 110.12 | 110.28 | 0.14 | 110.13 | 0.01 | 6.11 | 0 |
| 3 | 195.67 | 196.28 | 0.31 | 195.73 | 0.03 | 4.27 | 0 |
| 4 | 277.60 | 278.38 | 0.28 | 277.75 | 0.05 | 6.46 | 0 |
| Mode # | Exact ω (rad/s) | 1-Elem. Ω (rad/s) | Relative Error (%) | Corrected ω (rad/s) | Relative Error (%) | Distortion Factor γ (%) | Distorted Elements # |
|---|---|---|---|---|---|---|---|
| 1 | 161.75 | 162.68 | 0.57 | 161.81 | 0.04 | 125 | 1 |
| 2 | 438.18 | 551.89 | 25.95 | 471.27 | 7.55 | 2854 | 7 |
| 3 | 447.47 | 579.72 | 29.56 | 575.00 | 28.50 | 1.3 × 108 | 4 |
| 4 | 473.87 | 631.82 | 33.33 | 516.46 | 8.99 | 14,137 | 5 |
| Mode # | Exact ω (rad/s) | 1/2-Elem. ω (rad/s) | Relative Error | Corrected ω (rad/s) | Relat. Error | Distortion Factor γ | Distorted Elements # |
|---|---|---|---|---|---|---|---|
| 1 | 161.75 | 162.25 | 0.31% | 161.78 | 0.02% | 122% | 1 |
| 2 | 438.18 | 446.60 | 1.92% | 438.83 | 0.15% | 145% | 2 |
| 3 | 447.47 | 456.15 | 1.94% | 448.13 | 0.15% | 63% | 0 |
| 4 | 473.87 | 482.68 | 1.86% | 474.53 | 0.14% | 364% | 1 |
| Mode # | Exact 1 ω (rad/s) | 1-Elem. ω (rad/s) | Relative Error (%) | Corrected ω (rad/s) | Relative Error (%) | Distortion Factor γ (%) | Distorted Elements # |
|---|---|---|---|---|---|---|---|
| 1 | 97.41 | 97.59 | 0.19 | 97.42 | 0.01 | 3.48 | 0 |
| 2 | 97.41 | 97.59 | 0.19 | 97.42 | 0.01 | 3.52 | 0 |
| 3 | 140.11 | 140.45 | 0.24 | 140.14 | 0.02 | 6.40 | 0 |
| 4 | 580.82 | 672.56 | 15.79 | 583.93 | 1.38 | 101.45 | 4 |
| Mode # | Exact ω (rad/s) | 1-Elem. ω (rad/s) | Relative Error (%) | Corrected ω (rad/s) | Relative Error (%) | Distortion Factor γ (%) | Distorted Elements # |
|---|---|---|---|---|---|---|---|
| 1 | 28.51 | 28.51 | 0.01 | 28.51 | 0.00 | 8.20 | 0 |
| 2 | 28.51 | 28.51 | 0.01 | 28.51 | 0.00 | 8.20 | 0 |
| 3 | 31.81 | 31.82 | 0.02 | 31.81 | 0.00 | 2.01 | 0 |
| 4 | 89.08 | 89.20 | 0.14 | 89.09 | 0.01 | 67.43 | 0 |
| 5 | 89.08 | 89.20 | 0.14 | 89.09 | 0.01 | 64.86 | 0 |
| 6 | 91.72 | 91.85 | 0.14 | 91.73 | 0.01 | 50.67 | 0 |
| 7 | 98.90 | 99.05 | 0.15 | 98.91 | 0.01 | 4.79 | 0 |
| 8 | 129.38 | 129.72 | 0.26 | 129.41 | 0.02 | 11.55 | 0 |
| 9 | 137.88 | 138.27 | 0.29 | 137.91 | 0.02 | 56.25 | 0 |
| 10 | 137.88 | 138.27 | 0.29 | 137.91 | 0.02 | 55.71 | 0 |
| 11 | 155.42 | 156.00 | 0.38 | 155.46 | 0.03 | 189.21 | 4 |
| 12 | 155.42 | 156.00 | 0.38 | 155.46 | 0.03 | 99.61 | 0 |
| Mode # | Exact ω (rad/s) | 1-Elem. ω (rad/s) | Relative Error (%) | Corrected ω (rad/s) | Relative Error (%) | Distortion Factor γ (%) | Distorted Elements # |
|---|---|---|---|---|---|---|---|
| 1 | 124.49 | 125.17 | 0.54 | 124.54 | 0.04 | 47.18 | 0 |
| 2 | 126.75 | 127.42 | 0.53 | 126.79 | 0.04 | 59.22 | 0 |
| 3 | 146.27 | 147.08 | 0.55 | 146.33 | 0.04 | 80.42 | 0 |
| 4 | 151.65 | 152.58 | 0.61 | 151.71 | 0.04 | 76.67 | 0 |
| 5 | 184.03 | 185.26 | 0.67 | 184.13 | 0.06 | 182.87 | 1 |
| 6 | 212.50 | 214.77 | 1.07 | 212.67 | 0.08 | 185.24 | 6 |
| 7 | 245.42 | 248.36 | 1.20 | 245.69 | 0.11 | 273.57 | 13 |
| 8 | 276.69 | 281.67 | 1.80 | 277.20 | 0.18 | 729.64 | 18 |
| 9 | 366.95 | 402.78 | 9.77 | 372.53 | 1.52 | 1907.05 | 41 |
| 10 | 384.71 | 434.85 | 13.03 | 396.66 | 3.11 | 2970.10 | 51 |
| 11 | 392.67 | 454.37 | 15.72 | 423.86 | 7.94 | 1200.18 | 35 |
| 12 | 403.95 | 467.65 | 15.77 | 433.75 | 7.38 | 2018.34 | 42 |
| Mode # | Exact ω (rad/s) | 2-Elem. ω (rad/s) | Relative Error (%) | Corrected ω (rad/s) | Relative Error (%) | Distortion Factor γ (%) | Distorted Elements # |
|---|---|---|---|---|---|---|---|
| 1 | 124.49 | 124.54 | 0.03 | 124.50 | 0.00 | 2.35 | 0 |
| 2 | 126.75 | 126.79 | 0.03 | 126.75 | 0.00 | 4.65 | 0 |
| 3 | 146.27 | 146.33 | 0.04 | 146.28 | 0.00 | 3.94 | 0 |
| 4 | 151.65 | 151.71 | 0.04 | 151.66 | 0.00 | 4.33 | 0 |
| 5 | 184.03 | 184.13 | 0.05 | 184.04 | 0.00 | 6.87 | 0 |
| 6 | 212.50 | 212.66 | 0.08 | 212.52 | 0.01 | 4.66 | 0 |
| 7 | 245.42 | 245.67 | 0.10 | 245.44 | 0.01 | 7.20 | 0 |
| 8 | 276.69 | 277.13 | 0.16 | 276.73 | 0.01 | 17.03 | 0 |
| 9 | 366.95 | 368.89 | 0.53 | 367.08 | 0.04 | 9.62 | 0 |
| 10 | 384.71 | 387.27 | 0.67 | 384.89 | 0.05 | 16.12 | 0 |
| 11 | 392.67 | 395.59 | 0.74 | 392.87 | 0.05 | 3.82 | 0 |
| 12 | 403.95 | 407.28 | 0.82 | 404.18 | 0.06 | 4.83 | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Urruzola, J.; Garmendia, I. Improved FEM Natural Frequency Calculation for Structural Frames by Local Correction Procedure. Buildings 2024, 14, 1195. https://doi.org/10.3390/buildings14051195
Urruzola J, Garmendia I. Improved FEM Natural Frequency Calculation for Structural Frames by Local Correction Procedure. Buildings. 2024; 14(5):1195. https://doi.org/10.3390/buildings14051195
Chicago/Turabian StyleUrruzola, Javier, and Iñaki Garmendia. 2024. "Improved FEM Natural Frequency Calculation for Structural Frames by Local Correction Procedure" Buildings 14, no. 5: 1195. https://doi.org/10.3390/buildings14051195
APA StyleUrruzola, J., & Garmendia, I. (2024). Improved FEM Natural Frequency Calculation for Structural Frames by Local Correction Procedure. Buildings, 14(5), 1195. https://doi.org/10.3390/buildings14051195








