Machine Learning Insights: Exploring Key Factors Influencing Sale-to-List Ratio—Insights from SVM Classification and Recursive Feature Selection in the US Real Estate Market
Abstract
:1. Introduction
2. Literature Review
3. Materials and Methods
3.1. Support Vector Machines
3.2. Recursive Feature Elimination (RFE) and the Hybrid SVM-RFE Approach
3.3. Variables and Data
4. Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Sobieraj, J.; Metelski, D. Private Renting vs. Mortgage Home Buying: Case of British Housing Market—A Bayesian Network and Directed Acyclic Graphs Approach. Buildings 2022, 12, 189. [Google Scholar] [CrossRef]
- Bryx, M.; Sobieraj, J.; Metelski, D.; Rudzka, I. Buying vs. Renting a Home in View of Young Adults in Poland. Land 2021, 10, 1183. [Google Scholar] [CrossRef]
- Sobieraj, J.; Bryx, M.; Metelski, D. Preferences of Young Polish Renters: Findings from the Mediation Analysis. Buildings 2023, 13, 920. [Google Scholar] [CrossRef]
- Raza, S.A.; Guesmi, K. Guest editorial: Predictability of housing prices in the times of crises: New trends, methodologies, and techniques. Int. J. Hous. Mark. Anal. 2024, 17, 1–7. [Google Scholar] [CrossRef]
- Carrillo, P.E. To sell or not to sell: Measuring the heat of the housing market. Real Estate Econ. 2013, 41, 310–346. [Google Scholar] [CrossRef]
- Miller, N.; Sklarz, M. Integrating real estate market conditions into home price forecasting systems. J. Hous. Res. 2012, 21, 183–213. [Google Scholar] [CrossRef]
- Vinsand, E.; Sjong, H.H. Measuring The Heat of Oslo’s Housing Market: A Composite Indicator to Improve the Informational Efficiency in the Residential Real Estate Market. Master’s Thesis, Norwegian School of Economics, Bergen, Norway, 2021. [Google Scholar]
- Anenberg, E.; Ringo, D. Volatility in Home Sales and Prices: Supply or Demand? J. Urban Econ. 2024, 139, 103610. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, Y.; Yang, E.; Xu, S.; Yu, Y. Sale to list ratio, for-sale inventory, sale count, and housing value. International J. Hous. Mark. Anal. 2023, 1, 1–15. [Google Scholar] [CrossRef]
- Damen, S. The quality-adjusted price evolution of houses and apartments in Flanders from 2005q1 until 2021q2. SSRN Electron. J. 2021, 1–6. [Google Scholar] [CrossRef]
- Hattapoglu, M.; Hoxha, I. Hot and cold seasons in Texas housing markets. Int. J. Hous. Mark. Anal. 2021, 14, 317–332. [Google Scholar] [CrossRef]
- Schmidbauer, E. Time on the Market and List Prices in “Hot” Real Estate Markets. SSRN Electron. J. 2023, 4331752, 1–28. [Google Scholar] [CrossRef]
- Hoxha, I.; Yilmaz, S. Liquidity and pricing trends in the housing market in Pennsylvania. Pa. Econ. Rev. 2020, 27, 1–16. [Google Scholar]
- Huang, Y.; Yip, T.L.; Liang, C. Risk Perception and Property Value: Evidence from Tianjin Port Explosion. Sustainability 2020, 12, 1169. [Google Scholar] [CrossRef]
- Engerstam, S.; Warsame, A.; Wilhelmsson, M. Long-term dynamics of new residential supply: A case study of the apartment segment in Sweden. Buildings 2022, 12, 970. [Google Scholar] [CrossRef]
- Riccioli, F.; Fratini, R.; Boncinelli, F. The impacts in real estate of landscape values: Evidence from Tuscany (Italy). Sustainability 2021, 13, 2236. [Google Scholar] [CrossRef]
- Szczepańska, A.; Gościewski, D.; Gerus-Gościewska, M. A GRID-based spatial interpolation method as a tool supporting real estate market analyses. ISPRS Int. J. Geo-Inf. 2020, 9, 39. [Google Scholar] [CrossRef]
- Antipov, E.A.; Pokryshevskaya, E.B. Mass appraisal of residential apartments: An application of Random forest for valuation and a CART-based approach for model diagnostics. Expert Syst. Appl. 2012, 39, 1772–1778. [Google Scholar] [CrossRef]
- Truong, Q.; Nguyen, M.; Dang, H.; Mei, B. Housing price prediction via improved machine learning techniques. Procedia Comput. Sci. 2020, 174, 433–442. [Google Scholar] [CrossRef]
- Geerts, M.; De Weerdt, J. A Survey of Methods and Input Data Types for House Price Prediction. ISPRS Int. J. Geo-Inf. 2023, 12, 200. [Google Scholar] [CrossRef]
- Liu, G. Research on prediction and analysis of real estate market based on the multiple linear regression model. Sci. Program. 2022, 2022, 5750354. [Google Scholar] [CrossRef]
- Manjula, R.; Jain, S.; Srivastava, S.; Kher, P.R. Real estate value prediction using multivariate regression models. IOP Conf. Ser. Mater. Sci. Eng. 2017, 263, 042098. [Google Scholar] [CrossRef]
- Ghosalkar, N.N.; Dhage, S.N. Real estate value prediction using linear regression. In Proceedings of the 2018 Fourth International Conference on Computing Communication Control and Automation (ICCUBEA), Pune, India, 16–18 August 2018. [Google Scholar]
- Michele, L.; Andrea, L.; Pangallo, M. What do online listings tell us about the housing market? Int. J. Cent. Bank. 2022, 1, 1–53. [Google Scholar]
- Ho, W.K.; Tang, B.S.; Wong, S.W. Predicting property prices with machine learning algorithms. J. Prop. Res. 2021, 38, 48–70. [Google Scholar] [CrossRef]
- Alzain, E.; Alshebami, A.S.; Aldhyani, T.H.H.; Alsubari, S.N. Application of Artificial Intelligence for Predicting Real Estate Prices: The Case of Saudi Arabia. Electronics 2022, 11, 3448. [Google Scholar] [CrossRef]
- Yilmaz, O.; Talavera, O.; Jia, J.Y. Rental market liquidity, seasonality, and distance to universities. Int. J. Econ. Bus. 2022, 29, 223–239. [Google Scholar] [CrossRef]
- Anenberg, E.; Ringo, D. Housing Market Tightness During COVID-19: Increased Demand or Reduced Supply? Board of Governors of the Federal Reserve System: Washington, DC, USA, 2021.
- Ngai, L.R.; Sheedy, K.D. The decision to move house and aggregate housing-market dynamics. J. Eur. Econ. Assoc. 2020, 18, 2487–2531. [Google Scholar] [CrossRef]
- Gabrovski, M.; Ortego-Marti, V. Housing Market Dynamics with Search Frictions (No. 201804); University of California: Riverside, CA, USA, 2018; pp. 1–27. [Google Scholar]
- Ngai, L.R.; Tenreyro, S. Hot and cold seasons in the housing market. Am. Econ. Rev. 2014, 104, 3991–4026. [Google Scholar] [CrossRef]
- Guren, A. The Causes and Consequences of House Price Momentum; Harvard University: Cambridge, MA, USA, 2014; pp. 1–106. [Google Scholar]
- Diaz, A.; Jerez, B. House prices, sales, and time on the market: A search-theoretic framework. Int. Econ. Rev. 2013, 54, 837–872. [Google Scholar] [CrossRef]
- Bich, H.N.T.; Trong, H.N.; Thanh, H.T. The role of listing price strategies on the probability of selling a house: Evidence from Vietnam. Real Estate Manag. Valuat. 2020, 28, 63–75. [Google Scholar] [CrossRef]
- Leamer, E.E. Housing Is the Business Cycle (Working Paper 13428); National Bureau of Economic Research: Cambridge, MA, USA, 2007. [Google Scholar]
- Gilbukh, S.; Goldsmith-Pinkham, P. Heterogeneous Real Estate Agents and the Housing Cycle (No. w31683); National Bureau of Economic Research: Cambridge, MA, USA, 2023. [Google Scholar]
- Sklarz, M. Days on Market: The Unbearable Tightness of Inventory. Available online: https://www.blackknightinc.com/blog/the-unbearable-tightness-of-inventory/ (accessed on 10 April 2024).
- Schölkopf, B.; Smola, A.J.; Bach, F. Learning with Kernels: Support Vector Machines, Regularization, Optimization, and Beyond; MIT Press: Cambridge, MA, USA, 2002. [Google Scholar]
- Shin, K.S.; Lee, T.S.; Kim, H.J. An application of Support Vector Machines in bankruptcy prediction model. Expert Syst. Appl. 2005, 28, 127–135. [Google Scholar] [CrossRef]
- Osuna, E.; Freund, R.; Girosit, F. Training Support Vector Machines: An Application to Face Detection. Computer Vision and Pattern Recognition. In Proceedings of the IEEE Computer Society Conference, Los Alamitos, CA, USA, 17–19 June 1997. [Google Scholar]
- Karatzoglou, A.; Meyer, D.; Hornik, K. Support Vector Machines in R. J. Stat. Softw. 2006, 15, 1–28. [Google Scholar] [CrossRef]
- Platt, J. Sequential Minimal Optimization: A Fast Algorithm for Training Support Vector Machines; Technical Report MSR-TR-98-14; Microsoft Research: Redmond, WA, USA, 1998; pp. 1–21. [Google Scholar]
- Platt, J. Using analytic QP and sparseness to speed training of Support Vector Machines. Adv. Neural Inf. Process. Syst. 1999, 11, 557–563. [Google Scholar]
- Vishwanathan, S.V.; Smola, A.J.; Murty, M.N. Simple SVM. In Proceedings of the Twentieth International Conference on International Conference on Machine Learning, Washington, DC, USA, 21–24 August 2003. [Google Scholar]
- Vapnik, V. Statistical Learning Theory; Wiley: New York, NY, USA, 1998. [Google Scholar]
- Chapelle, O.; Vapnik, V. Model selection for Support Vector Machines. In Advances in Neural Information Processing Systems; Solla, S., Leen, T., Müller, K., Eds.; NIPS: Denver, CO, USA, 1999; pp. 230–236. [Google Scholar]
- Bousquet, O.; Boucheron, S.; Lugosi, G. Introduction to Statistical Learning Theory. In Advanced Lectures on Machine Learning; Bousquet, O., von Luxburg, U., Rätsch, G., Eds.; Springer: Berlin/Heidelberg, Germany, 2004; pp. 169–207. [Google Scholar]
- Gunn, S.R. Support Vector Machines for classification and regression. ISIS Tech. Rep. 1998, 14, 5–16. [Google Scholar]
- Salcedo-Sanz, S.; Rojo-Álvarez, J.L.; Martínez-Ramón, M.; Camps-Valls, G. Support Vector Machines in engineering: An overview. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 2014, 4, 234–267. [Google Scholar] [CrossRef]
- Brownlee, J. Recursive Feature Elimination (RFE) for Feature Selection in Python. Available online: https://machinelearningmastery.com/rfe-feature-selection-in-python/ (accessed on 10 December 2023).
- Huang, M.L.; Hung, Y.H.; Lee, W.M.; Li, R.K.; Jiang, B.R. SVM-RFE based feature selection and Taguchi parameters optimization for multiclass SVM classifier. Sci. World J. 2014, 1, 795624. [Google Scholar] [CrossRef]
- Sanz, H.; Valim, C.; Vegas, E.; Oller, J.M.; Reverter, F. SVM-RFE: Selection and visualization of the most relevant features through non-linear kernels. BMC Bioinform. 2018, 19, 432. [Google Scholar] [CrossRef]
- Fu, R.; Jin, G.Z.; Liu, M. Does Human-Algorithm Feedback Loop Lead to Error Propagation? Evidence from Zillow’s Zestimate; National Bureau of Economic Research: Cambridge, MA, USA, 2023; pp. 1–44. [Google Scholar]
- Yörük, B.K. Early effects of COVID-19 pandemic-related state policies on housing market activity in the United States. J. Hous. Econ. 2022, 57, 101857. [Google Scholar] [CrossRef]
- Knight, J.R. Listing price, time on market, and ultimate selling price: Causes and effects of listing price changes. Real Estate Econ. 2002, 30, 213–237. [Google Scholar] [CrossRef]
- Harker, P.T. The Fed and the Economy: Where We’re Going, Where We’ve Been (No. 95648); La Salle University: Philadelphia, PA, USA, 2023; pp. 1–10. [Google Scholar]
- Zillow. What Is Zillow’s Buyer-Seller Index, and How Is It Computed? Available online: https://www.zillow.com/research/understanding-the-zillow-buyer-seller-index-2883/ (accessed on 10 April 2024).
- Pariser, I. The Effect of School Quality on Prices versus Rents; University of California: Berkeley, CA, USA, 2019; pp. 1–48. [Google Scholar]
- Kotova, N.; Zhang, A.L. Liquidity in residential real estate markets. In Proceedings of the ASSA 2021 Annual Meeting, Held Virtually, 3–5 January 2021. [Google Scholar]
- Maxwell, T.; Segal, T. Sale-to-List Ratio: Why It Matters. Available online: https://www.bankrate.com/real-estate/sale-to-list-ratio/ (accessed on 20 November 2023).
- StreetEasy Team. What Is the Sale-to-List Price Ratio, and Why Does It Matter? Available online: https://streeteasy.com/blog/sale-to-list-price-ratio/ (accessed on 20 November 2023).
- Henriksson, E.; Werlinder, K. Housing Price Prediction over Countrywide Data: A Comparison of XGBoost and Random Forest Regressor Models; KTH, School of Electrical Engineering and Computer Science (EECS): Stockholm, Sweden, 2021. [Google Scholar]
- Anenberg, E. Information frictions and housing market dynamics. Int. Econ. Rev. 2016, 57, 1449–1479. [Google Scholar] [CrossRef]
- Paraschiv, C.; Chenavaz, R. Sellers’ and buyers’ reference point dynamics in the housing market. Hous. Stud. 2011, 26, 329–352. [Google Scholar] [CrossRef]
- Zheng, M.; Wang, H.; Wang, C.; Wang, S. Speculative behavior in a housing market: Boom and bust. Econ. Model. 2017, 61, 50–64. [Google Scholar] [CrossRef]
- Agnello, L.; Schuknecht, L. Booms and busts in housing markets: Determinants and implications. J. Hous. Econ. 2011, 20, 171–190. [Google Scholar] [CrossRef]
- Agnello, L.; Castro, V.; Sousa, R.M. Booms, busts, and normal times in the housing market. J. Bus. Econ. Stat. 2015, 33, 25–45. [Google Scholar] [CrossRef]
- Vaidynathan, D.; Kayal, P.; Maiti, M. Effects of economic factors on median list and selling prices in the US housing market. Data Sci. Manag. 2023, 6, 199–207. [Google Scholar] [CrossRef]
- Cervantes, J.; Garcia-Lamont, F.; Rodríguez-Mazahua, L.; Lopez, A. A comprehensive survey on support vector machine classification: Applications, challenges and trends. Neurocomputing 2020, 408, 189–215. [Google Scholar] [CrossRef]
- Durgesh, K.S.; Lekha, B. Data classification using support vector machine. J. Theor. Appl. Inf. Technol. 2010, 12, 1–7. [Google Scholar]
- Zhang, Y. Support vector machine classification algorithm and its application. In Proceedings of the Information Computing and Applications: Third International Conference, ICICA 2012, Chengde, China, 14–16 September 2012. [Google Scholar]
- Anthony, G.; Greg, H.; Tshilidzi, M. Classification of images using Support Vector Machines. arXiv 2007, arXiv:0709.3967. [Google Scholar]
- Han, Y.; Huang, L.; Zhou, F. A dynamic Recursive Feature Elimination framework (dRFE) to further refine a set of OMIC biomarkers. Bioinformatics 2021, 37, 2183–2189. [Google Scholar] [CrossRef]
- Guo, Y.; Zhang, Z.; Tang, F. Feature selection with kernelized multi-class support vector machine. Pattern Recognit. 2021, 117, 107988. [Google Scholar] [CrossRef]
- Lin, X.; Yang, F.; Zhou, L.; Yin, P.; Kong, H.; Xing, W.; Xu, G. A support vector machine-Recursive Feature Elimination feature selection method based on artificial contrast variables and mutual information. J. Chromatogr. B 2012, 910, 149–155. [Google Scholar] [CrossRef]
- Hakkoum, H.; Abnane, I.; Idri, A. Interpretability in the medical field: A systematic mapping and review study. Appl. Soft Comput. 2022, 117, 108391. [Google Scholar] [CrossRef]
- Abuali, K.M.; Nissirat, L.; Al-Samawi, A. Advancing Network Security with AI: SVM-Based Deep Learning for Intrusion Detection. Sensors 2023, 23, 8959. [Google Scholar] [CrossRef] [PubMed]
- Samuel, S.S.; Abdullah, N.N.; Raj, A. Interpretation of SVM Using Data Mining Technique to Extract Syllogistic Rules: Exploring the Notion of Explainable AI in Diagnosing CAD. In Proceedings of the International Cross-Domain Conference, CD-MAKE 2020, Dublin, Ireland, 25–28 August 2020. [Google Scholar]
- Valentin, S.; Harkotte, M.; Popov, T. Interpreting neural decoding models using grouped model reliance. PLoS Comput. Biol. 2020, 16, e1007148. [Google Scholar] [CrossRef] [PubMed]
- Jayaswal, V. Performance Metrics: Confusion Matrix, Precision, Recall, and F1 Score. Medium, towards Data Science. Available online: https://towardsdatascience.com/performance-metrics-confusion-matrix-precision-recall-and-f1-score-a8fe076a2262 (accessed on 15 February 2024).
- Silwal, D. Confusion Matrix, Accuracy, Precision, Recall & F1 Score: Interpretation of Performance Measures. Available online: https://www.linkedin.com/pulse/confusion-matrix-accuracy-precision-recall-f1-score-measures-silwal (accessed on 15 February 2024).
- Bonnet, A. Accuracy vs. Precision vs. Recall in Machine Learning: What is the Difference? Available online: https://encord.com/blog/classification-metrics-accuracy-precision-recall/ (accessed on 15 February 2024).
- Wu, J.Y. Housing Price Prediction Using Support Vector Regression; San José State University: San José, CA, USA, 2017. [Google Scholar]
- Yang, H.; Kang, D.; Hwang, K.; Yang, Z.; Jiang, Y. House Price Prediction with Creative Feature Engineering and Advanced Regression Techniques, NYC Data Science Academy. Available online: https://nycdatascience.com/blog/student-works/house-price-prediction-with-creative-feature-engineering-and-advanced-regression-techniques/ (accessed on 10 February 2024).
- Miller, T. Explanation in artificial intelligence: Insights from the social sciences. Artif. Intell. 2019, 267, 1–38. [Google Scholar] [CrossRef]
- Gao, L.; Guan, L. Interpretability of Machine Learning: Recent Advances and Future Prospects; IEEE MultiMedia: Washington, DC, USA, 2023; pp. 1–12. [Google Scholar]
- Alangari, N.; El Bachir Menai, M.; Mathkour, H.; Almosallam, I. Exploring Evaluation Methods for Interpretable Machine Learning: A Survey. Information 2023, 14, 469. [Google Scholar] [CrossRef]
- Yekkehkhany, B.; Safari, A.; Homayouni, S.; Hasanlou, M. A comparison study of different kernel functions for SVM-based classification of multi-temporal polarimetry SAR data. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2014, 40, 281–285. [Google Scholar] [CrossRef]
- Nalepa, J.; Kawulok, M. Selecting training sets for Support Vector Machines: A review. Artif. Intell. Rev. 2019, 52, 857–900. [Google Scholar] [CrossRef]
- Zillow. Why Do Pending Home Sales Fall Through? Available online: https://www.zillow.com/learn/why-pending-home-sales-fall-through/ (accessed on 15 February 2024).
- Keys, B.J.; Mulder, P. Neglected No More: Housing Markets, Mortgage Lending, and Sea Level Rise (No. w27930); National Bureau of Economic Research: Cambridge, MA, USA, 2020. [Google Scholar]
- Sirmans, G.S.; Benjamin, J. Determinants of market rent. J. Real Estate Res. 1991, 6, 357–379. [Google Scholar] [CrossRef]
- Yuan, J.; Zheng, X.; You, J.; Skibniewski, M.J. Identifying Critical Factors Influencing the Rents of Public Rental Housing Delivery by PPPs: The Case of Nanjing. Sustainability 2017, 9, 345. [Google Scholar] [CrossRef]
- Understanding Rental Rates: A Deep Dive into the Influencing Factors. Available online: https://www.assureshift.in/blog/factors-affecting-rental-prices (accessed on 20 February 2024).
- Grybauskas, A.; Pilinkienė, V.; Stundžienė, A. Predictive analytics using Big Data for the real estate market during the COVID-19 pandemic. J. Big Data 2021, 8, 105. [Google Scholar] [CrossRef]


| Variable | Units | Description | Substantiation |
|---|---|---|---|
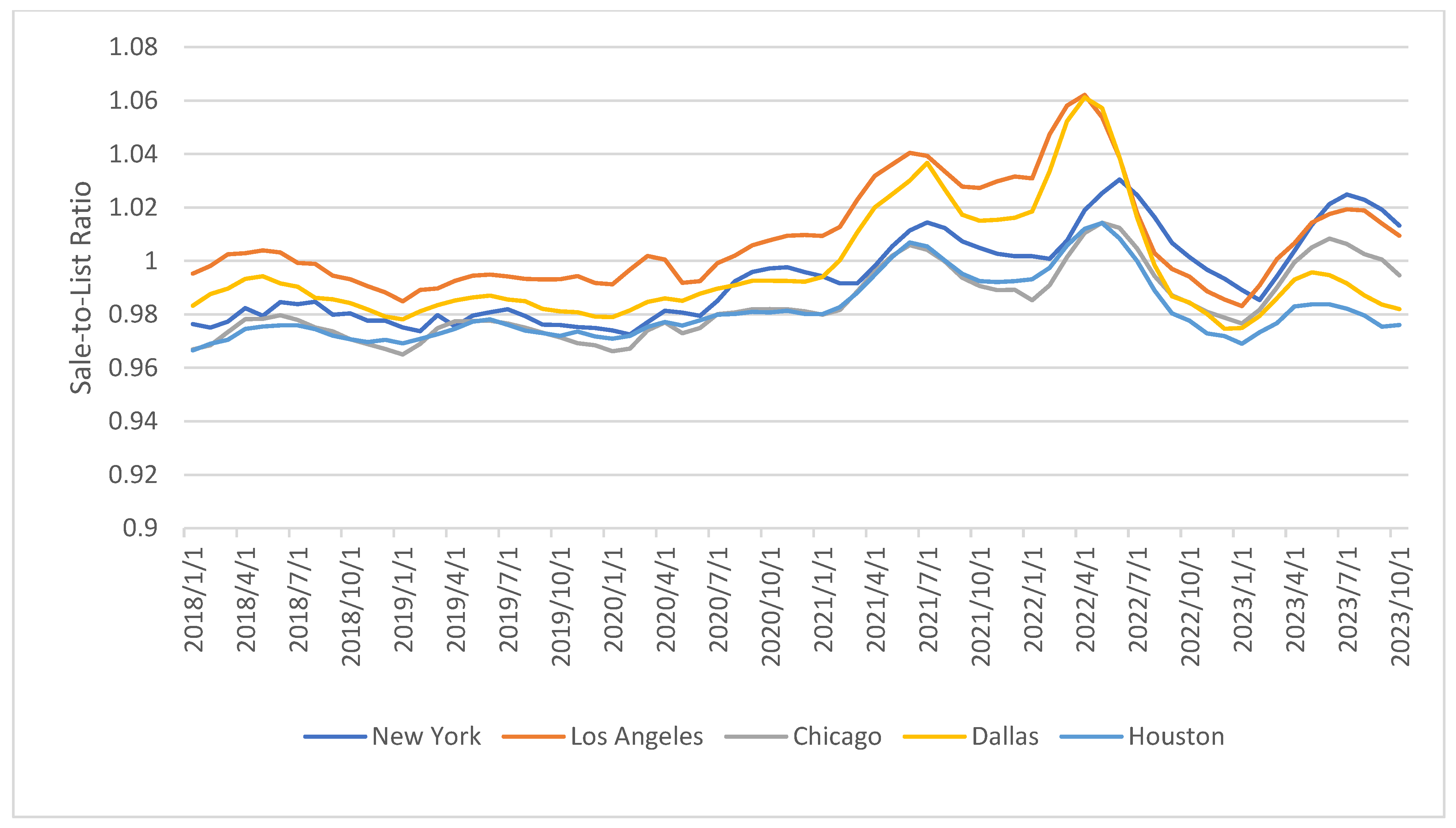
| Sale-to-List ratio (STL) | Percentage (%) | The sale-to-list ratio is a real estate metric that measures the final sale price of a home compared to its original listing price, expressed as a percentage. It can be viewed as a proxy for housing market tightness. Specifically, the sale-to-list ratio is calculated by dividing the final sale price by the initial asking price and expressing it as a percentage. | Anenberg and Ringo [8] discuss how market tightness, or the ratio of buyers to sellers, plays an important role in explaining short-run housing dynamics. Ngai and Tenreyro [31] highlight the importance of market tightness, noting that “a hot market is one with high prices, more buyers and sellers, and an unambiguously larger number of transactions”. |
| Days to Pending (DTP) | Days | The number of days between listing a property and accepting an offer. This metric is used to understand the speed of the housing market and the time it takes for homes to go under contract [53,54]. | Useful in predicting the sale-to-list ratio as it reflects the time it takes for a property to attract a buyer, which can indicate market demand and pricing accuracy. Gabrovski and Ortego-Marti’s [30] paper provides a sophisticated search-and-matching framework that directly relates the time on the market variable to housing market tightness and other key market conditions. This offers an alternative perspective to the more granular Zillow metrics (i.e., days to pending), while still capturing the overall dynamics of the housing sales process. |
| Days to Close (DTC) | Days | The number of days between accepting an offer and closing the sale [53]. | Useful in predicting the sale-to-list ratio as it reflects the efficiency of the sales process and the accuracy of initial pricing. Anenberg and Ringo [8] argue that slower sales, indicating that the market is not so tight, would inform them that they may need to lower prices to make a timely sale. This suggests that days on the market (or time to sell) is closely tied to the tightness of the housing market. Sklarz [37] directly discusses the relationship between days on market and housing market tightness. |
| For-Sale Inventory (FSI) | Number of homes | The number of properties available for sale [9]. | Ngai and Sheedy [29] appear to have established a theoretical framework linking housing market dynamics to the concept of market tightness. The listing rate nt is measured as the ratio of new listings Nt to the stock of owner-occupied houses not already for sale, that is, nt = Nt/(Kt − Ut) [where nt: The listing rate, which is the ratio of new listings (Nt) to the stock of owner-occupied houses not already for sale (Kt − Ut); Nt: The number of new listings; Kt: The total stock of owner-occupied houses; Ut: The number of houses already for sale]. This provides an indirect rationale for the association of the market tightness and for-sale inventory (FSI). |
| List Price (LP) | US Dollars ($) | The initial price at which a property is listed for sale [55]. | Useful in predicting the sale-to-list ratio as it directly influences the pricing dynamics and potential negotiation range. Bich et al.’s [34] study suggests that list price strategies likely play a crucial role in explaining market tightness, meaning that it potentially affects sale-to-list ratio (the study does not address the sale-to-list ratio explicitly). Ngai and Sheedy’s [29] study developed a theoretical model that examines how the listing rate, which is related to the ratio of buyers to sellers (i.e., market tightness), impacts the housing search and matching process. |
| Listing Price Cut (LPC) | US Dollars ($) | The reduction in the listing price [55]. | Useful in predicting the sale-to-list ratio as it reflects market responsiveness and pricing accuracy, and can indicate seller motivation and market conditions. Gabrovski and Ortego-Marti [30] provide evidence linking housing market tightness to housing price cuts and reductions. Gabrovski and Ortego-Marti [30] argue that “higher house prices drive entry of investors and lowers market tightness—or alternatively, they post more vacancies for any given number of buyers”. This indicates that as housing market tightness decreases, with more vacancies relative to buyers, sellers are more likely to offer price cuts or reductions to attract buyers. |
| New Constr. Sale Price (NCSP) | US Dollars ($) | The price at which a newly constructed property is sold. | Useful in predicting the sale-to-list ratio as it reflects the pricing dynamics and demand for new construction, which can impact overall market pricing. The study by Leamer [35] examines the relationship between housing starts, sales volumes, and prices. It shows that the sales volumes of new homes exhibit a clear cyclical pattern, with substantial dips during recessions, while home prices do not exhibit the same pronounced cyclicality. This suggests that housing market tightness, as reflected in sales volumes, is a more important driver of new construction prices than other factors. |
| New Constr. Sales Count (NCSC) | Number of homes | The number of newly constructed properties sold. | Useful in predicting the sale-to-list ratio as it indicates market activity and demand for new construction, which can impact overall market dynamics and pricing. The study by Anenberg and Ringo [8] provides a framework for understanding how the supply of homes (which NCSC would influence) can affect the overall tightness of the housing market and, in turn, housing prices and sales. The study indicates that NCSC, as a component of overall housing supply, would be expected to influence market tightness and, consequently, housing market outcomes. |
| Sale Price (SP) | US Dollars ($) | The price at which a property is sold. | Useful in predicting the sale-to-list ratio as it reflects the final market valuation and the accuracy of initial pricing and negotiation dynamics. The study by Gilbukh and Goldsmith-Pinkham [36] provides evidence linking housing sale prices to market tightness. It basically shows that an agent’s work experience is a key determinant of their ability to successfully sell homes, with more experienced agents having a significant advantage in sale probability compared to less experienced agents. Importantly, this experience gap varies significantly over the housing cycle—it is wider during market downturns and narrower during booms. This indicates that the distribution of agent experience in the market is a reflection of broader housing market conditions. When there are more experienced agents, it signals a tighter market where homes sell more quickly. Conversely, a predominance of inexperienced agents points to a looser market with slower home sales. In this way, an agent’s experience level serves as a proxy for the overall tightness or looseness of the housing market, providing insight into the balance of supply and demand. |
| Share of Listings With a Price Cut (SLPC) | Percentage (%) | The proportion of listings that have undergone a price cut [56]. | Useful in predicting the sale-to-list ratio as it reflects market conditions, seller flexibility, and pricing accuracy, and can indicate buyer negotiation power. The study by Gabrovski and Ortego-Marti [30] provides relevant evidence linking housing market tightness to the share of listings with price cuts (SLPC).The key points from that study are that higher house prices drive the increased entry of investors, which lowers market tightness by leading sellers to post more vacancies relative to the number of buyers. When market tightness decreases, with more vacancies compared to buyers, sellers become more likely to offer price cuts or reductions in order to attract buyers. This suggests that as housing market tightness decreases, with an oversupply of listings relative to buyer demand, sellers will be more inclined to cut listing prices in an effort to generate sales. The share of listings with price cuts can therefore be seen as an indicator of decreasing market tightness. By this logic, the share of listings with price cuts (SLPC) can be used as a proxy to infer changes in housing market tightness. When SLPC increases, it signals a loosening of the market and reduced tightness, as sellers compete for a limited pool of buyers by offering price reductions. |
| Size Rank (SR) | Ordinal ranking (1st, 2nd, 3rd, etc.) | The ranking of the MSA region compared to other MSA regions. | Useful in predicting the sale-to-list ratio as it reflects the size of a given MSA and its impact on pricing and market demand. Prior evidence has shown that there is a relationship between the sale-to-list ratio and MSA’s rank in that in larger, more populated housing markets, there is often a greater imbalance between housing supply and demand, leading to more competition among buyers and higher sale-to-list ratios [57,58]. |
| Zillow Home Value Index (ZHVI) | US Dollars ($) | The Zillow Home Value Index, which measures the typical value of homes in a given area. | Useful in predicting the sale-to-list ratio as it provides a benchmark for property valuation and market trends. Kotova and Zhang [59] use the ZHVI as a measure of home prices in their analysis. The researchers state that the ZHVI is “the price line in the year plots” and that their results are similar if they use other home price indices like the CoreLogic price index. This indicates that the ZHVI is a reliable proxy for tracking overall home price trends and movements in the housing market. Home prices are a key indicator of housing market tightness—higher prices generally signal a tighter market with lower inventory and higher demand. By using the ZHVI as a measure of home prices, Kotova and Zhang’s [59] study is indirectly linking it to housing market tightness. The ZHVI serves as a representation of the price dynamics in the housing market, which are closely tied to the balance between supply and demand, and overall market conditions. |
| Zillow Observed Rent Index (ZORI) | US Dollars ($) | The Zillow Observed Rent Index, which measures the typical rent in a given area. | Useful in predicting the sale-to-list ratio as it reflects rental market dynamics and can indicate property investment potential and market demand. Kotova and Zhang’s [59] paper also uses the Zillow Rent Index (ZRI) as a measure of rents, which are another important factor influencing housing market tightness. The relationship between home prices, rents, and other housing market variables examined in the paper further supports the idea that the ZHVI can be used as an indicator of market tightness. The article by Yilmaz et al. [27] found that higher rental market liquidity (an area closely related to ZORI) is associated with lower housing market tightness, suggesting a buyer’s market (a proxy for sale-to-list ratio). |
| Vars | n | Mean | sd | Median | Trimmed | Mad | Min | Max | Range | Skew | Kurtosis | se |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| STL | 6783 | 1.00 | 0.02 | 0.99 | 0.99 | 0.02 | 0.89 | 1.18 | 0.29 | 1.52 | 4.85 | 0.00 |
| SR | 7000 | 51.26 | 29.37406 | 51.5 | 51.225 | 37.8063 | 1 | 102 | 101 | −0.00328 | −1.19273 | 0.351087 |
| SP | 6961 | 306,462.2 | 175,654 | 255,000 | 275,301.2 | 100,075.5 | 95,000 | 1,550,000 | 1,455,000 | 2.688775 | 10.12511 | 2105.34 |
| DTP | 6853 | 39.6066 | 20.65162 | 36 | 37.43589 | 20.7564 | 8 | 154 | 146 | 1.052513 | 1.409263 | 0.249467 |
| DTC | 6773 | 36.20124 | 7.786966 | 35 | 35.48422 | 5.9304 | 9 | 72 | 63 | 1.059554 | 2.150149 | 0.094619 |
| LP | 6956 | 351,419.3 | 179,816.5 | 299,000 | 320,011.3 | 102,299.4 | 85,000 | 1,495,000 | 1,410,000 | 2.30421 | 7.069295 | 2156.005 |
| LPC | 6917 | 0.035423 | 0.008394 | 0.034245 | 0.03483 | 0.008081 | 0.016287 | 0.078596 | 0.062309 | 0.74521 | 0.746386 | 0.000101 |
| SLPC | 6964 | 0.184758 | 0.064211 | 0.179283 | 0.181576 | 0.063698 | 0.007576 | 0.488177 | 0.480601 | 0.544647 | 0.421007 | 0.000769 |
| FSI | 6952 | 7426.526 | 9963.77 | 4045.5 | 5257.462 | 3142.371 | 132 | 98,511 | 98,379 | 4.071141 | 22.45198 | 119.5003 |
| ZORI | 6990 | 1496.498 | 470.9466 | 1373.765 | 1428.191 | 373.0954 | 786.9547 | 3265.834 | 2478.879 | 1.355271 | 1.722398 | 5.632913 |
| ZHVI | 6858 | 315,443.9 | 182,042.5 | 262,792.3 | 283,041.6 | 104,144.7 | 103,085.5 | 1,521,706 | 1,418,621 | 2.527099 | 8.672603 | 2198.234 |
| NCS | 6636 | 267.4702 | 317.2863 | 160 | 203.7454 | 157.1556 | 5 | 2496 | 2491 | 2.775884 | 9.866544 | 3.894916 |
| NCSP | 5608 | 402,040 | 170,248.3 | 364,412.5 | 375,571.1 | 104,649.3 | 156,000 | 1,945,000 | 1,789,000 | 2.928937 | 13.14059 | 2273.416 |
| Statistic | Value |
|---|---|
| Accuracy | 0.8493 |
| 95% CI | (0.8295, 0.8676) |
| No Information Rate | 0.4407 |
| p-Value [Acc > NIR] | < |
| Kappa | 0.774 |
| Mcnemar’s Test p-Value | < |
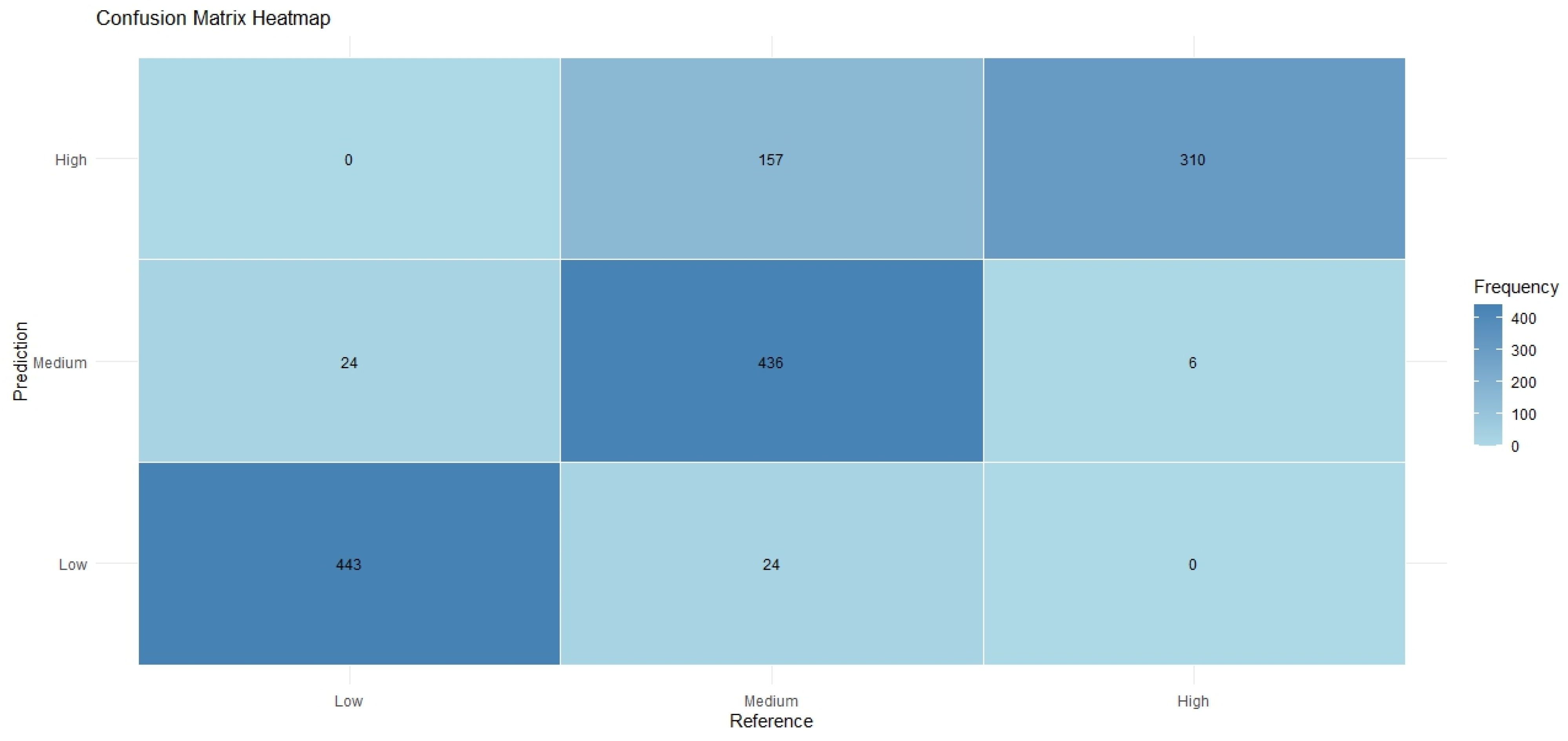
| Reference | Prediction | Frequency | Precision | Recall |
|---|---|---|---|---|
| Low | Low | 443 | 0.948608 | 1 |
| Low | Medium | 24 | 0.961686 | 1 |
| Low | High | 0 | 0.663812 | 1 |
| Medium | Low | 24 | 0.948608 | 1 |
| Medium | Medium | 436 | 0.961686 | 1 |
| Medium | High | 157 | 0.663812 | 1 |
| High | Low | 0 | 0.948608 | 1 |
| High | Medium | 6 | 0.961686 | 1 |
| High | High | 310 | 0.663812 | 1 |
| Class | Low | Medium | High |
|---|---|---|---|
| Sensitivity | 0.9486 | 0.7066 | 0.981 |
| Specificity | 0.9743 | 0.9617 | 0.8552 |
| Pos Pred Value | 0.9486 | 0.9356 | 0.6638 |
| Neg Pred Value | 0.9743 | 0.8062 | 0.9936 |
| Prevalence | 0.3336 | 0.4407 | 0.2257 |
| Detection Rate | 0.3164 | 0.3114 | 0.2214 |
| Detection Prevalence | 0.3336 | 0.3329 | 0.3336 |
| Balanced Accuracy | 0.9614 | 0.8342 | 0.9181 |
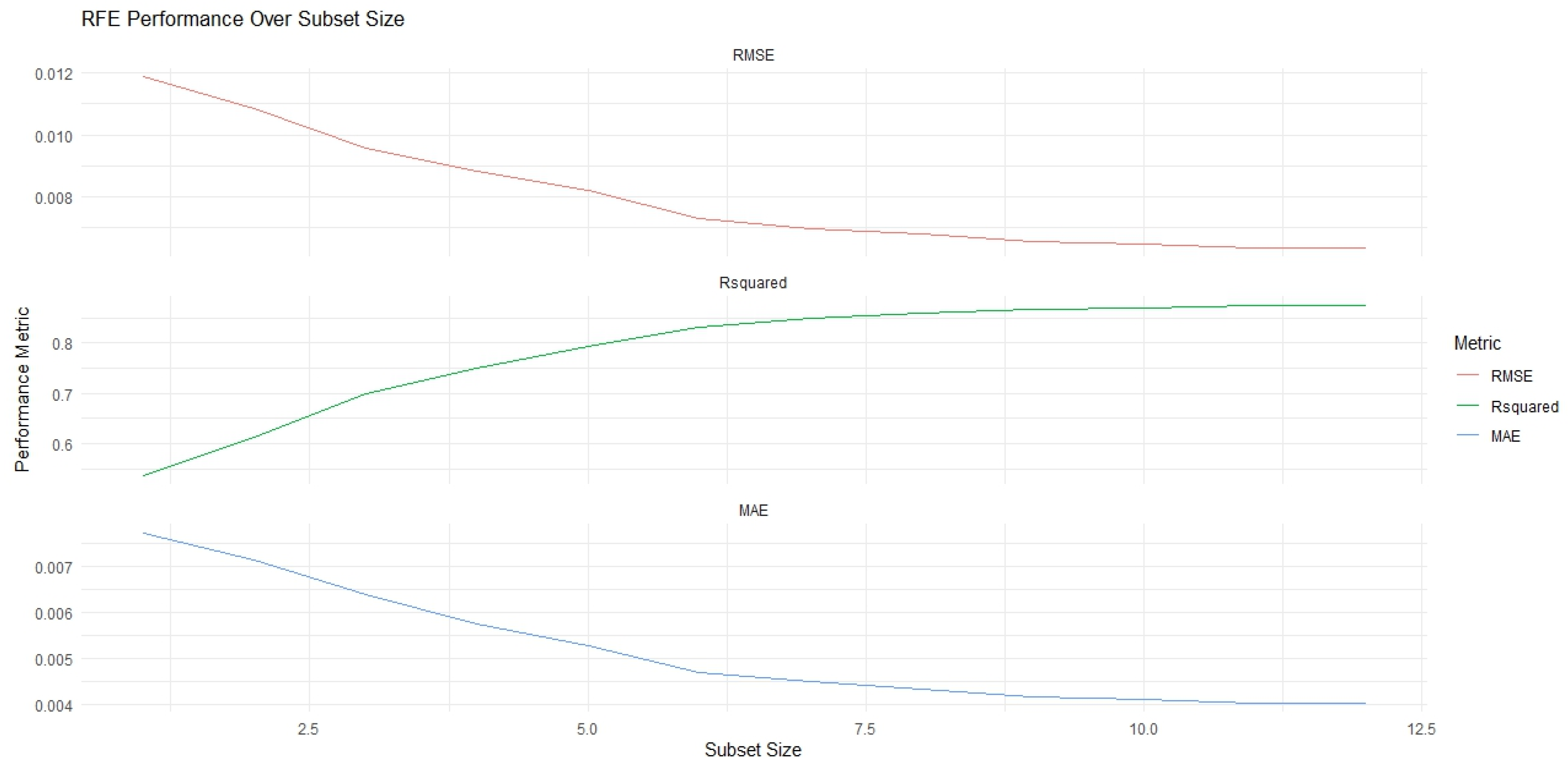
| Variables | RMSE | Rsquared | MAE | RMSESD | RsquaredSD | MAESD | RFE |
|---|---|---|---|---|---|---|---|
| Days to Pending (DTP) | 0.011863 | 0.535952 | 0.007721 | 0.001044 | 0.050047 | 0.000242 | * |
| Listing Price Cut (LPC) | 0.010833 | 0.613523 | 0.007126 | 0.000855 | 0.038162 | 0.000285 | * |
| Share of Listings With a Price Cut (SLPC) | 0.00956 | 0.69826 | 0.006382 | 0.000598 | 0.030582 | 0.000282 | * |
| Days to Close (DTC) | 0.008818 | 0.750748 | 0.005749 | 0.000592 | 0.024477 | 0.000204 | * |
| Zillow Observed Rent Index (ZORI) | 0.0082 | 0.792349 | 0.005257 | 0.000564 | 0.027883 | 0.000237 | * |
| For-Sale Inventory (FSI) | 0.007282 | 0.831117 | 0.004679 | 0.000427 | 0.02254 | 0.000216 | |
| New Constr. Sales Count (NCSC) | 0.006985 | 0.848399 | 0.004477 | 0.000446 | 0.017772 | 0.000179 | |
| New Constr. Sale Price (NCSP) | 0.006802 | 0.859017 | 0.004336 | 0.000439 | 0.014561 | 0.000136 | |
| Sale Price (SP) | 0.00654 | 0.866543 | 0.00416 | 0.000428 | 0.018364 | 0.000136 | |
| Size Rank (SR) | 0.006461 | 0.870519 | 0.004094 | 0.000454 | 0.015609 | 0.000164 | |
| Zillow Home Value Index (ZHVI) | 0.00637 | 0.875724 | 0.004027 | 0.000473 | 0.013964 | 0.000181 | |
| List Price (LP) | 0.006343 | 0.874604 | 0.004011 | 0.000457 | 0.014449 | 0.000168 |
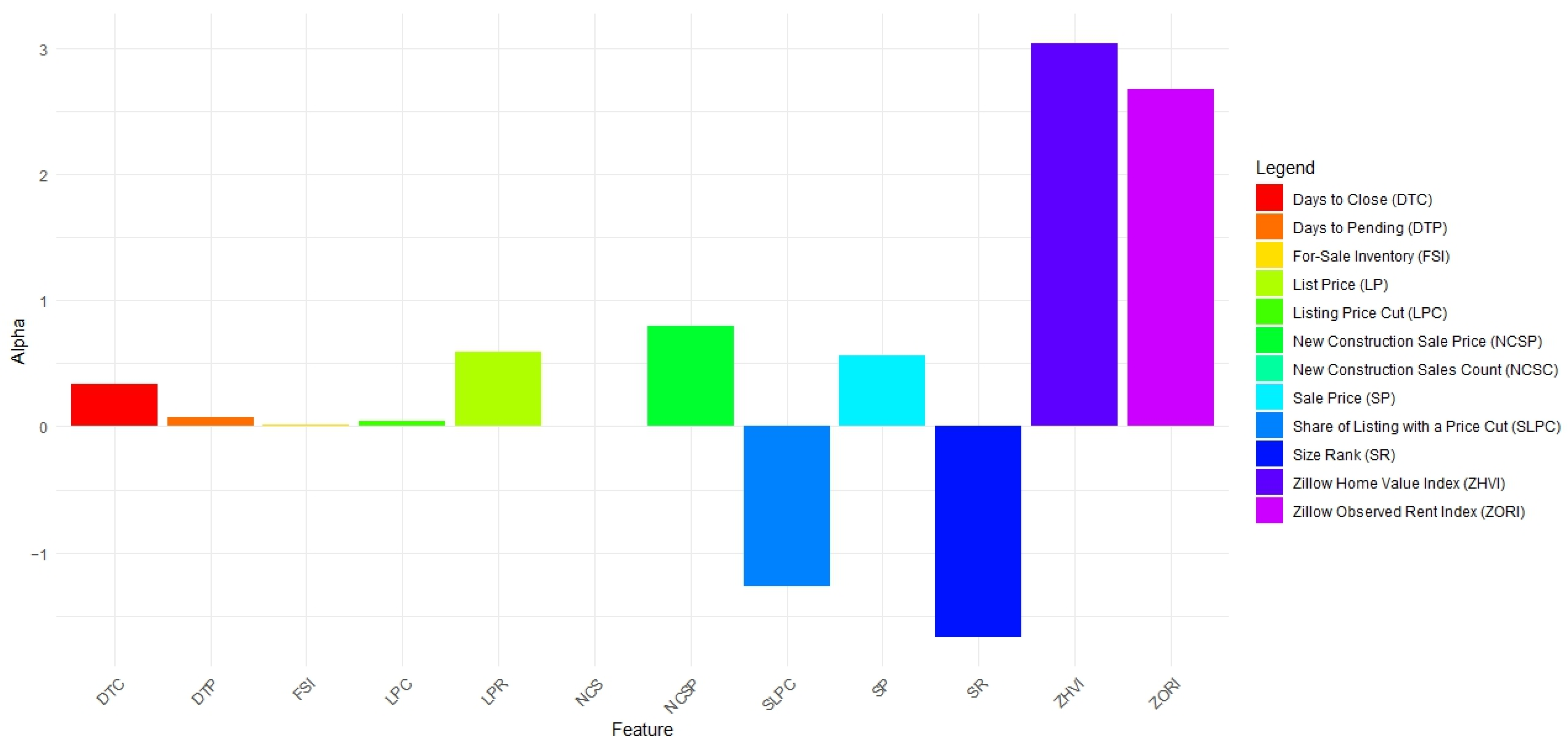
| SVM Model Feature | Alpha |
|---|---|
| Size Rank (SR) | −1.67285 |
| Sale Price (SP) | 0.558076 |
| Days to Pending (DTP) | 0.068493 |
| Days to Close (DTC) | 0.333333 |
| List Price (LP) | 0.592199 |
| Listing Price Cut (LPC) | 0.041028 |
| Share of Listings With a Price Cut (SLPC) | −1.26482 |
| For-Sale Inventory (FSI) | 0.009794 |
| Zillow Observed Rent Index (ZORI) | 2.677687 |
| Zillow Home Value Index (ZHVI) | 3.039253 |
| New Construction Sales Count (NCSC) | 0.003348 |
| New Construction Sale Price (NCSP) | 0.795975 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sobieraj, J.; Metelski, D. Machine Learning Insights: Exploring Key Factors Influencing Sale-to-List Ratio—Insights from SVM Classification and Recursive Feature Selection in the US Real Estate Market. Buildings 2024, 14, 1471. https://doi.org/10.3390/buildings14051471
Sobieraj J, Metelski D. Machine Learning Insights: Exploring Key Factors Influencing Sale-to-List Ratio—Insights from SVM Classification and Recursive Feature Selection in the US Real Estate Market. Buildings. 2024; 14(5):1471. https://doi.org/10.3390/buildings14051471
Chicago/Turabian StyleSobieraj, Janusz, and Dominik Metelski. 2024. "Machine Learning Insights: Exploring Key Factors Influencing Sale-to-List Ratio—Insights from SVM Classification and Recursive Feature Selection in the US Real Estate Market" Buildings 14, no. 5: 1471. https://doi.org/10.3390/buildings14051471
APA StyleSobieraj, J., & Metelski, D. (2024). Machine Learning Insights: Exploring Key Factors Influencing Sale-to-List Ratio—Insights from SVM Classification and Recursive Feature Selection in the US Real Estate Market. Buildings, 14(5), 1471. https://doi.org/10.3390/buildings14051471










