Risk Analysis and Simulation of Large Bridge Construction Based on System Dynamics
Abstract
1. Introduction
2. Risk Factor Analysis for Large Bridge Construction
2.1. Construction Risk Evolution Mechanism Analysis
2.2. Risk Factor Identification
3. System Dynamics Modelling of Large Bridge Construction Risks
3.1. Boundary Determination and Underlying Assumptions
3.2. Causal Loop Diagrams and Flow Diagrams Based on System Dynamics
3.3. Establishment of System Dynamics Equations
4. Construction Risk Simulation for Large Bridges
4.1. Project Case Overview
4.2. Parameter Determination and Variable Assignment
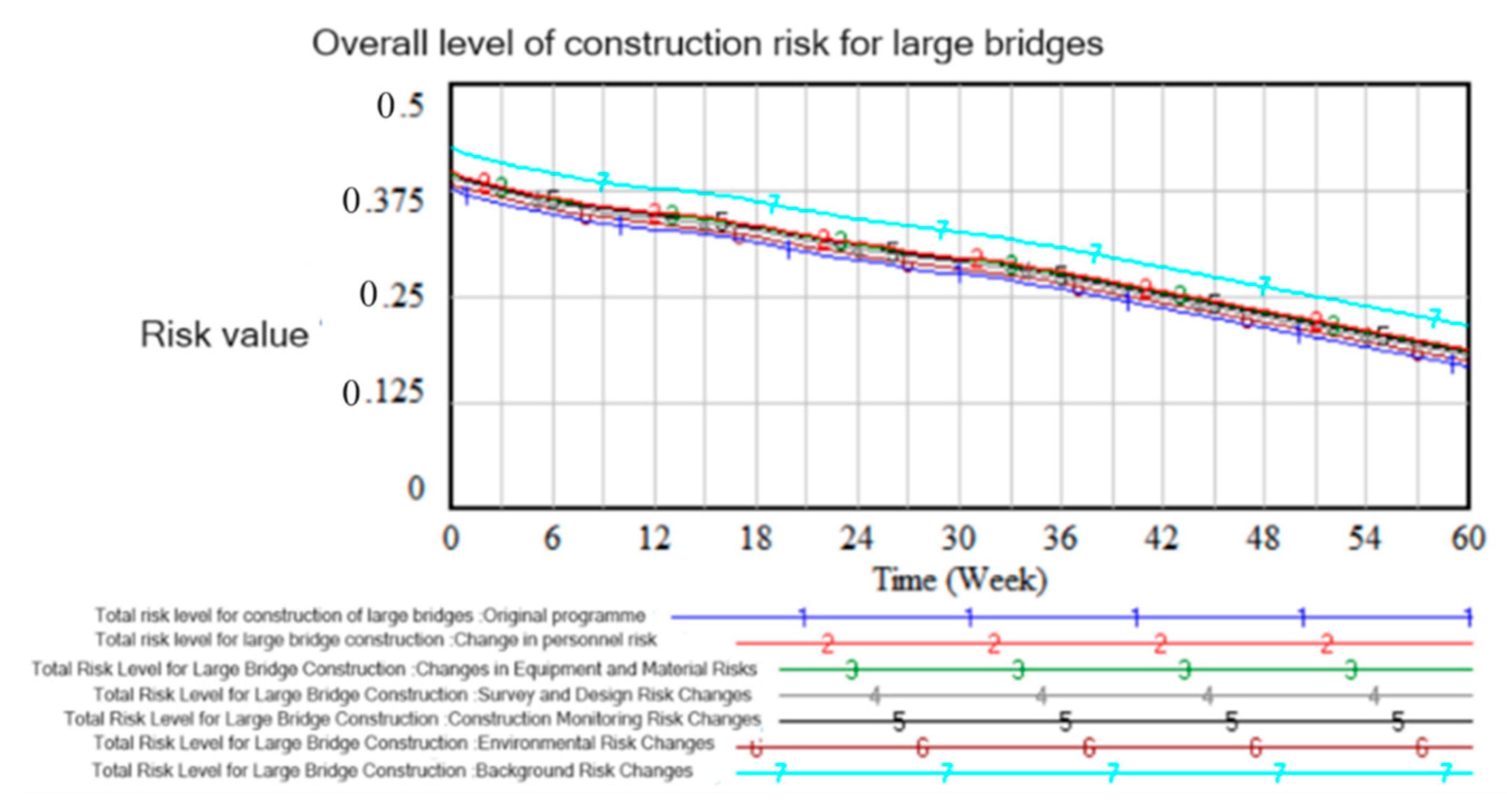
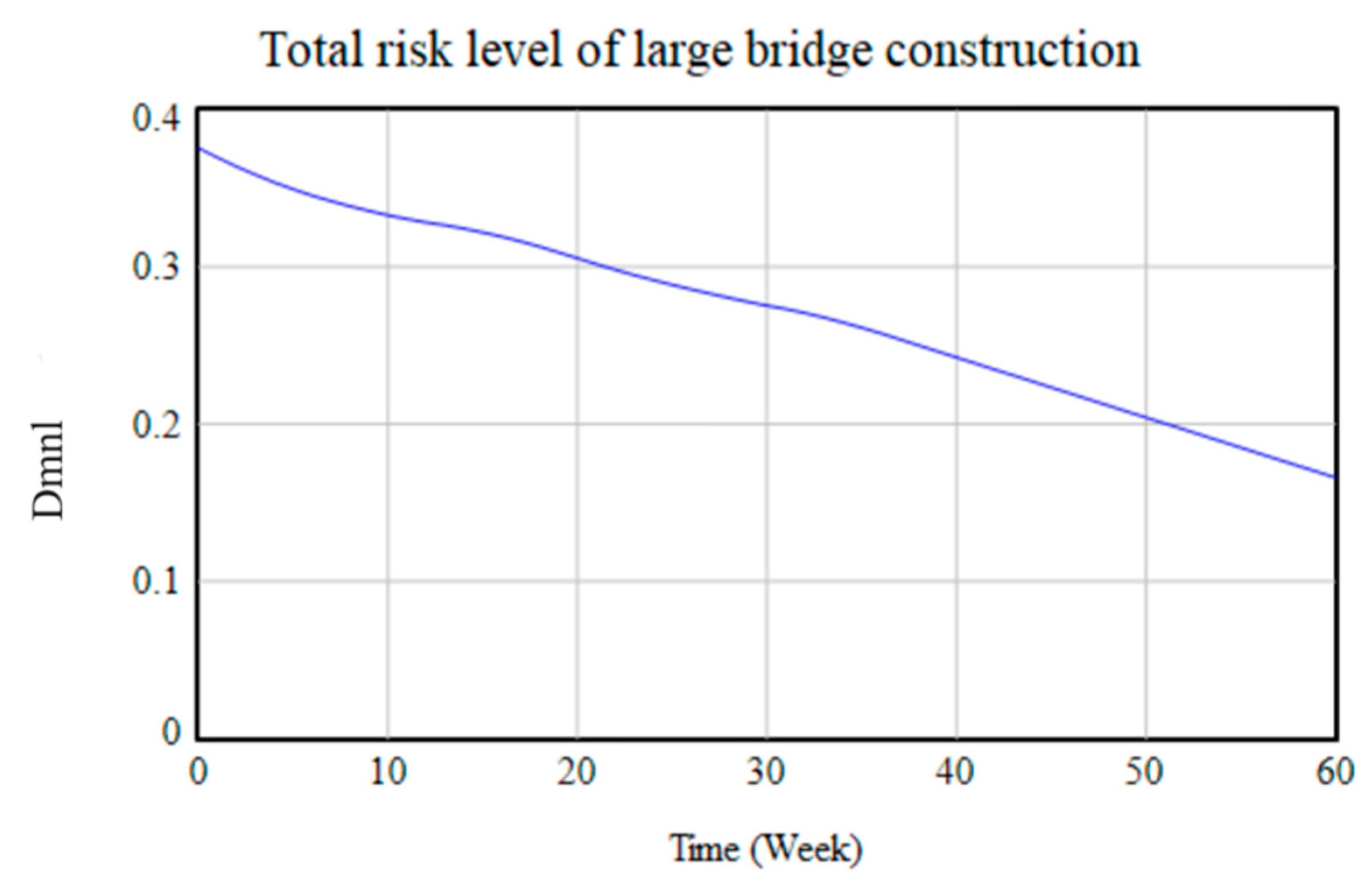
4.3. Model Simulation and Result Analysis
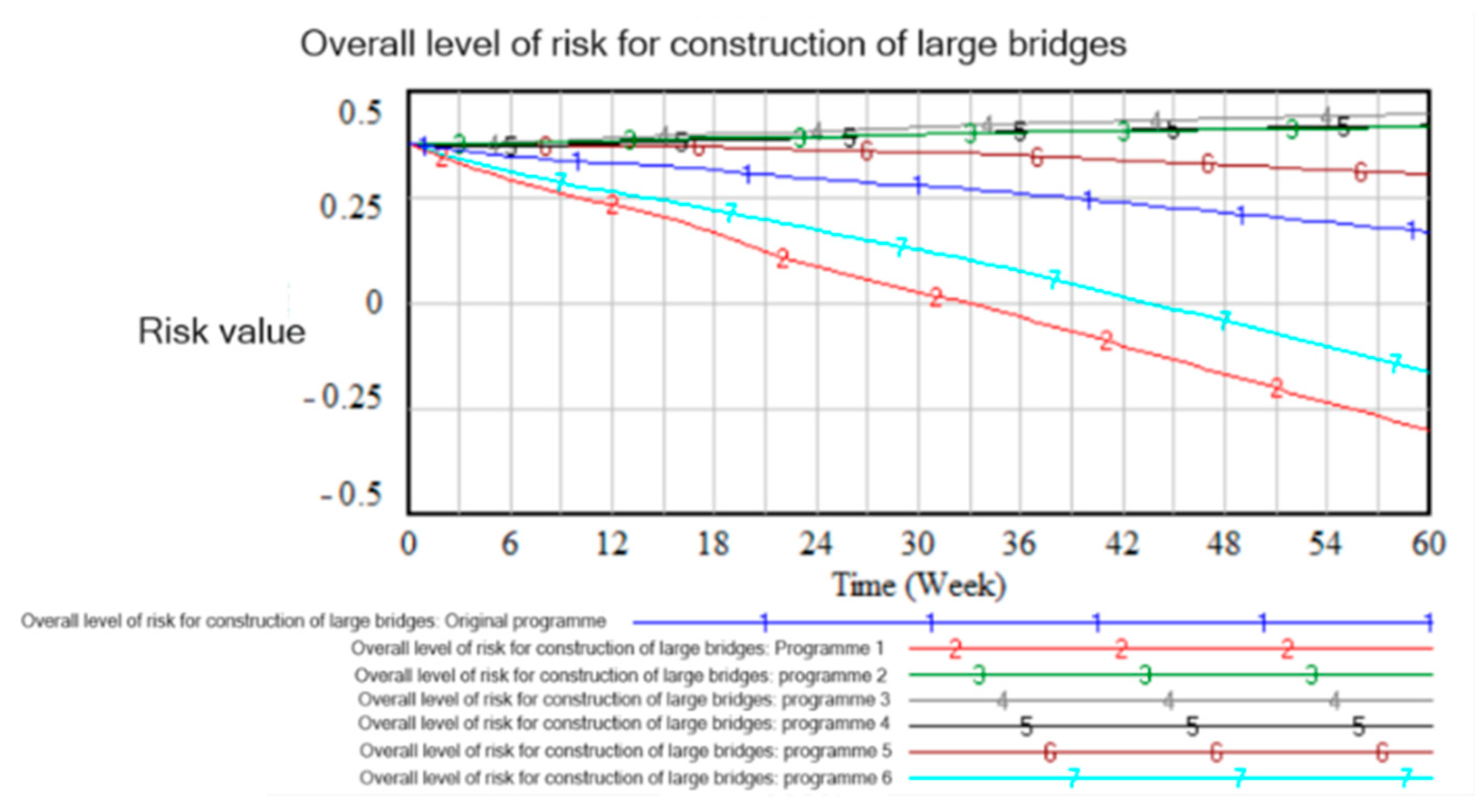
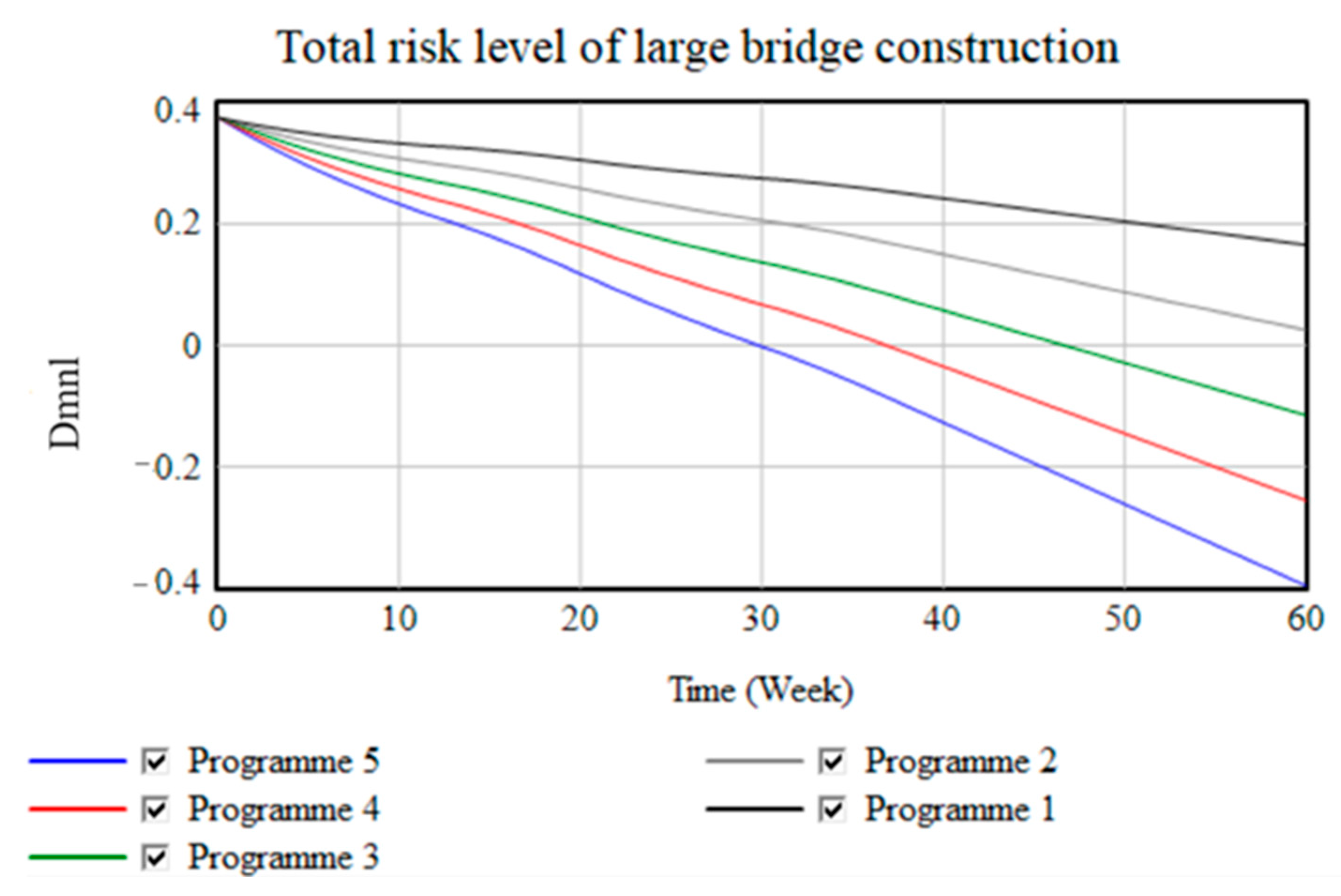
4.4. Risk Analysis and Simulation of Large Bridge Construction with Strategies for Optimizing Safety Investments
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, K.Y.; Yang, C.F. Research on the Application of AHP-DEA in Bridge Construction Risk Evaluation. J. Hebei Univ. Technol. 2014, 43, 102–106. [Google Scholar]
- Li, Y.C.; Feng, Z.R.; Wang, X.J. Construction Risk Evaluation of Highway Bridges Based on ANP 2D Cloud Modelling. J. Wuhan Univ. Technol. 2019, 41, 73–79. [Google Scholar]
- Chen, G.H.; Wu, W.S.; Xu, S.Y. HSE risk evaluation of cross-sea bridge project construction based on WBS-RBS and AHP. China Saf. Sci. J. 2013, 23, 51–57. [Google Scholar]
- Wang, C.B.; Song, Y.M. Research on bridge construction risk factors based on factor analysis method. J. Hunan Univ. Arts Sci. Nat. Sci. Ed. 2018, 30, 45–50. [Google Scholar]
- Bao, L.S.; Liu, K.T.; Yu, L. Multi-objective risk analysis and evaluation of bridge construction scheme based on grey hierarchical analysis method. J. Shenyang Jianzhu Univ. Soc. Sci. 2009, 25, 663–669. [Google Scholar]
- Feng, D.C.; Cao, X.Y.; Michael, B. An enhanced PDEM-based framework for reliability analysis of structures considering multiple failure modes and limit states. Probabilistic Eng. Mech. 2022, 70, 103367. [Google Scholar] [CrossRef]
- Cao, X.Y.; Xiong, C.Z.; Feng, D.C. Dynamic and probabilistic seismic performance assessment of precast prestressed reinforced concrete frames incorporating slab infuence through three-dimensional spatial mode. Bull. Earthq. Eng. 2022, 20, 6705–6739. [Google Scholar] [CrossRef]
- Yuan, H.C.; Zhang, W.L.; You, J.C. Safety Risk Evaluation of Bridge Construction Based on Improved Cloud Modelling. J. Eng. Stud. 2018, 10, 600–606. [Google Scholar] [CrossRef]
- Yuan, J.B.; Cui, G.; Fu, Q.S. Research on safety risk evaluation of road bridge construction based on network analysis method. Technol. Prog. Policy 2014, 31, 96–100. [Google Scholar]
- Wang, L.; Guo, Z.S.; Yang, G.J. Safety Risk Evaluation of Bridge Substructure in Loess Mountain Alluvial Terrain. Saf. Environ. Eng. 2022, 29, 26–32. [Google Scholar]
- Tang, T.M.; Guan, Y.N.; Wang, G.B. Safety Risk Assessment of Wuhan Qingshan Yangtze River Highway Bridge during Construction Phase. Bridge Constr. 2020, 50, 38–43. [Google Scholar]
- Zhu, Z.B.; Ma, C.F.; Wang, B. Safety Risk Assessment for Construction of Pingtan Strait Dual-purpose Bridge. Bridge Constr. 2017, 47, 12–16. [Google Scholar]
- Peng, W.Y.; Fan, Y.Y.; Li, H. Risk evaluation of large-span bridge construction phase based on grey clustering method. J. Eng. Manag. 2015, 29, 101–105. [Google Scholar]
- Bo, J.S. Research on Safety Risk Management of Long-Span Steel Box Arch Bridge Erection Construction Based on System Dynamics. Master’s Thesis, Chongqing Jiaotong University, Chongqing, China, 2023. [Google Scholar]
- Guo, Z.Q. Research on Safety Risk of Deep-Water Foundation Construction for Large-Span Cable-Stayed Bridges Based on System Dynamics. Master’s Thesis, Chongqing Jiaotong University, Chongqing, China, 2022. [Google Scholar]
- Liu, W.; Liu, Z.X. Simulation Analysis of Supply Chain Resilience of Prefabricated Building Projects Based on System Dynamics. Buildings 2023, 13, 2629. [Google Scholar] [CrossRef]
- Cheng, Y.F. Research on Cost Control of Bridge Engineering Construction Projects Based on System Dynamics. Master’s Thesis, Shenyang Jianzhu University, Shenyang, China, 2023. [Google Scholar]
- Zhao, C. Research on Safety Simulation of Elevated Bridge Construction Based on System Dynamics. Master’s Thesis, Zhengzhou University, Zhengzhou, China, 2022. [Google Scholar]
- Lin, K.Z.; Wang, Q.; Yang, H.Q. Risk Event Identification and Analysis in the Construction Process of Cross-Sea Bridges. J. Highw. Transp. Res. Dev. Appl. Technol. Ed. 2020, 16, 338–340+360. [Google Scholar]
- Wang, Y.M.; Zhang, Y.Y.; Zhu, B.M. Research on Construction Safety Risk Evaluation of Large-span Continuous Steel Truss Girder Bridges for Both Highway and Railway. Constr. Saf. 2023, 38, 76–82. [Google Scholar]
- Wu, D. Research on Construction Cost Control of Large Bridge Projects Based on System Dynamics. Master’s Thesis, Chongqing University, Chongqing, China, 2017. [Google Scholar]
- Chen, S.Z.; Wu, G.; Feng, D.C. Multi-Cross-Reference Method for Highway-Bridge Damage Identification Based on Long-Gauge Fiber Bragg-Grating Sensors. J. Bridge Eng. 2020, 6, 25. [Google Scholar] [CrossRef]
- Xu, X.H. Research on Risk Evaluation and Control of Steel Box Girder Bridge Construction Based on Step-by-Step Launching Technique. Master’s Thesis, Southeast University, Nanjing, China, 2023. [Google Scholar]
- Wang, Y.D.; Ibarra, L.; Pantelides, C. Seismic retrofit of a three-span RC bridge with buckling-restrained braces. J. Bridge Eng. 2016, 21, 11. [Google Scholar] [CrossRef]
- Kaviani, P.; Zareian, F.; Taciroglu, E. Seismic behavior of reinforced concrete bridges with skew-angled seat-type abutments. Eng. Struct. 2012, 45, 137–150. [Google Scholar] [CrossRef]
- Vincenzo, G.; Francesco, P.; Giulio, P. Multiple Tests for Dynamic Identification of a Reinforced Concrete Multi-Span Arch Bridge. Buildings 2022, 12, 833. [Google Scholar] [CrossRef]
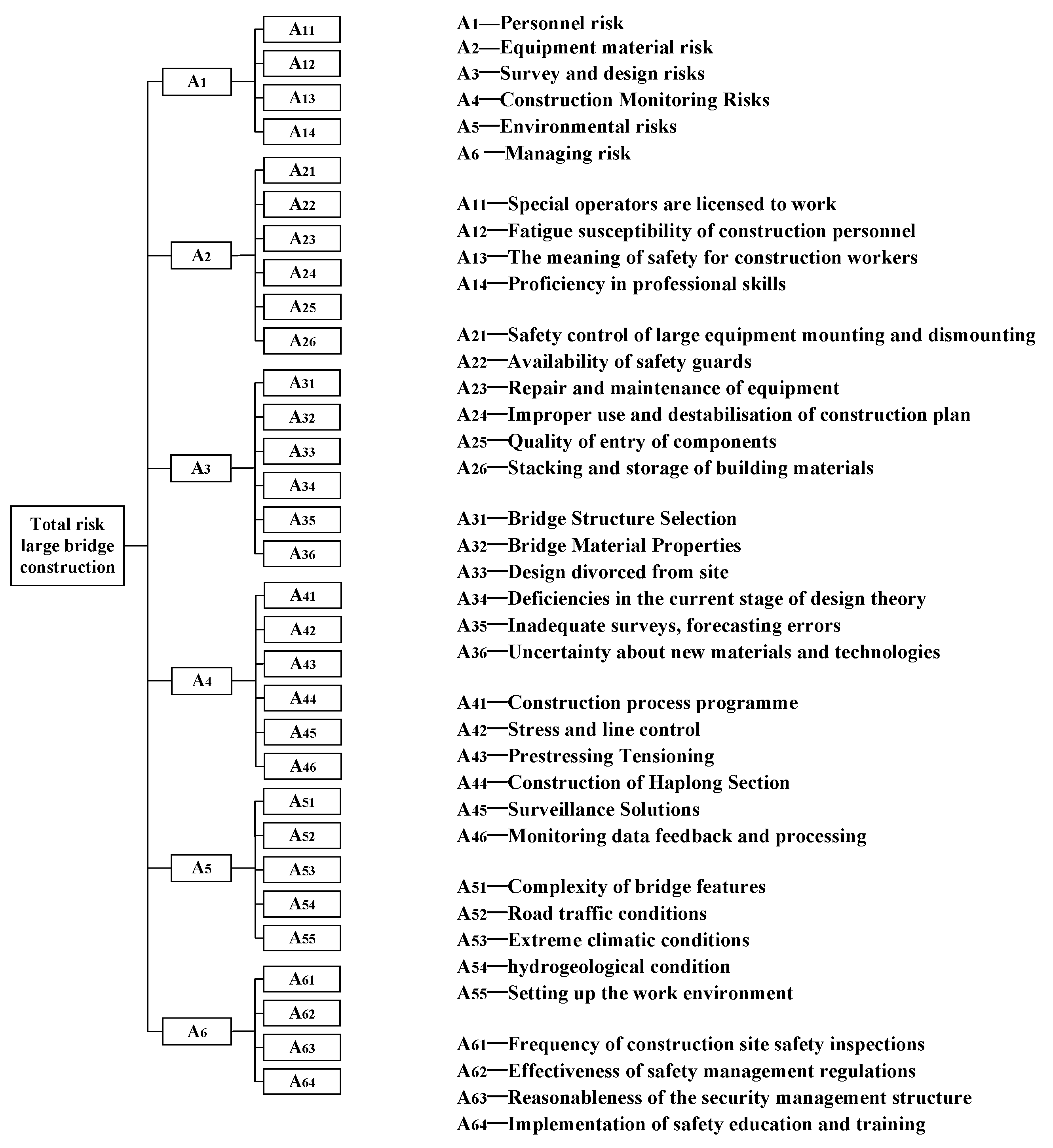



| S/N | Type | ID | Name | S/N | Type | ID | Name |
|---|---|---|---|---|---|---|---|
| 1 | Horizontal variable | S1 | Personnel risk level | 27 | Auxiliary Variables | I15 | Deficiencies in the current stage of design theory |
| 2 | S2 | Equipment material risk level | 28 | I16 | Inadequate surveys, forecasting errors | ||
| 3 | S3 | Survey and design risk level | 29 | I17 | Uncertainty about new materials and technologies | ||
| 4 | S4 | Construction monitoring risk level | 30 | I18 | Construction process program | ||
| 5 | S5 | Environmental risk level | 31 | I19 | Stress and line control | ||
| 6 | S6 | Managing the level of risk | 32 | I20 | Prestressing tensioning construction | ||
| 7 | Rate variables | R1 | Amount of change in personnel risk level | 33 | I21 | Construction of the closing section | |
| 8 | R2 | Amount of change in equipment material risk level | 34 | I22 | Surveillance solutions | ||
| 9 | R3 | Amount of change in level of survey and design risk | 35 | I23 | Monitoring data feedback and processing | ||
| 10 | R4 | Amount of change in the level of construction monitoring risk | 36 | I24 | Complexity of bridge features | ||
| 11 | R5 | Amount of change in the level of environmental risk | 37 | I25 | Road traffic conditions | ||
| 12 | R6 | Amount of change in the level of management risk | 38 | I26 | Extreme climatic conditions | ||
| 13 | Auxiliary variables | I1 | Total risk level for construction of large bridges | 39 | I27 | Hydrogeological conditions | |
| 14 | I2 | Special operators licensed to work | 40 | I28 | Setting up work environment | ||
| 15 | I3 | Fatigue susceptibility of construction personnel | 41 | I29 | Frequency of construction site safety inspections | ||
| 16 | I4 | Safety awareness among construction workers | 42 | I30 | Effectiveness of safety management regulations | ||
| 17 | I5 | Proficiency in professional skills | 43 | I31 | Reasonableness of security management structure | ||
| 18 | I6 | Safety control of large equipment mounting and dismounting | 44 | I32 | Investment in security management funds | ||
| 19 | I7 | Availability of safety guards | 45 | I33 | Implementation of safety education and training | ||
| 20 | I8 | Repair and maintenance of equipment | 46 | I34 | Security inputs | ||
| 21 | I9 | Improper use and destabilization of construction plant | 47 | I35 | Personnel security inputs | ||
| 22 | I10 | Quality of entry of components | 48 | I36 | Security inputs for equipment and materials | ||
| 23 | I11 | Stacking and storage of building materials | 49 | I37 | Survey and design safety inputs | ||
| 24 | I12 | Bridge structure selection | 50 | I38 | Construction monitoring security inputs | ||
| 25 | I13 | Bridge material properties | 51 | I39 | Safety inputs for environmental risks | ||
| 26 | I14 | Design divorced from site | 52 | I40 | Managing security inputs |
| Weights | Volume | Weights | Volume | Weights | Volume |
|---|---|---|---|---|---|
| W1 | 0.203 | W24 | 0.021 | W45 | 0.021 |
| W2 | 0.146 | W25 | 0.016 | W46 | 0.029 |
| W3 | 0.137 | W26 | 0.023 | W51 | 0.021 |
| W4 | 0.134 | W31 | 0.021 | W52 | 0.019 |
| W5 | 0.094 | W32 | 0.023 | W53 | 0.016 |
| W6 | 0.286 | W33 | 0.026 | W54 | 0.015 |
| W11 | 0.047 | W34 | 0.019 | W55 | 0.023 |
| W12 | 0.026 | W35 | 0.031 | W61 | 0.068 |
| W13 | 0.067 | W36 | 0.017 | W62 | 0.072 |
| W14 | 0.063 | W41 | 0.019 | W63 | 0.065 |
| W21 | 0.024 | W42 | 0.027 | W64 | 0.081 |
| W22 | 0.027 | W43 | 0.016 | ||
| W23 | 0.035 | W44 | 0.022 |
| S/N | Symbol | Variable Names | Initial Assignment |
|---|---|---|---|
| 1 | L01 | Personnel risk | 0.3 |
| 2 | L02 | Equipment material risk | 0.4 |
| 3 | L03 | Survey and design risks | 0.3 |
| 4 | L04 | Construction monitoring risks | 0.4 |
| 5 | L05 | Environmental risks | 0.2 |
| 6 | L06 | Managing risk | 0.5 |
| S/N | Subsystem Name | Proportion of Inputs | Symbol |
|---|---|---|---|
| 1 | Personnel risk | 0.15 | P1 |
| 2 | Equipment material risk | 0.17 | P2 |
| 3 | Survey and design risks | 0.16 | P3 |
| 4 | Construction monitoring risks | 0.19 | P4 |
| 5 | Environmental risks | 0.12 | P5 |
| 6 | Managing risk | 0.21 | P6 |
| Risk Factors | Unit Length Change | Risk Factors | Unit Length Change |
|---|---|---|---|
| Special operators licensed to work | 0.029 | Construction process program | 0.056 |
| Fatigue susceptibility of construction personnel | 0.037 | Stress and line control | 0.065 |
| Safety awareness among construction workers | 0.046 | Prestressing Tensioning Construction | 0.061 |
| Proficiency in professional skills | 0.033 | Construction of the closing section | 0.067 |
| Safety control of large equipment mounting and dismounting | 0.057 | Surveillance solutions | 0.063 |
| Availability of safety guards | 0.045 | Monitoring data feedback and processing | 0.059 |
| Repair and maintenance of equipment | 0.038 | Complexity of bridge features | 0.037 |
| Improper use and destabilisation of construction plant | 0.051 | Road traffic conditions | 0.035 |
| Quality of entry of components | 0.026 | Hydrogeological conditions | 0.034 |
| Stacking and storage of building materials | 0.031 | Setting up work environment | 0.043 |
| Bridge structure selection | 0.023 | Frequency of construction site safety inspections | 0.049 |
| Bridge material properties | 0.026 | Effectiveness of safety management regulations | 0.042 |
| Design divorced from site | 0.029 | Reasonableness of security management structure | 0.036 |
| Deficiencies in current stage of design theory | 0.021 | Implementation of safety education and training | 0.059 |
| Inadequate surveys, forecasting errors | 0.039 | ||
| Uncertainty about new materials and technologies | 0.033 |
| Program | Proportion of Inputs | |||||
|---|---|---|---|---|---|---|
| Personnel Risk | Equipment Material Risk | Survey and Design Risks | Construction Monitoring Risks | Environmental Risks | Managing Risk | |
| 1 | 0.5 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 |
| 2 | 0.1 | 0.5 | 0.1 | 0.1 | 0.1 | 0.1 |
| 3 | 0.1 | 0.1 | 0.5 | 0.1 | 0.1 | 0.1 |
| 4 | 0.1 | 0.1 | 0.1 | 0.5 | 0.1 | 0.1 |
| 5 | 0.1 | 0.1 | 0.1 | 0.1 | 0.5 | 0.1 |
| 6 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.5 |
| Name | Safety Investment/CNY 10,000 |
|---|---|
| Program 1 | 30 |
| Program 2 | 40 |
| Program 3 | 50 |
| Program 4 | 60 |
| Program 5 | 70 |
| Time | Program 1 | Program 2 | Program 3 | Program 4 | Program 5 |
|---|---|---|---|---|---|
| 0 | 0.3758 | 0.3758 | 0.3758 | 0.3758 | 0.3758 |
| 5 | 0.349528 | 0.336057 | 0.322586 | 0.309114 | 0.295643 |
| 10 | 0.333048 | 0.308064 | 0.283081 | 0.258097 | 0.233114 |
| 15 | 0.322133 | 0.28675 | 0.251366 | 0.215982 | 0.180599 |
| 20 | 0.305696 | 0.25881 | 0.211924 | 0.165038 | 0.118152 |
| 25 | 0.288767 | 0.230281 | 0.171796 | 0.113311 | 0.0548254 |
| 30 | 0.275563 | 0.206226 | 0.136889 | 0.0675516 | −0.00178533 |
| 35 | 0.26148 | 0.181119 | 0.100758 | 0.0203965 | −0.0599646 |
| 40 | 0.242582 | 0.150236 | 0.0578892 | −0.0344572 | −0.126803 |
| 45 | 0.22345 | 0.119072 | 0.0146935 | −0.0896848 | −0.194063 |
| 50 | 0.204318 | 0.0879081 | −0.0285022 | −0.144912 | −0.261322 |
| 55 | 0.185186 | 0.0567444 | −0.0716978 | −0.20014 | −0.328582 |
| 60 | 0.166055 | 0.0255806 | −0.114893 | −0.255368 | −0.395841 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fu, X.; Yang, M.; Liu, H.; Wang, L.; Li, Q. Risk Analysis and Simulation of Large Bridge Construction Based on System Dynamics. Buildings 2024, 14, 1488. https://doi.org/10.3390/buildings14051488
Fu X, Yang M, Liu H, Wang L, Li Q. Risk Analysis and Simulation of Large Bridge Construction Based on System Dynamics. Buildings. 2024; 14(5):1488. https://doi.org/10.3390/buildings14051488
Chicago/Turabian StyleFu, Xu, Meng Yang, Huanqin Liu, Lintai Wang, and Qian Li. 2024. "Risk Analysis and Simulation of Large Bridge Construction Based on System Dynamics" Buildings 14, no. 5: 1488. https://doi.org/10.3390/buildings14051488
APA StyleFu, X., Yang, M., Liu, H., Wang, L., & Li, Q. (2024). Risk Analysis and Simulation of Large Bridge Construction Based on System Dynamics. Buildings, 14(5), 1488. https://doi.org/10.3390/buildings14051488






