Deformation Characteristics and Energy Evolution Rules of Siltstone under Stepwise Cyclic Loading and Unloading
Abstract
1. Introduction
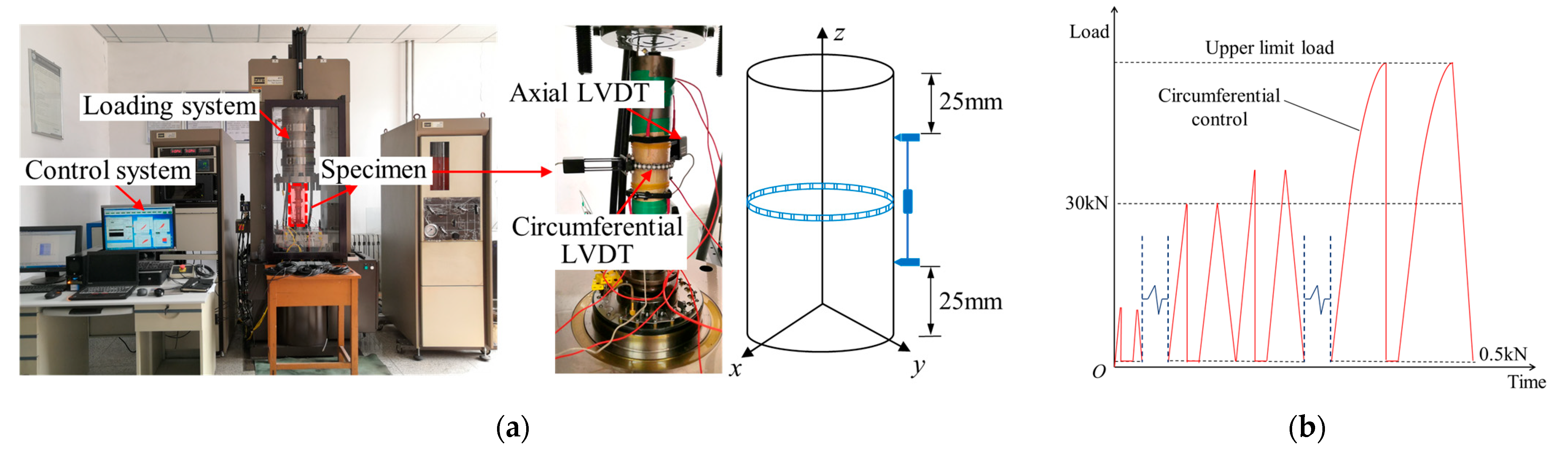
2. Uniaxial Step Loading and Unloading Test
2.1. Experimental Materials
2.2. Experimental Scheme
3. Mechanism and Evolution Characteristics of Siltstone Deformation at Different Loading and Unloading Stages
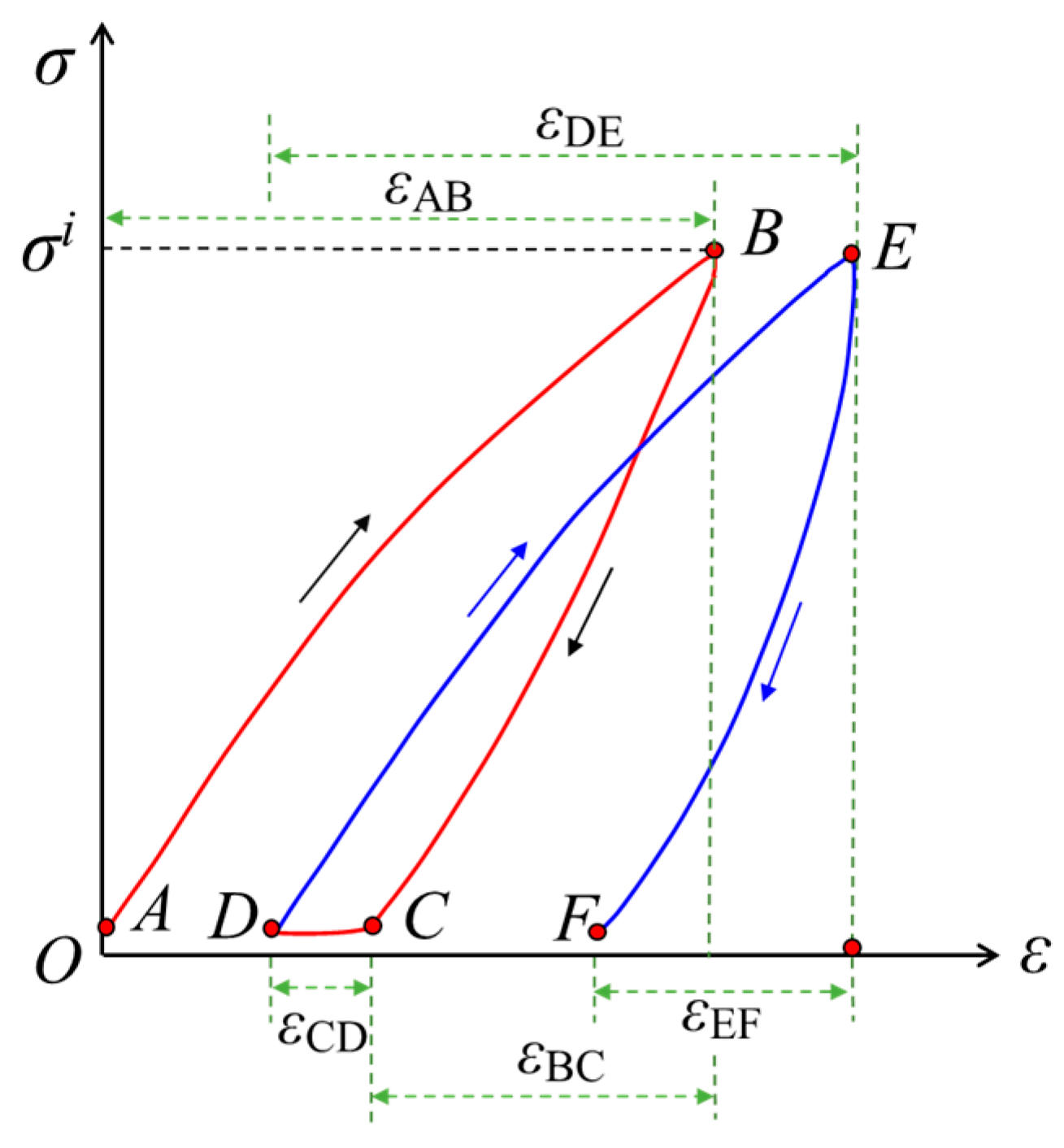
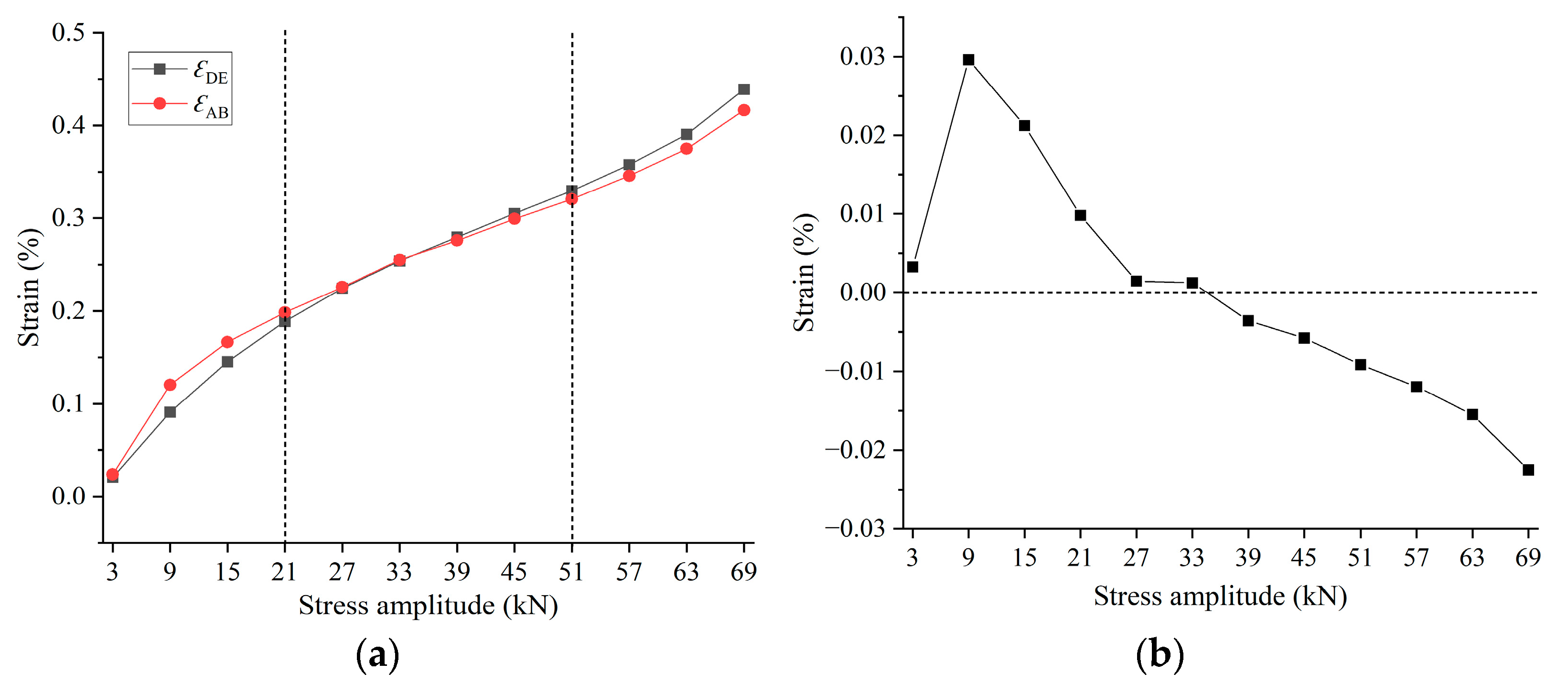
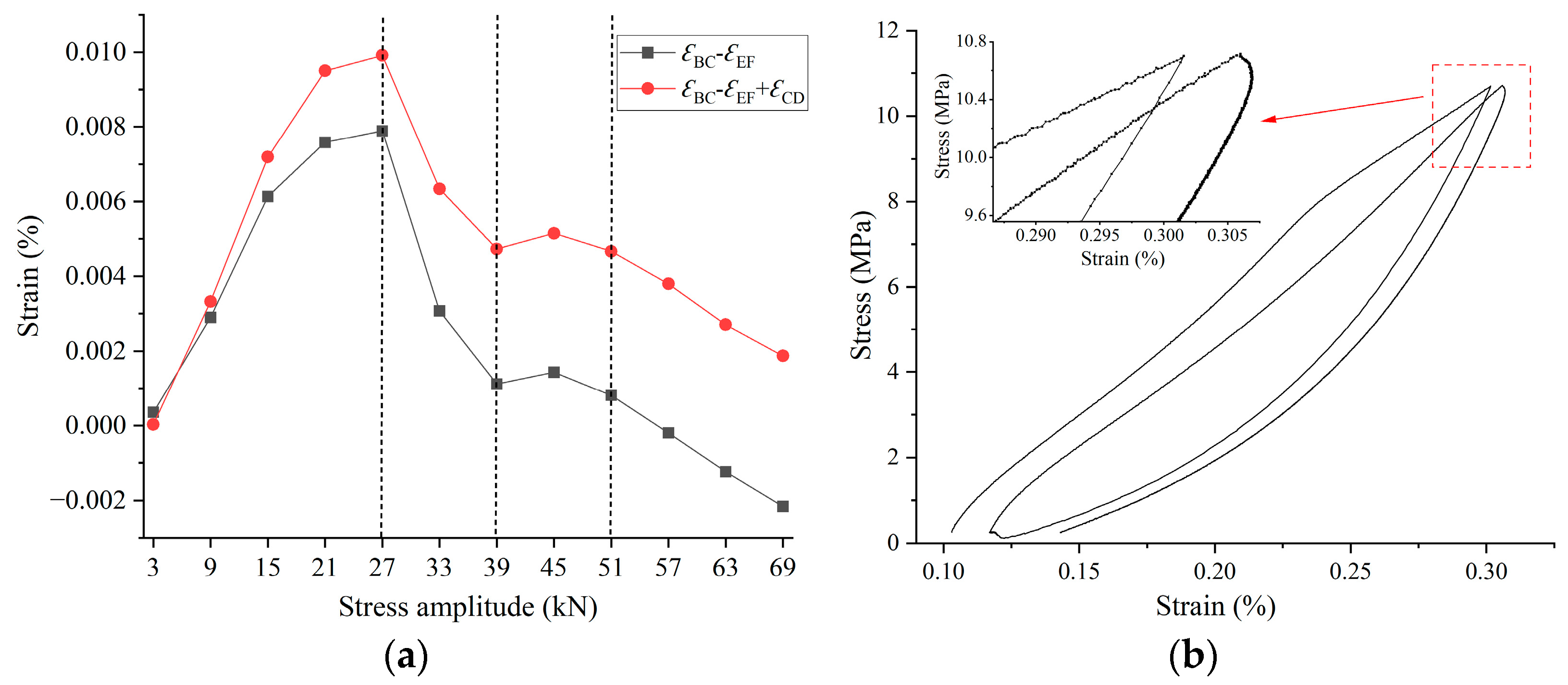
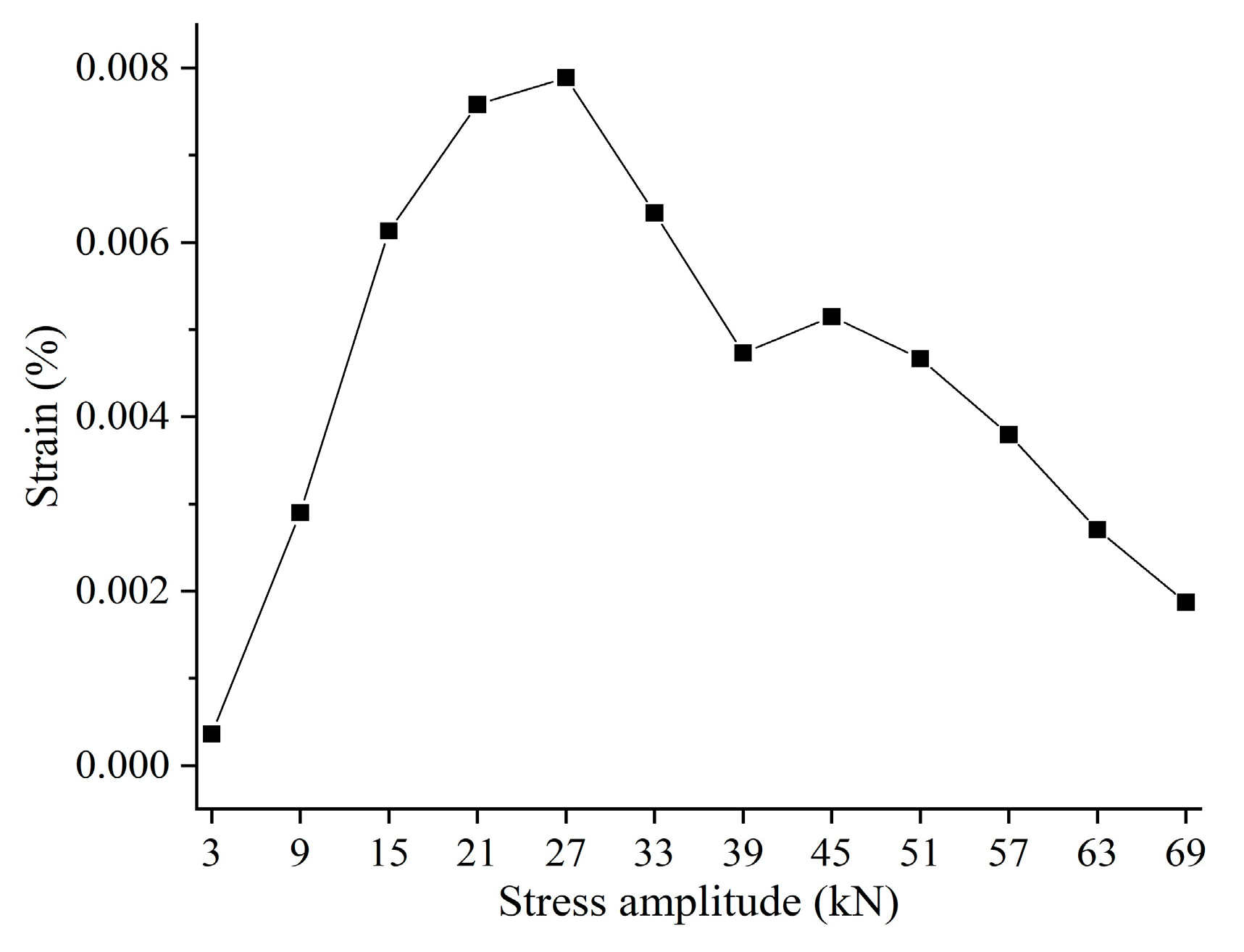
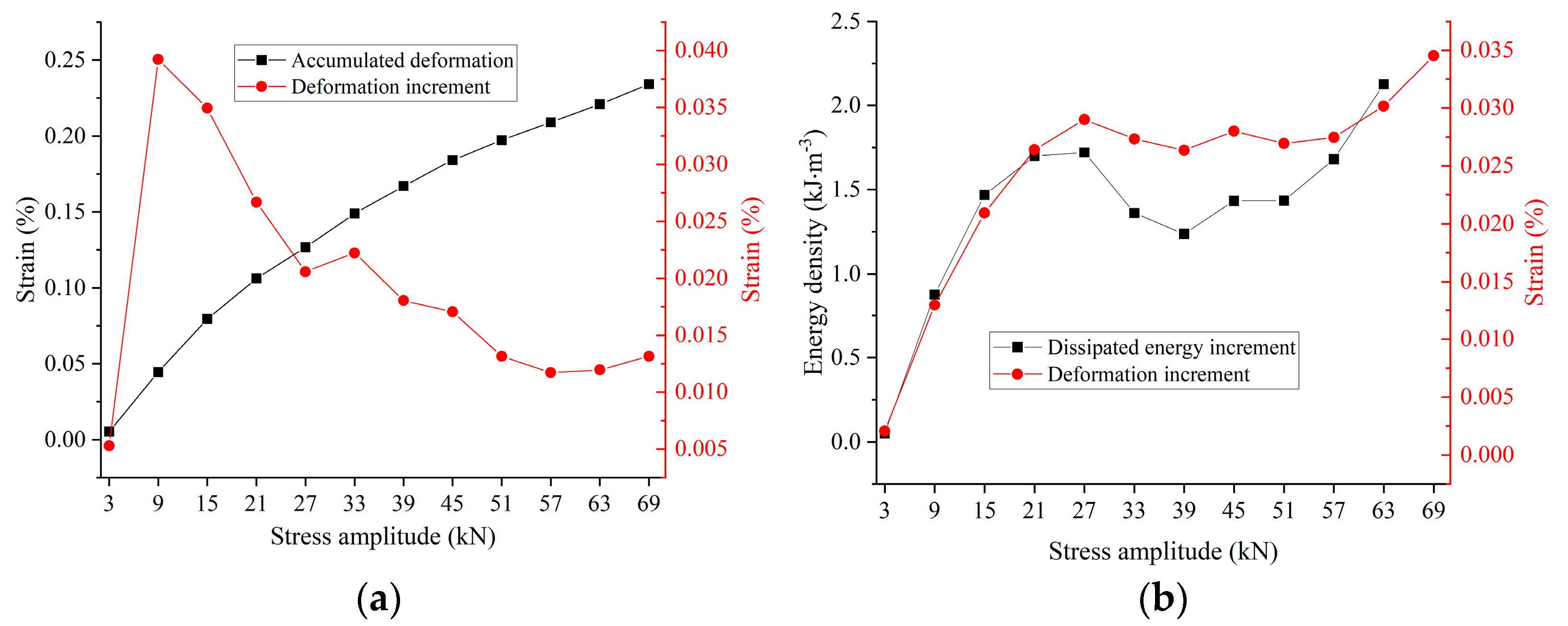
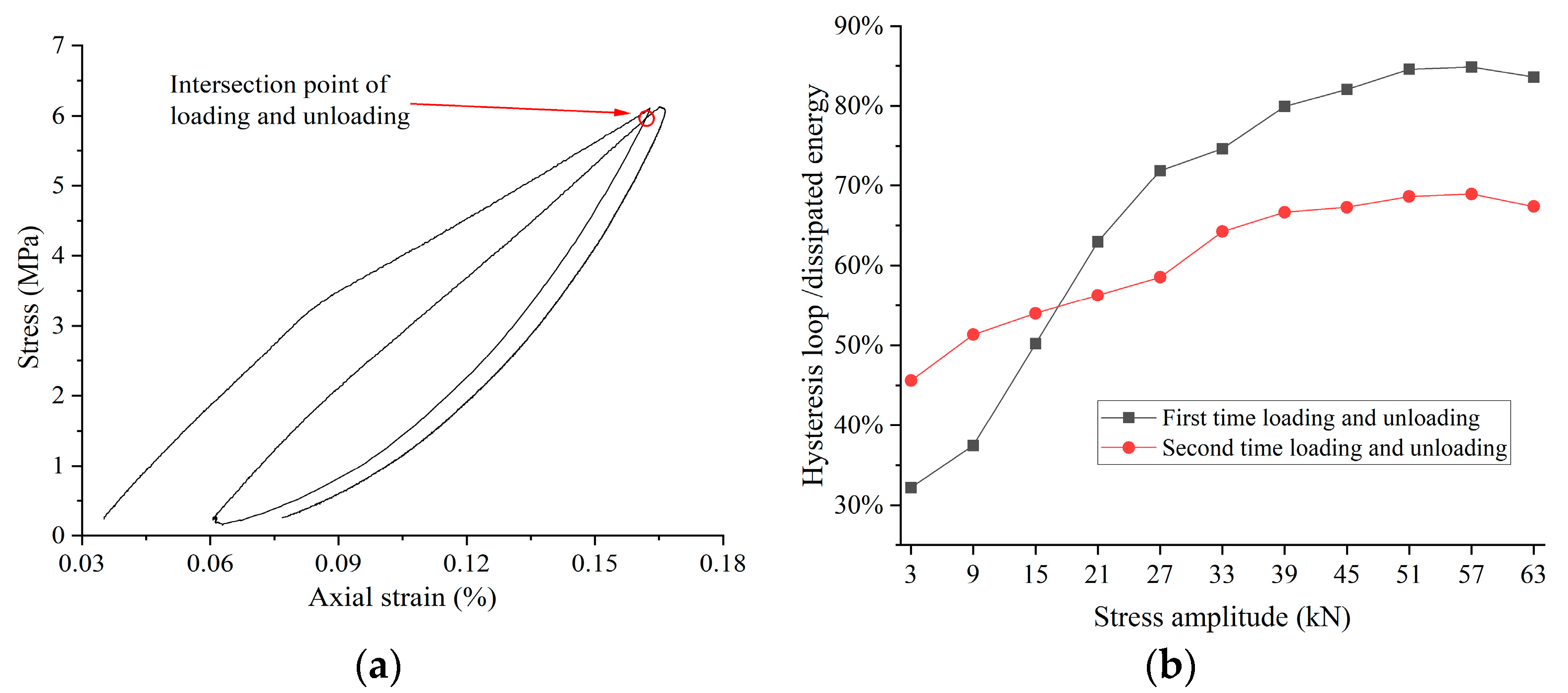
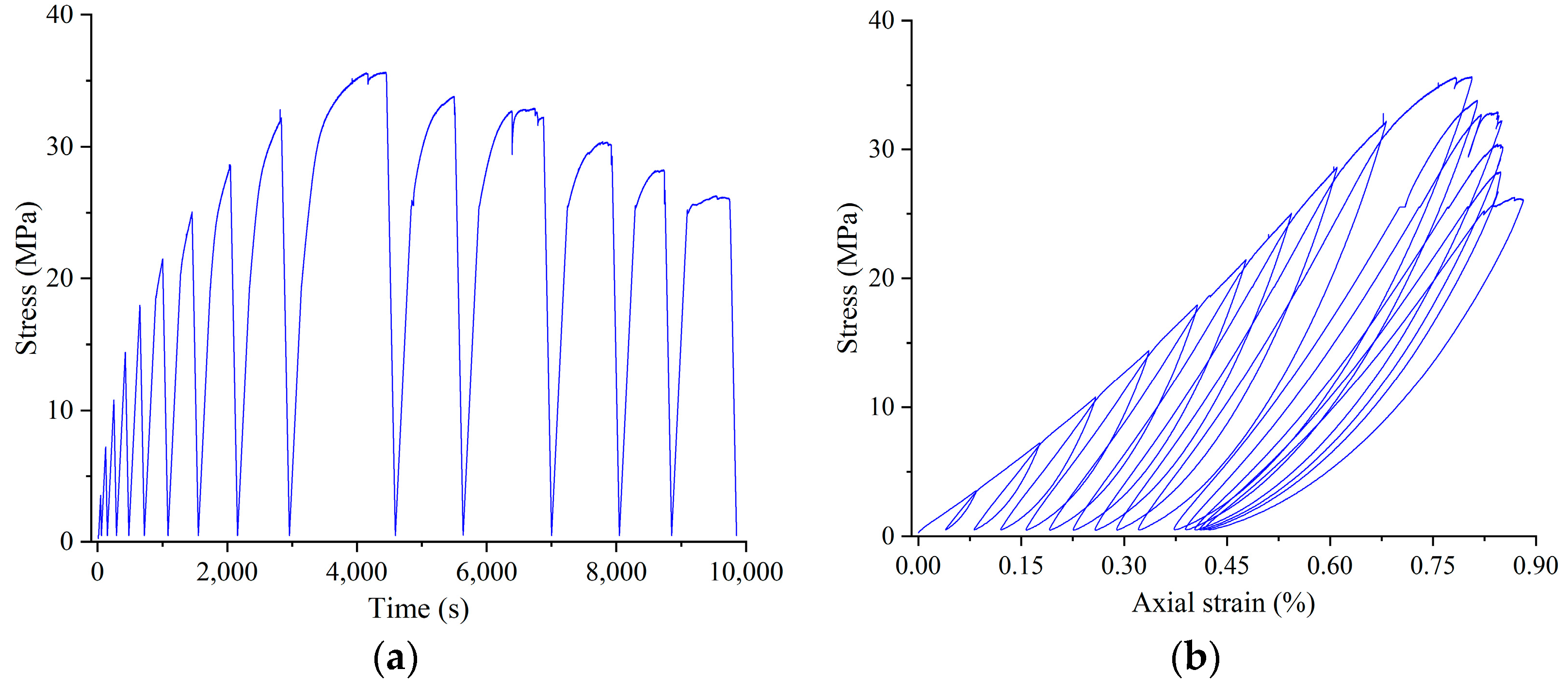
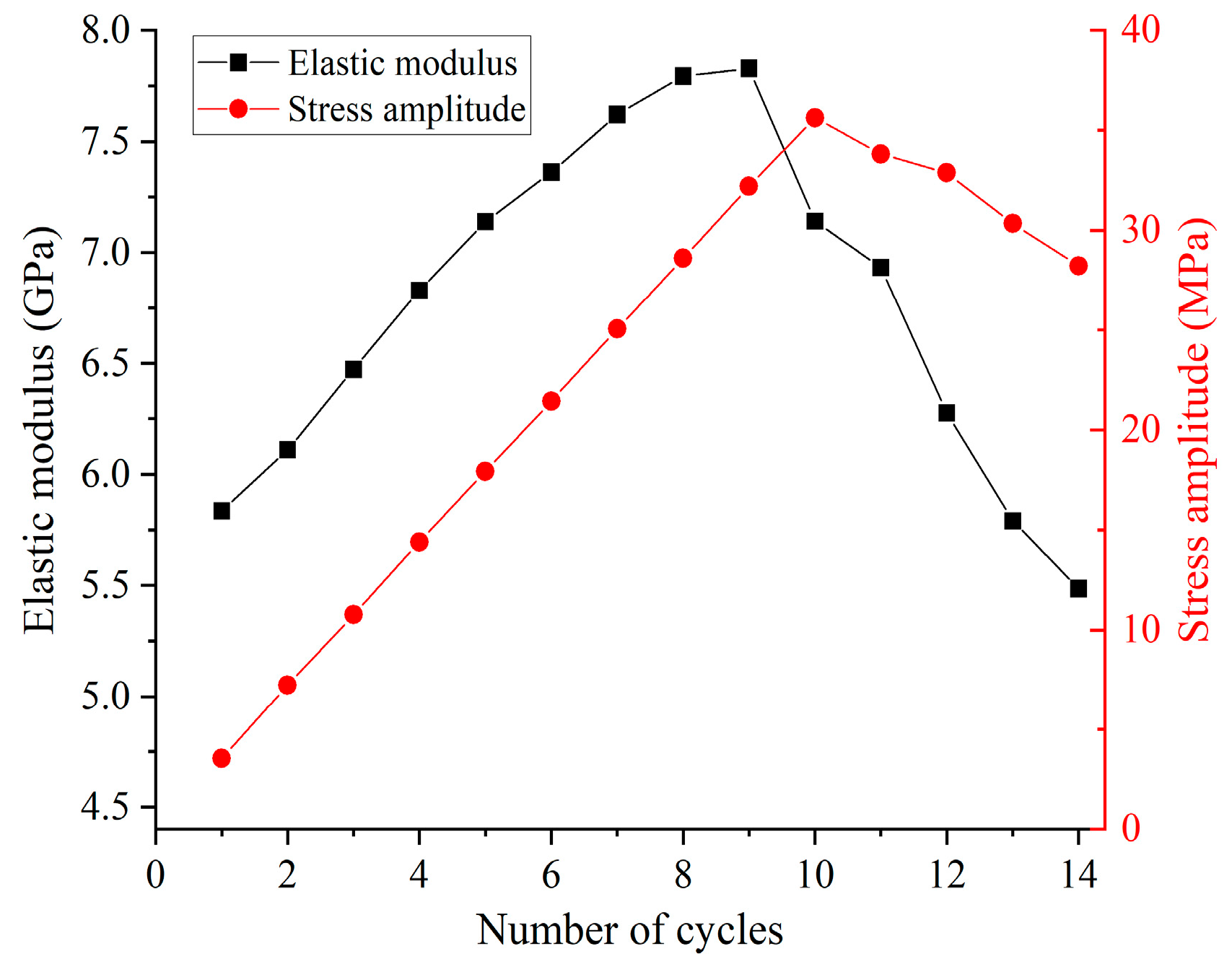
3.1. Deformation Characteristics of Siltstone Subjected to Stepped Cyclic Loading and Unloading
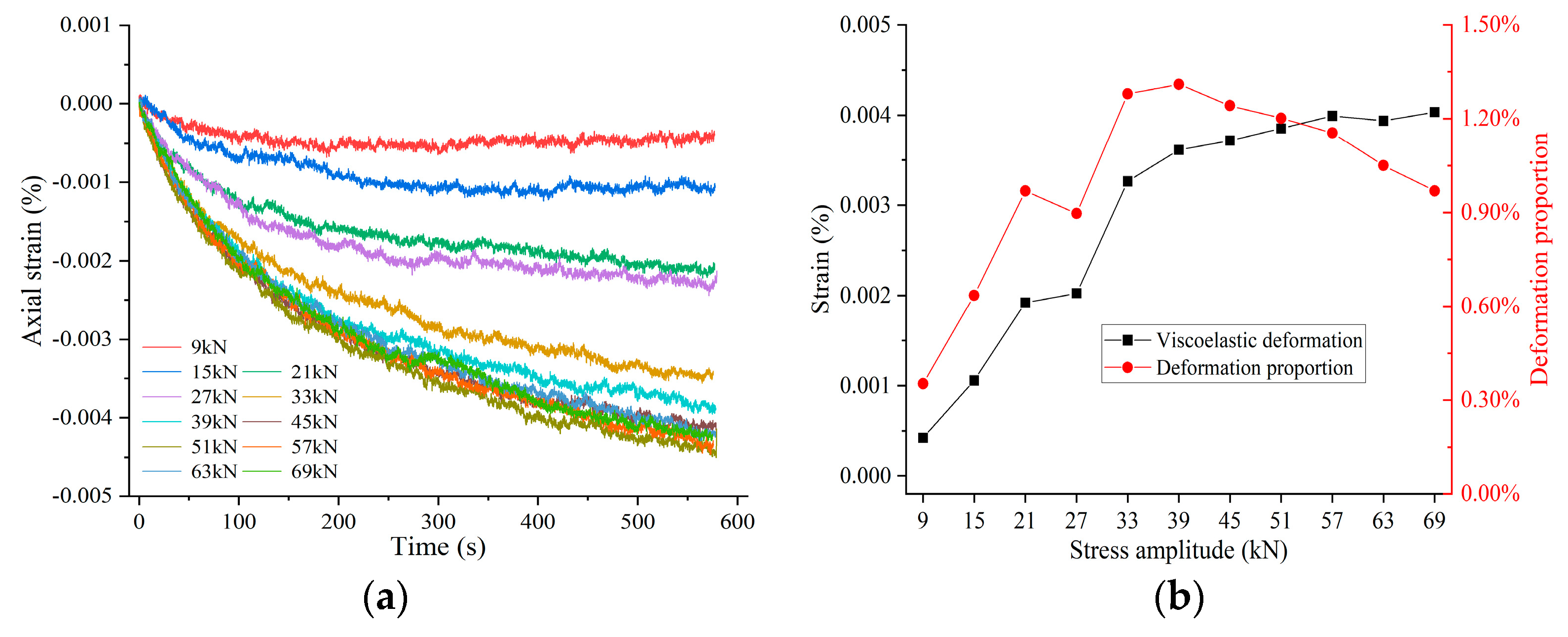
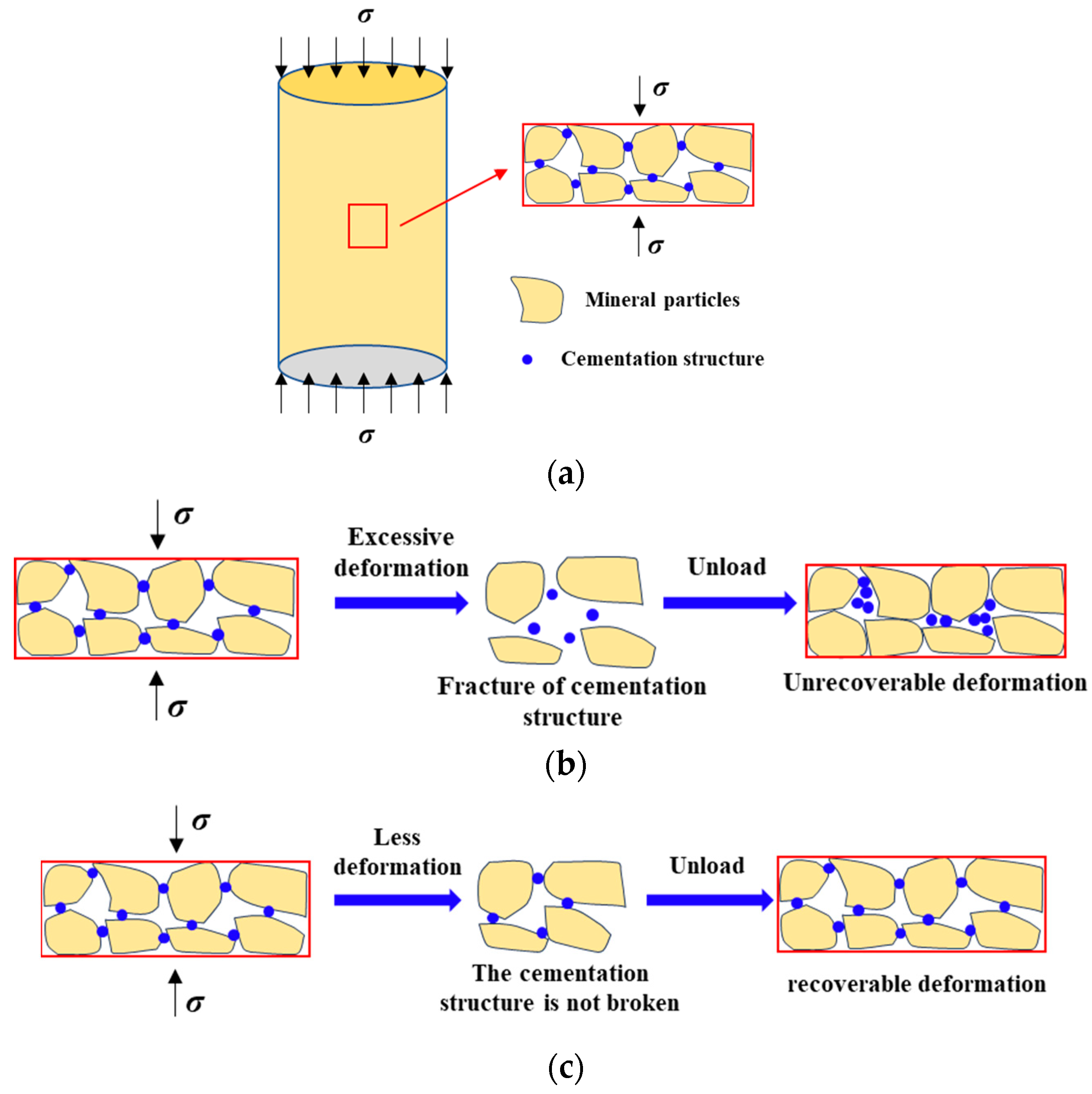
3.2. Deformation Mechanism of Siltstone under Uniaxial Loading and Unloading
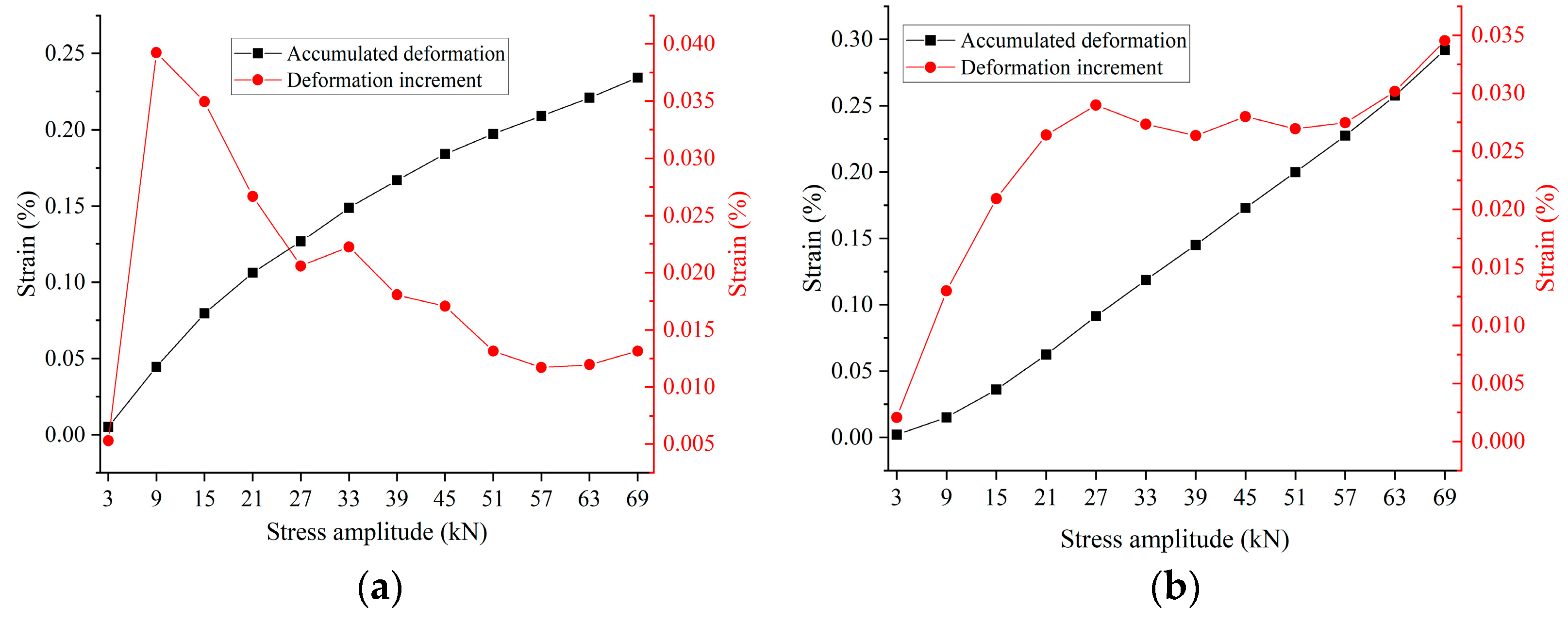
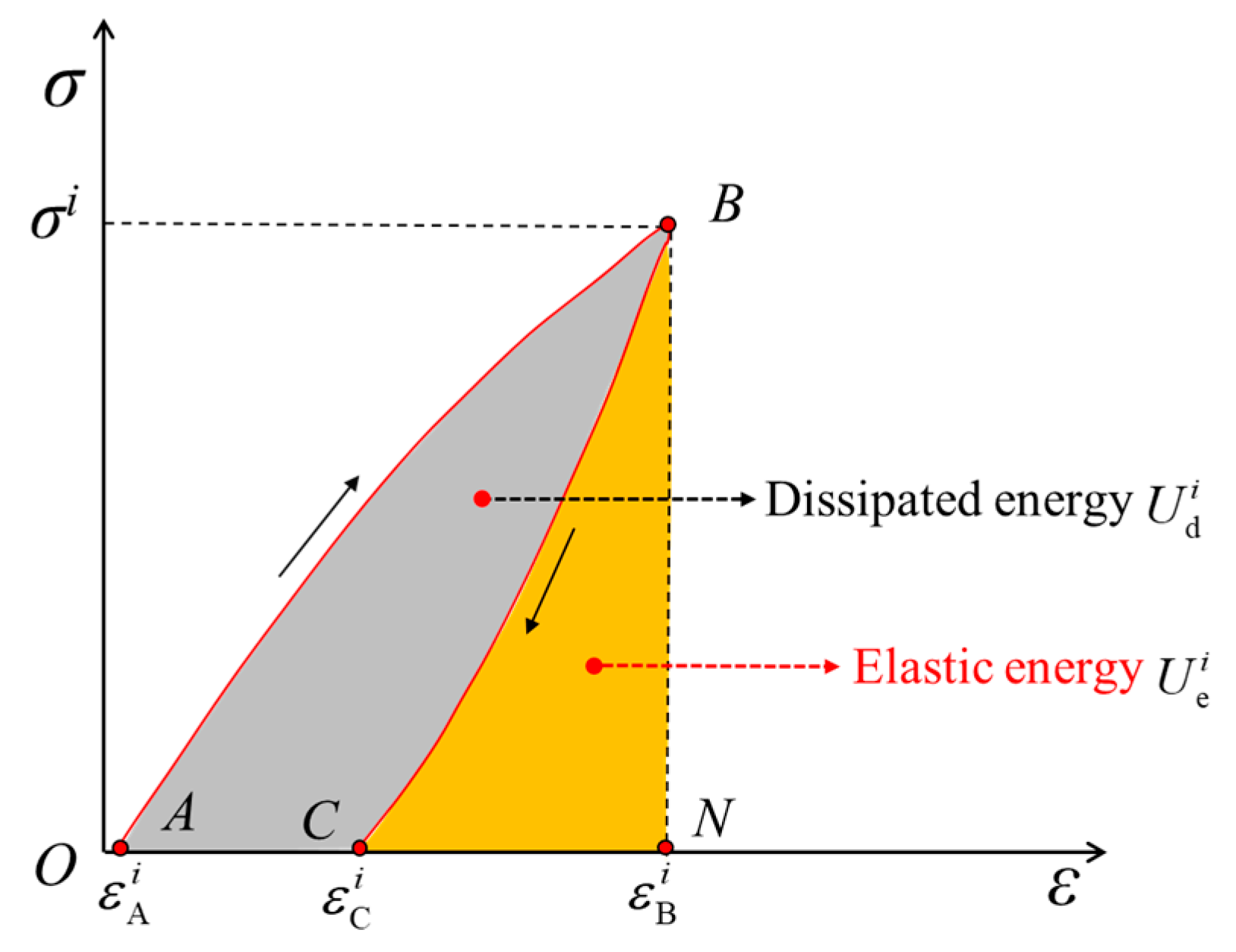
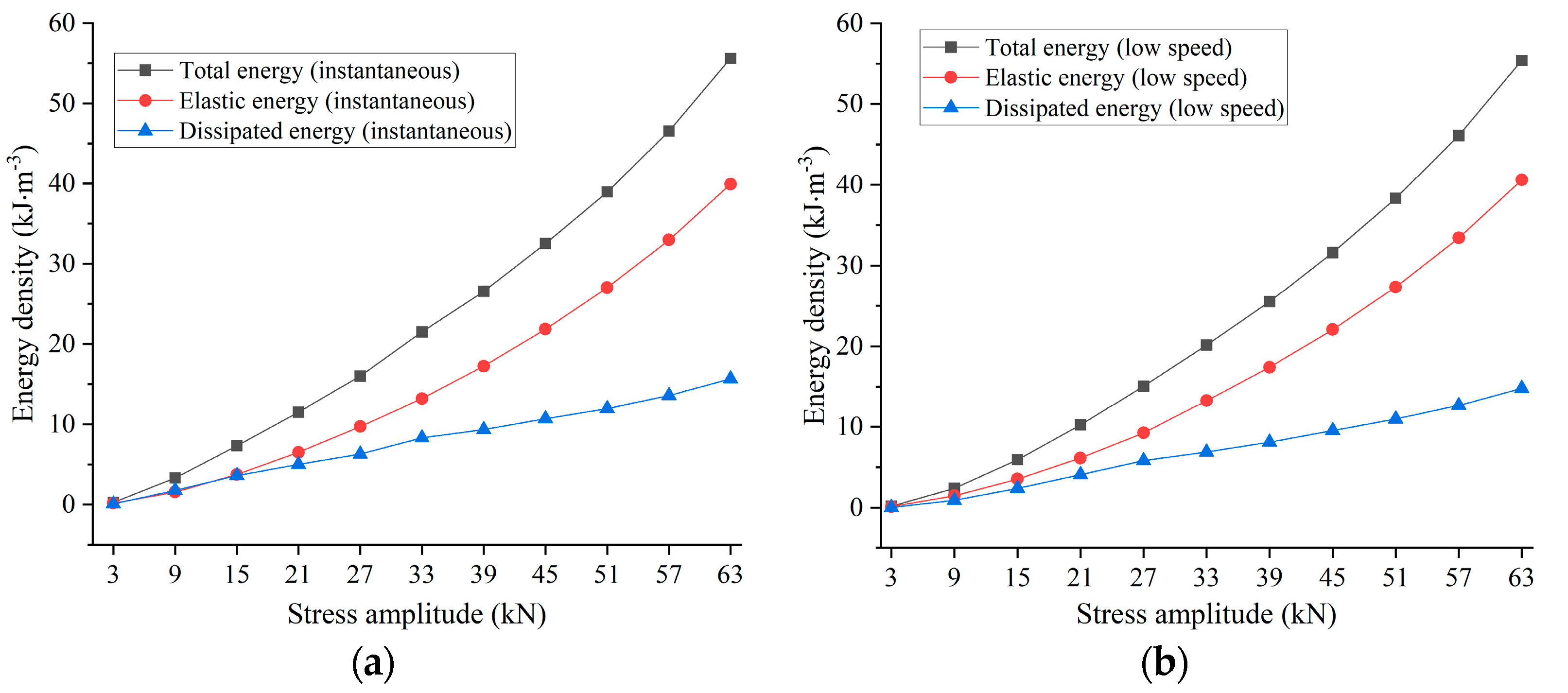
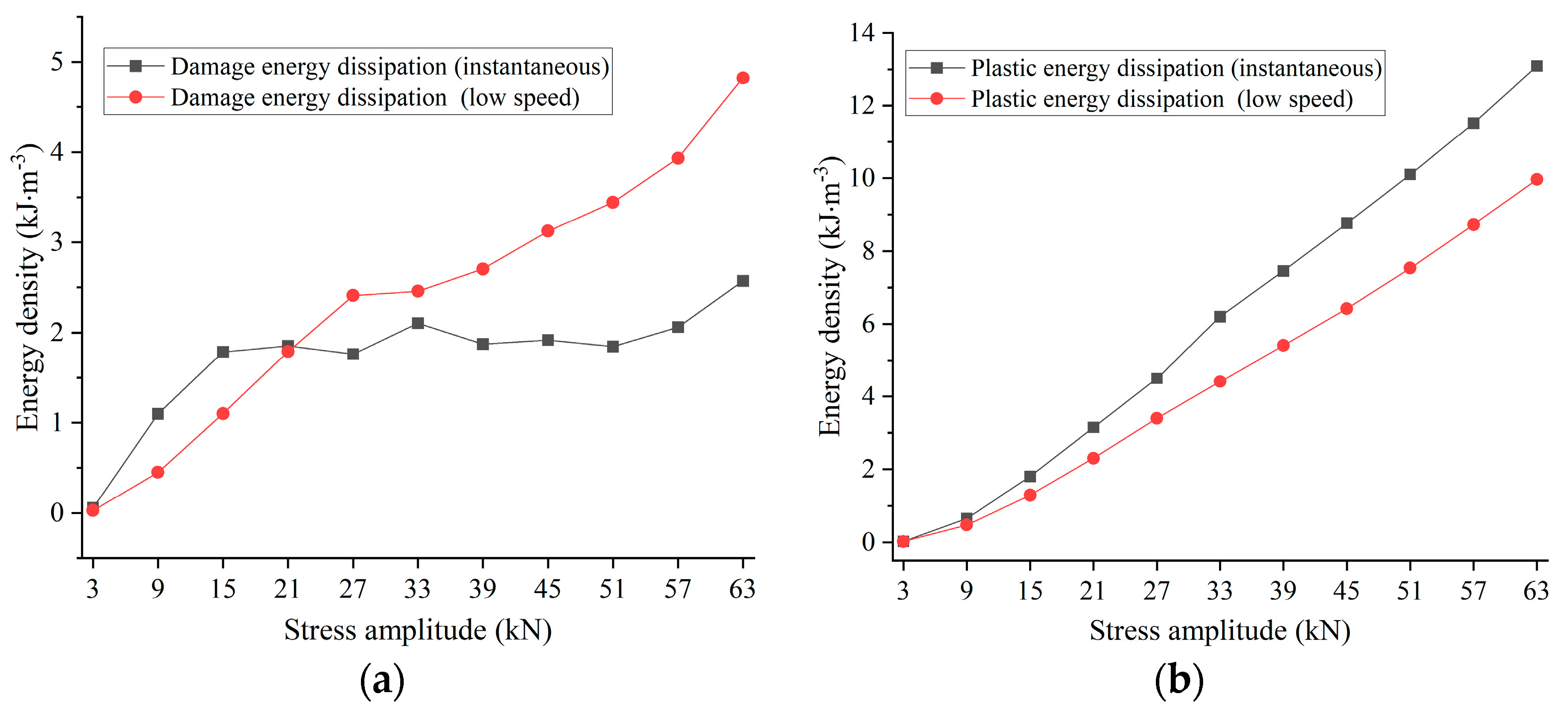
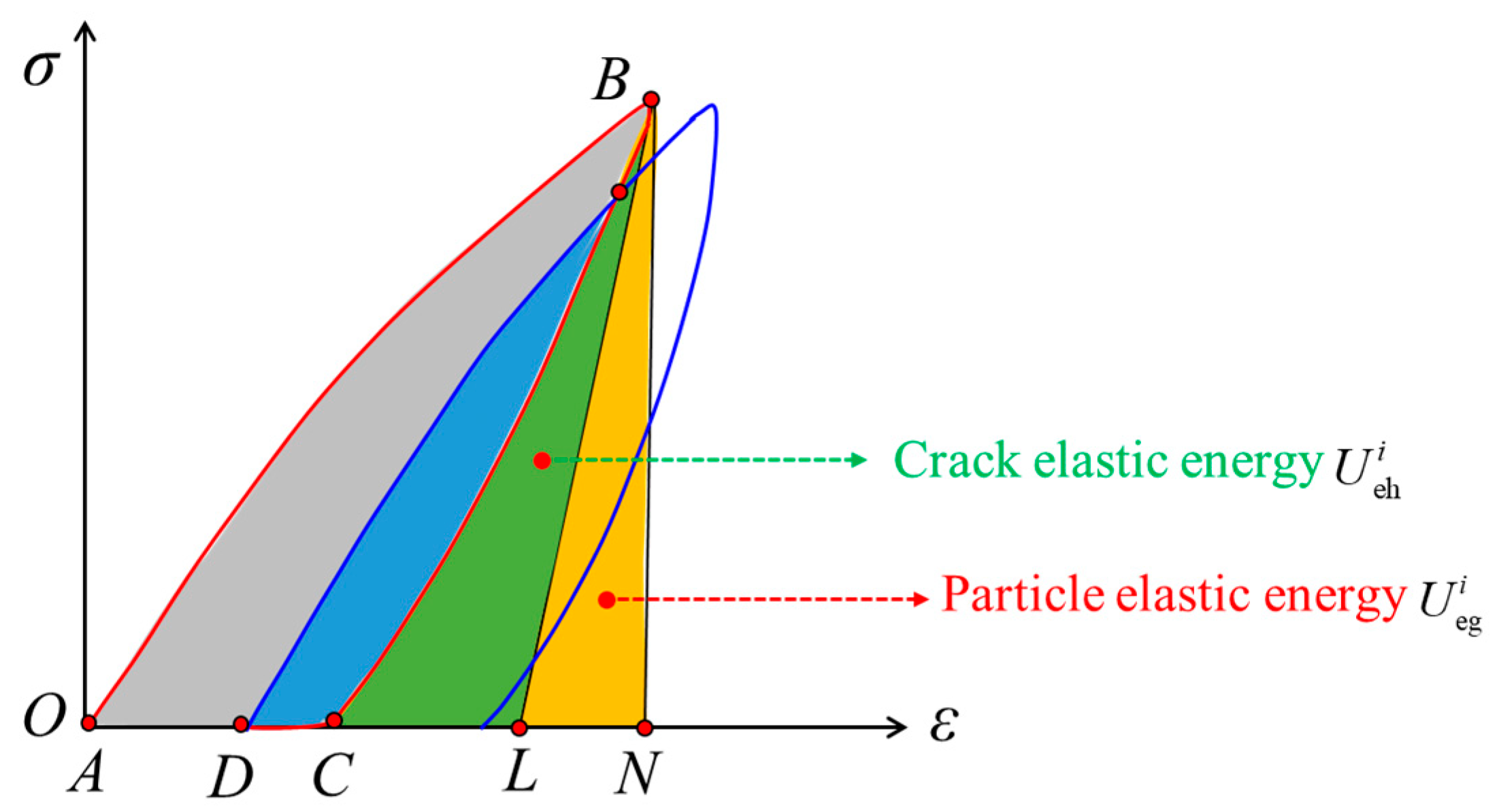
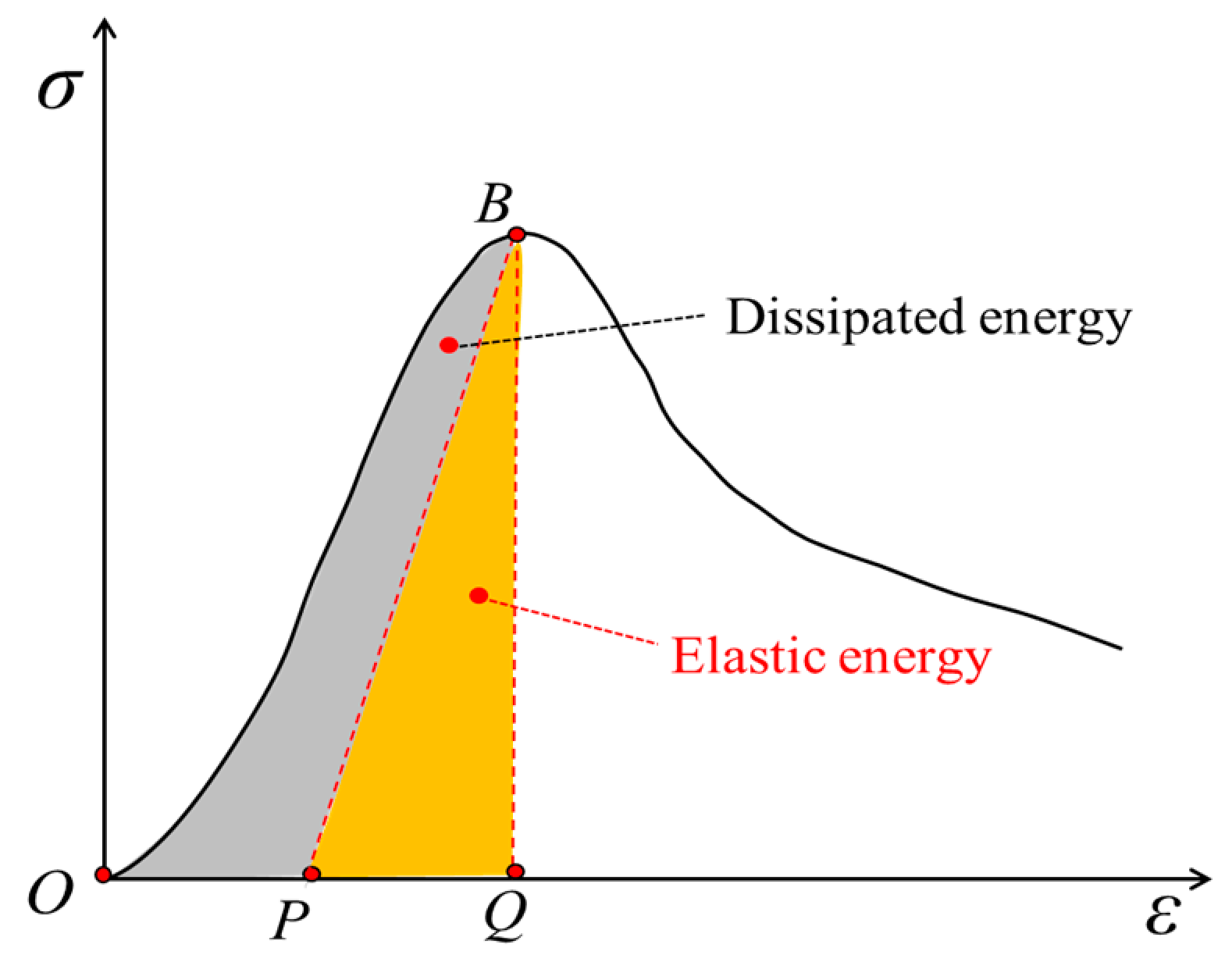
4. Calculation Method of Dissipative Energy and Elastic Energy Based on Deformation Evolution Characteristics
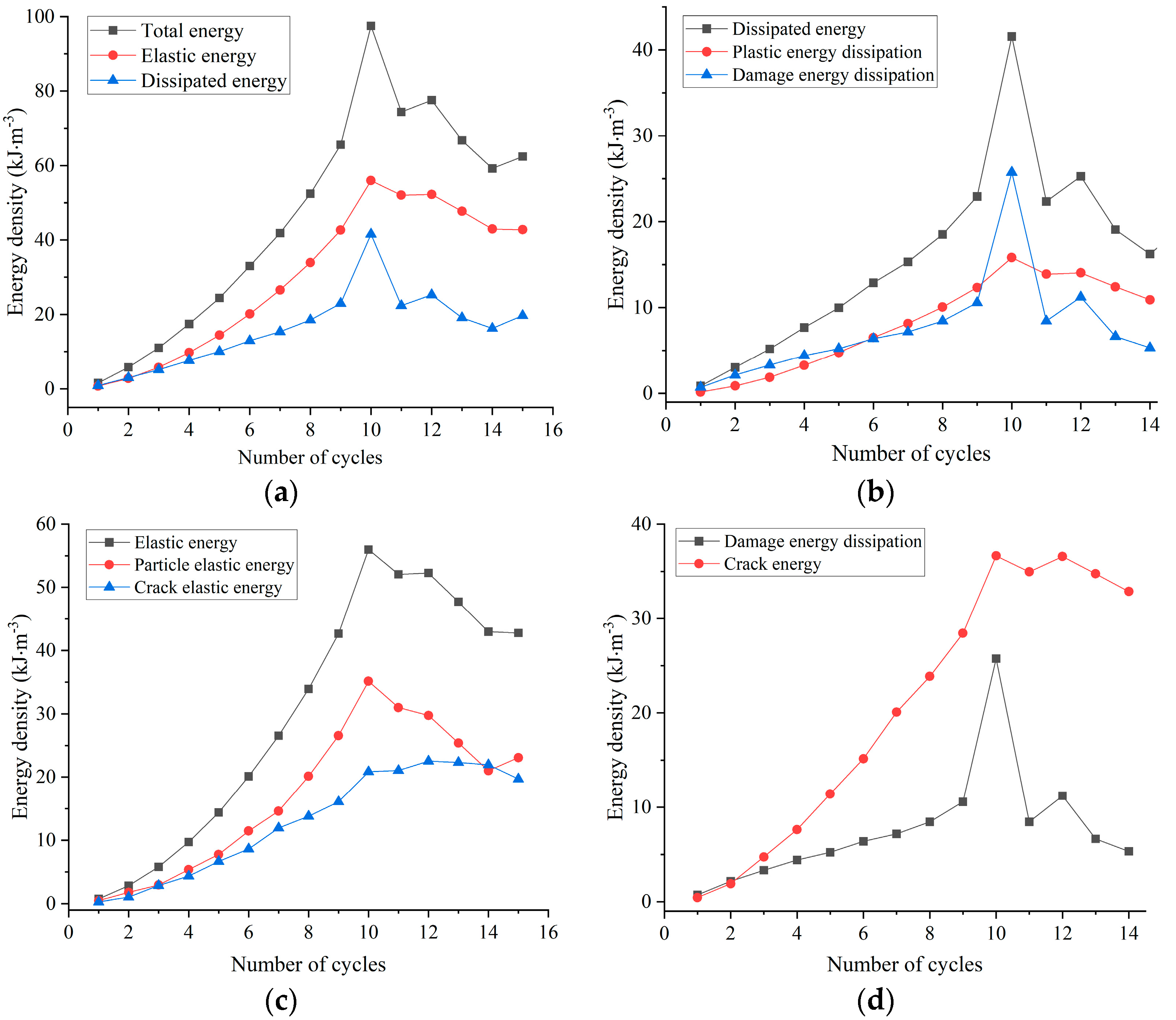
5. Damage Evolution Characteristics Based on Plastic Energy Dissipation and Crack Energy
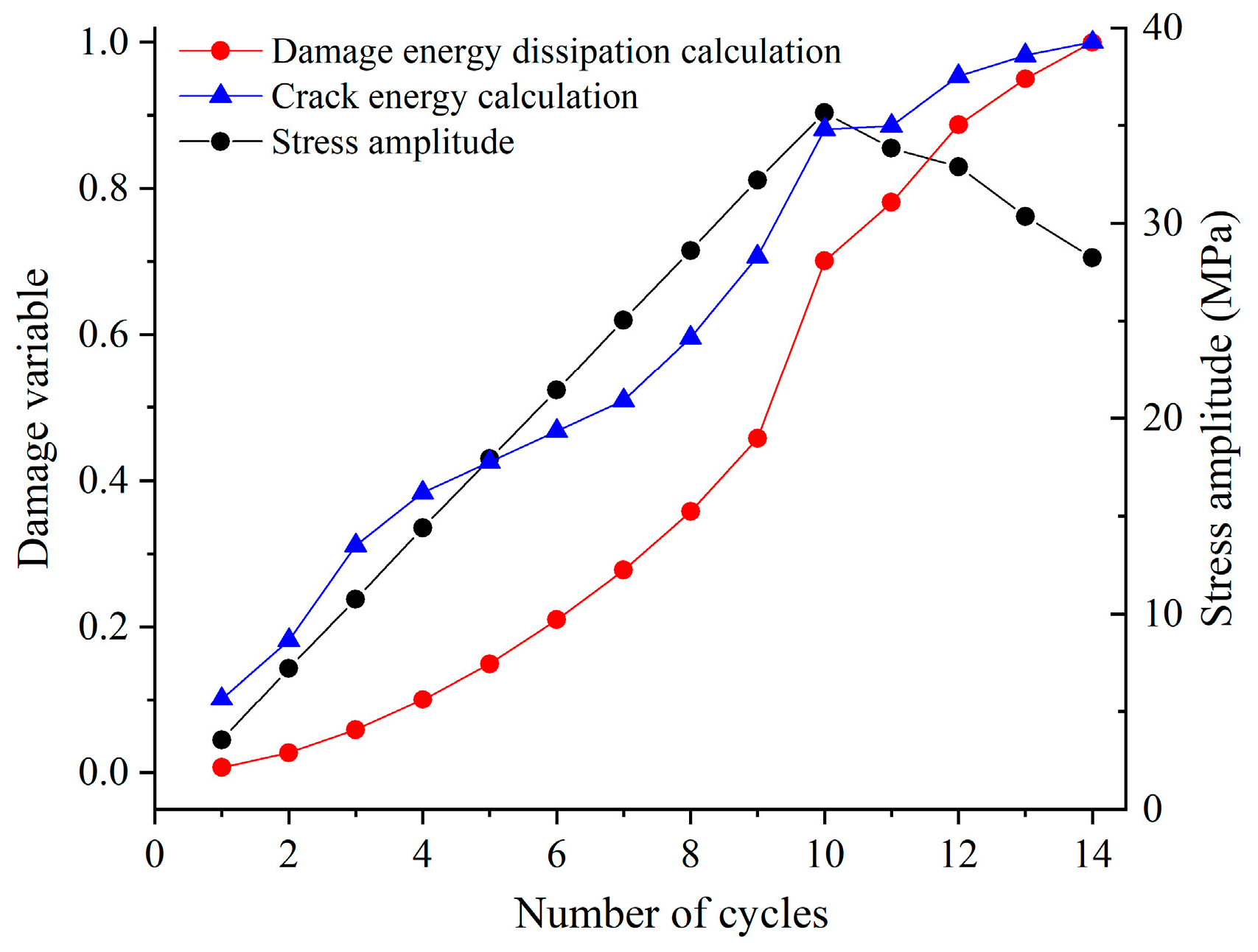
5.1. Definition of Damage Variables Based on Plastic Energy Dissipation and Crack Energy
5.2. Verification Test
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Cerfontaine, B.; Collin, F. Cyclic and fatigue behaviour of rock materials: Review, interpretation and research perspectives. Rock Mech. Rock Eng. 2018, 51, 391–414. [Google Scholar] [CrossRef]
- Geranmayeh Vaneghi, R.; Thoeni, K.; Dyskin, A.V.; Sharifzadeh, M.; Sarmadivaleh, M. Strength and damage response of sandstone and granodiorite under different loading conditions of multistage uniaxial cyclic compression. Int. J. Geomech. 2020, 20, 04020159. [Google Scholar] [CrossRef]
- Kim, I.B.; Ri, C.S.; So, Y.I. A damage mechanics model of materials with voids and cracks. Int. J. Damage Mech. 2016, 25, 773–796. [Google Scholar] [CrossRef]
- Xiong, L.F.; Wu, S.C.; Zhang, S.H. Mechanical behavior of a granite from wuyi mountain: Insights from strain-based approaches. Rock Mech. Rock Eng. 2019, 52, 719–736. [Google Scholar] [CrossRef]
- Ahmed, Z.; Wang, S.; Hashmi, M.Z.; Zishan, Z.; Chengjin, Z. Causes, characterization, damage models, and constitutive modes for rock damage analysis: A review. Arab. J. Geosci. 2020, 13, 806. [Google Scholar] [CrossRef]
- Gordon, R.B.; Davis, L.A. Velocity and attenuation of seismic waves in imperfectly elastic rock. J. Geophys. Res. 1968, 73, 3917–3935. [Google Scholar] [CrossRef]
- Elliott, G.M.; Brown, E.T. Further development of a plasticity approach to yield in porous rock. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1986, 23, 151–156. [Google Scholar] [CrossRef]
- Yoshinaka, R.; Tran, T.V.; Osada, M. Non-linear, stress- and strain-dependent behavior of soft rocks under cyclic triaxial conditions. Int. J. Rock Mech. Min. Sci. 1998, 35, 941–955. [Google Scholar] [CrossRef]
- Jia, C.; Xu, W.; Wang, R.; Wang, W.; Zhang, J.; Yu, J. Characterization of the deformation behavior of fine-grained sandstone by triaxial cyclic loading. Constr. Build. Mater. 2018, 162, 113–123. [Google Scholar] [CrossRef]
- Meng, Q.B.; Liu, J.F.; Ren, L.; Pu, H.; Chen, Y.L. Experimental study on rock strength and deformation characteristics under triaxial cyclic loading and unloading conditions. Rock Mech. Rock Eng. 2021, 54, 777–797. [Google Scholar] [CrossRef]
- Yang, P.; Miao, S.; Wang, H.; Li, C.; Shang, X.; Xia, D. Comparison of deformation behavior between creep and fatigue on siltstone and its modified damage model. Fatigue Fract. Eng. Mater. Struct. 2023, 46, 3815–3828. [Google Scholar] [CrossRef]
- Wang, Y.; Tan, W.H.; Liu, D.Q.; Hou, Z.Q.; Li, C.H. On anisotropic fracture evolution and energy mechanism during marble failure under uniaxial deformation. Rock Mech. Rock Eng. 2019, 52, 3567–3583. [Google Scholar] [CrossRef]
- Meng, Q.; Zhang, M.; Zhang, Z.; Han, L.; Pu, H. Research on non-linear characteristics of rock energy evolution under uniaxial cyclic loading and unloading conditions. Environ. Earth Sci. 2019, 78, 1–20. [Google Scholar] [CrossRef]
- Jiang, C.; Li, Z.; Wang, W.; Wen, Z.; Duan, M.; Geng, W. Experimental investigation of the mechanical characteristics and energy dissipation of gas-containing coal under incremental tiered cyclic loading. Geomech. Geophys. Geo-Energy Geo-Resour. 2021, 7, 1–15. [Google Scholar] [CrossRef]
- Thomas, A.; Filippov, L.O. Fractures, fractals and breakage energy of mineral particles. Int. J. Miner. Process. 1999, 57, 285–301. [Google Scholar] [CrossRef]
- Petrov, Y.V.; Morozov, N.F.; Smirnov, V.I. Structural macromechanics approach in dynamics of fracture. Fatigue Fract. Eng. Mater. Struct. 2003, 26, 363–372. [Google Scholar] [CrossRef]
- Xie, H.; Li, L.; Peng, R.; Ju, Y. Energy analysis and criteria for structural failure of rocks. J. Rock Mech. Geotech. Eng. 2009, 1, 11–20. [Google Scholar] [CrossRef]
- Zhang, L.; Cong, Y.; Meng, F.; Wang, Z.; Zhang, P.; Gao, S. Energy evolution analysis and failure criteria for rock under different stress paths. Acta Geotech. 2021, 16, 569–580. [Google Scholar] [CrossRef]
- Meng, Q.B.; Liu, J.F.; Huang, B.X.; Pu, H.; Wu, J.Y.; Zhang, Z.Z. Effects of confining pressure and temperature on the energy evolution of rocks under triaxial cyclic loading and unloading conditions. Rock Mech. Rock Eng. 2021, 55, 773–798. [Google Scholar] [CrossRef]
- Brantut, N.; Petit, L. Micromechanics of rock damage and its recovery in cyclic loading conditions. Geophys. J. Int. 2023, 233, 145–161. [Google Scholar] [CrossRef]
- Wang, Y.; Tang, P.; Han, J.; Li, P. Energy-driven fracture and instability of deeply buried rock under triaxial alternative fatigue loads and multistage unloading conditions: Prior fatigue damage effect. Int. J. Fatigue 2023, 168, 107410. [Google Scholar] [CrossRef]
- Wang, Y.; Cao, Z.; Mao, T.; Li, P.; Cai, M. Investigation of fatigue failure and energy characteristics of rock exposed to complicated stress disturbance paths: Cyclic stress amplitude effect. Fatigue Fract. Eng. Mater. Struct. 2023, 46, 2697–2713. [Google Scholar] [CrossRef]
- Zhang, M.; Dou, L.; Konietzky, H.; Song, Z.; Huang, S. Cyclic fatigue characteristics of strong burst-prone coal: Experimental insights from energy dissipation, hysteresis and micro-seismicity. Int. J. Fatigue 2020, 133, 105429. [Google Scholar] [CrossRef]
- Shirani, F.R.; Taheri, A.; Karakus, M. Failure behaviour of a sandstone subjected to the systematic cyclic loading: Insights from the double-criteria damage-controlled test method. Rock Mech. Rock Eng. 2021, 54, 5555–5575. [Google Scholar] [CrossRef]
- Hu, H.; Lu, Y.; Xia, B.; Luo, Y.; Peng, J.; Li, Y. Damage characteristics of sandstone with different crack angles subjected to true triaxial cyclic loading and unloading. Theor. Appl. Fract. Mech. 2022, 121, 103444. [Google Scholar] [CrossRef]
- Jiang, C.; Duan, M.; Yin, G.; Wang, J.G.; Lu, T.; Xu, J.; Zhang, D.; Huang, G. Experimental study on seepage properties, AE characteristics and energy dissipation of coal under tiered cyclic loading. Eng. Geol. 2017, 221, 114–123. [Google Scholar] [CrossRef]
- Shen, R.; Chen, T.; Li, T.; Li, H.; Fan, W.; Hou, Z.; Zhang, X. Study on the effect of the lower limit of cyclic stress on the mechanical properties and acoustic emission of sandstone under cyclic loading and unloading. Theor. Appl. Fract. Mech. 2020, 108, 102661. [Google Scholar] [CrossRef]
- Sun, Y.D.; Yang, Y. Energy and fatigue damage evolution of sandstone under different cyclic loading frequencies. Shock Vib. 2021, 2021, 5585983. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, D.; Han, J.; Li, C.; Liu, H. Effect of fatigue loading-confining stress unloading rate on marble mechanical behaviors: An insight into fracture evolution analyses. J. Rock Mech. Geotech. Eng. 2020, 12, 1249–1262. [Google Scholar] [CrossRef]
- Zhu, A.; Liu, J.; Wu, Z.; Wang, L.; Liu, H.; Xiao, F.; Deng, C. Energy dissipation and damage evolution characteristics of salt rock under uniaxial cyclic loading and unloading tension. Adv. Civ. Eng. 2021, 14, 1–9. [Google Scholar] [CrossRef]
- Yang, X.B.; Cheng, H.M.; Lv, J.Q.; Hou, X.; Nie, C.G. Energy consumption ratio evolution law of sandstones under triaxial cyclic loading. Rock Soil Mech. 2019, 40, 3751–3766. [Google Scholar]
- Lin, H.; Liu, J.; Yang, J.; Ran, L.; Ding, G.; Wu, Z.; Lyu, C.; Bian, Y. Analysis of damage characteristics and energy evolution of salt rock under triaxial cyclic loading and unloading. J. Energy Storage 2022, 56, 106145. [Google Scholar] [CrossRef]
- Liu, Y.; Dai, F.; Dong, L.; Xu, N.; Feng, P. Experimental investigation on the fatigue mechanical properties of intermittently jointed rock models under cyclic uniaxial compression with different loading parameters. Rock Mech. Rock Eng. 2018, 51, 47–68. [Google Scholar] [CrossRef]
- Cheng, C.; Li, X. Cyclic experimental studies on damage evolution behaviors of shale dependent on structural orientations and confining pressures. Energies 2018, 11, 160. [Google Scholar] [CrossRef]
- Yang, X.; Cheng, H.; Hou, X.; Nie, C.; Lv, J. Research on characteristic stress and constitutive equation of confined sandstone during damage evolution based on energy evolution analysis. Adv. Mater. Sci. Eng. 2019, 1, 1–13. [Google Scholar] [CrossRef]
- Wang, Y.; Yi, Y.F.; Li, C.H.; Han, J.Q. Anisotropic fracture and energy characteristics of a Tibet marble exposed to multi-level constant-amplitude (MLCA) cyclic loads: A labscale testing. Eng. Fract. Mech. 2021, 244, 107550. [Google Scholar] [CrossRef]
- Liu, X.S.; Ning, J.G.; Tan, Y.L.; Gu, Q.H. Damage constitutive model based on energy dissipation for intact rock subjected to cyclic loading. Int. J. Rock Mech. Min. Sci. 2016, 85, 27–32. [Google Scholar] [CrossRef]
- Li, T.; Pei, X.; Wang, D.; Huang, R.; Tang, H. Nonlinear behavior and damage model for fractured rock under cyclic loading based on energy dissipation principle. Eng. Fract. Mech. 2019, 206, 330–341. [Google Scholar] [CrossRef]
- Gong, F.Q.; Zhang, P.L.; Du, K. A novel staged cyclic damage constitutive model for brittle rock based on linear energy dissipation law: Modelling and validation. Rock Mech. Rock Eng. 2022, 55, 6249–6262. [Google Scholar] [CrossRef]
- Miao, S.; Xia, D.; Yang, P.; Liang, M. Acoustic emission and damage characteristics of granite under graded cyclic loading. Arab. J. Geosci. 2022, 15, 1–11. [Google Scholar] [CrossRef]
- Miao, S.; Liu, Z.; Zhao, X.; Ma, L.; Zheng, Y.; Xia, D. Plastic and damage energy dissipation characteristics and damage evolution of Beishan granite under triaxial cyclic loading. Int. J. Rock Mech. Min. Sci. 2024, 174, 105644. [Google Scholar] [CrossRef]
- Eberhardt, E.; Stead, D.; Stimpson, B. Quantifying progressive pre-peak brittle fracture damage in rock during uniaxial compression. Int. J. Rock Mech. Min. Sci. 1999, 36, 361–380. [Google Scholar] [CrossRef]
- Lemaitre, J.; Dufailly, J. Damage measurements. Eng. Fract. Mech. 1987, 28, 643–661. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Miao, S.; Shang, X.; Wang, H.; Liang, M.; Yang, P.; Liu, C. Deformation Characteristics and Energy Evolution Rules of Siltstone under Stepwise Cyclic Loading and Unloading. Buildings 2024, 14, 1500. https://doi.org/10.3390/buildings14061500
Miao S, Shang X, Wang H, Liang M, Yang P, Liu C. Deformation Characteristics and Energy Evolution Rules of Siltstone under Stepwise Cyclic Loading and Unloading. Buildings. 2024; 14(6):1500. https://doi.org/10.3390/buildings14061500
Chicago/Turabian StyleMiao, Shengjun, Xiangfan Shang, Hui Wang, Mingchun Liang, Pengjin Yang, and Chunkang Liu. 2024. "Deformation Characteristics and Energy Evolution Rules of Siltstone under Stepwise Cyclic Loading and Unloading" Buildings 14, no. 6: 1500. https://doi.org/10.3390/buildings14061500
APA StyleMiao, S., Shang, X., Wang, H., Liang, M., Yang, P., & Liu, C. (2024). Deformation Characteristics and Energy Evolution Rules of Siltstone under Stepwise Cyclic Loading and Unloading. Buildings, 14(6), 1500. https://doi.org/10.3390/buildings14061500





