Rubberized Concrete: Effect of the Rubber Size and Content on Static and Dynamic Behavior
Abstract
:1. Introduction
2. Methodology
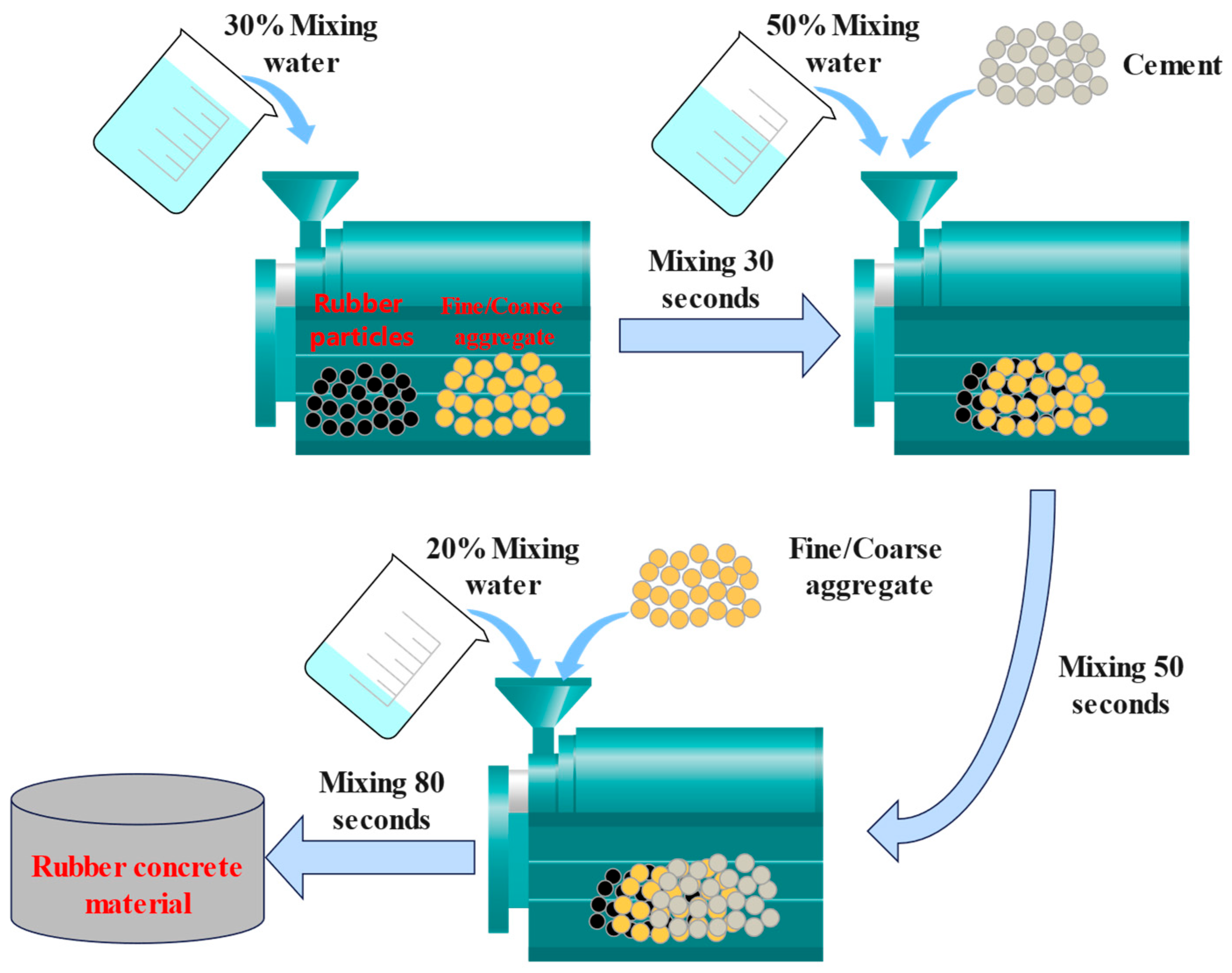
2.1. Material Preparation
2.2. Mechanical Testing
2.2.1. Quasi-Static Compressive Test
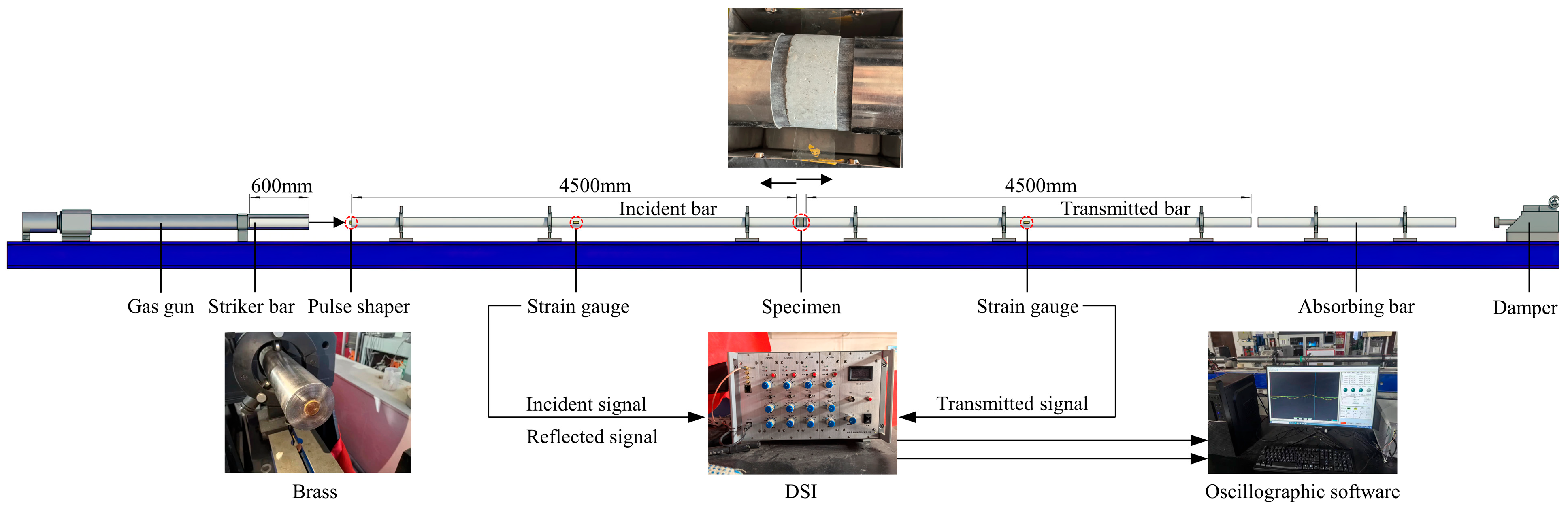
2.2.2. Dynamic Compressive Test
3. Results and Discussions
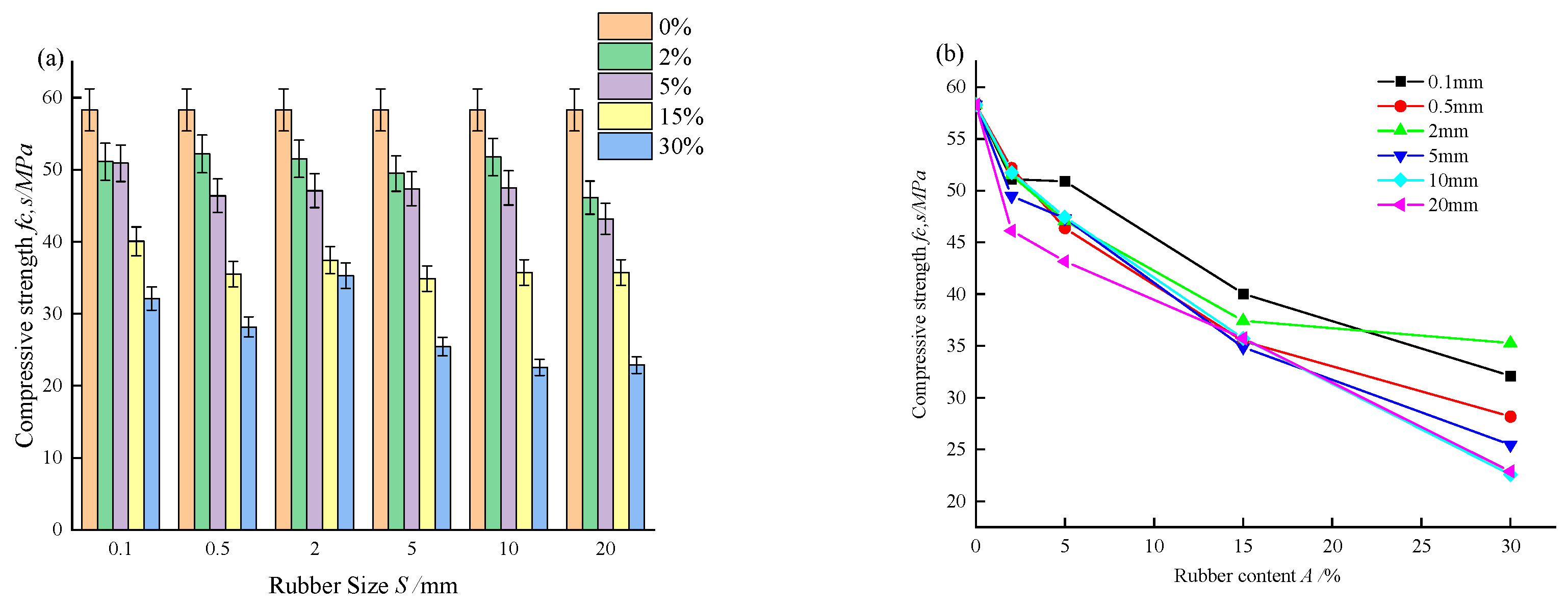
3.1. Static Compressive Strength
- (1)
- Rubber and concrete have different moduli of elasticity [56]. The elastic modulus of concrete is about 5000–24,000 times that of rubber. This difference makes RC prone to cracking around the rubber during the loading process, thereby accelerating the damage to the concrete during the loading process.
- (2)
- By observing the surface of the RC with a microscope, as shown in Figure 7, it can be found that there is a gap between rubber aggregate and cement paste. Because of the hydrophobic properties of rubber, the interface adhesion between rubber aggregate and cement slurry is low, resulting in a reduction in strength.
- (3)
- Aggregates mainly play a role similar to human skeleton in concrete, so good grading can help the accumulation of concrete to form the best state. The increase in rubber has disrupted the grading between the original sand and stone [57].

3.2. Compressive Strength Fitting Analysis
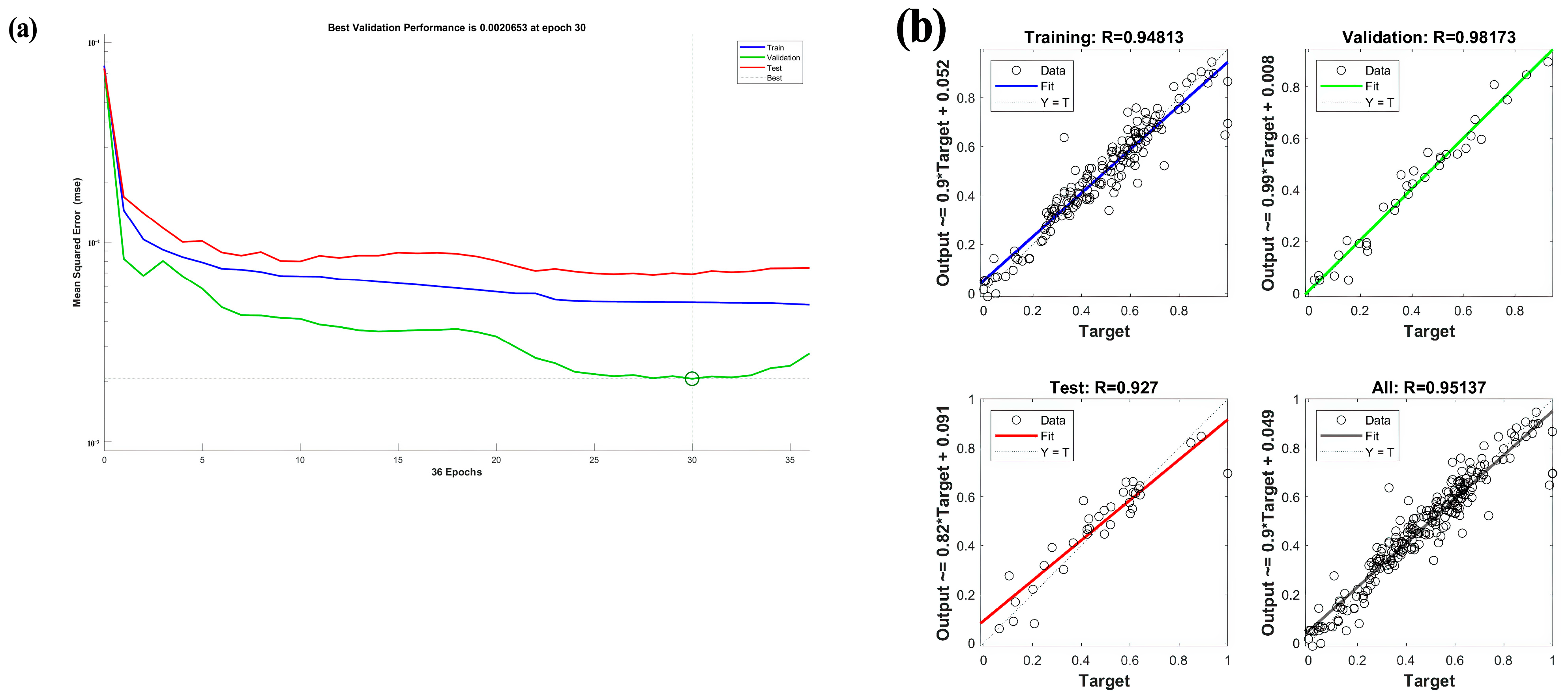
3.3. Compressive Strength ANN Analysis
3.3.1. Collection and Classification of Samples
3.3.2. Normalization of Sample Data
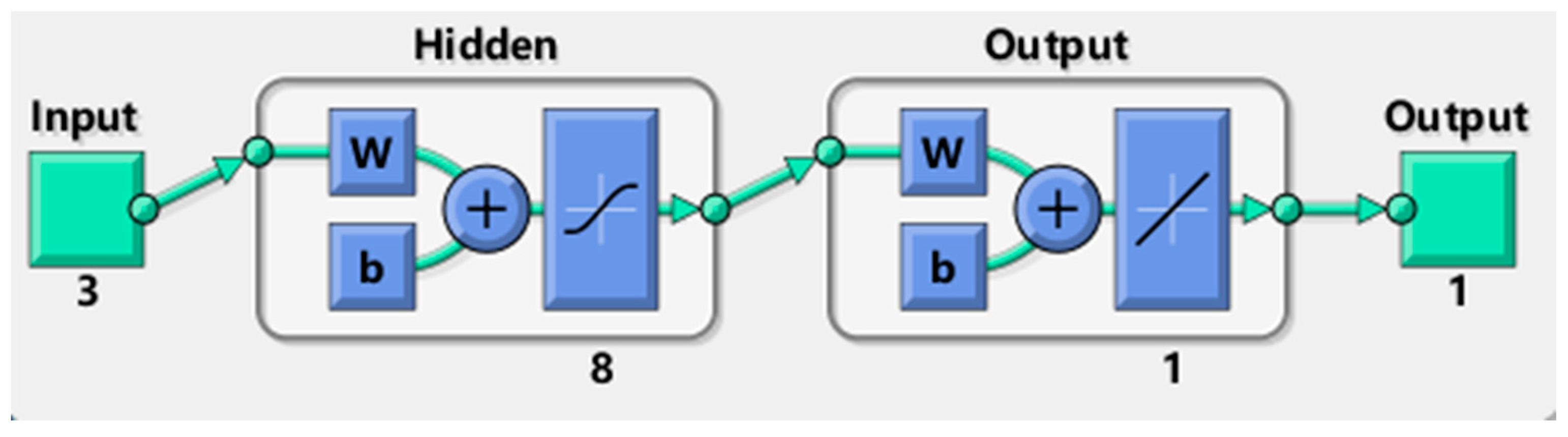
3.3.3. Model Building and Training
- (1)
- Input layer. The number of input nodes is three, including rubber size, content, and compressive strength of control samples.
- (2)
- Output layer. The number of output nodes is one, which is the compressive strength of RC.
- (3)
- Hidden layer. The hidden layer is one layer, and the number of nodes in the hidden layer is eight.
- (4)
- Training function. We adopt the Levenberg–Marquardt algorithm as a compromise between the Gauss–Newton and gradient descent methods to make the fastest adjustment possible.
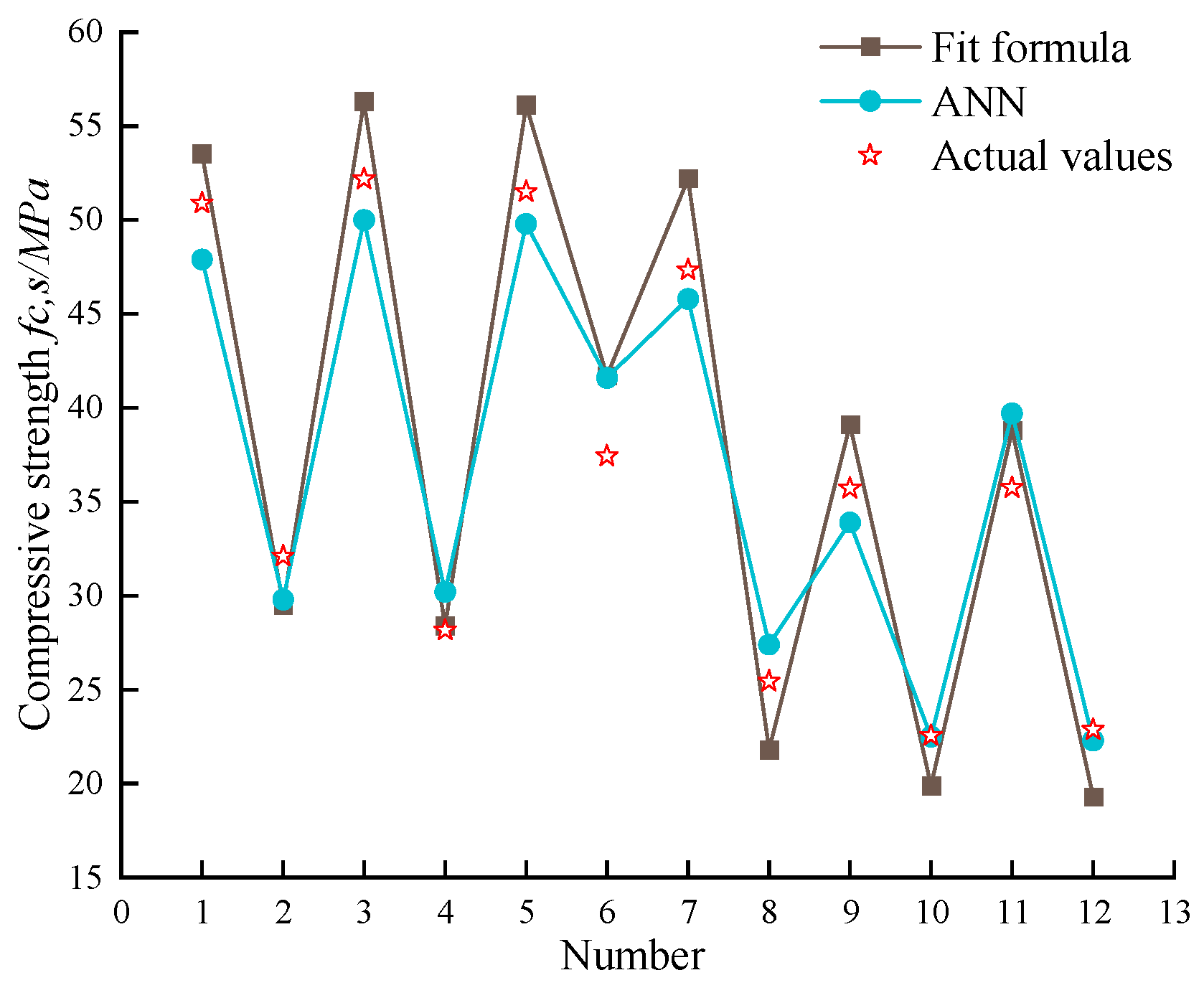
3.4. Model Testing
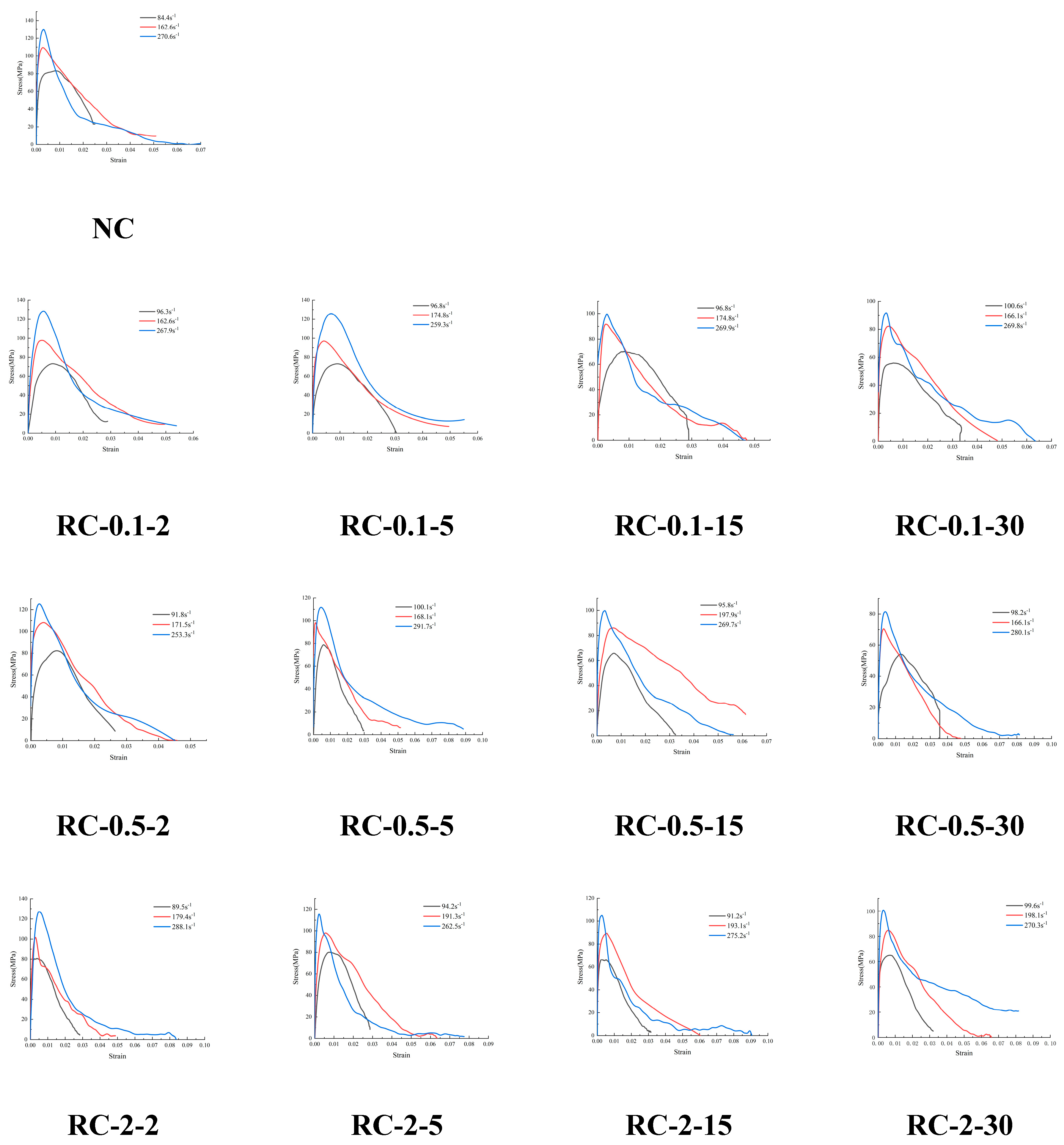
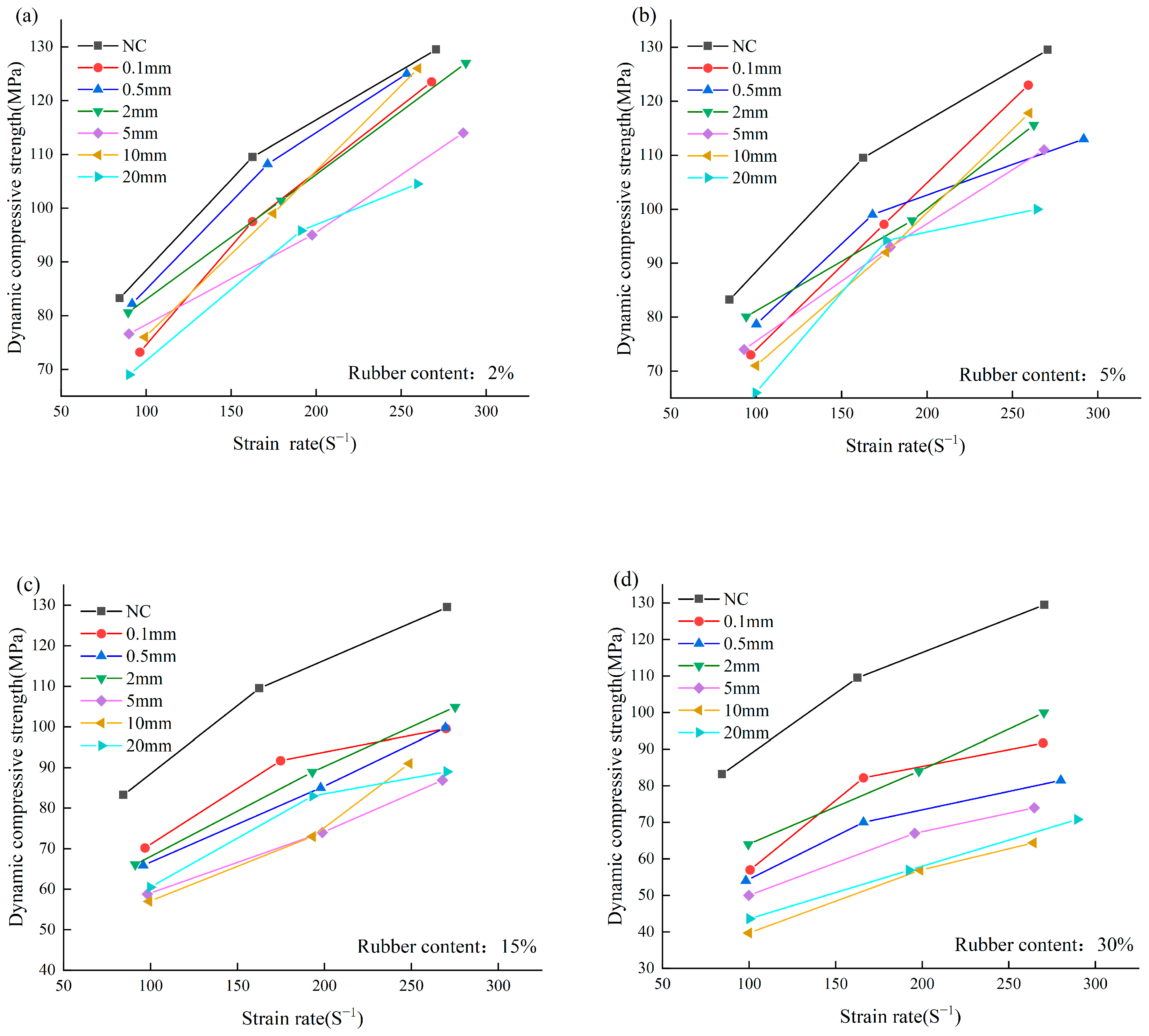
3.5. Dynamic SHPB Test Result
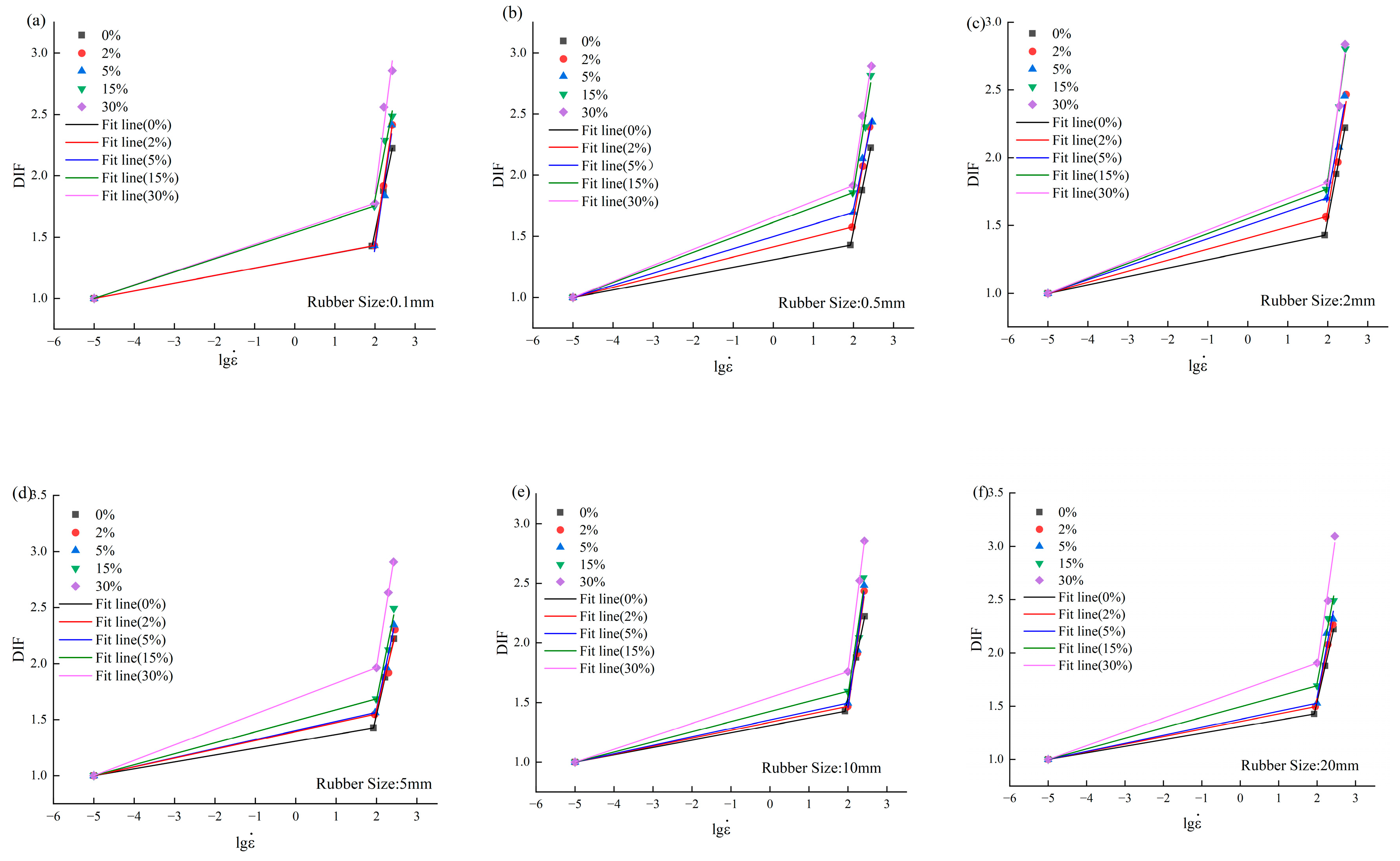
3.6. DIF of the RC
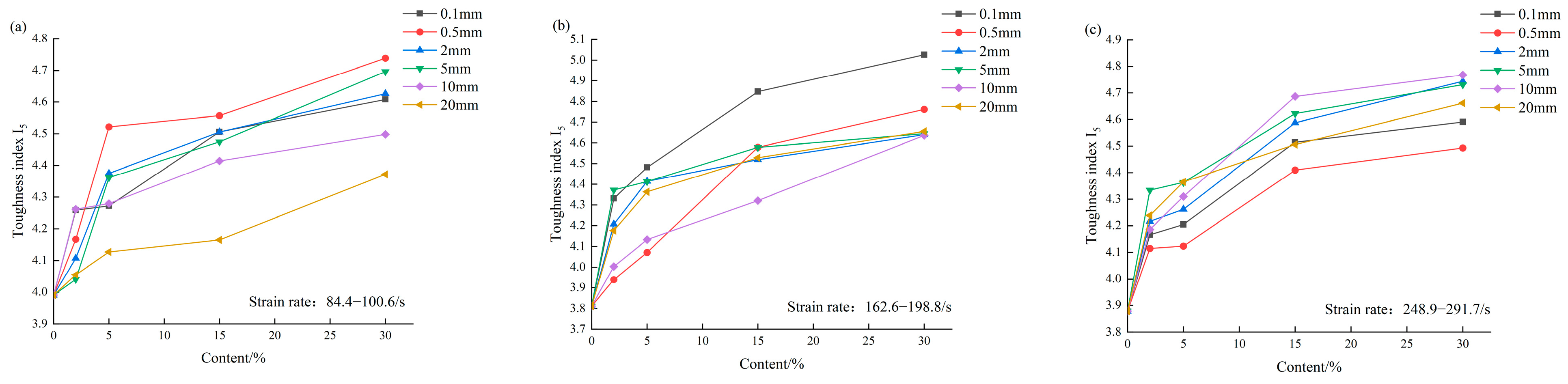
3.7. Analysis of Dynamic Toughness Index of RC
4. Conclusions
- (1)
- Rubber reduces the static strength of concrete, and the strength of RC decreases with an increase in rubber content. However, the effect of rubber particle size on the compressive strength of RC is irregular.
- (2)
- This article presents empirical equations for the compressive strength of concrete with varying rubber content and particle sizes. It uses BP neural networks combined with the literature data for neural network learning. The formula and neural network learning model can be used to predict the static compressive strength of concrete with different rubber particle sizes and contents.
- (3)
- In the dynamic test, the peak strain decreases with the increase in rubber content. When the rubber content is 30% and the rubber size is 10mm, the maximum strength reduction is 52.3%. The dynamic compressive strength of RC with a rubber particle size greater than 5mm is generally small, but the effect is insignificant. As the particle size increases, the interface transition zone becomes larger.
- (4)
- Compared to normal concrete, RC exhibits better impact resistance and energy absorption ability at high load rates. The main reason is that a large content of rubber particles is added to RC, which can play a role in energy absorption, slowing down the speed of crack propagation and progressive failure.
- (5)
- The DIF formula for RC with different rubber content and different rubber particle sizes was established through fitting methods. The formula can be used as a reference to predict the dynamic properties of RC under different strain rates in the future.
- (6)
- The toughness index of RC increases with an increase in rubber content. There is no clear relationship between RC’s toughness index and the rubber particles’ size. This phenomenon may mean that the energy absorption capacity of RC mainly depends on the added rubber content rather than particle size.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Li, Y.; Zhang, X.; Wang, R.; Lei, Y. Performance enhancement of rubberised concrete via surface modification of rubber: A review. Constr. Build. Mater. 2019, 227, 116691. [Google Scholar] [CrossRef]
- Rambabu, D.; Sharma, S.K.; Akbar, M.A. Evaluation of roller compacted concrete for its application as high traffic resisting pavements with fatigue analysis. Constr. Build. Mater. 2023, 401, 132977. [Google Scholar] [CrossRef]
- Topcu, I.B. The properties of rubberized concretes. Cem. Concr. Res. 1995, 25, 304–310. [Google Scholar] [CrossRef]
- Amini, K.; Vosoughi, P.; Ceylan, H.; Taylor, P. Effect of mixture proportions on concrete performance. Constr. Build. Mater. 2019, 212, 77–84. [Google Scholar] [CrossRef]
- Topçu, İ.B. Assessment of the brittleness index of rubberized concretes. Cem. Concr. Res. 1997, 27, 177–183. [Google Scholar] [CrossRef]
- Li, Y.; Li, Y. Experimental study on performance of rubber particle and steel fiber composite toughening concrete. Constr. Build. Mater. 2017, 146, 267–275. [Google Scholar] [CrossRef]
- Mu, C.; Zhou, H.; Ma, H. Prediction method for ground shock parameters of explosion in concrete. Constr. Build. Mater. 2021, 291, 123372. [Google Scholar] [CrossRef]
- Yang, F.; Feng, W.; Liu, F.; Jing, L.; Yuan, B.; Chen, D. Experimental and numerical study of rubber concrete slabs with steel reinforcement under close-in blast loading. Constr. Build. Mater. 2019, 198, 423–436. [Google Scholar] [CrossRef]
- Yang, F.; Ke, Z.; Feng, W.; Li, X.; Chen, S.; Li, H. Effects of crumb rubber particles on the dynamic response of reinforced concrete beams subjected to blast loads. Eng. Struct. 2024, 300, 117181. [Google Scholar] [CrossRef]
- Yao, J.; Zhang, J.; Huang, L.; Xu, J. Analysis of anti-collision performance of a new assembled rolling guardrail. In Structures; Elsevier: Amsterdam, The Netherlands, 2023; pp. 246–259. [Google Scholar]
- Khan, M.; Cao, M.; Xie, C.; Ali, M. Hybrid fiber concrete with different basalt fiber length and content. Struct. Concr. 2022, 23, 346–364. [Google Scholar] [CrossRef]
- Cui, D.; Wang, L.; Zhang, C.; Xue, H.; Gao, D.; Chen, F. Dynamic splitting performance and energy dissipation of fiber-reinforced concrete under impact loading. Materials 2024, 17, 421. [Google Scholar] [CrossRef] [PubMed]
- Shi, F.; Cao, P.; Wang, Z.; Gan, Y.; Zhou, C.; Liu, K. An experimental study of dynamic compression performance of self-compacting concrete. Materials 2020, 13, 3731. [Google Scholar] [CrossRef]
- Feng, S.; Zhou, Y.; Li, Q. Damage behavior and energy absorption characteristics of foamed concrete under dynamic load. Constr. Build. Mater. 2022, 357, 129340. [Google Scholar] [CrossRef]
- Yan, T.; Yin, X.; Zhang, X. Impact toughness and dynamic constitutive model of geopolymer concrete after water saturation. Sci. Rep. 2024, 14, 7117. [Google Scholar] [CrossRef] [PubMed]
- Dou, Y.; Feng, G.; Xu, L.; Yang, Y.; Zhang, Z.; You, L.; Zhong, S.; Gao, Y.; Cui, X. Modification of rubber particles and its application in rubberized concrete. J. Build. Eng. 2022, 51, 104346. [Google Scholar] [CrossRef]
- He, L.; Cai, H.; Huang, Y.; Ma, Y.; Van Den Bergh, W.; Gaspar, L.; Valentin, J.; Vasiliev, Y.E.; Kowalski, K.J.; Zhang, J. Research on the properties of rubber concrete containing surface-modified rubber powders. J. Build. Eng. 2021, 35, 101991. [Google Scholar] [CrossRef]
- Manjunatha, M.; Seth, D.; Balaji, K.; Roy, S.; Tangadagi, R.B. Utilization of industrial-based pvc waste powder in self-compacting concrete: A sustainable building material. J. Clean. Prod. 2023, 428, 139428. [Google Scholar] [CrossRef]
- Hayeemasae, N.; Salleh, S.Z.; Ismail, H. Sustainable use of chloroprene rubber waste as blend component with natural rubber, epoxidized natural rubber and styrene butadiene rubber. J. Polym. Environ. 2019, 27, 2119–2130. [Google Scholar] [CrossRef]
- Yang, G.; Fan, Y.; Li, X.; Xu, Y. Influence of rubber powder size and volume fraction on dynamic compressive properties of rubberized mortar. Powder Technol. 2023, 420, 118376. [Google Scholar] [CrossRef]
- Bušić, R.; Miličević, I.; Šipoš, T.K.; Strukar, K. Recycled rubber as an aggregate replacement in self-compacting concrete—Literature overview. Materials 2018, 11, 1729. [Google Scholar] [CrossRef] [PubMed]
- Mavukwana, A.-E.; Stacey, N.; Fox, J.A.; Sempuga, B.C. Thermodynamic comparison of pyrolysis and gasification of waste tyres. J. Environ. Chem. Eng. 2021, 9, 105163. [Google Scholar] [CrossRef]
- Chen, J.; Zhuang, J.; Shen, S.; Dong, S. Experimental investigation on the impact resistance of rubber self-compacting concrete. In Structures; Elsevier: Amsterdam, The Netherlands, 2022; pp. 691–704. [Google Scholar]
- Liu, F.; Chen, G.; Li, L.; Guo, Y. Study of impact performance of rubber reinforced concrete. Constr. Build. Mater. 2012, 36, 604–616. [Google Scholar] [CrossRef]
- Mendis, A.S.; Al-Deen, S.; Ashraf, M. Effect of rubber particles on the flexural behaviour of reinforced crumbed rubber concrete beams. Constr. Build. Mater. 2017, 154, 644–657. [Google Scholar] [CrossRef]
- Gao, Y.; Wang, B.; Liu, C.; Hui, D.; Xu, Q.; Zhao, Q.; Qin, Y.; Dong, W. Experimental investigation on static compressive toughness of steel fiber rubber concrete. Rev. Adv. Mater. Sci. 2022, 61, 576–586. [Google Scholar] [CrossRef]
- Bu, C.; Zhu, D.; Liu, L.; Lu, X.; Sun, Y.; Yu, L.; OuYang, Y.; Cao, X.; Wang, F. Research progress on rubber concrete properties: A review. J. Rubber Res. 2022, 25, 105–125. [Google Scholar] [CrossRef]
- Grincova, A.; Andrejiova, M.; Marasova, D. Failure analysis of the impact resistance of protective rubber panels. Eng. Fail. Anal. 2022, 139, 106481. [Google Scholar] [CrossRef]
- Zhai, S.; Liu, G.; Pang, B.; Liu, C.; Zhang, Z.; Zhang, L.; Liu, L.; Yang, Y.; Liu, Z.; Zhang, Y. Investigation on the influence of modified waste rubber powder on the abrasion resistance of concrete. Constr. Build. Mater. 2022, 357, 129409. [Google Scholar] [CrossRef]
- Yasser, N.; Abdelrahman, A.; Kohail, M.; Moustafa, A. Experimental investigation of durability properties of rubberized concrete. Ain Shams Eng. J. 2023, 14, 102111. [Google Scholar] [CrossRef]
- Angelin, A.; Miranda, E.J.P., Jr.; Santos, J.D.; Lintz, R.; Gachet-Barbosa, L. Rubberized mortar: The influence of aggregate granulometry in mechanical resistances and acoustic behavior. Constr. Build. Mater. 2019, 200, 248–254. [Google Scholar] [CrossRef]
- Feng, W.; Liu, F.; Yang, F.; Li, L.; Jing, L. Experimental study on dynamic split tensile properties of rubber concrete. Constr. Build. Mater. 2018, 165, 675–687. [Google Scholar] [CrossRef]
- Guo, J.; Huang, M.; Huang, S.; Wang, S. An experimental study on mechanical and thermal insulation properties of rubberized concrete including its microstructure. Appl. Sci. 2019, 9, 2943. [Google Scholar] [CrossRef]
- Mei, X.; Cui, Z.; Sheng, Q.; Zhou, J.; Li, C. Application of the improved poa-rf model in predicting the strength and energy absorption property of a novel aseismic rubber-concrete material. Materials 2023, 16, 1286. [Google Scholar] [CrossRef] [PubMed]
- Lai, D.; Demartino, C.; Xiao, Y. High-strain rate tension behavior of fiber-reinforced rubberized concrete. Cem. Concr. Compos. 2022, 131, 104554. [Google Scholar] [CrossRef]
- Pan, L.; Hao, H.; Cui, J.; Pham, T.M. Numerical study on dynamic properties of rubberised concrete with different rubber contents. Def. Technol. 2023, 24, 228–240. [Google Scholar] [CrossRef]
- Liu, Z.; Chen, X.; Wang, X.; Diao, H. Investigation on the dynamic compressive behavior of waste tires rubber-modified self-compacting concrete under multiple impacts loading. J. Clean. Prod. 2022, 336, 130289. [Google Scholar] [CrossRef]
- Pham, T.M.; Renaud, N.; Pang, V.L.; Shi, F.; Hao, H.; Chen, W. Effect of rubber aggregate size on static and dynamic compressive properties of rubberized concrete. Struct. Concr. 2022, 23, 2510–2522. [Google Scholar] [CrossRef]
- Su, H.; Yang, J.; Ling, T.-C.; Ghataora, G.S.; Dirar, S. Properties of concrete prepared with waste tyre rubber particles of uniform and varying sizes. J. Clean. Prod. 2015, 91, 288–296. [Google Scholar] [CrossRef]
- Thomas, B.S.; Gupta, R.C.; Kalla, P.; Cseteneyi, L. Strength, abrasion and permeation characteristics of cement concrete containing discarded rubber fine aggregates. Constr. Build. Mater. 2014, 59, 204–212. [Google Scholar] [CrossRef]
- Jin, H.; Wang, Z.; Zhao, C.; Xiao, J. Effect of rubber surface treatment on damping performance of rubber-mortar ITZ in rubberized concrete. J. Build. Eng. 2024, 83, 108441. [Google Scholar] [CrossRef]
- Chen, Z.; Li, L.; Xiong, Z. Investigation on the interfacial behaviour between the rubber-cement matrix of the rubberized concrete. J. Clean. Prod. 2019, 209, 1354–1364. [Google Scholar] [CrossRef]
- Gholampour, A.; Ozbakkaloglu, T.; Hassanli, R. Behavior of rubberized concrete under active confinement. Constr. Build. Mater. 2017, 138, 372–382. [Google Scholar] [CrossRef]
- Dong, Q.; Huang, B.; Shu, X. Rubber modified concrete improved by chemically active coating and silane coupling agent. Constr. Build. Mater. 2013, 48, 116–123. [Google Scholar] [CrossRef]
- Huang, B.; Shu, X.; Cao, J. A two-staged surface treatment to improve properties of rubber modified cement composites. Constr. Build. Mater. 2013, 40, 270–274. [Google Scholar] [CrossRef]
- Naderpour, H.; Poursaeidi, O.; Ahmadi, M. Shear resistance prediction of concrete beams reinforced by frp bars using artificial neural networks. Measurement 2018, 126, 299–308. [Google Scholar] [CrossRef]
- Naderpour, H.; Rafiean, A.H.; Fakharian, P. Compressive strength prediction of environmentally friendly concrete using artificial neural networks. J. Build. Eng. 2018, 16, 213–219. [Google Scholar] [CrossRef]
- Congro, M.; de Alencar Monteiro, V.M.; Brandão, A.L.; Santos, B.F.D.; Roehl, D.; de Andrade Silva, F. Prediction of the residual flexural strength of fiber reinforced concrete using artificial neural networks. Constr. Build. Mater. 2021, 303, 124502. [Google Scholar] [CrossRef]
- JGJ 55-2011; Standard for Design Specification for Mix Proportion of Ordinary Concrete. China Academy of Building Research: Beijing, China, 2011. (In Chinese)
- Ganjian, E.; Khorami, M.; Maghsoudi, A.A. Scrap-tyre-rubber replacement for aggregate and filler in concrete. Constr. Build. Mater. 2009, 23, 1828–1836. [Google Scholar] [CrossRef]
- GB/T 50081-2002; Standard for Test Method of Mechanical Properties on Ordinary Concrete. Ministry of Construction of the People’s Republic of China: Beijing, China, 2002. (In Chinese)
- GB/T 37783-2019; Metallic Materials-High Strain Rate Tensile Testmethod at Elevated Temperature. Ministry of Construction of the People’s Republic of China: Beijing, China, 2019. (In Chinese)
- Jiang, T.; Xue, P.; Butt, H. Pulse shaper design for dynamic testing of viscoelastic materials using polymeric SHPB. Int. J. Impact Eng. 2015, 79, 45–52. [Google Scholar] [CrossRef]
- Sun, X.; Zhao, K.; Li, Y.; Huang, R.; Ye, Z.; Zhang, Y.; Ma, J. A study of strain-rate effect and fiber reinforcement effect on dynamic behavior of steel fiber-reinforced concrete. Constr. Build. Mater. 2018, 158, 657–669. [Google Scholar] [CrossRef]
- Hassan, M.; Wille, K. Direct tensile behavior of steel fiber reinforced ultra-high performance concrete at high strain rates using modified split hopkinson tension bar. Compos. Part B Eng. 2022, 246, 110259. [Google Scholar] [CrossRef]
- Huang, W.; Huang, X.; Xing, Q.; Zhou, Z. Strength reduction factor of crumb rubber as fine aggregate replacement in concrete. J. Build. Eng. 2020, 32, 101346. [Google Scholar] [CrossRef]
- Li, L.; Ruan, S.; Zeng, L. Mechanical properties and constitutive equations of concrete containing a low volume of tire rubber particles. Constr. Build. Mater. 2014, 70, 291–308. [Google Scholar] [CrossRef]
- Ly, H.-B.; Nguyen, T.-A.; Tran, V.Q. Development of deep neural network model to predict the compressive strength of rubber concrete. Constr. Build. Mater. 2021, 301, 124081. [Google Scholar] [CrossRef]
- Chen, A.; Han, X.; Wang, Z.; Zhang, Q.; Xia, X.; Ji, Y.; Li, K. Analytical evaluation of compressive strength for concrete with rubber fine aggregates and the predictive model. Constr. Build. Mater. 2022, 345, 128359. [Google Scholar] [CrossRef]
- Karunarathna, S.; Linforth, S.; Kashani, A.; Liu, X.; Ngo, T. Effect of recycled rubber aggregate size on fracture and other mechanical properties of structural concrete. J. Clean. Prod. 2021, 314, 128230. [Google Scholar] [CrossRef]
- Ling, T.-C. Prediction of density and compressive strength for rubberized concrete blocks. Constr. Build. Mater. 2011, 25, 4303–4306. [Google Scholar] [CrossRef]
- Abbas, S.; Fatima, A.; Kazmi, S.M.S.; Munir, M.J.; Ali, S.; Rizvi, M.A. Effect of particle sizes and dosages of rubber waste on the mechanical properties of rubberized concrete composite. Appl. Sci. 2022, 12, 8460. [Google Scholar] [CrossRef]
- Feng, W.; Chen, Z.; Tang, Y.; Liu, F.; Yang, F.; Yang, Y.; Tayeh, B.A.; Namdar, A. Fracture characteristics of sustainable crumb rubber concrete under a wide range of loading rates. Constr. Build. Mater. 2022, 359, 129474. [Google Scholar] [CrossRef]
- Gesoglu, M.; Güneyisi, E.; Hansu, O.; İpek, S.; Asaad, D.S. Influence of waste rubber utilization on the fracture and steel–concrete bond strength properties of concrete. Constr. Build. Mater. 2015, 101, 1113–1121. [Google Scholar] [CrossRef]
- Al-Tayeb, M.; Bakar, B.A.; Akil, H.; Ismail, H. Performance of rubberized and hybrid rubberized concrete structures under static and impact load conditions. Exp. Mech. 2013, 53, 377–384. [Google Scholar] [CrossRef]
- Rezaifar, O.; Hasanzadeh, M.; Gholhaki, M. Concrete made with hybrid blends of crumb rubber and metakaolin: Optimization using response surface method. Constr. Build. Mater. 2016, 123, 59–68. [Google Scholar] [CrossRef]
- Issa, C.A.; Salem, G. Utilization of recycled crumb rubber as fine aggregates in concrete mix design. Constr. Build. Mater. 2013, 42, 48–52. [Google Scholar] [CrossRef]
- Girskas, G.; Nagrockienė, D. Crushed rubber waste impact of concrete basic properties. Constr. Build. Mater. 2017, 140, 36–42. [Google Scholar] [CrossRef]
- Taak, N.; Sharma, L. Influence of compression casting technique and chipped rubber usage on the strength parameters of concrete. Mater. Today Proc. 2021, 45, 3462–3468. [Google Scholar] [CrossRef]
- Xu, J.; Niu, X.; Yao, Z. Mechanical properties and acoustic emission data analyses of crumb rubber concrete under biaxial compression stress states. Constr. Build. Mater. 2021, 298, 123778. [Google Scholar] [CrossRef]
- Khatib, Z.K.; Bayomy, F.M. Rubberized portland cement concrete. J. Mater. Civ. Eng. 1999, 11, 206–213. [Google Scholar] [CrossRef]
- Wu, Y.-F.; Kazmi, S.M.S.; Munir, M.J.; Zhou, Y.; Xing, F. Effect of compression casting method on the compressive strength, elastic modulus and microstructure of rubber concrete. J. Clean. Prod. 2020, 264, 121746. [Google Scholar] [CrossRef]
- Feng, W.; Liu, F.; Yang, F.; Jing, L.; Li, L.; Li, H.; Chen, L. Compressive behaviour and fragment size distribution model for failure mode prediction of rubber concrete under impact loads. Constr. Build. Mater. 2021, 273, 121767. [Google Scholar] [CrossRef]
- Richardson, A.; Coventry, K.; Edmondson, V.; Dias, E. Crumb rubber used in concrete to provide freeze–thaw protection (optimal particle size). J. Clean. Prod. 2016, 112, 599–606. [Google Scholar] [CrossRef]
- Wu, G.-D.; Lo, S.-L. Effects of data normalization and inherent-factor on decision of optimal coagulant dosage in water treatment by artificial neural network. Expert Syst. Appl. 2010, 37, 4974–4983. [Google Scholar] [CrossRef]
- GB 50010-2010; Code for Design of Concrete Structures. Ministry of Construction of the People’s Republic of China: Beijing, China, 2010.










| Cement | Density (kg·m−3) | MgO (%) | SO3 (%) | Initial Setting (min) | Final Setting (h) | 3d (MPa) | 28d (MPa) |
|---|---|---|---|---|---|---|---|
| P·042.5 | 3100 | 3.0 | 3.5 | 60 | 6 | 21.5 | 44.5 |
| Specimen | Water | Cement | Coarse Aggregate | Fine Aggregate | Rubber |
|---|---|---|---|---|---|
| NC | 220 | 489 | 1113 | 523 | 0 |
| RC-0.1-2 | 220 | 489 | 1113 | 513 | 5 |
| RC-0.1-5 | 220 | 489 | 1113 | 487 | 11 |
| RC-0.1-15 | 220 | 489 | 1113 | 445 | 34 |
| RC-0.1-30 | 220 | 489 | 1113 | 366 | 68 |
| RC-0.5-2 | 220 | 489 | 1113 | 513 | 5 |
| RC-0.5-5 | 220 | 489 | 1113 | 487 | 11 |
| RC-0.5-15 | 220 | 489 | 1113 | 445 | 34 |
| RC-0.5-30 | 220 | 489 | 1113 | 366 | 68 |
| RC-2-2 | 220 | 489 | 1113 | 513 | 5 |
| RC-2-5 | 220 | 489 | 1113 | 487 | 11 |
| RC-2-15 | 220 | 489 | 1113 | 445 | 34 |
| RC-2-30 | 220 | 489 | 1113 | 366 | 68 |
| RC-5-2 | 220 | 489 | 1091 | 523 | 9 |
| RC-5-5 | 220 | 489 | 1057 | 523 | 23 |
| RC-5-15 | 220 | 489 | 946 | 523 | 70 |
| RC-5-30 | 220 | 489 | 779 | 523 | 140 |
| RC-10-2 | 220 | 489 | 1091 | 523 | 9 |
| RC-10-5 | 220 | 489 | 1057 | 523 | 23 |
| RC-10-15 | 220 | 489 | 946 | 523 | 70 |
| RC-10-30 | 220 | 489 | 779 | 523 | 140 |
| RC-20-2 | 220 | 489 | 1091 | 523 | 9 |
| RC-20-5 | 220 | 489 | 1057 | 523 | 23 |
| RC-20-15 | 220 | 489 | 946 | 523 | 70 |
| RC-20-30 | 220 | 489 | 779 | 523 | 140 |
| Size(mm) | Fit Method | |||
|---|---|---|---|---|
| 0.1 | Linear fitting | −0.96 | 58.3 | 0.99 |
| 0.5 | −0.99 | 58.3 | 0.99 | |
| 2 | −1.10 | 58.3 | 0.99 | |
| 5 | −1.22 | 58.3 | 0.99 | |
| 10 | −1.28 | 58.3 | 0.99 | |
| 20 | −1.30 | 58.3 | 0.98 |
| Number | Number of Specimens | Rubber Size/mm | Content/% | f28d/MPa | References |
|---|---|---|---|---|---|
| 1 | 3 | 2 | 5–15 | 34–40 | [26] |
| 2 | 2 | 2–4 | 15 | 28.7–35.8 | [38] |
| 3 | 3 | 0.3–3 | 20 | 54.6–55.3 | [39] |
| 4 | 24 | 1.48 | 2.5–20 | 17–41 | [40] |
| 5 | 3 | 20 | 5–10 | 25–33 | [50] |
| 6 | 20 | 0.25–2 | 20–80 | 2.8–22 | [56] |
| 7 | 25 | 0.17–4 | 2–10 | 25–40 | [57] |
| 8 | 13 | 0.15–3 | 1–6 | 16–32.3 | [59] |
| 9 | 4 | 4–15 | 2–4 | 29.26–33.38 | [60] |
| 10 | 24 | 3 | 5–50 | 9.5–35.4 | [61] |
| 11 | 9 | 1–8.5 | 10–30 | 22.1–44.6 | [62] |
| 12 | 5 | 0.5 | 10–50 | 17.91–37.76 | [63] |
| 13 | 6 | 1.5 | 5–30 | 30–50 | [64] |
| 14 | 3 | 1 | 5–20 | 29–35 | [65] |
| 15 | 2 | 1.16 | 15–30 | 21–30 | [66] |
| 16 | 4 | 0.1 | 15–100 | 5.3–26.7 | [67] |
| 17 | 6 | 3–5 | 5–20 | 20–55.2 | [68] |
| 18 | 5 | 15 | 10–50 | 11–25 | [69] |
| 19 | 2 | 1.84 | 5–10 | 37.9–41.5 | [70] |
| 20 | 16 | 1.5–15 | 2.16–57 | 2.7–34.9 | [71] |
| 21 | 8 | 12.5 | 10–100 | 3.8–24.13 | [72] |
| 22 | 5 | 0.85 | 10–50 | 18–37.76 | [73] |
| 23 | 5 | 0.25–2.25 | 0.6 | 35.12–36.37 | [74] |
| Number | Specimen | Actual Values | Fit Formula | ANN | ||||
|---|---|---|---|---|---|---|---|---|
| Prediction | Absolute Error | Relative Error/% | Prediction | Absolute Error | Relative Error/% | |||
| 1 | RC-0.1-5 | 50.9 | 53.5 | 2.6 | 5.1 | 47.9 | 3.0 | 5.9 |
| 2 | RC-0.1-30 | 32.1 | 29.5 | 2.6 | 8.1 | 29.8 | 2.3 | 7.2 |
| 3 | RC-0.5-2 | 52.18 | 56.3 | 4.1 | 7.9 | 50.0 | 2.2 | 4.2 |
| 4 | RC-0.5-30 | 28.17 | 28.4 | 0.2 | 0.8 | 30.2 | 2.0 | 7.1 |
| 5 | RC-2-2 | 51.51 | 56.1 | 4.6 | 8.9 | 49.8 | 1.7 | 3.2 |
| 6 | RC-2-15 | 37.44 | 41.7 | 4.3 | 11.5 | 41.6 | 4.1 | 11.0 |
| 7 | RC-5-5 | 47.34 | 52.2 | 4.9 | 10.3 | 45.8 | 1.5 | 3.2 |
| 8 | RC-5-30 | 25.44 | 21.8 | 3.7 | 14.5 | 27.4 | 2.0 | 7.7 |
| 9 | RC-10-15 | 35.72 | 39.1 | 3.4 | 9.4 | 33.9 | 1.9 | 5.2 |
| 10 | RC-10-30 | 22.55 | 19.9 | 2.7 | 11.9 | 22.5 | 0.1 | 0.4 |
| 11 | RC-20-15 | 35.74 | 38.8 | 3.1 | 8.6 | 39.7 | 4.0 | 11.1 |
| 12 | RC-20-30 | 22.87 | 19.3 | 3.5 | 15.5 | 22.3 | 0.6 | 2.6 |
| Number | Strain Rate 1 (s−1) | 1 (MPa) | DIF 1 | Strain Rate 2 (s−1) | 2 (MPa) | DIF 2 | Strain Rate 3 (s−1) | 3 (MPa) | DIF 3 | (MPa) |
|---|---|---|---|---|---|---|---|---|---|---|
| NC | 84.4 | 83.2 | 1.427 | 162.6 | 109.5 | 1.878 | 270.6 | 129.5 | 2.221 | 58.3 |
| RC-0.1-2 | 96.3 | 73.2 | 1.432 | 162.6 | 97.5 | 1.908 | 267.9 | 123.5 | 2.416 | 51.11 |
| RC-0.1-5 | 96.8 | 73.0 | 1.434 | 174.8 | 97.2 | 1.910 | 259.3 | 123.0 | 2.417 | 50.9 |
| RC-0.1-15 | 96.8 | 70.2 | 1.753 | 174.8 | 91.7 | 2.290 | 269.9 | 99.6 | 2.487 | 40.05 |
| RC-0.1-30 | 100.6 | 57.0 | 1.776 | 166.1 | 82.2 | 2.561 | 269.8 | 91.7 | 2.857 | 32.1 |
| RC-0.5-2 | 91.8 | 82.2 | 1.575 | 171.5 | 108.2 | 2.074 | 253.3 | 125.0 | 2.396 | 52.18 |
| RC-0.5-5 | 100.1 | 78.7 | 1.697 | 168.1 | 99.0 | 2.135 | 291.7 | 113.0 | 2.436 | 46.38 |
| RC-0.5-15 | 95.8 | 65.9 | 1.857 | 197.9 | 85.0 | 2.396 | 269.7 | 99.8 | 2.813 | 35.48 |
| RC-0.5-30 | 98.2 | 54.0 | 1.917 | 166.1 | 70.0 | 2.485 | 280.1 | 81.5 | 2.893 | 28.17 |
| RC-2-2 | 89.5 | 80.6 | 1.565 | 179.4 | 101.4 | 1.969 | 288.1 | 127.0 | 2.466 | 51.51 |
| RC-2-5 | 94.2 | 80.1 | 1.701 | 191.3 | 97.9 | 2.079 | 262.5 | 115.6 | 2.454 | 47.1 |
| RC-2-15 | 91.2 | 66.1 | 1.765 | 193.1 | 88.9 | 2.374 | 275.2 | 104.9 | 2.802 | 37.44 |
| RC-2-30 | 99.6 | 64.0 | 1.815 | 198.1 | 84.0 | 2.382 | 270.3 | 100.0 | 2.835 | 35.27 |
| RC-5-2 | 89.9 | 76.6 | 1.548 | 197.6 | 95.0 | 1.920 | 286.5 | 114.0 | 2.304 | 49.48 |
| RC-5-5 | 92.9 | 74.0 | 1.563 | 178.5 | 93.0 | 1.965 | 268.5 | 111.0 | 2.345 | 47.34 |
| RC-5-15 | 98.2 | 58.8 | 1.686 | 198.8 | 74.0 | 2.122 | 267.9 | 86.9 | 2.492 | 34.87 |
| RC-5-30 | 99.9 | 50.0 | 1.965 | 195.7 | 67.0 | 2.634 | 264.7 | 74.0 | 2.909 | 25.44 |
| RC-10-2 | 99.3 | 76.0 | 1.469 | 174.8 | 99.0 | 1.913 | 260.1 | 126.0 | 2.435 | 51.75 |
| RC-10-5 | 99.9 | 71.0 | 1.496 | 176.1 | 92.0 | 1.938 | 259.8 | 117.8 | 2.482 | 47.46 |
| RC-10-15 | 99.2 | 57.0 | 1.596 | 193.2 | 73.0 | 2.044 | 248.9 | 91.0 | 2.548 | 35.72 |
| RC-10-30 | 99.9 | 39.7 | 1.761 | 198.8 | 56.9 | 2.523 | 264.2 | 64.4 | 2.856 | 22.55 |
| RC-20-2 | 90.1 | 69.0 | 1.496 | 191.2 | 95.8 | 2.077 | 259.6 | 104.5 | 2.266 | 46.12 |
| RC-20-5 | 99.7 | 66.0 | 1.529 | 176.1 | 94.2 | 2.182 | 264.4 | 100.0 | 2.316 | 43.17 |
| RC-20-15 | 99.8 | 60.5 | 1.693 | 193.2 | 83.0 | 2.322 | 270.4 | 89.0 | 2.490 | 35.74 |
| RC-20-30 | 100.4 | 43.6 | 1.906 | 192.5 | 56.9 | 2.488 | 289.6 | 70.8 | 3.096 | 22.87 |
| Size (mm) | Rubber Content (%) | |||||
|---|---|---|---|---|---|---|
| 0.1 | 0 | 0.06 | 1.31 | 1.57 | −1.60 | 0.99 |
| 2 | 0.06 | 1.31 | 2.00 | −2.11 | 0.99 | |
| 5 | 0.06 | 1.31 | 2.07 | −2.23 | 0.95 | |
| 15 | 0.10 | 1.47 | 2.26 | −2.59 | 0.97 | |
| 30 | 0.11 | 1.55 | 2.91 | −3.21 | 0.94 | |
| 0.5 | 0 | 0.06 | 1.31 | 1.57 | −1.60 | 0.99 |
| 2 | 0.08 | 1.41 | 1.84 | −2.03 | 0.99 | |
| 5 | 0.10 | 1.50 | 1.79 | −1.90 | 0.98 | |
| 15 | 0.12 | 1.61 | 1.95 | −2.23 | 0.98 | |
| 30 | 0.15 | 1.76 | 2.34 | −2.73 | 0.99 | |
| 2 | 0 | 0.06 | 1.31 | 1.57 | −1.60 | 0.99 |
| 2 | 0.08 | 1.41 | 1.74 | −1.87 | 0.97 | |
| 5 | 0.09 | 1.48 | 1.81 | −1.92 | 0.95 | |
| 15 | 0.11 | 1.55 | 2.12 | −2.40 | 0.99 | |
| 30 | 0.13 | 1.69 | 2.28 | −2.77 | 0.98 | |
| 5 | 0 | 0.06 | 1.31 | 1.57 | −1.60 | 0.99 |
| 2 | 0.08 | 1.39 | 1.44 | −1.79 | 0.96 | |
| 5 | 0.08 | 1.40 | 1.67 | −1.98 | 0.99 | |
| 15 | 0.10 | 1.49 | 1.77 | −2.37 | 0.97 | |
| 30 | 0.17 | 1.84 | 2.28 | −2.61 | 0.99 | |
| 10 | 0 | 0.06 | 1.31 | 1.57 | −1.60 | 0.99 |
| 2 | 0.07 | 1.34 | 1.95 | −2.41 | 0.98 | |
| 5 | 0.07 | 1.35 | 2.00 | −2.51 | 0.97 | |
| 15 | 0.09 | 1.43 | 2.21 | −2.86 | 0.92 | |
| 30 | 0.11 | 1.54 | 2.59 | −3.41 | 0.99 | |
| 20 | 0 | 0.06 | 1.31 | 1.57 | −1.60 | 0.99 |
| 2 | 0.07 | 1.36 | 1.69 | −1.81 | 0.99 | |
| 5 | 0.08 | 1.38 | 1.91 | −2.24 | 0.93 | |
| 15 | 0.10 | 1.50 | 1.89 | −2.65 | 0.98 | |
| 30 | 0.13 | 1.65 | 2.54 | −3.21 | 0.98 |
| Size (mm) | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.1 | 0.18 | 0.06 | 0.92 | 0.90 | 1.30 | 0.95 | 3.77 | 1.77 | 0.91 | −4.65 | −1.86 | 0.92 |
| 0.5 | 0.26 | 0.08 | 0.91 | 1.35 | 1.38 | 0.92 | 2.20 | 1.67 | 0.91 | −3.24 | −1.76 | 0.90 |
| 2 | 0.20 | 0.07 | 0.91 | 1.12 | 1.37 | 0.91 | 2.23 | 1.67 | 0.92 | −3.68 | −1.73 | 0.95 |
| 5 | 0.33 | 0.06 | 0.95 | 1.65 | 1.32 | 0.95 | 2.52 | 1.48 | 0.93 | −3.21 | −1.73 | 0.92 |
| 10 | 0.06 | 0.15 | 0.99 | 0.76 | 1.31 | 0.99 | 2.83 | 1.77 | 0.88 | −4.83 | −2.06 | 0.83 |
| 20 | 0.22 | 0.06 | 0.99 | 1.10 | 1.32 | 0.99 | 2.86 | 1.62 | 0.91 | −5.09 | −1.77 | 0.94 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Du, T.; Yang, Y.; Cao, H.; Si, N.; Kordestani, H.; Sktani, Z.D.I.; Arab, A.; Zhang, C. Rubberized Concrete: Effect of the Rubber Size and Content on Static and Dynamic Behavior. Buildings 2024, 14, 1541. https://doi.org/10.3390/buildings14061541
Du T, Yang Y, Cao H, Si N, Kordestani H, Sktani ZDI, Arab A, Zhang C. Rubberized Concrete: Effect of the Rubber Size and Content on Static and Dynamic Behavior. Buildings. 2024; 14(6):1541. https://doi.org/10.3390/buildings14061541
Chicago/Turabian StyleDu, Tianyang, Yue Yang, Huidong Cao, Nan Si, Hadi Kordestani, Zhwan Dilshad Ibrahim Sktani, Ali Arab, and Chunwei Zhang. 2024. "Rubberized Concrete: Effect of the Rubber Size and Content on Static and Dynamic Behavior" Buildings 14, no. 6: 1541. https://doi.org/10.3390/buildings14061541






