Quality Risk Assessment of Prefabricated Steel Structural Components during Production Using Fuzzy Bayesian Networks
Abstract
:1. Introduction
2. Literature Review
3. Methodology
3.1. Bayesian Networks
3.2. Fuzzy Set Theory and the Fuzzy Bayesian Method
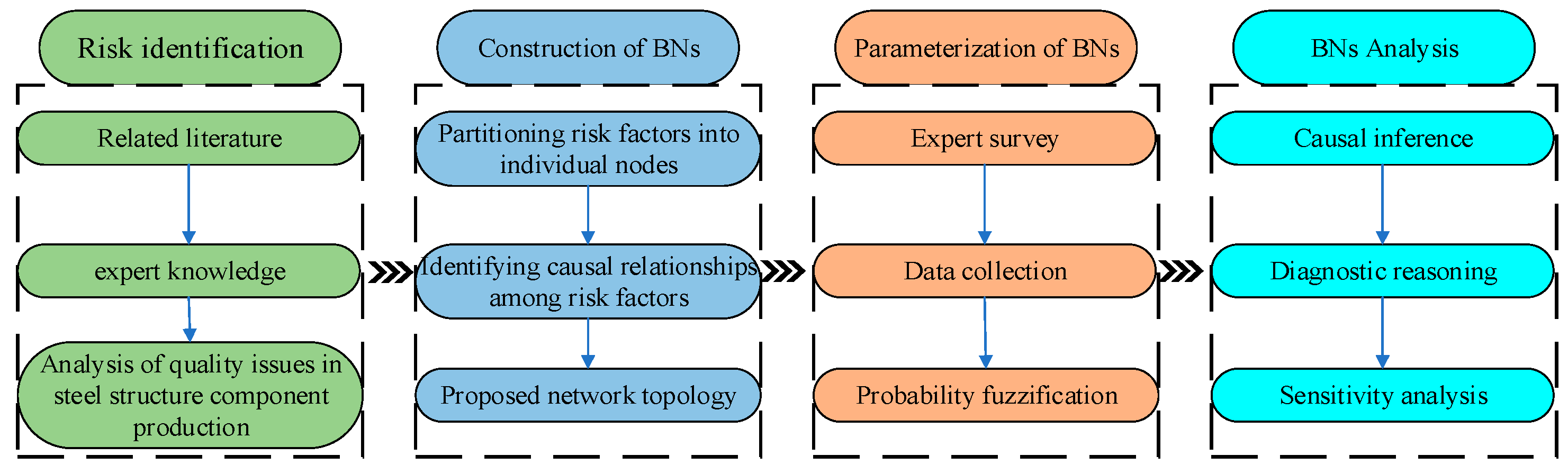
4. Model Construction
4.1. Risk Identification for the Quality of Steel Component Production
4.2. Structure of Bayesian Networks
4.3. Bayesian Network Parameter Learning
4.3.1. Determining the Prior Probabilities of Root Nodes
4.3.2. Determination of the CPTs for Intermediate and Target Nodes
4.4. BN Inference and Sensitivity Analysis
5. Application of BN Models
5.1. Prior Probabilities of BN Root Nodes
5.2. The Conditional Probabilities of the Leaf Nodes and the Target Nodes Are Determined
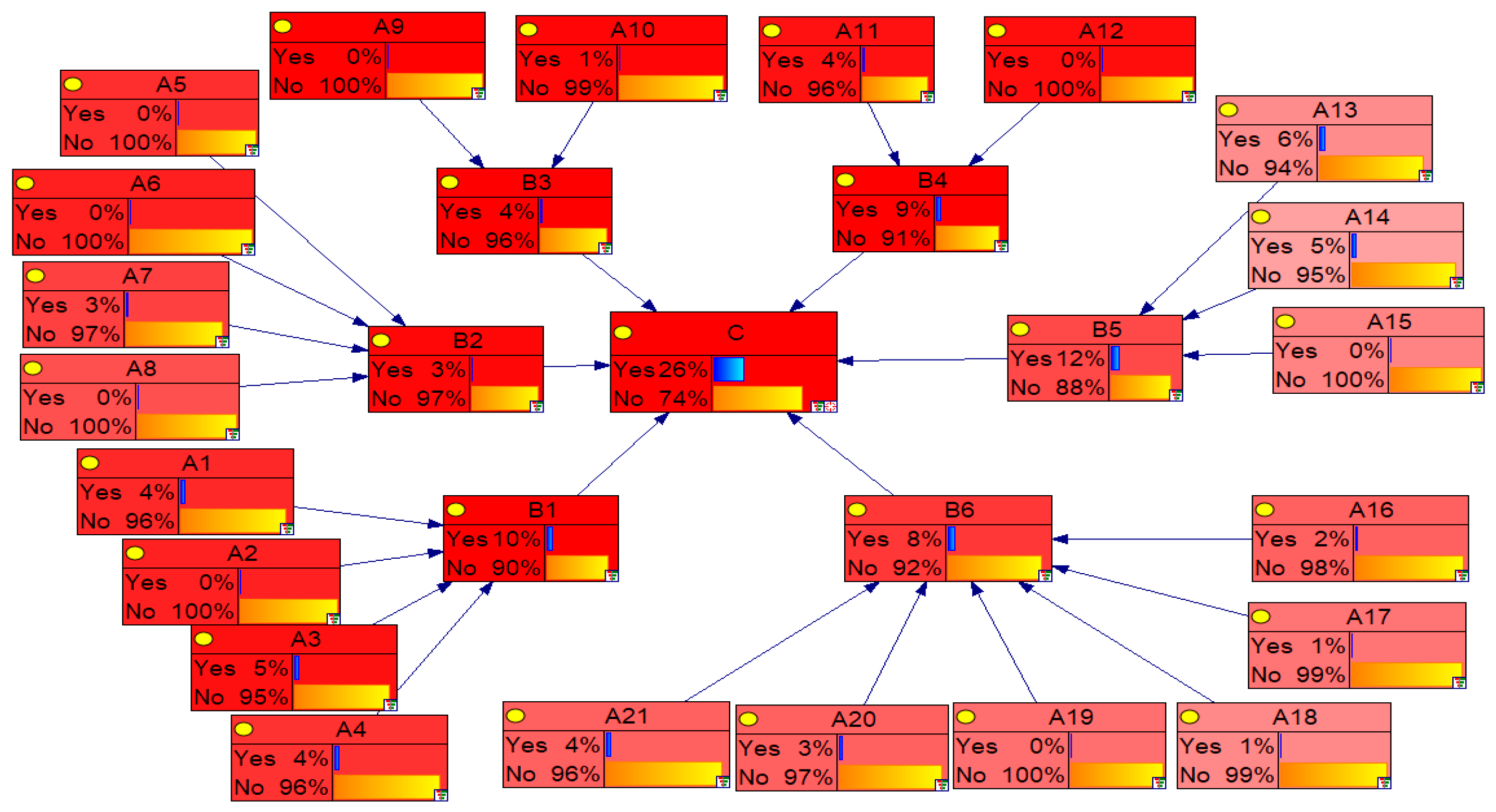
5.3. Inference Results
5.4. Diagnostic Reasoning
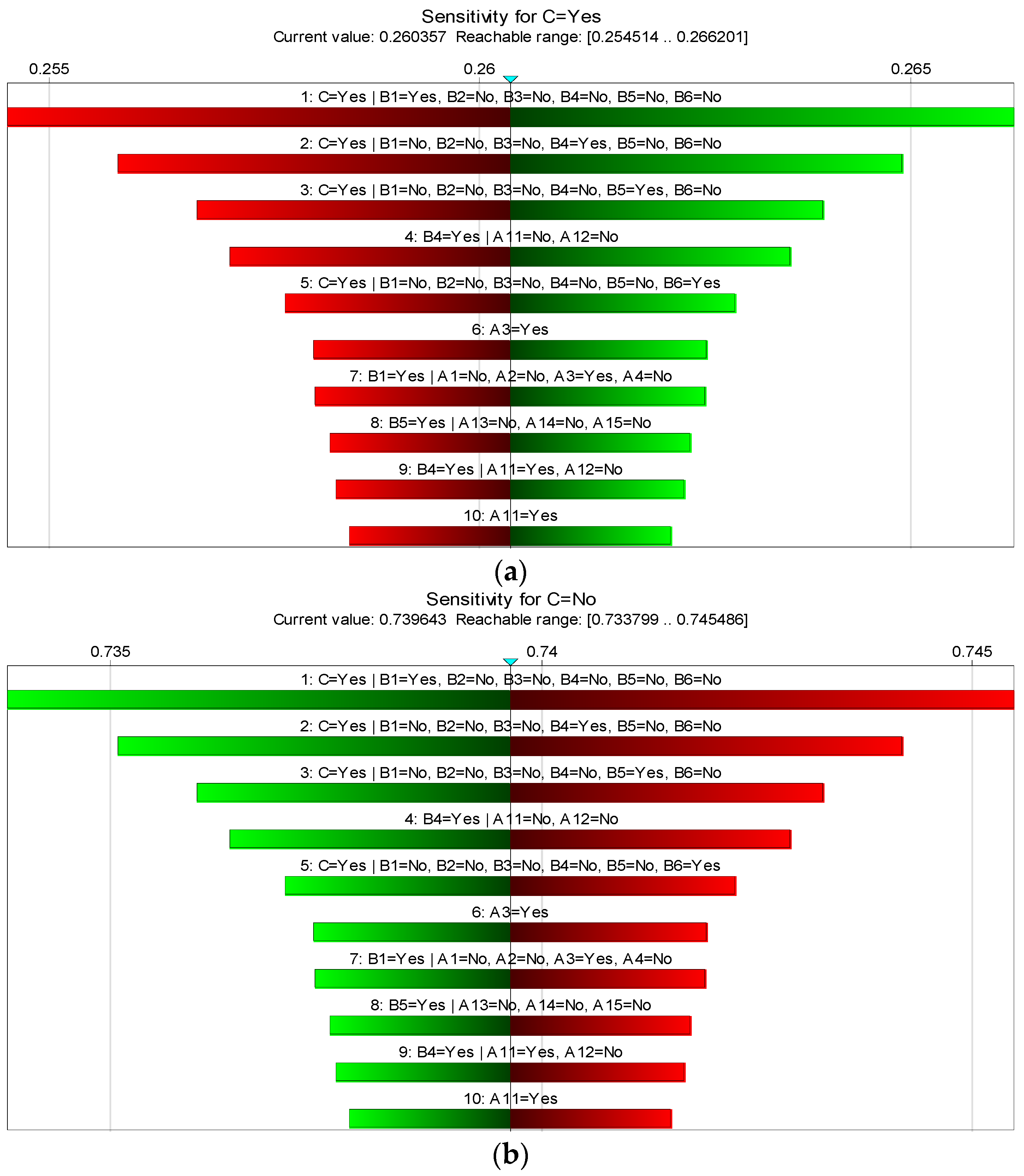
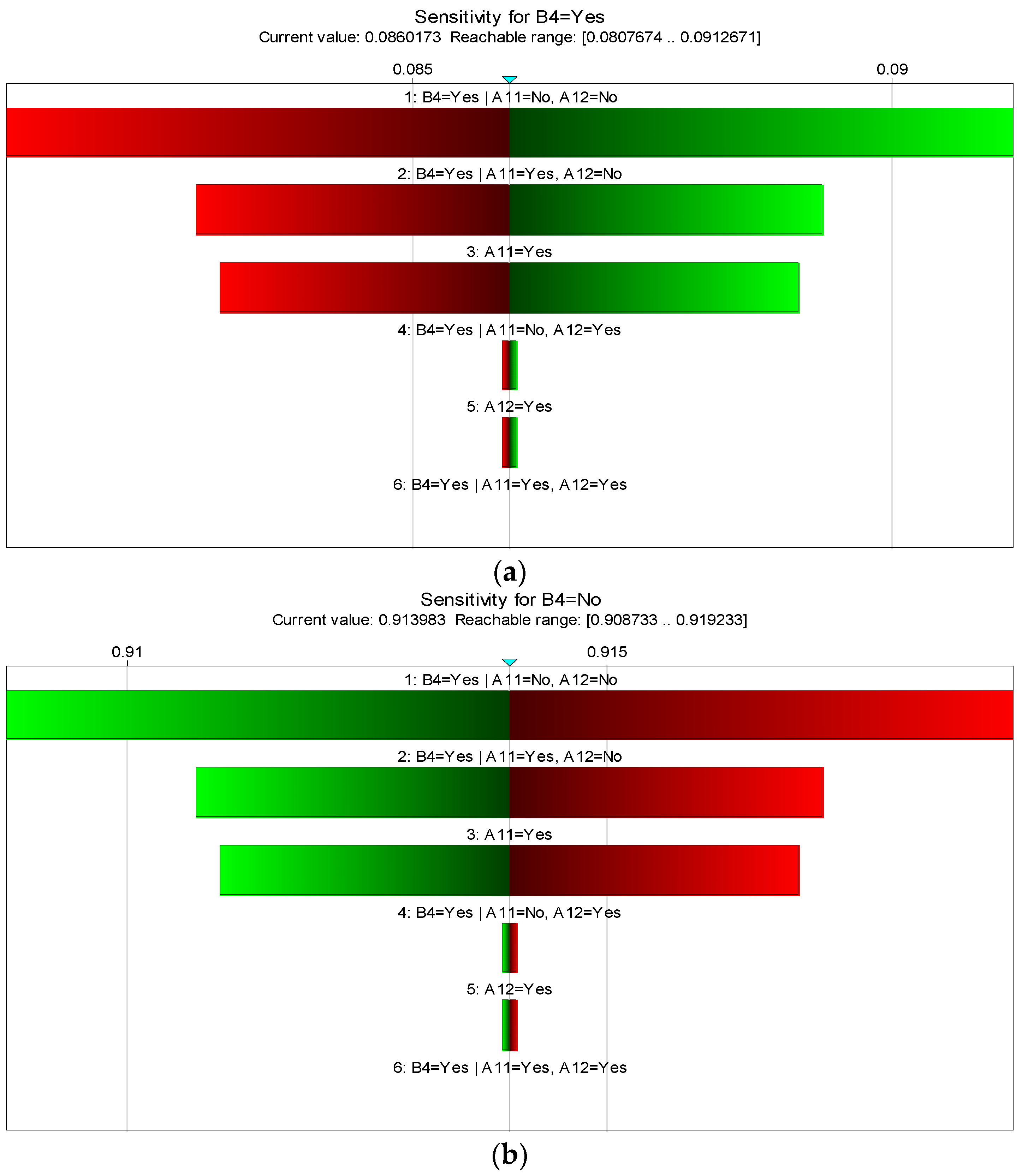
5.5. Sensitivity Analysis
5.6. Validation of the BN Model
6. Discussion
7. Conclusions and Recommendations
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Jiang, Z.-Q.; Niu, Z.-Y.; Cheng, K.-K.; Yan, T.; Zhang, A.-L. Experimental study of earthquake-resilient high ductility prefabricated opening-web steel channel beam-column joint. J. Build. Eng. 2022, 49, 104041. [Google Scholar] [CrossRef]
- Navaratnam, S.; Satheeskumar, A.; Zhang, G.; Nguyen, K.; Venkatesan, S.; Poologanathan, K. The challenges confronting the growth of sustainable prefabricated building construction in Australia: Construction industry views. J. Build. Eng. 2022, 48, 103935. [Google Scholar] [CrossRef]
- Darko, A.; Chan, A.P. Critical analysis of green building research trend in construction journals. Habitat Int. 2016, 57, 53–63. [Google Scholar] [CrossRef]
- Wuni, I.Y.; Shen, G.Q.; Hwang, B.-G. Risks of modular integrated construction: A review and future research directions. Front. Eng. Manag. 2020, 7, 63–80. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, M.; Zhao, L.; Chen, M. Analysis of factors affecting prefabricated building quality based on ISM-BN. Sustainability 2023, 15, 9682. [Google Scholar] [CrossRef]
- Rodríguez-Mariscal, J.; Canivell, J.; Solís, M. Evaluating the performance of sonic and ultrasonic tests for the inspection of rammed earth constructions. Constr. Build. Mater. 2021, 299, 123854. [Google Scholar] [CrossRef]
- Sacarea, A.I.; Oancea, G.; Parv, L. Magnetic particle inspection optimization solution within the frame of NDT 4.0. Processes 2021, 9, 1067. [Google Scholar] [CrossRef]
- Scislo, L. Single-point and surface quality assessment algorithm in continuous production with the use of 3D laser doppler scanning vibrometry system. Sensors 2023, 23, 1263. [Google Scholar] [CrossRef]
- Saba, N.; Jawaid, M.; Sultan, M.T.H. An overview of mechanical and physical testing of composite materials. Mechanical and Physical Testing of Biocomposites, Fibre-Reinforced Composites and Hybrid Composites; Elsevier: Amsterdam, The Netherlands, 2019; pp. 1–12. [Google Scholar]
- Vinod, S.; Shakor, P.; Sartipi, F.; Karakouzian, M. Object detection using esp32 cameras for quality control of steel components in manufacturing structures. Arab. J. Sci. Eng. 2023, 48, 12741–12758. [Google Scholar] [CrossRef]
- Scislo, L.; Szczepanik-Scislo, N. Quantification of Construction Materials Quality via Frequency Response Measurements: A Mobile Testing Station. Sensors 2023, 23, 8884. [Google Scholar] [CrossRef]
- Ayalp, G.G.; Ay, I. Model validation of factors limiting the use of prefabricated construction systems in Turkey. Eng. Constr. Archit. Manag. 2021, 28, 2610–2636. [Google Scholar] [CrossRef]
- Pinto, A. QRAM a Qualitative Occupational Safety Risk Assessment Model for the construction industry that incorporate uncertainties by the use of fuzzy sets. Saf. Sci. 2014, 63, 57–76. [Google Scholar] [CrossRef]
- Taillandier, F.; Sauce, G.; Bonetto, R. Risk-based investment trade-off related to building facility management. Reliab. Eng. Syst. Saf. 2019, 94, 785–795. [Google Scholar] [CrossRef]
- Pervez, H.; Ali, Y.; Pamucar, D.; Garai-Fodor, M.; Csiszárik-Kocsir, Á. Evaluation of critical risk factors in the implementation of modular construction. PLoS ONE 2022, 17, e0272448. [Google Scholar] [CrossRef]
- Tatari, A. Simulating Cost Risks for Prefabricated Construction in Developing Countries Using Bayesian Networks. J. Constr. Eng. Manag. 2023, 149, 04023037. [Google Scholar] [CrossRef]
- Zhang, Y. Application of risk management plan to technical risks in metro construction: Case study of the Grand Paris Express project. Tunn. Undergr. Space Technol. 2024, 147, 105716. [Google Scholar] [CrossRef]
- Leu, S.-S.; Chang, C.-M. Bayesian-network-based safety risk assessment for steel construction projects. Accid. Anal. Prev. 2013, 54, 122–133. [Google Scholar] [CrossRef]
- Kim, S.; Hwang, S.; Son, J. Safety Management Guidelines for Precast Concrete Production Plants Using Importance-Performance Analysis. J. Constr. Eng. Manag. 2022, 148, 04022038. [Google Scholar] [CrossRef]
- Shi, Y.; Stewart, M.G. Damage and risk assessment for reinforced concrete wall panels subjected to explosive blast loading. Int. J. Impact Eng. 2015, 85, 5–19. [Google Scholar] [CrossRef]
- Kontoleon, K.J.; Georgiadis-Filikas, K.; Tsikaloudaki, K.G.; Theodosiou, T.G.; Giarma, C.S.; Papanicolaou, C.G.; Triantafillou, T.C.; Asimakopoulou, E.K. Vulnerability assessment of an innovative precast concrete sandwich panel subjected to the ISO 834 fire. J. Build. Eng. 2022, 52, 104479. [Google Scholar] [CrossRef]
- O’Hegarty, R.; Kinnane, O.; Grimes, M.; Newell, J.; Clifford, M.; West, R. Development of thin precast concrete sandwich panels: Challenges and outcomes. Constr. Build. Mater. 2021, 267, 120981. [Google Scholar] [CrossRef]
- Balkos, K.D.; Sjaarda, M.; West, J.S.; Walbridge, S. Static and Fatigue Tests of Steel-Precast Composite Beam Specimens with Through-Bolt Shear Connectors. J. Bridge Eng. 2019, 24, 04019036. [Google Scholar] [CrossRef]
- Bechtel, A.; McConnell, J.; Chajes, M. Ultimate Capacity Destructive Testing and Finite-Element Analysis of Steel I-Girder Bridges. J. Bridge Eng. 2011, 16, 197–206. [Google Scholar] [CrossRef]
- Usefi, N.; Sharafi, P.; Mortazavi, M.; Ronagh, H.; Samali, B. Structural performance and sustainability assessment of hybrid-cold formed modular steel frame. J. Build. Eng. 2021, 34, 101895. [Google Scholar] [CrossRef]
- Wang, M.; Zhang, C.; Sun, Y.; Dong, K. Seismic performance of steel frame with replaceable low yield point steel connection components and the effect of structural fuses. J. Build. Eng. 2022, 47, 103862. [Google Scholar] [CrossRef]
- Tzortzinis, G.; Ai, C.; Brena, S.F.; Gerasimidis, S. Using 3D laser scanning for estimating the capacity of corroded steel bridge girders: Experiments, computations and analytical solutions. Eng. Struct. 2022, 265, 114407. [Google Scholar] [CrossRef]
- Gbagba, S.; Maccioni, L.; Concli, F. Advances in Machine Learning Techniques Used in Fatigue Life Prediction of Welded Structures. Appl. Sci. 2023, 14, 398. [Google Scholar] [CrossRef]
- Chen, M.-C.; Fang, W.; Yang, C.; Xie, L. Bayesian prediction and probabilistic model of fatigue cracks in steel structures. Eng. Fail. Anal. 2019, 103, 335–346. [Google Scholar] [CrossRef]
- Kabir, S.; Papadopoulos, Y. Applications of Bayesian networks and Petri nets in safety, reliability, and risk assessments: A review. Saf. Sci. 2019, 115, 154–175. [Google Scholar] [CrossRef]
- Borunda, M.; Jaramillo, O.A.; Reyes, A.; Ibargüengoytia, P.H. Bayesian networks in renewable energy systems: A bibliographical survey. Renew. Sustain. Energy Rev. 2016, 62, 32–45. [Google Scholar] [CrossRef]
- Amin, T.; Khan, F.; Imtiaz, S. Dynamic availability assessment of safety critical systems using a dynamic Bayesian network. Reliab. Eng. Syst. Saf. 2018, 178, 108–117. [Google Scholar] [CrossRef]
- Khakzad, N. Application of dynamic Bayesian network to risk analysis of domino effects in chemical infrastructures. Reliab. Eng. Syst. Saf. 2015, 138, 263–272. [Google Scholar] [CrossRef]
- Yazdi, M.; Kabir, S. A fuzzy Bayesian network approach for risk analysis in process industries. Process Saf. Environ. Prot. 2017, 111, 507–519. [Google Scholar] [CrossRef]
- Göksu, B.; Yüksel, O.; Şakar, C. Risk assessment of the Ship steering gear failures using fuzzy-Bayesian networks. Ocean Eng. 2023, 274, 114064. [Google Scholar] [CrossRef]
- Aydin, M.; Akyuz, E.; Turan, O.; Arslan, O. Validation of risk analysis for ship collision in narrow waters by using fuzzy Bayesian networks approach. Ocean Eng. 2021, 231, 108973. [Google Scholar] [CrossRef]
- Senol, Y.E.; Yasli, F. A risk analysis study for chemical cargo tank cleaning process using Fuzzy Bayesian Network. Ocean Eng. 2021, 235, 109360. [Google Scholar] [CrossRef]
- Pearl, J. From Bayesian Networks to Causal Networks. In Mathematical Models for Handling Partial Knowledge in Artificial Intelligence; Coletti, G., Dubois, D., Scozzafava, R., Eds.; Springer: New York, NY, USA, 1995; pp. 157–182. [Google Scholar] [CrossRef]
- Kitson, N.K.; Constantinou, A.C.; Guo, Z.; Liu, Y.; Chobtham, K. A survey of Bayesian Network structure learning. Artif. Intell. Rev. 2023, 56, 8721–8814. [Google Scholar] [CrossRef]
- van de Schoot, R.; Depaoli, S.; King, R.; Kramer, B.; Märtens, K.; Tadesse, M.G.; Vannucci, M.; Gelman, A.; Veen, D.; Willemsen, J.; et al. Bayesian statistics and modelling. Nat. Rev. Methods Primers 2021, 1, 1. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Diaz-Curbelo, A.; Andrade, R.A.E.; Municio, A.M.G. Role of Fuzzy Logic to Dealing with Epistemic Uncertainty in Supply Chain Risk Assessment: Review Standpoints. Int. J. Fuzzy Syst. 2020, 22, 2769–2791. [Google Scholar] [CrossRef]
- Omidvar, M.; Zarei, E.; Ramavandi, B.; Yazdi, M. Fuzzy bow-tie analysis: Concepts, review, and application. In Linguistic Methods Under Fuzzy Information in System Safety and Reliability Analysis; Springer: Cham, Switzerland, 2022; pp. 13–51. [Google Scholar]
- Mahmood, Y.A.; Ahmadi, A.; Verma, A.K.; Srividya, A.; Kumar, U. Fuzzy fault tree analysis: A review of concept and application. Int. J. Syst. Assur. Eng. Manag. 2013, 4, 19–32. [Google Scholar] [CrossRef]
- Ferdous, R.; Khan, F.; Veitch, B.; Amyotte, P.R. Methodology for computer aided fuzzy fault tree analysis. Process Saf. Environ. Prot. 2009, 87, 217–226. [Google Scholar] [CrossRef]
- Cho, H.-N.; Choi, H.-H.; Kim, Y.-B. A risk assessment methodology for incorporating uncertainties using fuzzy concepts. Reliab. Eng. Syst. Saf. 2002, 78, 173–183. [Google Scholar] [CrossRef]
- Gholamizadeh, K.; Zarei, E.; Omidvar, M.; Yazdi, M. Fuzzy sets theory and human reliability: Review, applications, and contributions. In Linguistic Methods Under Fuzzy Information in System Safety and Reliability Analysis; Springer: Cham, Switzerland, 2022; pp. 91–137. [Google Scholar]
- Halliwell, J.; Shen, Q. Linguistic probabilities: Theory and application. Soft Comput. 2009, 13, 169–183. [Google Scholar] [CrossRef]
- Lavasani, S.M.; Yang, Z.; Finlay, J.; Wang, J. Fuzzy risk assessment of oil and gas offshore wells. Process Saf. Environ. Prot. 2011, 89, 277–294. [Google Scholar] [CrossRef]
- Dombi, J.; Jónás, T. Ranking trapezoidal fuzzy numbers using a parametric relation pair. Fuzzy Sets Syst. 2020, 399, 20–43. [Google Scholar] [CrossRef]
- Mandal, S.; Maiti, J. Risk analysis using FMEA: Fuzzy similarity value and possibility theory based approach. Expert Syst. Appl. 2014, 41, 3527–3537. [Google Scholar] [CrossRef]
- Cao, P.; Shen, X.; Duan, G.; Liu, J.; Guo, K. Quality-integrated diagnostic platform for aerospace complex product assembly processes. Comput. Ind. Eng. 2024, 189, 109796. [Google Scholar] [CrossRef]
- Friederich, J.; Lazarova-Molnar, S. Reliability assessment of manufacturing systems: A comprehensive overview, challenges and opportunities. J. Manuf. Syst. 2024, 72, 38–58. [Google Scholar] [CrossRef]
- Dikmen, I.; Birgonul, M.T.; Han, S. Using fuzzy risk assessment to rate cost overrun risk in international construction projects. Int. J. Proj. Manag. 2007, 25, 494–505. [Google Scholar] [CrossRef]
- Dawes, J. Do Data Characteristics Change According to the Number of Scale Points Used? An Experiment Using 5-Point, 7-Point and 10-Point Scales. Int. J. Mark. Res. 2008, 50, 61–104. [Google Scholar] [CrossRef]
- Bai, L.; Kang, S.; Zhang, K.; Zhang, B.; Pan, T. Modeling for external stakeholder risk assessment of project portfolios. Eng. Constr. Archit. Manag. 2024, 31, 737–766. [Google Scholar] [CrossRef]
- Hsu, H.-M.; Chen, C.-T. Aggregation of fuzzy opinions under group decision making. Fuzzy Sets Syst. 1996, 79, 279–285. [Google Scholar] [CrossRef]
- Lu, M.; Jin, Y.; Lin, J.; Liu, Q.; Du, Y.; Yang, Y. Fuzzy fault tree analysis of EVAC system based on improved SAM- FFTA with butterfly optimization algorithm. Eng. Fail. Anal. 2023, 154, 107658. [Google Scholar] [CrossRef]
- Kumar, R.; Zarour, M.; Alenezi, M.; Agrawal, A.; Khan, R.A. Measuring security durability of software through fuzzy-based decision-making process. Int. J. Comput. Intell. Syst. 2019, 12, 627–642. [Google Scholar] [CrossRef]
- Belton, I.; MacDonald, A.; Wright, G.; Hamlin, I. Improving the practical application of the Delphi method in group-based judgment: A six-step prescription for a well-founded and defensible process. Technol. Forecast. Soc. Change 2019, 147, 72–82. [Google Scholar] [CrossRef]
- Palafox-Alcantar, P.G.; Hunt, D.V.L.; Rogers, C.D.F. The complementary use of game theory for the circular economy: A review of waste management decision-making methods in civil engineering. Waste Manag. 2020, 102, 598–612. [Google Scholar] [CrossRef]
- Zarei, E.; Yazdi, M.; Abbassi, R.; Khan, F. A hybrid model for human factor analysis in process accidents: FBN-HFACS. J. Loss Prev. Process Ind. 2019, 57, 142–155. [Google Scholar] [CrossRef]
- Runkler, T.A.; Glesner, M. A set of axioms for defuzzification strategies towards a theory of rational defuzzification operators. In Proceedings of the Second IEEE International Conference on Fuzzy Systems, San Francisco, CA, USA, 28 March–1 April 1993; pp. 1161–1166. [Google Scholar] [CrossRef]
- Varghese, A.; Varghese, R.R.; Balakrishnan, K.; Paul, J.S. Level identification of brain MR images using histogram of a LBP variant. In Proceedings of the 2012 IEEE International Conference on Computational Intelligence and Computing Research, Coimbatore, India, 18–20 December 2012; pp. 1–4. [Google Scholar] [CrossRef]
- Chen, P.; Zhang, Z.; Huang, Y.; Dai, L.; Hu, H. Risk assessment of marine accidents with Fuzzy Bayesian Networks and causal analysis. Ocean Coast. Manag. 2022, 228, 106323. [Google Scholar] [CrossRef]
- Onisawa, T. An application of fuzzy concepts to modelling of reliability analysis. Fuzzy Sets Syst. 1990, 37, 267–286. [Google Scholar] [CrossRef]
- Dimara, E.; Franconeri, S.; Plaisant, C.; Bezerianos, A.; Dragicevic, P. A task-based taxonomy of cognitive biases for information visualization. IEEE Trans. Vis. Comput. Graph. 2018, 26, 1413–1432. [Google Scholar] [CrossRef]
- Nyimbili, P.H.; Erden, T. Comparative evaluation of GIS-based best–worst method (BWM) for emergency facility planning: Perspectives from two decision-maker groups. Nat. Hazards 2021, 105, 1031–1067. [Google Scholar] [CrossRef]
- Lai, J.; Wang, K.; Xu, J.; Wang, P.; Chen, R.; Wang, S.; Beer, M. A failure probability assessment method for train derailments in railway yards based on IFFTA and NGBN. Eng. Fail. Anal. 2023, 154, 107675. [Google Scholar] [CrossRef]
- Chin, K.-S.; Tang, D.-W.; Yang, J.-B.; Wong, S.Y.; Wang, H. Assessing new product development project risk by Bayesian network with a systematic probability generation methodology. Expert Syst. Appl. 2009, 36, 9879–9890. [Google Scholar] [CrossRef]
- Zhang, J.; Li, M. Group decision-making method based on expert credibility with multi-granularity probabilistic linguistic Z-number preference relation. Inf. Sci. 2023, 650, 119664. [Google Scholar] [CrossRef]
- Li, M.; Wang, D.; Shan, H. Risk assessment of mine ignition sources using fuzzy Bayesian network. Process Saf. Environ. Prot. 2019, 125, 297–306. [Google Scholar] [CrossRef]
- Liwång, H. Survivability of an ocean patrol vessel—Analysis approach and uncertainty treatment. Mar. Struct. 2015, 43, 1–21. [Google Scholar] [CrossRef]


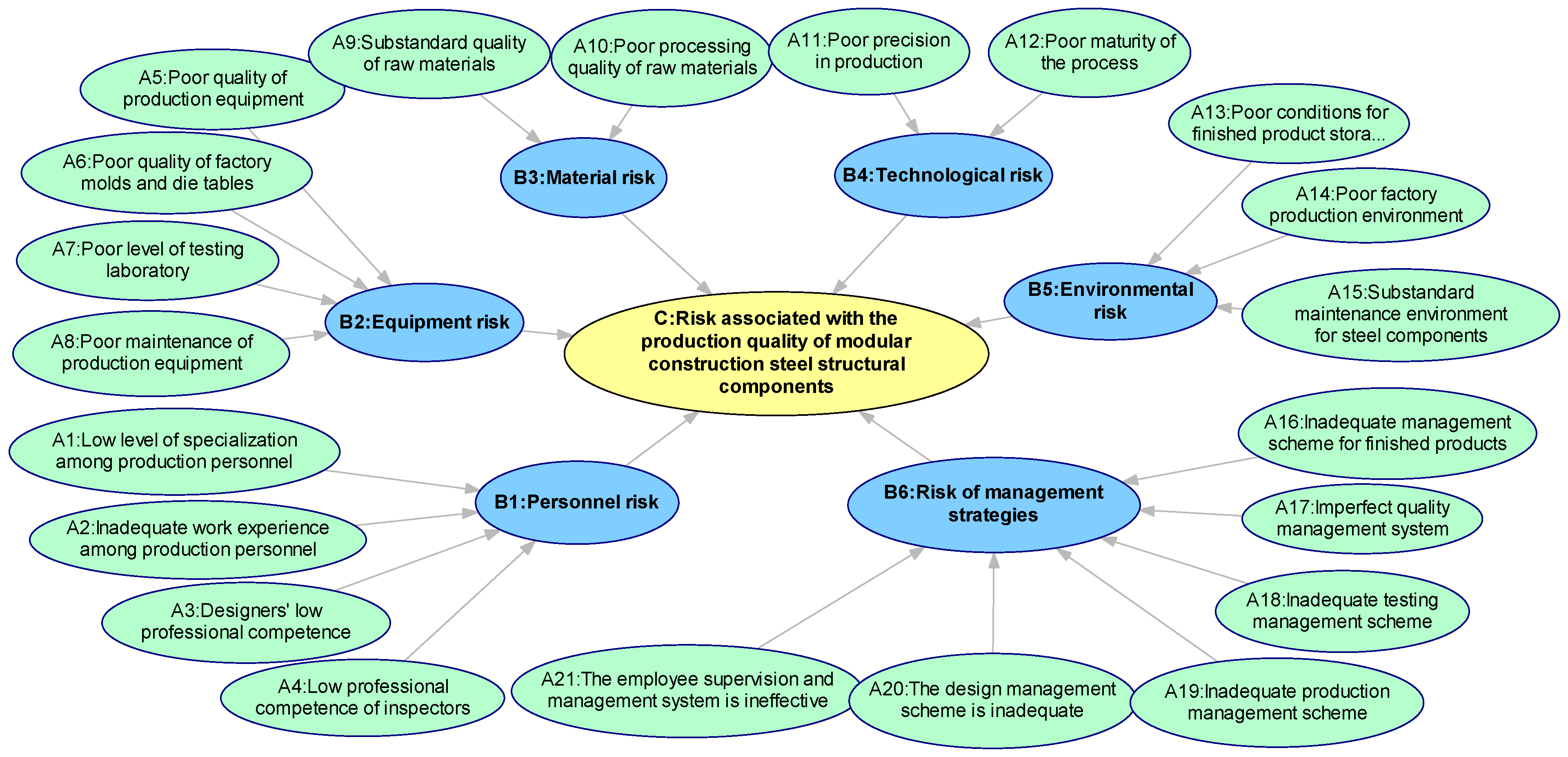





| Symbols | Variable Names | Descriptive Content |
|---|---|---|
| Human resource risk | Operators’ understanding of quality and level of technical proficiency | |
| Equipment risk | Precision and maintenance status of machinery, equipment, and testing instruments | |
| Material risk | Quality of raw materials, processing level, etc. | |
| Technological risk | Includes production processes, operating procedures, etc. | |
| Environmental risk | Temperature, humidity, lighting, cleanliness, and other conditions in the production area | |
| Risk of management strategies | Management of finished products, personnel, quality, production, and design |
| Symbols | Variable Names | Descriptive Content |
|---|---|---|
| Low level of specialization among production personnel | Refers to insufficient technical knowledge and operational skills of workers | |
| Inadequate work experience among production personnel | Typically, refers to a lack of practical experience among staff in production operations and problem-solving | |
| Designers’ low professional competence | Refers to a lack of professional knowledge, application abilities, and innovation awareness among designers | |
| Low professional competence of inspectors | Refers to a lack of professional knowledge, skills, and experience among quality inspection and control personnel | |
| Poor quality of production equipment | The failure rate, aging, and level of automation of equipment affect product quality | |
| Poor quality of factory molds and die tables | The quality of tools and equipment for shaping and supporting steel into the final product shape is inadequate | |
| Poor level of testing laboratory | The laboratory lacks in facilities, technology, and management system | |
| Poor level of testing laboratory | The production equipment lacks proper regular maintenance and necessary upkeep | |
| Substandard quality of raw materials | The materials used in production fail to meet industry standards or technical specifications | |
| Poor processing quality of raw materials | The processing of raw materials during production fails to meet industrial standards, leading to various defects and deficiencies | |
| Poor precision in production | Insufficiency in precision and meticulous execution in production activities | |
| Poor maturity of the process | The manufacturing and processing methods of steel structure components production have not reached a high level of precision and optimization | |
| Poor conditions for finished product storage | If the storage conditions, such as temperature and humidity, for finished products do not meet the ideal standards, it may compromise the quality and lifespan of the components | |
| Poor factory production environment | Whether the dust, temperature, and humidity in the factory production environment meet the requirements | |
| Substandard maintenance environment for steel components | The storage and maintenance environment of steel or components during maintenance do not meet standards, which may damage their quality and long-term performance | |
| Inadequate management scheme for finished products | The storage, transportation, and quality inspection of component finished products are unreasonable | |
| Imperfect quality management system | Systemic deficiencies in component and service quality assurance within the enterprise | |
| Inadequate testing management scheme | Inadequacies in the design, execution, personnel, technical application, and data analysis feedback of the inspection process | |
| Inadequate production management scheme | The management decisions regarding production processes and workflow scheduling have not effectively supported the completion of production tasks | |
| The design management scheme is inadequate | Whether the design scheme meets the relevant standards and the requirements of the construction unit | |
| The employee supervision and management system are ineffective | The systems, processes, or mechanisms employed by the enterprise to supervise and manage employees are not effectively implemented |
| Linguistic Variables | Fuzzy Set |
|---|---|
| Very Low (VL) | (0.0, 0.0, 0.1) |
| Low (L) | (0.0, 0.1, 0.3) |
| Fairly low (FL) | (0.1, 0.3, 0.5) |
| Moderate (M) | (0.3, 0.5, 0.7) |
| Fairly high (FH) | (0.5, 0.7, 0.9) |
| High (H) | (0.7, 0.9, 1.0) |
| Very high (VH) | (0.9, 1.0, 1.0) |
| Indicators | Description | Score | Indicators | Description | Score |
|---|---|---|---|---|---|
| Education Level | Doctor | 5 | Confidence in Assessment | Affirmative | 5 |
| Master | 4 | Almost certain | 4 | ||
| Bachelor | 3 | Very likely | 3 | ||
| College Diploma | 2 | Possibly | 2 | ||
| Other | 1 | Uncertain | 1 | ||
| Work Experience | ≥20 | 5 | Professional Title | Senior | 4 |
| 15–20 | 4 | Intermediate | 3 | ||
| 10–15 | 3 | Junior | 2 | ||
| 5–10 | 2 | Entry-level | 1 | ||
| ≤5 | 1 |
| Serial Number | Professional Title | Work Experience | Education Level | Confidence in Assessment | Score | Weight |
|---|---|---|---|---|---|---|
| Expert 1 | Senior | ≥20 | Doctor | Affirmative | 4 + 5 + 5 + 5 = 19 | 0.288 |
| Expert 2 | Senior | ≥20 | Master | Almost certain | 4 + 5 + 4 + 4 = 17 | 0.258 |
| Expert 3 | Senior | ≥20 | Bachelor | Very likely | 4 + 5 + 3 + 3 = 15 | 0.227 |
| Expert 4 | Senior | 15–20 | Bachelor | Almost certain | 4 + 4 + 3 + 4 = 15 | 0.227 |
| Root Node | Expert Judgment | Aggregated Fuzzy Numbers | |||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | ||||||
| H | FH | H | H | 0.653 | 0.853 | 0.978 | 0.82800 | 0.04338 | |
| M | FL | L | FL | 0.129 | 0.306 | 0.506 | 0.31367 | 0.00102 | |
| H | H | FH | VH | 0.703 | 0.880 | 0.979 | 0.85400 | 0.05284 | |
| H | H | FH | H | 0.655 | 0.856 | 0.978 | 0.8300 | 0.04402 | |
| FH | FL | VL | FL | 0.174 | 0.329 | 0.506 | 0.33633 | 0.00129 | |
| M | M | VL | FL | 0.186 | 0.343 | 0.526 | 0.35167 | 0.00151 | |
| H | FH | H | FH | 0.602 | 0.802 | 0.952 | 0.78533 | 0.03211 | |
| FH | M | L | M | 0.289 | 0.468 | 0.669 | 0.47533 | 0.00419 | |
| M | L | VL | FH | 0.195 | 0.322 | 0.499 | 0.33867 | 0.00133 | |
| FH | FH | M | FH | 0.456 | 0.656 | 0.856 | 0.65600 | 0.01395 | |
| H | H | FH | H | 0.655 | 0.856 | 0.978 | 0.82967 | 0.04391 | |
| M | L | L | M | 0.152 | 0.303 | 0.504 | 0.31967 | 0.00110 | |
| H | H | H | H | 0.701 | 0.901 | 1.000 | 0.86767 | 0.05897 | |
| FH | H | H | VH | 0.697 | 0.873 | 0.976 | 0.84867 | 0.05068 | |
| FH | FL | L | FL | 0.172 | 0.349 | 0.549 | 0.35667 | 0.00158 | |
| H | FH | FH | FH | 0.553 | 0.753 | 0.928 | 0.74500 | 0.02457 | |
| FH | M | M | FH | 0.402 | 0.602 | 0.802 | 0.60200 | 0.00990 | |
| FH | FH | M | FH | 0.456 | 0.656 | 0.856 | 0.65600 | 0.01395 | |
| M | FL | L | M | 0.181 | 0.359 | 0.559 | 0.36633 | 0.00173 | |
| FH | H | FH | H | 0.599 | 0.799 | 0.950 | 0.78300 | 0.03161 | |
| VH | FH | FH | H | 0.654 | 0.828 | 0.951 | 0.81100 | 0.03837 | |
| The expert judgments for “Poor Factory Production Environment ()” are as follows | |||||
| Expert 1 | FH | (0.5, 0.7, 0.9) | |||
| Expert 2 | H | (0.7, 0.9, 1.0) | |||
| Expert 3 | H | (0.7, 0.9, 1.0) | |||
| Expert 4 | VH | (0.9, 1.0, 1.0) | |||
| (1) is defined as the level of consensus between the opinions of each pair of experts, and . The similarity between experts is calculated as follows: | |||||
| (2) Calculate the average consensus of each expert’s assessment: | |||||
| (3) Calculate the relative consensus of each expert: | |||||
| (4) represents the weight of experts, where denotes the weight score of experts, with JT for job title, WE for work experience, EQ for educational background, and JC for judgment confidence, calculated as , as shown in Table 5. Calculate the consensus coefficient for each expert: | |||||
| (5) Summarize the judgment results: | |||||
| (6) Due to the output being a fuzzy number, the CoA method is utilized for defuzzification: | |||||
| (7) Ultimately, the failure probability, FP, is computed using Equations (4) and (5), representing the prior probabilities of each root node: | |||||
| The expert judgment on “Environmental Risk ()”, along with the aggregation of fuzzy numbers and , is assessed. | ||||||
| FL | FH | H | M | (0.394, 0.594, 0.771) | ||
| FL | FL | FH | FH | (0.291, 0.491, 0.691) | ||
| FH | M | FH | FH | (0.452, 0.652, 0.852) | ||
| Conditional probabilities are computed employing the noisy-OR gate model, as delineated in Formulas (6) and (7). | ||||||
| The conditional probability table associated with “Environmental Risk ()” is presented. , | ||||||
| As evidenced by Table 6: ; The probability of “Environmental Risk” occurrence is calculated using the BN formula. | ||||||
| Parental Nodes | Risk Events | Expert Assessment | Aggregated Fuzzy Numbers | ||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | ||||||
| M | FH | M | FH | 0.394 | 0.592 | 0.790 | 0.59220 | ||
| M | H | M | FH | 0.445 | 0.645 | 0.821 | 0.63684 | ||
| H | FH | M | FH | 0.506 | 0.706 | 0.881 | 0.69807 | ||
| FH | M | M | M | 0.351 | 0.551 | 0.751 | 0.55102 | ||
| FH | H | M | H | 0.556 | 0.757 | 0.906 | 0.73967 | ||
| H | H | H | FH | 0.655 | 0.855 | 0.978 | 0.82933 | ||
| FH | M | H | M | 0.445 | 0.645 | 0.822 | 0.63733 | ||
| M | M | H | M | 0.384 | 0.584 | 0.764 | 0.57733 | ||
| H | H | H | VH | 0.746 | 0.923 | 1.000 | 0.88967 | ||
| H | FH | H | FH | 0.602 | 0.802 | 0.951 | 0.78500 | ||
| M | H | H | FH | 0.557 | 0.761 | 0.915 | 0.74433 | ||
| H | FH | FH | H | 0.602 | 0.802 | 0.951 | 0.78500 | ||
| FL | FH | H | M | 0.394 | 0.594 | 0.771 | 0.58633 | ||
| FL | FL | FH | FH | 0.291 | 0.491 | 0.691 | 0.49100 | ||
| FH | M | FH | FH | 0.452 | 0.652 | 0.852 | 0.65200 | ||
| FH | FH | FH | FH | 0.500 | 0.700 | 0.900 | 0.70000 | ||
| M | FH | M | FH | 0.399 | 0.599 | 0.799 | 0.59900 | ||
| M | M | M | M | 0.300 | 0.500 | 0.700 | 0.50000 | ||
| M | H | M | FH | 0.445 | 0.645 | 0.801 | 0.63033 | ||
| M | FH | FH | H | 0.495 | 0.695 | 0.872 | 0.68760 | ||
| FH | M | FH | H | 0.498 | 0.698 | 0.875 | 0.69033 | ||
| C | H | H | FH | H | 0.655 | 0.856 | 0.978 | 0.82967 | |
| M | FH | FH | H | 0.495 | 0.695 | 0.872 | 0.68733 | ||
| FH | H | H | H | 0.650 | 0.850 | 0.976 | 0.82533 | ||
| FH | H | FH | H | 0.599 | 0.799 | 0.949 | 0.78233 | ||
| L | M | M | M | 0.228 | 0.404 | 0.604 | 0.41200 | ||
| FL | M | M | FH | 0.294 | 0.494 | 0.694 | 0.49400 | ||
| Primary Propagation Pathways | |
|---|---|
| Personnel Risk | |
| Equipment Risk | |
| Material Risk | |
| Technical Risk | |
| Environmental Risk | |
| Risk of management strategies | |
| 0.19170 | 0.24518 | 0.23804 | 0.20698 | 0.22015 | 0.23157 | |
| 0.07902 | 0.10178 | 0.06828 | 0.08041 | |
| 0.05577 | 0.08524 | |
| 0.09534 | 0.10441 | 0.12405 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhong, C.; Peng, J. Quality Risk Assessment of Prefabricated Steel Structural Components during Production Using Fuzzy Bayesian Networks. Buildings 2024, 14, 1624. https://doi.org/10.3390/buildings14061624
Zhong C, Peng J. Quality Risk Assessment of Prefabricated Steel Structural Components during Production Using Fuzzy Bayesian Networks. Buildings. 2024; 14(6):1624. https://doi.org/10.3390/buildings14061624
Chicago/Turabian StyleZhong, Chunling, and Jin Peng. 2024. "Quality Risk Assessment of Prefabricated Steel Structural Components during Production Using Fuzzy Bayesian Networks" Buildings 14, no. 6: 1624. https://doi.org/10.3390/buildings14061624
APA StyleZhong, C., & Peng, J. (2024). Quality Risk Assessment of Prefabricated Steel Structural Components during Production Using Fuzzy Bayesian Networks. Buildings, 14(6), 1624. https://doi.org/10.3390/buildings14061624





