Research on the Construction of a Risk Assessment Indicator System for Transportation Infrastructure Investment under Public–Private Partnership Model
Abstract
:1. Introduction
- How to establish a scientific and systematic risk assessment indicator system?
- Among the many risk factors, what are the key indicators for assessing the risk of investment in transportation infrastructure?
- This study comprehensively identifies and integrates the key risk factors of transportation infrastructure investment projects under the PPP model through a systematic literature review, expert interviews, and case studies. It constructs a comprehensive risk assessment indicator system covering six dimensions: economic, technical, management, policy, social environment, and market. This system not only comprehensively covers the main risks throughout the project lifecycle but also fills the gap of incomplete risk identification in existing research.
- This study is the first to combine principal component analysis (PCA) and the CRITIC-EWM method to screen and determine risk assessment indicators and their weights. This method not only improves the scientific and systematic nature of the indicator system but also simplifies the indicator structure through dimensionality reduction, highlighting key risk factors and making the risk assessment more accurate and operational.
2. Literature Review
- Many studies have adopted a static risk assessment framework, ignoring the impact of environmental and condition changes on risk factors in the project life cycle;
- Existing risk assessment methods often focus on specific types of risk but do not consider the interaction between risk factors and fail to form a comprehensive and systematic risk assessment system;
- Most studies rely on a single methodology, such as the analytical hierarchy process (AHP) or fuzzy logic, and fail to make full use of the advantages of multiple methodologies to improve the accuracy and reliability of risk assessment;
- Although some studies have mentioned the dynamic adaptability of risk assessment, specific implementation strategies and tools are still lacking, and it is difficult to cope with the changing risk environment during project implementation.
- The study constructs a dynamic risk assessment framework, with particular emphasis on changes and updates of risk factors in the project life cycle, to better reflect the actual risk situation.
- Through the comprehensive analysis of the multidimensional risk factors of transportation infrastructure investment, a comprehensive risk assessment indicator system is constructed, which covers the interaction between risk factors and reflects the concept of systematic risk management.
- The combination of principal component analysis (PCA) and CRITIC-EWM is used to improve the scientificity and precision of risk assessment through the complementary advantages of different methods.
- This paper constructs a method to construct a dynamic risk assessment indicator system, which can fully reflect the changes and updates of risk factors in the life cycle of investment projects in transportation infrastructure;
- Through the comprehensive analysis of the multidimensional risk factors of transportation infrastructure investment, a comprehensive risk assessment indicator system is constructed, which covers the interaction between risk factors and reflects the concept of systematic risk management;
- The combination of principal component analysis (PCA) and CRITIC-EWM is used to improve the scientificity and precision of risk assessment through the complementary advantages of different methods.
3. Methodology
3.1. Research Framework and Structural Design
3.1.1. Research Framework
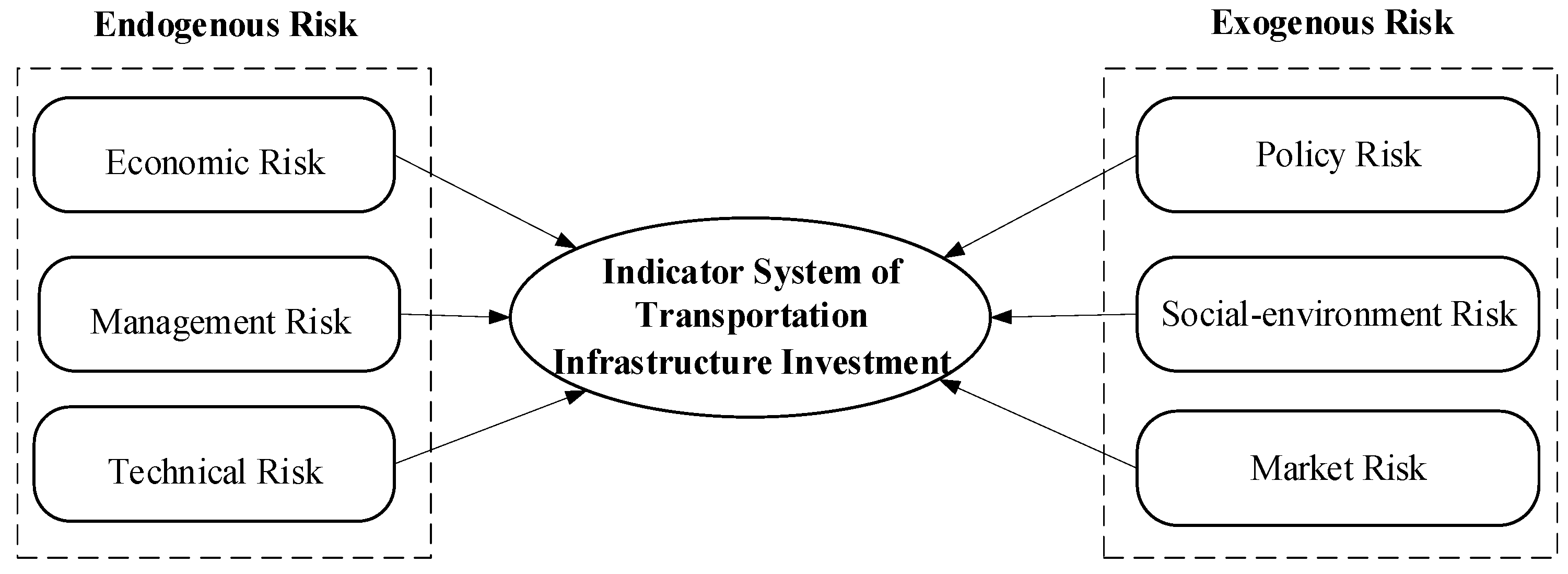
3.1.2. Structure of the Indicator System
- Economic risk reflects financial stability and cost-effectiveness in the investment implementation process, which is the key to investment success. The core of the risk concern in this dimension is capital liquidity and the economic feasibility of the project. In the context of global economic integration, economic risks cover factors such as return on investment, financing costs, and material price fluctuations that may be encountered in the transportation infrastructure investment process. These factors may lead to the project investment return not being as expected, increasing the project’s financial pressures and affecting the confidence of investors and related parties.
- Technical risk focuses on technical problems and challenges that can be encountered in the design, construction, and operation of investment projects in transportation infrastructure. This includes the feasibility of technical solutions, the uncertainty of technological innovation, the complexity of construction technology, and the reliability of equipment. Transportation infrastructure projects are usually large in scale, have high technical requirements, and involve many engineering and technical problems. Immaturity or improper selection of technology may lead to project delays, cost overruns, and even technical failure.
- Management risk focuses on organizational structure, the decision-making process, and the allocation of resources for transportation infrastructure investment projects. Management risk involves the efficiency and effectiveness of project management, including project planning, organization and coordination, resource allocation, schedule control, etc. Improper project management can lead to waste of resources, schedule delays, quality problems, etc., which in turn affect overall performance and return on investment of the project.
- Social environmental risks include the impact of project construction on the environment, the acceptance of the public, social stability, and other factors. Transportation infrastructure projects often have a significant impact on the local social environment. If the relationship with the local community is not properly handled or the impact on the environment is not effectively assessed and reduced, it may encounter public protests and legal proceedings, resulting in project delays or additional costs.
- Policy risk refers to the risk caused by changes in government policies and uncertainty of laws and regulations. Transportation infrastructure projects often require long-term planning and construction cycles, and policy changes can affect the legitimacy, economy, and sustainability of the project.
- Market risk involves changes in market demand, competitive situation, price fluctuations, and other factors. Investment in transportation infrastructure is huge, and the recovery cycle is long. Market risk is reflected mainly in the uncertainty of user demand and the fluctuation of operating income. Accurate prediction of market demand and in-depth analysis of the competitive environment are crucial to reducing market risks and ensuring project success.
3.1.3. Selection of Sample and Data Sources
3.2. Construction of an Indicator System Based on the PCA and CRITIC-EWM Method
3.2.1. Indicator Data Processing
- Standardization of positive indicator data
- 2.
- Standardization of negative indicator data
- 3.
- Standardization of interval indicator data
3.2.2. Degradation of the Indicator Dimension Based on the PCA Method
3.2.3. Calculation of the Weight of the Indicator System Based on the CRITIC-EWM Method
- The CRITIC method.
- 2.
- The EWM method.
- 3.
- Combination weight
3.3. Construction Indicator System
3.3.1. Standardization of Indicator Data
3.3.2. Dimensional Reduction of Risk Assessment Indicators
- Correlation test of indicators.
- 2.
- Extraction of principal components.
- 3.
- Calculation of weight coefficients
- 4.
- Establishment of the indicator system
4. Empirical Study
4.1. Theoretical Model and Research Hypotheses
4.2. Data Source and Reliability and Validity Test
4.2.1. Data Source
4.2.2. Reliability Test
4.2.3. Validity Test
4.3. Model Construction and Hypothesis Testing
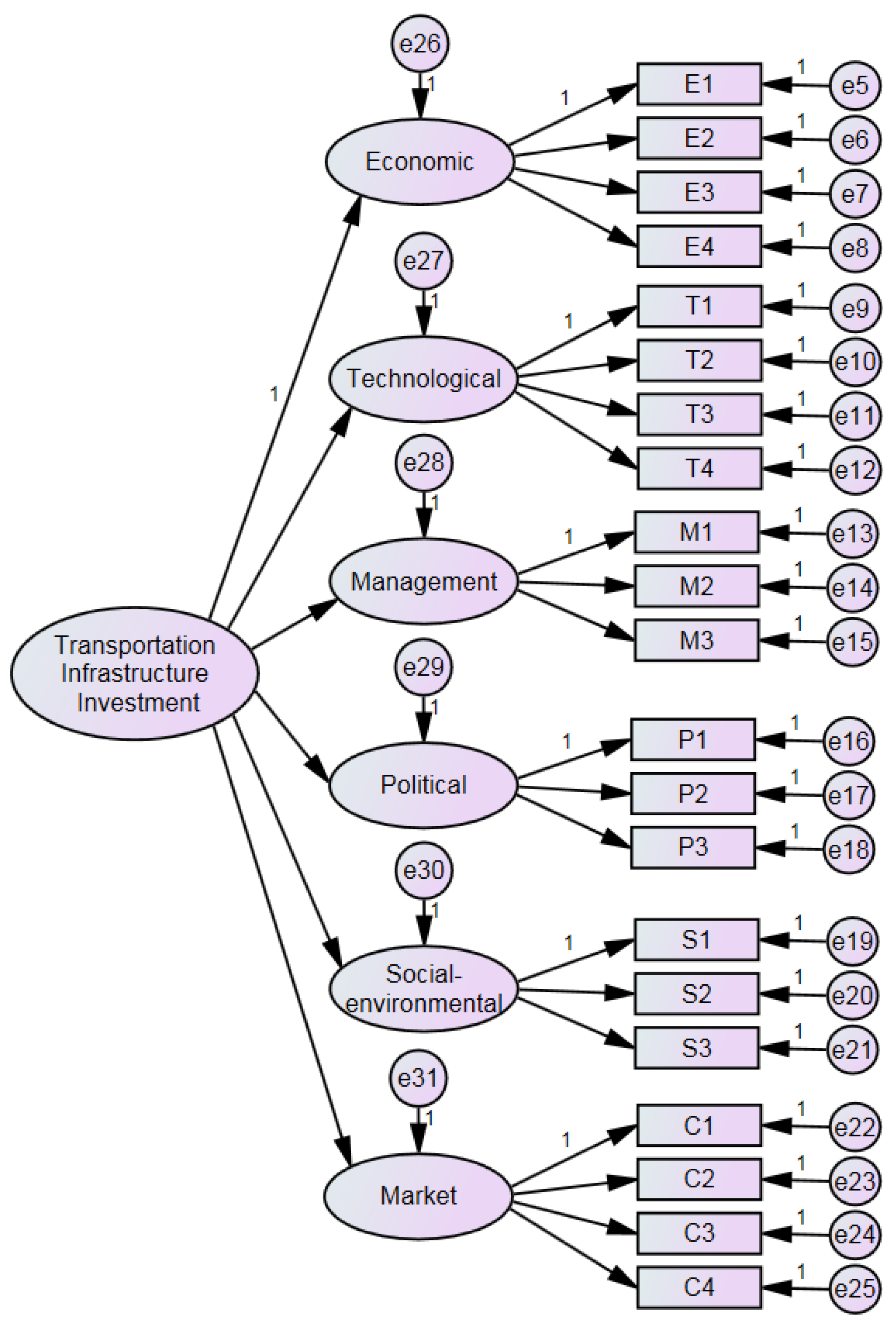
4.3.1. Model Construction
4.3.2. Fitting of the First-Order Structural Equation Model
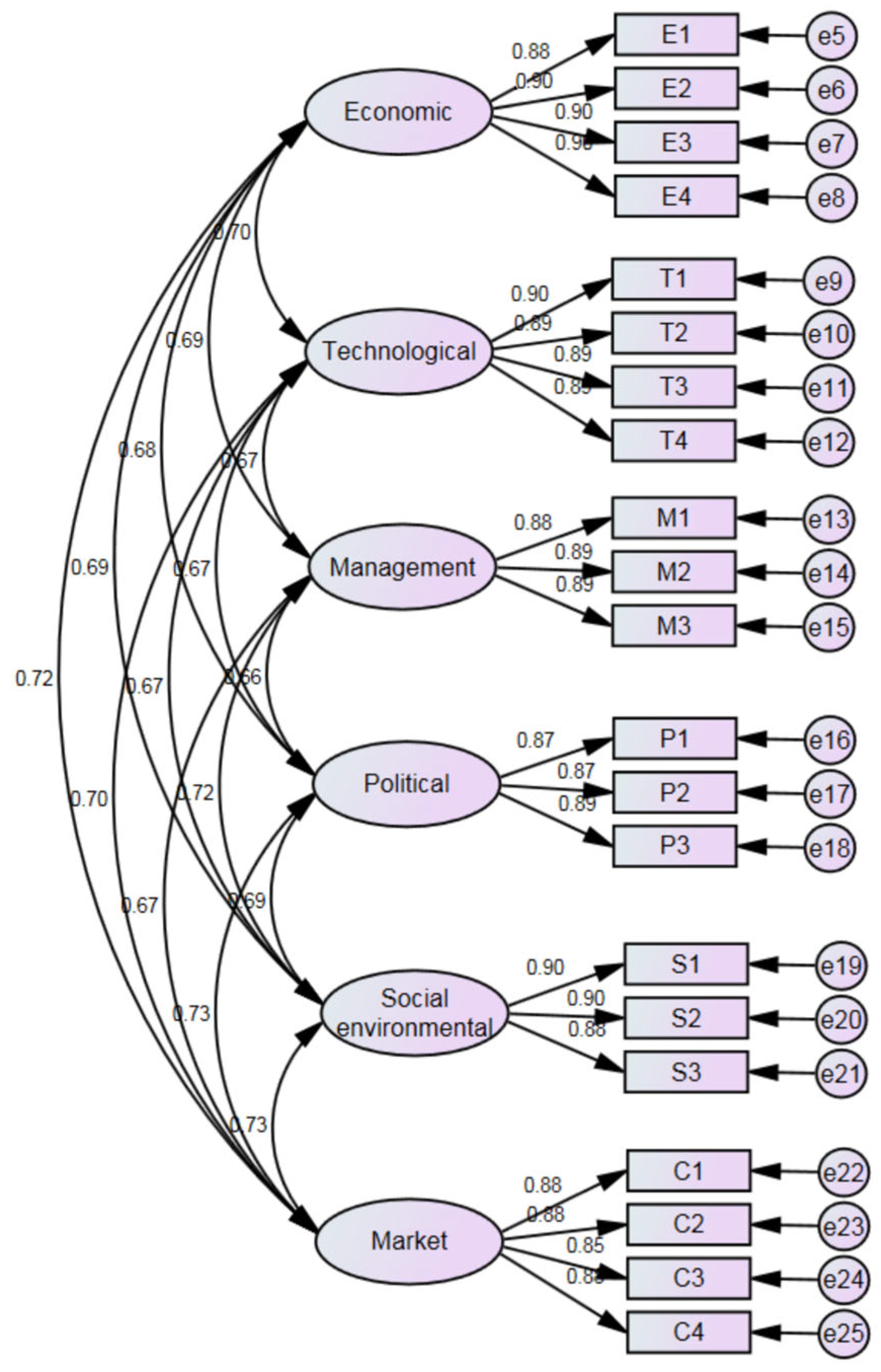
4.3.3. Fitting of the Second-Order Structural Equation Model
4.3.4. Hypothesis Testing
5. Conclusions
- This study successfully constructs an assessment indicator system containing multidimensional risk factors that can comprehensively reflect the risk status of transportation infrastructure investment projects in the PPP mode;
- By integrating the PCA and CRITIC-EWM methods, this study proposes a new method to build a risk assessment indicator system, improving the precision and practicality of risk assessment;
- The effectiveness of the constructed indicator system is tested using empirical data, verifying its application value in practical PPP project risk assessment.
- The risk assessment indicator system constructed in this study can serve as a reference tool for both government and private sectors in project decision-making and risk management, optimizing resource allocation and risk-sharing strategies;
- Establish a dynamic risk monitoring and assessment mechanism, regularly updating risk assessment indicators and their weights to adapt to changes during the project implementation process and in the external environment;
- Establish effective communication and coordination mechanisms among stakeholders to share risk information and collaboratively manage risks, enhancing project management transparency and synergy, thereby increasing the success rate of PPP projects.
- The empirical analysis in this study primarily relies on historical data from completed projects. The availability and quality of these data may affect the accuracy and generalizability of the research conclusions;
- While the PCA and CRITIC-EWM methods performed well in this study, their applicability may vary across different types of PPP projects, requiring further validation and optimization in the future;
- Although efforts were made to ensure the representativeness of the sample, the sample may still not fully represent all types and regions of transportation infrastructure investment projects due to limitations in data sources.
- Future research can further explore the applicability and reliability of the indicator system across different types and regions of the PPP projects.
- Investigate how to integrate other methods (such as Bayesian networks and machine learning) to optimize the risk assessment indicator system, improving the accuracy and flexibility of risk prediction.
- Consider the real-time and dynamic nature of data, further studying how to achieve real-time monitoring and dynamic adjustment of risk assessment through big data and artificial intelligence technologies.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Qin, Y. China’s Transport Infrastructure Investment: Past, present, and future. Asian Econ. Policy Rev. 2016, 11, 199–217. [Google Scholar] [CrossRef]
- International Transport Forum. Infrastructure Investment Data Reveal Contrasts Between Countries. 2020. Available online: https://www.itf-oecd.org/infrastructure-investment-data-reveal-contrasts-between-countries (accessed on 27 June 2022).
- Pricewaterhouse Coopers (PwC). Capital Project and Infrastructure Spending Outlook for 2025. 2018. Available online: https://www.pwc.com/my/en/assets/publications/cpi-spending-outlook-to-2025.pdf (accessed on 26 June 2018).
- Aven, T. Risk Assessment and Risk Management: Review of recent advances in their foundation. Eur. J. Oper. Res. 2016, 253, 1–13. [Google Scholar] [CrossRef]
- Sobieralski, J.B. Transportation Infrastructure and Employment: Are all investments created equal? Res. Transp. Econ. 2020, 88, 100927. [Google Scholar] [CrossRef]
- Čulo, K.; Skendrovi, V. Risk Management in Transport Infrastructure Projects. In Proceedings of the 5th International Conference on Road and Rail Infrastructure (CETRA 2018), Zadar, Croatia, 17–19 May 2018; pp. 1483–1489. [Google Scholar]
- Yucelgazi, F.; Yitmen, I. Risk Assessment for Large-Scale Transport Infrastructure Projects. IOP Conf. Ser. Mater. Sci. Eng. 2019, 471, 022005. [Google Scholar] [CrossRef]
- Boghean, F.; Boghean, C. Risk Management in the Decisional Process; IntechOpen Limited: London, UK, 2017. [Google Scholar] [CrossRef]
- Amiril, A.; Nawawi, A.H.; Takim, R.; Latif, S.N.F.A. Sustainability Factors and Performance of the Transportation Infrastructure Project. Procedia-Soc. Behav. Sci. 2014, 153, 90–98. [Google Scholar] [CrossRef]
- Chen, Y.; Zhu, L.; Hu, Z.; Chen, S.; Zheng, X. Risk Propagation in Multilayer Heterogeneous Network of Coupled System of Large Engineering Project. J. Manag. Eng. 2022, 38, 4022003. [Google Scholar] [CrossRef]
- Fisch-Romito, V.; Guivarch, C. Transportation Infrastructures in a Low-Carbon World: An Evaluation of Investment Needs and Their Determinants. Transp. Res. Transp. Environ. 2019, 72, 203–219. [Google Scholar] [CrossRef]
- Luo, J.; Wang, G.; Li, G.; Pesce, G. Transport infrastructure connectivity and conflict resolution: A machine learning analysis. Neural Comput. Appl. 2022, 34, 6585–6601. [Google Scholar] [CrossRef]
- Domnguez, R.; Gomez, C.; Cerezo, O. Risk Analysis Based on ETA, FTA and Bowtie Methodologies for the Bulk Coal Discharge Process. In Advances in Safety Management and Human Performance; Arezes, P.M., Boring, R.L., Eds.; Lecture Notes in Networks and Systems; Springer International Publishing: Cham, Switzerland, 2021; Volume 262, pp. 193–199. ISBN 978-3-030-80287-5. [Google Scholar]
- Hosseini, N.; Givehchi, S.; Maknoon, R. Cost-Based Fire Risk Assessment in Natural Gas Industry by Means of Fuzzy FTA and ETA. J. Loss Prev. Process Ind. 2020, 63, 104025. [Google Scholar] [CrossRef]
- Liu, P.; Han, Y.; Zhu, X.; Wang, S.; Li, Z. Research on Information System Risk Assessment Based on Improved AHP-Fuzzy Theory. J. Phys. Conf. Ser. 2020, 1693, 012046. [Google Scholar] [CrossRef]
- Ferreira, F.; Santos, S. Comparing Trade-Off Adjustments in Credit Risk Analysis of Mortgage Loans Using AHP, Delphi, and MACBETH. Int. J. Strateg. Prop. Manag. 2016, 20, 44–63. [Google Scholar] [CrossRef]
- Sun, G.; Sheng, L.; Luo, L.; Yu, H. Game Theoretic Approach for Multipriority Data Transmission in 5G Vehicular Networks. IEEE Trans. Intell. Transp. Syst. 2022, 23, 24672–24685. [Google Scholar] [CrossRef]
- Kim, M.; Kim, H.-J.; Park, K.-H.; Youn, H.-K.; Lee, S. Analysis of Fire Risk Assessment Indicators of Publicly-Used Establishments Using Delphi/AHP. Fire Sci. Eng. 2019, 33, 87–94. [Google Scholar] [CrossRef]
- Nadim, F.; Sousa, H.S.; Matos, J. Risk Assessment of Terrestrial Transportation Infrastructures Exposed to Extreme Events. Infrastructures 2021, 6, 163. [Google Scholar] [CrossRef]
- Guo, X.; Chen, B.; Feng, Y. Public-Private Partnership Transportation Investment and Low-Carbon Economic Development: An Empirical Study Based on Spatial Spillover and Project Characteristics in China. Sustainability 2022, 14, 9574. [Google Scholar] [CrossRef]
- Ding, R.; Ujang, N.; Hamid, H.B.; Manan, M.S.A.; Li, R.; Albadareen, S.S.M.; Nochian, A.; Wu, J. Application of Complex Networks Theory in Urban Traffic Network Researches. Netw. Spat. Econ. 2019, 19, 1281–1317. [Google Scholar] [CrossRef]
- Ma, X.; Dong, Z.; Quan, W.; Dong, Y.; Tan, Y. Real-time assessment of asphalt pavement moduli and traffic loads using monitoring data from Built-in Sensors: Optimal sensor placement and identification algorithm. Mech. Syst. Signal Process. 2023, 187, 109930. [Google Scholar] [CrossRef]
- Locatelli, G.; Invernizzi, D.C.; Brookes, N.J. Project Characteristics and Performance in Europe: Empirical Analysis for Large Transport Infrastructure Projects. Transp. Res. Part Policy Pract. 2017, 98, 108–122. [Google Scholar] [CrossRef]
- Gao, Z.; Zeng, H.; Zhang, X.; Wu, H.; Zhang, R.; Sun, Y.; Du, Q.; Zhang, Z.; Li, Z.; Zhao, F.; et al. Exploring tourist spatiotemporal behavior differences and tourism infrastructure supply–demand pattern fusing social media and nighttime light remote sensing data. Int. J. Digit. Earth 2024, 17, 2310723. [Google Scholar] [CrossRef]
- Rong, Y.; Xu, Z.; Liu, J.; Liu, H.; Ding, J.; Liu, X.; Luo, W.; Zhang, C.; Gao, J. Du-Bus: A Realtime Bus Waiting Time Estimation System Based on Multi-Source Data. IEEE Trans. Intell. Transp. Syst. 2022, 23, 24524–24539. [Google Scholar] [CrossRef]
- Love, P.E.D.; Smith, J.; Simpson, I.; Regan, M.; Olatunji, O. Understanding the Landscape of Overruns in Transport Infrastructure Projects. Environ. Plan. B Plan. Des. 2015, 42, 490–509. [Google Scholar] [CrossRef]
- Hwang, W.; Hsiao, B.; Chen, H.-G.; Chern, C.-C. Multiphase Assessment of Project Risk Interdependencies: Evidence from an ISD project of the University of Taiwan. Proj. Manag. J. 2016, 47, 59–75. [Google Scholar] [CrossRef]
- Zeng, Z.; Zio, E. Dynamic Risk Assessment Based on Statistical Failure Data and Condition Monitoring Degradation Data. IEEE Trans. Reliab. 2018, 67, 609–622. [Google Scholar] [CrossRef]
- Choueiri, E. Risks involved in financing public transport infrastructure projects. Rail Eng. Int. 2009, 38, 6–8. [Google Scholar]
- Lakshmanan, T. The Broader Economic Consequences of Transport Infrastructure Investments. J. Transp. Geogr. 2011, 19, 1–12. [Google Scholar] [CrossRef]
- Labanauskas, G.; Palaitis, R. Investment Risk Management and Economic Aspects of Transport Infrastructure Development. Transp. Telecommun. J. 2012, 13, 101–107. [Google Scholar] [CrossRef]
- Ang, G.; Marchal, V. Mobilising Private Investment in Sustainable Transport: The Case of Land-Based Passenger Transport Infrastructure; OECD Publishing: Paris, France, 2013. [Google Scholar] [CrossRef]
- Sharma, R. The Potential of Private Institutional Investors to Financing Transport Infrastructure; OECD Publishing: Paris, France, 2013. [Google Scholar] [CrossRef]
- Tran, D.Q.; Molenaar, K. Exploring Critical Delivery Selection Risk Factors for Transportation Design and Construction Projects. Eng. Constr. Archit. Manag. 2014, 21, 631–647. [Google Scholar] [CrossRef]
- Yucelgazi, F.; Yitmen, I. An ANP Model for Risk Assessment in Large-Scale Transport Infrastructure Projects. Arab. J. Sci. Eng. 2018, 44, 4257–4275. [Google Scholar] [CrossRef]
- De Vaus, D.A. Surveys in Social Research; Routledge: London, UK, 2013. [Google Scholar] [CrossRef]
- Bernard, H.R. Research Methods in Anthropology: Qualitative and Quantitative Approaches; Rowman & Littlefield: Lanham, MD, USA, 2017. [Google Scholar]
- Fisher, W.; Jackson, L.; Suter, G.; Bertram, P. Indicators for Human and Ecological Risk Assessment: A U.S. Environmental Protection Agency Perspective. Hum. Ecol. Risk Assess. Int. J. 2001, 7, 961–970. [Google Scholar] [CrossRef]
- Shi, X.; Wong, Y.; Li, M.; Chai, C. Key Risk Indicators for Accident Assessment Conditioned on Pre-Crash Vehicle Trajectory. Accid. Anal. Prev. 2018, 117, 346–356. [Google Scholar] [CrossRef]
- Reznikov, D. Assessment of Uncertainties and Risks Related to Implementation of Infrastructure Projects. IOP Conf. Ser. Mater. Sci. Eng. 2020, 972, 012062. [Google Scholar] [CrossRef]
- Mishra, S.; Khasnabis, S.; Dhingra, S.L. A Simulation Approach for Estimating Value at Risk in Transportation Infrastructure Investment Decisions. Res. Transp. Econ. 2013, 38, 129–138. [Google Scholar] [CrossRef]
- Ermolaeva, E.; Fateeva, I.; Bakhmetyev, A.; Kolosova, N.; Orlov, A. Risk-Based Methodology for Evaluating Transport Infrastructure Investment Projects. Transp. Res. Procedia 2022, 63, 1569–1574. [Google Scholar] [CrossRef]
- Jolliffe, I.T.; Cadima, J. Principal component analysis: A review and recent developments. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2016, 374, 20150202. [Google Scholar] [CrossRef]
- Diakoulaki, D.; Mavrotas, G.; Papayannakis, L. Determining objective weights in multiple criteria problems: The critic method. Comput. Oper. Res. 2018, 22, 763–770. [Google Scholar] [CrossRef]


| Related Research Literature | Risk Dimension Division |
|---|---|
| Choueiri (2009) [29] | Political Risk, Financial Risk, Technical Risk, Market Risk |
| Lakshmanan (2011) [30] | Economic Risk, Technical Risk, Market Risk |
| Labanauskas and Palšaitis (2012) [31] | Economic Risk, Political Risk, Market Risk, Operational Risk |
| Ang and Marchal (2013) [32] | Environmental Risk, Social Risk, Economic Risk |
| Sharma (2013) [33] | Legal Risk, Technical Risk, Economic Risk, Construction Risk |
| Tran and Molenaar (2014) [34] | Construction Risk, Design Risk, Policy Risk |
| Amiril (2014) [9] | Environmental Risk, Economic Risk, Social Risk, Management Risk |
| Yucelgazi and Yitmen (2018) [35] | Technical Risk, Financial Risk, Political Risk, Management Risk, Construction Risk, Legal Risk, Natural and Environmental Risk |
| No. | Object | Province | Average Investment (CNY Billion) |
|---|---|---|---|
| 1–29 | Expressway | Shandong Province, Henan Province, Guangdong Province, Anhui Province, Zhejiang Province, Guangxi Province, Shaanxi Province, Guizhou Province, Heilongjiang Province | 63.85 |
| 30–36 | Municipal highways | Beijing Municipality, Chongqing Municipality, Shandong Province, Zhejiang Province | 18.96 |
| 37–41 | Tunnels | Jiangsu Province, Guangdong Province, Hubei Province | 39.54 |
| 42–50 | Rail Transit | Shandong Province, Jilin Province, Xinjiang Uygur Autonomous Region, Shanxi Province, Gansu Province, Chongqing Municipality | 69.76 |
| 51–55 | Railway | Anhui Province, Zhejiang Province, Shanghai Municipality | 56.93 |
| 56–61 | Bridges | Shanxi Province, Guangdong Province, Hebei Province, Shandong Province, Jiangxi Province | 19.84 |
| 62–64 | Ports | Shandong Province, Jiangsu Province, Hainan Province | 32.53 |
| 65–71 | Channel | Shandong Province, Henan Province, Guangxi Province | 66.57 |
| 72–76 | Airports | Shaanxi Province, Sichuan Province, Guangdong Province, Guangxi Province, Hubei Province | 28.82 |
| Risk Dimensions | Evaluation Indicators | Indicator Attribute |
|---|---|---|
| Economic (E) | E11: Return on Investment | Positive |
| E12: Fund Flow Fluctuation | Positive | |
| E13: Inflation | Negative | |
| E14: Tax Policy | Negative | |
| E15: Financing Difficulty | Negative | |
| E16: Land Acquisition Costs | Negative | |
| E17: Investment Overrun | Negative | |
| E18: Labor Costs | Negative | |
| E19: Material Price Fluctuation | Negative | |
| E10: Cost of Capital Utilization | Negative | |
| Technical (T) | T21: Design Planning Deviation | Negative |
| T22: Technical Implementation Difficulty | Negative | |
| T23: Material Technology Qualification Rate | Positive | |
| T24: Technical Personnel Experience | Positive | |
| T25: Equipment Failure Rate | Negative | |
| T26: Geological Survey Error | Negative | |
| T27: Technical Environment Adaptability | Positive | |
| T28: Technical Standard Compliance Rate | Positive | |
| Management (M) | M31: Management Team Experience | Positive |
| M32: Decision Delay Rate | Negative | |
| M33: Contract Default Risk | Negative | |
| M34: Budget Overrun Rate | Negative | |
| M35: Key Personnel Attrition Rate | Negative | |
| M36: Supply Chain Management | Positive | |
| M37: Quality Management | Positive | |
| M38: Incomplete Management System | Negative | |
| Policy (P) | P41: Policy Support Level | Positive |
| P42: Policy Change Frequency | Negative | |
| P43: Positive Intensity of Policy Implementation Intensity | Positive | |
| P44: Policy Uncertainty | Negative | |
| P45: Regulatory Compliance Risk | Negative | |
| P46: Regional Policy Differences | Negative | |
| P47: Policy–Market Disconnect | Negative | |
| P48: Government Intervention Risk | Negative | |
| Social–environment (S) | S51: Public Opposition Degree | Negative |
| S52: Frequency of Social Conflict Events | Negative | |
| S53: Land Acquisition and Demolition Risk | Negative | |
| S54: Environmental Pollution Risk | Negative | |
| S55: Public Safety Incidents | Negative | |
| S56: Social Opinion Risk | Negative | |
| S57: Negative Social Responsibility Fulfillment | Negative | |
| S58: Social-Cultural Conflict | Negative | |
| Market (C) | C61: Market Demand Fluctuation | Negative |
| C62: Intensity of Market Competition | Negative | |
| C63: Price Fluctuation Risk | Negative | |
| C64: Market Acceptance | Positive | |
| C65: Market Regulation | Negative | |
| C66: Brand Image | Positive | |
| C67: Market Information Asymmetry | Negative |
| E11 | E12 | E13 | E14 | E15 | E16 | E17 | E18 | E19 | E10 | ||
|---|---|---|---|---|---|---|---|---|---|---|---|
| E | Mean | 4.97% | 5.02% | 5.10% | 4.99 | 5.06 | 50.4 | 5.08% | 5.05 | 5.1% | 5.10% |
| Max | 7.51% | 8.90% | 7.93% | 7.59 | 7.28 | 86.4 | 7.96% | 7.97 | 8.0% | 7.52% | |
| Min | 1.92% | 1.73% | 3.04% | 1.50 | 1.98 | 25.1 | 2.07% | 2.09 | 2.3% | 2.20% | |
| T | T21 | T22 | T23 | T24 | T25 | T26 | T27 | T28 | |||
| Mean | 10.06% | 9.92% | 9.92% | 9.95 | 9.81% | 9.88% | 9.94 | 9.92% | |||
| Max | 12.97% | 12.3% | 11.9% | 12.66 | 12.3% | 12.3% | 12.19 | 12.1% | |||
| Min | 7.08% | 7.56% | 7.22% | 7.09 | 7.45% | 7.39% | 7.06 | 7.11% | |||
| M | M31 | M32 | M33 | M34 | M35 | M36 | M37 | M38 | |||
| Mean | 6.88 | 6.89% | 7.02% | 7.0% | 6.97% | 6.95 | 6.93 | 6.95 | |||
| Max | 9.40 | 9.29% | 9.24% | 9.28% | 9.39% | 9.53 | 9.16 | 9.40 | |||
| Min | 4.65 | 4.78% | 5.19% | 4.25% | 4.81% | 4.31 | 4.49 | 4.27 | |||
| P | P41 | P42 | P43 | P44 | P45 | P46 | P47 | P48 | |||
| Mean | 2.90 | 3.01% | 3.11 | 3.08 | 3.07 | 2.99 | 3.06 | 3.16 | |||
| Max | 5.92 | 6.37% | 5.29 | 5.30 | 6.21 | 5.82 | 5.65 | 6.03 | |||
| Min | 0.23 | 0.16% | 1.01 | 0.04 | 0.16 | 0.76 | 0.54 | 0.80 | |||
| S | S51 | S52 | S53 | S54 | S55 | S56 | S57 | S58 | |||
| Mean | 6.02% | 5.83% | 5.90% | 6.02% | 5.88% | 6.01% | 5.92 | 6.06 | |||
| Max | 8.16% | 8.26% | 8.29% | 8.14% | 8.30% | 8.27% | 8.37 | 8.31 | |||
| Min | 2.87% | 3.64% | 3.56% | 3.74% | 3.26% | 3.66% | 3.68 | 3.92 | |||
| C | C61 | C62 | C63 | C64 | C65 | C66 | C67 | ||||
| Mean | 4.04% | 4.00% | 4.02% | 3.98% | 3.94 | 4.03 | 3.98 | ||||
| Max | 6.77% | 6.61% | 6.81% | 8.10% | 6.92 | 6.88 | 7.41 | ||||
| Min | 1.18% | 1.69% | 1.56% | 1.38% | 1.42 | 1.47 | 1.91 |
| E | T | M | P | S | C | ||
|---|---|---|---|---|---|---|---|
| KMO | 0.870 | 0.853 | 0.745 | 0.737 | 0.631 | 0.6448 | |
| Bartlett Sphericity Test | Chi-Square | 826.460 | 719.18 | 652.08 | 620.20 | 610.20 | 515.18 |
| DF | 45 | 43 | 37 | 52 | 38 | 36 | |
| p-value | 0.000 | 0.002 | 0.007 | 0.01 | 0.02 | 0.014 | |
| No. | Characteristic Root | Principal Component Extraction | ||||
|---|---|---|---|---|---|---|
| Characteristic | Variance | Accumulation | Characteristic | Variance | Accumulation | |
| 1 | 4.911 | 49.11 | 49.11 | 4.911 | 49.11 | 49.11 |
| 2 | 2.18 | 21.8 | 70.91 | 2.18 | 21.8 | 70.91 |
| 3 | 0.935 | 9.35 | 80.26 | 0.935 | 9.35 | 80.26 |
| 4 | 0.805 | 8.05 | 88.31 | 0.805 | 8.05 | 88.31 |
| 5 | 0.606 | 6.06 | 94.37 | - | - | - |
| 6 | 0.368 | 3.68 | 98.05 | - | - | - |
| 7 | 0.111 | 1.11 | 99.16 | - | - | - |
| 8 | 0.052 | 0.52 | 99.68 | - | - | - |
| 9 | 0.029 | 0.29 | 99.97 | - | - | - |
| 10 | 0.003 | 0.03 | 100 | - | - | - |
| No. | Principal Component | |||
|---|---|---|---|---|
| Component 1 | Component 2 | Component 3 | Component 4 | |
| E11 | 0.018 | 0.341 | 0.513 | 0.272 |
| E12 | −0.005 | −0.018 | 0.654 | 0.245 |
| E13 | −0.480 | −0.019 | −0.043 | −0.136 |
| E14 | 0.209 | 0.057 | −0.288 | 0.455 |
| E15 | −0.606 | 0.151 | 0.004 | 0.303 |
| E16 | 0.142 | 0.524 | −0.164 | 0.175 |
| E17 | 0.184 | 0.448 | 0.236 | −0.501 |
| E18 | 0.013 | 0.529 | −0.131 | −0.219 |
| E19 | 0.180 | −0.307 | 0.344 | −0.413 |
| E10 | 0.522 | −0.084 | −0.085 | 0.222 |
| Weight Coefficient | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| E1 | E2 | E3 | E4 | T1 | T2 | T3 | T4 | M1 | M2 | M3 | |
| 0.0543 | 0.0384 | 0.0512 | 0.0501 | 0.0467 | 0.0418 | 0.0550 | 0.0532 | 0.0399 | 0.0628 | 0.0519 | |
| 0.0603 | 0.0302 | 0.0536 | 0.0514 | 0.0446 | 0.0358 | 0.0619 | 0.0579 | 0.0325 | 0.0807 | 0.0550 | |
| 0.0653 | 0.0232 | 0.0547 | 0.0514 | 0.0416 | 0.0299 | 0.0679 | 0.0615 | 0.0259 | 0.1011 | 0.0570 | |
| P1 | P2 | P3 | S1 | S2 | S3 | C1 | C2 | C3 | C4 | ||
| 0.0418 | 0.0377 | 0.0563 | 0.0572 | 0.0398 | 0.0368 | 0.0546 | 0.0475 | 0.0483 | 0.0348 | ||
| 0.0358 | 0.0290 | 0.0648 | 0.0670 | 0.0323 | 0.0276 | 0.0610 | 0.0461 | 0.0477 | 0.0248 | ||
| 0.0299 | 0.0218 | 0.0728 | 0.0765 | 0.0257 | 0.0203 | 0.0664 | 0.0437 | 0.0460 | 0.0173 | ||
| Risk Dimensions | Indicator | Weight | Variance Contribution |
|---|---|---|---|
| Economic | E1: Financing Efficiency | 0.0653 | 88.31% |
| E2: Uncontrollable Investment Costs | 0.0232 | ||
| E3: Investment Benefit | 0.0547 | ||
| E4: Budget Overrun Rate | 0.0514 | ||
| Technological | T1: Technical Reliability | 0.0416 | 89.89% |
| T2: Technical Implementation Complexity | 0.0299 | ||
| T3: Engineering Quality Compliance Rate | 0.0679 | ||
| T4: Technical Compatibility Rate | 0.0615 | ||
| Management | M1: Decision Execution Efficiency | 0.0259 | 88.33% |
| M2: Management Efficiency | 0.1011 | ||
| M3: Stability of Core Team | 0.0570 | ||
| Political | P1: Policy Environment Stability | 0.0299 | 88.05% |
| P2: Policy Effectiveness | 0.0218 | ||
| P3: Adaptability to Policies and Regulations | 0.0728 | ||
| Social-environmental | S1: Social Stability Risk | 0.0765 | 86.37% |
| S2: Social Acceptance | 0.0257 | ||
| S3: Environmental Pressure Adaptability | 0.0203 | ||
| Market | C1: Market Stability | 0.0664 | 92.37% |
| C2: Market Responsiveness | 0.0437 | ||
| C3: Return Volatility | 0.0460 | ||
| C4: Market Regulation Intensity | 0.0173 |
| Information | Background | Sample Size | Percentage |
|---|---|---|---|
| Age | Under 25 | 22 | 7.01% |
| 26–34 | 68 | 21.66% | |
| 35–45 | 134 | 42.68% | |
| Over 45 | 90 | 28.66% | |
| Title | Junior | 55 | 17.52% |
| Intermediate | 72 | 22.93% | |
| Associate senior | 104 | 33.12% | |
| Senior | 83 | 26.43% | |
| Experience | Under 5 | 68 | 21.66% |
| 6–10 | 82 | 26.11% | |
| 11–15 | 93 | 29.62% | |
| Over 15 | 71 | 22.61% | |
| Education | Associate | 64 | 20.38% |
| Bachelor | 139 | 44.27% | |
| Master | 99 | 31.53% | |
| Doctorate | 12 | 3.82% |
| Latent Variable | Measured Variable | Cronbach’s α Coefficient | ||
|---|---|---|---|---|
| Economic | E1: Financing Efficiency | 0.9268 | 0.8271 | 0.9311 |
| E2: Uncontrollable Investment Costs | 0.9286 | |||
| E3: Investment Benefit | 0.9276 | |||
| E4: Budget Overrun Rate | 0.9269 | |||
| Technological | T1: Technical Reliability | 0.9272 | 0.8112 | |
| T2: Technical Implementation Complexity | 0.9274 | |||
| T3: Engineering Quality Compliance Rate | 0.9292 | |||
| T4: Technical Compatibility Rate | 0.9282 | |||
| Management | M1: Decision Execution Efficiency | 0.9272 | 0.7590 | |
| M2: Management Efficiency | 0.9287 | |||
| M3: Stability of Core Team | 0.9288 | |||
| Political | P1: Policy Environment Stability | 0.9289 | 0.7738 | |
| P2: Policy Effectiveness | 0.9274 | |||
| P3: Adaptability to Policies and Regulations | 0.9280 | |||
| Social-environmental | S1: Social Stability Risk | 0.9276 | 0.8174 | |
| S2: Social Acceptance | 0.9277 | |||
| S3: Environmental Pressure Adaptability | 0.9279 | |||
| Market | C1: Market Stability | 0.9281 | 0.7749 | |
| C2: Market Responsiveness | 0.9275 | |||
| C3: Return Volatility | 0.9279 | |||
| C4: Market Regulation Intensity | 0.9281 | |||
| Latent Variable | KMO | Bartlett’s Sphericity Test | ||
|---|---|---|---|---|
| Chi-Square | DF | p | ||
| Economic | 0.870 | 1141.45 | 6 | 0.000 |
| Technological | 0.862 | 1126.65 | 6 | 0.000 |
| Management | 0.761 | 673.72 | 3 | 0.001 |
| Political | 0.760 | 687.35 | 3 | 0.000 |
| Social–environmental | 0.763 | 699.53 | 3 | 0.000 |
| Market | 0.848 | 991.09 | 6 | 0.000 |
| Overall | 0.955 | 6596.81 | 210 | 0.000 |
| Path | Estimate | S.E | C.R. | p |
|---|---|---|---|---|
| Economic ↔ Technical | 0.701 | 0.125 | 9.135 | *** |
| Economic ↔ Management | 0.688 | 0.130 | 8.966 | *** |
| Economic ↔ Policy | 0.681 | 0.125 | 8.842 | *** |
| Economic ↔ Social–Environmental | 0.693 | 0.134 | 9.054 | *** |
| Economic ↔ Market | 0.719 | 0.128 | 9.195 | *** |
| Technical ↔ Management | 0.670 | 0.128 | 8.856 | *** |
| Technical ↔ Policy | 0.672 | 0.124 | 8.799 | *** |
| Technical ↔ Social–Environmental | 0.669 | 0.131 | 8.887 | *** |
| Technical ↔ Market | 0.700 | 0.126 | 9.086 | *** |
| Management ↔ Policy | 0.656 | 0.128 | 8.604 | *** |
| Management ↔ Social–Environmental | 0.722 | 0.141 | 9.269 | *** |
| Management ↔ Market | 0.674 | 0.130 | 8.817 | *** |
| Policy ↔ Social–Environmental | 0.687 | 0.134 | 8.905 | *** |
| Policy ↔ Market | 0.730 | 0.129 | 9.186 | *** |
| Social Environmental ↔ Market | 0.734 | 0.138 | 9.34 | *** |
| Indicator | Reference Range | Fitting Result | Model Fitness |
|---|---|---|---|
| X2/DF | ≤3.00 | 1.311 | Fit |
| GFI | ≥0.90 | 0.938 | Fit |
| RMR | ≤0.05 | 0.047 | Fit |
| RMSEA | ≤0.08 | 0.032 | Fit |
| AGFI | ≥0.90 | 0.918 | Fit |
| NFI | ≥0.90 | 0.966 | Fit |
| CFI | ≥0.90 | 0.992 | Fit |
| IFI | ≥0.90 | 0.992 | Fit |
| RFI | ≥0.90 | 0.959 | Fit |
| TLI | ≥0.90 | 0.990 | Fit |
| Path | Estimate | S.E | C.R. | p |
|---|---|---|---|---|
| Economic ← Transportation Infrastructure Investment | 0.837 | |||
| Technical ← Transportation Infrastructure Investment | 0.816 | 0.072 | 13.494 | *** |
| Market ← Transportation Infrastructure Investment | 0.861 | 0.074 | 13.98 | *** |
| Social-environmental ← Transportation Infrastructure Investment | 0.844 | 0.077 | 13.95 | *** |
| Policy ← Transportation Infrastructure Investment | 0.822 | 0.074 | 13.2 | *** |
| Management ← Transportation Infrastructure Investment | 0.815 | 0.075 | 13.348 | *** |
| E1 ← Economic | 0.881 | |||
| E2 ← Economic | 0.899 | 0.043 | 23.31 | *** |
| E3 ← Economic | 0.902 | 0.042 | 23.464 | *** |
| E4 ← Economic | 0.905 | 0.045 | 23.671 | *** |
| T1 ← Technicalssssssssssss | 0.893 | |||
| T2 ← Technical | 0.881 | 0.044 | 22.925 | *** |
| T3 ← Technical | 0.888 | 0.043 | 23.347 | *** |
| T4 ← Technical | 0.913 | 0.043 | 24.907 | *** |
| M1 ← Management | 0.892 | |||
| M2 ← Management | 0.892 | 0.043 | 22.49 | *** |
| M3 ← Management | 0.881 | 0.046 | 21.993 | *** |
| P1 ← Policy | 0.869 | |||
| P2 ← Policy | 0.914 | 0.047 | 22.516 | *** |
| P3 ← Policy | 0.887 | 0.049 | 21.391 | *** |
| S1 ← Social-environmental | 0.900 | |||
| S2 ← Social-environmental | 0.897 | 0.042 | 23.497 | *** |
| S3 ← Social-environmental | 0.883 | 0.042 | 22.754 | *** |
| C1 ← Market | 0.879 | |||
| C2 ← Market | 0.884 | 0.045 | 22.046 | *** |
| C3 ← Market | 0.851 | 0.046 | 20.439 | *** |
| C4 ← Market | 0.882 | 0.045 | 21.935 | *** |
| Indicator | Reference Range | Fitting Result | Model Fitness |
|---|---|---|---|
| X2/DF | ≤3.00 | 1.290 | Fit |
| GFI | ≥0.90 | 0.937 | Fit |
| RMR | ≤0.05 | 0.053 | Fit |
| RMSEA | ≤0.08 | 0.030 | Fit |
| AGFI | ≥0.90 | 0.920 | Fit |
| NFI | ≥0.90 | 0.965 | Fit |
| CFI | ≥0.90 | 0.992 | Fit |
| IFI | ≥0.90 | 0.992 | Fit |
| RFI | ≥0.90 | 0.960 | Fit |
| TLI | ≥0.90 | 0.991 | Fit |
| No. | Hypothesis | Result |
|---|---|---|
| H1 | Economic risk has explanatory power over the risk of investment in transportation infrastructure investment risk | Pass |
| H2 | Technical risk has explanatory power over the risk of investment in transportation infrastructure | Pass |
| H3 | Management risk has explanatory power over the risk of investment in transportation infrastructure | Pass |
| H4 | Social–environmental risk has explanatory power over the risk of investment in transportation infrastructure | Pass |
| H5 | Policy risk has explanatory power over the risk of investment in transportation infrastructure | Pass |
| H6 | Market risk has explanatory power over the risk of investment in transportation infrastructure | Pass |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Weng, X.; Yuan, C.; Li, X.; Li, H. Research on the Construction of a Risk Assessment Indicator System for Transportation Infrastructure Investment under Public–Private Partnership Model. Buildings 2024, 14, 1679. https://doi.org/10.3390/buildings14061679
Weng X, Yuan C, Li X, Li H. Research on the Construction of a Risk Assessment Indicator System for Transportation Infrastructure Investment under Public–Private Partnership Model. Buildings. 2024; 14(6):1679. https://doi.org/10.3390/buildings14061679
Chicago/Turabian StyleWeng, Xiangjian, Chunhui Yuan, Xiaolong Li, and Hui Li. 2024. "Research on the Construction of a Risk Assessment Indicator System for Transportation Infrastructure Investment under Public–Private Partnership Model" Buildings 14, no. 6: 1679. https://doi.org/10.3390/buildings14061679
APA StyleWeng, X., Yuan, C., Li, X., & Li, H. (2024). Research on the Construction of a Risk Assessment Indicator System for Transportation Infrastructure Investment under Public–Private Partnership Model. Buildings, 14(6), 1679. https://doi.org/10.3390/buildings14061679





