Critical Face Pressure of a Tunnel Driven by a Shield Machine Considering Seismic Forces and Tunnel Shape Influence
Abstract
:1. Introduction
2. Collapse Mechanism for an Arbitrarily Shaped Tunnel Face
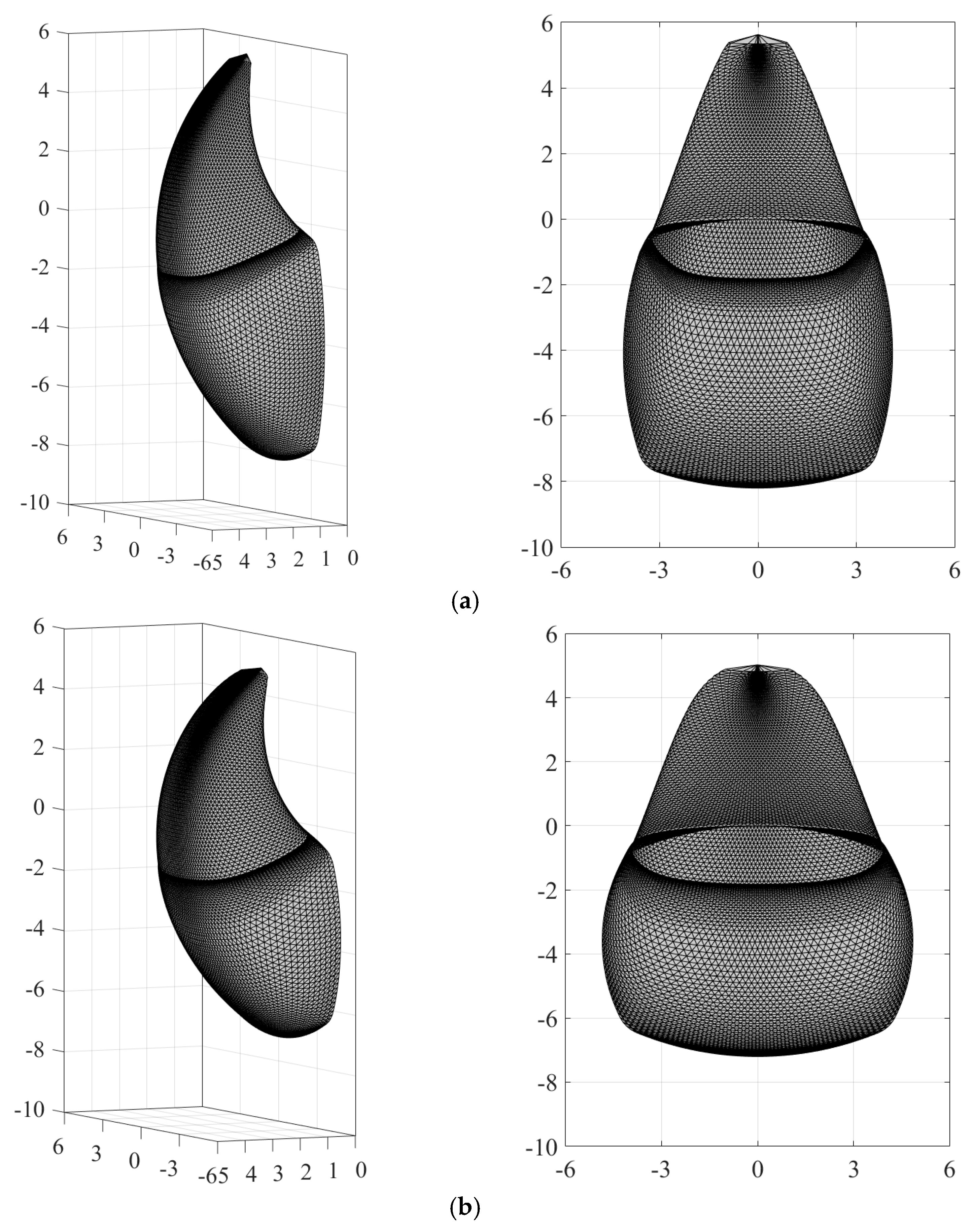
2.1. Generation of the 3D Failure Mechanism
2.2. The Work Rate Equation
3. Application and Comparison
3.1. Parametric Analysis on the Tunnel Shape
3.2. Critical Face Pressures
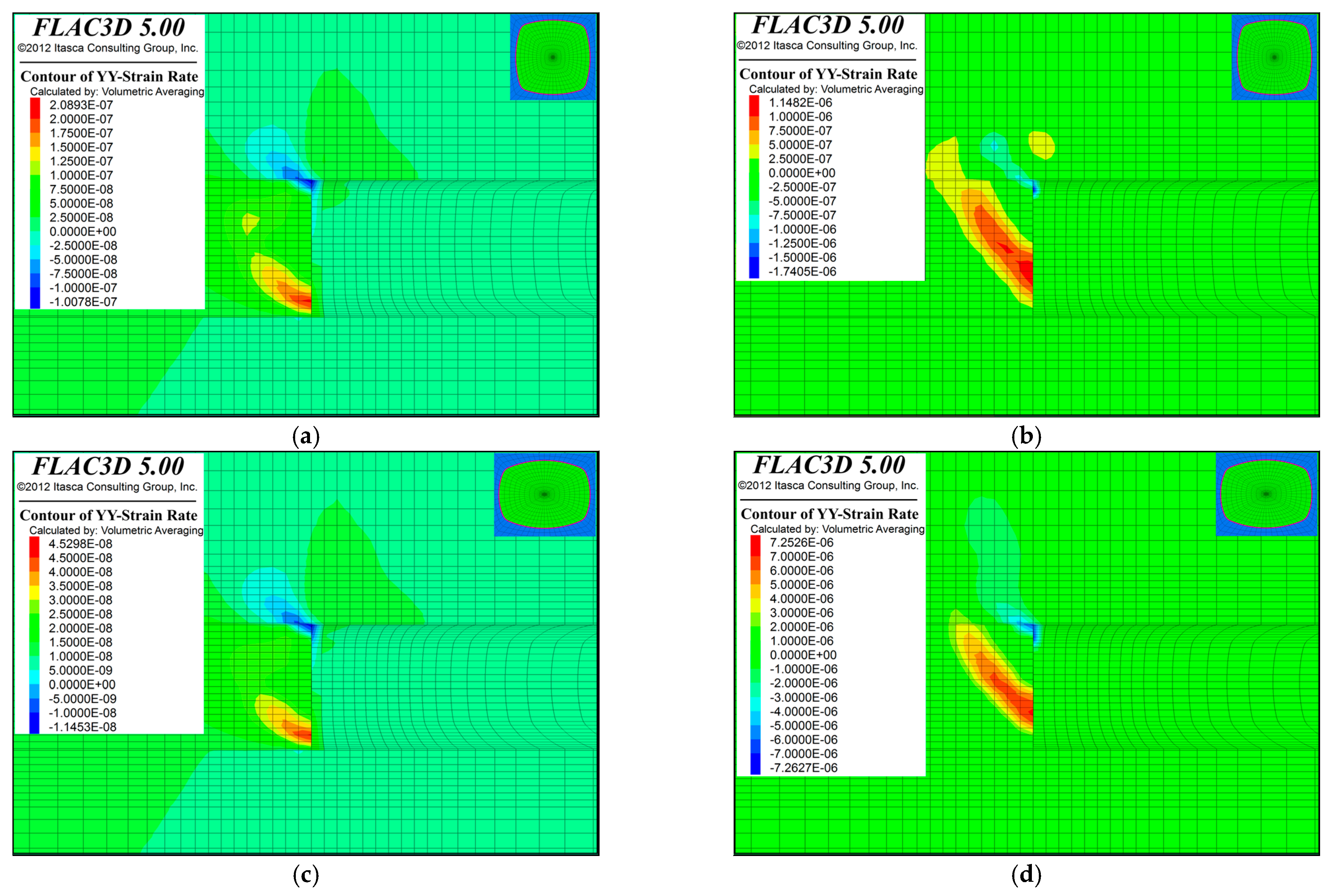
4. Validation with Numerical Simulations
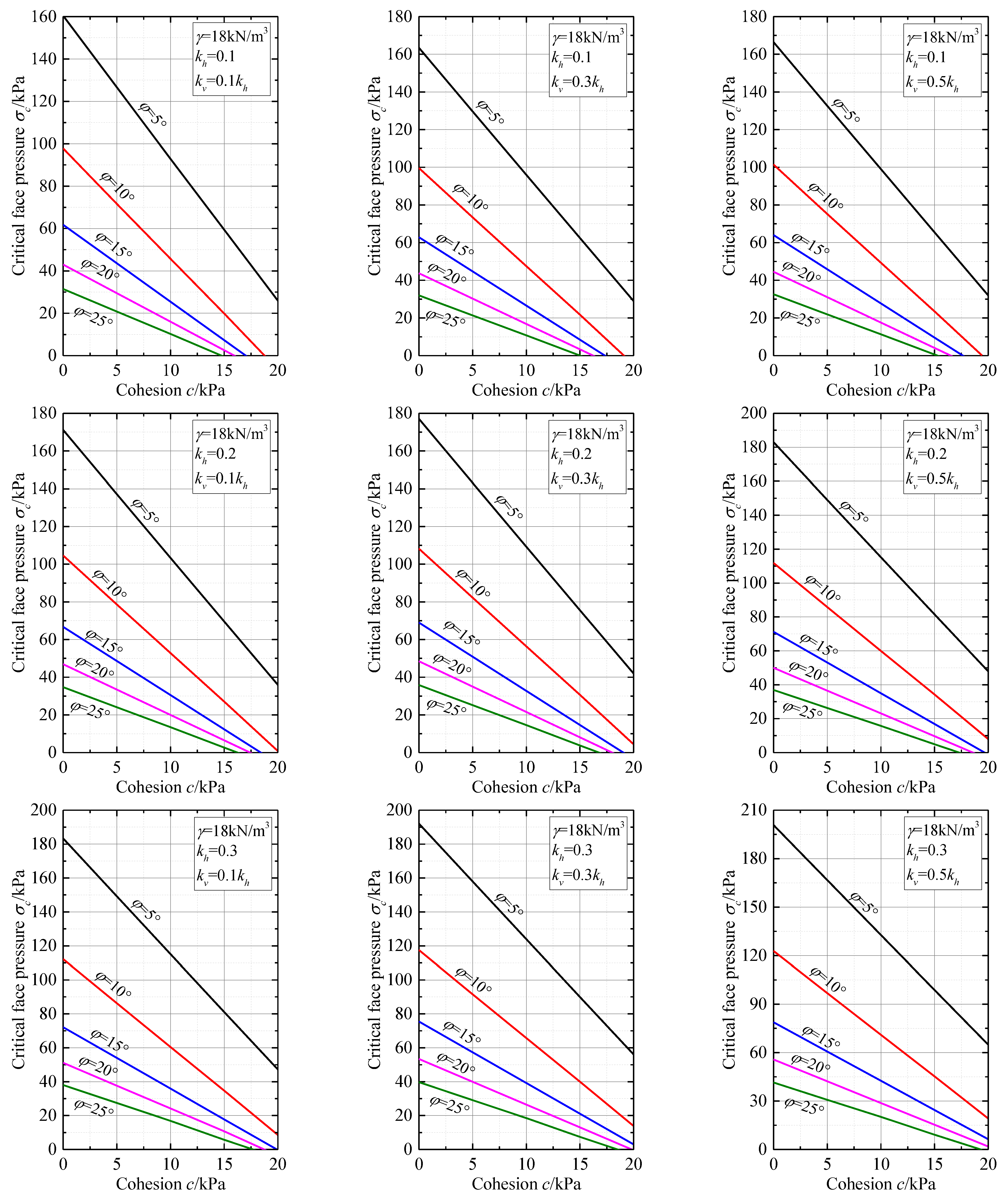
5. Seismic Stability Charts
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zakhem, A.M.; El Naggar, H. Effect of the constitutive material model employed on predictions of the behaviour of earth pressure balance (EPB) shield-driven tunnels. Transp. Geotech. 2019, 21, 100264. [Google Scholar] [CrossRef]
- Banerjee, S.K.; Chakraborty, D. Stability analysis of a circular tunnel underneath a fully liquefied soil layer. Tunn. Undergr. Space Technol. 2018, 78, 84–94. [Google Scholar] [CrossRef]
- Li, T.; Gong, W.; Tang, H.; Zhang, L. A meshed kinematical approach for 3D slope stability analysis. Int. J. Numer. Anal. Methods Geomech. 2022, 46, 2913–2930. [Google Scholar] [CrossRef]
- Moeinossadat, S.R.; Ahangari, K. Estimating maximum surface settlement due to EPBM tunneling by Numerical-Intelligent approach–A case study: Tehran subway line 7. Transp. Geotech. 2019, 18, 92–102. [Google Scholar] [CrossRef]
- Roateşi, S. Analytical and numerical approach for tunnel face advance in a viscoplastic rock mass. Int. J. Rock Mech. Min. Sci. 2014, 70, 123–132. [Google Scholar] [CrossRef]
- Soomro, M.A.; Ng, C.W.W.; Memon, N.A.; Bhanbhro, R. Lateral behaviour of a pile group due to side-by-side twin tunnelling in dry sand: 3D centrifuge tests and numerical modelling. Comput. Geotech. 2018, 101, 48–64. [Google Scholar] [CrossRef]
- Zuo, Y.; Xu, T.; Zhang, Y.; Zhang, Y.; Li, S.; Zhao, G.; Chen, C. Numerical study of zonal disintegration within a rock mass around a deep excavated tunnel. Int. J. Geomech. 2011, 12, 471–483. [Google Scholar] [CrossRef]
- Leca, E.; Dormieux, L. Upper and lower bound solutions for the face stability of shallow circular tunnels in frictional material. Geotechnique 1990, 40, 581–606. [Google Scholar] [CrossRef]
- Mollon, G.; Dias, D.; Soubra, A.H. Face stability analysis of circular tunnels driven by a pressurized shield. J. Geotech. Geoenviron. Eng. 2009, 136, 215–229. [Google Scholar] [CrossRef]
- Subrin, D.; Wong, H. Tunnel face stability in frictional material: A new 3D failure mechanism. Comptes Rendus Mec. 2002, 330, 513–519. [Google Scholar] [CrossRef]
- Mollon, G.; Dias, D.; Soubra, A.H. Rotational failure mechanisms for the face stability analysis of tunnels driven by a pressurized shield. Int. J. Numer. Anal. Methods Geomech. 2011, 35, 1363–1388. [Google Scholar] [CrossRef]
- Perazzelli, P.; Leone, T.; Anagnostou, G. Tunnel face stability under seepage flow conditions. Tunn. Undergr. Space Technol. 2014, 43, 459–469. [Google Scholar] [CrossRef]
- Pan, Q.; Dias, D. Three dimensional face stability of a tunnel in weak rock masses subjected to seepage forces. Tunn. Undergr. Space Technol. 2018, 71, 555–566. [Google Scholar] [CrossRef]
- Kargar, A.R.; Rahmannejad, R.; Hajabasi, M.A. A semi-analytical elastic solution for stress field of lined non-circular tunnels at great depth using complex variable method. Int. J. Solids Struct. 2014, 51, 1475–1482. [Google Scholar] [CrossRef]
- Lu, A.; Zhang, N.; Kuang, L. Analytic solutions of stress and displacement for a non-circular tunnel at great depth including support delay. Int. J. Rock Mech. Min. Sci. 2014, 70, 69–81. [Google Scholar] [CrossRef]
- Pan, Q.; Dias, D. Safety factor assessment of a tunnel face reinforced by horizontal dowels. Eng. Struct. 2017, 142, 56–66. [Google Scholar] [CrossRef]
- Ye, Z.K.; Ai, Z.Y. A matrix-form complex variable method for multiple non-circular tunnels in layered media. Appl. Math. Model. 2024, 131, 570–595. [Google Scholar] [CrossRef]
- Hou, C.; Yang, X.; Liu, M.; Chen, M.; Wu, Z.; Long, G. Stability assessment of a non-circular tunnel face with tensile strength cut-off subject to seepage flows: A comparison analysis. Comput. Geotech. 2023, 163, 105764. [Google Scholar] [CrossRef]
- Wu, Z.; Cui, Y.; Barrett, A.G.; Moreno, M.M.; Deng, Y. Role of surrounding soils and pore water in calcium carbonate precipitation in railway tunnel drainage system. Transp. Geotech. 2019, 21, 100257. [Google Scholar] [CrossRef]
- Lee, I.M.; Nam, S.W.; Ahn, J.H. Effect of seepage forces on tunnel face stability. Can. Geotech. J. 2003, 40, 342–350. [Google Scholar] [CrossRef]
- Shin, Y.J.; Song, K.I.; Lee, I.M.; Cho, G.-C. Interaction between tunnel supports and ground convergence—Consideration of seepage forces. Int. J. Rock Mech. Min. Sci. 2011, 48, 394–405. [Google Scholar] [CrossRef]
- Wijaya, H.; Rajeev, P.; Gad, E. Effect of seismic and soil parameter uncertainties on seismic damage of buried segmented pipeline. Transp. Geotech. 2019, 21, 100274. [Google Scholar] [CrossRef]
- Sahoo, J.P.; Kumar, J. Seismic stability of a long unsupported circular tunnel. Comput. Geotech. 2012, 44, 109–115. [Google Scholar] [CrossRef]
- Ganesh, R.; Prasad Sahoo, J. Seismic Passive Resistance of Cohesive-Frictional Soil Medium: Kinematic Limit Analysis. Int. J. Geomech. 2017, 17, 04017029. [Google Scholar] [CrossRef]
- Saada, Z.; Maghous, S.; Garnier, D. Pseudo-static analysis of tunnel face stability using the generalized Hoek–Brown strength criterion. Int. J. Numer. Anal. Methods Geomech. 2013, 37, 3194–3212. [Google Scholar] [CrossRef]
- Davoodi, M.; Senent, S.; Keshavarz, A.; Jimenez, R. Three-dimensional seismic face stability of shield tunnels in undrained clay. Undergr. Space 2024, 15, 26–43. [Google Scholar] [CrossRef]
- Vo-Minh, T.; Nguyen-Son, L.; Nguyen, T.A. Stable node-based smoothed finite element method for seismic stability analysis of a square tunnel in cohesive-frictional soils. Tunn. Undergr. Space Technol. 2023, 141, 105346. [Google Scholar] [CrossRef]
- Mollon, G.; Dias, D.; Soubra, A.H. Continuous velocity fields for collapse and blowout of a pressurized tunnel face in purely cohesive soil. Int. J. Numer. Anal. Methods Geomech. 2013, 37, 2061–2083. [Google Scholar] [CrossRef]
- Xu, J.; Yang, X. Seismic stability analysis and charts of a 3D rock slope in Hoek–Brown media. Int. J. Rock Mech. Min. Sci. 2018, 112, 64–76. [Google Scholar] [CrossRef]
- Li, T.; Gong, W.; Tang, H. Three-dimensional stochastic geological modeling for probabilistic stability analysis of a circular tunnel face. Tunn. Undergr. Space Technol. 2021, 118, 104190. [Google Scholar] [CrossRef]
- Li, A.J.; Lyamin, A.V.; Merifield, R.S. Seismic rock slope stability charts based on limit analysis methods. Comput. Geotech. 2009, 36, 135–148. [Google Scholar] [CrossRef]


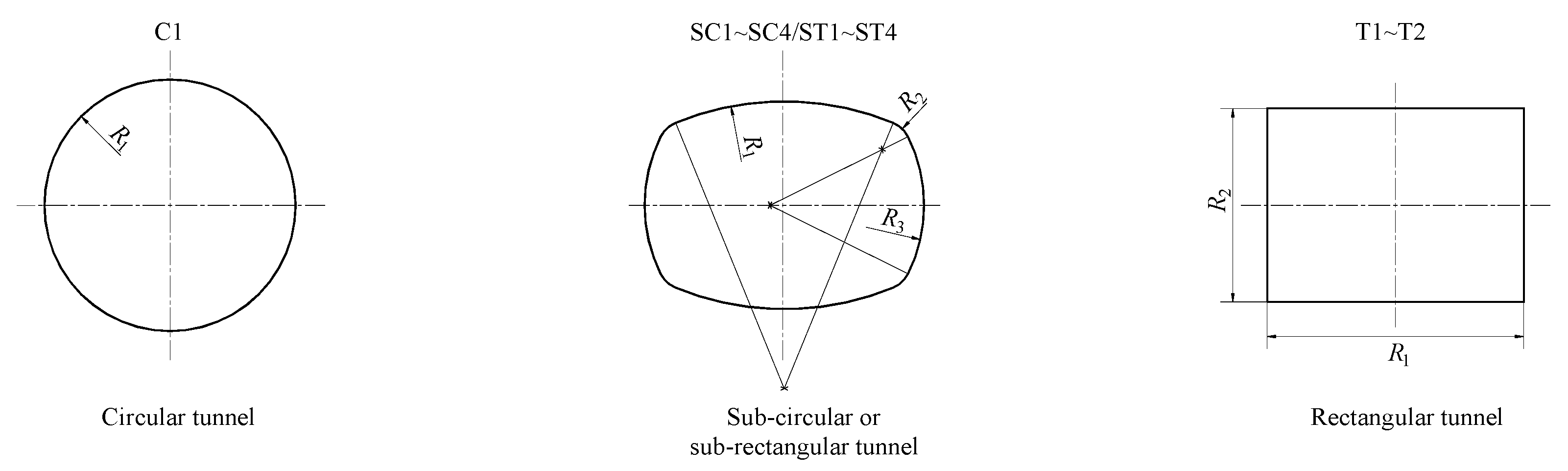
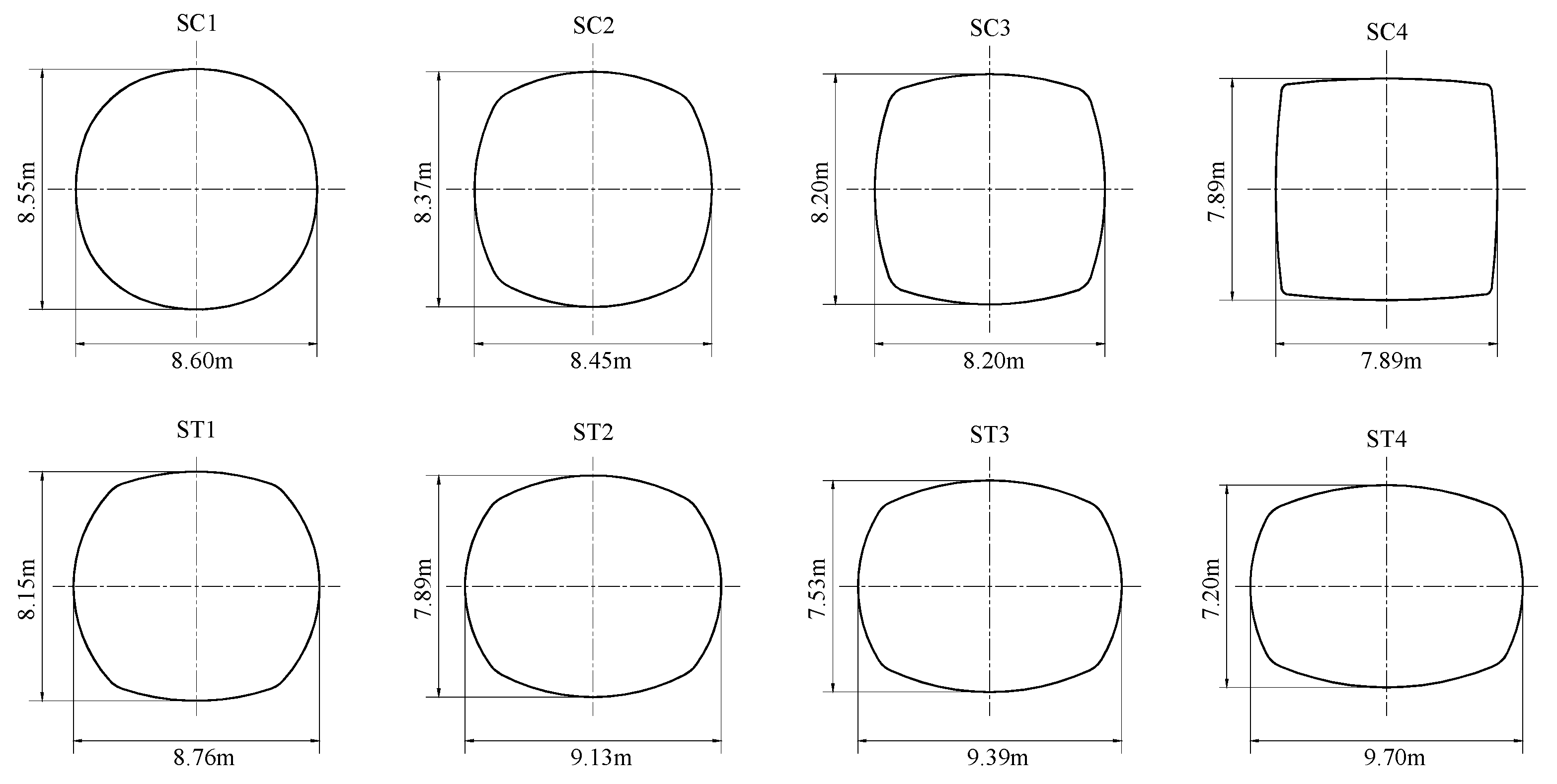
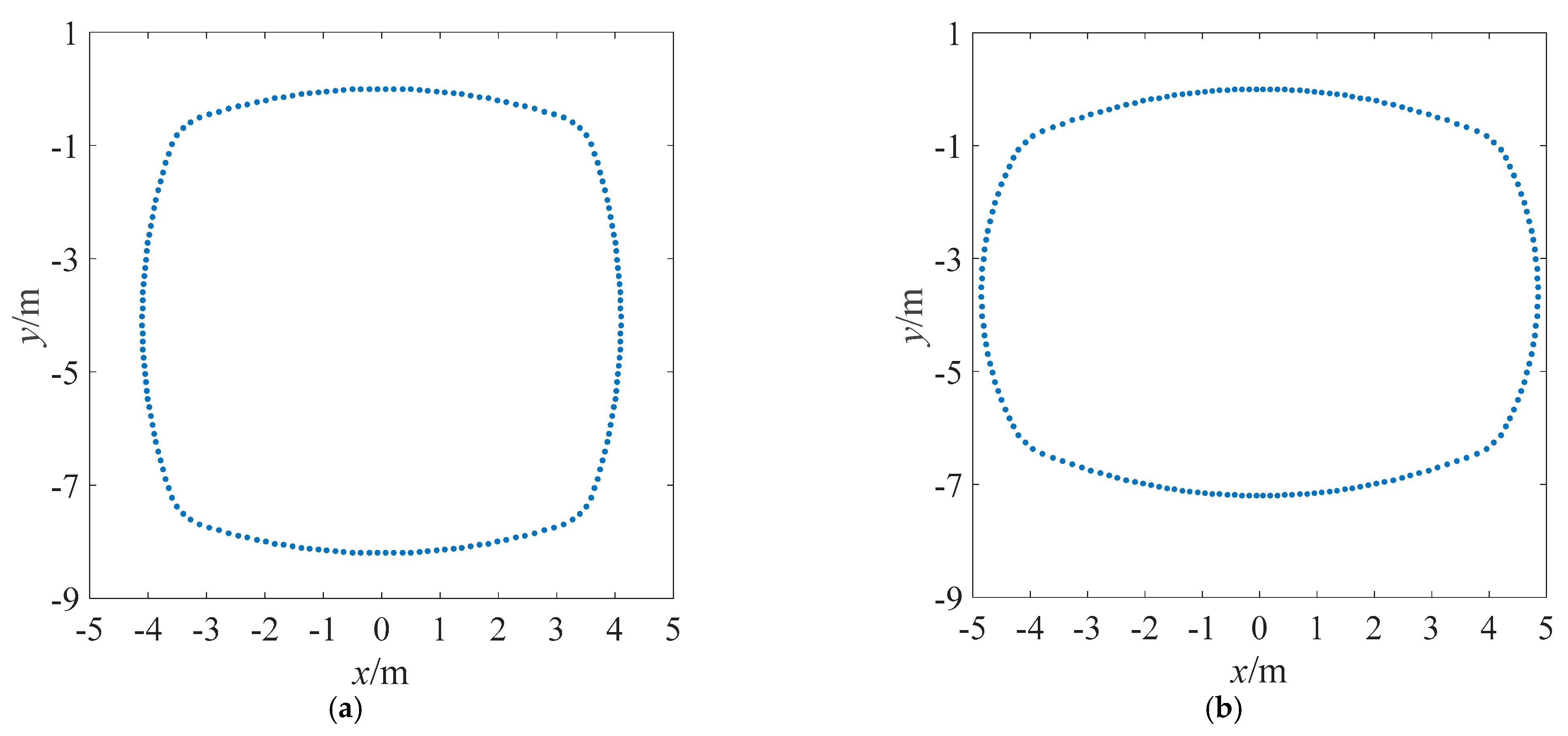

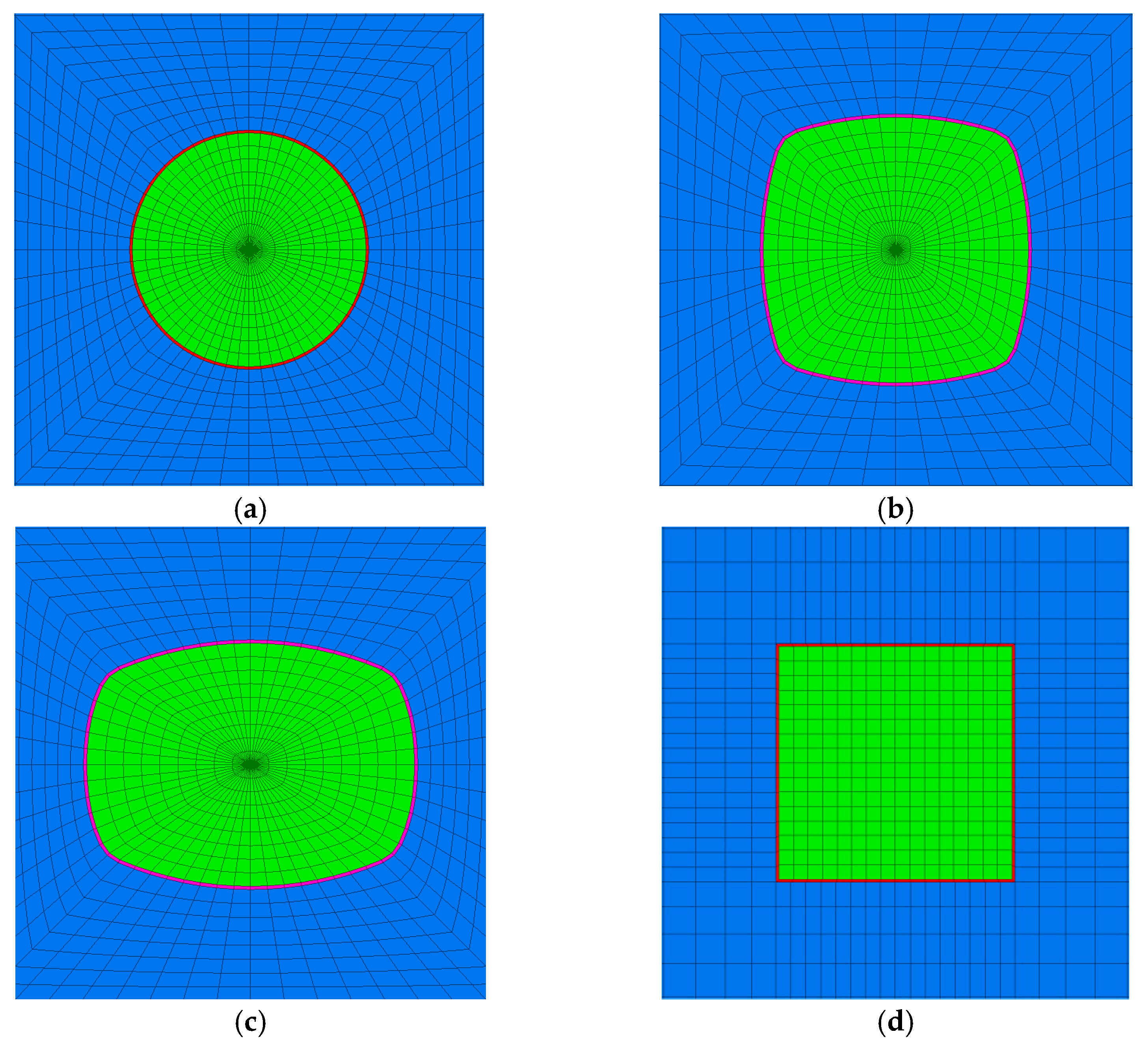
| Case | R1/m | R2/m | R3/m | L/m | L/H | Area/m2 | Type of Tunnel Shape | |
|---|---|---|---|---|---|---|---|---|
| L ≈ H | C1 | 4.36 | - | - | 8.72 | 1.00 | 59.786 | Circular (Reference case) |
| SC1 | 5.47 | 3.67 | 5.47 | 8.60 | 1.01 | 59.759 | Sub-circular | |
| SC2 | 6.56 | 1.23 | 6.56 | 8.45 | 1.01 | 59.795 | ||
| SC3 | 9.88 | 0.85 | 9.88 | 8.20 | 1.00 | 59.812 | ||
| SC4 | 25.83 | 0.25 | 25.83 | 7.89 | 1.00 | 59.778 | ||
| T1 | 7.73 | 7.73 | - | 7.73 | 1.00 | 59.753 | Rectangular (Reference case) | |
| L > H | ST1 | 8.36 | 1.02 | 4.99 | 8.76 | 1.07 | 59.788 | Sub-rectangular |
| ST2 | 7.09 | 1.23 | 4.81 | 9.13 | 1.16 | 59.757 | ||
| ST3 | 8.50 | 0.96 | 5.07 | 9.39 | 1.25 | 59.778 | ||
| ST4 | 9.95 | 1.00 | 5.35 | 9.70 | 1.35 | 59.786 | ||
| T2 | 10.00 | 5.98 | - | 10.00 | 1.67 | 59.786 | Rectangular (Reference case) | |
| Case | Cohesive–Frictional Soil | Frictional Soil | ||||
|---|---|---|---|---|---|---|
| kh = 0 | kh = 0.1 | Increment/% | kh = 0 | kh = 0.1 | Increment/% | |
| C1 | 30.38 | 35.89 | 18.14% | 17.22 | 20.02 | 16.24% |
| SC1 | 30.10 | 36.68 | 21.89% | 17.15 | 20.17 | 17.57% |
| SC2 | 29.36 | 35.85 | 22.10% | 16.84 | 19.77 | 17.38% |
| SC3 | 28.31 | 34.69 | 22.54% | 16.40 | 19.18 | 16.89% |
| SC4 | 26.47 | 32.38 | 22.32% | 15.87 | 18.31 | 15.63% |
| T1 | 25.62 | 31.65 | 23.53% | 14.65 | 17.77 | 21.31% |
| C1 | 30.38 | 35.89 | 18.14% | 17.22 | 20.02 | 16.24% |
| ST1 | 29.26 | 35.75 | 22.17% | 16.84 | 19.80 | 17.58% |
| ST2 | 28.64 | 35.07 | 22.44% | 16.63 | 19.56 | 17.63% |
| ST3 | 27.54 | 33.86 | 22.95% | 16.26 | 19.14 | 17.73% |
| ST4 | 26.36 | 32.55 | 23.46% | 15.86 | 18.70 | 17.87% |
| T2 | 21.48 | 26.99 | 25.66% | 13.54 | 16.05 | 18.58% |
| Case | Cohesive–Frictional Soil | Frictional Soil | ||||
|---|---|---|---|---|---|---|
| Limit Analysis | FLAC3D | Difference/% | Limit Analysis | FLAC3D | Difference/% | |
| C1 | 35.89 | 48.82 | −26.49% | 20.02 | 16.09 | 24.44% |
| SC3 | 34.69 | 43.75 | −20.71% | 19.18 | 15.08 | 27.16% |
| ST4 | 32.55 | 42.46 | −23.34% | 18.70 | 14.38 | 30.03% |
| T1 | 31.65 | 57.27 | −44.73% | 17.77 | 27.47 | −35.32% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jia, Y.; Pei, C.; Liang, F.; Li, T. Critical Face Pressure of a Tunnel Driven by a Shield Machine Considering Seismic Forces and Tunnel Shape Influence. Buildings 2024, 14, 1760. https://doi.org/10.3390/buildings14061760
Jia Y, Pei C, Liang F, Li T. Critical Face Pressure of a Tunnel Driven by a Shield Machine Considering Seismic Forces and Tunnel Shape Influence. Buildings. 2024; 14(6):1760. https://doi.org/10.3390/buildings14061760
Chicago/Turabian StyleJia, Yunfu, Chengyuan Pei, Feng Liang, and Tianzheng Li. 2024. "Critical Face Pressure of a Tunnel Driven by a Shield Machine Considering Seismic Forces and Tunnel Shape Influence" Buildings 14, no. 6: 1760. https://doi.org/10.3390/buildings14061760





