Exploring Historical Perspectives in Building Hygrothermal Models: A Comprehensive Review
Abstract
:1. Introduction
2. A Brief History of Hygrothermal Models
3. Classical Hygrothermal Models
3.1. Model of Philip and De Vries
- Hysteresis in the dependency of the moisture potential and volumetric water content is not taken into account.
- In the case of the deformed porous media and when having shrinkage and swelling porous material, the theory could not be applied.
- The porous medium must be homogeneous and isotropic in a macroscopic sense.
- Phenomena of boiling, freezing, and thawing are not included.
- Surface phenomena at the interface between the matrix and the liquid are not taken into account, nor are Knudsen effects.
3.2. Model of Luikov (or Lykov)
3.2.1. Luikov’s Model for Coupled Heat and Moisture Transfer in a Building Material
3.2.2. Luikov Model for Coupled Heat and Moisture Transfer in a Colloidal Porous Material
3.2.3. Luikov Model for Coupled Heat and Moisture Transfer in a Capillary Porous Material and General form of Equations
3.3. Model of Whitaker
3.4. Model of Künzel
3.5. Model of Rode
3.6. Model of Grunewald
4. Discussion on Building Hygrothermal Models
- Considering the three-dimensional hygrothermal analysis with an additional term of infiltration or air velocity in porous media.
- Taking into account the computational fluid dynamics (CFD) approach rather than the conventional 1D methods because the power of the computers has been improved. CFD offers detailed information on airflow, temperature, and humidity throughout the building environments and constructions.
- It is also not clear yet what the hysteresis effect is of sorption/desorption in moisture risk analysis of building materials.
- International efforts are needed to bring attention to assessing the hygrothermal models on various climate regions, especially in cold freezing regions.
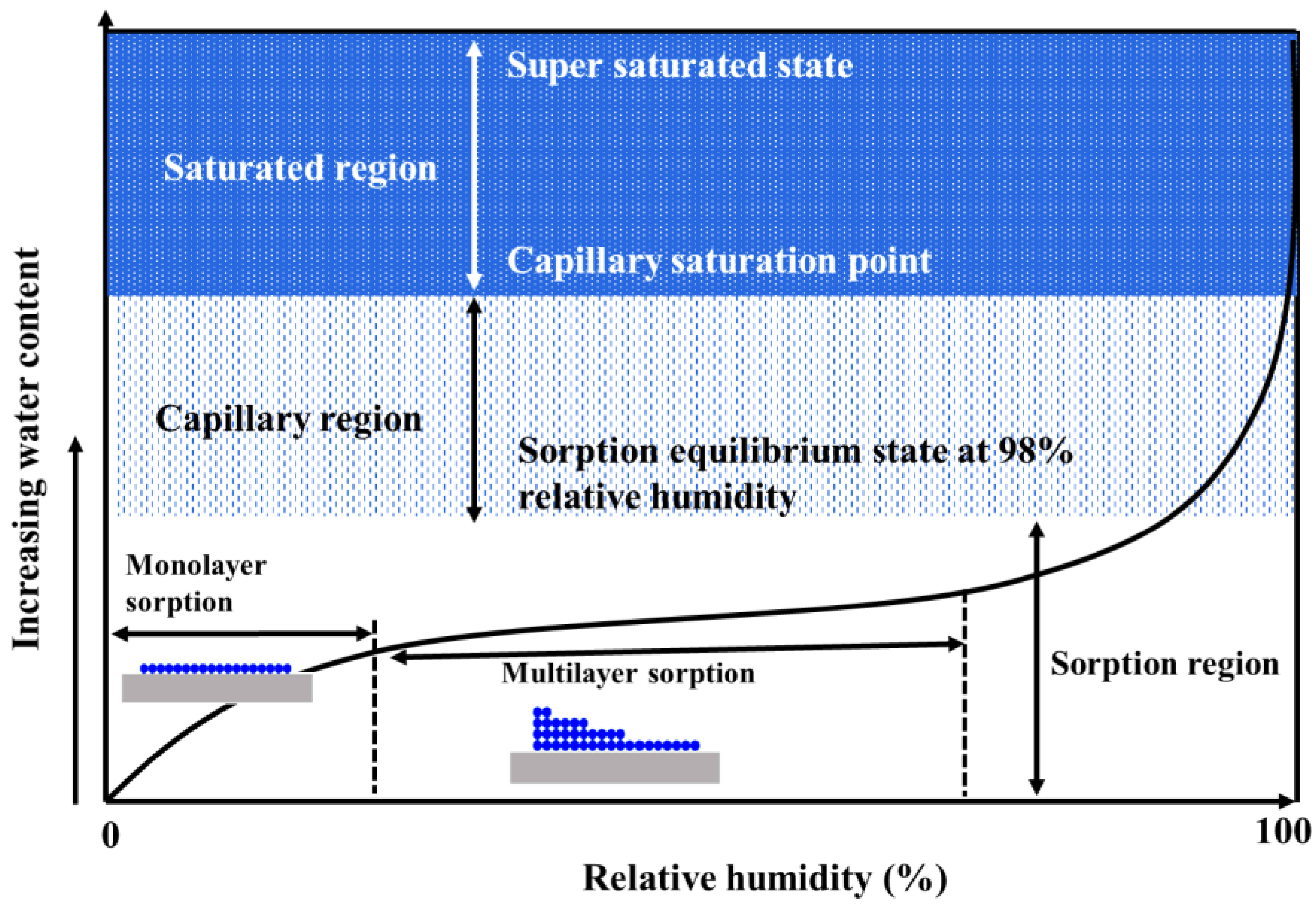
- The development of hygrothermal models encompasses all moisture states in porous materials, including the sorption, capillary, and saturated regions.
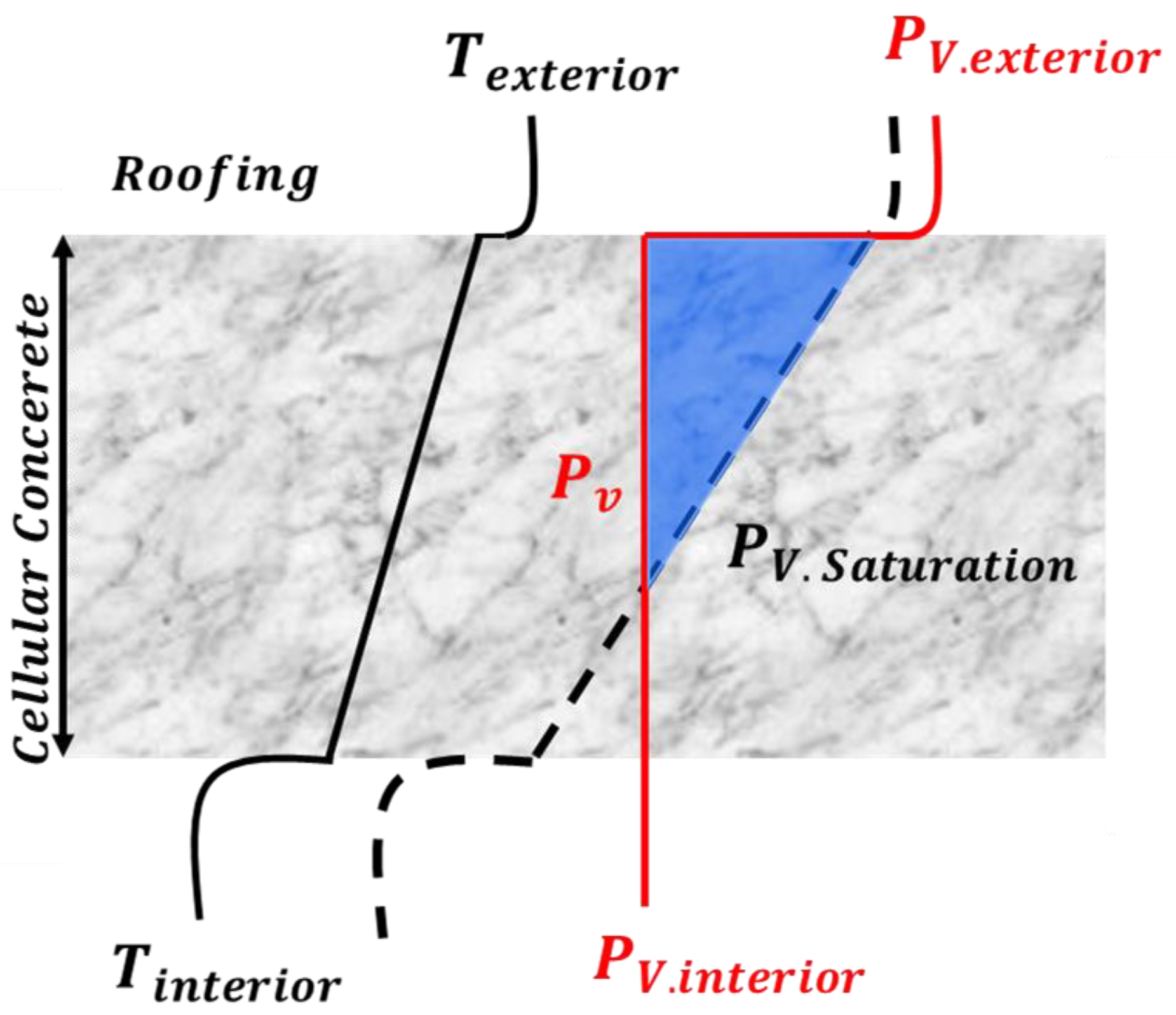
5. Advancements from Glaser Method to EN ISO 15026
- The variation of material properties with moisture content;
- Capillary suction and liquid moisture transfer, which whiten materials;
- Air movement from within the building into the component through gaps or air spaces;
- Hygroscopic moisture capacity of materials.
5.1. Benchmark No. 1 Insulated Roof
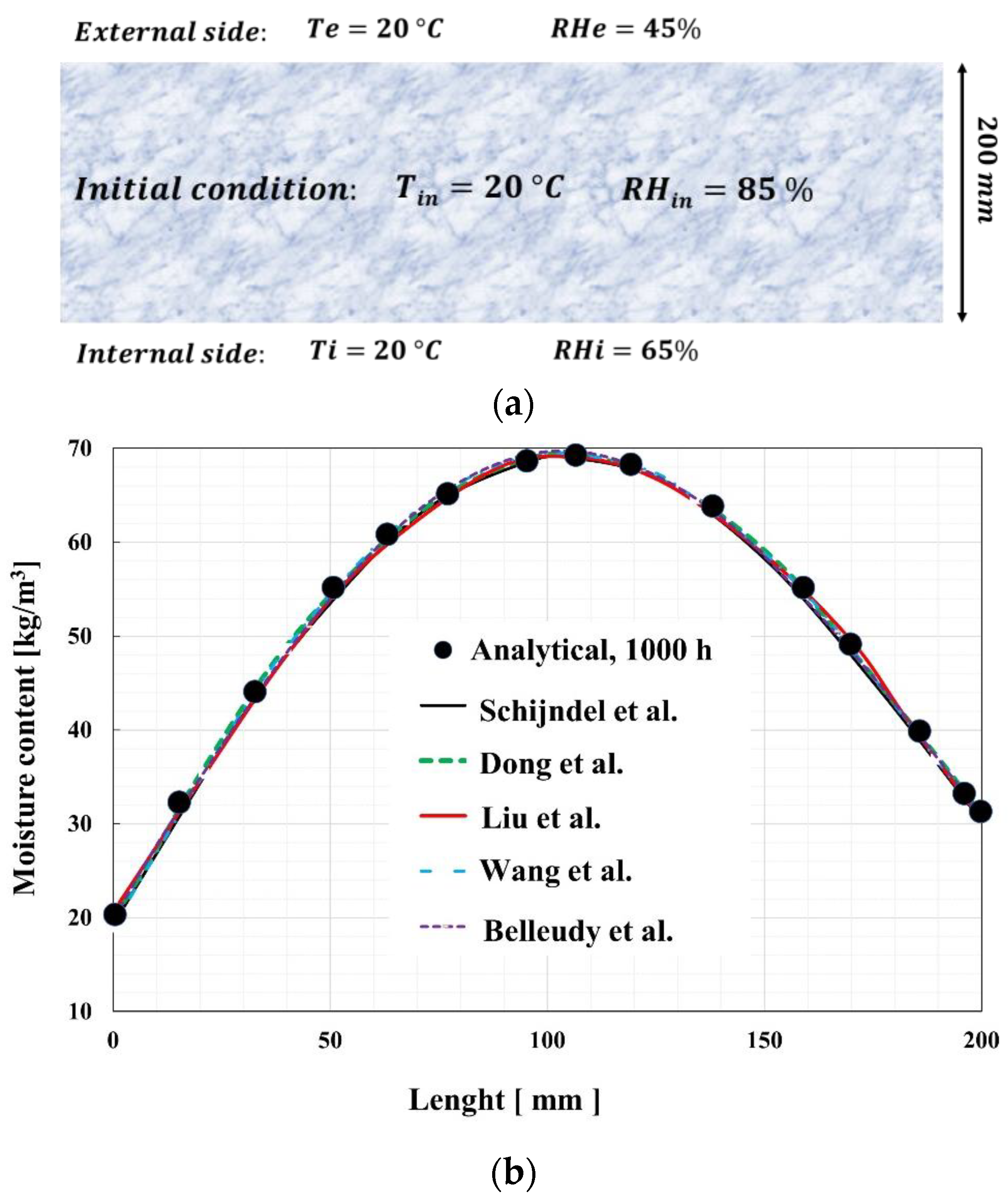
5.2. Benchmark No. 2 Analytical Case 1
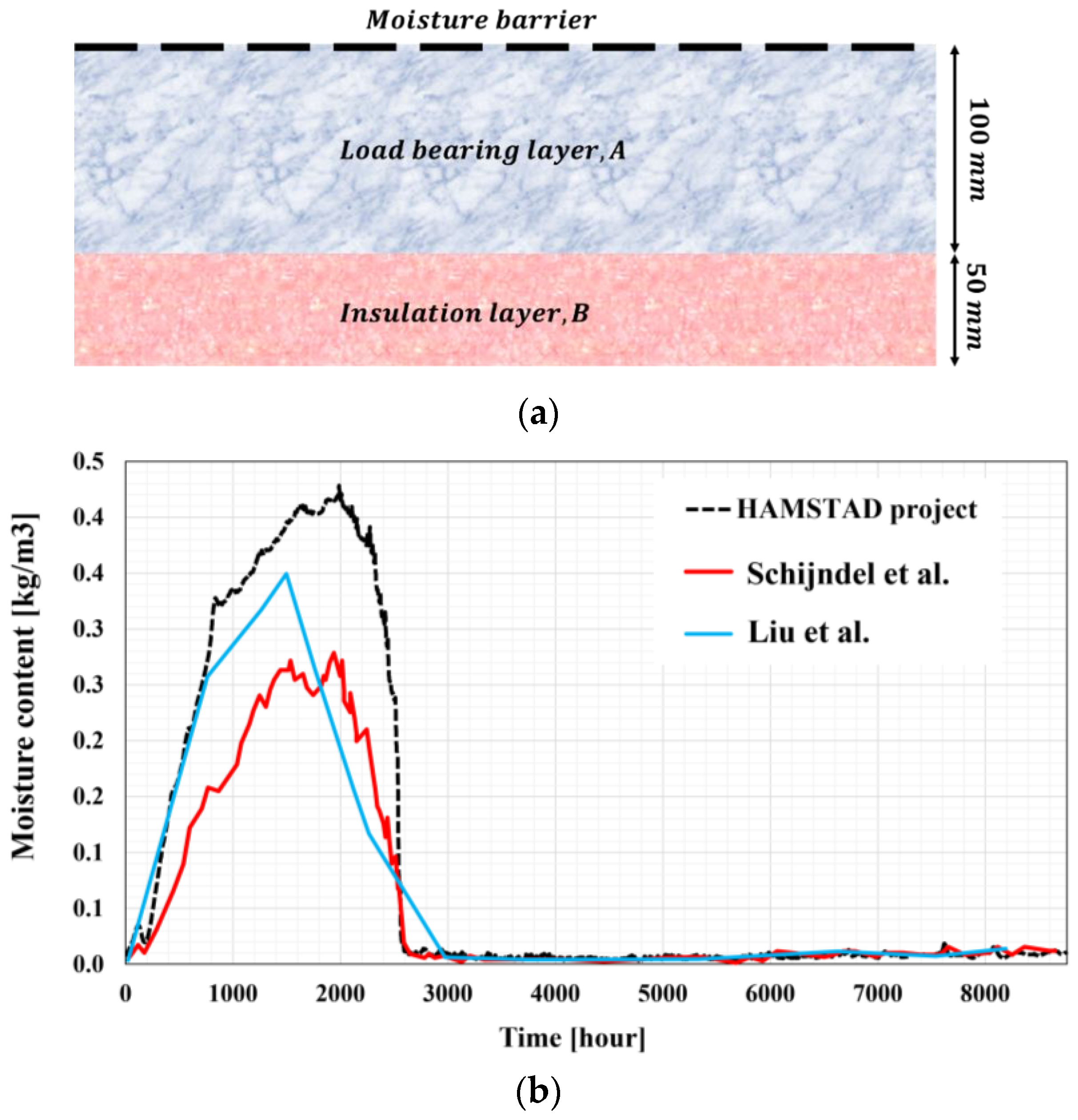
5.3. Benchmark No. 3 Lightweight Wall
5.4. Benchmark No. 4 Response Analysis
5.5. Benchmark No. 5 Capillary Active Inside Insulation
5.6. Benchmark No. 6 Analytical Case 2
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Saturated hydraulic conductivity (m·s−1) | |
| Hydraulic conductivity (m·s−1) | |
| Hydraulic head (m) | |
| Flow rate of water (m3·s−1) | |
| Capillary potential (J·kg−1) | |
| Gravitational potential (J·kg−1) | |
| Solute potential (J·kg−1) | |
| Electrochemical potential (J·kg−1) | |
| X | Mass moisture content (kg·kg−1) |
| Volumetric water content (m3/m3) | |
| Time (s) | |
| Temperature (K) | |
| Volumetric heat capacity of material (J·K−1·m−3) | |
| Thermal conductivity (W·m−1·K−1) | |
| Specific heat of liquid water (J·kg−1·K−1) | |
| Density of water (kg·m−3) | |
| Reference temperature (K) | |
| Water vapor pressure (Pa) | |
| Saturated water vapor pressure (Pa) | |
| Relative humidity (-) | |
| Molecular mass of water (kg·mol−1) | |
| Gravity (m/s2) | |
| Gas constant (J·mol−1·K−1) | |
| Total diffusivity of moisture transport due to a temperature gradient (m2·s−1·K−1) | |
| Total diffusivity of moisture transport due to a moisture gradient (m2·s−1) | |
| Diffusion of vapor under temperature gradient (m2·s−1·K−1) | |
| Diffusion of liquid under temperature gradient (m2·s−1·K−1) | |
| Isothermal vapor diffusivity (m2·s−1) | |
| Isothermal liquid diffusivity (m2·s−1) | |
| L | Latent heat of vaporization of liquid (J·kg−1) |
| Water vapor transmission coefficient (s) | |
| Volumetric air content (-) | |
| Temperature coefficient of surface tension (K−1) | |
| Tortuosity factor (-) | |
| Unitless parameter for the mass fraction of clay in the soil (-) | |
| Enhancement factor | |
| Water vapor diffusion coefficient in air (m2·s−1) | |
| Atmospheric pressure (Pa) | |
| Phenomenological coefficient (-) | |
| Slope of the water retention curve (J·kg−1) | |
| Slope of the water sorption curve (-) | |
| The criterion of the phase transition of fluid into vapor (-) | |
| Heat propagation (s) | |
| The moisture propagation in capillary porous media (s) | |
| Thermo gradient coefficient (K−1) | |
| Thermal diffusivity (m2·s−1) | |
| General moisture transfer coefficients (-) | |
| Density of solid phase (kg·m−3) | |
| Density of vapor phase (kg·m−3) | |
| Water vapor diffusivity (m2·s−1) | |
| Bound water diffusivity (m2·s−1) | |
| Dimensionless diffusivity tensor | |
| Liquid phase velocity (m·s−1) | |
| Specific enthalpy of the liquid phase (J·kg−1) | |
| Specific enthalpy of the vapor phase (J·kg−1) | |
| Specific enthalpy of the solid phase (J·kg−1) | |
| Specific enthalpy of the bound water (J·kg−1) | |
| Vapor mass fraction (kg/kg) | |
| Volume fraction of liquid (m3/m3) | |
| Volume fraction of vapor (m3/m3) | |
| Volume fraction of solid (m3/m3) | |
| Water vapor permeability (kg·Pa−1·m−1·s−1) | |
| Capillary coefficient (m2·s−1) | |
| Liquid conduction coefficient (kg·m−1·s−1) | |
| Moisture content (kg of moisture. (kg of dry material−1)) | |
| Dry density of material (kg·m−3) | |
| Water vapor permeability as a function of moisture content (kg·m−1·s−1·Pa−1) |
References
- Aceti, P.; Carminati, L.; Bettini, P.; Sala, G. Hygrothermal Ageing of Composite Structures. Part 1: Technical Review. Compos. Struct. 2023, 319, 117076. [Google Scholar] [CrossRef]
- Su, Y.; Tian, M.; Li, J.; Zhang, X.; Zhao, P. Numerical Study of Heat and Moisture Transfer in Thermal Protective Clothing against a Coupled Thermal Hazardous Environment. Int. J. Heat Mass Transf. 2022, 194, 122989. [Google Scholar] [CrossRef]
- Tadeu, A.; Simões, N.; Branco, F. Steady-State Moisture Diffusion in Curved Walls, in the Absence of Condensate Flow, via the BEM: A Practical Civil Engineering Approach (Glaser Method). Build. Environ. 2003, 38, 677–688. [Google Scholar] [CrossRef]
- Blocken, B.; Roels, S.; Carmeliet, J. A Combined CFD–HAM Approach for Wind-Driven Rain on Building Facades. J. Wind Eng. Ind. Aerodyn. 2007, 95, 585–607. [Google Scholar] [CrossRef]
- Janssen, H.; Blocken, B.; Roels, S.; Carmeliet, J. Wind-Driven Rain as a Boundary Condition for HAM Simulations: Analysis of Simplified Modelling Approaches. Build. Environ. 2007, 42, 1555–1567. [Google Scholar] [CrossRef]
- WUFI. Available online: https://wufi.de/en/ (accessed on 11 June 2024).
- EnergyPlus. Available online: https://energyplus.net/ (accessed on 11 June 2024).
- Chkeir, A.; Bouzidi, Y.; Akili, Z.E.; Charafeddine, M.; Kashmar, Z. Assessment of Thermal Comfort in the Traditional and Contemporary Houses in Byblos: A Comparative Study. Energy Built Environ. 2024, 5, 933–945. [Google Scholar] [CrossRef]
- Jiang, Q.; Li, Q.; Zhang, C.; Wang, J.; Dou, Z.; Chen, A.; Yang, Y.; Ren, H.; Zhang, L. Excavation of Building Energy Conservation in University Based on Energy Use Behavior Analysis. Energy Build. 2023, 280, 112726. [Google Scholar] [CrossRef]
- Du, C.; Wang, Y.; Li, B.; Xu, M.; Sadrizadeh, S. Grey Image Recognition-Based Mold Growth Assessment on the Surface of Typical Building Materials Responding to Dynamic Thermal Conditions. Build. Environ. 2023, 243, 110682. [Google Scholar] [CrossRef]
- Boonen, E.; Beeldens, A.; Dirkx, I.; Bams, V. Durability of Cementitious Photocatalytic Building Materials. Catal. Today 2017, 287, 196–202. [Google Scholar] [CrossRef]
- Adilkhanova, I.; Santamouris, M.; Yun, G.Y. Coupling Urban Climate Modeling and City-Scale Building Energy Simulations with the Statistical Analysis: Climate and Energy Implications of High Albedo Materials in Seoul. Energy Build. 2023, 290, 113092. [Google Scholar] [CrossRef]
- Aparicio-Fernández, C.; Torner, M.E.; Cañada-Soriano, M.; Vivancos, J.-L. Analysis of the Energy Performance Strategies in a Historical Building Used as a Music School. Dev. Built Environ. 2023, 15, 100195. [Google Scholar] [CrossRef]
- Kalair, A.R.; Seyedmahmoudian, M.; Stojcevski, A.; Mekhilef, S.; Abas, N.; Koh, K. Thermal Comfort Analysis of a Trombe Wall Integrated Multi-Energy Nanogrid Building. J. Build. Eng. 2023, 78, 107623. [Google Scholar] [CrossRef]
- Aggarwal, C.; Ge, H.; Defo, M. Assessing Mould Growth Risk of Wood-Frame Walls Using Partial Least Squares (PLS) Regression Considering Climate Model Uncertainties. Build. Environ. 2023, 238, 110374. [Google Scholar] [CrossRef]
- Friis, N.K.; Møller, E.B.; Lading, T. Hygrothermal Conditions in the Facades of Residential Buildings in Nuuk and Sisimiut. Build. Environ. 2023, 243, 110686. [Google Scholar] [CrossRef]
- Boardman, C.R.; Glass, S.V.; Lepage, R. Dose-Response Simple Isopleth for Mold (DR SIM): A Dynamic Mold Growth Model for Moisture Risk Assessment. J. Build. Eng. 2023, 68, 106092. [Google Scholar] [CrossRef]
- Urso, A.; Evola, G.; Costanzo, V.; Nocera, F. A Critical Analysis on the Use of Different Weather Datasets to Assess Moisture-Related Risks in Building Components for a Mediterranean Location. J. Build. Eng. 2023, 76, 107177. [Google Scholar] [CrossRef]
- Panico, S.; Larcher, M.; Herrera Avellanosa, D.; Baglivo, C.; Troi, A.; Maria Congedo, P. Hygrothermal Simulation Challenges: Assessing Boundary Condition Choices in Retrofitting Historic European Buildings. Energy Build. 2023, 297, 113464. [Google Scholar] [CrossRef]
- Urso, A.; Costanzo, V.; Nocera, F.; Evola, G. Moisture-Related Risks in Wood-Based Retrofit Solutions in a Mediterranean Climate: Design Recommendations. Sustainability 2022, 14, 14706. [Google Scholar] [CrossRef]
- Vandemeulebroucke, I.; Caluwaerts, S.; Van Den Bossche, N. Decision Framework to Select Moisture Reference Years for Hygrothermal Simulations. Build. Environ. 2022, 218, 109080. [Google Scholar] [CrossRef]
- Libralato, M.; De Angelis, A.; D’Agaro, P.; Cortella, G.; Saro, O. Multiyear Hygrothermal Performance Simulation of Historic Building Envelopes. IOP Conf. Ser. Earth Environ. Sci. 2021, 863, 012045. [Google Scholar] [CrossRef]
- Libralato, M.; De Angelis, A.; Tornello, G.; Saro, O.; D’Agaro, P.; Cortella, G. Evaluation of Multiyear Weather Data Effects on Hygrothermal Building Energy Simulations Using WUFI Plus. Energies 2021, 14, 7157. [Google Scholar] [CrossRef]
- Zeng, L.; Chen, Y.; Cao, C.; Lv, L.; Gao, J.; Li, J.; Zhang, C. Influence of Materials’ Hygric Properties on the Hygrothermal Performance of Internal Thermal Insulation Composite Systems. Energy Built Environ. 2023, 4, 315–327. [Google Scholar] [CrossRef]
- Philip, J.R.; De Vries, D.A. Moisture Movement in Porous Materials under Temperature Gradients. Trans. Am. Geophys. Union 1957, 38, 222. [Google Scholar] [CrossRef]
- Ng, C.W.W.; Menzies, B. Advanced Unsaturated Soil Mechanics and Engineering; CRC Press: Boca Raton, FL, USA, 2014; ISBN 978-0-203-93972-7. [Google Scholar]
- Ren, F.; Zhou, C.; Zeng, Q.; Wang, Z.; Wang, W. Numerical Investigations into the Physical Significance of Sorptivity for Cement-Based Materials Considering Water Sensitivity. J. Build. Eng. 2023, 66, 105952. [Google Scholar] [CrossRef]
- Hamrouni, I.; Ouahbi, T.; El Hajjar, A.; Taibi, S.; Jamei, M.; Zenzri, H. Water Vapor Permeability of Flax Fibers Reinforced Raw Earth: Experimental and Micro-Macro Modeling. Eur. J. Environ. Civ. Eng. 2023, 27, 3020–3039. [Google Scholar] [CrossRef]
- Carman, P.C. Fluid Flow through Granular Beds. Chem. Eng. Res. Des. 1997, 75, S32–S48. [Google Scholar] [CrossRef]
- Ruan, K.; Fu, X.-L. A Modified Kozeny–Carman Equation for Predicting Saturated Hydraulic Conductivity of Compacted Bentonite in Confined Condition. J. Rock Mech. Geotech. Eng. 2022, 14, 984–993. [Google Scholar] [CrossRef]
- Khan, W.A.; Yusuf, T.A.; Mabood, F.; Siddiq, M.K.; Shehzad, S.A. Chemically Reactive Water-Based Carbon Nanotubes Flow Saturated in Darcy-Forchheimer Porous Media Coupled with Entropy Generation. Chem. Phys. Lett. 2023, 830, 140808. [Google Scholar] [CrossRef]
- Purcell, W.R. Capillary Pressures—Their Measurement Using Mercury and the Calculation of Permeability Therefrom. J. Pet. Technol. 1949, 1, 39–48. [Google Scholar] [CrossRef]
- Buckingham, E. Studies on the Movement of Soil Moisture; US Department of Agriculture: Washington, DC, USA, 1907.
- Luo, S.; Lu, N.; Zhang, C.; Likos, W. Soil Water Potential: A Historical Perspective and Recent Breakthroughs. Vadose Zone J. 2022, 21. [Google Scholar] [CrossRef]
- Nimmo, J.R. Imperatives for Predicting Preferential and Diffuse Flow in the Unsaturated Zone: 1. Equal Emphasis. Hydrol. Process. 2020, 34, 5690–5693. [Google Scholar] [CrossRef]
- Nielsen, D.R.; Van Genuchten, M.T.; Biggar, J.W. Water Flow and Solute Transport Processes in the Unsaturated Zone. Water Resour. Res. 1986, 22, 89S–108S. [Google Scholar] [CrossRef]
- Nimmo, J.R.; Landa, E.R. The Soil Physics Contributions of Edgar Buckingham. Soil Sci. Soc. Am. J. 2005, 69, 328–342. [Google Scholar] [CrossRef]
- Richards, L.A. Capillary Conduction of Liquids through Porous Mediums. Physics 1931, 1, 318–333. [Google Scholar] [CrossRef]
- Walker, W.; Sabey, J.; Hampton, D. Studies of Heat Transfer and Water Migration in Soils. Final Report; Colorado State Univ., Fort Collins (USA). Solar Energy Applications Lab.: Fort Collins, CO, USA, 1981; p. DOE/CS/30139-T1, 6149346, ON: DE81023951. [Google Scholar]
- Krischer, O. Die Wissenschaftlichen Grundlagen der Trocknungstechnik; Springer: Berlin/Heidelberg, Germany, 1956; ISBN 978-3-662-23898-1. [Google Scholar]
- Hens, H.S.L.C.; Mukhopadhyaya, P.; Kumaran, M.K.; Dean, S.W. Vapor Permeability Measurements: Impact of Cup Sealing, Edge Correction, Flow Direction, and Mean Relative Humidity. J. ASTM Int. 2009, 6, 101893. [Google Scholar] [CrossRef]
- De Vries, D.A. The Theory of Heat and Moisture Transfer in Porous Media Revisited. Int. J. Heat Mass Transf. 1987, 30, 1343–1350. [Google Scholar] [CrossRef]
- Luikov, A.V. Application of Irreversible Thermodynamics Methods to Investigation of Heat and Mass Transfer. Int. J. Heat Mass Transf. 1966, 9, 139–152. [Google Scholar] [CrossRef]
- Ozaki, A.; Watanabe, T.; Hayashi, T.; Ryu, Y. Systematic Analysis on Combined Heat and Water Transfer through Porous Materials Based on Thermodynamic Energy. Energy Build. 2001, 33, 341–350. [Google Scholar] [CrossRef]
- Maref, W.; Lacasse, M.; Kumaran, M.K.; Swinton, M.C. Benchmarking of the Advanced Hygrothermal Model-hygIRC with Mid Scale Experiments; National Research Council of Canada: Ottawa, ON, Canada, 2002.
- Künzel, H.M. Simultaneous Heat and Moisture Transport in Building Components: One- and Two-Dimensional Calculation Using Simple Parameters; IRB Verlag: Stuttgart, Germany, 1995; ISBN 978-3-8167-4103-9. [Google Scholar]
- Rode, C.; Hansen, P.N.; Hansen, K.K. Combined Heat and Moisture Transfer in Building Constructions; Technical University of Denmark: Lyngby Denmark, 1990. [Google Scholar]
- Whitaker, S. Simultaneous Heat, Mass, and Momentum Transfer in Porous Media: A Theory of Drying. In Advances in Heat Transfer; Elsevier: Amsterdam, The Netherlands, 1977; Volume 13, pp. 119–203. ISBN 978-0-12-020013-9. [Google Scholar]
- Grunewald, J. Diffusiver und konvektiver Stoff- und Energietransport in Kapillarporösenbaustoffen. Ph.D. Thesis, Technische Universität Dresden, Dresden, Germany, 1997. [Google Scholar]
- Milly, P.C.D. Moisture and Heat Transport in Hysteretic, Inhomogeneous Porous Media: A Matric Head-Based Formulation and a Numerical Model. Water Resour. Res. 1982, 18, 489–498. [Google Scholar] [CrossRef]
- Fang, A.; Chen, Y.; Wu, L. Transient Simulation of Coupled Heat and Moisture Transfer through Multi-Layer Walls Exposed to Future Climate in the Hot and Humid Southern China Area. Sustain. Cities Soc. 2020, 52, 101812. [Google Scholar] [CrossRef]
- Zhang, X.; Zillig, W.; Künzel, H.M.; Mitterer, C.; Zhang, X. Combined Effects of Sorption Hysteresis and Its Temperature Dependency on Wood Materials and Building Enclosures-Part II: Hygrothermal Modeling. Build. Environ. 2016, 106, 181–195. [Google Scholar] [CrossRef]
- De Vries, D.A. Simultaneous Transfer of Heat and Moisture in Porous Media. Trans. Am. Geophys. Union 1958, 39, 909. [Google Scholar] [CrossRef]
- Edlefsen, N.E.; Anderson, A.B.C. Thermodynamics of Soil Moisture. Hilgardia 1943, 15, 31–298. [Google Scholar] [CrossRef]
- Cary, J.W. An Evaporation Experiment and Its Irreversible Thermodynamics. Int. J. Heat Mass Transf. 1964, 7, 531–538. [Google Scholar] [CrossRef]
- Cary, J.W. Onsager’s Relation and the Non-Isothermal Diffusion of Water Vapor 1. J. Phys. Chem. 1963, 67, 126–129. [Google Scholar] [CrossRef]
- Jury, W.A.; Letey, J. Water Vapor Movement in Soil: Reconciliation of Theory and Experiment. Soil Sci. Soc. Am. J. 1979, 43, 823–827. [Google Scholar] [CrossRef]
- Kay, B.; Groenevelt, P. On the Interaction of Water and Heat Transport in Frozen and Unfrozen Soils: I. Basic Theory; the Vapor Phase. Soil Sci. Soc. Am. J. 1974, 38, 395–400. [Google Scholar] [CrossRef]
- Sophocleous, M. Analysis of Water and Heat Flow in Unsaturated-Saturated Porous Media. Water Resour. Res. 1979, 15, 1195–1206. [Google Scholar] [CrossRef]
- Lykov, A.V. Mass and Heat Transfer in Building Materials. J. Eng. Phys. 1965, 8, 103–109. [Google Scholar] [CrossRef]
- Lykov, A.V. On Systems of Differential Equations for Heat and Mass Transfer in Capillary Porous Bodies. J. Eng. Phys. 1974, 26, 11–17. [Google Scholar] [CrossRef]
- Firoozabadi, A.F. Thermodynamics of Hydrocarbon Reservoirs; McGraw-Hill: New York, NY, USA, 1999. [Google Scholar]
- Sutera, S.P.; Skalak, R. The History of Poiseuille’s Law. Annu. Rev. Fluid Mech. 1993, 25, 1–20. [Google Scholar] [CrossRef]
- lrudayaraj, J.; Wu, Y. Analysis and Application OF Luikov’s Heat, Mass, and Pressure Transfer Model to a Capillary Porous Media. Dry. Technol. 1996, 14, 803–824. [Google Scholar] [CrossRef]
- Chaurasiya, V.; Singh, J. An Analytical Study of Coupled Convective Heat and Mass Transfer with Volumetric Heating Describing Sublimation of a Porous Body under Most Sensitive Temperature Inputs: Application of Freeze-Drying. Int. J. Heat Mass Transf. 2023, 214, 124294. [Google Scholar] [CrossRef]
- Younsi, R.; Kocaefe, D.; Kocaefe, Y. Three-Dimensional Simulation of Heat and Moisture Transfer in Wood. Appl. Therm. Eng. 2006, 26, 1274–1285. [Google Scholar] [CrossRef]
- Liu, J.Y.; Shun, C. Solutions of Luikov Equations of Heat and Mass Transfer in Capillary-Porous Bodies. Int. J. Heat Mass Transf. 1991, 34, 1747–1754. [Google Scholar] [CrossRef]
- Pandey, R.N.; Srivastava, S.K.; Mikhailov, M.D. Solutions of Luikov Equations of Heat and Mass Transfer in Capillary Porous Bodies through Matrix Calculus: A New Approach. Int. J. Heat Mass Transf. 1999, 42, 2649–2660. [Google Scholar] [CrossRef]
- Chang, W.-J.; Weng, C.-I. An Analytical Solution to Coupled Heat and Moisture Diffusion Transfer in Porous Materials. Int. J. Heat Mass Transf. 2000, 43, 3621–3632. [Google Scholar] [CrossRef]
- Qin, M.; Zhang, H. Analytical Methods to Calculate Combined Heat and Moisture Transfer in Porous Building Materials under Different Boundary Conditions. Sci. Technol. Built Environ. 2015, 21, 993–1001. [Google Scholar] [CrossRef]
- García-Alvarado, M.A.; Pacheco-Aguirre, F.M.; Ruiz-López, I.I. Analytical Solution of Simultaneous Heat and Mass Transfer Equations during Food Drying. J. Food Eng. 2014, 142, 39–45. [Google Scholar] [CrossRef]
- Pečenko, R.; Challamel, N.; Colinart, T.; Picandet, V. (Semi-)Analytical Solution of Luikov Equations for Time-Periodic Boundary Conditions. Int. J. Heat Mass Transf. 2018, 124, 533–542. [Google Scholar] [CrossRef]
- Conceição, R.S.G.; Macêdo, E.N.; Pereira, L.B.D.; Quaresma, J.N.N. Hybrid Integral Transform Solution for the Analysis of Drying in Spherical Capillary-Porous Solids Based on Luikov Equations with Pressure Gradient. Int. J. Therm. Sci. 2013, 71, 216–236. [Google Scholar] [CrossRef]
- Vargas-González, S.; Núñez-Gómez, K.S.; López-Sánchez, E.; Tejero-Andrade, J.M.; Ruiz-López, I.I.; García-Alvarado, M.A. Thermodynamic and Mathematical Analysis of Modified Luikov’s Equations for Simultaneous Heat and Mass Transfer. Int. Commun. Heat Mass Transf. 2021, 120, 105003. [Google Scholar] [CrossRef]
- Abahri, K.; Belarbi, R.; Trabelsi, A. Contribution to Analytical and Numerical Study of Combined Heat and Moisture Transfers in Porous Building Materials. Build. Environ. 2011, 46, 1354–1360. [Google Scholar] [CrossRef]
- Ferroukhi, M.Y.; Djedjig, R.; Limam, K.; Belarbi, R. Hygrothermal Behavior Modeling of the Hygroscopic Envelopes of Buildings: A Dynamic Co-Simulation Approach. Build. Simul. 2016, 9, 501–512. [Google Scholar] [CrossRef]
- Remki, B.; Abahri, K.; Tahlaiti, M.; Belarbi, R. Hygrothermal Transfer in Wood Drying under the Atmospheric Pressure Gradient. Int. J. Therm. Sci. 2012, 57, 135–141. [Google Scholar] [CrossRef]
- Koukouch, A.; Bakhattar, I.; Asbik, M.; Idlimam, A.; Zeghmati, B.; Aharoune, A. Analytical Solution of Coupled Heat and Mass Transfer Equations during Convective Drying of Biomass: Experimental Validation. Heat Mass Transf. 2020, 56, 1971–1983. [Google Scholar] [CrossRef]
- Qin, M.; Belarbi, R.; Aït-Mokhtar, A.; Seigneurin, A. An Analytical Method to Calculate the Coupled Heat and Moisture Transfer in Building Materials. Int. Commun. Heat Mass Transf. 2006, 33, 39–48. [Google Scholar] [CrossRef]
- Whitaker, S. The Method of Volume Averaging. In Theory and Applications of Transport in Porous Media; Springer: Dordrecht, The Netherlands, 1999; Volume 13, ISBN 978-90-481-5142-4. [Google Scholar]
- Perré, P. The Proper Use of Mass Diffusion Equations in Drying Modeling: Introducing the Drying Intensity Number. Dry. Technol. 2015, 33, 1949–1962. [Google Scholar] [CrossRef]
- Krus, M. Moisture Transport and Storage Coefficient of Porous Mineral Building Materials; IRB Verlag: Stuttgart, Germany, 1996. [Google Scholar]
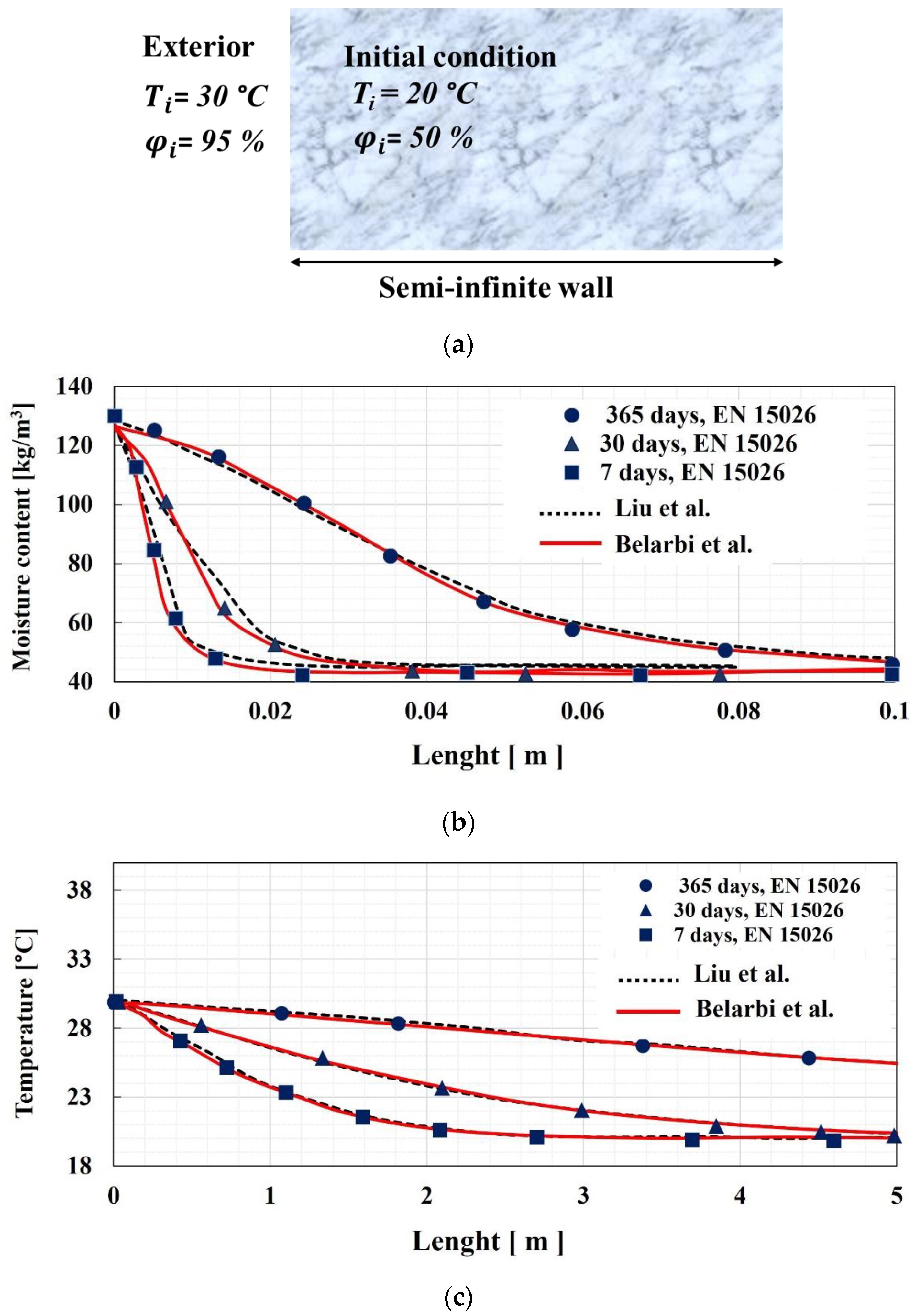
- EN 15026:2007; Hygrothermal Performance of Building Components and Building Elements—Assessment of Moisture Transfer by Numerical Simulation. The British Standards Institution: London, UK, 2007.
- Liu, X.; Chen, Y.; Ge, H.; Fazio, P.; Chen, G. Numerical Investigation for Thermal Performance of Exterior Walls of Residential Buildings with Moisture Transfer in Hot Summer and Cold Winter Zone of China. Energy Build. 2015, 93, 259–268. [Google Scholar] [CrossRef]
- Hagentoft, C.-E.; Kalagasidis, A.S.; Adl-Zarrabi, B.; Roels, S.; Carmeliet, J.; Hens, H.; Grunewald, J.; Funk, M.; Becker, R.; Shamir, D.; et al. Assessment Method of Numerical Prediction Models for Combined Heat, Air and Moisture Transfer in Building Components: Benchmarks for One-Dimensional Cases. J. Therm. Envel. Build. Sci. 2004, 27, 327–352. [Google Scholar] [CrossRef]
- Janssen, H. A Comment on “A Validation of Dynamic Hygrothermal Model with Coupled Heat and Moisture Transfer in Porous Building Materials and Envelopes”. J. Build. Eng. 2022, 47, 103835. [Google Scholar] [CrossRef]
- Dong, W.; Chen, Y.; Bao, Y.; Fang, A. Response to Comment on “A Validation of Dynamic Hygrothermal Model with Coupled Heat and Moisture Transfer in Porous Building Materials and Envelopes”. J. Build. Eng. 2022, 47, 103936. [Google Scholar] [CrossRef]
- Kuenzel, H.; Dewsbury, M. Moisture Control Design Has to Respond to All Relevant Hygrothermal Loads. UCL Open Environ. 2022, 4, e037. [Google Scholar]
- Woods, J.; Winkler, J.; Christensen, D. Evaluation of the Effective Moisture Penetration Depth Model for Estimating Moisture Buffering in Buildings; National Renewable Energy Lab.: Golden, CO, USA, 2013.
- Chang, S.J.; Kim, S. Hygrothermal Performance of Exterior Wall Structures Using a Heat, Air and Moisture Modeling. Energy Procedia 2015, 78, 3434–3439. [Google Scholar] [CrossRef]
- Zirkelbach, D.; Mehra, S.-R.; Sedlbauer, K.-P.; Künzel, H.-M.; Stöckl, B. A Hygrothermal Green Roof Model to Simulate Moisture and Energy Performance of Building Components. Energy Build. 2017, 145, 79–91. [Google Scholar] [CrossRef]
- Belleudy, C.; Kayello, A.; Woloszyn, M.; Ge, H. Experimental and Numerical Investigations of the Effects of Air Leakage on Temperature and Moisture Fields in Porous Insulation. Build. Environ. 2015, 94, 457–466. [Google Scholar] [CrossRef]
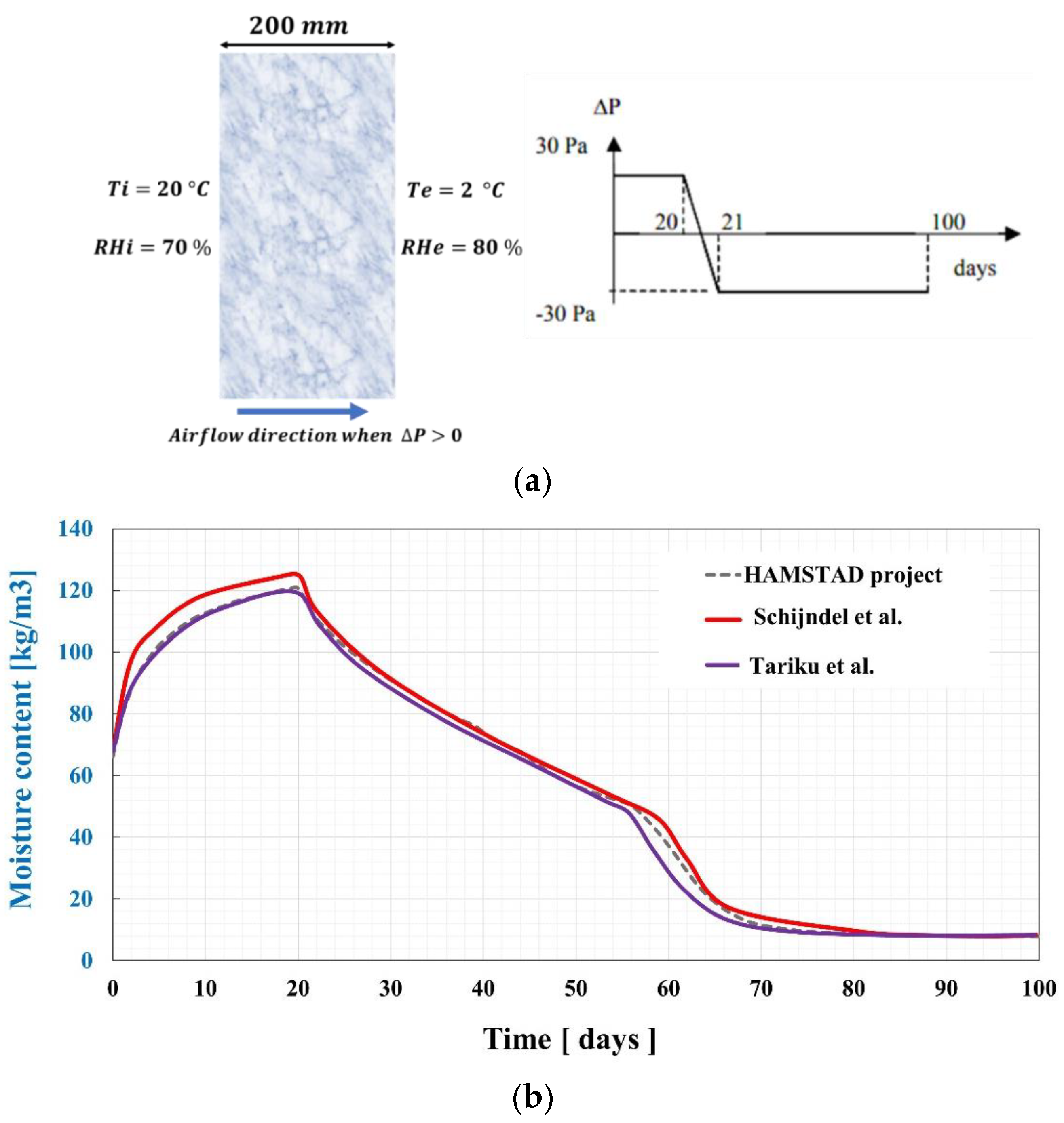
- Tariku, F.; Kumaran, K.; Fazio, P. Transient Model for Coupled Heat, Air and Moisture Transfer through Multilayered Porous Media. Int. J. Heat Mass Transf. 2010, 53, 3035–3044. [Google Scholar] [CrossRef]
- Hejazi, B.; Rodrigues Marques Sakiyama, N.; Frick, J.; Garrecht, H. Hygrothermal Simulations Comparative Study: Assessment of Different Materials Using WUFI and DELPHIN Software; IBPSA: Rome, Italy, 2019; pp. 4674–4681. [Google Scholar]
- Nicolai, A. Modeling and Numerical Simulation of Salt Transport and Phase Transitions in Unsaturated Porous Building Materials; Syracuse University: Syracuse, NY, USA, 2008. [Google Scholar]
- Rowley, F.B.; Algren, A.B.; Lund, C.E. Methods of Moisture Control and Their Application to Building Construction; University of Minnesota: Minneapolis, MN, USA, 1940. [Google Scholar]
- Egner, K.R. Feuchtigkeitsdurchgang Und Wasserdampfkondensation in Bauten; Franksche Verlagshandlung: Stuttgart, Germany, 1950. [Google Scholar]
- Cammerer, W.F. Die Untersuchung von Diffusionsvorgängen in Kühlraumwandungen Mit Hilfe Elektrischer Modellversuche. Kältetechnik 1951, 3, 197–200. [Google Scholar]
- Glaser, H. Zur Wahl Der Diffusionswiderstandsfaktoren von Mehrschichtigen Kühlraumwänden. Kaltetechnik 1959, 11, 214–222. [Google Scholar]
- Glaser, H. Graphisches Verfahren Zur Untersuchung von Diffusionsvorgängen. Kältetechnik 1959, 11, 345–349. [Google Scholar]
- Glaser, H. Vereinfachte Berechnung Der Dampfdiffusion Durch Geschichtete Wände Bei Ausscheidung von Wasser Und Eis. Kältetechnik 1958, 10, 358–364. [Google Scholar]
- Glaser, H. Temperatur Und Dampfdruckverlauf in Einer Homogene Wand Bei Feuchteausscheidung. Kältetechnik 1958, 6, 174–181. [Google Scholar]
- Cascione, V.; Marra, E.; Zirkelbach, D.; Liuzzi, S.; Stefanizzi, P. Hygrothermal Analysis of Technical Solutions for Insulating the Opaque Building Envelope. Energy Procedia 2017, 126, 203–210. [Google Scholar] [CrossRef]
- EN ISO 13788; Hygrothermal Performance of Building Components and Building Elements—Internal Surface Temperature to Avoid Critical Surface Humidity and Interstitial Condensation—Calculation Methods. International Organization for Standardization: Geneva, Switzerland, 2012.
- Hens, H.L.S.C. Combined Heat, Air, Moisture Modelling: A Look Back, How, of Help? Build. Environ. 2015, 91, 138–151. [Google Scholar] [CrossRef]
- Vos, B.H. Condensation in Flat Roofs under Non-Steady-State Conditions. Build. Sci. 1971, 6, 7–15. [Google Scholar] [CrossRef]
- Vos, B.H. Internal Condensation in Structures. Build. Sci. 1969, 3, 191–206. [Google Scholar] [CrossRef]
- Hens, H. Condensation in Concrete Flat Roofs. Batiment Int. Build. Res. Pract. 1978, 6, 292. [Google Scholar] [CrossRef]
- Hens, H. Theoretical and Experimental Study of the Hygrothermal Behavior of Building and Insulating Materials during Interstitial Condensation and Drying, with Application on Flat Roofs. Ph.D. Thesis, K.U.Leuven, Leuven, Belgium, 1975. [Google Scholar]
- Kooi, J.J.V.D. Moisture Transport in Cellular Concrete Roofs. Ph.D. Thesis, Eindhoven University of Technology, Eindhoven, The Netherlands, 1971. [Google Scholar] [CrossRef]
- Kiessl, K. Kapillarer und Dampfförmiger Feuchtetransport in Mehrsichtigen Bauteilen: Rechnerische Erfassung und Bauphysikalische Anwendung; Universität-Gesamthochschule Essen: Essen, Germany, 1983. [Google Scholar]
- Bruno, R.; Bevilacqua, P. Heat and Mass Transfer for the U-Value Assessment of Opaque Walls in the Mediterranean Climate: Energy Implications. Energy 2022, 261, 124894. [Google Scholar] [CrossRef]
- Hens, H. Heat, Air and Moisture Transfer in Highly Insulated Building Envelopes (Hamtie); FaberMaunsell Limited: Norwich, UK, 2002. [Google Scholar]
- Woloszyn, M.; Rode, C. Tools for Performance Simulation of Heat, Air and Moisture Conditions of Whole Buildings. In Proceedings of the Building Simulation; Springer: Berlin/Heidelberg, Germany, 2008; Volume 1, pp. 5–24. [Google Scholar]
- Barclay, M.; Holcroft, N.; Shea, A.D. Methods to Determine Whole Building Hygrothermal Performance of Hemp–Lime Buildings. Build. Environ. 2014, 80, 204–212. [Google Scholar] [CrossRef]
- Cóstola, D. External Coupling of Building Energy Simulation and Building Element Heat, Air and Moisture Simulation. Ph.D. Thesis, Eindhoven University of Technology, Eindhoven, The Netherlands, 2011. [Google Scholar] [CrossRef]
- Rode, C.; Hens, H.; Janssen, H. IEA Annex 41 Whole Building Heat, Air, Moisture Response: Closing Seminar, Nordic Building Physics Conference; Technical University of Denmark: Lyngby, Denmark, 2008. [Google Scholar]
- ISO 12572; Hygrothermal performance of building materials and products—Determination of water vapour transmission properties—Cup method. International Organization for Standardization: Geneva, Switzerland, 2016.
- EN ISO 15148:2002+A1:2016; Hygrothermal Performance of Building Materials and Products—Determination of Water Absorption Coefficient by Partial Immersion—Amendment 1. ISO: Geneva, Switzerland, 2016.
- Kreiger, B.K.; Srubar, W.V. Moisture Buffering in Buildings: A Review of Experimental and Numerical Methods. Energy Build. 2019, 202, 109394. [Google Scholar] [CrossRef]
- Van Schijndel, A.W.M.; Goesten, S.; Schellen, H.L. Simulating the Complete HAMSTAD Benchmark Using a Single Model Implemented in Comsol. Energy Procedia 2017, 132, 429–434. [Google Scholar] [CrossRef]
- Dong, W.; Chen, Y.; Bao, Y.; Fang, A. A Validation of Dynamic Hygrothermal Model with Coupled Heat and Moisture Transfer in Porous Building Materials and Envelopes. J. Build. Eng. 2020, 32, 101484. [Google Scholar] [CrossRef]
- Wang, Z.; Timlin, D.; Fleisher, D.; Sun, W.; Beegum, S.; Li, S.; Chen, Y.; Reddy, V.R.; Tully, K.; Horton, R. Modeling Vapor Transfer in Soil Water and Heat Simulations: A Modularized, Partially-Coupled Approach. J. Hydrol. 2022, 608, 127541. [Google Scholar] [CrossRef]
- Belleudy, C.; Woloszyn, M.; Chhay, M.; Cosnier, M. A 2D Model for Coupled Heat, Air, and Moisture Transfer through Porous Media in Contact with Air Channels. Int. J. Heat Mass Transf. 2016, 95, 453–465. [Google Scholar] [CrossRef]
- Tariku, F.; Kumaran, K.; Fazio, P. Development and Benchmarking of a New Hygrothermal Model. In Proceedings of the 11th International Conference on Durability of Building Materials and Components, Istanbul, Turkey, 11–14 May 2008. [Google Scholar]
- Belarbi, Y.E.; Sawadogo, M.; Poullain, P.; Issaadi, N.; Hamami, A.E.A.; Bonnet, S.; Belarbi, R. Experimental Characterization of Raw Earth Properties for Modeling Their Hygrothermal Behavior. Buildings 2022, 12, 648. [Google Scholar] [CrossRef]
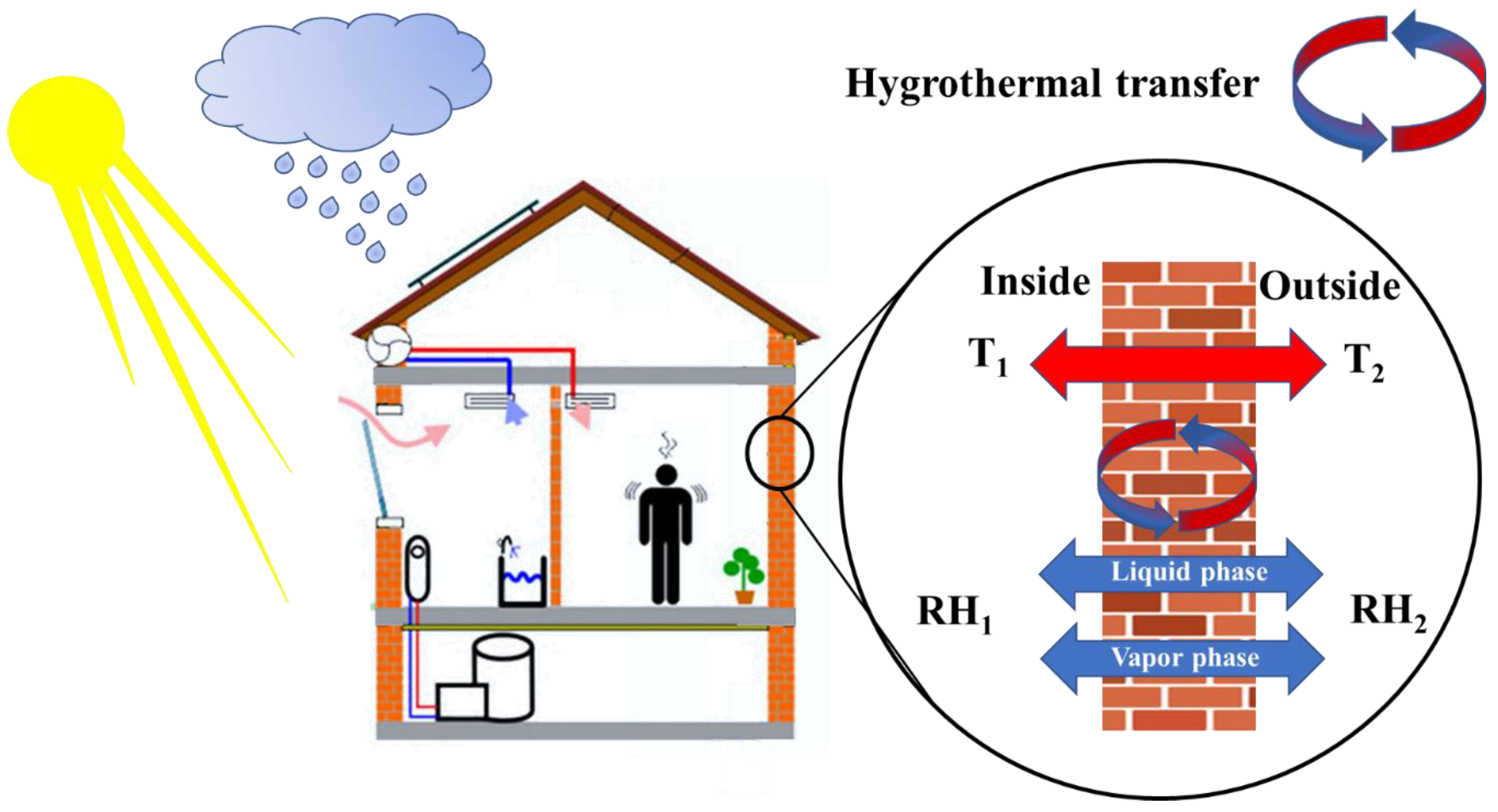


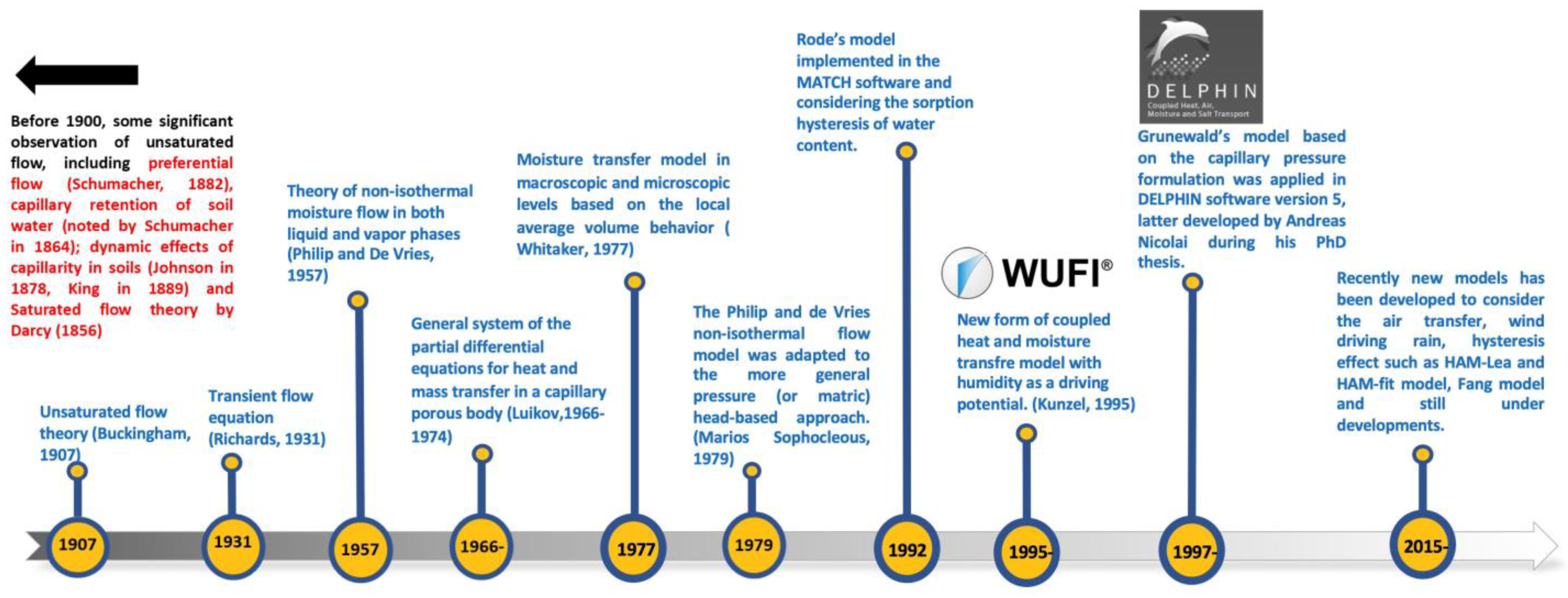
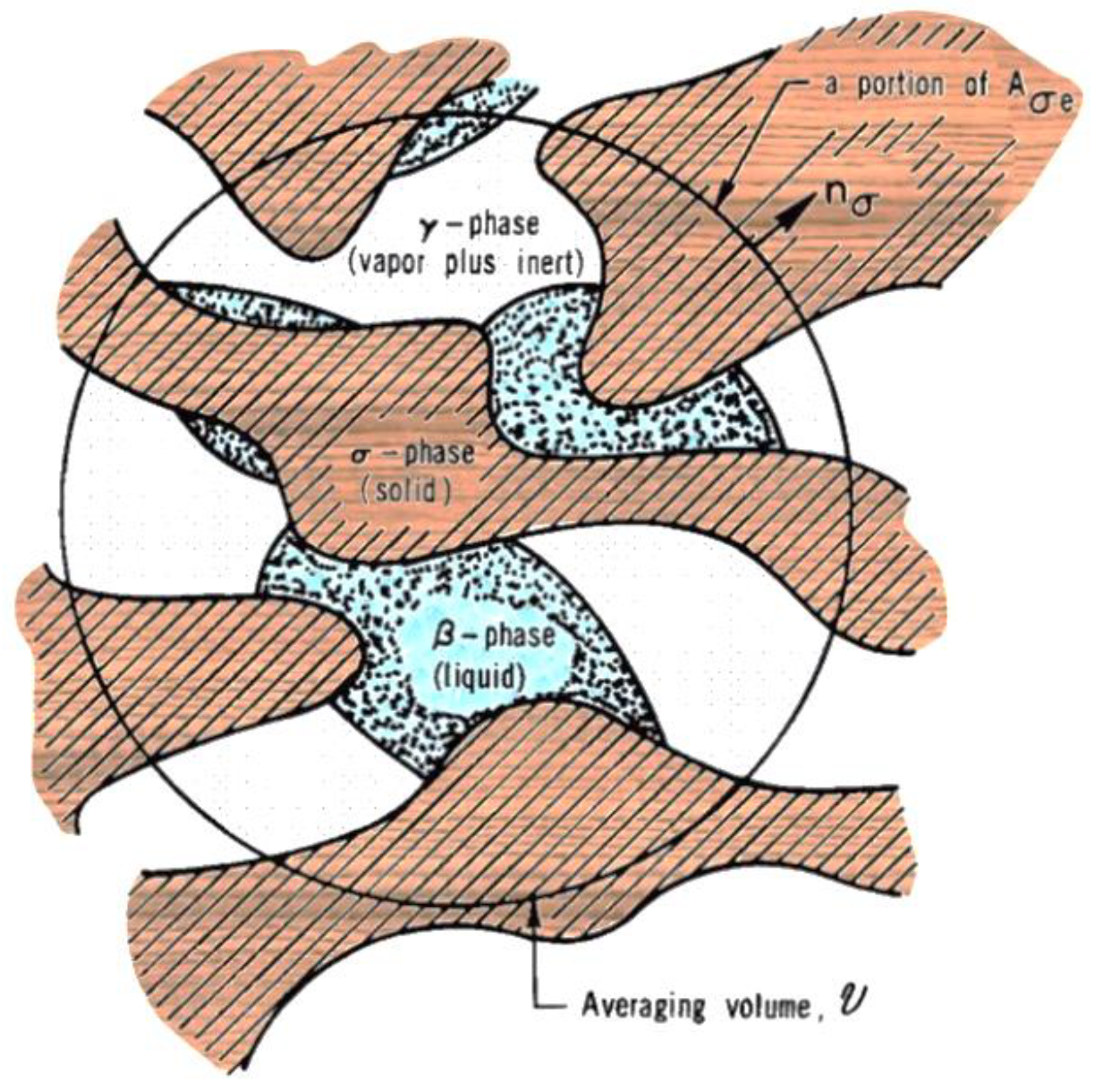
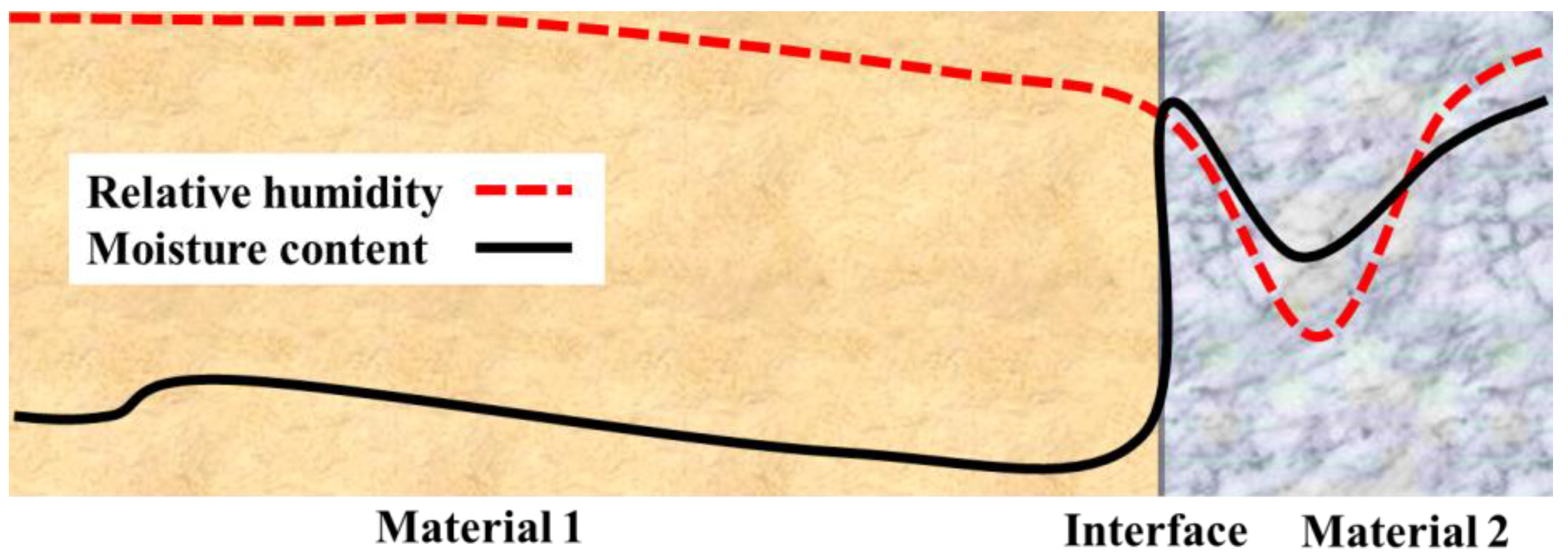



| Study | Year | Numerical | Analytical | Highlighted |
|---|---|---|---|---|
| R. Younsi et al. [66] | 2006 | * | - | Luikov model in three dimensions is applied to forecast temperature and moisture content profiles of wood under high heating rates. The numerical analysis utilized the FEMLAB software version 2 that operates within the MATLAB framework. The numerical results were in a good agreement with experimental results. |
| JEN Y. Liu and Shun Cheng [67] | 1991 | - | * | Luikov system of linear partial differential equations was solved analytically under the specified initial and boundary conditions. The method was tested by obtaining numerical results for spruce specimens and comparing them with published finite element solutions. |
| R.N. Pandey et al. [68] | 1999 | - | * | Luikov system of linear partial differential equations with various types of boundary conditions was analytically analyzed. The study demonstrates the influence of complex roots on dimensionless temperature, moisture content, and local drying rate. Benchmark results are provided for reference purposes. |
| Win-Jin Chang et al. [69] | 2000 | - | * | An analytical solution was obtained by applying Laplace transformation, which reduces the equations to ordinary differential equations. Next, a transformation function is introduced, which converts the equations into a fourth-order ordinary differential equation. Therefore, the temperature and moisture distributions in the transform domain can be determined easily. |
| Menghao Qin et al. [70] | 2015 | - | * | The paper introduces an analytical method for evaluating the combined hygrothermal transfer in porous building materials under diverse boundary conditions, including convection surface, adiabatic surface, and constant heat and moisture potential surface. The method considers the interaction between heat and moisture transport through the incorporation of a temperature gradient coefficient. |
| M.A. García-Alvarado [71] | 2014 | - | * | The solution for Luikov model is obtained using Laplace transform and complex inversion integral. Provided solution considers the temperature in the interface moisture content. The provided solution is compared with experimental data. |
| R. Pecenko et al. [72] | 2018 | - | * | The paper proposes a semi analytical approach based on Laplace transform to solve the time-periodic boundary conditions for simulating temperature and humidity oscillations in natural environments. The solution is obtained by solving some terms of the inverse Laplace transform using Gaussian quadrature. Convergence tests and validation of the proposed method are presented in the paper, along with its application to different building materials. |
| Renata S.G et al. [73] | 2013 | * | * | The Generalized Integral Transform Technique is used to obtain a hybrid solution for the Luikov equations, which takes into account pressure gradient effects during the drying of capillary–porous solids with spherical geometry. The accuracy of the numerical codes developed in the study is validated through comparisons with previous literature results. |
| S. Vargas-Gonzalez et al. [74] | 2021 | - | * | A modified Luikov equation was developed for simultaneous heat and mass transfer in solids based on interface thermodynamics. The equilibrium relation between air and (wet solid) can be approximated mathematically by two linear segments utilizing the thermodynamics theory. The implications of modified Luikov equations for thermodynamic and mathematical analysis of lumped equations were investigated. |
| K. Abahri et al. [75] | 2011 | - | * | A system of transient Luikov equations was solved analytically for Dirichlet boundary conditions. First, the Laplace transformation is introduced, followed by the potential function technique. By utilizing this method, the original mathematical problem can be reduced to a fourth-order ordinary differential equation, which is relatively simple to solve. The obtained solution was then utilized to evaluate the temporal moisture and temperature distributions within the materials. |
| Ferroukhi et al. [76] | 2016 | * | - | A novel approach was developed to predict the performance of buildings by utilizing two simulation tools, COMSOL Multiphysics and TRNSYS. The Luikov model is applied in the COMSOL software (version 4.3) to simulate the heat, air, and moisture transfer in multilayer porous walls, while the BES (Building Energy Simulation) model is used to simulate the hygrothermal behavior of the building. |
| B. Remki et al. [77] | 2012 | * | - | Finite element method was implemented by COMSOL Multiphysics software version 4.3 to solve the Luikov equation. The drying processes with high temperature and conventional boundary conditions as the normal climate conditions were regarded as two major cases during the analysis. |
| Abdelghani Koukouch et al. [78] | 2020 | - | * | Analytical solution for two different models were proposed for studying the moisture content and temperature distribution inside a biomass during forced convection drying. The thin-layer model assumes the biomass to be a uniform parallelepiped material, while the Luikov model considers it as a porous medium. Hermite’s zero-order approximation was used to obtain analytical solutions for the Luikov model equations. |
| Menghao Qin et al. [79] | 2006 | - | * | A new analytical approach has been suggested as a solution for Luikov equation using the Transfer Function Method. The coupled partial differential equations and their boundary conditions are first subjected to Laplace transformation. This approach enables the calculation of the transient distribution of temperature and moisture content within the building material. |
| Name of Model | Year | Moisture Transfer Driving Potential | Moisture Phase |
|---|---|---|---|
| Richard’s equation | 1931 | Capillary pressure | Only liquid phase |
| Philip and De Vries model | 1957 | Water content | Liquid + vapor phases |
| Luikov model | 1965–1974 | Water content | Liquid + vapor phases |
| Sophocleous and Milly’s model | 1977, 1982 | Capillary pressure | Liquid + vapor phases |
| Whitaker’s model | 1977 | Water content | Liquid + vapor + solid phases |
| Künzel model | 1995 | Relative humidity | Liquid + vapor phases |
| Model of Rode | 1992 | Vapor pressure–capillary pressure | Liquid + vapor phases |
| Model of Grunewald | 1997 | Capillary pressure | Liquid + vapor phases |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jalili, H.; Ouahbi, T.; Eid, J.; Taibi, S.; Hamrouni, I. Exploring Historical Perspectives in Building Hygrothermal Models: A Comprehensive Review. Buildings 2024, 14, 1786. https://doi.org/10.3390/buildings14061786
Jalili H, Ouahbi T, Eid J, Taibi S, Hamrouni I. Exploring Historical Perspectives in Building Hygrothermal Models: A Comprehensive Review. Buildings. 2024; 14(6):1786. https://doi.org/10.3390/buildings14061786
Chicago/Turabian StyleJalili, Habib, Tariq Ouahbi, Joanna Eid, Said Taibi, and Ichrak Hamrouni. 2024. "Exploring Historical Perspectives in Building Hygrothermal Models: A Comprehensive Review" Buildings 14, no. 6: 1786. https://doi.org/10.3390/buildings14061786
APA StyleJalili, H., Ouahbi, T., Eid, J., Taibi, S., & Hamrouni, I. (2024). Exploring Historical Perspectives in Building Hygrothermal Models: A Comprehensive Review. Buildings, 14(6), 1786. https://doi.org/10.3390/buildings14061786






