Numerical Investigation of the Seismic-Induced Rocking Behavior of Unbonded Post-Tensioned Bridge Piers
Abstract
:1. Introduction
2. Development of Numerical Models
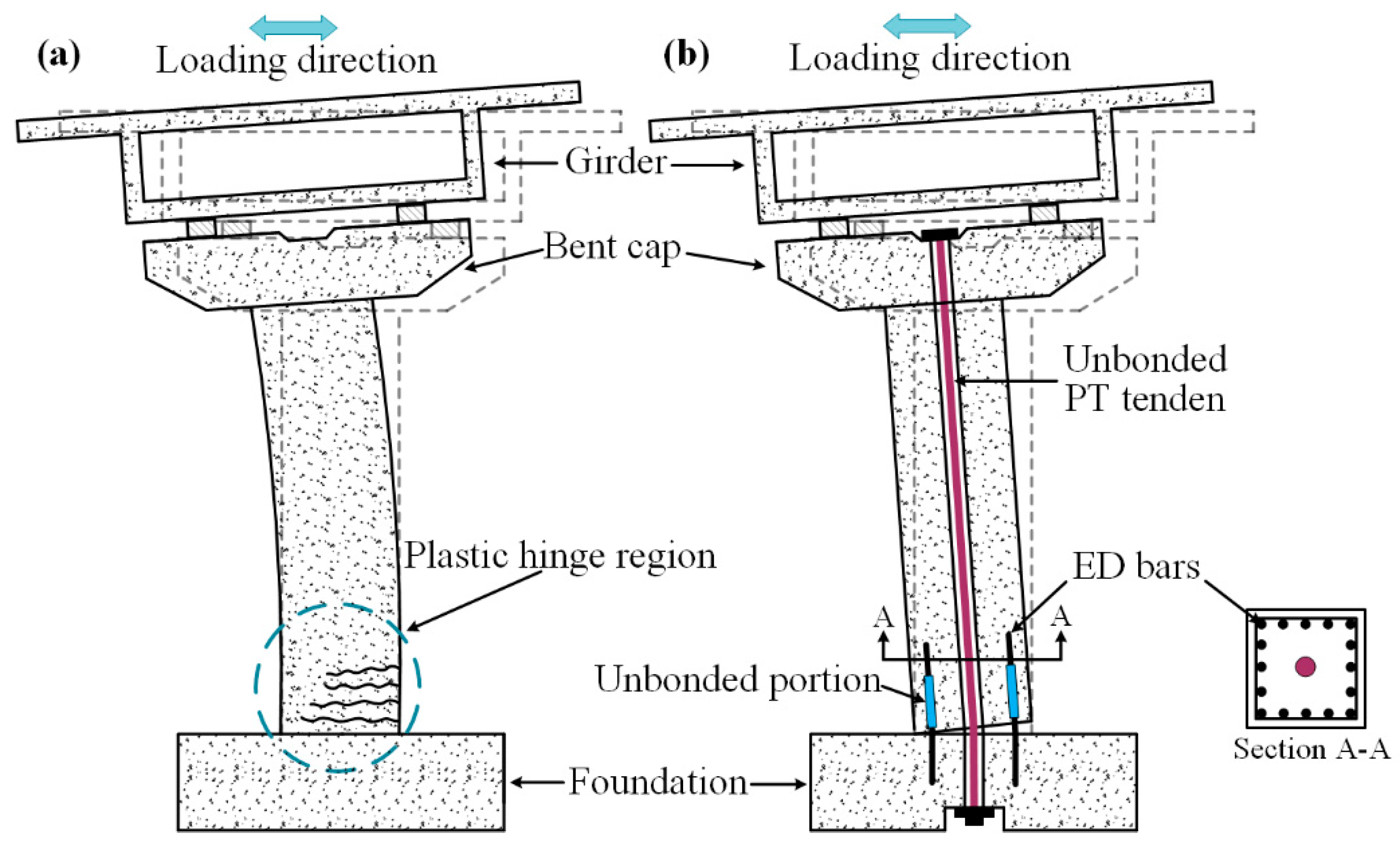
2.1. Description of Laboratory Test Specimens
2.1.1. Quasi-Static Test Specimen
2.1.2. Shaking Table Test Specimen
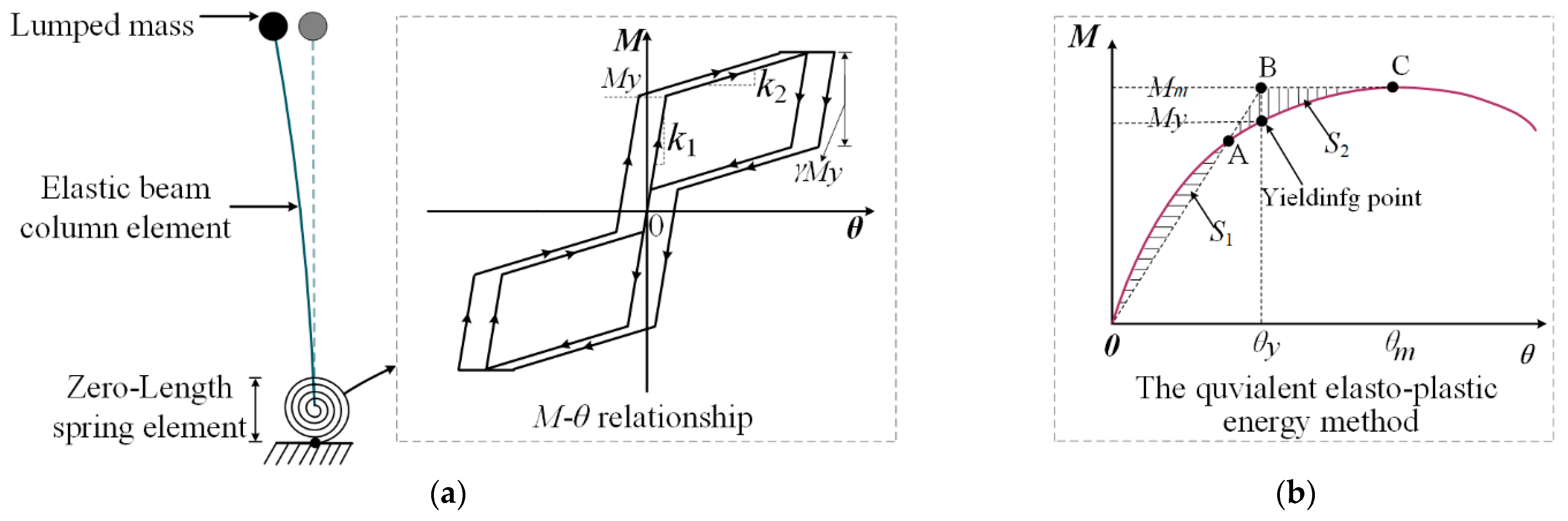
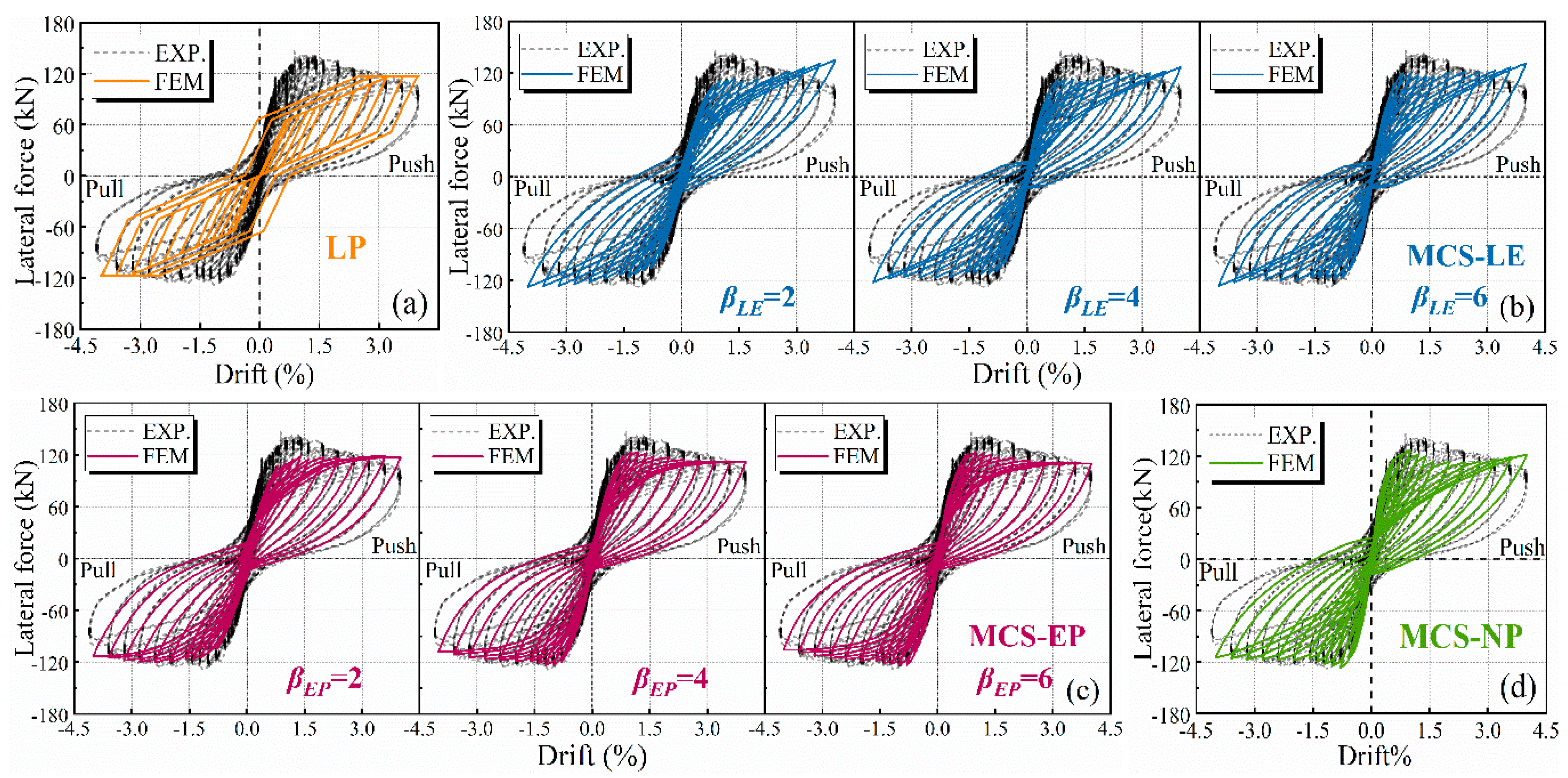
2.2. Lumped Plasticity (LP) Model
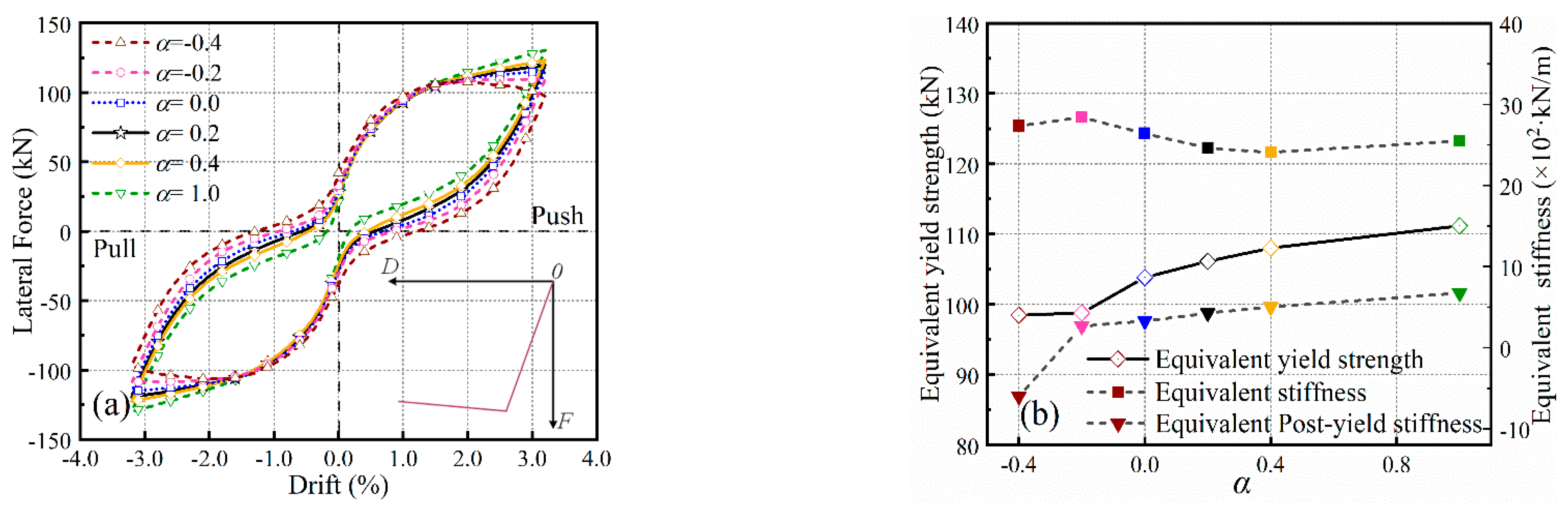
2.2.1. Modeling the Monotonic Behavior
2.2.2. Modeling the Cyclic Behavior
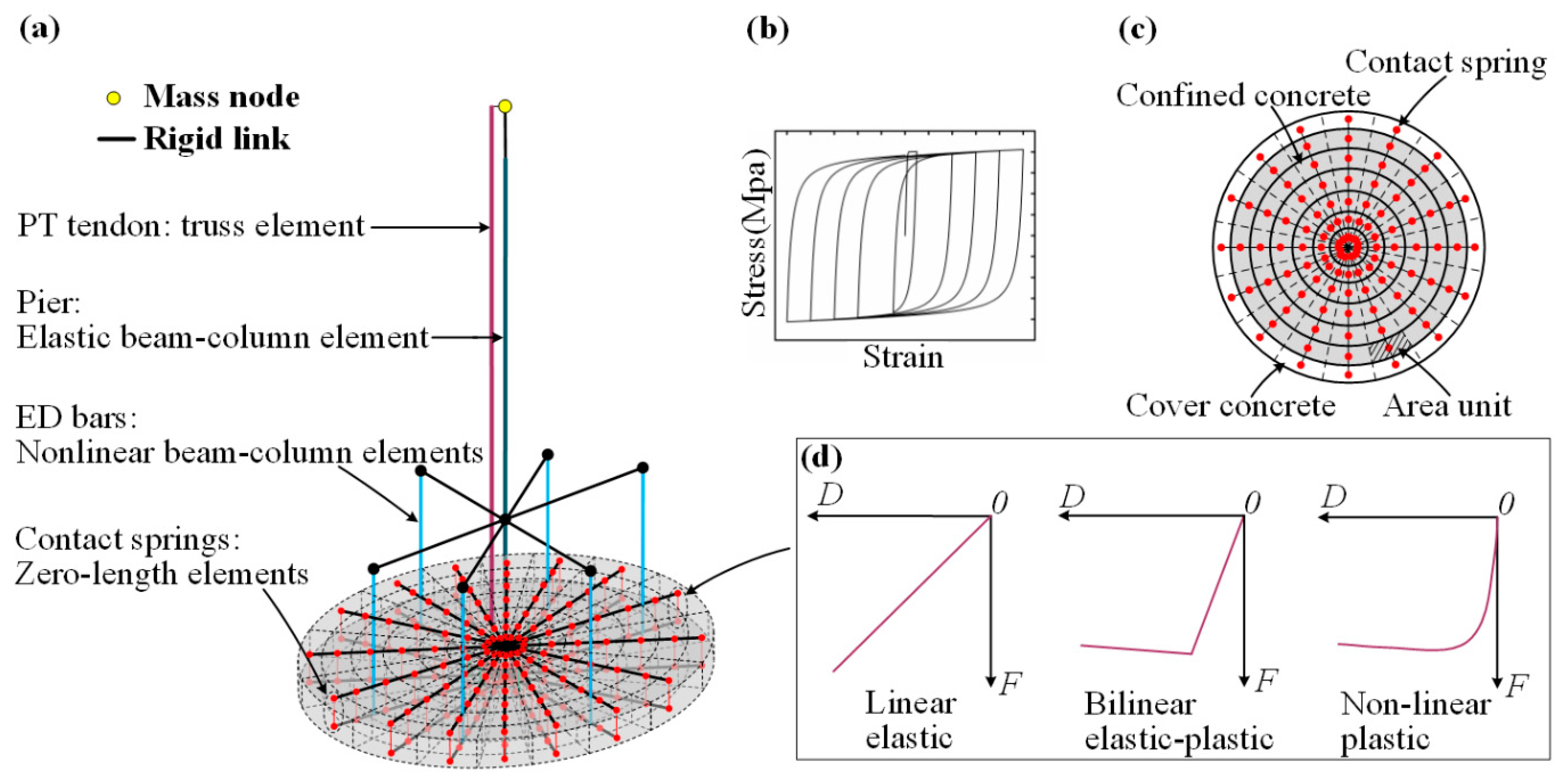
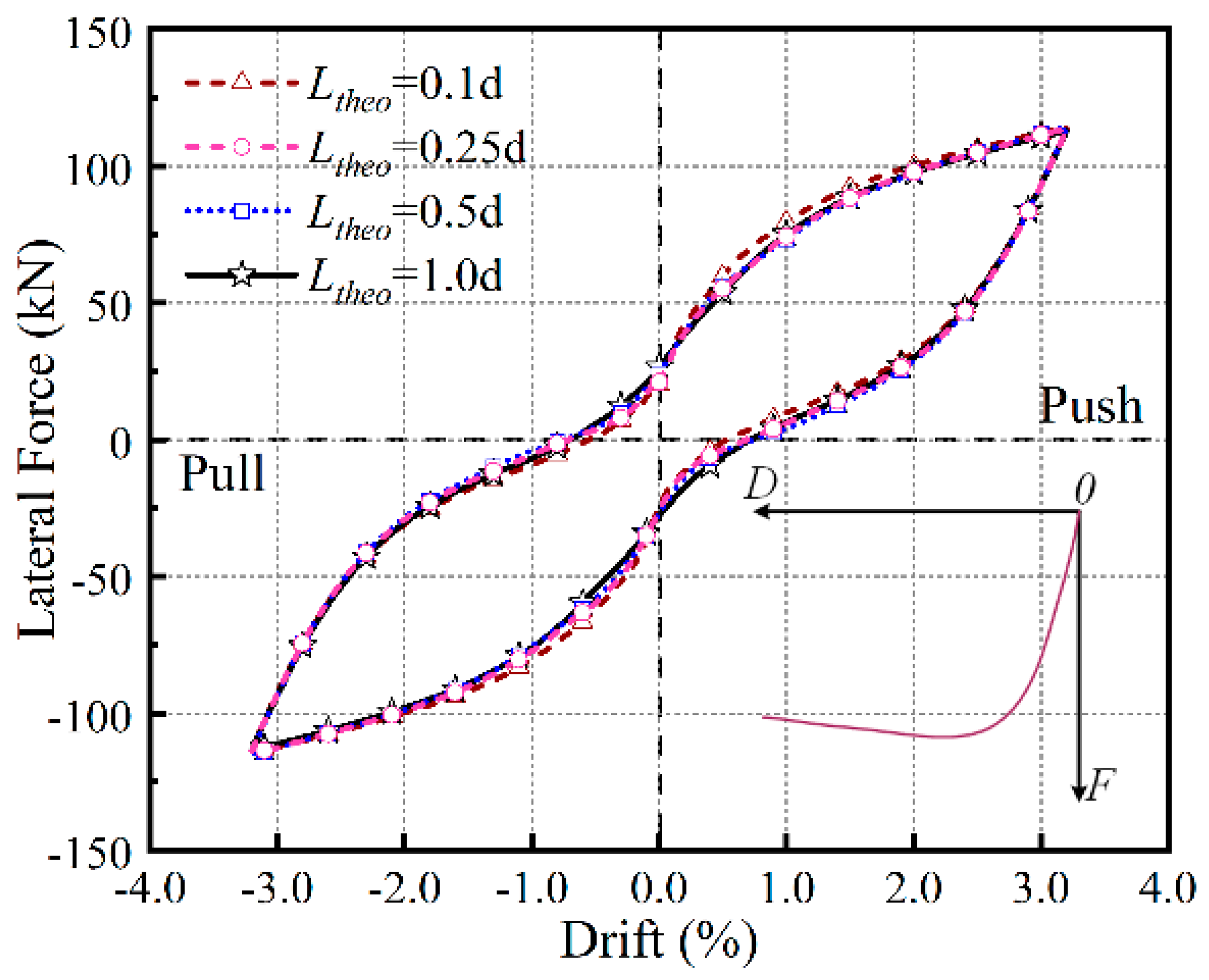
2.3. Multi-Contact Spring (MCS) Model
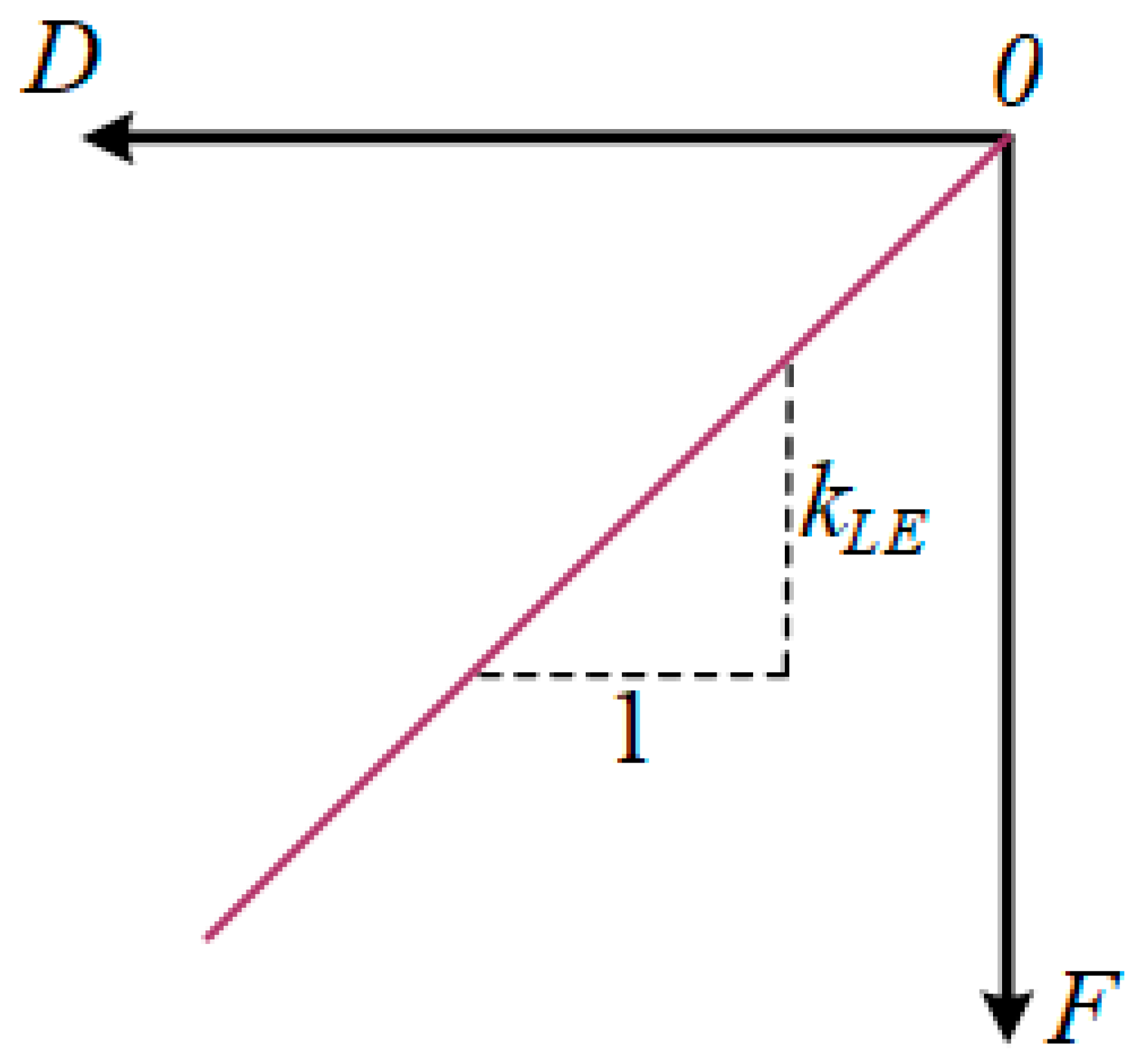
2.3.1. Linear Elastic (LE) Contact Spring
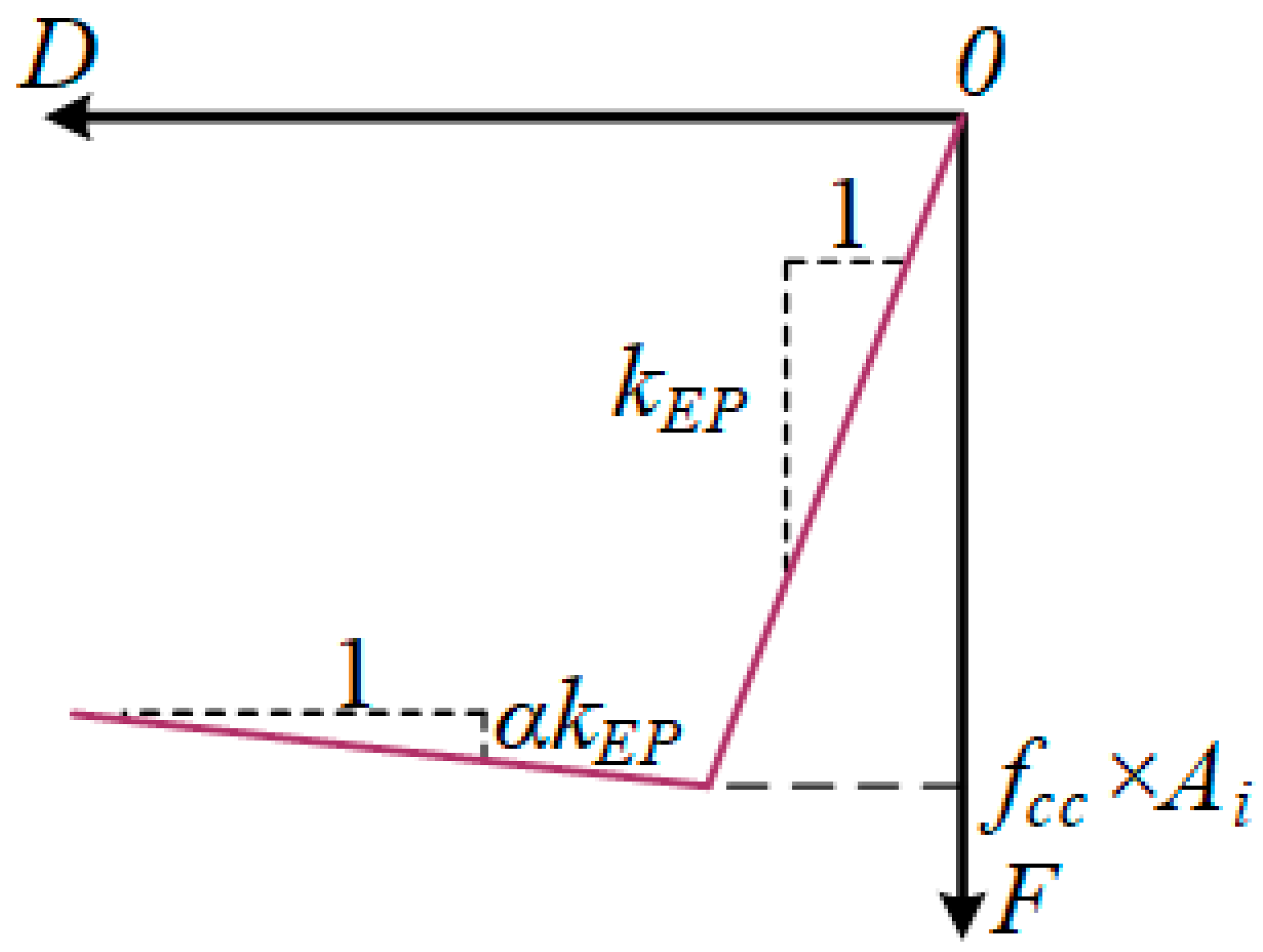
2.3.2. Bilinear Elastic–Plastic Contact (EP) Spring
2.3.3. Nonlinear Plastic (NP) Contact Spring
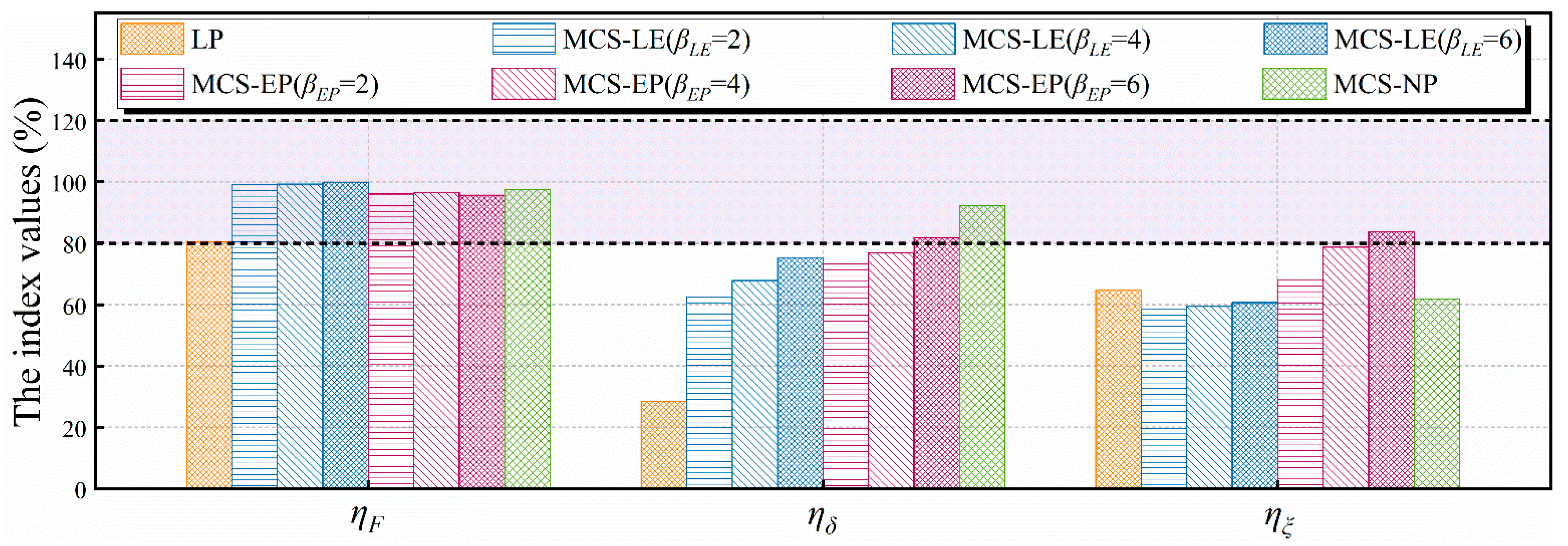
3. Comprehensive Performance Assessment of the MCS Models
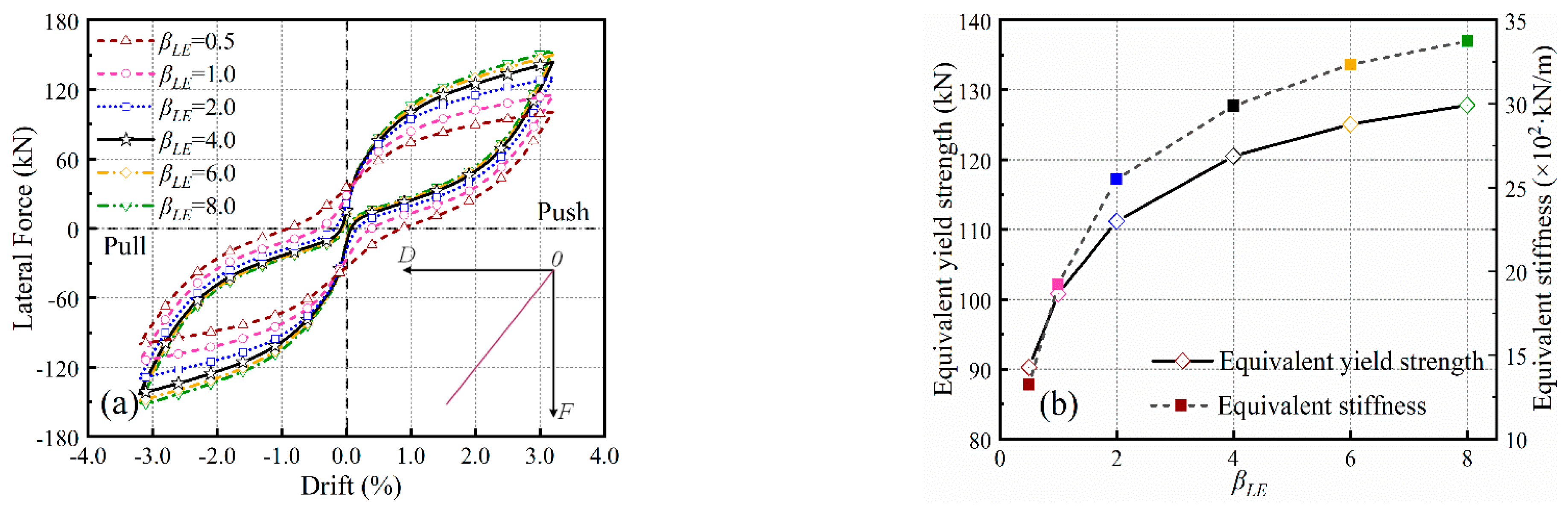
3.1. MCS-LE Model
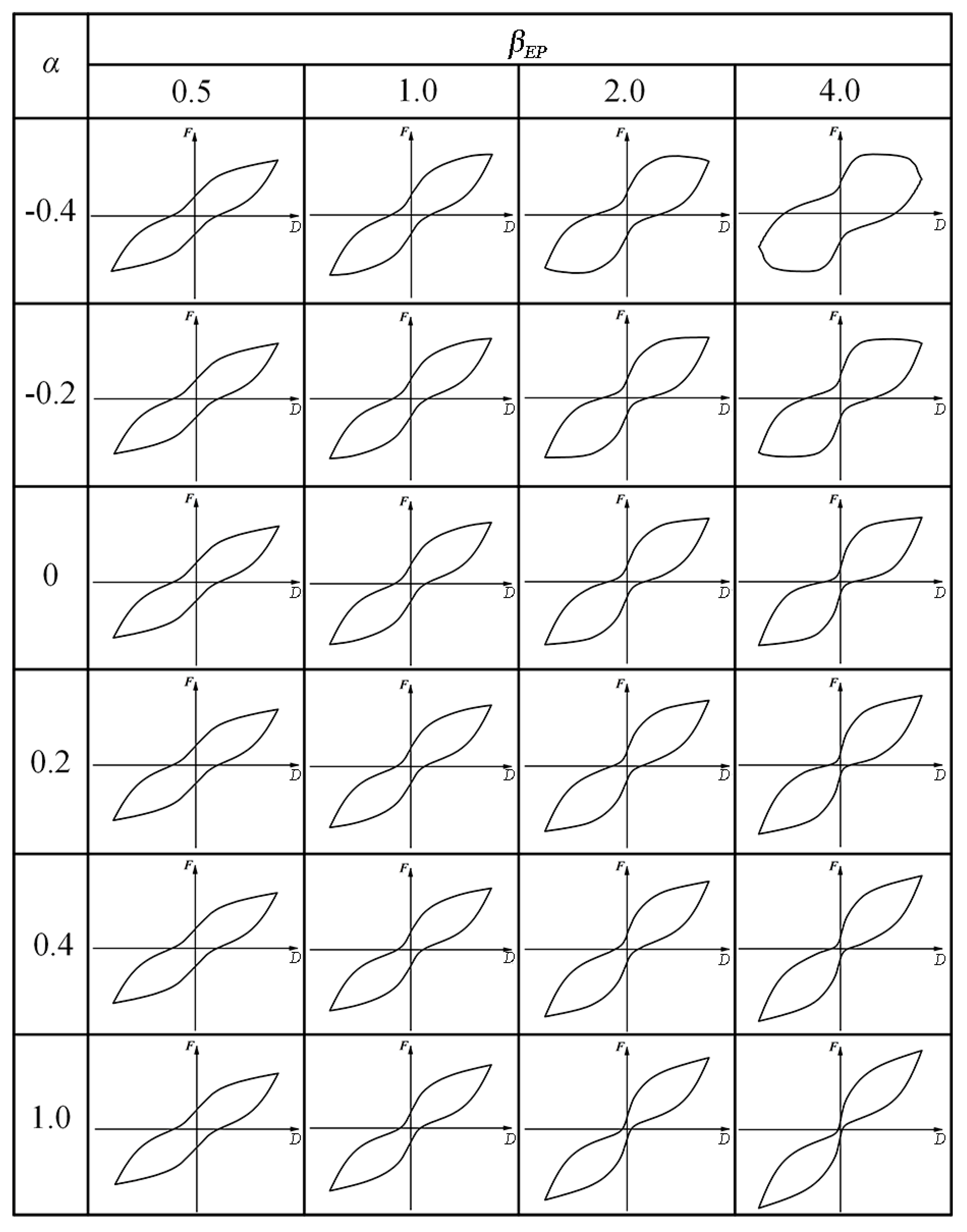
3.2. MCS-EP Model
3.3. MCS-NP Model
4. Validation of the Cyclic Responses
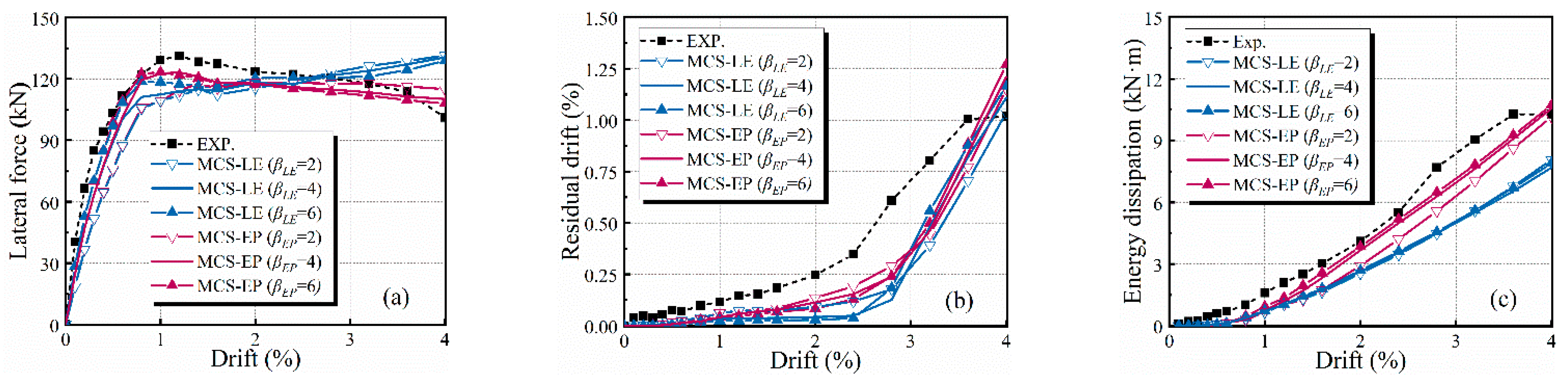
4.1. Force–Drift Relationship
4.2. Residual Drift and Energy Dissipation (ED)
4.3. Insight into the Modified Stiffness Factor
4.4. Validation Evaluation
5. Comparison with Shaking Table Testing Responses
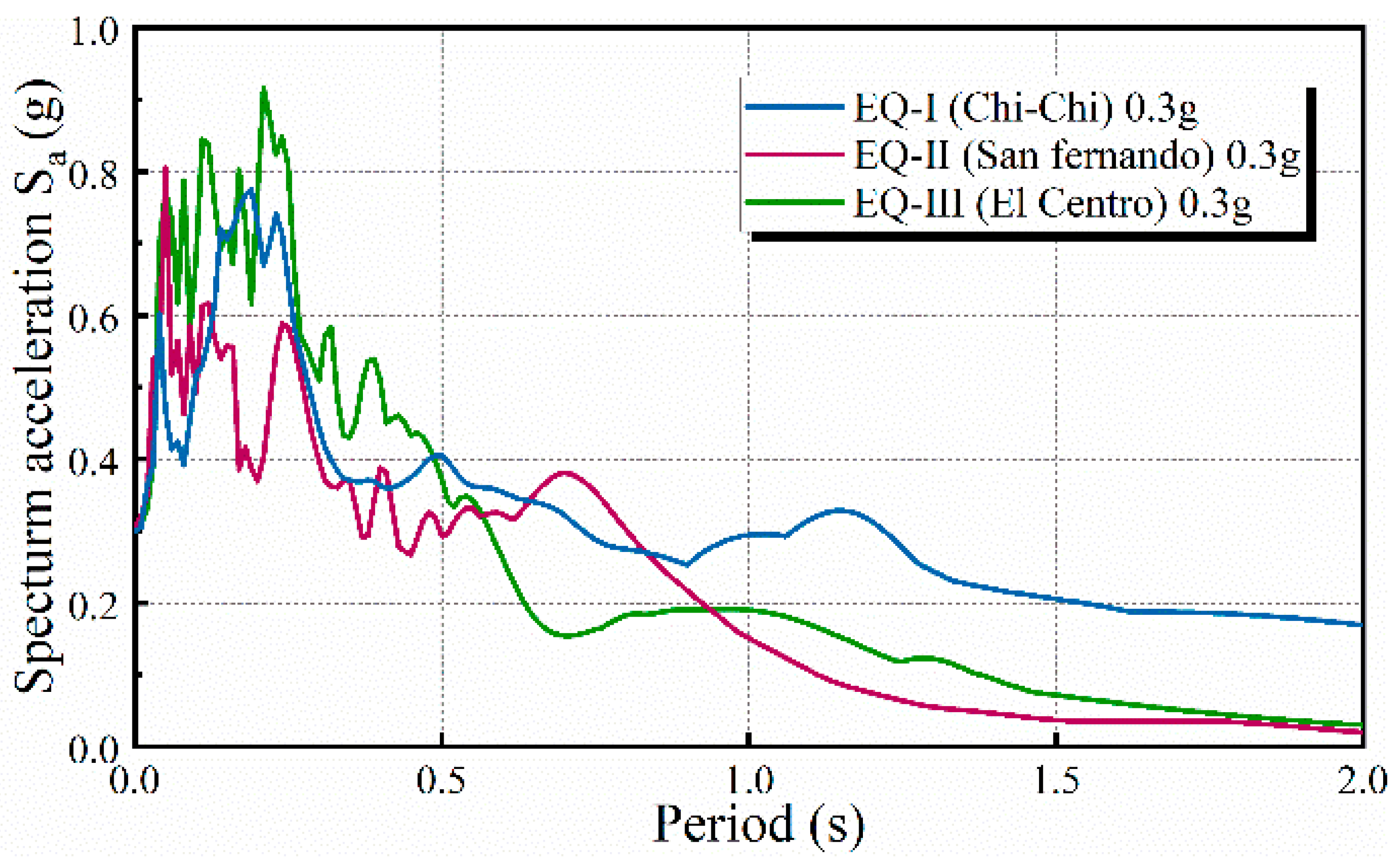
5.1. Input Ground Motions
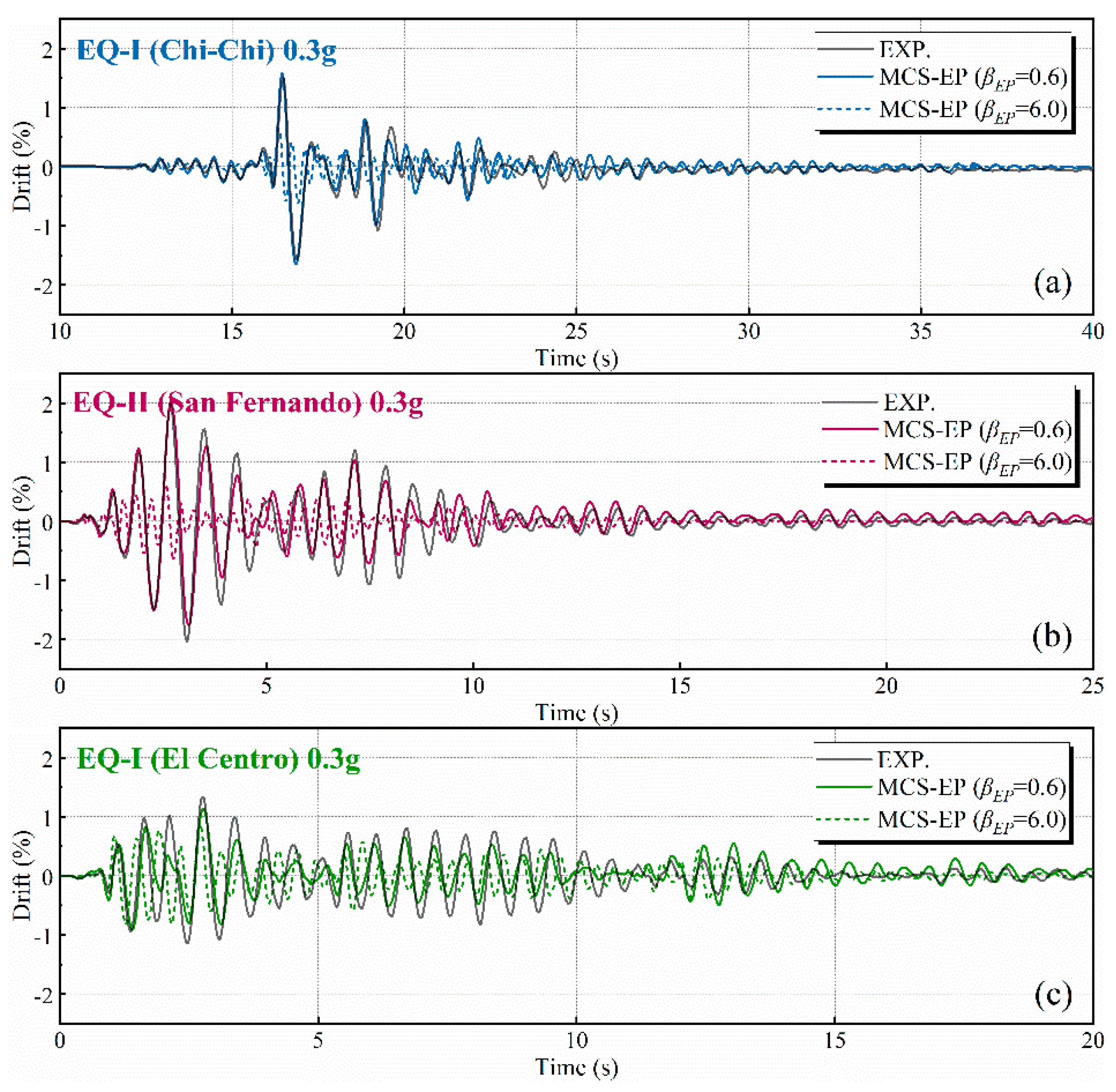
5.2. Nonlinear History Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Xia, X.; Zhang, X.; Shi, J.; Tang, J. Seismic isolation of railway bridges using a self-centering pier. Smart Struct. Syst. 2021, 27, 447–455. [Google Scholar]
- Xu, W.; Ma, B.; Duan, X.; Li, J. Experimental investigation of seismic behavior of UHPC connection between precast columns and footings in bridges. Eng. Struct. 2021, 2390, 112344. [Google Scholar] [CrossRef]
- Littleton, P.; Mallela, J. Iowa Demonstration Project: Accelerated Bridge Construction on US 6 Over Keg Creek; Department of Transportation, Faderal Highway Administration: Washington, DC, USA, 2013. [Google Scholar]
- Kagioglou, P.; Katakalos, K.; Mitoulis, S. Resilient connection for accelerated bridge constructions. Structures 2023, 33, 3025–3039. [Google Scholar] [CrossRef]
- Cao, L.; Li, C. A high performance hybrid passive base-isolated system. Struct. Control Health Monit. 2023, 29, e2887.1–e2887.26. [Google Scholar] [CrossRef]
- Li, C.; Chang, K.; Cao, L.; Hang, Y. Performance of a nonlinear hybrid base isolation system under the ground motions. Soil Dyn. Earthq. Eng. 2021, 143, 106589.1–106589.15. [Google Scholar] [CrossRef]
- Guo, A.; Gao, H. Seismic Behavior of Posttensioned Concrete Bridge Piers with External Viscoelastic Dampers. Shock Vib. 2016, 2016, 1823015.1–1823015.12. [Google Scholar] [CrossRef]
- Chen, X.; Xia, X.; Zhang, X.; Gao, J. Seismic performance and design of bridge piers with rocking isolation. Struct. Eng. Mech. 2020, 73, 447–454. [Google Scholar]
- Li, Y.; Li, J.J.; Shen, Y. Quasi-static and nonlinear time-history analyses of post-tensioned bridge rocking piers with internal ED bars. Structures 2021, 32, 1455–1468. [Google Scholar] [CrossRef]
- Wakjira, T.; Rahmzadeh, A.; Alam, M.; Tremblay, R. Explainable machine learning based efficient prediction tool for lateral cyclic response of post-tensioned base rocking steel bridge piers. Structures 2022, 44, 947–964. [Google Scholar] [CrossRef]
- Shi, X.; Song, L.; Guo, T.; Pan, Z. Seismic design of self-centering bridge piers considering soil-structure interaction. Structures 2022, 43, 1819–1833. [Google Scholar] [CrossRef]
- Priestley, M.J.N.; Sritharan, S.; Conley, J.R.; Pampanin, S. Preliminary Results and Conclusions From the PRESSS Five-Story Precast Concrete Test Building. PCI J. 1999, 44, 42–67. [Google Scholar] [CrossRef]
- Kwan, W. Unbonded posttensioned concrete bridge piers, I: Monotonic and cyclic analyses. J. Bridge Eng. 2003, 8, 92–101. [Google Scholar] [CrossRef]
- Roh, H.; Ou, Y.; Kim, J.; Kim, W. Effect of yielding level and post-yielding stiffness ratio of ED bars on seismic performance of PT rocking bridge piers. Eng. Struct. 2014, 81, 454–463. [Google Scholar] [CrossRef]
- Shen, Y.; Freddi, F.; Li, Y.; Li, J. Parametric experimental investigation of unbonded post-tensioned reinforced concrete bridge piers under cyclic loading. Earthq. Eng. Struct. Dyn. 2022, 51, 3479–3504. [Google Scholar] [CrossRef]
- Palermo, A.; Pampanin, S.; Marriott, D. Design, modeling, and experimental response of seismic resistant bridge piers with posttensioned dissipating connections. J. Struct. Eng. 2007, 133, 1648–1661. [Google Scholar] [CrossRef]
- Xu, F.; Zhang, X.; Xia, X.; Shi, J. Study on seismic behavior of a self-centering railway bridge pier with sacrificial components. Structures 2022, 35, 958–967. [Google Scholar] [CrossRef]
- Zhao, J.; Wu, B.; Ou, J. A novel type of angle steel buckling-restrained brace: Cyclic behavior and failure mechanism. Earthq. Eng. Struct. Dyn. 2011, 40, 1083–1102. [Google Scholar] [CrossRef]
- Roh, H.; Reinhorn, A. Hysteretic behavior of precast segmental bridge piers with superelastic shape memory alloy bars. Eng. Struct. 2010, 32, 3394–3403. [Google Scholar] [CrossRef]
- Govahi; Ehsan; Salkhordeh, M.; Mirtaheri, M. Cyclic performance of different mitigation strategies proposed for segmental precast bridge piers. Structures 2022, 36, 344–357. [Google Scholar] [CrossRef]
- Salkhordeh; Govahi, E.; Mirtaheri, M. Seismic fragility evaluation of various mitigation strategies proposed for bridge piers. Structures 2021, 33, 1892–1905. [Google Scholar] [CrossRef]
- Shen, Y.; Freddi, F.; Li, J. Experimental and numerical investigations of the seismic behavior of socket and hybrid connections for PCFT bridge columns. Eng. Struct. 2022, 253, 113833. [Google Scholar] [CrossRef]
- Marriott, D.; Pampanin, S.; Palermo, A. Quasi-static and pseudo-dynamic testing of unbonded post-tensioned rocking bridge piers with external replaceable dissipaters. Earthq. Eng. Struct. Dyn. 2009, 38, 331–354. [Google Scholar] [CrossRef]
- Marriott, D.; Pampanin, S.; Palermo, A. Biaxial testing of unbonded post-tensioned rocking bridge piers with external replacable dissipaters. Earthq. Eng. Struct. Dyn. 2011, 40, 1723–1741. [Google Scholar] [CrossRef]
- Jeong, H.; Mahi, S. Shaking Table Tests and Numerical Investigation of Self-Centering Reinforced Concrete Bridge Columns; PEER Report; Pacific Earthquake Engineering Research Center, University of California: Berkeley, CA, USA, 2008. [Google Scholar]
- Li, C.; Bi, K.; Hao, H. Seismic performances of precast segmental column under bidirectional earthquake motions: Shake table test and numerical evaluation. Eng. Struct. 2019, 187, 314–328. [Google Scholar] [CrossRef]
- Salkhordeh, M.; Mirtaheri, M.; Rabiee, N.; Govahi, E.; Soroushian, S. A Rapid Machine Learning-Based Damage Detection Technique for Detecting Local Damages in Reinforced Concrete Bridges. J. Earthq. Eng. 2023, 27, 3705–4738. [Google Scholar] [CrossRef]
- Dawood, H.; ElGawady, M.; Hewes, J. Behavior of Segmental Precast Posttensioned Bridge Piers under Lateral Loads. J. Bridge Eng. 2012, 17, 735–746. [Google Scholar] [CrossRef]
- ElGawady, M.; Dawood, H. Analysis of segmental piers consisted of concrete filled FRP tubes. Eng. Struct. 2012, 38, 142–152. [Google Scholar] [CrossRef]
- Hung, H.; Sung, Y.; Lin, K.; Jiang, C.; Chang, K. Experimental study and numerical simulation of precast segmental bridge columns with semi-rigid connections. Eng. Struct. 2017, 136, 12–25. [Google Scholar] [CrossRef]
- Ou, Y.; Chiewanichakorn, M.; Aref, A.; Lee, G. Seismic performance of segmental precast unbonded posttensioned concrete bridge columns. J. Struct. Eng. 2007, 133, 1636–1647. [Google Scholar] [CrossRef]
- Palermo, A.; Pampanin, S. Enhanced Seismic Performance of Hybrid Bridge Systems: Comparison with Traditional Monolithic Solutions. J. Earthq. Eng. 2008, 12, 1267–1295. [Google Scholar] [CrossRef]
- Zhao, L.; Bi, K.; Hao, H.; Li, X. Numerical studies on the seismic responses of bridge structures with precast segmental columns. Eng. Struct. 2017, 151, 568–583. [Google Scholar] [CrossRef]
- Mitra, N.; Lowes, L. Evaluation, calibration, and verification of a reinforced concrete beam–column joint model. J. Struct. Eng. 2007, 133, 105–120. [Google Scholar] [CrossRef]
- Guerrini, G.; Restrepo, J.; Vervelidis, A.; Massari, M. Self-Centering Precast Concrete Dual-Steel-Shell Columns for Accelerated Bridge Construction: Seismic Performance, Analysis, and Design; Report No. PEER 2015, 13; Pacific Earthquake Engineering Research Center, University of California: Berkeley, CA, USA, 2015. [Google Scholar]
- Bing, S.; Ming, G.; Zhi, S.; Min, D. Seismic response analysis of the rocking self-centering bridge piers under the near-fault ground motions. Eng. Mech. 2017, 33, 87–97. [Google Scholar]
- Fenves, G.; Mazzoni, S.; McKenna, F.; Scott, M. Open System for Earthquake Engineering Simulation OpenSees; University of California, Pacific Earthquake Engineering Research Center: Berkeley, CA, USA, 2004. [Google Scholar]
- Pampanin, S. Emerging Solutions for High Seismic Performance of Precast/Prestressed Concrete Buildings. J. Adv. Concr. Technol. 2005, 3, 207–223. [Google Scholar] [CrossRef]
- Shen, Y.; Freddi, F.; Li, Y.; Li, J. Enhanced Strategies for Seismic Resilient Posttensioned Reinforced Concrete Bridge Piers: Experimental Tests and Numerical Simulations. J. Struct. Eng. 2023, 149, 04022259. [Google Scholar] [CrossRef]
- Shen, Y. shaking Table Tests and Seismic Rocking Analysis of Posttensioning Self-Centering Bridge Piers. Ph.D. Dissertation, Tongji University, Shanghai, China, 2023. [Google Scholar]
- JTG/T 2231-01-2020; Specifications for Seismic Design of Highway Bridges. China Communications Press: Beijing, China, 2020.
- JTG B02-2013; MOT. Specification of Seismic Design for Highway Engineering. China Communications Press: Beijing, China, 2013.
- Pampanin, S.; Priestley, M.J.N.; Sritharan, S. Analytical modelling of the seismic behaviour of precast concrete frames designed with ductile connections. J. Earthq. Eng. 2001, 5, 329–367. [Google Scholar] [CrossRef]
- Priestley, M.; Seible, F.; Calvi, G.M. Seismic Design and Retrofit of Bridges; John Wiley & Sons, Inc.: New York, NY, USA, 1996. [Google Scholar]
- European Committee for Standardization. Design of Concrete Structures: Part 1-1: General Rules and Rules for Buildings; European Committee for Standardization: Brussels, Belgium, 2004. [Google Scholar]
- Lu, X.; Wei, K.; Xu, L. Lifetime seismic resilience assessment of a sea-crossing cable-stayed bridge exposed to long-term scour and corrosion. Ocean Eng. 2024, 295, 116990. [Google Scholar] [CrossRef]
- Fu, P.; Li, X.; Xu, L.; Wang, M. An advanced assessment framework for seismic resilience of railway continuous girder bridge with multiple spans considering 72h golden rescue requirements. Soil Dyn. Earthq. Eng. 2024, 177, 108370. [Google Scholar] [CrossRef]

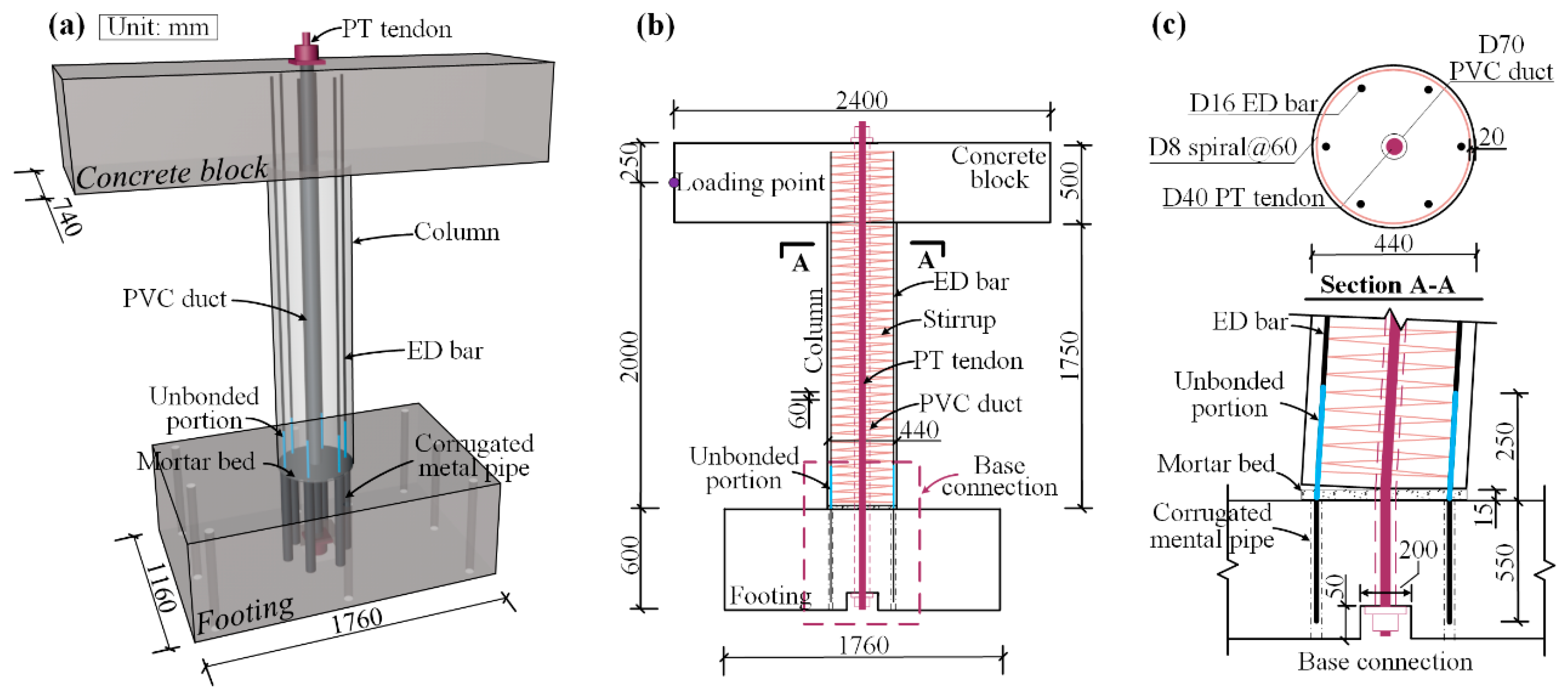








| Design Parameter | Monolithic Prototype | Specimen I | Specimen II |
|---|---|---|---|
| Pier diameter (m) | 2.1 | 0.44 | 0.44 |
| Pier clear height (m) | 8.3 | 1.75 | 1.35 |
| Pier effective height (m) | 9.5 | 2.0 | 2.04 |
| Axial gravity force (kN) [ratio (%)] | 7280 [7.5] | 323 [7.5] | 322.4 [7.5] |
| initial PT force | — | 749 [17.5] | 749 [17.5] |
| Longitudinal reinforcing steel [ratio (%)] | 36-D14 [1.32] | 6-D16 [0.79] | 6-D16 [0.79] |
| Transverse reinforcing steel [ratio (%)] | D18@80 [0.64] | D8@60 [0.84] | D8@60 [0.84] |
| PT steel [ratio (%)] | — | 1-D40 [0.82] | 1-D40 [0.82] |
| Longitudinal reinforcing + PT steel ratio | 1.32 | 1.61 | 1.61 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bao, Z.; Xu, W.; Gao, H.; Zhong, X.; Li, J. Numerical Investigation of the Seismic-Induced Rocking Behavior of Unbonded Post-Tensioned Bridge Piers. Buildings 2024, 14, 1833. https://doi.org/10.3390/buildings14061833
Bao Z, Xu W, Gao H, Zhong X, Li J. Numerical Investigation of the Seismic-Induced Rocking Behavior of Unbonded Post-Tensioned Bridge Piers. Buildings. 2024; 14(6):1833. https://doi.org/10.3390/buildings14061833
Chicago/Turabian StyleBao, Zehua, Wenjing Xu, Haoyuan Gao, Xueqi Zhong, and Jianzhong Li. 2024. "Numerical Investigation of the Seismic-Induced Rocking Behavior of Unbonded Post-Tensioned Bridge Piers" Buildings 14, no. 6: 1833. https://doi.org/10.3390/buildings14061833





