Effect of Soil–Bridge Interactions on Seismic Response of a Cross-Fault Bridge: A Shaking Table Test Study
Abstract
:1. Introduction
1.1. Design of Shaking Table Test
- This study attempts to simulate different ground motions on both sides of the fault with only one shaking table. The soil box is divided into two parts; one half is resting on the shaking table and the other half is fixed on the ground, connected with a steel strand in the middle. The displacement difference on both sides of the fault is used as the input of the shaking table to simulate the impact of the relative displacement and permanent displacement of the fault on the seismic response of the bridge structure, i.e., one-side input method.
- During the tests, displacement control shaking table input is adopted to ensure that the relative permanent displacement on both sides of the fault can be reproduced.
- In the tests, polymethyl methacrylate is used as the model material to improve the design stiffness of the test model.
- This test refers to the experimental similarity design method proposed by Xu, using the predominant period, time, and displacement of the site as the basic similarity conditions to maintain the main characteristics of the original site in the model soil, which can ensure partial similarity between the soil–structure system model and the prototype [26].
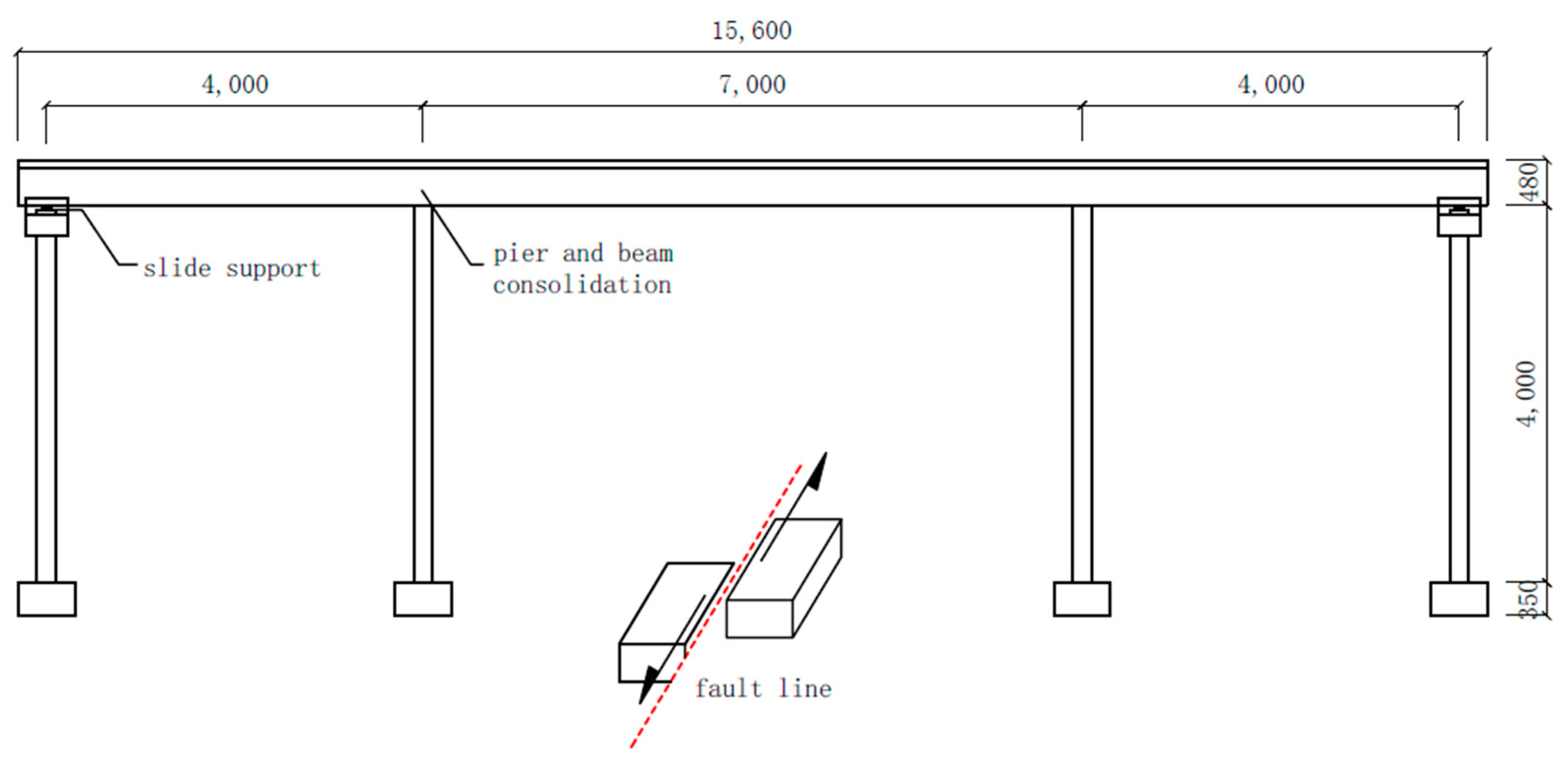
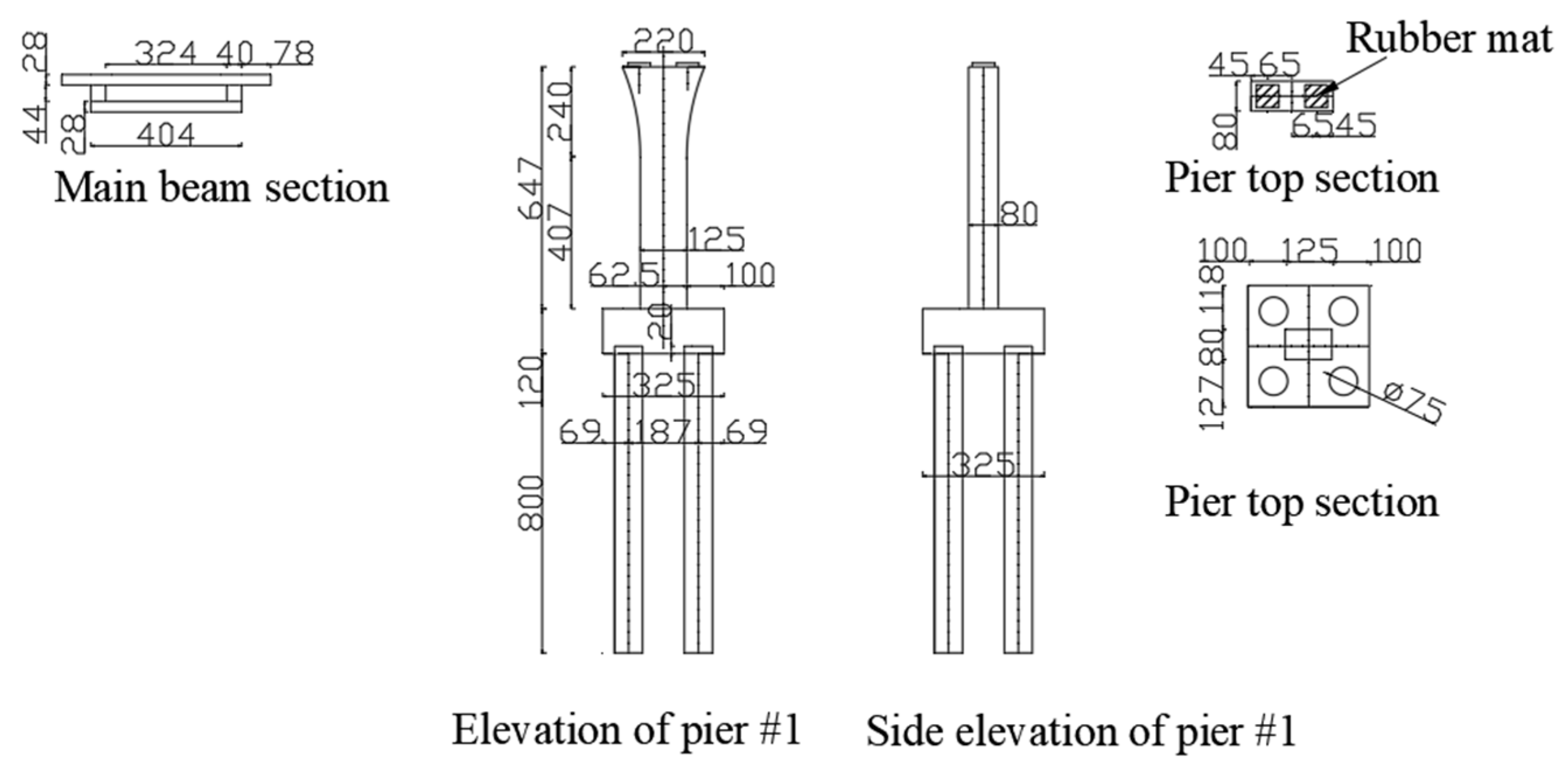
1.2. Prototype Bridge
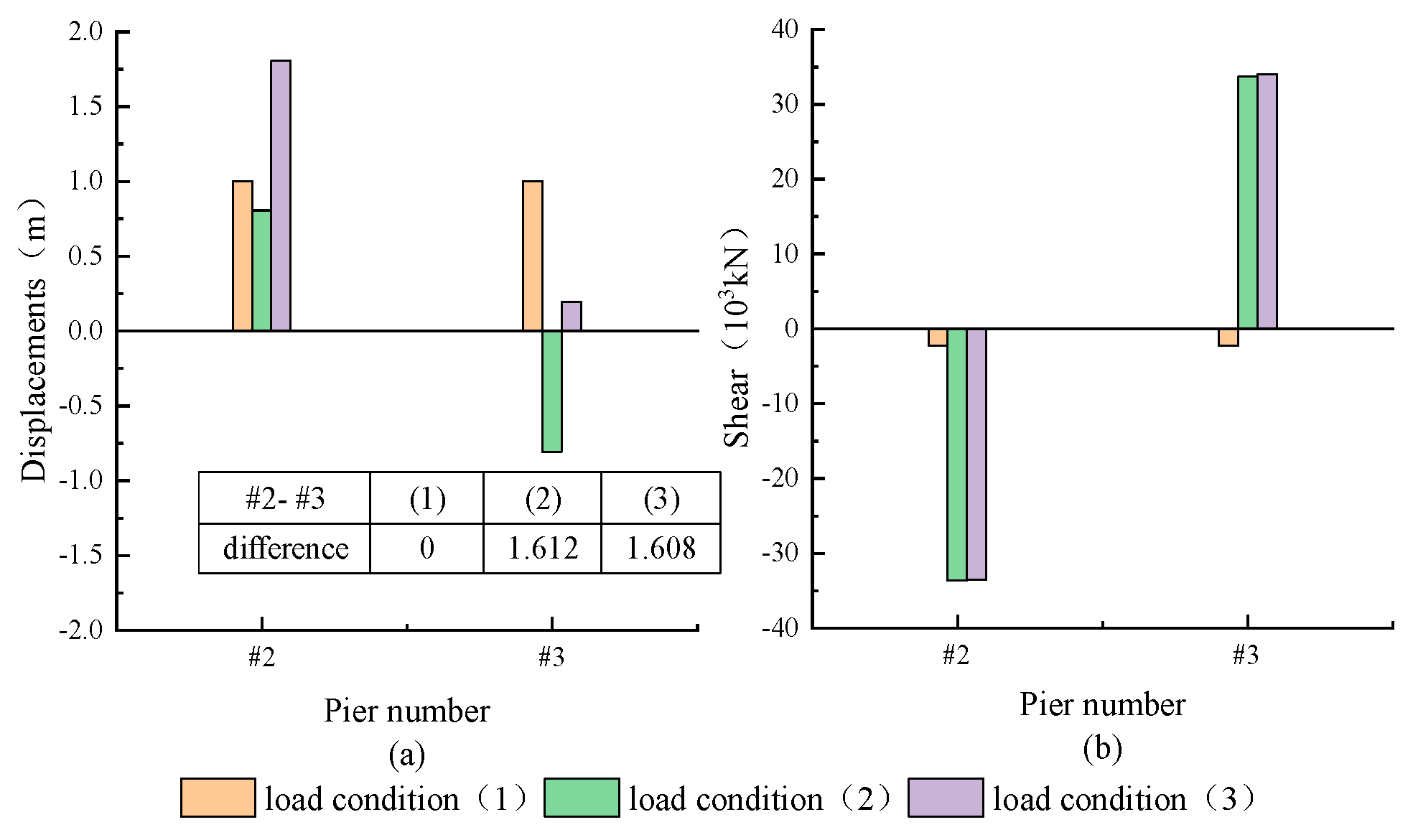
1.3. Numerical Confirmation of Single-Side Input Motion
1.4. Similarity Analysis
- (1)
- Bridge structural model similarity ratio design
- (2)
- Soil model similarity ratio design:
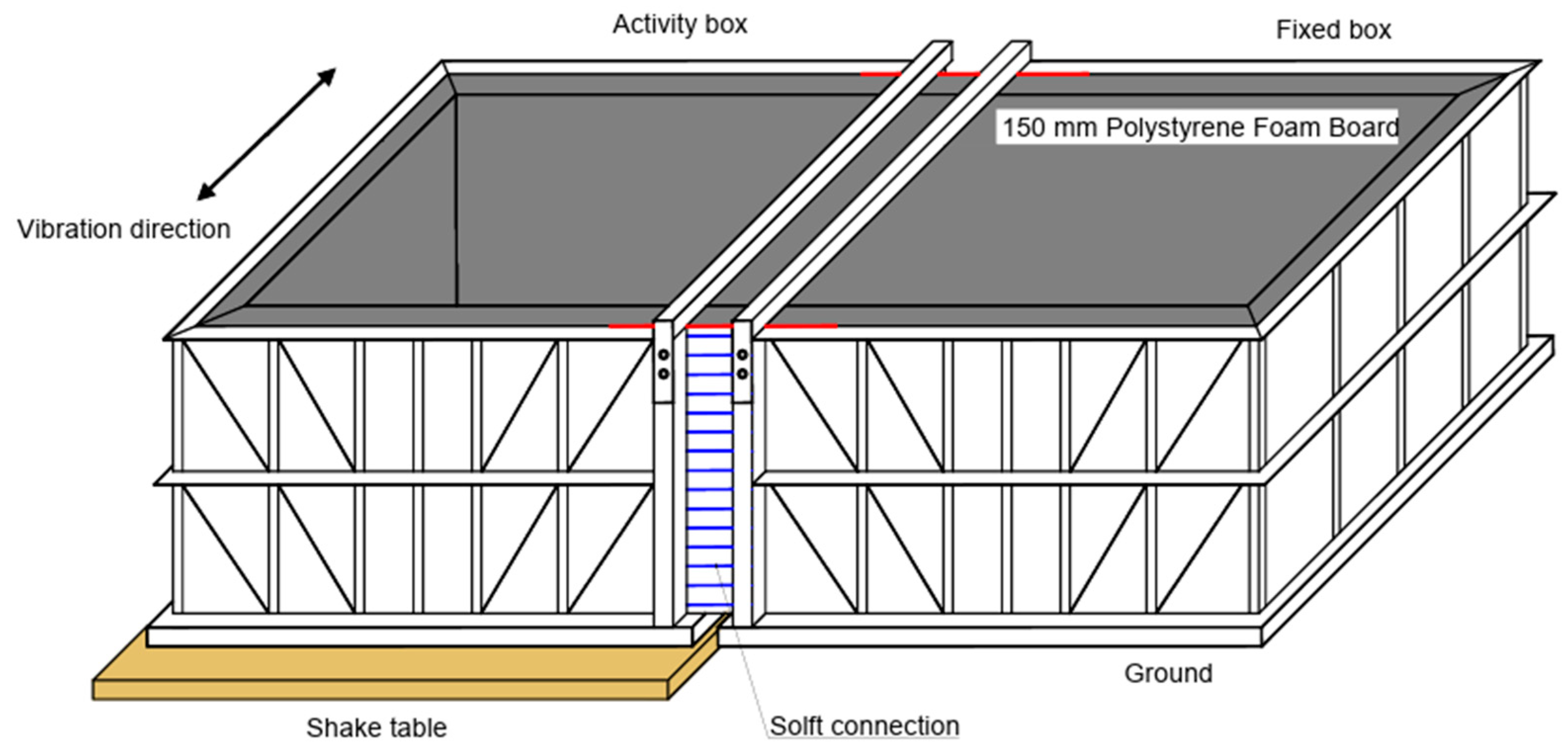
1.5. The Soil–Bridge Model
- (1)
- Soil boxes
- (2)
- The bridge model
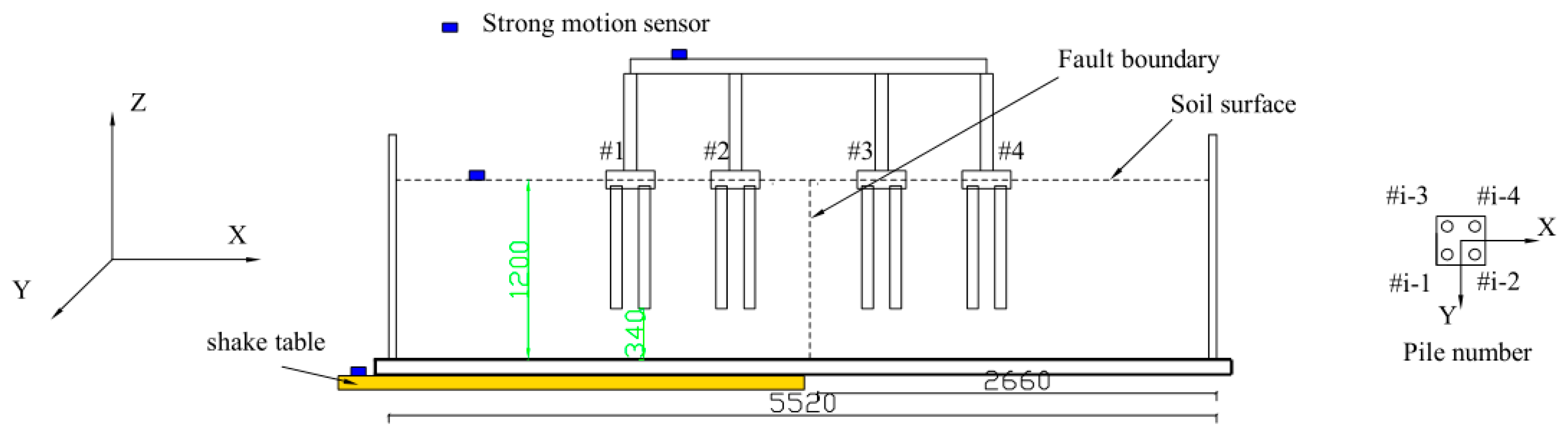
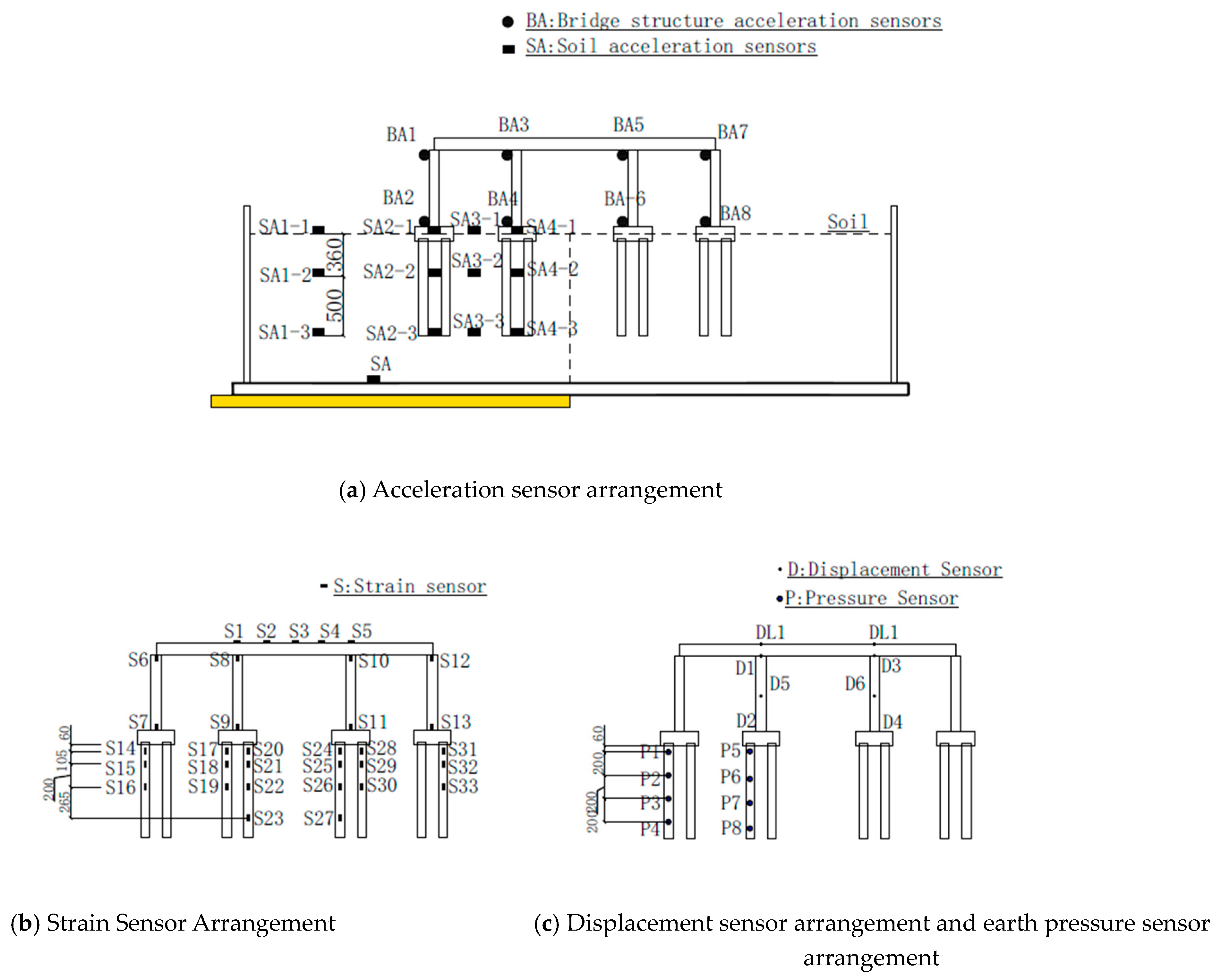
1.6. Instrument Deployments in the Test
1.7. Loading Scenarios for the Shaking Table Test
2. Test Results and Interpretation
2.1. Visual Observations
2.2. Soil–Bridge Response to White Noise
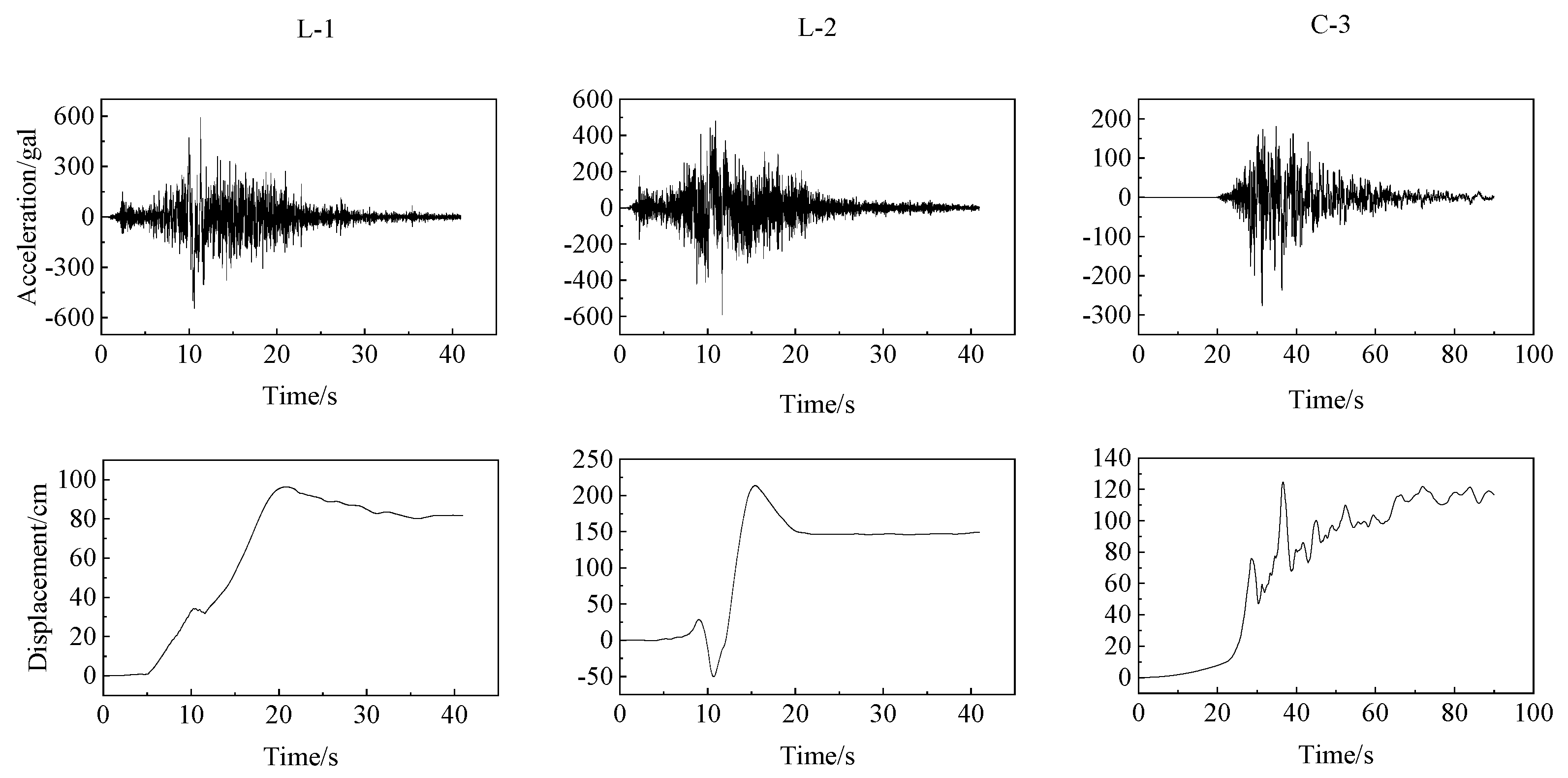
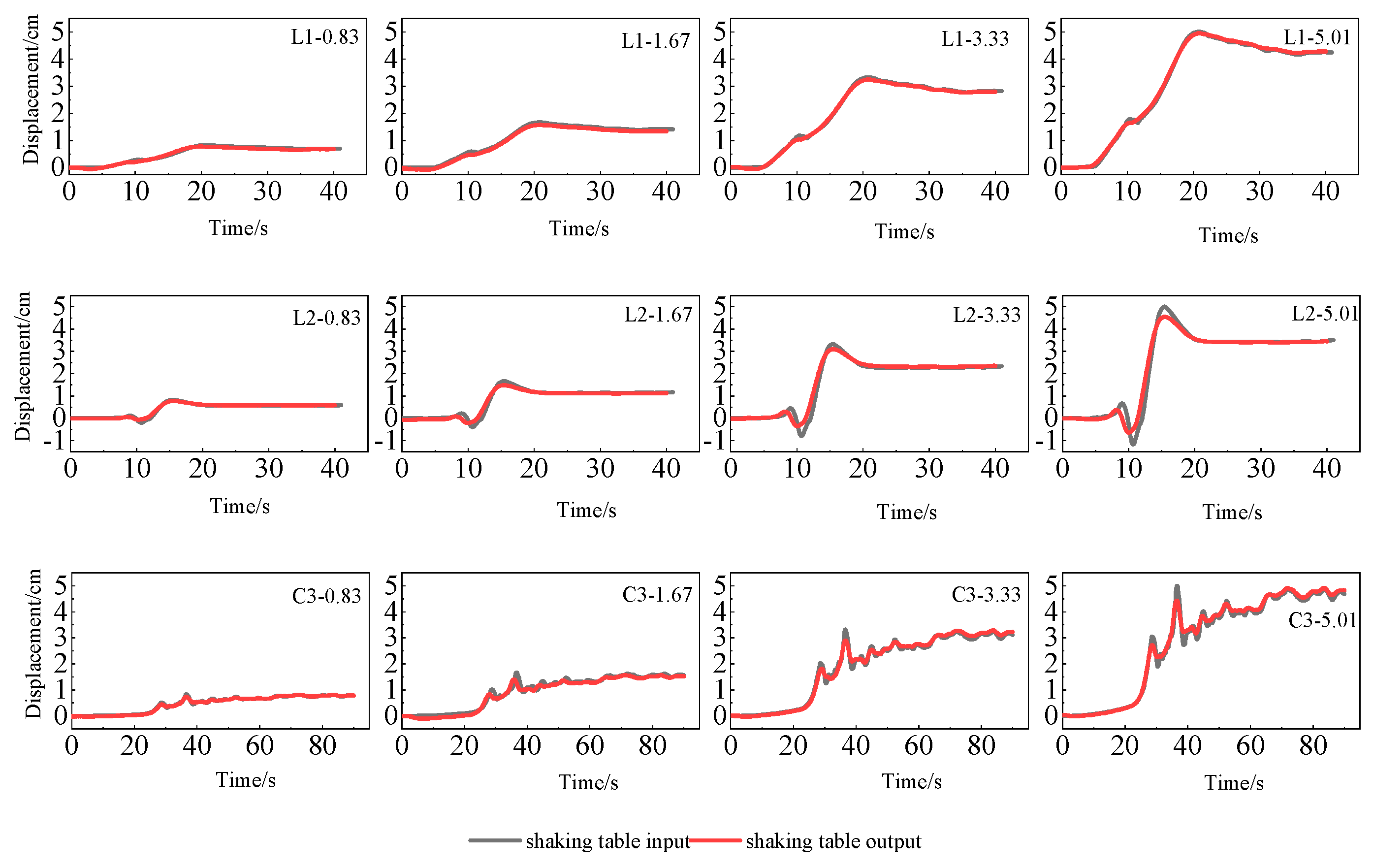
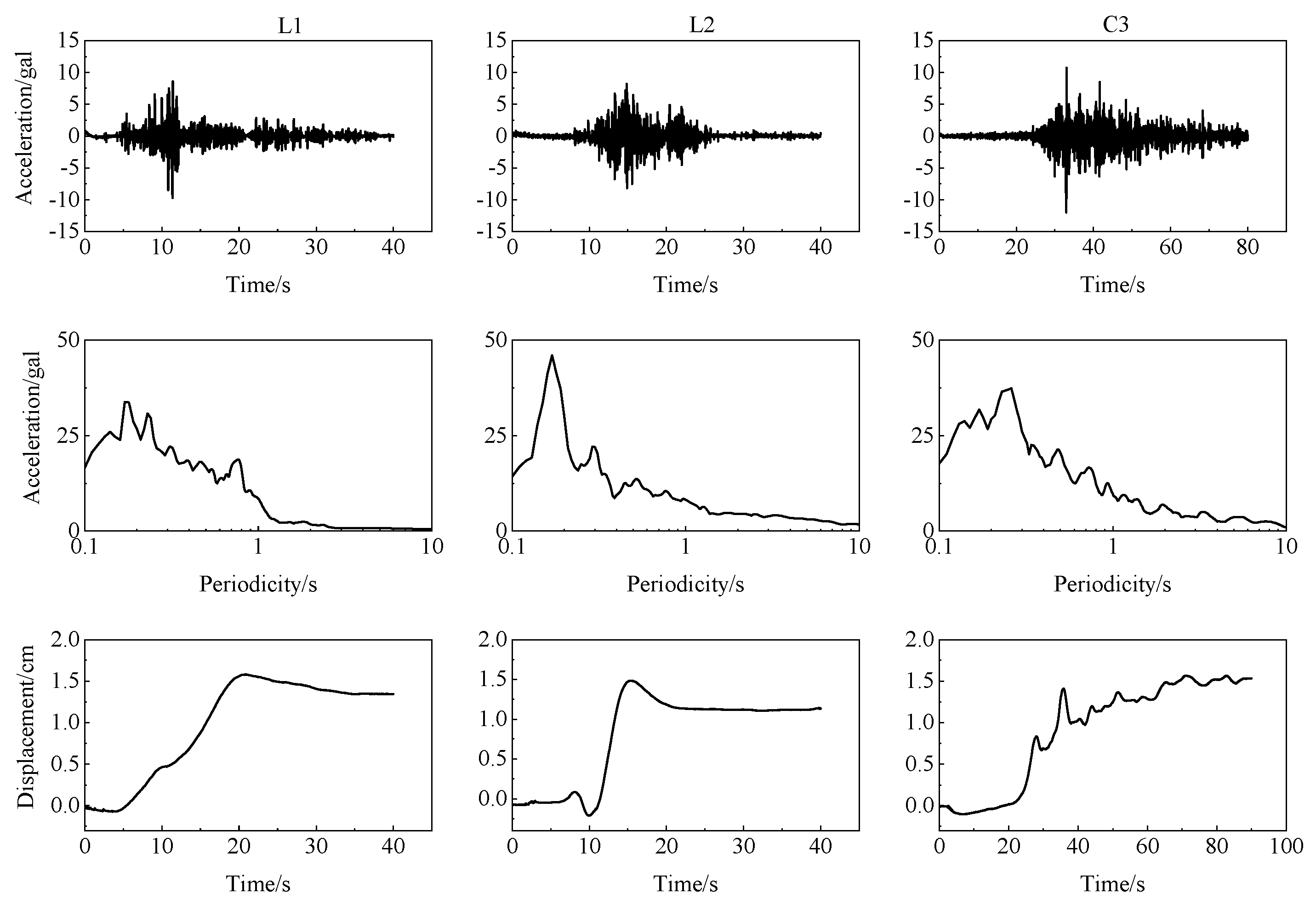
2.3. Inputs and Outputs of Shaking Table
2.3.1. Displacement Output of the Shaking Table
| Designed PGD (cm) | 0.83 | 1.67 | 3.33 | 5.01 | |
|---|---|---|---|---|---|
| Recorded PGD | L1 | 0.78 | 1.58 | 3.25 | 4.96 |
| L2 | 0.77 | 1.48 | 3.10 | 4.55 | |
| C3 | 0.81 | 1.57 | 3.29 | 4.92 | |
2.3.2. Seismic Response of Bridge Structures
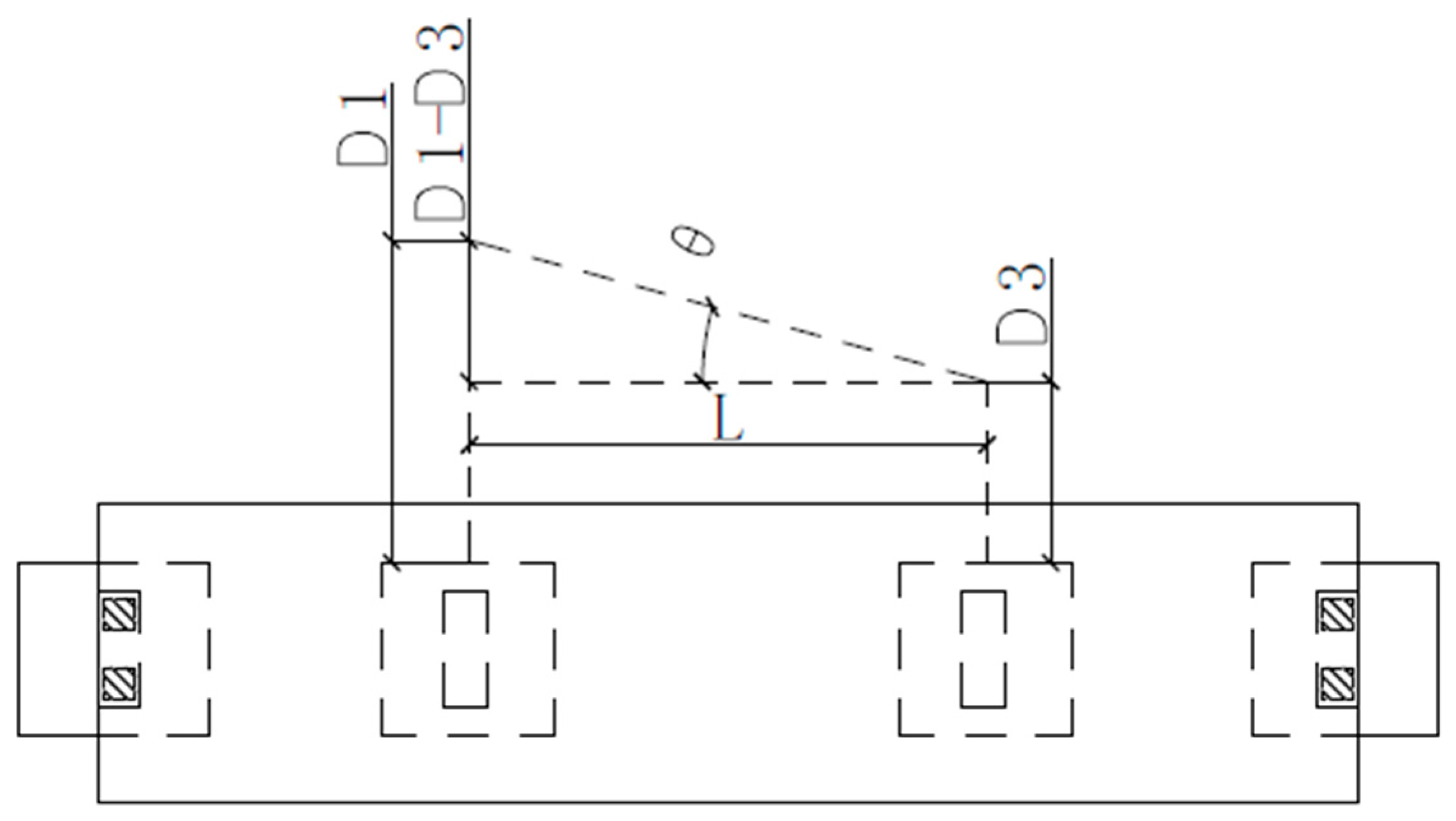
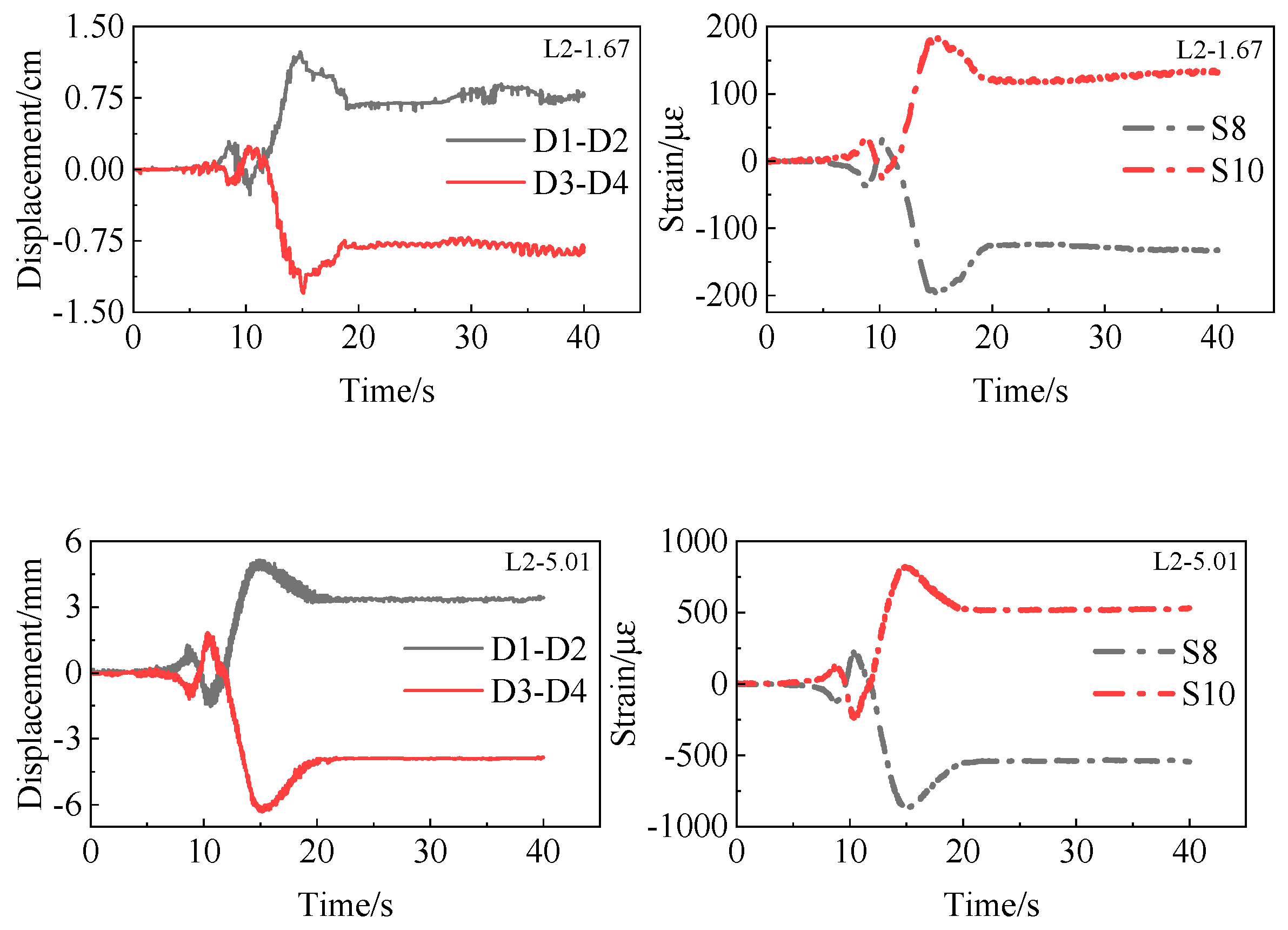
2.3.3. Lateral Displacement and Torsional Response of the Main Beam
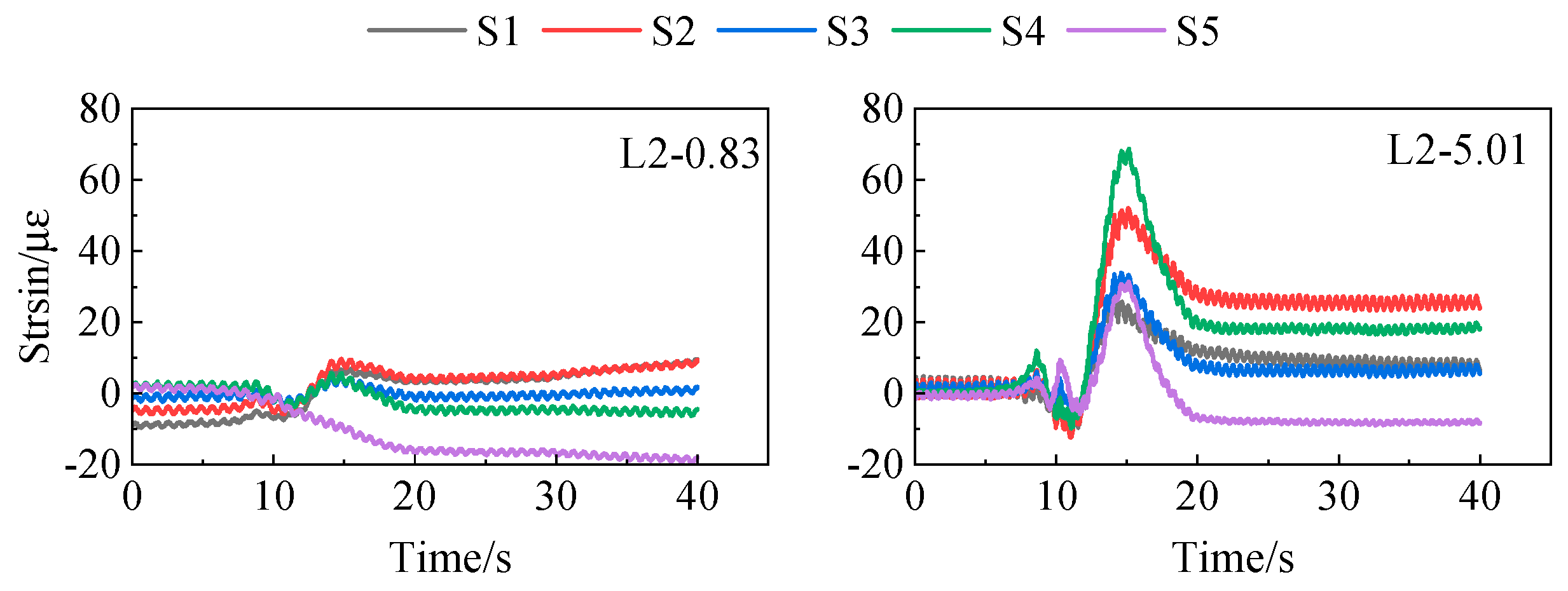
2.3.4. Displacement and Strain Response of the Main Beam on Both Sides of the Fault
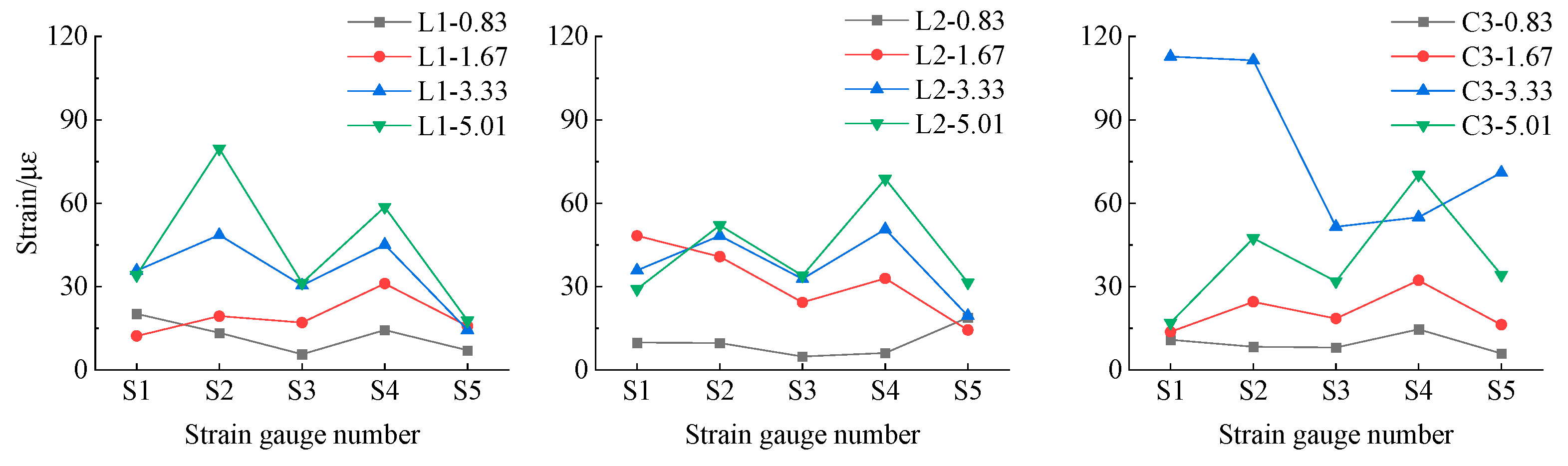
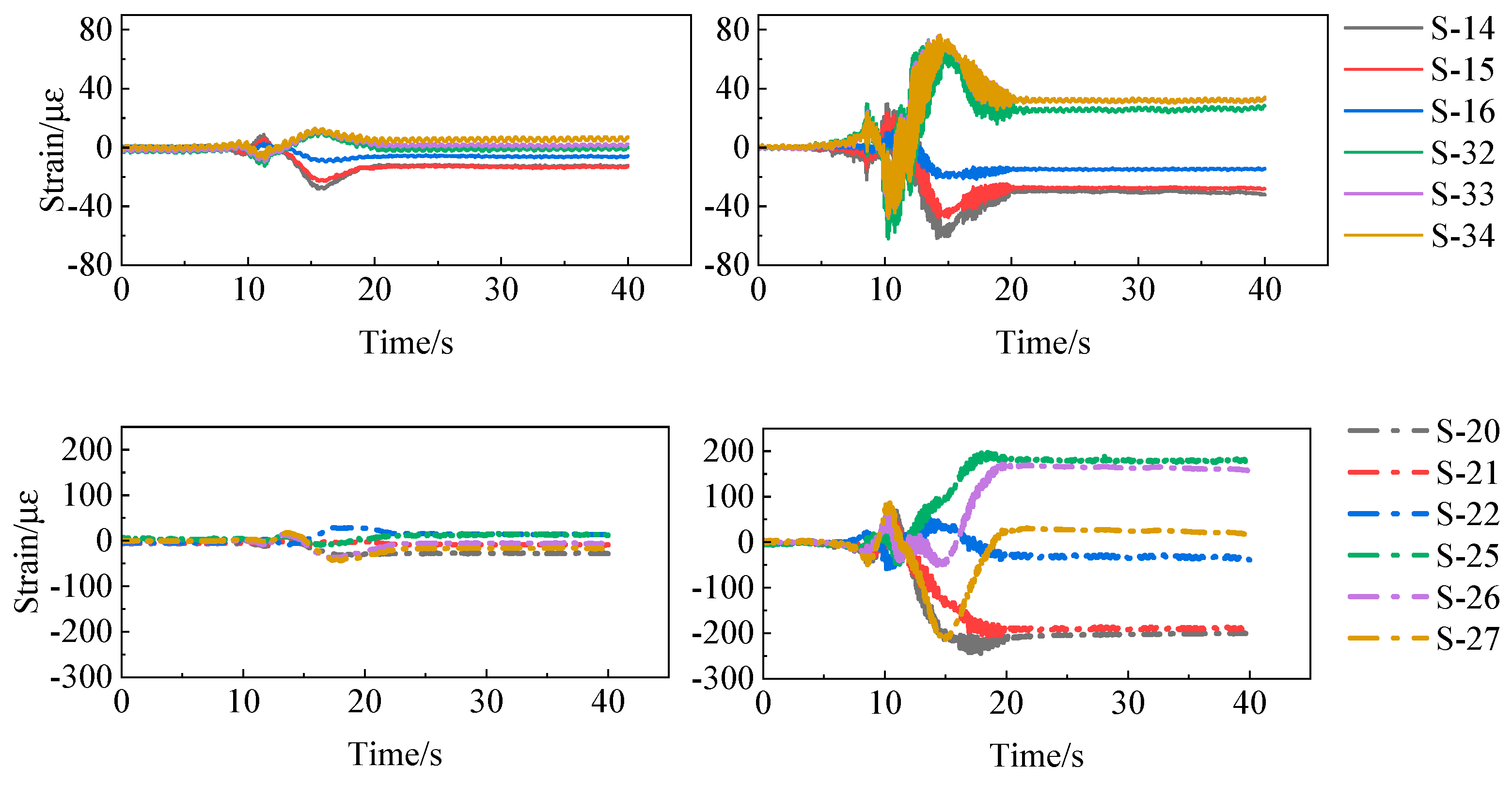
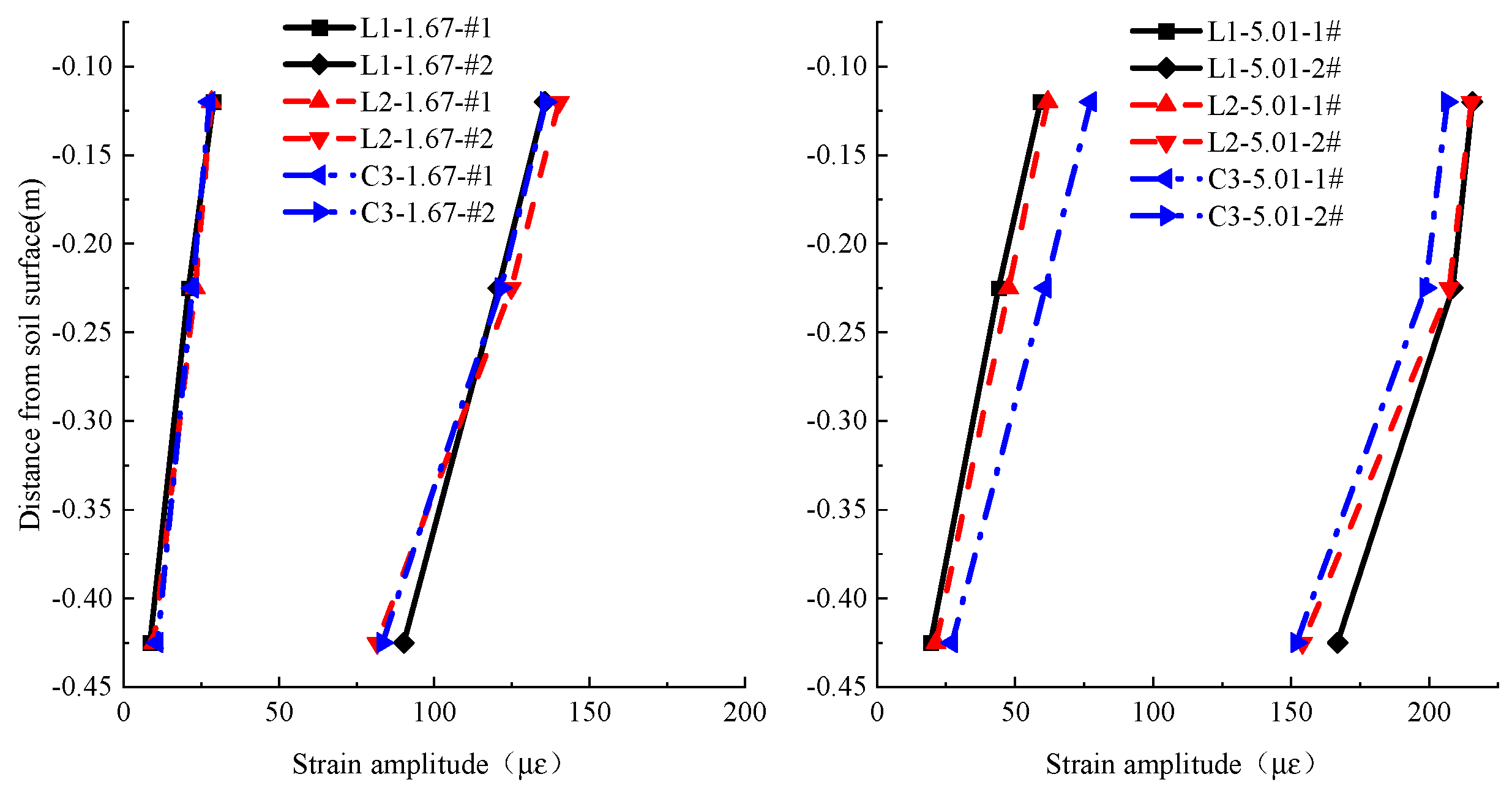
2.3.5. Comparison of Strain Response of Pile Body on Both Sides of the Fault
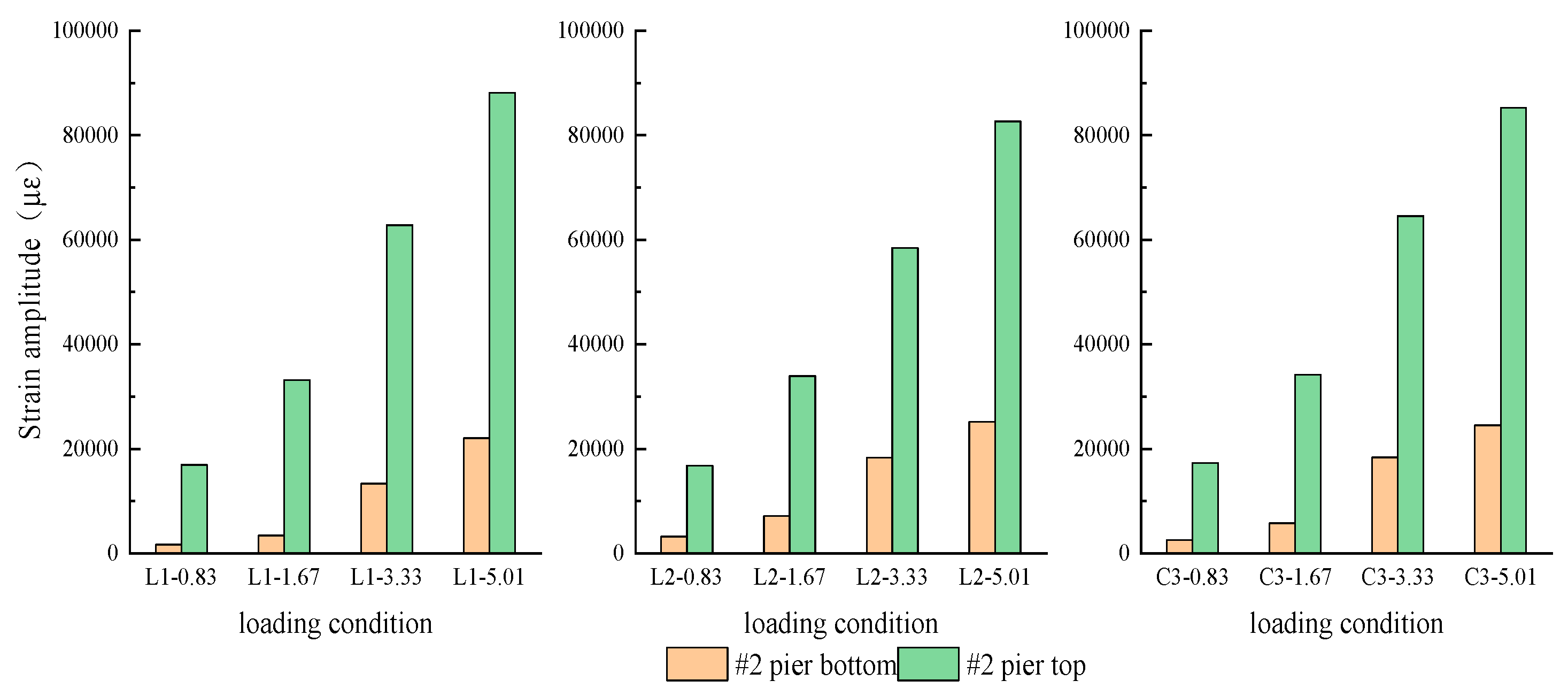
2.3.6. Pier Strain Variation

3. Effects of Soil–Structure Interaction on the Acceleration Response of Soils and Bridge Structures
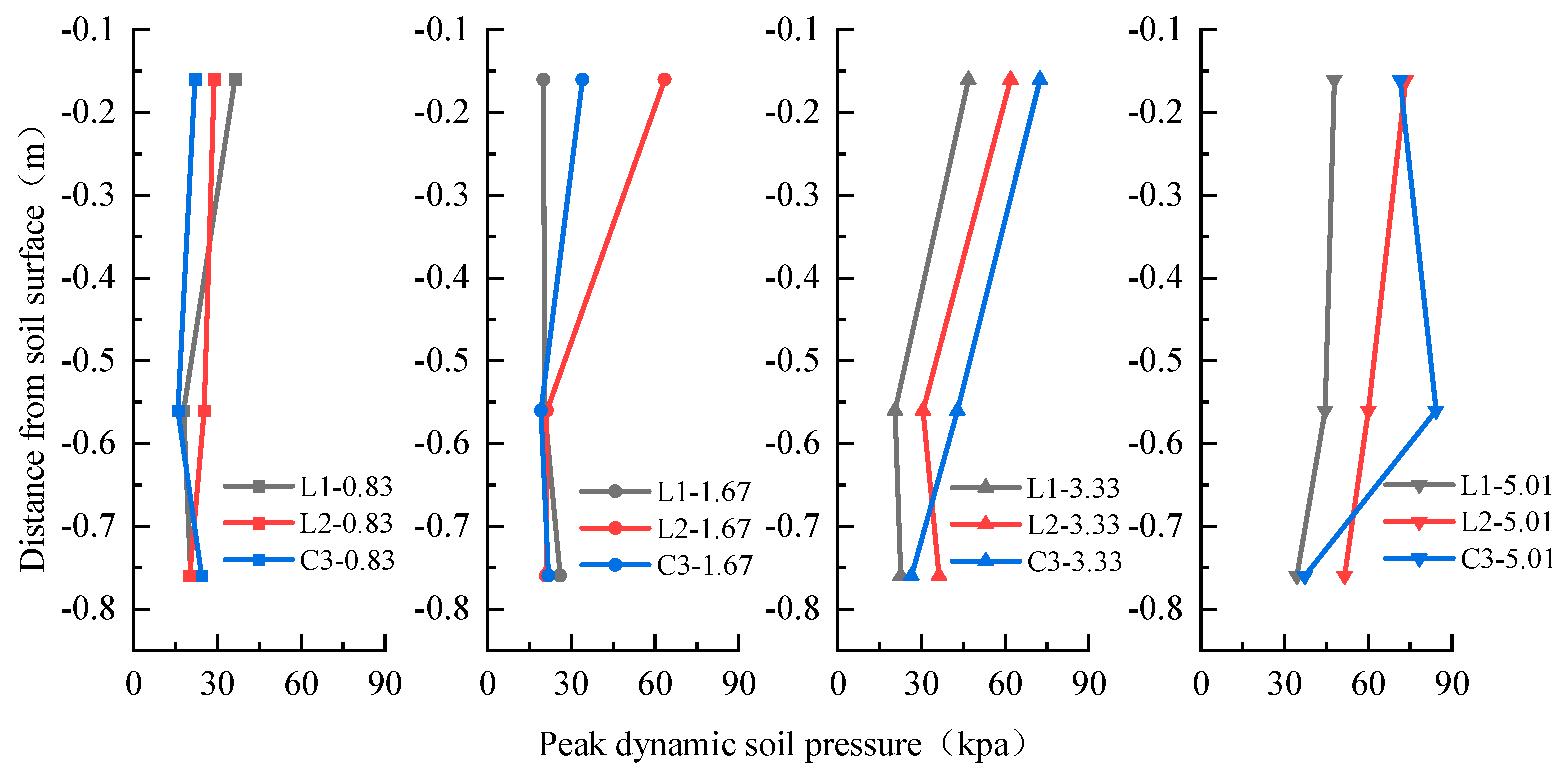
4. Variation in Dynamic Soil Pressure near the Pile
5. Conclusions
- The one-side input method proposed in this study can reproduce the different ground motions and permanent displacements on both sides of fault. This method can effectively simulate the ground motion on both sides of the fault. This provides a reference for conducting similar tests in the future.
- During the shaking table test, the actual shaking table motion is essentially the same as the input motion designed. But due to the limitations in the shaker’s own performance, it results in a missing structural dynamic response when using peak displacement as the input control. Since the seismic response of the bridge across the fault mainly comes from the proposed static component of ground shaking, the missing dynamic component has little effect on the test results. Additional calculations of the structural dynamic response of the bridge can be made subsequently via numerical simulation.
- The seismic behavior of a cross-fault bridge is markedly influenced by both quasi-static and dynamic effects. The quasi-static effect is the main factor that affects the acceleration amplification factor of the soil–structure system, the bridge’s displacement, torsion, and strain responses. Furthermore, the dynamic effect has a significant influence on the dynamic soil pressure.
- The highest strain is observed at the pile’s top, with the lowest at the bottom, indicating that strain decreases with depth from the top to the bottom of the pile. The peak displacement of the input seismic motion is the main factor that affects the strain response of the bridge structure. The strain response of the pile foundation close to the fault is considerably larger than that further away from the fault. For the seismic design of cross-fault bridges in practical engineering, it is recommended to focus on the seismic response of the pile foundation near the fault and to use seismic isolation bearings and other engineering techniques to increase the freedom of the pier and pile foundation and reduce their strain responses. The strain of the pier is generally greater than that of the pile foundation, indicating that the soil has an effect of resisting the motion of the pile foundation.
- The permanent displacement of ground motion has a greater impact on the torsional response of bridge structures compared to the PGD. Considering the special characteristics of the seismic response of cross-fault bridge structures, the maximum instantaneous inclination angle and the permanent inclination angle of the pier after the earthquake should be considered separately during the structural seismic design.
- The difference in seismic motions on both sides of the fault has a significant and complicated effect on the seismic response of the cross-fault bridge structure. The use of near-fault seismic motions with different characteristics may lead to significantly different seismic responses of the bridge structure. When analyzing the bridge structure that crosses active faults, the large deformation caused by fault slip and surface rupture should be fully considered to evaluate the seismic performance of the bridge.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hui, Y.X.; Tai, Y.J.; Wang, K.H.; Zhang, S. Discussion about Earthquake Resistance of the Bridges Crossing the Active Fault. China Earthq. Eng. J. 2017, 39, 870–875. [Google Scholar]
- European Committee for Standardization. Eurocode8: Design of Structures for Earthquake Resistance. Part 5: Foundation, Retaining Structures, and Geotechnical Aspects; EVN; European Committee for Standardization: Brussels, Belgium, 1998; pp. 14–20. [Google Scholar]
- Caltrans. Bridge Design Practice Manual; California Department of Transportation: Sacramento, CA, USA, 2012.
- Caltrans. Seismic Design Criteria: Version 1.9; California Department of Transportation: Sacramento, CA, USA, 2020.
- Yang, S.; Mavroeidis, G.P. Bridges crossing fault rupture zones: A review. Soil Dyn. Earthq. Eng. 2018, 113, 545–571. [Google Scholar] [CrossRef]
- Wang, N.; Elgamal, A.; Lu, J. Assessment of the Samoa Channel Bridge-foundation seismic response. Soil Dyn. Earthq. Eng. 2018, 108, 150–159. [Google Scholar] [CrossRef]
- Goel, R.K.; Chopra, A.K. Role of shear keys in seismic behavior of bridges crossing fault-rupture zones. Bridge Eng. 2008, 13, 398–408. [Google Scholar] [CrossRef]
- Deng, Q.D. Active Tectonics in China. Geol. Rev. 1996, 42, 295–299. [Google Scholar]
- Saiidi, M.S.; Vosooghi, A.; Choi, H.; Somerville, P. Shake Table Studies and Analysis of a Two-Span RC Bridge Model Subjected to a Fault Rupture. J. Bridg. Eng. 2014, 19, 1943–5592. [Google Scholar] [CrossRef]
- Tseng, W.S.; Penzien, J. Seismic analysis of long multiple-span highway bridges. Earthq. Eng. Struct. Dyn. 1975, 4, 1–24. [Google Scholar] [CrossRef]
- Murono, Y.; Miroku, A.; Konno, K. Experimental Study on Mechanism of Fault-Induced Damage of Bridges; Technical Report; Chuo Fukken Consultants: Osaka, Japan, 2005. [Google Scholar]
- Roussis, P.C.; Constantinou, M.C.; Erdik, M.; Durukal, E.; Dicleli, M. Assessment of Performance of Seismic Isolation System of Bolu Viaduct. J. Bridg. Eng. 2003, 8, 182–190. [Google Scholar] [CrossRef]
- Park, S.; Ghasemi, H.; Shen, J.; Somerville, P.; Yen, W.; Yashinsky, M. Simulation of the seismic performance of the Bolu Viaduct subjected to near fault ground motions. Earthq. Eng. Struct. Dyn. 2004, 33, 1249–1270. [Google Scholar] [CrossRef]
- Güney, D.; Acar, M.; Özlüdemir, M.; Çelik, R. Investigation of post-earthquake displacements in viaducts using Geodetic and Finite Element Methods. Nat. Hazards Earth Syst. Sci. 2010, 10, 2579–2587. [Google Scholar] [CrossRef]
- Hui, Y.X.; Wang, K.H. Study of Seismic Response Features of Bridge Crossing Faults. Bridge Constr. 2015, 45, 70–75. [Google Scholar]
- Hui, Y.X.; Wang, K.H. Earthquake motion input method for bridges crossing fault based on multi-support excitation displacement input model. J. Southeast Univ. 2015, 45, 557–562. [Google Scholar]
- Du, X.L.; Han, Q.; Li, X.Z.; Li, L.Y.; Chen, S.F.; Zhao, J.F. The Seismic Damage of Bridge in the 2008 Wenchuan Earthquake and Lessons from Its Damage. J. Beijing Univ. Technol. 2008, 34, 1270–1279. [Google Scholar]
- Zong, Z.H.; Lin, Y.Z.; Li, Y. Research Advances of across-fault Ground Motions and Their Effects on Bridge Structures. China J. Highw. Transp. 2023, 36, 80–96. [Google Scholar] [CrossRef]
- Lu, C.H.; Liu, K.Y.; Chang, K.C. Seismic performance of bridges with rubber bearings: Lessons learnt from the 1999 Chi-Chi Taiwan earthquake. J. Chin. Inst. Eng. 2011, 34, 889–904. [Google Scholar] [CrossRef]
- Goel, R.K.; Chopra, A.K. Nonlinear Analysis of Ordinary Bridges Crossing Fault-Rupture Zones. J. Bridg. Eng. 2009, 14, 216–224. [Google Scholar] [CrossRef]
- Goel, R.K.; Chopra, A.K. Linear Analysis of Ordinary Bridges Crossing Fault-Rupture Zones. J. Bridg. Eng. 2009, 14, 203–215. [Google Scholar] [CrossRef]
- Han, Q.; Du, X.; Liu, J.; Li, Z.; Li, L.; Zhao, J. Seismic damage of highway bridges during the 2008 Wenchuan earthquake. Earthq. Eng. Eng. Vib. 2009, 8, 263–273. [Google Scholar] [CrossRef]
- Lin, Y.; Zong, Z.; Bi, K.; Hao, H.; Lin, J.; Chen, Y. Experimental and numerical studies of the seismic behavior of a steel-concrete composite rigid-frame bridge subjected to the surface rupture at a thrust fault. Eng. Struct. 2019, 205, 110105. [Google Scholar] [CrossRef]
- Wang, Z.; Dueñas-Osorio, L.; Padgett, J.E. Influence of soil-structure interaction and liquefaction on the isolation efficiency of a typical multispan continuous steel girder bridge. J. Bridge Eng. 2014, 19, A4014001. [Google Scholar] [CrossRef]
- Zhang, Z.; Song, C.; Li, X.; Lan, R. Comparative study on the small radius curved bridge and simplified models by shaking table tests. J. Bridge Eng. 2021, 26, 04021039. [Google Scholar] [CrossRef]
- Xu, B.W. Shaking Table Test Studying Large-Scale Soil-Pile-Complex Structure Interaction; Tianjin University: Tianjin, China, 2009. [Google Scholar]
- Jiang, X.L.; Xu, B.W.; Jiao, Y. Analysis of shaking table test of large-scale soil-pile-complex structure interaction. China Civ. Eng. J. 2010, 43, 98–105. [Google Scholar] [CrossRef]
- Chen, G.; Chen, S.; Zuo, X.; Du, X.; QI, C.; Wang, Z. Shaking-table tests and numerical simulations on a subway structure in soft soil. Soil Dyn. Earthq. Eng. 2015, 76, 13–28. [Google Scholar] [CrossRef]
- LINSemih, E.; Murat, D. Effect of dynamic soil–bridge interaction modeling assumptions on the calculated seismic response of integral bridges. Soil Dyn. Earthq. Eng. 2014, 66, 42–55. [Google Scholar] [CrossRef]
- Zhang, F.; Li, S.; Wang, J.Q. Numerical analysis on seismic response of bridges crossing normal fault rupture zone. J. Build. Struct. 2022, 43, 205–216. [Google Scholar] [CrossRef]
- Guan, Z.G.; You, H.; Guo, H. Responses of Cable-Stayed Bridge Transversely Isolated with Elasto-Plastic Clabe Pairs and Fluid Viscous Damper Subjected to Near Fault Ground Motions. J. Tongji Univ. 2016, 44, 1653–1659. [Google Scholar]
- Li, X.J.; Sun, J.Y.; Wang, N.; Rong, M.S.; Dong, Q. Analysis of Seismic Response of Bridge across Earthquake Fault with Different Input Modes of Seismic Action. Technol. Earthq. Disaster Prev. 2023, 18, 203–214. [Google Scholar]
- Liu, G.; Li, H.N.; Lin, H. Comparison and evaluation of models for structural seismic responses analysis. Engineering Mechanics. 2009, 26, 10–15. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; Lu, M.; Wen, Z.; Luo, R. Characteristics of bridge damages in Wenchuan earthquake. J. Nanjing Univ. Technol. 2009, 31, 25–29. [Google Scholar]
- Li, J.Z.; Guan, Z.G. Performance-based seismic design for bridges. Eng. Mech. 2019, 28, 24–30. [Google Scholar]
- Mackie, K.R.; Lu, J.; Elgamal, A. Performance-based earthquake assessment of bridge systems including ground-foundation interaction. Soil Dyn. Earthq. Eng. 2012, 42, 184–196. [Google Scholar] [CrossRef]
- Sengupta, A.; Quadery, L.; Sarkar, S.; Roy, R. Influence of Bidirectional Near-Fault Excitations on RC Bridge Piers. J. Bridge Eng. 2016, 21, 04016034. [Google Scholar] [CrossRef]
- Lekidis, V.; Tsakiri, M.; Makra, K.; Karakostas, C.; Klimis, N.; Sous, I. Evaluation of dynamic response and local soil effects of the Evripos cable-stayed bridge using multi-sensor monitoring systems. Eng. Geol. 2005, 79, 43–59. [Google Scholar] [CrossRef]
- Wang, J.; Li, X.; Li, F.; Li, N. Analysis of the interaction effects between double shaking tables and test structure. J. Vib. Control. 2020, 27, 1407–1419. [Google Scholar] [CrossRef]
- Wu, J.; El Naggar, M.H.; Zhao, S.; Wen, M.; Wang, K. Beam–Unequal Length Piles—Soil Coupled Vibrating System Considering Pile–Soil–Pile Interaction. J. Bridg. Eng. 2021, 26, 04021086. [Google Scholar] [CrossRef]
- Zhou, G.L.; Bao, Y.X.; Li, X.J.; Peng, X.B. Review on dynamic analyses of structures under multi-support excitation. Word Earthq. Eng. 2009, 25, 25–32. [Google Scholar]
- Wang, N.; Elgamal, A.; Shantz, T. Recorded seismic response of the Samoa Channel Bridge-foundation system and adjacent downhole array. Soil Dyn. Earthq. Eng. 2017, 92, 358–376. [Google Scholar] [CrossRef]




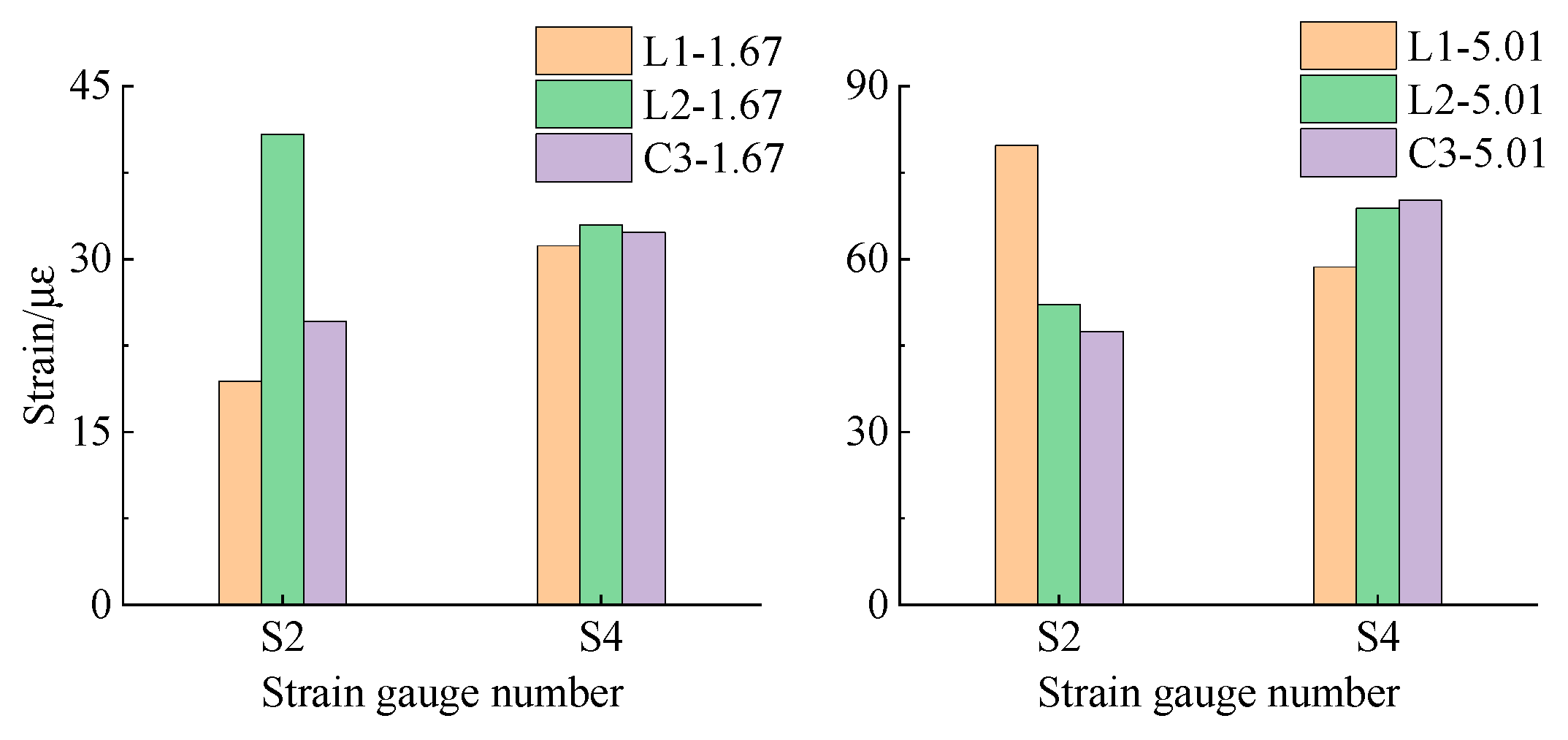


| Physical Quantities | Similarities | Bridge | Soil | Physical Quantities | Bridge | Structure | Soil |
|---|---|---|---|---|---|---|---|
| Young’s modulus similarity | 1/10 | 1/8 | Periodicity T | 0.053 | 0.047 | ||
| Equivalent density | 1 | 1 | Frequency f | 18.97 | 21.27 | ||
| Length | 1/60 | 1/60 | Acceleration a | 6 | 7.5 |
| Name | PGD (cm) | |||
|---|---|---|---|---|
| L1 | 0.83 | 1.67 | 3.33 | 5.01 |
| L2 | 0.83 | 1.67 | 3.33 | 5.01 |
| C3 | 0.83 | 1.67 | 3.33 | 5.01 |
| Loading Scenarios | PGD (cm) | L (cm) | Max D3 − D1 (cm) | (×10−3 rad) |
|---|---|---|---|---|
| L1 | 0.83 | 97.5 | 0.89 | 9.13 |
| 1.67 | 1.77 | 18.15 | ||
| 3.33 | 3.61 | 37.03 | ||
| 5.01 | 5.43 | 55.69 | ||
| L2 | 0.833 | 0.88 | 9.03 | |
| 1.67 | 1.68 | 17.23 | ||
| 3.33 | 3.44 | 35.28 | ||
| 5.01 | 4.84 | 49.64 | ||
| C3 | 0.833 | 0.81 | 8.31 | |
| 1.67 | 1.60 | 16.41 | ||
| 3.33 | 3.28 | 33.64 | ||
| 5.01 | 4.91 | 50.36 |
| Loading Scenarios | PGD (cm) | L (cm) | 2#Max D3 − D1 (cm) | (×10−3 rad) | 3#Max D3 − D1 (cm) | (×10−3 rad) |
|---|---|---|---|---|---|---|
| L1 | 0.83 | 64.7 | 0.12 | 1.8 | 0.12 | 1.8 |
| 1.67 | 0.21 | 3.2 | 0.2 | 3.1 | ||
| 3.33 | 0.36 | 5.6 | 0.41 | 6.3 | ||
| 5.01 | 0.49 | 7.6 | 0.64 | 9.8 | ||
| L2 | 0.833 | 0.13 | 2 | 0.14 | 2.1 | |
| 1.67 | 0.21 | 3.2 | 0.23 | 3.5 | ||
| 3.33 | 0.41 | 6.3 | 0.41 | 6.3 | ||
| 5.01 | 0.56 | 8.6 | 0.63 | 9.7 | ||
| C3 | 0.833 | 0.12 | 1.8 | 0.12 | 1.9 | |
| 1.67 | 0.22 | 3.4 | 0.22 | 3.4 | ||
| 3.33 | 0.39 | 6.0 | 0.41 | 6.3 | ||
| 5.01 | 0.51 | 7.8 | 0.63 | 9.7 |
| Loading Scenarios | PGD (cm) | L (cm) | 2#Max D3 − D1 (cm) | (×10−3 rad) | 3#Max D3 − D1 (cm) | (×10−3 rad) |
|---|---|---|---|---|---|---|
| L1 | 0.83 | 64.7 | 0.10 | 1.5 | 0.12 | 1.8 |
| 1.67 | 0.17 | 2.6 | 0.2 | 3.1 | ||
| 3.33 | 0.36 | 5.6 | 0.32 | 4.9 | ||
| 5.01 | 0.49 | 7.5 | 0.52 | 8.0 | ||
| L2 | 0.833 | 0.10 | 1.5 | 0.10 | 1.5 | |
| 1.67 | 0.15 | 2.3 | 0.18 | 2.8 | ||
| 3.33 | 0.25 | 3.9 | 0.24 | 3.7 | ||
| 5.01 | 0.56 | 8.7 | 0.48 | 7.4 | ||
| C3 | 0.833 | 0.11 | 1.7 | 0.11 | 1.7 | |
| 1.67 | 0.21 | 3.2 | 0.21 | 3.2 | ||
| 3.33 | 0.32 | 4.9 | 0.34 | 5.2 | ||
| 5.01 | 0.51 | 7.9 | 0.59 | 9.1 |
| Location | Name | ) | |||
|---|---|---|---|---|---|
| 0.83 cm | 1.67 cm | 3.33 cm | 5.01 cm | ||
| #1 pier bottom (SDX-5) | L1 | 1363 | 1407 | 1635 | 5409 |
| L2 | 1614 | 1562 | 2359 | 7691 | |
| C3 | 1478 | 1665 | 14,046 | 9996 | |
| #2 pier top (SDX-2) | L1 | 16,874 | 33,158 | 62,827 | 88,085 |
| L2 | 19,078 | 35,636 | 62,735 | 86,981 | |
| C3 | 17,282 | 34,192 | 64,535 | 85,272 | |
| #2 pier bottom (SDX-6) | L1 | 1623 | 3351 | 13,294 | 22,033 |
| L2 | 2187 | 4821 | 16,271 | 26,465 | |
| C3 | 2502 | 5751 | 18,362 | 24,473 | |
| #3 pier top (SDX-3) | L1 | 13,743 | 30,013 | 59,490 | 82,828 |
| L2 | 16,768 | 33,903 | 58,435 | 82,691 | |
| C3 | 14,875 | 31,690 | 76,204 | 79,618 | |
| #3 pier bottom (SDX-7) | L1 | 2621 | 4795 | 15,954 | 21,013 |
| L2 | 3163 | 7143 | 18,282 | 25,138 | |
| C3 | 3439 | 7244 | 16,401 | 23,822 | |
| #4 pier bottom (SDX-8) | L1 | 1646 | 2539 | 4828 | 8521 |
| L2 | 1938 | 2515 | 8674 | 14,724 | |
| C3 | 1684 | 2510 | 51,742 | 10,435 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, K.; Li, X.; Wang, N.; Wen, Z.; Wang, Y. Effect of Soil–Bridge Interactions on Seismic Response of a Cross-Fault Bridge: A Shaking Table Test Study. Buildings 2024, 14, 1874. https://doi.org/10.3390/buildings14061874
Guo K, Li X, Wang N, Wen Z, Wang Y. Effect of Soil–Bridge Interactions on Seismic Response of a Cross-Fault Bridge: A Shaking Table Test Study. Buildings. 2024; 14(6):1874. https://doi.org/10.3390/buildings14061874
Chicago/Turabian StyleGuo, Kunlin, Xiaojun Li, Ning Wang, Zengping Wen, and Yanbin Wang. 2024. "Effect of Soil–Bridge Interactions on Seismic Response of a Cross-Fault Bridge: A Shaking Table Test Study" Buildings 14, no. 6: 1874. https://doi.org/10.3390/buildings14061874






